Robust occurrence of ∆I = 2 bifurcation in scissors rotational bands

The geometric interpretation of scissors vibrational states was originally introduced through the two-rotor model [1], which describes the coupling between independent neutron and proton rotors mediated by a residual interaction. References [2−4] extended the framework of the original Projected Shell Model (PSM) [5, 6] to provide a microscopic description of the relative motion between the intrinsic states of neutrons and protons. Rather than employing a single BCS vacuum as the product state, angular-momentum projection was performed on separate neutron and proton BCS vacua. Although the use of two separately projected BCS vacua might appear to treat neutrons and protons as independent systems, the assumption of equal deformation in the deformed basis inherently reflects strong correlations between the two subsystems. To further account for neutron-proton interactions, the residual quadrupole-quadrupole interaction of the neutron-proton type is explicitly diagonalized within the basis constructed from the angular momentum-projected neutron and proton states (see discussions in Section II). This approach ensures a more comprehensive treatment of the collective dynamics and correlations between neutrons and protons. The calculations presented in Refs. [2, 3] successfully reproduce the conventional ground-state rotational band, which corresponds to the coherently coupled BCS condensate of neutrons and protons. Moreover, these calculations predict the emergence of novel states built upon a more intricate vacuum, incorporating fluctuations in the relative orientation of the neutron and proton intrinsic fields. This highlights the ability of the extended framework to capture richer collective dynamics beyond the traditional picture. In Ref. [4], we predicted that rotational bands based on nuclear scissors vibrations exhibit systematic splitting between neighboring spin states ($ \Delta I = 2 $ bifurcation) in which the energy levels of the scissors band in $ ^{156} {\rm{Gd}}$ oscillate between states with even and odd spins.

The present study systematically varies the deformation parameters and monopole-pairing force parameters in the theoretical model to perform an in-depth investigation of the influence of these critical parameters on the bifurcation behavior of the scissors rotational band. The results demonstrate that the occurrence of the $ \Delta I = 2 $ bifurcation phenomenon in the scissors rotational band is not restricted to certain nuclei but is a phenomenon that exists widely, insensitive to parameter changes. This work provides additional theoretical support for understanding the intrinsic physical mechanisms underlying the scissors mode.

The original PSM [5] calculation begins with the deformed Nilsson single-particle basis, with pairing correlations incorporated into the basis by a BCS calculation for the Nilsson states. To create deformed Nilsson single-particle states, the standard Nilsson model [7] is adopted with both the spin-orbit $ {\bf{l}}\cdot {\bf{s}} $ term and $ {\bf{l}}^{2} $ term in the potential. The quasiparticle (qp) vacuum state $ \left|0\right> $ of an axially deformed nucleus is taken to be a product of the Nilsson-BCS qp vacua $ \left|0_\nu\right> $ and $ \left|0_\pi\right> $, namely

The ground-state rotational band with angular momentum I is obtained by angular momentum projection onto $ \left|0\right> $:

where $ {\cal{N}}^I $ is the normalization and $ \hat P^I $ is the (one-dimensional) angular momentum projection operator [8].

The Hamiltonian employed in the PSM consists of the usual separable forces

where $ \hat H^0 $ is the spherical one-body term including the spin-orbit force, and the remainder is the two-body quadrupole+pairing interaction, which contains three parts: the quadrupole-quadrupole ($ QQ $) force and monopole and quadrupole pairing forces. The strength of the $ QQ $ force χ is determined in a self-consistent manner such that it is related to the deformation of the basis [5]. The monopole-pairing strength is taken to be $ G_M = [20.12 \mp 13.13(N-Z)/ A] /A $, with ''−'' for neutrons and ''+" for protons, which is determined such that it reproduces the known odd-even effect. Finally, it is assumed that the strength of the quadrupole pairing $ G_Q $ is proportional to $ G_M $, with the proportionality constant being fixed as $ 0.20 $ in this paper. The calculation is conducted in a model space that contains single-particle states from three major harmonic-oscillation shells ($ N = 4, 5 $ and 6 for neutrons and $ N = 3, 4 $ and 5 for protons).

In the second term of the Hamiltonian (1), the sum for the $ QQ $ interaction includes three parts: $ \hat Q^{\dagger}_\nu \hat Q_\nu $, $ \hat Q^{\dagger}_\pi \hat Q_\pi $, and $ \hat Q^{\dagger}_\nu \hat Q_\pi $. Equation (1) can be rewritten in the isospin formalism as $ \hat H = \hat H_\nu + \hat H_\pi + \hat H_{\nu\pi} $, where $ \hat H_\tau $ ($ \tau = \nu, \pi $) is the like-particle quadrupole+pairing Hamiltonian with inclusion of the quadrupole pairing:

and $ \hat H_{\nu\pi} $ is the n-p $ QQ $ residual interaction

Note that Eqs. (2) and (3) are rewritten based on Eq. (1) with no extra terms or new parameters introduced. The interaction strengths $ \chi_{\tau \tau} $ ($ \tau = \nu $ or π) are related self-consistently to the quadrupole deformation $ \varepsilon_2 $ by [5]

Following Ref. [5], the strength $ \chi_{\nu\pi} $ of the neutron-proton quadrupole–quadrupole residual interaction is calculated to be $ \chi_{\nu\pi} = (\chi_{\nu\nu} \chi_{\pi\pi})^{1/2} $, which determines the excitation energy of the $ 1^+ $ scissors state. Similar parameterizations were used in earlier works [9, 10].

To describe the microscopic neutron (proton) rotor, we first project out the neutron (proton) states $ \left|I_\nu\right> $ ($ \left|I_\pi\right> $) with angular momentum $ I_\nu $ ($ I_\pi $) from the vacuum-state $ \left|0_\nu\right> $ ($ \left|0_\pi\right> $). The projected states $ \left|I_\nu\right> $ and $ \left|I_\pi\right> $ are then coupled to form the basis states $ \left|(I_\nu \otimes I_\pi)I\right> $ for total angular momentum I. These basis states are used to construct the matrix of the total Hamiltonian of Eqs. (2) and (3)

The term $ \langle I_\nu | \hat H_\nu | I_\nu \rangle $ ($ \langle I_\pi | \hat H_\pi | I_\pi \rangle $) is the energy of the state $ | I_\nu \rangle $ ($ | I_\pi \rangle $) projected from the intrinsic state $ | 0_\nu \rangle $ ($ | 0_\pi \rangle $), with the neutron (proton) part of Hamiltonian $ \hat H_\nu $ ($ \hat H_\pi $) given by Eq. (5). The last term in Eq. (5) can be written explicitly as [11]

where $ {\cal{W}} $ is the re-coupling coefficient.

The Hamiltonian matrix of Eq. (5) is diagonalized and the resulting PSM eigenstates $ |\alpha, I \rangle $ are expressed as a linear combination of the basis states $ | ( I_\nu \otimes I_\pi) I \rangle $:

where α labels different eigenstates with the same angular momentum.

In the present work, we study the dependence of the scissors vibration band and its $ \Delta I = 2 $ oscillation characteristics by varying the model parameters, namely, the quadrupole deformation $ \varepsilon_2 $ and monopole-pairing interaction strength G (namely, $ G_M^\tau $ in Eq. (2)). We would like to confirm whether the results in Ref. [4] depend on a specific choice of model parameters or the predicted bifurcation behavior of the scissors rotational bands is truly an emergent phenomenon of a quantum many-body system, independently of model parameters.

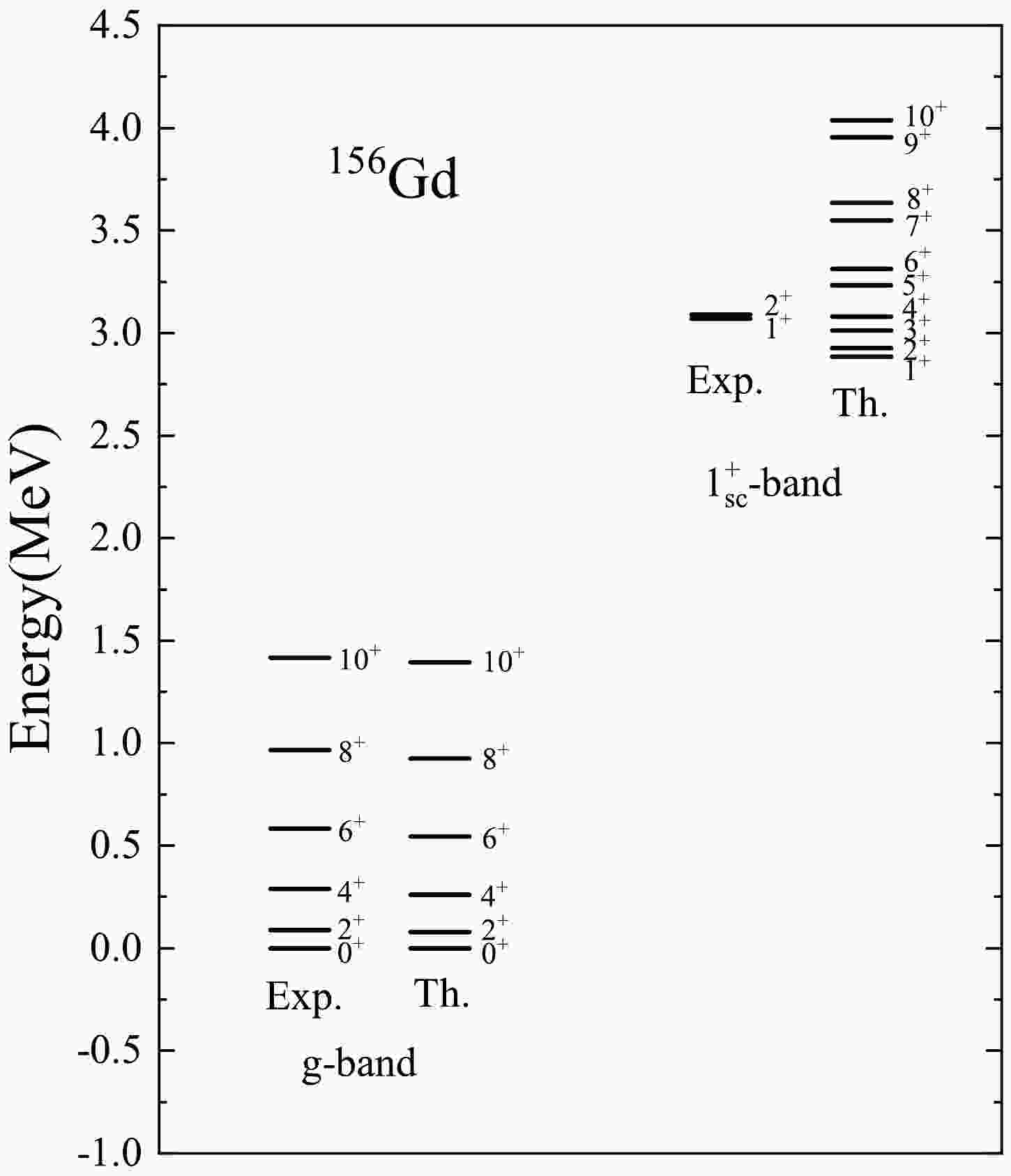
Figure 1 shows a comparison between the calculated and experimental energy spectra of the ground-state band and the $ 1^{+}_{\rm sc} $ scissors band in $ ^{156} {\rm{Gd}}$. In this calculation, quadrupole deformation is set to $ \varepsilon_2 = 0.275 $, and the strength of monopole-pairing is $ G_M^\nu = 0.1139 $ and $ G_M^\pi = 0.1441 $ MeV for neutrons and protons, respectively. From Fig. 1, it can be observed that, overall, the calculated results show excellent agreement with the experimental data. The theoretical values for the scissors band are slightly lower in energy than the experimental data. However, the important feature, that the $ 1^+ $ and $ 2^+ $ of the scissors rotational band are nearly degenerate [12], is reproduced correctly.

Figure 1.  Comparison of the calculated spectrum of the ground band and $ 1^{+}_{\rm sc} $-band in $ ^{156} {\rm{Gd}}$ with available experimental data. Data are taken from Refs. [12, 13].

Figure 2 shows the variations of the scissors band-head energy calculated with changing parameters. Panel (a) presents the evolution of the scissors band-head energy with the quadrupole deformation $ \varepsilon_2 $. It can be seen that within the range of $ \varepsilon_2 = 0.14 - 0.32 $, the calculated band-head energies change slowly, maintaining values close to 3 MeV, indicating that deformation variation in this range has a minimal impact on the band-head energy. However, when $ \varepsilon_2 $ falls below 0.14, the band-head energy shows a more rapid increase as the deformation decreases. Meanwhile, when $ \varepsilon_2 $ exceeds 0.32, the band-head energy shows a gradual upward trend with increasing deformation. These results suggest that in the large range of $ \varepsilon_2 = 0.14 - 0.32 $, the scissors mode band-head energy, $ 1^+_{\rm sc} $, remains stable around 3 MeV for this rare-earth nucleus. This is consistent with the conclusion from the systematic experimental observations [14]. Significant deviations from 3 MeV occur only when the deformation parameter is set unrealistically to be very small.

Figure 2.  Band-head energies of the scissors band, calculated with variation in input deformation parameter $ \varepsilon_2 $ (a) and monopole-pairing strength G (b). The horizontal line refers to the experimental value of the $ 1_{\rm sc}^+ $ energy [13].

In contrast, the monopole-pairing force has a relatively small effect on the scissors mode band-head energy, as demonstrated in Fig. 2(b). Calculations with different monopole-pairing strength G by applying a scaling factor, ranging from 0.9 to 1.1, to the strengths used in the results in Fig. 1 reveal a linear correlation between the scissors band-head energy and monopole-pairing strength: as G increases, the calculated $ 1^+_{\rm sc} $ energy increases gradually. The change is only moderate, with band-head energy variations ranging from 2.56 to 3.28 MeV, again around 3 MeV.

Figure 3 illustrates the $ \Delta I = 2 $ bifurcation behavior of the scissors rotational band based on the $ ^{156} {\rm{Gd}}$ example, represented by$ E(I)-E(I-1) $ plots as functions of (a) quadrupole deformation $ \varepsilon_2 $ and (b) monopole-pairing strength G. From Fig. 3, it can be observed that the oscillation characteristics exhibit the following pattern: As $ \varepsilon_2 $ decreases, the oscillation amplitude gradually increases, and the change is more pronounced in the small deformation region. When $ \varepsilon_2 $ exceeds 0.24, the oscillation amplitude changes less significantly and remains relatively stable. Notably, the oscillation amplitude of the odd-spin state consistently changes more than that of the even-spin state. In comparison, the effect of the pairing force on the oscillation (Panel (b)) is smaller.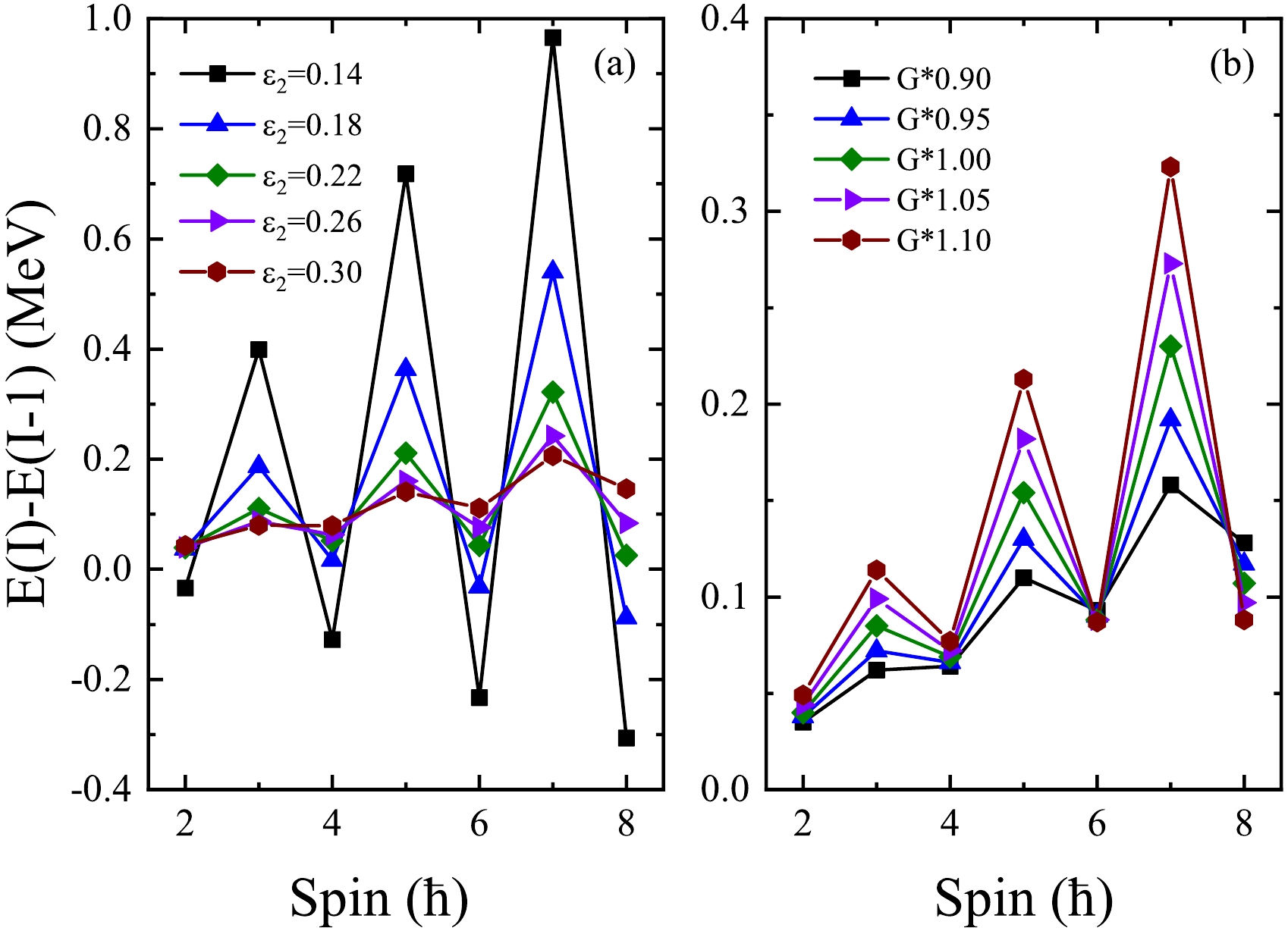

Figure 3.  (color online) Staggering behavior of the scissors rotational band shown by $ E(I)-E(I-1) $ as a function of spin I, calculated with changing parameters in the $ ^{156} {\rm{Gd}}$ calculation. (a) Change in deformation parameters $ \varepsilon_2 $. (b) Change with scaled monopole-pairing strengths G.

Because electromagnetic transitions play a significant role in understanding the scissors mode, we further investigate the influence of the deformation parameters and monopole-pairing force parameters on the electromagnetic transition values. Figure 4 illustrates the $ B(M1,1_{\mathrm{sc}}^+\rightarrow0_{\mathrm{gs}}^+) $ values calculated with variation in input deformation parameter $ \varepsilon_2 $ and monopole-pairing strength G. As the deformation parameter increases, the $ B(M1) $ values show a significant upward trend; meanwhile, with increasing strength of the monopole-pairing force, the $ B(M1) $ values exhibit a slight downward trend. It is clear that between these two factors, the influence of the deformation parameter on $ B(M1) $ values is substantially greater than that of the monopole-pairing force. The result that the $ B(M1,1_{\mathrm{sc}}^+\rightarrow0_{\mathrm{gs}}^+) $ values due to scissors vibration decrease quickly with decreasing deformation, while all other calculation conditions remain equal, is consistent with the recent conclusion of Chen et al. [15].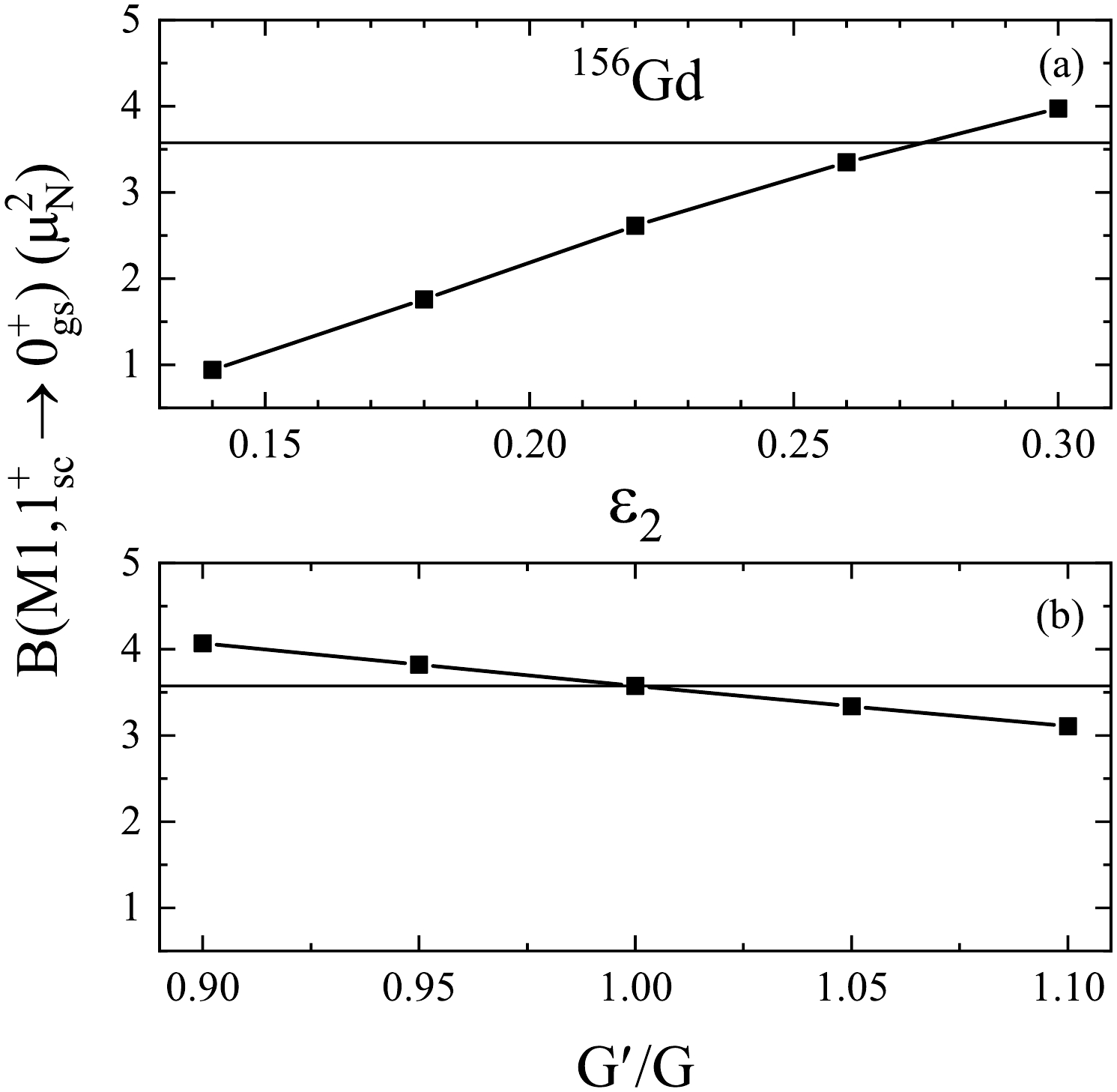

Figure 4.  $ B(M1,1_{\mathrm{sc}}^+\rightarrow0_{\mathrm{gs}}^+) $ values calculated with variation in input deformation parameter $\varepsilon_2$ (a) and monopole-pairing strength G (b). The horizontal line refers to the calculated value of $^{156}{\rm{Gd}}$[4].

Based on the current calculation, we conclude that deformation has a large impact on the band-head energy, oscillatory characteristics of the scissors rotational band, and $ B(M1,1_{\mathrm{sc}}^+\rightarrow0_{\mathrm{gs}}^+) $ values, while the effect from the pairing force is smaller. In particular, when the deformation is small, both the band-head energy and oscillatory characteristics of the scissors mode exhibit substantial changes. This indicates that deformation is the primary factor that influences the behavior of the scissors mode, whereas the influence of pairing is comparatively secondary.

It is important to note that regardless of how the deformation and pairing vary, the oscillatory characteristics exhibited by the rotational band of the scissors mode persist. Notably, although the parameters have large variations from the original ones (e.g., the G parameter reduces by a factor of 0.95 or smaller, or $ \varepsilon_2 $ reaches a higher value of 0.3), the energy oscillation effect, although with reduced amplitude, the basic characteristics remain preserved. This indicates a true physical effect, rather than a coincidence in the parameterization. As long as there is an appropriate restoring force between the two blades of the scissors (i.e., neutron and proton rotors), bifurcation phenomena will naturally occur. This further supports the hypothesis that this novel mode of collective nuclear motion may originate from some geometric effect, a direction that warrants further investigation. The main purpose of the present work is to show the robust existence of the scissors band oscillations against model parameter changes. In-depth theoretical research is still required and is of great importance for a comprehensive understanding of the quantum dynamical behavior of the scissors mode.

Of course, energy oscillation can also be seen in normal rotational bands. However, the scissors motion shows a completely different picture and therefore a different physical emphasis as the motion of normal rotational bands. The scissors motion emphasizes a relative motion between neutrons and protons in the rotating frame, whereas in normal rotation, neutrons and protons are stuck together as a unity. The important observation effect to distinguish the odd-even staggering in the scissors motion versus the normal rotation is that for usual odd-even energy staggerings of normal rotational bands, the staggering phase varies with orbits that the valence particles occupy. In contrast, the staggering phase of the scissors rotational bands is universally fixed (with even spins always favored), as shown in the present article.

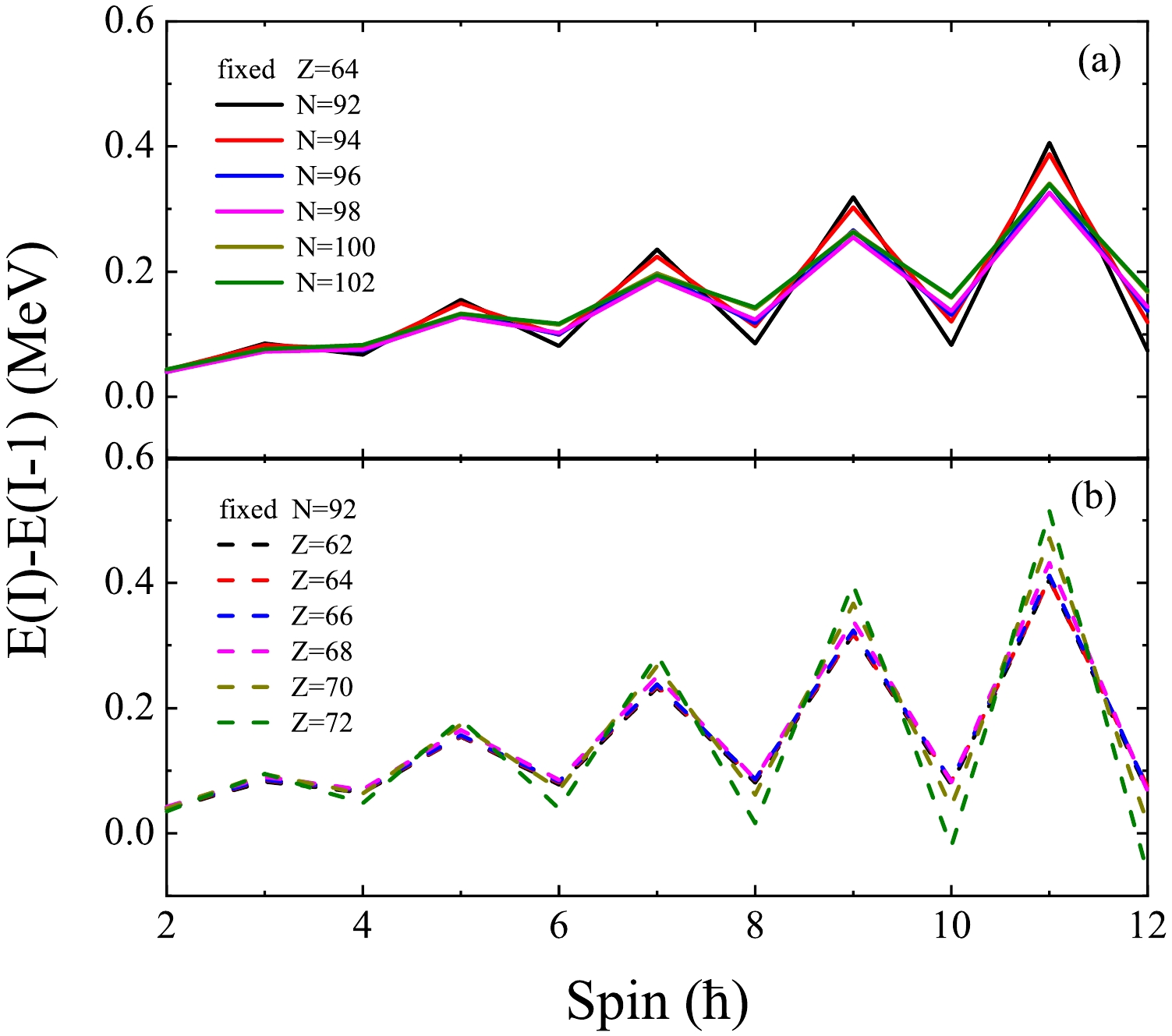
Figure 5 further illustrates the effect for systems with different neutron and proton numbers. We employ the same parameters as $ ^{156} {\rm{Gd}}$ for the calculation, with only the neutron or proton number altered. In this way, we compare the results for different proton and neutron systems, not realistic isotopes. As the figure shows, the amplitude of the scissors mode oscillation remains slightly reduced as the neutron number varies. In contrast, the amplitude of the scissors mode oscillation increases with the addition of protons. This behavior reflects the sensitivity of the scissors mode to the relative sizes of the proton and neutron systems, a sensitivity that varies oppositely in systems with fixed neutron and proton configurations. We expect that, with all other calculation conditions equal, the strongest oscillations would occur in nuclei with similar sizes of protons and neutrons, i.e., N = Z systems. This observation is based on current computational results. A more systematic investigation is required to fully understand the influence of neutron and proton numbers on the scissors mode and to provide a comprehensive analysis of their respective roles.

Figure 5.  (color online) Staggering behavior in scissors rotational bands. Solid lines denote the Gd ($ Z = 64 $) isotopes (a) and dashed lines denote the $ N = 92 $ isotones (b).

Through a systematic analysis of the scissors-mode rotational band in the nucleus of $ ^{156} {\rm{Gd}}$, as well as in some of its isotopes and isotones, we investigated the effects of quadrupole deformation and the strength of the monopole-pairing on its band-head energy and oscillatory characteristics. This study revealed that when the quadrupole deformation is relatively small, the band-head energy of the scissors rotational band increases significantly. Conversely, when the quadrupole deformation is larger, the band-head energy tends to stabilize, with only minor variations as the deformation changes. Therefore, for nuclei with large and stable deformations, the band-head energy of the scissors mode band typically remains within a certain energy range. Additionally, there is a clear dependence between the quadrupole deformation and oscillation amplitude of the scissors mode band: the smaller the deformation, the larger the oscillation amplitude. Notably, regardless of changes in deformation, the oscillatory characteristics of the scissors mode band persist, with only differences in oscillation amplitude. In comparison, the influence of the monopole-pairing strength on the band-head energy and oscillatory characteristics of the scissors mode band is relatively minor and can be considered a secondary factor compared to the effects of deformation.

The author is thankful for the many inspiring discussions with Professor Yang Sun and acknowledges collaboration with Professors F.-Q. Chen and M. Guidry.