Highlights
-
Transfer reaction products in the 40Ar + 232Th reaction
2025, 49(7): 074004. doi: 10.1088/1674-1137/adcb96
 The distribution of nuclei produced in the 40Ar + 232Th reaction has been studied at the gas-filled recoil separator (SHANS2) at the China Accelerator Facility for Superheavy Elements (CAFE2). The bombardment was carried out at a beam energy of 205 MeV with the detection system installed at the focal plane. Forty-four isotopes heavier than 208Pb were observed. These isotopes were identified as the transfer reaction (or target-like) products, and their relative cross-sections were extracted. Based on the mass distribution of these products, we exclude the possibility that they were produced by fusion-fission reactions; thus, they may originate from quasi-fission of the 40Ar + 232Th reaction.
The distribution of nuclei produced in the 40Ar + 232Th reaction has been studied at the gas-filled recoil separator (SHANS2) at the China Accelerator Facility for Superheavy Elements (CAFE2). The bombardment was carried out at a beam energy of 205 MeV with the detection system installed at the focal plane. Forty-four isotopes heavier than 208Pb were observed. These isotopes were identified as the transfer reaction (or target-like) products, and their relative cross-sections were extracted. Based on the mass distribution of these products, we exclude the possibility that they were produced by fusion-fission reactions; thus, they may originate from quasi-fission of the 40Ar + 232Th reaction. -
Pear shape and tetrahedral shape competition in actinide nuclei
2025, 49(7): 074110. doi: 10.1088/1674-1137/add5d0
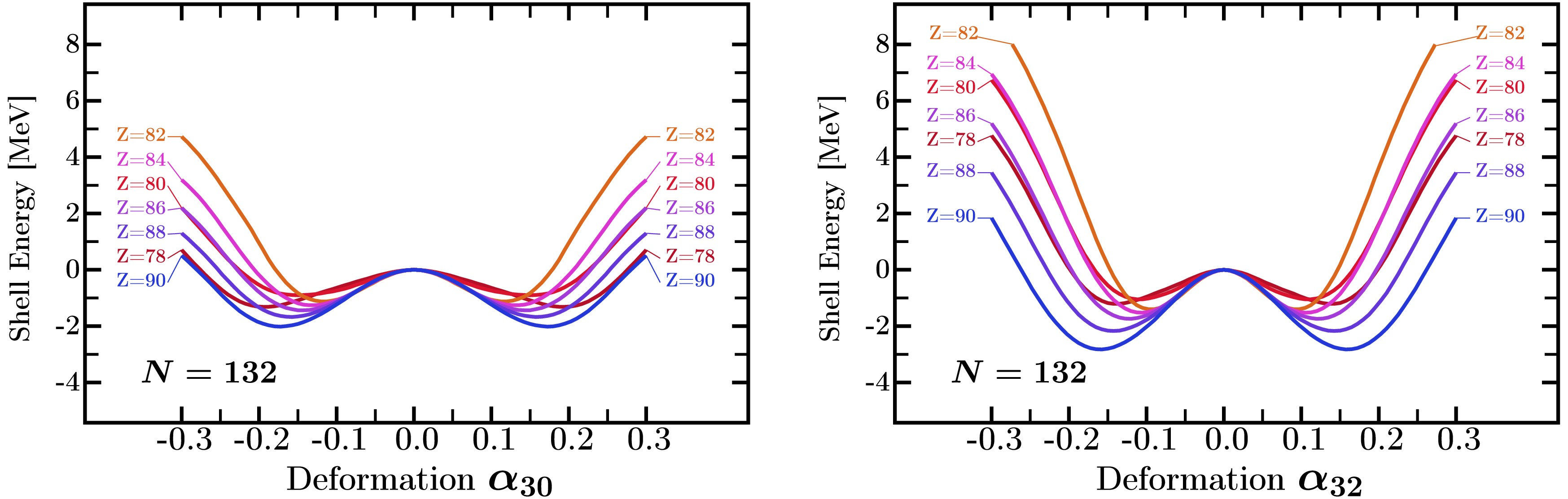 Shape competition and coexistence between the pear- and the tetrahedral-shape octupole deformations in actinide nuclei is investigated by employing the realistic nuclear mean-field theory with the phenomenological, so-called 'universal' Woods-Saxon Hamiltonian with newly adjusted parameters containing no parametric correlations. Both types of octupole deformations exhibit significant effects in
Shape competition and coexistence between the pear- and the tetrahedral-shape octupole deformations in actinide nuclei is investigated by employing the realistic nuclear mean-field theory with the phenomenological, so-called 'universal' Woods-Saxon Hamiltonian with newly adjusted parameters containing no parametric correlations. Both types of octupole deformations exhibit significant effects in$ N=132 $ ,$ N=134 $ , and$ N=136 $ isotones. Nuclear potential energy calculations within the multi-dimensional deformation spaces reveal that the tetrahedral deformation effects generally lead to deeper energy minima in most nuclei with$ N=134 $ and$ N=136 $ . Interestingly, in the nuclei$^{218}_{\;\;86}{\rm{Rn}}_{132} $ ,$^{222}_{\;\;88}{\rm{Ra}}_{134} $ , and$^{222}_{\;\;86}{\rm{Rn}}_{136} $ , selected for the illustration of the studied effects, the influence of pear-shape octupole deformation is comparable to that of tetrahedral octupole deformation. Consequently, the coexistence of both kinds of octupole shapes is predicted by the potential energy calculations. In particular, we have reproduced the experimental results known for pear-shape rotational bands obtaining in this way an estimate of the quality of the modelling parametrisation. With the same Hamiltonian, we have predicted the properties of the tetrahedral symmetry rotational bands. To facilitate the possible experiment-theory cooperation we have derived the exact spin-parity tetrahedral-band structures by applying the standard methods of the group representation theory for the Td point-group. -
Cluster radioactivity half-lives within deformed Gamow-like model
2025, 49(7): 074105. doi: 10.1088/1674-1137/adc097
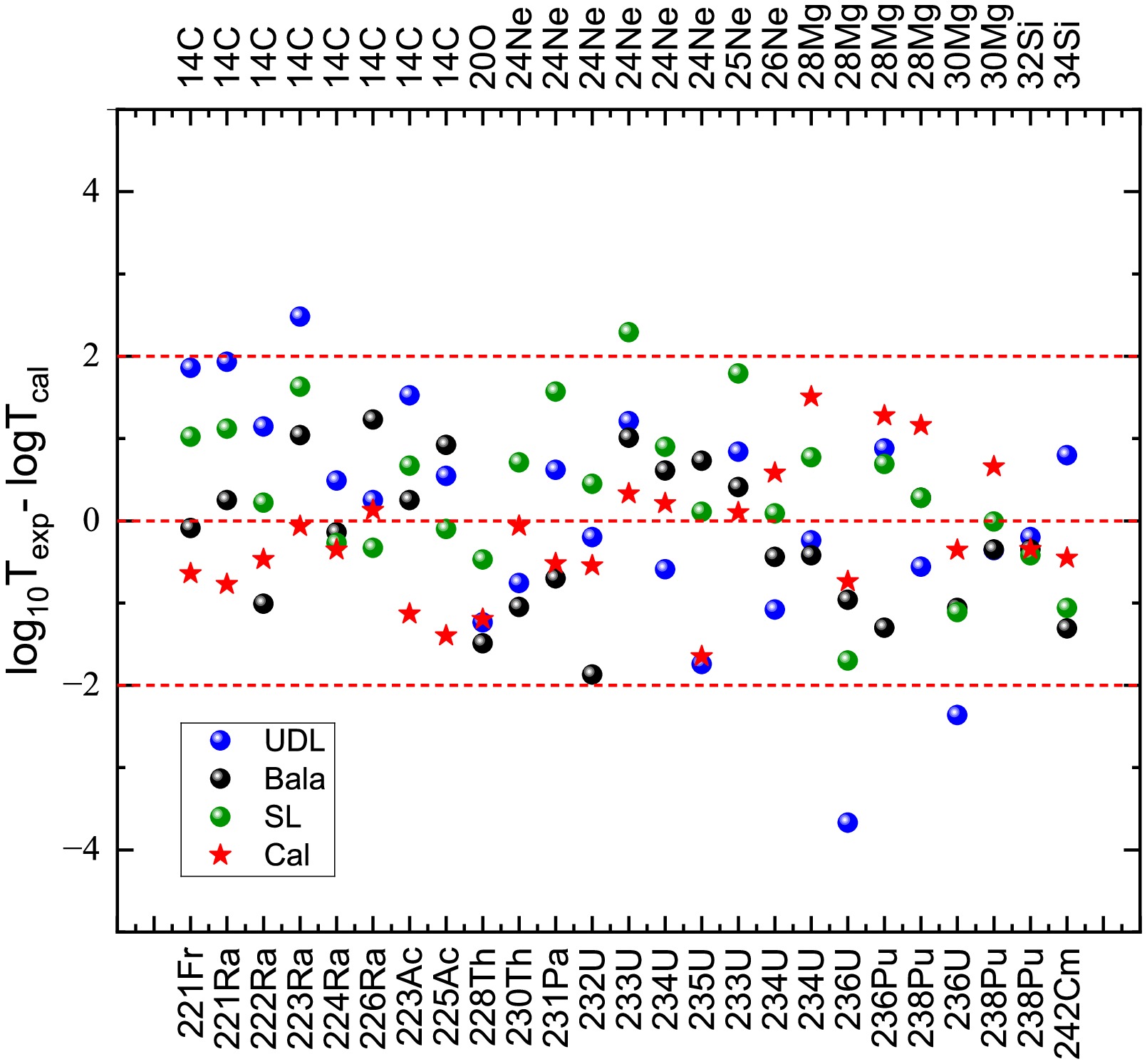 In the present work, based on a Gamow-like model, considering the deformation effect of Coulomb potential, where the effective nuclear radius constant is parameterized, we systematically investigate the cluster radioactivity half-lives of 25 trans-lead nuclei. For comparison, a universal decay law (UDL) proposed by Qi et al. [Phys. Rev. C 80, 044326 (2009)], a new semi-empirical formula for exotic cluster decay proposed by Balasubramaniam et al. [Phys. Rev. C 70, 017301 (2004)], and a scaling law proposed by Horoi [J. Phys. G: Nucl. Part. Phys. 30, 945 (2004)] are also used. The calculated results within the deformed Gamow-like model are in better agreement with the experimental half-lives. The deformation effect is also discussed within both the Gamow-like and deforemed Gamow-like models. Moreover, we extend this model to predict the cluster radioactivity half-lives of 49 nuclei whose decay energies are energetically allowed or observed but not yet quantified in NUBASE2020.
In the present work, based on a Gamow-like model, considering the deformation effect of Coulomb potential, where the effective nuclear radius constant is parameterized, we systematically investigate the cluster radioactivity half-lives of 25 trans-lead nuclei. For comparison, a universal decay law (UDL) proposed by Qi et al. [Phys. Rev. C 80, 044326 (2009)], a new semi-empirical formula for exotic cluster decay proposed by Balasubramaniam et al. [Phys. Rev. C 70, 017301 (2004)], and a scaling law proposed by Horoi [J. Phys. G: Nucl. Part. Phys. 30, 945 (2004)] are also used. The calculated results within the deformed Gamow-like model are in better agreement with the experimental half-lives. The deformation effect is also discussed within both the Gamow-like and deforemed Gamow-like models. Moreover, we extend this model to predict the cluster radioactivity half-lives of 49 nuclei whose decay energies are energetically allowed or observed but not yet quantified in NUBASE2020.
Just Accepted
More >
-
Gravitationally deformed polytropic models in extended teleparallel gravity and influence of decoupling parameters on constraining mass-radius relation
Published: 2025-06-26
-
The role and contribution of resonance effect for the decay process of
${ \bar {\boldsymbol B}^{\bf 0}_{\boldsymbol s} \boldsymbol\rightarrow \boldsymbol\pi^{+}\boldsymbol\pi^{-}{\boldsymbol P}}$ Published: 2025-06-26 -
An Unitary Coupled-Channel Approach to J/ψ Radiative decay to Pseudoscalar Pairs
Published: 2025-06-24
Recent
More >
-
Nature of X(3872) from recent BESIII data: considering the universal feature of an S-wave threshold resonance
2025, 49(7): 073103-073103-7. doi: 10.1088/1674-1137/adcb29Show AbstractWe analyze the recent data from the BESIII collaboration on the
$ X(3872) $ state in the$ J/\psi\pi^+\pi^- $ and$ D^0\bar{D}^0\pi^0 $ decay channels. The quantum number and mass of the$ X(3872) $ state allow us to exploit the universal feature of the very near-threshold$ D\bar D^* $ scattering in the S wave. The analysis of$ J/\psi\pi^+\pi^- $ and$ D^0\bar{D}^0\pi^0 $ data separately, as well as the combined analysis of these data together, all support the conclusion that$ X(3872) $ is an extremely weakly bound charm meson molecule. -
Effect of pressure anisotropy on quark star structure in the Starobinsky model
2025, 49(7): 074111-074111-13. doi: 10.1088/1674-1137/adcf8eShow AbstractThis paper discusses the structure and stability of quark stars (QSs) made of interacting quark matter. The discussion accounts for color superconductivity and perturbative QCD corrections. By combining this EoS with the Tolman-Oppenheimer-Volkoff (TOV) equations, we explore the mass-radius (
$ M-R $ ) relations of QSs. The analysis is conducted within the framework of$ R^2 $ gravity, where the model of gravity is described by$ f(R) = R + a R^2 $ . Our primary goal is to investigate how variations in the$ R^2 $ gravity parameter a affect the mass-radius and mass-central density ($ M-\rho_c $ ) relationships of QSs. Furthermore, we study the dynamical stability of these stars by analyzing the impact of the anisotropy parameter β and interaction parameter λ derived from the EoS on their stability. Our results demonstrate that the presence of pressure anisotropy is crucial for increasing the maximum mass of QSs. The results hint at the existence of super-massive pulsars. These findings are in agreement with recent astronomical observations, which suggest the possibility of neutron stars with masses exceeding$ 2M_{\odot} $ . -
Cross sections of the 148Sm(n,α)145Nd reaction in the 4.8–5.3 MeV neutron energy range
2025, 49(7): 074007-074007-6. doi: 10.1088/1674-1137/add09aShow AbstractThe cross sections of the 148Sm(n,α)145Nd reaction were measured for the first time at neutron energies ranging from 4.8 to 5.3 MeV. The experiment was carried out on the Van de Graaff accelerator EG–5 at the Frank Laboratory of Neutron Physics, Joint Institute for Nuclear Research. Fast neutrons were produced via the 2H(d,n)3He reaction with a deuterium gas target. A twin gridded ionization chamber was used as the charged particle detector, with back–to–back 148Sm samples mounted on tantalum backings at the common cathode. The absolute neutron flux was measured using the 238U3O8 sample. The obtained cross section data were compared with those from existing nuclear data libraries and theoretical calculations using the TALYS–1.96 code. The present results for the 148Sm(n,α)145Nd reaction are expected to resolve discrepancies among various nuclear evaluation data.
Archive