A three-body form factor at sub-leading power in the high-energy limit: planar contributions

The Standard Model (SM) of particle physics contains several massive particles at the electroweak scale, including the Higgs boson, the top quark, and the electroweak gauge bosons. An important goal in particle physics is to study the properties of these particles at the energy and luminosity frontiers with high precision and to probe new physics beyond the SM. This requires highly precise theoretical predictions for production processes involving these massive particles. However, calculating scattering amplitudes with massive particles is generally much more difficult than calculating massless scattering amplitudes. Owing to the high energies of the Large Hadron Collider (LHC) and future colliders, the particle masses are often small compared to other kinematic invariants in the scattering processes. With such scale hierarchies, perturbative scattering amplitudes and cross-sections can develop large logarithms involving the ratios between small masses and large kinematic invariants in the high-energy limit.

The standard approach to addressing scale hierarchies is the method of factorization. Such factorization can be organized into different orders using an expansion parameter, $ \lambda \sim m^2/E^2 $, where m denotes the low scale of the small masses and E denotes the high scale of other kinematic invariants. The leading power (LP) corresponds to order $ \lambda^0 $. The factorization formula at the LP is well understood [1−10]. It has been shown [10] that a massive scattering amplitude in the high-energy limit can be factorized into a massless amplitude, a soft function, and several collinear functions (one for each external leg). Such a factorization formula can be used to predict the structure of large logarithms of the form $ \ln(m/E) $ at higher orders in perturbation theory and also allows for the resummation of these logarithms at all orders.

Given the importance of the factorization approach, it is essential to investigate the behavior of massive amplitudes at sub-leading powers in λ. On the one hand, this allows us to understand the typical size of power corrections and thus provides an uncertainty estimate for calculations based on the LP factorization formula. On the other hand, once the factorization structure at sub-leading powers is understood, we can extrapolate high-energy approximations to intermediate energy ranges and eventually combine them with low-energy approximations based on threshold or soft factorization. This will lead to an adequate description of scattering amplitudes across the entire phase space.

In recent years, studies on small-mass factorization at next-to-leading power (NLP) in λ have emerged in the literature [11−28], either within the framework of soft-collinear effective theory (SCET) [29−35] or based on diagrammatic analysis. An analysis of sub-leading soft emissions was presented in [12]. The construction of an easy-to-use helicity operator basis was studied in [13−15]. Anomalous dimensions of sub-leading power N-jet operators were calculated in [17, 19]. Based on power counting and region analysis, an NLP factorization formula in the small-mass limit was proposed for the Yukawa theory [18] and quantum electrodynamics (QED) [22, 27]. An important ingredient in the QED factorization formula, namely, the NLP jet function, has recently been computed [28]. However, a general proof of the NLP factorization formula is still lacking.

An important validation of the factorization formula is to compare its fixed-order expansion with a direct computation of certain massive scattering amplitudes or form factors in the small-mass limit. The $ 1 \to 2 $ massive quark form factor has been computed at two loops [36−38], and three-loop calculations are in progress [7, 39−49]. However, $ 1 \to 2 $ kinematics does not capture all possible structures at the two-loop order and beyond. In this study, we analyzed a two-loop $ 1 \to 3 $ massive form factor at sub-leading powers. At two loops, non-trivial correlations can occur among at most three external particles. Therefore, the structure extracted from $ 1 \to 3 $ form factors is generic enough to be applied to other form factors and scattering amplitudes. To this end, our ultimate goal is to study the $ Q\bar{Q}g $ form factor in quantum chromodynamics (QCD), where Q represents a massive quark and g denotes a gluon. Owing to the complexity of this problem, we begin with a simpler one in QED, i.e., the $ e^+e^-\gamma $ form factor.

Scattering amplitudes involving massive electrons in QED are phenomenologically interesting on their own. Various high-energy and high-luminosity $ e^+e^- $ colliders have been proposed [50−56] as part of future plans for high-energy physics experiments. For these machines, it is important to understand standard QED processes as precisely as possible. These processes provide crucial inputs for calibrating the detectors and for better understanding beam parameters. The analyses presented in this paper are therefore valuable for these applications.

The remainder of the paper is organized as follows. In Section II, we introduce the notation and describe the method to determine independent coefficients in the small-mass expansion in Section III. In Section IV, we demonstrate the solution of the differential equations satisfied by the independent coefficients and discuss the final results. Finally, we briefly summarize this study in Section V and provide an outlook for future work.

Let us consider the $ 1 \to 3 $ QED process,

The independent kinematic variables are

where m is the mass of the electron. For convenience, we define the following dimensionless variables:

The results for tree-level amplitude $ {\cal{M}}^{(0)} $ and one-loop amplitude $ {\cal{M}}^{(1)} $ are well established [57, 58]. In this study, we focused on the two-loop amplitude $ {\cal{M}}^{(2)} $. We generated the relevant two-loop diagrams and corresponding amplitudes using $\mathrm{QGRAF}$ [59]. These diagrams can be categorized into eight integral families: five planar and three non-planar. We only considered the planar families in this study. The amplitudes containing Lorentz and Dirac indices can be decomposed into an appropriate basis with scalar coefficients (form factors). For simplicity, we demonstrated our method using the interference term in the squared-amplitude $ {\cal{F}}^{(2)} = \langle {\cal{M}}^{(0)} | {\cal{M}}^{(2)} \rangle $, where the indices are summed over. We used $\mathrm{FeynCalc}$ [60−63] and $\mathrm{FORM}$ [64, 65] to manipulate the expressions. The results are expressed in terms of two-loop scalar integrals. These scalar integrals can be expressed as

where $ a = \sum_i a_i $ and an appropriate power of $ (-s_{123}) $ is introduced to make the scalar integrals dimensionless. Each set $ \{D_i\} $ defines an integral family. There are five planar families involved in this study. The corresponding $ \{D_i\} $ are expressed as

Note that an integral family may contain several topologies; a topology is defined according to which $ D_i $ appear in the denominator of Eq. (4) (i.e., $ a_i > 0 $). The topologies belonging to each of the five families are illustrated in Fig. A1 of Appendix A.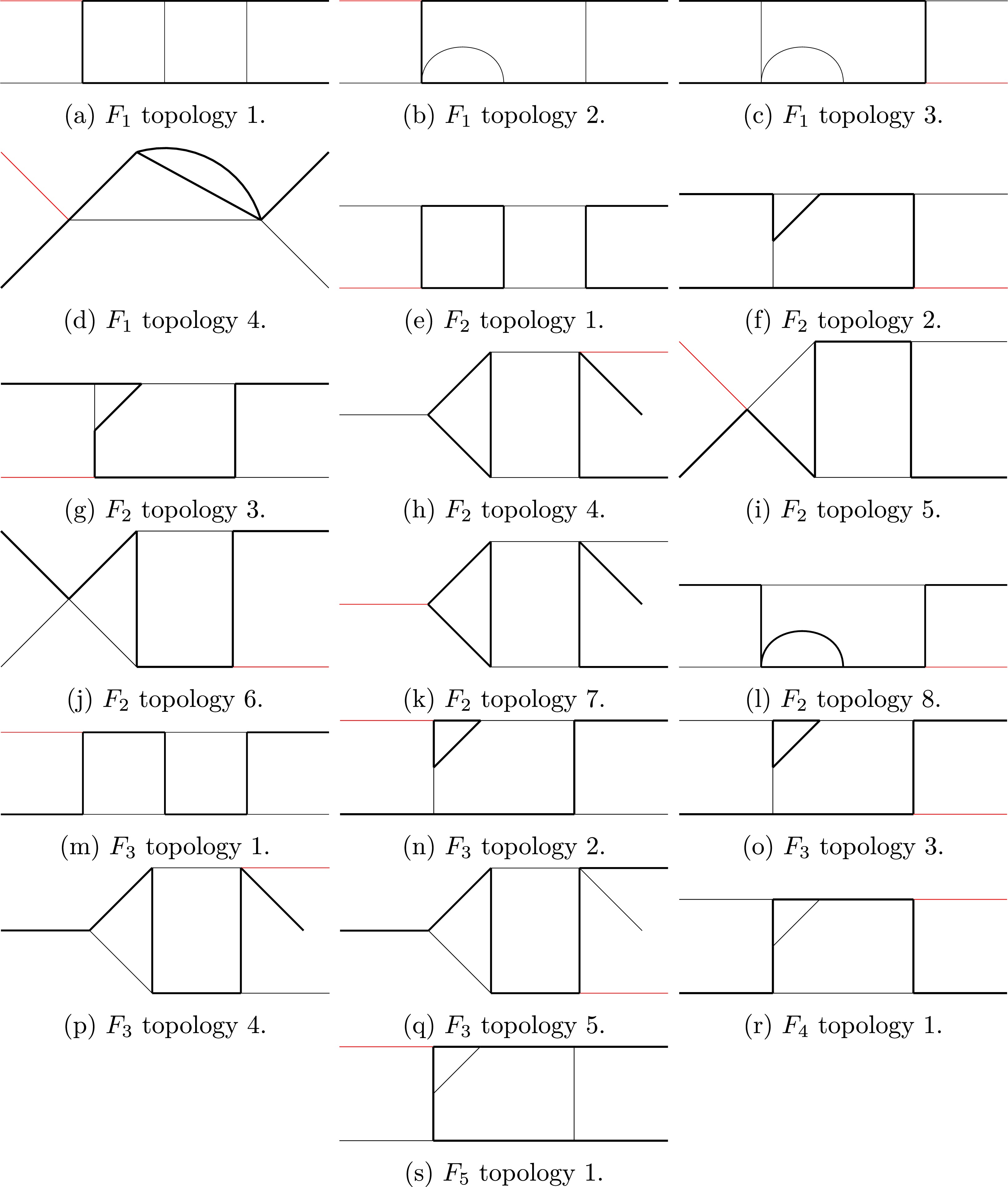

Figure A1.  (color online) Two-loop planar topologies. Thick lines represent propagators with mass m or external legs with $ p^2 = m^2 $. Thin lines represent massless propagators or external legs. Red lines represent external legs with $ p^2 = s_{123} $.

For each family, we used $ \mathrm{Kira} $ [66, 67] to reduce the scalar integrals to a set of MIs $ {\cal{I}}_i(x,y,z) $ by solving integration-by-parts (IBP) relations. Thus, the contribution from this family to the two-loop squared-amplitude can be decomposed as

where μ is the renormalization scale and coefficients $ {\cal{A}}_{i} $ are the rational functions which can be easily expanded in the limit of small values of x. The remaining task is to compute the master integrals in the high-energy limit $ x \to 0 $, while keeping the exact dependence on the variables y and z. To illustrate our method, we focused on the family (5c). There are 123 MIs in this family. In the high-energy limit, these MIs admit the following asymptotic expansion:

The objective of this study was to calculate the coefficients as a function of y and z. Note that the two-loop integrals considered in this study have no soft-collinear overlapped divergences, and the minimal power of $ \epsilon $ is $ -2 $. The integrals also have no power-like singularities in the limit $ m \to 0 $; therefore, the minimal power of x is $ 0 $. The maximal power of $ \log(x) $, $ n_{3,\max} $, depends on the values of $ n_1 $ and $ n_2 $. In practice, we truncated the series in $ \epsilon $ and x for calculating the squared-amplitude $ {\cal{F}}^{(2)} $ up to $ x^1 $ and $ \epsilon^0 $. This corresponds to the NLP in the high-energy expansion. Nevertheless, our method can be used to compute higher power terms as well.

To compute the coefficients, we adopted the method of differential equations [68−70]. From the IBP reduction, we can construct the differential equations of the MIs $ {\cal{I}}_i $ with respect to the variable $ t \in \{x,y,z\} $:

where $ {\cal{P}}^{(t)}_{i,j} $ are rational functions of $ \epsilon $, x, y, and z. The differential equations with respect to x lead to relations among the coefficients. Therefore, we only need to compute a set of independent coefficients, which is conceptually similar to the master integrals. After determining the set of independent coefficients, we can employ their differential equations with respect to y and z to obtain their analytic expressions.

Let us apply the expansion given by Eq. (7) into the differential equations in Eq. (8) for $ t = x $:

That is, taking derivative with respect to x always decreases the power of x, but may or may not decrease the power of $ \log(x) $. Meanwhile, the matrix elements $ {\cal{P}}^{(x)}_{i,j} $ may also contain poles at $ x = 0 $. Therefore, the differential equations with respect to x lead to linear relations among the coefficients $ {\cal{C}}_{i,n_1,n_2,n_3}(y,z) $. From these linear relations, we can determine a set of independent coefficients. We will refer to these independent coefficients as "master coefficients" (MCs) and express the remaining coefficients as linear combinations of the MCs.

Before solving the linear relations (there are an infinite number of them), we need to constrain the highest values of the integers $ n_1 $ and $ n_2 $ for each i, i.e., the maximal powers of $ \epsilon $ and x in the expansion of the master integral $ {\cal{I}}_i $ (note that the maximal power of $ \log(x) $ is naturally determined given the values of $ n_1 $ and $ n_2 $). The first constraint comes from the required orders in the expansion of the squared-amplitude $ {\cal{F}}^{(2)} $. As we have mentioned, we truncated the expansion in x up to the NLP, i.e., order $ x^1 $. In addition, we truncated the expansion in $ \epsilon $ up to order $ \epsilon^0 $. These requirements impose constraints on $ n_1 $ and $ n_2 $ for each master integral $ {\cal{I}}_i $. However, we found that these constraints are too tight for our purpose: the MCs determined from these constrained linear relations are not closed under differentiation. The reason is that there are cancellations among different topologies in a family when their contributions are introduced in Eq. (6).

To obtain a closed system of differential equations, we need to slightly loosen the constraints. For that purpose, we expand the coefficients in the differential equations as well:

The lowest values of k and l are crucial for the determination of the highest expansion orders. As an example, let us consider the differential equations with respect to x. The constraints from y and z can be similarly studied. Plugging Eqs. (7) and (10) into Eq. (8), we obtain

This is the master equation for relations among expansion coefficients. For this system to be closed, it is necessary that all coefficients contributing to a given $ (n_1,n_2,n_3) $ are incorporated in the above equation.

Let us focus on the equation for $ i=11 $, which arises from the differential equation of $ {\cal{I}}_{11} $ with respect to x. In this case, we have $ j \in \{1,8,11\} $ on the right-hand side of Eq. (11). Concerning the NLP accuracy of the squared amplitude, we require both $ {\cal{I}}_{11} $ and $ {\cal{I}}_{1} $ to be expanded to order $ x^3 $, given that the minimal power of x in $ {\cal{A}}_1 $ and $ {\cal{A}}_{11} $ is $ -2 $, which means that we need to consider the equation for $ n_2 = 3 $. However, the minimal value of l for $ i=11 $, $ j=1 $ is $ l=-2 $. Therefore, the coefficient for $ n_2-1-l=4 $ will appear on the right-hand side of the equation. For this reason, we need to expand $ {\cal{I}}_{1} $ up to order $ x^4 $.

Considerations similar to those mentioned above were also applied to the constrains on $ n_1 $, i.e., the expansion orders in $ \epsilon $. We performed such analysis for each sector and updated the constraints until all equations were closed. As a final outcome of such analyses, we provide the number of MCs for each integral family in Table 1.

Integral families	$ F_1 $	$ F_2 $	$ F_3 $	$ F_4 $	$ F_5 $
Number of MCs	247	359	383	158	199

Table 1.  Number of MCs in each integral family.

After obtaining a system of linear equations for the coefficients, we can solve the equations to express all coefficients in terms of the MCs. Before doing so, we need to establish a set of rules for selecting the MCs. This is similar to the criteria used for choosing MIs in Feynman integral reduction. In practice, this requires determining which of two coefficients is preferred over the other.

The choice of MCs significantly affects the process of solving their differential equations with respect to y and z. Ideally, the MCs should have the simplest possible analytic expressions. From experience, this corresponds to selecting coefficients with smaller $ n_1 $, smaller $ n_2 $, and larger $ n_3 $. Coefficients in lower sectors are also preferred over those in higher sectors.

After deciding the preference, we solved the linear system using the "user-defined system" functionality of $ \mathrm{Kira} $. We then constructed the system of differential equations of the MCs. For that, we had to re-express the derivatives of the MCs in terms of the MCs again. This step was accomplished using $ \mathrm{Kira} $ as well. For example, we can rewrite the differential equation of a MC with respect to y as

This equation was provided to $ \mathrm{Kira} $ along with other linear relations. We obtained the left-hand side expressed in terms of MCs. Finally, we obtained the following differential equations:

where $ I=(i,n_1,n_2,n_3) $ and $ J=(j,m_1,m_2,m_3) $ denote two subscript sequences that label the MCs.

After constructing the differential equations, we can find the analytic solutions for the MCs. Ideally, the solution procedure can be greatly simplified if connection matrices $ {\cal{A}}^{(y)}_{I,J}(y,z) $ and $ {\cal{A}}^{(z)}_{I,J}(y,z) $ take a strictly triangular form. In that case, the solutions can be easily expressed in terms of iterated integrals. This is similar in spirit to the concept of canonical differential equations [71]. However, the existing tools [72−76] for finding canonical differential equations do not easily adapt to the current case. Fortunately, the connection matrices are already in a block-triangular form with at most $ 3 \times 3 $ blocks. They can be iteratively converted to a strictly triangular form, as will be demonstrated next.

Let us first consider the simple cases where the derivatives of a MC only depend on themselves and the already-solved MCs:

where $ {\cal{G}}_{y} $ and $ {\cal{G}}_{z} $ come from the already-solved MCs. If coefficients $ {\cal{A}}_{y} $ and $ {\cal{A}}_{z} $ are both zero, the above equations can be easily solved by direct integration. This corresponds to a strictly triangular system, as discussed earlier. Let us consider the case where $ {\cal{A}}_{y} $ and $ {\cal{A}}_{z} $ are nonzero.

For convenience, we introduce the following functions:

Multiplying the MC by the two functions, the differential equations in Eq. (14) are transformed into

Note that only already-solved MCs appear on the right-hand side of the above two equations. We would like to find transformation function $ {\cal{T}}(y,z) $ such that

This is an example of a strictly triangular system of differential equations, where the derivatives of the transformed MCs only depend on already-solved ones. Comparing Eq. (17) with Eq. (16), we conclude that

where the function $ f_z(z) $ satisfies the differential equation

and a similar expression can be obtained for $ f_y(y) $. The fact that the right-hand side of the above equation is independent of y follows from the compatibility condition of Eq. (14):

which further follows from the linear-independence of $ {\cal{C}}(y,z) $ with respect to $ {\cal{G}}_y $, $ {\cal{G}}_z $ and their derivatives. From the above analysis, we can write

Building on this result, we obtain a general solution to the differential equations in Eq. (17):

where $ {\cal{C}}_{y}(y) $ is a function that only depends on y. This is also the case for $ {\cal{C}}_{z}(z) $. These two functions are related by the second equal sign in the above formula and are only fixed once the arbitrary constant terms of the indefinite integrals are chosen. Using the fact that $ {\cal{C}}_{y}(y) $ is independent of z, we can derive the differential equation of $ {\cal{C}}_{z}(z) $ with respect to z:

which allows us to determine the analytic expression of $ {\cal{C}}_{z} $ (as well as $ {\cal{C}}_{y} $) up to a constant of integration. This constant should be fixed by a boundary condition, as will be discussed later.

The above procedure of transforming the differential equations to a strictly triangular form can be naturally extended to $ 2 \times 2 $ and $ 3 \times 3 $ blocks, as will be discussed in the following subsections.

For $ 2 \times 2 $ blocks, the differential equations take the form

where $ t \in \{y, z\} $, $ {\cal{A}}^{(t)}_{ij} $ denotes rational functions of y and z, and $ {\cal{G}}^{(t)}_i $ results from already-solved MCs. To solve the equations, we would like to find a linear combination $ {\cal{C}}' = b_1 {\cal{C}}_1 + b_2 {\cal{C}}_2 $ with $ b_1 $ and $ b_2 $ being rational functions of y and z, such that the derivatives of $ {\cal{C}}' $ only depend on themselves. Taking the derivatives, we obtain

Therefore, we require

Once we find a suitable pair of $ b_1 $ and $ b_2 $, the differential equation of $ {\cal{C}}' $ becomes

The above equation resembles the one studied in Section IV.A. We can employ the method described there to remove term $ {\cal{A}}'_t {\cal{C}}' $ and effectively transform the differential equation into a strictly triangular form. After obtaining the solution of $ {\cal{C}}' $, we can use it to derive analytic expressions for $ {\cal{C}}_1 $ and $ {\cal{C}}_2 $. Taking $ {\cal{C}}_1 $ as an example, we have

Given that $ {\cal{C}}' $ is known, this equation can again be solved using the method presented in Section IV.A. The expression for $ {\cal{C}}_2 $ can be obtained from those of $ {\cal{C}}' $ and $ {\cal{C}}_1 $.

From the above discussion, it is clear that the task reduces to finding a particular solution of $ b_1 $ and $ b_2 $ that satisfies Eq. (26). Note that Eq. (26) is a differential equation for the ratio $ b_2/b_1 $ that can be rewritten as

This is the so-called Riccati equation. There are two procedures to find a solution of this equation.

Method one: brute-force solution. For the cases we addressed in this study, the Riccati equation can be solved using $\mathrm{Mathematica}$. As an example, we may need to solve the system with

For convenience, we set $ b_1 = 1 $, and the Riccati equation with respect to y becomes

Using $\mathrm{Mathematica}$, we obtained a general solution of the above equation that involves arbitrary functions of z. We require that the solution be rational and satisfy the corresponding equation with respect to z. This give rises to a particular solution:

In practice, this method may be slow. If this is the case, we may resort to the second method.

Method two: solution by ansatz. Given that the equation only constrains $ b_2/b_1 $, we can assume that both $ b_1 $ and $ b_2 $ are polynomials of y and z with integer coefficients. We can then apply the ansatz

where the coefficients $ c_{ij}^{(1)} $ and $ c_{ij}^{(2)} $ as well as the degree n are to be determined.

We start with a small value of n and substitute the ansatz into Eq. (26). This then leads to a system of quadratic equations of the coefficients. If the system of equations only allows a trivial solution (i.e., all coefficients are equal to zero), it means that the value of n is too small. We then increase the value of n until finding a non-trivial solution.

For the example considered above, we found that a non-trivial solution can be obtained for $ n=3 $:

which is equivalent to the result obtained from the first method.

Similar to the $ 2\times2 $ case, the differential equations for $ 3\times3 $ blocks have the form

The method for dealing with this system is analogous. First, we need to construct a linear combination $ {\cal{C}}' = b_1 {\cal{C}}_1 + b_2 {\cal{C}}_2 + b_3 {\cal{C}}_3 $ whose corresponding differential equations only involve themselves. This reduces to the following equation:

This equation can be rewritten as

Note that the two unknowns $ b_2/b_1 $ and $ b_3/b_1 $ are still coupled by both equations. Thus, this system is challenging to solve by brute force. Fortunately, the second method introduced in the previous subsection still works, offering an algorithmic procedure to address this type of problems. We can apply polynomial ansatz for $ b_1 $, $ b_2 $, and $ b_3 $, and solve for the coefficients from Eq. (36). Subsequently, we can solve for $ {\cal{C}}' $ using the method described in Sec. IV.A. As a result, we are left with a $ 2\times2 $ system of $ {\cal{C}}_1 $ and $ {\cal{C}}_2 $ that can be solved following the strategy described in Sec. IV.B.

Let us again demonstrate our approach using an example:

A particular solution can be found by using the ansatz for $ n=2 $:

This gives rise to a decoupled differential equation:

We do not go into the details of the remaining steps in this paper.

In this study, we did not encounter blocks greater than $ 3 \times 3 $. As can be seen, the method introduced above can be applied to more complex cases as well. The procedure is iterative: one first solves for a linear combination whose differential equation is decoupled, thereby reducing the system to a simpler form.

To obtain the solution to the system of differential equations, we still need to determine the boundary conditions for each coefficient. For that, we used $\mathrm{AMFlow}$ [77] to numerically compute the small-mass expansion of all MIs at a specific kinematic point. During this process, all variables (except $ m^2 $ but including $ \epsilon $), were set to exact values (rational numbers). For each value of $ \epsilon $, the output has the following structure:

where $ \alpha_i(\epsilon) $ is a linear function of $ \epsilon $, $ w_{ij}(\epsilon) $ depends on $ \epsilon $ and the kinematic variables (which we have suppressed), and $ j_{\max} $ is specified according the required expansion order (in $ m^2 $) of the MIs. By varying $ \epsilon $ with fixed kinematic variables, we can reconstruct the coefficients in $ \alpha_i(\epsilon) $ as well as the function $ w_{ij}(\epsilon) $ as a power series in $ \epsilon $:

To determine the coefficients $ a_{ijk} $, we need to sample at least $ (k_{\max}-k_{\min}+1) $ different values of $ \epsilon $. Note that the precision of the reconstructed $ a_{ijk} $ also depends on the number of samples. Therefore, we need to choose an appropriate number according to the required expansion order (in $ \epsilon $) of the MIs and the required precision for the coefficients. In practice, this number is approximately $ 50 $.

With the reconstructed coefficients, we can re-expand Eq. (41) in $ \epsilon $ and obtain the small-mass expansion of the MIs at the chosen kinematic point in the form

The minimal powers of $ \epsilon $ and x and the maximal powers of $ \log(x) $ for a given pair $ (n_1,n_2) $ can be read off from the above expansion. Note that $ f_{i,n_1,n_2,n_3} $ is coefficient $ {\cal{C}}_{i,n_1,n_2,n_3}(y,z) $ at a particular kinematic point, and the general solution of $ {\cal{C}}_{i,n_1,n_2,n_3}(y,z) $ has already been obtained from the differential equations. Such a solution can be written in terms of generalized polylogarithms (GPLs) with the help of $\mathrm{PolyLogTools}$ [78] up to some unknown constants. These constants can then be reconstructed as transcendental numbers by the PSLQ algorithm using high-precision numbers (about 100 decimal digits) of $ f_{i,n_1,n_2,n_3} $. The transcendental basis was generated from the elements $ \{\pi,\ln(2),\zeta_2,\zeta_3,\zeta_4,\text{Li}_4(1/2),\zeta_5\} $ up to weight 5. It is worth mentioning that the DEs may demand higher order coefficients in $ \epsilon $, as discussed in Sec. III.A. This is the reason why weight-5 functions and constants appear, despite the fact that two-loop amplitudes up to order $ \epsilon^0 $ only require weight-4 at most. Note that the form of the analytic expressions can differ in distinct kinematic regions. Specifically, we worked in the Euclidean region where all planar MIs have no imaginary part. The expressions in other kinematic regions can be obtained via analytic continuation. Given that our results are expressed in terms of GPLs, their analytic structure is well understood. The branch cuts of GPLs are uniquely determined by their symbols, and when one analytically continues across a branch cut, an additional term proportional to $ \pm {\rm i}\pi $ is generated, where the sign of $ {\rm i}\pi $ depends on the direction of crossing the cut. See [79−81] for further details.

With the analytic expressions for the MIs, we can combine them to obtain the planar contributions to the squared-amplitude $ {\cal{F}}^{(2)} $ up to order $ x^1 $ and $ \epsilon^0 $. It can be written in terms of GPLs up to weight $ 4 $ using the following symbol letters:

There are two additional letters $ \{1-y,\,2-y-z\} $ appearing in the MIs. However, they cancel out in the final expression for the squared amplitude. Note that the original massive amplitude involves elliptic integrals but the expanded amplitude can be expressed using GPLs up to the NLP. The result for the squared amplitude is compact, with a size of approximately 400 KB. We attach the expression as an electronic file to this paper.

We performed several sanity checks on our calculations. We applied our method to the one-loop amplitude, for which the complete result can be easily obtained. Upon expansion in the high-energy limit, the complete result agrees exactly with our calculations. We also numerically computed the MIs at different kinematic points other than the chosen boundary point. We found that the results agree with the outcomes from our analytic expressions. In particular, we verified kinematic points beyond the Euclidean region and found that the imaginary parts agree as well. These checks demonstrate the reliability of our method.

In this study, we initiate an analysis of sub-leading power contributions to multi-parton massive form factors in the high-energy limit, where the parton masses are much smaller than their energies. These form factors provide crucial information for formulating and validating sub-leading power factorization theorems for generic scattering amplitudes. Such factorization theorems are essential for resumming mass logarithms beyond the leading power and for generating approximate results for scattering amplitudes at higher loops.

While two-loop massive quark form factors are available, the $ 1 \to 2 $ kinematics is not generic enough to be extended to multi-parton scattering amplitudes. Therefore, we focused on $ 1 \to 3 $ form factors, for which two-loop multi-parton correlations can be studied. To establish the calculation procedures, we started with the two-loop planar contributions to a QED form factor $ \gamma^* \to e^+e^-\gamma $. Although only two-particle correlations are present in this case, it is sufficient to demonstrate that our method is capable of obtaining analytic expressions for the relevant loop integrals as a small-mass expansion.

Our calculations are based on the differential equations satisfied by the expansion coefficients of the master integrals. These equations can be derived to arbitrary order in the power expansion using the differential equations for the master integrals. The differential equations with respect to the mass m are then used to derive linear relations among the expansion coefficients. Similar to IBP reduction, these linear relations can be solved to express all coefficients in terms of a finite set of master coefficients. The differential equations of the master coefficients with respect to momentum invariants are then employed to obtain their analytic expressions. The solutions are expressed in terms of GPLs, which are then combined to yield a compact analytic result for the planar contributions to the form factor.

Several clear follow-ups to this study are in sight. A rigorous verification of factorization at NLP requires the inclusion of non-planar contributions to the amplitudes. Our method can readily be applied to the non-planar contributions to this form factor. The main obstacle in such a calculation lies in the IBP reduction. We have attempted to use state-of-the-art reduction tools such as $ \mathrm{Kira} $, $\mathrm{NeatIBP}$ [82, 83], and $\mathrm{Blade}$ [84], but we did not succeed within a reasonable amount of time. It is necessary to develop more efficient reduction methods for such cutting-edge calculations. Another evident generalization is to consider the $ Q\bar{Q}g $ form factor in QCD, for which genuine three-parton correlations can occur. This involves more integral families, but the method established in this work can still be applied straightforwardly. Finally, the differential equations for the master coefficients were solved by brute force in this study. It would be interesting to investigate whether these differential equations can be cast into a canonical form that allows direct solution as iterated integrals. We leave these investigations to future work.

As mentioned in the main text, we have five integral families that contain 19 planar topologies in total, as shown in Fig. A1. The MIs in each integral family are as follows: