Unveiling Extra Photon Rings: Optical images of Asymmetric Thin-Shell Wormholes with Non-Commutative Corrections

Black holes(BHs), extremely compact spacetime structures predicted by general relativity(GR), are a central object of study in theoretical physics and high-energy astrophysics. The Event Horizon Telescope (EHT) images of M87* [1, 2] and Sgr A* [3−8] provided the first direct visual evidence of BHs and offered observational constraints for analyzing crucial physical processes such as accretion disk radiation mechanisms and jet formation dynamics. Based on BH shadow images, we can clearly observe a central dark region surrounded by a light ring. The inner edge of this light ring is the critical curve, which is composed of photons bound by gravitational bending [9]. The central dark region is the BH shadow, which closely matches the predictions of GR. In fact, the study of such shadow images has a long history. As early as 1966, Synge’s work demonstrated that the shadow silhouette of a static spherically symmetric BH is a perfect circle [10]. He calculated the angular diameter of the shadow, expressing it as a function of the BH mass and the radial coordinate of the observer’s location. Subsequently, for rotating BHs, their spin effects can cause deformation of the BH shadow [11, 12]. Methods for calculating the photon sphere and shadow have become increasingly mature, and are continually being improved and refined [13]. Currently, these shadows have been widely proposed as an effective tool for cosmological studies. They serve as a natural cosmological ruler [14], enabling the measurement and testing of various cosmic phenomena [15]. Through observations of shadow images, researchers can rigorously test models in diverse gravitational environments and constrain relevant parameters [16].

In our real universe, BHs are usually surrounded by bright accretion flows, which result from the motion of matter within their accretion disks. Due to their strong gravitational fields, they continuously capture large amounts of gas, dust, and plasma from their surroundings. Under the influence of such intense gravity, this material gradually forms a rotating, flattened disk-like structure, known as an accretion disk. Luminet successfully simulated BH shadows by constructing a geometrically thin, optically thick standard accretion disk model [17]. His research revealed that the shapes of the shadow and photon rings depend on the location of the accretion flow. Subsequently, Narayan et al. established a spherically symmetric accretion flow model and systematically studied the shadow of a Schwarzschild BH [18]. They found that the optical appearance of a spherically accreting BH is independent of the inner radius at which the accreting gas ceases to radiate, meaning that the details of the accretion flow have little impact on the shadow size. In 2019, Gralla et al. investigated the shadow features of a Schwarzschild BH surrounded by a thin accretion disk [9]. Their results revealed that in addition to photon rings, lensing rings and a direct emission region also exist outside the shadow region. Using this thin accretion disk model, Zeng et al. investigated the shadow characteristics of BHs with Quintessence dark energy, focusing on discussing the influence of relevant physical parameters on the shadow [19]. Subsequently, this model has been extended to other modified gravity theories, and shadow features have been investigated using various emission models, such as spherical accretion flows, thick disks, and hot spots [20−43]. Furthermore, one has also analyzed the holographic properties of photon rings and examined the characteristics of Einstein rings in AdS spacetime, yielding some interesting research results [44−47].

Certain ultracompact objects (UCOs), such as wormholes [48−52] and boson stars [53−57], exhibit remarkably similar observational features to BHs under specific conditions, even disguising themselves as BHs in certain scenarios. Therefore, distinguishing BHs from their alternatives has become a central challenge in current high-energy astrophysics. Against this backdrop, the study of compact objects, such as wormholes, has gained new momentum [58−61]. In fact, a TSW is a hypothetical, traversable spacetime structure connecting two distinct regions of spacetime through a narrow throat [62]. This type of spacetime structure originates from Visser’s 1989 method to construct wormholes using a “cut-and-paste” technique, thereby successfully connecting two Schwarzschild spacetimes [63]. It is important to note that the passage of ordinary matter can cause wormholes to collapse into BHs, whereas exotic matter with negative energy density is required to maintain wormhole stability [64]. Visser et al. employed the Israel junction conditions to construct traversable static TSWs and analyze their stability [65]. Subsequently, Garcia et al. established a general framework for analyzing the stability of spherically symmetric TSWs, providing a foundational theoretical basis for future studies on the structural stability of other exotic spacetimes [66]. To further understand wormhole structures, Wang et al. studied the shadows of asymmetric thin-shell wormholes(ATWs) and compared the results with those of BH spacetimes [67]. Interestingly, Wielgus revealed the possibility of a double photon ring structure in ATW imaging, indicating that ATW images may contain a photon ring on the observer side and another photon ring originating from the far side of the wormhole [68]. Peng et al. conducted a systematic study of the observed appearance of accretion disks around the Schwarzschild ATW spacetime, finding extra photon rings and lensing bands in the ATW shadow images [69]. Therefore, systematically studying the shadows and optical images of ATWs can not only provide novel insights into exploring their internal structure, but also offer a theoretical basis for distinguishing wormholes from BHs and establish new theoretical templates for future astronomical observations.

In other hands, GR has successfully explained numerous astrophysical and gravitational phenomena, and several experimental results have largely corroborated the validity of the theory. However, some phenomena observed in reality remain inadequately explained within the framework of GR, including the nature of dark matter and dark energy, the accelerated expansion of the universe, and the singularity problem. In recent years, non-commutative spacetime has become increasingly important in the study of gravitational theories [70]. Serving as an effective approach to exploring spacetime quantization [71−76], its non-commutativity can be described by the algebraic relation $ [x^\mu,x^\nu] = i\theta^{\mu\nu} $ [72]. The influence of this non-commutativity on BH is particularly intriguing, and researchers have proposed various theoretical frameworks to implement non-commutative spacetime structures in gravitational theories [77−80]. Studies indicate that non-commutativity can be achieved within GR by modifying the matter source, thereby replacing the traditional Dirac delta function with a Gaussian distribution [81] or Lorentzian distribution [82]. The Lorentzian distribution offers a different perspective from the Gaussian distribution and better reflects the fundamental characteristics of non-commutative spacetime geometry. Currently, there are numerous studies on BHs with Lorentzian mass distribution in non-commutative spacetime, focusing on aspects such as quasinormal modes [83], thermodynamics [84−87], and geometric characteristics [88]. Naturally, there has been related work on shadow studies within this spacetime [27]. However, research on the observational intensity and appearance characteristics of wormholes surrounded by accreting matter in non-commutative spacetime remains limited. In particular, ATWs with higher-order non-commutative corrections under the Lorentzian mass distribution model have not yet been explored. This paper aims to systematically investigate the optical observational properties of such wormholes, considering a thin disk as the exclusive background light source. We focus on exploring the influence of spacetime-related parameters, such as the non-commutative parameter, mass ratio, and throat radius, on the observational characteristics of the wormhole, and compare the results with those of the BH spacetime. The goal is to provide a theoretical reference for distinguishing between BHs and ATWs with higher-order non-commutative corrections from the perspective of the shadow.

The organization of this paper is as follows. In section 2, we review the metric for the ATW within the framework of higher-order non-commutative corrected geometry, and then examine its effective potential and null geodesics. In section 3, we introduce the deflection of light and analyze the trajectories of photons in the ATW spacetime, as well as the transfer function and optical observations of the emission disk surrounding this wormhole. Subsequently, we also explored the impact of varying the mass asymmetry and throat radius on the optical appearance of the object. Finally, we present our conclusions in Section 4. In this paper, we set $ \hbar = G = c = 1 $.

Non-commutative geometry is a theory of spatiotemporal quantization, in which the commutations of spatiotemporal coordinate operators can be expressed as [72]

where $ \theta^{\mu\nu} $ represents the antisymmetric tensor, and θ denotes the non-commutative parameter, signifying the smallest scale of spacetime. In non-commutative geometry, the Lorentz distribution ρ of the mass density for spherically symmetric stars is given by [81, 83, 85]

where M represents the mass of the BH. The Einstein equation is

The Ricci tensor, $ R_{\mu\nu} $, describes the curvature of spacetime. $ g_{\mu\nu} $ is the metric of space time, $ T_{\mu\nu} $ is the energy-momentum tensor, which describes the distribution of matter and energy in spacetime. In non commutative scenarios, the spherically symmetric spacetime is

Substituting Eq. (4) in Eq. (3) yields

where

Here, $ T^0_0 $ represents energy density, and according to the Lorentz distribution formula in Eq. (2), we have

By substituting the above equation into the metric, we can obtain

or

When $ \theta\to 0 $, the spacetime geometry returns to the general Schwarzschild geometry.

The metric of the BH with high-order corrected non-commutative geometry is [86]

We constructed the ATW based on Visser’s cut-and-paste technique [63], joining two higher-order corrected spacetimes, denoted $ M_1 $ and $ M_2 $, with differing mass parameters. The metric of the resulting ATW spacetime, defined in the manifold $ M \equiv M_1 \cup M_2 $ is

where

In this context, $ i = 1 $ and $ i = 2 $ refer to two different higher-order non-commutative corrected spacetimes. The parameter R represents the location of the wormhole throat.

To study the optical observation appearance characteristics of wormholes, it is essential to first investigate the trajectories of photons within this spacetime background. For simplicity, it is assumed that the only interaction between photons and the throat is a gravitational interaction. Therefore, the four-momentum of the photon remains constant as it passes through the throat. In the context of non-commutative geometry, the higher-order corrected metric is continuous. This implies [67]

where the metrics in the $ M_1 $ and $ M_2 $ spacetimes are represented as $ g_{\mu\nu}^{M_1}(R) $ and $ g_{\mu\nu}^{M_2}(R) $, respectively.

For the photon, since the time t and azimuthal angle ϕ do not appear in the metric function $ f(r) $ for each spacetime, two conserved quantities arise, which are the energy $ E_i $ and the angular momentum $ L_i $ [27, 67, 69],

where the Lagrangian $ \mathcal{L}_i = \dfrac{1}{2} g^i_{\mu \nu} \dot{x}^\mu \dot{x}^\nu $. For a spherically symmetric spacetime, the motion of photons can be fixed in the equatorial plane, i.e., $ \theta = \pi/2 $. In this case, the null geodesics can be expressed as

Further, we have

where $ p_i^{r_i} = \dfrac{dr_i}{d\lambda} $ represents the photon’s four-momentum and λ is the affine parameter[67, 69]. From Eq. (17), we can express the radial component of the null geodesic as follows

where the parameter $ b_i = \frac{L_i}{E_i} $ represents the impact parameter of the photon in spacetime $ M_i $. The effective potential $ V_{effi}(r_i) $ is

Therefore, the photon ring orbit satisfies the critical condition of the effective potential, which is

To ensure the generality of our study on ATWs with higher-order non-commutative corrections, we set the mass parameters to $ M_1 = 1 $ and $ M_2 = k $, with $ k > 1 $. With this choice, the event horizon is obscured by the photon sphere. From Ref. [49], we know that the relationship between k and R is

In this paper, unless otherwise specified, we adopt $ M_2 = k = 1.2, M_1 = 1, R = 2.6 $ as the default values throughout this study. The impact parameters $ b_1 $ and $ b_2 $ in spacetimes $ M_1 $ and $ M_2 $ are related by the following equation [67]

Since $ M_1 < M_2 $, if a photon originating from the $ M_1 $ spacetime has an impact parameter $ b_1 $ that satisfies the condition $ b_1 < b_{c1} $, it will pass through the wormhole throat and enter the $ M_2 $ spacetime. However, when $ b_2 > b_{c2} $, the photon may return to spacetime $ M_1 $. Given the relation $ b_2 = b_1/Z $, the corresponding condition on $ b_1 $ in $ M_1 $ for this round-trip trajectory is

Using Eq. (20), we carefully calculated the critical impact parameter $ b_{ci} $ for different non-commutative parameters θ, as shown in Table 1. The result shows an inverse correlation between $ b_{ci} $ and θ. Furthermore, as θ increases, the values of the event horizon radius $ r_{h1} $ and the photon sphere radius $ r_{p1} $ decrease.

θ	$ r_{h1} $	$ r_{p1} $	$ b_{c1} $	$ b_{c2} $
0	2	3	5.19615	6.23538
0.01	1.74281	2.66245	4.76429	5.81148
0.03	1.49026	2.34456	4.37222	5.44504

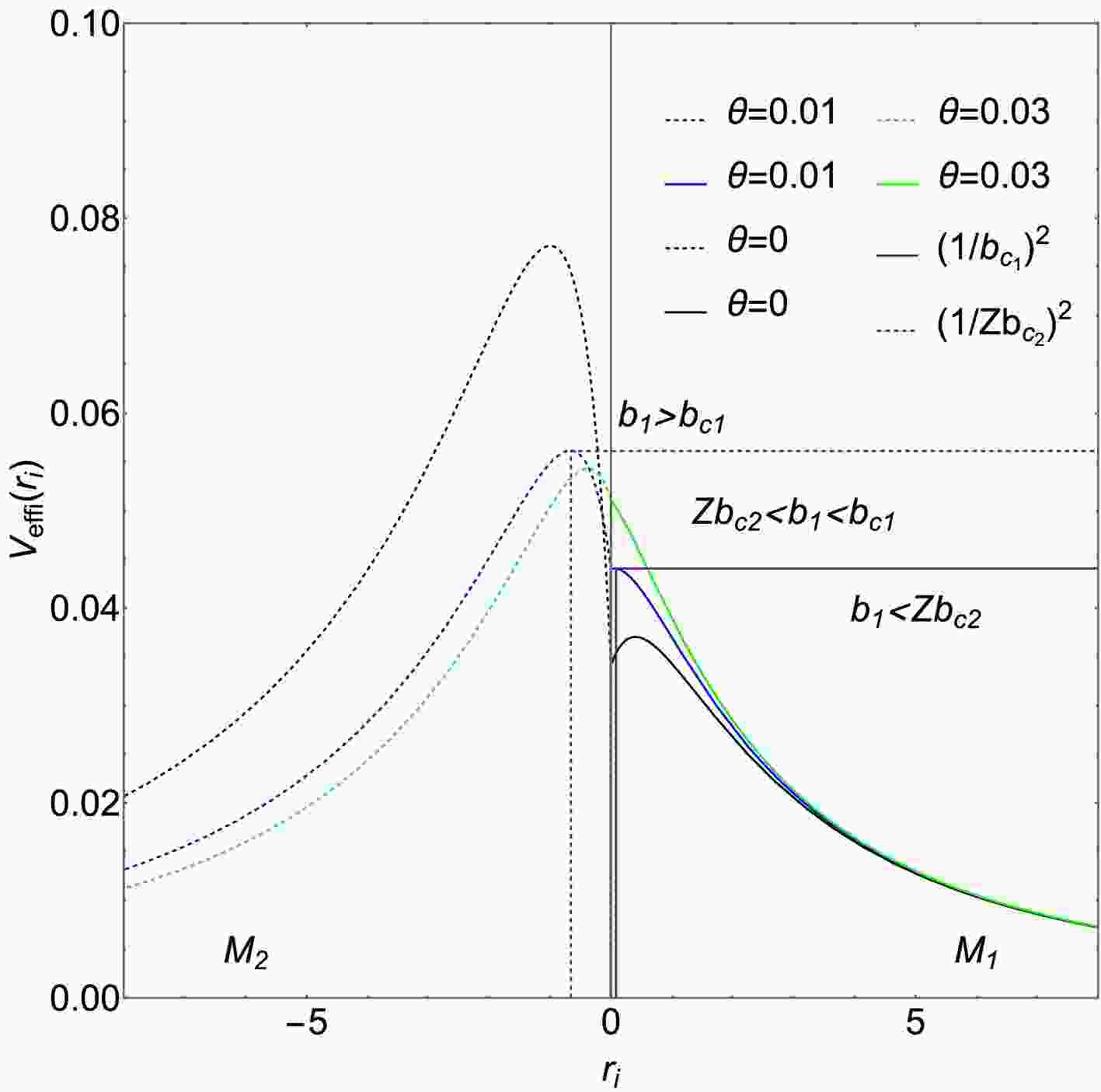
Table 1.  The table furnishes values for $ b_{ci} $, $ r_{h1} $, and $ r_{p1} $ corresponding to varying values of θ. The critical impact parameters for spacetimes $ M_1 $ and $ M_2 $ are denoted as $ b_{c1} $ and $ b_{c2} $, respectively. The event horizon radius and photon sphere radius of spacetime $ M_1 $ are $ r_{h1} $ and $ r_{p1} $,respectively.

Fig. 1 depicts the radial dependence of the effective potential for the ATW with higher-order non-commutative corrections, plotted for varying non-commutative parameter θ. When $ M_1 < M_2 $, the effective potential curve for the $ M_2 $ spacetime has a peak that is significantly higher than the curve for the $ M_1 $ spacetime, while the effective potential values at the wormhole throat remain equal for both. This allows a portion of the light rays emitted from the $ M_1 $ spacetime to pass through the $ M_2 $ spacetime and return to the $ M_1 $ spacetime. As θ increases, the peak difference between the $ M_1 $ and $ M_2 $ spacetimes decreases. Within a single spacetime, the peak effective potential increases with increasing θ.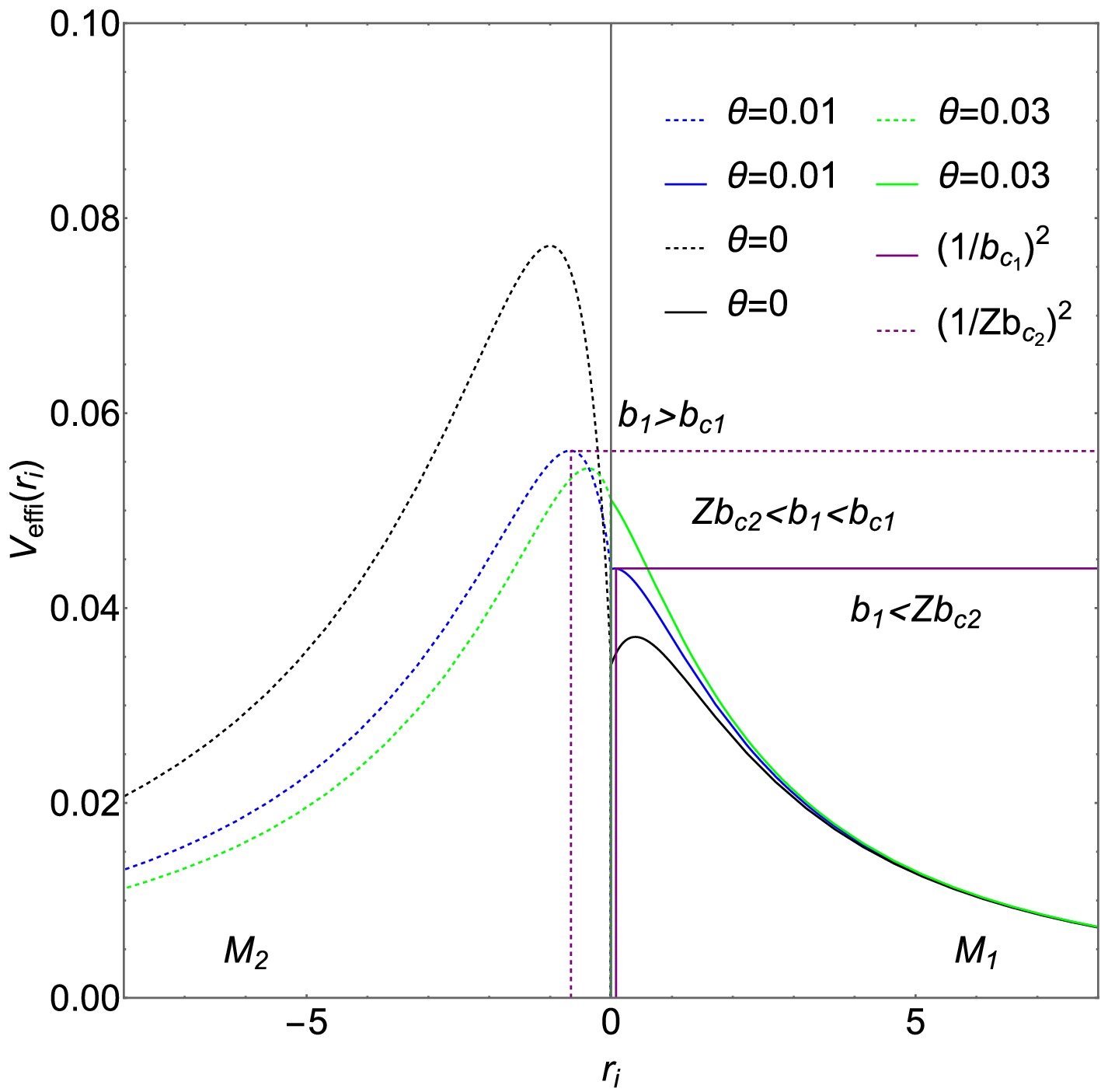

Figure 1.  (color online) The effective potential of the ATW with higher-order non-commutative corrections is studied as a function of radius, considering different non-commutative parameters. The left and right sides correspond to spacetimes with $ M_2 $ and $ M_1 $. When $ \theta = 0.01 $, $ b_{c1} = 4.76429 $ and $ Zb_{c2} = 4.22022 $, corresponding to the green solid and green dashed lines in the figure, respectively.

We introduce the parameter $ x_i = 1/r_i $ to simplify the calculations. Therefore, the equation of the photon trajectory becomes

where

In fact, the behavior of photons in the vicinity of the ATW spacetime with higher-order non-commutative corrections can be classified into three categories.

(1) $ b_1 > b_{c1} $: In spacetime $ M_1 $, photons originate from infinity and travel towards the wormhole throat. However, their trajectory is deflected near the throat, and they can ultimately be received by an observer at infinity in spacetime $ M_1 $.

(2) $ Zb_{c2} < b_1 < b_{c1} $: Starting from infinity in spacetime $ M_1 $, this trajectory passes through the wormhole throat into spacetime $ M_2 $. In spacetime $ M_2 $, its trajectory is deflected to a great extent before passing through the throat again and returning to infinity in spacetime $ M_1 $.

(3) $ b_1 < Zb_{c2} $: Trajectories that originate from infinity in spacetime $ M_1 $ that traverse the wormhole throat into spacetime $ M_2 $ and eventually propagate to infinity in spacetime $ M_2 $.

For $ b_1 > b_{c1} $, the photon’s motion is confined to the $ M_1 $ spacetime. The turning point in $ M_1 $ corresponds to the smallest positive real root of $ G_1(x_1) = 0 $, which is denoted as $ x_{1,\text{min}} $. According to Eq. (25), the total change in the azimuthal angle in spacetime $ M_1 $ can be expressed as

With $ Zb_{c2} < b_1 < b_{c1} $, the path of the photon is divided into two distinct portions. The deflection angle of the photon's trajectory in spacetime $ M_1 $ is calculated as

The turning point of the photon trajectory in spacetime $ M_2 $ is located at $ x_{2,\text{max}} $, corresponding to the largest positive real root of $ G_2(x_2) = 0 $. The deflection angle for the photon trajectory in spacetime $ M_2 $ is calculated as

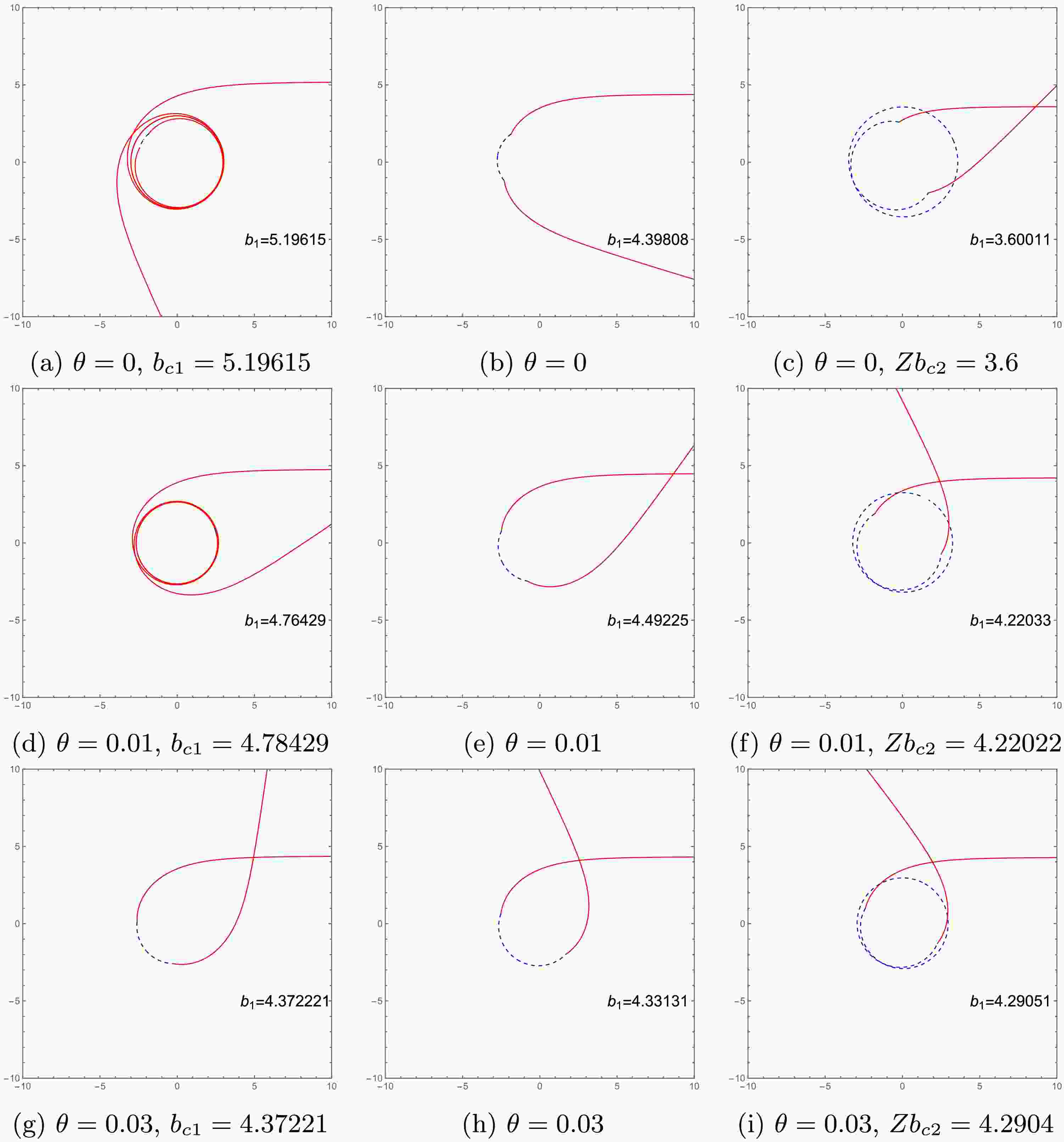
Fig. 2 depicts the trajectories of light rays around the ATW with higher-order non-commutative corrections. The simulations show that for photons emitted from infinity in spacetime $ M_1 $, when the impact parameter $ b_1 $ decreases while remaining within the range $ Zb_{c2} < b_1 < b_{c1} $, the resulting photon trajectories exhibit increased lengths spacetime $ M_2 $. From the left (Figs. 2a, 2d, 2g) and right (Figs. 2c, 2f, 2i) panels of Fig. 2, we observe that increasing the non-commutative parameter causes $ b_{c1} $ to decrease and $ Zb_{c2} $ to increase. This change ultimately causes the range of $ b_1 $ to gradually shrink.

Figure 2.  (color online) The figure shows photon trajectories within a certain impact parameter range ($ Zb_{c2} < b_1 < b_{c1} $) around the ATW with higher-order non-commutative corrections. Red and blue curves correspond to the light ray trajectories in $ M_1 $ and $ M_2 $, respectively.

In this spacetime, we consider a set-up consisting of a static observer and a thin accretion disk located in spacetime $ M_1 $. We assume that the thin accretion disk is situated in the equatorial plane of $ M_1 $, and that the observer is at the north pole of spacetime $ M_1 $. In order to obtain the optical appearance of the ATW with higher-order non-commutative corrections via ray-tracing techniques, we define the azimuthal change of a photon near the ATW as the orbital number. Therefore, the orbital number can be defined as

where $ n_2 $ and $ n_3 $ are additional orbit functions.

Based on the classification of light trajectories around BHs proposed by Gralla [9], we can divide light rays into three categories based on the number of intersections between the light ray and the accretion disk.

(1) Direct emission ($ n < 3/4 $): The light ray falls on the front side of the accretion disk and intersects the equatorial plane only once;

(2) Lensing ring ($ 3/4 < n < 5/4 $): The light ray falls on the back side of the accretion disk and intersects the equatorial plane twice;

(3) Photon ring ($ n > 5/4 $): The light ray intersects the equatorial plane at least three times.

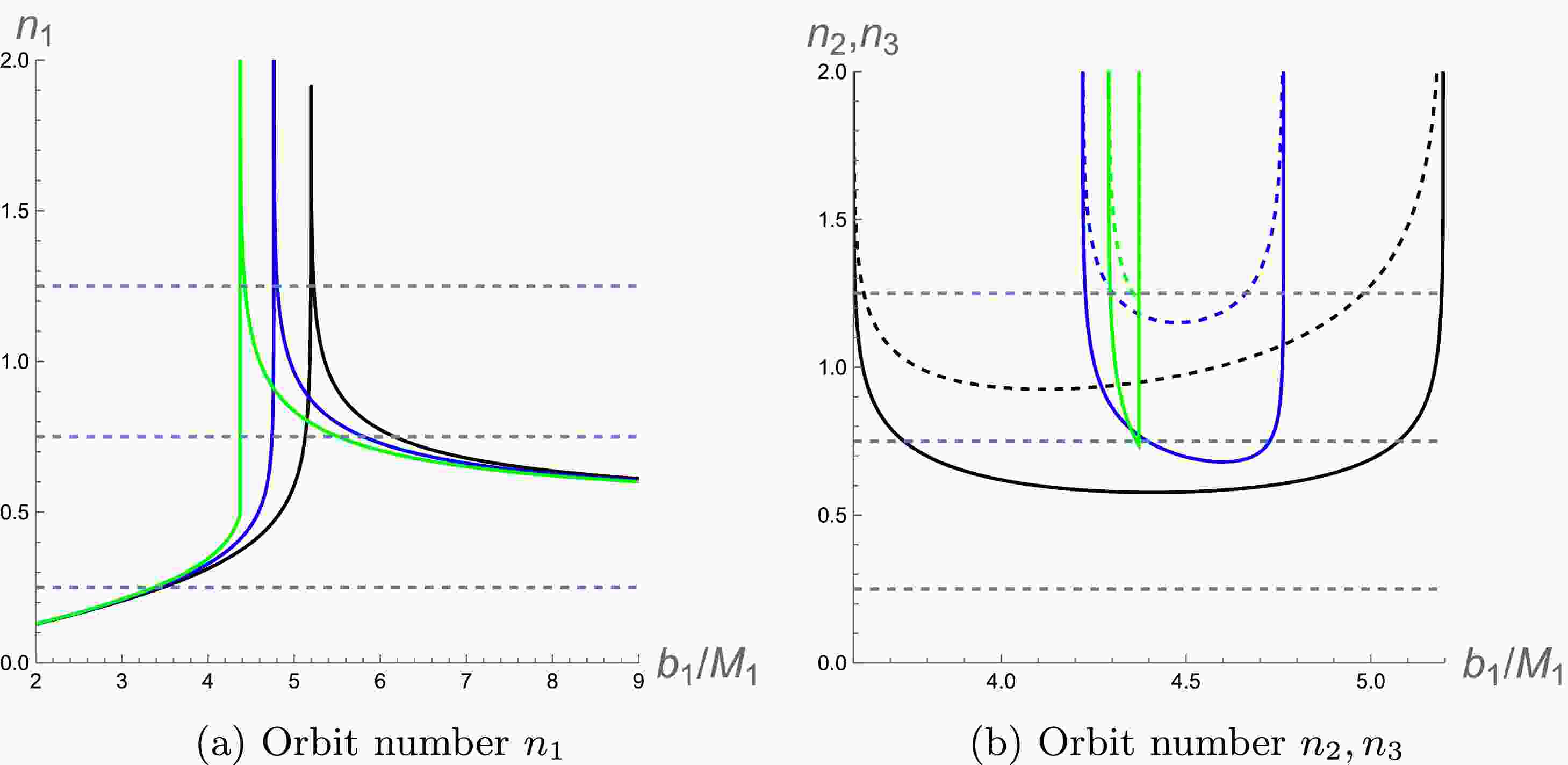
Fig. 3 illustrates the relationship between orbit numbers ($ n_1 $, $ n_2 $, $ n_3 $) and the impact parameter $ b_1 $ for the ATW with higher-order non-commutative corrections, considering various values of the non-commutativity parameter θ. Fig. 3a is a plot showing the relationship between the orbital number $ n_1 $ and the impact parameter $ b_1 $. In this situation, the photon motion is limited to the spacetime $ M_1 $, and its orbital behavior is equivalent to that of photons in a BH spacetime. Notably, as the non-commutative parameter increases, the value of $ b_1 $ corresponding to the peak of the orbital number $ n_1 $ decreases.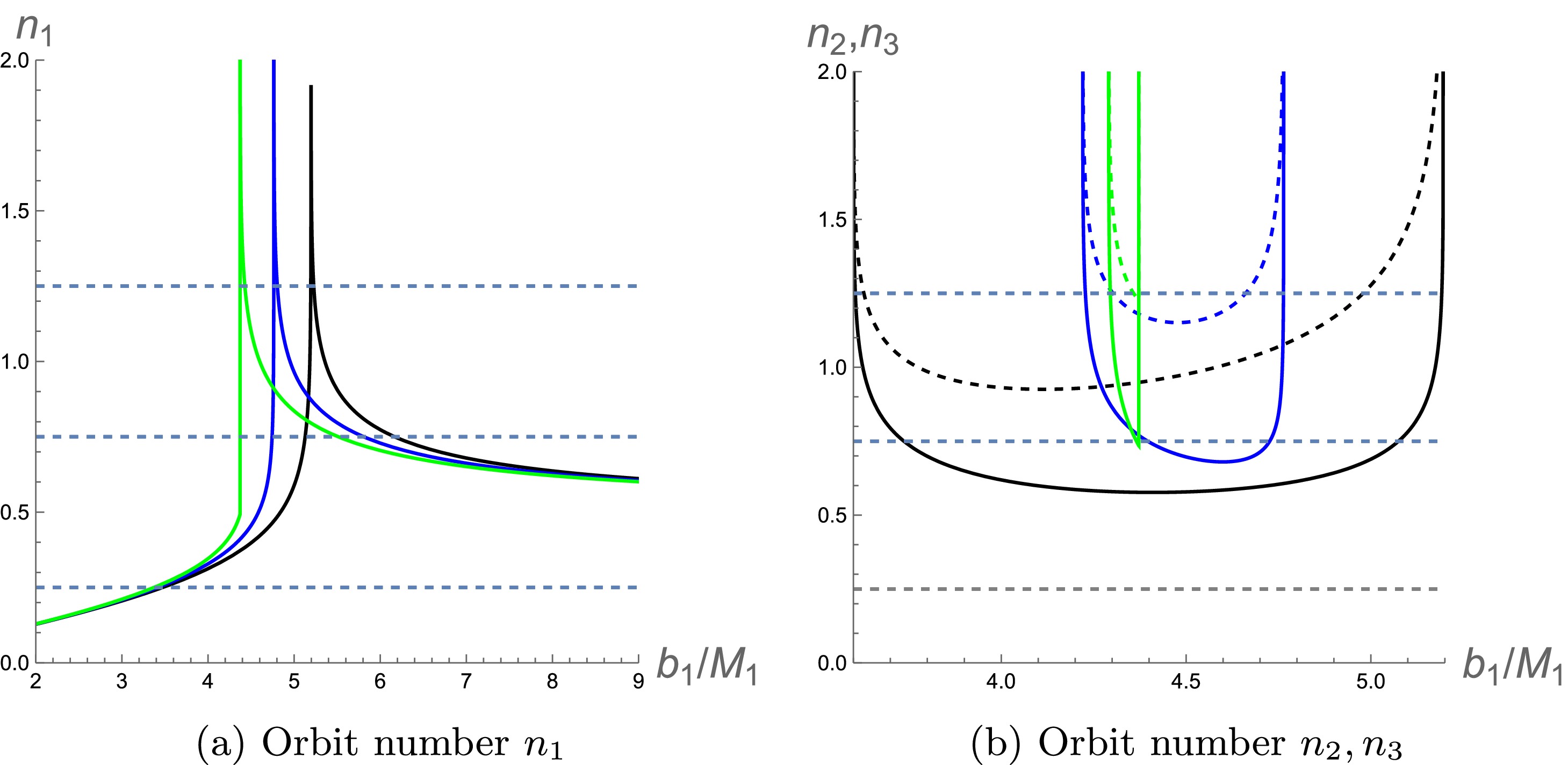

Figure 3.  (color online) For the orbit numbers of the ATW with higher-order non-commutative corrections, the black, blue, and green lines correspond to $ \theta = 0 $, $ \theta = 0.01 $, and $ \theta = 0.03 $, respectively. In the right-hand image, the solid lines represent $ n_2 $, and the dashed lines represent $ n_3 $.

Fig. 3b plots the relationship between the orbital numbers $ n_2 $ and $ n_3 $ and the impact parameter for varying non-commutative parameters θ. Solid and dashed lines represent the trends of $ n_2 $ and $ n_3 $, respectively. When photons travel from spacetime $ M_1 $ through the throat to $ M_2 $ and back to $ M_1 $, two distinct outcomes are possible. The first occurs when $ n_2 < 3/4 $ and $ n_3 > 3/4 $, where the photon falls into $ M_2 $, returns to $ M_1 $, and ultimately intersects with the back side of the accretion disk. The second occurs when $ n_2 < 5/4 $ and $ n_3 > 5/4 $, where the photon similarly falls into $ M_2 $ and returns to $ M_1 $, but ultimately intersects with the front side of the accretion disk. Moreover, it is apparent from Fig. 3b that the effective range of the impact parameter $ b_1 $ decreases as the non-commutative parameter θ increases. This result agrees with the analysis shown in Table 1 and Fig. 2. In addition, the U-shaped structures corresponding to $n_2$ and $n_3$ become narrower as the parameter θ increases. This is because the noncommutative correction alters the spacetime structure, causing the peaks of the effective potential in the two regions to move closer together, as shown in Fig. 1. As a result, the range of impact parameters allowing photons to return to region $M_1$ after crossing the throat becomes smaller, which means only fewer photons can return.

Each time a light ray passes through the thin disk, it obtain the additional luminosity from it. Therefore, the observed intensity received by an observer at infinity is the total brightness that the light ray acquires from the thin disk. The emission intensity and frequency of the accretion disk are denoted as $ I_e $ and v, respectively, while the corresponding quantities observed by a static observer are represented as $ I_o $ and $ v' = \sqrt{f(r)v} $. According to Liouville's theorem, $ I/v^3 $ is conserved along a light ray. Therefore, we have the following relationship

Based on the Eq. (32), we can express the observed specific intensity as

Thus, the observed intensity arising from a single intersection is

here, $ I_{\text{emv}} = \int I_e \, dv $ represents the total emitted intensity of the accretion disk. Consequently, the total observed intensity is

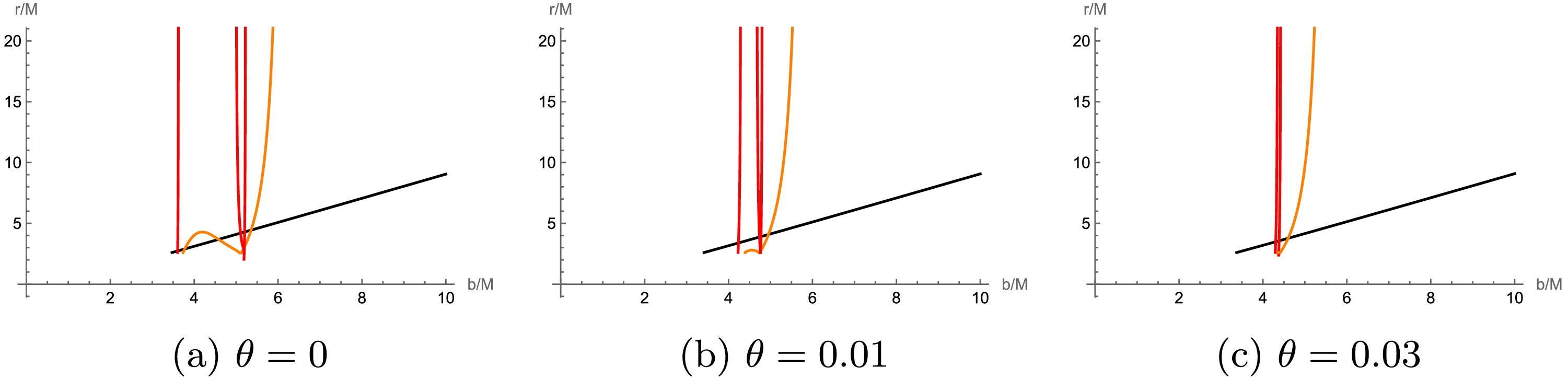
In the above equation, the term of $ r_n(b_1) $ is transfer function, which corresponds to the radial coordinate of the n-th intersection point of a light ray, with impact parameter $ b_1 $ and the accretion disk. The slope of the transfer function, $ dr/db_1 $ [9], represents the rate of change in the radial coordinate with respect to the impact parameter and is commonly referred to as the demagnification factor.

Fig. 4 shows the curves of the transfer function $ r_n(b_1) $ as a function of the impact parameter $ b_1 $ for different non-commutative parameters θ. Here, the first transfer function corresponds to the “direct image” of the accretion disk (represented by the black line in Fig. 4). In fact, it essentially reflects the redshift effect of the source profile at the minimum demagnification factor. The second transfer function describes a highly demagnified image of the back side of the accretion disk, known as the “lensing ring” because of its significant demagnification factor (represented by the orange line in Fig. 4). The third transfer function, on the other hand, presents an extremely demagnified image of the front side of the accretion disk, which possesses the largest demagnification factor and is called the “photon ring” (represented by the red line in Fig. 4). It is worth note that for the ATW with higher-order non-commutative corrections (as exemplified by Fig. 4b), when the impact parameter satisfies $ Zb_{c2} < b_1 < b_{c1} $, its new second transfer function is an irregular curve connecting to the lower end of the asymptote. Furthermore, there are two new third transfer functions within this impact parameter range, a finding that differs from the predictions for BHs. However, when the non-commutative parameter increases to $ \theta = 0.03 $ (as shown in Fig. 4c), only a new third transfer function exists. In particular, the results of the numerical analysis from Fig. 4 indicate that the demagnification factor of the new second transfer function increases with the non-commutative parameter θ.

Figure 4.  (color online) The first (black lines), second (orange lines), and third (red lines) transfer functions of the ATW with higher-order non-commutative corrections for different non-commutative parameters θ.

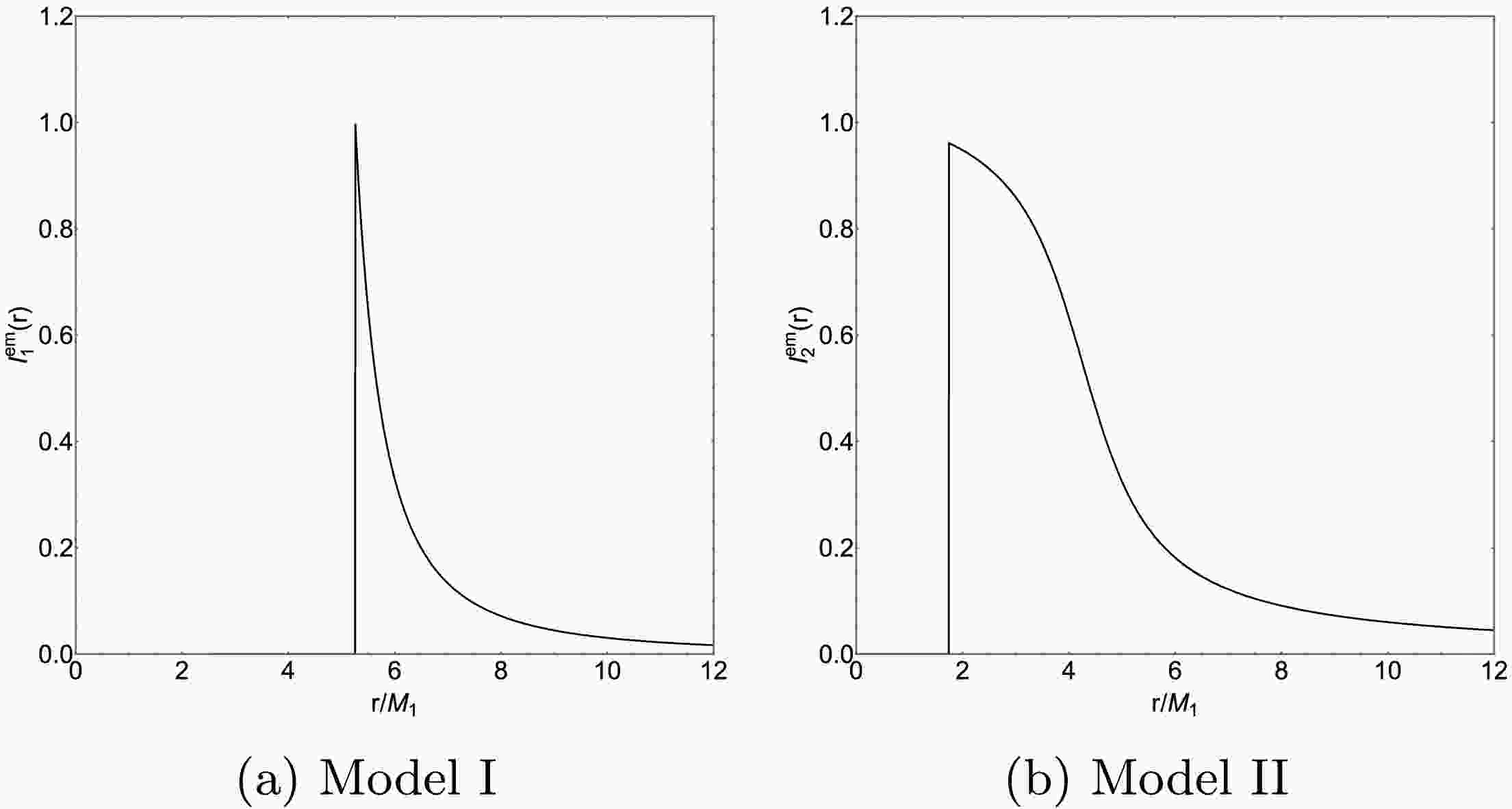
To analyze the optical appearance of the ATW with higher-order non-commutative corrections, we consider two typical emission models for thin accretion disks. Considering that the emission from a thin accretion disk can be reasonably approximated by a Gaussian function, we assume that the radiation process of the accretion disk ceases when the radius is smaller than the innermost stable circular orbit radius ($ r_{isco} $). Thus, the radiation function for emission model I ¹ can be expressed as [49]

where the innermost stable circular orbit radius, $ r_{isco} $, is expressed as [89]

In Fig. 5a, we plot the distribution of radiation intensity as a function of the radial coordinate, based on the theoretical framework of emission model I. We now turn our attention to emission model II. To distinguish it from emission model I, we consider emission model II with a smoother decay of the radiation function. Thus, the radiation function for emission model II can be expressed as

Figure 5.  The emission models.

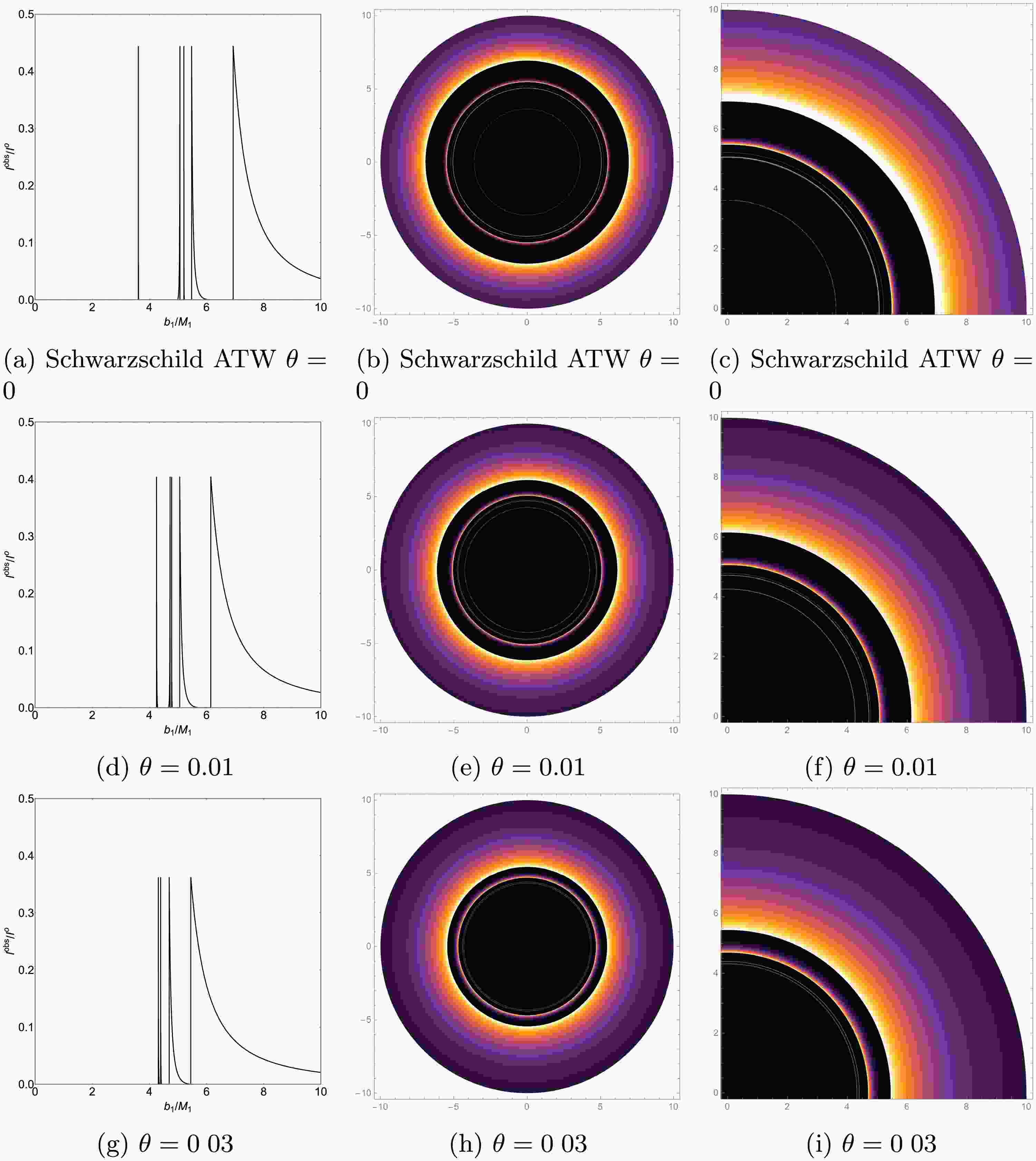
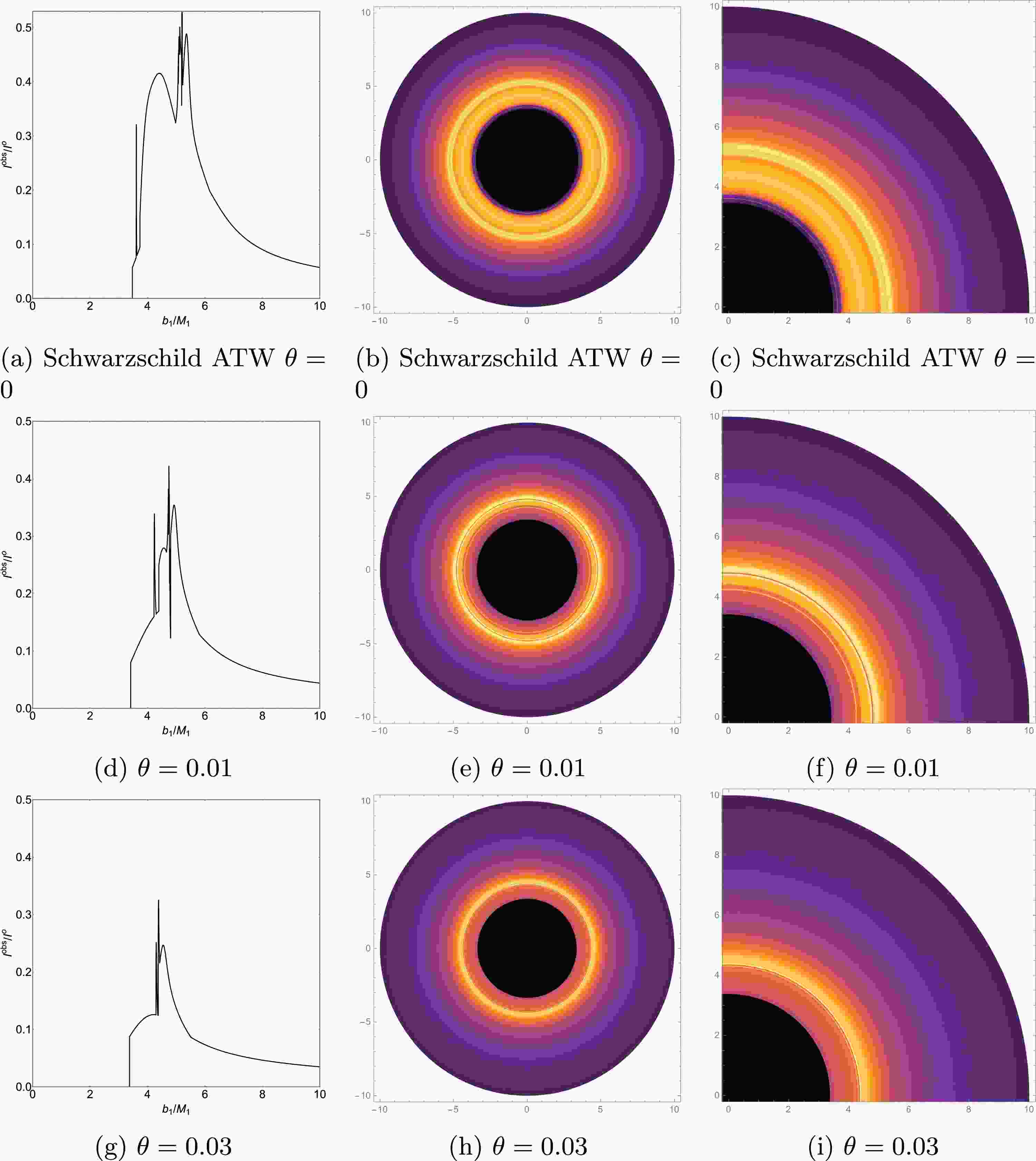
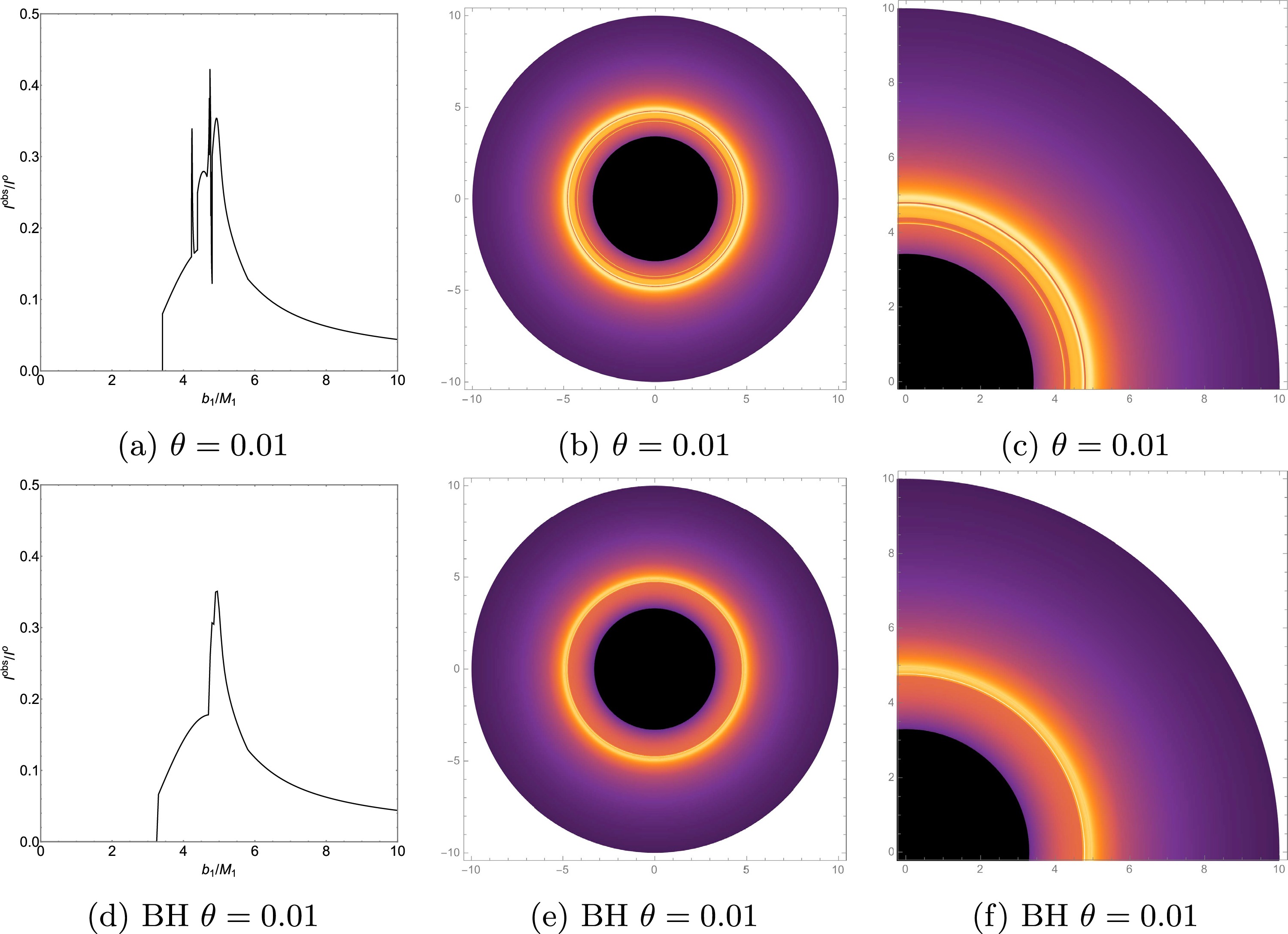
where $ r_h $ is the event horizon radius and $ r_p $ is the photon sphere radius. Notably, emission model II does not emit radiation within the event horizon. Fig. 5b clearly illustrates the radiation intensity distribution function for this emission model.

Using the radiation functions of emission models I and II, we numerically simulated the optical observational results of ATWs with higher-order non-commutative corrections for different values of the non-commutative parameter θ. We present their observational intensity, density plots, and local density plots in Figs. 6 and 7.

Figure 6.  (color online) Emission Model I - Observed intensities (the left panel), density plots (the middle panel), and local density plots (the right panel).

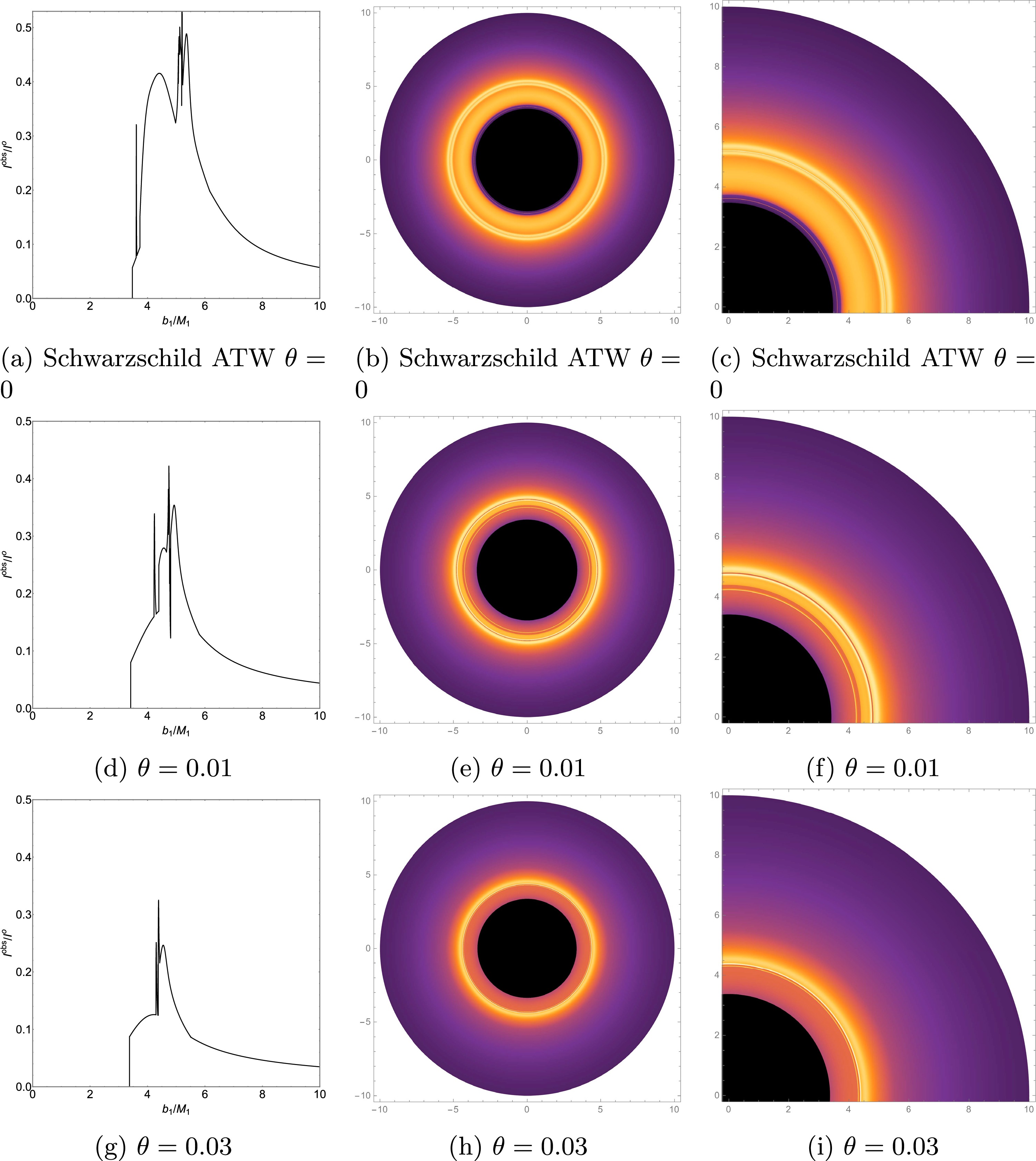
Figure 7.  (color online) Emission Model II - Observed intensities (the left panel), density plots (the middle panel), and local density plots (the right panel).

For the ATW with higher-order non-commutative corrections, using Fig. 6d as an example, for $ \theta = 0.01 $, we can clearly observe two extra photon rings. These extra photon rings are absent in BH spacetimes. The figure clearly shows the distinct regions associated with direct emission, the lensing ring, and the photon ring. In Fig. 6d, there are five peaks from left to right, corresponding in sequence to three photon rings, the lensing ring, and direct emission. Figs. 6d and 6g show that, with other parameters constant, increasing the non-commutative parameter θ decreases the size of the third photon ring, the lensing ring, and the directly emitted region. Furthermore, the study indicates that as the value of θ increases, the radius of the innermost extra photon ring increases, while the radius of the second extra photon ring decreases, resulting in reduction of the spacing between the two extra photon rings. However, for $ \theta = 0.03 $, the ATW optical observational image reveals the presence of only one extra photon ring. This phenomenon is more intuitively and clearly demonstrated in the local density plots in Figs. 6f and 6i. This phenomenon is in complete agreement with the trend of $ b_{ci} $ as a function of θ shown in Table. 1. By comparing the observational results of the Schwarzschild ATW (Fig. 6a) with those of the ATW with higher-order non-commutative corrections (Fig. 6d), a significant difference in the photon ring distribution can be found. Specifically, for the ATW with higher-order non-commutative corrections, the radius of the innermost extra photon ring is larger than that of the Schwarzschild ATW, while the radius of the second extra photon ring is smaller than that of the Schwarzschild ATW.

In Fig. 7, emission model II exhibits a multi-layered luminous ring structure formed by the superposition of the photon ring region, the lensing band region, and the direct emission region. Compared to emission model I, the observed intensity distribution curve for this model displays a more gradual and complex characteristic. 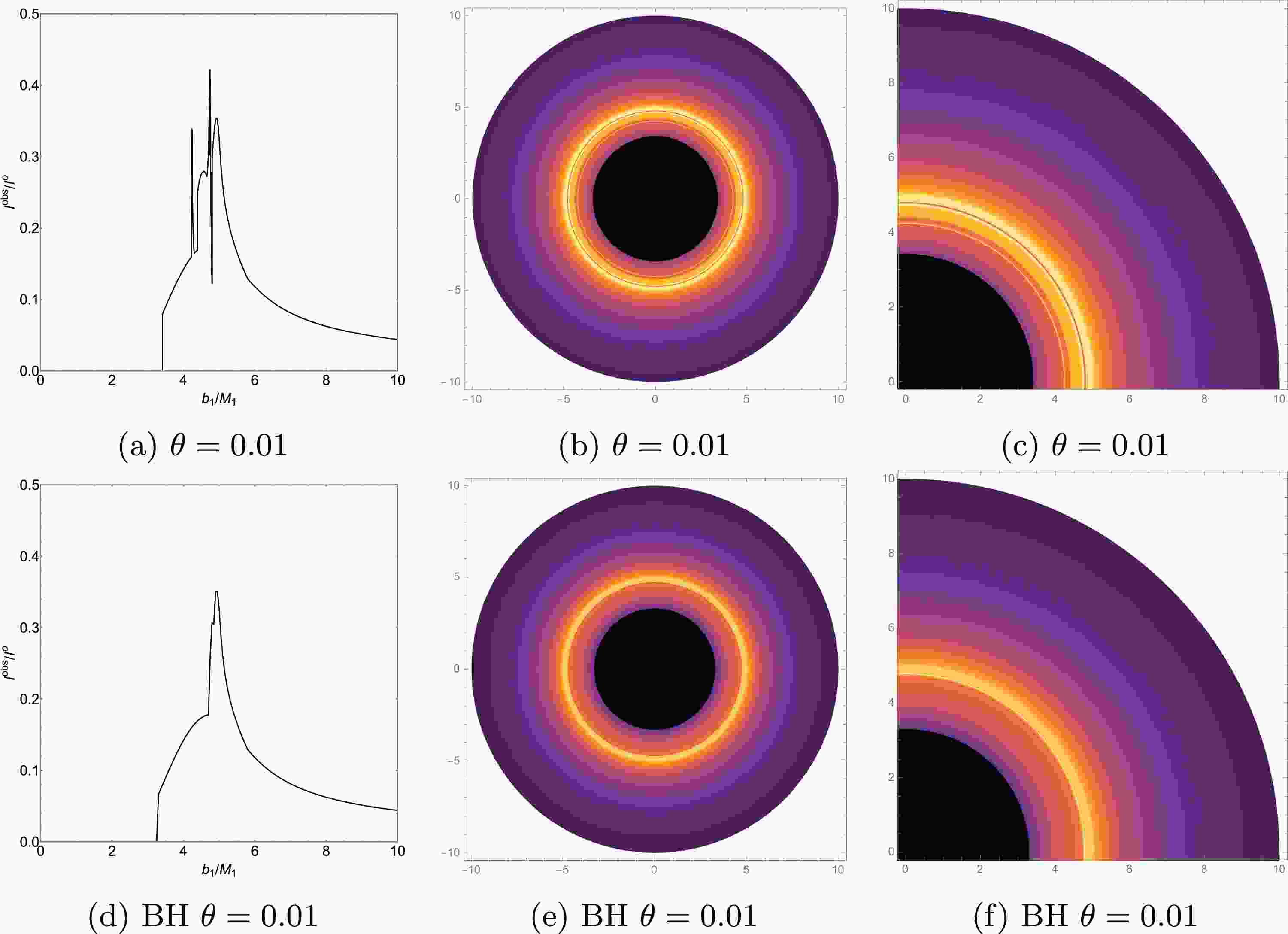The analysis reveals a new broad peak within the impact parameter range $ 4.22022 < b_1 < 4.76429 $ when $ \theta = 0.01 $. As shown in Fig. 7d, this feature originates from an extra lensing band produced by the new second transfer function. This phenomenon is more pronounced in Figs. 7e and 7f. Naturally, emission model II still exhibits two extra photon rings originating from the new third transfer function. By comparing the observational intensity curves of emission model II (Figs. 7d and 7g) reveals that as the non-commutative parameter θ increases, the extra lensing band of the ATW with higher-order non-commutative corrections narrows, and its corresponding observational intensity decreases. Figs. 7f and 7i more clearly demonstrate this phenomenon, revealing the influence of the non-commutative parameter on the optical observational characteristics of the ATW with higher-order non-commutative corrections. Compared to the Schwarzschild ATW in Fig. 7a, the ATW with higher-order non-commutative corrections under emission model II exhibits a narrower extra lensing band and a more distant first extra photon ring from the central black disk.

Next, to clearly distinguish the differences in optical observational characteristics between the ATW and BH with higher-order non-commutative corrections, this study systematically plotted and compared the observed intensity, density maps, and local density maps of both, based on the theoretical framework of emission model II (as shown in Fig. 8). The analysis of Figs. 8a and 8d highlights that the observed images of the ATW with higher-order non-commutative corrections are distinct from those of the BH with higher-order non-commutative corrections due to their more complex multi-ring structure and unique extra photon rings and lensing band features. This difference is particularly evident in Figs. 8c and 8f, further validating the fundamental distinction in optical observational features between the two. These results provide a reliable basis for effectively distinguishing between ATWs with higher-order non-commutative corrections, Schwarzschild ATWs, and BHs with higher-order non-commutative corrections in observations.

Figure 8.  (color online) Emission Model II - Observed intensities (the left panel), density plots (the middle panel), and local density plots (the right panel).

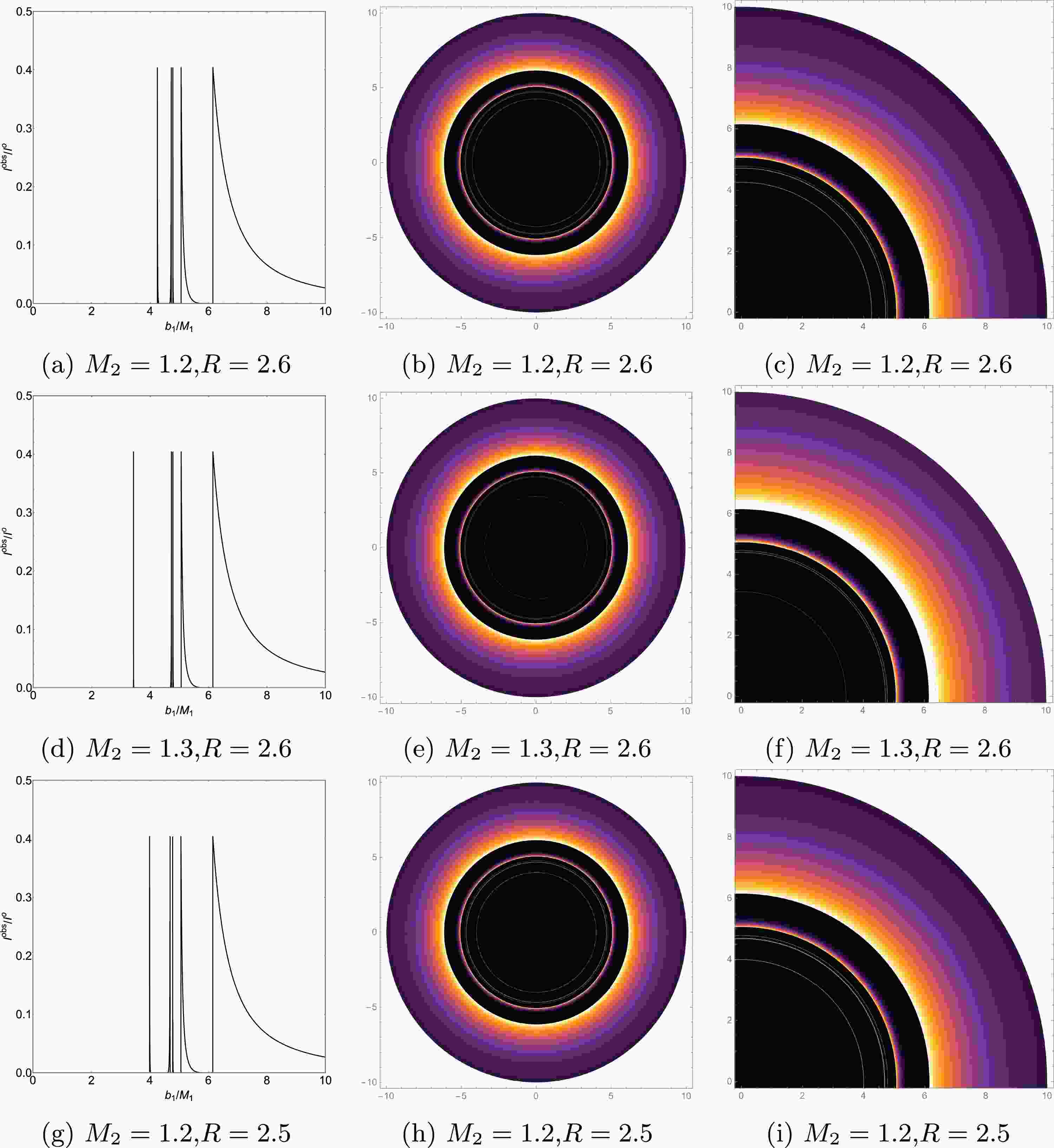
In this section, We will continue to examine the influence of changes in the mass ratio ($ {M_2}/{M_1} $) and throat radius R on optical features of the ATWs.

To investigate the impact of the mass ratio on the optical observational features of the ATW, this study controlled spacetime mass ratio by fixing the mass parameter $ M_1 = 1 $ and varying the mass parameter $ M_2 $. We set $ \theta = 0.01 $ and $ M_1 = 1 $ to ensure the reliability of the observational results under different mass ratios ($ {M_2}/{M_1} $). Comparing Figs. 9a and 9d reveals that as the mass ratio increases, the radius of the innermost extra photon ring decreases, while the radius of the second extra photon ring remains essentially unchanged. This phenomenon leads to a gradual widening of the spacing between the two extra photon rings, a trend that is particularly evident in Figs. 9c and 9f.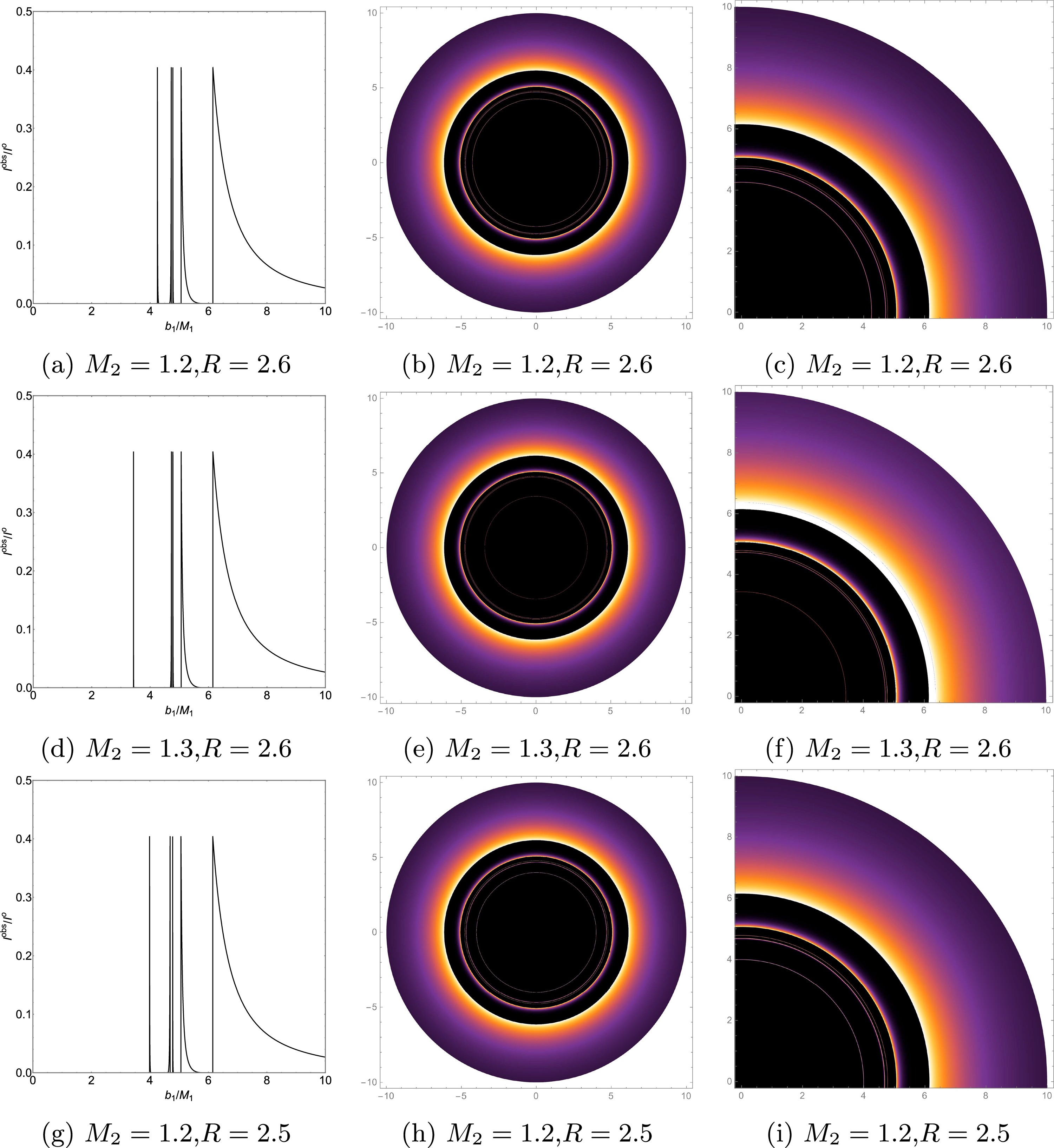

Figure 9.  (color online) Emission Model I - Observed intensities (the left panel), density plots (the middle panel), and local density plots (the right panel) for $ \theta=0.01$.

Keeping $ \theta = 0.01 $ and $ M_2 = 1.2 $, we now vary the throat radius R. Comparing Figs. 9a and 9g reveals that as the throat radius R increases, the radius of the innermost extra photon ring exhibits a significant increasing trend, whereas the radius of the second extra photon ring increases only slightly, leading to a gradual decrease in the spacing between the two extra photon rings. This trend is more clearly demonstrated in Figs. 9c and 9i. The analysis results presented in this section indicate that the mass ratio and parameter R selectively influence the two extra photon rings, primarily affecting the geometric properties of the innermost extra photon ring, while having a weaker impact on the second extra photon ring. It is noteworthy that the sizes of the third photon ring, the lensing ring, and the directly emitted region remain unchanged with variations in the mass ratio and throat radius.

This study investigates the optical observational characteristics of the ATW with higher-order non-commutative corrections. Using ray-tracing techniques, we investigated the influence of the non-commutative parameter θ, mass ratio ($ {M_2}/{M_1} $) and throat radius R on the optical appearance of the ATWs, with the corresponding optical observation images generated.

First, from Fig. 1, within a single spacetime, the effective potential peak gradually increases with the non-commutative parameter θ. The difference between the peak values in spacetimes $ M_1 $ and $ M_2 $ gradually decreases. In Table 1, as θ increases, both critical impact parameters $ b_{c1} $ and $ b_{c2} $ decrease. We employ a ray-tracing method to analyze the photon trajectory behavior of ATWs with higher-order non-commutative corrections. Based on the definition of the impact parameter $ b_1 $, we can discuss in detail the motion behavior of light rays in this spacetime. Especially, when the impact parameter $ b_1 $ is in the range $ Zb_{c2} < b_1 < b_{c1} $, photons originating from the $ M_1 $ spacetime can pass through the throat into the $ M_2 $ spacetime and then return to the $ M_1 $ spacetime. In Fig. 2, we found that within this range, as the impact parameter $ b_1 $ decreases, the photon trajectories generated within spacetime $ M_2 $ become longer. Furthermore, the increase of θ decreases $ b_{c1} $ and increases $ Zb_{c2} $. The results in Fig. 3 indicate that increasing the non-commutative parameter θ leads to a decrease in the $ b_1 $ value corresponding to the peaks of the orbital number $ n_1 $, and a shrinking of the effective range of the impact parameter $ b_1 $ corresponding to orbital numbers $ n_2 $ and $ n_3 $.

Next, we use the transfer function to distinguish the types of light rays near the ATW spacetime. Fig. 4 shows the variation of the transfer function $ r_n $ with respect to the impact parameter $ b_1 $. The analysis reveals that new second and third transfer functions emerge in the ATW with higher-order non-commutative corrections within the impact parameter range $ Zb_{c2} < b_1 < b_{c1} $. These functions correspond to the extra lensing band and the extra photon ring, respectively. In addition, we considered two emission models for the accretion disk. One scenario features radiation emerging from $ r_{isco} $ followed by a steep decay, and another starting at $ r_h $ and undergoing a relatively slow decay. Based on these two models, we obtained optical appearance images of ATWs with higher-order non-commutative corrections. In Fig. 6, the analysis based on emission model I reveals that as θ increases, the radius of the innermost extra photon ring increases, while the radius of the second extra photon ring decreases, resulting in a gradual reduction in the spacing between them. When $ \theta = 0.03 $, only one extra photon ring remains, which implies that the observed features of ATWs seem to become more and more visually similar to a BH as θ increased. Fig. 7 shows that, for emission model II, an extra lensing band emerges within the range $ Zb_{c2} < b_1 < b_{c1} $ and narrows with increasing θ. These findings offer new observational evidence into the optical characteristics of higher-order corrected ATW in a non-commutative geometry. Compared to a Schwarzschild ATW, an ATW with higher-order non-commutative corrections exhibits an innermost extra photon ring farther from the central black disk, a closer second extra photon ring, and a narrower extra lensing band. Furthermore, a comparative analysis of the optical images of the BH and ATW with higher-order non-commutative corrections reveals that only the latter exhibits a unique multi-ring structure. This difference provides a new observational basis for distinguishing between the two types of non-commutative spacetime structures.

In addition, we also investigate the impact of varying mass ratio ($ M_2/M_1 $) and the throat radius R on the optical observations of the ATW. The analysis indicates that increasing the mass ratio reduces the radius of the innermost extra photon ring, whereas increasing R increases the radius of the innermost extra photon ring. Notably, the variations in mass ratio and throat radius have a weaker impact on the position of the second extra photon ring, and no impact on the size of the third photon ring, the lensing ring, and the directly emitted region. These observational results of ATWs offer important theoretical support for distinguishing BHs higher-order non-commutative corrections, Schwarzschild ATWs and ATWs with higher-order non-commutative corrections in future astronomical observations, potentially providing deeper insights into the effects of quantum gravity.