Ab initio study of shell evolution in neutron-rich Si, S, Ar, and Ca isotopes near N = 32 and 34

The understanding of nuclear structure is fundamentally anchored in magic numbers or shell closures [1, 2]. The advent of rare isotope beams (RIB) has opened new avenues for studying nuclei with extreme neutron-to-proton ($ N/Z $) ratios, where well-established shell structures are significantly modified [3−5]. This shell evolution leads to the disappearance of traditional magic numbers, such as the $ N=8 $, 20, and 28 islands of inversion (IOIs) in the vicinity of $ ^{12} {\rm{Be}}$ [6], $ ^{32} {\rm{Mg}}$ [7], and $ ^{42} {\rm{Si}}$ [8], respectively. On the other hand, new magic numbers have been observed in neutron-rich nuclei, including $ N=14 $, 16, 32, and 34 [9−18]. These discoveries have not only profoundly advanced our understanding of nuclear physics but also challenged theoretical models, stimulating ongoing research into the shell evolution in exotic nuclei with extreme $ N/Z $ ratios.

In the calcium isotopic chain, both $ ^{40} {\rm{Ca}}$ and $ ^{48} {\rm{Ca}}$ are traditionally recognized as doubly magic nuclei. Recent experimental studies have further revealed that $ ^{36} {\rm{Ca}}$ [10], $ ^{52} {\rm{Ca}}$ [13, 14], and $ ^{54} {\rm{Ca}}$ [15, 18] also exhibit doubly magic characteristics, introducing new magic numbers at $ N=16 $, $ N=32 $, and $ N=34 $, respectively. As protons are removed from $ ^{40} {\rm{Ca}}$ down to $ ^{34} {\rm{Si}}$, the $ N=20 $ shell closure remains robust [19−21]. However, with the further removal of protons, the $ N=20 $ magic number disappears, as evidenced by the onset of deformation in $ ^{32} {\rm{Mg}}$, which is known as the $ N=20 $ IOI [7]. For the $ N=28 $ isotones, the magic number persists up to $ ^{56} {\rm{Ni}}$ when protons are added above $ ^{48} {\rm{Ca}}$ [4, 5]. Conversely, removing protons from $ ^{48} {\rm{Ca}}$ results in a substantial reduction in the excitation energy of the first $ 2^+ $ excited states ($ E(2_1^+) $), indicating that the $ N=28 $ shell closure present in $ ^{48} {\rm{Ca}}$ disappears in nuclei around $ ^{42} {\rm{Si}}$, forming the $ N=28 $ IOI [8]. Moreover, the strength of the $ N=32 $ sub-shell gradually diminishes as protons are added starting from $ ^{52} {\rm{Ca}}$, disappearing in $ ^{58} $Fe and heavier isotones [22−26]. Similarly, as protons are removed from $ ^{52} {\rm{Ca}}$, the $ N=32 $ sub-shell weakens in $ ^{50} {\rm{Ar}}$ [27, 28]. Additionally, the $ N=34 $ sub-shell has been observed only in $ ^{54} {\rm{Ca}}$ and $ ^{52} {\rm{Ar}}$ so far [15, 18, 28], and it has been confirmed to disappear in isotones heavier than $ ^{55} {\rm{Sc}}$ [26, 29, 30]. Meanwhile, experimental studies on the odd-mass P, Cl, and K isotopes suggest that the $ Z=16 $ sub-shell disappears in isotopes near $ N=28 $ [31−37], while the $ Z=16 $ shell gap is enhanced from $ ^{47} {\rm{K}}$ to $ ^{53} {\rm{K}}$ [31, 38]. On the other hand, the $ Z=14 $ sub-shell is present in $ ^{34} {\rm{Si}}$ [19−21] and $ ^{42} {\rm{Si}}$ [39], but experimental evidence for the $ Z=14 $ sub-shell in heavier Si isotopes is still lacking. Therefore, the evolution of the proton $ Z=14 $ and $ Z=16 $, as well as the neutron $ N=32 $ and $ N=34 $ sub-shells, in the neutron-rich Ar, S, and Si isotopes remains an intriguing open question. In particular, the enhancement of the $ N=34 $ magicity for isotones with smaller Z, as suggested theoretically in Ref. [40, 41], has been confirmed in $ ^{52} {\rm{Ar}}$ [28], with $ ^{48} {\rm{Si}}$ predicted to be a doubly magic nucleus [28, 40, 42].

Over the past decades, ab initio calculations, based on high-resolution interactions derived from the chiral effective field theory (χEFT), have made great progress [43−50], offering a comprehensive framework for understanding the properties of shell structures in exotic nuclei. The shell evolution of calcium isotopes and isotopes around calcium has attracted extensive theoretical studies, including mean-field methods [42, 51, 52], shell model (SM) [5, 30, 40, 53], Gamow SM [54], coupled-cluster theory [55], self-consistent Green’s function [56], and in-medium similarity renormalization group (IMSRG) [22, 25, 26, 28, 30, 41, 57]. However, for the neutron-rich $ N=32 $ and $ N=34 $ isotones, especially for $ ^{48} {\rm{Si}}$, precise and systematic ab initio calculations and evaluations are still required. In this paper, we performed systematical calculations for the shell evolution in the neutron-rich nuclei below Ca isotopes, using the valence-space IMSRG (VS-IMSRG) with nucleon-nucleon (NN) and three-nucleon (3N) forces derived from χEFT.

The paper is organized as follows: First, we provide a brief introduction to the framework of the VS-IMSRG. This is followed by $ E(2_1^+) $ calculations for neutron-rich Si, S, Ar, and Ca isotopes. Next, we present the effective single-particle energies (ESPE) for both neutrons and protons, followed by a discussion of the shell evolution. Subsequently, the low-lying states of neutron-rich Si, S, and Ar isotopes are examined. Finally, a summary is provided.

We start with the intrinsic A-body Hamiltonian

where $ {\boldsymbol{p}} $ is the nucleon momentum in the laboratory, m implies the nucleon mass, $ v^{NN} $ and $ v^{3N} $ corresponds to the NN and 3N interactions, respectively. In this work, we employ the EM1.8/2.0 interaction [59, 60], which reproduces ground-state (g.s.) energies of nuclei up to $ ^{132} {\rm{Sn}}$ remarkably well [61, 62]. Additionally, the NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}}_{\rm{lnl}} $ interaction [63] is also used, which shows a good description of g.s. energies up to nickel isotopes [63]. For NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}}_{\rm{lnl}} $, a large SRG scale of $ \lambda = $ 2.6 fm^-1 is adopted to neglect the induced 3N forces for the NN part, and the bare 3N interaction is employed. For both interactions, we take the harmonic-oscillator basis at $ \hbar \omega =16 $ MeV with $ e_{\rm{max}}= 2n + l = 14 $ and $ E_{3{\rm{max}}} = 14 $, which has been checked to be large enough for convergence, as presented in our previous work [64].

The Hamiltonian in Eq. (1) is rewritten as normal-ordered operators with respect to the Hartree-Fock reference state,

where $ E_0 $, f, Γ, and W correspond to the normal-ordered zero-, one-, two-, and three-body terms, respectively. The residual normal-ordered three-body term W is neglected in practical calculations and the contribution of $ 3N $ force can be effectively captured at the normal-ordered two-body level [65].

The normal-ordered Hamiltonian is then decoupled from the large Hilbert space to a small valence space by VS-IMSRG. This decoupling is achieved by solving the flow equation [46, 49, 50],

with an anti-Hermitian generator

In the present work, valence protons in the $ sd $ shell and neutrons in the $ pf $ shell above $ ^{28} $O inner core are adopted. In practical calculations, we use the Magnus formalism [66] of VS-IMSRG, truncating all operators at the two-body level while capturing the effects of the 3N force through ensemble normal ordering (ENO) [50], to generate consistently valence-space effective Hamiltonians, where the imsrg++ code is employed [67]. Subsequently, the nuclear observables are obtained using the large-scale SM code, KSHELL [68].

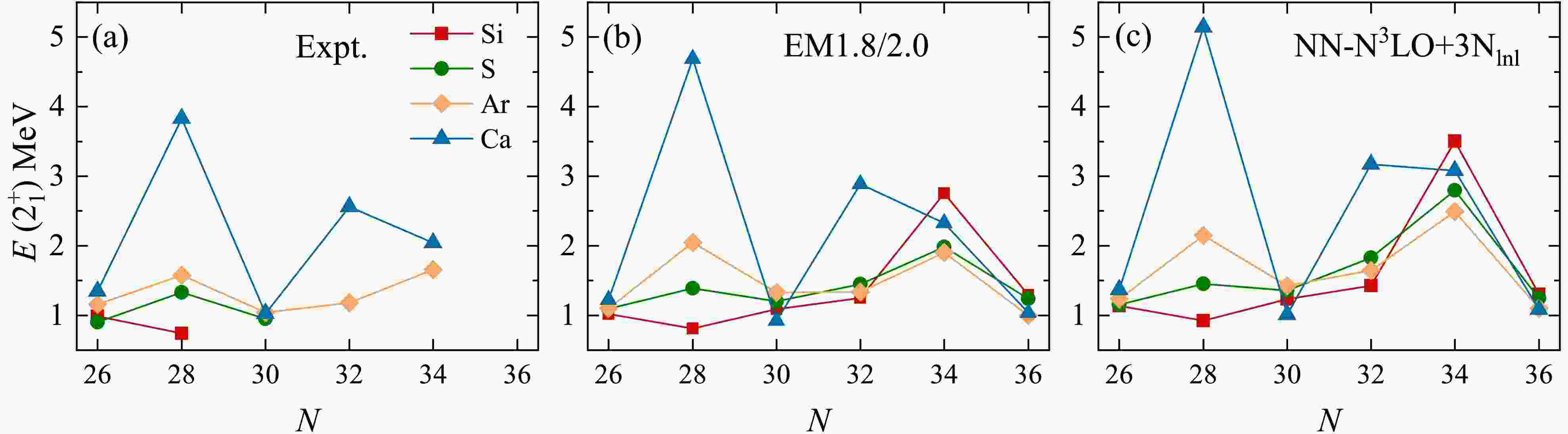
In the present work, we systematically investigate shell evolution at $ N=32 $ and $ N=34 $ in neutron-rich isotopes below Ca using the ab initio VS-IMSRG method. The $ E(2^+_1) $ in even-even nuclei, provides an important observable for characterizing shell structures, with a high $ E(2^+_1) $ value typically attributed to a large shell gap. Figure 1 represents the calculated $ E(2^+_1) $ values for even-even isotopes of Ca, Ar, Si, and S, compared to available experimental data. Our VS-IMSRG calculations with the EM1.8/2.0 and NN-$ {\rm{N}}^3{\rm{LO}}+3{\rm{N}}_{{\rm{lnl}}} $ interactions reasonably reproduce the measured $ E(2^+_1) $ values in these isotopes, although an overall overestimation is observed. To evaluate the uncertainty in the model space, we also performed VS-IMSRG calculations within the $ e_{\rm{max}}= 12 $, $ E_{3{\rm{max}}} = 12 $ model space. The difference in the calculated $ E(2^+_1) $ values is less than 200 keV compared to the results obtained with $ e_{\rm{max}}= 14 $, $ E_{3{\rm{max}}} = 14 $. However, the calculated $ E(2^+_1) $ for $ ^{54} {\rm{Ca}}$, using the EM1.8/2.0 and NN-$ {\rm{N}}^3{\rm{LO}}+3{\rm{N}}_{{\rm{lnl}}} $ interactions, differs by about 500 keV, indicating a larger uncertainty due to the underlying nuclear forces. Nevertheless, the trends for the $ E(2^+_1) $ states of these nuclei calculated using both interactions are consistent.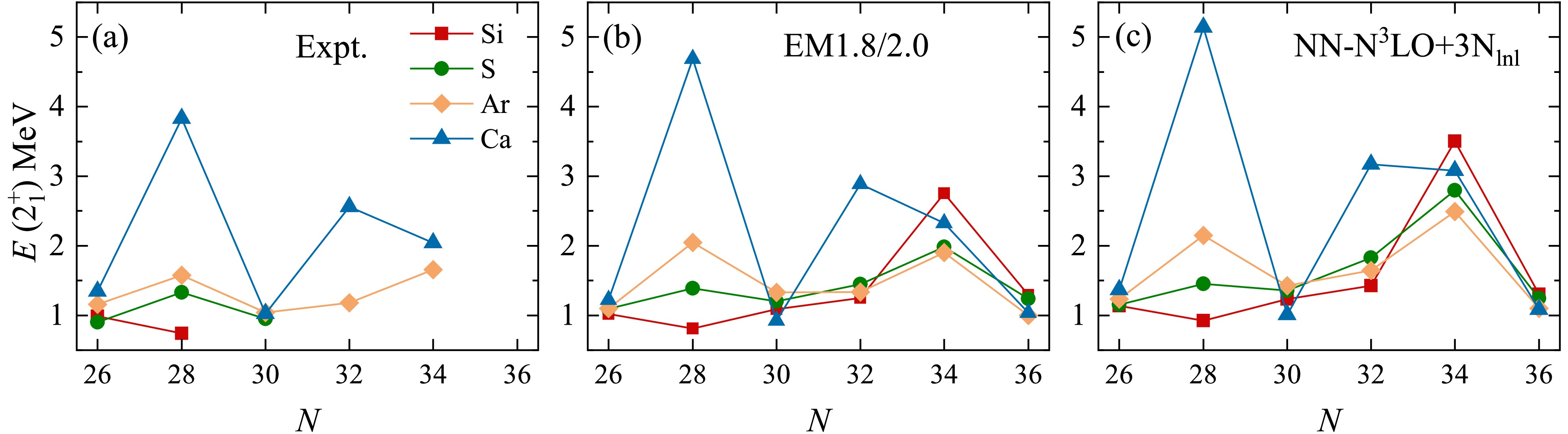

Figure 1.  (color online) $ E(2^+_1) $ values in Ca, Ar, S, and Si isotopes, calculated using ab initio VS-IMSRG based on the EM1.8/2.0 and NN-$ {\rm{N}}^3{\rm{LO}}+3{\rm{N}}_{{\rm{lnl}}} $ interactions, along with available experimental data [58].

When protons are removed from $ ^{48} {\rm{Ca}}$, the decreasing $ E(2^+_1) $ indicates the $ N=28 $ shell gap is shrinking and eventually disappears in $ ^{42} {\rm{Si}}$, which is well reproduced in our VS-IMSRG calculations, as discussed in our previous work [64]. For $ N=32 $, our results show that $ ^{52} {\rm{Ca}}$ clearly exhibits a sub-shell with a steep rise in $ E(2^+_1) $ compared to neighboring Ca isotopes, consistent with the experimental results [13]. In contrast, the calculated $ E(2_1^+) $ values for $ ^{50} {\rm{Ar}}$, $ ^{48} {\rm{S}}$, and $ ^{46} {\rm{Si}}$ are significantly reduced, much lower than that of $ ^{52} {\rm{Ca}}$. Furthermore, the calculated $ E(2_1^+) $ for $ ^{46} {\rm{Si}}$ is close to that of the nearby $ ^{44} {\rm{Si}}$, indicating the disappearance of the $ N=32 $ sub-shell in $ ^{46} {\rm{Si}}$. However, relativistic mean-field calculations [52] and large-scale SM studies [40] suggest that $ ^{46} {\rm{Si}}$ still exhibits a strong $ N=32 $ shell closure, which contrasts with our results. In Ref. [52], the relativistic mean field calculation gives a two proton shell gap $ \Delta_{2p} $ peak for $ ^{46} {\rm{Si}}$, associated with magic character, although it is slightly smaller than the peak for $ ^{52} {\rm{Ca}}$. However, the obtained isotopic shift $ \Delta E $ dose not support the magicity of $ ^{46} {\rm{Si}}$ in the relativistic mean field calculation [52]. In Ref. [40], SM calculations were performed with modifications to the phenomenological SDPF-MU interaction in order to reproduce existing experimental data. While this fit successfully reproduces the known experimental data, it may introduce greater uncertainty when predicting unknown nuclei, resulting in a relatively higher $ E(2^+_1) $ for $ ^{46} {\rm{Si}}$, which may similar to the situation of observed $ E(2_1^+) $ of $ ^{54} {\rm{Ca}}$ in Ref. [18].

The situation is different for $ N=34 $ isotones. The $ N=34 $ sub-shell has been experimentally observed in $ ^{54} {\rm{Ca}}$ [15, 18] and $ ^{52} {\rm{Ar}}$ [28], and it is predicted to be enhanced moving towards the more neutron-rich region [28, 40, 41]. Of particular interest are $ ^{50} {\rm{S}}$ and $ ^{48} {\rm{Si}}$, which may also exhibit double magicity. As shown in Fig. 1, the calculated $ E(2^+_1) $ of $ ^{48} {\rm{Si}}$ is even higher than that of $ ^{54} {\rm{Ca}}$, indicating that $ ^{48} {\rm{Si}}$ is a well-developed doubly magic nucleus, with shell strength comparable to those of observed doubly magic nuclei such as $ ^{52,54} {\rm{Ca}}$, and $ ^{78} {\rm{Ni}}$. Moreover, large-scale SM calculations based on the modified SDPF-MU interaction predict that the $ E(2_1^+) $ of $ ^{48} {\rm{Si}}$ is approximately 3 MeV [40], which is in good agreement with our calculations using the EM1.8/2.0 interaction, and smaller than the results obtained from the NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{\rm{lnl}} $ interaction. Notably, our previous works suggest that $ ^{48} {\rm{Si}}$ is a potential candidate for two-neutron halo [69]. For $ ^{50} {\rm{S}}$, a steep rise in $ E(2^+_1) $ is obtained from VS-IMSRG calculations using both interactions, indicating the persistence of the $ N=34 $ sub-shell. However, the $ E(2^+_1) $ of $ ^{50} {\rm{S}}$ calculated using the EM1.8/2.0 interaction is comparable to that of $ ^{52} {\rm{Ar}}$, whereas the calculations with the NN-$ {\rm{N}}^3{\rm{LO}}+3{\rm{N}}_{{\rm{lnl}}} $ interaction generally yield higher $ E(2^+_1) $ values, with the calculated $ E(2^+_1) $ of $ ^{50} {\rm{S}}$ being higher than that of $ ^{52} {\rm{Ar}}$. These discrepancies further raise doubts about the existence of the $ Z=16 $ sub-shell in $ ^{50} {\rm{S}}$, as discussed in detail in Fig. 3. Therefore, the properties of $ ^{50} {\rm{S}}$ and $ ^{48} {\rm{Si}}$ provide excellent test cases for ab initio methods and underlying nuclear forces, and future experiments are strongly encouraged. Recently, similar calculations have been done in Ref. [57] to discuss the shell evolution of $ N=32 $ and $ 34 $ sub-shells.

Figure 3.  (color online) The ESPEs of the proton $ \pi 0d_{5/2} $, $ \pi 1s_{1/2} $, and $ \pi 0d_{3/2} $ orbits in the Si and S isotopes, calculated by VS-IMSRG using the EM1.8/2.0 and NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{\rm{lnl}} $ interactions.

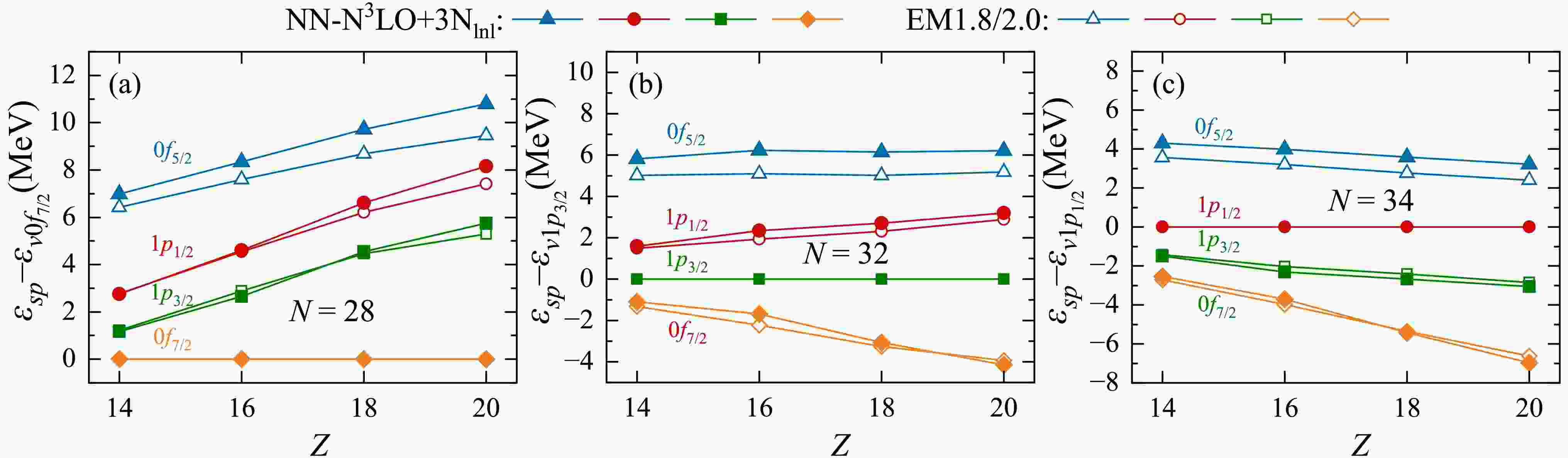
The ESPE offers a good reflection for the size of shell gaps [5, 70, 71]. In this paper, the ESPEs are calculated to gain further insight into the shell evolution in these exotic nuclei below Ca. First, the ESPEs of neutron single-particle states for $ N=28 $, $ N=32 $, and $ N=34 $ isotones are calculated and the results are presented in Fig. 2. For the $ N=28 $ isotones, it is clear that the $ N=28 $ shell gap rapidly diminishes with the removal of protons from $ ^{48} {\rm{Ca}}$, as shown in Fig. 2(a). These findings align with both theoretical and experimental investigations [8, 64], which demonstrate the collapse of the $ N=28 $ sub-shell in nuclei located below $ ^{48} {\rm{Ca}}$. Figure 2(b) shows the ESPEs relative to the neutron $ \nu1p_{3/2} $ orbital. Here, it is evident that the $ N=32 $ shell gap gradually decreases from approximately 3 MeV in $ ^{52} {\rm{Ca}}$, eventually disappearing in $ ^{46} {\rm{Si}}$, where the shell gap shrinks to about 1.5 MeV. Additionally, for the $ N = 32 $ isotones, as the proton number decreases, the neutron $ 0p0h $ (particle-hole) component across the $ N=32 $ subshell in the $ 0^+_1 $ state gradually decreases from about 85% in $ ^{52}\text{Ca} $ to about 20% in $ ^{46}\text{Si} $, with the $ 2p2h $ excitation across the $ N=32 $ subshell becoming the dominant configuration. In contrast, the $ N=34 $ shell gap increases as protons are removed from $ ^{54} {\rm{Ca}}$, as illustrated in Fig. 2(c). Correspondingly, the neutron $ 0p0h $ component across the $ N=34 $ subshell is dominant in the $ 0^+_1 $ states of all the $ N = 34 $ isotones. The $ N=34 $ shell gap increases from approximately 2.5 MeV in $ ^{54} {\rm{Ca}}$ to about 4 MeV in $ ^{48} {\rm{Si}}$, further enhancing the magicity of $ ^{48} {\rm{Si}}$. The results align with the relativistic Hartree–Fock–Bogoliubov calculations, which also predict $ N=34 $ shell gaps of 2.5 MeV in $ ^{54} {\rm{Ca}}$ and 4 MeV in $ ^{48} {\rm{Si}}$ [42].

Figure 2.  (color online) The ESPEs of the neutron $ \nu 0f_{7/2} $, $ \nu 1p_{3/2} $, $ \nu 1p_{1/2} $, and $ \nu 0f_{5/2} $ orbits in the $ N=28 $, $ N=32 $, and $ N=34 $ isotones, calculated by VS-IMSRG using the EM1.8/2.0 and NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ interactions.

The proton-neutron interaction matrix elements relevant to the evolution of $ N=32 $ and $ N=34 $ involve the proton $ \pi 0d_{3/2} $ and $ \pi 1s_{1/2} $ orbits $ vs. $ the neutron $ \nu 1p_{3/2} $, $ \nu 1p_{1/2} $, and $ \nu 0f_{5/2} $ orbits. The complex interactions between different orbits and various components of the nuclear force make it difficult to present a simple and clear picture for the physical reasons behind this shell evolution, as discussed in Ref. [40].

Similarly, the proton ESPEs for the Si and S isotopes are also investigated, with a focus on the evolution of the $ Z=14 $ and $ Z=16 $ sub-shells, as shown in Fig. 3. A significant $ Z=14 $ shell gap, approximately 5 MeV, is observed from calculations using both the EM1.8/2.0 and NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ interactions. Based on these results, we propose that $ ^{48} {\rm{Si}}$ is a doubly magic nucleus, with both $ Z=14 $ and $ N=34 $ shell closures. On the other hand, the behavior of the $ Z=16 $ shell gap in the S isotopic chain shows notable differences between the two interactions. Calculations with the EM1.8/2.0 interaction predict the $ Z=16 $ shell gap to be about 1.5 MeV around $ ^{50} {\rm{S}}$, while the NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ interaction gives a shell gap of approximately 3 MeV. In the latter case, the $ Z=16 $ shell gap in $ ^{50} {\rm{S}}$ is comparable to the $ N=32 $ sub-shell in $ ^{52} {\rm{Ca}}$. The EM1.8/2.0 interaction utilizes a nonlocal 3N regulator, while the NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ potential employs both local and nonlocal (lnl) 3N regulators. The difference in the treatment of the 3N force may play an important role in the observed variation in the $ Z = 16 $ shell gap. Nevertheless, the trends for the evolution of the $ Z=14 $ and $ Z=16 $ shell gaps with changing neutron number are consistent in the calculations using both interactions. In conclusion, whether $ ^{50} {\rm{S}}$ is a doubly magic nucleus remains uncertain in our theoretical calculations, requiring further experimental investigation.

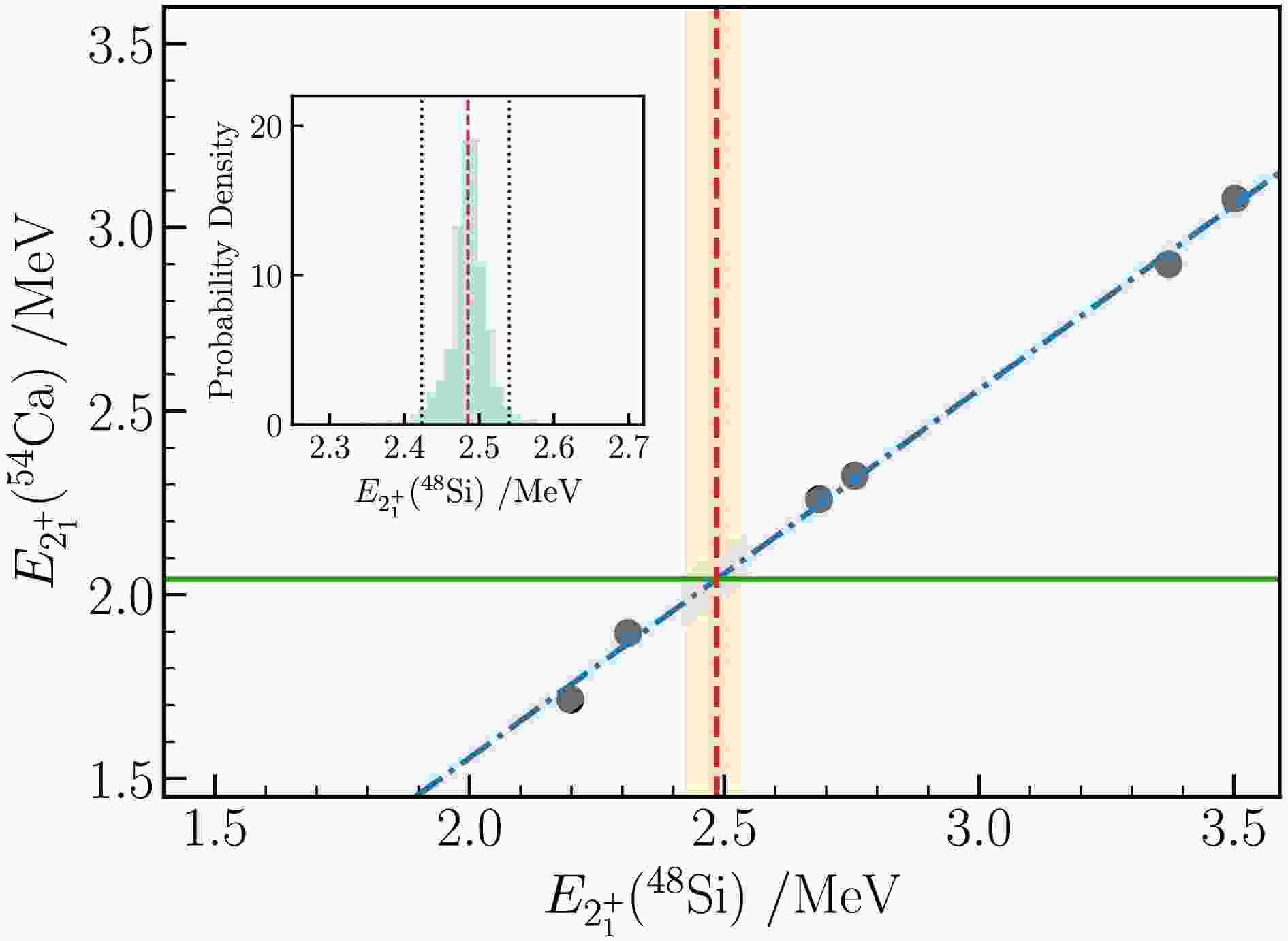
To precisely estimate the $ E(2_1^+) $ value of $ ^{48} {\rm{Si}}$, we used the EM1.8/2.0, NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $, and NN-${\rm{N}} ^4 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ [63] interactions to calculate the $ E(2_1^+) $ values for $ ^{48} {\rm{Si}}$ and $ ^{54} {\rm{Ca}}$ within both the $ e_{\rm{max}}= 14 $, $ E_{3{\rm{max}}} = 14 $ model space and the $ e_{\rm{max}}= 12 $, $ E_{3{\rm{max}}} = 12 $ model space. A robust linear correlation emerged between the calculated $ E(2_1^+) $ values for $ ^{48} {\rm{Si}}$ and $ ^{54} {\rm{Ca}}$. Therefore, we applied a Bayesian linear regression model, using the experimental value of $ E(2_1^+) $ for $ ^{54} {\rm{Ca}}$ (2.043 MeV) [18], to obtain the posterior distribution of the $ E(2_1^+) $ value for $ ^{48} {\rm{Si}}$. The probability density distribution and 95% confidence interval are shown in Fig. 4. We obtained the $ E(2_1^+) $ value for $ ^{48} {\rm{Si}}$ as $ E(2_1^+)=2.49 \pm 0.03 $ MeV.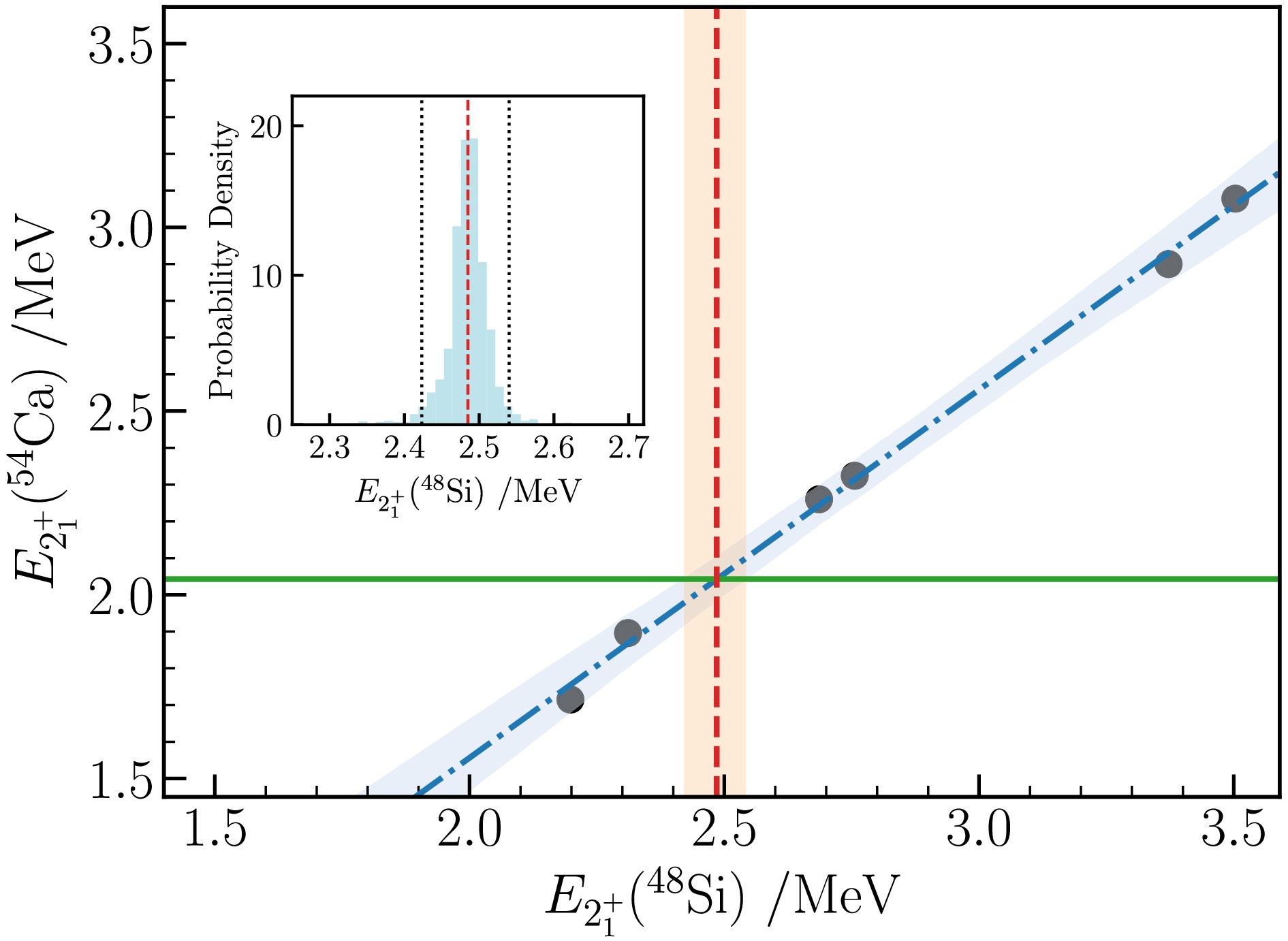

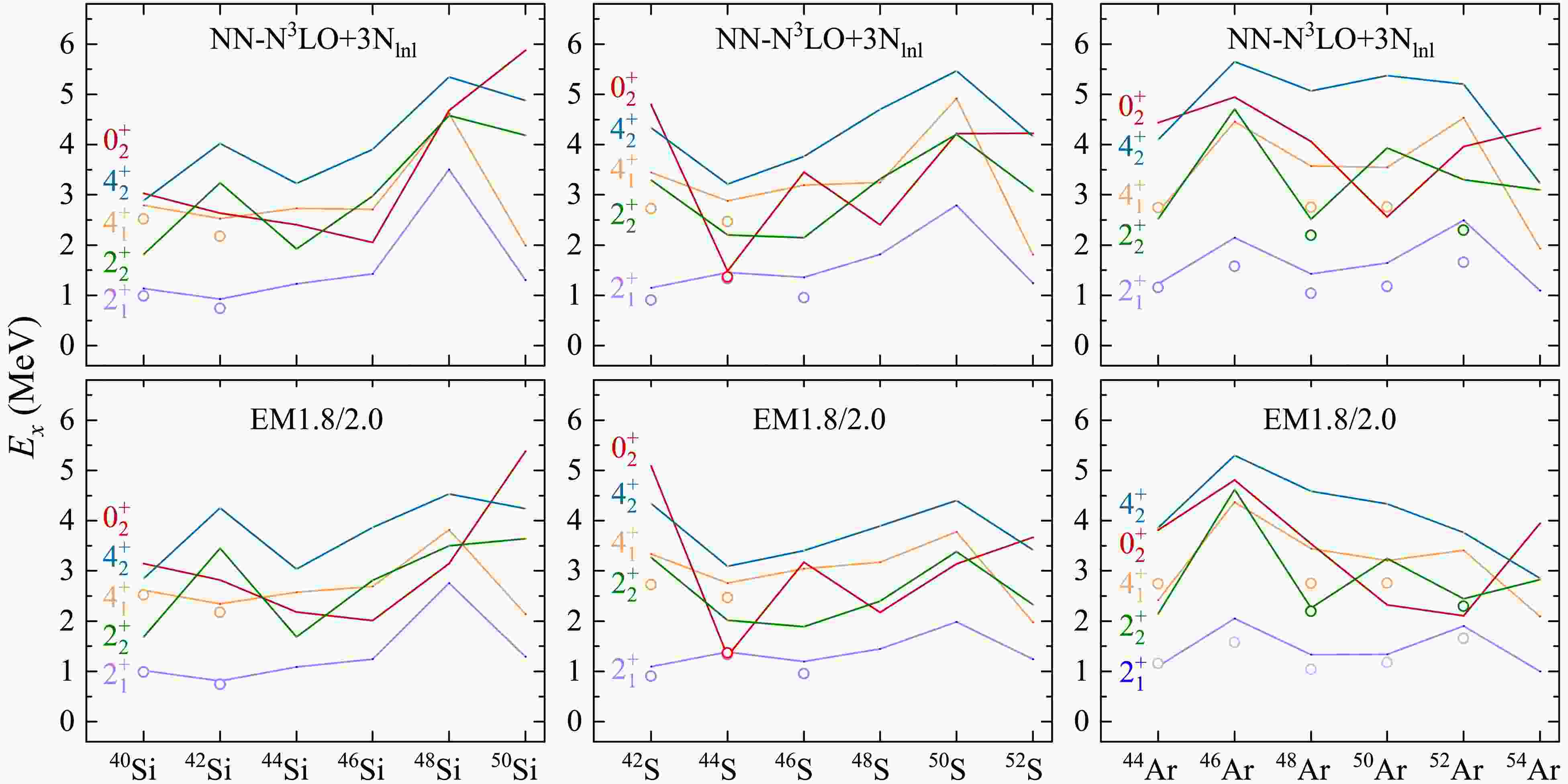
Figure 4.  (color online) Correlation between the $ E(2^+_1) $ values in $ ^{54} {\rm{Ca}}$ and $ ^{48} {\rm{Si}}$, derived from the VS-IMSRG calculations using the NN-${\rm{N}} ^4 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $, EM1.8/2.0, and NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ interactions within both the $ e_{\rm{max}}= 14 $, $ E_{3{\rm{max}}} = 14 $ model space and the $ e_{\rm{max}}= 12 $, $ E_{3{\rm{max}}} = 12 $ model space. Probability density distribution and 95% confidence interval for the $ E(2_1^+) $ value of $ ^{48} {\rm{Si}}$ in the inset panel are obtained using Bayesian linear regression, given the experimental $ E(2_1^+) $ value for $ ^{54} {\rm{Ca}}$ (2.043 MeV).

Furthermore, the evolution of the low-lying states in the neutron-rich Si, S, and Ar chains is also systematically investigated by ab initio VS-IMSRG calculations, and the results are depicted in Fig. 5, along with available experimental data. For these nuclei, experimental data are currently quite limited, but with advancements in experimental techniques, it is expected that more data will be accessible in the near future. As illustrated in Fig. 5, our calculations are in good agreement with the available experimental results. Notably, the calculated $ E(4_1^+)/E(2_1^+) $ ratios of $ ^{48} {\rm{Si}}$, $ ^{50} {\rm{S}}$, and $ ^{52} {\rm{Ar}}$ are all less than 2, approaching the vibrational limit, which indicates nearly spherical shapes. Furthermore, the predicted $ 0_2^+ $ states by VS-IMSRG calculations exhibit different behaviors among these isotopes. Specifically, the $ 0_2^+ $ states of Ar isotopes show a sharp descent, reaching a minimum at $ ^{52} {\rm{Ar}}$ with EM1.8/2.0 and at $ ^{50} {\rm{Ar}}$ with NN-N$ ^3 $LO+3N$ _{\rm{lnl}} $, which needs to be verified by future experiments. In addition, the $ 0_2^+ $ states of Si isotopes exhibit a steady decline from $ ^{40} {\rm{Si}}$ to $ ^{46} {\rm{Si}}$, followed by a rapid rise towards $ ^{50} {\rm{Si}}$. On the other hand, the $ 0_2^+ $ states of S isotopes display a staggering pattern. Moreover, the $ 2_2^+ $ states of Si and Ar isotopes also show a staggering. The lower $ 0_2^+ $ states indicate the disappearance of the magic number and the onset of shape coexistence in these isotopes, as discussed in our previous work [64]. In $ ^{52}\text{Ca} $, the $ 0^+_2 $ state is primarily dominated by the neutron $ 2p2h $ excitation (87%), while in $ ^{46}\text{Si} $, $ ^{48}\text{S} $, and $ ^{50}\text{Ar} $, the $ 0p0h $ and $ 1p1h $ configurations dominate, each contributing approximately 30%-40%. In contrast, for the $ N = 34 $ isotones, the $ 0^+_2 $ states are all dominated by the $ 2p2h $ excitation. These results will provide valuable information for future experiments in this region.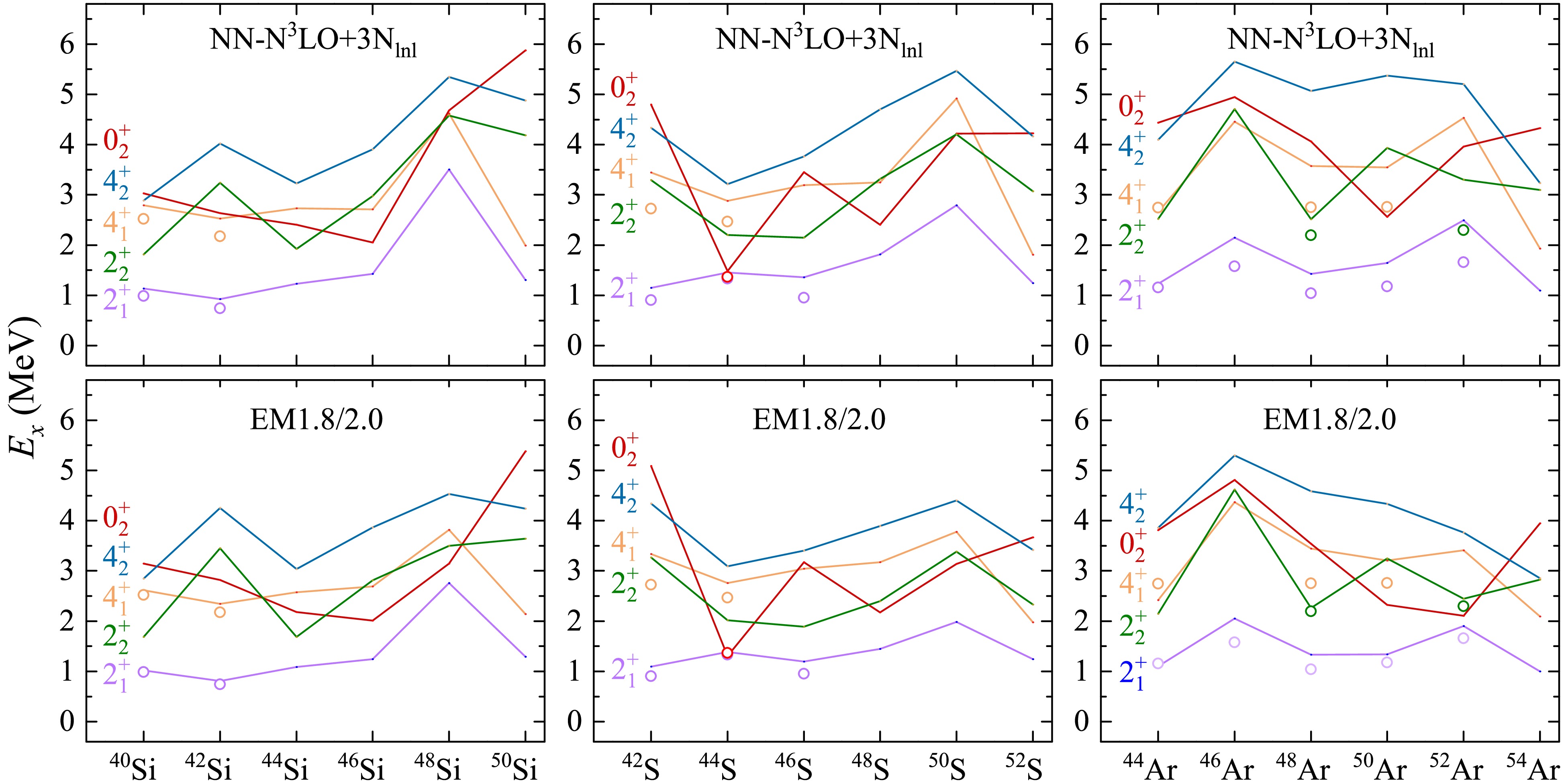

Figure 5.  (color online) Energy levels of neutron-rich Si, S, and Ar isotopes calculated by VS-IMSRG with the EM1.8/2.0 (lines in lower panels) and NN-N$ ^3 $LO+3N$ _{\rm{lnl}} $ (lines in upper panels) interactions, compared with the available experimental data [58]. Here, the open symbols represent experimental data [58].

We presented calculations for the neutron-rich Si, S, Ar, and Ca isotopes using the ab initio valence-space in-medium similarity renormalization group (VS-MSRG), based on chiral nucleon-nucleon and three-nucleon forces, specifically the EM1.8/2.0 and NN-${\rm{N}} ^3 {\rm{LO}}+3{\rm{N}} _{ {\rm{lnl}}} $ interactions. A detailed analysis of shell evolution at $ N=28 $, $ N=32 $, and $ N=34 $ in these isotopes is performed based on $ E(2_1^+) $ and effective single-particle energies. Our calculations well reproduce the reduction of the $ N=28 $ shell gap in the isotones below $ ^{48} {\rm{Ca}}$. Furthermore, our results indicate that the $ N=32 $ sub-shell also gradually weakens as we move from $ ^{52} {\rm{Ca}}$ to $ ^{46} {\rm{Si}}$, eventually disappearing in $ ^{46} {\rm{Si}}$. In contrast, the $ N=34 $ sub-shell is enhanced when moving from $ ^{54} {\rm{Ca}}$ to $ ^{48} {\rm{Si}}$, with the shell gap increasing from approximately 2.5 MeV in $ ^{54} {\rm{Ca}}$ to about 4 MeV in $ ^{48} {\rm{Si}}$. Given the fact that our calculations show that the $ Z=14 $ sub-shell is preserved in the Si isotopes, the doubly magic character of $ ^{48} {\rm{Si}}$ is highly proposed. Moreover, our calculations also reveal that the calculated $ E(2_1^+) $ values of $ ^{54} {\rm{Ca}}$ and $ ^{48} {\rm{Si}}$ with different interactions exhibit a robust linear correlation, with the $ E(2_1^+) $ of $ ^{48} {\rm{Si}}$ being approximately 400 keV higher than that of $ ^{54} {\rm{Ca}}$. Taking into account the uncertainties associated with the model space used in our calculations, as well as the linear correlation between the calculated $ E(2_1^+) $ values of $ ^{54} {\rm{Ca}}$ and $ ^{48} {\rm{Si}}$, we employed Bayesian linear regression to predict that the $ E(2_1^+) $ of $ ^{48} {\rm{Si}}$ is approximately 2.49 MeV, which is comparable to the values measured in other exotic doubly magic nuclei, such as $ ^{52,54} {\rm{Ca}}$ [13, 18], and $ ^{78} {\rm{Ni}}$ [72]. This result sparks significant interest for further experimental investigations. Additionally, the low-lying spectra of neutron-rich Si, S, and Ar isotopes are systematically calculated, providing valuable information for future experimental studies.