Universal momentum distributions for the spin-singlet NN channels

The problem of short-range correlations (SRC) is very relevant nowadays due to the recent theoretical and experimental achievements [1−8]. The new experiments allow to count correlated nucleon pairs with high relative momentum and small center of mass momentum. The theoretical description of the corresponding cross sections in quasi-elastic kinematics is reduced, in many cases, to treatment of the momentum distributions of nucleons in nuclei. This gave rise to the contact formalisms [9, 10] which occur to be quite convenient for practical calculations [5].

In this paper, we discuss one of the key aspects of the SRC problem. Two-nucleon momentum distribution $ \rho^A_{ { {NN}}} $ in the nucleus A depends on the relative momentum of nucleons k, the momentum of their center of mass Q, and the angle θ between them. These distributions have similar properties for different nuclei [11] and satisfy the factorization property at high relative momenta k and low Q [9, 12]:

where $ C^A_{ { {NN}}} $ is a constant depending on the nucleus A (the so-called nuclear contact), $ \rho^{A, { {NN}}}_{\rm{cm}}(Q) $ is a distribution of center-of-mass momentum for a pair of nucleons in the nucleus while $ \rho_{ { {NN}}}(k) $ represents a universal two-nucleon momentum distribution (UMD) which does not depend on A [9]. This distribution in its high-momentum part depends on the chosen model of $ NN $ interaction. In the case of the spin-triplet $ np $ pairs, this universal distribution coincides with the distribution of nucleons in the deuteron: $ \rho_{np}(k) = \rho_d(k) $. Since $ \rho_d(k) $ is normalized to 1, one can calculate explicitly a weight of the high-momentum part of the distribution $ a_2^d $ [13], which determines the magnitude of SRC.

At the same time, for spin-singlet $ ^1S_0 $ $ NN $ channels (i.e. $ np $, $ pp $ and $ nn $) bound states are absent, so there is a problem of determining the corresponding universal distributions [9], as well as estimating the magnitude of high-momentum components for such states for two-nucleon system. In [12], the corresponding momentum distributions at $ Q = 0 $ in $ ^4 {\rm{He}}$ were considered as universal distributions for $ pp $ (or $ nn $) pairs, and factorization (1) was used to calculate spectral functions for heavier nuclei up to $ ^{40} $Ca. Another approach to determining the UMD for spin-singlet pairs is proposed within the Generalized Contact Formalism (GCF) [5, 10] by using the two-body $ NN $ scattering wave functions at zero energy which are normalized by their high-momentum tails, i.e. by the integral from some $ p_0 $ (the boundary of the high-momentum region) to infinity. However, the question of quantitative evaluating the high-momentum components for spin-singlet channels, which would allow comparing different $ NN $ interactions in this respect, still remains open.

In the present study, we suggest the universal distribution for singlet $ NN $ channels which does not depend on the boundary of the high-momentum region $ p_0 $ and is determined directly by the momentum distribution for the virtual state. It should be noted, that such a distribution for a particular case of a separable $ NN $ interaction has been used as a two-body $ pp $-distribution in Ref. [14]. In a general case, to obtain the momentum distribution for virtual state, one can use the low-energy scattering wave functions.

For this purpose, we use the approach of Fäldt and Wilkin [15, 16] which establishes a relation between the scattering and bound state wave functions, and was applied to inelastic $ NN $ scattering calculations [17]. This approach gives an explicit factor (the Fäldt-Wilkin factor) which allows to approximately reproduce the bound- and virtual-state momentum distributions at high-momentum region by using the low-energy scattering wave functions. As a result of the developed technique, we introduce high-momentum constants for different $ NN $ interactions in the spin-singlet channel and compare quantitatively high-momentum parts of momentum distributions for different models of $ NN $ interactions. Our recently suggested treatment [18] for high-momentum components of the scattering wave functions is helpful on this way.

As a numerical illustration, we calculate the nuclear contacts for $ pp $ momentum distributions in $ ^3 {\rm{He}}$ with respect to the introduced two-nucleon momentum distributions for four realistic but essentially different models of $ NN $ and $ 3N $ interaction and show that these contacts have nearly the same values. Thus, the suggested formalism can be considered as an extension of the formalism presented in Ref. [9] for $ np $ triplet momentum distributions.

The structure of the paper is as follows. In Section II, we derive a relation between the scattering and bound- or virtual-state wave functions and define an explicit factor, i.e. the Fäldt–Wilkin factor. In Section III, the found relations are tested for the separable interaction when the virtual-state momentum distribution is found analytically and for the realistic $ NN $ interaction as well. In Section IV, the UMDs for the spin-singlet $ NN $ channels are introduced based on the developed formalism and the values of the high-momentum constants $ a_2^v $ are presented for four different models of $ NN $ interaction. In Section V, the nuclear contacts for $ ^3 {\rm{He}}$ nucleus are calculated based on the two-nucleon UMDs. The Summary is given in the last Section VI. For the reader convenience, a small Appendix A is given with the explicit relations between different universal momentum distributions.

Let's start with the definitions which we will use below.

For the spin-triplet bound state, the two-nucleon relative momentum distribution is naturally introduced by using the deuteron wave function with the S-wave and D-wave components $ u(k) $ and $ w(k) $, respectively:

The S-matrix $ S(p) $ for the spin-triplet $ np $-scattering (here $ p = \sqrt{2\mu E/\hbar^2} $ is the on-shell momentum) has a pole in a complex p-plane at $ p = i \varkappa_d $, where $ \varkappa_d\equiv \sqrt{-2\mu E_d/\hbar^2}>0 $ is the wave number corresponding to the bound-state energy $ E_d $, μ is the reduced mass of two nucleons.

The corresponding residues of the S-matrix elements at this pole determine the asymptotic normalization coefficients (ANCs) $ N_S $ and $ N_D $ (see Section II.D), which set amplitudes of components of the deuteron wave function in configuration space at $ r\to \infty $:

provided that the deuteron wave function is normalized to unity: $ \int_0^\infty [u^2(r)+w^2(r)]dr = 1 $.

There are no bound $ NN $ states in the spin-singlet channel $ ^1S_0 $. However, in this channel there is a virtual state $ u_v(r) $ with $ E_v<0 $ (for the $ np $ system $ E_v \approx -67 $ keV). The pole of the S-matrix corresponding to the virtual state lies on the unphysical energy sheet and on the negative imaginary semi-axis in the complex p-plane at $ p = i \varkappa_v $:

The function $ u_v(r) $ grows exponentially at the asymptotics:

in contrast to the bound-state case. However, the constant $ N_v $ in eq. (5) is the ANC for a virtual state which is related to the residue of the S-matrix $ S(p) $ for the singlet state at the pole $ p = i \varkappa_v $.

It should be mentioned, that although the virtual state function in the coordinate representation $ u_v(r) $ with the asymptotics (5) cannot be normalized, the virtual state wave function in the momentum representation $ u_v(k) $ is square integrable [19] (see also the example with a separable potential in Section III). One can also define a special Fourier transform procedure that relates the coordinate and momentum representations for the virtual-state wave function [20].

Therefore, one can consider the momentum distribution for the virtual state in a similar manner as for the bound-state (2) as follows

This distribution has the same dimension as for the bound-state, however, it is not normalized to unity. It would be convenient to define the UMD for the spin-singlet $ NN $ channels based on these distributions for virtual states. However, a practical calculation of such momentum distribution could be a complicated task for realistic $ NN $ interactions. Thus, further we will show how to reconstruct it in high-momentum region just from the low-energy scattering wave functions for the same interaction.

Finally, we should introduce here the scattering wave functions as well. Below we consider the radial parts of the scattering wave functions $ \psi_p^s $ and $ \psi_{p,l = 0,2}^t $ for two main $ NN $ configurations $ ^1S_0 $ and $ ^3S_1 $-$ ^3D_1 $ both in coordinate and momentum representations. In the momentum space these functions are normalized as follows:

where p is the on-shell momentum.

In the configuration space we will consider functions that satisfy the asymptotic condition of a standing wave. For a singlet channel this means:

where $ \phi(p) $ is the partial phase shift.

In Ref. [15], the authors found an explicit relation between bound-state and scattering wave functions for the same Hamiltonian in case of the S-wave interactions (without tensor coupling) by using an analytical continuation of the scattering wave function to the bound-state pole of the S-matrix. For our purposes, we also need the similar relation for the virtual state. So, let's reproduce briefly the derivation from Ref. [15] with some minor changes in notations.

Near the pole $ p = i \varkappa $ corresponding to the bound or virtual state the S-matrix can be presented in the form

For a bound state, the constant N in eq. (9) is a corresponding ANC (see [21, 22] and references therein). Near the pole, the relation (9) can also be written in a form:

where $ \varkappa>0 $ for a bound state and $ \varkappa<0 $ for a virtual state.

The asymptotics of the wave function of both bound and virtual states in the configuration space can be written in a unified way:

At the same time, the scattering wave function has the following asymptotics:

where in agreement with (8)

Near the pole $ p = i \varkappa $, $ \phi\to -i\infty $, $ C^{(-)}(p)\to 0 $, hence

Comparing Eqs. (10) and (13), one can find an explicit relation between $ C^{(+)} $ near the pole and ANC N:

The quantity

will be called below as the Fäldt-Wilkin's Factor (FWF).

Combining Eqs. (11), (14), and (15), we obtain the following relationship between the wave functions of the discrete and continuous spectrum:

Eq. (17) was derived in [15] for a bound state with $ u(r) $ normalized to unity. However, we have just shown that it is also valid for the virtual state for which the wave function $ u(r) $ is normalized according to (11) with ANC N related to a pole of the S-matrix (9). The transition from a bound state to a virtual one can be considered as an analytical continuation with respect to the variable $ \varkappa $ from $ \varkappa>0 $ to $ \varkappa<0 $ or, equivalently, with respect to some constant characterizing the strength of the interaction potential.

Since $ C^{(+)}(p) $ is real for imaginary values of p, it follows from (15) that ANC N is real for bound states ($ \varkappa > 0 $) and purely imaginary for virtual states ($ \varkappa < 0 $). The validity of this assertion can be illustrated by the example of the frequently used effective range approximation, within which

where $ r_{\rm{eff}} $ is an effective range. Applying the effective range approximation to the $ np $ system in the $ ^1S_0 $-state and using the experimental values of the singlet scattering length ($ a = -23.74 $ fm) and effective range ($ r_{\rm{eff}} = 2.77 $ fm) results in $ \varkappa = -0.0399 $ fm^-1 and $ N_v = i\cdot 0.268 $ fm$ ^{-1/2} $. ¹

The relation (17) is an equality at the complex pole $ p = i \varkappa $ only. However, it should be approximately satisfied in a certain region near the pole, including small real positive p. Indeed, in [16] it was shown that a similar approximate relationship between the scattering function $ \psi_p(r) $ at small p (low energies) and the weakly bound state function $ u(r) $ holds in the region of small values of r:

A similar relation must also be valid for wave functions in the momentum representation, and thus for momentum distributions, in the high-momentum area for both bound and virtual states:

where the squared FWF is introduced:

The approximation (20) can be explained as follows. The wave function of each type (i.e. the bound state, virtual state and scattering) satisfies the Schrödinger equation in the form:

where p is either an on-shell momentum (for the scattering wave function) or $ p = i \varkappa $ for the bound (virtual) state wave function. At $ k\gg |p| $ the second term in brackets on the left-hand side of the equation (22) can be neglected. Therefore the scattering and bound (or virtual) state wave functions for the same interaction potential should be the same at large momenta k up to some factors. According to (20) these factors are FWF for the wave functions and squared FWF for momentum distributions.

The realistic $ NN $ interaction includes the tensor term, so that the above S-wave formalism could not be applied directly for such a case. However, a generalisation of the approach can be done.

In particular, the total S-matrix is a matrix $ (2\times2) $ for the coupled $ ^3S_1 $-$ ^3D_1 $ channels. Near the bound-state pole $ p = i \varkappa_d $ it can be represented in a form [24, 25]:

where $ N_S $ and $ N_D $ are the ANCs introduced in Eq. (3). It can be shown that this S-matrix has one eigenvalue with a non-zero residue at $ p = i \varkappa_d $ corresponding to the so-called eigenchannel representation [25]. It seems that the procedure with a continuation to the bound-state pole can be applied and proved for one of the low-energy scattering states defined in this representation. Let's also note, that, at low positive energy, mixing in the S-matrix is very small, thus, the required momentum distribution can be calculated from the ordinary scattering wave function corresponding to the boundary condition with the incoming S-wave.

Thus, within the above assumptions, one can write the following approximate relation between the momentum distributions found from the scattering wave function and from the deuteron bound-state wave function in case of the realistic interaction:

Here we emphasize that this approximate equality should be valid only for one of the scattering states in the $ ^3S_1 $-$ ^3D_1 $ channels at given on-shell momentum p, i.e. the state corresponding to the incoming S-wave.

The approximate relations (20) and (24) between bound- and virtual-state momentum distributions and those found from the scattering wave functions represent the main result of this Section. In fact, these relations allow to obtain the high-momentum parts of the “basic” momentum distributions (2) and (6) from the low-energy scattering wave functions as we have initially suggested. Prior to introducing a new form for the universal momentum distributions, in the next Section we will test both relations numerically in a more detail.

In this section we demonstrate that the approximations (20) and (24) are valid for cases of the model and realistic $ NN $ interactions.

Using a simple example with a separable interaction, it is easy to test the considered approximations explicitly since all solutions are expressed in analytical form in this case. For the reader convenience, we give here the well-known formulas for a separable potential [26], however, supplementing them with the details of the virtual state calculation which seems to be less known.

Consider the S-wave attractive separable potential:

The unitary on-shell amplitude $ f_0(p)\equiv 1/(p\cot\phi_0-ip) $ is written in explicit form:

where $ E = p^2/(2\mu) $, μ is the reduced mass,

The bound state function $ u_b $ for the separable potential (25) is found from the homogeneous Lippmann–Schwinger equation (LSE), so that

where the normalization factor:

and the energy $ E_b $ is determined by the condition

The bound state exists for $ \lambda >\lambda_{\rm{min}} $ ($ \lambda_{\rm{min}} = \{\int_0^\infty g^2(k)dk\}^{-1} $ corresponds to $ \varkappa = 0 $), while for $ \lambda <\lambda_{\rm{min}} $ there is a virtual state with $ \varkappa<0 $, which corresponds to the pole of the t-matrix on the unphysical energy sheet.

The virtual state must satisfy the LSE continuated to the second (unphysical) sheet of the energy Riemann surface (or for $ {\rm{Im}}\ p < 0 $). As shown, for example, in work [20], the continuation to the second energy sheet is actually a continuation of the Cauchy-type integral and reduces to adding a separable energy-dependent term to the interaction. For the case of an initial separable potential, this is equivalent to modifying the coupling constant λ.

Therefore, in the case of a separable potential, the formulas for determining the functions on the second energy Riemann sheet remain the same as for the functions on the physical sheet, but a residue at the pole $ p = -i|\varkappa| $ (multiplied by $ 2i\pi $) must be added to all integrals over k which include the factor $ 1/(p^2-k^2) $. In particular, the equation (30) relating λ and $ \varkappa $ for the virtual state takes the form:

In this case, the virtual state function itself in the momentum representation has the same form as the bound state function (28):

i.e. it is a square-integrable (unlike the function in the coordinate representation). However, when calculating the normalization of this function, a residue (of the second order) at the pole $ p = -i|\varkappa| $ must be added to the integral:

In fact, here there is no need to use explicit formulas (32) or (33) to continue Cauchy-type integrals, since these integrals are given by analytical functions. Having calculated the integral in (30) for positive $ \varkappa $, one gets the analytic function $ \lambda^{-1}(\varkappa) $ that is defined for any values $ \varkappa $ and so determines the value of $ \lambda^{-1} $ corresponding to the bound (for $ \varkappa>0) $) or virtual state (for $ \varkappa<0 $). The same applies to the normalization factor (29).

Below we present some results for the Yamaguchi form factor [26]:

for which the explicit relations are well known in both configuration and momentum representations. In particular, the integrals (30) and (29) for the Yamaguchi form factor define functions

that are analytic in the entire $ \varkappa $-plane except for the pole at $ \varkappa = -\beta $. It should be noted that according to (35) the square of the normalization factor $ A^2_v $ for the virtual state function ($ \varkappa<0 $) is negative, i.e. the virtual state function $ u_v(k) $ and its ANC are purely imaginary (cf. (18)). The wave function of the bound (or virtual) state for the Yamaguchi potential in configuration space has a very simple form:

Note that the wave function (36) coincides with the wave function for the local Hulthén potential: $ V(r) = -V_0e^{-\beta r}/(1-e^{-\beta r}) $.

It is easy to show that the ANC $ N_{b(v)} $ for a separable potential is expressed in terms of the normalizing factor $ A_{b(v)} $ and the value of the form factor at the pole $ g(i\varkappa) $:

The S-wave scattering function $ |\psi^+_{p}\rangle $ for energy $ E = \frac{p^2}{2\mu} $ can be written in an explicit form, e.g. in terms of the amplitude $ f_0(p) $ (26):

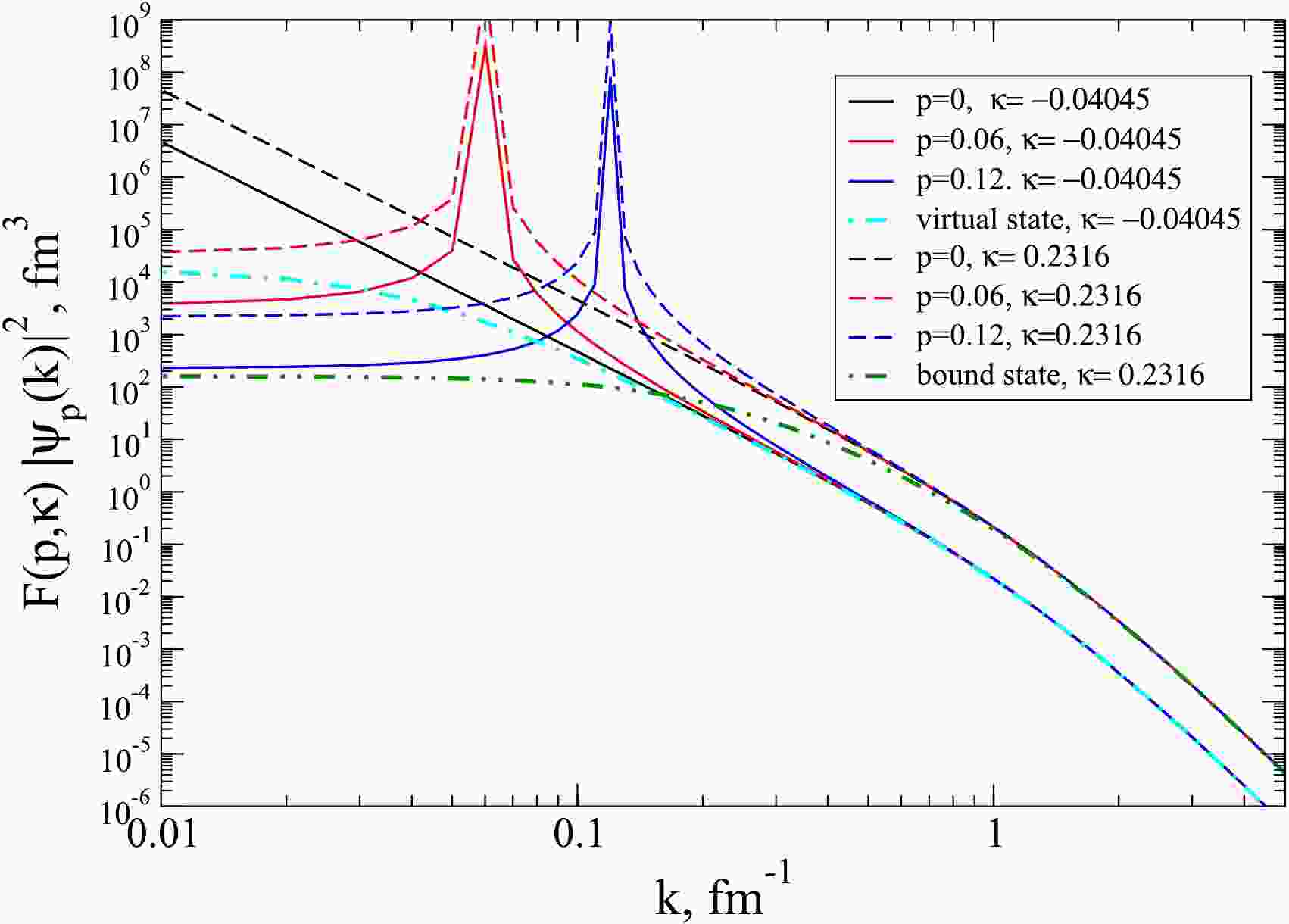
Let us check now the approximations (20) and (24). We use the Yamaguchi potential [26] with the parameter $ \beta = 1.4488 $ fm^-1 and two values of $ \varkappa $ corresponding to two main $ NN $-configurations (at $ \hbar^2/2\mu = 41.47 $ MeV fm$ ^{2} $): $ \varkappa = -0.04045 $ fm^-1, which corresponds to the singlet $ NN $-channel with a virtual state, and $ \varkappa = 0.2316 $ fm^-1, which gives a bound state with $ E_b = -2.2244 $ MeV.

Figure 1 shows the momentum distributions for the scattering wave functions: $ \rho_p(k) = F(p, \varkappa)|\psi_p(k)|^2 $, calculated for the two above-mentioned values of $ \varkappa $ and three energies corresponding to the values of the on-shell momentum: $ p = $0, 0.06, and 0.12 fm^-1 in comparison with the momentum distributions for the virtual state $ |u_v(k)|^2 $ and the bound state $ |u_b (k)|^2 $.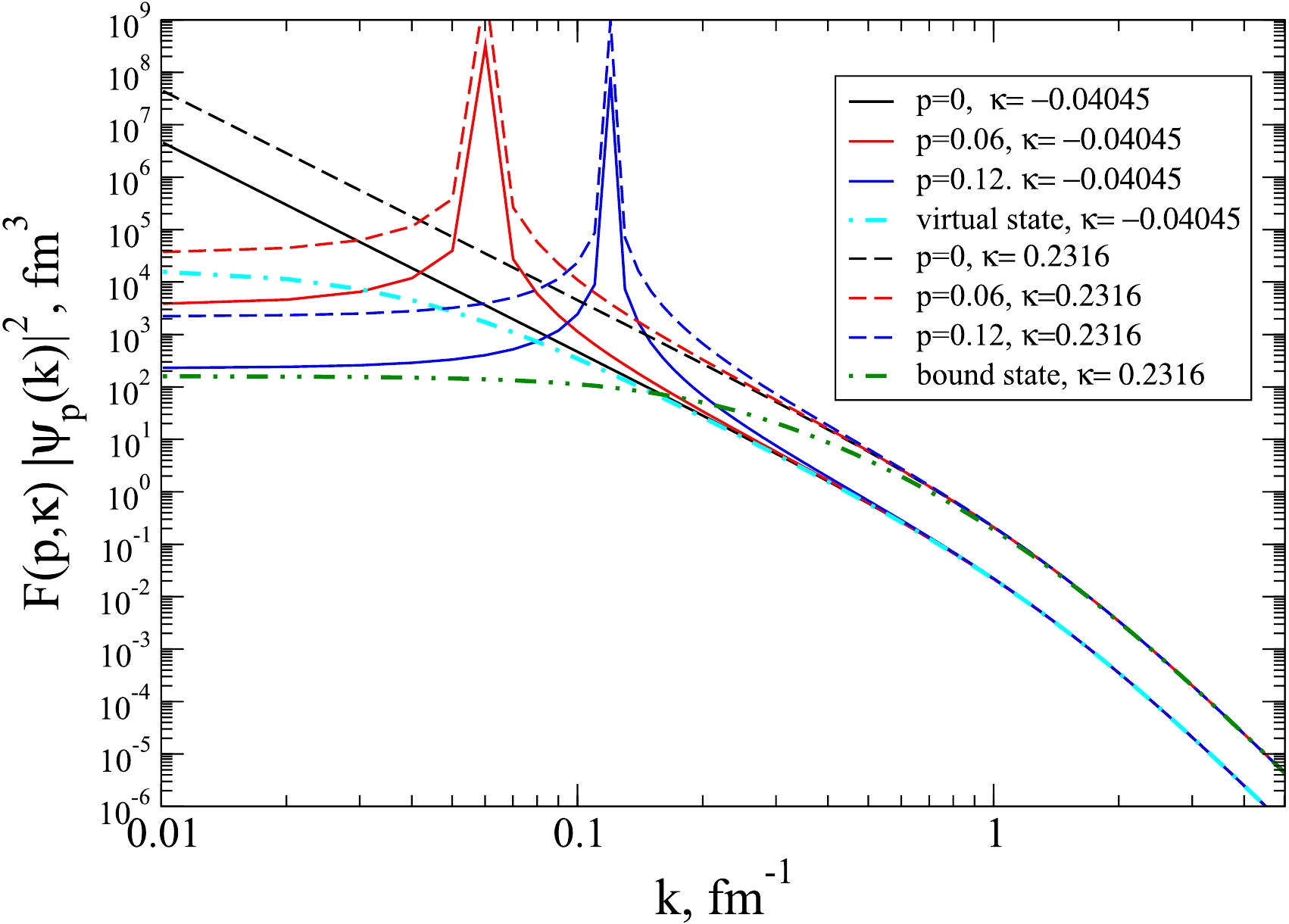

Figure 1.  (color online) The momentum distributions for the scattering functions $\rho_p(k)=F(p,\varkappa)|\psi_p(k)|^2$ for the Yamaguchi potential at three values $p=$0, 0.06 and 0.12 fm^-1 and for two values of $\varkappa$: -0.04045 fm^-1 (solid curves) and $\varkappa=0.2316$ fm^-1 (dashed curves) compared to the momentum distributions for the virtual state $|u_v(k)|^2$ and bound state $|u_b (k)|^2$.

As can be seen from Fig. 1, the momentum distributions $ \rho_p(k) = F(p, \varkappa)|\psi_p(k)|^2 $ found from the low-energy scattering wave functions do not depend on p at $ k>p $ and approaches (in absolute value) the corresponding momentum distribution for the virtual or bound state. Thus, the approximation based on the Fäldt–Wilkin equality does indeed work in the region of large momenta for both the bound and virtual states. Let's note that, as discussed above, a correct normalization of the virtual state wave function means that the integral $ \int_0^\infty|u_v(k)|^2k^2dk $ is not equal to unity in contrast to the bound-state. For example, such an integral of $ |u_v(k)|^2 $ with $ \varkappa = -0.04045 $ fm^-1, shown in the Fig. 1, is equal to 0.8377.

To demonstrate an accuracy of the approximation (20) we show in Fig. 2 the ratios of the momentum distributions $ \rho_p(k) $ at different p to the virtual-state momentum distribution $ \rho_v(k) $. This ratio has the form:

Figure 2.  (color online) The ratio of the momentum distributions for the scattering functions $\rho_p(k)=F(p,\varkappa)|\psi_p(k)|^2$ at $p=$0, 0.06 and 0.12 fm^-1 to the distribution for the virtual state $|u_v(k)|^2$ at $\varkappa=0.04045$ fm^-1.

where the function determining k dependence

monotonically approaches 1 (the faster, the smaller $ \varkappa^2+p^2 $). But at the same time, the ratio $ R_{p, \varkappa}(k) $ tends to the limit value $ A( \varkappa,p) $, which is slightly less than 1, even at zero energy $ p = 0 $, which is due to the non-zero value of $ \varkappa $.

The limit values $ A( \varkappa,p) $ for $ \varkappa = -0.0405 $ fm^-1 are 0.9998, 0.9994 and 0.9980 for $ p = 0 $, 0.06 and 0.12 fm ^-1, correspondingly. For comparison, the limit ratio $ A( \varkappa,0) $ at $ \varkappa = 0.2316 $ fm^-1, corresponding to the bound state, is 0.9971. As can be seen from Fig. 2, at $ p = 0 $ the ratio $ R_{p, \varkappa}(k) $ differs from 1 by less than one percent for all $ k>0.6 $ fm^-1. The above accuracy of the approximation (20) seem to be quite enough for calculations with such two-nucleon momentum distributions.

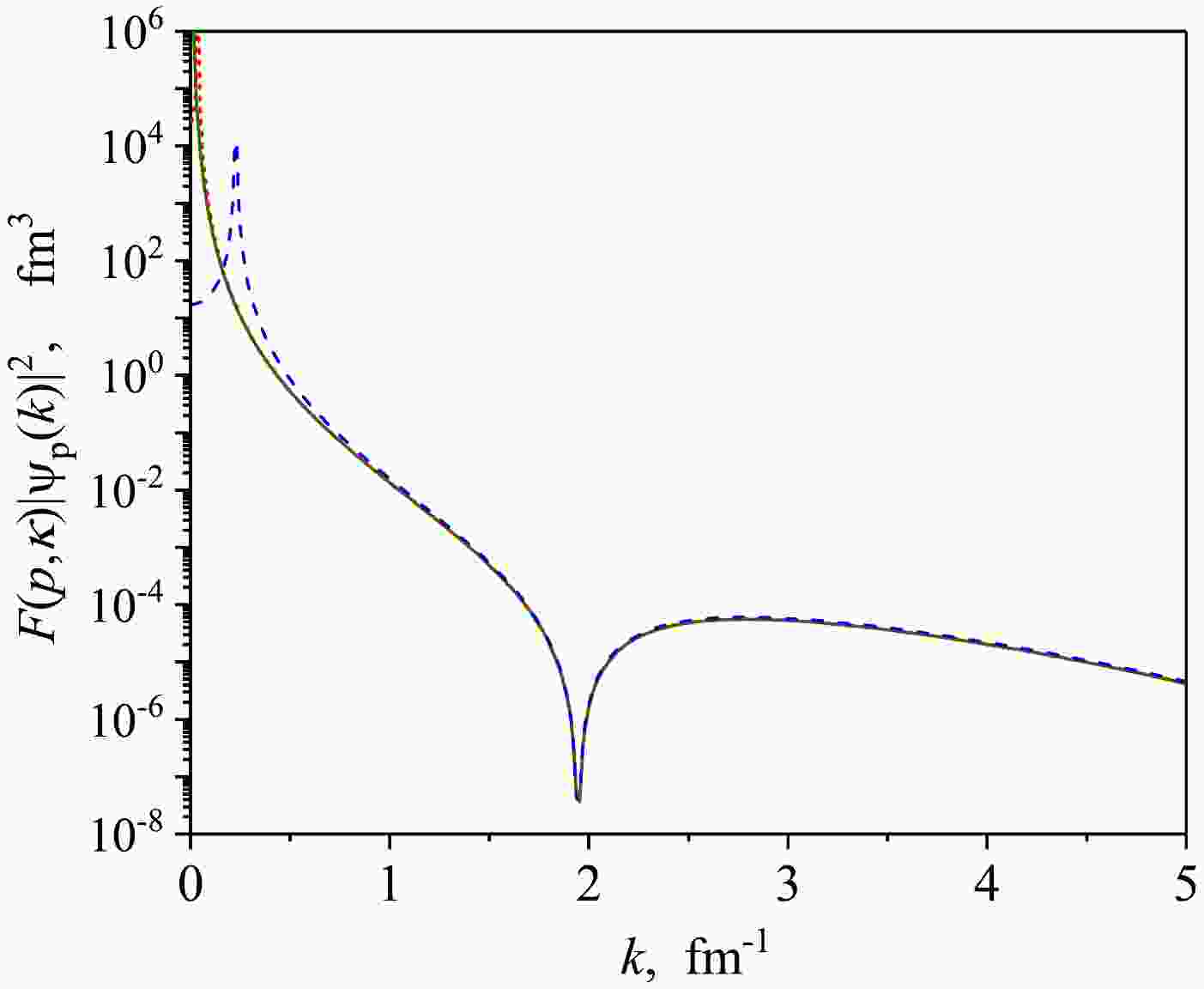
Let's now test the approximations based on the Fäldt–Wilkin factor for a realistic local $ NN $ interaction. In Fig. 3, we present the momentum distributions for the $ ^1S_0 $ $ np $ scattering wave functions with the factor (21) at three values of energy for the Argonne V18 (AV18) potential [28]. Here the wave number of the virtual state is equal $ \varkappa_{v} = -0.04 $ fm^-1. All three curves in this figure are almost indistinguishable in the region $ k>1 $ fm^-1. So that, the FWF indeed allows to get close momentum distributions at different small on-shell momenta. Based on the exact equality (17) and the results for separable interaction, we assume that the approximation (20) is also valid for realistic interaction. That is, the momentum distribution for the scattering state multiplied by the factor (21) is an approximation of the momentum distribution for the virtual state in this case.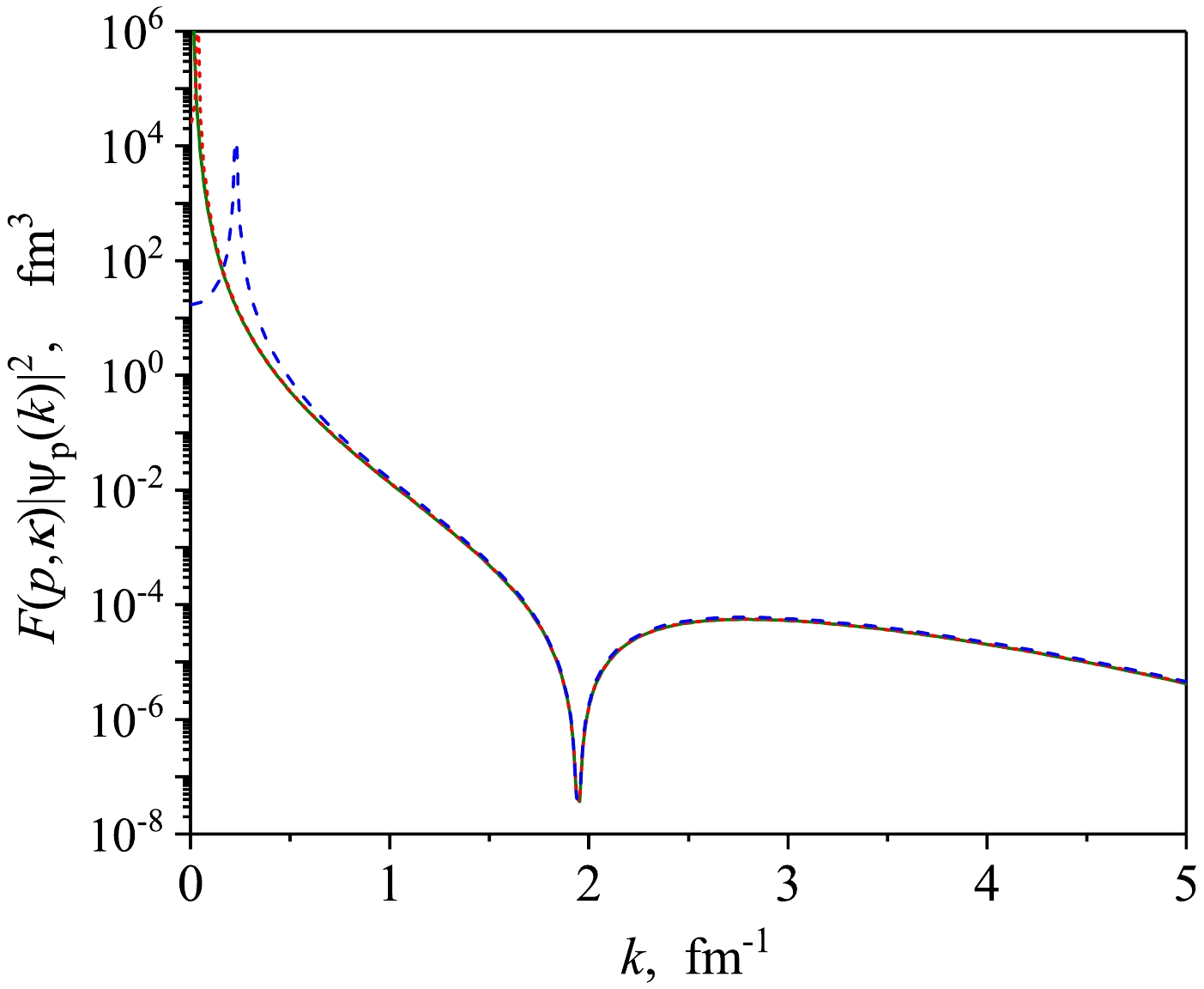

Figure 3.  (color online) Spin-singlet $np$ momentum distributions for the AV18 potential with the factor from Eq. (20) for three momenta: $p=0.008$ fm^-1 (solid curve), $p=0.041$ fm^-1 (dotted curve), p=0.23 fm^-1 (dashed curve).

In Fig. 4, we test the relation (24) for the $ ^3S_1 $-$ ^3D_1 $ coupled channels with AV18 $ NN $ interaction. Here $ \varkappa_d = 0.2316 $ fm^-1. Although all three curves are very close to each other in high k region, one can see a small deviation of the momentum distributions found from the scattering wave functions from the deuteron one even for the smallest p. Thus, the approximate relation (24) is also valid for realistic $ NN $-interaction. Here we can even estimate its error, which is about 5% for the case of zero energy.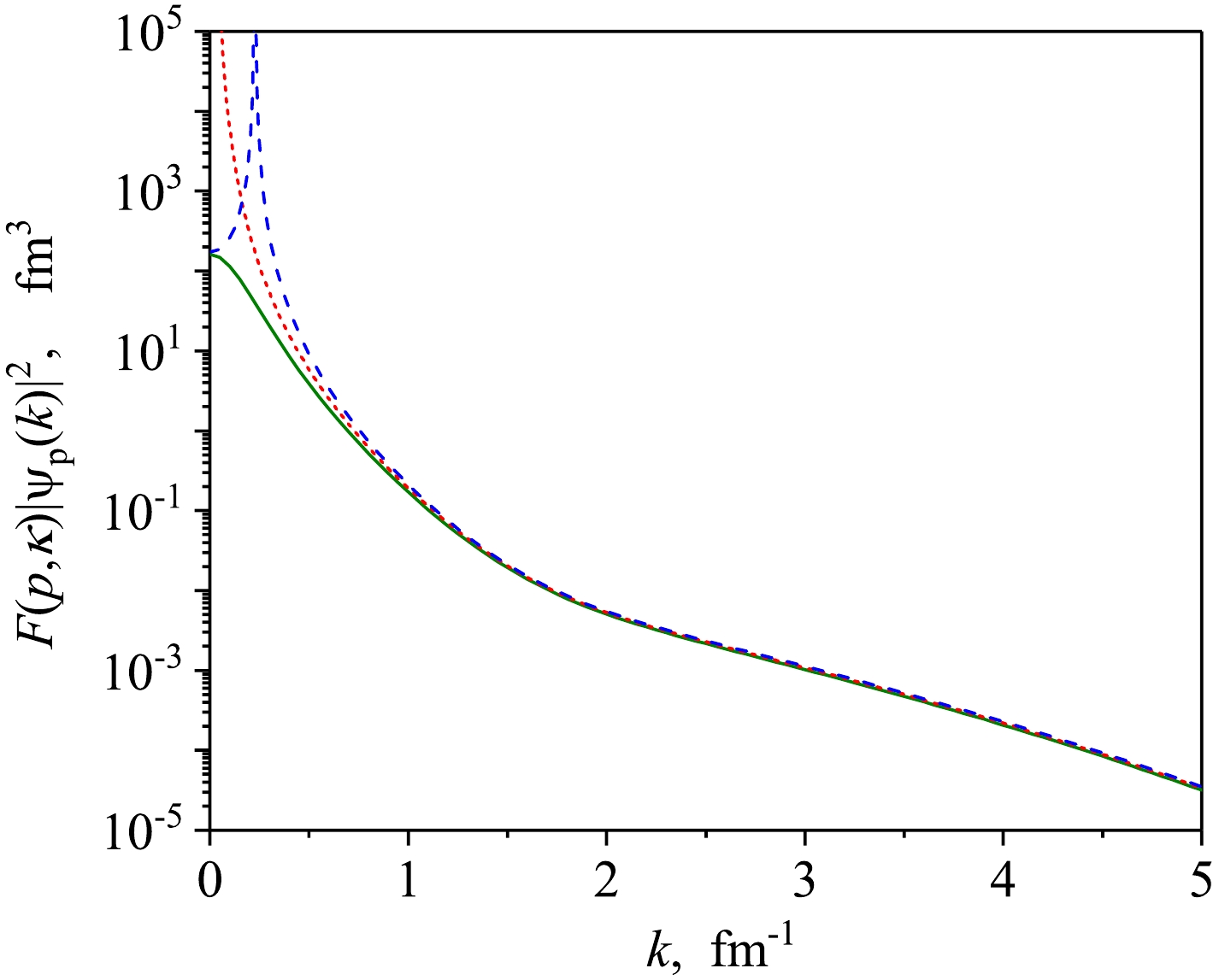

Figure 4.  (color online) Deuteron momentum distribution (solid curve) for AV18 potential in comparison with the momentum distributions found from the scattering wave functions according to Eq.(24): $p=0.041$ fm^-1 (dotted curve), $p=0.23$ fm^-1 (dashed curve).

Taking into account the above example with a separable potential, it can be concluded that the FWF-based approximation works slightly better for the spin-singlet channel due to the smaller value of $ | \varkappa| $. So the error for the spin-singlet channel should be no more than 2-3%.

The results of the previous sections allow us introducing a new form for UMD for the singlet $ NN $ channels based on the scattering wave functions at zero or small on-shell momentum p as follows:

Based on the results of the previous sections, in the high-momentum region these distributions should approximate the momentum distribution for the virtual state (6) (whose wave function in the configuration space is uniquely determined by the ANC (5)):

Here it should be noted that for the interactions which take into account charge dependence of $ NN $ forces, one will have three different singlet UMDs for $ pp $, $ np $ and $ nn $ pairs. The values $ \varkappa_v $ differ for these three cases as well.

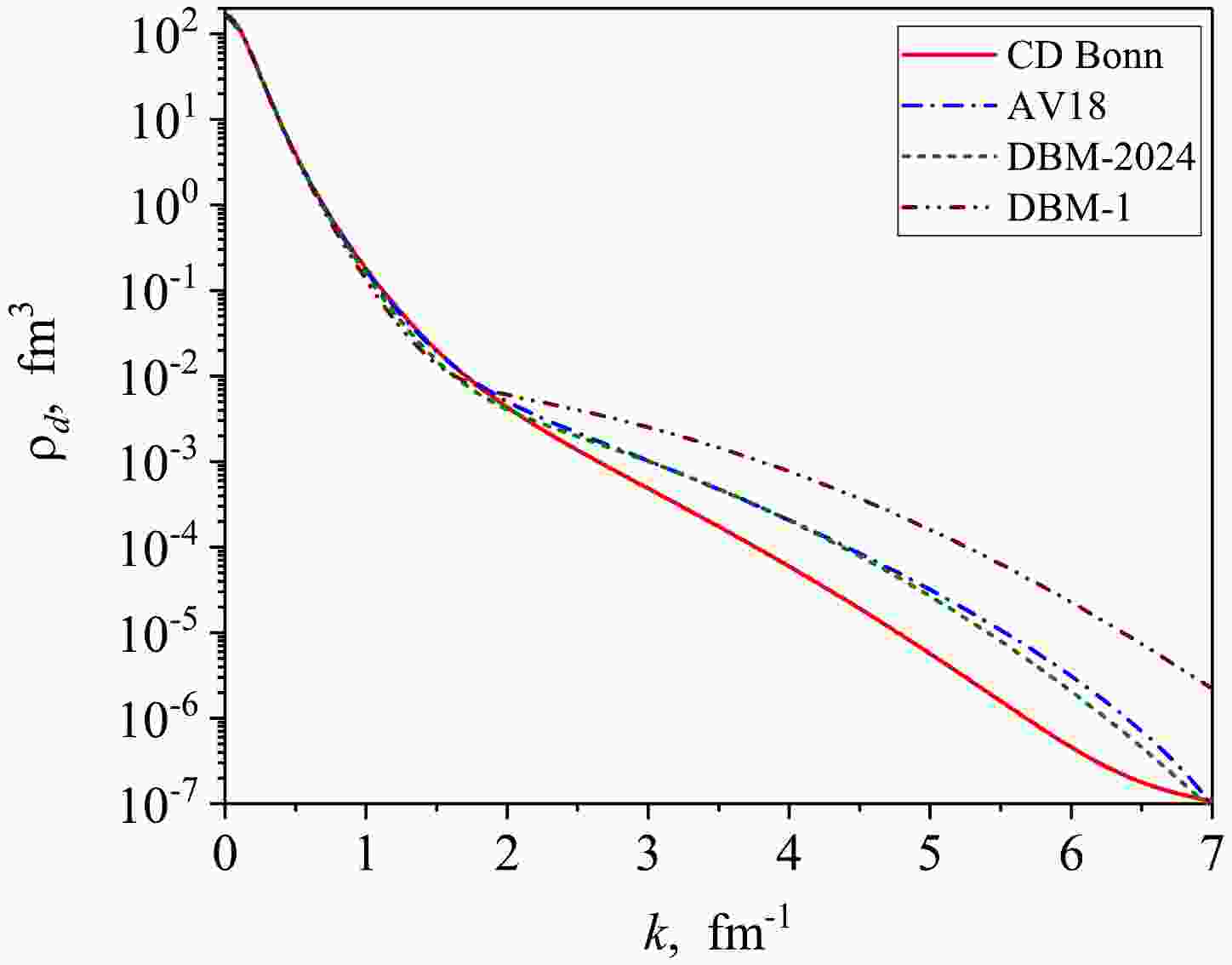
The corresponding UMD for the spin-triplet channel is just the deuteron momentum distribution. A comparison of the deuteron momentum distributions for different $ NN $ interactions is presented in Fig. 5. Below we consider four models for $ NN $ interactions, viz. the CD Bonn potential [27], AV18 potential [28] and two versions of the dibaryon model with energy dependent interactions DBM-1 and DBM-2024 (see details and further refs. in [30]). As is seen from Fig. 5, the deuteron momentum distributions at small relative momenta are nearly indistinguishable for the considered interactions while in high-momentum region, at $ k>1.3 $ fm^-1, all distributions show quite different behavior. Thus, we chose the above interactions with evidently different high-momentum properties for the further tests of the presented formalism.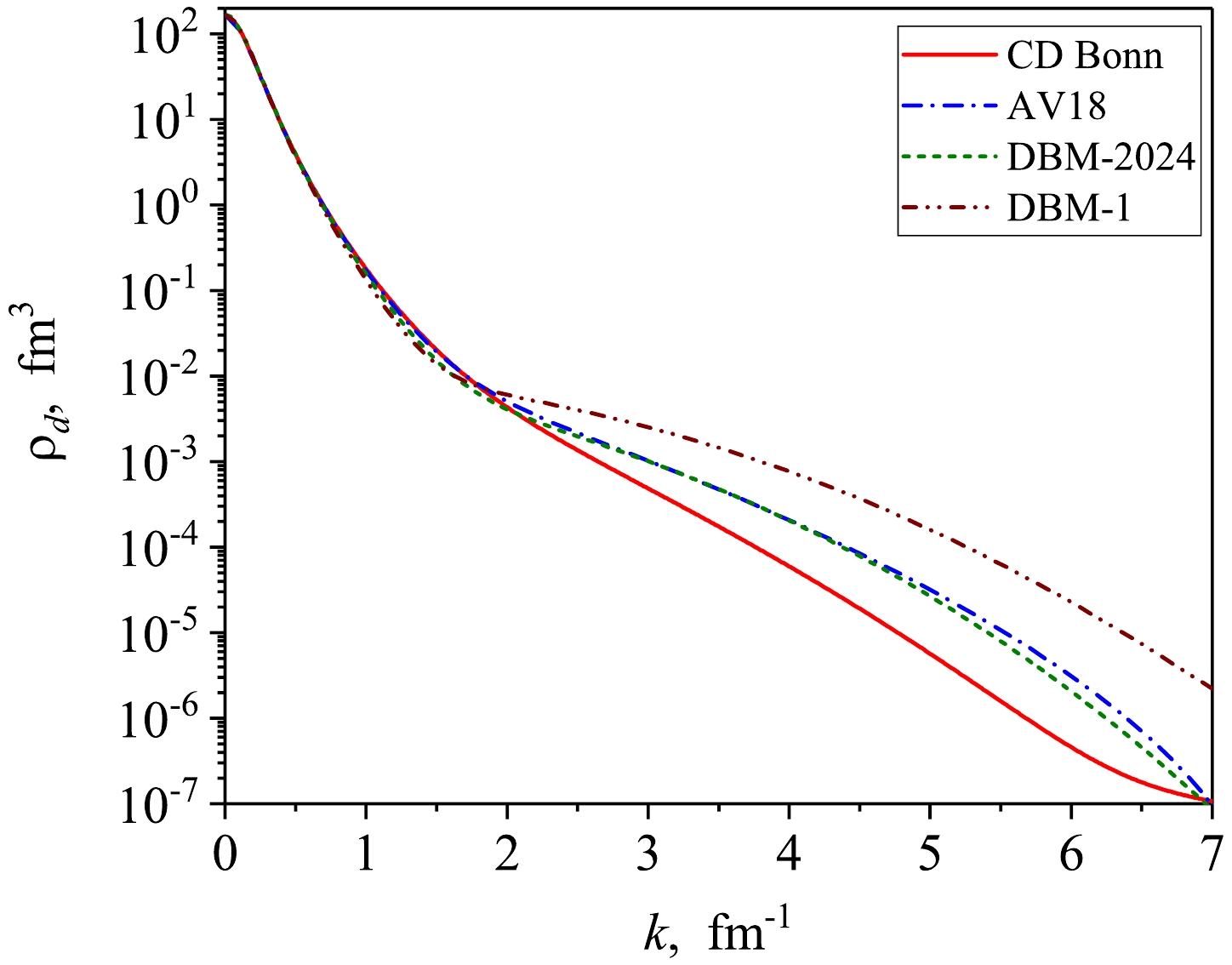

Figure 5.  (color online) Spin-triplet (deuteron) $np$-momentum distributions for different realistic $NN$-potentials: CD Bonn (solid curve), AV18 (dash-dotted curve), DBM-2024 (dashed curve) and DBM-1 (dash-dot-dotted curve).

A comparison of the spin-singlet $ np $ UMDs constructed from the scattering wave functions (calculated at $ p = 0.008 $ fm^-1) using the equation (41) for the four above interactions is shown in Fig. 6.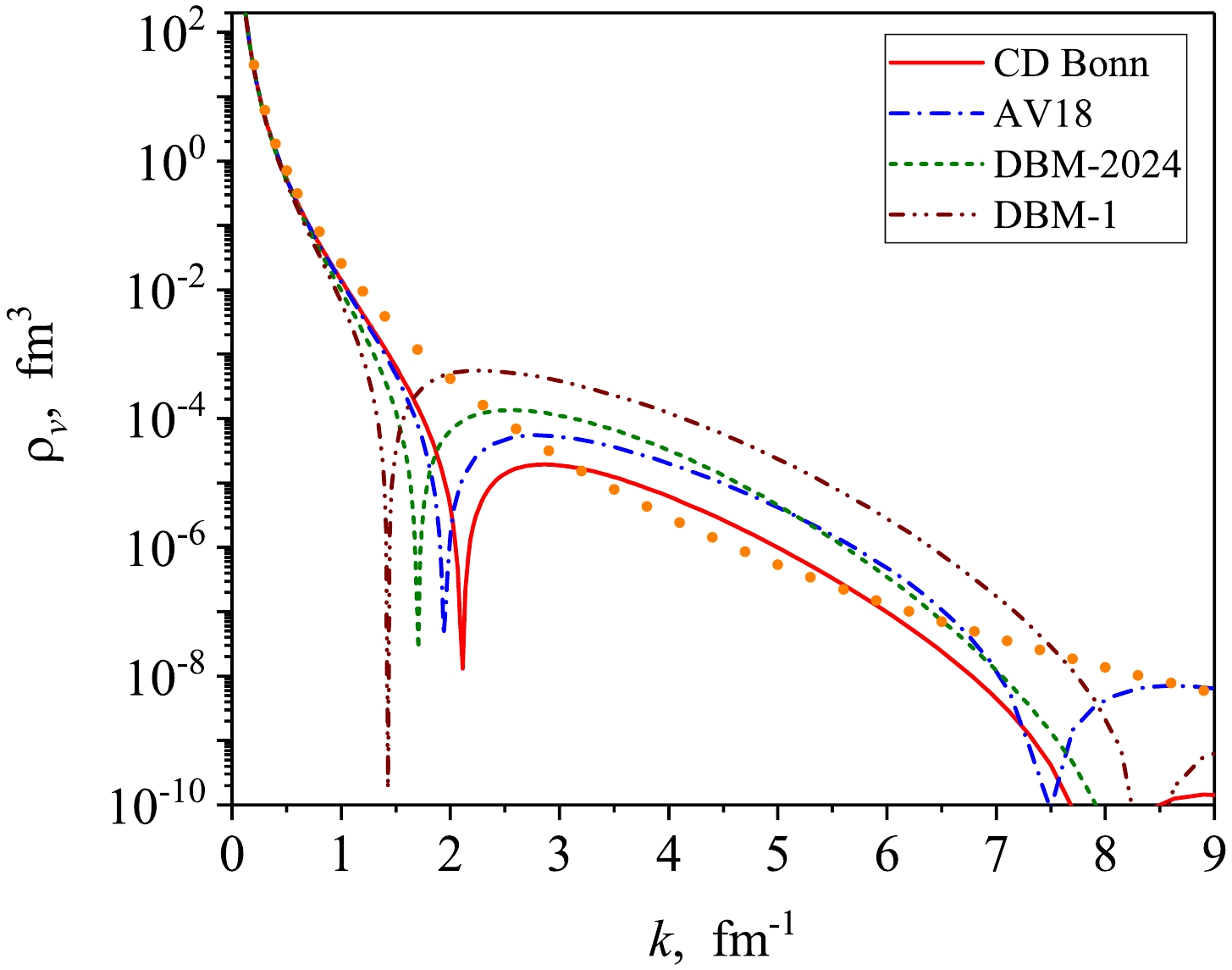

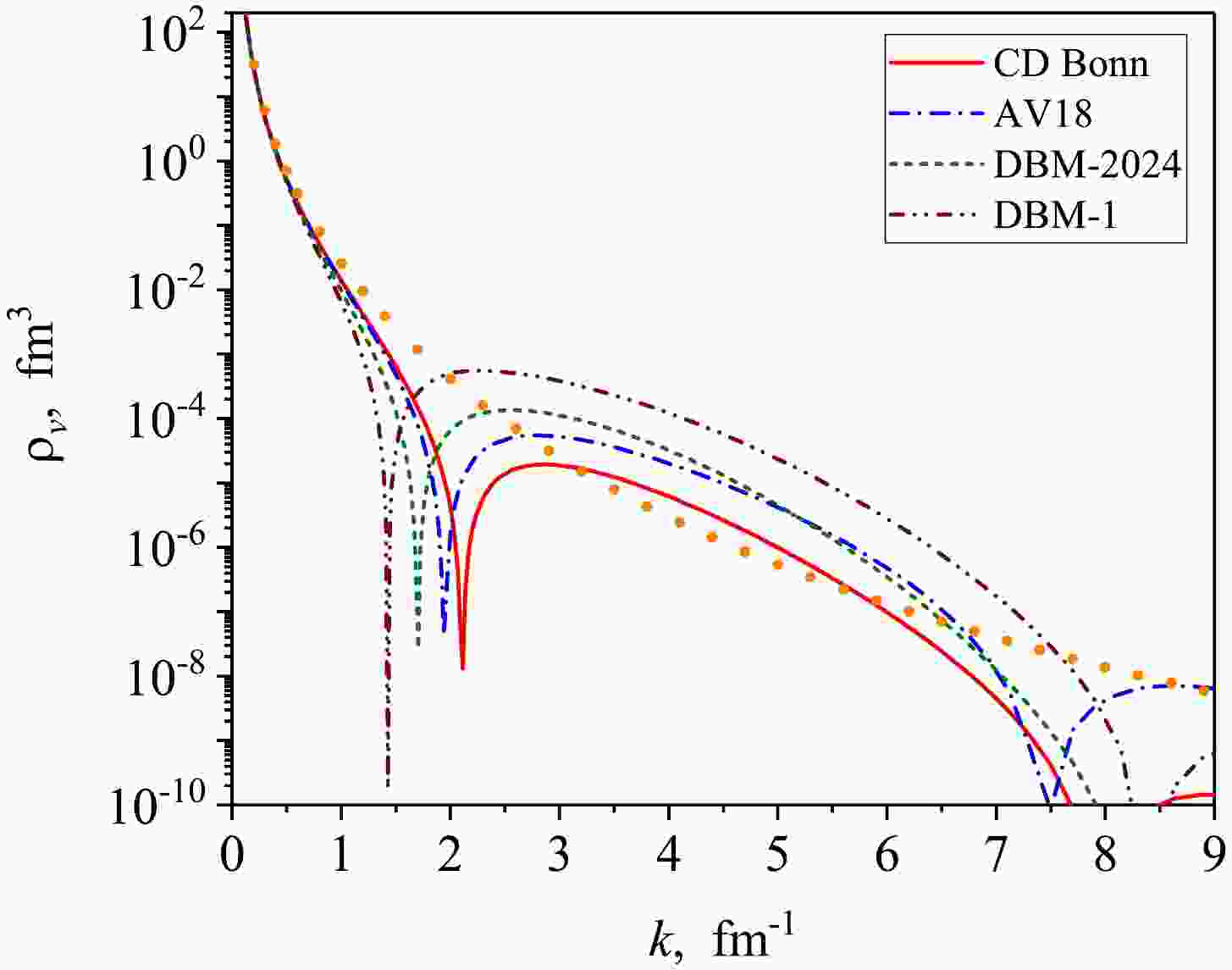
Figure 6.  (color online) Spin-singlet $np$ universal momentum distributions for different realistic $NN$-potentials. The notations are the same as in Fig. 3. The dots show the virtual-state momentum distribution for the Yamaguchi potential.

It is seen that the UMDs for different interactions are almost the same in the momentum region $ 0.2<k<0.6 $ fm^-1. Also in this region they are close to the exact distribution $ \rho_v(k) $ for the separable Yamaguchi potential, shown by dots. At the same time, at $ k >1 $ fm^-1 all distributions exhibit different behavior, which is primarily due to the difference in the position of the nodes of the corresponding wave functions.

Thus, by using the definition (41), one can evidently compare high-momentum components of the distributions in the spin-singlet channels for different $ NN $ interactions. Below we introduce constants which allow us to quantify these differences.

To consider high-momentum parts of the distributions, which just correspond to SRC, let's introduce the boundary of the high-momentum region as a constant $ p_0 $. Usually, it is taken to be comparable with the Fermi momentum $ k_F $ in nuclei [5, 13].

A high-momentum part of the deuteron (bound-state) distribution is defined by the integral:

which, due to normalization to unity (2), is simply the weight of the high-momentum components in the deuteron. The values of $ a_2^d $ are different for different realistic $ NN $-interactions [13].

Now one can consider the high-momentum parts of the singlet UMDs by taking the integral of the momentum distribution for the virtual state (6):

It should be emphasized that, unlike the triplet channel, the quantity $ a_2^v $ is not the weight of the high-momentum tail in the singlet channel. However, the quantity $ a_2^v $ is dimensionless and its value estimates the high-momentum contribution for different $ NN $ interactions.

For practical calculation of these quantities, let us consider high-momentum integrals of the squared modulus of scattering wave functions:

where $ p\ll p_0 $ is assumed, so that these integrals are finite. The functions $ c_2^{s(t)}(p) $ do not have the same meaning as values $ a_2^d $ and $ a_2^v $, as is already evident from their dimension (fm$ ^{-3} $), however, they contain quantitative information about the high-momentum components of the $ NN $ scattering states.

By using FWF, one can get an explicit approximate expression for the constant $ a_2^{v} $ for a virtual state:

The same approximate equality is also valid for the triplet channel, but there is no need for it there, since the high-momentum constant $ a_2^d $ is simply calculated from the deuteron momentum distribution.

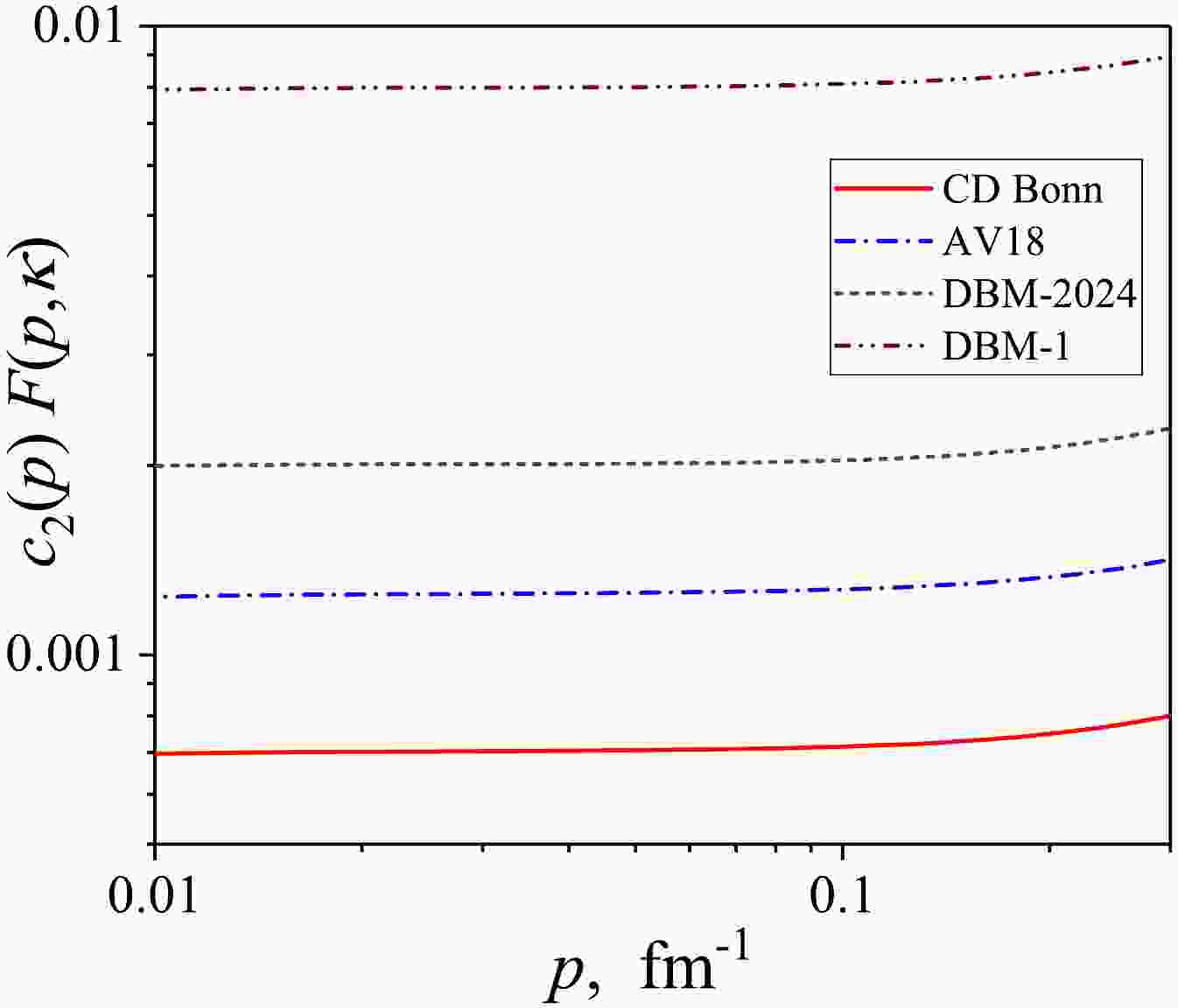
To check the relation (46), we show in Fig. 7 the function $ c_2^s(p)F(p, \varkappa_{np}) $ for the $ NN $ potentials considered here. As can be seen from the figure, these functions are practically constant at $ p<0.1 $ fm^-1, which allows us to calculate the values $ a_2^v $ for different potentials from the scattering wave functions.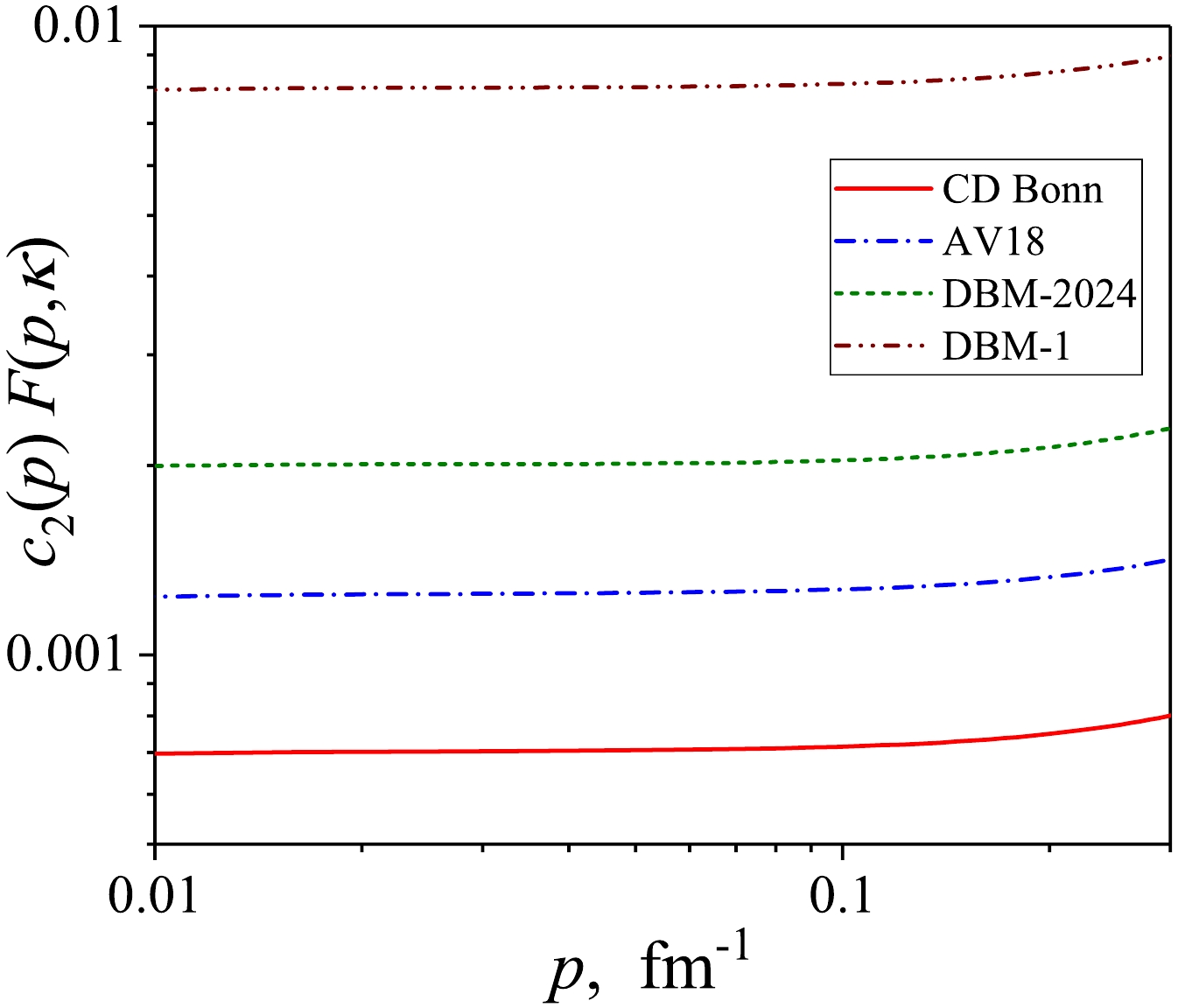

Figure 7.  (color online) Function $c_2^s(p)$ with the factor (21) at low on-shell momentum p for different $np$ potentials.

The values of $ a_2^v $ for different $ NN $ interactions in comparison with $ a_2^d $ found for the deuteron momentum distribution are given in Table 1. Here the high-momentum region boundary $ p_0 = 1.4 $ fm^-1 is used, which corresponds to the generally accepted value of $ k_F $ for nuclei. From Table 1 it can be seen that the spread of high-momentum constants for various interactions is different for triplet and singlet channels. In all cases, even for the traditional AV18 and CD Bonn models, the $ a_2^{v} $ constants differ from each other more than the $ a_2^d $ constants for the same potentials.

model	$ a_2^d \qquad $	$ a^{v(np)}_2\qquad $	$ a^{v(pp)}_2 \qquad $	$ a_2^{v(pp)}/a_2^d $
CD Bonn	0.031	0.0007	0.0009	0.03
AV18	0.041	0.0013	0.0016	0.04
DBM-2024	0.036	0.002	0.0026	0.07
DBM-1	0.068	0.008	0.011	0.16

Table 1.  High-momentum constants for different $ NN $ models for $ p_0=1.4 $ fm^-1.

Note also that the $ a_2^d $ value for DBM-2024 is a bit smaller than for AV18, while the $ a_2^v $ values are more than 1.5 times larger than for AV18. Thus, one can conclude that the value $ a_2^v $ represents an independent high-momentum characteristics of the $ NN $ interaction in spin-singlet channels.

In Table 1, the high-momentum constants for the $ pp $ interaction, $ a_2^{v(pp)} $, are also presented. These constants correspond ² to $ \varkappa_{pp}\approx - 0.054 $ fm^-1. It is clear that the ratio $ a_2^{v(pp)}/a_2^{v(np)} $ depends on the model very weakly.

Finally, in Table 1 we present the ratios of constants $ a_2^{v(pp)}/a_2^d $ which are discussed in the next subsection.

Recently [18] we have proposed a way to calculate the weight of high-momentum components for scattering wave functions via the integral over on-shell momentum p up to some small value q ($ q\ll{p_0} $):

Such an integral is dimensionless and can be compared with the $ a_2^d $ value for the bound-state wave function.

Now, one can also compare quantitatively the weight of high-momentum components for the singlet and triplet channels by using the ratio [18]:

The values in the numerator and denominator represent the cumulative weights of high-momentum components from all the states of the spectra up to the energy related to the considered on-shell momentum q in the singlet and the triplet $ NN $ channels correspondingly.

Using the relations (46) as approximation for both singlet and triplet functions $ c_2(p) $ at small values of p, one gets the following approximate expressions for the high-momentum integrals $ A(q) $ at small q:

This results in the relation for the ratio $ \eta(q) $:

The nice feature of this presentation is that the function ζ depends on the on-shell parameters $ \varkappa_v $ and $ \varkappa_d $ only, so that the dependence on q in the ratio η is the same for all the realistic $ NN $ interactions. Thus, the only difference in the values of $ \eta(q) $ for different $ NN $ interaction models is the ratio of the constants $ a_2^v/a_2^d $. At $ q = | \varkappa_{pp}| $ and $ q = \varkappa_d $ the corresponding ratios are the following:

One can see, the ratio of high-momentum weights $ \eta(q) $ increases with increasing q showing that spin-singlet channel contribution to high-momentum components grows faster with energy than the spin-triplet one. At the same time, the ratio $ a_2^{v(pp)}/a_2^d $ represents an informative characteristic for high-momentum components of the momentum distributions in continuum for the chosen model of the $ NN $ interaction.

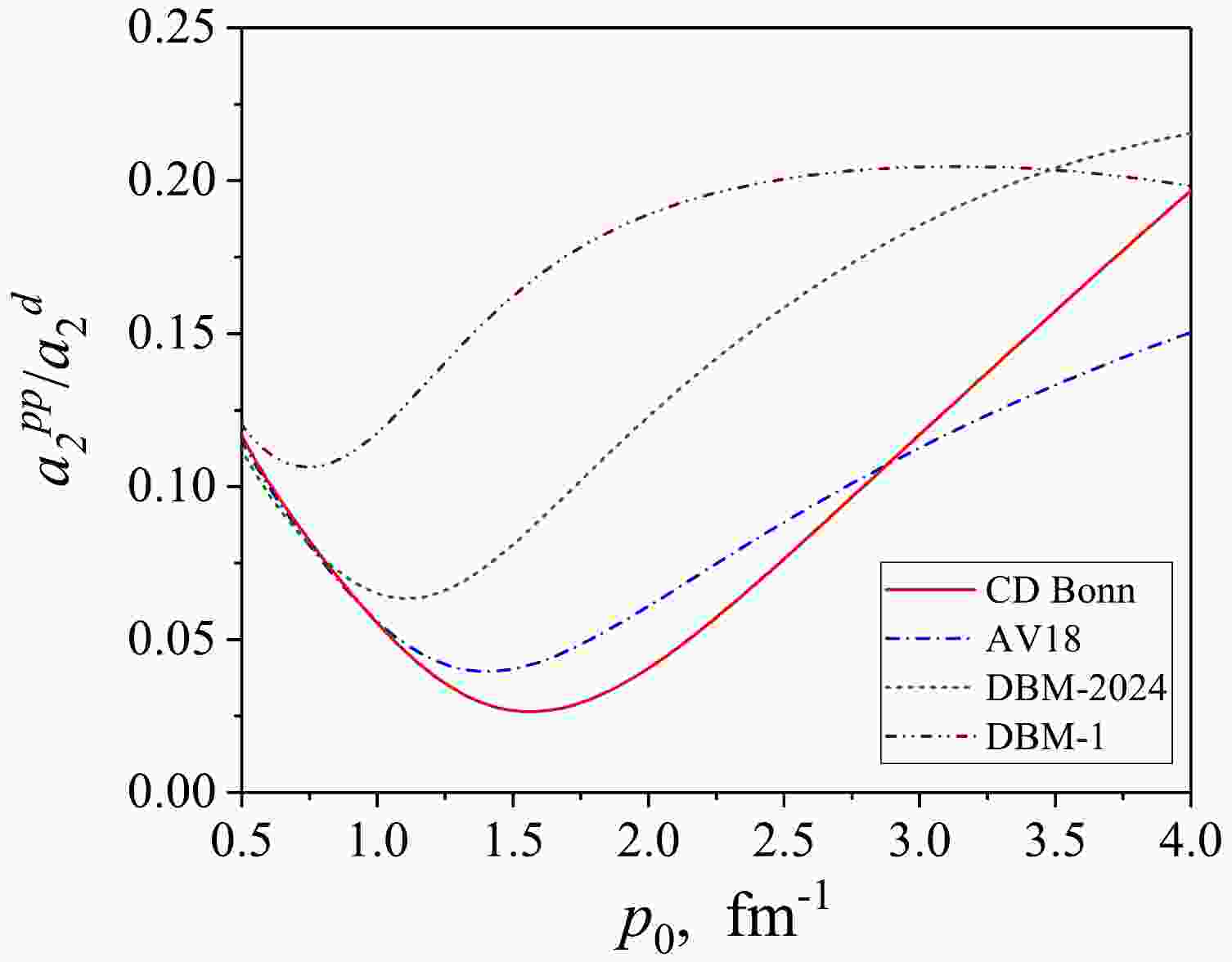
Using the data from Table 1, one can compare the ratios $ a_2^{v(pp)}/a_2^d $ at $ p_0 = 1.4 $ fm^-1 for different $ NN $ interactions. From the considered models, the minimal value of this ratio corresponds to the CD Bonn potential while the DBM-1 gives an essentially greater one. Based on the contact formalism, we may also expect that the use of an interaction with greater $ a_2^v/a_2^d $ ratio at two-nucleon level will lead to greater mean values for the ratios of $ pp $ and $ np $ momentum distributions in nuclei.

Also, we present in Fig. 8 the ratio $ a_2^{v(pp)}/a_2^d $ as a function of the high-momentum parameter $ p_0 $. One can see that the ratio $ a_2^{v(pp)}/a_2^d $ depends significantly on the value of $ p_0 $. It is interesting to note that the minimum of this ratio for the conventional AV18 and CD Bonn potentials corresponds just to the most frequently considered range of $ p_0 \sim 1.3-1.5 $ fm^-1 where the pp/np ratio is very sensitive to the chosen value of $ p_0 $.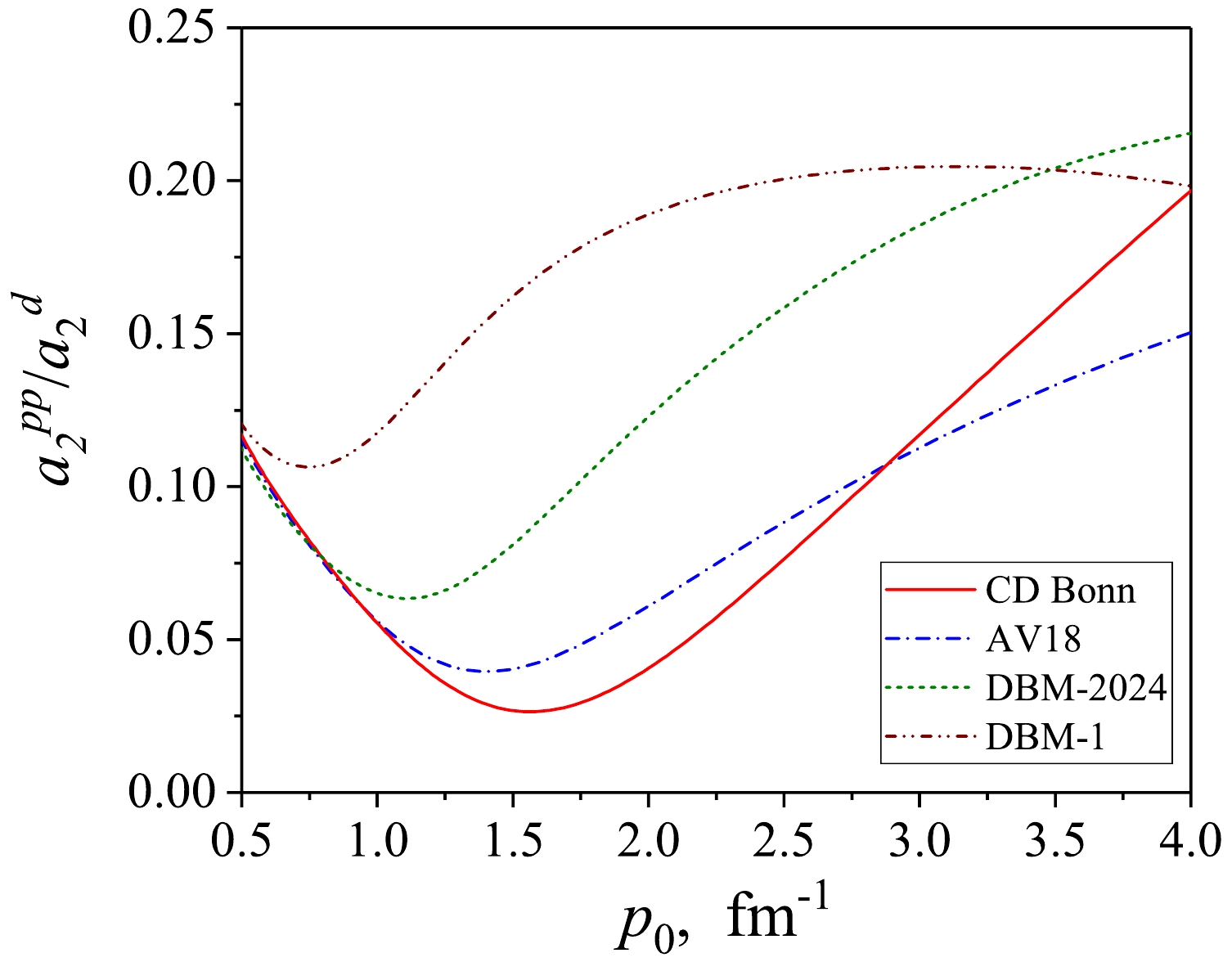

Figure 8.  (color online) Ratio of $a_2^{v(pp)}/a_2^d$ values as a function of high-momentum parameter $p_0$ for different $NN$ potentials.

Thus, the UMDs suggested in this Section is quite convenient for practical calculations. The developed formalism also allows to introduce a high-momentum constant $ a_2^v $ for the spin-singlet channel in addition to $ a_2^d $ for the deuteron channel. Besides, some estimations for the ratios of $ pp $ and $ np $ momentum distributions in nuclei for various models of $ NN $ interactions can be given already at the two-body level. In the next Section we show how the introduced UMDs can be employed within the contact formalism for analyzing $ NN $ distributions in $ ^3 {\rm{He}}$.

Here we will test the factorization property (1) of two-nucleon momentum distributions $ \rho^A_{ { {NN}}} $ for $ ^3 {\rm{He}}$ nucleus as an example and calculate the nuclear contacts $ C^{^3{\rm He}}_{ { {NN}}} $ for various interactions. We consider the distributions $ \rho^A_{ { {NN}}}(k,Q = 0) $ which corresponds just to back-to-back SRC pairs, where Q is the center-of-mass momentum of the pair.

In this case it is convenient to introduce the normalized distribution at $ Q = 0 $ as follows [9]:

where $ n_{ { {NN}}} $ is a number of nucleon pairs which is equal to 2 for $ NN = np $ and 1 for $ NN = pp $ correspondingly. Note that with such normalization, the distribution of the center-of-mass momentum of a pair of nucleons $ \rho^{A, { {NN}}}_{\rm{cm}}(Q) $ is assumed to be normalized to 1.

According to [9], the normalized momentum distribution is proportional to the UMD $ \rho_{ { {NN}}}(k) $ in the high-momentum region with the nuclear contact as a factor:

Since here we consider only the $ ^3 {\rm{He}}$ nucleus, we have omitted the index A, indicating the nucleus, in the notation of the distributions ρ and nuclear contacts C. Below we use the UMDs $ \rho_{np} = \rho_d $ and $ \rho_{pp} = \rho_{v(pp)} $ for $ np $- and $ pp $-pairs correspondingly.

We use the same four $ NN $ interactions: CD Bonn, AV18, DBM-1, and DBM-2024 listed in the previous Section and the $ ^3 {\rm{He}}$ $ NN $-distributions calculated using these interactions and the corresponding three-particle forces. The $ ^3 {\rm{He}}$ distributions for AV18 potential with UIX $ 3N $ force are taken from Ref. [29], the distributions for CD Bonn potential supplemented with $ 3N $ TM force are presented in Ref. [13], and the distributions for two versions of the DBM are obtained by the present authors from the variational calculations on an antisymmetrized Gaussian basis (see details in Ref. [30]).

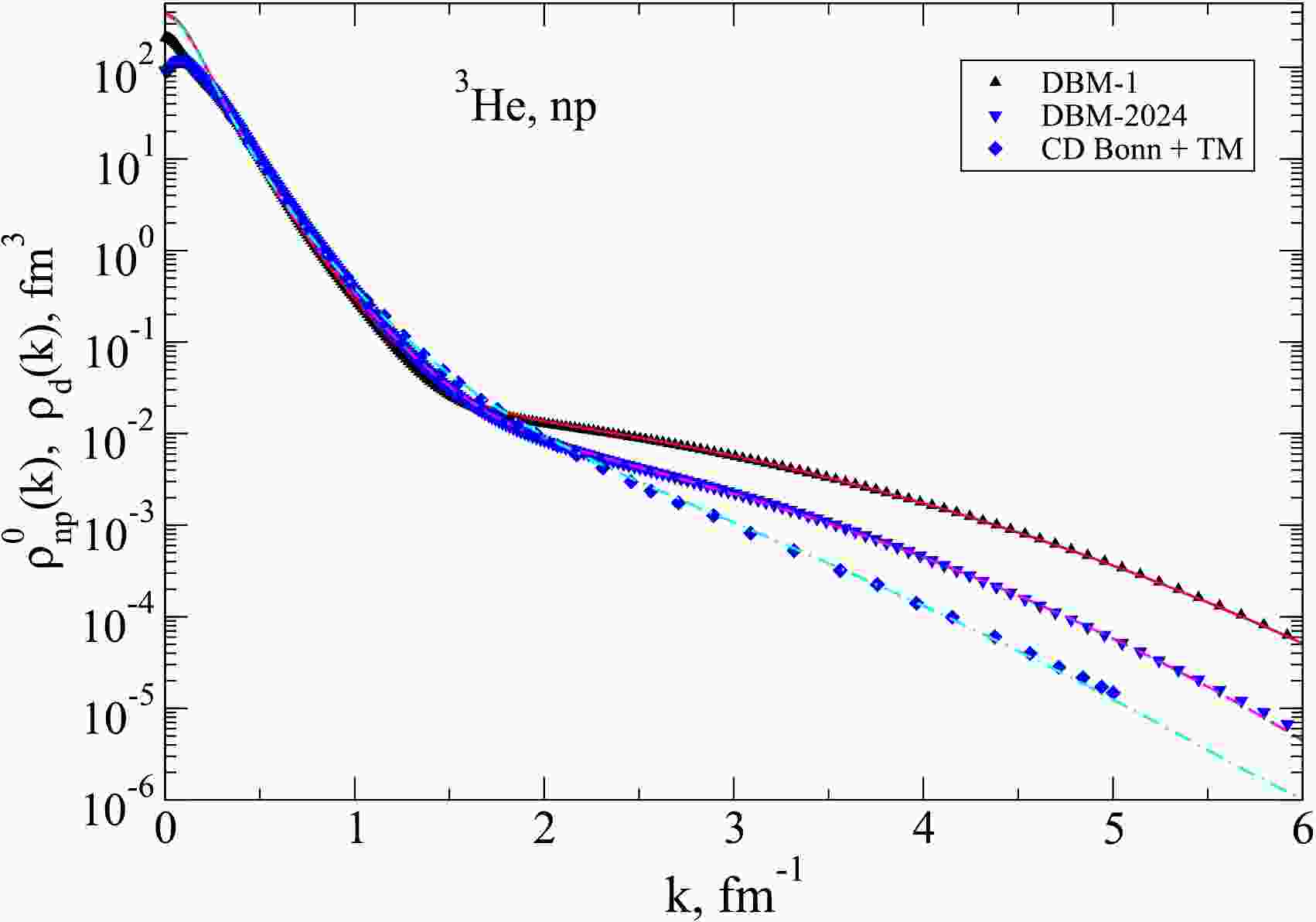
First, let us check how the factorization (53) is satisfied for $ np $ distributions, where the momentum distribution in the deuteron is used as the UMD. Fig. 9 shows the normalized momentum $ np $-distributions in $ ^3 {\rm{He}}$ at $ Q = 0 $, $ \rho^0_{np}(k) $, for the different interaction models in comparison with the corresponding deuteron distributions $ \rho_d(k) $ multiplied by the corresponding nuclear contacts $ C_{np} $.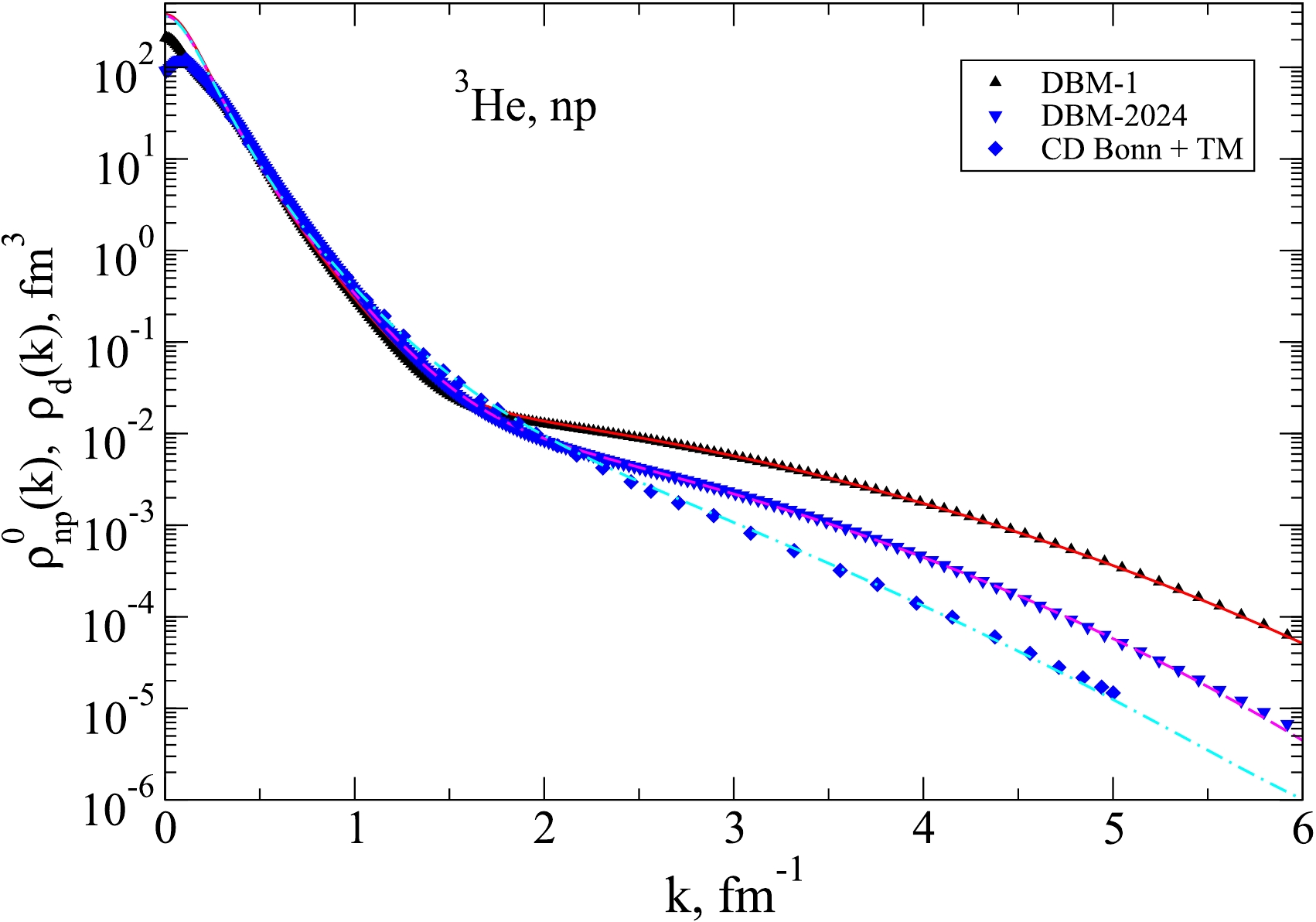

Figure 9.  (color online) The normalized momentum $np$-distributions in $^3$He at $Q=0$, $\rho^0_{np}(k)$, for three interaction models (DBM-1 – triangles-up, DBM-2024 – triangles-down, CD Bonn+TM – diamonds) in comparison with the corresponding deuteron distributions $\rho_d(k)$ multiplied by $C_{np}$ (solid curves).

Here, for all the interaction models considered, the $ ^3 {\rm{He}}$ momentum distributions achieve the deuteron “asymptotics” already at the relative momentum $ k \sim 1.5 $ fm^-1. Although high-momentum parts of the distributions for different interaction differ strongly, their ratios to their “own” deuteron momentum distributions in the high-momentum region (i.e. the nuclear contacts) are nearly independent on the interaction model. The found nuclear contacts $ C_{np} $ for all considered interaction models are close to 2, which agrees with the results of Ref. [9]. The values of $ C_{np} $ found in the present study are given in Table 2.

	AV18 + UIX	CD Bonn + TMa	DBM-1	DBM-2024
$ C_{np} $	$ 1.82\pm 0.07 $	2.2	$ 2.26\pm 0.03 $	$ 2.17\pm 0.04 $
$ C_{pp} $	$ 2.91\pm 0.16 $	3.1	$ 3.12\pm 0.03 $	$ 2.98\pm 0.05 $
aThe data on the distribution in $ ^3 {\rm{He}}$ are obtained by digitizing the figure in Ref. [13], so that the results are given without errors.

Table 2.  Nuclear contacts for $ ^3 {\rm{He}}$ for different models of $ NN $ and $ 3N $ interaction.

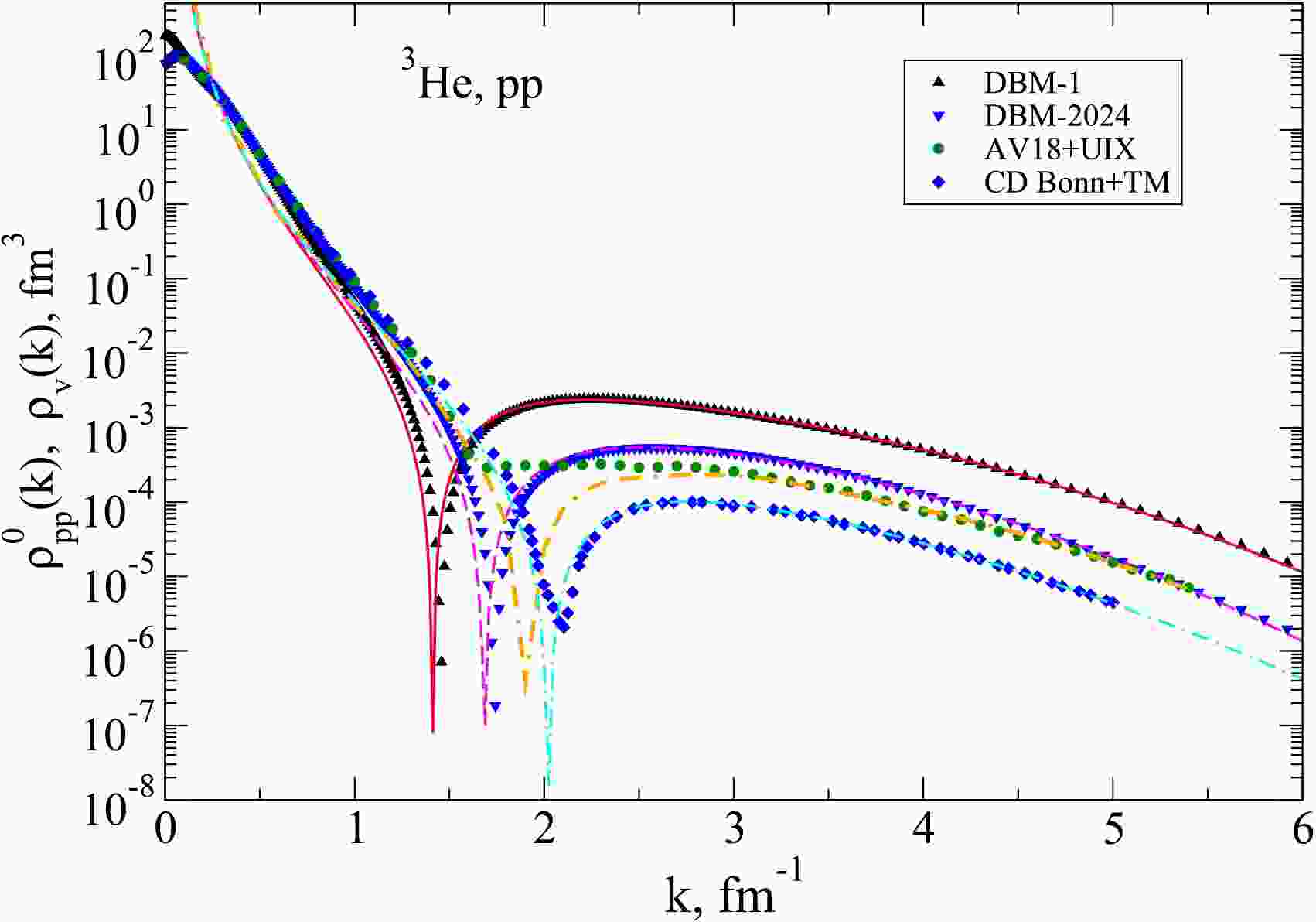
Now, having the UMD for the singlet channel $ \rho_v(k) $, one can compare the normalized momentum $ pp $-distributions in $ ^3 {\rm{He}}$ at $ Q = 0 $ with these UMDs and find the corresponding nuclear contacts $ C_{pp} $. Fig. 10 shows such a comparison for the four interaction models considered. Here the ratios of the $ pp $-distributions to the corresponding UMDs become nearly constant at values of $ k\geq 2.3 $ fm^-1. In Figure, we show the UMDs multiplied by the corresponding nuclear contacts $ C_{pp} $ the values of which are given in Table 2 and are close to 3.

Figure 10.  (color online) The normalized momentum $pp$ distributions in $^3$He at $Q=0$, $\rho^0_{pp}(k)$, for four interaction models in comparison with the corresponding singlet UMDs, multiplied by the contacts $C_{pp}$. The notations are the same as in Fig. 9 plus filled circles representing AV18+UIX.

As mentioned above, the values of the nuclear contacts found for the $ np $-pairs are consistent with the results of Ref. [9]. However, these values of both $ np $- and $ pp $-nuclear contacts differ from those given in Ref. [5] because the definitions of the corresponding UMDs and nuclear contacts are different there ³ (see also the relations between momentum distributions in Appendix A).

Thus, we have shown that the nuclear contacts for the $ ^3 {\rm{He}}$ nucleus, calculated with respect to the two-particle UMD corresponding to a virtual state are indeed almost identical for $ NN $ interactions, nevertheless the high-momentum components of the momentum distributions for those interactions differ significantly at $ k>p_0 $. Based on the results of the contact formalisms [5, 9], one may expect that this property will keep for heavier nuclei.

In this paper we have suggested a way to construct the momentum distributions for the spin-singlet $ ^1S_0 $ $ NN $ channels based on the virtual state from the low-energy scattering wave functions. The advantages of such momentum distributions are the followings.

$ ({\rm{i}}) $ The distribution is given by the square integrable function and does not depend on the boundary of the high-momentum region $ p_0 $.

$ ({\rm{ii}}) $ One can introduce a two-nucleon short-range constant $ a_2^v $ for spin-singlet channels, which characterizes the $ NN $ interaction with respect to high-momentum components of wave functions, similar to the value $ a_2^d $, well known for the deuteron channel.

$ ({\rm{iii}}) $ The ratio $ a_2^{v(pp)}/a_2^d $ differs for various realistic $ NN $ models and allows to estimate differences in ratios of $ pp $-and $ np $-momentum distributions in nuclei.

$ ({\rm{iv}}) $ In the low-momentum region, the momentum distribution for the virtual state depends only on the on-shell characteristics of the $ NN $-system, such as the wave number $ \varkappa $ and the scattering length, which are the same for all realistic $ NN $ interaction models. Thus, the introduced UMDs turn out to be the same for different models in the momentum region of 0.2-0.6 fm⁻¹, exhibiting obvious differences at high momenta.

$ ({\rm{v}}) $ Due to the previous property, the nuclear contacts calculated relatively to the introduced UMDs should be nearly the same for different realistic $ NN $ interactions.

The last property has been demonstrated for $ A = 3 $ nuclei with four essentially different models of $ NN $ interactions which correspond to the same observables in $ 2N $ and $ 3N $ systems. One can expect that a weak dependence of nuclear contacts on the $ NN $ interaction will also hold for heavier nuclei that should be studied and verified in future researches.

The above conclusion seems to differ from the results of Ref. [5] where a spread of the $ pp $-nuclear contacts for different $ NN $ interactions has been found. This is caused by the difference in the definitions of UMDs and nuclear contacts. At the same time, the relation (58) from the Appendix A shows that the ratio of nuclear contacts for two nuclei remains the same for differently defined UMDs. This result agrees with the findings of Ref. [5] where a very weak dependence on the interaction models for such ratios of the nuclear contacts was demonstrated.

The suggested spin-singlet universal distributions based on the momentum distribution for the virtual state can be considered as a supplement to the contact formalism presented in Ref. [9] for the triplet $ np $ distributions. Since the proposed UMDs do not depend on the high momentum boundary $ p_0 $, one can expect that our formalism will be suitable for calculations with $ NN $ models using various “low-k” approximations. In particular, the nuclear $ pp $-contacts for such interactions would be the same as for other realistic $ NN $ models, since the momentum distributions for the virtual state are nearly identical at low momenta for all realistic $ NN $ interactions. One may assume that the contacts will not depend on the cut-off parameters for this type of $ NN $ potentials as well.

Let's show how the introduced UMDs are related to other universal distributions used in the GCF.

The momentum distribution for the virtual state can be calculated by using the scattering wave function at zero energy $ \psi_{p = 0}^s(k) $ (normalized according to (7)) from the relation:

which is valid with high accuracy at $ k>0.5 $ fm⁻¹.

The universal momentum distributions normalized to unity in the region $ [p_0,\infty] $ can be calculated from the ratios [18]:

where functions $ c_2(p) $ are defined in Eq. (45). It has been shown [18] that these distributions do not depend on p in high-momentum region.

Thus, by using Eq. (46) for the spin-singlet channel, one gets that such 'tail-normalized' distribution is related to the density defined in Eq. (41) as follows:

which can be used at $ p = 0 $ as well. At the same time, the nuclear contacts defined relatively these two types of the universal distributions are recalculated as follows:

where $ \bar{C}_{pp}^A $ is a nuclear contact corresponding to the distribution $ \bar{\rho} $. This property shows that the ratios of the nuclear contacts for two nuclei $ A_1 $ and $ A_2 $ are the same for both distributions: