A Study on the Triggering of Nucleonic Direct Urca Processes in Neutron Stars of Specific Masses and Their Hyperon Dependence

Currently, global pulsar research has made significant progress: the Australia Telescope National Facility (ATNF) database has recorded over 3,700 certified pulsars [1]. Since China’s Five-hundred-meter Aperture Spherical Radio Telescope (FAST) came into operation [2], it has discovered about one thousand new pulsars, surpassing the combined discoveries of all other telescopes during the same period [3−6]. However, in stark contrast to these observational breakthroughs, the core questions about the internal composition of neutron stars remain unresolved. Although observations clearly confirm the extreme compactness of neutron stars — with radii of $ \sim $ 10 km and masses up to 2 $ M_{\odot} $ — direct observational constraints on their core composition, such as whether nucleons undergo hyperonization, deconfinement phase transitions, or form meson condensates, are still lacking [7, 8]. The presence of hyperons in neutron star cores stands as a pivotal scientific inquiry, whose resolution could revolutionize our understanding of dense matter physics and astrophysical phenomena. If confirmed, hyperons would not only soften the equations of state of neutron stars — thereby reshaping theoretical models of stellar structure — but also affect particle composition distributions, thermal evolution dynamics, and observable signatures such as rotational behaviors and gravitational wave emissions. Against this backdrop, neutron star equations of state, as theoretical frameworks describing the pressure-density relationship, play an irreplaceable role in understanding their overall structure and macroscopic properties [9−12]. In recent years, the relativistic mean-field (RMF) model has been frequently used to calculate the equation of state of neutron star matter containing hyperons, and it can well predict some properties of neutron stars [13−17]. However, due to the "hyperon puzzle", even when hyperon coupling constants are determined using the SU(6) spin-flavor symmetry based on the quark model, the maximum mass of neutron stars is still significantly reduced. For this reason, SU(3) flavor symmetry has been widely applied in studies on the properties of neutron stars with hyperons [18−24]. This is because SU(3) flavor symmetry modifies the coupling strengths between isoscalar, vector mesons (ω and ϕ) and the baryon octet, enabling the maximum mass of neutron stars containing hyperons to reach the inferred mass values of currently known massive pulsars. In recent years, mass and radius inferences for four pulsars—PSRs J0030+0451, J0740+6620, J0437-4715, and J1231-1411—from NASA’s Neutron Star Interior Composition Explorer (NICER) experiment have further constrained neutron star equations of state [24−29].

The thermal evolution and cooling processes of neutron stars serve as crucial probes of their core physical properties, maintaining profound and multi-dimensional links to the equations of state [30−34]. As a critical aspect in compact star evolution, the thermal evolution of neutron stars deeply reflects their internal matter states, microscopic interactions, and macroscopic energy transport mechanisms. Cooling processes not only record the initial high-temperature state after a supernova explosion but also continuously trace stellar structural evolution through mechanisms like neutrino radiation and photon emission. Notably, Potekhin et al. have conducted systematic studies on the cooling mechanisms of isolated and transient accreting neutron stars, suggesting the existence of neutron stars undergoing rapid cooling via baryonic direct Urca processes [35−37]. Marino et al. further proposed that the baryonic direct Urca processes may explain the anomalously low surface temperatures observed in young neutron stars such as PSR J0205+6449, PSR B2334+61, and CXOU J08524617 [32]. While considerable in-depth research has been conducted on the effects of hyperons and hyperonic direct Urca processes on the cooling of neutron stars [38−44], studies investigating the influence of hyperons on the radial distribution of neutrino emissivity and luminosity in the nucleonic direct Urca process of neutron stars with a fixed mass remain relatively scarce. In light of this current situation, this work attempts to conduct a preliminary exploration of the issues under two symmetries within the relativistic mean field model framework by integrating astronomical observations, hoping to provide some reference for searching for evidence of the existence of hyperons in pulsar observations.

The content of this work is structured as follows. In Section 2, we introduce the theoretical methods for deriving neutrino emissivity and luminosity in the nucleonic direct Urca processes within the framework of the relativistic mean field theory. In Section 3, we discuss the neutrino radiation properties of the nucleonic direct Urca processes, and investigate the potential impact of hyperons on three pulsars with known masses on the luminosity of the nucleonic direct Urca based on the selected GM1 and NL3 parameters under the SU(6) spin-flavor and SU(3) flavor symmetries. Section 4 presents the summary and conclusions.

The nucleonic direct Urca processes efficiently generate neutrinos via weak interactions among nucleons within the neutron star core, dominating the rapid cooling during the early neutrino-dominated era. The nucleonic direct Urca processes consist of beta decay and capture reactions [45]. Neutron β decay: a neutron decays into a proton, emitting a lepton ($ l = e^{-} $ and $ \mu^{-} $) and an antilepton neutrino ($ \bar{\nu}_{l} $). Proton lepton capture: A proton captures a lepton, converting into a neutron and emitting a neutrino ($ \nu_{l} $). The specific forms are as follows:

The two reactions persist in the neutron star core at densities exceeding the nuclear saturation density ($ n_{0} \approx 2.7 \times 10^{14} $ g cm^-3, corresponding to $ n_{0} \approx 0.16 $ fm^-3), forming a "cooling channel" for neutrino radiation. Each reaction produces neutrinos carrying energies far exceeding the typical energy of thermal photons, ensuring that neutrino radiation dominates the early cooling stage [46, 47]. The total relativistic neutrino emissivity Q per unit volume and time in both reactions (A1 and A2) can be expressed by the Fermi Golden Rule [41, 48], namely,

Here, the weak-coupling constant is $ G_{F}=1.436\times10^{-49} $ erg cm³, the Cabibbo factor $ C=\cos\theta_{C}=0.973 $, the threshold factor $ \Theta(x)=1 $ when $ x\geq0 $, the vector constant $ C_{V}=1 $, and the axial-vector constant $ C_{A}\simeq1.26 $. The nucleonic kinetic energy is given by $ \varepsilon_{F}=\sqrt{m_{N}^{*2}+P_{FN}^{2}} $.

The neutrino luminosity of the nucleonic direct Urca processes, $ L_{\nu}^{D} $, can be obtained by integrating the neutrino emissivity Q over the volume element $ dV= 4\pi r^{2}(1-\frac{2m}{r})^{-\frac{1}{2}} dr $ of a neutron star [49], namely,

Here, $ e^{\Phi}=\left(1-\dfrac{2m}{r}\right)^{\frac{1}{2}} $. $ R_{crit} $ denotes the critical radius at which the nucleonic direct Urca processes cease in a neutron star of a given mass.

Here, we apply the relativistic mean field approximation, which includes σ, ω, ρ, $ \sigma^{*} $, and ϕ mesons, to describe the properties of the cores of neutron stars. The total Lagrangian density can be expressed as

With $ \psi_{B(l)} $ the baryonic (leptonic) Dirac field, $ \gamma_{u} $ the Dirac matrices, $ \vec{I}_{B} $ the baryonic isospin matrix, and $ m_B(l) $ the baryonic (leptonic) mass. $ g_{\omega B} $, $ g_{\rho B} $, and $ g_{\phi B} $ denote separately the $ \omega- $, $ \rho- $, and $ \phi-B $ coupling constants. $ W_{\mu v} = \partial_\mu \omega_v - \partial_v \omega_\mu $, $ R_{\mu v} = \partial_\mu{\mathbf{\rho}}_v - \partial_v{\mathbf{\rho}}_\mu $, and $ P_{\mu v} = \partial_\mu \phi_v - \partial_v \phi_\mu $ correspond individually to the field strength tensors for the ω, ρ, and ϕ mesons. The sum B runs over N (neutron and proton), Λ, $ \Xi^{-} $, and $ \Xi^{0} $. We have not considered $ \Sigma^{+} $, $ \Sigma^{0} $, and $ \Sigma^{-} $ hyperons due to the potential uncertainty of Σ hyperons at saturation density in nuclear matter [39, 50, 51].

In the relativistic mean field approximation, the five meson fields are replaced by their expectation values ($ \sigma^{0}, \sigma^{*0}, \omega^{0}, \rho^{0}_{3} $, and $ \phi^0 $), which yields the following linear Dirac equation for the baryonic field:

where $ I_{3B} $ is the third component of the baryonic isospin. $ m_B^{*} $ denotes the baryonic effective mass and can be written as $ m_B^{*}=m_B-g_{\sigma B}\sigma-g_{\sigma^*B}\sigma^* $. $ g_{\sigma B} $ and $ g_{\sigma^{*}B} $ are the σ- and $ \sigma^{*} $-B coupling constants, respectively.

Thus, the five average meson fields are solutions of the following equations of motion:

$ p_{FB (l)} $ denotes the baryonic (leptonic) Fermi momentum.

The baryonic and leptonic chemical potentials are given by

The energy density ε and pressure P of neutron star matter can be shown as follows:

We can derive the equations of state under the conditions of electric neutrality and beta equilibrium in neutron stars. We can thereby obtain the required nucleonic effective mass, chemical potential, and Fermi momentum, as well as the leptonic chemical potential and Fermi momentum, for calculating the neutrino emissivity in the nucleonic direct Urca processes (as shown in Eq. 1). By solving the Tolman-Oppenheimer-Volkoff equation [52, 53], the mass-radius relationships of neutron stars can be further obtained. Moreover, the Keplerian frequency can be obtained from the Relativistic Roche model [54, 55], and its relationship with the mass and radius of a neutron star is expressed as $ f_{\mathrm{max}}^{\mathrm{Roche}} \approx 1.0\; \mathrm{kHz} \left(\dfrac{M}{M_\odot}\right)^{\frac{1}{2}}\left(\dfrac{R}{10\; \mathrm{km}}\right)^{-\frac{3}{2}} $.

In this work, we analyzed the influence of hyperons on the mass-radius, mass-density, mass-Kepler frequency, neutrino emissivity-radius, and neutrino luminosity-mass relationships of neutron stars, which are obtained using the relativistic mean field theory model with the parameter sets GM1 and NL3. To this end, we considered four different equations of state: (i) A neutron star consisting only of neutrons, protons, electrons, and muons, denoted as npeμ. (ii) A neutron star containing neutrons, protons, electrons, muons, and hyperons (Λ, $ \Xi^{-} $, and $ \Xi^{0} $). Regarding the baryon-meson coupling constants, five mesons, namely σ, ω, ρ, $ \sigma^{*} $, and ϕ, are included in the general SU(3) flavor symmetry. This case is denoted as SU3: npeμ+hyperons. (iii) Similar to case (ii), except that the hyperon-meson coupling constants in this case follow the SU(6) spin-flavor symmetry. Case (iii) is named SU6: npeμ+hyperons. (iv) Identical to case (iii), but without the $ \sigma^{*} $ and ϕ mesons, and is denoted as SU6-no $ \sigma^{*} $, ϕ: npeμ+hyperons. The specific values of the GM1 and NL3 parameter sets under the two symmetries can be referred to in Table 1 [18, 22]. For an in-depth discussion of hyperonization in neutron stars and related research under complex physical scenarios, Refs. [19, 20] provide a more comprehensive and systematic account.

Symmetries	$ g_{\omega N} $	$ g_{\phi N} $	$ g_{\sigma\Lambda} $	$ g_{\sigma\Xi} $	$ g_{\sigma^{\ast}\Lambda} $	$ g_{\sigma^{\ast}\Xi} $
GM1-SU(6)	10.61	—	5.84	3.06	3.73	9.67
GM1-SU(3)	10.26	-3.50	7.25	5.87	2.60	6.82
NL3-SU(6)	12.868	—	6.269	3.242	5.374	11.765
NL3-SU(3)	12.450	-4.250	7.853	6.408	4.174	8.378

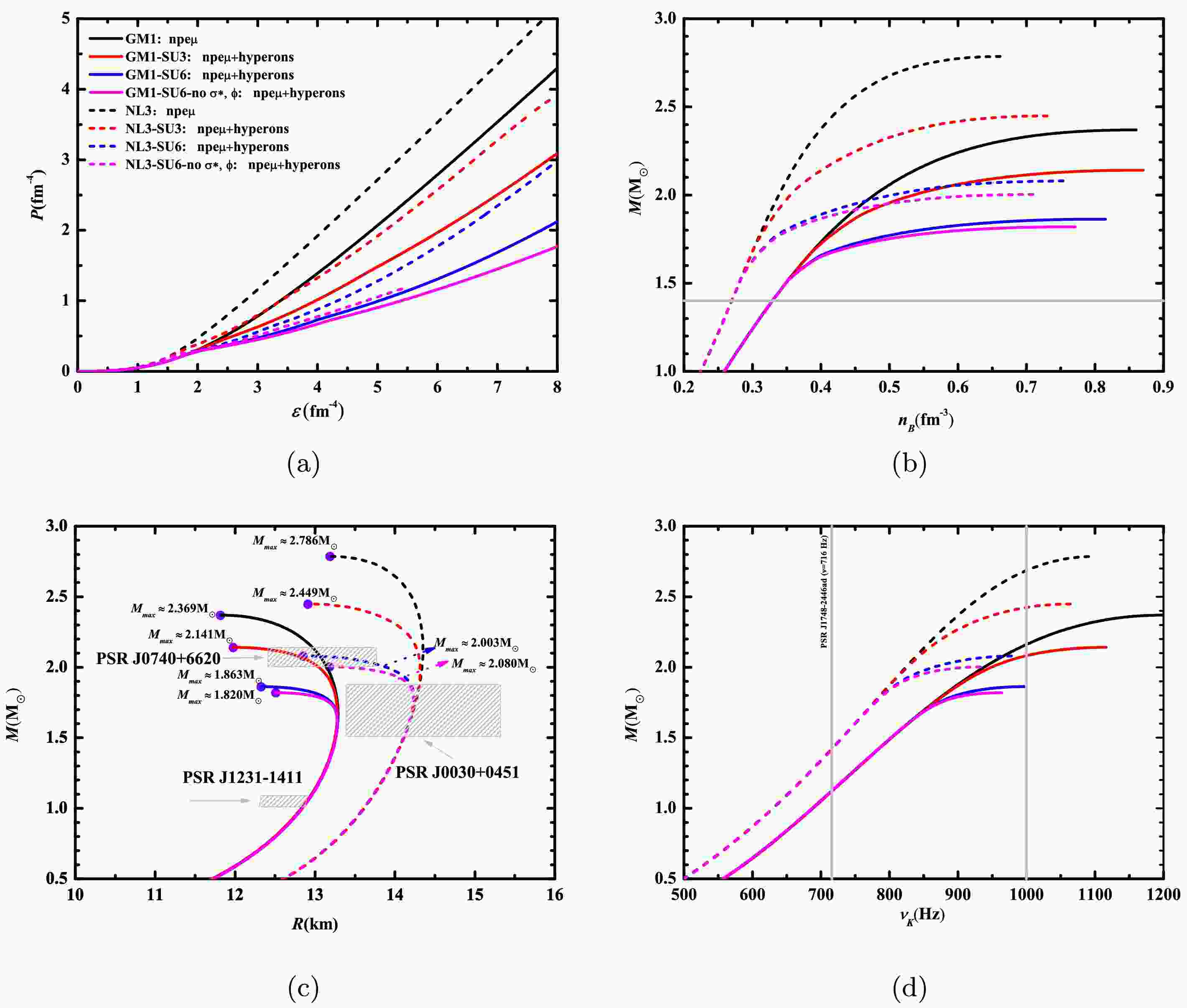
Table 1.  The two parameter sets are from [18, 22]. The values are as follows: $ m_{\sigma} $ = 550 MeV and 508.194 MeV, $ m_{\omega} $ = 783 MeV and 782.501 MeV, $ m_{\rho} $ = 770 MeV and 763 MeV, $ m_{N} $ = 939 MeV and 939 MeV, a = 12.28 $ \mathrm{fm}^{-1} $ and 10.431 $ \mathrm{fm}^{-1} $, b = -8.98 and -28.885, $ g_{\sigma N} $ = 9.57 and 10.217, $ g_{\rho N} $ = 4.10 and 4.474 in GM1 and NL3, respectively. The coupling relations are set to $ g_{\sigma^{*}N} = g_{\rho_{\Lambda}} = 0 $, and $ g_{\rho N} = g_{\rho_{\Xi}} $.

The possible equations of state, as well as the mass-radius, mass-density, and mass-Kepler frequency relationships for the above four cases under the GM1 and NL3 parameter sets, are shown in Figure 1. Additionally, Table 2 lists the threshold densities and mass values for the emergence of hyperons in cases (ii–iv) with the GM1 and NL3 parameter sets. Figure 1 shows that the equations of state of neutron star matter soften significantly when hyperons are present. Notably, in case (iv), under the SU(6) spin-flavor symmetry, it results in the softest equations of state and thus corresponds to the smallest neutron star mass among the four cases. The maximum masses of neutron stars obtained in the four cases of the GM1 and NL3 parameter sets are marked with purple dots in Figure 1c. In Figure 1c, the shaded regions represent the inferred mass and radius values of PSRs J1231-1411 ($ 1.04^{+0.05}_{-0.03} $ $ M_{\odot} $ with radius $ 12.6\pm0.3 $ km), J0030+0451 ($ 1.70^{+0.18}_{-0.19} $ $ M_{\odot} $ with radius $ 14.44^{+0.88}_{-1.05} $ km), and J0740+6620 ($ 2.073^{+0.069}_{-0.069} $ $ M_{\odot} $ with radius $ 12.49^{+1.28}_{-0.08} $ km), respectively. Based on Figure 1c and Table 2, the inferred mass and radius values of PSR J1231-1411 align with the mass-radius relations of the GM1 parameter set, indicating that it is likely to be a low-mass conventional neutron star within this theoretical framework. If the factor of hyperons is not taken into account, PSRs J0030+0451 and J0740+6620 are very likely to belong to the intermediate-mass and the massive traditional neutron stars, respectively. When hyperons are present in the interior of a neutron star, the inferred mass and radius values of PSR J0030+0451 exclusively match the mass-radius relationships of the NL3 parameter set. This suggests that it may be classified as an intermediate-mass hyperon star. Its interior will only have Λ hyperons under the SU(3) flavor symmetry, while it will have either Λ hyperons or both Λ and $ \Xi^{-} $ hyperons under the SU(6) spin-flavor symmetry. As for PSR J0740+6620, its inferred mass and radius values are consistent with the mass-radius relations of case (ii) under the GM1 parameter set and case (iii) under the NL3 parameter set. This strongly indicates that this pulsar is likely a massive hyperon star, with its interior containing Λ, $ \Xi^{-} $, or Λ, $ \Xi^{-} $, and $ \Xi^{0} $ hyperons. Figure 1d presents the mass-frequency relationships for the GM1 and NL3 parameter sets under both symmetry assumptions, incorporating the observational constraints from the currently known fastest-spinning pulsar: PSR J1748-2446ad with a spin frequency of ν = 716 Hz [56]. Under our model and parameter settings, PSR J1748-2446ad is likely a conventional neutron star with a relatively small mass. As shown in Figure 1d, when the Keplerian frequency exceeds 1000 Hz, the possible mass range of neutron stars varies significantly. According to the calculation results of the GM1 and NL3 parameter sets, the mass range of sub-millisecond pulsars with $ f= $ 1000 Hz is approximately between 1.86 $ M_{\odot} $ and 2.70 $ M_{\odot} $, falling within the category of medium to high mass.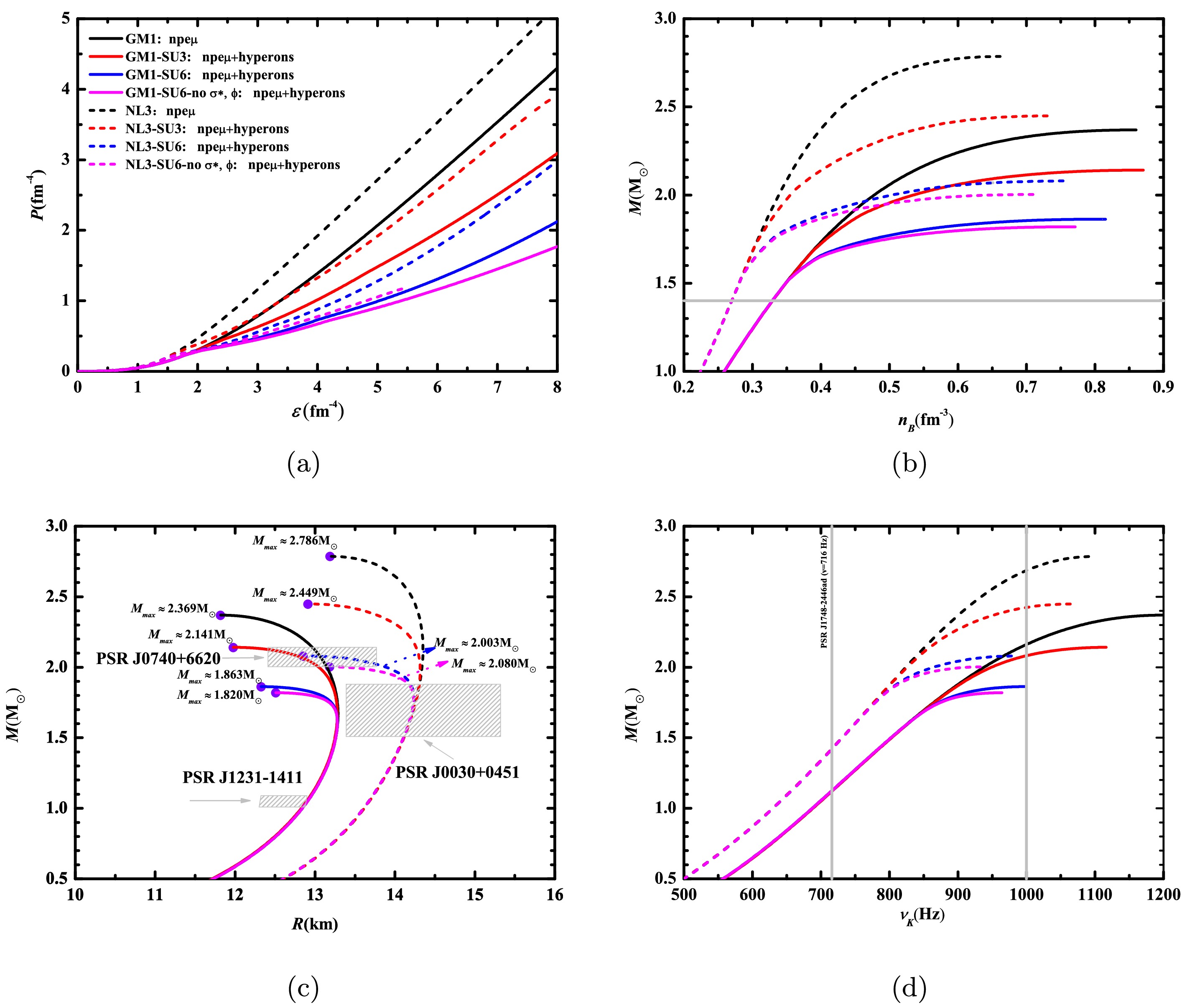

Figure 1.  (color online) The equations of state, mass-density, mass-radius, and mass-frequency relations of neutron stars are presented for four cases using the GM1 and NL3 parameter sets. The purple dots in Figure 1c represent the maximum mass values of neutron stars in each case.

Parameter Set	Hyperon	case(ii)			case(iii)			case(iv)
		$ n_B $ (fm−3)	$ M_c(M_\odot) $		$ n_B $ (fm−3)	$ M_c(M_\odot) $		$ n_B $ (fm−3)	$ M_c(M_\odot) $
GM1	Λ	0.386	1.671		0.349	1.502		0.349	1.502
	$ \Xi^{-} $	0.459	1.888		0.398	1.653		0.396	1.644
	$ \Xi^{0} $	0.791	2.136		0.704	1.856		0.730	1.819
NL3	Λ	0.303	1.702		0.285	1.538		0.285	1.538
	$ \Xi^{-} $	0.360	2.023		0.334	1.767		0.334	1.759
	$ \Xi^{0} $	0.575	2.403		0.567	2.042		0.590	1.989

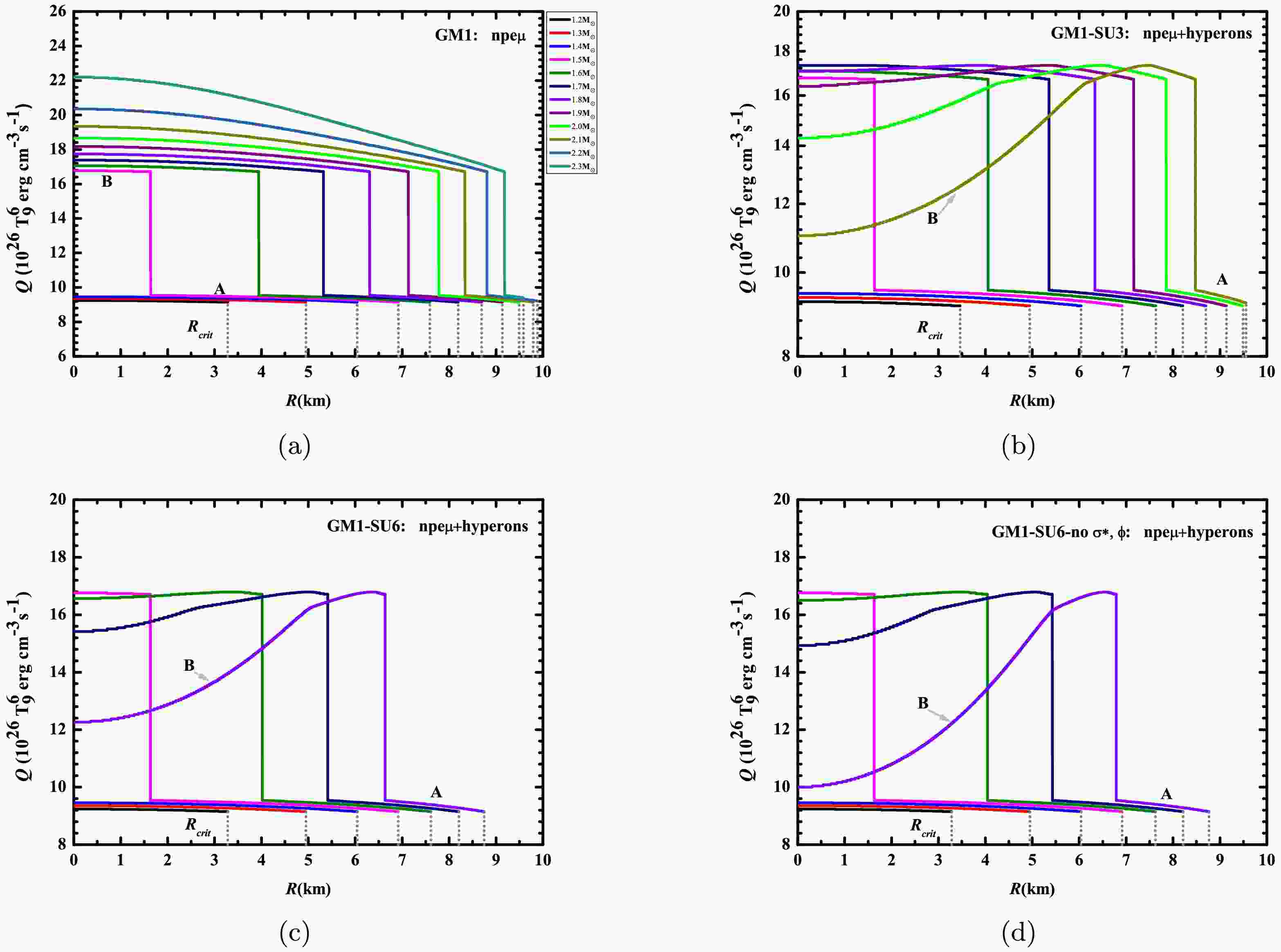
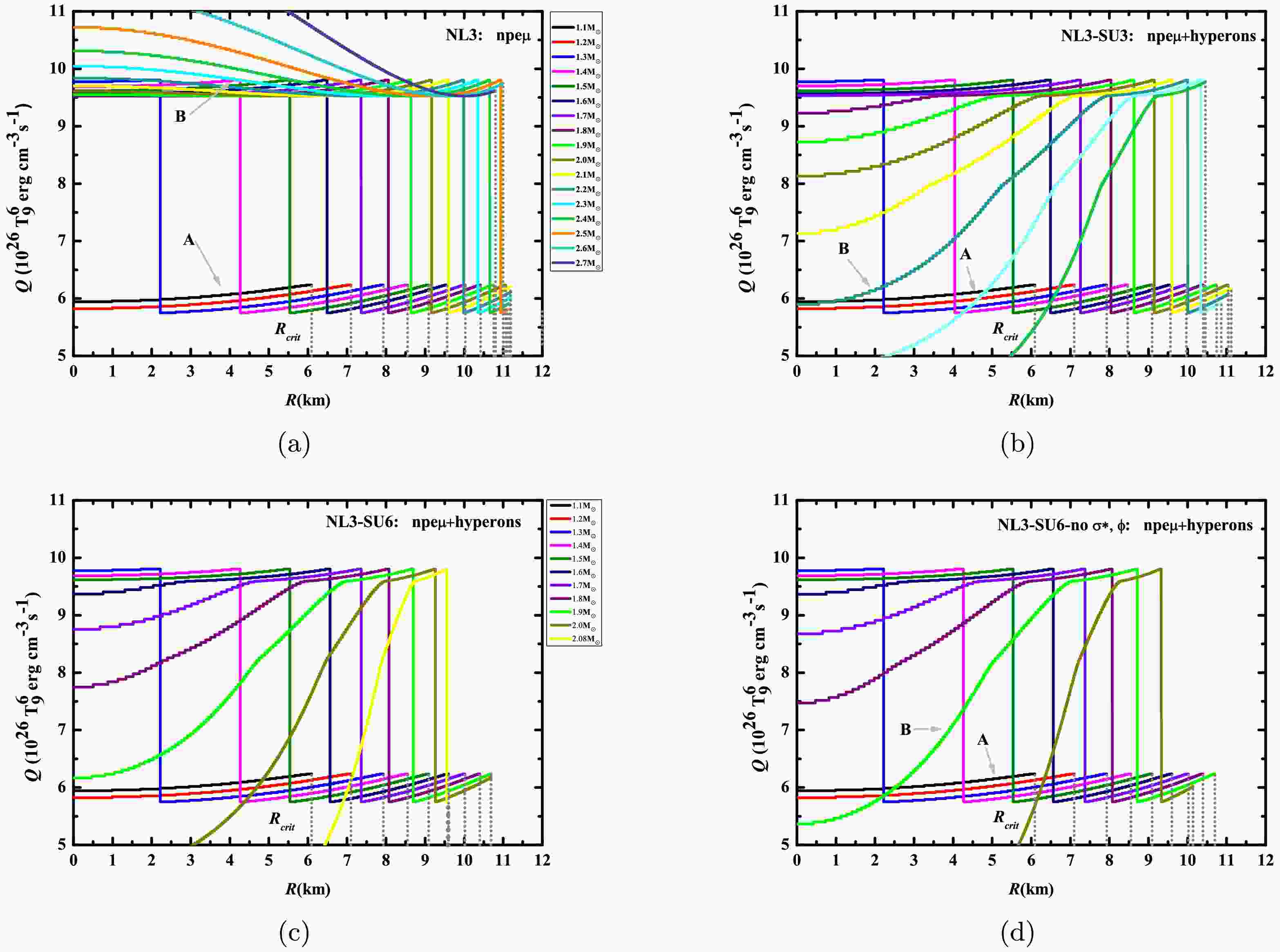
Table 2.  Threshold density and mass values for the emergence of Λ, $ \Xi^{-} $, and $ \Xi^{0} $ hyperons for three cases: SU3: npeμ+hyperons, SU6: npeμ+hyperons, and SU6-no $ \sigma^{*} $, ϕ: npeμ+hyperons.

The neutrino emissivity of the nucleonic direct Urca processes as a function of stellar radius for the four cases under the GM1 and NL3 parameter sets is presented in Figures 2 and 3, respectively. It should be noted that each curve comprises two distinct components (labeled A and B). Specifically, $ e^{-} $ is present throughout the interior of a neutron star, whereas $ \mu^{-} $ requires higher threshold densities: 0.129 fm^-3 (GM1) and 0.111 fm^-3 (NL3), respectively. Consequently, component A corresponds to the contribution of the nucleonic direct Urca processes with $ e^{-} $ to neutrino emissivity, while component B incorporates the combined contributions from the nucleonic direct Urca processes with both $ e^{-} $ and $ \mu^{-} $ to neutrino emissivity. Table 3 lists the critical radius values at which the nucleonic direct Urca processes cease, corresponding to each curve in Figures 2 and 3. It is shown that only the nucleonic direct Urca processes with $ e^{-} $ occur in neutron stars with masses spanning 1.2 $ M_{\odot} $–1.4 $ M_{\odot} $ within the GM1 equations of state framework (1.1 $ M_{\odot} $–1.2 $ M_{\odot} $ under NL3 parameters), maintaining a relatively stable neutrino emissivity. However, when the central density of the neutron star approaches the threshold density of $ \mu^{-} $, a significant enhancement in neutrino emissivity arises from the nucleonic direct Urca processes involving $ \mu^{-} $, causing an abrupt rise in the total neutrino emissivity. Furthermore, it might illustrate that there is an inverse correlation between the hyperonic fraction and the neutrino emissivity of the B section, as shown by the comprehensive analysis of the hyperon threshold densities and critical masses across four cases in Table 2 and Figures 2 and 3, where a greater hyperonic fraction induces stronger suppression of the neutrino emissivity for the nucleonic direct Urca processes. Since the threshold mass required for the appearance of hyperons under the SU(3) flavor symmetry is higher than that under the SU(6) spin-flavor symmetry, we will examine the change in the neutrino emissivity within a neutron star with a mass of 1.8 $ M_{\odot} $ as an example to illustrate this in detail. In case (ii), the hyperonic fraction inside this hyperon star with a mass of 1.8 $ M_{\odot} $ is relatively low. As a result, there is almost no difference in the intensity of neutrino energy loss during the nucleonic direct Urca processes in their cores for a traditional neutron star and a hyperon star, both with a mass of 1.8 solar masses. In contrast, in cases (iii) and (iv), the threshold mass required for the appearance of hyperons is reduced, significantly increasing the hyperonic fraction inside the hyperon star with a mass of 1.8 $ M_{\odot} $. Therefore, there is a significant difference in the intensity of neutrino energy loss during the nucleonic direct Urca processes in their cores for a traditional neutron star and a hyperon star, both with a mass of 1.8 $ M_{\odot} $, and hyperons will evidently suppress the neutrino emission intensity of the hyperon star with a mass of 1.8 $ M_{\odot} $. In addition, since the nucleonic and leptonic Fermi momenta within PSR J1231-1411 do not satisfy the momentum conservation condition in Eq.1, the nucleonic direct Urca processes are prevented from occurring within this pulsar. According to the numerical results of the GM1 or NL3 parameter set, a canonical neutron star with a mass of 1.4 $ M_{\odot} $ is categorized as a traditional neutron star, and its neutrino emissivity for the nucleonic direct Urca processes is found to be between (9.154 - 9.457) $ \times $ $ 10^{26} $ T$ ^{6}_{9} $ erg cm^-3 s$ ^{-1} $ or (5.752 - 9.803) $ \times $ $ 10^{26} $ T$ ^{6}_{9} $ erg cm^-3 s$ ^{-1} $. Because the inferred mass range of PSR J0030+0451 (1.51 $ M_{\odot} $ - 1.88 $ M_{\odot} $) has a large span, it gives rise to obvious fluctuations in the hyperonic fraction. As depicted in Figure 3, this leads to significant changes in the intensity of the neutrino emissivity of the nucleonic direct Urca processes, with the maximum change occurring in case (iv). Similarly, the inferred mass range of PSR J0740+6620 (2.004 $ M_{\odot} $ - 2.142 $ M_{\odot} $) has a smaller span compared to that of PSR J0030+0451. Therefore, the fluctuations of the hyperonic fraction are also smaller. Figure 2 and Figure 3 indicate that the change in the intensity of the neutrino emissivity of the nucleonic direct Urca processes is also relatively small.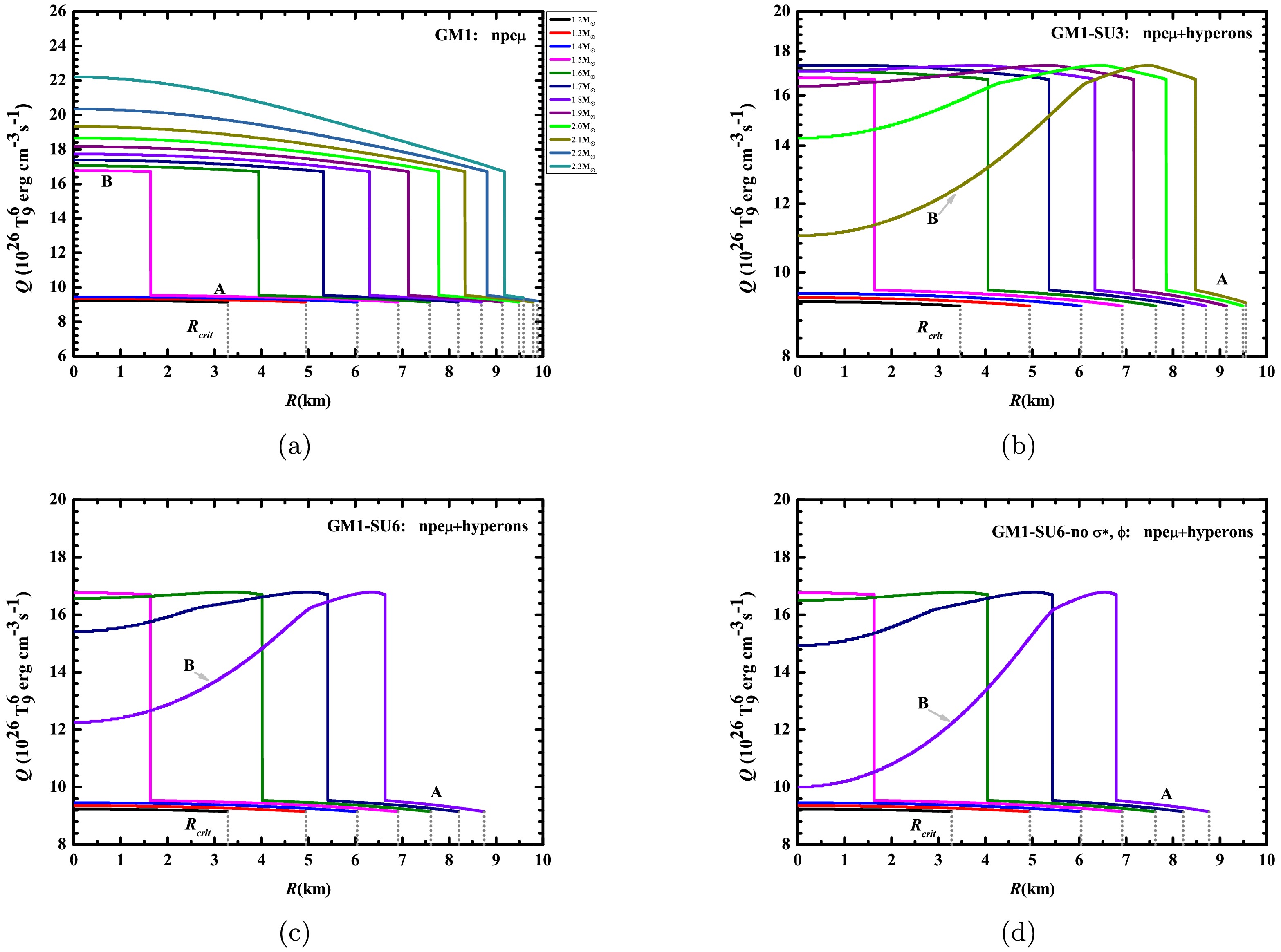

Figure 2.  (color online) Radial variation diagrams of the neutrino emissivity in the nucleonic direct Urca processes within the core of neutron stars are presented for four cases of the GM1 parameter set. The gray dotted lines represent the critical radius values at which the nucleonic direct Urca processes cease in neutron stars with different masses.

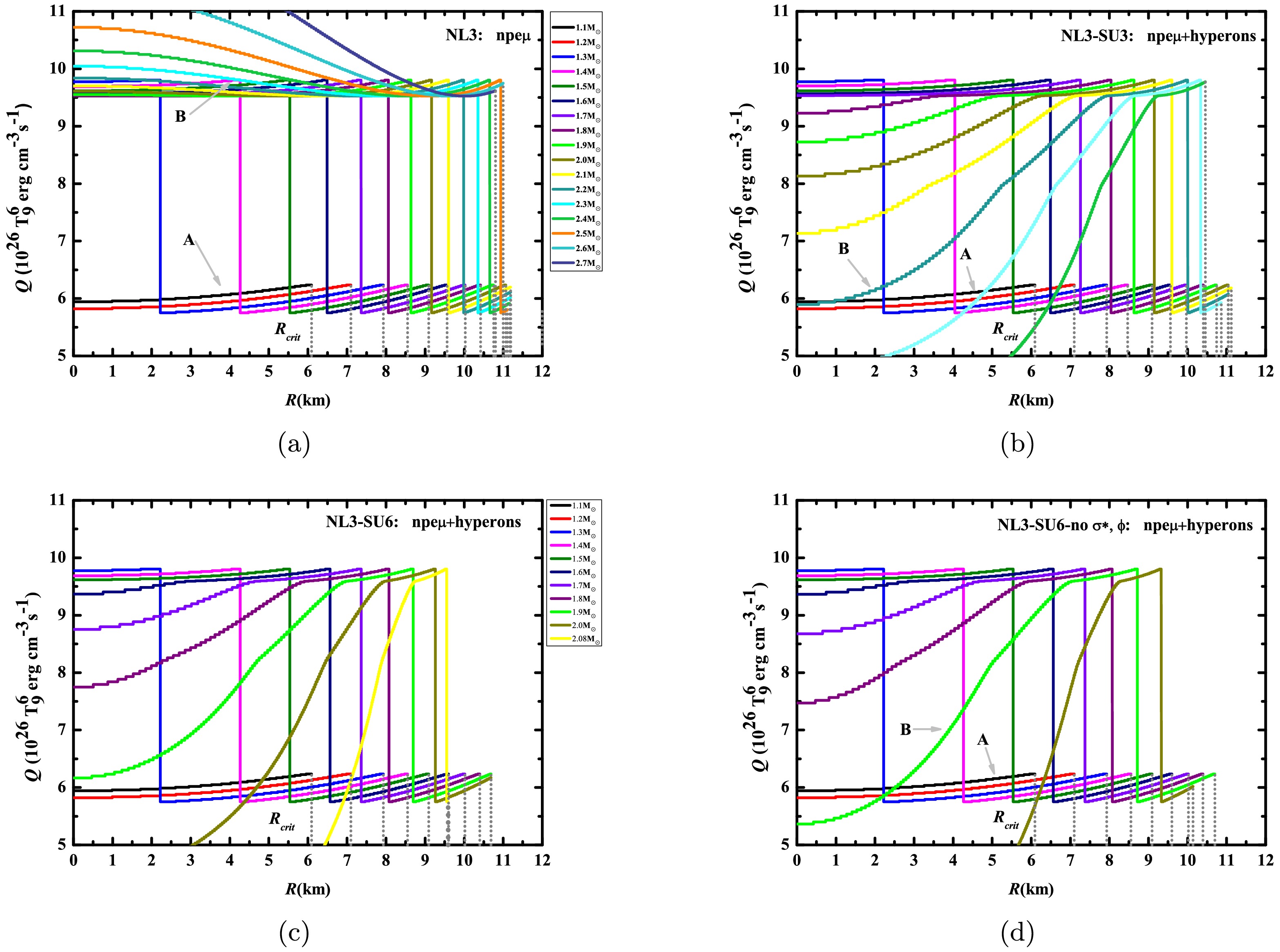
Figure 3.  (color online) Radial variation diagrams of the neutrino emissivity in the nucleonic direct Urca processes within the core of neutron stars are shown for four cases of the NL3 parameter set. The gray dotted lines represent the critical radius values at which the nucleonic direct Urca processes cease in neutron stars with different masses, respectively.

	M ($ M_{\odot} $)	$ R_{\text{crit}}(R) $ (km) (GM1)					$ R_{\text{crit}}(R) $ (km) (NL3)
		case (i)	case (ii)	case (iii)	case (iv)		case (i)	case (ii)	case (iii)	case (iv)
Sure, please provide the section that needs proofreading.	1.1	−	−	−	−		6.092 (13.726)	6.093 (13.734)	6.092 (13.726)	6.092 (13.726)
	1.2	3.283 (13.067)	3.461 (13.062)	3.283 (13.067)	3.283 (13.067)		7.099 (13.840)	7.100 (13.849)	7.099 (13.840)	7.099 (13.840)
	1.3	4.946 (13.154)	4.945 (13.141)	4.946 (13.154)	4.946 (13.154)		7.931 (13.946)	7.932 (13.953)	7.931 (13.946)	7.931 (13.946)
	1.4	6.040 (13.215)	6.040 (13.205)	6.040 (13.215)	6.040 (13.215)		8.552 (14.030)	8.469 (14.025)	8.552 (14.030)	8.552 (14.030)
	1.5	6.916 (13.259)	6.915 (13.249)	6.915 (13.260)	6.915 (13.260)		9.091 (14.105)	9.092 (14.110)	9.091 (14.105)	9.091 (14.105)
	1.6	7.589 (13.282)	7.634 (13.274)	7.612 (13.280)	7.623 (13.280)		9.561 (14.169)	9.562 (14.175)	9.600 (14.173)	9.597 (14.174)
	1.7	8.193 (13.287)	8.209 (13.277)	8.210 (13.257)	8.212 (13.251)		10.024 (14.230)	9.971 (14.229)	10.017 (14.219)	10.023 (14.219)
	1.8	8.690 (13.269)	8.701 (13.255)	8.747 (13.076)	8.767 (12.954)		10.418 (14.280)	10.405 (14.282)	10.398 (14.236)	10.394 (14.231)
	1.9	9.135 (13.223)	9.138 (13.191)	−	−		10.752 (14.315)	10.742 (14.309)	10.686 (14.173)	10.698 (14.133)
	2.0	9.492 (13.150)	9.492 (13.051)	−	−		11.065 (14.340)	11.040 (14.314)	10.686 (13.893)	10.140 (13.390)
	2.1	9.794 (13.034)	9.557 (12.661)	−	−		11.190 (14.350)	11.122 (14.289)	−	−
	2.2	9.882 (12.853)	−	−	−		11.190 (14.347)	11.045 (14.205)	−	−
	2.3	9.584 (12.542)	−	−	−		11.190 (14.325)	10.863 (14.020)	−	−
	2.4	−	−	−	−		11.165 (14.284)	10.455 (13.617)	−	−
	2.5	−	−	−	−		11.107 (14.209)	−	−	−
	2.6	−	−	−	−		10.999 (14.083)	−	−	−
	2.7	−	−	−	−		10.801 (13.867)	−	−	−
Note: "–" indicates that the value exceeds the maximum mass under the selected parameters, meaning the star does not form and the nucleonic direct Urca processes do not occur

Table 3.  The values of the mass, the critical radius at which the nucleonic direct Urca processes cease, as well as the radius of neutron stars are considered under four cases for the GM1 and NL3 parameter sets.

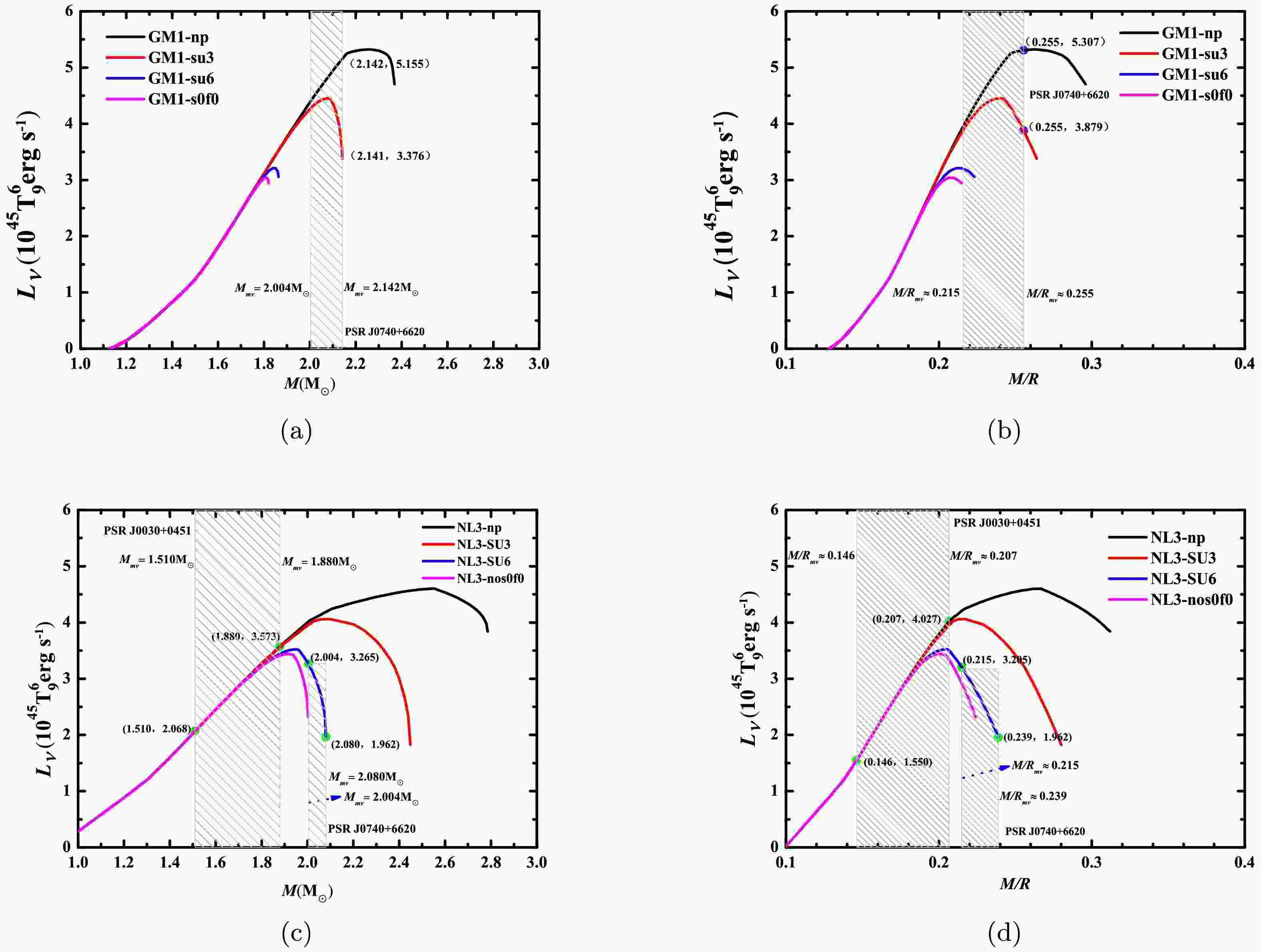
The neutrino luminosities of the nucleonic direct Urca processes, which are functions of the stellar mass and compactness (the mass-to-radius ratio), for the four cases under the GM1 and NL3 parameter sets are plotted in Figure 4. As shown in Figure 4, regardless of whether hyperons are present in the core of a neutron star, the neutrino luminosities from the nucleonic direct Urca processes in neutron stars display a non-monotonic variation trend as the stellar mass or compactness increases. Under the GM1 and NL3 parameter sets, Table 4 shows the possible values and ranges of the neutrino luminosity of the nucleonic direct Urca processes in PSRs J0030+0451 and J0740+6620, combined with the inferred mass and radius values of these two pulsars and the maximum mass values of neutron stars obtained in four cases. Under the NL3 parameter set, the $ L_{\nu}^{D} $ of PSR J0030+0451 in case (ii) is almost the same as that in case (i), and it is not affected by the hyperonic fraction. However, compared with case (i), the $ L_{\nu}^{D} $ of this star in case (iii) or case (iv) is obviously suppressed by the hyperonic fraction when $ M_{mv} \geq 1.8 M_{\odot} $ or $ (M/R)_{mv} \geq 0.18 $. For the heavier pulsar PSR J0740+6620 in case (ii) under the GM1 parameter set, as the values of $ M_{mv} $ or $ (M/R)_{mv} $ increase, the hyperonic fraction significantly rises, which greatly suppresses $ L_{\nu}^{D} $. This leads to a gradual expansion of the difference in $ L_{\nu}^{D} $ between case (i) and case (ii). For this pulsar in case (iii) under the NL3 parameter set, as the values of $ M_{mv} $ or $ (M/R)_{mv} $ increase, $ L_{\nu}^{D} $ shows a rapid decreasing trend. It should be emphasized that all theoretical value ranges presented in this study are based on the selected models and parameters and must be systematically validated and refined through the accumulation and analysis of future astronomical observational data. If we can obtain relevant observational information about the neutrino emissivity or luminosity of pulsars in the future with the advancement of astronomical observations, our results offer a possible perspective for judging whether a pulsar contains hyperons and hyperonic species as well as constraining nuclear physics parameters.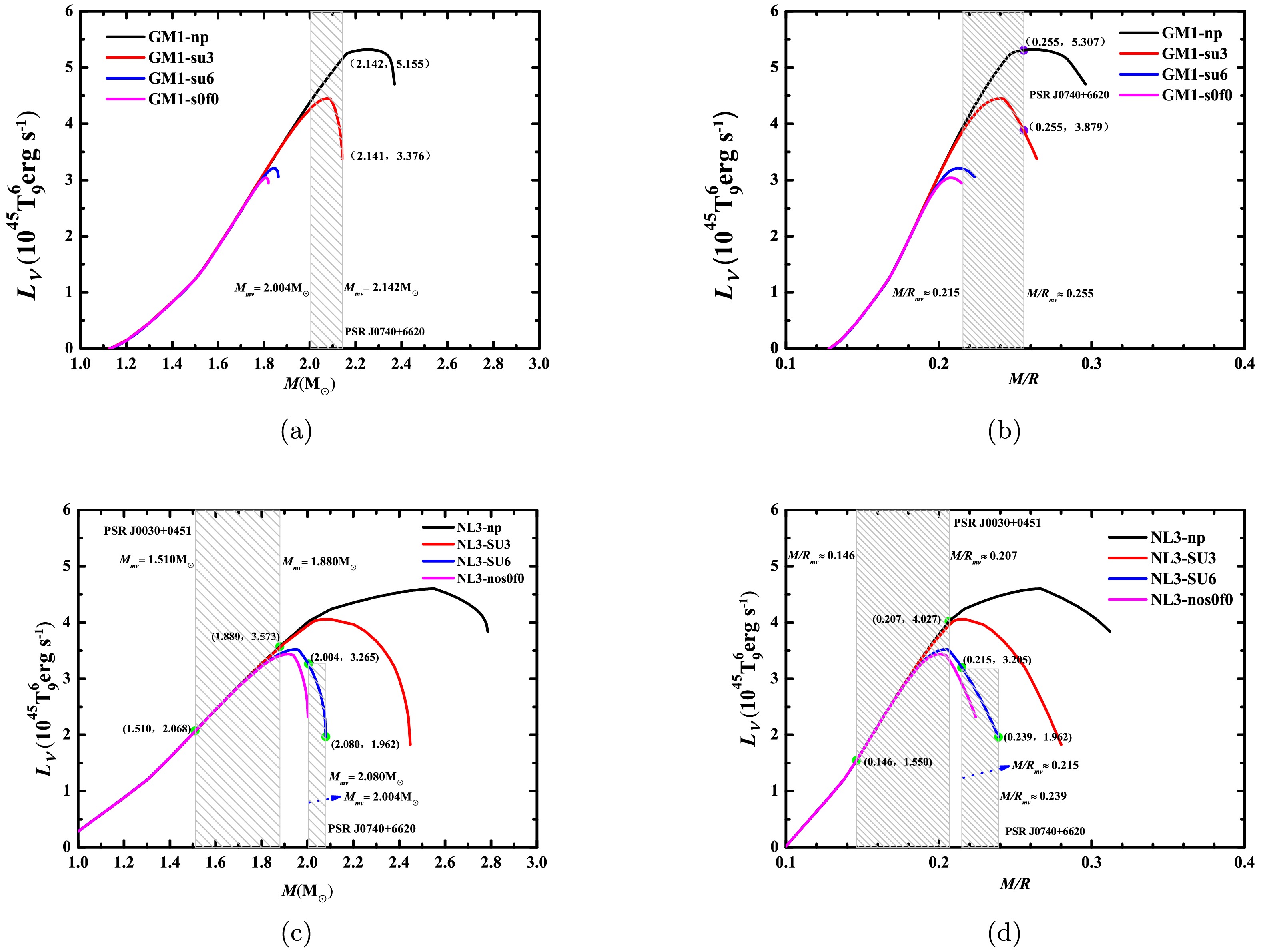

Figure 4.  (color online) Neutrino luminosity-mass and neutrino luminosity-compactness relations for four cases of the GM1 and NL3 sets are presented. Purple and green circles denote the theoretical prediction ranges of the neutrino luminosities for the nucleonic direct Urca processes in PSRs J0030+0451 and J0740+6620.

Parameter Sets	Constraint Types	J0030$ + $0451,J0740$ + $6620	$ L_{\nu}^{D} $ ($ 10^{45} $ T$ _{9}^{6} $ erg s$ ^{-1} $)
			J0030$ + $0451	J0740$ + $6620
GM1	$ M_{mv} $ ($ M_{\odot} $)	1.510–1.880, 2.004–2.142	–	3.376–5.155
	$ (M/R)_{mv} $	0.146–0.207, 0.215–0.255	–	3.879–5.307
	$ M_{mv}^{c} $ ($ M_{\odot} $)	1.700, 2.073	–	4.449–4.795
	$ (M/R)_{mv}^{c} $	0.174, 0.245	–	4.359–5.193
NL3	$ M_{mv} $ ($ M_{\odot} $)	1.510–1.880, 2.004–2.080	2.068–3.573	1.962–3.265
	$ (M/R)_{mv} $	0.146–0.207, 0.215–0.239	1.550–4.027	1.962–3.205
	$ M_{mv}^{c} $ ($ M_{\odot} $)	1.700, 2.073	2.869	2.407
	$ (M/R)_{mv}^{c} $	0.174, 0.245	2.760	–
Note: "--" denotes no values for the corresponding pulsar under the given constraints.

Table 4.  Neutrino luminosity $ L_{\nu}^{D} $ for nucleonic direct Urca processes in PSRs J0030$ + $0451 and J0740$ + $6620 is constrained by the inferred mass $ M_{mv} $, central mass $ M_{mv}^{c} $, compactness $ (M/R)_{mv} $, and central compactness $ (M/R)_{mv}^{c} $ (GM1 and NL3 parameter sets).

In this work, we mainly investigate the potential effects of hyperons on the neutrino emissivity and luminosity in neutron stars using the GM1 and NL3 parameter sets under the two flavor symmetries of SU(6) and SU(3) in the framework of mean field theory. We analyzed the feasibility of the nucleonic direct Urca processes and their associated neutrino emission properties, focusing on three representative PSRs: J1231-1411, J0030+0451, and J0740+6620. Under the GM1 and NL3 parameter sets, the nucleonic direct Urca processes will not occur inside PSR J1231-1411 due to the non-satisfaction of the momentum conservation conditions. Considering the factor of hyperons, the nucleonic direct Urca processes with both $ e^{-} $ and $ \mu^{-} $ will occur in PSR J0030+0451 under the NL3 parameter set. Due to the large span of its mass measurement values, the hyperon abundance fluctuates significantly, leading to a significant change in the intensity of the neutrino emissivity of the nucleonic direct Urca process inside it. If the inferred mass of PSR J0030+0451 is greater than approximately 1.8 $ M_{\odot} $, the neutrino luminosity of its internal nucleonic direct Urca processes under the SU(3) flavor symmetry is almost unchanged compared to the situation of npeμ matter. However, it shows an obvious hyperon dependence under the SU(6) spin-flavor symmetry. The neutrino luminosity of the nucleonic direct Urca processes inside PSR J0740+6620 decreases faster with the increase of the hyperonic fraction than in npeμ matter under the GM1 parameter set, and its luminosity also shows a monotonically decreasing trend under the NL3 parameter set. The above results and analysis demonstrate that the hyperonic fraction exerts differential effects on the properties of the neutrino emissivity and luminosity for the nucleonic direct Urca processes in neutron stars of different masses. If future astronomical observations could provide precise measurements of the neutrino emissivity or surface thermal radiation for pulsars, this work could not only help confirm the hyperonic species in neutron stars but also offer valuable insights for the nuclear physics parameter determinations.