-
The lack of Coulomb interactions makes neutrons unique probes for investigating various salient features of the nuclear structure with the (n,
$ \gamma $ ) reaction [1]. The compound nucleus mechanism, characterized by statistical quantities of level density and$ \gamma $ -strength function, is dominant in the neutron capture process up to the incident neutron energy of several MeV for nuclei with a reasonably high valence particle number (e.g., A$ \geqslant $ 40 and not near a double-closed shell). The resonance regions at low neutron energies, however, show obvious non-statistical processes, such as potential, valence capture, and doorway states. The intermediate structure with a 2p-1h configuration in the doorway state might result in the quenching of the E1 dipole strength [2].The radiative neutron capture process has primarily been investigated at thermal (
$ E_{n} $ = 0.0253 eV) energies, at which s-wave neutrons couple with the bound orbits of the target nucleus [1, 3-5]. It has been reported that incident p-wave neutrons may play an unusual role in the capture reaction mechanism [1]. For instance, the neutron strengths for s-wave resonances as a function of the nucleus mass number A have peaks emerging at A = 55 and A = 150; however, the p-wave resonance shows a descending trend in these mass regions [6]. The origin of this contrasting feature held by s- and p-wave neutrons has not been fully investigated.In the vicinity of A = 55 nuclei, the last neutron is in the
$ fp $ sub-shell, where the space can be occupied by excited neutrons from the$ sd $ shell. This situation may be well-suited to the formation of a 2p-1h doorway state, which is an excited state involving two particles and one hole in the resonance process. Once the doorway capture states are formed, radiative decay can occur either due to neutron transition in the excited nucleus or particle-hole annihilation. When the incident particle undergoes many interactions, and a large number of particle-hole configurations are produced, a statistical model must be utilized to take into account the intrinsic pattern. The p-h pair may be blocked due to the fully filled upper shell in heavier nuclei and the large shell-energy gap that must be overcome to excite nucleons in light nuclei. Therefore, the 2p-1h doorway excitation would be a bright feature for the neutron capture mechanism in the A = 55 mass region.With regard to the
$ \gamma $ -strength function, significant effort has been made to gain insight into the intrinsic process through various formulations. Charged particle inelastic scattering (3He, 3He$ \gamma $ ) and particle-transfer (3He,$ \alpha\gamma $ ) were utilized to determined the$ \gamma $ -strength function at low$ \gamma $ -ray energies [7, 8]. The enhancement of the$ \gamma $ -strength function below 3 MeV was measured due to the increase in the B(M1) strength of low-energy M1 transitions. This outcome was confirmed by the (d, p) reaction on the 95Mo target [9]. The enhancement, however, is strangely not observed in neutron capture experiments [10, 11]. This inconsistency might result from the role of the reaction mechanisms, reflected by the$ \gamma $ -strength function induced by keV neutrons, where the non-statistical and statistical effects coexist.A model-independent approach reflecting the
$ \gamma $ -strength function was applied [9]. The ratio of the$ \gamma $ -strength function for two different primary transitions from the same initial state ($ E_{\rm i} $ ) to discrete low-lying levels ($ E_{\rm L1} $ and$ E_{\rm L2} $ ), is formulated as:$ R = \frac{f(E_{\rm i}-E_{\rm L1})}{f(E_{\rm i}-{E_{\rm L2}})} = \frac{N_{\rm L1}(E_{\rm i})(E_{\rm i}-E_{\rm L2})^{3}}{N_{\rm L2}(E_{\rm i})(E_{\rm i}-E_{\rm L1})^{3}}, $

(1) where
$ N_{\rm L1}(E_{\rm i}) $ and$ N_{\rm L2}(E_{\rm i}) $ are the intensities of the two primary transitions, and their transition energies are$ E_{\rm i}-E_{\rm L1} $ and$ E_{\rm i}-E_{\rm L2} $ . In this study, we observed, for the first time, an extraordinary quenching of the$ \gamma_{0} $ transition only for the p-wave neutron radiative capture in 57Fe. The quenching was observed from the pronounced enhancement of the$ \gamma $ -strength function ratio R for$ f_{\gamma_{1}}/f_{\gamma_{0}} $ and$ f_{\gamma_{2}}/f_{\gamma_{0}} $ , with respect to the nearly uniform distribution of the mixed neutron resonances (narrow p-wave resonances overlying a wide s-wave resonance). The enhancement results from the doorway mechanism formed by capture-neutron coupling to the core-neutron p-h excitation configuration, dominated by strong E1 transitions of$ \gamma_{1} $ and$ \gamma_{2} $ . However, the$ \gamma_{0} $ transition seems tremendously suppressed due to the absence of a doorway mechanism for the induction of p-wave neutron resonance. We also found that the low-energy$ \gamma $ -rays in the neutron capture reaction mostly arose from the cascade decay of low-lying states, rather than from the primary transition to the high-lying states, which explains why the enhancement of the low energy$ \gamma $ -strength function does not occur in the neutron capture reaction. -
The measurement was carried out at the 3 MV Pelletron accelerator in the Research Laboratory for Nuclear Reactors at the Tokyo Institute of Technology [12]. A proton beam with an energy of 1.903 MeV hitting a lithium target created by evaporating metallic lithium (isotopic 7Li enrichment 99.9%) on a copper disk generates 2–90 keV continuous neutrons. This spectrum is similar to the Maxwellian-Boltzmann distribution [12]. Hence, this neutron generator provides a realistic condition for the astrophysical environment of the slow neutron-capture (s-) process. The astro-nuclear reaction rate could be constrained from the experimental total and partial neutron capture cross-sections. The energy of incident neutrons on a 57Fe-enriched sample with a thickness of 0.373 mm was measured using the time-of-flight (TOF) method with a mini 6Li-glass scintillation detector located 30 cm from the neutron target. A large anti-Compton spectrometer [12] consisting of a central main NaI(Tl) detector with a 15.2 cm diameter by 30.5 cm length and a circular arrangement of NaI(Tl) detectors with a 33.0 cm outer diameter by 35.6 cm length was used to detect
$ \gamma $ -rays from the neutron capture reactions. A low peak-efficiency less than 3.5% ensured access to only one$ \gamma $ -ray in each cascade decay. A good signal-to-noise ratio (full energy peak efficiency: 3.3% at 1.173 MeV from 60Co; 2.7% at 6.02 MeV from the 27Al(p,$ \gamma $ )28Si reaction [13]) was obtained owing to the powerful shield composed of borated paraffin, borated polyethylene, cadmium, and potassium-free lead. Additionally, a 6LiH cylinder that effectively absorbed the neutrons scattered by the sample was added to the collimator of the spectrometer shielding shell. The spectrometer was placed at an angle of$ 125^{\circ} $ with respect to the proton beam direction based on the kinematics, because the second Legendre polynomial is zero at this angle. The measurement obtained at this angle approximates the integrated$ \gamma $ -ray spectrum for the dipole transition, which is assumed to represent the majority of statistical$ \gamma $ -rays. The distance between the centre of the neutron capture sample and the front surface centre of the main NaI(Tl) detector was fixed at 78.5 cm.The total and partial neutron capture cross-sections for certain ranges of neutron energy are extracted from the capture yield [14]. Because the number and individual energies of emitted
$ \gamma $ -rays differ according to the cascade mode, the efficiency for detecting capture events depends on the decay mode. The pulse height weighting method [15] was used to obtain the detection efficiency, which is proportional to the energy dissipated in the detector. The lowest two to three excited states in 57Fe will be excited by the neutron spectrum via the inelastic scattering. These contributions are likely significant and may account for the large contributions to the$ \gamma $ -ray spectrum below 1 MeV. The threshold of the$ \gamma $ -ray measurement was set to be 0.5 MeV to block the background from the noise and the inelastic-scattering$ \gamma $ -ray contribution. The linear extrapolation is applied for the estimation of the$ \gamma $ -ray yield below the threshold in the extraction of the cross-sections. The net$ \gamma $ -ray spectra were extracted by subtracting the background spectrum normalized with the digital gate widths of the foreground spectrum. The net$ \gamma $ -ray spectrum after unfolding with the response function matrix is shown in Fig. 1, which highlights the strong primary transitions from the neutron capture states to the ground state (0$ ^{+}_{\rm GS} $ ), and the first and second excited states ($2 ^{+}_{1} $ and$ 2^{+}_{2} $ ). -
The intensity of the primary transition is proportional to the
$ \gamma $ -strength function of$ f(E_{\rm i}-E_{{\rm L}j}) $ , the transition energy of$ (E_{\rm i}-E_{{\rm L}j})^{3} $ as well as$ \sum_{J\pi}\sigma_{J\pi}(E_{\rm i}) $ , which is the cross-section for populating the levels with the given spin and parity at excitation energy$ E_{\rm i} $ [9]. The most populated neutron capture state of 1$ ^{-} $ in 58Fe is created when an incident s-wave neutron couples to 57Fe. Because$ \sigma_{1^{-}}(E_{\rm i}) $ remains almost as constant for different modes of cascade$ \gamma $ -ray decay with the dominant E1 transitions, the ratio of$ \gamma $ -strength functions R in Eq. (1) can be extracted from the intensities and energies of the primary transitions from the neutron capture state to the low-lying states with a specific spin and parity. It is essential to investigate the intrinsic characteristics of$ \gamma $ -transitions for the s- and p-wave neutron, especially for the primary transitions from a common initial state to final states with the same spin and parity. Fig. 2 shows the distributions of$ R_{2_{1}^{+}/0_{\rm GS}^{+}} $ ,$ R_{2_{2}^{+}/0_{\rm GS}^{+}} $ , and$ R_{2_{1}^{+}/2_{2}^{+}} $ depending on neutron resonance energy reflecting the s- and p- wave neutron’s remarkably different coupling features. A distinct enhancement in$ R_{2_{1}^{+}/0_{\rm GS}^{+}} $ at the p-wave resonance is exhibited comparatively with the slightly varied amplitude of the superimposing resonances of the s and p-waves. The distribution of$ R_{2_{2}^{+}/0_{\rm GS}^{+}} $ is similar to that of$ R_{2_{1}^{+}/0_{\rm GS}^{+}} $ , but with a weaker strength. The slightly higher ratio of the p-wave with respect to the s-wave in the$ R_{2_{1}^{+}/2_{2}^{+}} $ distribution indicates the$ \gamma $ -strength functions from the initial capture state to the low-lying states with the same spin and parity induced by the p-wave neutron, which exhibits larger variations than the s-wave neutron.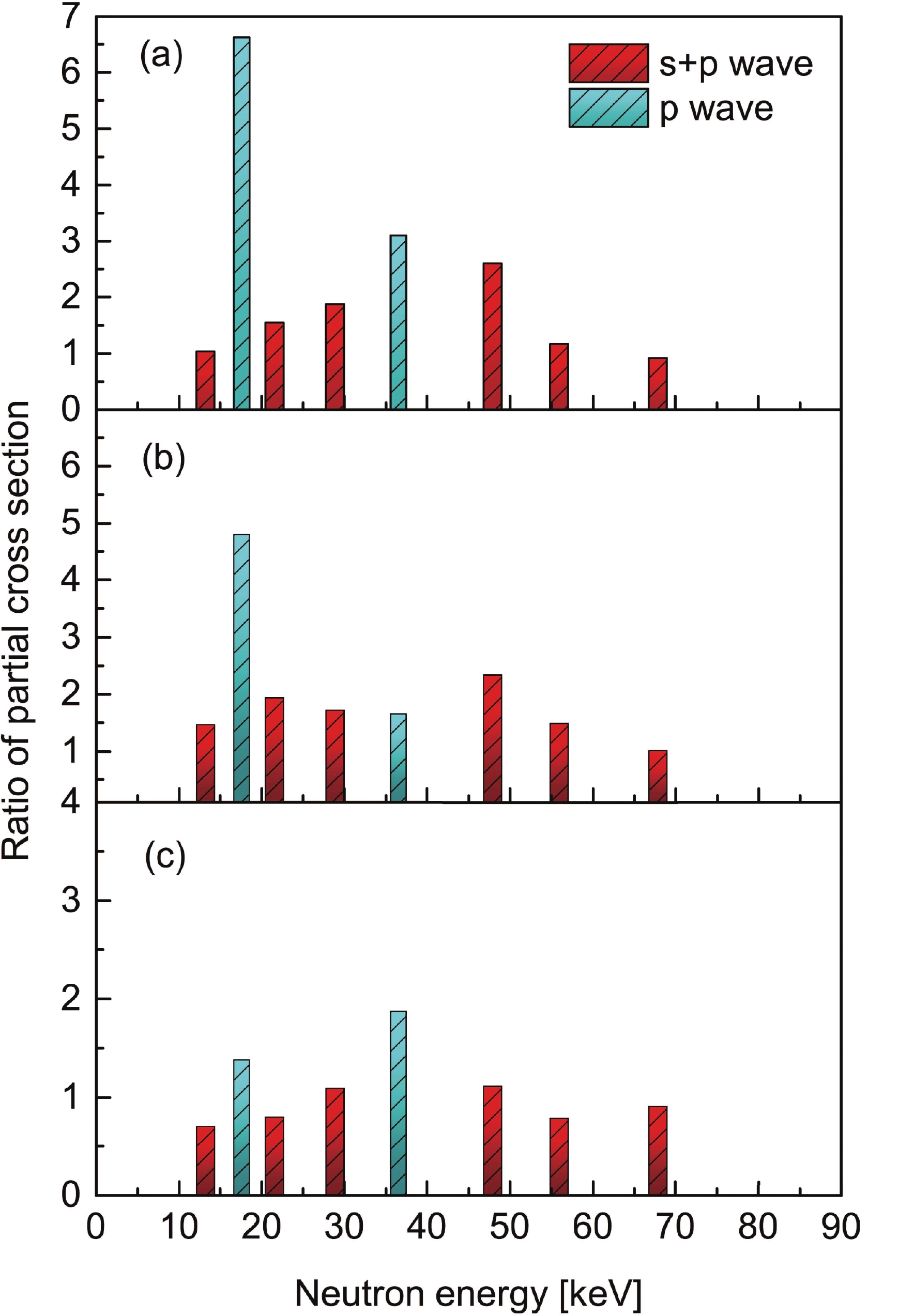
Figure 2. (color online) Distributions of R ratio of
$ \gamma $ -strength functions depending on neutron resonance energies: (a)$ R_{2_{1}^{+}/0_{\rm GS}^{+}} $ , (b)$ R_{2_{2}^{+}/0_{\rm GS}^{+}} $ and (c)$ R_{2_{1}^{+}/2_{2}^{+}} $ .Neutron capture resonance initial and final states can be represented as single neutron states coupled to the target ground state, as well as quadrupole and octupole excitations. These collective states are coherent superpositions of 2p-1h qusiparticle states [16, 17]. If certain p-h configurations are dominant, they may occur with unperturbed energies significantly larer than those of the collective states [16, 17]. In the
$ fp $ shell region, possible 2p-1h configurations that can decay with E1 annihilation are (2p$ _{1/2} $ ; 2s$ _{1/2}^{-1} $ ), (2p$ _{1/2} $ ; 1d$ _{3/2}^{-1} $ ), and (1f$ _{5/2} $ ; 1d$ _{3/2}^{-1} $ ) neutron particle-hole pairs coupled to one neutron in the 2p$ _{1/2} $ , 2p$ _{3/2} $ , or 1f$ _{5/2} $ orbit. The energy differences of the p-h components range from 8-10 MeV according to the neutron binding energies of each level, which are exactly consistent with the observed$ \gamma $ -ray energies of the primary transitions ($ E_{\gamma_{0}} $ = 10.072$ \pm $ 0.002 MeV), ($ E_{\gamma_{1}} $ = 9.235$ \pm $ 0.001 MeV), and ($ E_{\gamma_{2}} $ = 8.362$ \pm $ 0.001 MeV) in the present measurement of 57Fe(n,$ \gamma $ )58Fe reaction. If the annihilation energy of the paired neutron-hole for the 2p-1h configuration is comparable to the observed$ \gamma $ -ray energies, the corresponding doorway states are expected to be strongest.The configurations of doorway states corresponding to the primary transitions of
$ 1_{\rm CS}^{-}\rightarrow2_{1}^{+} $ ,$ 1_{\rm CS}^{-}\rightarrow2_{2}^{+} $ in 58Fe are neutrons (2p$ _{3/2}^{3} $ , 1f$ _{5/2}^{2} $ , 2s$ _{1/2}^{-1} $ ) and (2p$ _{3/2}^{3} $ , 2p$ _{1/2}^{2} $ , 1d$ _{3/2}^{-1} $ ), respectively, as shown in Fig. 3, where$ 1_{\rm CS}^{-} $ is the s-wave neutron−s initial capture state and$2 _{1}^{+} $ and$2 _{2}^{+} $ are the first and second excited states, respectively. One incident neutron initiates the particle-hole excitation from the$2{{s}} _{1/2} $ sub-shell to the$ 1{{f}}_{5/2} $ sub-shell to form a 2p-1h configuration for the$ 1_{\rm CS}^{-}\rightarrow2_{1}^{+} $ transition. A similar excitation mechanism is shown for the$ 1_{\rm CS}^{-}\rightarrow2_{2}^{+} $ transition. Several narrow p-wave resonances superpose on the wide s-wave resonance; therefore, the denotation of the$ s+p $ wave is used to distinguish from the p-wave resonance in Fig. 2. The remarkable enhancement of$ R_{2_{1}^{+}/0_{\rm GS}^{+}} $ and$ R_{2_{2}^{+}/0_{\rm GS}^{+}} $ for the p-wave neutron resonance essentially results from the quenching the intensity of$ \gamma_{0}(1_{\rm CS}^{+}\rightarrow0_{\rm GS}^{+}) $ . This is caused by the absence of a doorway excitation mechanism due to the capture-neutron filling in 2p$ _{3/2} $ to produce a full sub-shell and non-coupling with the neutron p-h pair of (2p$ _{1/2}^{1} $ , 2s$ _{1/2}^{-1} $ ), as shown in Fig. 3. In contrast, the transition intensity of$ \gamma_{0}(1_{\rm CS}^{+}\rightarrow0_{\rm GS}^{+}) $ for the p-wave neutron with M1 transition is weaker than that of$ \gamma_{0}(1_{\rm CS}^{-}\rightarrow0_{\rm GS}^{+}) $ for the s-wave neutron with the E1 transition due to the low magnetic-to-electric dipole transition probability of$ \lambda $ (M1):$ \lambda $ (E1). Because M1 transitions will be hindered with respect to E1 transitions, the$ E_{\gamma}^{(2l+1)} $ energy dependence will result in a significant difference between the s- and p- wave total radiative widths. This difference also exists in the strength of the s- and p-wave neutrons. The averaged width of$ <\Gamma_{\gamma}(s)>\sim3<\Gamma_{\gamma}(p)> $ was found in the$ fp $ shell region [16, 17], where there are correlations between the reduced neutron widths and radiative widths of the s-wave resonance. In contrast, the doorway excitation mechanism with neutron 2p-1h configurations of (2p$ _{3/2}^{3} $ , 1f$ _{5/2}^{2} $ , 2s$ _{1/2}^{-1} $ ) and (2p$ _{3/2}^{3} $ , 2p$ _{1/2}^{2} $ , 1d$ _{3/2}^{-1} $ ), shown in Fig. 3 of$ \gamma_{1}(1_{\rm CS}^{-}\rightarrow2_{1}^{+}) $ and$ \gamma_{2}(1_{\rm CS}^{-}\rightarrow2_{2}^{+}) $ , leads to strong transitions and high intensities to populate the final states of$ 2_{1}^{+} $ and$ 2_{2}^{+} $ shown in Fig. 1. The transitions of$ 2_{1}^{+}\rightarrow0_{\rm GS}^{+} $ and$ 2_{2}^{+}\rightarrow0_{\rm GS}^{+} $ in the cascade decays are interpreted as the capture-neutron jumping from 1f$ _{5/2} $ and 2p$ _{1/2} $ to 2p$ _{3/2} $ , forming the full sub-shell of 2p$ _{3/2} $ .
Figure 3. (color online) Configurations of doorway states corresponding to primary transitions and cascade of low-lying states: (a)
$ 1_{\rm CS}^{-}\rightarrow0^{+} $ , (b)$ 1_{\rm CS}^{-}\rightarrow2_{1}^{+} $ ,$ 2_{1}^{+}\rightarrow0^{+}, $ (c)$ 1_{\rm CS}^{-}\rightarrow2_{2}^{+} $ ,$ 2_{2}^{+}\rightarrow0^{+} $ in 58Fe. Blue circles indicate neutrons of the target nucleus filled/excited on the sub-shell; red circles denote the incident neutron coupled with the particle-hole pair, and dashed circles are holes. The arrows indicate the particle-hole annihilation and neutron transition.From the doorway mechanism point of view, the neutron capture reaction in the keV region is dominated by 2p-1h excitation, where the
$ \gamma $ -rays are emitted mostly by the annihilation of a neutron particle-hole pair with$ E_{\gamma} $ $ \sim $ 8-10 MeV. The core excitation results in the continuum region at the middle of the$ \gamma $ spectrum shown in Fig. 1. However, the low-energy$ \gamma $ -rays are mostly produced by the cascade decay of low-lying states, rather than from the primary transition to the high-lying state, which is why the enhancement of the low-energy$ \gamma $ -strength function does not occur in the neutron capture reaction. It is distinct that the primary M1 transitions with$ E_{\gamma} $ $ < $ 3 MeV can be populated to a great extent in the charged particle inelastic scattering reactions [7-9].Non-statistical and statistical effects coexist in the keV neutron resonance. The statistical aspects are also distinct for the neutron radiative capture reaction of 57Fe. Here, the experimental total and partial cross-sections to the three lowest
$ 0^{+} $ (CS$ \rightarrow $ GS) and$ 2^{+} $ (CS$ \rightarrow $ 1st ex. and 2nd ex.) are compared to the calculation using the statistical model code TALYS [18], as shown in Fig. 4. There are several options for the level density models, the optical models and the$ \gamma $ -ray strength functions for the input to TALYS that typically represents an error band for the cross-section predictions of a factor of 5-10. We applied many option-associations from these three main items for the TALYS calculations, and the final selected conditions are as follows. To test the consistence between the theoretical calculation and the results of the measurement, we use the evaluations method via minimum$ \chi^{2} $ =$ \sum $ $ \frac{(O_{\rm i}-E_{\rm i})^{2}}{E_{\rm i}} $ , where$ O_{\rm i} $ and$ E_{\rm i} $ are the values of the calculation and measurement for the total cross-sections. The microscopic level densities of the temperature-dependent Hartree-Fock-Bogoliubov with Gogny force, the E1 strength function from the Hartree-Fock-BCS with a scaling factor equal to 0.85, and the active Semi-microscopic optical model (JLM) neutron potential are adopted in the calculations. The calculation for the partial and total cross-sections is fairly consistent with the experimental data. However, the partial cross-sections of CS$ \rightarrow $ 2nd ex. are underestimated by TALYS, as the spin transfer is not included in the statistical mechanism frame.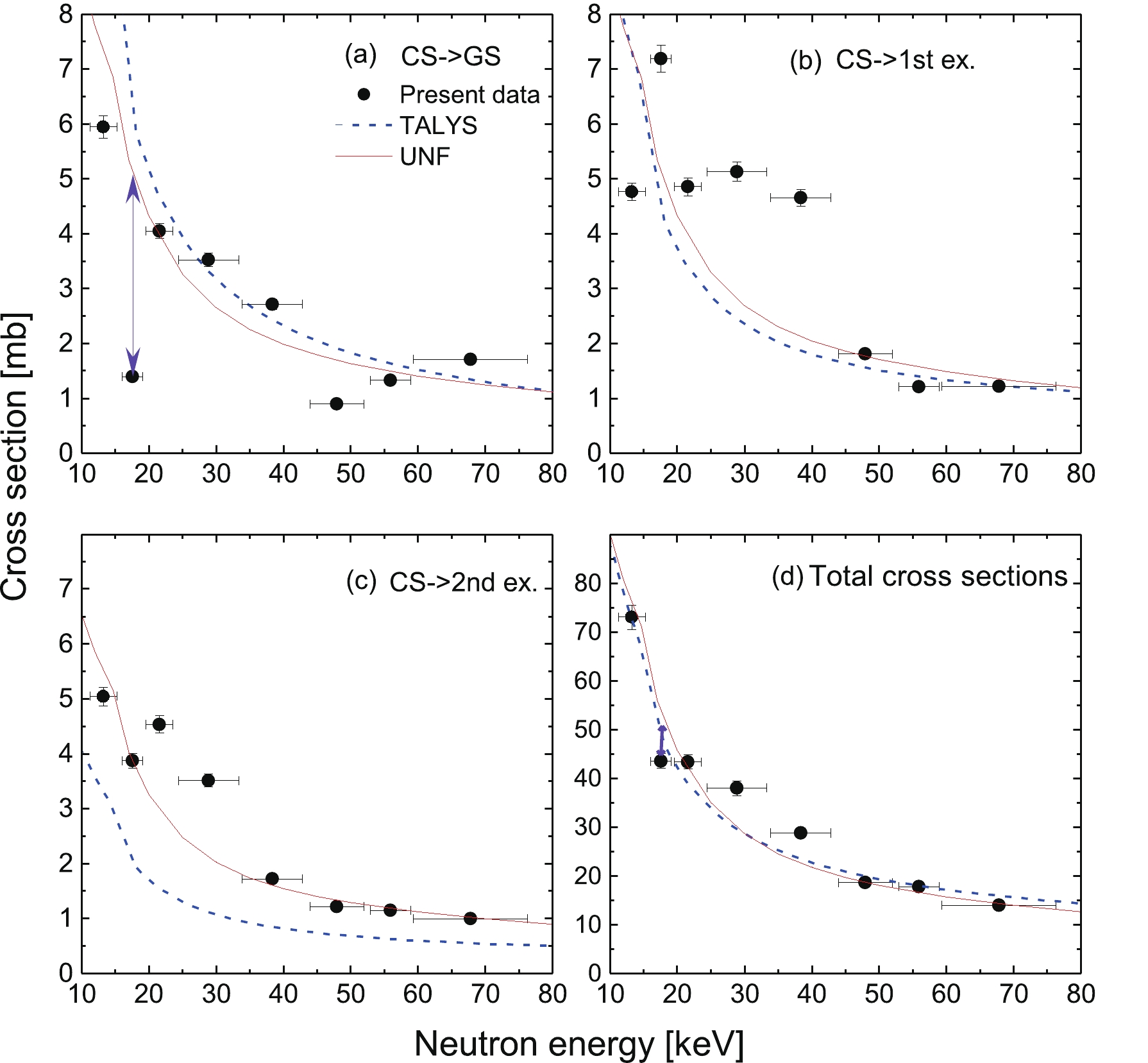
Figure 4. (color online) Experimental partial cross-sections to the three lowest
$ 0^{+} $ ($ 1_{\rm CS}^{-}\rightarrow0^{+}_{\rm GS} $ ) and$ 2^{+} $ ($ 1_{\rm CS}^{-}\rightarrow2_{1}^{+} $ and$ 1_{\rm CS}^{-}\rightarrow2_{2}^{+} $ ) in (a), (b), (c) and the total cross-section in (d) are compared to the calculation using the statistical model codes TALYS [18] and UNF [19]. The arrow lines indicate the difference in the cross-sections caused by the quenching$ \gamma_{0} $ transition.Recent progress made by employing a quantum mechanical approach for the treatment of spin-transfer into the excitation model has brought about a good reproduction of the cross-sections of neutron-induced reactions at low energies [19-21]. Spin-transfer effects have been revealed to be significant for accurate calculation of
$ \gamma $ -ray partial cross-sections with the statistical Hauser-Feshbach model [22]. The pre-equilibrium process may be modelled by the well-known statistical multistep direct (MSD) theory from Feshbach, Kerman, and Koonin (FKK), Tamura, Udagawa, and Lenske (TUL), and Nishioka, Weidenm$ \ddot{u} $ ller and Yoshida (NWY), in which the bombarding projectile initiates a series of particle-hole excitations in the target nucleus [21]. Different statistical assumptions for an intermediate state in the multistep reactions are utilized in these theories. These differences mainly cause effects at the high incident energies [20, 21]; however, descriptions of the first step (one-step producing 1p1h excitation) are the same in principle [20, 21]. Therefore, at low incident energies, the one-step process along with the multistep compound (MSC) process can be adopted to analyze experimental data. The spin-transfer in the preequilibrium process can be calculated with the FKK model using the UNF code [19], where the calculated spin distribution is combined with the Hauser-Feshbach statistical model. The one-step MSD cross-section is calculated as a distorted-wave Born approximation (DWBA) cross-section, representing the excitation of a certain p-h pair in the shell structure with an angular momentum transfer of$ \lambda $ ; the cross-section is given by [19-21]$ \begin{split} \left(\frac{{\rm d}^{2} \sigma}{{\rm d}\Omega {\rm d}E}\right) = &\sum\limits_{\lambda}\frac{2J_{B}+1}{(2J_{A}+1)(2s_{a}+1)}\frac{\mu_{a} \mu_{b}}{(2\pi \hbar ^{2})^{2}}\frac{k_{b}}{k_{a}}\\ &\times \overline{\sum\limits_{\lambda mm_{b}m_{a}}|T^{mm_{b}m_{a}}_{\lambda}(\theta)|^{2}}\rho(1,1,E_{x},J)R_{2}(\lambda), \end{split} $

(2) where a and b denote the incident and emitting particles; A and B indicate the target state (0p-0h) and the residual state (1p-1h); k is the wave number,
$ \mu $ the reduced mass, m the z-component of spin, and$ \lambda $ the total spin transfer.$ T^{mm_{b}m_{a}}_{\lambda}(\theta) $ are the DWBA matrix elements$ <\psi_{f} |f_{\lambda} (r)|\psi_{i}> $ , which represent the excitation of a 1p-1h state, where$ f_{\lambda} (r) $ is the particle-hole excitation form factor.$ \rho(1,1,E_{x},J) $ is the density of the 1p-1h state in the residual system at the excitation energy$ E_{x} $ .$ R_{2} (\lambda) $ is the spin distribution for two excitons (2 = 1p+1h). We adopt a Gaussian distribution for$ R_{2} (\lambda) $ with the spin cut-off factor$ \sigma^{2} $ =$ 0.24\times2\times $ $ A^{2/3} $ [20] in the UNF calculation [19].$R_{2} (\lambda) = \frac{2\lambda+1}{\sqrt{2\pi}2\sigma^{2}}{\rm exp}\left[\frac{-(\lambda+\frac{1}{2})^{2}}{2\sigma^{2}}\right]. $

(3) Comparisons of the calculation using the UNF code with experimental data, shown in Fig. 4, indicate a fairly good consistency between the partial/total
$ \gamma $ -ray cross-sections and the experimental data. The input parameters for the UNF code calculation are: GDR parameters for double peaks (σ1= 55.0 mb; E$ _{1} $ = 16.82 MeV; G$ _{1} $ = 4.33 MeV; σ2= 45.0 mb; E$ _{2} $ = 20.9 MeV; G$ _{2} $ = 6.09 MeV), energy level parameter a = 7.056 (1/MeV), pair correction$ \Delta $ = –0.03 (MeV). The underestimation for the CS$ \rightarrow $ 2nd ex. transition from the TALYS calculation indicates the significance of the application of the spin-transfer in the Hauser-Feshbach statistical model plus exciton model for the accurate calculation of partial$ \gamma $ -ray cross-sections. The capture states in the residual 58Fe nuclei populated by the neutron capture can be formed through either a compound 58Fe* that decays by$ \gamma $ -ray emission, or a preequilibrium process that proceeds mainly through the creation of a 1p-1h pair. These two processes generate rather different spin distributions; the momentum transfer in the preequilibrium process is smaller than that in the compound reaction. This difference in the spin population must have a significant impact on the$ \gamma $ -ray deexcitation cascade, and therefore on the partial$ \gamma $ -ray cross-sections [21]. -
In summary, a clear and strong quenching of the
$ \gamma_{0} $ transition in the p-wave neutron resonances is observed, for the first time, with respect to the high intensities of$ \gamma_{1} $ and$ \gamma_{2} $ transitions owing to the effect of non-statistical 2p-1p doorway excitation mechanism. The enhancement of the low-energy$ \gamma $ -strength function does not occur in the neutron capture reaction due to populating cascade transitions of low-lying states, rather than primary transitions. The application of spin-transfer into the Hauser-Feshbach statistical model and the exciton model reproduces the partial and total$ \gamma $ -ray cross-sections fairly well compared to the experimental data.The authors thank the Pelletron accelerator crew at the Tokyo Institute of Technology for their help with the steady operation of the accelerator. The authors gratefully appreciate financial support from the China Scholarship Council.
Quenching of ${ \gamma_{0}}$ transition results from 2p-1h doorway mechanism by p-wave neutron excitation
- Received Date: 2020-05-15
- Available Online: 2020-10-01
Abstract: The ratio of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
























 DownLoad:
DownLoad: