Nuclear dynamics and impact of ⁷Li breakup and triton transfer in ⁷Li + ²⁸Si systems

The lithium-7 isotope is a weakly bound (WB) nucleus, characterized by having a single-bound excited state at an excitation energy (E_x) of 0.4776 MeV [1]. This state precedes the formation of the ⁷Li cluster structure, which transitions to α + t at E_x = 2.467 MeV [2]. These properties highlight the importance of breakup processes in systems involving ⁷Li. Previous studies have shown that systems with WB nuclei such as ⁷Li exhibit distinct characteristics that differ markedly from those with tightly bound nuclei. One key difference is the absence of the normal threshold anomaly (TA) [3], where the real part of the nuclear potential exhibits a localized peak near the Coulomb barrier energy (V_B), and the imaginary part increases progressively with energy until reaching a plateau. In contrast, systems involving ⁷Li projectiles demonstrate a breakup threshold anomaly (BTA) [4], characterized by an increasing depth of the imaginary potential as the energy decreases below V_B.

Another key finding in systems with ⁷Li projectiles is the need to reduce the real potential strength by ~ 30%–60% (depending on the bombarded target and incident energy) to accurately reproduce measured angular distribution (AD) data [5–8]. These phenomena are attributed to the breakup of the ⁷Li nucleus into α + t in the presence of the studied targets, where strong coupling to the breakup channel creates a dynamic polarization potential (DPP) that considerably reduces the strength of the real potential. Recent studies on systems induced by ⁷Li projectiles [9–10] have also explored the influence of triton transfer instead of ⁷Li breakup on the elastic scattering channel for the ⁷Li + ⁹³Nb [9], ⁷Li + ²⁰⁹Bi [10], and ⁷Li + ¹⁴⁴Sm [11] systems.

In this study, we revisited the ⁷Li + ²⁸Si system, which has been the subject of extensive experimental and theoretical investigations [12–24] focused on its characteristics at energies below and near V_B. Pakou et al. [12] measured the elastic scattering ADs for the ⁷Li + ²⁸Si system at various energies close to the barrier. Their analysis, which employed the continuum discretized coupled channels (CDCC) method in conjunction with the double-folding optical model (DFOM) using the BDM3Y1 interaction, provided significant insights into the interaction dynamics. Notably, the depth of the imaginary potential was found to decrease as the energy approached the barrier, while the real part of the scattering potential remained largely constant, with only a minor reduction.

Further experimental investigations examined different energy ranges. For instance, Sinha et al. [13] measured ADs in the laboratory energy (E_lab) range of 11.5–26 MeV, analyzing their data with an optical potential (OP) model that included both imaginary surface and volume potentials. Additionally, CDCC calculations were conducted, focusing solely on the projectile breakup. In another study [14], scattering data for the ⁷Li + ²⁸Si system at energies E_lab = 20 and 36 MeV were compared to optical model calculations, demonstrating good agreement.

At higher energies, specifically E_lab = 45 and 48 MeV [15], the ⁷Li + ²⁸Si ADs were analyzed using real folded potentials, achieving a satisfactory renormalization that matched experimental cross-sections. Notably, at even higher energy, E_lab = 350 MeV [16], the ADs exhibited diffractive oscillations at forward angles, followed by an exponential falloff at larger angles. Zerva et al. [17] expanded this analysis by investigating the excitation functions for quasielastic scattering of ⁷Li + ²⁸Si at angles of 150° and 170°, further exploring barrier distributions through both coupled reaction channel (CRC) and CDCC methods, which take into account transfer reactions and breakup.

Numerous theoretical studies [18–24] have also explored the ⁷Li + ²⁸Si system. Farid and Hassanain [18] employed a real double-folded (DF) potential alongside an imaginary Woods-Saxon (WS) potential to analyze the elastic scattering ADs of ⁷Li on various targets, including ²⁸Si. The same authors applied the S1Y effective nucleon-nucleon (NN) interaction using the coupled channels (CC) method to fit experimental data [19]. Pakou et al. [20] introduced a phenomenological DPP to explain the observed reduction in potential strength in their analysis of the ⁷Li + ²⁸Si system. In another investigation [21], the elastic scattering AD at E_lab = 350 MeV was analyzed using the CDCC method, achieving a reasonable fit to the data. Kuterbekov et al. [22] studied the ⁷Li + ²⁸Si ADs within the energy range of 7.5–32 MeV using the WS optical model with the SPI-GENOA code. W. Chen et al. [23] applied a microscopic approach to model the OP for ⁷Li scattering from various nuclei, predicting the ADs for ⁷Li scattered from targets ranging from ²⁷Al to ²⁰⁸Pb without any free parameters.

The ⁷Li + ²⁷Al system, closely related to the ⁷Li + ²⁸Si system, has also been extensively investigated through both experimental [25–29] and theoretical [23, 30–33] studies in the energy range of 6–89 MeV. Pakou et al. [31] explored the interaction mechanisms of WB ^6,7Li and ^7,9Be nuclei as they scatter off ²⁷Al and ²⁸Si targets, using the microscopic BDM3Y1 framework. Their CDCC calculations effectively described the experimental elastic scattering data, revealing that only the ⁶Li projectile exhibits significant coupling to the continuum. In contrast, the ⁷Li and ⁷Be projectiles show weak couplings, while the ⁹Be projectile has an extremely weak coupling. The reaction cross-section (σ_R) values did not show significant enhancement when appropriately reduced, indicating that continuum effects vary across different projectiles and systems. In another study [33], the ADs for ⁶Li and ⁷Li projectiles on heavy targets (A ≥ 40) were studied using a single-folding model based on the Jeukenne–Lejeune–Mahaux (JLM) potential, accurately reproducing the ADs and σ_R for both stable and unstable nuclei.

While some systems induced by ⁷Li projectiles, such as ⁷Li + ¹²C [8], ⁷Li + ²⁷Al [25], ⁷Li + ²⁸Si [34], and ⁷Li + ¹³⁸Ba [35], exhibit a breakup threshold anomaly BTA, others, including ⁷Li + ⁵⁹Co [36], ⁷Li + ⁸⁰Se [37], ⁷Li + ¹³⁴Ba [38], and ⁷Li + ²⁰⁸Pb [39], exhibit the usual TA. These contrasting results regarding the occurrence of the BTA in ⁷Li-induced systems remain an active area of research [31, 40].

In addition, advancements in theoretical nuclear reaction models continue to evolve. Notably, the CDCC method, traditionally used for three-body scattering problems involving WB projectiles, is now being extended to address more complex four-body systems. This includes scenarios where the projectiles consist of three-body nuclei, such as ⁶He [41, 42] and ⁹Be [43–45], as well as two-body systems such as ¹¹Be + d [46]. Overall, the ⁷Li + ²⁸Si system, alongside other related systems, has become a focal point in the investigation of nuclear reactions at sub-barrier energies. Both experimental and theoretical developments are enhancing our understanding of these reactions, shedding light on the role of the Coulomb barrier, the interactions between breakup and transfer reactions, and phenomena such as BTA. These advancements significantly contribute to the broader understanding of WB projectiles and their scattering dynamics.

Building upon a previous study of ours [24], where we conducted a comprehensive analysis of the ⁷Li + ²⁸Si ADs using various interaction potentials to identify the nature of threshold anomalies—whether normal or indicative of breakup—we focused in the present study on the effects of both ⁷Li breakup within ²⁸Si target and the ²⁸Si(⁷Li, α)³¹P triton stripping reaction on the elastic ADs for the ⁷Li + ²⁸Si system at energies ranging from 8.5 to 36 MeV [12–14]. The manuscript is organized as follows: Sec. II outlines the methodology used in the analyses; Sec. III presents the results and their implications; and Sec. IV concludes with a summary and conclusions.

The calculations conducted in this study are based on the CDCC method, which has proven effective for analyzing nuclear reactions involving nuclei with low breakup thresholds, such as ^6,7Li [31]. This method allows researchers to investigate how projectile breakup influences the scattering channels by incorporating explicit couplings to continuum states. The CDCC method can successfully address projectile breakup through various mechanisms, including elastic scattering, breakup, and transfer reactions. Over the years, it has become a powerful tool for replicating experimental results related to the scattering of both unstable and stable nuclei. Originally, the CDCC was designed to model three-body systems consisting of a target and a two-body projectile. Since then, it has been adapted for four-body reactions, where the projectile dissociates into three fragments within the field of the target, leading to the development of the four-body CDCC. However, solving the CDCC equation becomes notably complex for systems involving more than three bodies. The primary challenge lies in obtaining a set of discretized continuum states for multi-body projectiles. Three main discretization methods have been proposed to address this challenge: the pseudostate (PS) [47], average (Av) [48], and midpoint (Mid) [49] methods. The PS approach replaces states with pseudostates generated by diagonalization of the internal Hamiltonian of the projectile, providing an alternative to the Av and Mid techniques.

In our previous study [24], the ⁷Li + ²⁸Si ADs were investigated using the cluster folding potential (CFP), which was normalized using two factors: N_RCF for the real component and N_ICF for the imaginary component. The analysis indicated that the real CFP strength must be reduced by approximately 60% to adequately describe the ⁷Li + ²⁸Si ADs. A similar pattern emerged in the analysis using the double folding potential (DFP) and São Paulo potential (SPP); it was found that the real DFP and SPP strength require reductions of approximately 63% and 48%, respectively, for proper representation of the ⁷Li + ²⁸Si ADs. These reductions in real potential strengths were attributed primarily to the ⁷Li breakup. To further investigate the impact of ⁷Li breakup on the ²⁸Si target, the CDCC method, which incorporates the couplings to continuum states above the ⁷Li breakup into the t + α structure, was considered, obtaining an excitation energyE_x =2.467 MeV. These couplings are significant as they generate a DPP, which in turn reduces the real potential strength. The ⁷Li + ²⁸Si ADs at energies ranging from 8.5 to 36 MeV [12–14] were analyzed using the CDCC method. A key requirement for performing these calculations is the determination of the core (α) + target (²⁸Si) and valence (t) + target (²⁸Si) potentials, denoted as $U_{a+^{{28}} {\rm{Si}}} $ and $U_{t+^{28} {\rm{Si}}} $, at the appropriate energies, E_α = 4/7$ E_{^7\mathrm{Li}} $ and E_t=3/7$ E_{^7\mathrm{Li}} $. These potentials are generated through the standard single cluster folding (CF) procedure, leading to the formulation of central and coupling potentials as follows:

In this context, R represents the separation between ⁷Li and ²⁸Si nuclei, while r denotes the distance between (t) and (α) in the ⁷Li ground state. The potential that binds α and t was modeled using a standard real Woods-Saxon shape, characterized by a radius R_V = 1.83 fm and a diffuseness a_V = 0.65 fm. The depth of this potential was adjusted to accurately reproduce the cluster binding energy. The $U_{a+^{{28}} {\rm{Si}}} $ and $U_{t+^{{28}} {\rm{Si}}} $ potentials at E_α = 4/7$ E_{^7\mathrm{Li}} $ and E_t = 3/7$E_{^7\mathrm{Li}} $, respectively, were extracted from earlier studies [50, 51]. The FRESCO code [52] and SFRESCO search code were employed to analyze the data and determine the optimal potential parameters by minimizing the χ² value, which quantifies the deviation between experimental data and calculated results.

As discussed in our aforementioned previous study [24], the required reductions for the real DFP, SPP, and CFP strengths, as observed through calculations using the (Real DF + Imag. DF), (Real SPP + Imag. SPP), and (Real CFP + Imag. CFP) methods, are due to significant coupling effects related to the ⁷Li breakup channel. This coupling can be addressed either by incorporating a DPP derived from the continuum coupling or by applying the microscopic CDCC method. We considered both approaches in this study to model the coupling effects. According to Feshbach theory regarding microscopic optical model potentials, the nucleus-nucleus interaction that contributes to the dynamic polarization potential is represented by the following equation [53]:

The first term in Eq. (2) describes the interaction between the projectile and target nuclei when both are in their ground states, $ \varphi {\,_P}_0 $ and $ \varphi {\,_T}_0 $, typically characterized by the DF integral. The operator Q projects onto the ground state, E_c.m. represents the total center-of-mass energy, and $ \varepsilon $ is an infinitesimal value that ensures time retardation in the excluded channels. The second term captures the complex contributions from all allowed inelastic channels; it is known as DPP. Numerous studies, particularly those focused on weakly bound nuclei, have investigated this potential (see, for example, Refs. [54–57]). In this study, a straightforward semi-microscopic approach was employed for modeling the DPP by introducing an additional repulsive (U^DPP) term. This potential is derived from the differentiation of the real and imaginary CFPs as follows:

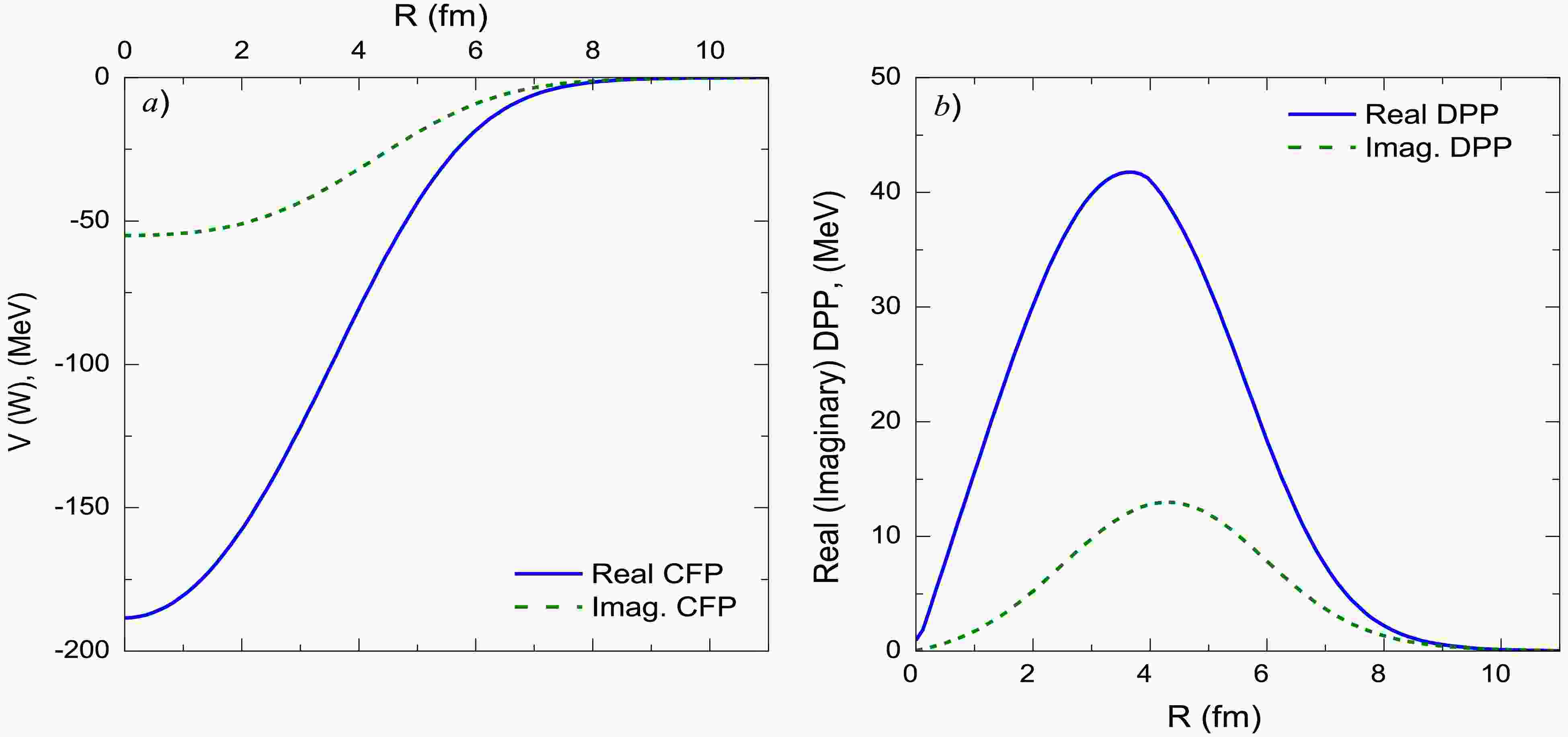
The implemented DPP in this study was modeled as a factor multiplied by the derivative of the real and imaginary CFPs, as expressed in Eq. (3). The employed CFP and DPP are depicted in Fig. 1.

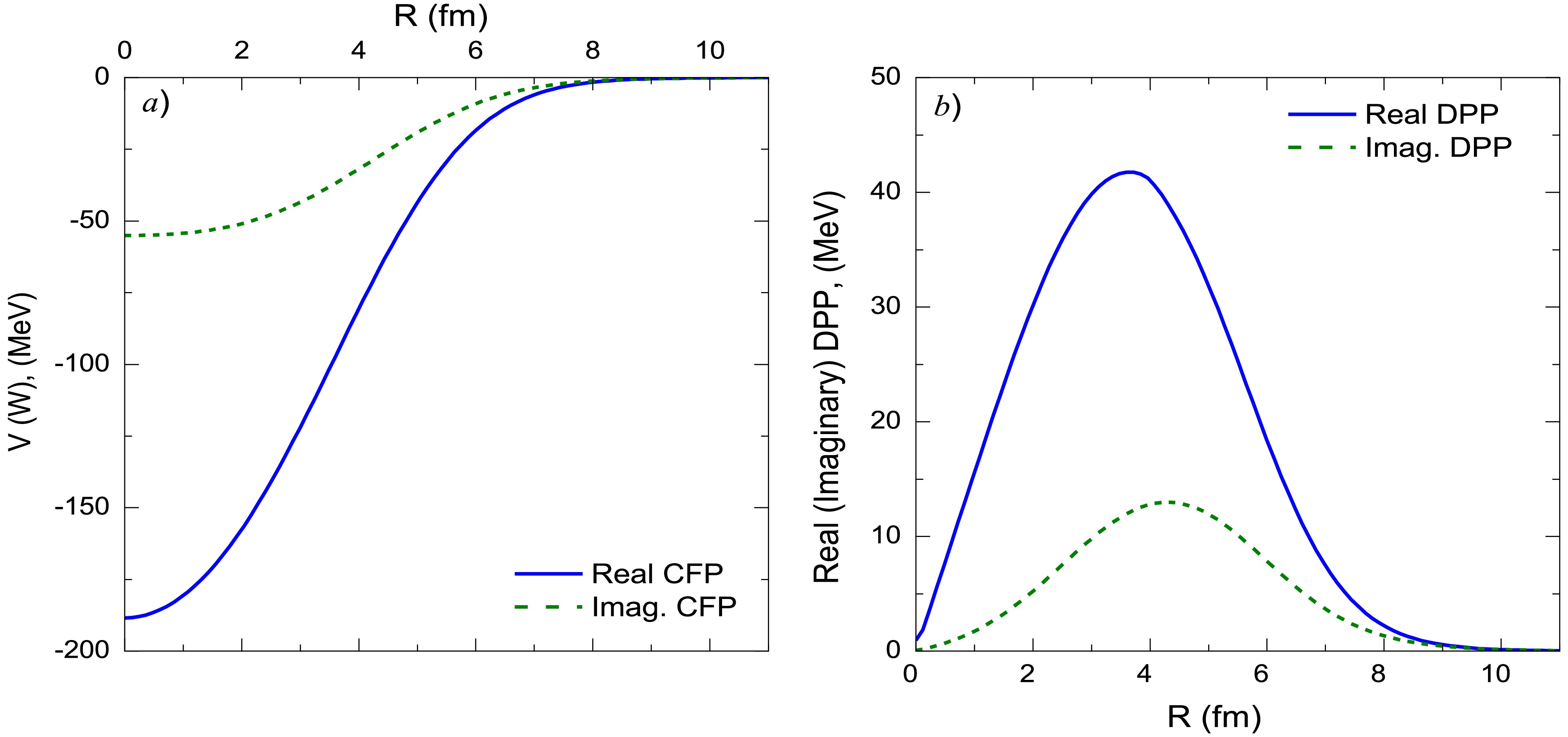
Figure 1.  (color online) Real and imaginary parts for (a) CFPs for the ⁷Li + ²⁸Si system, (b) DPPs used in the computation within the (non-normalized CFPs + DPP) approach.

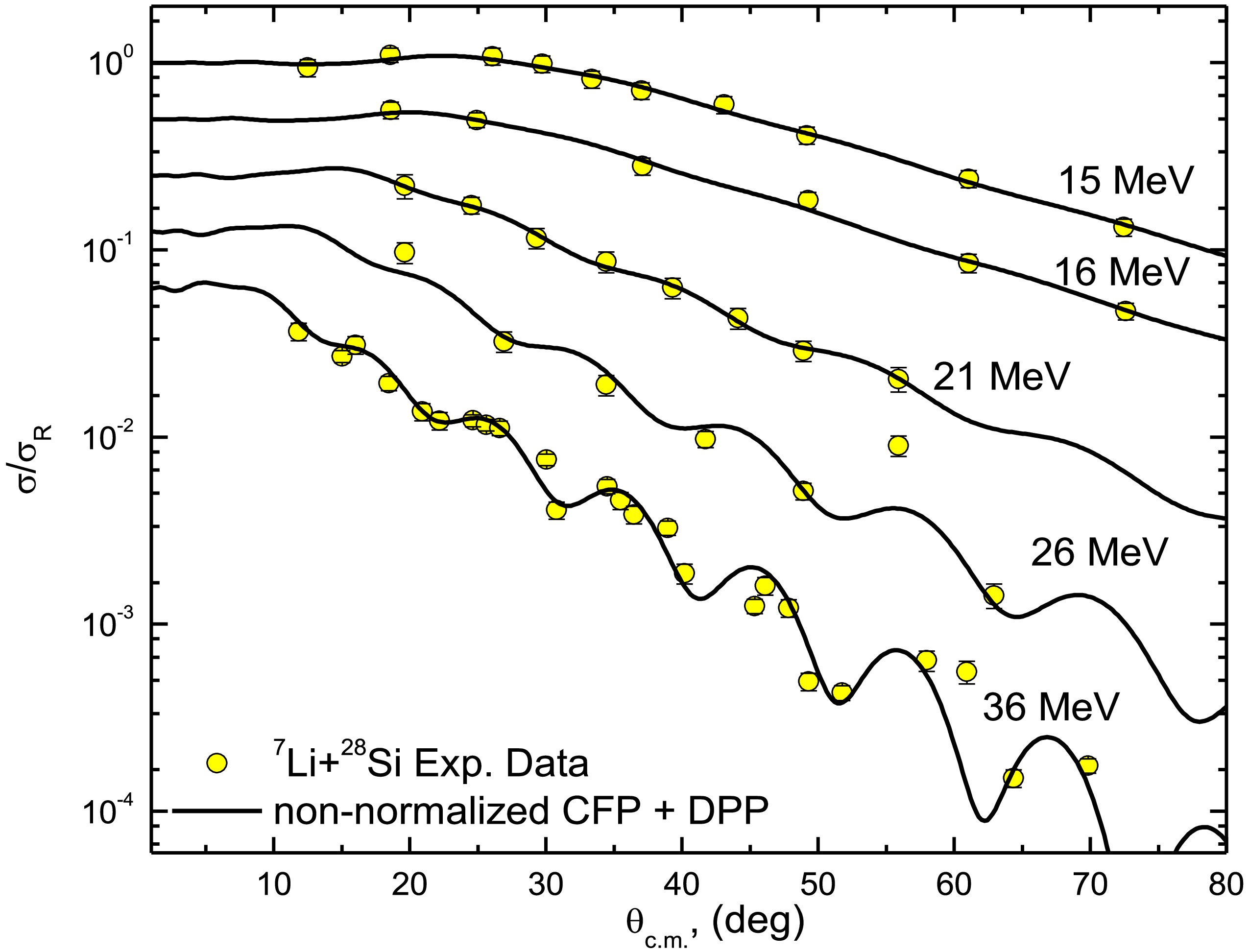
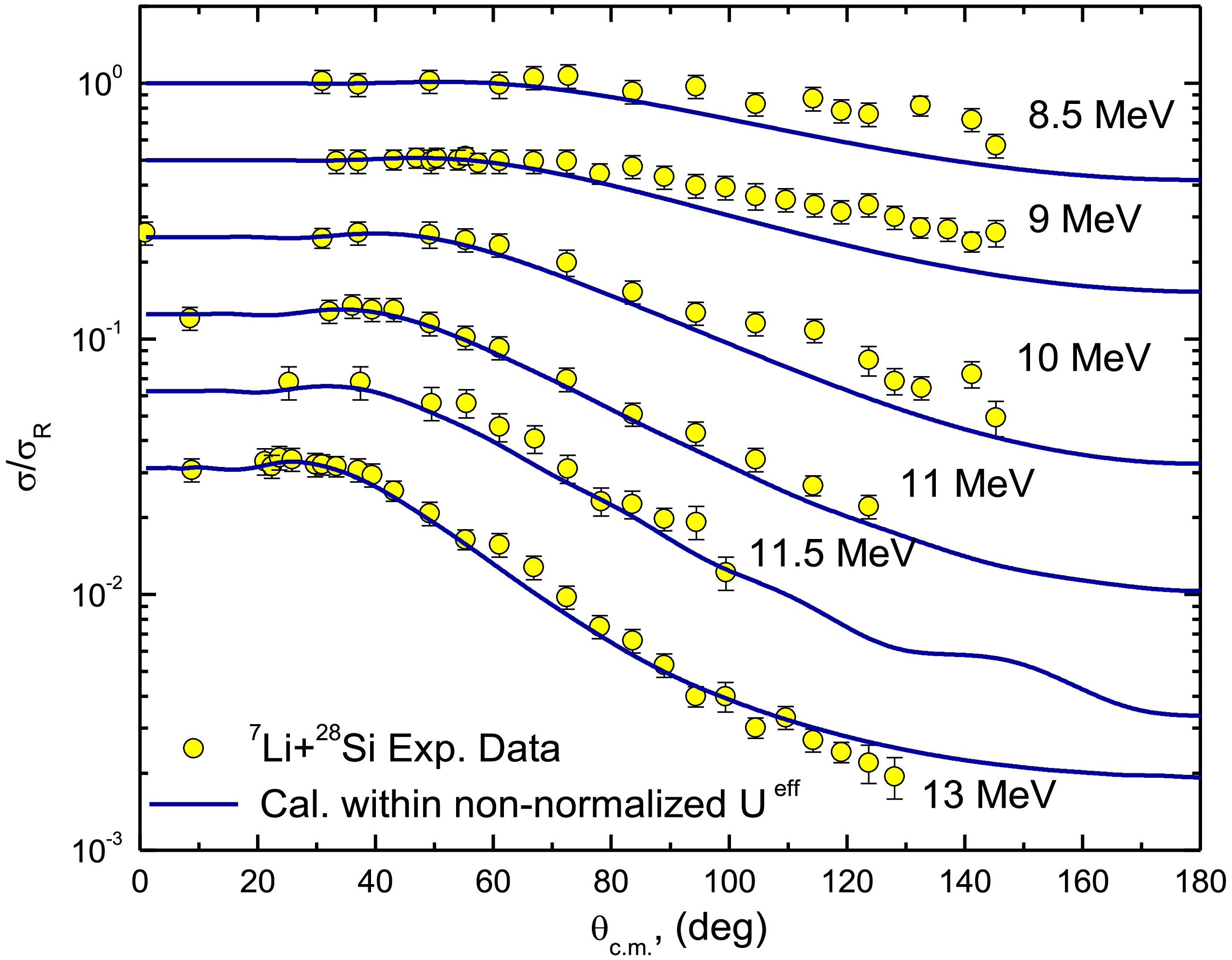
As shown in Ref. [24], the ⁷Li + ²⁸Si ADs can be reasonably described using the CFP, with reductions of approximately 60% for the real CFP strength and 32% for the imaginary CFP strength. In the present study, the inclusion of the DPP allowed for the data to be described using non-normalized real and imaginary CFPs such that “both N_RCF and N_ICF are fixed to unity”. This same approach was adopted in Ref. [58], which introduced two parameters — N_RDPP and N_IDPP — as renormalization factors for the repulsive surface DPP. Figures 2 and 3 show good agreement between the experimental ⁷Li + ²⁸Si ADs and the calculations based on non-normalized real and imaginary CFPs combined with the DPP, with the optimal potential parameters summarized in Table 1. At E_lab = 36 MeV, we obtained χ²/N= 6.8, which is higher than values at other studied energies. Nevertheless, our calculations successfully reproduce experimental AD data across the full angular range. The elevated value of χ²/N likely reflects the significantly smaller experimental uncertainties in the 36 MeV dataset.

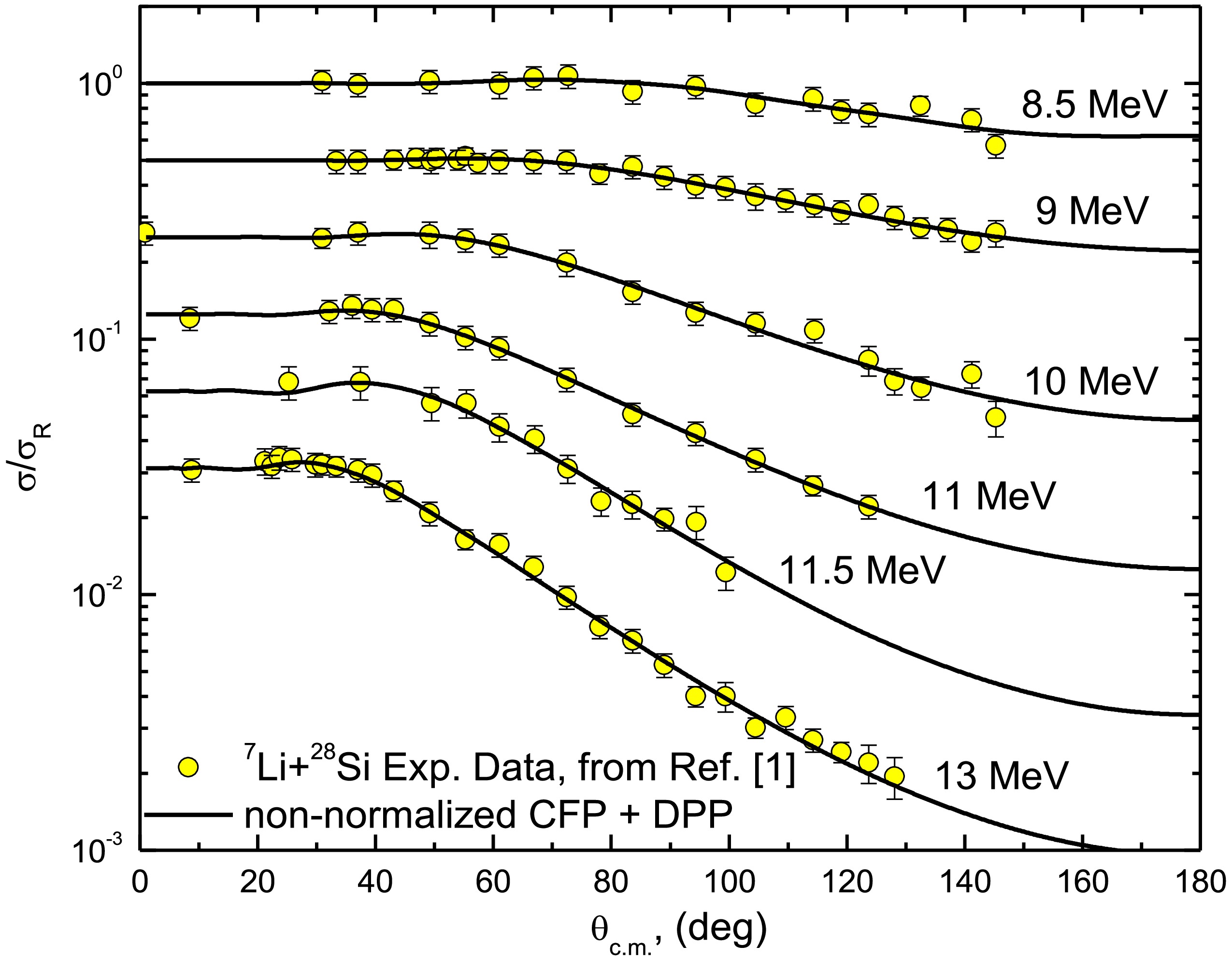
Figure 2.  (color online) Experimental ²⁸Si(⁷Li,⁷Li)²⁸Si elastic scattering ADs at E_lab= 8.5, 9, 10, 11, 11.5, and 13 MeV versus calculations using the (non-normalized CFPs + DPP) approach. The data are displaced by a factor of 0.5.

Figure 3.  (color online) Same as Fig. 2 but at E_lab= 15, 16, 21, 26, and 36 MeV.

The CDCC method [59–62] is an advanced technique widely used to study processes involving WB projectiles. It incorporates couplings to continuum states, allowing for a detailed examination of how projectile breakup affects scattering channels. The CDCC calculations were carried out using the FRESCO code, which includes coupling to resonant states (7/2^–, E_x= 4.652 MeV and 5/2^–, E_x = 6.604 MeV) with width of ∆k, 0.2, and 2 MeV, respectively; bound non-resonant state (1/2^–, E_x= 0.4776 MeV); and non-resonant continuum states with orbital momentum up to L=3. The bins with higher L were found to have a weak effect. The diagonal and coupling potentials were calculated using Eq. (1). The α + t continuum above the breakup threshold (2.467 MeV) was discretized into several momentum bins according to the momentum $ \hbar k $ of the α + t relative motion. Each bin was treated as an excited state. We adopted the model space proposed by Kelly et al. [63]. The binding potentials for t + ²⁸Si, α + ²⁸Si, and α + t correspond to those used in the CF calculations [(Eq. (1)].

An important aspect that must be carefully tested is the convergence of the CDCC calculations. These calculations should not depend on the choice of parameters, such as numerical parameters (e.g., matching radius, R_match; and integration step-size, hcm) or model space parameters (e.g., momentum-bin width, Δk; maximum momentum, k_max; and the inclusion of pseudo-states with different orbital angular momentum, L). The test calculations performed indicate that convergence is achieved for R_match = 40 fm, as shown in Fig. 4(a). These results do not depend on the hcm parameter; we set hcm = 0.04 fm. As shown in Fig. 4(b), the CDCC calculations include pseudo-states with L = 0, 1, 2, 3, 4 to examine the accumulative contributions from these states, showing convergence at L = 3. Additionally, tests were conducted with different momentum-bin widths (Δk = 0.15, 0.2, and 0.25 fm^–1). The results show that convergence is achieved for Δk = 0.25 fm^–1. Generally, values of Δk between 0.1 and 0.3 fm^–1 are suitable. The CDCC calculations in this study featured hcm = 0.04 fm, R_match = 40 fm, Δk = 0.25 fm^–1, and included the cumulative contributions from pseudo-states with L = 0, 1, 2, 3. It is important to note that the number of momentum bins considered varies depending on the bombarding energy. For bombarding energies between 8.5 and 16 MeV, the momentum space (k) above the ⁷Li breakup threshold is truncated at k_max = 1.0 fm⁻¹ (corresponding to E_max = 12.19 MeV). For higher energies (E_lab = 21, 26, and 36 MeV), the values of k_max are 1.25 fm⁻¹ (E_max = 19.05 MeV), 1.5 fm⁻¹ (E_max = 27.43 MeV), and 1.75 fm⁻¹ (E_max = 37.34 MeV), respectively.

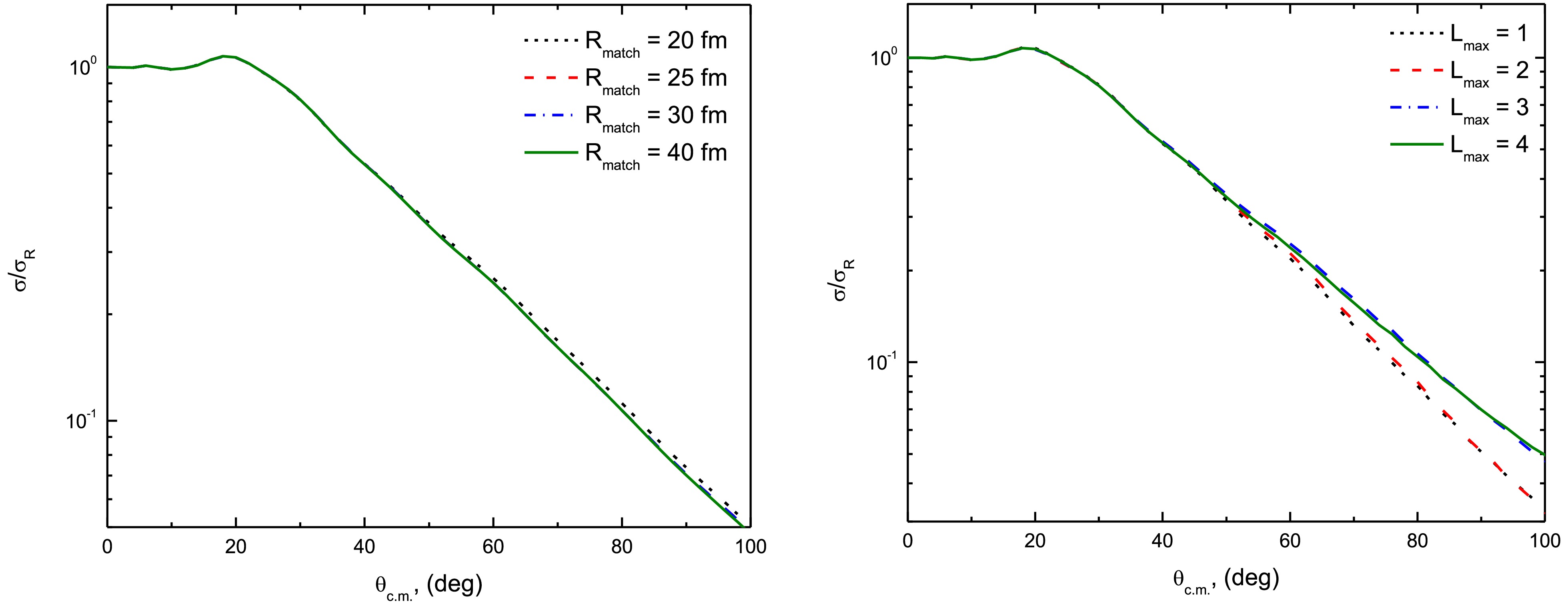
Figure 4.  (color online) Convergence test of the CDCC calculations for the ⁷Li + ²⁸Si system at E_lab = 16 MeV, showing a) convergence with respect to the matching radius (R_match) and b) the accumulative effect of the pseudo-states with various (L_max).

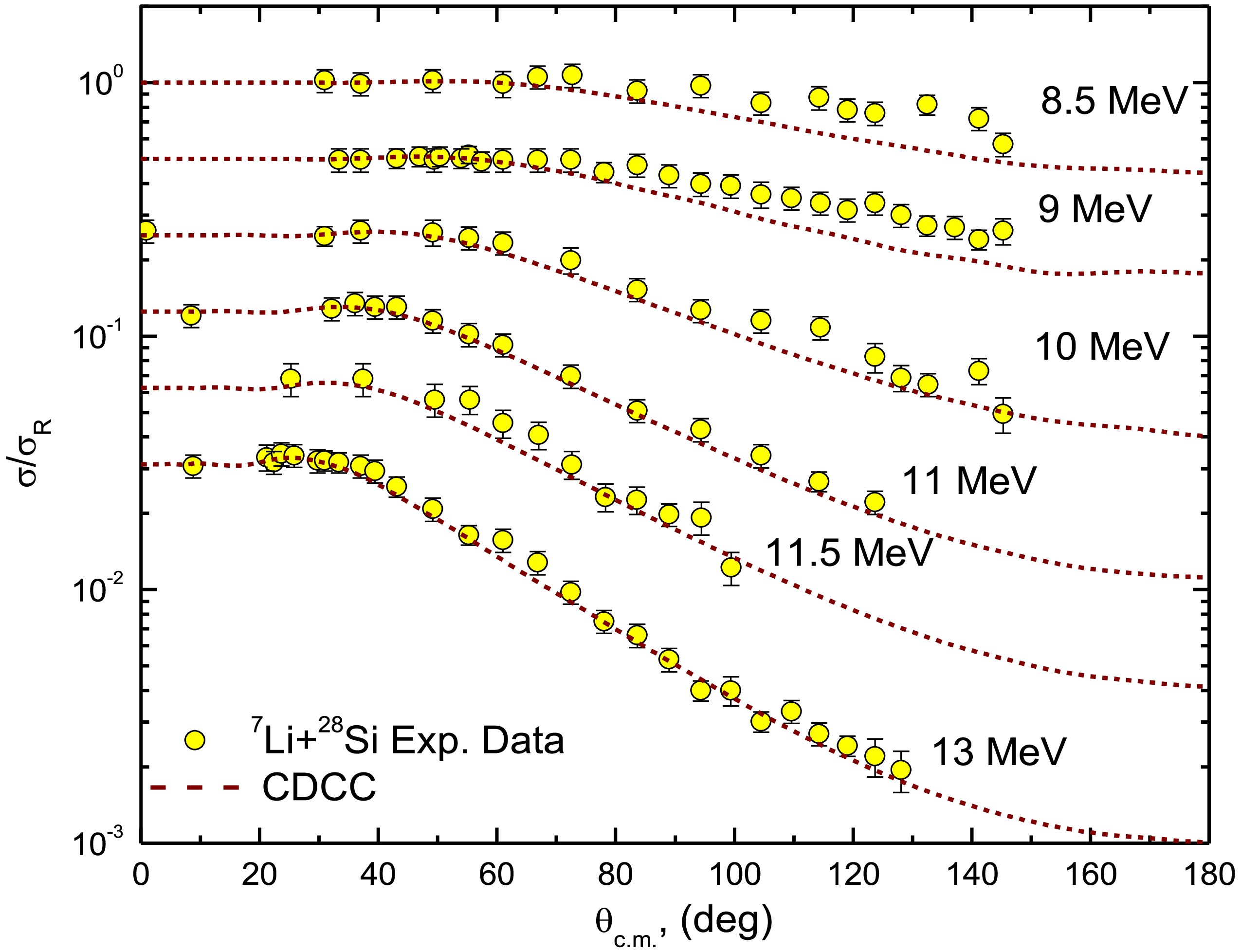
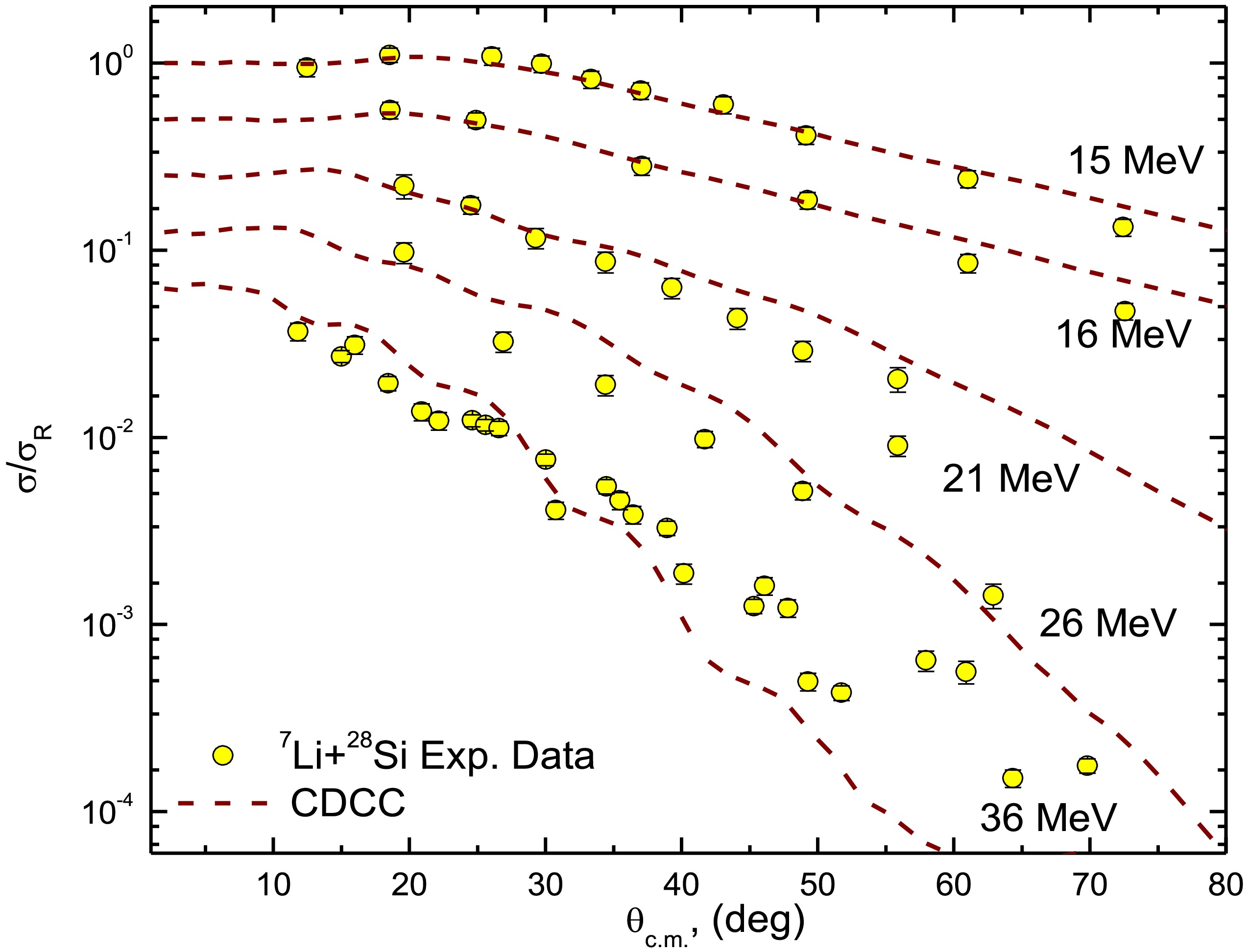
The outcomes of the calculations are shown in Figs. 5 and 6. Overall, the CDCC calculations show reasonable agreement with the experimental data across all energies examined, except for the lowest three energies (8.5, 9, and 10 MeV), where the calculations tend to underestimate the measured data, particularly at angles greater than 90°. This discrepancy may be attributed to the formation of the compound nucleus, which is not accounted for in standard CDCC calculations. Similar effects have been observed in reactions with WB [64–66]), where CN contributions dominate over direct processes. Although a better fit for the angular distributions at these lower energies could be achieved by reducing the strength of the imaginary potential, we believe it is more physically accurate to present the CDCC results without making adjustments to the potential parameters.

Figure 5.  (color online) Experimental ²⁸Si(⁷Li,⁷Li)²⁸Si elastic scattering ADs at E_lab= 8.5, 9, 10, 11, 11.5, and 13 MeV versus calculations based on the CDCC method.

Figure 6.  (color online) Same as Fig. 5 but at E_lab= 15, 16, 21, 26, and 36 MeV.

We reanalyzed the ⁷Li + ²⁸Si elastic scattering ADs using an effective potential (U^eff). This U^eff was constructed as the sum of two components: cluster folding potential (U^CF) and dynamic polarization potential (U^DPP), both derived from CDCC calculations. U^DPP was obtained from the coupling to the continuum states and generated using the trivially equivalent local potential (TELP) approach [67]. The expression for U^eff is

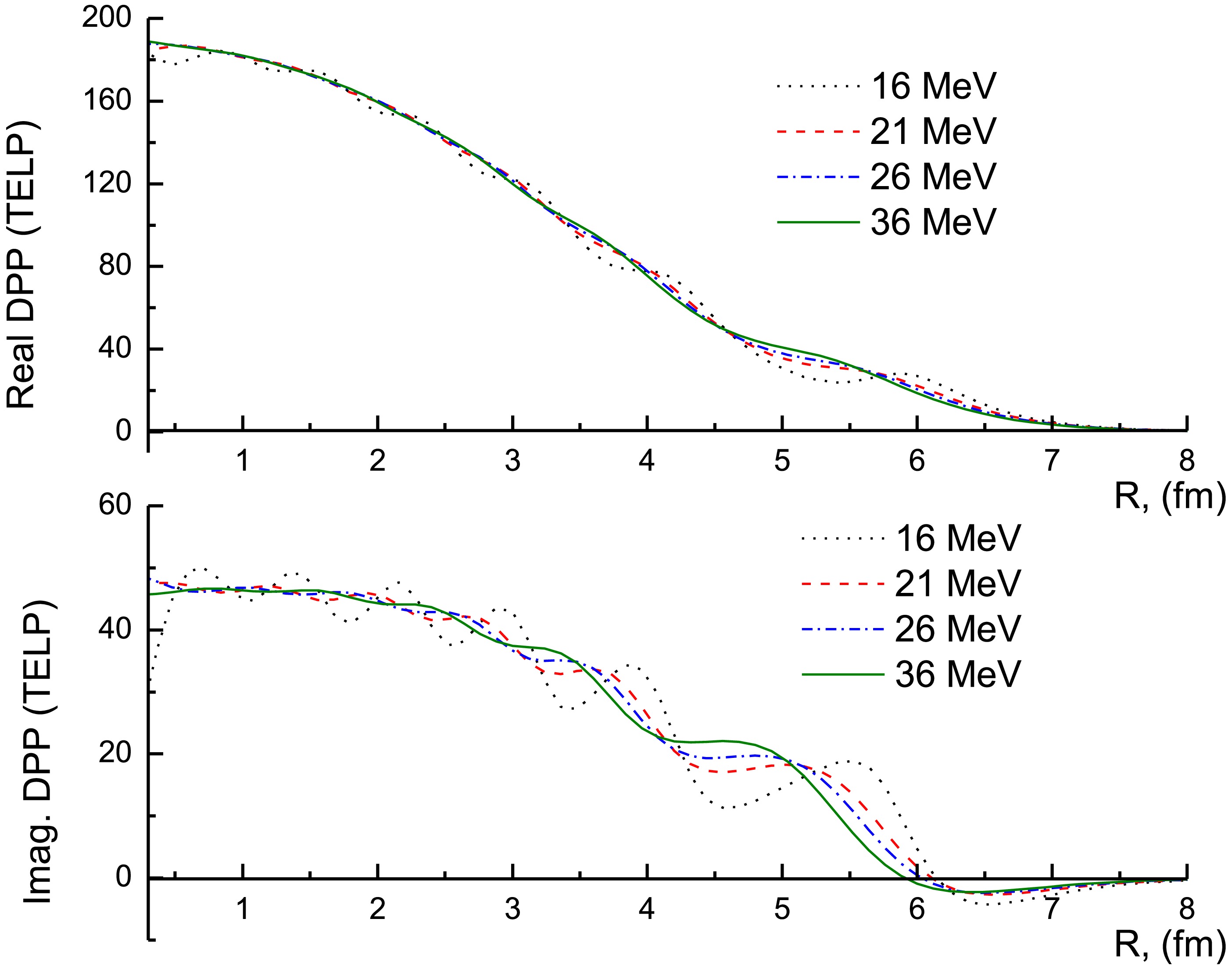
Figures 7 and 8 illustrate the generated U^DPP for the ⁷Li + ²⁸Si system. The characteristics of U^DPP are significantly influenced by the target and incident energy. At E_lab = 16, 21, 26, and 36 MeV, the general behavior for the real and imaginary parts of the generated U^DPP is close to each other, while at the lowest studied energies, E_lab ≤ 15 MeV, this behavior is completely different, and U^DPP exhibits a clear oscillatory nature.

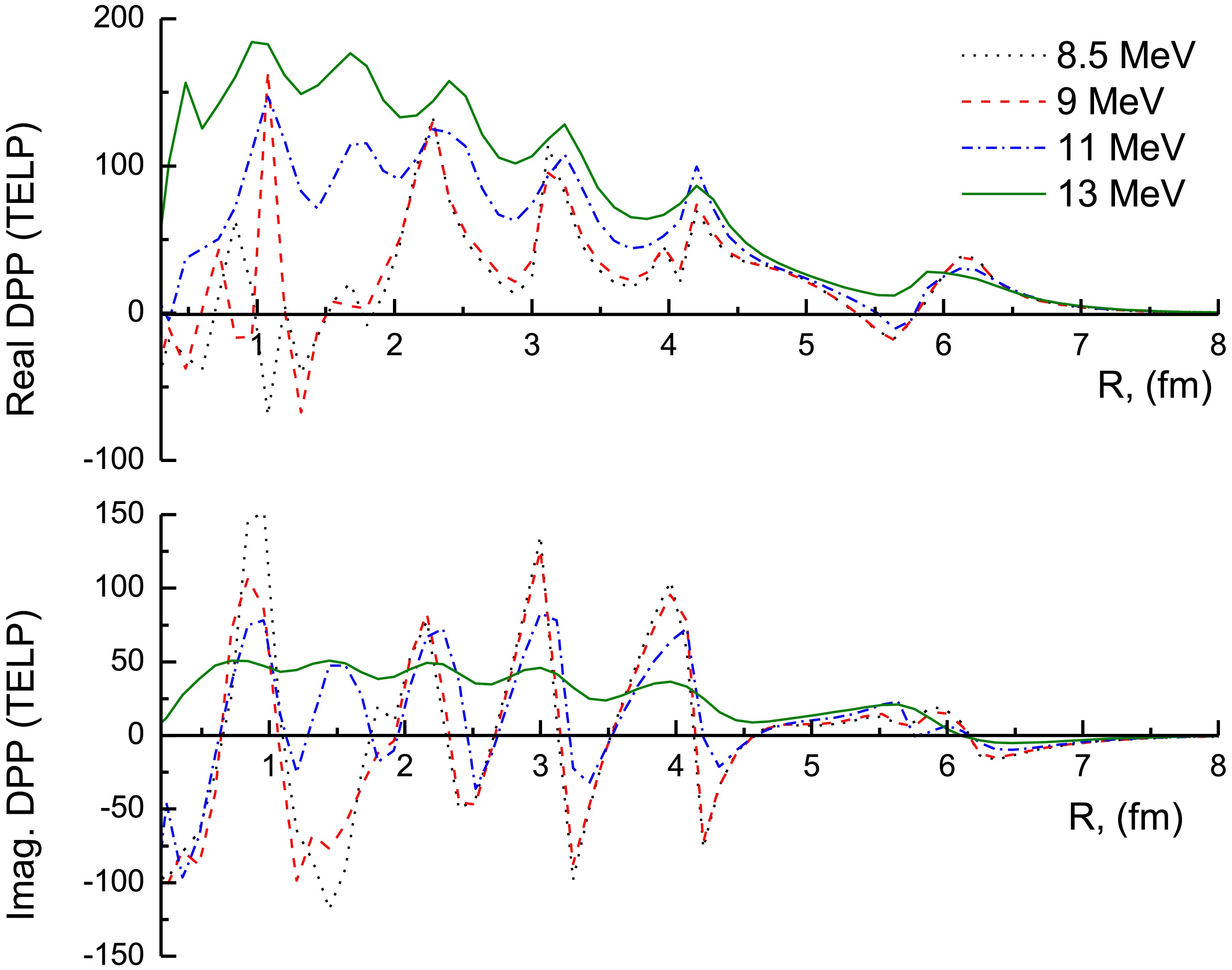
Figure 7.  (color online) U^DPP obtained from the CDCC computations for the ⁷Li + ²⁸Si system at E_lab = 8.5, 9, 11, and 13 MeV.

Figure 8.  (color online) Same as Fig. 7 but at E_lab = 16, 21, 26, and 36 MeV.

The ⁷Li + ²⁸Si elastic scattering ADs were reproduced using a non-normalized effective potential, U^eff, characterized by two factors: N_R and N_I, both set to unity (N_R = 1.0 and N_I = 1.0) for the real and imaginary U^eff components, respectively. A comparison between the calculated ⁷Li + ²⁸Si ADs using the non-normalized U^eff and experimental data reveals good agreement, as presented in Figs. 9 and 10. These calculations demonstrate the suitability of U^eff, which explicitly accounts for the ⁷Li breakup effects arising from the coupling to continuum states above the ⁷Li →α + t breakup threshold, replicating experimental AD data over a wide range of energies.

Figure 9.  (color online) Experimental ²⁸Si(⁷Li,⁷Li)²⁸Si elastic scattering ADs (circles) at E_lab= 8.5, 9, 10, 11, 11.5, and 13 MeV versus calculations within non-normalized U^eff (curves).

Figure 10.  (color online) Same as Fig. 9 but at E_lab= 15, 16, 21, 26, and 36 MeV.

A recent study [10] investigated the breakup of ⁷Li in the presence of a heavy mass target, ²⁰⁹Bi, revealing a significant population in a region accessible solely through direct triton stripping, distinct from breakup followed by triton capture. The analysis highlighted the direct cluster-stripping mechanism as a major source of alpha production. Similar results were observed in the ⁷Li + ¹⁴⁴Sm reaction [11], emphasizing the role of the triton transfer mechanism. In the ⁷Li + ²⁸Si system, both the breakup of ⁷Li and combined effects of ⁷Li breakup and triton transfer in the reaction ²⁸Si(⁷Li, α)³¹P on the elastic ⁷Li+²⁸Si channel are depicted in Fig. 11. The triton was modeled as being transferred as a single entity from the ⁷Li ground state to a t + ²⁸Si configuration in ³¹P. For the entrance channel (⁷Li + ²⁸Si), non-normalized U^eff incorporating the ⁷Li breakup was used, while for the exit channel (α + ³¹P), a standard potential (SPP) [68] with standard normalization factors (N_R = 1.0 and N_I = 0.78) was employed. The bound state potentials for the ⁷Li→ α + t and ³¹P→ ²⁸Si + t configurations were modeled using the WS form, with R_V = 1.25, a_V = 0.65 fm, and the depth adjusted to reproduce the binding energies of 2.467 and 17.897 MeV, respectively, for the considered overlap $ \left\langle {{{}^{\text{7}}{\text{Li}}}} \mathrel{\left | {\vphantom {{{}^{\text{7}}{\text{Li}}} {\alpha + t}}} \right. } {{\alpha + t}} \right\rangle $ and$ \left\langle {{{}^{{\text{31}}}{\text{P}}}} \mathrel{\left | {\vphantom {{{}^{{\text{31}}}{\text{P}}} {^{28}{\text{Si}} + t}}} \right. } {{^{28}{\text{Si}} + t}} \right\rangle $.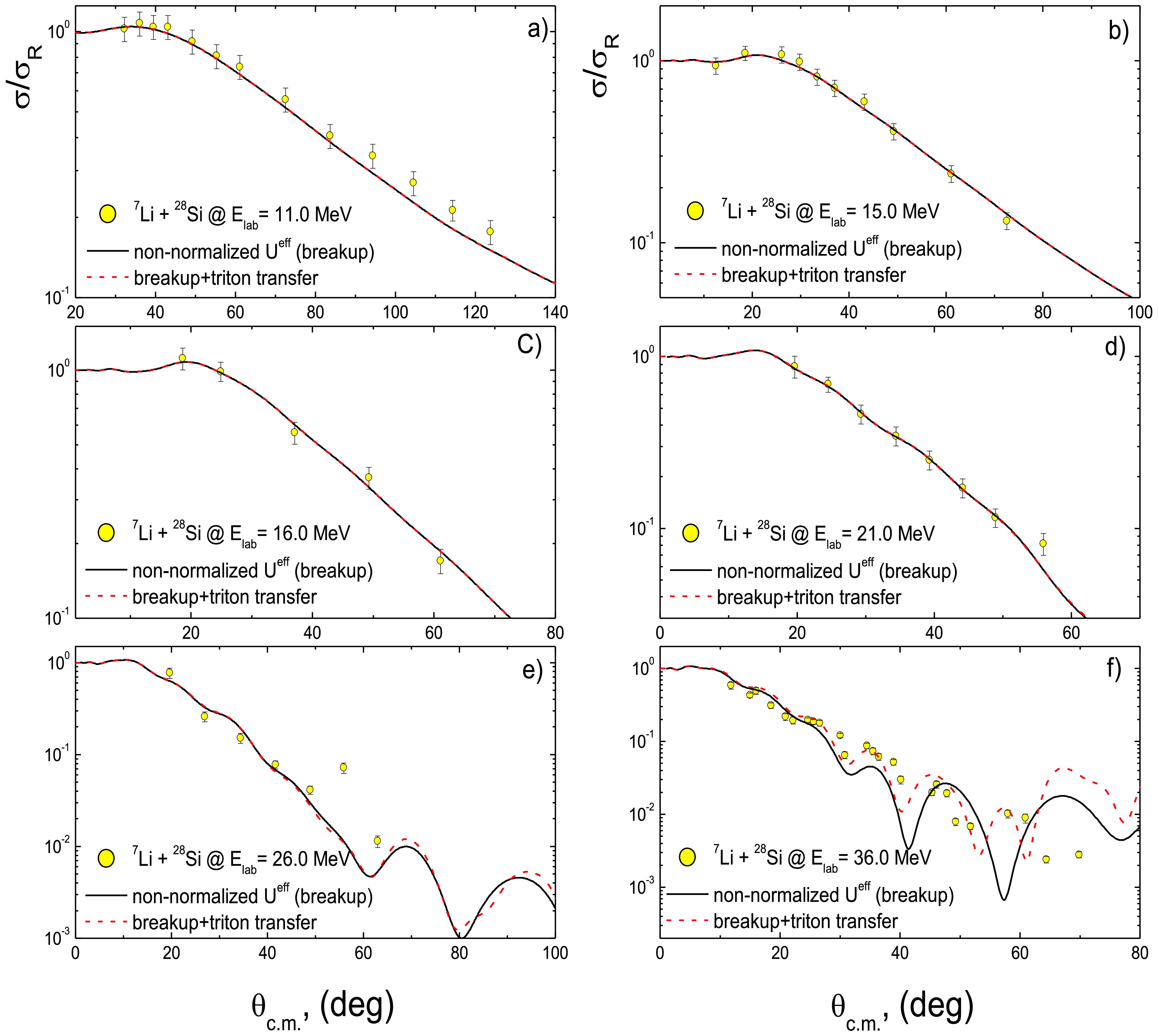

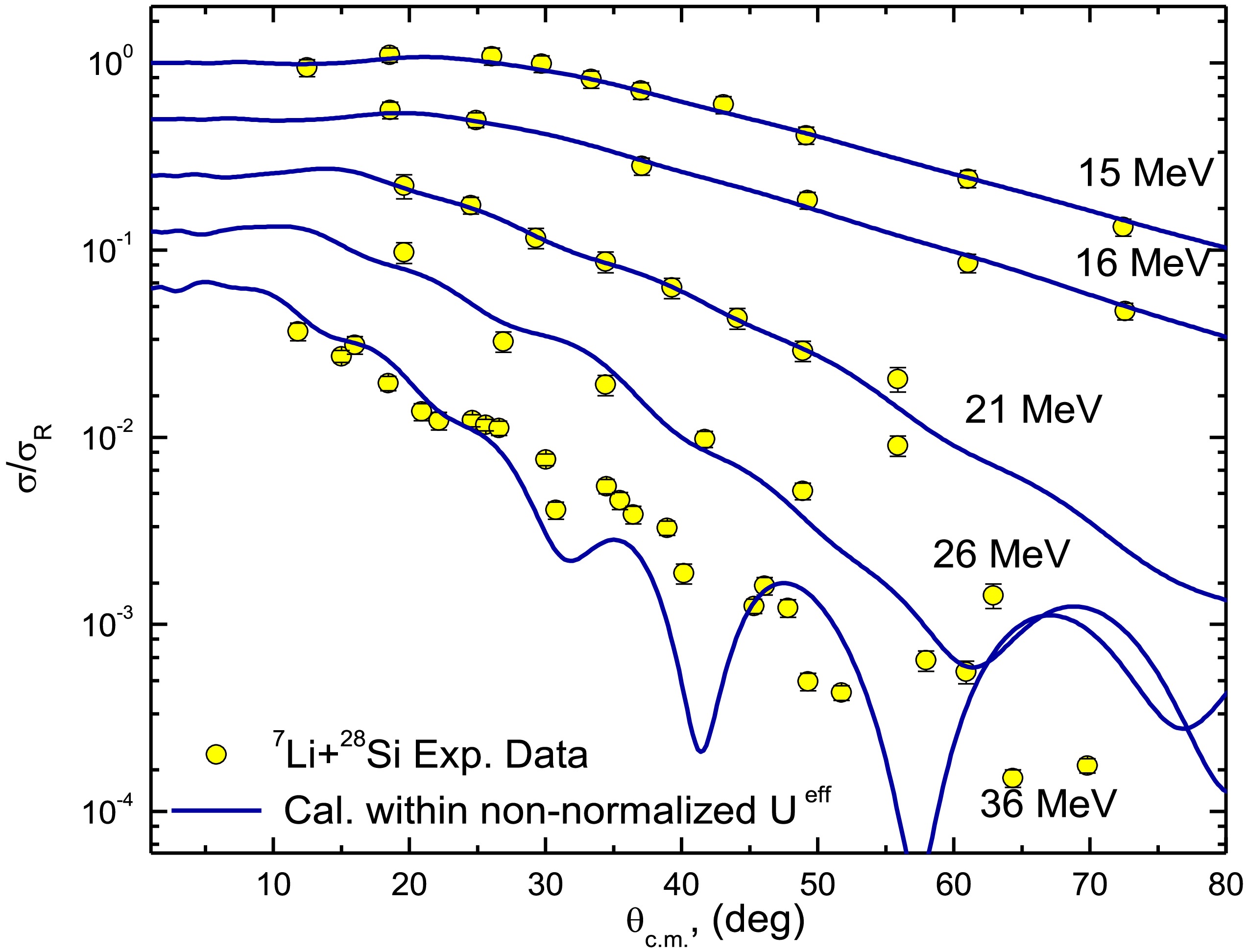
Figure 11.  (color online) ²⁸Si(⁷Li,⁷Li)²⁸Si experimental ADs at E_lab = 11, 15, 16, 21, 26, and 36 MeV versus the calculations within non-normalized U^eff that explicitly consider the ⁷Li breakup effect (solid curves) in comparison with the combined effects of breakup and triton transfer (dashed curves).

The calculations considering the combined effects of ⁷Li breakup and triton transfer were conducted at various incident energies, namely E_lab = 11, 15, 16, 21, 26, and 36 MeV, to assess their energy dependence. As shown in Fig. 11, at all the studied energies, the dominant contributions emerged from breakup, while those from triton transfer were negligible. With increasing bombarding energy, especially at larger angles (Figs. 11(e) and (f)), the effects of triton transfer began to emerge. In conclusion, at energies near or below the breakup threshold, breakup is the predominant mechanism, with limited effects at higher energies. Compared to heavier systems such as ⁷Li + ²⁰⁹Bi [10] and ⁷Li + ¹⁴⁴Sm [11], the influence of triton transfer is negligible in the lighter (⁷Li + ²⁸Si) system, particularly at low energies. To confirm the increasing role of triton transfer at higher energies, we compared the relative contributions of breakup and transfer processes by analyzing the ratio of the breakup cross-section $ \left( {{\sigma _{{\text{BU}}}}} \right) $ to the total breakup+transfer cross-section $ \left( {{\sigma _{{\text{BU}} + {\text{TR}}}}} \right) $ across the studied energies (Table 2). The results reveal a clear trend: as the energy increases, the $ \left( {{{{\sigma _{{\text{BU}}}}} \mathord{\left/ {\vphantom {{{\sigma _{{\text{BU}}}}} {{\sigma _{{\text{BU}} + {\text{TR}}}}}}} \right. } {{\sigma _{{\text{BU}} + {\text{TR}}}}}}} \right) $ ratio increases, indicating a growing contribution from triton transfer. This enhanced transfer leads to a suppression of the overall cross-section values, consistent with the observed energy-dependent behavior.

E/MeV	$ {\sigma _{{\text{BU}}}} $/mb	$ {\sigma _{{\text{BU}} + {\text{TR}}}} $/mb	$ \left( {{{{\sigma _{{\text{BU}}}}} \mathord{\left/ {\vphantom {{{\sigma _{{\text{BU}}}}} {{\sigma _{{\text{BU}} + {\text{TR}}}}}}} \right. } {{\sigma _{{\text{BU}} + {\text{TR}}}}}}} \right) $
11	711.0	711.6	0.999
15	1140	1123	1.015
16	1208	1192	1.013
21	1442	1424	1.013
26	1558	1531	1.018
36	1677	1538	1.090

Table 2.  Breakup cross-sections$ \left( {{\sigma _{{\text{BU}}}}} \right) $, total breakup+transfer cross-sections$ \left( {{\sigma _{{\text{BU}} + {\text{TR}}}}} \right) $, and their ratios at E_lab = 11–36 MeV

In this study, we conducted a detailed analysis on the elastic scattering ADs for the ⁷Li + ²⁸Si system at near-barrier energies. The focus was put on examining the influences of the breakup of ⁷Li in the field of the ²⁸Si target and triton stripping reaction ²⁸Si(⁷Li, α)³¹P on the ⁷Li + ²⁸Si elastic ADs. Based on a previous study [24], it was determined that the strengths of the real DFP, SPP, and CFP needed reductions of 63%, 72%, and 55%, respectively. This reduction in potential strength is a characteristic feature of systems involving WB projectiles such as ⁷Li, arising from coupling to the continuum that generates a DPP. In this analysis, two methodologies were employed to simulate these effects. The first approach involves reproducing the data using a non-normalized CFP ''N_RCF and N_ICF =1''. Additionally, surface-shaped real and imaginary DPPs were included, modeled as factors multiplied by the derivative of the real and imaginary CFPs. The second approach is based on the continuum discretized coupled channels (CDCC) method with freely adjustable parameters to reproduce the elastic ADs. The analysis revealed that the characteristics of the real and imaginary DPPs exhibit a strong dependence on the bombarding energy. Moreover, we found that the U^eff potential—without any adjustments—successfully reproduces the ⁷Li + ²⁸Si ADs data, supporting its suitability for this nuclear system. Furthermore, the analysis included an investigation on the influence of the triton transfer reaction ²⁸Si(⁷Li, α)³¹P on the ⁷Li+²⁸Si elastic scattering channel. The results indicate that below and near the barrier, breakup is the dominant mechanism, while the effects of triton transfer become increasingly significant with higher bombarding energy.

This work was funded by the University of Jeddah, Jeddah, Saudi Arabia, under Grant No. (UJ-24-DR-3076-1). The authors, therefore, acknowledge with thanks the University of Jeddah for technical and financial support.