Implication of radioactive nuclear reaction ¹¹C(α, p)¹⁴N in Supernova ν-process nucleosynthesis

The boron in the solar system possibly originates from two primary astrophysical sources: spallation reactions in galactic cosmic ray (GCR), i.e. the collisions of high-energy charged particles with abundant p, ⁴He and CNO nuclei in the interstellar medium (ISM) [1−3], and neutrino-induced nucleosynthesis (ν-process) in CCSN, i.e., the neutrino spallation reactions in CCSN such as ${\rm \nu+^{12}C\rightarrow {^{11}B}}+n,\ ^{11} $C+p (¹¹C is a short-lived radioactive nucleus) [4] and the reaction chain such as $ \rm ^4He(\nu_e, \mathit{p}) \rm ^3H(\alpha,\ \gamma)^7Li(\alpha,\ \gamma)^{11}B $ [5, 6]. Therefore, the two stable boron isotopes ^10,11B can serve as suitable probes for studying the explosion mechanism and ν-process nucleosynthesis in the CCSN.

Type X silicon carbide grains (hereafter X grains) are discovered in primitive meteorites [7, 8], and the isotopic ratios in X grains are valuable signatures that they are formed in the ejecta from CCSN [9]. The ¹¹B/¹⁰B isotopic ratios measured in those X grains is 4.68 ± 0.31 [10, 11], which exceeds the solar values $ \rm (^{11}B/^{10}B)_{\odot}\approx 4.04 $ [12] by 2σ (here we take $ \sigma\approx 0.31 $). Standard GCR spallation models predict $ \rm (^{11}B/^{10}B)_{GCR}\approx 2.5 $ [2], which is significantly lower than both observed ratios in the solar system and X grains. This discrepancy may indicate that the ν-process in the CCSNe could be a dominant contribution to the solar system ¹¹B [3, 13, 14]. It has recently been indicated theoretically that the isotopic ratios such as $ \rm ^{11}B/^{10}B $, ¹³⁸La/¹³⁹La, etc. could help to constrain the still unknown neutrino mass hierarchy [15]. However, the existence of laboratory contamination in meteoritic observation prevents a clear conclusion on the origin of X grains [10, 11]. If the uncertainties from X grain data and theoretical calculation of the isotopic abundances can be reduced, these intrinsic ¹¹B/¹⁰B ratios obtained from X grains will provide a unique window to study the explosive nucleosynthesis and the explosion mechanism of CCSN, and the chemical evolution in the early solar system.

Boron is a fragile nucleus and can be easily destroyed by the reactions such as ¹⁰B$ (p,\alpha)^7 $Be and ¹¹B$ (p,2\alpha)^4 $He during the hydrogen burning process in the stellar evolution [12, 16, 17]. This also applies to the explosive SN ν-process nucleosynthesis because once ¹⁰Be ($ \tau_{1/2}=1.51 $ My), ¹⁰B, ¹⁰C ($ \tau_{1/2}=19.3 $ s), ¹¹Be ($ \tau_{1/2}=13.8 $ s), ¹¹B and ¹¹C ($ \tau_{1/2}=20.34 $ m) are produced by the ν-spallation reactions, some fractions are quickly consumed by secondary destruction reactions. During the supernova explosion, the ^6,7Li, ⁷Be, ^10,11B are produced and/or destroyed efficiently by the time when the temperature drops to $ T\sim0.2 $ GK. After this time, the temperature and density quickly decrease as the materials are ejected into interstellar space (see Figure 1 of [5]). Therefore, even the fragile nuclei Li and B do not suffer further nuclear destruction processes and survive in the cooled materials until the SiC X grains condense and form after a few years but within 30 years [9, 18, 19]. Fujiya et al. discovered the ^6,7Li and ^10,11B isotopes in SiC X grains [11]. Our previous paper [15] discussed supernova nucleosynthesis of ^6,7Li and ^10,11B and their observability in X grains. The sensitivity of ¹¹B and ¹¹C abundances to the related nuclear reactions has not been studied in the literature and needs further careful investigation, particularly at the astrophysically important temperature range $ T\leq 1 $ GK for SN nucleosynthesis. We studied all the 43 nuclear reactions related to ¹¹B and ¹¹C from the JINA reaclib [20], and our analysis revealed that the secondary nuclear reaction, ¹¹C$ (\alpha,p)^{14} $N, is one of the most efficient reactions that destroys the ¹¹C and affect the final ¹¹B abundance. The present precision of experimental measurement of the reaction cross section is quite limited, especially at astrophysical low energies 0.23−1.24 MeV of Gamow window corresponding to $ T=0.2-1 $ GK. The sensitivity of ¹¹C abundance to the ¹¹C$ (\alpha,p)^{14} $N reaction rate requires further detailed study both experimentally and theoretically.

In the present work, we calculated the ¹¹C$ (\alpha,p)^{14} $N S-factor by including the contributions from low energy resonances, which were ignored in the previous studies, and estimated the corresponding reaction rate and its associated uncertainty. Additionally, we investigated the impact of the new rate on the CCSN nucleosynthesis of the A=10 and A=11 nuclear systems to infer the sensitivity of ¹¹B production to the reaction rate. In Section II, we present the calculation of ¹¹C$ (\alpha,p)^{14} $N S-factor and nuclear reaction rate in detail. In Section III, we discuss the effects of our new ¹¹C$ (\alpha,p)^{14} $N rate on ¹¹B and ¹¹C production as well as their sensitivities in CCSN nucleosynthesis. The conclusion is given in Section IV.

We perform a systematic study for all the 43 nuclear reactions related to the ¹¹B and ¹¹C production by enlarging and reducing each reaction rate by two orders of magnitude. These large multiplication factors are artificially introduced to identify the most sensitive nuclear reaction clearly, since the non-linear effect due to multiple reactions makes it challenging to find the net change of the A=11 nuclear abundances by only a single reaction if a much smaller factor is adopted. 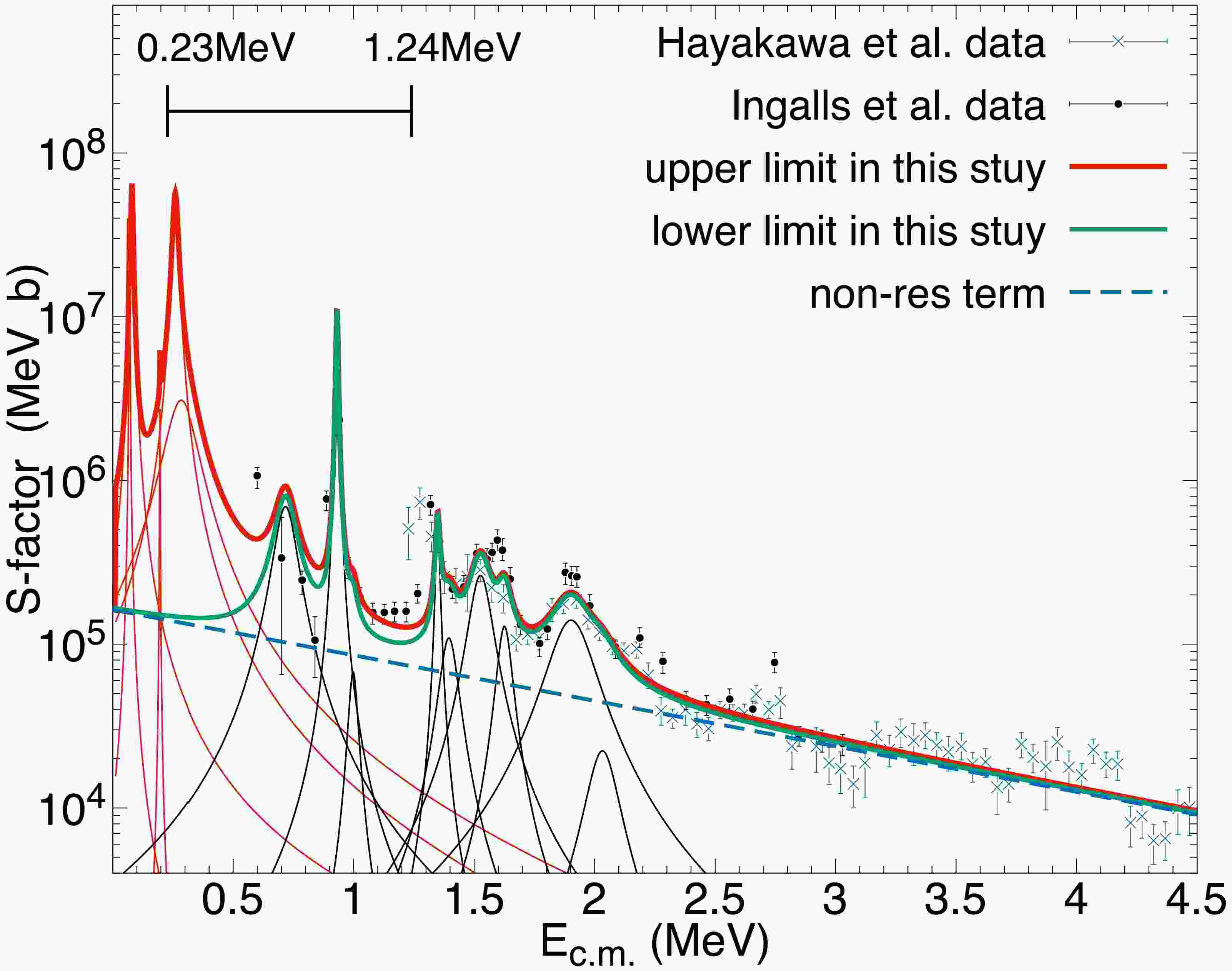The reaction cross section for ¹¹C$ (\alpha,p)^{14} $N has not been measured at astrophysical low energies $ E\leq 0.6 $ MeV as shown in Fig. 1. If we take account of five resonances at much lower energies, which were not included in the previous studies of SN nucleosynthesis, the uncertainties of thermally averaged reaction rate could be as large as 1−2 orders of magnitude at $ T_9\sim0.2 $ as displayed in Fig. 2. The sensitivity of the nuclear abundance of $ ^{\rm A}X $ is defined by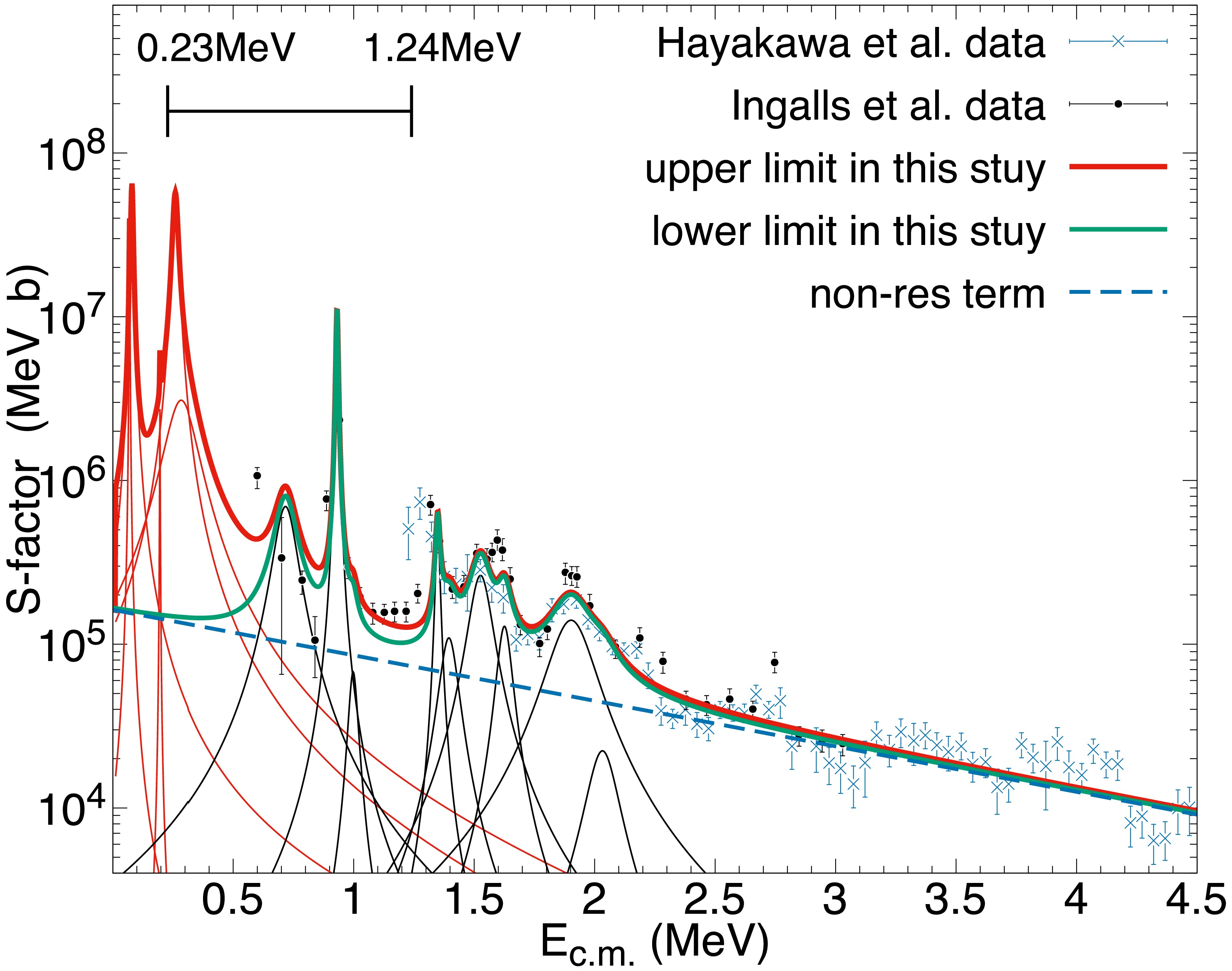

Figure 1.  (color online) Astrophysical S-factor of the reaction ¹¹C$ (\alpha,p)^{14} $N. Experimental data are from Ingalls data (black dots) and Hayakawa data (blue cross). The thick red line is the best fitting S-factor of the upper limit ($ \theta^2_{\alpha}=1 $ for i = 1−5). The thick dashed blue line is the non-resonant contribution. The thick green line is the lower limit of S-factor, which does not include the contribution of the lowest five resonances ($ \theta^2_{\alpha}=0 $). Thin red curves are the contributions from the lowest five resonances, while thin black lines represent higher resonance contributions. The horizontal bar in the upper left corner shows the range of the Gamow window for the $ \rm ^{11}C $($ \alpha,p)^{14} $N reaction, i.e., 0.23–1.24 MeV, corresponding to $ T_9= $0.2–1.

Figure 2.  (color online) The upper panel shows the ratios of the ¹¹C($ \alpha,p)^{14} $N reaction rates to the rate of CF88 as a function of temperature $ T_9=T/10^9 $K. Thick red lines represent the upper and lower limits. The black hatched range represents the uncertainty in Hayakawa data. The area between the gray dashed lines shows an extrapolated band to lower temperature based on their data. The thick dashed blue line corresponds to the non-resonant contribution. The lower panel shows the contribution from the 1st-5th resonances to the total reaction rate, the sum of other resonances at higher energies, and the non-resonance contribution.

where $ Y_0({\rm{^{A}X}}) $ and $ Y({\rm{^{A}X}}) $ are the abundances calculated by using the default and the enlarged or reduced rate. The results are listed in Table A1 of the Appendix. There are nine reactions with superscripts a−d in the last column, including ¹¹C$ (\alpha,p)^{14} $N, whose absolute δ-values are more than 20%. Their corresponding experimental uncertainties of the reaction rate at $ T=0.2 $ GK are in the last column. Although we artificially changed each reaction rate by a factor of 100 or 0.01, the error bars of measured reaction cross sections are smaller, except for our target reaction ¹¹C$ (\alpha,p)^{14} $N (No. 35 in Table A1), ¹¹C$ (n,p)^{11} $B (No. 32), and ¹¹C$ (n,2\alpha)^{4} $He (No. 41) whose rates are poorly known or unmeasured at relevant low energies. Among all the 43 reactions, the ¹¹C$ (\alpha,p)^{14} $N plays a predominant role in depleting ¹¹C and critically impacts on the final ¹¹B abundance.

Index	Reaction name	$ \delta(^{11}\rm{B}) $			$ \delta(^{11}\rm{C}) $		uncertainty
		×100	×0.01		×100	×0.01
1	11Be$ (\beta^-)^{11} $B	0.00%	0.00%		−0.02%	−0.00%
2	11C$ (\beta^+)^{11} $B	24.74%	−0.77%		−91.20%	2.51%	±0.02%a
3	11N$ (\beta^+)^{11} $C	−0.00%	0.00%		0.00%	−0.01%
4	11Be$ (\gamma,\alpha)^{7} $Li	0.00%	0.00%		−0.01%	−0.00%
5	12Be$ (\gamma,n)^{11} $B	−0.00%	0.00%		0.01%	0.00%
6	11B$ (\gamma,n)^{10} $B	0.00%	0.00%		−0.01%	0.00%
7	11B$ (\gamma,p)^{10} $Be	−0.00%	0.00%		0.01%	−0.01%
8	11B$ (\gamma,\alpha)^{7} $Li	−0.00%	0.00%		0.00%	−0.00%
9	12B$ (\gamma,n)^{11} $B	0.03%	0.01%		−0.02%	0.02%
10	11C$ (\gamma,p)^{10} $B	0.00%	0.00%		−0.00%	−0.00%
11	11C$ (\gamma,\alpha)^{7} $Be	0.00%	0.00%		−0.00%	−0.01%
12	12C$ (\gamma,n)^{11} $C	−0.00%	0.00%		0.00%	−0.00%
13	12C$ (\gamma,p)^{11} $B	−0.00%	0.00%		0.00%	−0.01%
14	12N$ (\gamma,p)^{11} $C	0.01%	−0.01%		1.14%	−1.59%
15	7Li$ (\alpha,\gamma)^{11} $B	13.97%	−33.01%		2.99%	4.21%	±15%b
16	7Be$ (\alpha,\gamma)^{11} $C	−2.09%	0.30%		78.25%	−20.02%	+163%b−60%
17	10Be$ (p,\gamma)^{11} $B	0.00%	−0.00%		0.00%	0.01%
18	10B$ (n,\gamma)^{11} $B	0.00%	0.00%		0.00%	−0.01%
19	10B$ (p,\gamma)^{11} $C	−0.01%	−0.01%		0.03%	0.01%
20	11B$ (n,\gamma)^{12} $B	−0.01%	0.01%		0.01%	−0.01%
21	11B$ (p,\gamma)^{12} $C	−1.94%	0.02%		0.37%	−0.01%
22	11C$ (n,\gamma)^{12} $C	−0.00%	0.01%		−0.08%	−0.02%
23	11C$ (p,\gamma)^{12} $N	−0.01%	−0.00%		0.02%	0.01%
24	8Li$ (\alpha,n)^{11} $B	0.01%	−0.01%		−0.01%	0.00%
25	9Be(t,n)11B	0.02%	0.00%		0.00%	−0.02%
26	8B$ (\alpha,p)^{11} $C	0.00%	0.00%		−0.00%	−0.00%
27	11B(n,t)9Be	−0.00%	−0.00%		0.00%	0.01%
28	11B$ (n,\alpha)^{8} $Li	0.00%	−0.00%		−0.00%	0.02%
29	11B(p,n)11C	−0.00%	0.00%		0.01%	−0.00%
30	11B$ (\alpha,n)^{14} $N	−71.95%	26.22%		−10.85%	22.10%	±21%b
31	11B$ (\alpha,p)^{14} $C	−49.47%	6.72%		22.56%	−4.79%	±10%c
32	11C(n,p)11B	2.53%	−0.15%		−75.24%	4.36%	—d
33	11C$ (p,\alpha)^{8} $B	−0.00%	−0.00%		0.00%	0.01%
34	11C$ (\alpha,n)^{14} $O	0.00%	−0.00%		−0.01%	0.02%
35	11C$ (\alpha,p)^{14} $N	−0.99%	1.27%		−87.52%	139.93%	most uncertain$ ^d $
36	14C$ (p,\alpha)^{11} $B	−0.00%	0.00%		0.00%	−0.01%
37	14N$ (n,\alpha)^{11} $B	0.00%	−0.00%		−0.00%	0.01%
38	14N$ (p,\alpha)^{11} $C	0.00%	0.00%		0.00%	−0.01%
39	14O$ (n,\alpha)^{11} $C	0.02%	0.01%		2.41%	−0.11%
40	11B$ (p,2\alpha)^{4} $He	−88.21%	102.83%		16.94%	−7.44%	±12%b
41	11C$ (n,2\alpha)^{4} $He	−0.87%	0.07%		−76.58%	4.89%	—d
42	4He$ (2\alpha,n)^{11} $C	0.00%	0.00%		−0.01%	−0.01%
43	4He$ (2\alpha,p)^{11} $B	0.00%	0.00%		−0.01%	−0.01%

Table A1.  Sensitivity result in the 20$ M_{\odot} $ core-collapse supernova. The last column indicates the reaction rate uncertainties inferred from experiments. a: Valverde et al., Phy. Rev. C 97, 035503 (2018) [37]. b: NACRE II database [38]. c: Wang et al., Phy. Rev. C 43, 2 (1991) [39]. d: uncertainties unknown experimentally.

Current ¹¹C$ (\alpha,p)^{14} $N rates reported in the JINA reaclib and Caughlan and Fowler [21] (we hereafter refer to CF88) are based on the experiments using indirect methods through time-reversal reaction of ¹⁴N$ (p,\alpha)^{11} $C [22]. The first direct measurement of ¹¹C$ (\alpha,p)^{14} $N reaction rates has been performed by Hayakawa et al. [23]. These two experiments provide the data on this reaction, in Fig. 1, which shows the S-factor vs. the center-of-mass energy $ E\rm_{c.m.} $ (hereafter abbreviated as E) beyond 0.6 MeV. Blue crosses are from direct measurement [23] (hereafter referred to as the Hayakawa data), and black dots are from inverse reaction experiment [22] (hereafter referred to as the Ingalls data). We note here that according to the energy levels of the compound state of ¹⁵O [24], there are still five resonances below E = 0.5 MeV. The featured temperature for ¹¹C and ¹¹B production in the SN explosion environment is $ T_9=(T/10^9 {\rm{K}})= $ 0.2−1 [5]. The corresponding Gamow peak energy (i.e., the energy range where nuclear reactions operate most effectively, see Ref. [25].) is $ E_0=(bkT/2)^{2/3} $ = 0.23 MeV with $ b^2=E_G= 2\mu(\pi e^2 Z_{^{11}\rm{C}}Z_{\alpha}/\hbar)^2 $ at $ T_9=0.2 $, which is much lower than 0.5 MeV. Therefore, five low-energy resonances below 0.5 MeV make an additional contribution to the reaction S-factor of ¹¹C$ (\alpha,p)^{14} $N, and the uncertainty of this reaction rate at low temperature needs to be verified.

The total cross-section consists of both non-resonant and resonant parts:

where $ S(E) $ is so-called astrophysical S-factor, η is the Sommerfeld factor, $ \eta=Z_{^{11}\rm{C}}Z_{\alpha}e^2/\hbar v $, $ {-\!\!\!\!\lambda}^2=\lambda/2\pi=\hbar/\sqrt{2\mu E} $ is the de Broglie wavelength, and μ is the reduced mass of ¹¹C and α particle. We take a simple form of non-resonant S-factor

following CF88 [21], where A and B are treated as free parameters and calibrated to best fit the experimental data at higher energies $ E \geq $ 2.5 MeV (Fig. 1). The resonant S-factor is given by

in the Breit-Wigner formula [25] with the information of resonances of ¹⁵O [24], where $ \omega_{\rm{i}} =\ (2J_{\rm{i}} +1) /\{[2J(^{11}\rm{C})+1] [2J(^4\mathrm{He})+1]\} $ is the statistical weight factor, $ i $ is the label of the corresponding resonance and $ E_{\rm i} $ is the corresponding resonance energy, $ J_{\text{i}}(^{15} $O) is the spin of the corresponding compound state of ¹⁵O, and $ J(^{11}\mathrm{C})=3/2 $ and $ J(^4\mathrm{He})=0 $ are the spins of the corresponding ground states of ¹¹C and ⁴He, respectively. $ \Gamma_{\alpha}^i(E)=2\gamma^2_{\alpha}P_{\alpha}(E;l)\theta^2_{\alpha} $ is the partial width for the α-entrance channel, and $ \gamma^2_{\alpha} $ is the reduced width. In this article, we take $ \gamma^2_{\alpha}=3{\hbar^2}/2{\mu R^2} $ and R is set to be the channel radius [26]. $ P_\alpha(E;l) $ is the Coulomb penetration factor of the α particle in the $ \rm ^{11}C+\alpha $ system, which depends on the energy above the threshold and the corresponding orbital angular momentum l for each resonance. The l value depends on the difference between $ J(^{11} $C) and $ J_{\rm i}(^{15} $O), and it is constrained by parity conservation for each resonance. The Coulomb penetration factor is calculated by solving the Schrödinger equation. In this study, we applied the Coulomb function to calculate the penetration factor (Chap.9 of [27])

where $ F_l $ and $ G_l $ are the regular and irregular Coulomb functions ¹. The channel radii of entrance and exit channels are 3.92 fm for ¹¹C+α and 3.35 fm for ¹⁴N+p, respectively [28, 29]. The dimensionless reduced width $ \theta^2_{\alpha} $ is taken to be a parameter ranging from 0 to 1 for the lowest five resonances (see Table 1).

No.	$ E_x $/MeV	$ E_{\rm{i}} $/MeV	$ J^{\pi} $	$ \Gamma^{\text{i}}_{\text{tot}} $/keV	$ \theta^2_{\alpha} $
1	10.290	0.071	5/2−	3	−
2	10.300	0.081	5/2+	11	−
3	10.416	0.197	9/2+	2	−
4	10.480	0.261	3/2−	25	−
5	10.506	0.287	3/2+	140	−
6	10.917	0.698	7/2+	90	0.00E+00
7	10.938	0.719	1/2+	99	3.88E-01
8	11.025	0.806	1/2−	25	0.00E+00
9	11.151	0.932	1/2+	10	7.03E-01
10	11.218	0.999	3/2+	40	8.71E-03
11	11.569	1.350	5/2−	20	1.38E-01
12	11.616	1.397	3/2−	80	1.39E-02
13	11.748	1.529	5/2+	99	7.35E-02
14	11.846	1.627	5/2−	65	1.24E-01
15	11.980	1.761	5/2−	20	0.00E+00
16	12.129	1.910	5/2+	200	1.00E-01
17	12.255	2.036	5/2+	135	1.12E-02
18	12.471	2.252	5/2−	77	0.00E+00

Table 1.  Resonance parameters of the excited status of ¹⁵O above the $ ^{11}\rm{C}+\alpha $ threshold energy. The excitation energy $ E_x $ of compound state ¹⁵O, resonance energy $ E_{i} $, spin and parity $ J^{\pi} $, and total widths $ \Gamma^{\rm{i}}_{\rm{tot}} $ from Ajzenberg-Selove (1991) [24]. The dimensionless reduced width $ \theta^2_{\alpha} $ for the other resonances at higher excitation energies are the results from $ \chi^2 $-fitting to the measured cross sections at $ E_{\rm{c.m.}}\ge 0.6 $ MeV as shown in Fig. 1. Note that in our upper and lower limits of reaction rate, the $ \theta^2_{\alpha} $ values for the 1^st-5^th resonances are 1 and 0, respectively. $ E_x=E_{\rm{i}}+S_{\alpha} $ with the threshold energy $ S_{\alpha}=10.219 $ MeV in the entrance α-channel.

$ \Gamma_p^{\text{i}}(E_{\text{i}})=\Gamma_{\text{tot}}^{\text{i}}(E_{\text{i}})-\Gamma_{\alpha}^{\text{i}}(E_{\rm i}) $ is the partial width for the proton-emission channel at the corresponding resonance energy, and $ \Gamma^{\text{i}}_p(E)=\Gamma^{\text{i}}_p(E_{\rm i})P_p(E;l)/P_p(E_{\rm i};l) $ is applied to the energies out of resonance energy. $ \Gamma_{\rm tot}^{\rm i} $ is the total width which is given by the measured ¹⁵O resonance width [24]. $ E_x $ is the excitation energy of the corresponding resonance $ E_x=E_{\text{i}}+S_{\alpha} $ with the α threshold energy $ S_{\alpha}=10.219 $ MeV [30] in the entrance α-channel. For the S-factor at $ E> $ 0.6 MeV, since $ E_{\rm{i}} $ and $ \Gamma\rm{_{tot}} $ are known [24] as summarized in Table 1 and $ \sigma{_{\rm tot}}(E) $ is given experimentally [22, 23], the only free parameters are $ \theta^2_{\alpha} $ in addition to A and B of the non-resonant S-factor.

To match the experimental data of S-factor in the Breit-Wigner form, we applied the $ \chi^2 $-fitting method in our study to determine the values of $ \theta^2_{\alpha} $ at energy $ E> $0.6 MeV for the resonances i = 6−18 in Table 1, as well as parameters A and B associated with non-resonant contribution. The fitting results for $ \theta^2_{\alpha} $ values are summarized in Table 1, and A = −0.640 $ \rm MeV^{-1} $ and B = 0.484. We applied the Wigner limit $ \theta^2_{\alpha}=1 $ for the lowest five resonances to estimate the conservative upper limit of ¹¹C($ \alpha,p)^{14} $N S-factor. $ \theta^2_{\alpha}=0 $ was assumed for the lower limit of resonant contribution from i = 1−5.

In Fig. 1 we present the fitted ¹¹C($ \alpha,p)^{14} $N S-factor, together with experimental data from Ingalls data (black dots) and Hayakawa data (blue cross). The thick red and thin green lines are the upper and lower limits, respectively. The dashed blue line is the non-resonant contribution. Thin red curves are the contributions from the lowest five resonances, while thin black curves represent those from the higher resonances. The horizontal bar in the upper left corner shows the range of the Gamow window for the $ \rm ^{11}C $($ \alpha,p)^{14} $N reaction, i.e., 0.23–1.24 MeV, corresponding to $ T_9= $0.2–1.

Our theoretical S-factors at $ E\sim $ 0.6 MeV ($ 5^{\rm th} $ and 6^th), 1.1−1.3 MeV (between resonances the 10^th and 11^th) and ~1.6 MeV ($ 13^{\rm{th}} $ and $ 14^{\rm{th}} $) underproduce Ingalls data because these energies are out of known resonance-energies and because the observed total widths of nearby resonances are narrow (see Table 1). For the same reasons, the theoretical S-factor underproduces Hayakawa data around $ E\sim $ 1.2−1.3 (between $ 10^{\rm th} $ and $ 11^{\rm th} $ resonances) MeV. Our S-factor near the resonance at $ E\sim $ 1.910 MeV ($ 16^{\rm th} $) cannot fit the resonance shape of Ingalls data because total width is too large $ \Gamma^{ {i=16}}_{\rm tot}= $ 200 keV. We adopt the non-resonant S-factor in the same parametrization as Caughlan and Fowler (1988), which fits the average behavior of S-factors rather well at higher energies 2.5 MeV $ <E $. As a consequence of the $ \chi^2 $-fitting in terms of extrapolated smooth non-resonant S-factor to the low energies plus resonance contributions, our total S-factor overproduces the data at $ E\sim $ 0.8−0.9 MeV. Although there is a resonance at E = 0.806 MeV with $ J^{\rm{\pi}}=1/2^- $, the incident s-wave between ¹¹C($ 3/2^- $) and ⁴He($ 0^+ $) cannot form this resonance and the d-wave is the smallest orbital angular momentum to form this resonance. However, at this low energy $ E< $ 1.0 MeV, d-wave could not contribute effectively. Therefore, the dimensionless reduced width of this resonance turns out to be almost zero in our $ \chi^2 $ fit ($ 8^{\rm th} $ of Table 1).

With this S-factor, we calculated the thermonuclear reaction rate:

The upper panel of of Fig. 2 shows the ratio of our new estimated ¹¹C$ (\alpha,p)^{14} $N reaction rate to the rate of CF88. Red lines represent the upper and lower limits. The black solid line and hatched region represent the ratio of the rate to CF88 and its uncertainty from Hayakawa data. The calculated upper and lower rates of ¹¹C$ (\alpha,p)^{14} $N are given in Table A2, together with the central value from Hayakawa data. Our result agrees with this estimation at around $ T_9=0.7-2 $, although slightly higher than the CF88 rate. Because of the newly added five resonances at lower energies, our estimated rate significantly differs from the CF88 rate at $ T_9\leq 0.6 $. In our SN model, the featured temperature for ¹¹C production is about $ T_9= 0.2-1 $, where the estimated uncertainty can be different from others as much as one order of magnitude. This uncertainty calls for a more precise measurement of this reaction rate in the astrophysically interesting temperature range. In the lower panel of Fig. 2, we show each contribution from the 1st-5th resonances to the total reaction rate, the sum of the other resonances (black line) at higher energies, and the non-resonant contribution (blue dashed line). It is shown that the $ 4^{\rm{th}} $ and $ 5^{\rm{th}} $ resonances in Table 1 and Fig. 1 dominate the total reaction rate at $ T_9=0.2-0.5 $.

Temperature $ T_9 $	Central value	Upper limit	Lower limit
5.0E-02	1.22E-21	7.35E-21	3.71E-22
5.5E-02	2.71E-20	8.55E-20	5.20E-21
6.0E-02	2.80E-19	8.28E-19	5.37E-20
6.5E-02	2.20E-18	6.87E-18	4.33E-19
7.0E-02	1.42E-17	4.99E-17	2.85E-18
7.5E-02	7.61E-17	3.23E-16	1.57E-17
8.0E-02	3.13E-16	1.89E-15	7.51E-17
8.5E-02	1.15E-15	9.96E-15	3.16E-16
9.0E-02	5.18E-15	4.72E-14	1.19E-15
9.5E-02	1.91E-14	2.01E-13	4.09E-15
1.0E-01	4.36E-14	7.71E-13	1.29E-14
1.1E-01	4.57E-13	8.44E-12	1.03E-13
1.2E-01	2.90E-12	6.54E-11	6.49E-13
1.3E-01	1.48E-11	3.80E-10	3.36E-12
1.4E-01	6.43E-11	1.75E-09	1.48E-11
1.5E-01	2.40E-10	6.65E-09	5.69E-11
1.6E-01	7.46E-10	2.16E-08	1.95E-10
1.7E-01	2.14E-09	6.15E-08	6.05E-10
1.8E-01	6.80E-09	1.57E-07	1.72E-09
1.9E-01	1.85E-08	3.66E-07	4.56E-09
2.0E-01	3.77E-08	7.90E-07	1.13E-08
2.1E-01	1.01E-07	1.59E-06	2.63E-08
2.2E-01	2.25E-07	3.04E-06	5.83E-08
2.3E-01	4.33E-07	5.52E-06	1.24E-07
2.4E-01	9.61E-07	9.61E-06	2.51E-07
2.5E-01	1.63E-06	1.61E-05	4.93E-07
2.6E-01	3.47E-06	2.63E-05	9.34E-07
2.7E-01	5.55E-06	4.15E-05	1.72E-06
2.8E-01	1.11E-05	6.41E-05	3.09E-06
2.9E-01	1.74E-05	9.68E-05	5.41E-06
3.0E-01	3.16E-05	1.43E-04	9.28E-06
3.1E-01	5.03E-05	2.09E-04	1.56E-05
3.2E-01	7.92E-05	3.00E-04	2.58E-05
3.4E-01	1.86E-04	5.96E-04	6.70E-05
3.6E-01	4.63E-04	1.13E-03	1.64E-04
3.8E-01	1.02E-03	2.09E-03	3.82E-04
4.0E-01	1.88E-03	3.74E-03	8.46E-04
4.2E-01	4.01E-03	6.54E-03	1.79E-03
4.4E-01	7.59E-03	1.12E-02	3.63E-03
4.6E-01	1.31E-02	1.89E-02	7.08E-03
4.8E-01	2.43E-02	3.13E-02	1.33E-02
5.0E-01	3.78E-02	5.09E-02	2.41E-02
5.2E-01	6.78E-02	8.15E-02	4.24E-02
5.4E-01	1.01E-01	1.28E-01	7.22E-02
5.6E-01	1.71E-01	1.99E-01	1.20E-01
5.8E-01	2.49E-01	3.03E-01	1.93E-01
6.0E-01	3.95E-01	4.55E-01	3.04E-01
6.5E-01	1.03E+00	1.17E+00	8.58E-01
7.0E-01	2.41E+00	2.76E+00	2.14E+00
7.5E-01	5.14E+00	5.94E+00	4.82E+00
8.0E-01	9.92E+00	1.19E+01	9.92E+00
9.0E-01	3.53E+01	3.92E+01	3.39E+01
1.0E+00	9.34E+01	1.05E+02	9.31E+01
1.1E+00	2.27E+02	2.43E+02	2.17E+02
1.2E+00	4.86E+02	4.98E+02	4.50E+02
1.3E+00	9.43E+02	9.37E+02	8.50E+02
1.4E+00	1.70E+03	1.64E+03	1.50E+03
1.5E+00	2.86E+03	2.73E+03	2.50E+03
1.6E+00	4.54E+03	4.33E+03	3.98E+03
1.7E+00	7.12E+03	6.61E+03	6.09E+03
1.8E+00	1.08E+04	9.76E+03	9.01E+03
1.9E+00	1.55E+04	1.40E+04	1.29E+04
2.0E+00	2.15E+04	1.95E+04	1.81E+04
2.1E+00	2.99E+04	2.66E+04	2.48E+04
2.2E+00	3.98E+04	3.56E+04	3.31E+04
2.3E+00	5.24E+04	4.66E+04	4.34E+04
2.4E+00	6.78E+04	5.99E+04	5.59E+04
2.5E+00	8.56E+04	7.58E+04	7.09E+04

Table A2.  The $ ^{11}\text{C}(\alpha,p)^{14}\text{N} $ reaction rates in this study as a function of temperature in $ T_9\equiv10^9 $ K. The central value is taken from [23]. The upper and lower limits are calculated in this study. The rates are given in units of $ \rm cm^3\,s^{-1}\,mol^{-1} $.

Hayakawa data takes account of resonances at $ E=2.5-4.5 $ MeV in the estimated reaction rate as shown in Fig. 1, while we do not consider these resonances because the relevant Gamow window energy for the ¹¹C$ (\alpha,p)^{14} $N reaction is much lower, $ E= 0.23-1.24 $ MeV, as shown by the arrows in Fig. 1, corresponding to the temperature $ T_9= 0.2-1 $ in Fig. 2. Therefore, there is a slight difference between our rates and theirs at $ T_9> $ 1.5. We confirmed that the deviation between the two rates around $ T\sim2 $ GK does not change the final ¹¹C abundance in our SN model calculation.

The purpose of the present study is to set the upper and lower limits to the reaction rate for ¹¹C($ \alpha,p)^{14} $N which affects the astrophysical uncertainty in the ¹¹B/¹⁰B ratio to be measured in SiC X grains. Using the larger rate for this reaction, ¹¹C is more strongly destroyed. We therefore assume the incoherence among resonant and non-resonant components in the total S-factor by ignoring the interference in order to set a conservative upper limit, leading to the maximum effect on destruction. On the other hand, the lower limit could be smaller than the present estimate ignoring the interference. Although the thermal average of the S-factor or equivalently the cross section tends to smear out the interference effect on the calculated reaction rate, it is an interesting question to constrain a more reliable lower limit to the S-factor both experimentally and theoretically. The present study suggests and motivates the importance of further studies of this reaction in the future.

To demonstrate the impact of the ¹¹C$ (\alpha,p)^{14} $N reaction and its sensitivity to the SN explosive nucleosynthesis, we incorporate the upper and lower limits of the reaction rate into our CCSN nucleosynthesis model. This SN model is the same as that used in [15] based on pre-SN model [31] and the hydrodynamic model of [5], which is a successful model for SN 1987A with a 20 $ M_{\odot} $ and metallicity $ Z=Z_{\odot}/4 $ progenitor star. The hydrodynamic model simulates the temperature and density evolution during the explosion (see [5] for the temperature and density profile). This calculation stops at 50 s after the core bounce. After 50 s, the temperature and density become very low, and most nuclear reactions do not proceed anymore, except for β decays. The ν-process such as $ \nu+^{12} $C and $ \nu+^{4} $He [5, 32] are included. We also include the newly estimated $ \nu+^{16} $O and $ \nu+^{20} $Ne reaction rates from a new shell model study [33]. The effects of neutrino flavor change, such as MSW effect [13] and collective flavor oscillation effect [6], have also been considered in the present model. The neutrino total energy is $ 3\times10^{53} $ erg, and the decay timescale of neutrino luminosity is 3 s. The initial neutrino temperatures shown in $ E=kT $ for $ \nu_e $, $ \bar{\nu}_e $ and $ \nu_x $ are 3.2, 5.0 and 6.0 MeV, respectively [32] where x stands for the μ- and τ-neutrinos and their anti-particles. All neutrino flavors are assumed to be equally partitioned in the initial luminosities, and their spectra obey Fermi-Dirac distribution with zero-chemical potentials.

In the measured ¹²C$ (\nu_e,e^-)^{12} $N$ _{g.s.} $ and ¹²C$ (\nu,\nu')^{12} $C* reaction cross sections, uncertainties in charged current (CC reaction induced by the exchange of $ W^{\pm} $ bosons) and neutral current (NC reaction induced by the exchange of neutral $ Z^0 $ bosons) interaction reactions are ±10% and ±20%, respectively [34]. In this study, we also assumed that ν-induced reaction cross sections for $ \nu+^4 $He, $ \nu+^{12} $C, $ \nu+^{16} $O and $ \nu+^{20} $Ne are subject to the same uncertainties of ± 10% and ± 20% for CC and NC, respectively.

Figure 3 shows the calculated mass fractions of (a)¹⁰B, (b)¹⁰C ($ \tau_{1/2} $ = 19.30 secs), (c)¹¹B and (d)¹¹C ($ \tau_{1/2} $ = 20.34 mins) at 50 s after the CCSN explosion started as a function of mass coordinate $ M_r $ in the units of $ M_{\odot} $. For the convenience of comparison with other SN models, we adopted the same definition of the layers as Meyer et al. (1995) [35] and Yao et al. (2025) [15], i.e., we divide the stellar interior into five regions, O/Ne, O/C, C/He, He/C, and He/N layers, marked as I~V, which depend on the most abundant nuclei in each layer. The blue and red lines represent the results under normal (blue) and inverted (red) neutrino mass hierarchies, respectively. The solid lines represent the central values (i.e., with ¹¹C$ (\alpha,p)^{14} $N rate from Hayakawa data). The associated bands of the ¹¹C abundance present the calculated results including uncertainties of both ¹¹C$ (\alpha,p)^{14} $N and ν-induced reactions. The larger rate of the ¹¹C$ (\alpha,p)^{14} $N reaction results in more efficient destruction of ¹¹C, while the larger rate of the ν-induced reactions like ¹²C$ (\nu_i,\nu_in)^{11} $C results in more efficient production of ¹¹C, and vice versa. Because of this mechanism, the lower limit of the ¹¹C abundance in Fig. 3 (d) corresponds to the upper limit of the ¹¹C$ (\alpha,p)^{14} $N rate and lower limit of the ν-induced reaction rates, i.e. ±10% (CC) and ±20% (NC), vice versa, independently of the neutrino mass hierarchy. We also present the calculated results (dashed lines) using the ¹¹C$ (\alpha,p)^{14} $N rate from CF88.

Figure 3.  (color online) The mass fraction of (a)¹⁰B, (b)¹⁰C, (c)¹¹B, and (d)¹¹C at 50 s after the core-bounce in the SN model calculation. The red and blue colors represent the inverted and normal hierarchies of the neutrino mass. The solid lines indicate the central values. The uncertainties of isotopic production are displayed by the colored bands, which are induced by the uncertainties of ¹¹C$ (\alpha,p)^{14} $N reaction rate and the ν-induced reaction rate. The dashed lines represent the results using the CF88 rate for ¹¹C$ (\alpha,p)^{14} $N. Note that the vertical axes in each panel are of different scales.

The ¹⁰B and ¹⁰C are mainly produced in regions II and III, as shown in Fig. 3 (a) and (b), while ¹¹B and ¹¹C are mainly produced in regions II and IV where plenty of ⁴He exist (see Fig. 3 (c) and (d)). In our calculation, most of ¹¹B is produced via $ \rm ^4He(\nu,\mathit{p})^3H(\alpha,\gamma)^7Li(\alpha,\gamma)^{11}B $ and destroyed via ¹¹B$ (\alpha,n)^{14} $N. Similarly, ¹¹C is mostly involved in the reaction chain of $ \rm ^4He(\nu,\mathit{n})^3He(\alpha,\gamma)^7Be(\alpha,\gamma)^{11}C $ and subsequent destruction by ¹¹C($ \alpha,p)^{14} $N. Both ¹¹B and ¹¹C mass fractions calculated by using our new rate (solid lines) are lower than those obtained by adopting CF88 rate (dashed lines) at $ M_r<4.3\ M_{\odot} $, particularly in O/Ne (region I) and O/C (region II) layers, for both normal and inverted hierarchies. This is because our new ¹¹C$ (\alpha,p)^{14} $N rate is higher than CF88 and ¹¹C is destroyed more efficiently at temperatures $ T_9>0.6 $ when the shock arrives at these regions I and II (see Fig. 2). Although ¹⁰B and ¹⁰C abundances are subject primarily to the uncertainties of ν-induced reactions, ¹¹B and ¹¹C abundances depend on both uncertainties of the ¹¹C$ (\alpha,p)^{14} $N reaction and the ν-induced reactions.

Figure 4 (a) $ \delta(^{11}\rm{B})_{\nu} $ and (b) $ \delta(^{11}\rm{C})_{\nu} $ correspond to those by taking account of the uncertainties of ν-induced reactions (CC±10%, NC±20%), and Figs. 4 (c) $ \delta(^{11}\rm{B})_{(\mathit{\alpha,p})} $ and (d) $ \delta(^{11}\rm{C})_{(\mathit{\alpha,p})} $ correspond to the calculated results by taking account of the uncertainty for the ¹¹C$ (\alpha,p)^{14} $N reaction rate shown in Fig. 2. The definition of $ \delta({\rm{^{A}X}}) $ is similar to Eq. (1), but for the different change of the reaction rates for ¹¹C$ (\alpha,p)^{14} $N displayed in Fig. 2 and ν-induced reactions of ±10% (CC) and ±20% (NC) displayed in Fig. 4. The default ¹¹C$ (\alpha,p)^{14} $N rate is taken from Hayakawa data. The sensitivities $ \delta(^{A}\rm{X})_{(\mathit{\alpha,p})} $ for the CF88 rate are also shown by dashed lines in these Figures.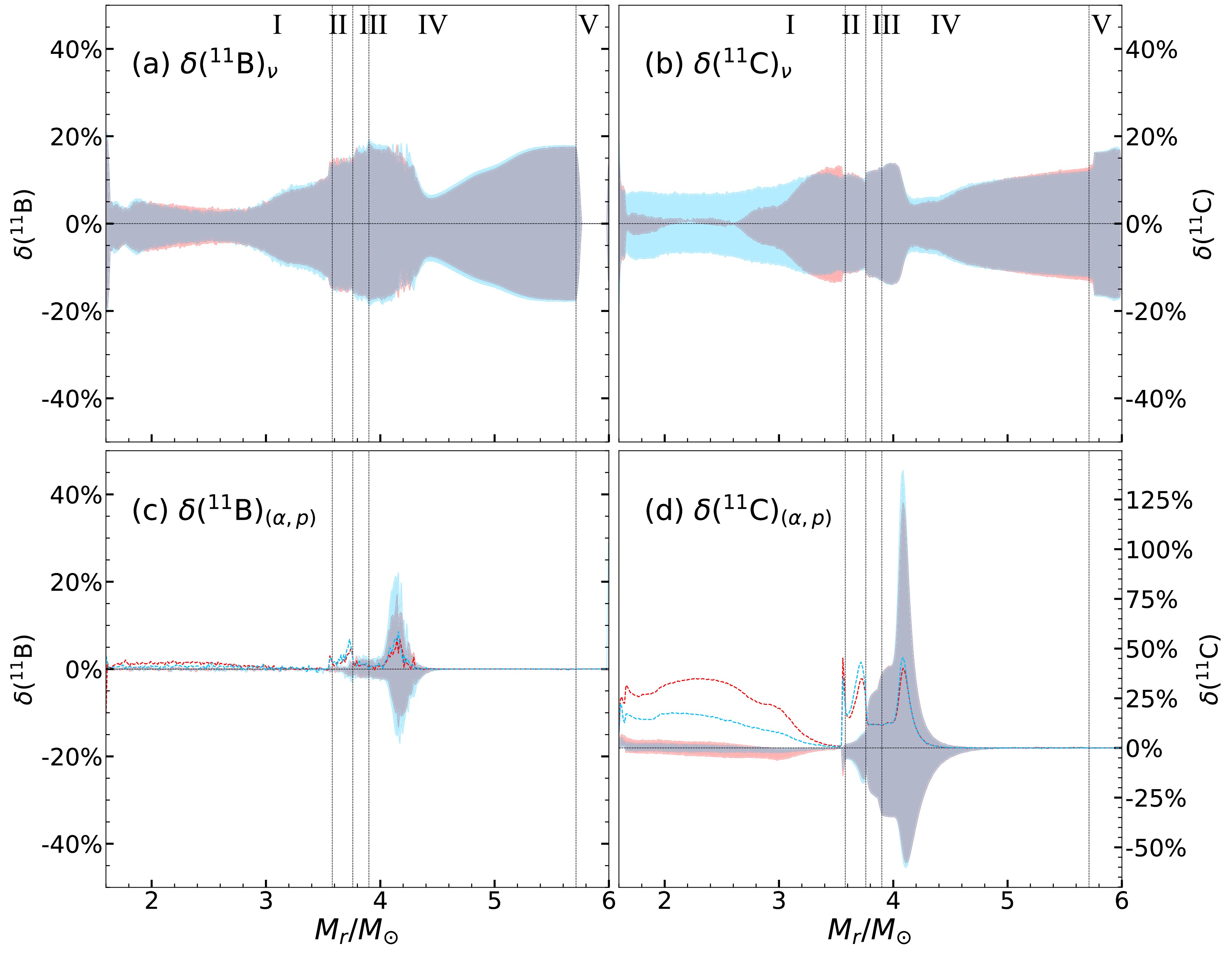

Figure 4.  (color online) The sensitivities (a) $ \delta(^{11}\rm{B})_{\nu} $ and (b) $ \delta(^{11} $C)_ν of the ν-induced reaction uncertainties (CC ± 10% and NC ± 20%), (c) $ \delta(^{11} $B)$ _{(\alpha,p)} $ and (d) $ \delta(^{11} $C)$ _{(\alpha,p)} $ of only the ¹¹C$ (\alpha,p)^{14} $N reaction uncertainty. The line-color convention follows Fig. 3. The blue and red colors represent the results for normal and inverted hierarchies, respectively.

In general, the ¹¹B and ¹¹C abundance uncertainties arising from ν-process are limited. As in Fig. 4 (a) and (b), the $ \delta(^{11} $B)_ν and $ \delta(^{11} $C)_ν are less than ±20%. As for the $ (\alpha,p) $ reaction uncertainties, it is clear that the ¹¹B abundance is not substantially affected by this reaction, as shown in Fig. 4 (c), so that the uncertainty of ¹¹B is mainly contributed by ν-induced reaction uncertainty, except for the region $ 3.78\ M_{\odot}<M_r<4.4M_{\odot} $ where the $ \delta(^{11} $B)$ _{(\alpha,p)} $ is slightly larger than $ \delta(^{11} $B)_ν.

The sensitivity of the ¹¹C abundance to $ (\alpha,p) $ rate is as large as –50% to 140%, as shown in Fig. 4 (d), particularly in region III and inner part of region IV at 3.8 $ M_{\odot}<M_r<4.2\ M_{\odot} $. This is much larger than the sensitivity ±20% induced by the ν-process as shown in Fig. 4 (b). It is to be noted that the vertical scale of Fig. 4 (d) $ \delta(^{11} $C)$ _{(\alpha,p)} $ is different from the other Figs. 4 (a), (b) and (c). These results are attributed to the following mechanism of the different efficiency of destruction of ¹¹C by the ¹¹C$ (\alpha,p)^{14} $N reaction which depends on the effective temperature in each region at the shock arrival.

In O/Ne (region I) and O/C (region II) layers, the peak temperature at the shock arrival is around $ T_9=0.6 $ (see Fig. 2 in [5]). The uncertainty of the ¹¹C$ (\alpha,p)^{14} $N rate is tiny in these layers at this temperature as shown in Fig. 2. However, in C/He (region III) and inner part of He/C ($ M_r<4.4M_{\odot} $) layers, the peak temperature is about $ T_9=0.2-0.5 $. The ¹¹C$ (\alpha,p)^{14} $N rate uncertainty becomes as large as factor ~ 2 to 10 (see Fig. 2). Due to the abundant ⁴He in these layers, ¹¹C$ (\alpha,p)^{14} $N destroys ¹¹C as soon as ¹¹C is produced by ⁷Be$ (\alpha,\gamma)^{11} $C. In the outer region of He/C layer (region IV) and He/N layer (region V) at ($ M_r>4.4M_{\odot} $), the temperature becomes low enough $ \boldsymbol{T}_\mathbf{9}\mathbf{\sim0.2} $ where ¹¹C$ (\alpha,p)^{14} $N rate shows large uncertainty (Fig. 2). However, the ¹¹C$ (\alpha,p)^{14} $N reaction is much weaker than ⁷Be$ (\alpha,\gamma)^{11} $C because the temperature becomes lower and the Coulomb barrier of $ \alpha+^{11} $C is higher than that of $ \alpha+^{7} $Be. After the explosion shock arrives at these layers, ¹¹C$ (\alpha,p)^{14} $N destroys only small amount of ¹¹C.

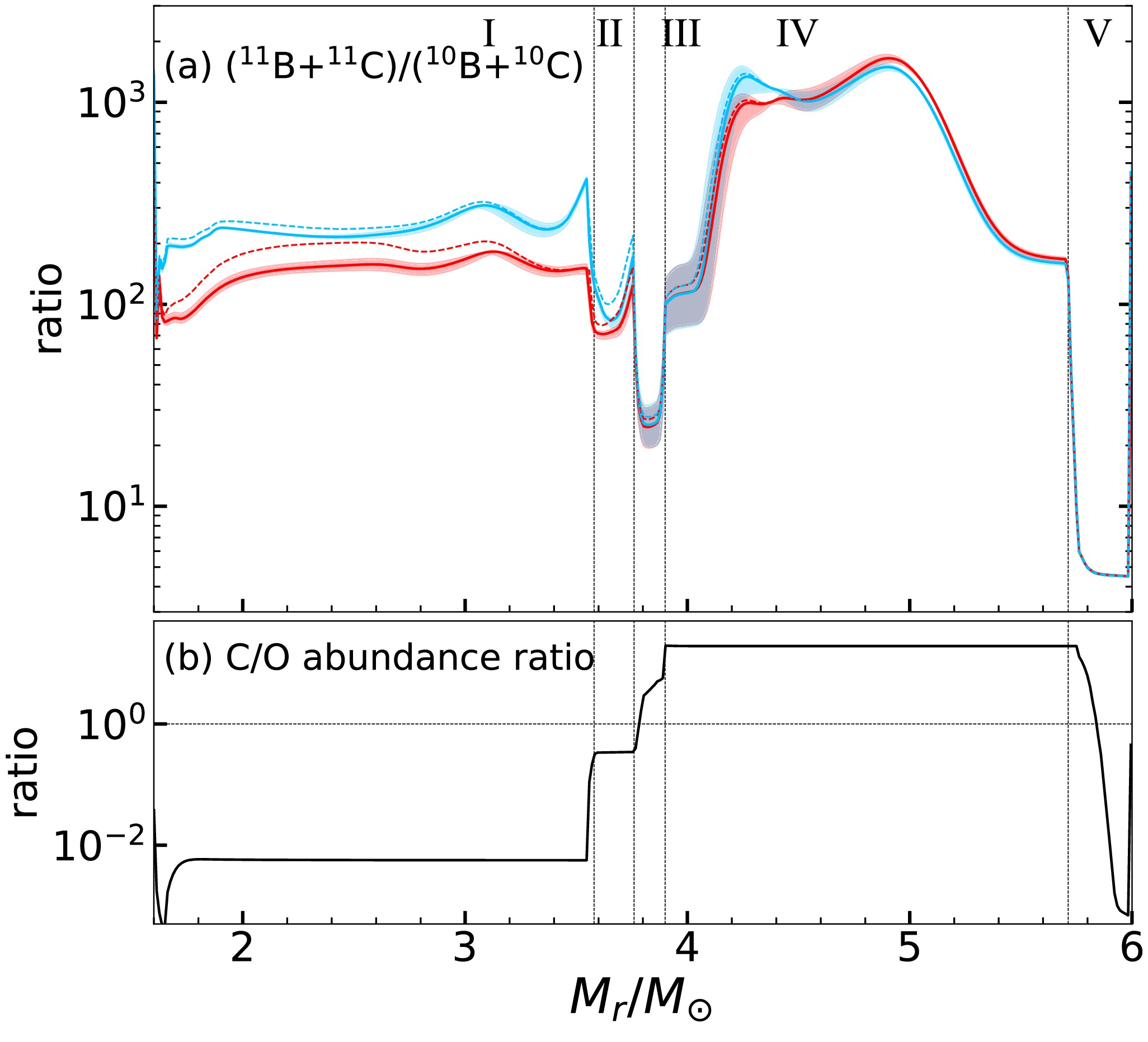
The isotopic signature preserved in X grains, particularly the ¹¹B/¹⁰B ratio, reflects the nucleosynthesis during the explosion [15]. This ratio can reveal details about the nucleosynthesis in the SN nucleosynthesis. We note here that the formation of X grains is believed to require a carbon-rich environment, on the condition of Carbon to Oxygen ratio C/O > 1 [36]. Figure 5 illustrates the mass fraction ratio of (¹¹B+¹¹C)/(¹⁰B+¹⁰C) (panel a) and C/O ratio (panel b) at 50 s after the explosion as a function of mass coordinate. Regions III and IV satisfy the condition of X grain formation C/O >1. The distinct separation of the (¹¹B+¹¹C)/(¹⁰B+¹⁰C) ratio between the two neutrino mass hierarchies occurs near the carbon production peak region (mass coordinate $ M_r\sim4.2-4.6\ M_{\odot} $) in the He/C layer. However, the (¹¹B+¹¹C)/(¹⁰B+¹⁰C) ratio displays significant uncertainty in the range $ 3.90 M_{\odot}<M_r<4.4 M_{\odot} $ of regions III and IV. This uncertainty is primarily attributed to the ¹¹C$ (\alpha,p)^{14} $N as discussed previously. These reaction rate uncertainties would affect the interpretation of X grains in the meteorite study. To reduce the model uncertainty, a more precise measurement of the ¹¹C$ (\alpha,p)^{14} $N reaction cross-section at lower energies $ E_{\rm c.m.}\leq 0.6 $ MeV (Fig. 1) corresponding to temperatures $ T_9\lessapprox 0.6 $ (Fig. 2) is desirable in laboratory experiments. If observational evidence confirms that some X grains originated from this region, a more precise measurement of the ¹¹C$ (\alpha,p)^{14} $N reaction rate could help improve the interpretation of X grains in the meteorite study and provide critical constraints on the neutrino mass hierarchy. For this purpose, we propose that the uncertainty of both upper and lower bounds of the ¹¹C$ (\alpha,p)^{14} $N reaction rate should be more strictly reduced by at least 20% of its current value.

Figure 5.  (color online) The mass ratio of (a) (¹¹B+¹¹C)/ (¹⁰B+¹⁰C) and of (b) C/O as a function of mass coordinate $ M_r $ in units of $ M_{\odot} $ at 50 s after the core-bounce. The line-color convention follows Figs. 3 and 4.

We investigated both the nuclear reactions and ν-induced reactions, which play significant roles in the nucleosynthesis of A=11 nuclei in CCSNe. We found that ¹¹C$ (\alpha,p)^{14} $N is the most sensitive nuclear reaction to the nucleosynthesis among 43 light-mass nuclear reactions which we studied in the present work. We adopted the Breit-Wigner formula and $ \chi^2 $-fitting to nuclear resonance parameters of the ¹¹C$ (\alpha,p)^{14} $N reaction, and estimated the uncertainty of temperature-dependent thermonuclear reaction rate at astrophysical temperature $ T=0.2-1 $ GK. These uncertainties originate from the low-energy resonances in the ¹⁵O compound nucleus, which could change the ¹¹C$ (\alpha,p)^{14} $N reaction rate by one order of magnitude at the Wigner limit. We further applied our new ¹¹C$ (\alpha,p)^{14} $N rate to our CCSN nucleosynthesis model and analyzed the sensitivity of ^10,11B and ^10,11C abundances to the ¹¹C$ (\alpha,p)^{14} $N rate and ν-induced reaction rate. The upper limit of the ¹¹C$ (\alpha,p)^{14} $N rate destroys ¹¹C efficiently at $ M_r=3.78-4.4\ M_{\odot} $, which leads to a significant uncertainty in the (¹¹B+¹¹C)/(¹⁰B+¹⁰C) ratio. This isotopic ratio is featured in the X grains and provides insight into the origin of presolar grains and still unknown neutron-mass hierarchy. Therefore, we call for a new measurement of the ¹¹C$ (\alpha,p)^{14} $N reaction cross section at astrophysical low energies $ E_{\rm{c.m.}}\leq 0.6 $ MeV.

In the appendix, we provide extended data tables which are referred to in the main text.