Lepton-number-violating pion decay and type-I seesaw mechanism in chiral perturbation theory

The charged fermions in the Standard Model (SM) of particle physics acquire mass via their Yukawa coupling with the Higgs field after the breaking of electroweak symmetry. The SM predicts massless neutrinos due to the absence of right-handed neutrinos. However, neutrino oscillation observed over two decades [1−3] convincingly confirms that the masses of neutrinos are non-zero. The simplest way to accommodate neutrinos with nonvanishing masses is the well-known type-I seesaw mechanism [4−8] or so-called neutrino-extended SM (νSM), which introduces two or more right-handed neutrino fields $ \nu_R $ manifested as gauge singlets under the SM gauge transformation such that the SM gauge symmetry is preserved. In addition to explaining the origin of the tiny masses of active neutrinos, the sterile neutrinos can be utilized to explain the baryon asymmetry of the universe and dark matter [9, 10]. Another attractive characteristics is that the type-I seesaw mechanism can naturally capture the Majorana neutrinos that induce the neutrinoless double beta ($ 0\nu\beta\beta $) decay [11].

As a promising probe of the lepton number violation (LNV), the hadronic $ 0\nu\beta\beta $ decay plays an important role in particle and nuclear physics. For this process, both the GERDA [12] and KamLAND-Zen [13] projects, which use $ ^{76}\text{Ge} $ and $ ^{136}\text{Xe} $ isotopes, respectively, provide the current best limits on the half-lives up to $ 10^{26} $ years. In the future, ton-scale facilities are expected to improve this sensitivity by one or two orders of magnitude [14, 15]. On the theoretical side, an effective field theory (EFT) roadmap for matching various LNV models at high energy to the nuclear operators at low energy was accomplished in Refs. [16, 17]. Starting with the chiral EFT framework, the $ 0\nu\beta\beta $ nuclear matrix elements (NMEs) of the nuclei relevant for experiments are available with ab initio nuclear many-body methods [18−21]. Despite significant progress, accurately predicting NMEs remains a significant challenge because of the nonperturbative effects in nuclear systems (for a comprehensive review see Ref. [22]).

Compared with the nuclear $ 0\nu\beta\beta $ decay, the process involving only mesons can be treated in a perturbative manner, providing a simpler method of probing the LNV mechanism (see Refs. [23−25]). Because the transition $ \pi^-\pi^-\to e^-e^- $ (or unphysical transition $ \pi^-\to\pi^+e^-e^- $) dominates the nuclear $ 0\nu\beta\beta $ decay induced by the short-range LNV mechanisms, such as the R-parity violation supersymmetry mechanism [26], we explore this transition within the chiral perturbative theory (ChPT). Moreover, Refs. [27, 28] (Ref. [29]) calculated the long-range (short-range) contribution to the low-energy transition using the lattice QCD method. Such results can be used to determine the low-energy constants (LECs) that appear in the amplitude for the long- and short-distance mechanisms, respectively.

The intriguing features of the type-I seesaw mechanism have prompted many investigations into the impact of sterile neutrinos on the $ 0\nu\beta\beta $ decay rate [23−25, 30−35]. Most of the studies focus on the tree-level effects of sterile neutrinos on the hadronic decay rate. In this work, we move the calculation of the process $ \pi^-\pi^-\to e^-e^- $ in the context of the type-I seesaw mechanism to the one-loop level, corresponding to $ \mathcal{O}(Q^2/\Lambda_\chi^2) $ in ChPT. Introducing sterile neutrinos leads to a mass-dependent description and consequently imposes more constraints on $ 0\nu\beta\beta $ decay. Based on the competition between the sterile neutrino mass with the breakdown scale $ \Lambda_\chi $, as is commonly performed, we integrate the neutrinos with masses above $ \Lambda_\chi $ at the quark level, whereas the neutrinos with masses below $ \Lambda_\chi $ are kept as explicit degrees of freedom in ChPT. We note that a description of this process within the standard mechanism of the SM neutrino of $ 0\nu\beta\beta $ decay is presented up to the one-loop level in Ref. [36].

The remainder of this paper is organized as follows. In Sec. II, we present the theoretical formalism of the $ 0\nu\beta\beta $ amplitude and interpolation formula. This is followed by results and discussions in Sec. III. Finally, we summarize the paper in Sec. IV.

The central concept of the type-I seesaw mechanism to address the limitations of SM is to introduce sterile neutrinos. In this model, the effective Lagrangian consists of the SM Lagrangian and its extension based on the k right-handed neutrino fields $ N_{Ri} $ :

where $ \psi_L=(\nu_{L},e_L)^T $ denotes the left-handed lepton doublet, $\widetilde{H}={\rm i}\tau_2H^*$ the conjugate state of the Higgs doublet H, $ Y_D $ is a $ 3\times k $ Yukawa coupling matrix, and $ M_R $ is a symmetric $ k\times k $ matrix. The charge conjugation of the fermion field is defined as $ \psi^c=C\bar{\psi}^T $ in terms of the charge conjugation operator $C={\rm i}\gamma_2\gamma_0$. After the electroweak symmetry breaking, the neutrinos acquire masses

where $ M_D=\dfrac{v}{\sqrt{2}}Y_D $ denotes the Dirac mass, in which $ v=246 $ GeV is the Higgs vacuum expectation value. Using the unitary mixing matrix $ \mathcal{U} $, we can diagonalize the $ (3+k)\times(3+k) $ mass matrix:

where $ \hat{M}_\nu=\text{diag}(m_1, m_2, m_3) $ is the mass matrix of the three generations of the active neutrino, and $ \hat{M}_N=\text{diag}(M_1, M_2, ..., M_k) $ is the mass matrix of the k flavors of sterile neutrinos. U is the so-called light neutrino mixing matrix, i.e., the PMNS matrix [37, 38]. Note that the U matrix is no longer unitary owing to the existence of sterile neutrinos. R, a $ 3\times k $ matrix, represents the mixing of sterile neutrinos in the charged current (CC). Specifically, the neutrino flavor eigenstate $ \nu_\alpha $ $ (\alpha= e, \mu, \tau) $ is related to the neutrino mass eigenstate via

In the context of Majorana neutrinos, the propagators can be expressed as [39]

where $ S_F(x-y) $ is the standard fermion propagator.

Additionally, according to Eq. (3), such a model requires the neutrino masses and mixing matrix elements to satisfy the relation

This seesaw relation implies that at least two sterile neutrinos must be in the mechanism. For the scenario with multiple sterile neutrinos, the amplitude results from the sum of the contributions of individual neutrinos, e.g., see Refs. [32, 34]. Moreover, although Eq. (6) imposes a constraint on the masses of sterile neutrinos, their specific values are model-dependent owing to the existence of undetermined parameters. For example, $ M_i\sim\mathcal{O}(10^{15}) $ GeV occurs naturally under the assumption $ Y_D\sim\mathcal{O}(1) $, whereas kiloelectronvolt-scale masses become viable through soft $ L_e-L_\mu-L_\tau $ flavor symmetry breaking [40]. Therefore, in this work, we focus on the mass dependence of the amplitude to provide essential inputs adaptable to various models.

To describe the effects of physics beyond the SM much larger than the electroweak scale at a low-energy scale, Refs. [16, 17] formed a systematic EFT framework. With this approach, the beyond-SM operators are first matched to a low-energy EFT (LEFT) with $ SU(3)_c\times U(1)_\text{em} $ gauge symmetry via integrating heavy SM particles whose masses are comparable to the electroweak scale such as Higgs particles. Furthermore, the LEFT operators are evolved to the QCD scale using the renormalization group equations and then rewritten as chiral effective operators based on chiral symmetry. Note that the degrees of freedom have been changed from quarks to hadrons (pions, nucleons, etc.) after matching the LEFT onto ChPT owing to the nonperturbative effects of QCD.

In the seesaw model, the ChPT description of a sterile neutrino depends on its mass $ M_i $. For $ M_i<\Lambda_\chi $, the (light) sterile neutrino as a degree of freedom in ChPT mediates the $ 0\nu\beta\beta $decay of a pion. The relevant Lagrangian spelled by pion fields $u=\text{exp}({\rm i}\pmb{\tau}\cdot\pmb{\pi}/(2F_0))$ and leptonic charged current $ l^\mu=-2\sqrt{2}G_FV_{ud}\tau^+\,\overline{e_L}\,\gamma_\mu\nu_{eL} $ can be expressed as

where $ F_0 $ is the pion decay constant in the chiral limit and Fermi constant $ G_F=1.166\times10^{-5} $ $ \text{GeV}^{-2} $, quark mixing matrix element $ V_{ud}=0.97 $, and

Constant B ( $ \simeq $ 2.8 GeV) connects the leading order pion mass M to the light quark masses via $ M^2= B(m_u+m_d) $, called the quark condensate. For clarity, we expand the Lagrangian in the pion field and split it into two parts: the pure strong interaction

describing the coupling between pion fields and the CC operators

Again, the sterile neutrino couples with the hadron through neutrino mixing in Eq. (4).

We note that the operators in the second-order Lagrangian only provide the corrections to constants $ F_0 $ and M. Within the accuracy we operate with, as in Ref. [36], we can replace these constants with their physical values to account for these subleading corrections, such as the diagrams involving a pure mesonic loop and the subleading operator insertions. Therefore, we hide the expression of the subleading Lagrangian and, henceforth, make the substitution $ F_0\to f_\pi=92.2\;{\rm MeV} $, $ M\to m_\pi=138\;{\rm MeV}$.

Moreover, the light sterile neutrino would be integrated if its momentum approaches or exceeds $ \Lambda_\chi $ before matching to ChPT. This implies an additional contribution that describes the neutrino exchange in the region less than $ 1/\Lambda_\chi $; thus, it is called the hard neutrino exchange contribution. By dissecting the chiral symmetry of the quark operator in the amplitude with two insertions of the weak charge current, as in Ref. [31], we can obtain the pionic operator with two derivatives [36], which dominates the contributions of hard neutrinos,

where $ g_\nu^{\pi\pi} $ denotes an LEC encoding hard-neutrino exchange and

Through a naive dimensional analysis (NDA) of LEC $ g_\nu^{\pi\pi}\sim \mathcal{O}(1) $, which can be fixed by experiment and lattice QCD simulations. Because of the non-perturbative effects of QCD, the mass dependence of $ g_\nu^{\pi\pi} $ in the type-I seesaw mechanism is currently unknown. We note the lattice QCD calculation for the mass-dependent $ g_\text{LR}^{\pi\pi} $ of the $ \pi-\pi $ coupling in the left-right symmetry model in Ref. [41] and expect the prediction of $ g_\nu^{\pi\pi}(M_i) $ from the lattice QCD. In addition to the Lagrangian in the pion sector, the hard neutrino can also induce chiral operators involving nucleon fields, which are independent of this work.

Similar to the hard-neutrino case, the sterile neutrino with mass $ M_i > \Lambda_\chi $ is no longer an appropriate low-energy degree of freedom in ChPT. Integrating out the heavy neutrino in LEFT leads to a dimension-nine operator with the same form as the $ O_1 $ operator defined in Refs. [16, 17]. Consequently, the heavy-neutrino contribution relevant to this work—parameterized through an LEC $ g_1^{\pi\pi} $—can be expressed in ChPT as

where we have ignored the scale dependence of the matching coefficient because this dependence is mild [33, 35], and

We can now calculate the amplitude for process $ \pi^-(p_a)\pi^-(p_b)\to e^-(p_1)e^-(p_2) $ with massless electrons $ p_1^2= p_2^2=0 $ in the type-I seesaw mechanism. Similar to the case of the light-neutrino exchange, the amplitude of the transition mediated by sterile neutrinos is straightforward via performing a substitution

Following Ref. [36], we define the transition amplitude as follows:

where $ T_\text{lept}=4G_F^2V_{ud}^2\,\overline{u}_L(p_1)u_L^c(p_2)\,\mathcal{U}_{ei}^2M_i $ with the spinor of electron $ u_L(p) $. Dimensionless amplitude $ S_{\pi\pi} $ can be expanded in the powers of the momentum:

where $ S_{\pi\pi}^{(\nu)} $ denotes the correction with magnitude of $ \mathcal{O}(Q^\nu/\Lambda^\nu_\chi) $, called N$ ^\nu $LO correction henceforth for convenience.

For the light sterile neutrino mediating the LNV decay of a pion, the diagrams up to N²LO are shown in Fig. 1. Figure 1(a) shows the tree-level contribution, and these remains are subleading contributions. Unlike for nuclear $ 0\nu\beta\beta $ decay, the hard-neutrino contribution occurs at N²LO and cancels the ultraviolet (UV) divergence of the one-loop diagrams. Again, additional one-loop level diagrams extended from Fig. 1(a), which are not explicitly shown, provide the corrections to constants $ F_0 $ and M, and these corrections are incorporated by taking their physical values.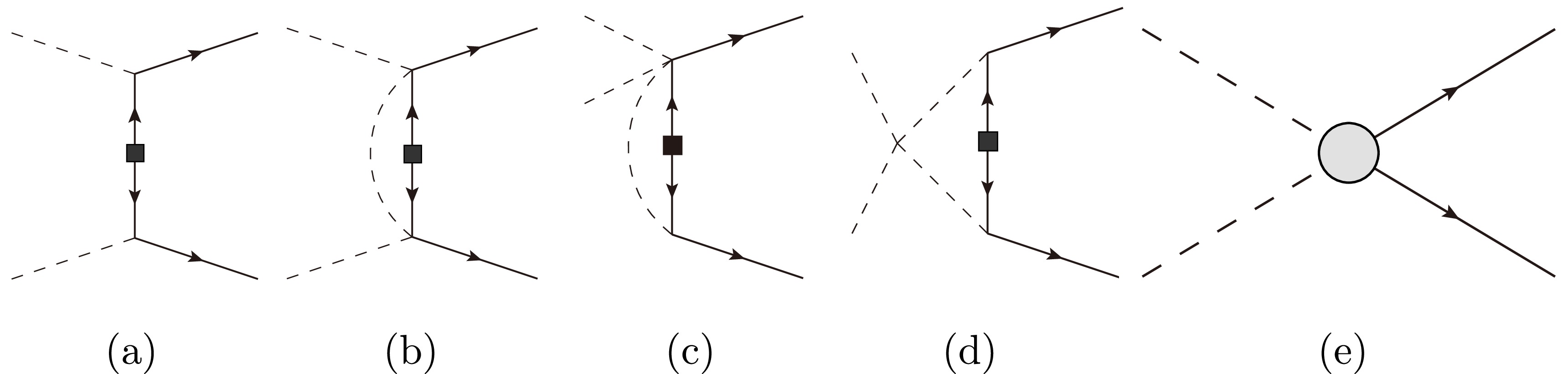

Figure 1.  Transitions $ \pi^-+\pi^-\to e^-+e^- $ up to N²LO. The dashed and solid lines represent pion and lepton fields, respectively. The black square denotes an insertion of the neutrino Majorana mass, and the gray circles sketch the contributions of heavy or hard neutrinos.

Adopting the Mandelstam symbols,

the tree-level amplitude can be expessed as

At N²LO, the amplitude is composed of the one-loop and hard-neutrino contributions,

in which one-loop contribution $ S_{\pi\pi}^\text{loop} $ is the sum of the following amplitudes:

The full expressions of the above amplitudes based on the Mandelstam variables are not listed explicitly because of their complexity. For the hard-neutrino contribution, it can be expressed as

Using the $ \overline{\text{MS}} $ scheme, the hard-neutrino term absorbs the UV divergences such that $ S_{\pi\pi}^{(2)} $ is a finite and μ-independent quantity.

At the threshold, corresponding to $ s=4m_\pi^2 $, $ t=u= -m_\pi^2 $, the above amplitudes can be expressed as

where $ \widetilde{g}_\nu^{\pi\pi}(0)=0.45 $ obtained by matching on the lattice result in Ref. [27] and $ x_i=M_i/m_\pi $; function $ \mathcal{V}_{\pi\pi}(x) $ is defined as

with dilogarithm function $ \text{Li}_2(x) $. As $ x_i\to0 $, the result under the standard mechanism given by Ref. [36] will be recovered.

One of the main features of the seesaw model is that the ChPT description originating from it is based on not only the pre-set expansion in $ Q/\Lambda_\chi $ but also another expansion in $ M_i/\Lambda_\chi $. This is because the loop integral results in the positive power of the neutrino mass such that this additional expansion becomes possible. For the light neutrino, $ M_i/\Lambda_\chi $ is an expansion parameter of ChPT. Therefore, we can expand LEC $ \widetilde{g}_\nu^{\pi\pi} $ in the powers of $ M_i $ as follows [35]:

The second term in the above expansion can be considered a low-mass truncation error of ChPT. Moreover, using NDA, the amplitude up to the one-loop level we calculate accepts an additional uncertainty with $ \mathcal{O}(M_i^4/\Lambda^4_\chi) $ resulting from the next order such as two-loop corrections. Thus, the amplitude with error can be expressed as

Note that the procedure above adopts a conservative perspective of estimating the effects of the mass of a sterile neutrino on the amplitude. The construction of consistent power counting that accommodates the massive sterile neutrino effects remains crucial in ChPT.

In the context of the heavy neutrino, the amplitude of the pion decay up to N²LO is given by

where $ g_1^{\pi\pi}=0.36 $ at the scale $ \mu=2 $ GeV extracted from the lattice calculation in Ref. [29].

In principle, we can now obtain the mass-dependent amplitude of the pionic $ 0\nu\beta\beta $ decay within the type-I seesaw mechanism based on ChPT. However, owing to expansion parameter $ M_i/\Lambda_\chi $, the ChPT description would break down when the neutrino mass approaches $ \Lambda_\chi $. Consequently, the amplitude of the pion decay in the region where the neutrino mass is close to $ \Lambda_\chi $ must be modeled.

An intuition exists that the evolution of the amplitude from the light-neutrino to heavy-neutrino area is continuous. Therefore, with the constraint of the heavy-neutrino asymptotic behavior,

we can construct the following $ M_i $ dependence in the $ M_i<\Lambda_\chi $ region

where $ S_{\pi\pi}(0)=S^{(0)}_{\pi\pi}(0)+S^{(2)}_{\pi\pi}(0) $ given by ChPT. Based on the above intuition, we can utilize the matching condition

to pin down parameter $ m_a $ at $ M_i=2 $ GeV.

We consider Eq. (29) because this interpolation formula, which has been widely used to predict the mass-dependent NMEs of the nuclear $ 0\nu\beta\beta $ decay, e.g., see Refs. [30, 32, 34, 42–45], captures the main features of the amplitude in the light- and heavy-neutrino regions. Because of the unknown dependence of LEC $ g_\nu^{\pi\pi} $ on the neutrino mass so far, we do not plan to discern the $ M_i $ dependence of the long- and short-range contributions, as performed in Refs. [31, 33, 35].

The actual breakdown scale of EFT is often lower than theoretical expectation $ \Lambda_\chi $ for a given process. For example, in $ \pi - \pi $ scattering, the theoretical range is associated with the ρ-meson mass, whereas in nucleon-nucleon scattering, this range is approximately 500 MeV [46]. Determining the realistic breakdown scale of ChPT in a specific process is essential because it limits the range of theory and provides an input to the uncertainty estimation. Hence, we first focus on the mass dependence of the tree-level and one-loop contributions to the process in which two pions convert to two electrons at the threshold under the light sterile neutrino exchange mechanism.

As shown in Fig. 2, both tree-level and one-loop contributions in $ M_i\lesssim 50 $ MeV exhibit less sensitivity to neutrino mass than the regime of $ M_i\sim m_\pi $. This is unsurprising because the neutrino mass is smaller than the typical momentum $ \sim m_\pi $ in these cases. Furthermore, the one-loop contribution becomes zero for $ M_i\simeq 200 $ MeV $ \sim m_\pi $. In the range of $ M_i\gtrsim m_\pi $, the tree-level amplitude still decreases with increasing $ M_i $, whereas the one-loop correction increases logarithmically. When $ M_i $ approaches $ 500\ \text{MeV} $, we find that the magnitude of the one-loop correction is comparable to the tree-level contribution. In principle, up to this scale, the mesons with masses heavier than $ m_\pi $ (such as K and η mesons) can be created and should be included as the explicit degrees of freedom in ChPT. We naturally expect that the one-loop correction may be changed owing to the contributions of these heavier mesons, thereby ensuring the validity of the perturbative expansion. However, using the chiral Lagrangian in the three-flavor case, we confirmed that the K and η mesons do not generate extra contributions to this process up to the one-loop level.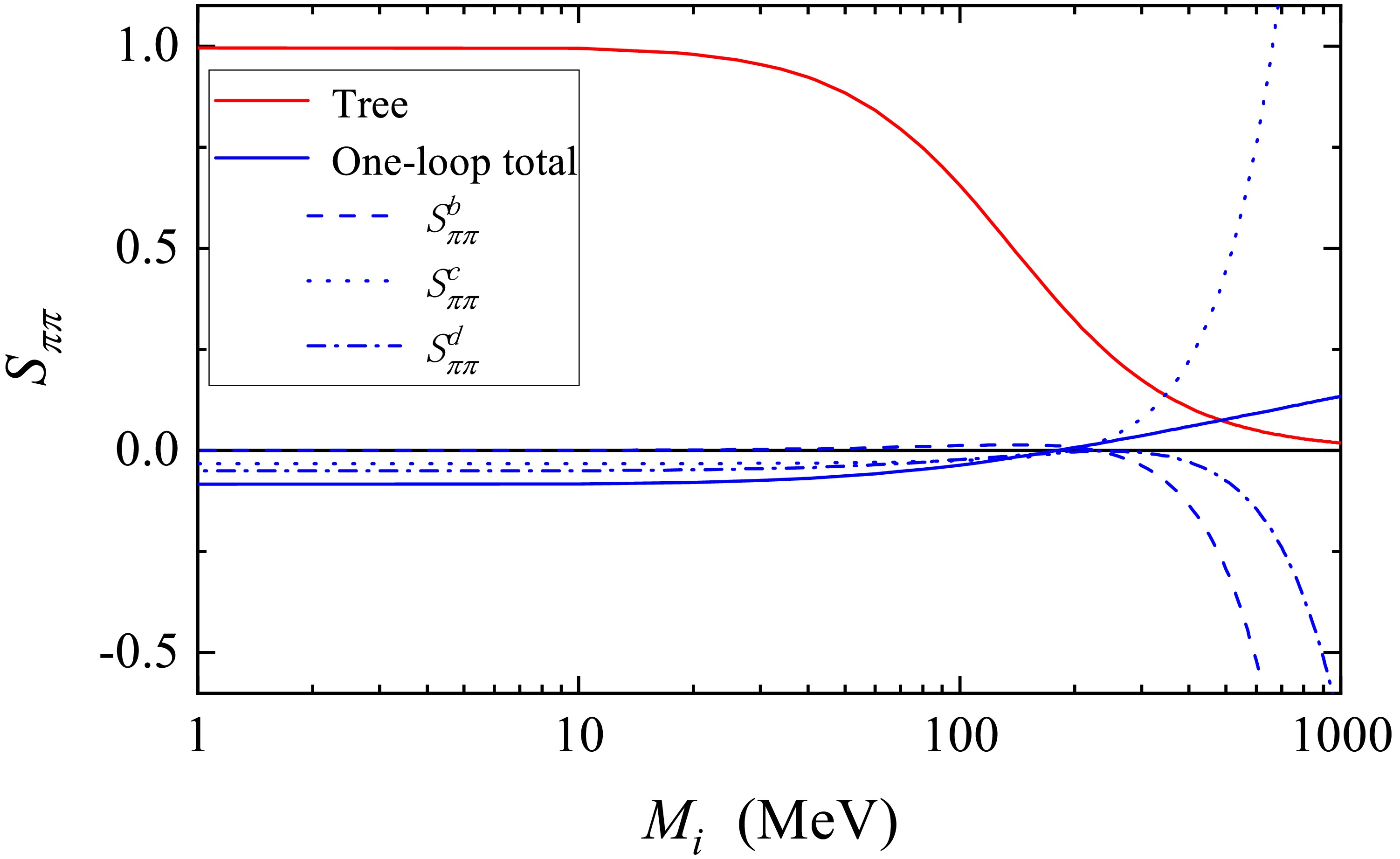

Figure 2.  (color online) Dependence of threshold amplitude $ S_{\pi\pi} $ on sterile neutrino mass $ M_i $, showing the contributions from tree-level and one-loop diagrams (sub-diagrams (b), (c), and (d)) based on ChPT calculations.

To gain insight into the effects of various one-loop diagrams on this sub-leading contribution, we illustrate in Fig. 2 the mass dependence of different amplitudes $ S_{\pi\pi}^b $, $ S_{\pi\pi}^c $, and $ S_{\pi\pi}^d $ in Eq. (21) denoted by dotted, dashed, and dot-dash lines, respectively. The mass independence of these contributions from three diagrams can be observed in the range of $ M_i\lesssim 50 $ MeV. Meanwhile, $ S_{\pi\pi}^b $ is nearly negligible, and $ S_{\pi\pi}^c $ is almost equivalent to the contribution of $ S_{\pi\pi}^d $. Notably, for $ M_i\simeq 200 $ MeV $ \sim m_\pi $, the contributions of three one-loop diagrams approach zero, leading to a tiny one-loop correction at this point. This behavior occurs because a loop integral in Eq. (21) vanishes after renormalization when $ M_i $ approaches $ m_\pi $. In the heavier mass region, the contributions of various diagrams change dramatically, and the cancellation between $ S_{\pi\pi}^c $ and the remaining amplitudes leads to a mild mass dependence of the total correction (a logarithmical increase with $ M_i $). Moreover, $ S_{\pi\pi}^b $ and $ S_{\pi\pi}^c $ will exceed the tree-level contribution when $ M_i\gtrsim 400 $ MeV. This simply implies that the neutrino with mass $ M_i\gtrsim 3m_\pi $ is no longer a suitable light degree of freedom in ChPT and the neutrino may be treated as an explicit heavy degree of freedom in a manner similar to the treatment of the $ \Delta(1232) $ resonance in ChPT.

In addition to the one-loop correction at N²LO, a contact contribution results from the hard-neutrino exchange. According to the interpolation formulae of the hard-neutrino LECs discussed in Ref. [31] and the lattice simulation [41], we can foresee that the hard-neutrino contribution is negatively related to $ M_i $. In contrast, this contact term does not change the scenario of the breaking of perturbative expansion for ChPT. Consequently, we suggest that breakdown scale Λ in this framework is about 500 MeV, and $ \Lambda_\chi $ will be replaced by Λ in the following analysis.

We fix the value of parameter $ m_a $ in Eq. (29) to 112 MeV from our calculation of the amplitude at the threshold; thus, it is comparable to the pion mass. In Fig. 3, we depict the $ M_i $ dependence of amplitude $ S_{\pi\pi} $ based on ChPT and Eq. (29).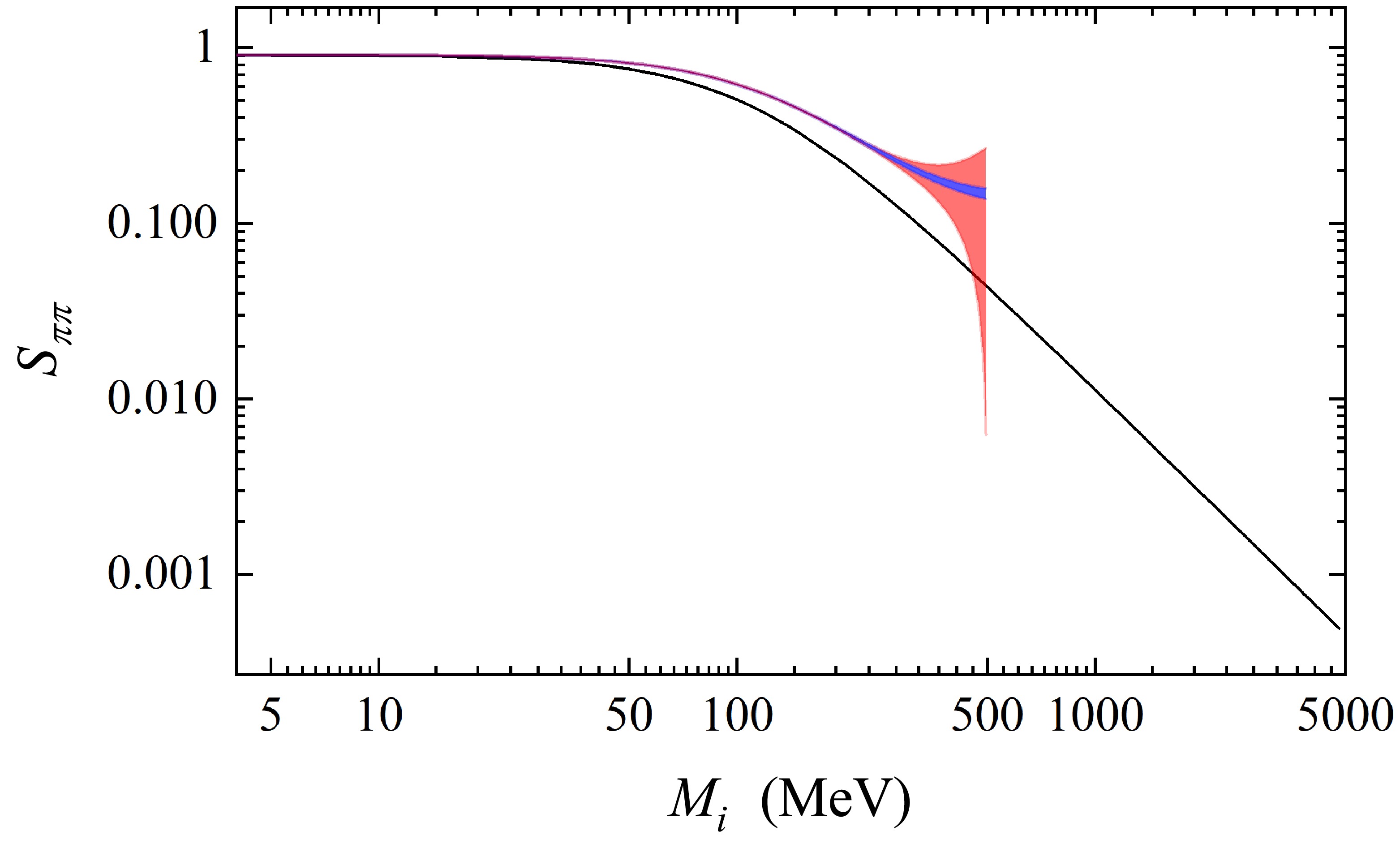

Figure 3.  (color online) Amplitude $ S_{\pi\pi} $ at the threshold predicted by Eq. (29) as a function of the sterile neutrino mass compared with the amplitude based on ChPT. The blue and red bands represent the results with the low-mass truncation errors of $ \widetilde{g}_\nu^{\pi\pi} $ and amplitude, respectively. The black curve denotes the prediction of the interpolation formula.

To survey the validity of the interpolation formula, we also include the uncertainty estimation based on Eq. (26), in which the blue (red) band denotes the low-mass truncation error of $ \widetilde{g}_\nu^{\pi\pi} $ (amplitude). The truncation error of $ \widetilde{g}_\nu^{\pi\pi} $ given by Eq. (25) has a minor effect on the amplitude; this again suggests that the contribution of the hard neutrino cannot easily cure the breakdown of the expansion in $ M_i $. Moreover, the ChPT result, as specified by Eq. (26), remains nearly invariant in the $ M_i \lesssim 50\ \text{MeV} $ region, and the interpolation formula is in excellent agreement with the ChPT calculations. However, the difference between this interpolation and ChPT predictions emerges when $ M_i\gtrsim50 $ MeV. Particularly, for the mass region in which ChPT is still valid, such as $ M_i\simeq m_\pi $, the prediction of the interpolation formula deviates significantly from the ChPT results, meaning a demand for a more reliable interpolation formula. Furthermore, the low-mass truncation error of the amplitude displays a divergent trend in the region with $ M_i\gtrsim300 $ MeV, reflecting the conclusions drawn from Fig. 2 regarding the breakdown of the perturbative approach. For the heavy neutrino, amplitude $ S_{\pi\pi} $ from the interpolation is consistent with ChPT.

As mentioned in Sec. II, the interpolation formula Eq. (29) uses only the data of two extreme cases, the amplitudes under the light- and heavy-neutrino exchange, to predict the mass dependence of the amplitude. Although correctly describing the main behavior of the amplitude, this method may be under-fitting. In addition, Eq. (29) adopts the most economic assumption that the ratio of the long-range contribution over the hard-neutrino contribution is independent of $ M_i $. This means that for the light sterile neutrino, $ g_\nu^{\pi\pi} $ can be expressed as an expansion in powers of $ M_i/m_a $ rather than $ M_i/\Lambda $, which contradicts NDA. Therefore, the form of Eq. (29) is insufficient for the pionic $ 0\nu\beta\beta $ decay mediated by a sterile neutrino. We also note that a similar conclusion is shown in the two-nucleon case by Refs. [33, 35].

In this work, we have studied the pionic $ 0\nu\beta\beta $ decay induced by the sterile neutrinos with masses $ M_i $ in the framework of ChPT. Thus far, the sterile neutrino mass has not been stringently limited in experimental and theoretical aspects such that we explore this process in a broad mass range. Because the mass dependence of the amplitude can be derived analytically for the heavy sterile neutrino, we have focused on the mass region below a few gigaelectronvolts. We calculate the transition amplitude under the light- and heavy-neutrino mechanism up to N²LO.

The amplitude associated with heavy neutrinos up to N²LO is given by the contact term. Its mass dependence is scaled as $ M_i^{-2} $. For a light neutrino, which is an active degree of freedom in ChPT, the one-loop correction as a subleading contribution would be over the leading-order contribution in the intermediate mass region with $500\;\text{MeV} \lesssim M_i\lesssim\Lambda_\chi$. Thus, we recommend $ \Lambda=500 $ MeV as the breaking scale of ChPT in the LNV pion decay process mediated by light sterile neutrino.

Because of the ChPT expansion breakdown in the intermediate mass region, we employ a naive interpolation formula to connect the amplitude based on ChPT across the light and heavy sterile neutrino mass regions. This interpolation formula, which assumes that the long- and short-range contributions share the same functional form of mass, does not recover the ChPT prediction well in the light mass region. Differing from it, a form of interpolation that distinguishes the mass dependence of the long- and short-range contributions is presented in Refs. [31, 33, 35]. More studies on the mass dependence of the amplitude, particularly for short-range contributions, are required to accurately describe the $ 0\nu\beta\beta $ decay under the seesaw mechanism.