The rotation effect on the thermodynamics of the QCD matter

In recent years, there has been a growing interest in the study of matter under extreme conditions, particularly in the context of intense rotational scenarios within the field of Quantum Chromodynamics (QCD). QCD matter produced in non-central collisions exhibits a non-negligible angular momentum on the order of $ 10^{4} \sim 10^{5}\hbar $, with local angular velocities ranging from 0.01~0.1 GeV [1−5]. The orbital angular momentum of the Quark-Gluon Plasma (QGP) can be transferred to the spin of constituent particles through spin-orbit coupling, a phenomenon known as the Barnett effect [6, 7]. Consequently, quarks and anti-quarks become polarized along the direction of the reaction plane. In 2005, Liang and Wang [1] predicted that spin–orbit coupling would lead to the polarization of strange quarks produced in non-central heavy ion collisions. Subsequently, in 2008, Becattini and colleagues [3] highlighted that within a hydrodynamic framework, local thermodynamic equilibrium implies a relationship between spin polarization and the rotational flow structure.Significant progress has also been made in theoretical investigations of QCD matter under rotation, attracting considerable attention in recent years. Studies have explored various phenomena such as pion superfluidity [8−10], $ \rho $ meson superconductivity [11, 12], chiral and deconfinement transitions [13−24], among others.

Experimentally, in 2017, the STAR Collaboration published the first observation of global polarization resulting from non-central heavy-ion collisions [25], in 2020, the ALICE Collaboration reported spin alignment of vector mesons $ \phi $ and $ K^{*0} $ [26], and in 2023, the STAR Collaboration also measured the spin alignment of $ \phi $ and $ K^{*0} $ [27]. Additionally, there have been advancements in lattice simulations of rotating systems [28−32]. These advances have led to the exploration of numerous spin-related quantum phenomena and remarkably strong fluid vorticity structures. For example, hydrodynamic simulations have been widely used to investigate vorticity and spin polarization in heavy-ion collisions. Hydrodynamic models [33−47] and transport models [48−56] have made significant progress in the study of vorticity and polarization observable.

The QCD thermodynamic quantities reflect the physical characteristics of QCD phase transition. The knowledge of thermodynamic quantities at finite temperature, chemical potential and angular velocity is needed when we study the non-central collisions. Some of thermodynamic quantities, such as the trace anomaly and speed of sound, are sensitive to the phase transition, which provide candidate signals for experimental study of phase transition and determining the critical endpoint. Experimentally determining the speed of sound in the QGP is proposed in [57−61]. Besides, the QCD thermodynamic quantities, such as the pressure and the speed of sound, are crucial inputs for the hydrodynamic simulations and transport models [62−65]. Therefore, it is significant to investigate the rotation effect on the thermodynamics of strong interaction matter.

According to the lattice simulations [66, 67] and functional renormalization group theory [68−71], at low momentum or renormalization group scale, the gluons are decoupled from the system due to the finite mass gap. The QCD system, which includes degrees of freedom of quarks and gluons, is transformed into a system composed by quarks and hadrons, which can be described by the low energy effective field models. The low energy effective field models, such as the Nambu–Jona-Lasinio (NJL) model [14, 72−76] and quark meson model [77−79], offer alternative approaches to exploring strong interaction matter, which capture the crucial features of QCD and provide insights into the QCD phase structure at finite temperature, density and angular velocity.

In this paper, we use the three-flavor NJL model to study the thermodynamic quantities of strong interaction matter under rotation, such as the speed of sound, angular momentum and moment of inertia. Our work is organized as follows. In II, we introduce the formalism of the three-flavor NJL model and derive the detailed expressions for thermodynamics in the presence of rotation. In III, we present the numerical results and discussions on thermodynamic quantities. Finally, in IV, we summarize our findings and conclude the paper.

First, we provide a very brief sketch of the basis for studying the rotating matter in an effective model. The general idea is to conduct the study in a reference frame that rotates with the system [14, 23, 80, 81]. In this frame of reference, the rotation can be described in relation to an external gravitational field. The metric tensor can describe the structure of space-time under a rotating frame reads

where $ v_i $ is the velocity. Our starting point is the partition function

here, S denotes the quark action, which is the integration of the Lagrangian density $ {\cal{L}} $. When extending to the case of rotating fermions [14, 80, 82] with non-zero chemical potential, the Lagrangian in the three-flavor NJL model is given by

here, $ \psi $ is the quark field, $ \bar{\gamma}^\mu=e_{a}^{\ \mu} \gamma^a $ with $ e_{a}^{\ \mu} $ being the tetrads for spinors and $ \gamma^{a} $ represents the gamma matrix, $ \Gamma_\mu $ is defined as $ \Gamma_\mu=\dfrac{1}{4}\times\dfrac{1}{2}[\gamma^a,\gamma^b] \ \Gamma_{ab\mu} $, which is the spinor connection, where $ \Gamma_{ab\mu}=\eta_{ac}(e^c_{\ \sigma} G^\sigma_{\ \mu\nu}e_b^{\ \nu}-e_b^{\ \nu}\partial_\mu e^c_{\ \nu}) $, and $ G^\sigma_{\ \mu\nu} $ is the affine connection determined by $ g^{\mu\nu} $. m is the bare quark mass matrix, $ \mu $ denotes the chemical potential, and G represents the coupling constant of four-point interaction term. $ \lambda ^a(a=1,...8) $ are the Gell-Mann matrices in flavor space. The last term corresponds to the 't Hooft interaction with coupling strength K, which is a determinant in flavor space. Considering a system with an angular velocity along the fixed z-axis, then $ \vec{v}=\vec{\omega}\times \vec{x} $. By choosing $ e^{a}_{\ \mu}=\delta^a_{\ \mu}+ \delta^a_{\ i}\delta^0_{\ \mu} \, v_i $ and $ e_{a}^{\ \mu}=\delta_a^{\ \mu} - \delta_a^{\ 0}\delta_i^{\ \mu} \, v_i $, and expanding the Lagrangian to first-order in angular velocity, we get the following expression:

where $ {\overset{\rightharpoonup }{\mathop{S}}} _{4 \times 4} = \dfrac{1}{2}\left( {\begin{array}{*{20}c} {\overset{\rightharpoonup }{\mathop{\sigma}}} & 0 \\ 0 & {\overset{\rightharpoonup }{\mathop{\sigma}}} \\ \end{array}} \right) $ is the spin operator. With the technique of the path integral formulation for Grassmann variables theory and the mean field approximation, the linearization is done to a 4-quark interaction and 6-quark interaction, we get the expression of $ \log {\cal{Z}} $ as follows:

The inverse fermion propagator $ {D^{ - 1} } $ in Eq. (5) can be derived as follows,

where we introduce Matsubara frequency $ {\boldsymbol{{\omega_{l}}}}=-ip_{0}= (2l+1){\pi}T $ with the temperature T, and M denotes the dynamical mass of the quark

To find solutions of the Dirac equation, we start by choosing a complete set of commutating operators consisting of $ \hat{H} $, which can be obtained from Eq. (4) by using the relation $ {\cal H} = \bar \psi \left( {i\gamma ^0 \partial _0} \right)\psi-{\cal{L}} $, the momentum in the z-direction $ \hat{p}_{z} $, the square of transverse momentum $ \hat{p}_{t}^{2} $, the z-component of the total angular momentum $ \hat{J}_{z} $ and the transverse helicity $ \hat{h}_{t} $, where $ {\hat h_t} = {\gamma ^5}{\gamma ^3}{{\overset{\rightharpoonup }{\mathop{p}}} _t} \cdot {\overset{\rightharpoonup }{\mathop{S}}} $, and $ {\gamma ^5}=i{\gamma ^0}{\gamma ^1}{\gamma ^2}{\gamma ^3} $. By solving the eigenvalue equations of the complete set of commuting operators {$ \hat{H} $, $ \hat{p}_{z} $, $ \hat{p}_{t}^{2} $,$ \hat{J}_{z} $, $ \hat{h}_{t} $}, we obtain the positive and negative energy solutions of the Dirac field as follows: In cylindrical coordinates, the general spinor eigenstates can be written as

Here, $ s=\pm1 $ represent the transverse helicity values, n denotes the z-direction angular momentum quantum number. After the summation of all the Matsubara frequencies and carrying out the general approach of the finite temperature fields [83], it can be shown that the grand thermodynamic potential ($ \Omega=-\dfrac{T}{V} \log {\cal{Z}} $) has following form:

Here, the quark quasiparticle energy $ {E_f } = \sqrt {M_f^2 + p_t^2 + p_z^2} $. For simplicity we also introduce the quark quasiparticle energy under rotation as follows,

Note that the above expression of grand thermodynamic potential contains an explicit cutoff dependence, due to the NJL model being nonrenormalizable. Here, our thermodynamic potential naturally separates into the vacuum piece and the temperature-dependent matter part, which is very helpful in calculating the thermodynamic quantities. The three-momentum cutoff in the vacuum piece should be chosen to reproduce observables, such as pion mass, pion decay constant, and so on, also, in principle, the cutoff in the matter part should take the infinite value. Here, $ \Lambda $ is the three-momentum cutoff of the vacuum part in the potential.

Then, we consider the gap equations which will be required to minimize the grand potential, the dynamical quark mass $ M_{f} $ can be determined by solving the stationary condition, and we also require the solutions satisfy to get the minimum of the potential, namely,

which leads to the following coupled gap equations:

here, $ n_f $ and $ \bar n_f $ denote the quark and anti-quark distribution functions:

This set of coupled equations is then solved for the fields as functions of temperature T, quark chemical potential $ \mu $, and angular velocity $ \omega $. Now we turn to the thermodynamics of the rotating system, when we extend to the rotating system, the vorticity should also be considered a further intensive thermodynamic quantity which is necessary for the description of the local fluid, so, some corrections may need to be carried out for the energy density as follows [16, 84, 85]:

Here, n denotes quark number density, J presents the (polarization) angular momentum density.

From the standard thermodynamic relations, the pressure, and (polarization) angular momentum density (the angular velocity can be regarded as an "effective chemical potential", similarly, we can define the angular momentum by a derivative with respect to the angular velocity of the grand canonical potential) and the quark number density are given as follows,

note here, to get a physical pressure, we have renormalized the thermodynamical potential, and the subscript represents keeping the chemical potential and angular velocity fixed during taking the partial differentiation, and the trace anomaly can be defined as

For each flavor, the explicit formulae of entropy density and quark number density, and the angular momentum along the z-axis are listed in A.

Once we get the expression of the angular momentum, then we can directly obtain the moment of inertia of the rotating system

For the description of the expansion of dense matter created in heavy ion collisions, a fundamental quantity that determines the expansion of hot dense matter is the speed of sound

another quantity of interest is the specific heat

Here, we don't list the detailed expressions of them, and one can easily get that from the above expressions.

In this section, we will present our numerical results for the dynamical quark mass and chiral transition in the three-flavor NJL model under rotation. In our calculations, the input parameters in the NJL are the coupling constants G, the light quark mass $ m_{q} $ (throughout, we ignore isospin breaking effects and work with $ m_{u}=m_{d}=m_{q} $), the strange quark mass $ m_{s} $ and the three-momentum cutoff $ \Lambda $ and the 't Hooft term coupling constant. We use the model parameters reported in Ref. [86], which have been estimated by the fitting in light of the following observations: $ m_{\pi}=138 $ MeV, $ f_{\pi}=92 $ MeV, $ m_{K}=495 $ MeV and $ m_{\eta'}=958 $ MeV, the input parameters are as follows: $ m_q = 0.005\; {\rm{GeV}},\; m_s = 0.1283\; {\rm{GeV}}, \; G = 3.672\; {\kern 1pt} {\rm{GeV}}^{ - 2}, \ \; K = 59.628\; {\kern 1pt} {\rm{GeV}}^{ - 5}, \; \Lambda = 0.6816\; {\rm{GeV}} $. Throughout the text, unless otherwise specified, the radius r is taken as $ 0.1\; {\rm{GeV}}^{ - 1} $.

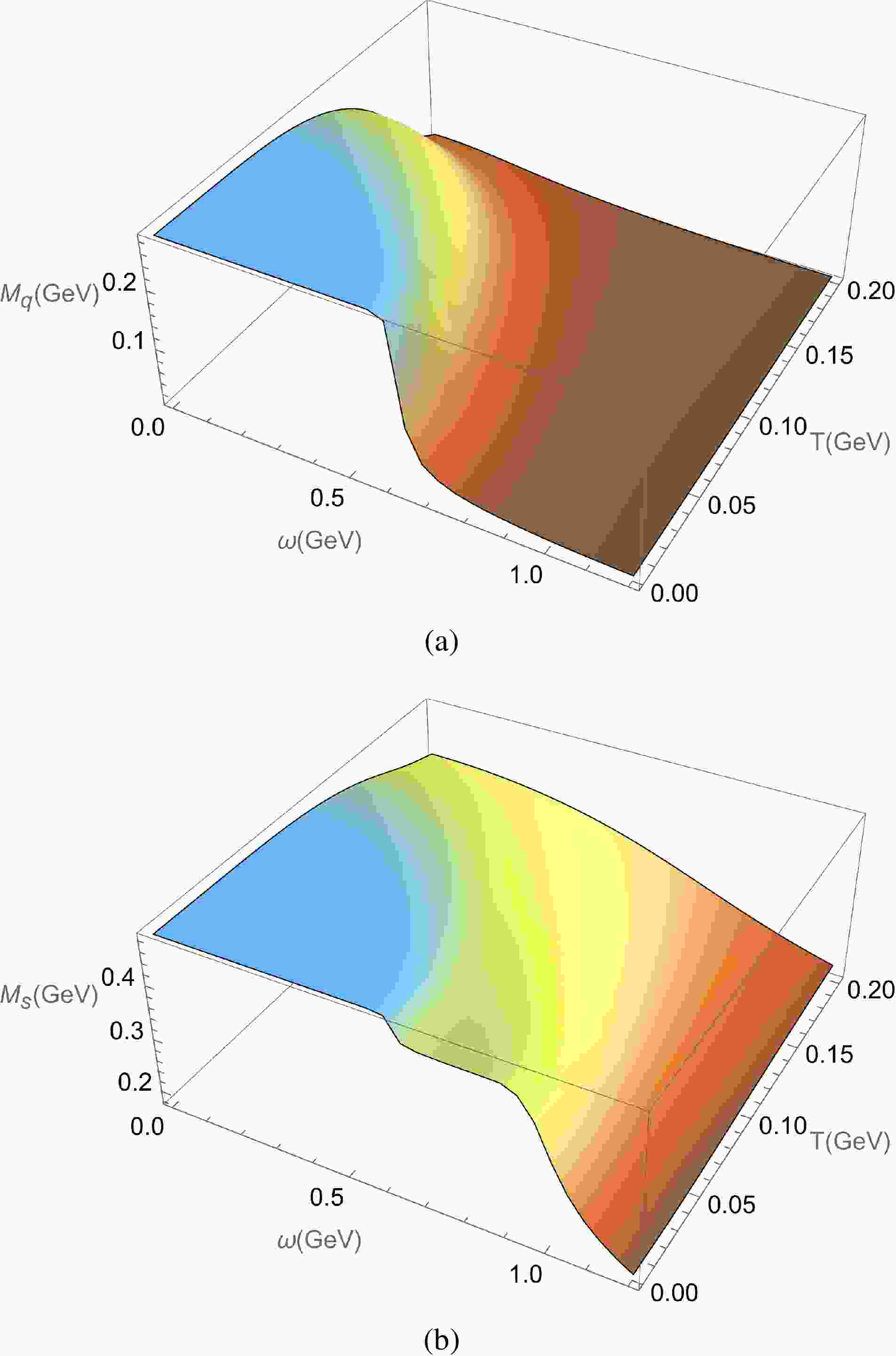
We present the evolution of the light quark mass with respect to T, $ \omega $ in Fig. 1(a), and the strange quark mass in Fig. 1(b). We observe a decrease in mass as the temperature or angular velocity increases, indicating the restoration of chiral symmetry at high temperatures or large angular velocities. It is remarkable that there exist fast transitions in the low temperature and large angular velocity region, while in the high temperature and small angular velocity region only exhibits a very slow change. It is easy to see that when we fix the temperature is very low, the restoration of chiral symmetry experiences a fast transition with rapid rotation. This can be seen as the continuous crossover becoming steeper with increasing angular velocity, eventually merging into a fast transition at large angular velocity. By comparing the critical angular velocities $ \omega_{c} $ for the light and strange quarks, we find that the decrease is faster for the light quark, which suggests that the chiral symmetry restoration is more efficient for the light quark compared to the strange quark.

Figure 1.  (Color online) The effective mass of light quark and strange quark according to temperature T and angular velocity $ \omega $ with $ \mu=0.01 $ GeV.

Then, we extended the investigation of effective quark mass to the $ \omega-\mu $ plane. In Fig. 2, we show the evolution of the effective masses for the light quark and strange quark as functions of the angular velocity and quark chemical potential. Clearly, at sufficiently large angular velocity or (and) sufficiently large quark chemical potential the quark effective mass is very small. When angular velocity is small, we can find there is a very swift change for the light quark around $ \mu=0.3 $ GeV, and for the strange effective quark there are two quickly change regions. We can also observe similar transition regions of small quark chemical potential and large angular velocity as shown in the left rear side of the figure.

Figure 2.  (Color online) The effective mass of light quark and strange quark according to angular velocity $ \omega $ and quark chemical potential $ \mu $ with T=0.01 GeV.

The temperature and chemical potential dependence of the light and strange quark effective masses at $ \omega=0.1 $ GeV is depicted in Fig. 3, one sees that at low temperature and small quark chemical potential, the chiral symmetry is spontaneously broken, with increasing temperature or quark chemical potential, the effective mass of strange quark is only mildly dependent on them while the light quark shows more sensitive to them compared the strange quark. It can be found that in the low temperature region, the effective mass of the light quark has a sharp drop at certain values of $ \mu $ with increasing $ \mu $. One can see at high temperature or large quark chemical potential the effective mass of these quarks become small, and at sufficiently high temperature or sufficiently large chemical potential the effective mass of light quark almost approaches its current mass, while the strange quark still with a heavy effective mass, this indicates that the current mass of the quark plays an important role in the chiral transition.

Figure 3.  (Color online) The effective mass of light quark and strange quark according to temperature T and quark chemical potential $ \mu $ with $ \omega=0.1 $ GeV.

The quark condensate $ \langle {\bar{q}q} \rangle $ or $ \langle {\bar{s}s} \rangle $ is often treated as an order parameter for spontaneous chiral symmetry breaking. The temperature-dependence of the order parameters for different values of the rotational speed are shown in Fig. 4. It shows a rapid cross-over with a critical angular velocity at about $ 0.6 $ GeV and $ 1.0 $ GeV for the light quark and strange quark condensate, respectively. At low temperatures and small angular velocities, the chiral symmetry is spontaneously broken. While at high temperatures or (and) large angular velocities, chiral symmetry may gradually be restored.

Figure 4.  (Color online) Condensates of light quark and strange quark as functions of temperature for different values of the rotational speed.

Next, we determine the chiral phase transition temperature in the presence of angular velocity in Fig. 5. The definition of $ T_{pc} $ in this context is determined by the maximum of $ \left| {\dfrac{{d{\phi _f}}}{{dT}}} \right| $, here, $ f=u,d,s $ and $ {\phi _u} ={\phi _d} = \langle {\bar{q}q} \rangle , {\phi _s} = \langle {\bar{s}s} \rangle $. From Fig. 5 we can see the pseudocritical temperature decreases as angular velocity becomes larger. At small angular velocity region, the pseudocritical temperature of strange quark is about $ 0.1 $ GeV larger than that of the light quark, even at a large angular velocity around $ 0.6 $ GeV, where the pseudocritical temperature of light quark is very small and by contrast the pseudocritical temperature of strange is still very large. Thus, a conclusion seems to be that the rotation can lead to an obvious change to the chiral transition of light quarks compared to that of strange quark due to whose mass is heavier.

Figure 5.  (Color online) The pseudocritical temperatures for the chiral transition of rotating quark matter as functions of the angular velocity.

As can be seen in Fig. 6, the scaled pressure, energy, and entropy densities increase with increasing temperature. These quantities start to increase rapidly with temperature and then gradually grow as the temperature continues to rise after passing through the transition region. The observable rotation enhances these scaled quantities, at low temperatures, the enhancements are significant, while at high temperatures, the enhancements are less pronounced. The scaled trace anomaly exhibits a peak in the transition region, as the temperature continues to increase, the scaled trace anomaly decreases for all different angular velocities. It is evident that at low temperatures the variation in angular velocity can result in significant deviations of the scaled trace anomaly, and this effect diminishes as the firing temperature increases.

Figure 6.  (Color online) Scaled pressure, energy density, entropy density and trace anomaly as functions of temperature at zero chemical potential for different angular velocities.

The specific heat is an important quantity in thermodynamics as it can be considered a response function of the phase transition, its variation with temperature is presented in Fig. 7(a). As the angular velocity increases, the peak of the specific heat, which occurs at the transition temperature, shifts towards lower temperatures, this indicates that the transition temperature decreases with an increase in angular velocity. In Fig. 7(b), the speed of sound squared increases with temperature and shows little sensitivity to the chosen angular velocities. However, this observation may be attributed to the consideration of only small values of angular velocity. It is evident that the speed of sound squared approaches the conformal limit of 1/3 for different angular velocities at high temperature limits.

Figure 7.  (Color online) Scaled specific heat and speed of sound squared as functions of temperature at zero chemical potential for different angular velocities.

An intriguing quantity in the rotating system is the angular momentum. Fig. 8(a) displays the results of the scaled angular momentum as functions of temperature at zero chemical potential for various angular velocities. The scaled angular momentum initially increases with temperature and reaches its peak across the chiral transition region ($ T \sim 150 $ MeV) for all angular velocities. Beyond this temperature, it decreases with further temperature increment. The moment of inertia is also of interest in our calculation as it represents the linear response of the system's angular momentum J to the angular velocity $ \omega $. Fig. 8(b) displays the results of the moment of inertia as functions of temperature at zero chemical potential for various angular velocities. It is evident that the scaled moment of inertia always increases with temperature for different angular velocities. Moreover, for a fixed temperature, the scaled moment of inertia becomes larger with increasing angular velocity.

Figure 8.  (Color online) Scaled angular momentum and moment of inertia as functions of temperature at zero chemical potential for different angular velocities.

In the transverse directions to the axis of rotation, the radius of rotation must be constrained by the causal condition $ \omega r<1 $, resulting in a finite value. Consequently, a system of QCD matter undergoing rotation must always possess a finite volume. To gain a deeper understanding of the characteristics of QCD matter produced in non-central heavy-ion collisions, it is essential to investigate the impact of finite volume effects on thermodynamic properties. Several studies have extensively examined the influence of system size on its thermodynamic behavior and other physical quantities [87−89].

In the standard NJL model, these thermodynamic quantities are functions of temperature and quark chemical potential. However, in a rotating system, these thermodynamic quantities should also depend on the finite size. Due to the cylindrical symmetry, these quantities are dependent on the transverse radius r. It would be interesting to investigate how the various thermodynamic quantities in a strongly interacting rotating matter depend on the radius of the rotating system. The properties as a function of the radius of the rotating system may be related to experimental observations in the future. Additionally, the radius should drastically change the angular momentum and the momentum of the inertia. Therefore, it becomes important to study how the various thermodynamic quantities in the QCD matter under rotation depend on the rotation radius of the system.

We show the densities of the scaled pressure, energy, entropy, and trace anomaly as functions of temperature at zero chemical potential for different radii in Fig. 9. As can be seen, the radius effect is visible and enhances these thermodynamic quantities. The radius effect does not qualitatively affect the behavior of these thermodynamic quantities even in the high-temperature region; it just shifts these thermodynamics at a given temperature. It is also noted that the differences for each thermodynamic quantity between different radii seem unchanged even in the high-temperature region.

Figure 9.  (Color online) Scaled pressure, energy density, entropy density and trace anomaly as functions of temperature at zero chemical potential for different radii.

The scaled angular momentum and moment of inertia, which are functions of temperature at zero chemical potential for different radii, are plotted in Fig. 10. In Fig. 10(a) we find that there is a rapid change near the chiral transition region (around 150 MeV) for the scaled specific heat. It can be seen that there exists a characteristic where the location of the summits almost has no change with increasing radius. In Fig. 10(b), it is remarkable that the speed of sound squared curves seem the same around the chiral transition region. It is also found that at extremely high temperatures, for different angular velocities, all the values of the speed of sound squared approach the Stefan-Boltzmann limit, whose value is 1/3. This indicates that the speed of sound squared of quark matter at high temperature is not sensitive to the transverse radius.

Figure 10.  (Color online) Scaled specific heat and speed of sound squared as functions of temperature at zero chemical potential for different radii.

From Fig. 11(a), one could also infer the dependence of the scaled angular momentum on the radius. Unlike other thermodynamics, the angular momentum has a strong dependence on the system radius. At low temperatures, the angular momentum increases smoothly with increasing radius. At high temperatures, the angular momentum becomes stronger. It is also evident that the scaled moment of inertia always increases with increasing temperature for different radii from Fig. 11(b). In the region of high temperature, the scaled moment of inertia shows a strong radius dependence. As the temperature increases, the difference between any two curves in the figure becomes larger for the scaled angular momentum and the scaled moment of inertia.

Figure 11.  (Color online) Scaled angular momentum and moment of inertia as functions of temperature at zero chemical potential for different radii.

Studying the thermodynamics at finite chemical potential in the rotating system is important for understanding the phase structure of QCD, modeling compact stars, and interpreting heavy ion collision experiments. In Fig. 12 we show the densities of scaled pressure, energy, entropy, and trace anomaly as functions of temperature at $ \omega=0.2 $ GeV for different chemical potentials. A notable feature is that, in the low temperature region, there can be a nontrivial contribution from the chemical potential. It is shown that the pressure, energy, and entropy density increase with increasing temperature for different chemical potentials, and these quantities are also enhanced by the chemical potential. An increase in the chemical potential leads to increases in these thermodynamics, which can be easily understood as more degrees of freedom are active. In the rotating system, the trace anomaly is enhanced by the chemical potential below the critical transition region, while across the transition region, it can be found the trace anomaly is suppressed by the chemical potential, in addition, with increasing chemical potential, the crossover pattern evolves to lower transition temperatures. For all the quantities in this figure show that below the crossover temperature they exhibit a strong chemical potential dependence. In Fig. 13 we show scaled specific heat and speed of sound squared as functions of temperature at $ \omega=0.2 $ GeV for different chemical potentials. As shown in Fig. 13(a), scaled specific heat increases with increasing temperature and reaches a peak at the chiral transition region. Then it first decreases quickly around the critical chiral transition and finally changes little with temperature. The figure shows that the peak position moves to a smaller temperature as quark chemical potential increases. From Fig. 13(b), we can see there is a significant increase in the speed of sound squared for increased quark chemical potential, even near the transition region, which means in the finite chemical potential may have an important effect on the thermalization of the QCD matter in the rotating system. Here, the speed of sound squared also conveys relevant information: it displays no local minimum at a crossover transition for the quark chemical potential considered, due to first is that the system is not an infinite volume as the standard NJL model, another reason is that the energy density has been modified, i.e., we add the contribution of $ J\omega $. It is not hard to see there is a trend when increasing chemical potential in the rotating system, there will appear a local minimum in the phase transition. From this figure, we can see the speed of sound squared will approach the conformal limit of 1/3 for different angular velocities at a large temperature limit.

Figure 12.  (Color online) Scaled pressure, energy density, entropy density and trace anomaly as functions of temperature at $ \omega=0.2 $ GeV for different chemical potentials.

Figure 13.  (Color online) Scaled specific heat and speed of sound squared as functions of temperature at $ \omega=0.2 $ GeV for different chemical potential.

Another basic thermodynamic quantity is the angular momentum and moment of inertia, these quantities measure the breaking of conformal symmetry in the interaction theory. In Fig. 14, we show the scaled angular momentum and moment of inertia as functions of the temperature for different chemical potential at finite angular velocities. They have similar characteristics as scaled quantities in Fig. 12 below the critical transition. When continuously increasing the temperature, the scaled angular momentum slowly decreases, while the scaled moment of inertia always keeps increasing with temperature.

Figure 14.  (Color online) Scaled angular momentum and moment of inertia as functions of temperature at $ \omega=0.2 $ GeV for different chemical potential.

Another possible signature of the chiral transition is offered by the behavior of the quark number densities. In Fig. 15 we show the results of the scaled quark number density as a function of the temperature at $ \omega=0.2 $ GeV for different values of chemical potential, from the figure we can see when quark chemical potential equals to zero, the corresponding quark number density is always zero. In the presence of finite quark chemical potential, the scaled quark number densities increase slightly until $ T=150 $ MeV and decrease again with growing temperature. It is obvious that the chemical potential enhances the quark number density in the rotating system.

Figure 15.  (Color online) Scaled quark number density as a function of temperature at $ \omega=0.2 $ GeV for different values of chemical potential.

In the following, we will present a systematic analysis of the thermodynamic quantities of QCD matter under large angular velocity. The system's total pressure and energy density during rotation are simply the sum of the contributions from each quark flavor. In order to have a clearer picture of the effects of rotation on different quark flavors, we will investigate each individual contribution as well as the total contribution.

From the strong rotational behavior depicted in Fig. 16, it is evident that the bulk thermodynamic properties, such as the scaled pressure, energy density, and trace anomaly, increase with increasing angular velocity at a temperature of T=0.01 GeV and quark chemical potential $ \mu=0 $ GeV. Notably, the scaled pressure, energy, and trace anomaly of both the light quark and strange quark increase as the angular velocity rises. In the mid-region of angular velocity, below approximately 0.8 GeV, the light quark predominantly contributes to these thermodynamic quantities. However, at sufficiently large angular velocities, the contributions from different flavors become almost the same. It can also be found that the angular momentum of the system also has a very similar character in Fig. 17. It is evident that the angular momentum in the chiral broken phase is lower than the angular momentum in the chiral restored phase. Furthermore, it is worth noting that the contribution of the light quark to the angular momentum is remarkable in the mid-region of the angular velocity, while that of the strange quark is moderate.

Figure 16.  (Color online) Scaled pressure, energy density, entropy density and trace anomaly as functions of angular velocity at T=0.01 GeV and $ \mu=0 $ GeV for the light, strange and total quarks, respectively.

Figure 17.  (Color online) Scaled moment of inertia as functions of angular velocity at T=0.01 GeV and $ \mu=0 $ GeV for the light, strange and total quarks, respectively.

There is a descent for the scaled entropy density after exceeding the critical point around $ \omega=0.6 $ GeV because, in this region, the rate of increase of the quantity pressure is slowing down. We can also observe a slight increase (not clearly visible in the figure) followed by a decrease in the entropy density around $ \omega=1.0 $ GeV. The trace anomaly increases with increasing angular velocity, which is because we have set T=0.01 GeV, in such low temperature, the strange quark is still in a phase with partly broken chiral symmetry if the temperature is high, we will see that the trace anomaly becomes small.

We show the behavior of the scaled specific heat as a function of $ \omega $ in T=0.01 GeV for vanishing chemical potential. The evolution of the scaled specific heat increases from zero to a maximum value around $ \omega=0.6 $ GeV then down to a minimum value and then gradually increases to another sub-maximum value around $ \omega=1.0 $ GeV and finally tends to gradually decrease at large angular velocity. From the figure, we can clearly see that the light quark rises steeply across the chiral transition and for the strange quark only there is a flatter peak at a more relatively broad region. It is known that if one has a sharp crossover phenomenon with a rapid change in thermodynamic quantities over a small interval, there is some chance for measurable effects in experiments, so the specific heat may provide relevant signatures for phase transitions in the rotating system.

The speed of sound squared changes with the angular velocity for the light and strange quarks is plotted in Fig. 18(b). It is known that in the transition region of the QCD matter, the characteristics of the speed of sound squared undergo significant changes, it is evident that the speed of sound squared shows a (pronounced) dip near the chiral transition. There are two local minima of the speed of sound squared becomes deeper in the vicinity of the critical angular velocity, which correspondingly to the light quark and strange quark, respectively. At small angular velocity, the speed of sound squared increases with an increase in the angular velocity. However, at a large angular velocity, the speed of sound squared subtly decreases with an increase in the angular velocity. Our numerical results indicate that the dependence of the speed of sound squared on the angular velocity can be indicative of QCD chiral transition. To probe this dependence further, we show the results of calculations for different temperatures in Fig. 19, the figure exhibits markedly behavior of the quark matter under rotation, and it can be found that the maximum value of the speed of sound is dominated by features associated with the chiral transitions. In addition, the speed of sound squared increases as angular velocity increases in the small angular velocity region, while decreases with angular velocity increases in the large angular velocity region. In the low angular velocity region, there is a significant difference in the speed of sound corresponding to different temperatures. However, in the high angular velocity region, the difference in the speed of sound becomes smaller for different temperatures and ultimately converges to the same value. Thus, a key conclusion can be made that the speed of sound exhibits a nonmonotonic behavior as the angular velocity changes.

Figure 18.  (Color online) (a) Scaled specific heat as a function of angular velocity at T=0.01 GeV and $ \mu=0 $ GeV for the light, strange and total quarks, respectively. (b) The corresponding result of speed of sound squared for the total quarks.

Figure 19.  (Color online) Speed of sound squared as a function of angular velocity at $ \mu=0 $ GeV for different temperatures.

In order to investigate the expansion of the plasma formed in ultra-relativistic heavy-ion collisions with noncentral impact, it is crucial to compute the thermodynamic properties within a rotating system. This paper focuses on formulating and exploring the thermodynamics of the three-flavor NJL model under rotation. We present the outcomes concerning diverse thermodynamic observables as a function of temperature, considering various angular velocities, radii, and finite quark chemical potentials. Additionally, we examine the thermodynamic behaviors of the light and strange quarks in relation to the angular velocities, respectively.

To summarize, we have presented an analytical calculation of the thermodynamics in the three-flavor NJL model in the presence of the rotational effect. We systematically analyze the equation of state in the parameter space of temperature T, chemical potential $ \mu $, and the angular velocity $ \omega $ in the rotational system. The calculations provide a physical picture of the chiral transition under rotation, and our findings indicate that the effect of rotation plays an important role in thermodynamics. By studying the changes in thermodynamic quantities of a rotating system, we can gain insights into the properties and behaviors of QCD matter. In the rotating system, the scaled thermodynamic quantities are visibly influenced by rotation, and an important quantity is the moment of inertia, which exhibits a strong dependence on the angular velocity even at high temperatures. The thermodynamic properties of light and heavy quarks differ with respect to different angular velocities, and this distinction strongly influences the thermodynamic quantities. However, for sufficiently strong rotation, these distinctions for each flavor vanish. The speed of sound plays a crucial role in studying the thermodynamic properties and phase transitions of QGP. As a main finding of our analysis, the speed of sound squared exhibits a nonmonotonic feature with respect to the angular velocity.

It should be mentioned that, in the study of the properties of QCD matter, the effective volume effect and boundary conditions are of crucial importance. They not only influence the phase structure and thermodynamic properties of QCD matter but also are closely related to experimental phenomena [90−104]. As demonstrated in Ref. [101], chiral condensation can display either catalysis or inverse catalysis depending on the boundary conditions, while a quantized first-order phase transition emerges specifically under periodic boundary conditions. Ref. [103] took into account the finite size effect with periodic, quasi-periodic, and anti-periodic boundary conditions, and the results indicated that the phase structure of the system exhibited significant differences under different boundary conditions. For rotating QCD matter, the rotational system must satisfy the causality condition $ \omega r < 1 $. Thus, in principle, the boundary conditions should be taken into account. In Ref. [98], it has been found that in the rotating system, the boundary effects can cause the quark chiral condensation to exhibit oscillatory behavior near the boundaries. In Ref. [105], lattice results on QCD matter under rotation were investigated, and three types of boundary conditions, including open boundary condition, periodic boundary condition, and Dirichlet boundary condition, were considered. In the holographic QCD model under rotation [104], the finite size effects and boundary conditions have been discussed. Under Neumann or Dirichlet boundary conditions, different (inverse)catalysis effects on the chiral condensation occur. The finite volume effect with different boundary conditions also influences the momentum distribution of particles in the system, thereby affecting thermodynamic properties.

More importantly, the finite volume effect and boundary conditions are closely related to experimental phenomena. In experiments such as heavy-ion collisions, the QCD matter produced is under extreme conditions, and both its volume and boundary conditions are special. Various phenomena observed in the experiments, such as particle production, distribution, and collective flow, are closely associated with the finite volume effect and boundary conditions. Therefore, understanding the impact of finite volume and boundary conditions is crucial for linking experimental observations to the QCD phase diagram and thermodynamics. For simplicity, we did not take into account the boundary effect of the system here, we plan to conduct comprehensive and in-depth studies in this research area in the near future. Such investigations will not only advance our fundamental theoretical understanding of strong interaction dynamics in rotating QCD systems, but also provide a robust theoretical framework for interpreting and predicting phenomena observed in non-central heavy-ion collision experiments.

So far, we have developed the NJL model taking into account only fermion-antifermion scalar interactions for the chiral transition. It is necessary to note that the vector interactions [106−108] may play an important role on the chiral transition of three-flavor NJL model in the presence of rotation, and we also leave it as our further study. In addition, the Polyakov-Nambu-Jona-Lasinio (PNJL) model [109−115] incorporates the Polyakov loop integral based on the NJL model, considering the coupling between quark degrees of freedom and gluon degrees of freedom. The PNJL model shows features of both chiral symmetry restoration and deconfinement phase transition, so this may allow the PNJL model to better describe the properties of QCD matter under rotation at high temperatures and finite chemical potentials. The PNJL model under rotation has been proposed in Refs. [21, 116], thus, it is meaningful to calculate the thermodynamic quantities in this model. Although there is still controversy on how rotation affects the deconfinement transition at present, we hope the lattice QCD provides more clues on the Polyakov loop. Finally, to make this research available in the PNJL model.

We greatly thank Mei Huang, Jingfeng Liao, Yin Jiang, Kun Xu and Jie Mei for useful discussions.

We list the detailed expressions of the entropy density, quark number density, and the angular momentum along the z-axis: