Explanation of the nature of the island of inversion exhibited by ³²Mg at the Hartree-Fock-Bogoliubov level and beyond

The fundamental challenge in the field of nuclear physics is understanding how nucleons interact and combine to form an atomic nucleus. Nuclei far from the stability line, also known as exotic or unstable nuclei, exhibit a wide range of novel phenomena, including the disappearance of traditional magic shells and the appearance of new (semi-) magic shells [1−9]. The unstable nucleus of interest, namely $ ^{32} {\rm{Mg}}$ [10, 11], exhibits a typical feature called the island of inversion [12−14]. In particular, experimental evidence, including the large $B(E2:2_1^+\to 0^{+}_{1})$ value, low-lying $ 2_1^+ $ excited state, and rotational band [3, 15−21], has established a well-deformed ground state (g.s.) for $ ^{32} {\rm{Mg}}$, from which the persistence of a spherical magic shell $ N = 20 $ is ruled out consistently. All these findings offer valuable insights into the mechanisms that govern the binding of the nucleus.

In theory, a remarkable cross-shell excitation from neutron $ sd $ to $ pf $ shells for $ ^{32} {\rm{Mg}}$ has been proposed for the deformed g.s. $ 0_1^+ $ using the shell model with the SDPF-M interaction [22, 23]. Based on the picture of the cross-shell excitation, the intrusion of the $ pf $-shell is frequently observed in the deformed mean-field calculations of $ ^{32} {\rm{Mg}}$. Nevertheless, the g.s. deformation remains inadequately described. For instance, the angular momentum projection (AMP) based on the mean-field models can reproduce the deformed g.s. for $ ^{32} {\rm{Mg}}$ [24−26] but cannot reproduce the low-lying excitation energies. This indicates that the underlying mechanism responsible for the island of inversion properties exhibited by $ ^{32} {\rm{Mg}}$ remains challenging.

As one of the representative nuclear models, the relativistic mean field (RMF) theory [27−34], based on the meson-propagated diagram of nuclear force [35], provides a simple yet efficient modeling of nuclear binding through a covariant representation of the strong attractive scalar and repulsive vector interactions. This picture provides a natural explanation of the strong spin-orbit couplings in nuclei [36, 37] and the origin of pseudo-spin symmetry (PSS) [38, 39]. In particular, as indicated by the conservation conditions, namely $ V+S = 0 $ [40] or $ {\rm d}(V+S)/{\rm d}r = 0 $ [41] with the scalar (S) and vector (V) potentials, the approximate PSS in realistic nuclei is a natural consequence of the relativistic modeling of nuclear binding. However, the Fock terms, integral parts of the meson-propagation diagram, were excluded from the RMF models for simplicity, thereby neglecting the important degrees of freedom associated with the π and ρ-tensor (ρ-T) couplings.

The incorporation of the Fock terms, which account for the exchange correlations, has led to the relativistic Hartree-Fock (RHF) and relativistic Hartree-Fock-Bogoliubov (RHFB) theories [42−45]. With the proposed RHF Lagrangians PKOi ($ i = 1,2,3) $ [43, 46] and PKA1 [44], comparable quantitative precision as the RMF theory has been achieved by the RHF and RHFB theories in describing a range of nuclear phenomena [47]. To understand the role of the Fock terms, PKO2, which contains the σ-scalar (σ-S), ω-vector (ω-V), and ρ-vector (ρ-V) couplings, was set to share the same degrees of freedom as popular RMF Lagrangians. PKO1 additionally considers the π-pseudo-vector (π-PV) coupling, which is gradually enhanced in PKO3, and PKA1 further considers the ρ-T coupling [automatically the ρ-vector-tensor (ρ-VT) couplings], which implements the meson exchange diagram of nuclear force. Note that the π-PV and ρ-T couplings contribute almost fully via the Fock terms, which are considered the exchange degrees of freedom.

An early study established that the Fock terms can significantly enhance the isovector contributions of the energy functional [48]. Practically, the modeling of nuclear binding remains largely unaltered from the RMF models to the PKO series [43, 49], providing a comparable description of the PSS restoration in nuclear structures [50]. However, owing to the strong ρ-T coupling, the in-medium balance between nuclear attractive and repulsive interactions, which determines the binding of nucleus, is significantly altered from the popular RMF and PKO models to PKA1 [49]. Consequently, PKA1 correctly restores the PSS for the high-l states, which eliminates the spurious shell closures $ {{N(Z)}} = 58 $ and $ 92 $ predicted by the RMF and PKO calculations [44, 49, 51]. Thus, the development of new Lagrangians DD-LZ1 [52] and PCF-PK1 [53] was prompted, with restored PSS for the high-l states and eliminated spurious shell closures.

Recently, both the RHF and RHFB theories have been extended to accommodate axially deformed nuclei, leading to the D-RHF and D-RHFB models [54, 55], respectively. In particular, both the π-PV and ρ-T couplings associated with the exchange correlations have been shown to exert a considerable influence on deformed nuclei [54−56]. The D-RHFB model with PKA1 [44] has been demonstrated to reproduce both the even-parity g.s. and halo structure [56] and has been used to elucidate the coherence between the parity inversion and the halo/cluster structures in $ ^{11} {\rm{Be}}$ [57]. More recently, the RHF theory has been extended to include the configuration interactions, leading to the configuration-interaction relativistic Hartree-Fock (CI-RHF) model [58]. We must highlight that the configuration interactions are constrained by an existing Lagrangian, such as PKA1, in a manner analogous to that employed in Refs. [59−63]. Thus, using the same Lagrangian, a robust methodology for an insight into the g.s. and the low-lying excitations is obtained from the combination of the D-RHFB and CI-RHF models, as well as for the underlying mechanism responsible for the island of inversion properties exhibited by $ ^{32} {\rm{Mg}}$.

The remainder of this paper is organized as follows. In Sec. II, the CI-RHF model is introduced briefly, with comments on the relation to D-RHFB calculations. The low-lying excitation properties and g.s. deformation of $ ^{32} {\rm{Mg}}$ are discussed in Sec. III, with a special focus on the relation between the breaking of the PSS predicted for spherical $ ^{32} {\rm{Mg}}$ and the island of inversion properties of $ ^{32} {\rm{Mg}}$. Finally, the conclusions and perspectives are given in Sec. IV.

In this section, we briefly introduce the CI-RHF model [58]. Similar to the conventional shell model, the CI-RHF calculations are restricted to a truncated Hilbert space, namely the model space, on top of a frozen doubly magic core. Consequently, an effective Hamiltonian is introduced to account for the configurations excluded from the model space. Note that the model space is constructed on the single-particle basis given by the spherical RHF calculations, and then, the energy of the frozen core is consistently determined.

Starting with a complete set of single-particle basis, the pairing, quadrupole, and octupole correlations can be captured through the configuration mixing in a relatively small model space, namely the P-space:

where $ \left|{\text{core}}\right> $ represents the frozen core, and the creation operators ($ c^\dagger $) are restricted within the valence space. However, owing to the limited model space, an effective Hamiltonian must be considered to incorporate the important correlations associated with the configurations excluded from the model space. To account for the cross-shell excitation, we apply the extended Kuo-Krenciglowa (EKK) method [64, 65] to derive the multi-shell effective Hamiltonian for the CI-RHF calculations:

where the sum on the right side is the folded terms, the index l represents the step of the iterations, and the Bloch-Horowitz Hamiltonian is defined as $ H^{\text{BH}}(E) = PH_{0}P + \widehat{Q}(E) $, where $ H_{0} $ is the unperturbed Hamiltonian. Correspondingly, the effective interaction $ V^{\text{eff}} $ can be calculated as $ V^{\text{eff}} = H^{\text{eff}}- PH_0P $. In practice, the $ \widehat Q $-box is frequently approximated as an expansion around $ H_0 $:

The effective Hamiltonian $ H^{\text{eff}} $ in Eq. (2) is independent of the starting energy $ E_{0} $. Therefore, we may tune the value of $ E_{0} $ to avoid the divergences of energy denominator in the $ \widehat{Q} $-box. In the practical calculations of $ \widehat{Q} $-box, we consider only the second-order core-polarization corrections to 80 MeV in the single particle energy [58]. Moreover, the folding terms with $ k\ge10 $ are terminated in Eq. (2).

Beyond the Hartree-Fock level, the main components of pairing, quadrupole, and even octupole correlations can be naturally included through configuration mixing in the model space. Meanwhile, the correlations associated with high-energy particle-hole excitations, which are excluded from the model space, are incorporated by the effective Hamiltonian. Thus, we expect that the CI-RHF model provides a reasonable description of the low-lying excitations. In the D-RHFB model, the RHF mean field and pairing correlations are treated within the Bogoliubov scheme in a unified manner [55]. In the intrinsic framework, the quadruple correlations are considered with the presence of quadruple deformation. This, to a certain extent, indicates some consistency between the D-RHFB and CI-RHF calculations, particularly with the same Lagrangian. In particular, the g.s. and low-lying excitations can be well described by the CI-RHF model, whereas the D-RHFB model can provide us an intuitive deformation picture. Consequently, we must understand the nature of the island of inversion exhibited by $ ^{32} {\rm{Mg}}$ through the application of the CI-RHF and D-RHFB models.

In this study, the RHF Lagrangians PKOi ($ i = 1,2,3 $) [43, 46] and PKA1 [44] are utilized in both the D-RHFB and CI-RHF calculations. To provide a more complete understanding, we also perform the D-RHFB calculations with the RMF Lagrangian DD-ME2 [66] and DD-LZ1 [52] for the nucleus of interest, $ ^{32} {\rm{Mg}}$. However, because the Fock terms are missing, it is difficult to expect that the off-diagonal two-body interaction matrix elements (TBMEs), namely $ \bar V_{abcd} = V_{abcd}-V_{abdc} $, can be properly evaluated with the RMF Lagrangians, such as DD-ME2 and DD-LZ1, in which the exchange correlations are incorporated phenomenologically by the parameterizations, rather than an explicit treatment. Therefore, the RMF Lagrangians will not be applied in the current CI-RHF calculations.

Within the D-RHFB model, the Bogoliubov quasi-particle orbits, as well as the canonical single-particle ones, are expanded on the spherical Dirac Wood-Saxon (DWS) basis [67]. The details of the space truncations are available in Ref. [55]. Moreover, the central part of the finite-range Gogny force D1S [68] is utilized as the pairing force in the D-RHFB calculations. For the CI-RHF calculations of $ ^{32} {\rm{Mg}}$, the neutron (ν) valence orbits include both the $ sd $ ($ \nu2s_{1/2} $, $ \nu1d_{3/2} $ and $ \nu1d_{5/2} $) and $ pf $ orbits ($ \nu1f_{7/2} $ and $ \nu2p_{3/2} $) to account for the cross-shell excitation, and the proton valence space is set as the $ sd $ shell, on top of the frozen core $ ^{16} {\rm{O}}$.

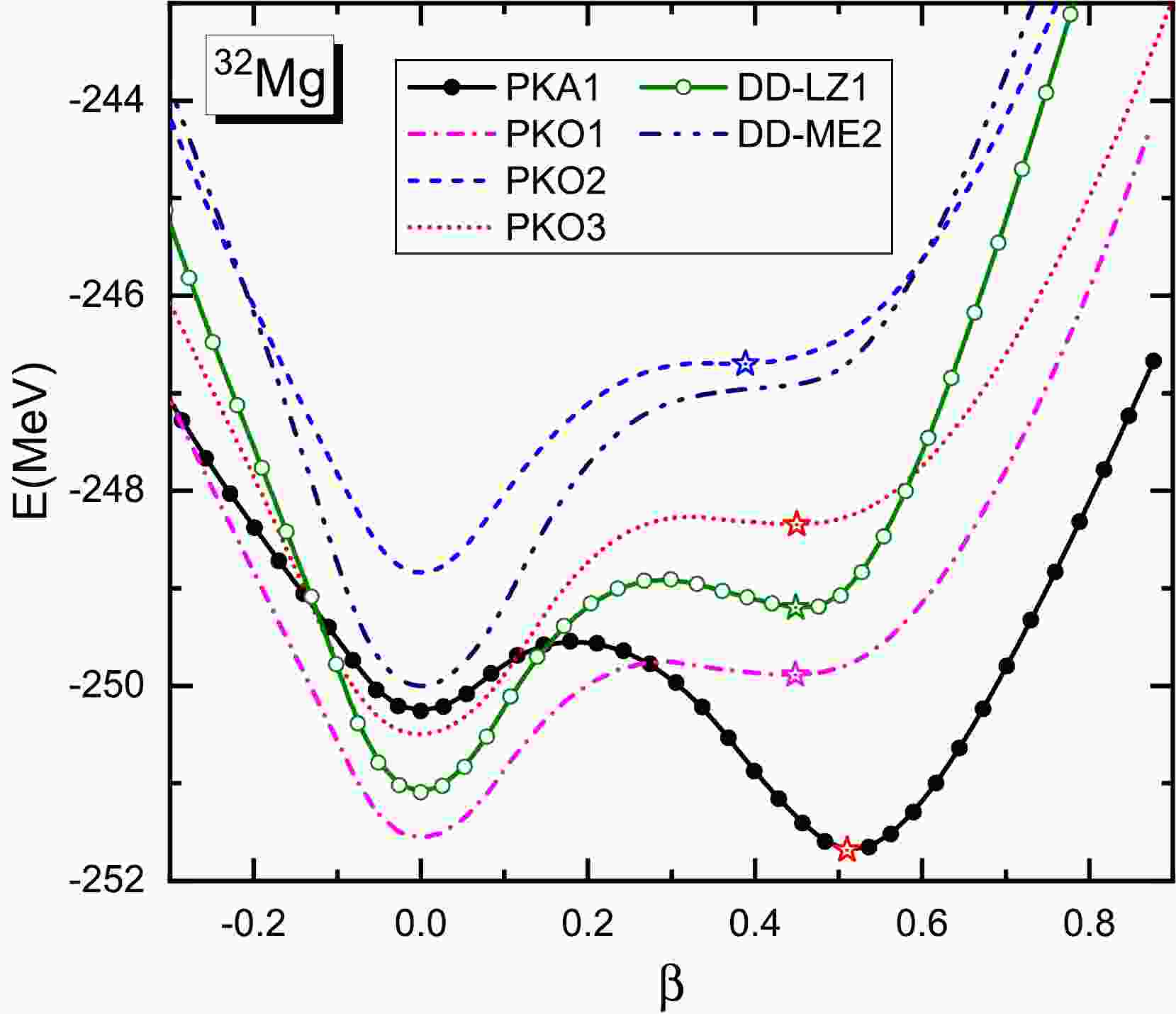
Figure 1 shows the total energies E (MeV) as functions of the quadruple deformation β, given by the shape-constrained D-RHFB calculations. We observe that PKA1 produces a clear global prolate minimum, displaying a stable deformation for the g.s. of $ ^{32} {\rm{Mg}}$. In particular, the deformation given by PKA1 agrees closely with the experimental values of $ \beta = 0.512(44) $ [3] and $ \beta = 0.51(3) $ [18]. In contrast, all the other selected Lagrangians predict spherical global minima and a shoulder-like structure or weak local minimum with prolate deformation. The deformed calculation with the Lagrangian PCF-PK1 [53] does not support a stable deformation for the g.s. of $ ^{32} {\rm{Mg}}$, either. We also observe in Fig. 1 that the RMF Lagrangian DD-LZ1 [52] presents a more visible prolate minimum compared with the other selected models except PKA1. In contrast, as indicated by the AMP calculations [24, 26], a global deformed minimum for $ ^{32} {\rm{Mg}}$ can be produced with these Lagrangians if we further consider the correlations beyond the D-RHFB scheme.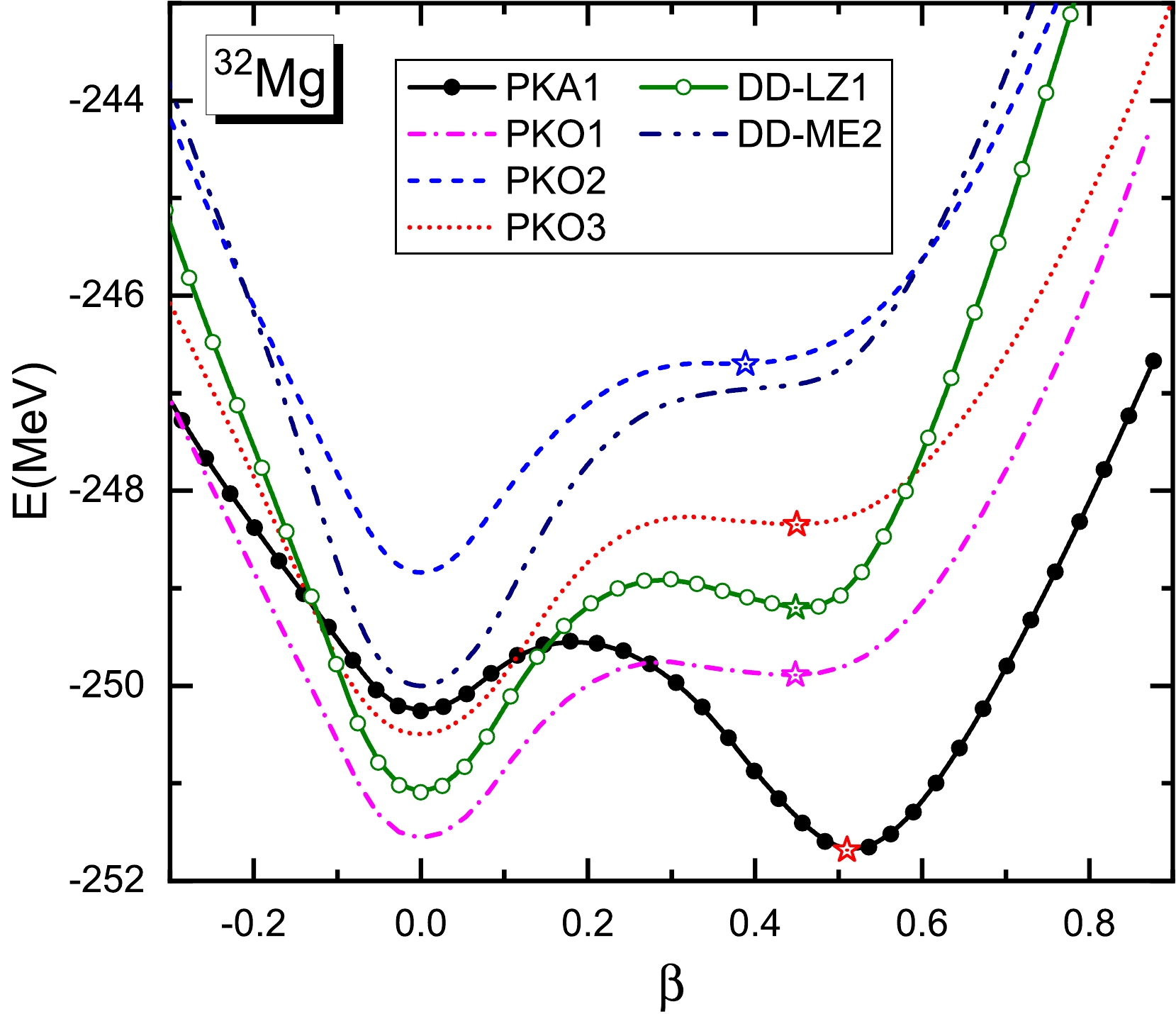

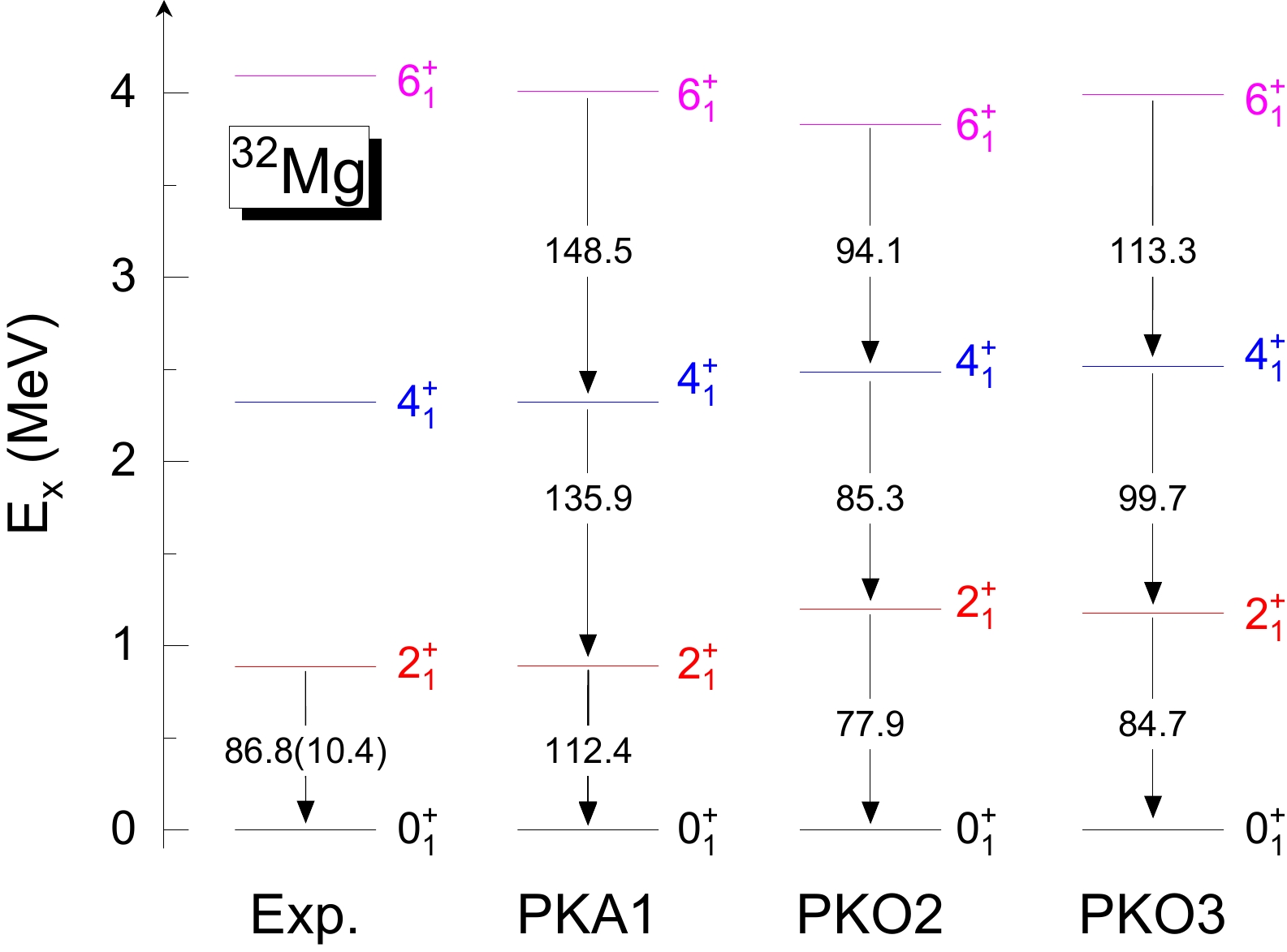
Figure 1.  (color online) Total energies E (MeV) of ³²Mg as functions of the quadruple deformation β given by the D-RHFB calculations with the RHF Lagrangians PKA1 and PKOi ($i = 1,2,3$) and the RMF Lagrangians DD-ME2 and DD-LZ1. The stars denote the prolate minima.

Figure 2 depicts the low-lying excitation spectra and reduced transition probabilities $ B(E2) $ given the CI-RHF calculations with PKA1, PKO2, and PKO3 compared with the experimental data [15, 19, 69]. The $ B(E2) $ values are calculated with the effective charges 1.35 and 0.35 for protons and neutrons, respectively [22]. The results of PKO1 are not shown owing to them having a description similar to that of PKO3. Moreover, Table 1 lists the numbers of neutrons populating the valence orbits for the g.s. $ 0_1^+ $. For better understanding, the ratios $ R = E(4_1^+)/E(2_1^+) $ are also shown in the last column of Table 1. As shown in Fig. 2 and Table 1, the experimental measurements, including the low-lying spectrum, the ratio R, and $ B(E2: 2_1^+\to 0_1^+) $, indicate a rotational collectivity rather than a vibrational one for $ ^{32} {\rm{Mg}}$. The low-lying excitation energies and R given by PKA1 are in excellent agreement with the experimental data [19, 69]. With reference to the most recently reported value [15], PKA1 overestimates the $B(E2: 2_1^+\to 0_1^+)$ value but is more consistent with the earlier measured value of 124.4(18.0) $ e^2 $fm⁴ [21]. In particular, a notable cross-shell excitation is predicted by PKA1 for the g.s. $ 0_1^+ $, with about two neutrons populating the $ pf $ shell. It supports a deformed g.s. for $ ^{32} {\rm{Mg}}$, being consistent with global prolate minimum given by the PKA1 results in Fig. 1. Consistently, the CI-RHF and D-RHFB calculations with PKA1 yield similar intrinsic electric quadruple momentums $ Q^i $, $ 68.9 $ efm² and 65.8 efm², respectively. These results are consistent with the previous shell model calculations [22, 23]. Moreover, PKA1 predicts a considerable neutron population on the $ 2p_{3/2} $ orbit. Note that the measured cross section of the g.s. of $ ^{32} {\rm{Mg}}$ can only be reproduced with a discernible $ 2p_{3/2} $ contribution [69].

Figure 2.  (color online) Low-lying excitation spectra and reduced transition probabilities $B(E2)$ (in $e^2\text{fm}^4$) of ³²Mg given by the CI-RHF calculations with PKA1, PKO2, and PKO3 compared with the experimental data [15, 19, 69].

	$1d_{5/2}$	$2s_{1/2}$	$1d_{3/2}$	$1f_{7/2}$	$2p_{3/2}$	R
$\text{PKA}$1	5.75	1.91	2.27	1.50	${\bf{0.56}}$	2.61
$\text{PKO}$2	5.73	1.92	2.38	1.81	0.16	2.07
$\text{PKO}$3	5.73	1.92	2.56	1.57	0.23	2.14

Table 1.  Numbers of neutrons populating the $sd$ and $pf$ orbits for the $0_1^+$ state of ³²Mg given by the CI-RHF calculations with PKA1, PKO2, and PKO3. The ratio $R = E(4_1^+)/E(2_1^+)$ is also shown in the last column, and the experimental value is $2.62$ [19, 69].

In contrast, Table 1 and Fig. 2 show that PKO2 and PKO3 predict not only a notable cross-shell excitation from the $ sd $ to the $ pf $ shells for the g.s. $ 0_1^+ $ but also fairly large values of $ B(E2:2_1^+\to0_1^+) $. Specifically, these $ B(E2) $ values are consistent with the reported measurements of 90.8(15.6) $ e^2 $fm⁴ [3], 66.6(15.6) $ e^2 $fm⁴ [16], 89.4(11.4) $ e^2 $fm⁴ [18], and 86.8(10.4) $ e^2 $fm⁴ [15] but are smaller than the value 124.4(18.0) $ e^2 $fm⁴ reported in Ref. [21]. In contrast to the weak local minima in Fig. 1, these results also support a deformed g.s. for $ ^{32} {\rm{Mg}}$ after implementing the many-body correlations within the CI-RHF scheme. However, as shown in the last column of Table 1, the R-values given by PKO2 and PKO3 are close to the vibration limit ($ 2.0 $), which indicates nearly pure vibration collectivity for $ ^{32} {\rm{Mg}}$. This is consistent with the calculations of the AMP based on the RMF approach [70]. Meanwhile, the low-lying spectra given by PKO2 and PKO3 in Fig. 2 are nearly equally spaced, representing a typical feature of the vibration band. Thus, we deduce that the CI-RHF calculations with both PKO2 and PKO3 predict a soft deformation for $ ^{32} {\rm{Mg}}$, which is not as stable as indicated by the measured low-lying excitation spectrum [19].

To provide an insight into the g.s. deformation and the collectivity of $ ^{32} {\rm{Mg}}$, Table 2 lists the contributions (MeV) of the energy functional, as given by the D-RHFB calculations with PKA1, PKO3, and DD-LZ1, where the first and second rows for each Lagrangian correspond to the spherical and deformed minima, respectively. Evidently, the total bindings described by PKA1, PKO3, and DD-LZ1 are not significantly different for $ ^{32} {\rm{Mg}}$. As shown in Table 2, the modeling of nuclear binding remains largely unaltered from DD-LZ1 to PKO3, although the isovector contributions in PKO3 are enhanced by the Fock terms. However, the contributions of the ρ-couplings in PKA1, owing to the ρ-T and ρ-VT couplings, become competitive with the interplay of the strong attractive σ-S and repulsive ω-V couplings. Note that the $ E_\rho $ term described by PKA1 is reduced from the spherical to the deformed cases, whereas the $ E_{\sigma+\omega} $ term is significantly enhanced, leading to the deformed g.s. for $ ^{32} {\rm{Mg}}$. This reveals that the modeling of nuclear binding undergoes a significant alteration with the presence of the Fock terms, particularly for the exchange degrees of freedom associated with the ρ-T and ρ-VT couplings.

	$E_{\text{kin.}}$	$E_{\sigma+\omega}$	$E_\rho$	$E_\pi$	$E_{\text{oth.}}$	E
PKA1	400.8	$-$417.0	$-$217.5	$-$31.5	14.9	$-$250.2
	409.6	$-$434.4	$-$214.4	$-$29.9	17.4	$-$251.7
PKO3	438.1	$-$606.1	$-$59.7	$-$37.2	14.4	$-$250.5
	448.7	$-$616.3	$-$59.2	$-$36.1	14.6	$-$248.3
DD-LZ1	412.6	$-$701.3	18.3	$-$	19.4	$-$251.1
	414.1	$-$702.7	17.6	$-$	21.8	$-$249.2

Table 2.  Contributions (MeV) of the energy functional E, including the kinetic term $E_{\text{kin.}}$, sum of the isoscalar σ-S and ω-V couplings, isovector ρ- and π-couplings, and others $E_{\text{oth.}}$ for the sum of the other channels, namely, the Coulomb field, pairing correlations, and center-of-mass corrections. The results are given by the D-RHFB calculations with PKA1, PKO3, and DD-LZ1, where the first and second rows correspond to the spherical and deformed minima, respectively.

As an extensive illustration beyond the Hartree-Fock-Bogoliubov level, Fig. 3 shows the main $ sd $-to-$ pf $ cross matrix elements as given by PKA1 (left pillars), PKO3 (middle pillars), and PKO2 (right pillars). The contributions from the exchange degrees of freedom, namely, the ρ-T (automatically including ρ-VT) and π-PV couplings, are indicated by the patterns, and the black color represents the sum of the dominant channels (d.c.), which includes the degrees of freedom considered in the popular RMF models and PKO2, namely, the σ-S, ω-V, and ρ-V couplings. In particular, the black bars overlapping the red patterns indicate the cancellations between the d.c. and the ρ-T coupling, and the length of the pillars, after the cancellations, represents the total results.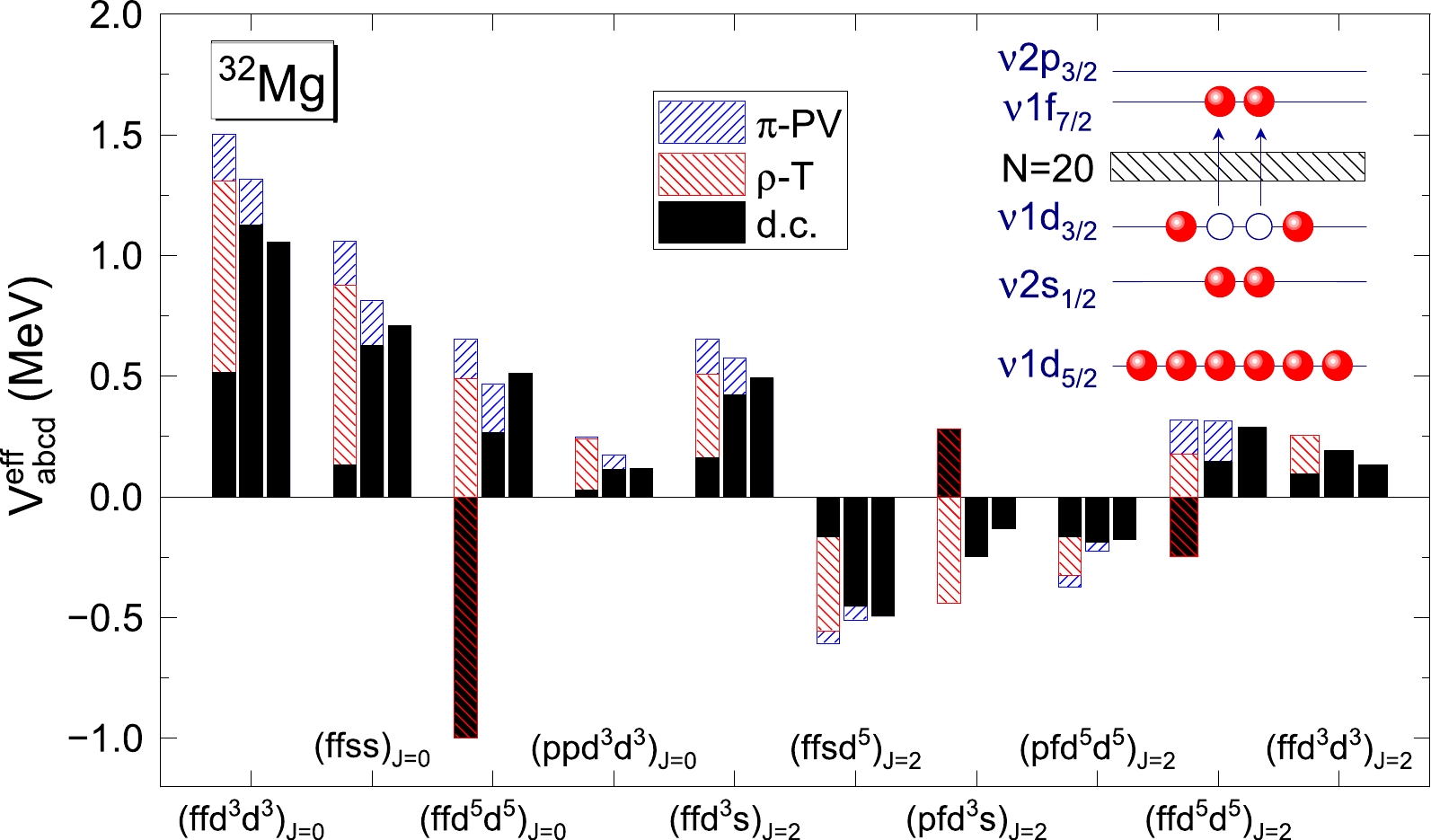

Figure 3.  (color online) Schematic of the cross-shell excitation and the main $sd$-to-$pf$ cross-shell matrix elements given by PKA1 (left pillars), PKO3 (middle pillars), and PKO2 (right pillars), where f, p, s, $d^{3}$, and $d^{5}$ represent the neutron orbits $1f_{7/2}$, $2p_{3/2}$, $2s_{1/2}$, $1d_{3/2}$, and 1$d_{5/2}$, respectively. The dominant channel (d.c.) contains the σ-S, ω-V, and ρ-V couplings.

As shown in Fig. 3, the configuration interactions given by PKA1 are predominantly shaped by the ρ-T coupling. Moreover, the π-PV coupling also makes discernible contributions, despite its relatively weak coupling strength [44, 46]. With the presence of the π-PV coupling, the d.c. contributions are slightly changed from PKO2 to PKO3 but are notably reduced for (ff$ \text{d}^5\text{d}^5 $)$ _{J = 0} $ and (ff$ \text{d}^5\text{d}^5 $)$ _{J = 2} $. This indicates the significance of the π-PV coupling in determining some configuration interactions. Furthermore, for PKA1, which incorporates the ρ-T and ρ-VT couplings, the contributions of the d.c. are remarkably changed from PKO3 for most cases. This is consistent with the underlying alteration of the nuclear binding in Table 2, where the sum of the dominant σ-S and ω-V contributions is reduced significantly from PKO3 to PKA1. In particular, for (ff$ \text{d}^5\text{d}^5 $)$ _{J = 0} $, (ff$ \text{d}^3\text{d}^5 $)$ _{J = 2} $, and (ff$ \text{d}^5\text{d}^5 $)$ _{J = 2} $, notable cancellations appear between the contributions from the d.c. and the ρ-T and π-PV couplings. This indicates that the exchange degrees of freedom associated with the π-PV and ρ-T couplings can exert even more important effects in determining the configuration interactions compared with the modeling of nuclear binding at the Hartree-Fock-Bogoliubov level, as shown in Table 2. Furthermore, this also demonstrates the significance of the Fock terms, particularly the exchange degrees of freedom that are absent at the Hartree level.

As discussed earlier, the exchange degrees of freedom play a significant role in determining both the nuclear binding and configuration interactions. However, the reason PKA1 predicts a stable deformation and consistent collectivity with the experimental measurements whereas the PKO models prefer a near pure vibration collectivity with soft quadruple deformation for $ ^{32} {\rm{Mg}}$ is not easy to understand. This necessitates a further investigation on the microscopic single-particle structure given by the D-RHFB calculations.

Based on the results in Table 1, the cross-shell excitation supports the occurrence of the deformation for the g.s. of $ ^{32} {\rm{Mg}}$ under the CI-RHF scheme. Among the selected Lagrangians, PKA1 achieves an excellent agreement with the experimental data for both the deformation and the low-lying excitation energies. In contrast, regarding the ratio $ R = E(4_1^+)/E(2_1^+) $ in Table 1 and the low-lying spectra in Fig. 2, PKO2 and PKO3 predict a vibration band for $ ^{32} {\rm{Mg}}$. To better understand the nature of the island of inversion exhibited by $ ^{32} {\rm{Mg}}$, Fig. 4 shows the evolution of neutron canonical single-particle orbits with respect to the deformation β. The results are extracted from the D-RHFB calculations with PKA1 (solid lines) and PKO3 (dashed lines), the representatives of the selected models.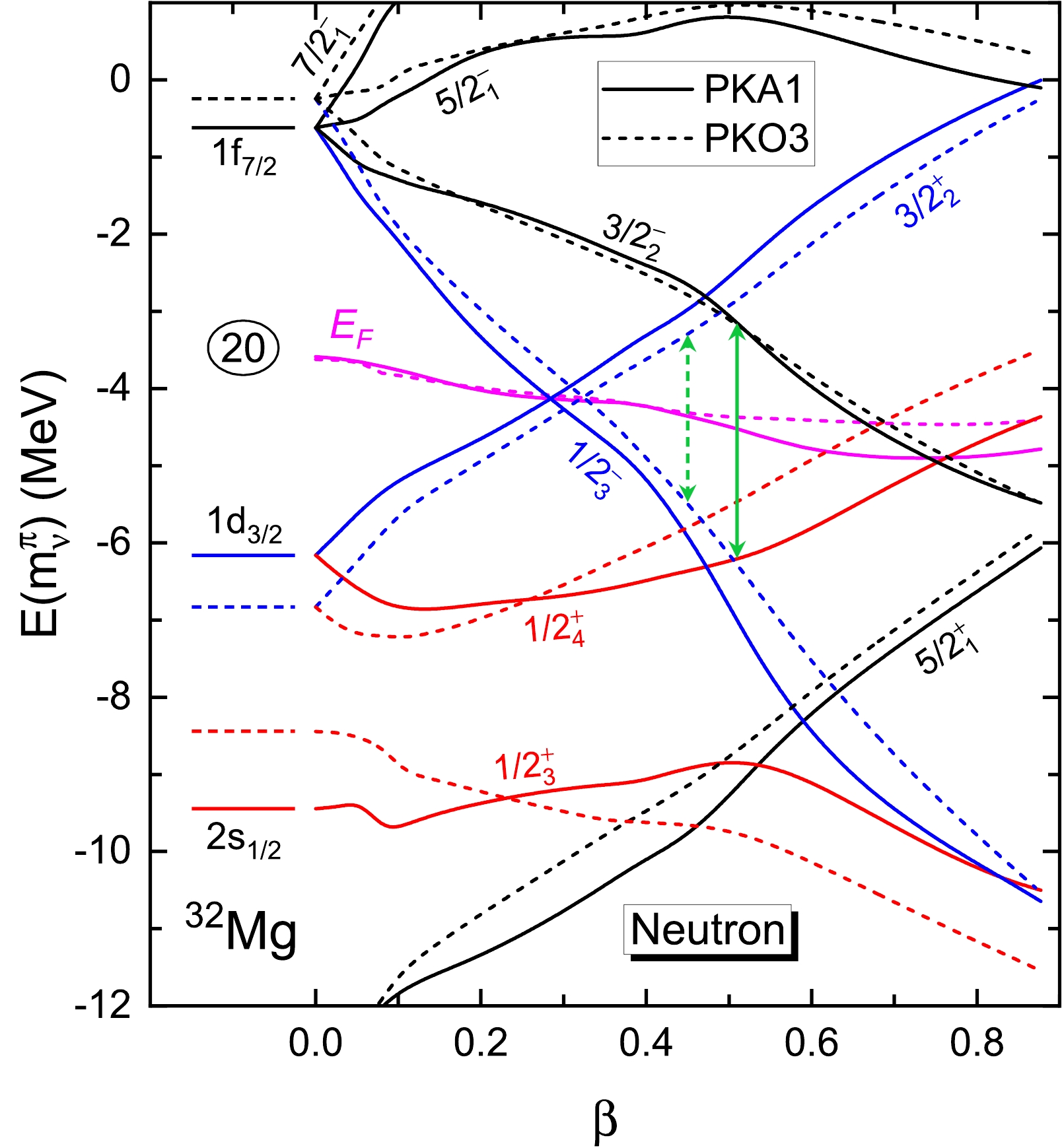

Figure 4.  (color online) Neutron canonical single-particle energies of ³²Mg as functions of the deformation β, as given by PKA1 (solid lines) and PKO3 (dotted lines). The arrows mark the shell gap at the prolate minima ($\beta = 0.51$ for PKA1 and $0.45$ for PKO3).

As shown in Fig. 4, the intrusion of the $ pf $ shell, namely, the $ 1/2_3^- $ orbit, is observed in both the PKO3 and PKA1 results. This intrusion is consistent with the $ sd $-to-$ pf $ cross-shell excitation given by the spherical CI-RHF calculations in Table 1. Moreover, because of the smaller spherical shell gap of $ N = 20 $, an accelerated intrusion of the $ 1/2_3^- $ orbit is predicted by PKA1 compared with PKO3, which results in an earlier intersection of the orbits $ 1/2_3^- $ and $ 3/2_2^+ $. This, to a certain extent, is meaningful for the occurrence of a stable deformation in $ ^{32} {\rm{Mg}}$. More significantly, PKA1 presents a much flatter shape evolution than PKO3 for both the orbits $ 1/2_3^+ $ and $ 1/2_4^+ $, which branch from the pseudo-spin (PS) partners $ 2s_{1/2} $ and $ 1d_{3/2} $. In particular, the $ 1/2_4^+ $ orbit described by PKA1 remains more deeply bound than the spherical $ 1d_{3/2} $ state before reaching the global minimum. Thus, PKA1 produces a more notable shell gap (marked in arrows) at the prolate minimum than PKO3. Although much less pronounced than the spherical one $ N = 20 $, this notable shell gap is still essential for stabilizing the g.s. deformation of $ ^{32} {\rm{Mg}}$. Accordingly, as indicated by the PKA1 results in Fig. 1, the energy of the system is predicted to increase rapidly when the deformation deviates from the prolate minimum. This explain why the nucleus $ ^{32} {\rm{Mg}}$ described by PKA1 exhibits the rotational rather than the vibrational collectivity, which is consistent with the low-lying spectra in Fig. 2.

To provide a deep understanding for the occurrence of a stable deformation in $ ^{32} {\rm{Mg}}$, Fig. 5 (a) shows the quadruple moment $ Q_2 $ (fm$ ^{2} $) as a function of the deformation β for both neutron orbits $ 1/2_{3}^+ $ and $ 1/2_{4}^+ $, and Fig. 5 (b) shows the proportions of main spherical DWS waves in the orbit $ 1/2_{4}^+ $. It is known well that the mixture of spherical waves subsequent to the deformation is sensitive to the presence of a spherical shell gap. As shown on the left of Fig. 4, PKA1 yields a much more distinct splitting between the spherical PS partners ($ 1d_{3/2} $, $ 2s_{1/2} $) than PKO3, thereby illustrating a notable breaking of the PSS. Consequently, as shown in Fig. 5 (b), this prevents the mixture of the $ 2s_{1/2} $ wave into the $ 1/2_4^+ $orbit as described by PKA1. Similarly, the mixture of the $ 1d_{3/2} $ wave into the $ 1/2_3^+ $ orbit predicted by PKA1 is less than that by PKO3. Consistently, the $ Q_2 $ values given by PKA1 and PKO3 differ significantly for both the $ 1/2_3^+ $ and $ 1/2_4^+ $ orbits, as shown in Fig 5 (a).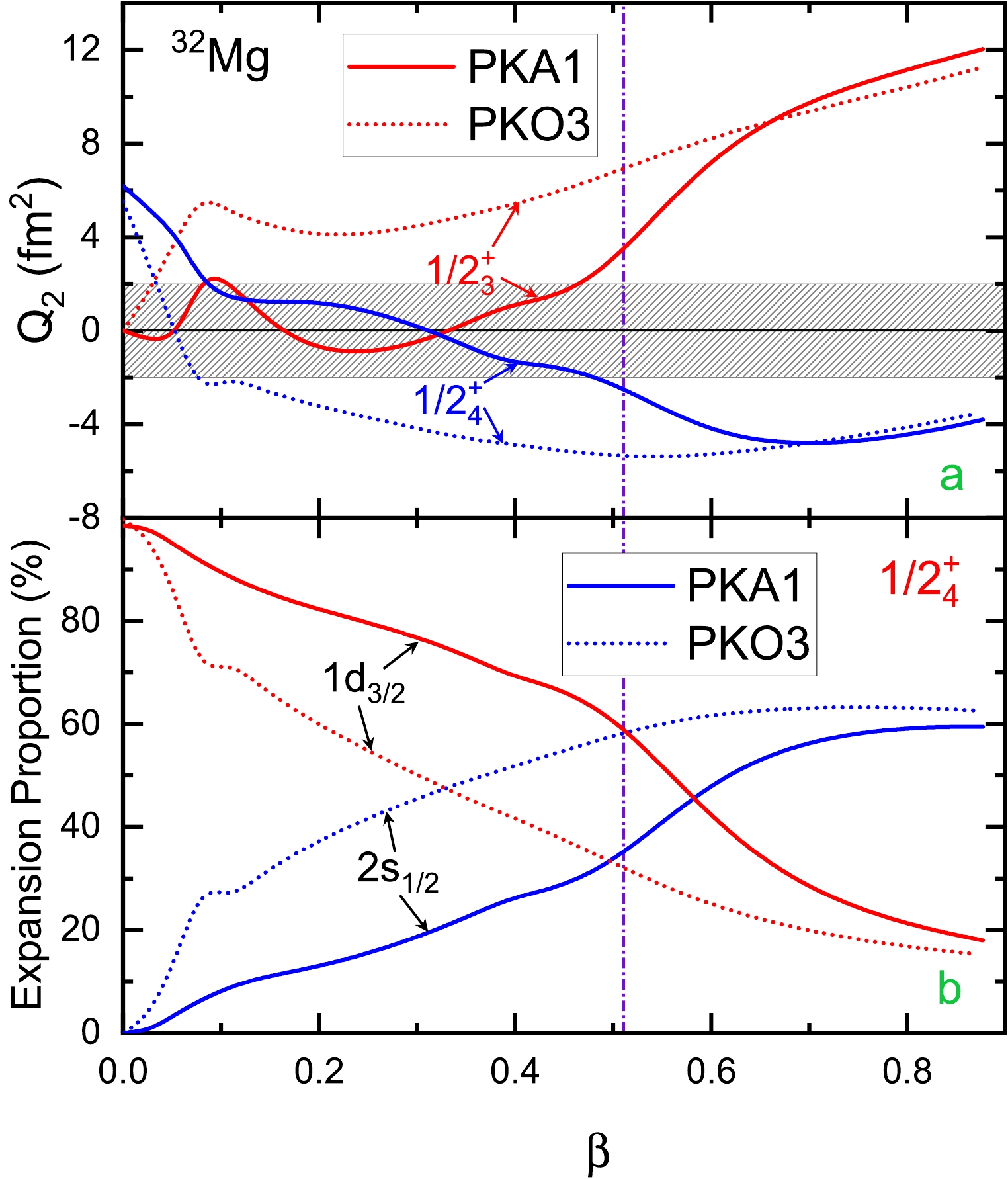

Figure 5.  (color online) Quadruple moment $Q_2$ (fm²) for neutron orbits $1/2_{3}^+$ and $1/2_{4}^+$ (plot a) and the proportions (in percentage) of main spherical DWS waves in the orbit $1/2_{4}^+$ of ³²Mg as given by PKA1 (solid lines) and PKO3 (dotted lines).

Combined with the $ Q_2 $ values in Fig. 5 (a), the shape evolutions of the $ 1/2_3^+ $ and $ 1/2_4^+ $ orbits in Fig. 4 are easily understood. As deduced from the $ Q_2 $ values in Fig. 5 (a), PKO3 predicts the $ 1/2_4^+ $ orbit exhibiting oblate distribution, which thus becomes increasingly less bound when the nucleus $ ^{32} {\rm{Mg}}$ is increasingly prolately deformed, and vice versa for the $ 1/2_3^+ $ orbit. However, both the $ 1/2_3^+ $ and $ 1/2_4^+ $ orbits described by PKA1 exhibit near spherical nature before reaching the prolate minimum. Consistently, as shown in Fig. 4, both the $ 1/2_3^+ $ and $ 1/2_4^+ $ orbits described by PKA1 exhibit much flattened shape evolutions. The flat evolution of the $ 1/2_4^+ $ orbit is essential for producing the distinct deformed shell gap and further the stable deformation in $ ^{32} {\rm{Mg}}$.

As previously stated, the cross-shell excitation or the $ pf $ intrusion is essential for the occurrence of a deformation in $ ^{32} {\rm{Mg}}$. In addition, the stability of the deformation, which plays a crucial role in determining the collectivity of $ ^{32} {\rm{Mg}}$, is intrinsically connected with the PSS breaking between neutron spherical PS partners $ (2s_{1/2}, 1d_{3/2}) $. Thus, a new insight into the nature of the island of inversion exhibited by $ ^{32} {\rm{Mg}}$ is implemented from the PSS breaking, which is a consequence of nuclear binding as indicated by the PSS conditions [40, 41]. Moreover, as shown in Table 2 and Fig. 3, the ρ-T couplings are essential in determining both the nuclear binding and the configuration interactions. This also reveals the role of the exchange degrees of freedom in determining the island of inversion properties of $ ^{32} {\rm{Mg}}$.

In contrast, the Lagrangians PCF-PK1 and DD-LZ1 can properly restore the PSS for the high-l states as PKA1 [52, 53]. However, PCF-PK1, as well as DD-ME2, PKO1, and PKO2, presents similar descriptions of the splitting of the PS partners $ (1d_{3/2},2s_{1/2}) $ and the $ N = 20 $ shell in spherical $ ^{32} {\rm{Mg}}$. Thus, we do not expect PCF-PK1 to provide a description equivalent to that provided by PKA1 for the nucleus of interest,$ ^{32} {\rm{Mg}}$. In contrast, similar to PKA1, DD-LZ1 produces notable PSS breaking and flat shape evolutions for the deformed orbits $ 1/2_3^+ $ and $ 1/2_4^+ $. However, as mentioned earlier, the RMF Lagrangian DD-LZ1 is not a proper choice to derive an effective Hamiltonian for the CI-RHF calculations.

The nature of the island of inversion exhibited by the unstable nucleus $ ^{32} {\rm{Mg}}$, namely, a well-deformed ground state with vanishing neutron shell $ N = 20 $, is investigated through the application of the axially deformed relativistic Hartree-Fock-Bogoliubov (D-RHFB) and configuration-interaction relativistic Hartree-Fock (CI-RHF) models. Using the same Lagrangian PKA1, the D-RHFB and CI-RHF models adequately reproduce the stable deformation and low-lying excitations of $ ^{32} {\rm{Mg}}$ at the Hartree-Fock-Bogoliubov level and beyond, respectively. In addition to the picture of the $ pf $ intrusion or the cross-shell excitation, a new insight into the occurrence of a stable deformation in $ ^{32} {\rm{Mg}}$ is implemented from the breaking of the pseudo-spin symmetry (PSS). We find that, owing to the notable PSS breaking, a notable deformed shell gap is predicted by PKA1, which stabilizes the deformation of $ ^{32} {\rm{Mg}}$ and produces rotational collectivity, as revealed by the experimental measurements.

In particular, we show that the degrees of freedom associated with the exchange correlations, particularly the ρ-tensor coupling, present significant contributions to the nuclear binding and the configuration interactions, which are essential to producing the PSS breaking and cross-shell excitation for $ ^{32} {\rm{Mg}}$, respectively. This reveals the significance of exchange correlations in understanding the nature of the island of inversion, as well as for the binding of the nucleus, a fundamental problem in the field of nuclear physics. Finally, we comment that the CI-RHF calculation with PKA1 yields an excitation energy $ E(0_2^+) $ similar to that obtained with the shell model calculations with the SDPF-M interaction [22, 23], which deserves an extensive study in the future.