Growing evidence for a Higgs triplet

The established theoretical description of Nature at microscopic scales, the Standard Model (SM), with its gauge symmetry group $ SU(3)_c\times SU(2)_L\times U(1)_Y $ includes the strong, weak, and electromagnetic interactions of matter particles (spin-1/2 fermions) via mediators (spin-1 particles, called gauge bosons). The gauge bosons of the electromagnetic and strong interactions — the photon and gluons — are massless, while those of the weak interactions, the W and Z bosons, are heavy. ¹ The SM has been (with a few exceptions [1]) very successful in describing the results of the vast majority of particle physics experiments [2].

In 2012, the final missing particle of the SM, the Higgs boson, was observed by the ATLAS [3] and CMS [4, 5] collaborations at the Large Hadron Collider (LHC) at CERN. It is important to recall that this discovery took place several decades after the Higgs was predicted by the mechanism of spontaneous symmetry breaking via a scalar field, as proposed in 1964 by Brout and Englert [6], Higgs [7, 8] and Guralnik, Hagen and Kibble [9], and implemented in the SM by Glashow [10] Weinberg [11] and Salam [12]. The Higgs was so difficult to find because its mass of 125 GeV lies beyond the reach of electron-positron colliders like LEP [13] at CERN, and its suppressed production cross-section prevented an observation at the Tevatron [14] at Fermilab. In fact, the Higgs discovery at the LHC was only possible this time because its signal strengths are predicted by the SM, so CMS and ATLAS were able to combine the di-photon ($ \gamma\gamma $) with the 4-lepton channel. Furthermore, the obtained Higgs mass was consistent with the expectation from the global electroweak fit, which provided a search range and indirect confirmation that it is really the SM Higgs. This substantiates the importance of an ultraviolet-complete and predictive model as well as indirect hints for new particles to facilitate discovery in statistically limited searches.

On the theoretical side, the Higgs boson of the SM is an elementary scalar, a type of particle that had never been observed before. It gives masses to the W and Z bosons while keeping the theory renormalizable (i.e. theoretically consistent), as shown by 't Hooft and Veltman [15, 16] in 1971. Furthermore, the elementary fermions acquire their masses via their so-called Yukawa interactions with the Higgs field [11, 17], which is an essential requirement for the existence of complex structures and processes in our Universe.

However, the SM cannot be the ultimate theory of Nature. For example, it does not account for the fact that more gravitationally interacting matter than visible matter is observed at astrophysical scales, leading to the conjecture of the existence of Dark Matter. Non-vanishing neutrino masses necessitated by neutrino oscillations also require an extension of the SM. Furthermore, the dominance of matter over anti-matter in the universe cannot be explained, and the SM does not include gravity. Therefore, it should be considered an effective description that must be superseded by a more comprehensive theory. While no unambiguous direction for such an extension has been established, any heavy new physics poses a problem for fundamental scalar particles because they are subject to quantum corrections involving the corresponding scale, which can be many orders of magnitude larger than the electroweak (EW) scale ($ \sim 100 $ GeV). Therefore, the mass of the Higgs boson is puzzlingly small. Moreover, no theoretical principle or symmetry requirement guarantees the minimality of the SM Higgs sector. Solving these puzzles is part of the motivation for many new physics models and future experiments and accelerators.

Additional scalar bosons must play a subleading role in the spontaneous breaking of the weak interactions. One reason for this is that in the SM, the W mass can be calculated in terms of the Z mass and the weak and electromagnetic interaction strengths, and the result agrees well (on an absolute scale) with the corresponding measurement. Nonetheless, the W boson was found to be slightly heavier than expected by the CDF-II collaboration at Fermilab, which prefers a small new physics contribution. ² In this context, the scalar $S U(2)_L$ triplet with hypercharge 0 [27−34] is particularly interesting since it is the most minimal extension of the SM that predicts a positive definite shift in the W mass at tree-level (i.e. at leading order in the expansion of quantum corrections) [35−47]. Furthermore, it has been shown that it can lead to a strong first-order phase transition, [48−50] which is an essential ingredient of weak-scale Baryogenesis, a mechanism that can explain the matter-antimatter asymmetry in the universe. Last but not least, the so-called "multi-lepton anomalies" [1, 51] suggest the existence of a new scalar with a mass range of 140 GeV to 160 GeV [52−55] that decays dominantly to W bosons and is produced in association with lepton, bottom quarks, and missing energy [56]. Both the production and decay modes are in agreement with the $ Y=0 $ triplet hypothesis [57]. Importantly, these indirect hints for a new scalar reduce the look-elsewhere effect.

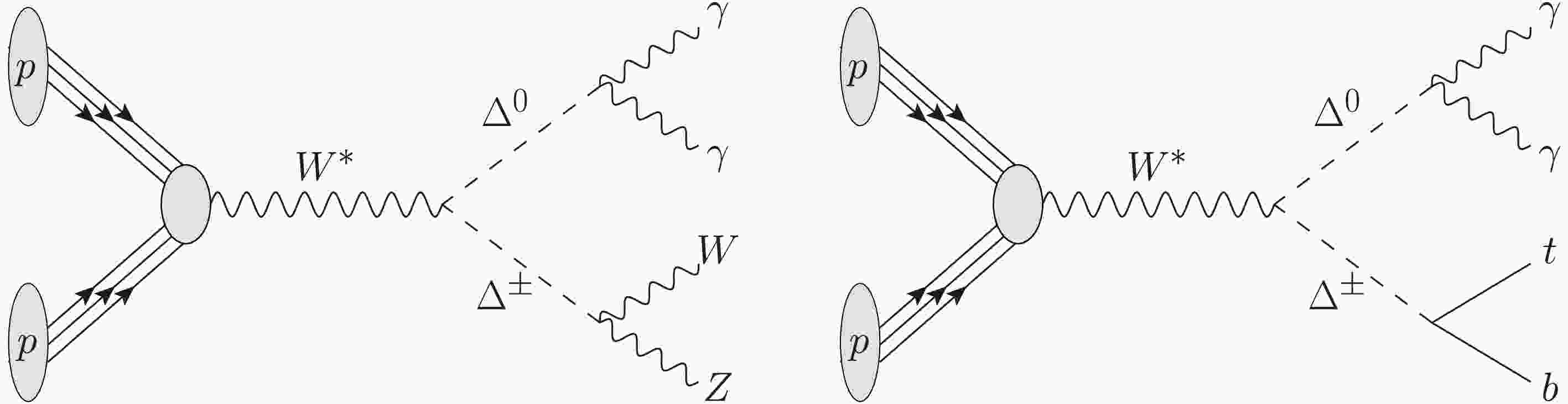
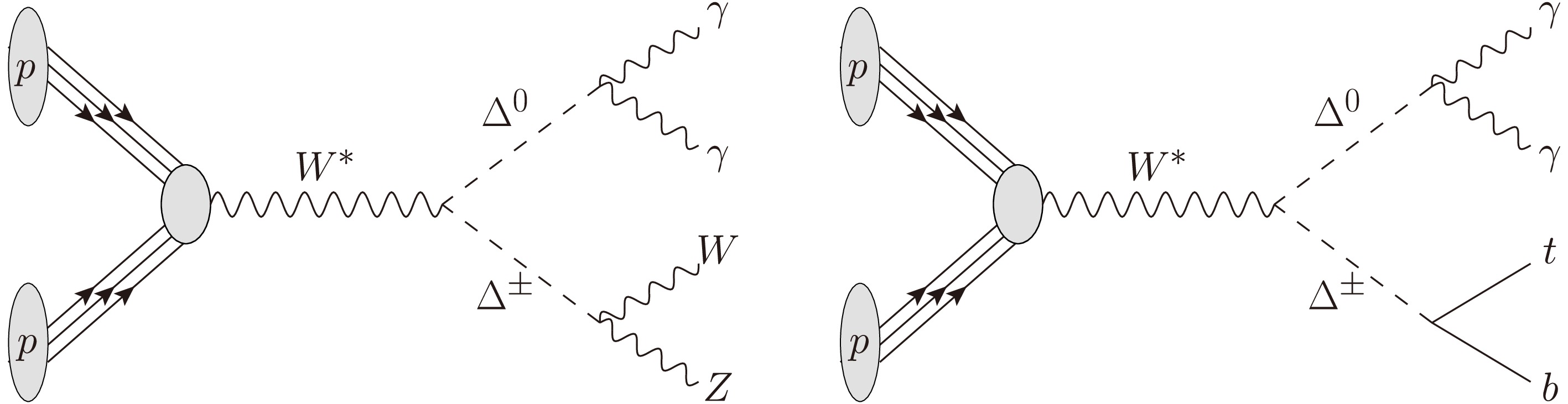
The SM extended by a $S U(2)_L$ triplet with zero hypercharge is a very predictive model since it contains (in addition to the SM) only one neutral and one charged scalar with no direct couplings to SM fermions. This leads to suppressed production rates, allowing it to evade LEP and current LHC bounds [58]. However, it has distinct collider signatures due to its unavoidable production in proton-proton collisions via off-shell EW gauge bosons and the photon, called Drell-Yan production. This leads to the associated production of di-photons with leptons, missing energy, and/or jets [57] (see Fig. 1). Note that searching for these exclusive signatures significantly improves the new physics sensitivity by reducing the SM backgrounds owing to the requirement of additional particles in the final state.

Figure 1.  Feynman diagrams showing the Drell-Yan production and decays of the triplet Higgses: $ pp\to W^*\to (\Delta^{\pm}\to tb, WZ)(\Delta^{0}\to\gamma\gamma) $, which we search for using the side-bands of the SM Higgs analyses of ATLAS [59, 60].

In this article, we search for the scalar triplet in associated production channels with di-photons in the mass range suggested by the multi-lepton anomalies. For this, we use the comprehensive ATLAS analysis of Ref. [59] as well as the latest result for di-photons plus single tau and single lepton channels of Ref. [60] presented at the Moriond conference. ³

The SM supplemented by a $S U(2)_L$ triplet scalar with hypercharge 0 is commonly referred to as the ΔSM [27−34]. ⁴ During spontaneous electroweak symmetry breaking, the $S U(2)_L$ doublet SM Higgs and the triplet Higgs acquire their vacuum expectation values of v and $ v_\Delta $, respectively. While the former gives rise to both $ m_W $ and $ m_Z $, the latter contributes only to $ m_W $; it is thus said to violate the custodial symmetry. More specifically, it leads to a positive definite shift in $ m_W $:

w.r.t. the SM prediction [2]. This is in agreement with the current global average for the W mass by the LHC-TeV MW Working Group [62], which indicates a positive effect of 44.7 MeV with a significance of $ 3.5\sigma $. This implies that$ v_\Delta \sim \mathcal{O}({\rm{GeV}}) $ such that $ v_\Delta\ll v $. Note that the exact value for $ v_\Delta $ is immaterial for this work.

The ΔSM contains, in addition to the SM(-like) Higgs (h), a charged Higgs ($ \Delta^\pm $) and a neutral one ($ \Delta^0 $). Because h and $ \Delta^0 $ have the same quantum numbers, they mix after EW symmetry breaking by an angle α, that is, the mass eigenstates are linear superpositions of the neutral components of the triplet and doublet Higgses (the interaction eigenstates). However, since this mixing is generally small, ⁵ we will use the same labels for the mass and interaction eigenstates. Furthermore, because the mass splitting between $ \Delta^0 $ and $ \Delta^\pm $ is of the order of $ v_\Delta $, we can assume both components to be degenerate, that is, $ m_{\Delta^0}\approx m_{\Delta^\pm}\equiv m_{\Delta} $, as far as LHC searches are concerned.

Owing to its quantum numbers, the triplet Higgs cannot have direct couplings to quarks or leptons. Consequently, it is dominantly produced at the LHC via the Drell-Yan processes $ pp\to W^*\to \Delta^0\Delta^\pm $ and $pp\to Z^*/\gamma^*\to \Delta^\pm\Delta^\mp$ ⁶ since it transforms non-trivially under $ S U(2)_L $ (see Fig. 1). Because the couplings of $ \Delta^\pm $ to SM particles are mixing-induced by $ v_\Delta $, the dominant decay modes are $ WZ $, $ tb $, $ \tau\nu $, and $ cs $, and the only free parameter is $ m_\Delta $ entering through phase space factors. ⁷ The resulting branching ratios are shown in Fig. 2. The dominant decay widths of $ \Delta^0 $ ($ WW $, $ bb $ and $ ZZ $ for our mas range of interest) depend on $ v_\Delta $ and α. However, we are interested in $ \Delta^0\to\gamma\gamma $, which constitutes a particularly clean signature with controlled backgrounds in experiments. This decay is loop-induced and depends, in addition to α and $ v_\Delta $, critically on $ m_{\Delta^0}-m_{\Delta^\pm} $ (because the mass difference is related to the trilinear couplings $ \Delta^0\Delta^\pm\Delta^\mp $). ⁸ Therefore, in the following, we subsume these parameter dependencies into the di-photon branching ratio Br$ (\Delta^0\to\gamma\gamma) $ and consider the latter as a free parameter.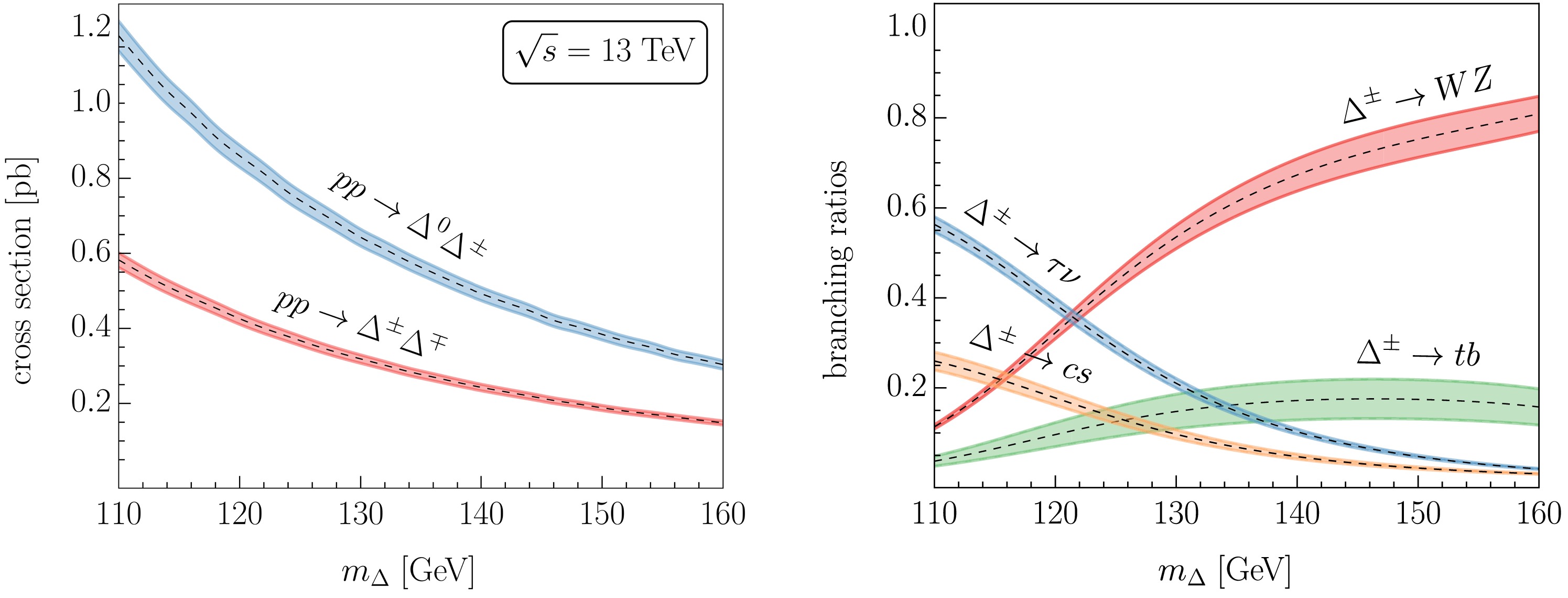

Figure 2.  (color online) Left: Production cross-section for $ pp\to \Delta^0 \Delta^\pm $ and $ pp\to \Delta^\pm \Delta^\mp $ as a function of the triplet mass including the NNLL and NLO QCD correction factor and uncertainties of Refs. [63, 64]. Right: Dominant branching ratios of the charged component $ \Delta^\pm $ as a function of its mass. The errors are estimated from the decays for a SM Higgs with a higher (hypothetical) mass from $ h\to tt^*, ZZ^* $ and $ h\to cc $ [65]. While these uncertainties are sizable, we checked that their impact on the final significance is very small ($ \approx $0.1σ).

We consider searches for the production of photon pairs (di-photons) at the LHC in association with additional particles or missing energy. ⁹ Since we are interested in the on-shell production of a new Higgs that decays to photons, we can look for a peak in the invariant mass spectrum of the di-photons. In this context, an extensive analysis of the associated production of the SM Higgs was performed in Ref. [59], containing 22 different channels ($ \gamma\gamma+X $ where X stands for leptons, missing energy, jets, etc.). In addition, recently, ATLAS released another search targeting various channels, including $ \gamma\gamma+\tau $ [60], which was not included in Ref. [59]. ¹⁰ The figures given in the ATLAS papers [59] show the observed and expected number of events as a function of the invariant mass of the di-photon system between $ 105\, $GeV and $ 160\, $GeV, therefore covering our region of interest motivated by the multi-lepton anomalies. ¹¹

We simulated the processes $ pp\to W^*\to (\Delta^\pm\to XY)(\Delta^0\to \gamma\gamma) $with $ \Delta^\pm $ decaying according to its (mass-dependent) branching ratios (see Fig. 2) using $ \mathtt{MadGraph5aMC@NLO} $ [66] with the parton showering performed by $ \mathtt{Pythia8.3} $ [67] and performed the ATLAS detector simulation [59] with $ \mathtt{Delphes} $ [68] ¹². The UFO model file at NLO for the ΔSM was built using $ \mathtt{FeynRules} $ [69−71]. ¹³ Considering that Z and W bosons decay (according to their known branching ratios) to leptons, missing energy, and jets, we expect that the ATLAS signal regions targeting leptons, missing transverse energy ($ E_T^{\rm{miss}} $), and high jet activity are the most sensitive. Furthermore, at higher values of $ m_{\Delta} $, the categories addressing top quarks become relevant. ¹⁴ In fact, we find that of the 23 categories, the eight listed in Table 1 are relevant to our model for the considered mass range. The di-photon invariant mass distributions of the relevant signal regions are shown in Fig. 3.

Target	Signal region	Detector level	Correlation
High jet activity[59]	$ \ge 4j $	$ n_{\text jet} \ge 4 $, $ |\eta_{\rm{jet}}| <2.5 $	−
Top[59]	$ \ell b $	$ n_{\ell=e, \mu} \ge 1 $, $ n_{b\text{-jet}} \ge 1 $	−
	$ t_\text{lep} $	$ n_{\ell=e, \mu}=1 $, $ n_\text{ jet}=n_{b\text{-jet}}=1 $
Lepton	$ 2\ell $[59]	$ ee, \mu\mu $ or $ e\mu $	<26%
	$ 1\ell $[60]	$ n_{\ell=e, \mu}=1 $, $ n_{\tau_{\text{had}}} = 0 $, $ n_{b\text{-jet}}=0 $, $ E_\text{T}^\text{miss}> 35\text{ GeV} $ (only for e-channel)
$ E_\text{T}^\text{miss} $[59]	$ E_\text{T}^\text{miss}> 100 \text{ GeV} $	$ E_\text{T}^\text{miss}> 100 \text{ GeV} $	29%
	$ E_\text{T}^\text{miss}> 200 \text{ GeV} $	$ E_\text{T}^\text{miss}> 200 \text{ GeV} $
Tau [60]	1$ \tau_{\text{had}} $	$ n_{\ell=e, \mu} = 0 $, $ n_{\tau_{\text{had}}} = 1 $, $ n_{b\text{-jet}}=0 $, $ E_\text{T}^\text{miss}> 35 \text{ GeV} $	−

Table 1.  The signal regions of the ATLAS analyses [59, 60] sensitive to the Drell-Yan production of the scalar triplet within our mass range of interest. $ E_T^{\rm{miss}} $ represnts the missing transverse energy, t represents the top quark, and $ \ell=e, \mu $ represents an electron or a muon. $ n_{(b)}\text{-jet} $ denotes the number of (bottom quark-initiated) jets and $ \eta_{\rm{jet}} $ the rapidity of the jet. The subscripts 'had' and 'lep' stand for the corresponding hadronic decays of tau leptons and the leptonic decays of top quarks.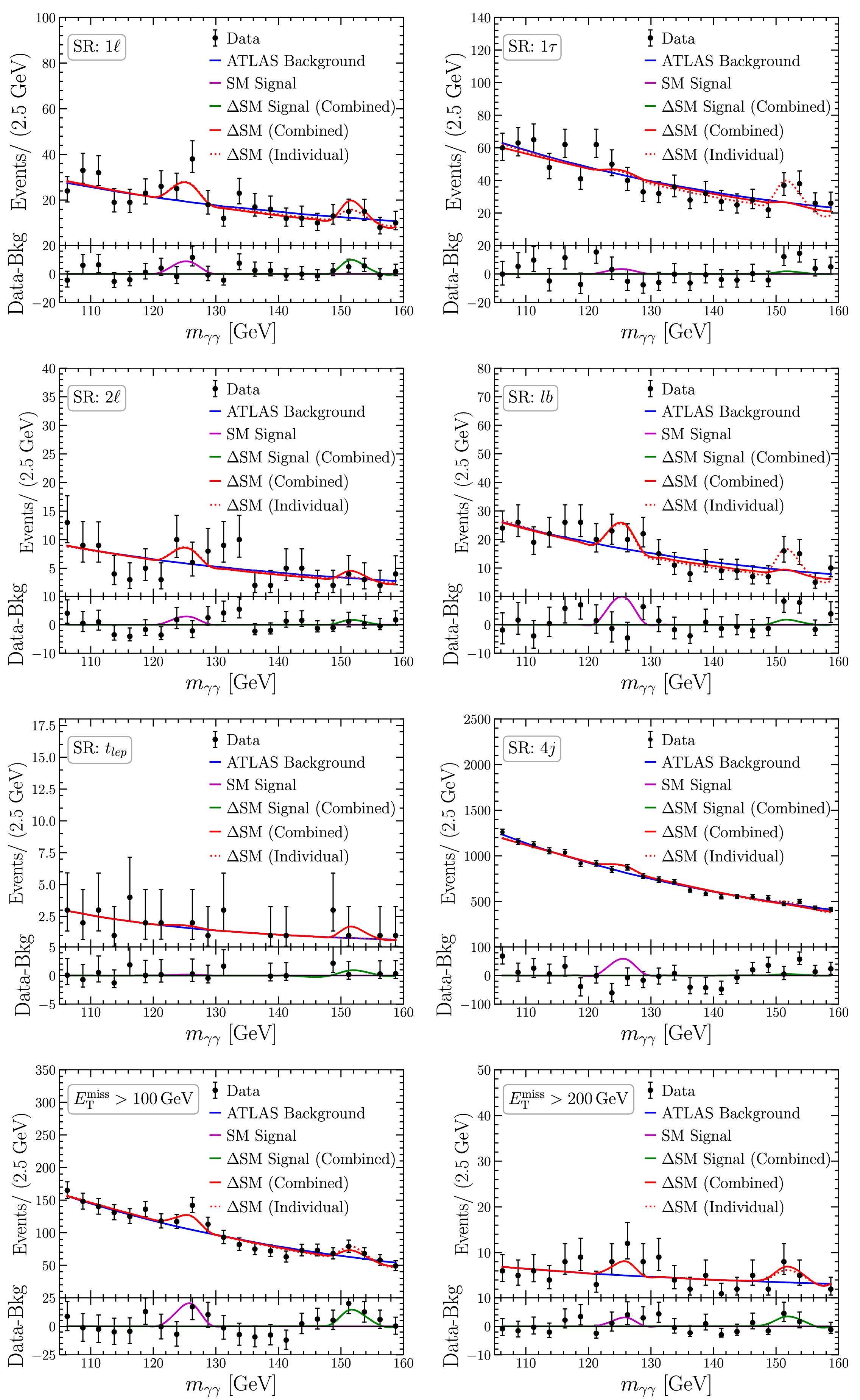

Figure 3.  (color online) Di-photon invariant mass distributions for the eight relevant signal regions. The data (black) is shown together with the continuum background (blue) from the ATLAS analyses and the total ΔSM events (red). The latter is comprised of the refitted background (not shown for brevity), the predicted SM Higgs signals at 125 GeV (magenta) and 152 GeV (green). The solid (dotted) lines correspond to combined (individual) best-fit signals.

The backgrounds (including the SM Higgs for our purpose) given by ATLAS were obtained under the hypothesis that there is a single resonance at 125 GeV. Since we assume, in addition, a second resonance with a different mass and signal strength, the background must be redetermined. For this, we subtract from the measured number of events per bin ($ N_i^{\rm{exp}} $) the predicted number of SM Higgs events as well as the new physics signal (depending on $ m_\Delta $ and Br[$ \Delta^0\to \gamma\gamma $]) and fit the outcome to the continuous function

with the free parameters $ a_0, a_1 $, and b, $ s=13 $ TeV and is the LHC run-2 center-of-mass energy, and m is the invariant mass of the di-photon pair. In Fig. 3, we show the fit to the di-photon invariant mass distributions for the eight relevant signal regions. The continuum backgrounds obtained from the ATLAS analyses are in blue, and the overall fitted ΔSM signal-plus backgrounds are in red. The figure also shows the 125 GeV SM Higgs and 152 GeV triplet Higgs signals.

To determine (for a given mass) the preferred range for Br$ (\Delta^0\to \gamma\gamma) $, we perform a likelihood-ratio test using Poisson statistics for each signal region . Thus, the theory prediction for the number of events in a bin i (including the continuous background of Eq. (2), the SM Higgs signal, and the new physics signal from the triplet Higgs) corresponds to the mean of the Poisson distribution, and we calculate the ratio

Here, $ \mathcal{L} $ is the likelihood described by the Poisson distribution, $ N_i^{\rm{SM}} $ ($ N_i^{\rm{NP}} $) is the number of expected events in the SM (ΔSM), and $ N_i^{\rm{exp}} $ is the number of events measured by ATLAS.

The resulting 68% and 95% confidence level (CL) regions of Br$ (\Delta^0\to \gamma\gamma) $, calculated by requiring that $ \Delta\chi^2=-2\ln(\mathcal{L}_R)=1 $ and $ \Delta\chi^2=-2\ln(\mathcal{L}_R)=4 $, respectively, are shown in Fig. 4. ¹⁵ Interestingly, all relevant distributions display a preference for a non-zero decay rate to $ \gamma\gamma $ at $ \approx $152 GeV. Combing all eight signal regions, including the relevant correlations among them, we obtain the best-fit range for Br$ (\Delta^0\to \gamma\gamma) $ as a function of $ m_\Delta $ in Fig. 5. One can see a strong preference for a non-zero signal strength, which is most pronounced at $ \approx $152 GeV with a corresponding significance of $ \approx4\sigma $.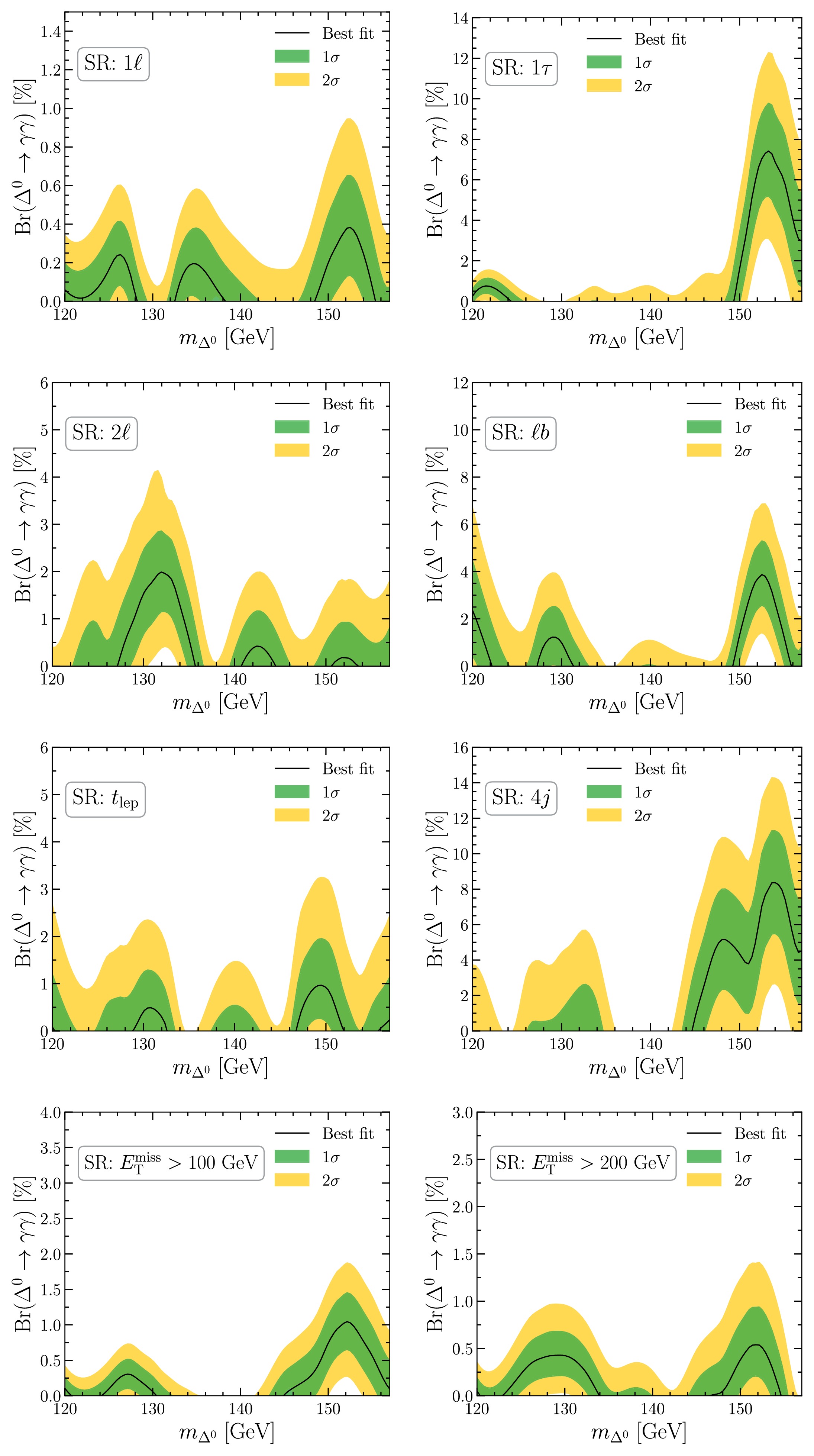

Figure 4.  (color online) Preferred range for the branching ratio of $ \Delta^0 \to \gamma \gamma $ for the eight signal regions sensitive to the our model's signal. Note that four of the signal regions show significant excesses at $ \approx $152 GeV while the other channels will be included as constraints in the combined fit.

Figure 5.  (color online) Statistical combination of the eight relevant channels including their correlations within the ΔSM, resulting in a significance of $ \approx 4\sigma $ at $ m_\Delta\approx152 $ GeV. Note that this significance includes the slight tensions between the different signal regions shown in Fig. 4.

The $ 4\sigma $ significance obtained for a new Higgs at $ \approx $152 GeV within the ΔSM is the highest at the LHC for a narrow resonance within a simple but ultraviolet-complete extension of the SM. Note that, because of the mass range and final state signatures predicted by the multi-lepton anomalies, the look-elsewhere effect is negligible. Consequently, we were able to combine the different channels without a penalty for additional degrees of freedom. Furthermore, the ΔSM can account for a positive shift in W and lead to a strong first-order phase transition required for generating matter anti-matter asymmetry via Baryogenesis.

So far, we have subsumed the free parameters of our model into Br$ [\Delta^0\to\gamma\gamma] $. Let us now have a closer look at how the preferred decay rate for photons can be obtained. Br$ [\Delta^0\to\gamma\gamma] $ is only a function of the mixing angle α and the mass splitting between the charged and neutral components of the triplet (for a given mass and $ v_\Delta $). Looking at the corresponding parameter space for two representative values of $ v_\Delta $ shown in Fig. 6, one can see that the 2σ region preferred by the associated di-photon production can lead to an unstable vacuum and only slightly overlaps within the non-perturbative regime. While vacuum stability should not be taken at the same level as an experimental observable since it is sensitive to physics at arbitrary high scales, this indicates that while we have growing evidence for a 152 GeV Higgs produced via Drell-Yan in association with leptons (e, μ and τ), missing energy and b quarks, the ΔSM should be extended. In fact, while it can lead to a strong first-order phase transition, it cannot account for the additional charge-parity violation [72] required for Baryogenesis since all the triplet interactions are real. Thus, while ΔSM is not expected to be the final theory of Nature and does not solve several of the SM problems mentioned in the introduction, it provides an important indication of the direction in which the SM should be extended.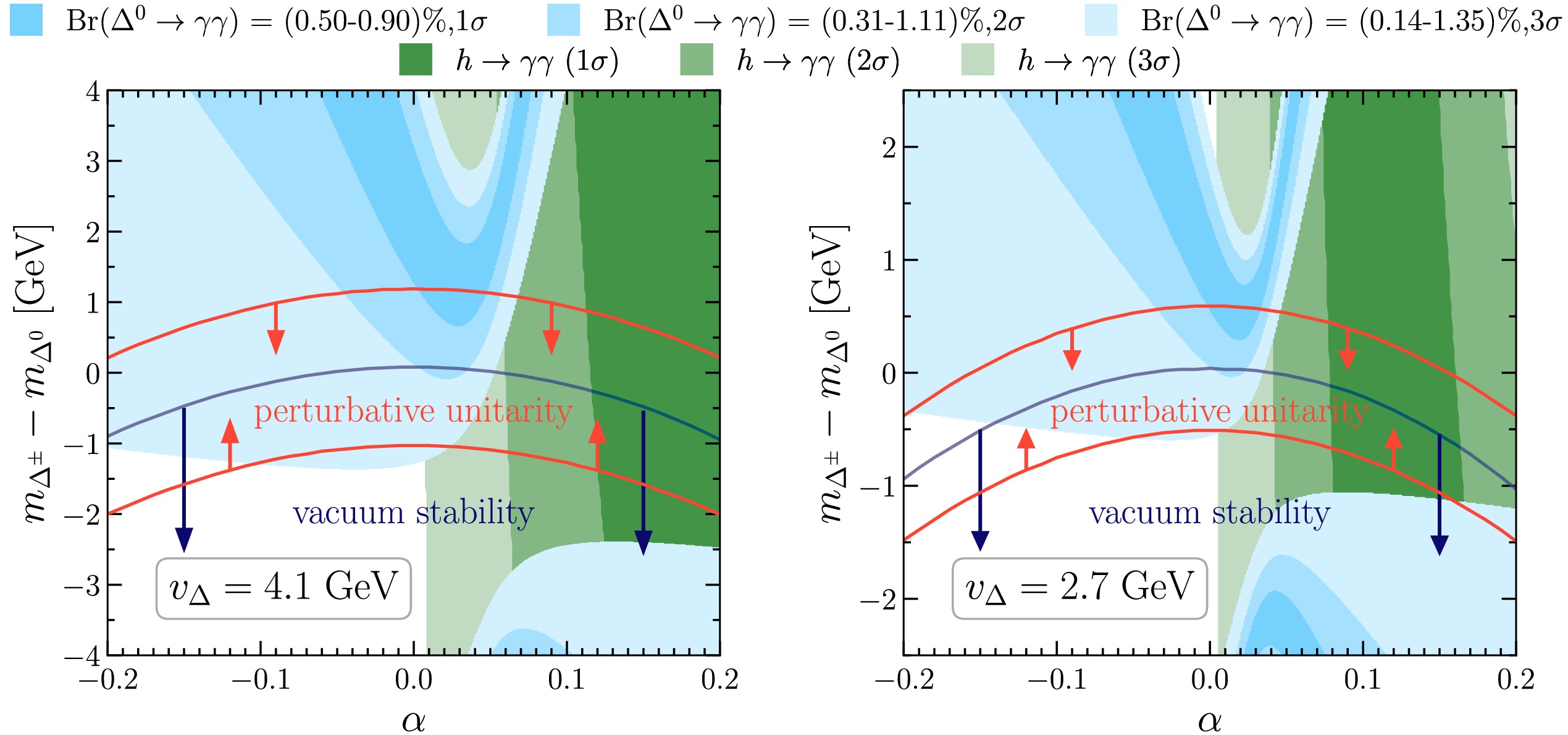

Figure 6.  (color online) Preferred regions in the α vs $ m_{\Delta^\pm}-m_{\Delta^0} $ plane for $ m_{\Delta^0} = 152 $ GeV and two values of $ v_\Delta $: 4.1 GeV (left) and 2.7 GeV (right), corresponding to the central value obtained from the global electroweak fit with and without including the CDF-II measurement. The band between the two orange lines satisfies perturbative unitarity and the one below the blue line leads to a stable vacuum at the electroweak scale. The green regions are allowed by the SM Higgs signal strength to photons ($ h \rightarrow \gamma \gamma $) [73, 74] at the $ 1\sigma $ (1.02−1.15), $ 2\sigma $ (0.96−1.22), and $ 3\sigma $ (0.90−1.29) levels. The $ 1\sigma $, $ 2\sigma $, and $ 3\sigma $ regions for Br$ (\Delta^0\to \gamma\gamma) $ are shown in violet. Note that both Br$ (\Delta^0\to \gamma\gamma) $ and Br$ (h \rightarrow \gamma \gamma) $ are sensitive to mass splitting since this determines the tri-linear Higgs coupling entering the processes via the $ \Delta^\pm $ loop.

While the 152 GeV excess is consistent with, and motivated by, the multi-lepton anomalies, the ΔSM is insufficient to explain the latter. A more comprehensive model addressing these problems could be the Δ2HDMS model [75], where the SM is extended not only by a triplet but also by a singlet and a second doublet. This model can explain the tensions between the theory predictions of the differential $ WW $ [76] and top-quark distribution and their measurements [75], which are seperate from the multi-lepton anomalies. Furthermore, it can successfully give rise to weak-scale Baryogenesis [77] and e. Furthermore, the charged Higgs coming from the second $ S U(2)_L $ doublet can modify Br$ (\Delta^0\to \gamma\gamma) $ significantly (via the tri-linear term $ H_1^\dagger\Delta^0H_2 $) to avoid problems with vacuum stability and perturbative unitarity.

Finally, a new Higgs boson in general, and our ΔSM in particular, significantly strengthens the physics case for future particle experiments. While the signals of the charged component are difficult to reconstruct at the LHC [58, 78], its properties could be determined with great precision at future $ e^+e^- $ accelerators, such as the Circular Electron-Positron Collider (CEPC) [79, 80], the Compact Linear Collider (CLIC) [81], the Future Circular Collider (FCC-ee) [82, 83], and the International Linear Collider (ILC) [84, 85]. Furthermore, these colliders can be used to determine the properties of the SM Higgs very precisely (which are, in general, altered in our model), produce many top quarks within a clean environment to test the related multi-lepton anomalies, and clarify the preference of new physics in the global electroweak fit, in particular the W mass where a positive-definite shift w.r.t. the SM is predicted.

A.C. thanks Daniel Litim for useful discussion concerning vacuum stability and Sezen Sekmen for help with the Delphes card.