Energy dependence of fission product yields in ²³⁵U(n, f ) within the Langevin approach incorporated with the statistical model

Nuclear fission produces hundreds of primary fragments with different yields $ Y(Z, A, KE) $ of charge, mass, and kinetic energy, and the fragments are highly excited and neutron-rich to the extent that they quickly de-excite via sequential emission of prompt neutrons and γ-rays to reach the ground or isomer states. The yield of the fission product after emitting prompt particles but before β decay, $ i.e. $, the independent fission yield $ Y_I(Z, A) $, is one of the most important observables for testing the theoretical models describing the entire fission process. Additionally, the independent fission yield is one of the key nuclear data for application of nuclear power such as evaluating the decay heat in nuclear reactor and developing the advanced reactor.

Current nuclear data libraries such as ENDF/B-VIII.0 [1], JEFF-3.3 [2], and JENDL-5.0 [3] include the independent fission yield data of major actinides at the thermal, fast, and 14-MeV neutron energies. However, the yield data at more neutron energy points are required in new applications. Fortunately, in the last decade, considerable experimental and theoretical progress [4−6] have been made in nuclear fission. Most of the fragment deexcitation models and codes [7−15] can provide a good reproduction of prompt fission observables by inputting the primary fragment yields $ Y(A, TKE) $ obtained from either the experimental data or systematic methods with parameters estimated by fitting available experimental data. Furthermore, these models can generate extensive nuclear data, including independent fission yields and the multiplicity and energy spectra of prompt particles. However, they are rarely used to study the dependence of prompt fission observables on incident neutron energy due to the limited availability of experimental data on primary fragment yields across a range of neutron energies.

Furthermore, the dynamical approaches of nuclear fission, especially Langevin approach [16−26] and random walk on the potential energy surface [27−29] within the macroscopic-microscopic model, shed light on the description of the primary fragment yields for any fissioning system at any excitation energy in a reasonable computation time. In recent years the Brownian shape motion model have been coupled with the statistical evaporation model to perform calculations of the prompt neutron observables [23, 24, 26, 28−32] at a given incident neutron energy. In this work, the Langevin approach incorporated with the statistical model is used to investigate the independent fission yields for a large quantity of fission products, the dependence of the independent mass yields, the cumulative yields for select isotopes, the average TKE and average prompt neutron multiplicity in $ ^{235} $U(n, f) on the incident neutron energy. There is an overall agreement between the calculated results and data from the experiments, the evaluation, and the GEF model [7], which verifies the predictive power of the present model in describing the fission product yield and its dependence on the incident neutron energy.

The paper is organized as follows. We present the methods briefly in Sec. II. The calculated results for the independent fission yield and the energy dependence of the fission observables as well as some discussions are provided in Sec. III. Finally, a summary of the present study is presented in Sec. IV.

In this study, the primary fragment yields are obtained by simulating the dynamical process of the fissioning system with the Langevin approach, where the slow evolution of the nuclear shape is treated as the motion of a Brownian particle in "heat bath". The nuclear shape during the fission process is described within the two-center shell model parametrization (TCSMP) [33], in which there are totally five shape parameters: the elongation parameter $ Z_0 $ defined as the distance between centers of pre-fragments, fragment deformation parameters $ \delta_1 $ and $ \delta_2 $ of the left and right semi-ellipsoid ends, mass asymmetry η, and neck parameter $ \epsilon $.

In this study, we fix $ \epsilon $ as 0.35 [34] and consider $ \delta_1=\delta_2=\delta $ simultaneously, similar to that in Refs. [16, 18, 21, 23], to save computation time. Thus, three free shape parameters, $ i.e. $, $ \{Z_0/R_0, \delta, \eta\} $, are used for the generalized coordinates of the Langevin equation, which takes the following form,

where $ p_i $ denotes the generalized momentum conjugate to the generalized coordinate $ q_i $. The summation convention for repeated indices is considered in Eq. (1) and in the following equations. Here, V denotes the potential energy of deformation obtained within the macroscopic-microscopic model, in which the macroscopic energy is evaluated with finite range liquid drop model [35, 36], and the microscopic shell and pairing correction energy are calculated with Strutinsky method [37] and Bardeen-Cooper-Schrieffer (BCS) method [38], respectively, based on the single-particle levels obtained from TCSM. The microscopic correction energy is highly dependent on the nuclear temperature at low-excitation energies, which is described by following Ignatyuk prescription [39] in this study. Additionally, the inertia tensor $ m_{ij} $ and friction tensor $ \gamma_{ij} $ are calculated with Werner-Wheeler method [40] and wall-and-window model [41], respectively. The normalized random force $ \Gamma_j (t) $ is assumed as white noise and its strength $ g_{ij} $ is obtained from the fluctuation-dissipation theorem:

where $ T^* $ denotes the effective nuclear temperature evaluated from the following form [42, 43]:

in which the quantum effect is considered at low excitation energy. Furthermore, ϖ denotes the local frequency of the collective motion and we use $ \hbar\varpi $ = 2 MeV [18]. Temperature T is obtained from the Fermi gas model: $E_{\rm int}=aT^2$. The level density parameter a of the fissioning nucleus is considered from Ref. [44] and local intrinsic excitation energy $E_{\rm int}$ is calculated at each time step along the Langevin trajectory according to the energy conservation as follows:

where $ E^* $ denotes the total excitation energy of the fissioning nucleus, V and the $E_{\rm coll}$ denote the potential energy of deformation and the collective kinetic energy of the fissioning nucleus, respectively. In this study, we introduce the contribution of the multi-chance fission, which plays an important role for the fissioning system wherein the excitation energy is higher than the neutron separation energy. At each step, the neutron emission is judged by asking whether a random number ξ is less than the ratio of time step τ to the neutron decay time $ \tau_n(\tau_n= {\hbar}/{\Gamma_n}) $: $ \xi< {\tau}/{\tau_n}(0\leq\xi\leq1) $ [45]. If this is the case, a neutron is emitted, and its kinetic energy is obtained by randomly sampling from the decay width of neutron emission within the Weisskopf model [46]. The energy carried away by the evaporated neutron, $ i.e. $, $E_{\rm evap}$, is the sum of the neutron separation energy and its kinetic energy. It should be noted that in the current approach, if the i-th neutron evaporates during the fission process, then the evaporation-residue nucleus will follow a new trajectory by solving the Langevin equation for a system with charge number Z and neutron number $ (N-i) $, which has a potential energy surface of thenucleus $ (Z, N-i) $ and total excitation energy of $E^*_i = (E^*_{i-1}-E^i_{\rm evap})$. Specifically, the charge number Z and neutron number N are that of compound nucleus.

In the dynamical calculation, the initial position is set as $ \{Z_0/R_0=0.5, \delta=0.2, \eta=0\} $ near the ground state and the scission point is determined by a fixed neck radius as 0.5 fm [21, 47]. The number of Langevin trajectories reaches at least 3.0$ \times $10$ ^5 $ per fissioning system, which guarantees sufficient statistics for the calculation of the primary fragment distributions and following prompt neutron observables.

In addition to multi-chance fission, the Weisskopf statistical model is employed to describe prompt neutron emission during the de-excitation process. This is based on the characteristics of the primary fragments: their mass and TKE are obtained from Langevin calculations, while their charge and excitation energy are determined using empirical formulas.

The charge probability distribution for the fragments with a given mass number $ A_f $ is generally assumed to be a Gaussian function [48, 49],

with the standard deviation considered as $ \sigma_z=0.5 $ [9, 48]. The most probable charge $ \bar{Z}_f $ of the distribution is determined from the unchanged-charge distribution (UCD) corrected with the charge polarization, $ i.e. $, $\bar{Z}_f(A_f)= \dfrac{Z_{CN}}{A_{CN}}A_f+\Delta Z$. Within the Wahl's systematics [49], the charge polarization $ \Delta Z $ of the fission fragments, heavier than A=130, approximates to be -0.5 for Uranium isotopes, and $ \Delta Z $ of the fragments around the symmetric fission region equals to 0. In the this study, a simple linear interpolation is adopted for a smooth transition of $ \Delta Z $ for the fragments between A=130 ($ \Delta Z=-0.5 $) and $ A=A_{CN}/2 $ ($ \Delta Z=0 $), and $ \Delta Z $ equals to –0.5 for the fragments heavier than A=130. Thus, the charge number $ Z_H $ of the heavy fragment is obtained by using the random sampling according to the expression of Eq. (5) and that of the complementary light fragment is determined by $Z_L= Z_{CN}-Z_H$. It should be noted that the odd-even effect in the fragment charge distribution is not considered, which plays a significant role in the fissioning system at the lower excitation energy.

According to the energy conservation, the total excitation energy (TXE) for each pair of fission fragments is obtained by subtracting TKE from the Q-value of the fission reaction: $ TXE=Q-TKE $. The TXE is then partitioned between the two complementary fragments based on the anisothermal parameter $ R_T $ [50] , which is defined as the ratio of the temperatures of the fission fragments:

with the energy-dependent level density parameter a as follows:

where $ \tilde{a} $ denotes the asymptotic level density parameter, $ \delta W $ and γ denote the shell correction energy and shell damping parameter, respectively, U denotes the effective excitation energy, which is defined as the difference between the excitation energy and paring energy, $ i.e. $, $ U=E_x-\Delta $. Specifically, $ \tilde{a} $, $ \delta W $, Δ, and γ in Eq. (7) are consistently taken from TALYS calculations [51] with the Back-shifted Fermi gas model for each fragment $ (Z_i, A_i) $. The excitation energy $ E_x $ in each fragment is obtained by an iterative procedure according to Eq. (6). Considering that TXE partition is highly correlated with the prompt neutron multiplicity distribution $ \nu(A) $, $ R_T $ is considered as mass dependent in order to effectively reproduce the prompt neutron multiplicity distribution.

The highly excited primary fragments first deexcite through sequential emission of neutrons. The emission probability of the neutron with the kinetic energy $ \varepsilon_n $ for a fragment with a excitation energy $ E^*_M $ can be obtained via Weisskopf formula [47]:

where μ denotes the reduced mass of the neutron, and $\sigma_{\rm inv}$ denotes the neutron inverse cross section which is obtained from the optical model calculation using TALYS code [52]. Furthermore, $ \rho_M $ and $ \rho_D $ denote the level densities of parent and daughter nuclei, respectively.

The sequential neutron emission is assumed to take place until the excitation energy of the fragment is less than its neutron separation energy.

The independent yields of hundreds of fission products in 14 MeV n+$ ^{235} $U fission are calculated with the present model, as well as the primary isotopic yields. We show the primary and independent fission yields on the proton and neutron number $ (Z_f - N_f) $ plane in the upper and middle panel of Fig. 1, respectively. It can be observed that the distribution of the independent fission yields $ Y_I(Z,A) $, and it is obviously shifted 2−3 units to the left side relative to the primary fragment distribution, and thereby, the distribution of $ Y_I(Z,A) $ is closer to β-stability line. The maximum independent fission yields corresponding to the heavy products are distributed in the region around $ Z=54, N=82 $, which verifies that the proton shell around $ Z=54 $ plays a significant role in the origin of the asymmetric fission of the actinides [7, 53] in addition to the well-known neutron shell closure $ N=82 $. Furthermore, the results of $ Y_I(Z,A) $ are compared to the evaluated data from ENDF/B-VIII.0, which is shown in the bottom panel of Fig. 1. The overall distribution of $ Y_I(Z,A) $ is consistent with that of the evaluated data with the exception that the range of the fission products with lower yields is less than the evaluated data. This results from limitation of the number of Langevin trajectories in a reasonable computation time.

Figure 1.  (color online) Calculated primary isotopic yield in 14 MeV n+$ ^{235} $U fission on the proton and neutron number $ (Z_f-N_f) $ plane (top). The independent yield $ Y_I(Z,A) $ in 14 MeV n+$ ^{235} $U fission calculated with the present model (middle) and from ENDF/B-VIII.0 (bottom).

A more detailed comparison of the calculated independent fission yield $ Y_I(Z,A) $ with the GEF calculations and evaluated data from ENDF/B-VIII.0 is shown in Figs. 2−4. Figure 2 shows the comparison of $ Y_I(Z,A) $ around the peak regions $ (Z=34-41, 50-57) $ of the charge distribution in 14 MeV n+$ ^{235} $U fission, together with the $ Y_I(Z,A) $ calculated without the neutron emission during the fission process, $ i.e. $, without the multi-chance fission. It can be observed that there is no obvious difference between $ Y_I(Z,A) $ calculated with and without the multi-chance fission for 14 MeV n+$ ^{235} $U fission, indicating that the multi-chance fission has slight effect on$ Y_I(Z,A) $ for the fissioning system at low excitation energy. This is consistent with the case of the mass yields [32, 54]. The effect of the multi-chance fission for high-energy neutron induced fission will be discussed in future studies. It can be observed in Fig. 2 that $ Y_I(Z,A) $ for most fission products are effectively reproduced via the present model, though the isotopic distributions of the $ Y_I(Z,A) $ for $ Z=38-41 $ are shifted toward the left side by approximately 2 units when compared to the evaluated data and GEF calculations. Moreover, the distribution of the isotopic yields appears to be Gaussian-like shape, which is similar to the charge distribution of fission products for a given mass number. The results for the independent yields around the valley and wing regions are shown in the logarithmic scale in Fig. 3. Similar to that in the peak regions, there is an overall agreement among the calculated results, evaluated data, and GEF calculations, especially that the calculation results for $ Z=46-49 $ are in better agreement with the evaluated data than GEF calculations. The accurate reproduction of $ Y_I(Z,A) $ for 14 MeV n+$ ^{235} $U fission indicates validity of the present model in evaluating the charge and TXE partition between the two complementary fragments in addition to primary fragment yields. Moreover, we calculate the independent yields for thermal n+$ ^{235} $U fission. Figure 4 shows the calculation results of $ Y_I(Z,A) $ around the peak regions when compared to the evaluated data and GEF calculations. There is a slightly larger difference among the calculation results, evaluated data, and GEF calculations for thermal n+$ ^{235} $U fission when compared to that for 14 MeV n+$ ^{235} $U fission. This is potentially due to the fact that the calculated mass yields primary fragments in lower-energy neutron induced fission deviate from the experimental data to a certain extent, whereas the reproduction of the mass yields becomes better as the incident neutron energy increases. This will be shown and discussed later in Fig. 5.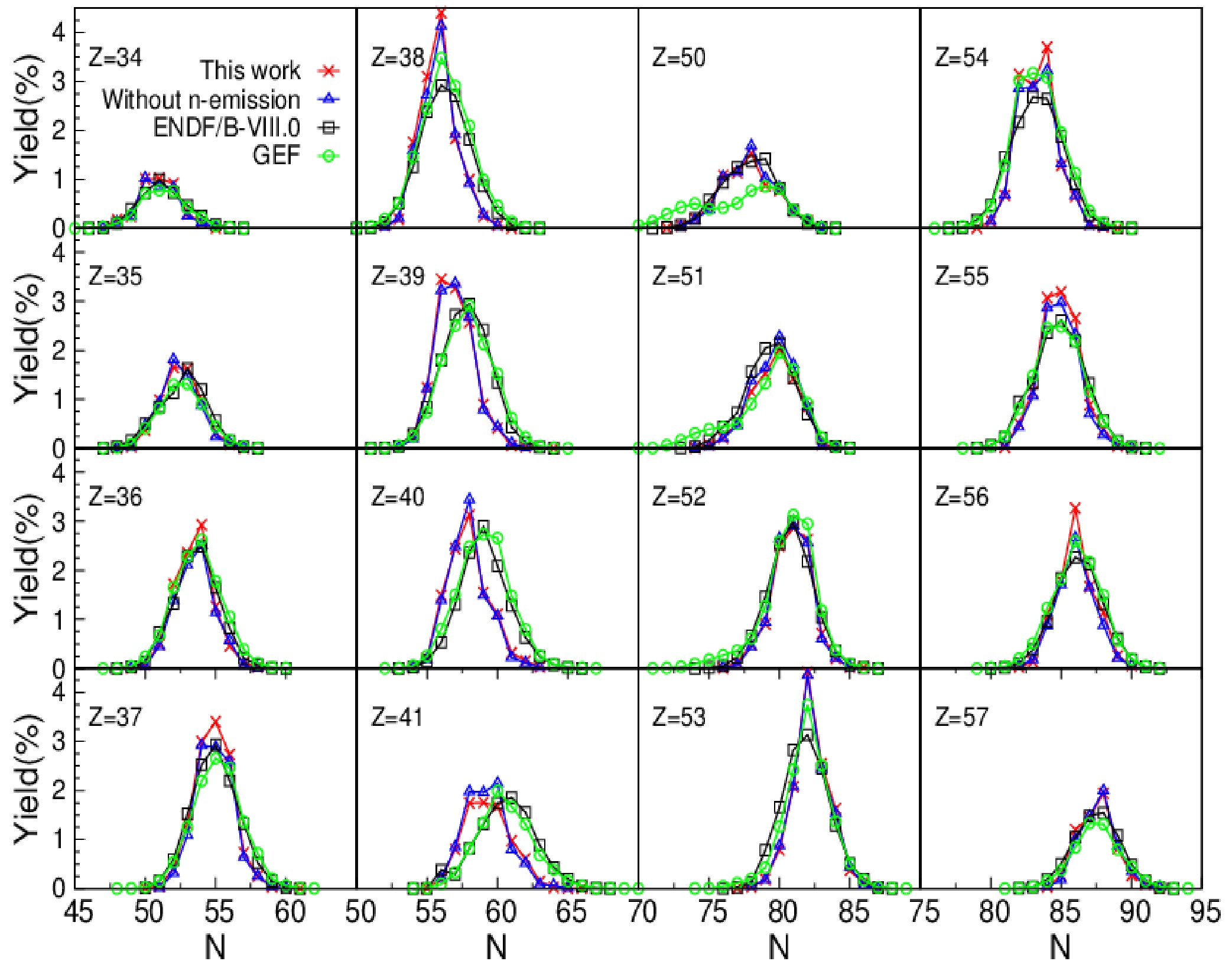

Figure 2.  (color online) Calculated independent yields (red curve) for a given isotope chain around the light peak region $ (Z=34-41) $ and heavy peak region $ (Z=50-57) $ of the charge distribution in 14 MeV n+$ ^{235} $U fission when compared to the corresponding results obtained from the GEF model and ENDF/B-VIII.0. The blue curve denotes the independent yields without the neutron emission along the Langevin trajectory.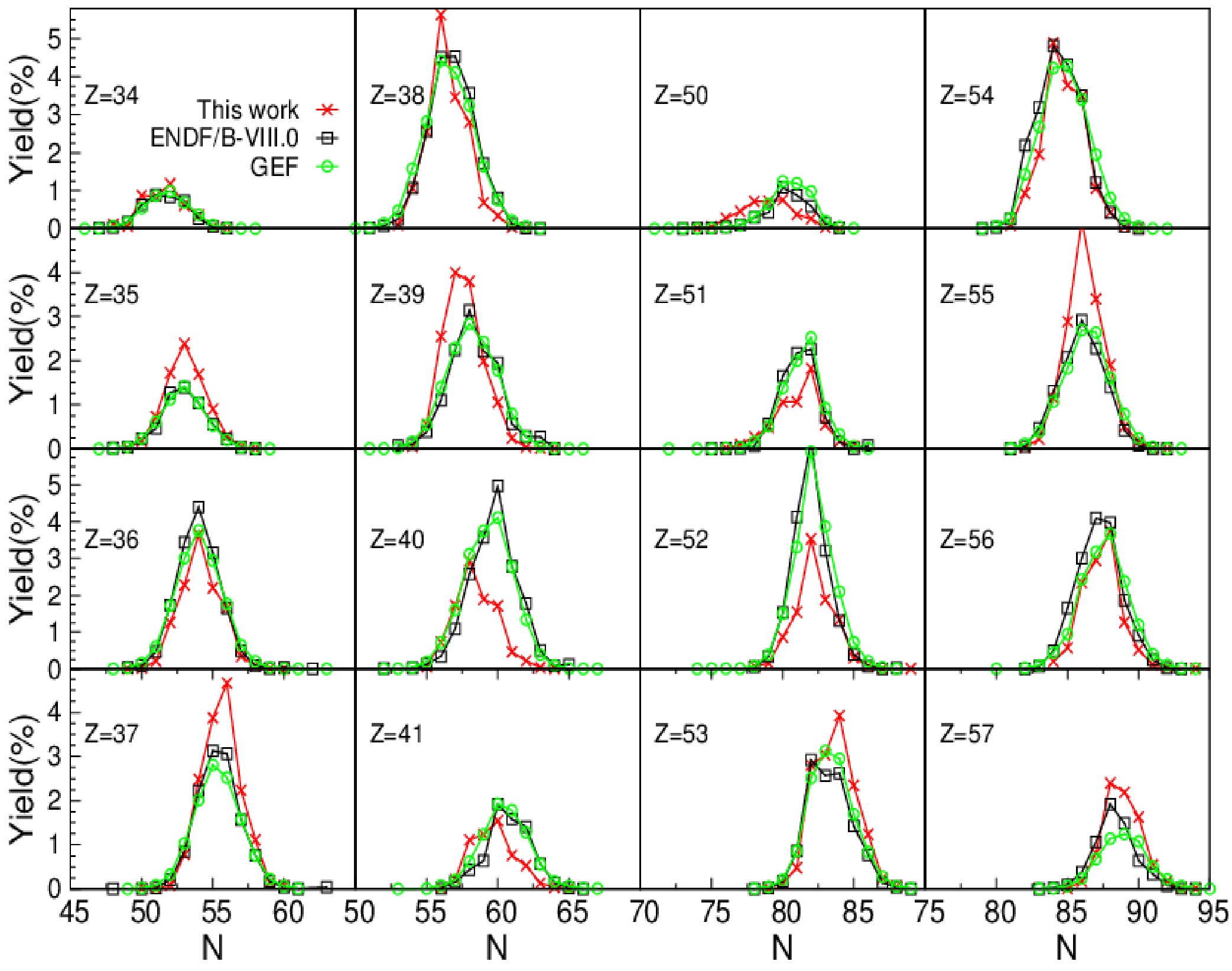

Figure 4.  (color online) Similar to Fig. 2 but in thermal n+$ ^{235} $U fission.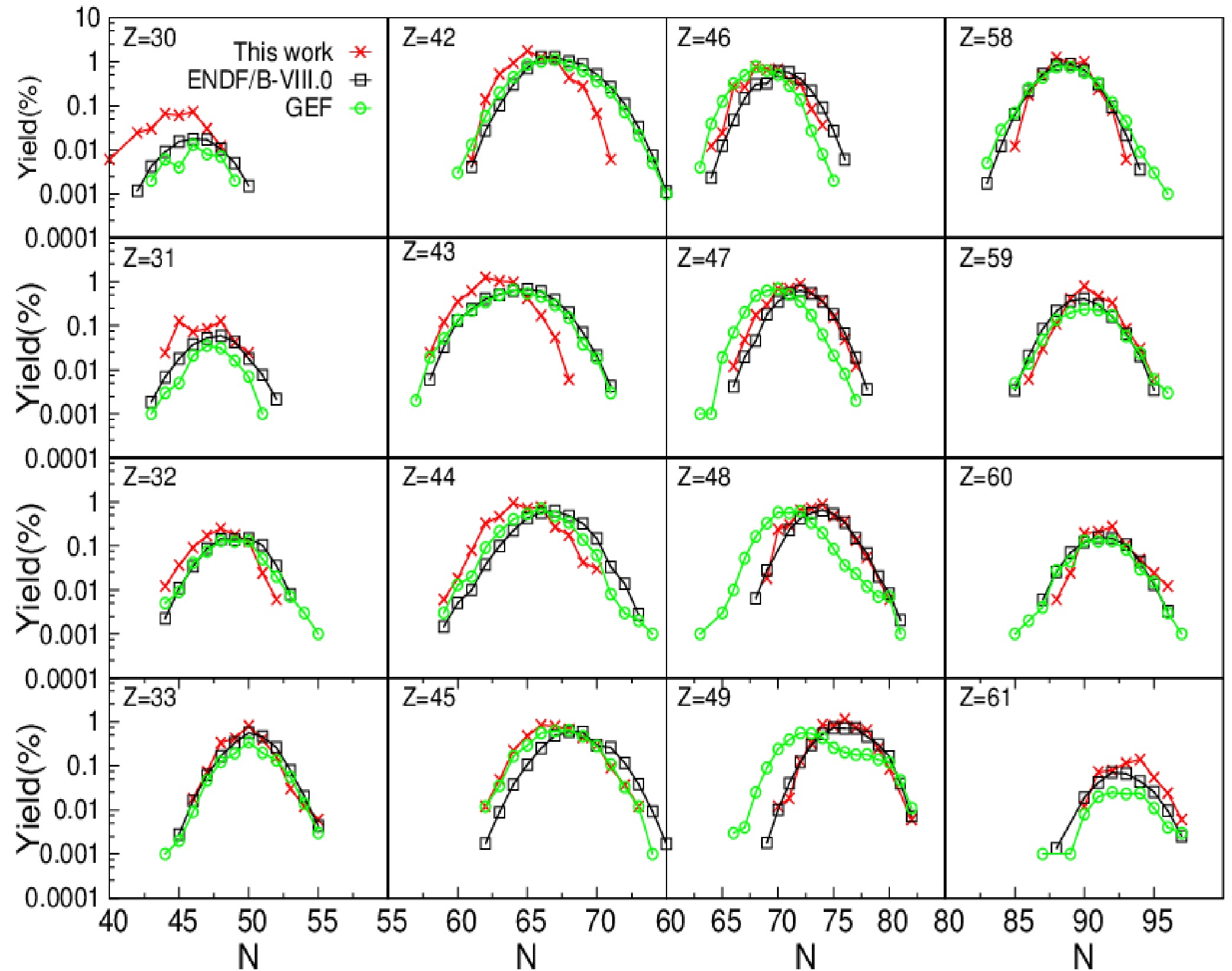

Figure 3.  (color online) Similar to Fig. 2 but for the isotope chains around the valley region $ (Z=42-49) $ and wing regions $ (Z=30-33, 58-61) $ of the charge distribution in 14 MeV n+$ ^{235} $U fission.

Figure 5.  (color online) The calculated primary fragment mass yields (green curve) and independent mass yields (red curve) in $ ^{235} $U(n, f) for incident energies of thermal [32] (a), 5 MeV (b), 8.1 MeV (c), 14 MeV [32] (d), 15.1 MeV (e) and 19.1 MeV (f), together with the independent mass yields obtained from the GEF model, ENDF/B-VIII.0 or experiments [55−57].

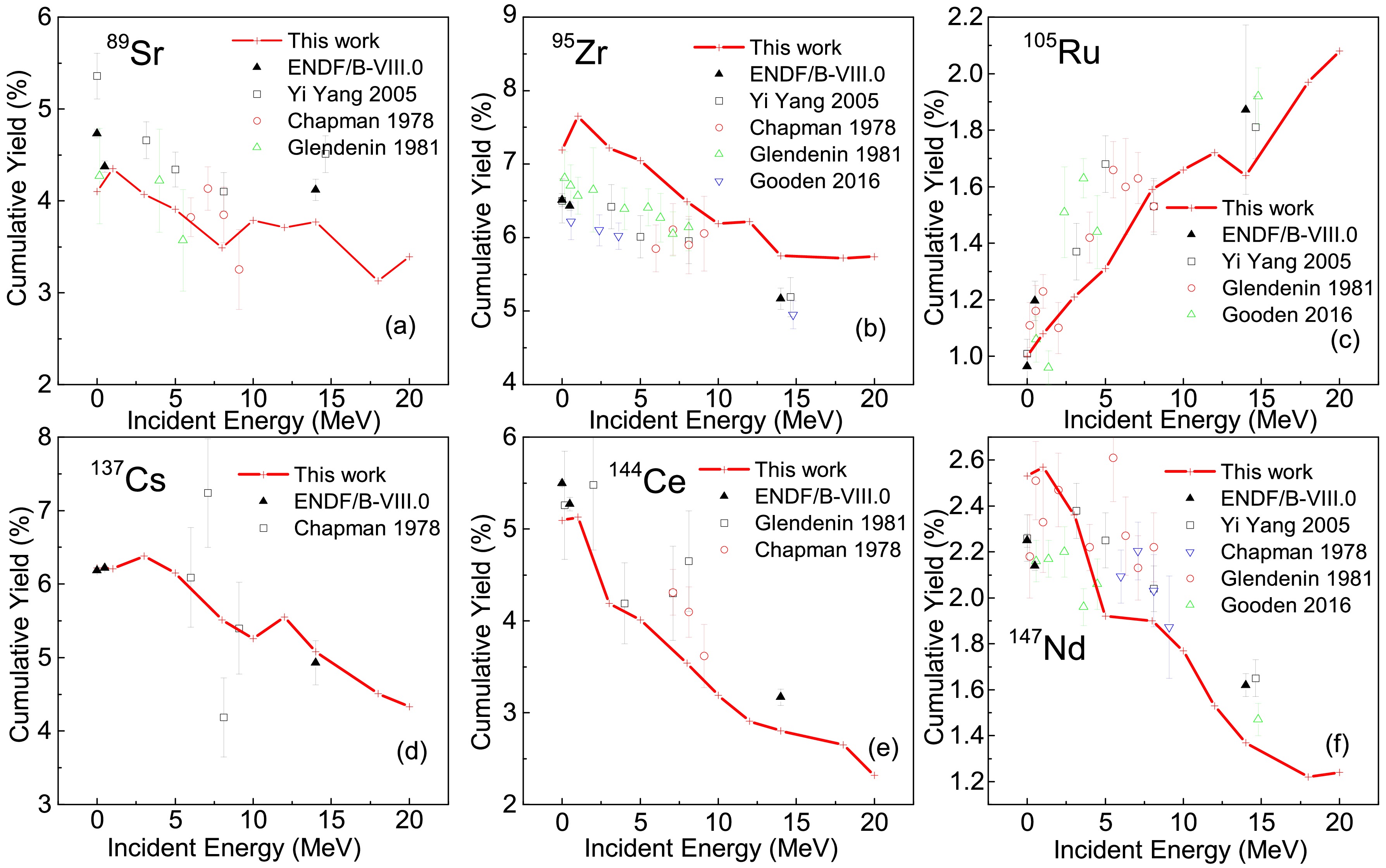
The evolution of mass yields of primary fragments and independent mass yields with the increase in incident neutron energy in $ ^{235} $U(n, f) is shown in Fig. 5 when compared to the independent mass yields obtained from GEF model, ENDF/B-VIII.0 or experiments. The distributions of independent mass yields are generally shifted to the left relative to the primary fragment mass distributions due to prompt neutron emission. As the incident neutron energy increases, yields in the symmetric fission region increase, while those near the peak regions decrease, and the overall distribution broadens. The calculated results show good agreement with GEF calculations, evaluated data, and experimental data—particularly for neutron-induced fission at 14 MeV, 15.1 MeV, and 19.1 MeV. This consistency supports the validity of incorporating temperature dependence in the potential energy as well as multi-chance fission in the present model. For neutron-induced fission at thermal energies, 5 MeV, and 8.1 MeV, the independent mass yields in the wing regions and peak heights are well reproduced. However, slight deviations are observed in the symmetric region yields and peak widths when compared to evaluated and experimental data. These discrepancies may stem from the unavailability of macroscopic transport coefficients at lower energies. Incorporating microscopic effects, such as shell and pairing contributions to the transport coefficients, could improve the model’s accuracy for low-energy fission.

Furthermore, we show the dependence of the cumulative yields on the incident neutron energy for several nuclides with available experimental data across a range of neutron energies in Fig. 6. It should be noted that, in the present study, the independent mass yield is assumed to correspond to the cumulative yield of either the final product of β decay (generally a stable nucleus) or a long-lived nucleus adjacent to the stable isotope within the same mass chain. The model successfully reproduces the general trend of the cumulative yield's dependence on incident neutron energy for the selected isotopes, despite some discrepancies in the absolute yield values compared to experimental data. This demonstrates the model's feasibility in capturing the energy dependence of fission yields.

Figure 6.  (color online) Cumulative fission yield as a function of incident energy in $ ^{235} $U(n, f) for select isotopes $ ^{89} $Sr (a), $ ^{95} $Zr (b), $ ^{105} $Ru (c), $ ^{137} $Cs (d), $ ^{144} $Ce (e), and $ ^{147} $Nd (f) when compared to the experimental data [55, 58−60].

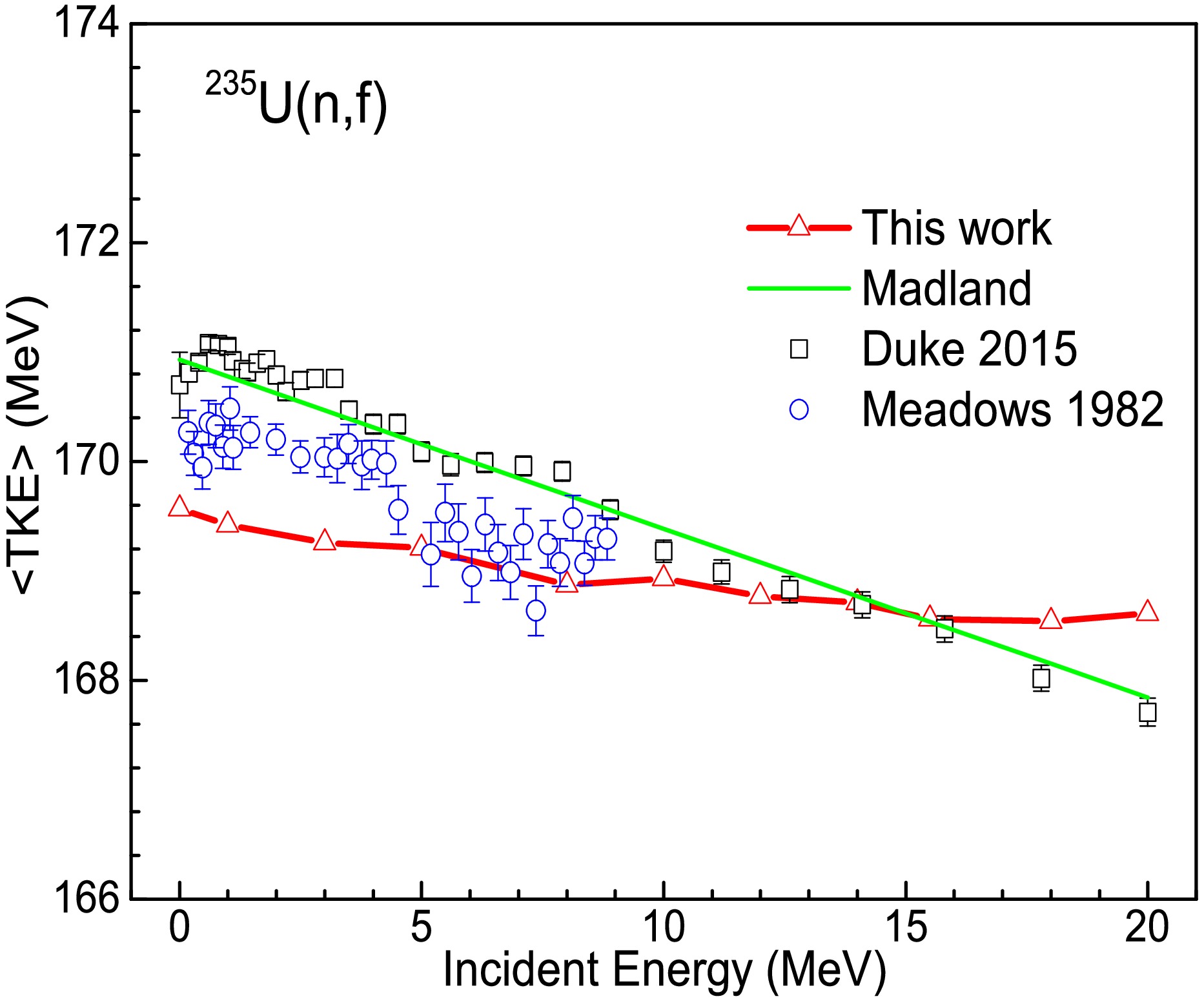
In addition to the fission yields, the average TKE and average prompt neutron multiplicity as a function of the incident neutron energy are investigated in this study. Figure 7 shows the energy dependence of the average TKE of fission fragments in $ ^{235} $U(n, f) when compared to the Madland systematics and experimental data. The calculated TKE decreases with the increase in the incident neutron energy, which is physically reasonable because the shapes of abundant heavy fragments change from almost spherical for lower excitation energy to highly prolate for higher excitation energy. This leads to an increase in the distance between two pre-fragments, and thereby, the decrease in TKE as proposed in Refs. [22, 25]. The slope of the tendency curve is less than those from systematics and experimental data, and the maximum difference between the calculation results and the experimental data is approximately 1.6 MeV.

Figure 7.  (color online) Average TKE of primary fragments as a function of incident energy in $ ^{235} $U(n, f) when compared to Madland systematic results [61] and experimental data [62, 63].

Moreover, the average prompt neutron multiplicity $ \bar{\nu}_p $ as a function of the incident neutron energy is shown in Fig. 8, together with the evaluated data from ENDF/B-VIII.0 and experimental data. The nearly linear tendency of the dependence of $ \bar{\nu}_p $ on the incident energy is well reproduced, and the slope is consistent with the evaluated data and experimental data. However, the calculated $ \bar{\nu}_p $is generally 0.5 larger than the evaluated data and experimental data in the entire range of the incident neutron energy. The excessive prompt neutron emission is potentially due to the present model not accounting for the competition between neutron and γ-ray emission, which will be addressed in future work.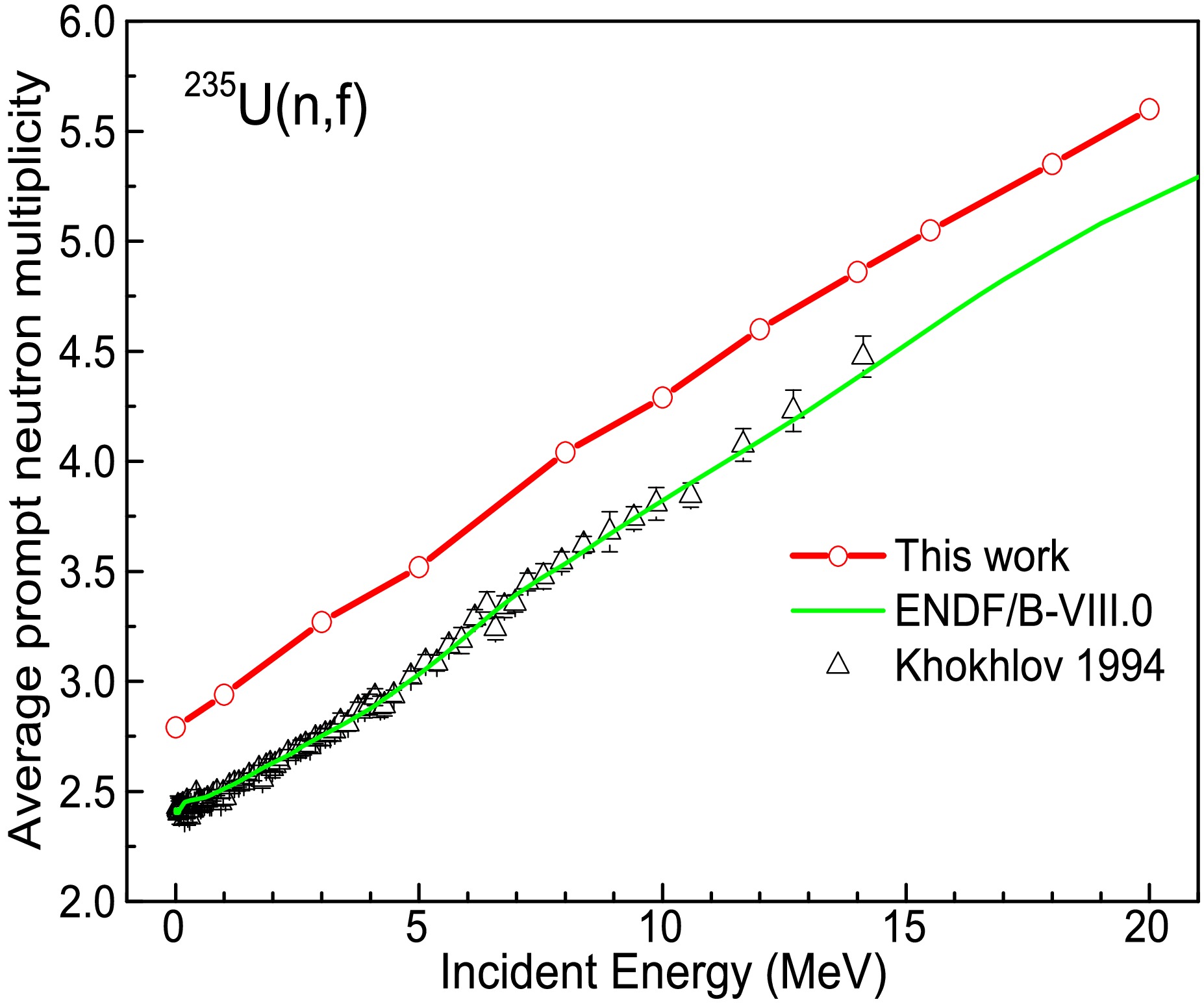

Figure 8.  (color online) Average prompt neutron multiplicity as a function of incident energy in $ ^{235} $U(n, f) when compared to the evaluated data from ENDF/B-VIII.0 and experimental data [64].

In this study, the Langevin approach, combined with a statistical model, is employed to investigate the independent fission yields of a wide range of fission products, as well as the dependence of independent mass yields, cumulative yields for selected isotopes, average total kinetic energy (TKE), and average prompt neutron multiplicity on the incident neutron energy in $ ^{235} $U(n, f).

Firstly, the independent fission yields in 14 MeV n+$ ^{235} $U fission on the proton-neutron number plane are calculated, showing that the maximum yields corresponding to the heavy products are distributed in the region around $ Z=54, N=82 $. It verifies that the proton shell around $ Z=54 $ plays a significant role in the origin of the asymmetric fission of the actinides in addition to the well-known neutron shell closure $ N=82 $. Moreover, the independent fission yields of the isotopes from $ Z= 30-61$ are generally in good agreement with the evaluated data from ENDF/B-VIII.0 and GEF calculations, which indicates validity of the present model in evaluating the charge and TXE partition between the complementary fragments, in addition to the primary fragment yields.

Additionally, the evolution of the independent fission mass yields with the incident neutron energy in $ ^{235} $U(n, f) is described well, especially that there is a good agreement between the calculation results and experimental data for the fissioning system at higher excitation energies. Furthermore, the tendency of the dependence of the cumulative yields for select isotopes on the incident neutron energy is consistent with the experimental data, demonstrating the feasibility of using the present model to describe the energy dependence of fission yields.

Finally, the average TKE and average prompt neutron multiplicity $ \bar{\nu}_p $ as a function of the incident neutron energy are investigated in this study. The average TKE decreases with a less slope as the incident neutron energy increases. The linearly increasing tendency of $ \bar{\nu}_p $ with respect to the increase in the incident neutron energy is reproduced effectively, and the slope is consistent with the experimental data. However, the calculated results are generally 0.5 higher across the entire range of the incident neutron energies. It should be improved by considering the competition between the neutron and γ-ray emission, which will be examined in future studies.