Comparative analysis of jet and underlying event properties across various models as a function of charged particle multiplicity at 7 TeV

The history of hadron production is broad and extensive in high-energy and nuclear physics. A comprehensive understanding of hadron and multiparticle production in hadron-hadron collisions remains an open area of research in the field of high-energy particle physics. At the energies attained in the Large Hadron Collider (LHC), proton-proton collisions predominantly result in inelastic interactions, giving rise to jets stemming from hard parton-parton scatterings with momentum exchanges of the order of several GeV/c. The soft interactions between partons and remnants account for underlying events [1, 2]. Additionally, at low momentum transfer, diffractive processes and multi-parton interactions (MPIs) play pivotal roles in particle production. These partons originate from the strong interaction within hadrons [3]. Theoretical modeling of particle production in such environments relies on theoretical models that are calibrated to match experimental data. In high-energy interactions, momentum transfer between partons occurs at the scale of many GeV/c, which is described by perturbative quantum chromodynamics (pQCD). Understanding particle production in proton-proton collisions at LHC energies necessitates a complete understanding of the transition between the hard processes, governed by pQCD, and soft processes, described by non-perturbative models of QCD. Jets are narrow, cone-shaped sprays of particles produced when high-energy quarks or gluons fragment and hadronize after being scattered in particle collisions. Modern jet substructure techniques such as grooming and the soft-drop algorithm offer sophisticated methods for studying the properties of jets in addition to the standard jet definitions used in this analysis. These methods are especially useful for improving the resolution of jet mass and other observables and minimizing contamination from soft, wide-angle radiation. The soft-drop algorithm removes the softer, wide-angle components from the jet by applying specific criteria to the transverse momentum and the angular separation of jet constituents. This process results in a cleaner jet structure, which is important for precisely identifying and measuring the properties of the originating particles, particularly in high-background environments such as the LHC [4]. Enhancements have been made to the original soft-drop technique, such as recursive soft drop (RSD). RSD improves mass resolution and robustness against non-perturbative effects by repeatedly applying the soft-drop condition [5]. The probability associated with the creation of a specific number of particles in a collision is referred to as multiplicity distributions [6, 7]. These distributions encapsulate all relevant information regarding particle correlations. In the context of hadron-hadron and heavy ion collisions, multiplicity distributions play a crucial role in understanding particle production mechanisms. The mechanism governing particle production is linked to the probability $p_{n}$ , denoting the number of charged particles produced in the medium. The distributions of charged particle multiplicities encompass detailed information about both soft and hard interactions. These multiplicity distributions stand as fundamental and ubiquitous observables in high-energy physics experiments. Moreover, they provide insights into various aspects of the particle production mechanism and the process of hadronization. In this study, we conduct a comprehensive analysis of jets and underlying events as a function of charged particle multiplicity in proton-proton collisions at $ \sqrt{s}=7 $ TeV. Various Monte Carlo (MC) models, namely, Pythia8.3, EPOS4$_{\rm Hydro}$, EPOS4$_{\rm noHydro}$, EPOS1.99, and EPOSLHC, are employed for simulation, and their results are compared with CMS data. The simulation encompasses 1 million events. Although this study focuses on standard jet definitions, incorporating soft-drop and related grooming techniques in future analyses could potentially provide deeper insights and more precise measurements of the underlying event and jet properties. The remainder of this paper is structured as follows. Section II describes the methods and models utilized, Section III presents the results and subsequent discussion, and the conclusion is provided in Section IV.

Pythia [8] is the most widely used event generator in high-energy physics and related areas and can be used to simulate proton-proton collisions, as well as proton-antiproton and $e^{+}e^{-}$ collisions. Pythia primarily simulates parton showers and the interactions between partons. Its ability to analyze MPIs [9] and the Lund string fragmentation model [10, 11] is used for hadronization. Pythia simulates particle collisions through the following steps: hard scattering, parton showers, initial state radiation (ISR), final state radiation (FSR) [12, 13], and finally, hadronization. It employs the $p_{T}$-ordered approach [14] for parton showers and uses the original impact parameter for MPIs [15]. The Lund string fragmentation model is used for hadronization [11, 16], which is the final step of fragmentation. For particle collisions, the energy of the particles must be greater than 10 GeV because below this threshold, particles go into hadronic resonance and Pythia fails to provide accurate results. Therefore, 10 GeV is chosen as the limit for the standard scale. In $e^{+}e^{-}$ annihilation, this limit can be reduced; however, in proton-proton collisions below this limit, the Pythia model is not reliable. Conversely, Pythia is suitable for higher energy ranges and can be tested up to a center-of-mass energy of 100 TeV [17−21]. There is no internal facility for proton-nucleus and nucleus-nucleus collisions, but several programs interface with specific Pythia models, especially for decay processes, and string fragmentation algorithms are available. Users must either use the HEPMC [22] interface or write their own interface for simulation programs. Pythia events are always applicable at both the partonic and particle levels. Pythia8.3, written in C++, uses matching and merging techniques for parton showers and matrix elements.

EPOS is an event generator used for both cosmic ray air shower (EAS) simulations and heavy ion interactions. High-energy hadronic interactions are described by the EPOS model, which includes parton remnants [23]. EPOS is based on the string and quantum multiple scattering approach for various particle production mechanisms. It employs the Gribov-Regge-parton-based theory (GRPT) [24] for soft interactions. The EPOS model also accounts for energy conservation at the amplitude level and centrality dependence in heavy ion collisions.

In EPOS1.99 [23], the data are tuned to Tevatron energies. EPOSLHC [25] is an updated version of EPOS1.99, designed for LHC energies [26]. In EPOSLHC, different flow parameterizations for the core (small system but high-density matter) are introduced in proton-proton collisions compared to heavy ion collisions. The EPOSLHC model is tuned to 8 TeV; however, some parameters are still missing for 13 TeV. In EPOSLHC, minimum bias results are reproduced for particles with transverse momentum distributions ranging from 0 to a few GeV/c [25, 27]. The EPOSLHC model is also more accurate in reproducing multiplicity distributions at 7 TeV.

EPOS4 is an advanced MC model framework [28−30] designed to simulate the full evolution of high-energy heavy ion collisions, including both initial and final state interactions. In the EPOS4 approach, multiple scatterings, either partonic or nucleonic, occur in parallel, based on elementary considerations related to time scales. EPOS4 combines S-matrix theory (related to parallel scattering) with modern pQCD approaches and saturation concepts. This parallel scattering approach distinguishes between "primary scattering" and "secondary scattering". In parallel scattering, the initial primary nucleon and its partonic constituents are involved, occurring instantaneously at very high energies. The S-matrix is a theoretical tool that uses a specific form of proton-proton scattering S-matrix (Gribov-Regge theory) [30−33], which can also be used for nucleon-nucleon (AA) collisions. This feature offers a solid framework for understanding the initial dynamics of quark-gluon plasma (QGP) and its hadronization. The EPOS4 model can mainly be used in two versions: EPOS4$_{\rm Hydro}$ and EPOS4$_{\rm noHydro}$. In EPOS4 with Hydro, full hydrodynamic evolution, a hadronic cascade, the core-corona procedure, and equation of state are activated, whereas the other version operates without these. These two versions allow flexible simulations for different physical scenarios [34]. EPOSLHC, and EPOS4 are designed for LHC experiments and offer sophisticated features such as event-by-event fluctuations and complex initial state treatments. They are also flexible for cosmic ray simulations.

In our analysis, we utilize Rivet [35] to validate MC event generators and compare the model predictions with the experimental data. RIVET has an extensive code library that compares event generator predictions with experimental data available on HEPData.

We present a comprehensive analysis of jet and underlying event properties as a function of $ N_{\rm ch} $ at $\sqrt{s} = 7 $ TeV in pp collisions. Different MC models (Pythia8.308, EPOS1.99, EPOSLHC, and EPOS4) are used for simulations, and the MC predictions are compared with CMS data [36].

Jet and underlying event properties for charged particles:

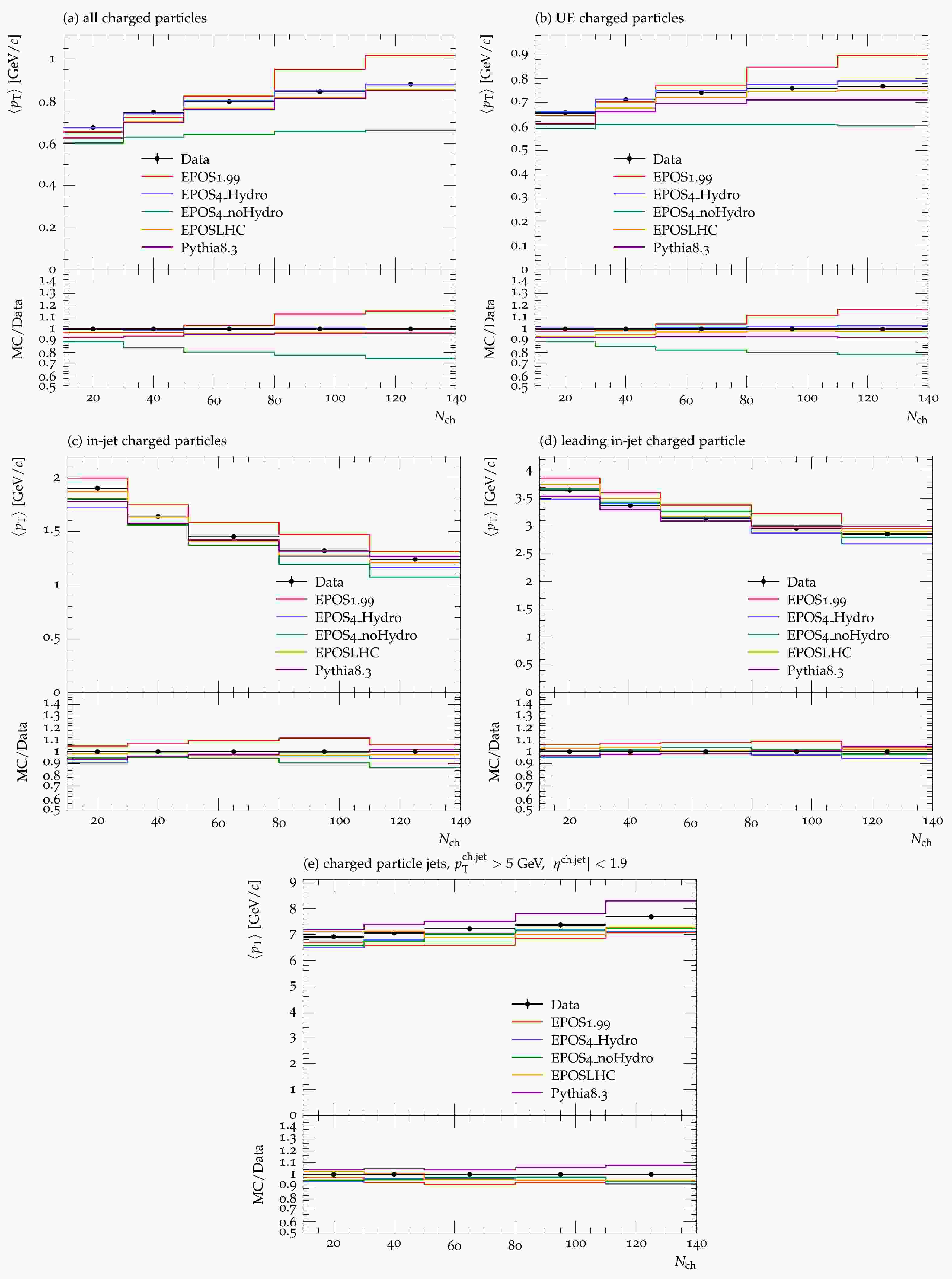
Figure 1 illustrates the mean transverse momentum ($ <p_T> $) for (a) all charged particles, (b) underlying event (UE) charged particles, (c) intra-jet charged particles, (d) leading intra-jet charged particles, and (e) charged particle jets as a function of charged particle multiplicity $ N_{\rm ch} $. $ <p_T> $ increases with an increase in charged multiplicity for all charged particles and underlying events (Fig. 1(a), (b)) and decreases with increasing charged multiplicity for jets (Fig. 1(c), (d), (e)). When comparing the MC models with the data for all charged particles, all models show good agreement with the experimental data except EPOS1.99, which overpredicts for $ N_{\rm ch}> $ 80, and EPOS4$ _{\rm Hydro} $ , which underpredicts for $ N_{\rm ch}> $30. For underlying event charged particles, all models exhibit good predictions at low $ N_{\rm ch} $, whereas EPOS4$ _{\rm Hydro} $ and EPOSLHC accurately reproduce the data over the entire range. The Pythia8 model produces comparatively better predictions than EPOS1.99 and EPOS4$ _{\rm noHydro} $. EPOS1.99 overpredicts and EPOS4$_{\rm noHydro}$ underpredicts the data. For intra-jet and leading intra-jet charged particles, the model comparison with the data reveals that all models accurately reproduce the data; however, EPOS1.99 overpredicts and EPOS4$ _{\rm Hydro} $ underpredicts at higher $N_{\rm ch} > 100$. This means that the EPOS4$ _{\rm Hydro} $, EPOSLHC, and Pythia8 models reproduce the data for the underlying event and intrajet charged particles for all given $ N_{\rm ch} $. As shown in Fig. 1, EPOS4$_{\rm Hydro}$ accurately reproduces the results for higher $ N_{\rm ch} $ because the hydro option increases the multiplicity and converts some energy into flow, resulting in the blue curve being considerably stronger than the other curves.

Figure 1.  (color online) Mean transverse momentum for (a) all charged particles, (b) underlying event (UE) charged particles, (c) intra-jet charged particles, (d) leading intra-jet charged particles, and (e) charged particle jets as a function of charged particle multiplicity $ N_{\rm{ch}} $. Different Monte Carlo models, that is, Pythia8.308 [8], EPOS1.99 [23], EPOSLHC [25], and EPOS4 [28], are compared with the experimental data [36].

Jet properties for charged particles:

In this section, we focus on the jet properties for charged particles, including the number of jets per event, differential jet $ p_T $ spectra, mean transverse momenta of jets, and jet widths. Figure 2 illustrates the charged jet rate per event plotted as a function of $N_{\rm ch}$ for $p^{\rm ch.jet}_{T} > 5$ GeV/c and $p^{\rm ch.jet}_{T} > 30$ GeV/c. The number of jets per event increases with increasing charged-particle multiplicity. This implies that a higher number of jets are generated for larger values of $N_{\rm ch}$. The jet rates increase from 0.05 to 4 jets/event as the charged particle multiplicity increases. In the case of $p^{\rm ch.jet}_{T} > 5~{\rm GeV/c}$, all models perform well in predicting the data, except the EPOS$4_{\rm noHydro}$ model, which underestimates the results when $N_{\rm ch} > 20$. Models such as Pythia8, EPOS$4_{\rm Hydro}$, EPOSLHC, and EPOS1.99 successfully reproduce the results for all given charged particle multiplicity distributions.

Figure 2.  (color online) Both panels show the number of charged particle jets vs. charged particle multiplicity for (a) $p^{\rm ch.jet}_{T} > 5$ GeV/c and (b) $p^{\rm ch.jet}_{T} > 30$ GeV/c in the region $|\eta| < 1.9$. The predictions of different Monte Carlo models (Pythia8.308 [8], EPOS1.99 [23], EPOSLHC [24], and EPOS4 [28]) are compared with the experimental data [36].

For $p^{\rm ch.jet}_{T} > 30~{\rm GeV/c}$, at low $ N_{\rm{ch}} $, only EPOSLHC effectively reproduces the results, whereas EPOS4$ _{\rm{Hydro}} $ disagrees with the data. At higher charged particle multiplicities, all models disagree except for EPOS4$_{\rm{Hydro}}$ and EPOSLHC, which show strong agreement with the data. Figure 3 illustrates differential jet $ p_{T} $ spectra for inclusive charged particles in an event for (a) $ 10<N_{\rm{ch}}\leq30 $ , (b) $ 30<N_{\rm{ch}}\leq50 $ , (c) $ 50<N_{\rm{ch}}\leq80 $ , (d) $ 80<N_{\rm{ch}}\leq110 $ , and (e) $ 110<N_{\rm{ch}}\leq150 $. When comparing MC models to the data, we find that for $ 10<N_{\rm{ch}}\leq30 $, all the models show good agreement with the data at $ p_{T}<10 $ GeV/c. The EPOSLHC model tends to overestimate the data for $ 10<p_{T}<25 $ GeV/c and underestimate for $ 25<p_{T}<35 $ GeV/c. The EPOS4$ _{\rm{Hydro}} $ model accurately reproduces the data for the $ 5<p_{T}<35 $ GeV/c range, whereas Pythia8 overestimates and EPOS4$ _{\rm{noHydro}} $ underestimates the data for $ p_{T}>10 $ GeV/c. For $ 30<N_{\rm{ch}}\leq50 $ and $ 50<N_{\rm{ch}}\leq80 $, all the models accurately predict the data at $ p_{T}<10 $ GeV/c. For the $ 10<p_{T}<35 $ GeV/c range, EPOSLHC and EPOS1.99 reproduce the results well, whereas EPOS4$ _{\rm{noHydro}} $ underestimates and Pythia8 overestimates the data. EPOS4$ _{\rm{Hydro}} $ disagrees with the data in the $ N_{\rm{ch}}>15 $ region. For $ 80<N_{\rm{ch}}\leq110 $ and $ 110<N_{\rm{ch}}\leq150 $, all models reproduce the data well for $ 5<p_{T}<10 $ GeV/c. For the intermediate and high $ p_{T} $ regions, Pythia8 overestimates and EPOS4$ _{\rm{Hydro}} $ and EPOS4$ _{\rm{noHydro}} $ agree well with the data. EPOS1.99 underestimates the data for the $ 15<p_{T}<35 $ GeV/c region, and for the higher $ p_{T} $ region, it fails to reproduce the results. Figure 4 illustrates the normalized charged-particle jet $ p_{T} $ density as a function of the distance to the jet axis R for events in five $ N_{\rm{ch}} $ intervals. The results of the MC predictions are compared with the data. The jet ρ increases as $ N_{\rm{ch}} $ increases. For the $ 10 < N_{\rm{ch}} \leq 30 $ and $ 30 < N_{\rm{ch}} \leq 50 $ intervals, when different MC predictions are compared with the data, we observe that for $ R < 0.05 $, EPOS4$_{\rm{Hydro}}$ and EPOSLHC provide good predictions, whereas Pythia8 underestimates and EPOS4$_{\rm{noHydro}}$ overestimates the data. For larger distances, the Pythia8 model overestimates the data, whereas the remaining models show excellent agreement with the data. EPOS4$_{\rm{Hydro}}$ and EPOS1.99 accurately reproduce the data for the entire distance. For the $ 50 < N_{\rm{ch}} \leq 80 $ and $ 80 < N_{\rm{ch}} \leq 110 $ ranges, when $ R < 0.1 $, EPOS4$_{\rm{Hydro}}$ and EPOSLHC provide good predictions, whereas Pythia8 underestimates and EPOS4$_{\rm{noHydro}}$ overestimates the data. For the $ 0.1 < R < 0.45 $ region, all models accurately reproduce the data. EPOS1.99 underestimates the data for greater distances from the jet axis. For the $ 110 < N_{\rm{ch}} \leq 140 $ range, all models overestimate the data except for EPOS4$_{\rm{Hydro}}$. However, in the intermediate region, EPOS4$_{\rm{Hydro}}$, EPOS4$_{\rm{noHydro}}$, Pythia8, and EPOSLHC provide good predictions, whereas EPOS1.99 underestimates the data. For larger values of R, EPOS4$_{\rm{noHydro}}$, EPOS4$_{\rm{Hydro}}$, EPOSLHC, and Pythia8 show good agreement with the data. However, EPOS1.99 performs differently, failing to reproduce the data for the $ R > 0.25 $ range.

Figure 3.  (color online) Differential jet $p_{T}$ spectra for inclusive charged particles in an event for (a) $10<N_{\rm{ch}}\leq30$ , (b)$30<N_{\rm{ch}}\leq50$ , (c) $50<N_{\rm{ch}}\leq80$ , (d) $80<N_{\rm{ch}}\leq110$ , and (e) $110<N_{\rm{ch}}\leq150$. Results of different Monte Carlo models (Pythia8.308 [8], EPOS1.99 [23], EPOSLHC [25], and EPOS4 [28]) compared with the experimental data [36].

Figure 4.  (color online) Normalized charged-particle jet $ p_{T} $ density ρ as a function of distance to the jet axis R for (a) $ 10<N_{\rm{ch}}\leq30 $ , (b) $ 30<N_{\rm{ch}}\leq50 $ , (c) $ 50<N_{\rm{ch}}\leq80 $ , (d) $ 80<N_{\rm{ch}}\leq110 $ , and (e) $ 110<N_{\rm{ch}}\leq140 $. Results of different Monte Carlo models (Pythia8.308 [8], EPOSLHC [25], EPOS1.99 [23], and EPOS4 [26]) compared with the experimental data [36].

In this study, we conduct a comprehensive analysis of jets and underlying events as a function of charged particle multiplicity in proton-proton (pp) collisions at a center-of-mass energy of $\sqrt{s} = 7$ TeV. Various MC event generators, including Pythia8.308, EPOS1.99, EPOSLHC, EPOS4$_{\rm{Hydro}}$, and EPOS4$_{\rm{noHydro}}$, are employed to predict particle production. The predictions from these models are compared with experimental data from the CMS collaboration. The produced particles are divided into two classes: those associated with underlying events and those associated with jets. The charged particles are tracked within $|\eta| < 2.4$ and $p_{T} > 0.25 \, \text{GeV}/\rm c$, whereas charged particle jets are calculated with $p_{T} > 5 \, \text{GeV}/\rm c$ using only charged particle information. We present jet $p_{T}$ distributions, the mean $p_{T}$ of underlying event and jet particles, jet rates, and normalized charged density as a function of $N_{\rm{ch}}$. We find that the mean transverse momentum for all charged particles and underlying event charged particles increases with charged-particle multiplicity. This indicates that at higher $N_{\rm{ch}}$, MPIs increase, and hard scattering occurs. When comparing the MC predictions with the CMS data, we find that all models agree well with the data at low $ N_{\rm{ch}} $. However, at higher $ N_{\rm{ch}} $, only EPOS4$_{\rm{Hydro}}$ and EPOSLHC generally align with the data. In contrast, the mean $ p_{T} $ for intra-jet and leading charged particle jets decreases logarithmically as the charged particle multiplicity increases. This indicates an opposite trend: a larger number of MPIs occur owing to softer processes. Consequently, the production of final state hadrons is attributed to (mini)jets. EPOS4$_{\rm{Hydro}}$, Pythia8, and EPOSLHC reproduce the results, whereas EPOS1.99 overestimates and EPOS4$_{\rm{noHydro}}$ underestimates the data; for charged particle jets, EPOS4$_{\rm{Hydro}}$ and EPOSLHC align with the data. These results suggest that EPOS models with a hydrodynamic component perform best as the charged particle multiplicity increases. This is because "turning on Hydro" increases the multiplicity, converting some energy into the flow, which allows EPOS4$_{\rm{Hydro}}$ to closely match the data and produce accurate results at higher $ N_{\rm{ch}} $ compared to other models. The similarity between the Pythia8 and EPOSLHC models arises from their use of partonic methods and perturbative approaches for describing hard collisions. When studying the charged jet rates, we observe that for the $ p^{\text{ch.jet}} > 5 \, \text{GeV}/\rm c $ range, Pythia8 and EPOS4$_{\rm{Hydro}}$ perform the best, with EPOSLHC also fitting the results well. EPOS1.99 initially under-predicts and then over-predicts the data, whereas EPOS4$_{\rm{noHydro}}$ consistently underestimates the data and does not perform well. For $ p^{\text{ch.jet}} > 30 \, \text{GeV}/\rm c $, no MC model performs best at low $ N_{\rm{ch}} $; however, at higher charged particle multiplicity, only EPOS4$_{\rm{Hydro}}$ performs well. This is due to the "Hydro = on" option, which reduces the multiplicity and converts some energy into flow, making the blue curve considerably stronger than the other curves. The EPOSLHC model also describes the data well owing to its incorporation of new collective flow effects and correlated flow treatment, which contrasts with the EPOS1.99 model. In the study of differential jet $ p_{T} $ spectra over five intervals, we find that for the selected intervals, all the given MC models agree well with the results at low and intermediate $ p_{T} $; however, for higher $ p_{T} $, EPOSLHC, EPOS4$ _{\rm{Hydro}} $, and EPOS4$ _{\rm{noHydro}} $ well agree with the data. Pythia8 overestimates whereas EPOS1.99 and EPOS4$ _{\rm{Hydro}} $ underestimate the data and do not effectively reproduce the results for higher $ p_{T} $. In the study of normalized charged $ p_{T} $ jet density over five intervals, we observe that only EPOS4$ _{\rm{Hydro}} $ and EPOSLHC perform well at low $ p_{T} $ however, at larger $ p_{T} $, all the given MC models agree well with the data. EPOS1.99 under-predicts the data with increasing $ N_{\rm{ch}} $. The EPOSLHC model describes the data well owing to the new collective flow effects, correlated flow treatment, and parameterization, compared to EPOS1.99. This suggests that each model has its advantages and limitations, which vary depending on the specific physical scenario. The suitability of a particular model is determined by the context of the investigation.