-
As we know from the last century, black holes have been proposed to be not only strong gravitational systems but also thermodynamic systems that satisfy the four laws of thermodynamics [1, 2]. In 1983, Hawking and Page [3] proved a phase transition between a pure AdS spacetime and stable large black hole state, i.e., Hawking-Page phase transition. Subsequently, it was explained as a confinement/deconfinement phase transition in the gauge theory [4]. This has led to more attention being paid to black holes. Because of the lack of pressure in traditional black hole thermodynamics, the authors of [5] expanded black hole thermodynamics into the expanded phase space by regarding the negative cosmological constant as pressure. Especially, the thermodynamical properties of AdS black holes in the expanded phase space have been widely investigated [6−18]. Recently, the holographic thermodynamics [19, 20] and restricted phase space thermodynamics [21−24] of AdS black holes have been proposed to give a holographic interpretation of black hole thermodynamics. Meanwhile, based on the ϕ-map topological flow theory [25], the authors of [26] presented that black hole solutions are just defects described by winding numbers. The corresponding winding number of local stable black holes is +1, while it is –1 for local unstable black holes. The topological number is simply the sum of all winding numbers to reveal the global topological nature of a black hole. Black hole solutions may be classified by topological numbers. Based on these results, we investigate the topological properties of charged AdS black holes under different gravity frames in the restricted phase space.
Recently, the authors of [27] investigated the restricted phase space thermodynamics in the higher dimensions and higher-order curvature gravities [28−30]. The subclass of Lanczos-Lovelock models with some particular choices of the coupling coefficients, known as the class of black hole scan models, was adopted to be a simple example for the application of extended-phase-space thermodynamics in higher-dimension and higher-order curvature gravity models with the characteristic parameters of (
$ d,k $ ). Parameter d represents the spacetime dimension, and k is an integer under condition$ 1\leq k\leq [(d-1)/2] $ , which represents the highest order of Lanczos-Lovelock densities appearing in the action. In the restricted phase space, the thermodynamics of three typical models with$ (d,k)=(5,1),\; (5,2),\; (6,2) $ , which are representative of the Einstein-Hilert (EH), Chern-Simons (CS), and Born-Infield (BI) like gravity models, were investigated. From the thermodynamical results, it is proven that the EH and BI like models seemingly belong to the same universality class, while the CS like models do not. Meanwhile, the RN-AdS black hole is the typical solution in the EH gravity model. Hence, in this work, we probed the topology of RN-AdS black holes and investigated whether the EH and BI like models belong to the same class from the perspective of topology in different ensembles.Inspired by these, in Sec. II, we first investigate the topology of the RN-AdS black hole under the restricted phase space frame in two different ensembles. Then, from the perspective of topology, we investigate whether two typical models with
$ (d,k)=(5,1),\; (6,2) $ belong to the same class in two different ensembles. A brief summary is given in Sec. IV. -
In this section, we discuss the topology of the RN-AdS black hole in different ensembles under the restricted phase space.
-
The metric of the four-dimensional RN-AdS black hole has the following form:
$ {\rm d}s^2=-f(r)c^2 {\rm d}t^2+f^{-1}(r) {\rm d}r^2+r^2\left( {\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2\right), $

(1) $ \begin{aligned}[b]& h(r)=1-\frac{2GM}{r}+\frac{G\bar q^2}{r^2}+\frac{r^2}{l^2},\; \; A^\mu=(\bar\phi(r)/c,0,0,0),\\& \bar\Phi(r)=\frac{\bar q}{r}, \end{aligned} $

(2) where l is related to the cosmological constant via
$ l^2=-3/\Lambda $ . As$ M>\bar q/\sqrt{G} $ , function$ h(r) $ has two distinct real zeros at$ r=r_{\pm} $ , where$ r_+ $ corresponds to the black hole event horizon radius. The black hole mass parameter can be described as$ M=\frac{r_+}{2G}\left(1+\frac{G\bar q^2}{r_+^2}+\frac{r_+^2}{l^2}\right). $

(3) In the restricted phase space for the RN-AdS black hole, the macro states are characterized by three pairs of dual thermodynamical parameters:
$ (S,T),\; (Q,\Phi), $ and$ (\mu,N) $ . The corresponding first law of thermodynamics and Smarr formula are$ \begin{array}{*{20}{l}} {\rm d} M=T {\rm d} S+\Phi {\rm d}Q+\mu {\rm d}N,\; \; M=TS+\Phi Q+\mu N \end{array} $

(4) with
$ \begin{aligned}[b]& M(S,Q,N)=\frac{S^2+\pi SN+\pi^2Q^2}{2\pi^{3/2}l(SN)^{1/2}},\\& T(S,Q,N)=\frac{3S^2+\pi SN-\pi^2Q^2}{4\pi^{3/2}lS(SN)^{1/2}}, \end{aligned} $

(5) $ \Phi=\left(\frac{\pi}{SN}\right)^{1/2},\; \; \mu=-\frac{S^2-\pi SN+\pi^2Q^2}{4\pi^{3/2}lN(SN)^{1/2}}, $

(6) $ G=\frac{l^2}{N},\; \; S=\frac{\pi r_+^2}{G},\; \; Q=\frac{ql}{\sqrt{G}}. $

(7) If parameters
$ S,\; Q,\; N $ are scaled as$S\rightarrow \lambda S$ ,$Q\rightarrow \lambda Q, N\rightarrow \lambda N$ , respectively, from Eq. (7), we can see that the mass parameter will also be scaled as$ M\rightarrow \lambda M $ , and$ T,\; \Phi,\; \mu $ will not be scaled. Hence, the first-order homogeneity of the mass parameter and zeroth-order homogeneity of$ T,\; \Phi,\; \mu $ are clear. Note that the zeroth-order homogeneous functions are intensive at the critical point$ S_c=\frac{\pi N}{6},\; \; T_c=\frac{\sqrt{6}}{3\pi l},\; \; Q_c=\frac{N}{6},\; \; F_c=\frac{\sqrt{6}N}{18l}. $

(8) Introducing relative parameters
$ s=S/S_c,\; t=T/T_c, \; q=Q/Q_c $ and the Legendre transform of Eq. (7), the relative parameter of free energy is given as [23]$ f\equiv\frac{F}{F_c}=\frac{q^2+s^2+6s-4ts^{3/2}}{4s^{1/2}}, \; \; F(T,Q,N)=M(T,Q,N)-TS. $

(9) To uncover the thermodynamical topology, vector field mapping
$ \phi:\; X=\{(s,\theta)|0<s<\infty, \;\; 0< \theta< \pi\}\rightarrow \mathbb{R}^2 $ is defined as [26, 31−34]$ \phi(s,\theta)=\left(\frac{\partial f}{\partial s},-\cot\theta\csc\theta\right). $

(10) When parameter s is used to characterize an AdS black hole, it becomes the first parameter of the domain of mapping ϕ. Another parameter θ serves as an auxiliary function and is utilized to construct the second component of the mapping. Component
$ \phi^\theta $ is divergent at$ \theta=0,\; \pi $ ; thus, the direction of the vector points outward there. It is obvious that the zero point of ϕ corresponds to a black hole with a temperature of$ T=\tau^{-1} $ as$ \theta=\pi/2 $ . Therefore, the zero point of the mapping can be used to characterize the black hole solution with a given parameter, τ. Based on Duan's$ \phi- $ mapping topological current theory [25, 35], the zero point of mapping ϕ is linked to the topological number. The topological number can be obtained by the weighted sum of the zero points of mapping ϕ. The weight of each zero point is determined by its nature. A saddle point has a weight of negative one, and conversely, the weight of an extremum point is one. A topological current can be described in the following form:$ j^\mu=\frac{1}{2}e^{\mu\nu\rho}\epsilon_{ab}\partial_\nu n^a \partial_\rho n^b,\; \; \; \; \mu,\nu,\rho=0,1,2,\; \; a,b=1,2, $

(11) where n is the unit vector
$ (n^s,n^\theta) $ with$ n^s=\phi^s/\parallel\phi\parallel $ and$ n^\theta=\phi^\theta/\parallel\phi\parallel $ . Further, it satisfies the conserve law:$ \partial_\mu j^\mu=0 $ . As shown in Refs. [36, 37], the topological current is a δ-function of the field configuration$ j^\mu=\delta^2(\phi)J^\mu\left(\frac{\phi}{x}\right), $

(12) where the three-dimensional Jacobian reads
$ \epsilon^{ab}J^\mu\left(\frac{\phi}{x}\right)= \epsilon^{\mu\nu\rho}\partial_\nu \phi^a \partial_\rho \phi^b $ . As$ \phi^a(x_i)=0 $ , the topological current equals zero. The topological number in parameter region Σ can be calculated by the following expression:$ W=\int_\Sigma j^0 {\rm d}^2x=\sum\limits^{\bar N}_{i=1}\beta_i\eta_i=\sum\limits^{\bar N}_{i=1}w_i, $

(13) where
$ j^0=\sum\limits^{\bar N}_{i=1}\beta_i\eta_i\delta^2\left(\overrightarrow{x}-\overrightarrow{s}_i\right) $ is the density of the topological current, and$ \beta_i $ is the Hopf index, which is always positive.$ s_i $ is the i-th zero point of mapping ϕ, and$\eta_i={\rm sign} J^0(\phi/x)_{s_i}=\pm 1$ is the Brouwer degree. For the i-th zero point of the vector, winding number$ w_i $ is determined by the stability of the black hole state.In the canonical ensemble, substituting Eq. (9) into Eq. (10), we have
$ \phi^s=\frac{\partial f}{\partial s}=-\frac{q^2}{8s^{3/2}}+\frac{3s^{1/2}}{8}+\frac{3}{4s^{1/2}}-\frac{1}{\tau}, \; \; \phi^\theta=-\cot\theta\csc\theta. $

(14) The zero points are determined by the expression:
$ \phi^s=0 $ . Thus, we have$ \frac{1}{\tau}=-\frac{q^2}{8s^{3/2}}+\frac{3s^{1/2}}{8}+\frac{3}{4s^{1/2}}. $

(15) It is obvious that there are two extremes:
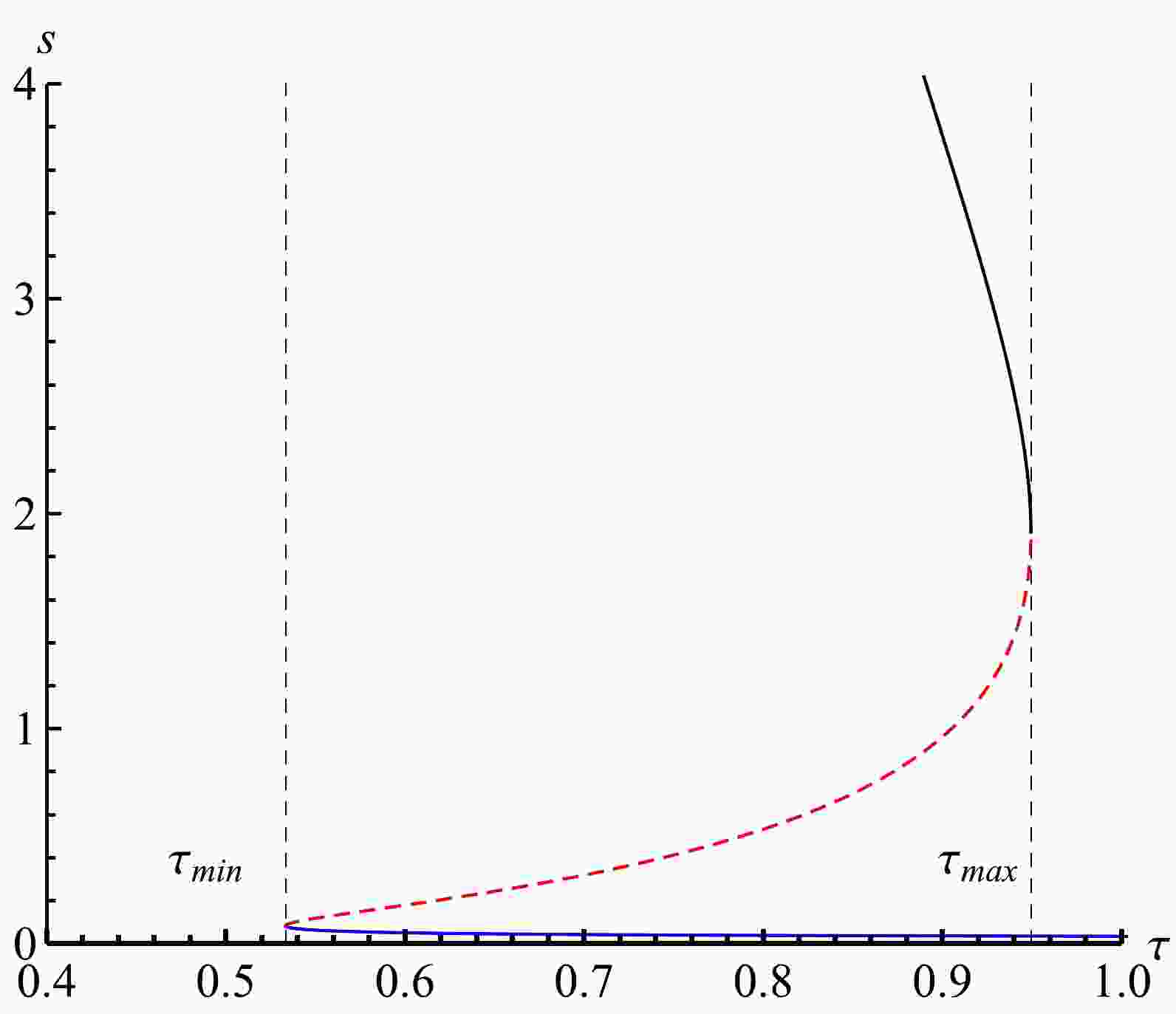
$\tau_{\rm min,max}=\dfrac{2\left(1\mp\sqrt{1-q^2}\right)^{3/2}}{3(1\mp\sqrt{1-q^2})-q^2}$ . As$ q=1 $ ,$\tau_{\rm min}=\tau_{\rm max}= \tau_c=1$ . Note that the generation point satisfies constraint conditions$ \dfrac{\partial\tau}{\partial s}=0,\; \dfrac{\partial^2\tau}{\partial s^2}>0 $ , and the annihilation point obeys conditions$ \dfrac{\partial\tau}{\partial s}=0,\; \dfrac{\partial^2\tau}{\partial s^2}<0 $ . The zero points of$ \phi^s $ in the diagram of$ \tau-s $ is displayed in Fig. 1.$\tau_{\rm min}$ is related to the generation point, and$\tau_{\rm max}$ is related to the annihilation point. As$ \tau_{\min}<\tau<\tau_{\max} $ , there are three intersection points for the RN-AdS black hole in the canonical ensemble. The black, red dashed, blue lines represent a low-potential black hole (LPSB), intermediate-potential black hole (IPBH), and high-potential black hole (HPBH), respectively, which are the stable, unstable, and stable black hole states, respectively, and the corresponding winding numbers are 1, –1, 1, respectively. Thus, the topological number is$ W=1-1+1=1 $ as$ \tau_{\min}<\tau<\tau_{\max} $ . The intersection points exactly satisfy the equation$ \tau=1/T $ . For$\tau=\tau_{\rm min,max}$ , the three intersection points for the RN black hole coincide, and they will disappear as$\tau < \tau_{\rm min}$ or$\tau > \tau_{\rm max}$ ; the three branches of black holes reduce to the one stable black hole, and the topological number is still one. These results are consistent with those of Ref. [38]. -
We proceed to investigate the topology of the RN-AdS black hole in the grand canonical ensemble. For the given values of Φ and N, from Eq. (7), the minimum temperature reads [23]
$ T_{\rm min}=\frac{\sqrt{3}}{2}\frac{\left(1-l^2\Phi^2\right)^{1/2}}{\pi l}.$

(16) The corresponding minimum entropy, mass parameter, and free energy are
$S_{\rm min}=\frac{\pi N}{3}\left(1-l^2\Phi^2\right),\; \; M_{\rm min}=\frac{N\left(2+l^2\Phi^2\right)}{3\sqrt{3}l}\left(1-l^2\Phi^2\right)^{1/2}, $

$ F_{\rm min}=\frac{N\left(1+5l^2\Phi^2\right)}{6\sqrt{3}l}\left(1-l^2\Phi^2\right)^{1/2}. $

(17) By introducing relative parameters
$t=T/T_{\rm min},\; s=S/S_{\rm min}, m=M/M_{\rm min},\; f=F/F_{\rm min}$ , we can obtain the following expression:$ f=\frac{s^{1/2}\left[3+s+(3-s)l^2\Phi^2\right]}{1+5l^2\Phi^2}-\frac{3ts\left(1-l^2\Phi^2\right)^{1/2}}{1+5l^2\Phi^2}. $

(18) Thus, the component of mapping
$ \phi^s $ reads$ \phi^s=\frac{3\left[1+s(1-l^2\Phi^2)+l^2\Phi^2\right]} {2s^{1/2}(1+5l^2\Phi^2)}-\frac{3t\left(1-l^2\Phi^2\right)^{1/2}}{1+5l^2\Phi^2}.$

(19) Hence, we have
$ \tau=\frac{2s^{1/2}\left(1-l^2\Phi^2\right)^{1/2}}{\left[1+s(1-l^2\Phi^2)+l^2\Phi^2\right]}. $

(20) There exists one extreme:
$\tau_{\rm extr}=\sqrt{\frac{\left(1-l^4\Phi^4\right)}{\left(1+l^4\Phi^4\right)}}$ . The zero points of$ \phi^s $ in the diagram of$ \tau-s $ are displayed in Fig. 2.$\tau_{\rm extr}$ is related to the annihilation point. As$\tau < \tau_{\rm extr}$ , there are two intersection points for the RN-AdS black hole in the grand canonical ensemble. The red and blue lines represent the LPSB and HPBH, respectively, which are the stable and unstable black hole states, respectively. and the corresponding winding numbers are 1 and –1, respectively. Thus, the topological number is$ W=1-1=0 $ as$\tau < \tau_{\rm extr}$ . For$\tau=\tau_{\rm extr}$ , the two intersection points for the RN black hole coincide. Furthermore, there is no black hole as$\tau > \tau_{\rm extr}$ . -
Recently, the restricted phase space thermodynamics was shown to be applicable to a large class of higher-dimension and higher-order curvature gravity models with coupling to the Maxwell field [27, 39], which are known as black hole scan models [40] and are labeled by spacetime dimension d and highest order k of the Lanczos-Lovelock densities appearing in the action.
$ (d, k) = (5, 1) $ ,$ (5, 2) $ , and$ (6, 2) $ are chosen as example cases and studied here in detail. These cases are the representatives of EH, CS, and BI like gravity models. However, the CS like$ (5, 2) $ model behaves quite differently. This seems to indicate that the EH and BI like models belong to the same universality class, while the CS like model does not. In this section, we determine whether the EH and BI like models belong to the same universality class from a topological perspective.Specifically, the metric function of black holes in higher dimensions and higher-order curvature gravities with coupling to Maxwell's field was given in Refs. [27, 39, 40] as follows:
$ \begin{aligned}[b]& {\rm d}s^2_{(d,k)}=-f_{(d,k)}(r){\rm d}t^2+f_{(d,k)}^{-1}(r){\rm d}r^2+r^2{\rm d}\Omega^2_{d-2},\\& f_{(d,k)}(r)=1+\frac{r^2}{l^2}-\left(\frac{2G_{(d,k)}M+\delta_{d-2,k,1}}{r^{d-2k-1}} -\frac{G_{(d,k)}Q^2}{(d-3)r^{2(d-k-2)}}\right)^{1/k},\\& \Phi=\frac{Q}{(d-3)r^{d-3}}, \end{aligned} $

(21) where
$ G_{(d,k)} $ is the Newton constant, and$ \delta_{d-2,k,1} $ is the Kronecker delta function. Q and M are the charge and mass parameters of the black hole, respectively. Note that for$ k=1 $ , the three-dimensional black hole [41, 42] and Schwarzschild-AdS solutions of the higher-dimensional EH action with negative cosmological constant can both be recovered. Moreover, when setting$ k=\left[\dfrac{d-1}{2}\right] $ , we can also obtain the black hole solutions corresponding to BI and CS theories [43].Black hole horizon
$ r_h $ is located at one of the zero points of$ f_{(d,k)}(r) $ . By solving equation$ f_{(d,k)}(r_h)=0 $ , the black hole mass parameter can be obtained as follows:$ M(r_h,G_{(d,k)},Q)=-\frac{\delta_{d-2,k,1}}{2G_{(d,k)}} +\frac{r_h^{d-2k-1}\left(1+r_h^2/l^2\right)^k}{2G_{(d,k)}} +\frac{Q^2}{2(d-3)r_h^{d-3}}. $

(22) The temperature of the black hole can be evaluated by the Euclidean period method, which gives
$ \begin{aligned}[b] T=\;&\frac{1}{4\pi k r_h^{2d-1}}\left(1+r_h^2/l^2\right)^{1-k} \Big[(d-2k-1)r_h^{2d}\left(1+r_h^2/l^2\right)^{k}\\&-G_{(d,k)}Q^2r_h^{2k+4}\Big] +\frac{r_h}{2\pi l^2}. \end{aligned} $

(23) The entropy of the black hole was given in Ref. [39] in the following form:
$ S=\frac{2\pi k}{G_{(d,k)}}\int_0^{r_h}r^{d-2k+1} \left(1+r^2/l^2\right)^{k-1} {\rm d} r. $

(24) To establish the restricted phase space thermodynamics (RPST) of the
$ (d,k)- $ models, we introduce two thermodynamical parameters: effective number of the microscopic degrees of freedom N and chemical potential μ, which are defined as$ N=\frac{L^{d-2k}}{G_{(d,k)}},\; \; \mu=(M-TS-\Phi Q)/N. $

(25) Here, L is a constant that is introduced to make N dimensionless. The corresponding re-scaled charge and potential are
$ \widetilde{Q}=\frac{QL^{(d-2k)/2}}{\sqrt {G_{(d,k)}}},\; \; \widetilde{\Phi}=\frac{Q\sqrt {G_{(d,k)}}}{(d-3)L^{(d-2k)/2}r_h^{d-3}}. $

(26) The thermodynamical parameters satisfy the following expressions:
$ \begin{array}{*{20}{l}} M=TS+\widetilde{\Phi}\widetilde{Q}+\mu N,\; \; {\rm d} M=T{\rm d}S+\widetilde{\Phi}{\rm d}\widetilde{Q}+\mu {\rm d}N. \end{array} $

(27) Note that the above equations indicate that the RPST formalism holds for the
$ (d,k)- $ models with$ d>3 $ . -
Setting
$ (d,k)=(5,1) $ , Eq. (21) becomes$ f_{(5,1)}=1+\frac{r^2}{l^2}+\frac{G_{(5,1)}Q^2}{2 r^4} -\frac{2G_{(5,1)}M}{r^2}. $

(28) This is the black hole solution in the EH gravity theory, and the entropy is
$ S=A/4G $ with Newton constant$ G=3\pi G_{(5,1)}/4 $ . Through the transformations$ \begin{aligned}[b]& r_h=[3SL^3/(2\pi N)]^{1/3},\;\; G_{(5,1)}=L^3/N, \\&Q=\widetilde{Q}/\sqrt{N}, \;\; \widetilde{S}=(3SL^3/N)^{1/3}, \end{aligned} $

(29) the temperature and mass parameter of the black hole can be rewritten as
$ T=\frac{\widetilde{S}}{2(2\pi)^{2/3}} \left(2+4\widetilde{S}^2(2\pi)^{-2/3}/l^2 -\frac{(2\pi)^{4/3}L^3\widetilde{Q}^2}{N^2\widetilde{S}^4}\right), $

(30) $ M=\frac{\widetilde{S}^2N}{2(2\pi)^{2/3}L^3} \left(1+\frac{(2\pi)^{-2/3}\widetilde{S}^2}{l^2} +\frac{(2\pi)^{4/3}L^3\widetilde{Q}^2}{2N^2\widetilde{S}^4}\right),$

(31) It is clear that when
$ \widetilde{S}\rightarrow \lambda\widetilde{S}, \; \widetilde{Q}\rightarrow \lambda\widetilde{Q},\; N\rightarrow \lambda N $ , the mass parameters behave as$ M\rightarrow \lambda M $ , while the temperature remains unchanged under these re-scalings. From these thermodynamical parameters, we can obtain the critical point$ \begin{aligned}[b]& \widetilde{S}_c=\frac{(2\pi)^{1/3}l}{\sqrt{3}},\; \; \widetilde{Q}_c=\sqrt{\frac{2}{135}}\frac{l^2N}{L^{3/2}},\\& T_c=\frac{4\sqrt{3}}{5\pi l},\; \; M_c=\frac{7l^2N}{30L^3},\; \; F_c=\frac{l^2N}{18L^3}. \end{aligned} $

(32) With relative parameters
$ t=T/T_c,\; s=S/S_c, \; q=Q/Q_c, \widetilde{\phi}=\widetilde{\Phi}/\widetilde{\Phi}_c,\; m=M/M_c,\; f=F/F_c $ , the relative free energy reads as$ f=mM_c/F_c-tsT_cS_c/F_c=s^{4/3}+3s^{2/3}+\frac{q^2}{5s^{2/3}}-\frac{16s}{5\tau}. $

(33) From the above equation, the components of mapping ϕ can be written as
$ \phi^s=\frac{4s^{1/3}}{3}+\frac{2}{s^{1/3}}-\frac{2q^2}{15s^{5/3}}-\frac{16}{5\tau},\; \; \phi^\theta=-\cot\theta\csc\theta. $

(34) The zero points of mapping ϕ can be calculated by
$ \phi^s=0 $ . We solve this and get$ \tau=\frac{5s^{1/3}}{12}+\frac{5}{8s^{1/3}}-\frac{q^2}{24s^{5/3}}. $

(35) In Fig. 3, we can see that there are three branches as
$ \tau_{\min}<\tau<\tau_{\max} $ , a large black hole branch for$ \tau<\tau_{\min} $ , and a small black hole branch for$ \tau>\tau_{\max} $ . This indicates the existence of a phase transition in the region of$ \tau_{\min}<\tau<\tau_{\max} $ . The winding numbers of the large black hole branch for$ \tau<\tau_{\min} $ and small black hole branch for$ \tau>\tau_{\max} $ , which are stable, both read$ w=1 $ . The corresponding topological number equals one. Meanwhile, for the system in the region of$ \tau_{\min}<\tau<\tau_{\max} $ , there exist the stable large and small black holes and the unstable intermediate black hole; thus, the corresponding winding numbers are$ w=1,1,-1 $ . The topological number is$ W=1 $ . These results are consistent with those for the RN-AdS black hole in the canonical ensemble. -
In the grand canonical ensemble, using Eqs. (25), (26), and (29), we can obtain
$ Q^2=\frac{4N\widetilde{\Phi}^2}{(2\pi)^{4/3}} \left(\frac{3L^3S}{N}\right)^{4/3},\; \; \widetilde{S}=L\left(\frac{3S}{N}\right)^{1/3}.$

(36) Then, substituting them into Eqs. (30) and (31), the temperature and mass parameter become
$ T=\left(\frac{3\pi^2NL^3}{2S}\right)^{1/3} \left(2+\frac{4L^2}{l^2}\left[\frac{3S}{2\pi N}\right]^{2/3} -4\widetilde{\Phi}^2L^3\right), $

(37) $ M=\frac{N}{2L}\left(\frac{3S}{2\pi N}\right)^{2/3} \left(1+\frac{L^2}{l^2}\left[\frac{3S}{2\pi N}\right]^{2/3}+2\widetilde{\Phi}^2L^3\right). $

(38) From the above equation, the minimum temperature is determined by
$\dfrac{\partial T}{\partial S}=0$ , yielding$ T_{\rm min}=\frac{\sqrt{2(1-2\widetilde{\Phi}^2L^3)}}{\pi l}, $

(39) and the corresponding minimum entropy, mass, and free energy read
$ \begin{aligned}[b] S_{\rm min}=\frac{\pi Nl^3\left(1-2\widetilde{\Phi}^2L^3\right)^{3/2}}{3\sqrt{2}L^3},\end{aligned} $

$ \begin{aligned}[b] M_{\rm min}=\;&\frac{Nl^2(1-2L^3\widetilde{\Phi}^2)(3+2L^3\widetilde{\Phi}^2)}{8L^3},\\ F_{\rm min}=\;&\frac{N(1+5l^2\widetilde{\Phi}^2) \left(1-\widetilde{\Phi}^2l^2\right)^{1/2}}{6\sqrt{3}l}. \end{aligned} $

(40) With definitions
$f=F/F_{\rm min}=(M-TS)/F_{\rm min},\; 1/\tau= t=T/T_{\rm min},\; s=S/S_{\rm min}$ , we can obtain the components of mapping ϕ as follows:$ \phi^s=\frac{\partial f}{\partial s}=\frac{1}{F_{\rm min}} \left(\frac{\partial M}{\partial s}-\frac{T_{\rm min}S_{\rm min}}{\tau}\right),\; \; \phi^\theta=-\cot\theta\csc\theta. $

(41) The zero points of mapping ϕ can be calculated by
$ \phi^s=0 $ . Solving this, we get$ \tau=\frac{\sqrt{2}s^{1/3}(1-2L^3\widetilde{\Phi}^2)} {1+2L^3\widetilde{\Phi}^2+s^{2/3}(1-2L^3\widetilde{\Phi}^2)}. $

(42) As
$ s=(1+2L^3\widetilde{\Phi}^2)^{3/2}/(1-2L^3\widetilde{\Phi}^2)^{3/2} $ ,$\tau=\tau_{\rm max}= \dfrac{\sqrt{2}}{ \left(\left[\frac{1+2L^3\widetilde{\Phi}^2}{1-2L^3\widetilde{\Phi}^2}\right]^{1/3} +\left[\frac{1+2L^3\widetilde{\Phi}^2}{1-2L^3\widetilde{\Phi}^2}\right]^{2/3}\right)}$ . The zero points of$ \phi^s $ in the diagram of$ \tau-s $ are displayed in Fig. 4.$\tau_{\rm max}$ is related to the annihilation point. As$\tau < \tau_{\rm max}$ , there are two intersection points for the AdS black hole under the$ (5,1) $ -model frame in the grand canonical ensemble. The red and blue lines represent the LPSB and HPBH, which are the stable and unstable black hole states, respectively, and the corresponding winding numbers are 1, –1, respectively. Thus, the topological number is$ W=1-1=0 $ as$\tau < \tau_{\rm max}$ . For$\tau=\tau_{\rm max}$ , the two intersection points for this type of AdS black holes coincide. Furthermore, there is no black hole as$\tau > \tau_{\rm max}$ . -
When adopting
$ (d,k)=(6,2) $ , the Wald entropy for the charged spherically symmetric AdS black hole solution was given in Ref. [27] as$ S=\pi\sqrt{\frac{8Mr_h^3-2Q^2/\pi}{G_{(6,2)}l^4}}-\frac{r_h^4}{G_{(6,2)}l^2} . $

(43) With definitions
$ \bar S=L^2S/N+\pi l^2,\; \bar Q=Q/N $ , the corresponding radiation temperature and mass parameter are$ T=\frac{5\bar S^2-14\pi^{1/2}l\bar S^{3/2}+13\pi l^2\bar S-4\pi^{3/2}l^3\bar S^{1/2}-\pi^2L^2\bar Q^2}{8\pi^{5/4}l^{3/2}\bar S^{1/2}\left(\bar S^{1/2}-\pi^{1/2}l\right)^{5/2}}, $

(44) $ M=N\frac{3\bar S^2-6\pi^{1/2}l\bar S^{3/2}+3\pi l^2\bar S+\pi^2L^2\bar Q^2}{6\pi^{5/4}l^{3/2}L^2\left(\bar S^{1/2}-\pi^{1/2}l\right)^{3/2}}. $

(45) From these thermodynamical parameters, the critical point reads
$ \bar S_c=(0.9058+\pi)l^2,\; \bar Q=0.0358l^2/L,\; T_c=0.1747/l, $

(46) $ \widetilde{\Phi}_c=0.2406/(lL),\; M_c=0.241lN/L^2,\; F_c=0.0828lN/L^2. $

(47) By introducing relative parameters
$ f=F/F_c= (M-TS)/F_{c},\; 1/\tau=t=T/T_{c},\; s=\bar S/\bar S_{c},\; q=\bar Q/\bar Q_c $ , the component of mapping$ \phi^s $ reads$ \begin{aligned}[b]\\ \phi^s=\frac{\partial }{\partial s}\frac{3(0.9058+\pi)^2s^2 -6\sqrt{\pi}(0.9058+\pi)^{3/2}s^{3/2} +3\pi(0.9058+\pi)s+(0.0358q\pi)^2} {0.4968\pi^{5/4}\left[\sqrt{(0.9058+\pi)s}-\sqrt{\pi}\right]^{3/2}} -\frac{1.91115}{\tau}. \\\end{aligned} $ 
(48) The zero points of mapping ϕ can be calculated by
$ \phi^s=0 $ . In Fig. 5, we can see that there are three branches as$ \tau_{\min}<\tau<\tau_{\max} $ , a large black hole branch for$ \tau<\tau_{\min} $ , and a small black hole branch for$ \tau>\tau_{\max} $ . This indicates the existence of a phase transition in the region of$ \tau_{\min}<\tau<\tau_{\max} $ . The winding numbers of the large and small black hole branches, which are stable, both read$ w=1 $ . The corresponding topological number equals one. While for the system in the region of$ \tau_{\min}<\tau<\tau_{\max} $ , there exist the stable large and small black holes and the unstable intermediate black hole; thus, the corresponding winding numbers are$ w=1,1,-1 $ . The topological number is$ W=1 $ . These results are consistent with those for the RN-AdS and AdS black holes under the$ (5,1) $ -model in the canonical ensemble. -
In this section, we consider the topology of the charged AdS black hole for the case of
$ (6,2) $ -model in the grand canonical ensemble. From Eq. (24), we have$ r_h^2=l^2\left(-1+\sqrt{1+\frac{SG_{(6,2)}}{\pi l^2}}\right). $

(49) With the above equation, Eqs. (25) and (26), and definition
$ \widetilde{S}=\bar S/(\pi l^2)=\dfrac{L^2S}{\pi l^2N}+1,\; \bar Q=Q/N $ , Eqs. (44) and (45) can be rewritten as$ M=\frac{Nl\left[\widetilde{S}^2-2\widetilde{S}^{3/2}+\widetilde{S} +3\widetilde{\Phi}^2N^2l^2L^2(\sqrt{\widetilde{S}}-1)^3\right]} {2L^2(\sqrt{\widetilde{S}}-1)^{3/2}}, $

(50) $ T=\frac{5\widetilde{S}^2-14\widetilde{S}^{3/2}+13\widetilde{S} -4\widetilde{S}^{1/2}-9\widetilde{\Phi}^2N^2l^2L^2(\sqrt{\widetilde{S}}-1)^3} {8\pi l\sqrt{\widetilde{S}}(\sqrt{\widetilde{S}}-1)^{5/2}}. $

(51) Through redefinitions
$ f(\widetilde{S})=F{\text Ł}^2/(lN),\; m(\widetilde{S})= M{\text Ł}^2/(lN), 1/\tau=t(\widetilde{S})=TlN $ , the components of mapping ϕ read$ \begin{aligned}[b]&\phi^{\widetilde{S}}=\frac{\partial f(\widetilde{S})}{\partial\widetilde{S}}=\frac{\partial m(\widetilde{S})}{\partial\widetilde{S}}-\frac{1}{\tau}.\\& \phi^\theta=-\cot\theta\csc\theta,\end{aligned} $

(52) From the zero-point equation of mapping
$ \phi^{\widetilde{S}}=0 $ , we can obtain$ \frac{1}{\tau}=\frac{5\widetilde{S} +\sqrt{\widetilde{S}}(9\widetilde{\Phi}^2N^2l^2L^2-4) -9\widetilde{\Phi}^2N^2l^2L^2} {8\sqrt{\widetilde{S}}\sqrt{\sqrt{\widetilde{S}}-1}}. $

(53) The zero points of
$ \phi^{\widetilde{S}} $ in the diagram of$ \tau-\widetilde{S} $ are displayed in Fig. 6.$\tau_{\rm max}$ is related to the annihilation point. As$\tau < \tau_{\rm max}$ , there are two intersection points for the AdS black hole under the$ (6,2) $ -model frame in the grand canonical ensemble. The red and blue lines represent the LPSB and HPBH, respectively, which are the stable and unstable black hole states, respecitvely, and the corresponding winding numbers are 1, –1. Thus, the topological number is$ W=1-1=0 $ as$\tau < \tau_{\rm max}$ . For$\tau=\tau_{\rm max}$ , the two intersection points for this type of AdS black holes coincide. Furthermore, there is no black hole as$\tau > \tau_{\rm max}$ . -
In this work, under the restricted phase space frame, we investigated the thermodynamical topology of the RN-AdS black hole as well as two typical models of
$ (d,k)=(5,1),\; (6,2) $ in higher dimensions and higher-order curvature gravities. The results showed that the topology numbers for these black holes in the canonical and grand canonical ensembles are different. For the charged AdS black holes (both the RN-AdS black hole and two others with$ (d,k)=(5,1),\; (6,2) $ ) in the canonical ensemble, the topological number is +1, while it is zero for the charged AdS black holes in the grand canonical ensemble. This also proves that the EH and BI like models belong to the same gravitational classification from the thermodynamical topology perspective. -
We would like to thank Prof. Ren Zhao for his indispensable discussions and comments.
Topology of charged AdS black hole in restricted phase space
- Received Date: 2024-03-11
- Available Online: 2024-09-15
Abstract: The local topological properties of black hole systems can be expressed through winding numbers as defects. To date, AdS black hole thermodynamics are often depicted by the dual parameters of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: