-
The tau (
$ \tau^\pm $ ) lepton, as the heaviest and third-generation lepton within the Standard Model (SM), is considered a crucial gateway to uncovering new physics (NP). Various NP models postulate the involvement of the tau lepton in mechanisms that either alter SM predictions for tau-related processes or introduce novel interactions. Notably, these include the presence of an additional gauge boson$ Z' $ , which exhibits either flavor-conserving or flavor-changing interactions, additional scalar particles that facilitate flavor-changing interactions [1−8], and quantum-induced dipole interactions [9, 10]. Moreover, recent experimental observations indicate deviations from the lepton flavor universality, exemplified by discrepancies in$ R_D $ ($ R_{D^\ast} $ ) and$ R_K $ ($ R_{K^\ast} $ ) ratios [11−13]. These findings not only challenge the completeness of the SM but also highlight the tau lepton's pivotal role in probing NP. Furthermore the long standing muon$ g-2 $ anomaly [14−16] stimulates interests in testing the tau lepton dipole moments [17−20].The low-energy lepton colliders, such as Belle-II and the super tau charm factory (STCF) with collision energies of 4−7 GeV [21, 22], are considered promising platforms for these types of measurements, as billons of tau leptons will be produced based on the process
$e^-e^+\to \tau^-\tau^+$ , contributing from quantum electrodynamics current interactions. Additionally, increasing interest has been directed toward exploring both the direct and indirect potentials of low-energy lepton colliders in various NP searches. Research into NP manifestations in meson decays [23] or through non-standard interactions [24] has been thoroughly pursued. The potential for directly detecting additional vector bosons, such as the dark photon$ A' $ or$ Z' $ , has been investigated at the STCF [21, 22].In this study, we explore the capabilities of low-energy lepton colliders in probing dipole operators and four-fermion operators, with a particular emphasis on their contribution to process
$ e^+e^- \rightarrow \tau^+\tau^- $ . Instead of specific NP models, we utilize effective field theory (EFT) [25], in which high dimension operators are utilized to depict the NP effects, to characterize these types of interactions. It provides a model independent and flexible frame, and it is particularly advantageous at lower energies [26, 27]. Diverse EFTs, each pertinent to its energy scale and symmetry, are employed to address various aspects of NP. For example, the standard model effective field theory (SMEFT) [28], which adheres to$ S U(2)_L \times U(1)_Y $ gauge symmetry, is applicable above the electroweak scale, whereas Low Energy Effective Field Theory (LEFT), manifesting$ U(1)_{\rm{EM}} $ symmetry, is relevant below the electroweak scale. These frameworks are interconnected via a rigorous ''matching'' process, facilitating the translation of findings across different energy scales [29−32]. Initially, our focus will be on identifying and analyzing the implications of specific operators within the LEFT that are indicative of NP. Subsequently, we will extend our analysis to the SMEFT, employing the established “matching” results to correlate the Wilson coefficients in the LEFT with those in the SMEFT.We focus on two types of operators, namely four-fermion and lepton dipole operators in the LEFT. In Table 1, we enumerate six operators, which can be involved in the process
$ e^+e^-\rightarrow\tau^+\tau^- $ and might alter SM predictions. Notably, the chirality of the lepton in each operator is flipped. In the SM contribution, the leptons have identical chiralities due to the current interactions. It is expected that the interference between the high dimension operators and SM is suppressed by the lepton mass, particularly for massless electron limit. Then, the leading order contribution from those operators is represented by the square terms and is inversely proportional to the fourth power of the cut-off scale, rendering weak constraints on the operators. Recent investigations have delved into dipole operators with the polarization asymmetry of beams at the future electron-positron collider, particularly at a center-of-mass energy of$ \sqrt{s} = 250 $ GeV [33]. A noteworthy observation is that the azimuthal angle of the final state particles with respect to the beam polarization direction exhibits asymmetric distribution for interference terms. This idea has been extended at the forthcoming Electron-Ion Collider (EIC) to study four-fermion operators and dipole operators [34, 35]. In the present study, the single transverse spin asymmetry is used to explore the potential on operators listed in Table 1 at low-energy lepton colliders. Specifically, two points should be noted. First, the tau lepton magnetic dipole operators can interfere with SM contribution as a massive lepton, and the total event numbers, as opposed to asymmetric distribution, are utilized to constrain the operators even with the polarized beams. Furthermore, for the electric dipole operators indicating charge-parity ($ CP $ ) violation, they exhibit no interference with the SM even with polarized beams. To maintain unity, we utilize the total event numbers instead of the asymmetric distribution of azimuthal angle to constrain the operators. Second, although it can be expected that the constraints for electron dipole operators in the present study would be much weaker than those from the electron electric dipole moment (EDM) and magnetic dipole moment (MDM) measurements [36−38], these electron dipole operators are also listed in Table 1 for completeness.${\cal{O} }_V: (\bar{e}_L\gamma^{\mu}\tau_L)(\bar{\tau}_R\gamma_{\mu}e_R)+ {\rm h.c.}$ 

${\cal{O} }_S: (\bar{e}_L\tau_R)(\bar{\tau}_Le_R)+{\rm h.c.}$ 

${\cal{O}}_{\tau \gamma}: \bar{\tau}\sigma^{\mu\nu}\tau F_{\mu\nu}$ 

${\cal{O}}_{\tau \gamma}^a: \bar{\tau}\sigma^{\mu\nu}i\gamma_5\tau F_{\mu\nu}$ 

${\cal{O}}_{e \gamma}:\bar{e}\sigma^{\mu\nu}e F_{\mu\nu}$ 

${\cal{O}}_{e \gamma}^a: \bar{e}\sigma^{\mu\nu} i\gamma_5 e F_{\mu\nu}$ 

Table 1. Operators in LEFT [30] are listed, which contribute to the process
$e^-e^+\to \tau^-\tau^+$ . The cut-off scale of the operators is the electroweak scale$v\;(v=246~\text{GeV})$ .The contribution of the four-fermion operators
$ {\cal{O}}_V $ and$ {\cal{O}}_S $ to the EDM and MDM of the electron at the one-loop level is well established. Hence, precision measurements of the electron EDM and MDM offer indirect methods to constrain these operators [39−41]. For instance, the real and imaginary parts of the Wilson coefficient associated with$ {\cal{O}}_V $ are constrained to orders of$ 10^{-5} $ and$ 10^{-11} $ , respectively, and those for$ {\cal{O}}_S $ are of orders of$ 10^{-4} $ and$ 10^{-10} $ , respectively. These constraints are typically more stringent than those obtainable through direct searches at colliders. However, it is crucial to recognize that indirect constraints on$ {\cal{O}}_V $ and$ {\cal{O}}_S $ may be influenced by correlations between operators or hidden new physics. For example, while analyses typically consider contributions only from the tau lepton, electrons, muons, quarks, and even new fermions or scalars may enter the loops and significantly alter these constraints. This observation underscores the necessity of directly examining each operator, which is the focus of our research.The rest of this paper is organized as follows. In Sec. II, we review the general fermion polarization formula and asymmetric observables. In Sec. III, we show the analytical results, and then, in Sec. IV, we present the numerical calculations. Finally, we present our conclusions.
-
In this section, we initially discuss the polarizations of electrons and positrons, especially their transverse polarizations. With the aid of the polarizations of beams, the asymmetric observable can be defined, which behaves like the forward-backward asymmetry. Two asymmetric observables are defined, and statistical uncertainty is provided.
-
The polarizations of electrons are discussed in [42−44], where the longitudinal and transverse polarizations of the electrons and positrons are explored. The longitudinal polarization
$ \lambda_e(\bar{\lambda}_e) $ corresponds to the spin projection on the beam momentum direction, representing the helicity$ \pm 1 $ . The beam transverse polarization of the initial electron (positron) beam is defined by the polarization vector$s_e(\bar{s}_e)$ :$ \begin{aligned}[b]& s_e = (0, b_T\cos\phi_s, b_T\sin\phi_s, 0), \\& \bar{s}_e = (0,\bar{b}_T\cos\phi_s,\bar{b}_T\sin\phi_s, 0), \end{aligned} $

(1) where
$ \phi_s $ denotes the transverse polarized angle, and$ b_T(\bar{b}_T) $ denotes the magnitude of the polarization for the initial electron (position).With the polarizations in Eq. (1), the density matrices for a massless electron and positron are as follows:
$ \rho_e = \frac{1}{2} \begin{pmatrix} 1+\lambda_e & s_e {\rm e}^{-{\rm i}\phi_s} \\ s_e {\rm e}^{{\rm i}\phi_s} & 1-\lambda_e \end{pmatrix}, \; \bar{\rho}_e = \frac{1}{2} \begin{pmatrix} 1+\bar{\lambda}_e & \bar{s}_e {\rm e}^{{\rm i}\phi_s}\\ \bar{s}_e {\rm e}^{-{\rm i}\phi_s} & 1-\bar{\lambda}_e \end{pmatrix}. $

(2) Furthermore, the spinor summation rules are as follows:
$ \begin{aligned}[b]& \rho_{e}u_{\lambda_e}(p)\bar{u}_{\lambda_e}(p) = \not {p}\frac{1-\lambda_e\gamma_5+\gamma_5\not {s}_e}{2},\\& \bar{\rho}_{e}v_{\bar{\lambda}_e}(p)\bar{v}_{\bar{\lambda}_e}(p) = \not {p}\frac{1-\bar{\lambda}_e\gamma_5+\gamma_5\not {\bar{s}}_e}{2}, \end{aligned} $

(3) where p denotes the momentum of the electron or positron. Based on the aforementioned equation, it can be clearly shown that the transverse polarization vectors mix different helicity states and this will render the interference contribution, which is forbidden in the helicity basis.
-
Considering the effects of the polarized initial beams on the operators, the total differential scattering cross section including the SM and NP operator contributions will depend on the difference between the azimuthal angle and transverse polarization angle as follows:
$ \frac{2\pi {\rm d}\sigma}{\sigma {\rm d}\phi} = 1+A_{\rm{LR}} \cos(\phi-\phi_s)+A_{\rm{UD}} \sin(\phi-\phi_s), $

(4) where ϕ denotes the azimuthal angle of the tau lepton. Here, the transverse polarization angle of beams is selected as
$ \phi_s = 0 $ without loss of generality. It is emphasized that NP has no contribution to the total cross section at the order of$ 1/v^2 $ , while it will alter the azimuthal distribution of the final state. With the asymmetric distribution, we can define the asymmetric observables as [33, 45]$ \begin{aligned}[b] &A_{\rm{LR}} = \frac{N(\cos\phi>0)-N(\cos\phi<0)}{N(\cos\phi>0)+N(\cos\phi<0)},\\ & A_{\rm{UD}} = \frac{N(\sin\phi>0)-N(\sin\phi<0)}{N(\sin\phi>0)+N(\sin\phi<0)}, \end{aligned}$

(5) where N denotes the total event number, and the statistical uncertaintity of the observables can be obtained as
$ \delta A_{\rm{LR(UD)}} = \sqrt{\frac{1-A_{\rm{LR(UD)}}}{N}}, $

(6) which becomes
$ \dfrac{1}{\sqrt{N}} $ if we take the approximation$A_{\rm{LR(UD)}} \simeq 0$ in the SM. -
In this section, we provide analytical results, namely asymmetric observables and total event numbers for the operators in Table 1. Before delving into the interference contributions between the SM and high dimensional operators, it is important to note that the Z contribution to the process
$ e^-e^+\to \tau^-\tau^+ $ is negligible when compared with that from γ at low-energy lepton colliders. Therefore, we only consider the process$ e^-e^+\to \gamma^\ast \to \tau^-\tau^+ $ in the SM, which is a pure quantum electrodynamics process.Based on electron and positron chiralities, it is clearly shown that the four-fermion operators and electron dipole operators, as listed in Table 1, do not interfere with the SM contribution for the process
$ e^-e^+ \rightarrow \tau^- \tau^+ $ for unpolarized beams. The characteristic absence of interference is apparent from the fermion chirality structure. In the SM, fermion chirality is conserved in electroweak interactions. Conversely, the operators in question cause a flip in the chirality of electrons. Given the correspondence between chirality and helicity in the massless limit of fermions, it leads to no interference in the helicity basis. With polarized beams, a transversely polarized electron becomes a superposition state of different helicity states, and this will lead to an extra interference contribution to the distribution of final state particles.Before displaying the differential cross section with polarized beams, it is important to note that the four-fermion operators listed in Table 1 independently induce
$ e^-e^+ \rightarrow \tau^- \tau^+ $ , and their interferences with the SM process are correlated, as described by the following Fierz identities:$ \begin{aligned}[b] (\bar{e}_L\tau_R)(\bar{\tau}_Le_R) =\;& -\frac{1}{8}(\bar{e}_L\sigma^{\mu\nu}e_R)(\bar{\tau}_L\sigma_{\mu\nu}\tau_R)\\&-\frac{1}{2}(\bar{e}_Le_R)(\bar{\tau}_L\tau_R),\\ (\bar{e}_L \gamma_{\mu} \tau_L)(\bar{\tau}_R \gamma^{\mu} e_R) =\;& 2(\bar{e}_L e_R)(\bar{\tau}_R \tau_L). \end{aligned} $

(7) The operator
$ (\bar{e}_L\sigma^{\mu\nu}e_R)(\bar{\tau}_L\sigma_{\mu\nu}\tau_R) $ in the aforementioned equation does not interfere with the SM contribution even for polarized beams. Therefore, the radio of the interference amplitudes from$ {\cal{O}}_V $ and$ {\cal{O}}_S $ is$ 4:1 $ . In our analysis, we use the first operator$ {\cal{O}}_V $ as the benchmark, and the results for$ {\cal{O}}_{S} $ can be obtained via rescaling.The differential cross section from the interference between the SM and operator
$ {\cal{O}}_V $ contribution is as follows:$ \frac{{\rm d}\sigma}{{\rm d}\sin\phi} = \frac{e^2m_{\tau}(4m_{\tau}^2-s)}{32v^2s\sqrt{s}}\times \text{Re}[L_V](b_T\bar{\lambda}_e+\bar{b}_T\lambda_e), $

(8) $ \frac{{\rm d}\sigma}{{\rm d}\cos\phi} = \frac{e^2m_{\tau}(4m_{\tau}^2-s)}{32v^2s\sqrt{s}}\times \text{Im}[L_V](\bar{b}_T\lambda_e-b_T\bar{\lambda}_e), $

(9) where
$ L_V $ denotes the Wilson coefficient for the operator$ {\cal{O}}_V $ , e denotes the electron and tau lepton charge,$ \sqrt{s} $ denotes the collision energy, and v denotes the electroweak symmetry breaking scale as the cut-off scale of the LEFT. It can be shown that the interference term is proportional to$ m_\tau $ due to the tau lepton chirality flip as the chiralities of tau leptons are flipped in the operators while they are conserved in the QED. With the differential cross section, the asymmetric observables can be obtained as follows:$ A_{\rm{LR}}^{V} = \frac{-3m_{\tau}s\sqrt{s-4m_{\tau}^2}\times \text{Re}[L_V](\bar{b}_T\lambda_e+b_T\bar{\lambda}_e)}{2e^2 v^2 (\lambda_e\bar{\lambda}_e+1)(2m_\tau^2+s) }, $

(10) $ A_{\rm{UD}}^{V} = \frac{3 m_{\tau}s\sqrt{s-4m_{\tau}^2}\times \text{Im}[L_V](\bar{b}_T\lambda_e-b_T\bar{\lambda}_e)}{ 2e^2 v^2 (\lambda_e\bar{\lambda}_e+1)(2m_\tau^2+s)}. $

(11) Next, we explore the electron dipole operators
$ {\cal{O}}_{e\gamma} $ and$ {\cal{O}}_{e\gamma}^a $ , whose interference with the SM for polarized beams can be expressed as$ \frac{{\rm d}\sigma}{{\rm d}\cos\phi} = -\frac{e^3\sin2\theta(s-4m_{\tau}^2)^{\frac{3}{2}}}{32\pi v s^2}\times L_{e\gamma}(\bar{b}_T\lambda_e+b_T\bar{\lambda}_e), $

(12) $ \frac{{\rm d}\sigma}{{\rm d}\sin\phi} = -\frac{e^3\sin2\theta(s-4m_{\tau}^2)^{\frac{3}{2}}}{32\pi v s^2}\times L_{e\gamma}^a(\bar{b}_T\lambda_e-b_T\bar{\lambda}_e), $

(13) where θ denotes the polarization angle of the tau lepton, and
$ L_{e\gamma} $ and$ L_{e\gamma}^a $ denote the Wilson coefficients of$ {\cal{O}}_{e\gamma} $ and$ {\cal{O}}_{e\gamma}^a $ , respectively. With the differential cross section, the asymmetric observables are obtained as follows:$ A_{\text{LR}}^{e\gamma} = \frac{-2\sqrt{s}(s-4m_{\tau}^2)\times L_{e\gamma}(b_T\bar{\lambda}_e+\bar{b}_T\lambda_e)}{\pi e v(1+\lambda_e\bar{\lambda}_e)(s+2m_{\tau}^2)}, $

(14) $ A_{\text{UD}}^{e\gamma} = \frac{2\sqrt{s}(s-4m_{\tau}^2)\times L_{e\gamma}^a (\bar{b}_T\lambda_e-b_T\bar{\lambda}_e)}{\pi e v(1+\lambda_e\bar{\lambda}_e)(s+2m_{\tau}^2)}. $

(15) It is important to note that the asymmetric observables discussed are dependent on both transverse and longitudinal polarizations. This dependency arises because our analysis is confined to the pure QED contributions within the SM, specifically the photon mediation processes, which are parity-conserving. Conversely, an asymmetric variant that depends uniquely on transverse polarization emerges when incorporating the contribution of the Z gauge boson into the SM processes [33].
For the τ dipole operators
$ {\cal{O}}_{\tau\gamma} $ and$ {\cal{O}}_{\tau\gamma}^a $ , as stated above, total event numbers are used. The production rates of the process$ e^+ e^-\to \tau^+\tau^- $ are as follows:$ \begin{aligned}[b] \sigma({\cal{O}}_{\tau\gamma}) =\;& \sqrt{\frac{s-4m_{\tau}^2}{s}} \times\frac{\left[(s+8m_\tau^2)L_{\tau\gamma}^2+6evm_{\tau}L_{\tau\gamma}\right]}{6\pi sv^2} \\&\times e^2\left(1+\lambda_e\bar{\lambda}_e\right), \\ \sigma({\cal{O}}_{\tau\gamma}^a) =\;& \sqrt{\frac{s-4m_{\tau}^2}{s}} \times\frac{(s-4m_\tau^2){(L_{\tau\gamma}^{a}})^2}{6\pi sv^2} e^2\left(1+\lambda_e\bar{\lambda}_e\right), \end{aligned} $

(16) where
$ L_{\tau\gamma} $ and$ L_{\tau\gamma}^a $ denote the Wilson coefficients of$ {\cal{O}}_{\tau\gamma} $ and$ {\cal{O}}_{\tau\gamma}^a $ , respectively. Notably, the magnetic dipole moment operator interferes with the SM, while the electric dipole moment operator does not. -
In this section, we explore the sensitivity of low-energy lepton colliders to high dimension operators numerically. We first focus on the LEFT operators shown in Table 1, and then deduce the potential impact on operators within the SMEFT framework via a ''matching'' procedure. The collison setup is chosen to be similar to that of Belle-II and STCF [46, 47]. The integrated luminosity of 3000 fb–1 is adopted. The beam polarization parameters are set as
$(\lambda_e, \bar{\lambda}_e, b_T, \bar{b}_T) = $ (0.5, 0.5, 0.8, 0.3) for the polarized case. Furthermore, an$ \sqrt{s} $ value of 7 GeV is utilized as the benchmark collision energy. Additionally, we consider τ lepton decay and reconstruction. Among the rich phenomenology of τ lepton decay modes, we focus on the decay modes$\tau^- \rightarrow \pi^- \nu_{\tau}$ ,$\tau^- \rightarrow \pi^- \pi^0 \nu_{\tau}$ , and$\tau^- \rightarrow \pi^- \pi^+ \pi^- \nu_{\tau}$ , which collectively represent a significant portion of τ decay, with a cumulative branching ratio of 45.8% [48]. Specifically, these decay channels exhibit advantages for analysis due to their minimal backgrounds from the$e^-e^+ \rightarrow q\bar{q}$ process [49]. By exclusively focusing on these decay modes, we enhance our experimental sensitivity to potential new physics signals. Accordingly, coupled with a high reconstruction efficiency of the tau lepton pair, which is approximately 85% [50−53], we estimate the number of observable events ($N$ ) as$N = \sigma(e^-e^+ \rightarrow \tau^- \tau^+) \times {\cal{L}} \times $ 45.8%×45.8%×85%×85%$\approx 0.15 \times \sigma(e^-e^+ \rightarrow \tau^- \tau^+) \times {\cal{L}}$ . -
Firstly, we use
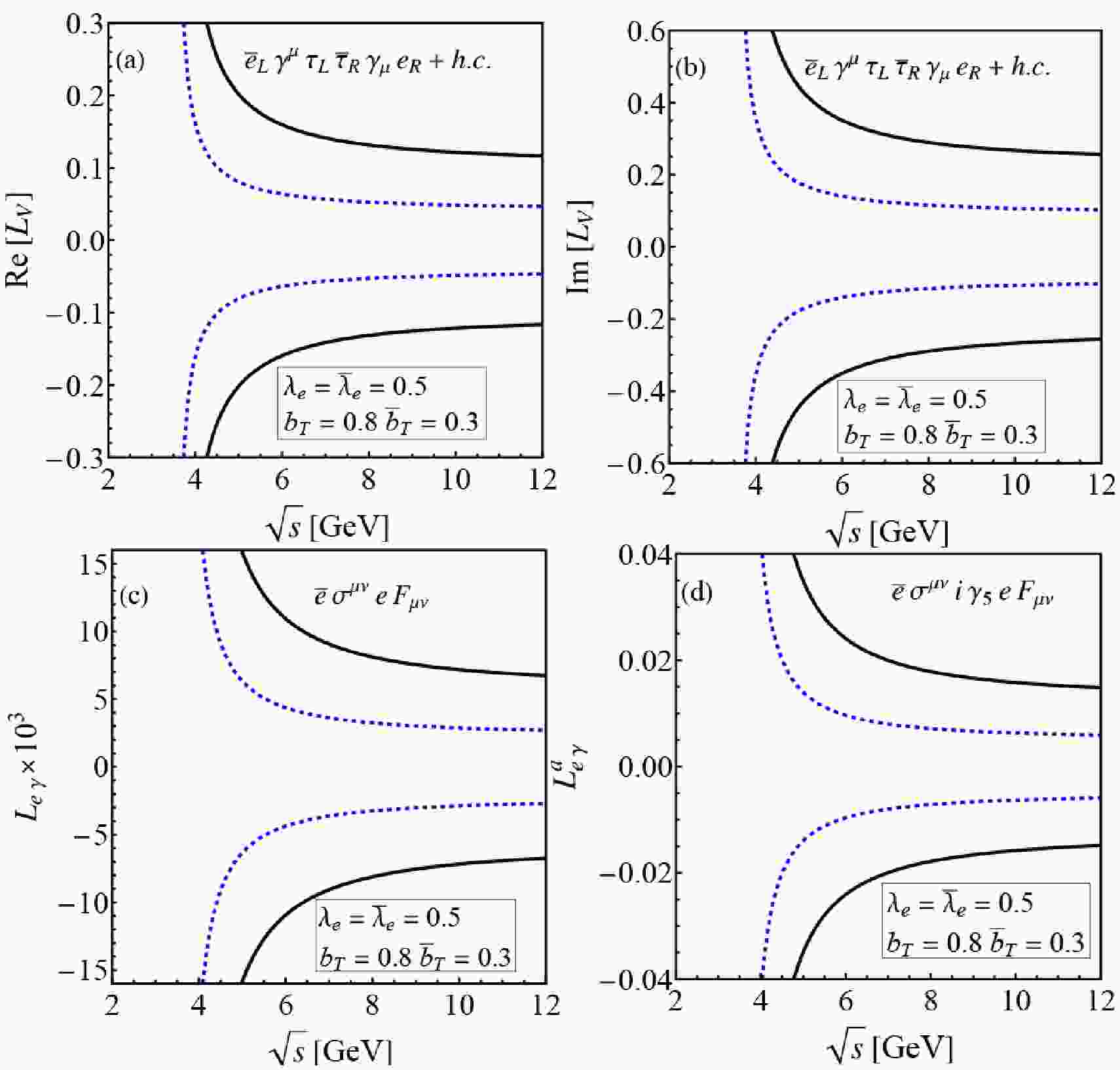
$ A_{\rm{LR(UD)}}/\delta A_{\rm{LR(UD)}} $ to evaluate the potential of the low-energy lepton collider in probing the Wilson coefficients of operators listed in Table 1. Figure 1 displays the$5\sigma$ discovery and$2\sigma$ exclusion potentials as functions of the varying collision energy$ \sqrt{s} $ for operators$ {\cal{O}}_V $ ,$ {\cal{O}}_{e\gamma} $ , and$ {\cal{O}}_{e\gamma}^a $ , whose Wilson coefficients are$ L_V $ ,$ L_{e\gamma} $ , and$ L_{e\gamma}^a $ , respectively. The black lines denote the$5\sigma$ discovery potential for the$e^+e^-$ collider at various collision energies, while the dashed blue lines represent the$2\sigma$ testing capacity for these operators. The potential of the Wilson coefficient increases with the collision energy near the$\tau$ mass threshold and tends to stabilize for$\sqrt{s} \gg m_\tau$ . This trend is attributed to the phase space expansion with increasing$\sqrt{s}$ near the$m_\tau$ threshold. This leads to a higher event count, thereby enhancing the collider capacity for Wilson coefficients. For$\sqrt{s} \gg m_\tau$ , the asymmetric observables manifest as follows:
Figure 1. (color online) Potential on the Wilson coefficients as a function of the collision energy
$\sqrt{s}$ , assuming${\cal{L}}=3000~\text{fb}^{-1}$ and the cut-off scale is the electroweak scale v. The black lines denote the$5\sigma$ discovery capacity boundary, and the dashed blue lines represent the$2\sigma$ potential boundary.$ A_{\rm{LR}} \sim A_{\rm{UD}} \sim L_V\frac{m_\tau \sqrt{s}}{v^2}, $

(17) for four-fermion operators, and
$ A_{\rm{LR}} \sim A_{\rm{UD}} \sim L_{e\gamma}/L_{e\gamma}^a \frac{\sqrt{s}}{v}, $

(18) for dipole operators. The total event number can be expressed as
$ N \sim \frac{{\cal{L}}}{s}. $

(19) Given the dependence of asymmetric observables and total event number on
$s$ , the constraint on Wilson coefficients approach a constant value. Furthermore, Fig. 1 indicates that the constraint on$ \text{Im}[L_V] $ is looser when compared to that on$ \text{Re}[L_V] $ , wherein the boundary for$ \text{Im}[L_V] $ is approximately two times that of$ \text{Re}[L_V] $ . A similar trend is observed for$ L_{e\gamma} $ and$ L_{e\gamma}^a $ . This observation is confirmed by the results in Table 2 based on the 7 GeV$e^+e^-$ collider. This discrepancy is due to the fact that$ \text{Re}[L_V] $ and$ L_{e\gamma} $ indicate$ CP $ -even effects in the four-fermion and electron dipole operators, respectively, whereas$ \text{Im}[L_V] $ and$ L_{e\gamma}^a $ indicate the$ CP $ -odd effects. These$ CP $ -even and$ CP $ -odd components exhibit different dependencies on beam polarizations, specifically$\lambda_e \bar{b}_T + \bar{\lambda}_eb_T$ and$\lambda_e \bar{b}_T - \bar{\lambda}_e b_T$ . In our numerical calculations, we set the beam polarizations as$(\lambda_e, \bar{\lambda}_e, b_T, \bar{b}_T) = (0.5, 0.5, 0.8, 0.3)$ , which elucidates the observed factor of two differences.$|\text{Re}[L_V]|<0.057$ 

$|\text{Re}[L_V]|>0.141$ 

$|\text{Im}[L_V]|<0.12$ 

$|\text{Im}[L_V]|>0.31$ 

$|L_{e\gamma}|<0.0036$ 

$|L_{e\gamma}|>0.0091$ 

$|L_{e\gamma}^a|<0.008$ 

$|L_{e\gamma}^a|>0.020$ 

$|L_{\tau\gamma}|<0.0012$ 

$|L_{\tau\gamma}|>0.0031$ 

$|L_{\tau\gamma}^a|<0.16$ 

$|L_{\tau\gamma}^a|>0.25$ 

Table 2.
$2\sigma$ (left side) and$5\sigma$ (right side) potentials on Wilson coefficients at the$e^+e^-$ collider with a collision energy of 7 GeV and an integrated luminosity of 3000 fb–1.Figure 2 illustrates the constraints on the tau lepton magnetic and electric dipole operators, with solid black lines indicating the
$ 5\sigma $ discovery potential for anomalous interactions as a function of collision energy$ \sqrt{s} $ . Dashed lines delineate the$ 2\sigma $ limits on the Wilson coefficients, predicated in the absence of deviations from SM predictions at the collider. Notably, the constraints on the magnetic dipole moment operator,$ {\cal{O}}_{\tau\gamma} $ , is significantly more stringent than those for the electric dipole moment operator,$ {\cal{O}}_{\tau\gamma}^a $ . This distinction is attributed to the interference of$ {\cal{O}}_{\tau\gamma} $ with SM processes, a phenomenon not observed with$ {\cal{O}}_{\tau\gamma}^a $ due to its differing$ CP $ properties. Moreover, the figure reveals a variation in constraints with the collision energy. For$ {\cal{O}}_{\tau\gamma} $ , constraints weaken as$ \sqrt{s} $ increases, a relationship quantitatively described by$ N_s/\sqrt{N_b} \propto 1/\sqrt{s} $ . This trend indicates that the signal-to-background ratio diminishes with higher collision energies. Conversely, constraints on$ {\cal{O}}_{\tau\gamma}^a $ strengthen with increasing$ \sqrt{s} $ , following the relationship$ N_s/\sqrt{N_b} \propto \sqrt{s} $ . Here,$ N_s $ represents the number of signal events generated by operator contributions, while$ N_b $ denotes the number of background events predicted by the SM.
Figure 2. (color online) Potentials on the Wilson coefficients as a function of collision energy
$\sqrt{s}$ , assuming${\cal{L}}=3000~\text{fb}^{-1}$ ; the cut-off scale is the electroweak scale v. The black lines denote the$5\sigma$ discovery capacity boundary, and the dashed blue lines represent the$2\sigma$ potential boundary.To elucidate the constraints on the Wilson coefficients more effectively, Table 2 details the
$ 5\sigma $ discovery potential and$ 2\sigma $ exclusion limits at a benchmark collision energy of$ \sqrt{s} = 7 $ GeV. -
In this subsection, we explore the derivation of constraints on dim-6 operators in the SMEFT [28] by utilizing results obtained in the LEFT [26, 27]. We assume the cut-off scale (Λ) for operators in the SMEFT to be 1 TeV in numerical calculations. This derivation is facilitated through the application of ''matching'' [29−31]. The “matching” process should ensure that the coefficients of corresponding operators in the LEFT and SMEFT are of the same order of magnitude. Specifically, as the coefficient in the LEFT is of the order
$ 1/v^2 $ , we retain results in the SMEFT up to the order of$ 1/\Lambda^2 $ . It should be noted that the operator$ {\cal{O}}_S $ cannot be obtained from the SMEFT dim-6 operators. Then, we utilize the results from the other 5 operators of the LEFT, as listed in Table 1, which were derived for the 7 GeV lepton collider with an integrated luminosity of 3000 fb–1 to constrain the corresponding operators in the SMEFT.For the four-fermion operator
$ {\cal{O}}_V $ , the matching results are$ \frac{1}{v^2}\text{Re}[L_V] = \; \frac{1}{\Lambda^2}\text{Re}\left[C_{le}^{e\tau\tau e}\right], $

(20) $ \frac{1}{v^2}\text{Im}[L_V] = \; \frac{1}{\Lambda^2}\text{Im}\left[C_{le}^{e\tau\tau e}\right], $

(21) up to the order of
$ 1/\Lambda^2 $ , where$ C_{le}^{e\tau\tau e} $ denotes the Wilson coefficient of the operator$ (\bar{l}_e\gamma^{\mu}l_{\tau})(\bar{\tau}\gamma_{\mu}e)+{\rm h.c.} $ in the SMEFT. Here,$ l_e\; (l_{\tau}) $ denotes left hand electron (tau) lepton, and$ e\; (\tau) $ denotes the right hand electron (tau) lepton. Based on the constraints on the real and imaginary parts of$ L_V $ , we can obtain that the 5σ discovery region for$ C_{le}^{e\tau\tau e} $ is as follows:$ | \text{Re}\left[C_{le}^{e\tau\tau e}\right] | > 2.33,\; \; \; |\text{Im}\left[C_{le}^{e\tau\tau e}\right]|>5.12. $

(22) Given the null result, the
$ 2\sigma $ consistent region is as follows:$ | \text{Re}\left[C_{le}^{e\tau\tau e}\right] | < 0.94,\; \; \; |\text{Im}\left[C_{le}^{e\tau\tau e}\right]| < 1.98. $

(23) Next, we focus on the tau lepton magnetic and electric dipole operators
$ {\cal{O}}_{\tau\gamma} $ and$ {\cal{O}}_{\tau\gamma}^a $ . They can be derived from$ (\bar{l}_{\tau}\sigma^{\mu\nu}\tau)\tau^I HW_{\mu\nu}^I $ and$ (\bar{l}_{\tau}\sigma^{\mu\nu}\tau)HB_{\mu\nu} $ , referred to as$ {\cal{O}}_{\tau W} $ and$ {\cal{O}}_{\tau B} $ in the SMEFT. The correspondence between the Wilson coefficients for these operators in the LEFT and SMEFT are established via the following matching relations:$ \frac{1}{v}L_{\tau\gamma} = \frac{v}{\sqrt{2}\Lambda^2 }\left[c_W\text{Re}\left[C_{\tau B}\right]-s_W\text{Re}\left[C_{\tau W}\right]\right], $

(24) $ \frac{1}{v}L_{\tau\gamma}^a = \frac{v}{\sqrt{2} \Lambda^2}\left[c_W\text{Im}\left[C_{\tau B}\right]-s_W\text{Im}\left[C_{\tau W}\right]\right], $

(25) where
$ s_W = \sin\theta_W $ and$ c_W = \cos\theta_W $ . Specifically,$ \theta_W $ denotes the weak mixing angle, and$ C_{\tau B} $ and$ C_{\tau W} $ denote the Wilson coefficients of$ {\cal{O}}_{\tau W} $ and$ {\cal{O}}_{\tau B} $ , respectively. We display the constraints on$ {\cal{O}}_{\tau W} $ and$ {\cal{O}}_{\tau B} $ in Fig. 3. The gray shaded area represents the parameter space that could be probed with a$ 5\sigma $ confidence level. Conversely, the blue shaded area indicates the parameter space that aligns with SM predictions, assuming a null result at a$ 2\sigma $ confidence level.
Figure 3. (color online) Potentials on the real part (a) and image part (b) of Wilson coefficients
$C_{\tau W}$ and$C_{\tau B}$ under SMEFT with respect to the collision energy$\sqrt{s}$ , assuming${\cal{L}}= $ $ 3000~\text{fb}^{-1}$ and$\Lambda=1~\text{TeV}$ . The gray diagonal area denotes the$5\sigma$ discovery capacity boundary, and the blue diagonal area represents the$2\sigma$ potential boundary.Finally, we discuss the electron magnetic and electric dipole operators
$ {\cal{O}}_{e\gamma} $ and$ {\cal{O}}_{e\gamma}^a $ , respectively, which are derived from the operators$ (\bar{l}_{e}\sigma^{\mu\nu}e)\tau^I HW_{\mu\nu}^I $ and$ (\bar{l}_{e}\sigma^{\mu\nu}e)HB_{\mu\nu} $ , respectively. The relations between Wilson coefficients are similar to those in the τ lepton case and can be expressed as$ \frac{1}{v}L_{e\gamma} = \frac{v}{\sqrt{2}\Lambda^2}\left[c_W\text{Re}\left[C_{eB}\right]-s_W\text{Re}\left[C_{eW}\right]\right], $

(26) $ \frac{1}{v}L_{e\gamma}^a = \frac{v}{\sqrt{2}\Lambda^2}\left[c_W\text{Im}\left[C_{eB}\right]-s_W\text{Im}\left[C_{eW}\right]\right], $

(27) where
$ C_{eB} $ and$ C_{eW} $ denote the Wilson coefficients of$ {\cal{O}}_{eB} $ and$ {\cal{O}}_{eW} $ , respectively.The constraints on
$ {\cal{O}}_{e B} $ and$ {\cal{O}}_{e W} $ are illustrated in Fig. 4, where the gray shaded area represents the parameter space that could be probed with a$ 5\sigma $ confidence level. Conversely, the blue shaded area indicates the parameter space that aligns with SM predictions, assuming a null result at a$ 2\sigma $ confidence level.
Figure 4. (color online) Potentials on the real part (a) and image part (b) of Wilson coefficients
$C_{eW}$ and$C_{eB}$ under SMEFT with respect to collision energy$\sqrt{s}$ , assuming${\cal{L}}=3000~\text{fb}^{-1}$ and$\Lambda=1~\text{TeV}$ . The gray diagonal area denotes the$5\sigma$ discovery capacity boundary, and the blue diagonal area represents the$2\sigma$ potential boundary. -
In this study, we explored four-fermion operators and dipole operators through the process
$ e^+e^-\to \tau^+\tau^- $ at the STCF and Belle II with a benchmark collison energy of$ \sqrt{s} = 7 $ GeV. Instead of specific NP models, we selected high dimension operators to characterize the interactions. We focused on the operators which cannot interfere with the SM process. They are mainly derived from QED current interactions, namely operators that include different chiralities. To highlight the operators' contributions at the leading order, we considered the collision of polarized initial beams, where the interference between NP and the SM begins. First, we investigated the potential on the four-fermion operators$ {\cal{O}}_V $ and$ {\cal{O}}_S $ as well as the magnetic and electric dipole moments of the tau and electron leptons in the LEFT, although the magnetic and electric dipole moments of the electron were significantly more constrained [39−41] with EDM and MDM measurements. For completeness, we also included these operators in our analysis. We then translated the results for the operators in the LEFT to constraints on the operators in the SMEFT using the "matching" expressions, which provide the relations of the Wilson coefficients in these two bases.
Probing dipole operators and four-fermion operators at low-energy lepton colliders
- Received Date: 2024-03-15
- Available Online: 2024-09-15
Abstract: In this study, we explore the potentials of dipole operators and four-fermion operators at low-energy lepton colliders such as Belle II and the Super Tau Charm Facility (STCF). We utilize high-dimension operators to characterize such anomalous interactions, focusing on those that do not interfere with the Standard Model (SM) contributions. With polarized beams, the four-fermion operators and dipole moment operators can be tested with high precision.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: