-
It has been widely regarded, for an extended period, that the standard model (SM) of particle physics, despite its remarkable success in explaining a vast array of phenomena, fails to provide a complete description of the fundamental aspects of the universe. Consequently, the search for new physics beyond the SM (BSM) has become a crucial direction in modern physics research.
The discovery of a Higgs boson with properties consistent with SM predictions at the large hadron collider (LHC) in 2012 significantly bolstered our understanding of the SM [1−4]. Nevertheless, this milestone also intensified the debate regarding the possible existence of additional Higgs bosons. These scalar particles are theoretically predicted by a large number of natural BSM models, which aim to address the limitations and unresolved questions on the SM, including the Minimal Supersymmetric Standard Model (MSSM) [5−16], Next-to-MSSM (NMSSM) [17−32], Minimal Dilaton Model (MDM) [33−37], and Little Higgs Models (LHMs) [38, 39]. The experimental search for heavy neutral Higgs bosons has focused on decay channels such as
$ \tau^+\tau^- $ [40, 41],$ t\bar{t} $ ,$ b\bar{b} $ ,$ \mu^+\mu^- $ ,$ ZZ $ ,$ WW $ ,$ hh $ , and$ hV $ , which are reviewed in [42, 43]. Recently, evidence for a new scalar around 151 GeV was accumulated with significances of$ 4.3\sigma $ locally and$ 3.9\sigma $ globally [44], subsequently revised to$ 4.1\sigma $ locally and$ 3.5\sigma $ globally [45].The exploration of new physics phenomena, particularly the detection of heavy Higgs bosons, requires colliders with higher energies. Future high-energy colliders, designed to exceed the capabilities of current facilities, will be able to examine these heavy particles. Notably, the Future Hadron-Hadron Circular Collider (FCC-hh) at CERN [46] and Super-
$ pp $ -Collider (SppC) [47, 48] in China are among the most ambitious projects in this direction. Both initiatives aim to construct a 50−100 TeV$ pp $ collider [49], promising a significant leap in the energy frontier and potentially uncovering phenomena beyond the SM. Moreover, the concept of a multi-TeV muon collider provides an innovative approach to high-energy physics experiments [50, 51]. Extensive research has been conducted on the detection of heavy Higgs bosons at future colliders. In particular, the studies described in Ref. [52] examined the$ pp\to b\bar{b}H/A\to b\bar{b}\tau\tau $ and$pp\to b\bar{b}H/A\to b\bar{b}t\bar{t}$ channels at a 100 TeV$ pp $ collider and proposed pushing the exclusion limits for heavy Higgs searches up to$ M_H \sim 10 \; {\rm{TeV}} $ , with exceptions in regions of low$ \tan\beta $ . Furthermore, the analysis in Ref. [13] explored the$ pp\to H/A \to \tilde{\chi}_1^0\tilde{\chi}_2^\mp $ process, revealing the$4\ell+ \not {E}$ signal at a 100 TeV hadron collider, demonstrating its ability to probe new supersymmetric model sectors. In addition, the study in Ref. [53] explored the potential of a multi-TeV muon collider to discover heavy Higgs bosons within Two Higgs Doublet Models (2HDMs) and assess the discriminative power among different 2HDM types.This study extend the investigation initiated in our previous study on heavy Higgs bosons within the framework of the semi-constrained NMSSM (scNMSSM) [54]. The NMSSM incorporates an additional singlet superfield to the MSSM, thereby enriching the Higgs and neutralino sectors. Our analysis focuses on the computational evaluation of production cross sections and decay branching ratios for these heavy Higgs bosons. Through these calculations, we aim to provide a comprehensive understanding of the behavior and detectability of heavy Higgs bosons within the scNMSSM. Furthermore, we delve into the exploration of the discovery potential of these heavy Higgs bosons through the
$pp\to b\bar{b}H/A\to b\bar{b}t\bar{t}$ channel at a future 100 TeV collider. The selection of a 100 TeV collider is driven by its exceptional ability to achieve the high energy levels required for producing such massive particles, which provides new avenues for their discovery.The remainder of this manuscript is organized as follows. In Sec. II, we provide a brief overview of the scNMSSM, outlining its fundamental aspects and theoretical significance. In Sec. III, we present a detailed description of our computational methodology, followed by a comprehensive discussion on the results obtained from our analysis. In Sec. IV, we conclude the paper by summarizing the main results and their implications for future research in this area.
-
The NMSSM extends the MSSM by introducing an additional singlet superfield, denoted as
$ \hat{S} $ , where the superpotential of the$ \mathbb{Z}_3 $ -symmetric NMSSM is defined as$ \begin{array}{*{20}{l}} W_{{\rm{NMSSM}}} = W_{{\rm{MSSM}}}|_{\rm{\mu=0}} + \lambda\hat{S} \hat{H}_{u} \cdot \hat{H}_{d} + \dfrac{\kappa \hat{S}^{3}}{3} \,, \end{array} $

(1) where
$ W_{{\rm{MSSM}}}|_{\rm{\mu=0}} $ is the superpotential of the MSSM without the μ-term, λ and κ are coupling constants,$ \hat{H}_{u} $ and$ \hat{H}_{d} $ are the doublet Higgs superfields, and$ \hat{S} $ is the added singlet superfield. After electroweak symmetry breaking, the singlet scalar's vacuum expectation value (VEV), denoted as$ v_{s} $ , dynamically generates the massive μ-term [55, 56]$ \begin{array}{*{20}{l}} \mu \equiv \lambda v_s \, . \end{array} $

(2) Concurrently, the scalar components
$ H_{u} $ and$ H_{d} $ also attain VEVs, labeled as$ v_{u} $ and$ v_{d} $ , respectively. This leads to the introduction of a new parameter$ \tan \beta $ , defined as$ \begin{array}{*{20}{l}} \tan\beta \equiv v_u/v_d \, , \end{array} $

(3) where the sum of their squares is
$ v_u^2 + v_d^2 = v^2 = $ $(174 {\rm{GeV}})^2$ .The NMSSM introduces specific soft supersymmetry (SUSY) breaking terms, distinct from those in the MSSM, expressed by
$ \begin{aligned}[b] - {\cal L}_{{\rm{N M S S M}}}^{{\rm{s o f t}}}=\;&-{\cal L}_{{\rm{M S S M}}}^{{\rm{s o f t}}} |_{\mu=0}+m_{S}^{2} | S |^{2} \\ &+\lambda A_{\lambda} S H_{u} \cdot H_{d} +\frac{1} {3} \kappa A_{\kappa} S^{3}+{\rm{h. c.}} \,, \end{aligned} $

(4) where
$ {\cal L}_{{\rm{MSSM}}}^{{\rm{soft}}} |_{\mu=0} $ denotes the MSSM's soft SUSY breaking terms with the μ parameter set to zero. The symbols$ H_{u} $ and$ H_{d} $ refer to the scalar components of the Higgs doublets,$ A_{\lambda} $ and$ A_{\kappa} $ represent the trilinear coupling constants with mass dimension, and$ m_{S} $ is the mass of the singlet scalar field.In the scNMSSM, the Higgs sector is allowed to deviate from universality at the Grand Unified Theory (GUT) scale, a characteristic also known as NMSSM with non-universal Higgs masses. Specifically, the soft masses for the Higgs fields,
$ m_{H_{u}}^2 $ ,$ m_{H_{d}}^2 $ , and$ m_{S}^2 $ , can differ from$ M_0^2 + \mu^2 $ . Furthermore, the trilinear coupling constants$ A_{\lambda} $ and$ A_{\kappa} $ may vary independently from$ A_0 $ . Consequently, the parameter space of the scNMSSM is defined by nine parameters:$ \begin{array}{*{20}{l}} \lambda, \ \kappa, \ \tan \beta, \ \mu, \ A_{\lambda}, \ A_{\kappa}, \ A_{0}, \ M_{1/2}, \ M_{0} \, . \end{array} $

(5) Here, the last five parameters are set at the GUT scale.
$ M_{1/2} $ and$ M_{0} $ represent the universal sfermion mass and universal gaugino mass, respectively, while$ A_{0} $ denotes the universal trilinear coupling constant in the sfermion sector. This set of nine parameters at the GUT scale effectively constrains the NMSSM. Through the renormalization group equations (RGEs) to the SUSY scale, these parameters determine mass spectra at lower energy scales.The Higgs sector within the NMSSM is predictedto contain three CP-even Higgs bosons, two CP-odd Higgs bosons, and a pair of charged Higgs bosons. For convenience, the scalar components of the superfields
$ H_u $ ,$ H_d $ , and S are often rotated so that they can be represented as$ H_{1} = \cos \beta H_{u} + \varepsilon \sin \beta H_{d}^{*} = \left( \begin{matrix} H^+ \\ \dfrac{S_{1} + {\rm i} P_{1}^{\,}}{\sqrt{2}} \end{matrix} \right), $

(6) $ H_{2} = \sin \beta H_{u} - \varepsilon \cos \beta H_{d}^{*} = \left( \begin{matrix} G^+ \\ v + \dfrac{S_{2} + {\rm i} G^{0}}{\sqrt{2}} \end{matrix} \right), $

(7) $ H_{3} = S = v_{s} + \frac{S_{3} + {\rm i} P_{2}}{\sqrt{2}}, $

(8) where
$ \varepsilon = \left(\begin{smallmatrix} 0 & 1 \\ -1 & 0 \end{smallmatrix} \right) $ , and$ S_1 $ ,$ S_2 $ , and$ S_3 $ create the CP-even basis, while$ P_1 $ and$ P_2 $ establish the CP-odd basis.$ H_2 $ is identified as the SM-like Higgs,$ H_1 $ represents a new Higgs doublet field, and$ H_3 $ introduces a new singlet field.The CP-even Higgs mass matrix
$ M_S^2 $ in the basis$ (S_1, S_2, S_3) $ is expressed by [21, 57]$ M_{S, 11}^{2}= M_{A}^{2}+( m_{Z}^{2}-\lambda^{2} v^{2} ) {\rm{s i n}}^{2} 2 \beta, $

(9) $ M_{S, 12}^{2}= - \frac{1} {2} ( m_{Z}^{2} - \lambda^{2} v^{2} ) {\rm{s i n}} 4 \beta, $

(10) $ M_{S, 13}^{2}= - \left( \frac{M_{A}^{2}} {2 \mu/ {\rm{s i n}} 2 \beta} + \kappa v_{s} \right) \lambda v {\rm{c o s}} 2 \beta, $

(11) $ M_{S, 22}^{2}=m_{Z}^{2} \operatorname{c o s}^{2} 2 \beta+\lambda^{2} v^{2} {\rm{sin}}^{2} 2 \beta, $

(12) $ M_{S, 23}^{2}=2 \lambda\mu v \left[ 1-\left( \frac{M_{A}} {2 \mu/ {\rm{sin}} 2 \beta} \right)^{2}-\frac{\kappa} {2 \lambda} {\rm{sin}} 2 \beta\right], $

(13) $ \begin{aligned}[b] M_{S, 33}^{2}=\;&\frac{1} {4} \lambda^{2} v^{2} \left( \frac{M_{A}} {\mu/ {\rm{sin}} 2 \beta} \right)^{2}+\kappa v_{s} A_{\kappa}+4 ( \kappa v_{s} )^{2} \\ & -\frac{1} {2} \lambda\kappa v^{2} {\rm{sin}} 2 \beta, \end{aligned} $

(14) where
$ M_A^2 $ is defined as$ M_A^2 = \frac{2 \mu( A_{\lambda}^{\rm{SUSY}} + \kappa v_{s} )} {{\rm{sin}} 2 \beta}. $

(15) Notably,
$ A_\lambda^{\rm{SUSY}} $ is the SUSY scale equivalent of$ A_\lambda $ , derived from the GUT scale parameters by running through RGEs.The CP-odd Higgs mass matrix
$ M_P^2 $ in the basis$ (P_1, P_2) $ is expressed by$ M_{P, 1 1}^{2}=M_{A}^{2} \, , $

(16) $ M_{P, 1 2}^{2}=\lambda v ( A_{\lambda}-2 \kappa v_{s} ) \, , $

(17) $ M_{P, 2 2}^{2}=\lambda( A_{\lambda}+4 \kappa v_{s} ) \frac{v_{u} v_{d}} {v_{s}}-3 \kappa v_{s} A_{\kappa} \,. $

(18) Three CP-even mass eigenstates
$ h_1 $ ,$ h_2 $ , and$ h_3 $ ($ m_{h_1}<m_{h_2}<m_{h_3} $ ) are derived from the mixture of$ (S_1, S_2, S_3) $ , and two CP-odd mass eigenstates$ a_1 $ and$ a_2 $ ($ m_{a_1}<m_{a_2} $ ) are derived from$ (P_1, P_2) $ . This can be represented as$ \begin{pmatrix} h_{1} \\h_{2} \\h_{3} \\ \end{pmatrix} = S_{ij}\begin{pmatrix}S_{1} \\S_{2} \\S_{3} \\ \end{pmatrix}, $

(19) $ \begin{pmatrix}a_{1} \\a_{2} \\ \end{pmatrix} = P_{ij}\begin{pmatrix}P_{1} \\P_{2} \\ \end{pmatrix}, $

(20) where
$ S_{ij} $ and$ P_{ij} $ are the mixing matrices that diagonalize the mass matrices$ M_S^2 $ and$ M_P^2 $ , respectively. For corrections to Higgs boson masses, we consider adjustments using a combination of full one-loop top/bottom, leading-log two-loop top/bottom, and leading-log one-loop electroweak effects [55], which have been implemented in the$\textsf{NMSSMTools-6.0.2}$ package.Among the three CP-even Higgs bosons (
$ h_i $ , where$ i=1,2,3 $ ), the$ 125 \; {\rm{GeV}} $ SM-like Higgs could be either$ h_1 $ or$ h_2 $ , both of which are predominantly doublet-dominated scalars. The remaining CP-even Higgs bosons include another doublet-dominated scalar and a singlet-dominated scalar. For the two CP-odd Higgs bosons ($ a_i $ , where$ i=1,2 $ ), one is doublet-dominated, and the other is singlet-dominated. The singlet-dominated Higgs boson rarely couples to fermions because the singlet S interacts only with the Higgs sector. This property makes it difficult to detect at the LHC. In contrast, the doublet-dominated Higgs boson couples to fermions, which facilitates its detection. Our study focuses only on the heavy doublet-dominated CP-even Higgs H and CP-odd Higgs A because of their detectability. The couplings to up/down-type fermions of these heavy Higgs bosons, H and A, are defined as follows:$ C_{Huu}^{\rm SUSY} = {\rm i} \frac{m_{u}} {v} \cot \beta $

(21) $ C_{Hdd}^{\rm SUSY} = {\rm i} \frac{m_{d}} {v} \tan \beta $

(22) $ C_{Auu}^{\rm SUSY} = \frac{m_{u}} {v} \cot \beta \gamma_{5} $

(23) $ C_{Add}^{\rm SUSY} = \frac{m_{d}} {v} \tan \beta \gamma_{5} $

(24) The reduced couplings of these heavy Higgs bosons, H and A, are defined as follows:
$ C_{Huu}=C_{Huu}^{\rm SUSY}/C_{Huu}^{\rm SM} = \cot \beta $

(25) $ C_{Auu}=C_{Auu}^{\rm SUSY}/C_{Auu}^{\rm SM} = \cot \beta $

(26) $ C_{Hdd}=C_{Hdd}^{\rm SUSY}/C_{Hdd}^{\rm SM} = \tan \beta $

(27) $ C_{Add} = C_{Add}^{\rm SUSY}/C_{Add}^{\rm SM} = \tan \beta $

(28) Furthermore, when
$ \tan \beta $ is significantly larger than 1 ($ \tan \beta \gg 1 $ ),$ M_{S, 11}^2 $ closely approximates$ M_A^2 $ . In addition, the Higgs bosons H and A become degenerate, which implies that they have the same mass and exhibit identical couplings to quarks. -
In this study, we explore the detectability of the heavy doublet-dominated CP-even Higgs (H) and CP-odd Higgs (A) in the scNMSSM, at a 100 TeV hadron collider. We set the upper mass limit for the Higgs at 10 TeV, represented as
$ \begin{array}{*{20}{l}} h_i, a_j < 10 \; {\rm{TeV}} \quad \text{for }~ i = 1, 2, 3;\; j=1, 2. \end{array} $

(29) Therefore, we consider the relevant parameter space in the scNMSSM as follows:
$ \begin{array}{*{20}{l}} 0.0<\lambda<0.7, \quad |\kappa|<0.7, \quad 1<\tan\beta <60 \, , \\ 0.0<\mu, \,\, M_0, \,\, M_{1/2} < 10 \; {\rm{TeV}} \, , \\ |A_0|,\,\, |A_\lambda|,\,\, |A_\kappa| < 10 \; {\rm{TeV}} \, . \end{array} $

λ is set to be positive to ensure that
$ \mu > 0 $ . κ is allowed to be either positive or negative, providing a more comprehensive exploration of the parameter space.We use the package
$\textsf{NMSSMTools-6.0.2}$ [58−61] to scan the parameter space and calculate relevant quantities, considering the following constraints: (i) theoretical constraints including vacuum stability and without Landau pole below the GUT scale [58, 59]; (ii) flavor constraints from rare B-meson decays and D-meson mass differences [62−65]; (iii) 123−127 GeV Higgs boson with signal predictions that are globally consistent with LHC Higgs data [3, 4, 66−69]; (iv) constraints from searches for additional Higgs bosons and exotic decays of the SM-like Higgs, using$\textsf{HiggsBounds-5.5.0}$ , including a limit of 10.7% on invisible Higgs decay [69−74]; (v) upper bounds on the dark matter relic density from WMAP/ Planck [75, 76]; (vi) direct dark matter search constraints from XENON1T [77, 78], PICO-60 [79], PandaX-4T [80, 81], and LUX-ZEPLIN [82]; and (vii) constraints from direct SUSY searches at the LHC and LEP, using the package$\textsf{SModelS-v2.2.1}$ [83−89].For the samples satisfying the above theoretical and experimental constraints, we observe the following properties.
● The squarks of the first two generations are heavier than
$ 2.2 \; {\rm{TeV}} $ , with the lightest squark,$ \tilde{t}_1 $ , exceeding$ 1 \; {\rm{TeV}} $ . These mass limits are a direct result of constraints from LHC searches and naturalness requirements.● The third-generation sleptons can be as light as approximately
$ 170 \; {\rm{GeV}} $ , constrained by LHC search data.● The gluino mass exceeds
$ 2 \; {\rm{TeV}} $ , constrained by LHC search data. Consequently, given the universal gaugino mass condition at the GUT scale, the bino and wino masses exceed$ 340 \; {\rm{GeV}} $ and$ 620 \; {\rm{GeV}} $ , respectively.● The mass range for the lightest neutralino varies from
$ 4 \; {\rm{GeV}} $ to$ 4 \; {\rm{TeV}} $ , typically dominated by bino and singlino compositions, with some higgsino admixture. This range is constrained by dark matter experiments, such as relic density and direct searches, and by the composition of the neutralino itself.● In the Higgs sector, we categorize the samples into two types, a classification emerging from the extended Higgs sector of the NMSSM:
-
$ h_1 $ is the$ 125 \; {\rm{GeV}} $ SM-like Higgs.$ h_2 $ and$ h_3 $ are heavy CP-even Higgs bosons, while$ a_1 $ and$ a_2 $ are heavy CP-odd Higgs bosons.-
$ h_2 $ is the$ 125 \; {\rm{GeV}} $ SM-like Higgs. The light CP-even Higgs$ h_1 $ and light CP-odd Higgs$ a_1 $ are typically singlet-dominant. The heavy CP-even Higgs$ h_3 $ and light CP-odd Higgs$ a_2 $ are typically doublet-dominant.In this study, we focus on doublet-dominant heavy Higgs due to the difficulty of detecting singlet-dominant Higgs. There are two types to consider. In the first type,
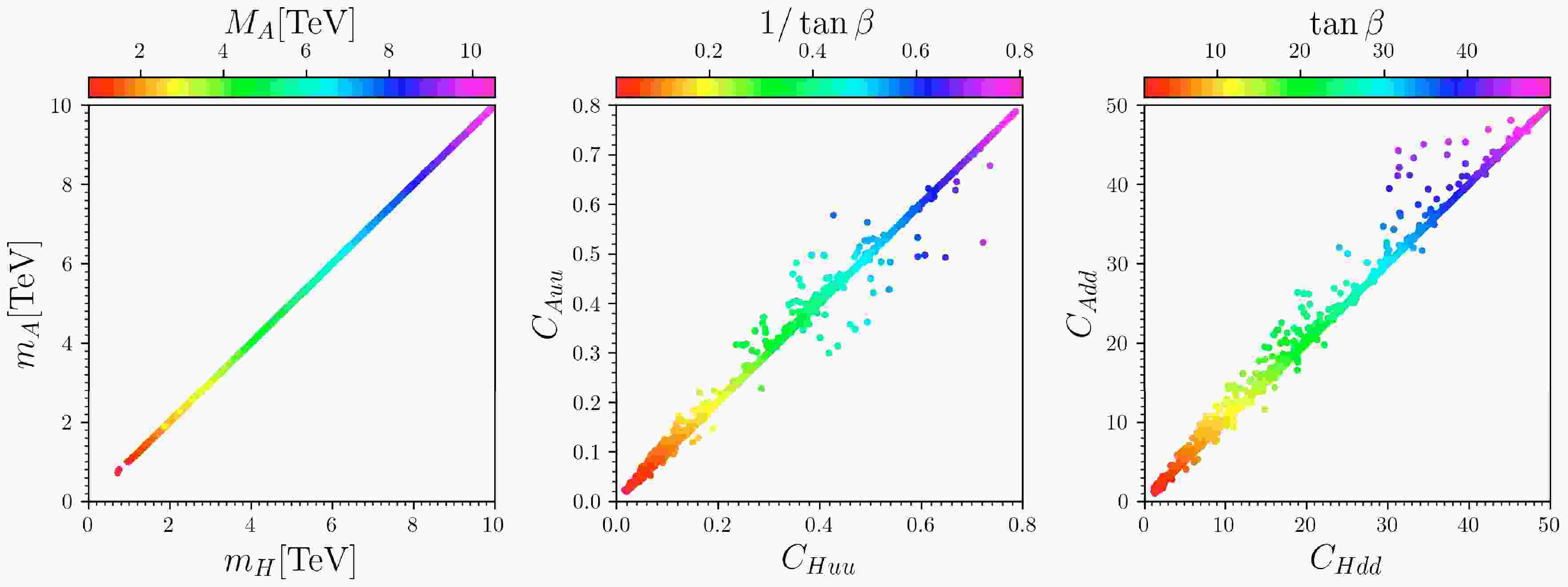
$ h_1 $ resembles the SM-like Higgs, with either$ h_2 $ or$ h_3 $ being doublet-dominant; the same is valid for$ a_1 $ and$ a_2 $ , where one of them is doublet-dominant. We label the heavy CP-even and CP-odd doublet-dominant Higgs bosons as H and A, respectively. In the second type,$ h_2 $ acts as the SM-like Higgs, with$ h_3 $ and$ a_2 $ typically being doublet-dominant, also denoted as H and A. Thus, H and A represent the heavy CP-even and CP-odd doublet-dominant Higgs bosons in subsequent discussions. For the heavy Higgs bosons H and A, which have masses ranging from$ 0.6 \; {\rm{TeV}} $ to$ 10 \; {\rm{TeV}} $ , we calculate their production cross sections and decay branching ratios. We also compare the$ pp\to b\bar{b}H\to b\bar{b}t\bar{t} $ signal with simulation results in Ref. [52].In Fig. 1, we show the mass and reduced coupling of the heavy doublet-dominated Higgs bosons H and A in the scNMSSM. The observations from these figures can be summarized as follows.

Figure 1. (color online) Surviving samples are shown in the planes of
$ m_A $ versus$ m_H $ (left), reduced coupling$ C_{Auu} $ versus$ C_{Huu} $ (middle), and reduced coupling$ C_{Add} $ versus$ C_{Hdd} $ (right). From left to right, the colors represent$ M_A $ ,$ 1/\tan \beta $ , and$ \tan \beta $ respectively. Samples with larger values of$ \tan \beta $ are plotted on top of those with smaller values.● In the left panel, the surviving samples are plotted on the
$ m_A $ versus$ m_H $ plane, with colors indicating$ M_A $ . H and A have nearly identical masses, approximately equal to the parameter$ M_A $ . This similarity arises because, according to Eq. (16),$ P_1 $ is the CP-odd doublet-dominated Higgs; as A is also denoted as the CP-odd doublet-dominated Higgs, it follows that$ m_A \approx M_A $ . Furthermore,$ S_1 $ is the CP-even doublet-dominated Higgs, labeled here as H. According to Eq. (9), when$ \tan\beta \gg 1 $ ,$ m_H \approx M_A $ . The mass of H and A is between$ 0.6 \; {\rm{TeV}} $ and$ 10 \; {\rm{TeV}} $ .● In the middle panel, the surviving samples are displayed on the plane of reduced coupling with up-type fermions for A versus H, with the colors indicating
$ 1/\tan \beta $ . For most samples,$ C_{Auu} $ and$ C_{Huu} $ are approximately equal to$ 1/\tan \beta $ . This approximation arises because the doublet components of H and A are neither exactly equal nor exactly equal to 1. Furthermore, the values of the reduced couplings$ C_{Huu} $ and$ C_{Auu} $ range from 0 to 0.8.● In the right panel, the surviving samples are plotted on the plane of reduced coupling with down-type fermions for A versus H, with colors representing
$ \tan \beta $ . The results are similar to those in the middle panel; for most samples,$ C_{Add} $ and$ C_{Hdd} $ approximate$ \tan \beta $ . This approximation is also due to the doublet components of H and A not being exactly equal or exactly equal to 1. Additionally, the values of the reduced couplings$ C_{Hdd} $ and$ C_{Add} $ vary from 0 to 50.In Fig. 2, we show the decay properties of the CP-even doublet-dominated heavy Higgs H in the scNMSSM, with colors representing
$ \tan \beta $ . As both heavy Higgs bosons A and H are doublet-dominated, their couplings to fermions show a very small difference. The only difference is that$ {\rm Br} (A\to VV/\tilde{V}\tilde{V})=0 $ . However, this difference is minimal due to the small coefficient$ C_{HVV} $ . Consequently, the decay properties of the CP-odd doublet-dominated heavy Higgs A are very similar to those of H. Therefore, the plot for A is omitted. The observations from these figures can be summarized as follows.
Figure 2. (color online) Surviving samples in the planes of branching ratios versus
$ m_H $ , with colors representing$ \tan\beta $ . The branching ratios pertain to the decays of the heavy CP-even Higgs H into$ t\bar{t} $ ,$ b\bar{b} $ ,$ \tau^+ \tau^- $ , all possible lighter Higgs bosons, and all possible SUSY particles, respectively. Samples with larger values of$ \tan \beta $ are plotted over those with smaller values.● The dominant branching ratios consistently arise from the decays to
$ t\bar{t} $ ,$ b\bar{b} $ and SUSY particles. These branching ratios reach values close to 1.● In the upper left panel, the branching ratio of H to
$ t\bar{t} $ is inversely proportional to$ \tan\beta $ ; that is, a smaller$ \tan\beta $ corresponds to a larger branching ratio$ {\rm Br}(H \to t\bar{t}) $ . This relationship is due to$ C_{Huu} $ being directly proportional to$ 1/\tan\beta $ . Consequently, when$ \tan\beta < 10 $ , the branching ratio${\rm Br}(H \to t\bar{t})$ exceeds 0.2. As$ \tan\beta $ approaches 1, the branching ratio${\rm Br}(H \to t\bar{t})$ tends toward 1.● In the upper middle and right panels, the branching ratios of H to
$ b\bar{b} $ and$ \tau^+ \tau^- $ are proportional to$ \tan\beta $ ; a larger$ \tan\beta $ corresponds to higher branching ratios${\rm Br}(H \to b\bar{b})$ and${\rm Br}(H \to \tau^+ \tau^-)$ . This proportionality is due to$ C_{Hdd} $ being directly proportional to$ \tan\beta $ . Additionally, when$ \tan\beta $ exceeds 40, the maximum branching ratio${\rm Br}(H \to b\bar{b})$ can reach 0.8, while the maximum branching ratio$ {\rm Br}(H \to \tau^+ \tau^-) $ can reach only 0.2. Furthermore, the branching ratio$ {\rm Br}(H \to \tau^+ \tau^-) $ is generally lower than$ {\rm Br}(H \to b\bar{b}) $ due to the lower mass of τ compared to b, as the coupling strength of Higgs with fermions is proportional to their mass.● In the lower left panel, the branching ratios of H to light Higgs bosons are relatively small, reaching a maximum of approximately 0.6. Additionally, for samples where
$ \tan\beta $ exceeds 40, the maximum branching ratio${\rm Br}(H \to \text{light Higgs})$ is only 0.1.● In the lower right panel, the maximum branching ratios of H to SUSY particles can approach 0.8. Additionally, when
$ \tan\beta $ ranges from 10 to 30, the branching ratios${\rm Br}(H \to \text{SUSY})$ can approach this maximum value of 0.8, remaining above 0.5. When$ \tan\beta $ is smaller than 10, the heavy Higgs H predominantly decays into$ t\bar{t} $ ; conversely, when$ \tan\beta $ exceeds 30, it primarily decays into$ b\bar{b} $ .We calculate the cross sections for the process
$pp \to b\bar{b} H$ in the SM with$ m_H $ ranging from$ 0.5 $ to$ 10 \; {\rm{TeV}} $ at$ \sqrt{s} = 100 \; {\rm{TeV}} $ using MG5_aMC_v2.6.7 [90, 91]. We used the "SM" model in MadGraph to conduct these calculations. The calculated cross section for$ m_H $ or$ m_A $ in our samples is multiplied by the square of the reduced coupling$ C_{Hbb} $ and branching ratio$ {\rm Br}(H/A \to t\bar{t}) $ . As the masses and various couplings of the heavy Higgs bosons H and A are very similar, along with nearly identical branching ratios$ {\rm Br}(H \to t\bar{t}) $ and$ {\rm Br}(A \to t\bar{t}) $ and similar reduced couplings$ C_{Hbb} $ and$ C_{Abb} $ , the heavy Higgs bosons H and A are considered degenerate in the detection channel$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ . Therefore, the cross section for the$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ channel is twice that of the individual H or A channels. Production rates for our samples in the$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ channel are presented in the left panel of Fig. 3, where colors indicate$ \tan\beta $ . The red and green curves represent the model-independent exclusion and discovery reaches, respectively, with an integrated luminosity of$ 3 {\; {\rm{ab}}}^{-1} $ at$ 100 \; {\rm{TeV}} $ , as depicted in Fig. 9 of Ref. [52]. In the calculation of the SM cross section, we employed both four-flavor scheme (4FS) and five-flavor scheme (5FS) cross sections [92], and combined them using the formula from Ref. [93]:
Figure 3. (color online) Surviving samples are shown in the planes of
$1/\tan^2 \beta / \Gamma_{\rm tot}(H)$ versus${\rm Br}(H \to t\bar{t})$ (left), heavy Higgs total decay width$\Gamma_{\rm tot}(H)$ versus heavy Higgs mass$ m_H $ (middle), and cross section of$ pp \to b\bar{b}H \to b\bar{b}t\bar{t} $ versus heavy Higgs mass$ m_H $ (right), where the colors of the samples indicate$ \tan\beta $ . The red and green curves represent the model-independent exclusion and discovery ranges, respectively, for the$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ channel, with an integrated luminosity of$ 3 {\; {\rm{ab}}}^{-1} $ at$ 100 \; {\rm{TeV}} $ , according to Fig. 9 in Ref. [52]. Samples with larger values of$ \tan \beta $ are plotted on top of those with smaller values.$ \sigma = \frac{\sigma^{\rm{4FS}} + \omega \sigma^{\rm{5FS}}}{1+\omega}, $

(30) where
$ \omega = \ln(m_H/m_b) - 2 $ .In Fig. 3 we show the cross section for the
$pp \to b\bar{b}H/A \to b\bar{b}t\bar{t}$ channel of the CP-even doublet-dominated heavy Higgs$ H/A $ in the scNMSSM, with colors representing$ \tan \beta $ . As the heavy Higgs A and H are considered degenerate, the cross section$\sigma(pp \to b\bar{b}H/ A \to b\bar{b}t\bar{t}) = 2\sigma(pp \to b\bar{b}H \to b\bar{b}t\bar{t})$ . The observations from these plots can be summarized as follows.● In the left panel,
$1/\tan^2 \beta / \Gamma_{\rm tot}(H)$ appears to be directly proportional to${\rm Br}(H \to t\bar{t}) $ , because the decay diagram for$ {\rm Br}(H \to t\bar{t}) $ includes a coupling vertex$ C_{Huu} $ . In the calculation of the decay cross-section, a$ C_{Huu}^2 $ term is introduced. Thus,$ {\rm Br}(H \to t\bar{t}) $ is proportional to$ 1/\tan^2 \beta $ . Additionally, the branching ratio$ {\rm Br}(H \to t\bar{t}) $ is inversely proportional to the total decay width$ \Gamma_{\rm tot}(H) $ , which is represented as$ {\rm Br}(H \to t\bar{t}) = \frac{\sigma(H \to t\bar{t})}{\Gamma_{\rm tot}(H)} \sim \frac{1/\tan^2\beta}{\Gamma_{\rm tot}(H)} \, . $

(31) ● In the middle panel, the total decay width
$\Gamma_{\rm tot}(H)$ of the heavy Higgs increases exponentially with$ \tan\beta $ . Additionally, when$ \tan\beta $ remains constant,$\Gamma_{\rm tot}(H)$ increases with the mass of the heavy Higgs$ m_H $ .● In the right panel, the cross section
$\sigma(pp \to b\bar{b}H/A \to b\bar{b}t\bar{t})$ decreases rapidly as the mass of the heavy Higgs$ m_H $ increases. The cross section for$pp \to b\bar{b}H \to b\bar{b}t\bar{t}$ can be approximated as follows:$ \begin{aligned}[b] & \sigma(pp \to b\bar{b}H \to b\bar{b}t\bar{t}) \\ \approx\; & \sigma^{\rm SM}(pp \to b\bar{b}H) \cdot C_{Hdd}^2 \cdot {\rm Br} (H \to t\bar{t}) \\ \approx \;& \frac{\sigma^{\rm SM}(pp \to b\bar{b}H)}{\Gamma_{\rm tot}(H)} \end{aligned} $

(32) This decline is because
$ \sigma(pp \to b\bar{b}H \to b\bar{b}t\bar{t}) $ is proportional to$\sigma^{\rm SM}(pp \to b\bar{b}H)$ , and the production cross section$\sigma^{\rm SM}(pp \to b\bar{b}H)$ diminishes with an increase in mass. Samples with the smaller$ \tan\beta $ values have larger cross sections$ \sigma(pp \to b\bar{b}H \to b\bar{b}t\bar{t}) $ , because$\sigma(pp \to b\bar{b}H \to b\bar{b}t\bar{t})$ is inversely proportional to the total decay width$ \Gamma_{\rm tot}(H) $ , and$ \Gamma_{\rm tot}(H) $ exponentially increases as the$ \tan\beta $ increases.● In the right panel, the regions above the green and red curves indicate where the samples can be covered by 2 σ and 5 σ, respectively, with an integrated luminosity of
$ 3 {\; {\rm{ab}}}^{-1} $ at$ 100 \; {\rm{TeV}} $ . This implies that, through the$pp \to b\bar{b}H/A \to b\bar{b}t\bar{t}$ channel in the scNMSSM, samples with a heavy Higgs mass$ m_H < 2 \; {\rm{TeV}} $ can be tested at the$ 100 \; {\rm{TeV}} $ collider with an integrated luminosity of$ 3 {\; {\rm{ab}}}^{-1} $ . Samples with the heavy Higgs mass$ m_H > 7 \; {\rm{TeV}} $ are below the exclusion and discovery curves, and thus, they cannot be discovered or excluded. Samples with the heavy Higgs mass in the range of$ 2-7 \; {\rm{TeV}} $ and$ \tan\beta < 20 $ can be tested at the$ 100 \; {\rm{TeV}} $ collider with an integrated luminosity of$ 3 {\; {\rm{ab}}}^{-1} $ .In Table 1, we present four benchmark samples detailing the Higgs sector, where
$ \sigma(X) $ represents the cross section$ \sigma(pp \to b\bar{b}X \to b\bar{b}t\bar{t}) $ . The heavy Higgs bosons H and A, corresponding to$ h_3 $ and$ a_2 $ , respectively, are doublet-dominated, while$ S_{33}^2 $ and$ P_{22}^2 $ indicate the singlet components in H and A. H and A have minimal singlet components, which suggests that$ h_2 $ and$ a_1 $ are primarily singlet-dominated. Owing to their weak coupling to fermions, these singlet-dominated bosons,$ h_2 $ and$ a_1 $ , are difficult to detect at colliders.P1 P2 P3 P4 λ 0.61 0.21 0.10 0.10 κ 0.36 −0.21 −0.42 0.67 $ \tan\beta $ 

2.07 4.98 20.02 47.91 $ \mu/{\rm{GeV}} $ 

361 345 295 498 $ M_0/{\rm{GeV}} $ 

8072 1506 5811 9596 $ M_{12}/{\rm{GeV}} $ 

3402 5569 3017 9289 $ A_0/{\rm{GeV}} $ 

7306 −6275 539 9862 $ A_\lambda/{\rm{GeV}} $ 

4961 1230 4983 2357 $ A_\kappa/{\rm{GeV}} $ 

2720 252 3769 −3588 $ m_{h_1}/{\rm{GeV}} $ 

124 124 124 125 $ m_{h_2}/{\rm{GeV}} $ 

341 648 1942 6796 $ m_{H}/{\rm{GeV}} $ 

720 2025 4030 7950 $ m_{a_1}/{\rm{GeV}} $ 

512 277 2920 1860 $ m_{A}/{\rm{GeV}} $ 

716 2026 4031 7950 $ S_{31}^2 $ 

0.99 1.00 1.00 1.00 $ S_{32}^2 $ 

0.00 0.00 0.00 0.00 $ S_{33}^2 $ 

0.01 0.00 0.00 0.00 $ P_{21}^2 $ 

1.00 1.00 1.00 1.00 $ P_{22}^2 $ 

0.00 0.00 0.00 0.00 $ C_{h_2uu} $ 

0.1 0.0 0.0 0.0 $ C_{Huu} $ 

−0.5 −0.2 −0.1 0.0 $ C_{a_1uu} $ 

0.0 0.0 0.0 0.0 $ C_{Auu} $ 

0.5 0.2 0.0 0.0 $ C_{h_2dd} $ 

0.4 0.1 0.0 0.3 $ C_{Hdd} $ 

2.0 5.0 20.0 47.9 $ C_{a_1dd} $ 

0.0 −0.2 −0.3 0.1 $ C_{Add} $ 

2.1 5.0 20.0 47.9 ${\rm Br}(h_2\to t\bar{t})$ 

0 0.01 $ 4.4 \times 10^{-4} $ 

$ 7.9 \times 10^{-8} $ 

Continued on next page Table 1. Four benchmark points for surviving samples, where
$ \sigma(X) $ denotes the cross section$ \sigma(pp \to b\bar{b}X \to b\bar{b}t\bar{t}) $ . H and A represent the doublet-dominated heavy Higgs bosons, while$ S_{33}^2 $ and$ P_{22}^2 $ indicate the singlet components in H and A, respectively. -
In this study, we explored the potential for detecting heavy Higgs bosons in the
$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ channel at a 100 TeV hadron collider within the semi-constrained NMSSM. First, we scanned the relevant parameter space with the$\textsf{NMSSMTools}$ package, which includes theoretical constraints such as vacuum stability and Landau poles, as well as experimental constraints such as Higgs data, B physics, sparticle searches, dark matter relic density, and direct detection experiments. We observed that singlet-dominated Higgs bosons S are difficult to detect due to their limited interactions outside the Higgs sector. Therefore, our analysis primarily focused on the more detectable heavy doublet-dominated CP-even Higgs H and CP-odd Higgs A, limiting their masses to below$ 10 \; {\rm{TeV}} $ to remain detectable. The presence of a CP-even Higgs ($ h_1 $ or$ h_2 $ ) resembling the 125 GeV SM-like Higgs does not affect these findings. As the heavy Higgs H and A are nearly identical in mass and couplings, the cross section for the combined channel$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ is effectively double that of the single H channel.We calculated their decay branching ratios and production rates, and compared them with the simulation results in Ref. [52]. We can summarize the following conclusions about the heavy Higgs bosons A and H, with masses ranging from 0.6 to 10 TeV, in the semi-constrained NMSSM.
● When the heavy Higgs bosons are doublet-dominated, their reduced couplings with up-type fermions,
$ C_{Huu} $ and$ C_{Auu} $ , are approximately equal to$ 1/\tan \beta $ . This relationship causes the branching ratio of$ H/A $ to$ t\bar{t} $ to be inversely proportional to$ \tan\beta $ ; a smaller$ \tan\beta $ results in a larger branching ratio${\rm Br}(H \to t\bar{t})$ . Conversely, the reduced couplings with down-type fermions,$ C_{Hdd} $ and$ C_{Add} $ , approximate to$ \tan \beta $ , leading to branching ratios of H to$ b\bar{b} $ and$ \tau^+ \tau^- $ that are directly proportional to$ \tan\beta $ .● When
$ \tan\beta $ is smaller than 10, the heavy Higgs H predominantly decays into$ t\bar{t} $ , with the branching ratio${\rm Br}(H \to t\bar{t})$ reaching 1. When$ \tan\beta $ exceeds 30, it primarily decays into$ b\bar{b} $ , with a branching ratio${\rm Br}(H \to b\bar{b})$ up to 0.8 and${\rm Br}(H \to \tau^+ \tau^-)$ up to 0.2. For$ \tan\beta $ values between 10 and 30, the branching ratio${\rm Br}(H \to \rm SUSY)$ is dominant, reaching 0.8.● The branching ratio
${\rm Br}(H \to t\bar{t})$ is proportional to$ 1/\tan^2 \beta $ and inversely proportional to the total decay width$ \Gamma_{\text{tot}}(H) $ . Furthermore, the total decay width of the heavy Higgs,$ \Gamma_{\text{tot}}(H) $ , increases exponentially with$ \tan\beta $ .● The cross section
$ \sigma(pp \to b\bar{b}H/A \to b\bar{b}t\bar{t}) $ decreases rapidly as the mass of the heavy Higgs ($ m_H $ ) increases and is inversely proportional to the total decay width$ \Gamma_{\text{tot}}(H) $ . Consequently, this cross section also decreases exponentially with an increase in$ \tan\beta $ .● For the
$ pp \to b\bar{b}H/A \to b\bar{b}t\bar{t} $ channel at a 100 TeV collider with an integrated luminosity of 3 ab$ ^{-1} $ in the semi-constrained NMSSM.● Heavy Higgs bosons with a mass
$ m_H < 2 $ TeV can be tested.● Heavy Higgs bosons with a mass
$ m_H > 7 $ TeV are below the exclusion and discovery thresholds and therefore cannot be discovered or excluded.● For heavy Higgs masses in the range of 2−7 TeV, those with
$ \tan\beta \lesssim 20 $ can be tested, while those with$ \tan\beta \gtrsim 20 $ cannot be discovered or excluded.
Exploration of heavy Higgs bosons at a 100 TeV hadron collider withinthe semi-constrained next-to-minimal supersymmetric standard model
- Received Date: 2024-04-19
- Available Online: 2024-09-15
Abstract: In this study, we explore the detectability of heavy Higgs bosons in the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: