Bulk-boundary and RPS thermodynamics from topology perspective

Thermodynamics of black holes is the study of how black holes behave as thermodynamic systems, including investigation of their temperature, entropy, heat capacity, and other properties. One of the main challenges is to understand the phase transitions and critical points of black holes in different contexts, such as anti-de Sitter (AdS) or de Sitter (dS) space, with or without electric charge, and nonlinear electromagnetic fields. Some important concepts in thermodynamics are critical points and phase transitions. A phase transition is a change of state of matter from one phase to another, such as from liquid to gas or from solid to liquid [1−15]. In thermodynamics, phase transitions are characterized by discontinuities or singularities in some thermodynamic quantities, such as pressure, volume, and temperature. Phase transitions can be classified into different orders depending on the behavior of these quantities near the transition point. A recent approach to studying the thermodynamics and phase transitions of black holes involves the use of Duan's topological current-mapping theory. This theory introduces topology to the study of black hole thermodynamics by assigning a topological charge to each critical point in the phase diagram. This method can reveal new features and classifications of black hole thermodynamics that are not captured by conventional methods. For example, it can distinguish between conventional and novel critical points, which have different implications for the first-order phase transition. It can also classify different types of black holes into different topological classes based on their topological charges. Many important works have investigated thermodynamics from the point of view of topology, exploring different aspects of this topic. For further details, you can refer to the following references: [16−44]. In this article, we study thermodynamics by comparing two different spaces, namely, bulk-boundary and restricted phase space (RPS), for different types of black holes, which have not been investigated so far. We will compare the results with each other and with those of other works in the literature.

Restricted phase space thermodynamics (RPST) is a new formalism for studying the thermodynamics of AdS black holes. The construction is based on Visser's holographic thermodynamics, but with the AdS radius being fixed. This means that the pressure and conjugate volume are excluded from the thermodynamic variables, and only central charge C of the dual CFT and chemical potential μ are included. The RPST formalism has several advantages over the conventional extended phase space (EPS) formalism, which treats the cosmological constant as pressure and introduces an extra pair of state variables (P, V). For example, the RPST formalism can avoid some ambiguities and inconsistencies in the EPS formalism, such as the definition of mass, Smarr relation, and first law of thermodynamics. The RPST formalism can also automatically satisfy the Euler relation, and it explicitly demonstrates the first-order homogeneity of mass and zeroth-order homogeneity of intensive variables. The RPST formalism can be applied to various types of AdS black holes, such as Kerr-AdS and RN-AdS [45, 46], and reveal some interesting thermodynamic behaviors and phase transitions. For example, it can show that there is a first-order supercritical phase equilibrium in the $ T-S $ processes at a fixed nonvanishing charge or angular momentum; however, at vanishing charge or angular momentum or at fixed potentials, there is always a non-equilibrium transition from a small unstable black hole state to a large stable black hole state. Moreover, there is a Hawking-Page phase transition in the $ \mu-C $ processes. The RPST formalism can also classify different types of black holes into different topological classes based on their topological charges of critical points [8, 45−50].

Bulk-boundary thermodynamic equivalence is a concept that states that, from the point of view of topology, the thermodynamics and phase transitions of AdS black holes in the bulk gravity theory are equivalent to those of the dual CFT on the boundary. This means that the bulk and boundary thermodynamics have the same topological charges of critical points, which can be calculated using the residue method. This concept was proposed by Zhang and Jiang in their paper [51] "Bulk-boundary thermodynamic equivalence: a topology viewpoint." In their work, they set both the cosmological constant and Newton's constant to be dynamical and developed mass/energy formulas in terms of thermodynamic state functions for three different scenarios: extended thermodynamics, which includes both pressure and volume; mixed thermodynamics, which includes only pressure; and boundary CFT thermodynamics, which includes neither pressure nor volume. They applied these formulas to study the thermodynamics and phase transitions of charged AdS black holes in various dimensions and with various charges or angular momenta and compared them with existing findings in the literature. They used the residue method to study the topological properties of phase transitions. They defined vector field φ on complex plane z, which is related to temperature T and entropy S. They also defined complex function Ω on z, which is related to different thermodynamic potentials for extended thermodynamics, mixed thermodynamics, and boundary CFT thermodynamics. They used these definitions to calculate the residues of $ \varphi/\Omega $ at different critical points on the z-plane and used them as topological charges to classify different types of phase transitions. They found that the bulk and boundary thermodynamics are topologically equivalent for both criticalities and first-order phase transitions in the canonical ensembles, as well as for the Hawking-Page (like) phase transitions in the grand canonical ensembles. They also found that these three kinds of phase transitions are distinguished by their unique topological charges. They claimed that their results exemplify the gravity-gauge duality in terms of topology [51−53].

Therefore, we consider different black holes and study their topological behavior in two spaces, bulk-boundary and RPS, and compare the results.

In [51], it was shown that the total topological charge remains constant in extended, mixed, and CFT thermodynamics. In contrats, we show that in RPS thermodynamics, the total topological charge changes in comparison with other thermodynamics. This effect may arise from the fixed cosmological constant.

One of the proposed methods to investigate the thermodynamics of a black hole is the use of topology, which leads to our prognostic of the phase structure of a black hole. Therefore, in this study, we tried to choose black holes so that they have a different phase structure. As the charged black hole and (4 and 5)-dimensional Gauss-Bonnet AdS black holes have similar behaviors in the phase structure. We chose the charged black hole to investigate the thermodynamic behavior of its topology with the 6-dimensional Gauss-Bonnet AdS black hole in two EPSs and RPSs.

Based on the above concepts, we organize the paper as follows:

In Sec. II, we briefly explain thermodynamic topology. In Sec. III, we perform calculations related to thermodynamic topology from the perspective of bulk-boundary for two black holes, namely, the R-N AdS black hole and charged Gauss-Bonnet AdS black hole. In Sec. IV, we undergo a similar process for the RPS and compare the results with each other and with the latest findings in the literature. Finally, we summarize the results in Sec. V.

The critical points of the phase diagram of thermodynamic systems can be classified into three categories: conventional, novel, and neutral, based on the topological charge given by the winding number of Duan's ϕ-mapping theory. This theory uses scalar thermodynamic function Φ and vector field ϕ to study the topological features and stability conditions of black hole solutions in various gravity theories. The zero points of ϕ correspond to the critical points of Φ, and the topological charge is determined by the deflection angle of ϕ along a closed contour around the zero point. The conventional class has a negative charge, the novel class has a positive charge, and the neutral class has a zero charge. Different gravity theories and parameters may affect the topological class of black hole solutions [16, 21, 54]. Researchers have recently discovered that black holes can be classified into two types based on their thermodynamic behaviors. These types are called conventional and novel, and they are determined by the topological charge of the critical points on the phase diagram. The phase diagram shows how the temperature of the black hole depends on other properties like entropy, pressure, and some extra parameters ($ x^{i} $), which vary depending on the gravity theory and black hole solution. These properties are considered as variables in extended thermodynamic systems. The temperature function for these systems is given by [16]

An important fact is that the critical points in the phase diagram of a thermodynamic system, i.e., where the system changes abruptly from one phase to another, can be found by solving the conditions for a stationary point of inflection,

Next, we represent the newly introduced thermodynamic function as Φ, where pressure P has been removed according to Eq. (2),

The above equation is obtained by eliminating variable P using Eq. (2) and adding factor $ \dfrac{1}{\sin\theta} $ to simplify the analysis. A new vector field is also introduced to develop the framework of Duan's ϕ-mapping theory:

where

Also, the charge can be considered as

where $ \eta_{i} $ is the sign of the zero component of topological current $ J^{0}(\phi/x)_{z_{i}} $ at the i-th zero point of ϕ, and it can be either $ +1 $ or $ -1 $. $ \beta_{i} $ and $ \omega_{i} $ are the positive integers (Hopf index) that count the number of loops and winding number around the i-th zero point of ϕ. The above equation shows that topological charge $ Q_{t} $ is non-zero only at the zero points of ϕ. Thus, each critical point has a topological charge given by the winding number, which can be positive or negative. This leads to two different topological classes (conventional and novel), where the negative charge corresponds to conventional and positive charge corresponds to novel. To visualize these topological classes, one can use a plot of $ (\theta-r) $ or $ (\theta-S) $ with some smooth curves C that go around the zero points in a positive direction. As a simplification, C is chosen to be an ellipse centered at $ (r_{0}, \dfrac{\pi}{2}) $ with parameter ϑ that ranges from $ 0 $ to $ 2\pi $ [54]:

Therefore, the topological charge given by the winding number can be obtained by calculating deflection $ \Omega(\vartheta) $ of vector field ϕ. Thus,

where

Now, we apply the equations introduced in this section to two types of black holes: R-N AdS black hole and charged Gauss-Bonnet AdS black hole. We use the bulk-boundary and RPS and describe the results of our work in detail in the following sections.

Bulk-boundary thermodynamics is a formalism that relates the thermodynamic quantities of AdS black holes in the bulk to those of the dual CFT on the boundary via the AdS/CFT correspondence. The bulk quantities include the mass, temperature, entropy, angular momentum, and electric potential of the black hole, while the boundary quantities include the energy, temperature, entropy, angular velocity, and chemical potential of the CFT. The bulk-boundary thermodynamics shows that the first law of thermodynamics and Smarr relation are satisfied by both the bulk and boundary quantities. The bulk-boundary thermodynamics also reveals some interesting phase transitions and critical behaviors of AdS black holes and their dual CFT.

A notable discovery in the past few years is that negative cosmological constant Λ results in thermodynamic pressure P that is positive:

where G is the Newton gravitational constant and $ \ell $ is the radius of the d-dimensional AdS space (setting $ \hbar=c=1 $). Building on the AdS/CFT concept and adopting the methodology outlined in [55, 56], we utilize the duality correlation presented in [57] to express central charge C in the following manner:

The value of factor k is influenced by the specific characteristics of the holographic system. The first law of black hole thermodynamics, under the condition that $ \ell $ and G are both variables for a black hole with the characteristics of mass M, electric charge Q, angular momentum J, area A, and Gauss-Bonnet constant $ \tilde{\alpha}=(d-3)(d-4)\alpha $, is as follows:

where $\kappa,\; \Omega,\; V, \;\Phi, \;\frac{\beta}{G}$, and γ are the surface gravity, conjugate angular velocity, thermodynamic volume, electric potential, conjugate to G, and conjugate variable of $ \tilde{\alpha} $, respectively. When G and J are both variables, according to Refs. [55, 56, 58], we can use the definition of ${\cal{M}}= M(A,\sqrt{G}Q,GJ, \Lambda,\tilde{\alpha})$ in bulk, in which case Eq. (12) can be rewritten [55],

By dividing each side by Newton's constant G, we can derive the variation in mass M as

By comparing Eqs. (12) and (14), beta can be obtained as

Also, for the central charge to play a role in the first law of thermodynamics, we need to use Eqs. (10) and (11). Thus, we have [56]

Therefore, by using Eqs. (12), (14), and (16) and $ T=\dfrac{\kappa}{2\pi}, S=\dfrac{A}{4G} $, we can obtain the first law of thermodynamics in the form of bulk and boundary as follows [55, 56]:

where

are chemical potential μ and new thermodynamic volume $ V_c $. Next, we examine the topology thermodynamics of two R-N AdS and charged Gauss-Bonnet AdS black holes in the bulk-boundary space.

An R-N AdS black hole is a type of charged black holes that has a negative cosmological constant. It is a solution to the Einstein-Maxwell equations that describe the gravitational field of a charged, non-rotating, spherically symmetric body. It has two event horizons: an inner and outer one. The R-N AdS black hole has some interesting properties, such as casting a shadow, exhibiting a phase transition similar to the van der Waals system, and having quantum gravitational corrections to its metric. Now, we apply the equations mentioned in Section II to the R-N AdS black hole. The metric of the R-N AdS black hole is given by [49]

where $ {\rm d}\Omega^2_2 $ is the metric of a unit two-sphere, and

where M and Q are related to the mass and charge of the black hole, respectively, and $ \ell $ is the radius of the AdS space. Thus, the temperature of this black hole is expressed in the following form:

We remove the $ \ell $ parameter by setting $ \dfrac{\partial T}{\partial r_h}=0 $ and consider the Φ function as follows:

Then, using Eq. (20), we obtain vector fields$ \phi^r=\dfrac{\partial \Phi}{\partial r_h} $ and $ \phi^{\theta}=\dfrac{\partial \Phi}{\partial \theta} $:

The normalized vector field is therefore $ n=\Bigg(\dfrac{\phi^r}{\|\phi\|}, \dfrac{\phi^{\theta}}{\|\phi\|} \Bigg) $. Thus, we have

To determine the topological charge of a critical point (where $ \phi^r=\phi^{\theta}=0 $), it is necessary to find its winding number $ w_i $. For this purpose, we seek assistance from the orthogonal $ \theta-r_h $ plane. In the following discussion, we set $ P=1 $ and $ \ell=\sqrt[4]{\dfrac{3 C}{8 \pi }} $. As shown in Fig. 1, the topological charge for the R-N AdS black hole in bulk-boundary thermodynamics is $ Q_t=-1 $. In fact, this finding aligns with the topological charge obtained in the extended black hole thermodynamics outlined in [16].

Figure 1.  (color online) Vector field n is represented by the arrows on the $ r_h-\theta $ plane, where $ Q=1, C=1, P=1 $

A charged Gauss-Bonnet AdS black hole is a type of charged black holes that has a negative cosmological constant and Gauss-Bonnet term in the action. The charged Gauss-Bonnet AdS black hole has some interesting properties, such as thermodynamic geometry, exhibiting a phase transition similar to that of the R-N AdS black hole, and having effects on the shadow, energy emission rate, and quasinormal modes of the black hole. The metric of the 6-dimensional charged Gauss-Bonnet AdS black hole is given by [17, 55]

where $ \tilde{\alpha}=6\alpha $ , M, Q are related to the mass and charge of the black hole, respectively, α is the Gauss-Bonnet coupling parameter, and $ \ell $ is the radius of the AdS space. To simplify, the area of a 6-dimensional unit sphere is denoted as $ \Sigma_k=1 $. We refer to studies [17, 55] and derive the temperature of the charged Gauss-Bonnet AdS black holes in six dimensions:

By setting $ \dfrac{\partial T}{\partial r_h}=0 $, we eliminate the $ \ell $ parameter and focus on the Φ function:

and

We also obtain the normalized vector field as follows:

Then, to determine the topological charge of the critical points, we draw the $ r_h-\theta $ diagram using Eq. (26). As shown in [55], for the 6D charged Gauss-Bonnet AdS black hole in bulk-boundary thermodynamics, when $ Q<Q_3 $, we have three critical points, whereas when $ Q>Q_3 $, we have only one critical point. According to Fig. 2, we find that in all cases in bulk-boundary thermodynamics, the total topological charge is –1 $ (Q_t=-1) $. This result is consistent with that reported by [17], in that the total topological charge of the 6D charged Gauss-Bonnet AdS black hole in the extended thermodynamics is $ -1\; (Q_t=-1) $ in all cases.

Figure 2.  (color online) Vector field n is represented by the arrows on the $ r_h-\theta $ plane, where $ C=30, P=0.015, \tilde{\alpha}=0.5 $: (a) $ Q=0.04 $ and (b) $ Q=1 $.

RPS is a new formalism for thermodynamics of AdS black holes that excludes the pressure and conjugate volume as thermodynamic variables but includes the central charge of the dual CFT and chemical potential as intensive variables. The RPS formalism is based on Visser’s holographic thermodynamics, but the AdS radius must be fixed. The RPS formalism has some advantages over the EPS formalism, such as avoiding the ambiguity of the Smarr relation and Euler relation, and making the scaling properties of the equations of state explicit. The RPS formalism has been applied to various AdS black hole solutions, such as R-N AdS and Kerr-AdS, and revealed some interesting thermodynamic behaviors, such as phase transitions, criticalities, and Hawking-Page transitions. Now, we perform the same process as in the previous sections for the mentioned black hole but in RPS. We compare the results with those of other works in the literature.

Visser developed a new version of the EPS formalism, which takes into account the AdS/CFT correspondence [58, 59]. This innovation includes the addition of CFT central charge C and conjugate chemical potential μ as new thermodynamic parameters. The volume and pressure are also changed to that of the CFT, where $ {\cal{V}} $ is proportional to $ \ell^{d-2} $ (with $ \ell $ being the AdS radius) and $ {\cal{P}} $ is determined by the CFT equation of states (EOS) $ E = (d -2){\cal{P}}{\cal{V}} $, where d represents the dimension of the bulk spacetime. In RPS thermodynamics, the relationship between the central charge of the black hole and Newton's constant is as follows:

While both $ \ell $ and G are considered to be variable in [58], the RPS formalism keeps $ \ell $ fixed and only G is allowed to vary. Physically, G is proportional to $ (\ell_p^{d-2}) $, where $ \ell_p $ represents the Planck length. Therefore, C has an intuitive interpretation as the number of pieces of the size of Planck “area” that a hypersurface of radius $ \ell $ can be divided into, with each such piece representing a single microscopic degree of freedom [60]. Varying G implies changing the Planck length, which in turn changes the number of pieces mentioned above [60]. As we are considering Gauss-Bonnet and R-N AdS black holes, the first law of thermodynamics in this formalism is

Electric charge $ \tilde{Q} $ and electric potential $ \tilde{\Phi} $ have been appropriately rescaled. In the RPS proposed in [49, 50], the radius AdS is considered fixed, in which case the first law of thermodynamics is rewritten as [49, 50]

The rescaled electric potential $ \hat{\Phi} $and re-scaled electric charge $ \hat{Q} $ are defined by the dual CFT quantities [49, 50, 56]:

In the following, we examine the topology thermodynamics for the considered black holes in the RPS.

We use [49], and for temperature, in the RPS formalism, we have

First, we remove the $ \hat{Q} $ parameter when condition $ \dfrac{\partial T}{\partial S}=0 $ is met and form the ϕ function as follows:

Then, utilizing Eq. (31), we construct the vector field as

and

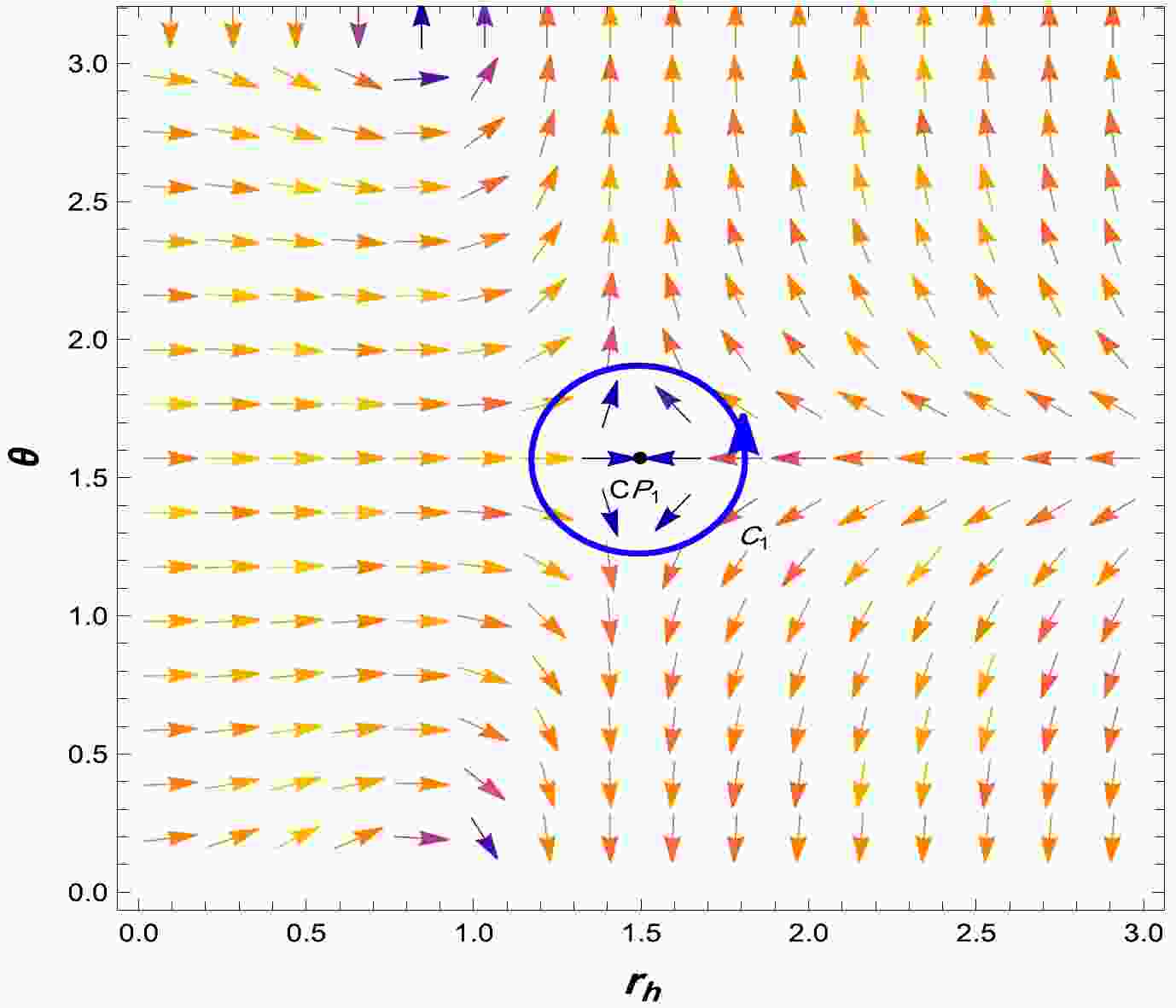
According to Eq. (33), we determine that the critical point is $ (S, \theta)=\left(\dfrac{C}{6},\dfrac{\pi}{2}\right) $. The obtained result is consistent with that reported by [49]. As shown in Fig. 3, this critical point possesses a topological charge of +1 $ Q_t=+1 $. This finding contradicts [16], implying that in the RPS formalism, it results in a modification of the topological charge.

Figure 3.  (color online) Vector field n represented by the arrows on the $ S-\theta $ plane, where $ C=1. $

We use [55] with definition $ \hat{Q}=Q \sqrt{C} $ [49], and we have

Then, by utilizing Eq. (2), we eliminate $ \hat{Q} $. Furthermore, in accordance with Eq. (2), we obtain the function as

We also have normalized vector fields:

According to Fig. 4, we find that there is only one critical point with a topological charge of +1 $ (Q_t=+1) $.

Figure 4.  (color online) Vector field n represented by the arrows on the $ r_h-\theta $ plane, where $ \ell=1 $ and $ \tilde{\alpha}=0.5 $.

In the following, for further investigation between these two formalisms, we will draw the $ T-S $ or $ T-r_h $ diagram and discuss it.

From Fig. 5(a), we can observe that the R-N AdS black hole exhibits a maximum point in bulk-boundary thermodynamics with a topological charge of –1. According to [16], a first-order phase transition occurs within it. However, for the RPS formalism in Fig. 5(b), the critical point is located at the minimum of $ T-S $. As the cosmological constant is considered fixed in the RPS formalism, we do not associate the black hole with the concept of volume. Therefore, the processes considered in RPS are not related to any volume work. Therefore, in this formalism, there is a behavior similar to that of van der Waals. Also, this critical point can show us the phase transition, as stated in [49]. Such phase transitions are considered as non-equilibrium transitions. From Figs. 6(a) and 6(b), it is evident that the number of critical points and total topological charge for charged Gauss-Bonnet AdS black holes in bulk-boundary thermodynamics are identical to those in extended thermodynamics. Furthermore, their phase transitions exhibit similar behavior. However, as shown inFig. 6(c), the behavior of the critical point and its topological charge is entirely distinct between boundary and RPS thermodynamics.

Figure 5.  (color online) (a) Spinodal curve for the R-N AdS black hole in bulk-boundary thermodynamics, where $ Q=C=1 $. (b) Spinodal curve for the R-N AdS black hole in RPS thermodynamics, where $ C=\ell=1 $.

Figure 6.  (color online) Spinodal curve for the charged Gauss-Bonnet AdS black hole in bulk-boundary thermodynamics, where $ C=30, \tilde{\alpha}=0.5 $: (a) $ Q=0.04 $ and (b) $ Q=1 $. (c) Spinodal curve for the charged Gauss-Bonnet AdS black hole in RPS thermodynamics, where $ \ell=1, \tilde{\alpha}=0.5 $.

In fact, when comparing two black holes in two different thermodynamic systems, we observe that the behavior of the number of critical points and total topological charge of the black hole are the same in both the boundary and extended thermodynamics. However, in the RPS formalism, the behavior differs between the boundary and extended thermodynamics. We also find that in the RPS formalism, there is only one critical point with a topological charge of +1 $ (Q_t=+1) $.

We investigated R-N AdS and charged Gauss-Bonnet AdS black holes in bulk-boundary and RPS thermodynamics. We found that the number of critical points and total topological charge of the two black holes considered in bulk-boundary thermodynamics are the same as those in the extended thermodynamics, and this result is in agreement with that reported by [51]. However, the topological charge of these two black holes in the RPS formalism differs from that of the bulk-boundary and extended thermodynamics. Also, in the RPS formalism, we only find one critical point with a topological charge of +1 for the charged AdS black hole.

These three thermodynamics are considered to be the same in one respect: additional terms and parameters for charged AdS black holes do not affect the topological class of the black hole. However, there is a difference between bulk-boundary and extended thermodynamics. In both cases, the total topological charge for the black hole is –1 $ (Q_t=-1) $ in all modes. Conversely, in RPS thermodynamics, the total topological charge is +1 $ (Q_t=+1) $.

The cosmological constant plays a significant role in the topological charge. As the cosmological constant is variable in both bulk-boundary and extended thermodynamics, their total topological charges are the same, but in RPS thermodynamics, the cosmological constant is fixed; hence, its total topological charge is different from the other two thermodynamics.

We are grateful to Prof Shao-Wen Wei for providing some valuable points.