-
In 2018, the Belle Collaboration observed a new excited hyperon
$ \Omega(2012)^- $ decaying into$ \Xi^0K^- $ and$ \Xi^-\bar{K}^0 $ with a mass of$ 2012.4\pm 0.7(\mathrm{stat})\pm 0.6(\mathrm{syst}) $ MeV and a width of$ \Gamma=6.4^{+2.5}_{-2.0}(\mathrm{stat})\pm1.6(\mathrm{syst}) $ MeV [1]. In 2021, evidence of$ \Omega(2012)^- $ was observed in the$ \Omega_c $ weak decay process$ \Omega_c\to \pi^+\Omega(2012)\to \pi^+(\Xi^0 K^-) $ at Belle [2], following the proposal suggested in Ref. [3]. According to the previous mass spectrum predicted in various models and methods, e.g., the Skyrme model [4], quark model [5–14], lattice gauge theory [15, 16], and so on [17–22], the newly observed$ \Omega(2012) $ may be a good candidate of the first orbital ($ 1P $ ) excitations of$ \Omega(1672) $ .The discovery of
$ \Omega(2012) $ immediately attracted a great deal of attention from the hadron physics community. The Okubo-Zweig-Iizuka (OZI)-allowed two body strong decays of the low-lying P- and D-wave Ω baryon states were analyzed within the chiral quark model [23, 24] and$ ^3P_0 $ model [25] by combining the mass spectrum analysis. It is found that the$ \Omega(2012) $ resonance favors the assignment of the$ 1P $ -wave state with spin-parity$ J^P=3/2^- $ , i.e.,$ \Omega^*|1P_{3/2^-}\rangle $ . Furthermore, the newly measured ratio$\mathcal{B}[\Omega_c\to \Omega(2012)\pi^+ \to (\Xi\bar{K})^-\pi^+]/ \mathcal{B}[\Omega_c \to \Omega \pi^+]$ at Belle was understood to be well within the three-quark picture in a recent study [26]. The conclusion is consistent with that based on the framework of QCD sum rules [27, 28], the constituent quark model including relativistic corrections [29], and the flavour SU(3) analysis [30]. Additionally, in literature, the$ \Omega(2012) $ was interpreted as a hadronic molecule [31–41]. In the hadronic molecular picture, the decay rate into the three-body final state$ \Xi \pi \bar{K} $ is predicted to be similar to that of the two-body final state$ \Xi \bar{K} $ . In contrast, in the three-quark picture, the decay rate for the OZI-allowed two-body final state$ \Xi \bar{K} $ should be dominant, and the decay rate of$ \Omega(2012)\to \Xi^*(1530)\bar{K} \to \Xi \pi \bar{K} $ should be suppressed because of the limited phase space of the intermediate hadron state$ \Xi^*(1530) $ .To test the decay properties of
$ \Omega(2012) $ predicted within different pictures, the three-body channel$ \Xi \pi \bar{K} $ through the decay chain$ \Omega(2012)\to \Xi^*(1530)\bar{K}\to \Xi\pi \bar{K} $ was observed by the Belle Collaboration. The first observation was carried out in 2019 [42]. The collaboration observed no significant$ \Omega(2012) $ signals in the three-body final state$ \Xi \pi \bar{K} $ and set an upper limit at a 90% confidence level on the branching fraction ratio$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}}\equiv \mathcal{B}[\Omega(2012)\to \Xi^*(1530)\bar{K}\to \Xi\pi\bar{K}]/\mathcal{B}[\Omega(2012)\to \Xi\bar{K}]<11{\text%} $ , which se-ems to be consistent with expectation in the three-quark picture. However, in a recent measurement, they observed significant$ \Omega(2012) $ signals in the three-body decay chain$ \Omega(2012)\to \Xi^*(1530)^0K^-\to \Xi^-\pi^+K^- $ [43]. A rather large ratio,$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}}=0.97\pm 0.24\pm 0.07 $ , was extracted from the observations, which seems to be consistent with the expectation in the hadronic molecular picture [3, 32, 35].In previous studies [23, 24], we did not investigate the three-body decay process
$ \Omega^*|1P_{3/2^-}\rangle\to \Xi^*(1530)\bar{K}\to \Xi\pi \bar{K} $ . It is unclear how large the decay rate of the$ \Xi\pi \bar{K} $ mode is within the three-quark picture. Furthermore,$ \Omega(2012) $ , as a conventional three-quark state, can couple to the$ \Xi^{*}(1530)\bar{K} $ ,$ \Xi \bar{K} $ , and$ \Omega\eta $ channels; then,$ \Omega(2012) $ may contain significant molecular components due to coupled-channel effects. To uncover these puzzles and better understand the nature of$ \Omega(2012) $ , in the three-quark picture, we further study the three-body decays of$ \Omega^*|1P_{3/2^-}\rangle\to \Xi \pi \bar{K} $ and the coupled-channel effects from nearby channels$ \Xi \bar{K} $ ,$ \Omega\eta $ , and$ \Xi^{*}(1530)\bar{K} $ . For self-consistency, we adopt the same framework, i.e., the chiral quark model [44], as in our previous studies for the excited Ω state studies [23, 24]. In this model an effective chiral Lagrangian is introduced to account for the quark-meson coupling at the baryon-meson interaction vertex. The light pseudoscalar mesons, i.e.,$ \pi,K $ , and η, are treated as Goldstone bosons. Since the quark-meson coupling is invariant under the chiral transformation, some of the low-energy properties of QCD are retained [45–47].This paper is organized as follows. In Sec. II, a brief review of the chiral quark model is given; then, by using this model, the two-body and three body strong decays of
$ \Omega^*|1P_{3/2^-}\rangle $ are estimated. In Sec. III, the coupled-channel effects on$ \Omega^*|1P_{3/2^-}\rangle $ are evaluated by combining the simplest version of the coupled-channel model with the chiral quark model. Finally, we provide a short discussion and summary in Sec. IV. -
In the chiral quark model [44], the low-energy quark-pseudoscalar-meson interactions in the SU(3) flavor basis are described by the effective Lagrangian [45–47]
$ \mathbf{{\cal L}}=\sum\limits_j \frac{1}{f_m}\bar{\psi}_j\gamma^{j}_{\mu}\gamma^{j}_{5}\psi_j\vec{\tau}\cdot\partial^{\mu}\vec{\phi}_m. $

(1) In the above effective Lagrangian,
$ \vec{\tau} $ is an isospin operator,$ \psi_j $ represents the jth quark field in the hadron,$ \phi_m $ is the pseudoscalar meson field, and$ f_m $ is the pseudoscalar meson decay constant. In this study, the decay constants for π, K, and η mesons are taken as$ f_{\pi}=132 $ MeV and$ f_{K}=f_{\eta}=160 $ MeV, respectively. To match the nonrelativistic wave functions of the initial and final hadron states, we adopt the nonrelativistic form of the Lagrangian:$ \begin{aligned}[b] \mathbf{{\cal H}}_{m}^{nr}=&\frac{{\rm i} \delta\sqrt {(E_f+M_f)(E_i+M_i)}}{f_m}\sum\limits_j\bigg\{\frac{\omega_m}{E_f+M_f} \sigma _j\cdot {P}_f \\& + \frac{\omega_m}{E_i+M_i} \sigma _j \cdot {P}_i- \sigma _j \cdot {q} +\frac{\omega_m}{2\mu_q} \sigma _j\cdot {p}'_j\bigg\}I_j \phi_m, \end{aligned} $

(2) where
$ \omega_m $ and$ {q} $ are the energy and three momentum of the final state pseudoscalar meson, respectively;$ E_i $ and$ M_{i} $ are the energy and mass of the initial heavy hadron, respectively;$ E_f $ and$ M_f $ represent the energy and mass of the final state heavy hadron, respectively;$ P_i $ and$ P_f $ are the momenta of the inial and final baryons, respectively;$ \sigma _j $ is the spin operator for the jth quark of the baryon system; and$ \mu_q $ is a reduced mass expressed as$1/\mu_q= 1/m_j+ 1/m'_j$ , with$ m_j $ and$ m'_j $ being the masses of the jth quark in the initial and final baryons, respectively.$ {p}'_j $ is the internal momentum operator of the jth quark;$ {p}'_j $ can be related to the jth quark momentum$ {p}_j $ and center-of-mass momentum$ {P}_{c.m.} $ of a hadron with the relation$ {p}'_j\equiv {p}_j- m_j/M {P}_{c.m.}$ . The plane wave part of the emitted light meson is$\phi_m= {\rm e}^{-{\rm i} {q}\cdot {r}_j}$ , and$ I_j $ is an isospin operator defined in the SU(3) flavor space [46, 48, 49]. δ as a global parameter accounts for the strength of the quark-meson couplings.For an excited baryon state, within the chiral quark model, its two-body OZI-allowed strong decay amplitudes with the emission of a light pseudoscalar meson
$ \mathbb{M} $ can be described by$ \begin{array}{*{20}{l}} \mathcal{M}\left[\mathcal{B} \rightarrow \mathcal{B}^{\prime} \mathbb{M}\right] =\langle\mathcal{B}^{\prime}\left|\mathbf{{\cal H}}_{m}^{n r}\right| \mathcal{B}\rangle, \end{array} $

(3) where
$ | \mathcal{B}\rangle $ and$ |\mathcal{B'}\rangle $ stand for the initial and final baryon states, respectively. With the decay amplitudes derived from Eq. (3), the partial decay width for the$ \mathcal{B} \rightarrow \mathcal{B}^{\prime} \mathbb{M} $ process can be calculated with$ \Gamma=\frac{1}{8 \pi} \frac{\left|\mathbf{q}\right|}{M_{i}^{2}}\frac{1}{2J_i+1}\sum\limits_{J_{i z} J_{f z}}\left|\mathcal{M}_{J_{i z} J_{f z}}\right|^{2}, $

(4) where
$ J_i $ is the total angular momentum quantum number of the initial baryon, and$ J_{i z} $ and$ J_{f z} $ represent the third components of the total angular momenta of the initial and final baryons, respectively.The OZI-allowed two-body strong decay for the Ω resonances has been evaluated under the framework of the chiral quark model in our previous studies [23, 24]. It is found that the newly observed
$ \Omega(2012) $ resonance favors the assignment of the$ 1P $ -wave state with$ J^P=3/2^- $ (i.e.,$ \Omega^*|1P_{3/2^-}\rangle $ listed in Table 1) in the Ω baryon family [23]. Considering$ \Omega(2012) $ as$ \Omega^*|1P_{3/2^-}\rangle $ ,$ \Xi \bar{K} $ is the only OZI allowed two-body decay channel, which is shown in Fig. 1, while the$ \Omega(2012) \to \Xi^{*}(1530)\bar{K} $ decay process is forbidden since the mass of$ \Omega(2012) $ lies below the$ \Xi^{*}(1530)\bar{K} $ threshold. Thus, the total width should be nearly saturated by the$ \Xi \bar{K} $ channel.$ \Omega^*|1^2P_{ 3/2^{-}}\rangle =\dfrac{1}{\sqrt{2}}\left\{ \psi_{000}^{\rho} \psi_{01m_{\lambda}}^{\lambda} \chi_{\frac{1}{2}S_z}^{\lambda} \phi_{\Omega}^{s} +\psi_{01m_{\rho}}^{\rho} \psi_{000}^{\lambda} \chi_{\frac{1}{2}S_z}^{\rho} \phi_{\Omega}^{s} \right\} $ 

$ \Omega|1^4S_{3/2^{+}}\rangle =\psi_{000}^{\rho} \psi_{000}^{\lambda} \chi_{\frac{3}{2}S_z}^{s} \phi_{\Omega}^{s} $ 

$ \Xi^{*}(1530)|1^4S_{3/2^{+}}\rangle =\psi_{000}^{\rho} \psi_{000}^{\lambda} \chi_{\frac{3}{2}S_z}^{s}\phi_{\Xi^{*}}^{s} $ 

$ \Xi|1^2S_{1/2^{+}}\rangle =\dfrac{1}{\sqrt{2}} \left\{ \psi_{000}^{\rho} \psi_{000}^{\lambda} \chi_{\frac{1}{2}\frac{1}{2}}^{\rho} \phi_{\Xi}^{\rho} +\psi_{000}^{\rho} \psi_{000}^{\lambda} \chi_{\frac{1}{2}\frac{1}{2}}^{\lambda} \phi_{\Xi}^{\lambda} \right\} $ 

Table 1. The baryon wave functions involved in our calculations.
$ \psi_{n_{\rho}l_{\rho}m_{\rho}}^{\rho} $ and$ \psi_{n_{\lambda}l_{\lambda}m_{\lambda}}^{\lambda} $ represent the radial wave functions of ρ-mode and λ-mode, respectively, while$ \chi_{SS_z}^{\sigma} $ and$ \phi_{\Omega,\Xi^*,\Xi}^{\sigma} $ express the spin and flavor wave functions of the baryon system, respectively. The details can be found in Ref. [50].
Figure 1. The OZI-allowed two-body decay process
$\Omega^*|1P_{3/2^-}\rangle $ $ \to \Xi K$ at (i) the hadronic level and (ii) the quark level.By using the wave function calculated from the potential model [23], within the chiral quark model, the partial width of
$ \Omega^*|1P_{3/2^-}\rangle\to \Xi \bar{K} $ is predicted to be$ \begin{array}{*{20}{l}} \Gamma_{\Xi \bar{K}}=\Gamma_{\Xi^0 K^-}+\Gamma_{\Xi^- \bar{K}^0}\simeq(3.0+2.7) \ \ \mathrm{MeV}, \end{array} $

(5) which is consistent with the measured width
$ \Gamma_{\rm exp.}= 6.4^{+2.5}_{-2.0}\pm 1.6 $ MeV of$ \Omega(2012) $ [51]. It should be mentioned that, in the calculations, to be consistent with the mass spectrum predicted in the potential model [23], the constituent quark masses of$ u/d $ and s quarks are adopted to be$ m_{u}=m_{d}=350 $ MeV and$ m_{s}=600 $ MeV. The decay constants for π, K, and η mesons are taken as$ f_{\pi}=132 $ MeV and$ f_{K}=f_{\eta}=160 $ MeV, respectively. The masses of the final and initial states are taken as the measured values from experiments [51], which are listed in Table 2. The global parameter in Eq. (2) is considered to have the same value as that determined in Refs. [23, 24, 50], i.e.,$ \delta = $ 0.576. The spatial wave functions of the baryons appearing in the initial and final states are in the form of a harmonic oscillator. For the Ξ and$ \Xi^*(1530) $ states, the harmonic oscillator strength parameter$ \alpha_{\rho} $ is taken as$ \alpha_{\rho}= $ 400 MeV, while the parameter$ \alpha_{\lambda} $ for the λ oscillator is related to$ \alpha_{\rho} $ via$ \alpha_{\lambda}=\sqrt[4]{3m_u/(2m_s+m_u)}\alpha_{\rho} $ [48]. For the$ \Omega^*|1P_{3/2^-}\rangle $ state, we take$ \alpha_{\rho}=\alpha_{\lambda}=411 $ MeV, which is fitted by reproducing the root-mean-square radius of the ρ-mode excitations from the potential model [23].Hadron $ J^{P} $ 

Mass/MeV $ \pi^{0},\pi^{\pm} $ 

$ 0^{-} $ 

$ 135.0,139.6 $ 

$ \bar{K}^{0},K^{\pm} $ 

$ 0^{-} $ 

$ 497.6,493.6 $ 

η $ 0^{-} $ 

$ 547.9 $ 

$ \Xi^{-},\Xi^{0} $ 

$ 1/2^{+} $ 

$ 1321.7,1314.9 $ 

$ \Xi^{*-},\Xi^{*0} $ 

$ 3/2^{+} $ 

$ 1535.0,1531.8 $ 

$ \Omega^{-} $ 

$ 3/2^{+} $ 

$ 1671.7 $ 

$ \Omega(2012) $ 

$ 3/2^{-} $ 

$ 2012.4 $ 

Table 2. Masses (MeV) of the hadrons adopted in this study. The data are taken from the Particle Data Group [51].
-
Recently, the Belle Collaboration observed a rather large three-body decay rate in the
$ \Omega(2012)\to \Xi^*(1530)^0K^- \to \Xi^-\pi^+K^- $ process. To test the nature of$ \Omega(2012) $ using the new data, we further evaluate the decay chain$ \Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}(1530)K \to [\Xi \pi] \bar{K} $ within the chiral quark model. For the cascade decay process$ \Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}(1530)\bar{K} \to [\Xi \pi] \bar{K} $ , as shown in Fig. 2, the decay amplitude can be expressed as
Figure 2. The three-body decay process
$ \Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}(1530)K $ $ \to [\Xi \pi] K $ at (i) the hadronic level and (ii) the quark level.$ \mathcal{M}_{\Omega^*|1P_{3/2^-}\rangle \to \Xi \pi \bar{K}}=\frac{\mathcal{M}_{\Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}\bar{K}}\mathcal{M}_{\Xi^* \to \Xi\pi}}{2M_{\Xi^*}\left( M_{\Xi \pi}- M_{\Xi^*}+i \tilde{\Gamma}_{\Xi^* \to \Xi\pi} / 2\right)}, $

(6) where
$ \mathcal{M}_{\Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}(1530)\bar{K}} $ and$ \mathcal{M}_{\Xi^* \rightarrow \Xi\pi} $ are the amplitudes defined in Eq. (3). It should be emphasized that the$ \Xi^*(1530) $ baryon mass$ M_{\Xi^*} $ in$ \mathcal{M}_{\Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}K} $ and$ \mathcal{M}_{\Xi^* \to \Xi\pi} $ is replaced with the invariant mass$ M_{\Xi\pi} $ of the$ \Xi\pi $ system, since the intermediate state$ \Xi^*(1530) $ can be slightly off-shell. Adopting the wave functions listed in Table 1, one can calculate the$ \mathcal{M}_{\Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}(1530)\bar{K}} $ and$ \mathcal{M}_{\Xi^* \rightarrow \Xi\pi} $ within the chiral quark model. Moreover,$ \tilde{\Gamma}_{\Xi^*(1530) \rightarrow \Xi\pi} $ depends on the invariant mass of$ M_{\Xi\pi} $ , and it can be obtained by Eq. (4).Then, the three-body decay width of the
$ \Omega^*|1P_{3/2^-}\rangle $ resonance in its rest frame was obtained as$ {\rm d} \Gamma_{\Xi \pi \bar{K}}=\frac{M_{\Xi \pi}^{2}}{M_{\Omega^*}^{2}} \frac{|\mathbf{q}_{K}|}{4 \pi^{2}} \frac{\tilde{\Gamma}_{\Xi^{*} \rightarrow \Xi \pi}\overline{\left|\mathcal{M}_{\Omega^*|1P_{3/2^-}\rangle \rightarrow \Xi^{*} \bar{K}}\right|^{2}}}{4 M_{\Xi^{*}}^{2}\left[\left(M_{\Xi \pi}-M_{\Xi^{*}}\right)^{2}+\tilde{\Gamma}_{ \Xi^{*} \rightarrow \Xi \pi}^{2}/4 \right]} {\rm d} M_{\Xi \pi}, $

(7) where the magnitude of the momentum for the final K meson is given by
$ |\mathbf{q}_{K}|=\frac{\sqrt{\left[M_{\Omega^*}^{2}-\left(m_{K}+M_{\pi \Xi}\right)^{2}\right]\left[M_{\Omega^*}^{2}-\left(m_{K}-M_{\pi \Xi}\right)^{2}\right]}}{2 M_{\Omega^*}}. $

(8) Integrating the right hand side of Eq. (7) from
$ M_{\Xi}+m_{\pi} $ to$ M_{\Omega^*}-m_{K} $ , one can easily calculate the three-body decay width of the cascade decay process$ \Omega^*|1P_{3/2^-}\rangle \to \Xi^{*}(1530)\bar{K} \to [\Xi \pi] \bar{K} $ . Our results are listed in Table 3.Channel $ \Xi^{-}\pi^{+}K^{-} $ 

$ \Xi^{0}\pi^{0}K^{-} $ 

$ \Xi^{-}\pi^{0}\bar{K}^{0} $ 

$ \Xi^{0}\pi^{-}\bar{K}^{0} $ 

$ \mathbf{Sum} $ 

$ \Gamma_i $ /MeV

$ 0.25 $ 

$ 0.18 $ 

$ 0.07 $ 

$ 0.17 $ 

$ \mathbf{0.67} $ 

$ \overline{\Gamma}_i $ /MeV

$ 0.21 $ 

$ 0.11 $ 

$ 0.11 $ 

$ 0.21 $ 

$ \mathbf{0.64} $ 

Table 3. The partial widths (MeV) of three-body final states for the
$ \Omega^*|1P_{3/2^-}\rangle $ state.$ \Gamma_i $ stands for the results including isospin breaking effects (i.e., considering the mass differences for the isospin multiplet in the final states). While$ \overline{\Gamma}_i $ stands for the results without the isospin breaking effects, the mass for the isospin multiplet in the final states is adopted as the average value of different charged states.$ \Omega(2012) $ as the$ \Omega^*|1P_{3/2^-}\rangle $ state has a sizeable partial decay width when decaying into the three-body final state$ \Xi \pi \bar{K} $ ,$ \begin{array}{*{20}{l}} \Gamma_{\Xi\pi\bar{K}}\simeq 0.67 \ \ \mathrm{MeV}. \end{array} $

(9) Combining it with the two-body decay width predicted in Eq. (5), the total width is predicted to be
$ \begin{array}{*{20}{l}} \Gamma_{\rm total} \simeq 6.37 \ \ \mathrm{MeV}, \end{array} $

(10) which is in good agreement with the data
$ \Gamma_{\rm exp.}=6.4^{+2.5}_{-2.0}\pm $ 1.6 MeV [51]. Then, the predicted ratio,$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}}\equiv\frac{\mathcal{B}[\Omega^*|1P_{3/2^-}\rangle\to \Xi^*(1530)\bar{K}\to \Xi\pi\bar{K}]}{\mathcal{B}[\Omega^*|1P_{3/2^-}\rangle\to \Xi\bar{K}]}\simeq 12\%, $

(11) is close to the previous value
$ (6.0\pm 3.7\pm 1.3)\% $ measured by the Belle Collaboration in 2019 [42]; however, it is$ 4 \sim 8 $ times smaller than the value measured in 2022, i.e.,$ 0.97\pm 0.24\pm 0.07 $ [43].In a recent study [29], the three-body decay of
$ \Omega(2012)\to \Xi\pi\bar{K} $ was also investigated within a constituent quark model by including relativistic corrections; a small ratio,$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}}\simeq 4.5\% $ , was obtained with the$\Omega^*| 1P_{3/2^-}\rangle$ assignment. It should be mentioned that the isospin breaking effects (i.e., considering the mass differences of the isospin multiplet in the final states) on the partial widths of the three-body decays are evident because the phase space of the three-body decay is very small; the magnitude of the K-meson momentum appearing in the phase space is sensitive to the the masses of the baryons ($ \Xi^{-} $ ,$ \Xi^{0} $ ) and mesons ($ \bar{K}^{0} $ ,$ K^{\pm} $ ,$ \pi^{0} $ ,$ \pi^{\pm} $ ) with different charges in the$ \Xi\pi\bar{K} $ final state. The results in Table 3 show that there are significant differences between the partial widths with and without consideration of the isospin breaking effects.It should be mentioned that the recent measured ratio,
$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}} $ , at Belle [43] seems to be compatible with the molecular interpretation for$ \Omega(2012) $ proposed in Refs. [38–41], where similar branching fractions for$ \Omega(2012) $ decay into$ \Xi \pi \bar{K} $ and$ \Xi \bar{K} $ were predicted. -
In the following, we will further explore the molecular components of
$ \Omega^*|1P_{3/2^-}\rangle $ due to coupled-channel effects. First, we provide a brief review of the coupled-channel model adopted in this study. A bare baryon state$ |A\rangle $ predicted in the quark model can couple to the two-hadron continuum$ BC $ via hadronic loops, as shown in Fig. 3. In the simplest version of the coupled-channel model [52–56], the wave function of the physical state is given by
Figure 3. The hadronic loop for a bare baryon state
$ |A\rangle $ coupling to two-hadron continuum$ BC $ at (i) the hadronic level and (ii) the quark level.$ \begin{equation} \begin{aligned} | \Psi \rangle =c_A |A\rangle + \sum\limits_{BC}\int c_{BC}(\mathbf{p})d^3\mathbf{p} |BC,\mathbf{p}\rangle , \end{aligned} \end{equation} $

(12) where
$ \mathbf{p}=\mathbf{p}_B=-\mathbf{p}_C $ is the final two-hadron relative momentum in the initial hadron static system;$ c_A $ and$ c_{BC}(\mathbf{p}) $ denote the probability amplitudes of the bare valence state$ |A\rangle $ and$ |BC,\mathbf{p}\rangle $ continuum, respectively.The coupling between the bare state
$ |A\rangle $ and the continuum components sectors$ |BC,\mathbf{p}\rangle $ is achieved by creating light quark pairs. This coupling, as an effective coupling for the quark-meson interactions, can be described with the chiral interactions expressed in Eq. (2) in the chiral quark model. Thus, the full Hamiltonian of the physical state$ | \Psi \rangle $ can be written as$ \begin{equation} \begin{aligned} \mathbf{{\cal H}} = \left( \begin{matrix}\mathbf{{\cal H}}_0\; \; \; \; \; \; \mathbf{{\cal H}}_m^{nr} \\ \mathbf{{\cal H}}_m^{nr}\; \; \; \; \; \; \mathbf{{\cal H}}_c \end{matrix}\right), \end{aligned} \end{equation} $

(13) where
$ \mathbf{{\cal H}}_0 $ is the Hamiltonian of the bare state$ |A\rangle $ in the potential model, while$ \mathbf{{\cal H}}_c $ is the Hamiltonian for the continuum state$ |BC,\mathbf{p}\rangle $ . Neglecting the interaction between the hadrons B and C, one has$ \begin{equation} \begin{aligned} \mathbf{{\cal H}}_{c}|BC,\mathbf{p}\rangle&=E_{BC}|BC,\mathbf{p}\rangle, \end{aligned} \end{equation} $

(14) where
$ E_{BC}=\sqrt{m_B^2+p^2}+\sqrt{m_C^2+p^2} $ represents the energy of$ BC $ continuum.The Schrödinger equation of a mixed system can be written as
$ \begin{aligned}[b] &\left( \begin{matrix}\mathbf{{\cal H}}_0\; \; \; \; \; \; \mathbf{{\cal H}}_m^{nr} \\ \mathbf{{\cal H}}_m^{nr}\; \; \; \; \; \; \mathbf{{\cal H}}_c \end{matrix}\right) \; \left( \begin{matrix} c_A |A\rangle \\ \sum\limits_{BC}\int c_{BC}(\mathbf{p}) d^3\mathbf{p} |BC,\mathbf{p}\rangle \end{matrix}\right)\\ =&M \left( \begin{matrix} c_A |A\rangle \\ \sum\limits_{BC}\int c_{BC} (\mathbf{p}) d^3\mathbf{p}|BC,\mathbf{p}\rangle \end{matrix}\right). \end{aligned} $

(15) From Eq. (15), we have
$ \begin{aligned}[b] \langle A | \mathbf{{\cal H}} | \Psi \rangle =&c_A M \\ =& c_A M_A+ \sum\limits_{BC}\int c_{BC}(\mathbf{p})d^3\mathbf{p} \langle A | \mathbf{{\cal H}}_m^{nr} | BC,\mathbf{p}\rangle , \end{aligned} $

(16) $ \begin{aligned}[b] \langle BC,\mathbf{p} | \mathbf{{\cal H}} | \Psi \rangle =&c_{BC}(\mathbf{p}) M \\ =&c_{BC}(\mathbf{p}) E_{BC}+ c_A\langle BC,\mathbf{p}| \mathbf{{\cal H}}_m^{nr} | A \rangle. \end{aligned} $

(17) Deriving
$ c_{BC}(\mathbf{p}) $ from Eq. (17) and substituting it into Eq. (16), we obtain a coupled-channel equation$ \begin{equation} \begin{aligned} M=M_A+\Delta M(M), \end{aligned} \end{equation} $

(18) where the mass shift
$ \Delta M(M) $ is given by$ \begin{aligned}[b] \Delta M(M) =& \mathrm{Re} \sum\limits_{BC}\int_0^{\infty} \frac{|\langle BC,\mathbf{p} |\mathbf{{\cal H}}_m^{nr}| A \rangle|^2}{(M-E_{BC})} p^2 {\rm d} p {\rm d}\Omega_p, \\ =& \mathrm{Re} \sum\limits_{BC}\int_0^{\infty} \frac{\overline{|\mathcal{M}_{A\to BC}(\mathbf{p})|^2}}{(M-E_{BC})} p^2 {\rm d}p , \end{aligned} $

(19) and
$ M_A $ is the bare mass of the baryon state$ |A\rangle $ , which can be predicted within the potential model. By plotting$ \Delta M(M) $ and$ M-M_A $ as functions of M, the physical mass$M_{\rm phy}$ and the mass shift$ \Delta M $ due to coupled-channel effects are both determined at the intersection point of two curves, as shown in Fig. 4.
Figure 4. (color online) Determination of the mass shift for the
$ \Omega^*|1P\rangle_{3/2^{-}} $ state using two methods: (i) cut off at the inflection point (left hand side); (ii) with a suppressed factor (right hand side).$ \Delta M(M) $ and$ M-M_A $ as functions of M are indicated as thick and thin solid curves, respectively, while the partial mass shift functions for the$ \Xi \bar{K} $ ,$ \Omega \eta $ , and$ \Xi^* \bar{K} $ channels are shown with dotted, dash-dot-dotted, and dashed curves, respectively.To provide more details about the mass shift due to coupled-channel effects, in Fig. 5 , we plot the integrand
$ \Delta \tilde{M}(p)\equiv \dfrac{\overline{|\mathcal{M}_{A\to BC}(\mathbf{p})|^2}}{(M-E_{BC})} p^2 $ of Eq. (19) as a function of momentum$ p=|\mathbf{p}| $ . It can be seen that the coupled-channel effects significantly contribute to the hadron mass shift in a wide momentum range,$ p\simeq (0 - 2000) $ MeV. There is a bump structure in the higher p range of$ p\simeq (500 - 2000) $ MeV. Most of the contribution from the bump structure may be nonphysical because the quark pair production rates via the nonperturbative interaction$ \mathcal{H}_{m} $ should be strongly suppressed in the high momentum region [52, 57–59]. The main contribution of the coupled-channel effects may come from the low momentum region around the pole position.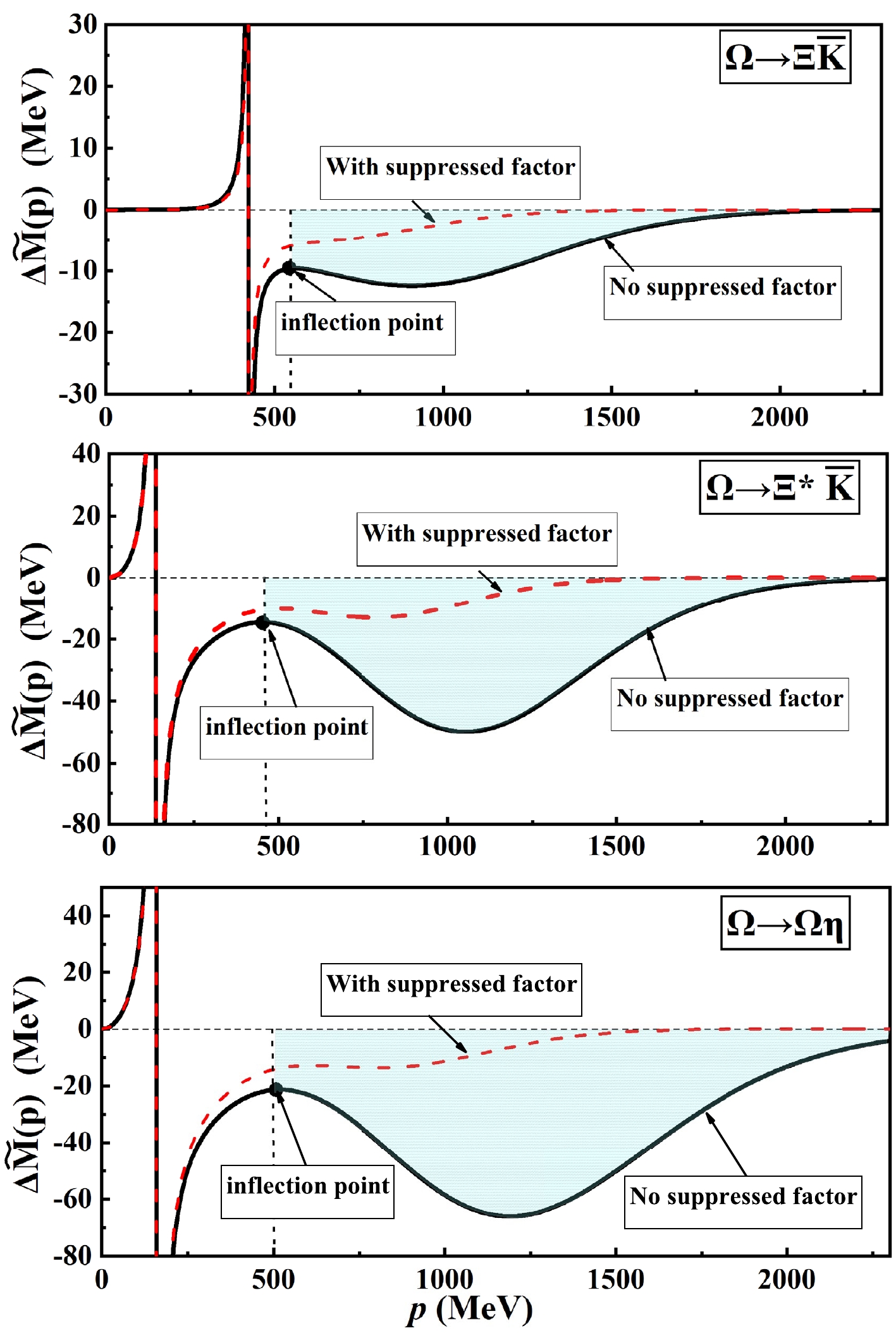
Figure 5. (color online) The integrand
$ \Delta \tilde{M}(p)\equiv \frac{\overline{|\mathcal{M}_{A\to BC}(\mathbf{p})|^2}}{(M-E_{BC})} p^2 $ as a function of the momentum$ p=|\mathbf{p}| $ for the$ \Xi \bar{K} $ ,$ \Xi^{*}(1530)\bar{K} $ , and$ \Omega\eta $ channels, respectively. The dashed line indicates the results with a suppressed factor${\rm e}^{-p^{2}/2\Lambda}$ (Λ=780 MeV), while the solid line indicates the results without suppressed factors. The shadow area represents the high momentum region, which may include non-physical contributions.To suppress the nonphysical contributions of the coupled-channel effects at the high momentum region, in literature [52, 57–59], a suppressed factor
${\rm e}^{-p^2/(2 \Lambda^2)}$ was introduced in the decay amplitudes, i.e.,$ \begin{array}{*{20}{l}} \mathcal{M}_{A \rightarrow B C}(\mathbf{p}) \to \mathcal{M}_{A \rightarrow B C}(\mathbf{p}) {\rm e}^{-\frac{p^2}{2 \Lambda^2}}. \end{array} $

(20) Here, Λ is the cut-off parameter. In Fig. 5, we also plot
$ \Delta \tilde{M}(p) $ as a function of momentum$ p=|\mathbf{p}| $ by introducing a suppressed factor${\rm e}^{-p^2/(2 \Lambda^2)}$ . In this study, we adopt$ \Lambda=780 $ MeV, which is determined from our recent study of the heavy-light meson spectrum with coupled-channel effects [60]. The cut-off parameter adopted in the present study is slightly smaller than the value of$ \Lambda=840 $ MeV used in Refs. [58, 59]. From Fig. 5, it is seen that the coupled-channel effects are suppressed to be negligibly small at the high momentum range of$ p>800 $ MeV, while the contributions at the low momentum range of$ p<500 $ MeV are almost not affected by the suppressed factor. In a previous study [61], the contribution of the high momentum range was directly cut off at the inflection point as shown in Fig. 5. With this method, from Table 4, it is seen that the predicted mass shift is approximately 2 times smaller than that predicted using a suppressed factor. To see the nonphysical contributions, in Table 4, we also present the results without any suppressions in the high momentum range. The nonphysical contributions may be very significant. The mass shift without any suppressions is approximately one order of magnitude larger than that with a suppressed factor.Channel $ \Xi \bar{K} $ 

$ \Xi^{*}(1530)\bar{K} $ 

$ \Omega\eta $ 

Baryon core $ \mathbf{Total} $ 

$Cut\text{-}off ~~at ~~inflection ~~point$ 

$ \Delta M $ /MeV

$ -2.2 $ 

$ -9.4 $ 

$ -3.0 $ 

$ \mathbf{...} $ 

$ \mathbf{-14.6} $ 

Proportion $ (\%) $ 

$ 1.8 $ 

$ 13.5 $ 

$ 0.8 $ 

$ \mathbf{83.9} $ 

$ \mathbf{100} $ 

$ With ~~ a ~~ suppressed ~~factor $ 

$ \Delta M $ /MeV

$ -5.6 $ 

$ -21.5 $ 

$ -8.8 $ 

$ \mathbf{...} $ 

$ \mathbf{-35.9} $ 

Proportion $ (\%) $ 

$ 1.4 $ 

$ 14.6 $ 

$ 1.3 $ 

$ \mathbf{82.6} $ 

$ \mathbf{100} $ 

$ Without ~~any ~~ suppressions $ 

$ \Delta M $ /MeV

$ -17.5 $ 

$ -75.5 $ 

$ -51.3 $ 

$ \mathbf{...} $ 

$ \mathbf{-144.3} $ 

Proportion $ (\%) $ 

$ 3.0 $ 

$ 18.7 $ 

$ 3.8 $ 

$ \mathbf{74.5} $ 

$ \mathbf{100} $ 

Table 4. The proportions of different components and mass shifts for the
$ \Omega^*|1P_{3/2^-}\rangle $ state predicted with three methods: (i) cut off at the inflection point; (ii) with a suppressed factor; (ii) without any suppressions. The cut-off momenta for the$ \Xi \bar{K} $ ,$ \Xi^{*}(1530)\bar{K} $ , and$ \Omega\eta $ channels are determined as$ 550 $ ,$ 450 $ , and$ 500 $ MeV, respectively.To estimate the baryon core and baryon-meson continuum components in the physical state, for below-threshold states, deriving
$ c_{BC}(\mathbf{p}) $ from Eq. (17) and substituting it into normalized constants containing two Fock components,$ \begin{equation} \begin{aligned} |c_A|^2+\sum\limits_{BC}\int |c_{BC}(\mathbf{p})|^2 d^3\mathbf{p} =1, \end{aligned} \end{equation} $

(21) we obtain the probability of hadron A component,
$ \begin{equation} P_A=|c_A|^2= \left( 1+ \sum\limits_{BC} \int \frac{\overline{|\mathcal{M}_{A\to BC}(\mathbf{p})|^2}}{(M-E_{BC})^2} p^2 {\rm d} p \right)^{-1}. \end{equation} $

(22) Further, combining Eq. (17) and Eq. (22), we can obtain the probability of the
$ |BC,\mathbf{p}\rangle $ continuum components,$ \begin{equation} \begin{aligned} P_{BC}=|c_A|^2 \int \frac{\overline{|\mathcal{M}_{A\to BC}(\mathbf{p})|^2} }{(M-E_{BC})^2} p^2 {\rm d} p . \end{aligned} \end{equation} $

(23) With Eqs. (22) and (23), one can estimate the probabilities of the bare baryon components and
$ BC $ hadron pair components of a physical state. However, the integrands in Eqs. (22) and (23) are only well defined for$ M<m_B+ m_C $ . For states above the$ BC $ hadron pair threshold, as suggested in Ref. [37], we replace the real M with its complex counterpart,$M+{\rm i}\,\Gamma/2$ , where Γ is the decay width of the physical state.By using the above coupled-channel model, we study the coupled-channel effects on the
$ \Omega^*|1P_{3/2^-}\rangle $ . The bare state$ |A\rangle $ is considered to be the$ 1P $ -wave state with$ J^P=3/2^- $ (i.e.,$ \Omega^*|1P_{3/2^-}\rangle $ ) predicted within the quark model. Three nearby channels$ \Xi \bar{K} $ ,$ \Omega\eta $ , and$ \Xi^{*}(1530)\bar{K} $ are considered. The strong coupling amplitudes$\langle \Xi K /\Xi^{*}(1530)\bar{K}/ \Omega\eta |\mathbf{{\cal H}}_m^{nr} |\Omega^*1P_{3/2^-}\rangle$ can be easily obtained within the chiral quark model by using the same parameter set. Using this, we further extract the mass shift of the bare state$ |\Omega^*1P_{3/2^-}\rangle $ due to the coupled-channel effects and the proportion of various components. Our results are listed in Table 4.It is found that the coupled-channel effects on
$ \Omega(2012) $ is not very large if one considers it as the$ \Omega^*|1P_{3/2^-}\rangle $ state. The mass shift due to coupled-channel effects is predicted to be$ \Delta\in(-144,-15) $ MeV, which is mainly contributed by the S-wave channel$ \Xi^{*}(1530)\bar{K} $ . The components of$ \Omega(2012) $ may be dominated by the baryon core$ \Omega^*|1P_{3/2^-}\rangle $ , the proportion of which is predicted to be$\sim 75%-84\%$ , while the proportion of the$ \Xi^{*}(1530)\bar{K} $ component is only$\sim 14%-19\%$ . -
With the
$ \Omega^*|1P_{3/2^-}\rangle $ assignment, both the observed mass and total width of$ \Omega(2012) $ can be well explained [23–25]. Furthermore, the newly measured ratio$ \mathcal{B}[\Omega_c\to \Omega(2012)\pi^+ \to (\Xi\bar{K})^-\pi^+]/\mathcal{B}[\Omega_c\to \Omega \pi^+] $ at Belle can be well understood [26]. The decay width is nearly saturated by the two-body decay channel$ \Xi K $ . In the present study, to further understand the nature of$ \Omega(2012) $ resonance, we investigate the three-body decays of$ \Omega^*|1P_{3/2^-}\rangle\to \Xi \pi \bar{K} $ and coupled-channel effects from nearby channels$ \Xi \bar{K} $ ,$ \Omega\eta $ , and$ \Xi^{*}(1530)\bar{K} $ .It is found that, considering the
$ \Omega(2012) $ resonance as a conventional$ 1P $ -wave state$ \Omega^*|1P_{3/2^-}\rangle $ , it has sizeable decay rates into the three-body final state$ \Xi \pi \bar{K} $ . The partial width and branching fraction are predicted to be$ \Gamma_{\Xi \pi \bar{K}}\simeq 0.67 $ MeV and$ \mathcal{B}[\Omega(2012)\to \Xi \pi \bar{K}]\simeq 12\% $ , respectively. The predicted ratio$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}}=\mathcal{B}[\Omega(2012)\to \Xi^*(1530)\bar{K} \to \Xi\pi\bar{K}]/\mathcal{B}[\Omega(2012)\to \Xi\bar{K}]\simeq0.12 $ is close to the previous value$ (6.0\pm 3.7\pm 1.3)\% $ measured by Belle in 2019 [42]; however, it is too small to be comparable to the recent value$ 0.97\pm 0.24\pm 0.07 $ measured by Belle in 2022 [43].Note that the newly measured ratio
$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}}= 0.97\pm 0.024\pm 0.07 $ at Belle seems to be consistent with the molecular interpretation for the$ \Omega(2012) $ resonance proposed in Refs. [38–41]. However, our results show that the molecular component of$ \Omega(2012) $ is no more than$ 30\% $ if we consider the$ \Omega(2012) $ resonance as a dressed baryon core of$ \Omega^*|1P_{3/2^-}\rangle $ . It should be mentioned that the mass and strong decay behaviors of the$ \Omega(2012) $ resonance were investigated in a coupled-channel approach in a recent study [62]. The results of that study indicate that both the three-quark core and$ \Xi^{*}(1530)\bar{K} $ channel are important and play essential roles in describing the mass and strong decay behaviors of the$ \Omega(2012) $ resonance. It is expected that further studies on the coupled-channel effects, especially based on the quark models, are needed. Precise measurements of the ratio$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}} $ can be used to clarify this issue. In addition, the latest observations by the Belle Collaboration [43] make the situation more complicated for the$ \Omega(2012) $ resonance, and it is hoped that the ratio$ R_{\Xi\bar{K}}^{\Xi\pi\bar{K}} $ can be tested by other experiments as well.
Further study of ${{\boldsymbol{\Omega^*}} \boldsymbol{|1P_{\bf 3/2^-}\rangle} }$ within a chiral quark model
- Received Date: 2022-12-17
- Available Online: 2023-06-15
Abstract: In our previous studies, we analyzed the two-body strong decays of the low-lying Ω baryon states within a chiral quark model. The results showed that the mass, total width, and two body decay







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






























 DownLoad:
DownLoad: