-
In the past two decades, a large number of new hadronic states have been observed by large-scale scientific facilities, several of which cannot be categorized as conventional mesons or baryons. The states that do not meet the expectations of conventional hadrons in the quark model are known as exotic states. Theorists have conducted numerous studies in an attempt to explain the mysterious properties of these exotica. The experimental and theoretical effort required makes the study of these exotic states an intriguing field in hardonic physics. These achievements and progresses provide good opportunities for us to investigate the internal structures of exotica, and recent experimental and theoretical statuses can be found in reviews [1–10].
Among the new hadronic states, charmonium-like states are particularly fascinating and attract wide attention both experimentally and theoretically. Various approaches have been adopted to study their properties, including phenomenological quark models, effective field theories, QCD sum rules, and lattice QCD, and several different interpretations have been proposed to reveal their natures, such as compact tetraquarks, meson-meson molecular states, conventional charmonia, hybrid states, and kinematic effects. These investigations on charmonium-like states covered masses, decay behaviors, production processes, and magnetic moments. Although previous studies have not provided a unified explanation, it is essential to explore every aspect of these states with different configurations because this can help us to better understand them and search for additional undetected particles.
Besides mass spectra and production, strong decay behaviors reflect the internal structures of charmonium-like states and hence have been attracting increasing attention. In literature, two-meson decay channels have been widely studied [11–23]. For molecular states, these decays usually occur through meson exchange processes, and the fall-apart mechanism is generally assumed to estimate the partial decay widths of compact tetraquarks. Moreover, a charmonium-like state can decay into one light meson plus one charmonium-like state, and yet there are few studies on this type of decay. Under the molecular hypothesis, the authors calculated the processes using the effective Lagrangian approach [24, 25]. However, these processes have not been investigated within compact tetraquark configurations. In fact, the light meson emissions of these
$ XYZ $ states not only help us distinguish between compact tetraquarks and loosely bound molecules, but also play an essential role as the connecting bridges between different charmonium-like states. Hence, it is important to study these decay processes for charmonium-like states within compact tetraquark configurations.Experimentally, several candidates have been observed for excited compact tetraquarks. In 2016, a
$ J^{PC } $ =$ 0^{++} $ structure$ X(4700) $ was discovered in the$ B^{+} \rightarrow J/\psi \phi K^{+} $ decay process by the LHCb Collaboration [26, 27], which had a mass of$ 4704 \pm 10^{+14}_{-24} $ MeV and a width of$ 120 \pm 31^{+42}_{-33} $ MeV. Because$ X(4700) $ was found in the$ J/\psi \phi $ invariant mass, it may include both a$ c \bar c $ pair and$ s \bar s $ pair and be regarded as a radially excited$ c \bar c s \bar s $ compact tetraquark [28–31]. Another radially excited candidate is the resonance$ Z_{c}(4430) $ , which was first observed in the$ B \rightarrow K \pi^- \phi(2S) $ decay process by the Belle Collaboration in 2007 [32]. This resonance was then confirmed in the same process by the LHCb Collaboration and in the$ B^{0} \rightarrow K^{-}\pi^{+}J/\psi $ decay by the Belle Collaboration [33, 34]. Its mass and decay width were remeasured to be$ 4478^{+15}_{-18} $ MeV and$ 181 \pm31 $ MeV, respectively [35]. For$ P $ -wave candidates, there have been several$1^{--}$ charmonium-like states. For instance, Y(4260) was reported in the process$ e^{+}e^{-} \rightarrow \pi^{+}\pi^{-} J/ \psi $ by the BaBar Collaboration and subsequently confirmed by the Belle and BESIII Collaborations [36–38]. With increasing experimental data, Y(4260) was renamed Y(4230), with a mass of$ (4219.6 \pm 3.3 \pm 5.1) $ MeV and a width of$ (56.0 \pm 3.6 \pm 6.9) $ MeV, respectively [35]. Moreover, the decay branching fraction$\Gamma_{e^{+}e^{-}} \mathcal{B}[Y(4230) \rightarrow \pi^{+}\pi^{-}h_c]$ was measured to be$ (4.6^{+2.9}_{-1.4} \pm 0.8) $ eV in the$ \pi^{+}\pi^{-}h_c $ channel [39]. Y(4390) was found in the$ e^{+}e^{-} \rightarrow \pi^{+}\pi^{-} h_c $ cross sections at approximately 4.22 and 4.39 GeV by the BESIII Collaboration [39], with a mass of$ 4391.5^{+6.3}_{-6.8} \pm 1.0 $ MeV and a width of$ 139.5^{+16.2}_{-20.6} \pm 0.6 $ MeV, respectively. This structure was also observed in the$ e^{+}e^{-} \rightarrow \eta J/\psi $ and$e^{+}e^{-} \rightarrow \pi^{+}\pi^{-}D^+ D^-$ processes [40, 41]. Experimental information on the other$ P $ -wave candidates$ Y(4360) $ and$ Y(4660) $ can be found in [38, 42–49].In this study, we apply the
$ ^3P_0 $ model to four-body systems and calculate the selected decays of the resonances$ X(4700) $ ,$ Z_c(4430) $ ,$ Y(4230) $ ,$ Y(4360) $ ,$ Y(4390) $ , and$ Y(4660) $ . The final states are light mesons plus$ Z_c(3985) $ ,$ Z_c(4020) $ ,$ Z_{cs}(3900) $ , or$ Z_{cs}(4000) $ . According to previously theoretical and experimental studies, these charmonium-like states are good candidates of compact tetraquarks. Here, we adopt compact tetraquark configurations to investigate the decay processes among these$ XYZ $ states. We find that the pion/kaon decay widths of$ X(4700) $ and$ Z_c(4430) $ are relatively small, whereas the partial decay widths of$ Y(4230) $ ,$ Y(4360) $ ,$ Y(4390) $ , and$ Y(4660) $ are significant.This paper is organized as follows: The formalism for the strong decays of compact tetraquarks in the
$ ^3P_0 $ model is introduced in Sec. II. We present the numerical results and discussions for the selected charmonium-like states in Sec. III. Finally, a short summary is given in the last section. -
In this study, we adopt the
$ ^3P_0 $ model to calculate the Okubo-Zweig-Iizuka-allowed strong decays of compact tetraquark states. In this model, a quark-antiquark pair with the quantum number$ J^{PC} $ =$ 0^{++} $ is created from vacuum and then goes into the final states [50]. This model has been widely employed to study strong decays for different types of hadronic systems with notable success [51–66]. Moreover, several previous studies adopted the formalism for compact tetraquarks [53, 67–69]. In the nonrelativistic limit, to describe the decay process$ A\rightarrow BC $ for a compact tetraquark, the transition operator T in the$ ^3P_0 $ model can be expressed as [58, 62–66]$ \begin{aligned}[b] T=&-3\gamma\sum_m\langle 1m1-m|00\rangle\int {\rm d}^3\boldsymbol{p}_5{\rm d}^3\boldsymbol{p}_6\delta^3(\boldsymbol{p}_5+\boldsymbol{p}_6)\\&\times {\cal{Y}}^m_1\left(\frac{\boldsymbol{p}_5-\boldsymbol{p}_6}{2}\right)\chi^{56}_{1,-m}\phi^{56}_0\omega^{56}_0b^\dagger_{5i}(\boldsymbol{p}_5)d^\dagger_{6j}(\boldsymbol{p}_6), \end{aligned} $

(1) where γ is the dimensionless
$ q_5\bar{q}_6 $ quark pair production strength, and$ \boldsymbol{p}_5 $ and$ \boldsymbol{p}_6 $ are the momenta of the created quark$ q_5 $ and antiquark$ \bar{q}_6 $ , respectively. Here, i and j are the color indices of the created quark and antiquark,$ \phi^{56}_{0}=(u\bar u + d\bar d +s\bar s)/\sqrt{3} $ ,$ \omega^{56}=\delta_{ij} $ , and$ \chi_{{1,-m}}^{56} $ are the flavor singlet, color singlet, and spin triplet wave functions of the quark-antiquark pair, respectively.${\cal{Y}}^m_1(\boldsymbol{p})\equiv |p|Y^m_1(\theta_p, \phi_p)$ is the solid harmonic polynomial reflecting the$ P- $ wave momentum-space distribution of the$ q_5\bar{q}_6 $ pair.There are five possible rearrangements of the strong decays of the compact tetraquarks
$ c q \bar c \bar q $ :$ A(c_1,q_2,{\bar c}_3,{\bar q}_4)+ P(q_5,{\bar q}_6)\rightarrow B(q_2,q_5,{\bar c}_3,{\bar q}_4)+C(c_1,{\bar q}_6), $

(2) $ A(c_1,q_2,{\bar c}_3,{\bar q}_4)+ P(q_5,{\bar q}_6)\rightarrow B(c_1,q_5,{\bar c}_3,{\bar q}_4)+C(q_2,{\bar q}_6), $

(3) $ A(c_1,q_2,{\bar c}_3,{\bar q}_4)+ P(q_5,{\bar q}_6)\rightarrow B(c_1,q_2,{\bar q}_4,{\bar q}_6)+C(q_5,{\bar c}_3), $

(4) $ A(c_1,q_2,{\bar c}_3,{\bar q}_4)+ P(q_5,{\bar q}_6)\rightarrow B(c_1,q_2,{\bar c}_3,{\bar q}_6)+C(q_5,{\bar q}_4), $

(5) $ A(c_1,q_2,{\bar c}_3,{\bar q}_4)+ P(q_5,{\bar q}_6)\rightarrow B(c_1,q_2,q_5)+C(\bar{c}_3,{\bar q}_4, {\bar q}_6). $

(6) In Fig. 1, we present all possible rearrangements, that is, charmed(-strange) meson emissions, light meson emissions, and baryon-antibaryon processes. Owing to the limited phase space of the selected charmonium-like states, we only focus on light meson emissions in this study.
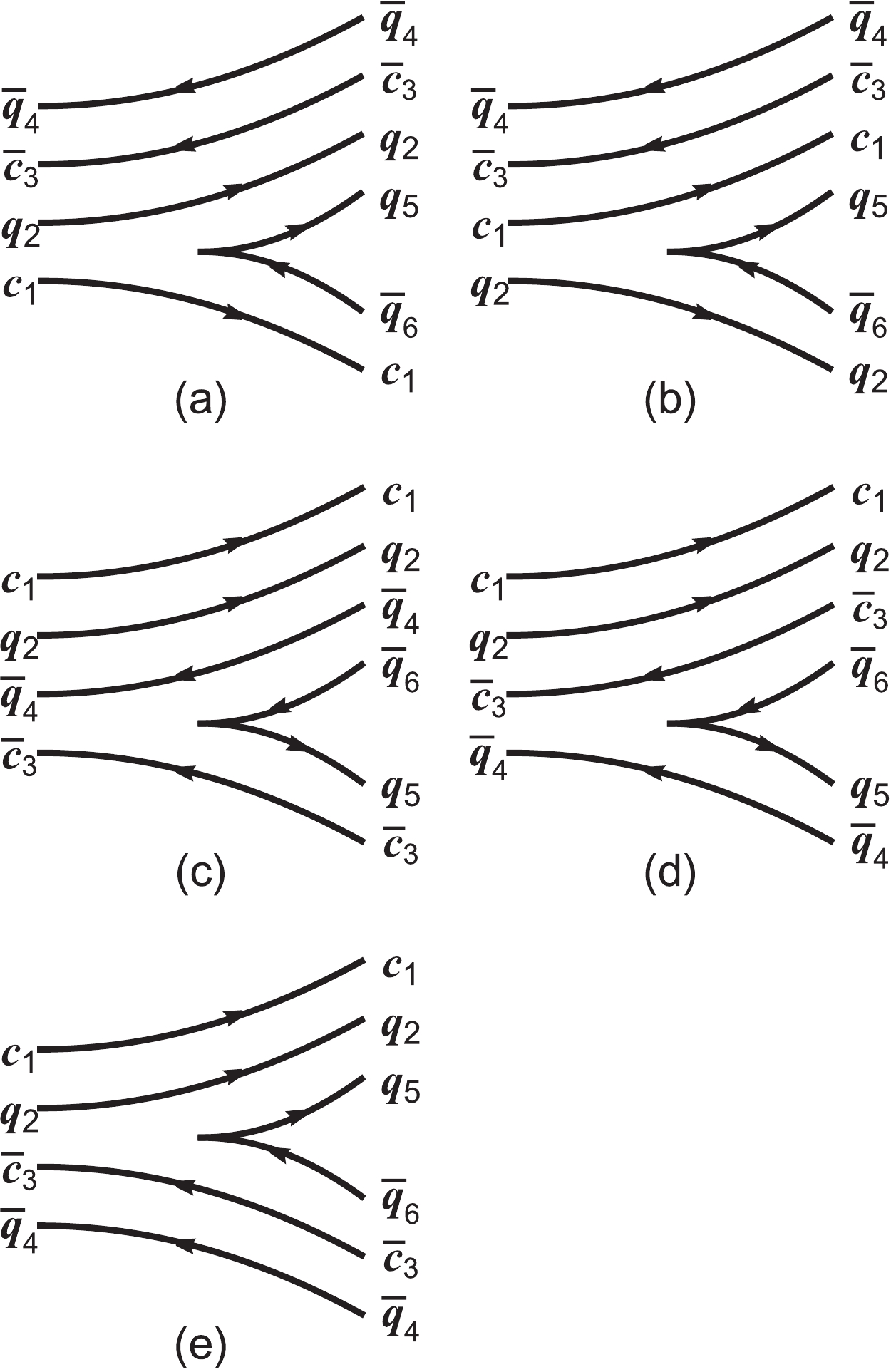
Figure 1. Five possible rearrangements. (a) and (c) are charmed(-strange) meson emissions, (b) and (d) are light meson emissions, and (e) represents the baryon and anti-baryon decay modes.
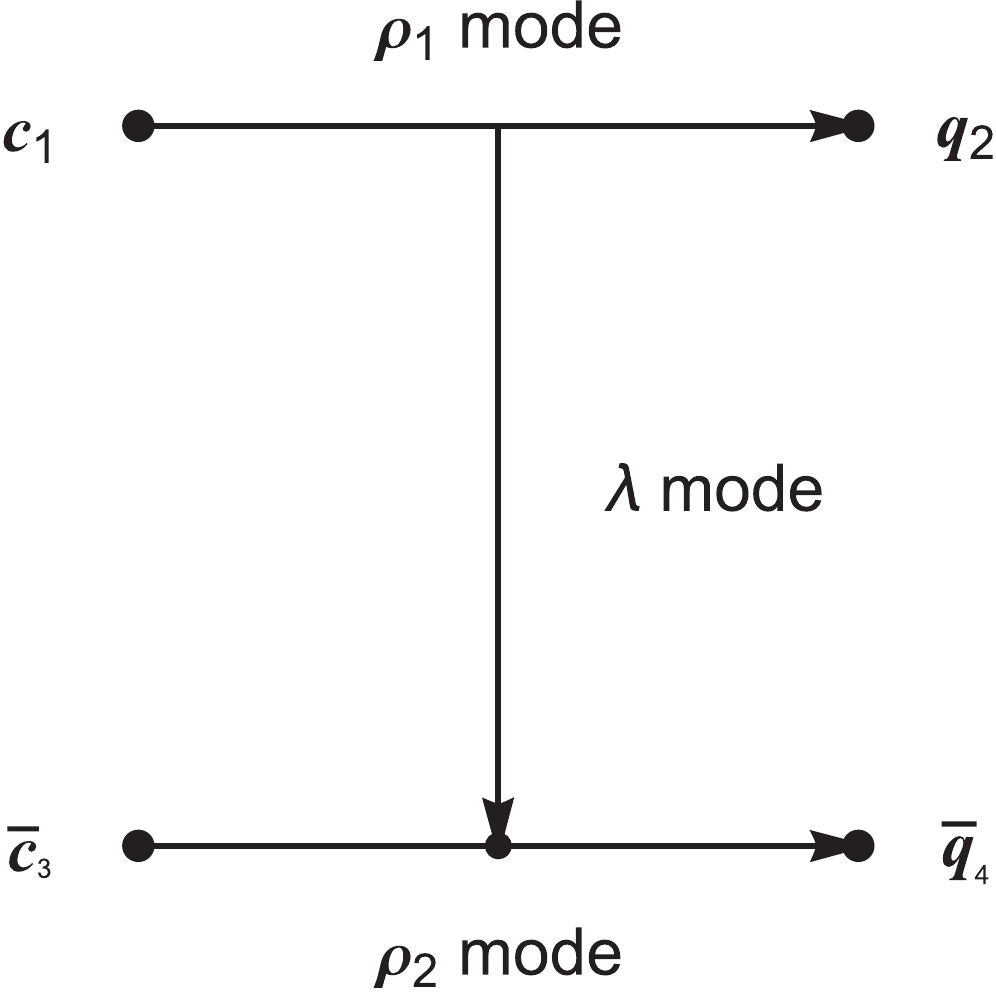
To investigate the strong decay behaviors of compact tetraquarks, we present the Jacobi coordinates in Fig. 2. Here,
$ c_1 $ and$ q_2 $ denote quarks, and$ \bar c_3 $ and$ \bar q_4 $ correspond to antiquarks.$ \boldsymbol \rho_1=\boldsymbol{r_1}-\boldsymbol{r_2} $ is the relative coordinates between two quarks,$ \boldsymbol{\rho_2}=\boldsymbol{r_3}-\boldsymbol{r_4} $ is the relative coordinates between two antiquarks, and$\boldsymbol \lambda= \dfrac{m_1\boldsymbol{r_1}+m_2\boldsymbol{r_2}}{m_1+m_2}-\dfrac{m_3\boldsymbol{r_3}+m_4\boldsymbol{r_4}}{m_3+m_4}$ represents the relative coordinates between quarks and antiquarks. With this definition, we can classify the excitations of compact tetraquarks into three types:$ \rho_1- $ mode,$ \rho_2- $ mode, and$ \lambda- $ mode. Empirically, the observations for$ \rho- $ mode excitations are scarce for heavy-light systems. For instance, most observed singly heavy baryons in experiments can be assigned as λ-mode excitations, and no$ \rho- $ mode heavy baryon has previously been confirmed. In this study, we only consider λ-mode excitations for the initial states, that is,$ n_{\rho_{A1}}=l_{\rho_{A1}}=n_{\rho_{A2}}=l_{\rho_{A2}}=0 $ and$ L_A = L_{\lambda_A} $ . Furthermore, owing to phase space constraints, all the final states are ground states.With the transition operator T, the helicity amplitude
$ {\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}} $ is defined as$ \begin{eqnarray} \langle BC|T|A\rangle=\delta^3(\boldsymbol{P}_A-\boldsymbol{P}_B-\boldsymbol{P}_C){\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}}. \end{eqnarray} $

(7) Here, we take the diagram (d) in Fig. 1 as an example. Similar to the strong decays of conventional hadrons [58, 62–66], the explicit formula of the helicity amplitude
$ {\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}} $ can be expressed as$ \begin{aligned}[b] & {\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}}\\= &- \gamma \sqrt{8E_AE_BE_C}\sum_{M_{L_A}}\sum_{M_{S_1}}\sum_{M_{S_2}}\sum_{M_{S_3}}\sum_{M_{S_4}}\sum_{m}\\ &\times \langle S_1 M_{S_1} S_2 M_{S_2}|S_{12} M_{S_{12}}\rangle \langle S_3 M_{S_3} S_4 M_{S_4}|S_{34}M_{S_{34}}\rangle \\ &\times \langle S_{12} M_{S_{12}} S_{34} M_{S_{34}}| S_A M_{S_A}\rangle\times \langle L_A M_{ L_A} S_A M_{S_A} |J_A M_{J_A}\rangle\\ & \times \langle S_1 M_{S_1} S_2 |M_{S_2} S_{12} M_{S_{12}} \rangle \times \langle S_3 M_{S_3} S_6 M_{S_6} |S_{36} M_{S_{36}}\rangle \\ & \times \langle S_{12} M_{S_{12}} S_{36} M_{S_{36}} |J_B M_{J_B}\rangle \times \langle S_4 M_{S_4} S_5 M_{S_5} |J_C M_{J_C}\rangle \\ &\times \langle S_5 M_{S_5} S_6 M_{S_6} |1 -m\rangle \times \langle 1 m 1 -m |0 0\rangle \\ &\times \langle \phi_B^{1236} \phi_C^{45}|\phi_A^{1234}\phi_0^{56}\rangle I^{M_{L_A}m}_{M_{L_B}M_{L_C}}(\boldsymbol{p}), \end{aligned} $

(8) where
$ \langle \phi_B^{1236} \phi_C^{45}|\phi_A^{1234}\phi_0^{56}\rangle $ is the overlap of the flavor wave functions.$ I^{M_{L_A}m}_{M_{L_B}M_{L_C}}(\boldsymbol{p}) $ represents the spatial overlaps of initial and final states, and relevant analytical expressions are listed in the appendix. The decay width$ \Gamma (A \rightarrow BC) $ can then be calculated directly,$ \begin{eqnarray} \Gamma= \pi^2\frac{p}{M^2_A}\frac{1}{2J_A+1}\sum_{M_{J_A},M_{J_B},M_{J_C}}|{\cal{M}}^{M_{J_A}M_{J_B}M_{J_C}}|^2, \end{eqnarray} $

(9) where
$ p=|\boldsymbol{p}|=\frac{\sqrt{[M^2_A-(M_B+M_C)^2][M^2_A-(M_B-M_C)^2]}}{2M_A} $ , and$ M_A $ ,$ M_B $ , and$ M_C $ are the masses of the hadrons A, B, and C, respectively.In the
$ ^3P_0 $ model, we require the quark pair creation strength γ, harmonic oscillator parameters in the orbital wave functions of the initial and final states, and different types of quark masses to calculate the decays numerically. In literature,$ \gamma = 0.4\times \sqrt{96 \pi} $ and$ \alpha= 0.4\; \rm{GeV} $ are widely used to investigate the strong decays of conventional mesons [60], where the factor$ \sqrt{96 \pi} $ originates from different conventions. For conventional baryons,$ \alpha=0.4/\sqrt{2} $ GeV is commonly adopted, where$ \sqrt{2} $ originates from the different definitions of the relative coordinates [70–74]. In compact tetraquarks, there is no experimental information to restrict these parameters via the known decay processes. In the$ cq \bar c \bar q $ states, the$ \rho_{1} $ and$ \rho_{2} $ modes are similar to the excitations of conventional baryons, whereas the λ mode is analogous to conventional meson systems. Thus, we adopt$ \alpha_{\rho_1} $ =$ \alpha_{\rho_2} $ =0.4/$ \sqrt{2} $ GeV and$ \alpha_\lambda=0.4 $ GeV for the compact$ cq \bar c \bar q $ states,$ \alpha= $ 0.4 GeV for light mesons, and$ \gamma = 0.4\times \sqrt{96 \pi} $ for the overall strength. Moreover, the quark masses$ m_{u/d} $ =0.22 GeV,$ m_{s} $ =0.418 GeV, and$ m_{c} $ =1.628 GeV are employed in the calculations [60, 75, 76]. Here, we adopt as few parameters as possible to semi-quantitatively estimate the strong decays of$ cq \bar c \bar q $ tetraquarks and provide theoretical information for future explorations.In this study, we investigate the decay behaviors of the charmonium-like states
$ X(4700) $ ,$ Z_c(4430) $ ,$ Y(4230) $ ,$ Y(4360) $ ,$ Y(4390) $ , and$ Y(4660) $ . Combining experimental data and theoretical information, we tentatively regard$ X(4700) $ as a$ cs \bar c \bar s(2S) $ state;$ Z_c(4430) $ as a$ cq \bar c \bar q(2S) $ state;$ Y(4230) $ ,$ Y(4360) $ ,$ Y(4390) $ , and$ Y(4660) $ as$ cq \bar c \bar q(1P) $ states; and$ Y(4660) $ as a$ cs \bar c \bar s(1P) $ state. The possible quantum numbers of these states are listed in Table 1. Here, in the notation$ \chi^{S_{12}S_{34}}_S $ ,$ S_{12} $ ,$ S_{34} $ , and S represent the spin of$ c_1 q_2 $ , spin of$ \bar c_3 \bar q_4 $ , and total spin, respectively. The explicit expressions of$ \chi^{S_{12}S_{34}}_S $ are as follows:State $ J^{PC} $ 

$ n_\lambda $ 

$ L_\lambda $ 

Spin Candidate $ X^{SS}_S $ 

$ 0^{++} $ 

1 0 $ \chi^{00}_{0} $ 

$ {X(4700)} $ 

$ X^{AA}_S $ 

$ 0^{++} $ 

1 0 $ \chi^{11}_{0} $ 

$ Y^{SS}_S $ 

$ 1^{–} $ 

0 1 $ \chi^{00}_{0} $ 

$\left(\begin{array}{c} Y(4660)\\ Y(4230)\\ Y(4360)\\ Y(4390) \end{array} \right)$ 

$ Y^{AA}_S $ 

$ 1^{–} $ 

0 1 $ \chi^{11}_{0} $ 

$ Y^{AA}_T $ 

$ 1^{–} $ 

0 1 $ \chi^{11}_{2} $ 

$ Y^{AS}_A $ 

$ 1^{–} $ 

0 1 $ \sqrt{\frac{1}{2}}(\chi^{10}_{1}+\chi^{01}_{1}) $ 

$ Z^{AS}_A $ 

$ 1^{+-} $ 

1 0 $ (\chi^{10}_{1}-\chi^{01}_{1})/\sqrt{2} $ 

$Z_c(4430)$ 

$ Z^{AA}_A $ 

$ 1^{+-} $ 

1 0 $ \chi^{11}_{1} $ 

Table 1. Notations and quantum numbers of the initial states. The superscripts and subscripts S, A, and T in the states correspond to spins 0, 1, and 2, respectively.
$ \chi^{00}_0={|{(c_1 q_2)}_0{(\bar c_3 \bar q_4)}_0\rangle} _0, $

(10) $ \chi^{11}_0={|{(c_1 q_2)}_1{(\bar c_3 \bar q_4)}_1\rangle} _0, $

(11) $ \chi^{01}_1={|{(c_1 q_2)}_0{(\bar c_3 \bar q_4)}_1\rangle} _1, $

(12) $ \chi^{10}_1={|{(c_1 q_2)}_1{(\bar c_3 \bar q_4)}_0\rangle} _1, $

(13) $ \chi^{11}_1={|{(c_1 q_2)}_1{(\bar c_3 \bar q_4)}_1\rangle} _1, $

(14) $ \chi^{11}_2={|{(c_1 q_2)}_1{(\bar c_3 \bar q_4)}_1\rangle} _2. $

(15) Furthermore,
$ Z_c(3985) $ ,$ Z_c(4020) $ ,$ Z_{cs}(3900) $ , and$ Z_{cs}(4000) $ are assumed to be the ground states of compact tetraquarks, which are all$ J^{P(C)}= 1^{+(-)} $ resonances. Under these assignments, the$ Z_c(3900) $ and$ Z_{cs}(3985) $ resonances have the spin wave function$ (\chi^{10}_{1}-\chi^{01}_{1})/\sqrt{2} $ , and the spin wave function for the$ Z_c(4020) $ and$ Z_{cs}(4000) $ resonances is$ \chi^{11}_{1} $ . -
In literature, the
$ X(4700) $ resonance is usually explained as a radially excited compact$ cs \bar c \bar s $ tetraquark,$ P $ -wave conventional charmonium,$ D- $ wave$ cs \bar c \bar s $ tetraquark state, or ground tetraquark state [28–31, 77–80]. In the constituent quark model, there are two λ-model$0^{++}\; cs \bar c \bar s$ states, which are predicted to be close to each other. The partial decay widths of the$ Z_{cs}(3985) K $ and$ Z_{cs}(4000) K $ channels are estimated and listed in Table 2. All of these partial widths are relatively small, which suggests that the fall-apart process with two meson final states may dominate. The small partial decay widths of the$ X(4700) $ resonance may be caused by the radial$ 2 S $ excitations and$ P $ -wave suppression of the decay amplitude. Although the predicted partial decay widths are small, these decay channels have the opportunity to be observed in future experiments. Moreover, we find that the$ Z_{cs}(4000) K $ decay mode is forbidden at the tree level under the$ X^{SS}_S $ assignment, and this selection rule is independent of the parameters of the quark pair creation model.Decay mode X(4700) $ X^{SS}_S $ 

$ X^{AA}_S $ 

$ Z_{cs}(3985) K $ 

0.25 0.08 $ Z_{cs}(4000) K $ 

0 0.12 Total 0.25 0.20 Table 2. Predictions of the
$ X(4700) \rightarrow Z_{cs}(3985)/Z_{cs}(4000) K $ processes in MeV.Recently, the LHCb Collaboration observed a new resonance
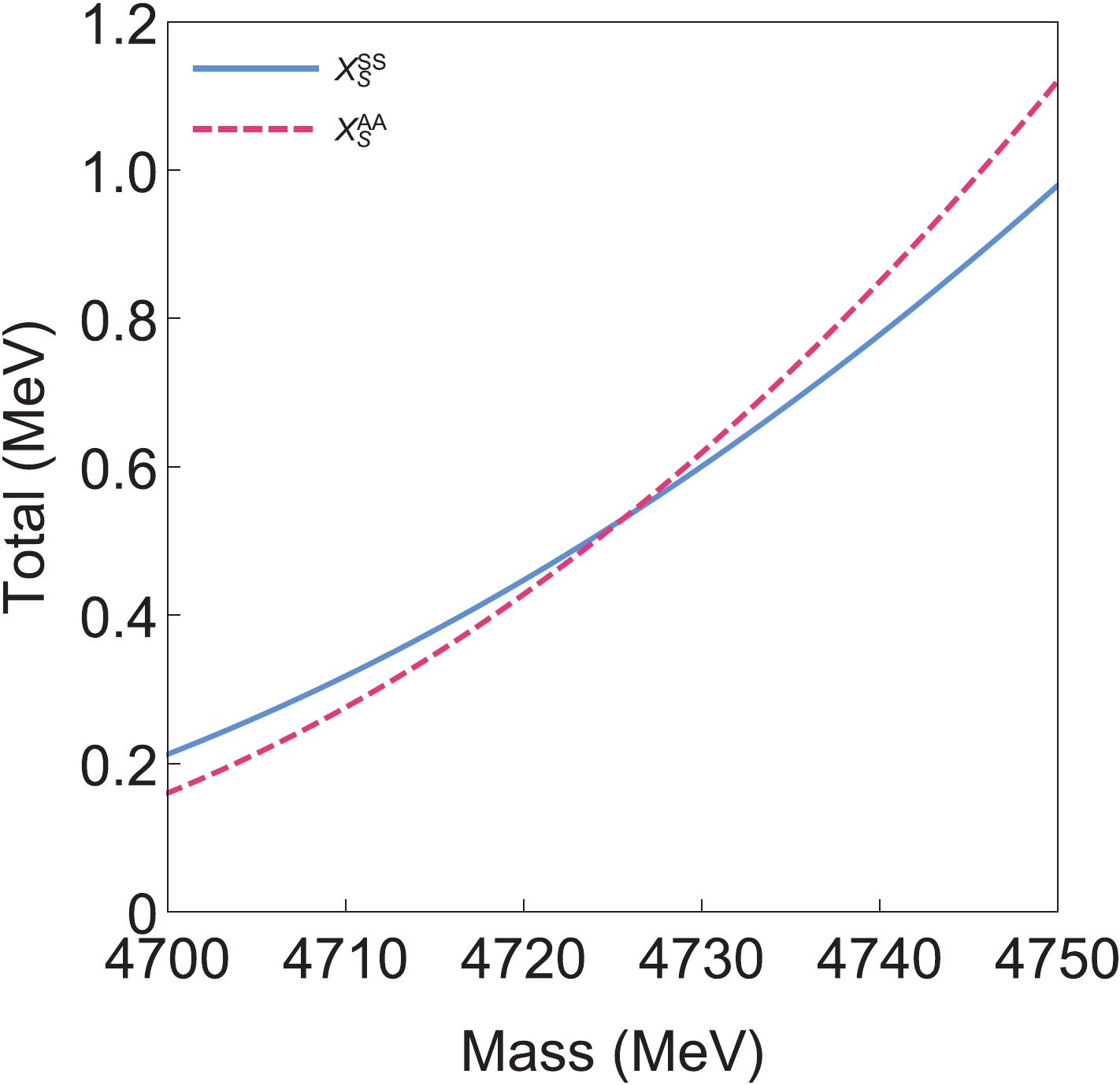
$ X(4740) $ in the$ J/\psi \phi $ mass spectrum [81, 82], which is probably the same state as$ X(4700) $ . This resonance may be explained as another radially excited compact$0^{++} \; cs \bar c \bar s$ tetraquark, or even a$ 2^{++} $ tetraquark. We plot the mass dependence of the partial decay widths of two$ 0^{++} $ states in Fig. 3. As shown, the total widths of the$ Z_{cs}(3985) K $ and$ Z_{cs}(4000) K $ channels remain small when the mass varies from 4700 to 4750 MeV. We hope that these estimations can provide a valuable clue to better understand the resonances$ X(4700) $ and$ X(4740) $ , and more theoretical and experimental efforts are required to reveal the relationship between observed resonances and predicted states in the quark model. -
In the constituent quark model, two
$ \lambda $ -model$ 1^{+-} $ radially excited compact$ cn \bar c \bar n $ tetraquarks lie at approximately 4.5 GeV. With these two assignments, the partial decay widths of$ Z_c(4430) $ are calculated and presented in Table 3. Similar to the$ X(4700) $ case, these partial decay widths are also small owing to radial excitations. Usually, decay behaviors can help distinguish different assignments for a new hadronic state. However, for the resonance$ Z_c(4430) $ under two$ 1^{+-} $ assignments, its decays exhibit the same behaviors. This situation can be understood via the Clebsch-Gordan coefficient in the helicity amplitudes. Although these two assignments have different quantum numbers, the helicity amplitudes are found to be the same after tedious calculations. Because of the small partial decay widths and same decay behaviors, other decay channels may be more suitable for clarifying the nature of$ Z_c(4430) $ .Decay mode $ Z_c(4430) $ 

$ Z^{AS}_A $ 

$ Z^{AA}_A $ 

$ Z_{c}(3900) \pi $ 

$ 2.72\times 10^{-3} $ 

$ 2.72\times 10^{-3} $ 

$ Z_{c}(4020) \pi $ 

$ 8.60\times 10^{-2} $ 

$ 8.60\times 10^{-2} $ 

Total $ 8.87\times 10^{-2} $ 

$ 8.87\times 10^{-2} $ 

Table 3. Theoretical predictions of the strong decays of the
$ Z_c(4430) $ states in MeV.Decay mode $ Y(4360) $ 

$ Y^{SS}_S $ 

$ Y^{AA}_S $ 

$ Y^{AA}_T $ 

$ Y^{AS}_A $ 

$ Z_{c}(3900) \pi $ 

4.73 1.20 0.11 1.20 $ Z_{c}(4020) \pi $ 

0 0.64 0.68 0.64 Total 4.73 1.84 0.79 1.84 Table 5. Theoretical predictions of the strong decays of the Y(4360) states in MeV.
-
For
$ \lambda $ -model$ P $ -wave excitations, there are four$1^{--} \; cn \bar c \bar n$ compact tetraquarks in the constituent quark model. We tentatively assign$ Y(4230) $ ,$ Y(4360) $ , and$ Y(4390) $ as these configurations and calculate the partial decay widths of the$ Z_{c}(3900) \pi $ and$ Z_{c}(4020) \pi $ channels. The results are presented in Tables 4 to 6. The partial decay widths are predicted to be approximately$ 0.11 \sim 5.64 $ MeV, except in the forbidden channels, which are significant enough to be tested in forthcoming experiments. Moreover, the$ Y^{AA}_S $ and$ Y^{AS}_A $ assignments exhibit the same decay behaviors for pion emissions.Decay mode $ Y(4230) $ 

$ Y^{SS}_S $ 

$ Y^{AA}_S $ 

$ Y^{AA}_T $ 

$ Y^{AS}_A $ 

$ Z_{c}(3900) \pi $ 

1.27 0.65 0.76 0.65 $ Z_{c}(4020) \pi $ 

0 0.58 0.96 0.58 Total 1.27 1.23 1.72 1.23 Table 4. Theoretical predictions of the strong decays of the Y(4230) states in MeV.
Decay mode $ Y(4390) $ 

$ Y^{SS}_S $ 

$ Y^{AA}_S $ 

$ Y^{AA}_T $ 

$ Y^{AS}_A $ 

$ Z_{c}(3900) \pi $ 

5.64 1.47 0.22 1.47 $ Z_{c}(4020) \pi $ 

0 0.63 0.50 0.63 Total 5.64 2.10 0.72 2.10 Table 6. Theoretical predictions of the strong decays of the Y(4390) states in MeV.
In Ref. [83], the authors calculated the process
$ Y(4230) \to Z_{c}(3900) \pi $ in the tetraquark scheme with the quark-pion axial vector interaction and obtained an$ 8 ^{+10}_{-4} $ MeV partial decay width. When we adopt the same assignment, our result is 0.76 MeV, which is different from theirs. Under the$ D\bar D_1 (2420) + H.c. $ . molecular scenario, we also investigate the decay$ Y(4230) \to Z_{c}(3900) \pi $ using an effective Lagrangian approach [25] and obtain a width of$ 3.15\pm0.45 $ MeV. For the$ Y(4390) $ resonance, the$ D^* \bar D_1 + H.c. $ molecular interpretation is also popular in literature. In a previous study [24], the partial decay width of the$ \pi^{+} \pi^{-} h_{c} $ process was estimated to be 0.74 to 0.85 MeV with an effective Lagrangian approach. By subducting the branch ratio, one can obtain the width of the$ Y(4390) \to Z_{c}(4020) \pi $ process as approximately 10 MeV, which is also larger than the present results under compact tetraquark configurations. It should be emphasized that$ Y(4390) \to Z_c(3900)\pi $ is significant under compact tetraquark configurations, whereas the$ Zc(3900)\pi $ mode should be suppressed for the$ D^* \bar{D}_1 + H.c. $ molecular interpretation [24]. Thus, the$ Y(4390) \to Z_c(3900)\pi $ channel can help discriminate the nature of$ Y(4390) $ and$ Z_c(3900) $ . More precise theoretical calculations and experimental information are required to clarify their internal structures. -
$ Y(4660) $ is a good candidate of P-wave$ c s \bar c \bar s $ compact tetraquarks. This state is divided into two structures,$ Y(4660) $ and$ Y(4630) $ ; however, several studies have indicated that$ Y(4630) $ should be the same structure as$ Y(4660) $ [84–87]. Here, we follow the assignment of the Review of Particle Physics, which suggests that only one resonance$ Y(4660) $ exists in this energy region [35]. The calculated partial decay widths are shown in Table 7. These partial decay widths are significant, and the decay behaviors are similar to those of their non-strange partners$ Y(4230) $ ,$ Y(4360) $ , and$ Y(4390) $ . Compared with the total width$ 62 ^{+9}_{-7} $ MeV, the total branch ratios of the$ Z_{cs}(3985) K $ and$ Z_{cs}(4000) K $ channels are approximately$ 0.06 \sim 0.14 $ , which can be tested in future experiments.Decay mode $ Y(4660) $ 

$ Y^{SS}_S $ 

$ Y^{AA}_S $ 

$ Y^{AA}_T $ 

$ Y^{AS}_A $ 

$ Z_{cs}(3985) K $ 

8.81 2.78 1.42 2.78 $ Z_{cs}(4000) K $ 

0 2.89 2.46 2.89 Total 8.81 5.67 3.88 5.67 Table 7. Theoretical predictions of the strong decays of the Y(4660) states in MeV.
-
Our present calculations are based on the resonances
$ Z_c(3900) $ /$ Z_{cs}(3985) $ with a spin structure of$ (\chi^{10}_{1}-\chi^{01}_{1})/\sqrt{2} $ , and$ Z_c(4020) $ and$ Z_{cs}(4000) $ with a spin structure of$ \chi^{11}_{1} $ . This is the normal mass hierarchy for$ J^{P(C)}= 1^{+(-)} $ compact tetraquarks. However, these spin structures may be inversed in realistic calculations, that is,$ Z_c(3900) $ /$ Z_{cs}(3985) $ with$ \chi^{11}_{1} $ , and$ Z_c(4020) $ /$ Z_{cs}(4000) $ with$ (\chi^{10}_{1}-\chi^{01}_{1})/\sqrt{2} $ . Fortunately, because of the nearly equal masses of these states, this does not change the results significantly.In the constituent quark model, the commonly used interaction is the Cornell potential, which can reproduce the low-lying spectra of heavy quarkonium well. With realistic wave functions, one can obtain the effective αs predicted to be approximately 400 MeV. Considering the similarity between λ-mode compact tetraquarks and charmonia, we expect that the mass pattern and hierarchy can be reproduced. Indeed, several previous studies [29, 80] based on the diquark-antiquark pictures have revealed masses and αs in these ranges, and the experimental data of charmonia also support the mass differences of compact tetraquarks. We investigate the dependence on the harmonic oscillator parameter
$ \alpha_\lambda $ for$ Y(4230) $ and$ Y(4390) $ by fixing the relation$ \alpha_\lambda = \sqrt{2} \alpha_\rho $ in Fig. 4. When$ \alpha_\lambda $ varies in the large reasonable range$ 300 \sim 500 $ MeV, the decay widths exhibit some changes, but our conclusions remain the same.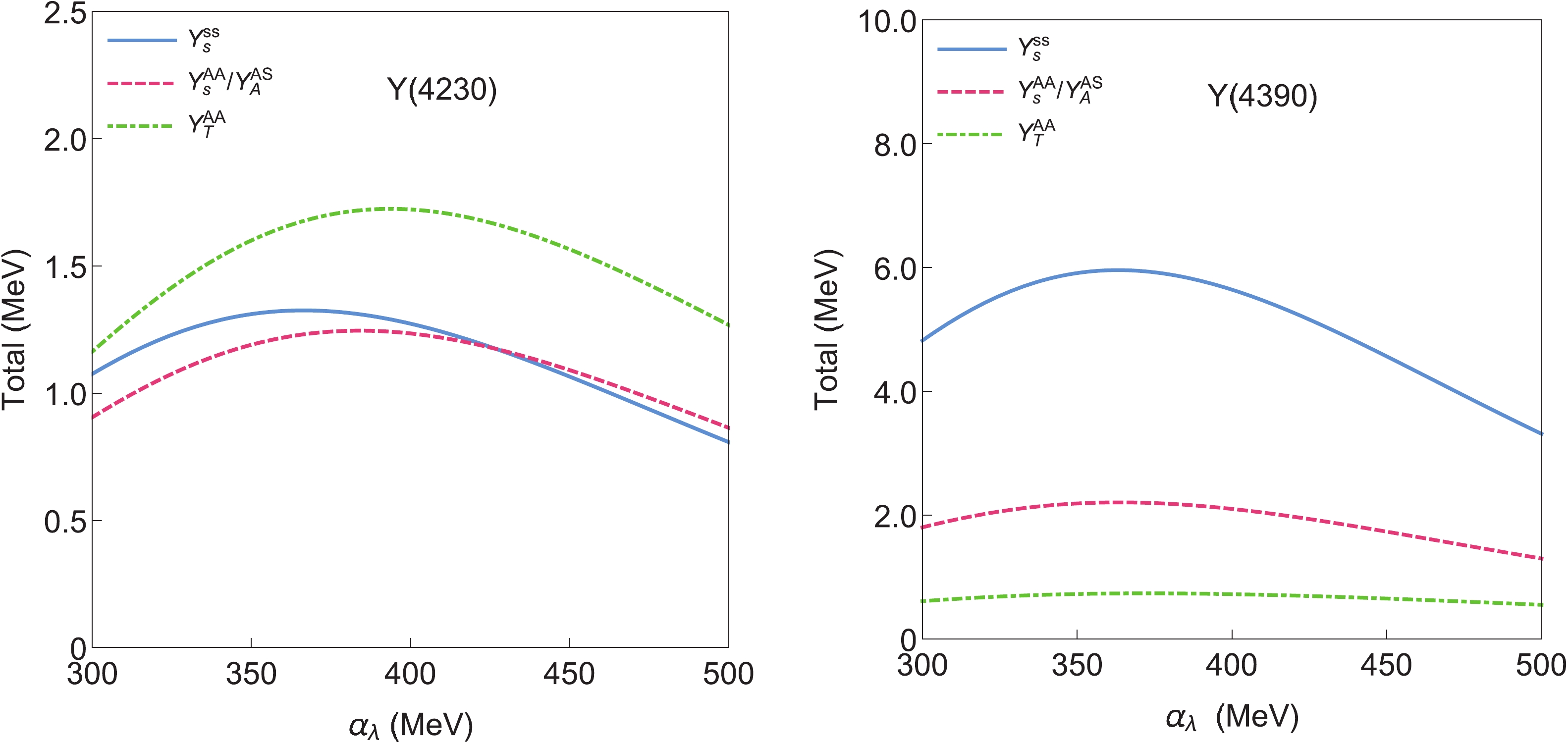
Figure 4. (color online) Dependence on the harmonic oscillator parameter
$ \alpha_\lambda $ for$ Y(4230) $ and$ Y(4390) $ .Here, we apply the quark pair creation model to study the decay behaviors of compact tetraquarks in an attempt to estimate the light meson emissions of charmonium-like states. There are a few investigations on light meson emissions among compact tetraquarks, both theoretically and experimentally. However, this type of process is important for studying the relationships of compact tetraquarks and requires more attention in future.
-
In this study, we adopt the
$ ^3P_0 $ model to investigate the light meson emissions of the charmonium-like states$ X(4700) $ ,$ Z_c(4430) $ ,$ Y(4230) $ ,$ Y(4360) $ ,$ Y(4390) $ , and$ Y(4660) $ under compact tetraquark configurations. We find that the pion/kaon decay widths of the radially excited states are relatively small, whereas the partial decay widths of P-wave excitations are significant. Based on our calculations, we expect that the$Y(4390) \to Z_c(3900)/Z_c(4020)\pi$ decay channels are more likely to be measured by the BESIII and Belle II Collaborations, which can provide valuable information to clarify the nature of$ Y(4390) $ ,$ Z_c(3900) $ , and$ Z_c(4020) $ .Our present calculations are preliminary. Here, we employ a widely accepted approach and relevant parameters to semi-quantitatively estimate the magnitudes of transitions between these charmonium-like states. Current theoretical results and experimental data are not sufficient to give definitive interpretations. We hope that our preliminary explorations can provide information for further research, and more theoretical and experimental studies are encouraged to further discuss this topic.
-
We would like to thank Xian-Hui Zhong and Rui Chen for valuable discussions.
-
Harmonic oscillator wave functions for compact tetraquarks in the momentum representation can be expressed as
$ \begin{aligned}[b] &\psi _{n_{L}M_{L}}(n_{\rho _{1}},l_{\rho _{1}},m_{\rho _{1}},n_{\rho _{2}},l_{\rho _{2}},m_{\rho _{2}},n_{\lambda },l_{\lambda },m_{\lambda })\\=&(-1)^{n_{\rho _{1}}}(-i)^{l_{\rho _{1}}}p_{\rho _{1}}^{^{l_{\rho _{1}}}}\Bigg[ \frac{2n!}{\Gamma (n_{\rho _{1}}+l_{\rho _{1}}+\frac{3}{2})}\Bigg]^{\frac{1}{2} }\times \Bigg(\frac{1}{\alpha _{\rho _{1}}}\Bigg)^{\frac{3}{2}+l_{\rho _{1}}} \\ &(-1)^{n_{\rho _{2}}}(-i)^{l_{\rho _{2}}}p_{\rho _{2}}^{^{l_{\rho _{2}}}}\Bigg[ \frac{2n!}{\Gamma (n_{\rho _{2}}+l_{\rho _{2}}+\frac{3}{2})}\Bigg]^{\frac{1}{2} }\times \Bigg(\frac{1}{\alpha _{\rho _{2}}}\Bigg)^{\frac{3}{2}+l_{\rho 2}} \\ &(-1)^{n_{\rho _{\lambda }}}(-i)^{l_{\rho _{\lambda }}}p_{\rho _{\lambda }}^{^{l_{\rho _{\lambda }}}}\Bigg[\frac{2n!}{\Gamma (n_{\rho _{_{\lambda }}}+l_{\rho _{_{\lambda }}}+\frac{3}{2})}\Bigg]^{\frac{1}{2}}\times \Bigg(\frac{1}{ \alpha _{\rho _{_{\lambda }}}} \Bigg)^{\frac{3}{2}+l_{\rho _{\lambda }}} \\ &Y_{l_{\rho _{1}}}^{m_{\rho _{1}}}(\vec p_{\rho _{1}}) Y_{l_{\rho _{2}}}^{m_{\rho _{2}}}(\vec p_{\rho _{2}})Y_{l_{\rho _{\lambda }}}^{m_{\rho _{\lambda }}}(\vec p_{\lambda } )L_{n_{\rho _{1}}}^{l_{\rho _{1}}+\frac{1}{2}}(p_{\rho _{1}}^{2}/\alpha _{\rho _{1}}^{2}) L_{n_{\rho _{2}}}^{l_{\rho _{2}}+\frac{1}{2}}(p_{\rho _{2}}^{2}/ \alpha _{\rho _{2}}^{2}) \\ &L_{n_\lambda }^{l_\lambda+\frac{1}{2}} (p_\lambda^2 / \alpha _\lambda ^{2}) \times \exp \Bigg(-\frac{ \vec p_{\rho _{1}}^{2}}{2\alpha _{\rho _{1}}^{2}}-\frac{ \vec p_{\rho _{2}}^{2}}{2\alpha _{\rho _{2}}^{2}}-\frac{ \vec p_{\rho _{\lambda}}^{2}}{2\alpha _{\rho _{\lambda}}^{2}}\Bigg), \end{aligned}\tag{A1} $

where
$ \vec{p}_{\rho_1}=\frac{m_{2}\vec{p}_{1}- m_{1}\vec{p}_{2}}{m_{1}+ m_{2}}, \tag{A2} $

$ \vec{p}_{\rho_2}=\frac{m_{4}\vec{p}_{3}- m_{3}\vec{p}_{4}}{m_{3}+ m_{4}}, \tag{A3}$

$ \vec{p}_{\lambda}=\frac{(m_{3}+m_{4})(\vec{p}_{1}+\vec{p}_{2})- (m_{1}+m_{2})(\vec{p}_{3}+\vec{p}_{4})}{m_{1}+ m_{2}+ m_{3}+ m_{4}}. \tag{A4} $

Similarly, the harmonic oscillator wave function for ground mesons in the momentum representation can be written as
$ \psi \left(0,0,0\right)=\left( \frac{1}{\pi \alpha^{2}}\right) ^{\frac{3}{4}}\exp \left( - \frac{\vec{p}_{\rm rel}^{2}}{2\alpha^{2}}\right),\tag{A5} $

where
$ \vec{p}_{rel} $ represents the relative momentum between the quark and antiquark in the final mesons.In this study, all the final states are ground states, that is,
$ n_{\rho_{B1}}=l_{\rho_{B1}}=n_{\rho_{B2}}=l_{\rho_{B2}}=n_{\lambda_ B}=l_{\lambda_ B}=n_{C}=L_{C}=0 $ . More-over, we only consider λ-mode excitations for the initial states, and then$ n_{\rho_{A1}}=l_{\rho_{A1}}=n_{\rho_{A2}}=l_{\rho_{A2}}=0 $ . Here, we denote the spatial overlap integrals$ I^{M_{L_A},m}_{M_{L_B},M_{L_C}}(\vec{p}) $ as$\Pi(n_{\lambda _A}, l_{\lambda_A}, m_{\lambda_A}, m)$ , and the relevant formulas for the low-lying states are presented below. We define$ c_{1} =\frac{m_{2}}{m_{1}+m_{2}}, \tag{A6} $

$ c_{2} =\frac{m_{1}+m_{2}}{2m_{1}+m_{2}+m_{5}}, \tag{A7} $

$ c_{3} =\frac{m_{1}}{m_{1}+m_{5}}, \tag{A8}$

$ c_{4} =\frac{m_{2}}{m_{2}+m_{5}}, \tag{A9} $

$ c_{5} =\frac{m_{1}}{m_{1}+m_{2}}-c_{3}, \tag{A10} $

$ \lambda _{1} =\frac{1}{\alpha _{\lambda }^{2}}+\frac{1}{2\alpha _{\rho }^{2}}c_{5}^{2}+\frac{1}{2\alpha ^{2}}c_{1}^{2}, \tag{A11} $

$ \lambda _{2} =\frac{1}{\alpha _{\rho }^{2}}+\frac{1}{2\alpha ^{2}}, \tag{A12} $

$ \lambda _{3} =\frac{1}{2\alpha _{\rho }^{2}}c_{3}^{2}+\frac{1}{2\alpha _{\lambda }^{2}}c_{2}^{2}+\frac{1}{2\alpha ^{2}}c_{4}^{2}, \tag{A13} $

$ \lambda _{4} =\frac{1}{\alpha _{\rho }^{2}}c_{3}c_{5}-\frac{1}{\alpha _{\lambda }^{2}}c_{2}-\frac{1}{\alpha ^{2}}c_{1}c_{4}, \tag{A14} $

$ \lambda _{5} =\frac{1}{\alpha ^{2}}c_{1}-\frac{1}{\alpha _{\rho }^{2}}c_{5}, \tag{A15} $

$ \lambda _{6} =-\frac{1}{\alpha _{\rho }^{2}}c_{3}-\frac{1}{\alpha ^{2}} c_{4}, \tag{A16} $

$f_{1} =\frac{\lambda _{5}}{2\lambda _{1}}, \tag{A17} $

$ f_{2} =\frac{\lambda _{4}}{2\lambda _{1}}, \tag{A18} $

$ f_{3} =\lambda _{2}-\frac{f_{1} \lambda _{5}}{2},\tag{A19}$

$ f_{4} =\frac{\lambda _{6}-f_{2}\lambda _{5}}{2f_{3}}, \tag{A20} $

$ f_{5} =\lambda _{3}-\frac{f_{2} \lambda _{4}}{2}-f_{4}^{2}f_{3}, \tag{A21} $

and then, we can easily obtain the spatial overlap integrals,
$ \Pi (0,0,0,0)=\sqrt{\frac{3}{4\pi }}(1+f_{4}+c_{1}f_{2}-c_{1}f_{1}f_{4}) \left\vert \vec{P}\right\vert \Delta _{00}, \tag{A22} $

$ \begin{aligned}[b] \Pi (1,0,0,0) =&\Bigg[-2(1+f_{4}+c_{1}f_{2}-c_{1}f_{1}f_{4})(f_{2}-f_{1}f_{4})\left\vert \vec{P}\right\vert^2 \\ & -\frac{ f_{1}(c_{1}f_{1}-1)}{f_{3}}-\frac{c_{1}}{\lambda _{1}}\Bigg]\Delta _{10}^{\lambda }, \end{aligned}\tag{A23} $

$ \Pi (0,1,1,-1) =\Pi (0,1,-1,1) =\Bigg[ \frac{f_{1}(c_{1}f_{1}-1)}{f_{3}}+\frac{c_{1}}{\lambda _{1}} \Bigg ]\Delta_{10}^{\lambda }, \tag{A24} $

with
$ \begin{aligned}[b] \Delta _{00} =& \Bigg( \frac{1}{\pi \alpha _{\rho }^{2}} \Bigg)^{3} \Bigg(\frac{1}{\pi \alpha _{\lambda }^{2}}\Bigg)^{\frac{3}{2}} \Bigg(\frac{1}{\pi \alpha ^{2}}\Bigg)^{\frac{3}{4}} \Bigg(\frac{\alpha _{\rho }^{2}\pi ^{3}}{\lambda_{1}f_{3}} \Bigg)^{\frac{3}{2}} \\ &\times \exp \Bigg[-\Big(f_{5}\left\vert \vec{P} \right\vert ^{2}\Big) \Bigg], \end{aligned}\tag{A25} $

$ \begin{aligned}[b] \Delta _{10}^{\lambda } =&-i\Bigg(\frac{1}{\pi \alpha _{\rho }^{2}}\Bigg)^{3} \Bigg(\frac{ 1}{\alpha _{\lambda }}\Bigg)^{\frac{5}{2}}\Bigg(\frac{\alpha _{\rho }^{2}\pi ^{3}}{ \lambda _{1}f_{3}}\Bigg)^{\frac{3}{2}} \Bigg(\frac{1}{\pi \alpha _{\lambda }^{2}}\Bigg)^{ \frac{3}{4}}\Bigg(\frac{1}{\pi \alpha ^{2}}\Bigg)^{\frac{3}{4}} \\&\times \exp \Bigg[-\Big(f_{5}\left\vert \vec{P}\right\vert ^{2}\Big) \Bigg] \times \Bigg(\frac{8}{3\sqrt{\pi }}\Bigg)^{\frac{1}{2}}\Bigg(\frac{3}{8\pi }\Bigg). \end{aligned}\tag{A26} $

Light meson emissions of selected charmonium-like states within compact tetraquark configurations
- Received Date: 2022-12-10
- Available Online: 2023-06-15
Abstract: We adopt the quark pair creation model to investigate the light meson emissions of several charmonium-like states. The quark pair creation model is applied to four-body systems, and we calculate the pion/kaon emissions of






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: