-
In modern physics, black holes (BH) are considered important objects as they represent a complex system of temperature, entropy, specific heat, and enthalpy [1]. These are the types of extended space that have aroused the interest of scientists for decades. The broad connection between thermodynamics, Einstein gravity, and quantum physics is evident in the formation of all four laws of BH thermodynamics. A common connection, as Einstein described, is the only time theory of the space of gravity. Within the dark holes, there is an event horizon at that point in the same direction, as no one can return or escape its gravitational pull, even at the speed of light. To solve the problem of singularity by taking the usual model without singularity, as this model provides the appropriate division into the final phase of the fall of gravity to remove future singularity, was proposed by Sakharov [2] and Gliner [3]. Using this concept, Bardeen provides a solution for the BH that reveals the horizon but lacks singularity.
Various modified theories of general relativity (GR), such as the Einstein-Gauss-Bonnet theory (EGB) [4–7],
$ f(T) $ gravity theory [8],$ f(R) $ gravity [9], and Newmann-Jeans algorithm for rotating BH [10, 11], were used to obtain standard solutions of the BH. Phase modification has been used to discuss the thermodynamics of BH for a long time. The term "phase change" refers to a change in the basic state of an entity. Hawking and Page [12] identified the thermodynamic features of the Anti-de-Sitter (AdS) BH in detecting phase changes in the phase space. The first phase change was exposed by the BH of the charged RN-AdS [13, 14]. In [15–17], the cosmological constant successfully refers to thermodynamic pressure. This is a major source of inspiration for calculating the volume of the BH and thermodynamic pressure, as well as for the re-introduction of the P-V term in BH thermodynamics [18–20].The universal effects of non-linear electrodynamics (NLED) theory are completely reviewed. The subject of universal evolution, as evidenced by the Born-Infeld theory [21–23], has been studied. The non-linear interaction of the electromagnetic field (EM) creates the cosmic conditions, which are necessary for the event to take place. Recent research has shown the importance of NLED in two of the most important aspects of cosmology, which are related to the transition time of large and very small regions. A powerful magnetic field has already been shown to win the chance for a single region in Maxwell's field on NLED. Cosmological models containing NLED have attracted considerable attention over the last few years [24–26]. Interest in studying the NLED in the context of cosmology has grown significantly as a result of these important findings [24, 26, 27–35]. It was discovered that the original singularity of the Big Bang could not have been avoided if the original universe had been ruled by a non-linear magnetic field [36–44].
In the cosmos, NLED fields may play an important role. However, when seen from the BH, Einstein's solutions for the gravitational force and the NLED field are surprising. This is because in order to comprehend such solutions, the functional relationship between nonlinear events in strong magnetic fields and electromagnetic fields must be understood. Other solutions for charged BHs and black strings are present in [45–49]. It has been found that with the use of the NLED field, not only the singularity of the Big Bang but also the singularity of the BH can be prevented. As a result, some common BH solutions have been found [50–55] that are regular and singularity free. The Kerr-Newman-de Sitter space-time has an inner horizon, an event horizon, and a cosmic horizon. The BHs with many horizons in NLED fields were investigated in Refs. [9, 56–59]. Gunasekaran et al. [60] studied charged BH thermodynamics, including the effect of NLED, and analyzed the critical behavior of charged and rotating BHs.
This research focuses on the thermodynamic behavior of the NLED BH. The effects of the coupling constant α have been used to discuss the stability and phase transition of the BH. The thermal stability has been discussed through two conditions: isothermal pressure and heat capacity
$ Cv $ . The remainder of this paper is organized as follows. In Sec. II, we present a precise review of the BH solution in Einstein's gravitational field with the NLED field. Additionally, we discuss the thermodynamical quantities of the NLED BH in Sec. III. Sec. IV deals with the$ P\text{-}V $ criticals and critical parameters. The last section summarizes our findings. -
In this section, we examine the NLED BH solution [61] that comes from the action of NLED theories that have been coupled with gravity:
$ S= \frac{1}{16 \pi} \int \sqrt{-g}\Big(R + K(\psi)\Big) {\rm d}^{4}x, $

(1) where
$ \begin{array}{*{20}{l}} \psi = F_{\mu\nu} F^{\mu\nu}, \,\,\, F_{\mu\nu}= A_{\nu;\mu}- A_{\mu;\nu}. \end{array} $

(2) Here,
$ A_{\mu} $ gives the Maxwell field, Ricci scalar R, and ψ function$ K(\psi) $ . The field equations of Einstein are given by the change of action relating to the metric$ G_{\mu \nu} = -2K_{, \psi} F_{\mu \lambda} F_{\nu}^{\lambda}+ \frac{1}{2}g_{\mu\nu}K,\quad\quad K_{, \psi}\equiv \frac{{\rm d}K}{{\rm d}\psi}. $

(3) The Maxwell general equations are determined by the field:
$ \begin{array}{*{20}{l}} (K_{, \psi} F^{\mu\nu})_{;\mu}=0. \end{array} $

(4) The spherically symmetric and static background metric [61] is given by
$ {\rm d}s^{2}= -N(r){\rm d}t^{2}+ \frac{1}{N(r)}{\rm d}r^{2}+ f(r)^{2}{\rm d}\Omega_{2}^{2}, $

(5) The only non-zero component of the Maxwell field tensor
$ A_{\mu} $ is given by$ \begin{array}{*{20}{l}} A_{0}= -\phi(r), \end{array} $

(6) $ \begin{array}{*{20}{l}} \psi = -2\varphi'^{2}. \end{array} $

(7) The field equations of Einstein and the generalized equations of Maxwell [61] were also handled:
$ \frac{-N'f'}{f}-\frac{2N f''}{f} + \frac{1}{f^{2}}-\frac{N f'^{2}}{f^{2}}= 2K_{,\psi} \phi'^{2}+ \frac{1 }{2}K, $

(8) $ \frac{-N'f'}{f}+ \frac{1}{f^{2}}-\frac{N f'^{2}}{f^{2}} = 2K_{,\psi} \phi'^{2}+ \frac{1 }{2}K, $

(9) $ \frac{-N'f'}{f}+\frac{Nf''}{f} +\frac{1}{2} N'' = - \frac{1 }{2}K, $

(10) $ \begin{array}{*{20}{l}} (f''K_{, \psi}\phi')' = 0. \end{array} $

(11) The prime symbol denotes differentiation with respect to r. The Maxwell field of Eq. (11) defines the electric charge:
$ \begin{array}{*{20}{l}} Q = f^{2} \phi' K_{, \psi}. \end{array} $

(12) From the difference of Eqs. (8) and (9), we obtain
$ \begin{array}{*{20}{l}} f''(r)=0. \end{array} $

(13) As a result, the solution to f is
$ \begin{array}{*{20}{l}} f(r)=r. \end{array} $

(14) We assume the Maxwell Lagrangian K form to solve the field equations:
$ \begin{eqnarray} K= 2\sqrt{2\alpha}\sqrt{-\psi}-\psi- 2\Lambda, \end{eqnarray} $

(15) where α has the dimension of length. The theory is reduced to Maxwell's equation when
$ \alpha=0 $ (see Eq. (2) for details), and$ 2\Lambda $ is the cosmological constant factor. Ultimately,$ \begin{eqnarray} \phi=r\sqrt{\alpha}+\frac{Q}{r}, \end{eqnarray} $

(16) $ N(r)= 1-\frac{2 M}{r}+\frac{Q^2}{r^2} +\frac{r^2}{l^2}+2 \sqrt{\alpha } Q-\frac{\alpha r^2}{3}. $

(17) Here Q, α, and Λ are the electric charge, coupling constant, and cosmological constant, respectively. If one vanishing
$ \alpha\rightarrow 0 $ , its nothing but just RN-AdS solution, and$ Q=0 $ reveals the Schwarzschild AdS BH solution. -
Now, we discuss the thermodynamical properties of the NLED BH [61] .
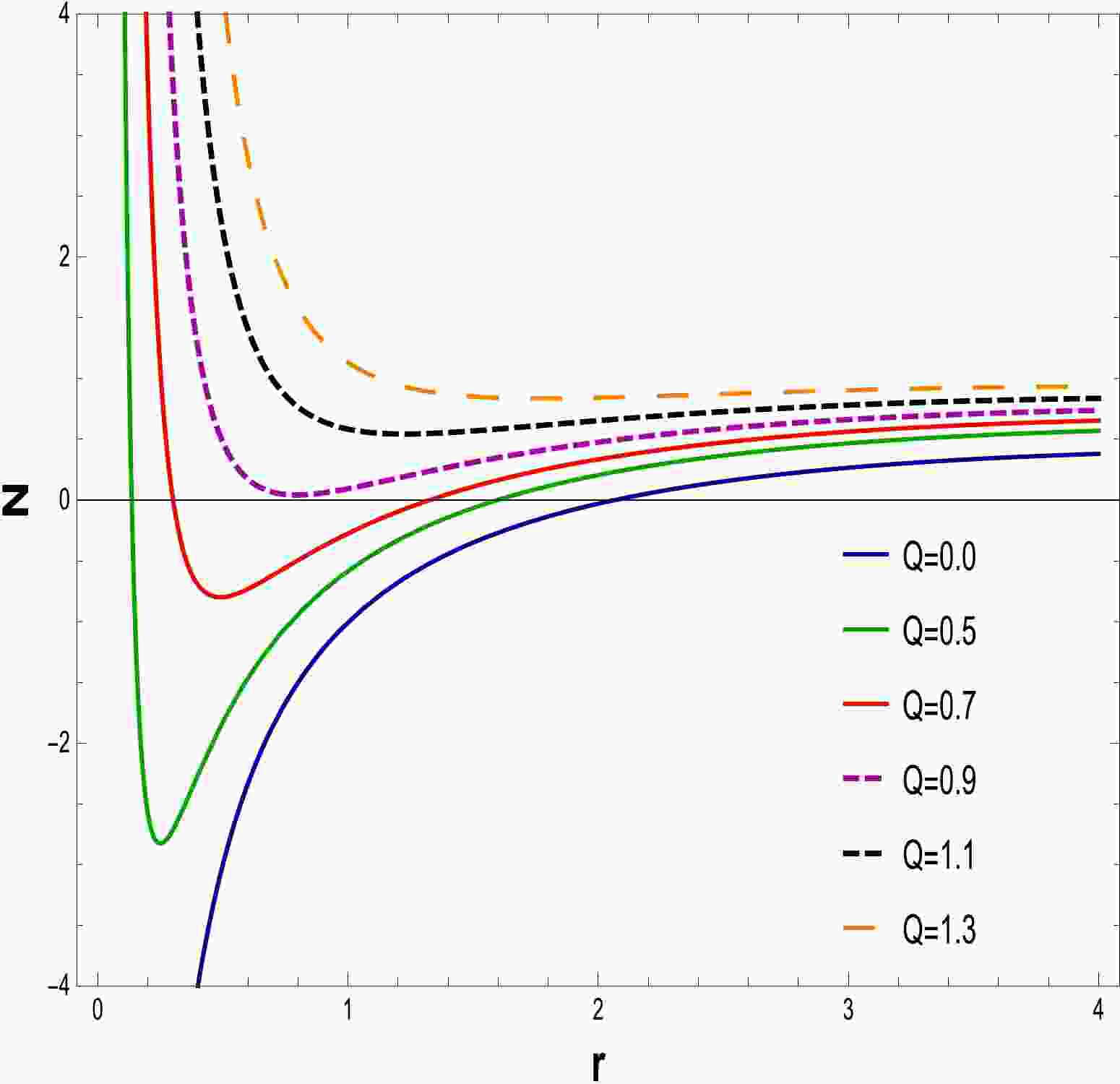
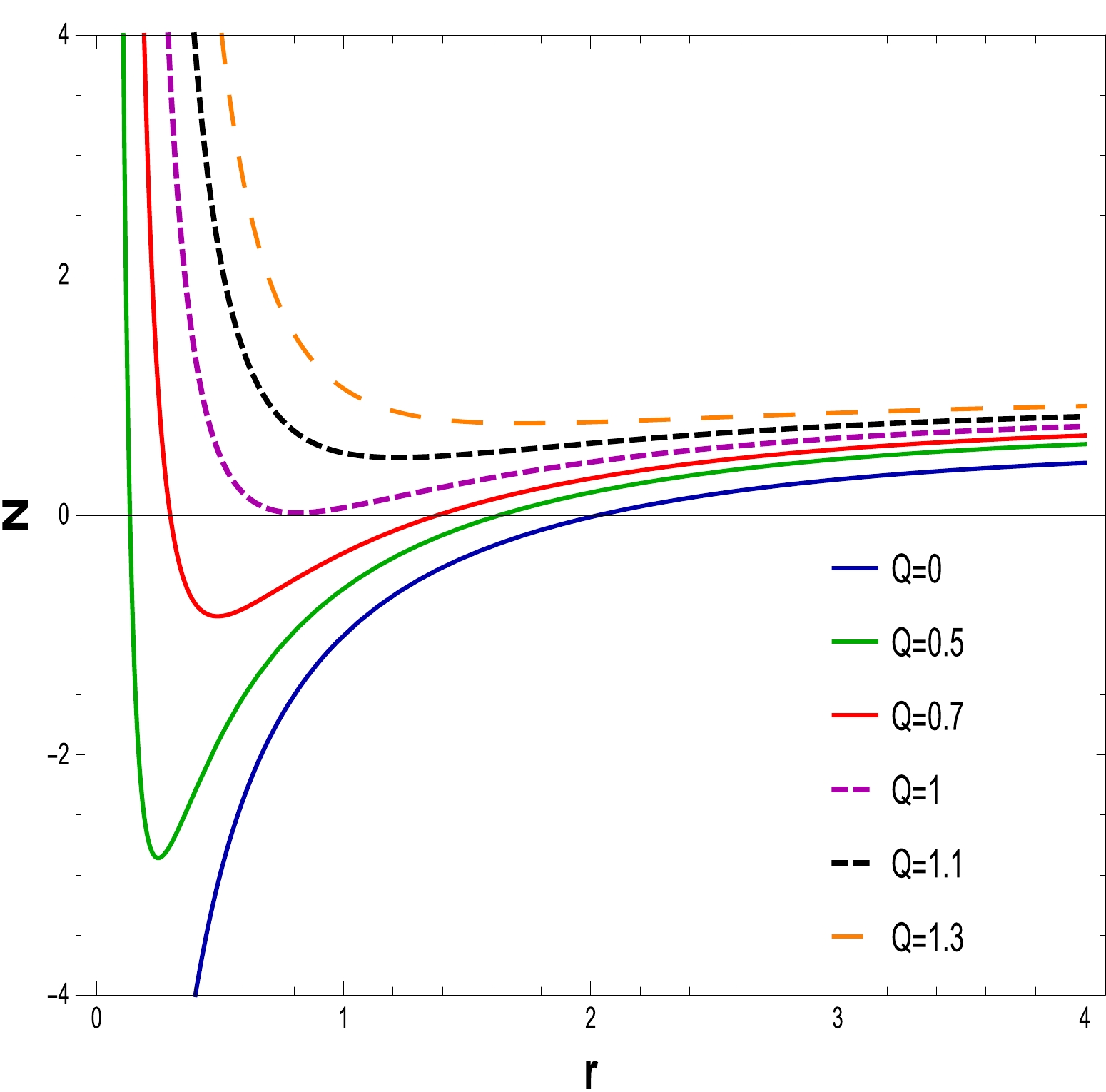
Using Eq. (17) with
$ N(r)=0 $ , one may determine the physical characteristics of a BH event horizon. The equations are solved by changing the values of the parameters Q, α, and$ l=20 $ . The behavior of the discovered solution for a fixed value of α is depicted in Figs. 1–3. It is evident that as the charge Q is increased, the BH size grows. From Figs. 1 and 2, we can deduce from the answer that it shows a naked singularity at$ Q=1.1 $ and$ Q=1.2 $ , which means that it gives no event horizon, hence no black holes, when$ Q>Q_{c} $ ; one double zero, which corresponds to an extreme BH, for$ Q=Q_{c} $ ; and two simple zeros, corresponding to two event horizons, which denote a non-extreme BH, for$ Q<Q_{c} $ . In Fig. 3 , as$ \alpha=0 $ and$ Q=0 $ demonstrate event horizons of the RN-BH and the Schwarzschild BH, respectively, two categories of BH solutions appear: extremal and non-extremal.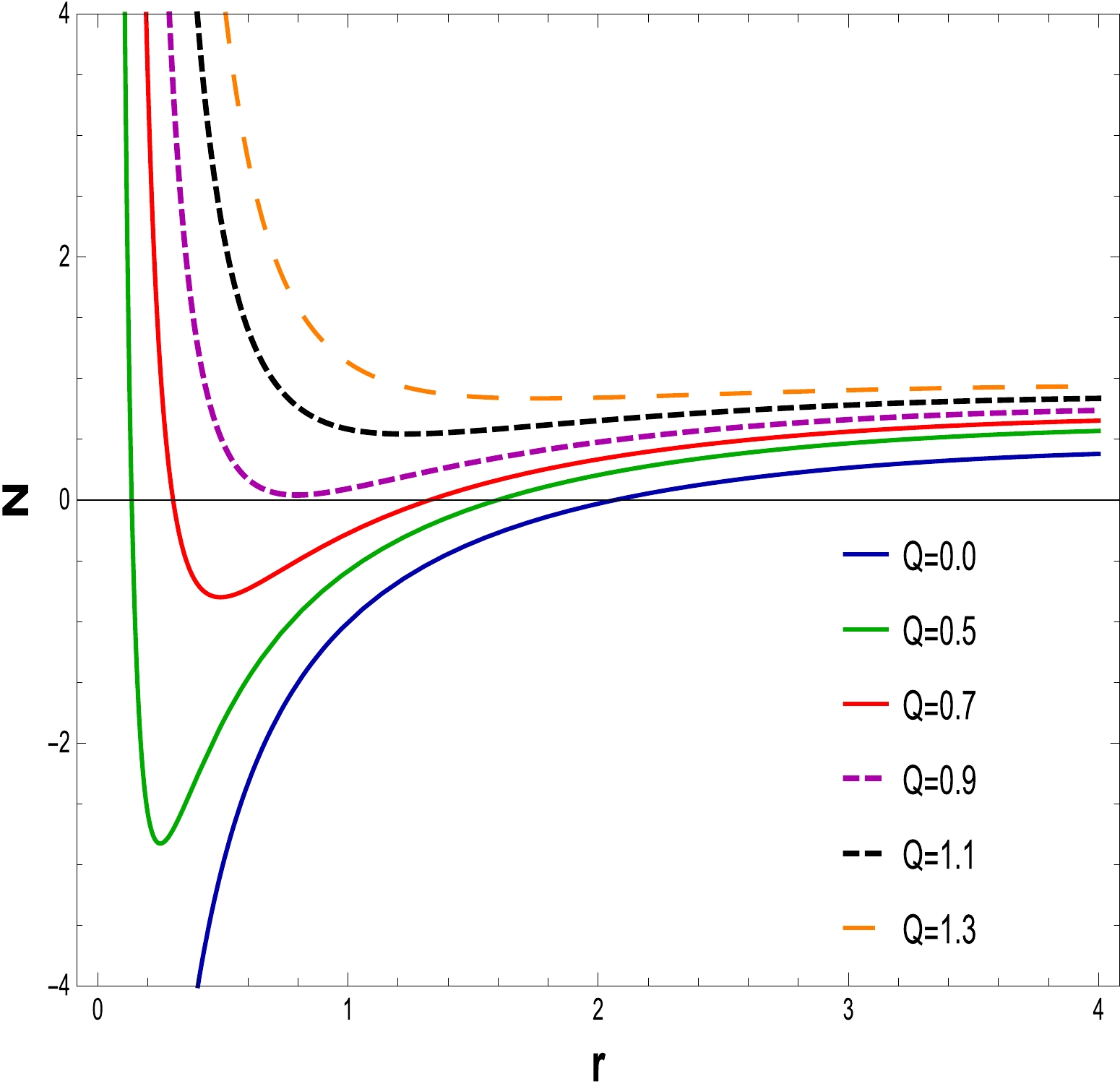
Figure 1. (color online) The graph of N as a function of r for
$ \alpha=0.030 $ ,$ l=20 $ , and$ M=1 $ .
Figure 2. (color online) The graph of N as a function of r for
$ \alpha=0.040 $ ,$ l=20 $ , and$ M=1 $ .Taking
$ N(r_{+})=0 $ enables us to determine the BH's mass and obtain$ M=\frac{1}{2} r_+ \left(\frac{r_+^2}{l^2}+\frac{Q^2}{r_+^2}+2 \sqrt{\alpha } Q-\frac{\alpha r_+^2}{3}+1\right). $

(18) We obtain the BH temperature from
$ T=\dfrac{k}{2\pi}=\dfrac{N'(r_{+})}{4\pi} $ , where k is the surface gravity. Thus, the temperature takes the following form:$ T=\frac{1}{{4 \pi r_+}}\Big(1+\frac{3 r_+^2}{l^2}-\frac{Q^2}{r_+^2}+2 \alpha Q-\alpha r_+^2\Big). $

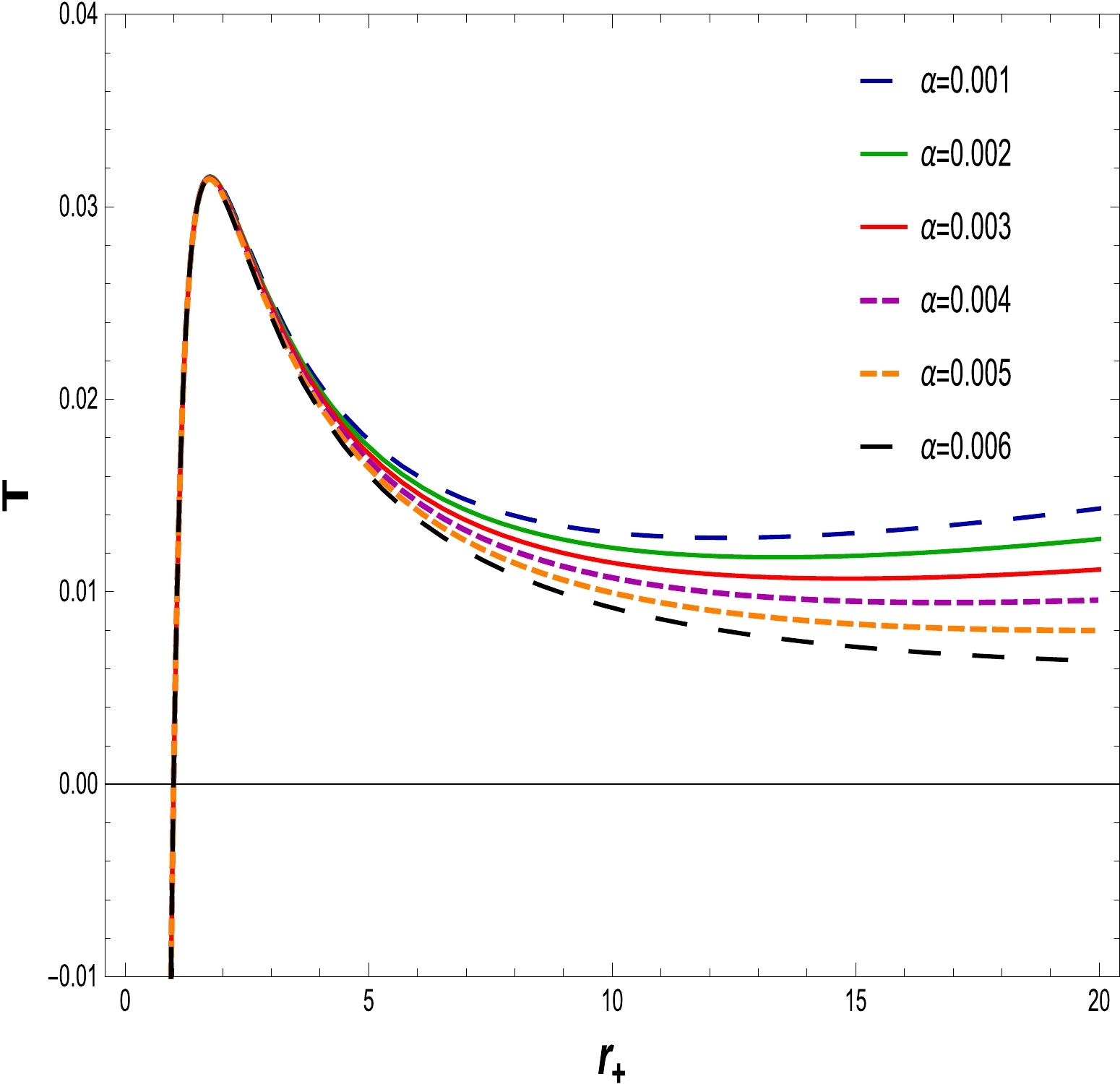
(19) In Figs. 4, 5, 6 and 7, we plot the NLED charged BH Hawking temperature for a small radius BH, as well as a large radius BH, for different values of the charge Q and coupling constant α with
$ l=20 $ . From Figs. 4 and 5, it is clear that the Hawking temperature of the BH increases (decreases) to the maximum (minimum) value when the charge Q decreases (increases) with the increase in the horizon radius. It is worthy to mention that, with a fixed NLED coupling constant$\alpha=0.0020,~0.0030$ and the electric charge start varying from$ Q=0 $ to$ Q=1.3, $ the Hawking temperature of Schwarzschild and RN BHs is explained. Figures 6 and 7 reveal the behavior of the Hawking temperature with fixed values of the charge, i.e.,$ Q=0.5 $ and$ 1 $ , and the NLED coupling parameter varying from$ \alpha=0.0010 $ to$ \alpha=0.0060 $ , describe the increasing behavior of the Hawking emperature as the coupling parameter decreases with the increase in the horizon radius (from small to large BH), and exhibit the universal pattern of stability. Hence, the system remains stable for small as well as large BHs.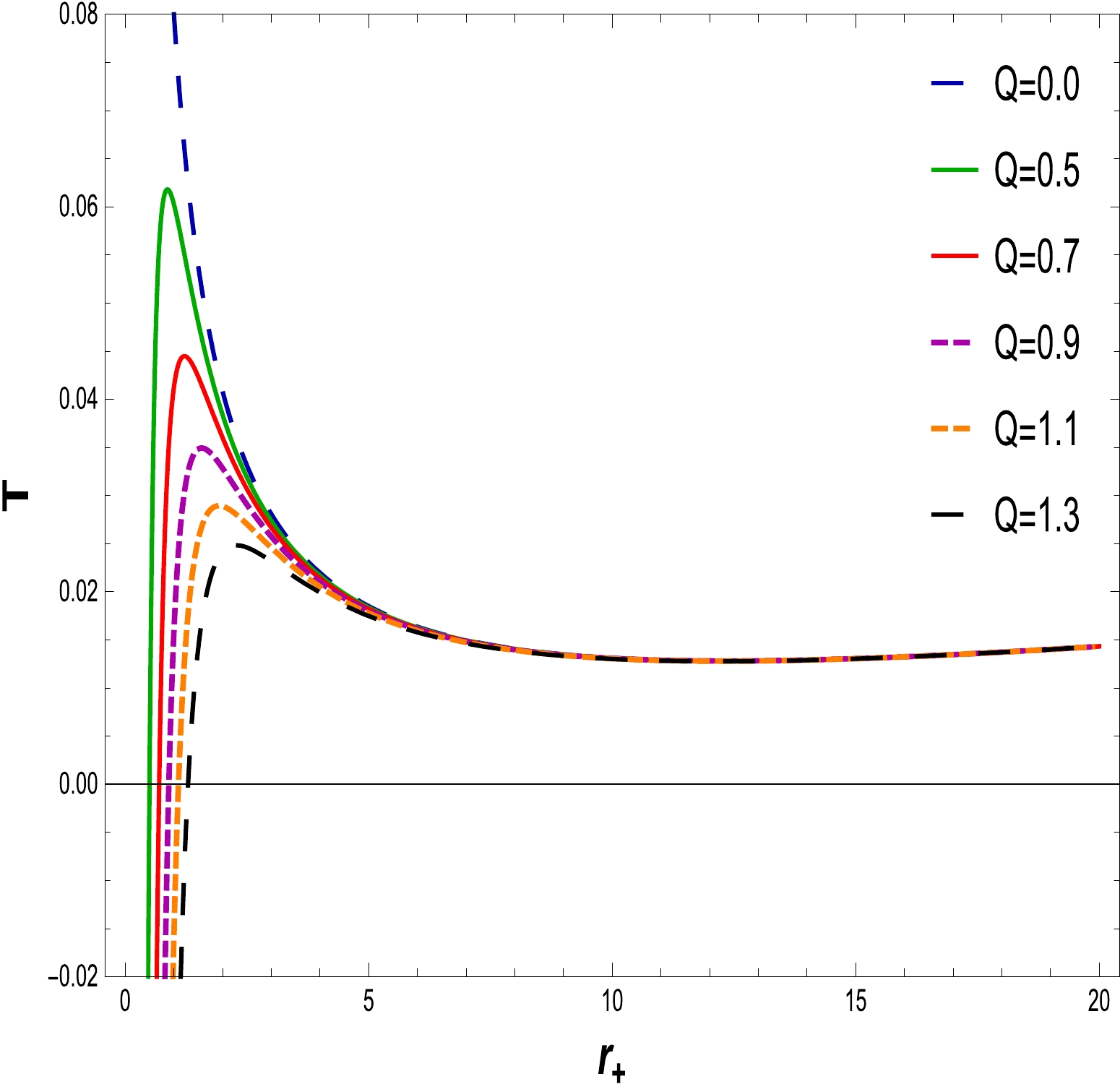
Figure 4. (color online) The graph of T with respect to
$ r_{+} $ for$ \alpha=0.0020 $ and$ l=20 $ .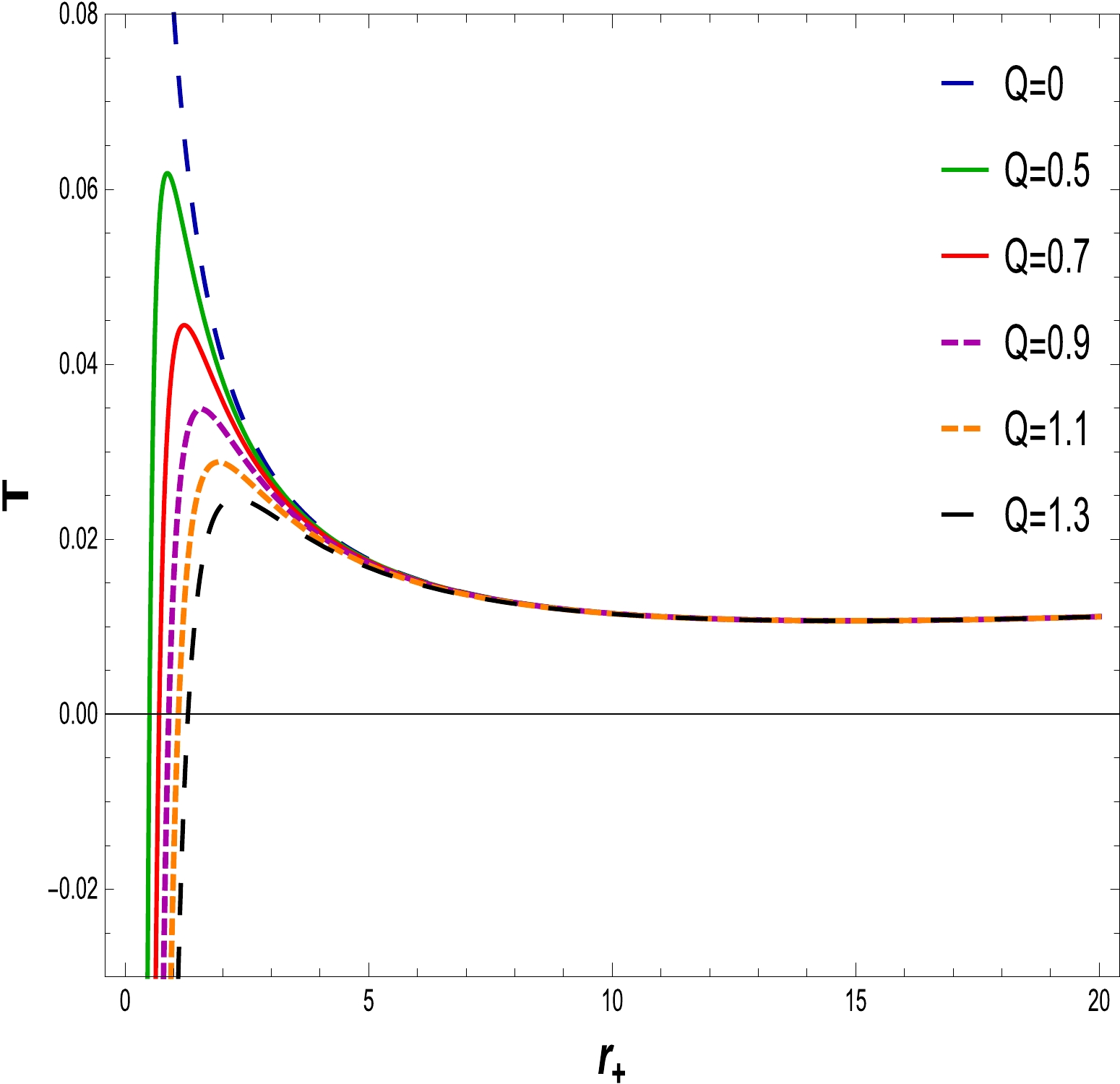
Figure 5. (color online) The graph of T with respect to
$ r_{+} $ for$ \alpha=0.0030 $ and$ l=20 $ .The BH entropy is derived from
${\rm d}M=T{\rm d}S,$ which is integrated to give$S=\int\dfrac{{\rm d}M}{T}{\rm d}r_{+},$ $ \begin{array}{*{20}{l}} S=\pi r_+^{2}. \end{array} $

(20) The concept of heat capacity can be studied as
$ C=\dfrac{\partial M}{\partial T} $ , which simplifies to$ C=\frac{2 \pi r_+^2 \left(l^2 \left(Q^2-2 \sqrt{\alpha } Q r_+^2+\alpha r_+^4-r_+^2\right)-3 r_+^4\right)}{l^2 \left(-3 Q^2+2 \sqrt{\alpha } Q r_+^2+\alpha r_+^4+r_+^2\right)-3 r_+^4}. $

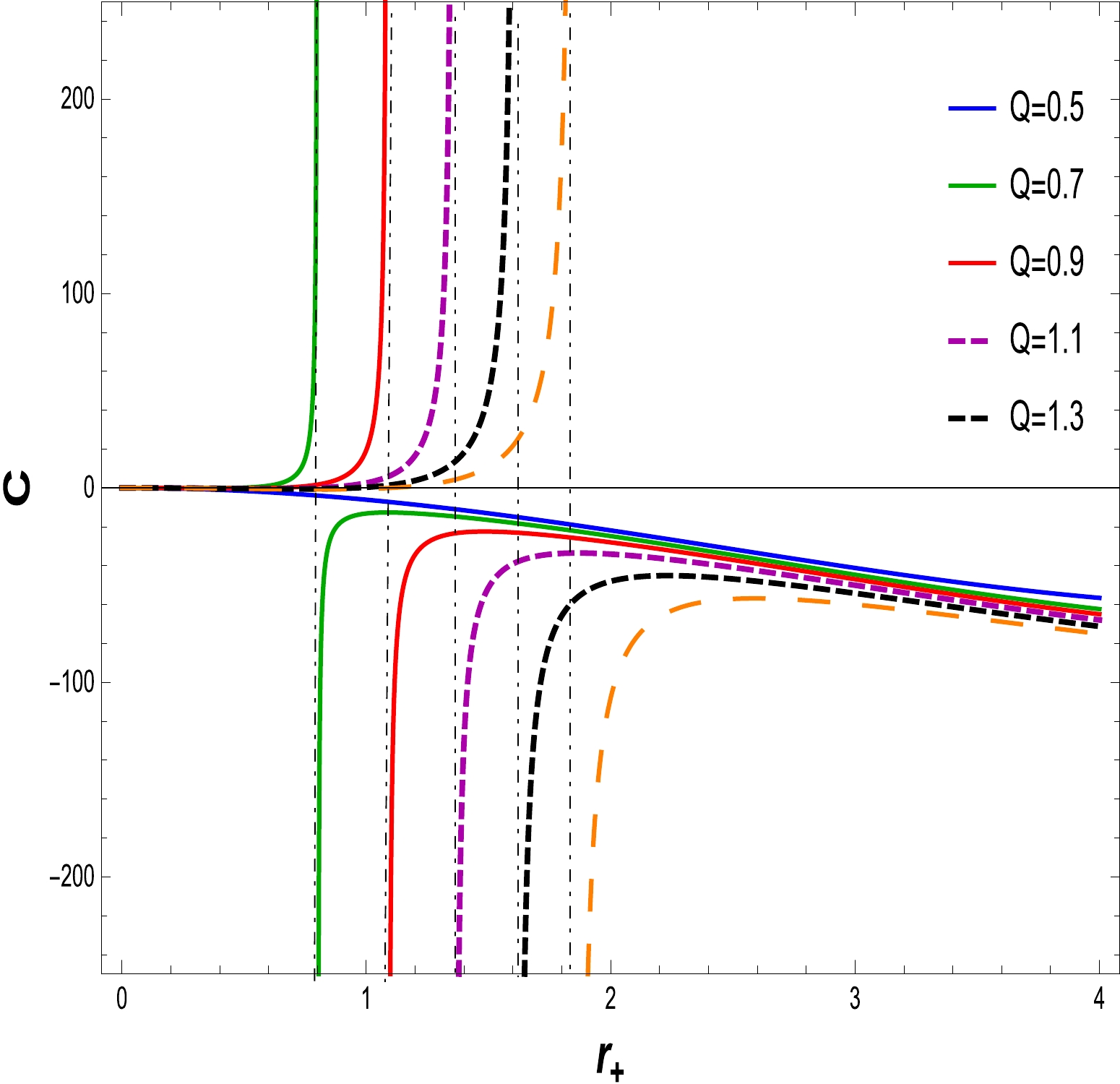
(21) We now analyze the thermodynamical consistency of the BH solution to Einstein gravity with the NLED field. For this purpose, we turn our attention by reckoning that heat capacity indicates BH solution thermal stability. The thermodynamic stability of the BH is contingent on the behavior of the heat capacity. If
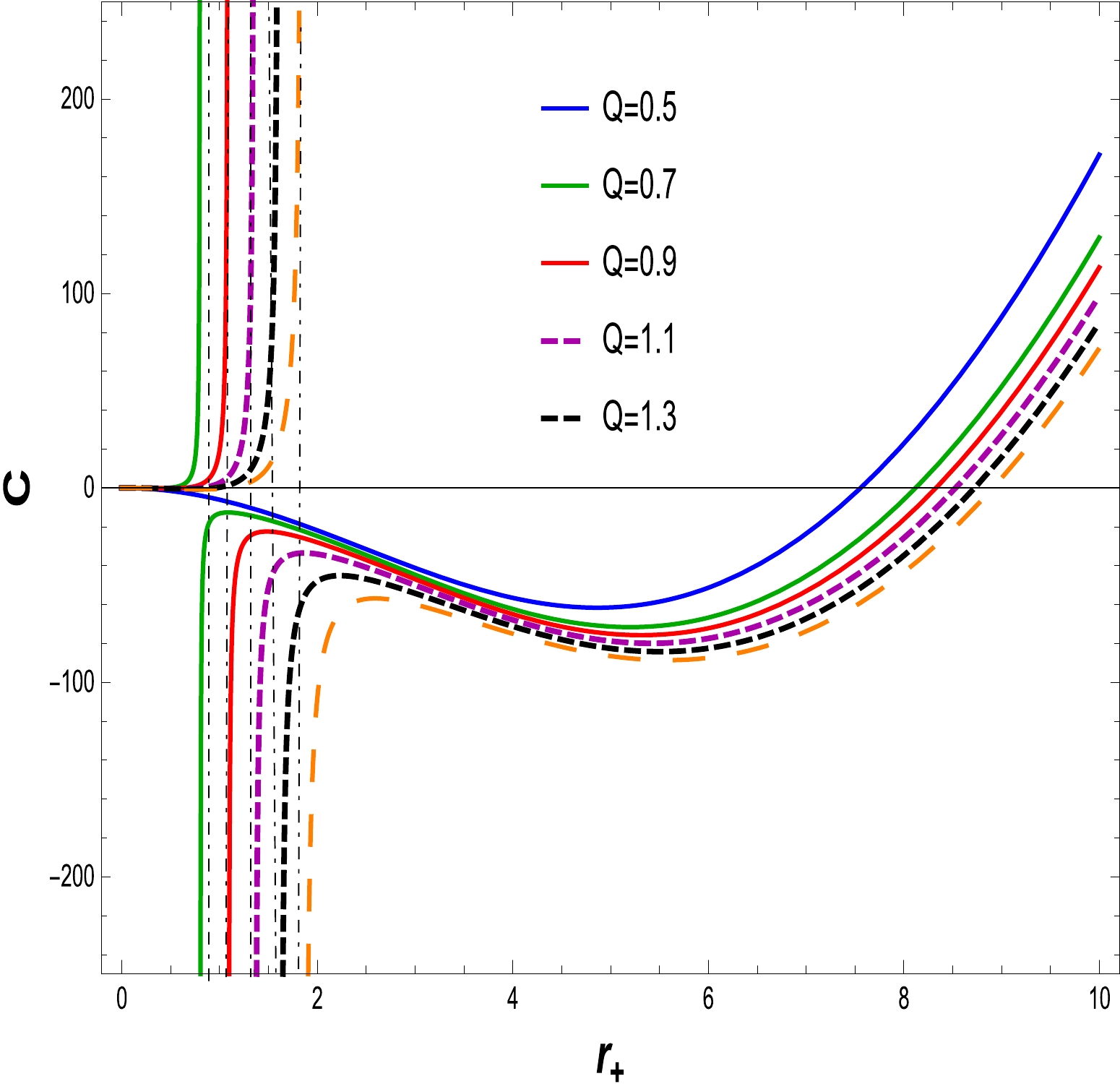
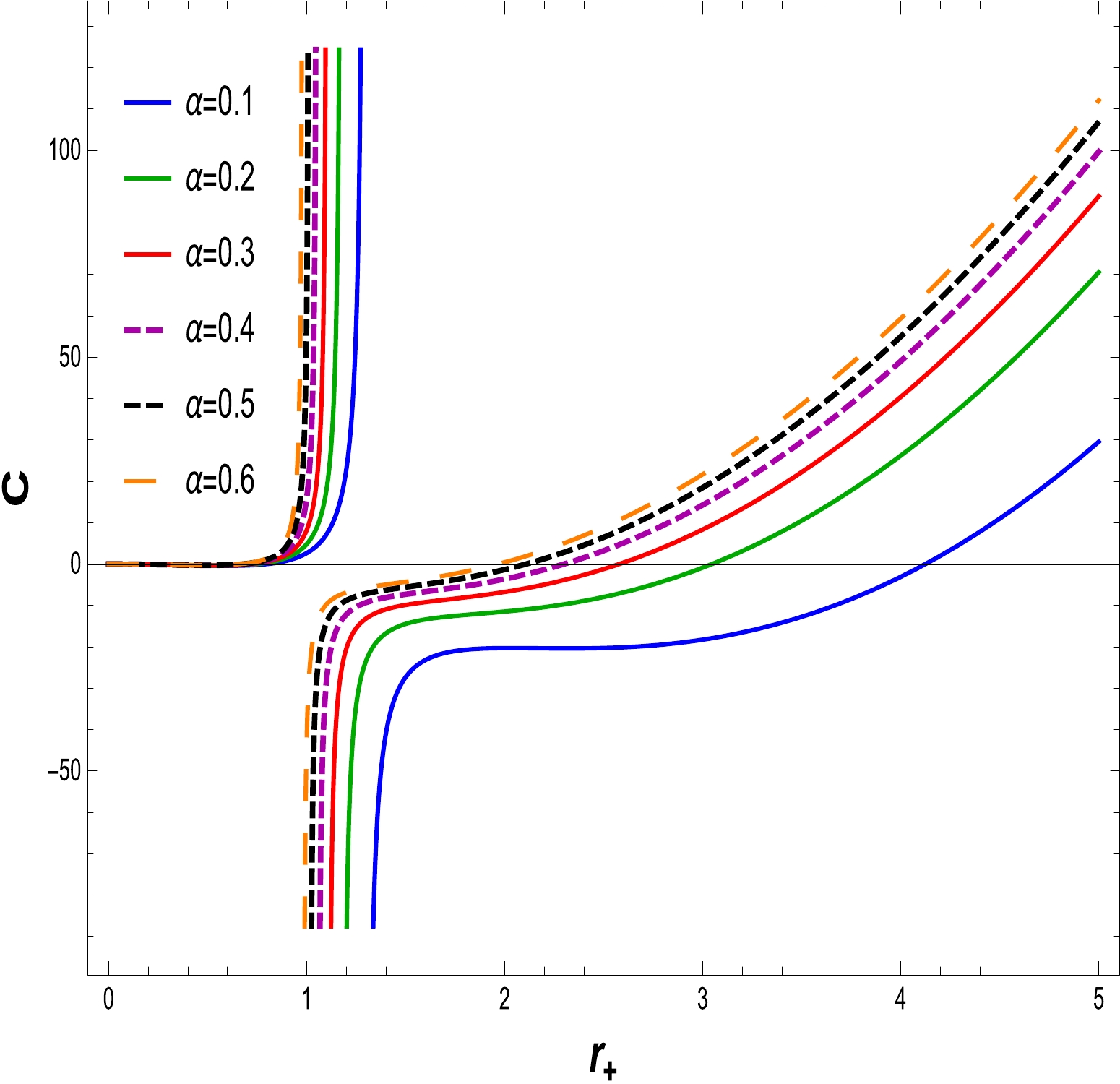
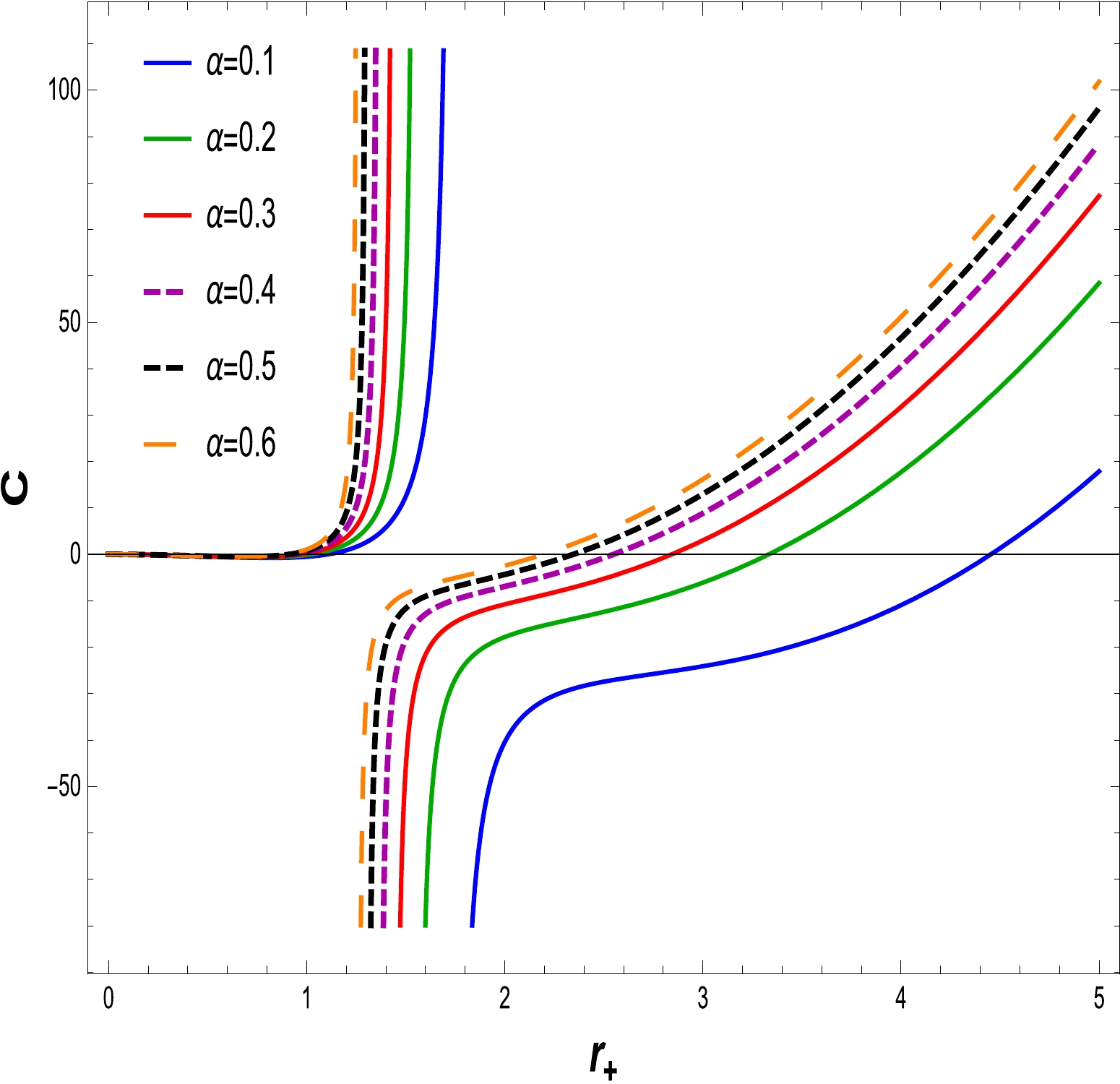
$ C > 0, $ the thermodynamical system is locally stable, whereas it become unstable when the specific heat is$ C < 0 $ . To identify the stability of the specific heat, the graphical representation as shown in Figs. 8–11. We have plotted specific heat C versus$ r_{+} $ for different amounts of electric charge Q and NLED coupling constants$ \alpha. $ If the electric charge is$ Q=0 $ , the heat capacity is that of the Schwarzschild AdS BH. Corresponding to the maximum temperature, critical values discontinue heat capacity curves$ r_{+} = r_{c} $ . At critical values, the specific heat diverges, as shown in Figs. 8 and 10. We find that as the electric charge increases, so does the critical radius. In Figs. 9 and 11, express the stability at initial phase and the second phase change occurs from unstable region to stable region for large BH with variations in the charge Q and fixed values of the NLED parameter α. A similar behavior is observed in Figs. 12 and 13, where the NLED parameter is varied with a fixed value of the charge parameter Q. As a consequence, the large BH in the presence of charge and the coupling parameter tends to be in the stable region compared with the small BH.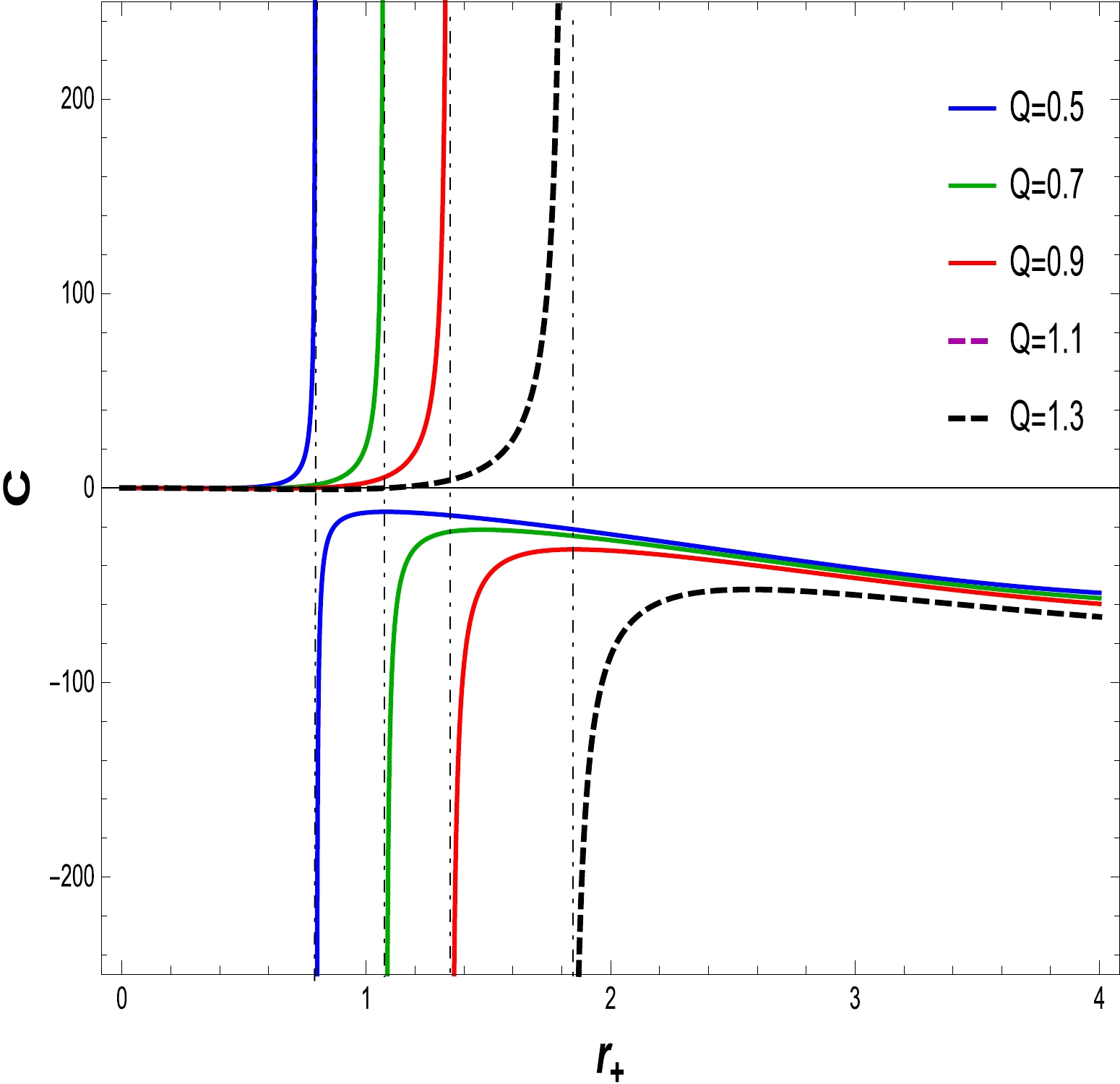
Figure 8. (color online) The graph of C with respect to
$ r_{+} $ for$ \alpha=0.030 $ and$ l=20 $ .
Figure 9. (color online) The graph of C with respect to
$ r_{+} $ for$ \alpha=0.030 $ and$ l=20 $ .Free energy is also known as Gibbs free energy (GFE). Using thermodynamical quantities such as the temperature, mass, and entropy of the BH, the relation
$ G= M-TS, $

takes the form
$ G= \frac{1}{12} \Big(r_+^3(\alpha-8\pi P)+\frac{9Q^2}{r_+}-6\alpha-2\sqrt{\alpha}Qr_++3r_+\Big). $

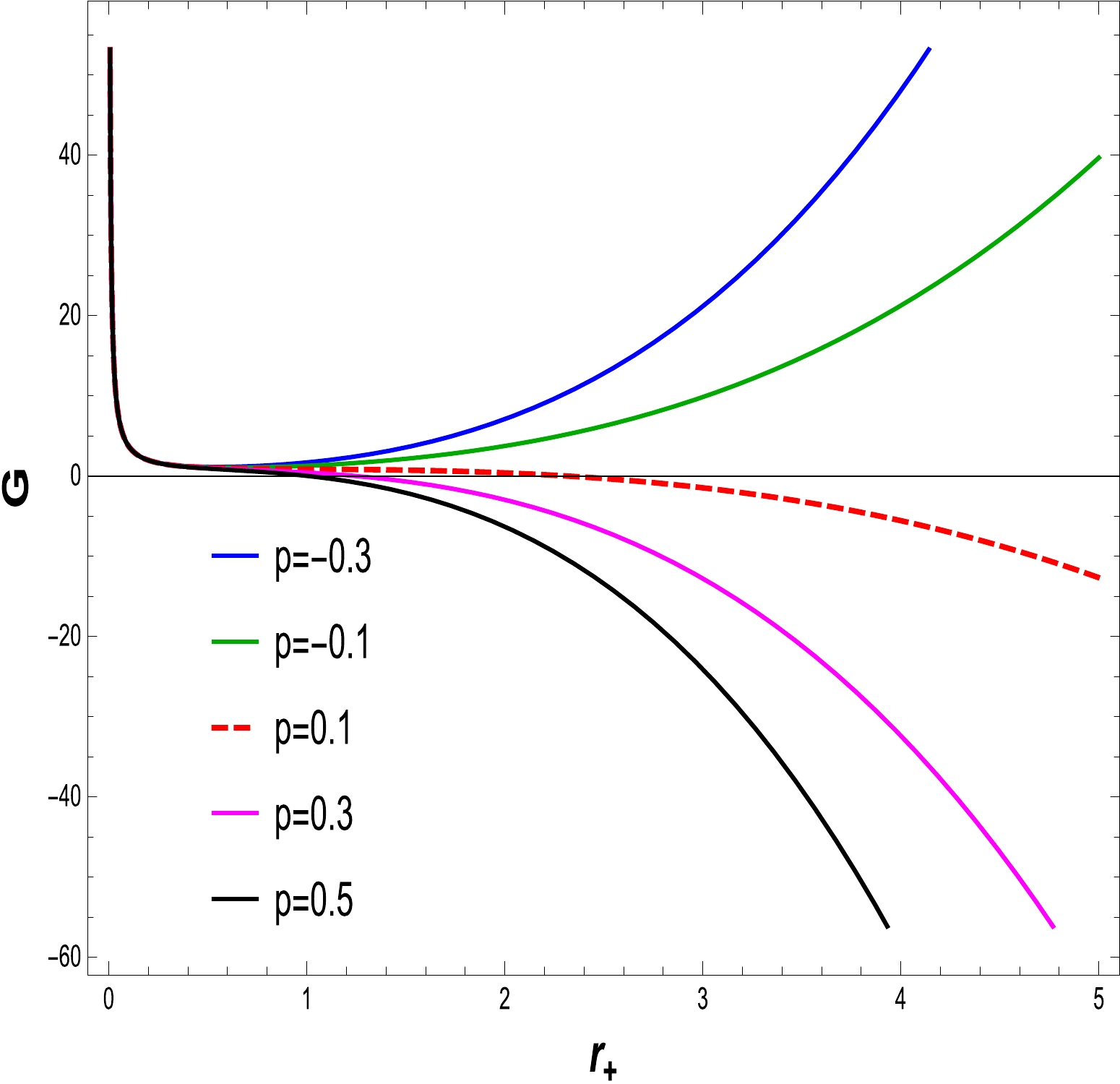
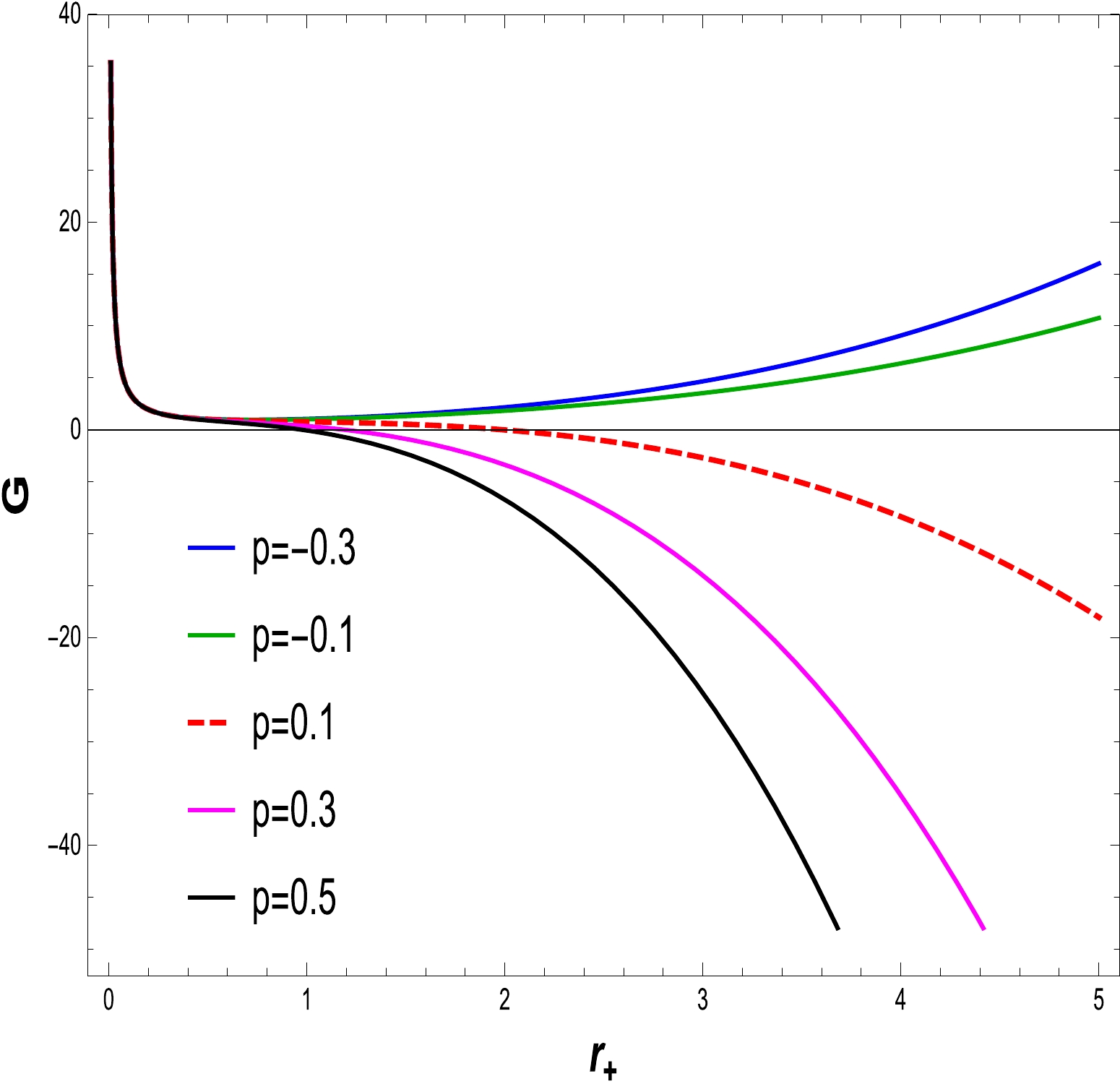
(22) To recognize the thermodynamic stability of the BH, we must investigate the GFE interactions. The effect of BH parameters plays an important role in the stability of transition. To analyze the behavior of the GFE, we draw a plot of the GFE G as a function of the BH temperature. We vary the electric charge Q and fix
$ \alpha= 1 $ and$ \alpha= 0.5 $ . Figures 14 and 15 show the curves associated with different values of pressure. The positive region of the GFE shows stability, while the negative region of the GFE indicates thermodynamic instability. Hence, the BHs with negative GFE release energy to the surroundings to obtain the low energy state, and BHs with a positive GFE are globally stable. -
The extensive state space pressure takes the form
$ P= \frac{-\Lambda}{8\pi} = \frac{3}{8\pi l^{2}}, $

and using Eq. (19), we obtain
$ P(r_+, T)= \Big(\frac{\alpha }{8 \pi }+\frac{Q^2}{8 \pi r_+^4}-\frac{\alpha Q}{4 \pi r_+^2}-\frac{1}{8 \pi r_+^2}+\frac{T}{2 r_+}\Big),\,\,\,\,\,\, v=2r_+. $

(23) Additionally,
$ P(v, T)= \Big(\frac{\alpha}{8\pi}+\frac{2Q^2}{\pi v^4}-\frac{\alpha Q}{\pi v^2}+\frac{T}{v}-\frac{1}{2\pi v^2}\Big). $

(24) To find the critical values, we use
$ \frac{\partial P}{\partial r_+}|_{T} =0 \,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\, \frac{\partial^{2} P}{\partial r_+^{2}}|_{T} =0. $

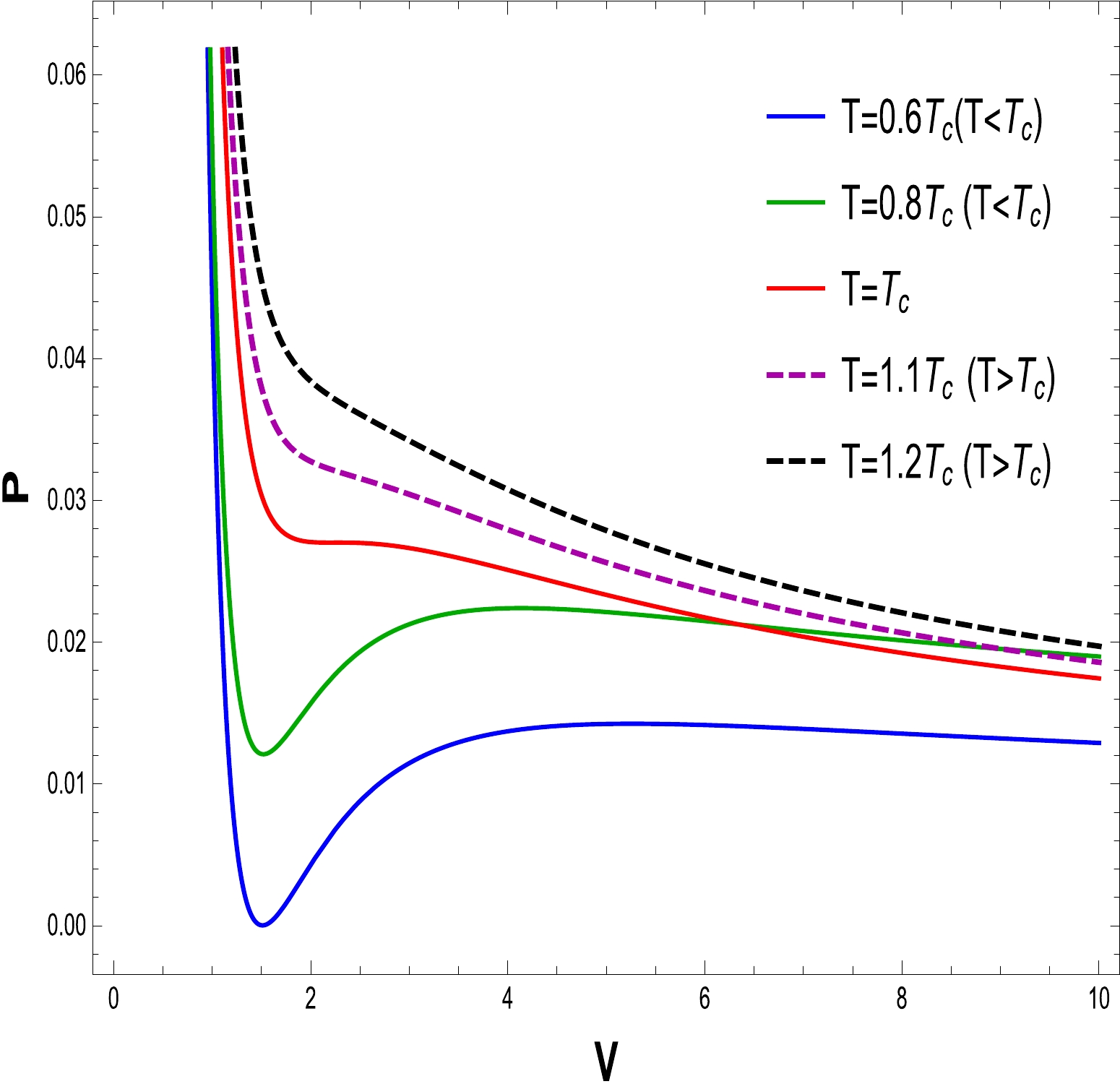
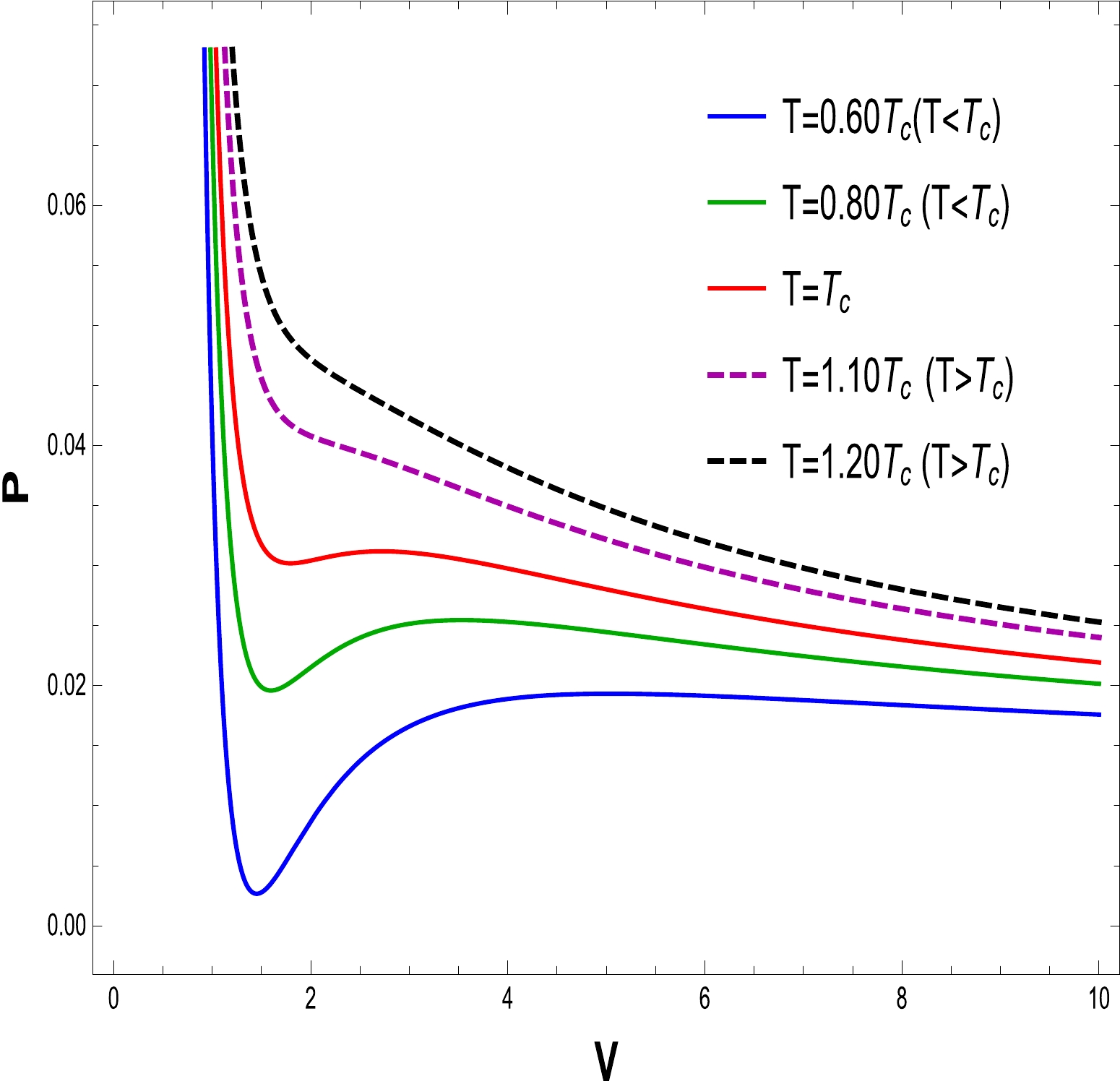
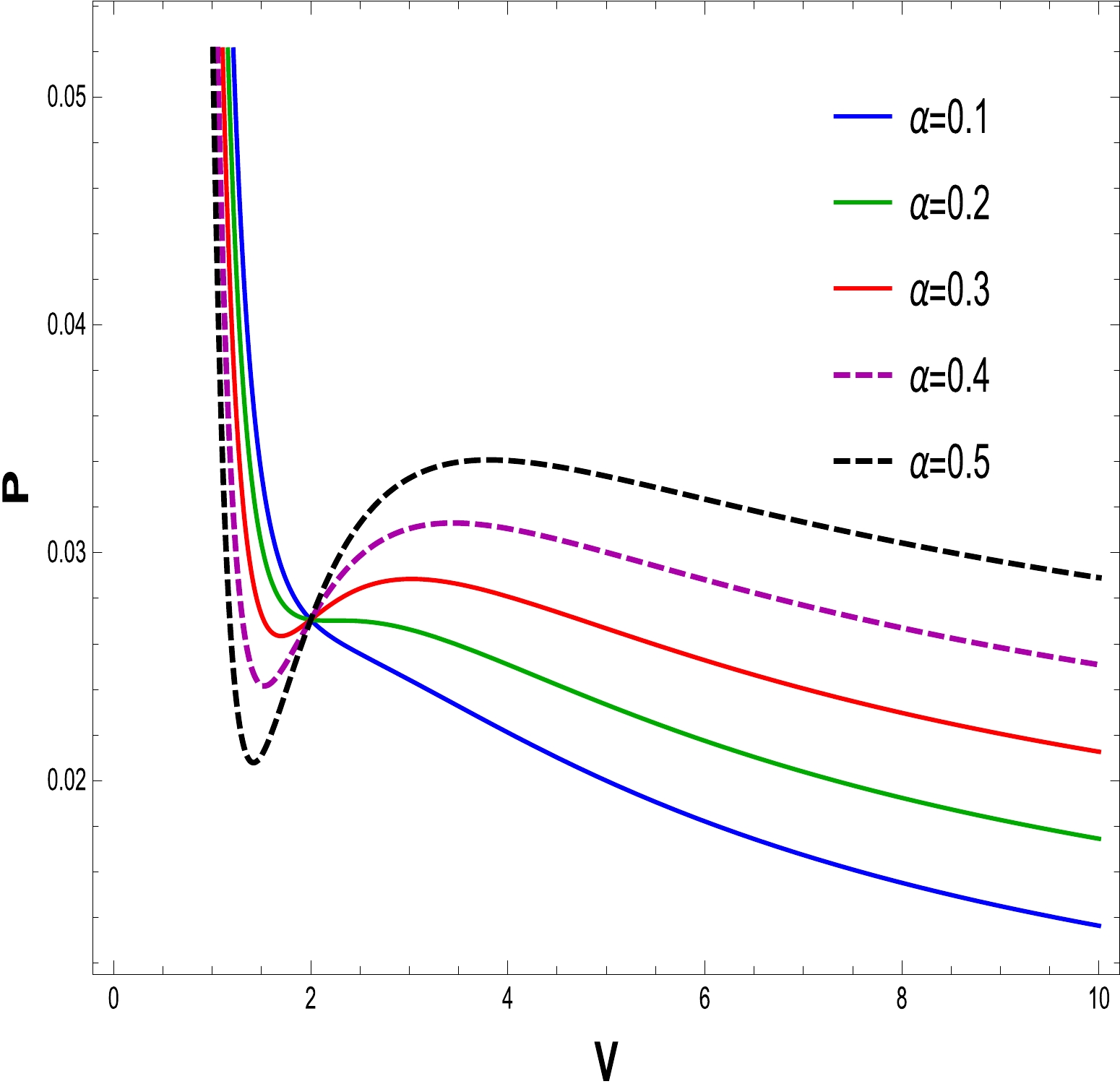
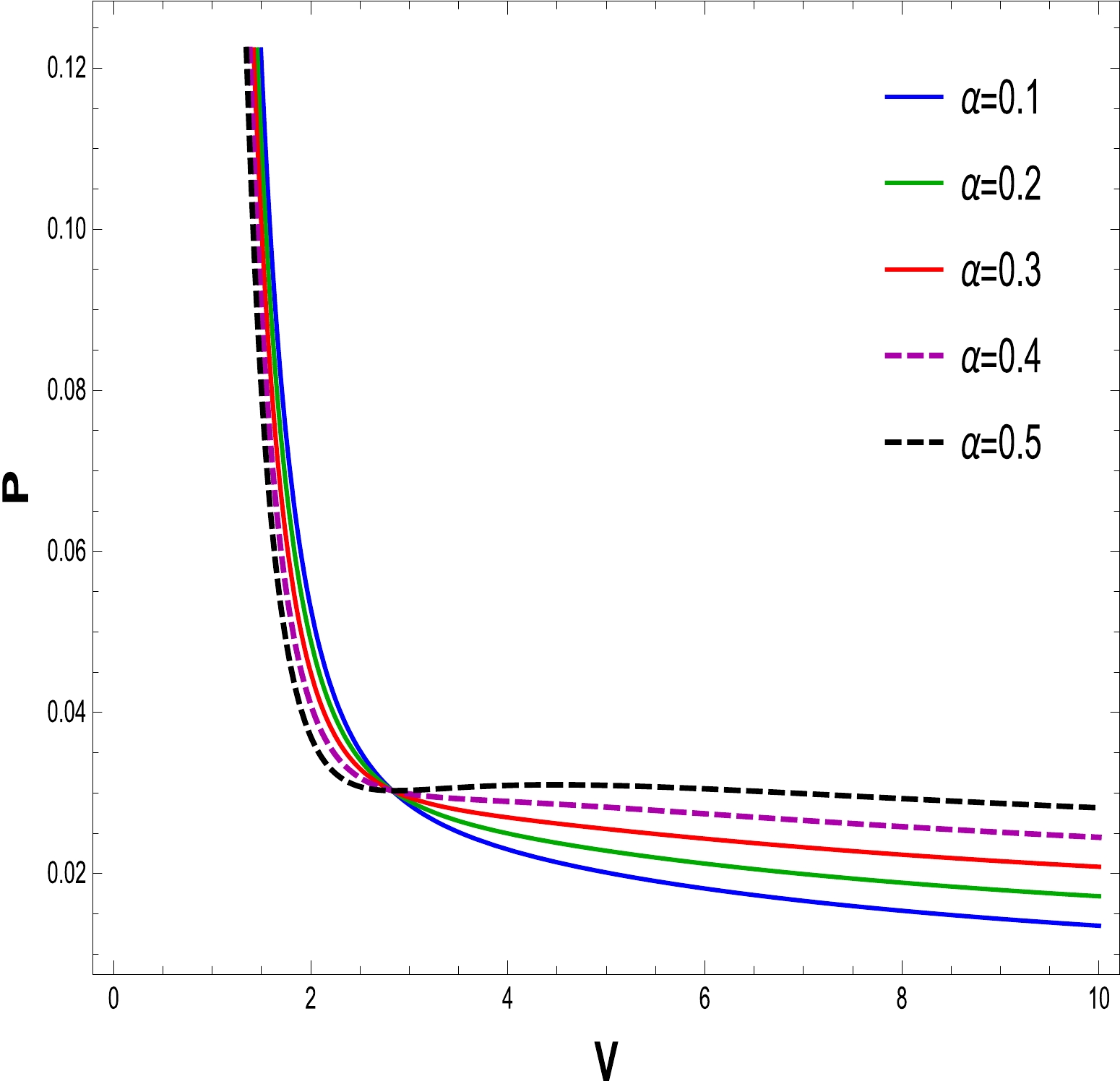
(25) To comprehend the phase transition of the BH solution, we are looking for specific properties. Using the equations for pressure, volume, and temperature, we plot
$ P\text{-}V $ diagrams in Figs. 16–21 to evaluate the critical behavior and the critical characteristics of the NLED AdS BH. From Figs. 16 and 19, it is obvious that a thermodynamic system behaves as an ideal gas and is stable when$ T > T_{c} $ . When$ T = T_{c} $ , the critical isotherm has an inflection point, and when$ T <T_{c} $ , the unstable zone exists in the system and we observe that the small/large BH phase transition occurs. To understand this more clearly, a phase transition is displayed in the right plots in Figs. 17 and 20. It may noted that$ P\text{-}V $ criticality has stable and unstable regions. The stability can be seen in the regions$ V\in[0,a] $ and$ [b, \infty] $ corresponding to the small and large BHs, respectively. Meanwhile, there is instability in the region$ V \in[a, b] $ , and the phase transition can coexist for the unstable region of small and large BHs. To show the impact of the NLED parameter α in$P\text{-}V$ criticality is plotted in Figs. 18 and 21 to show phase transition. The$P\text{-}V$ diagrams in Figs. 16 and 19 show that the stationary points of inflection are at the same locations where the critical points of the equation of the state occur. Now, to determine the critical values, we differentiate Eq. (23) and obtain
Figure 17. (color online) The graph of P as a function of V for
$ Q=0.50 $ ,$ \alpha=0.20 $ , and$ T=0.06828 $ .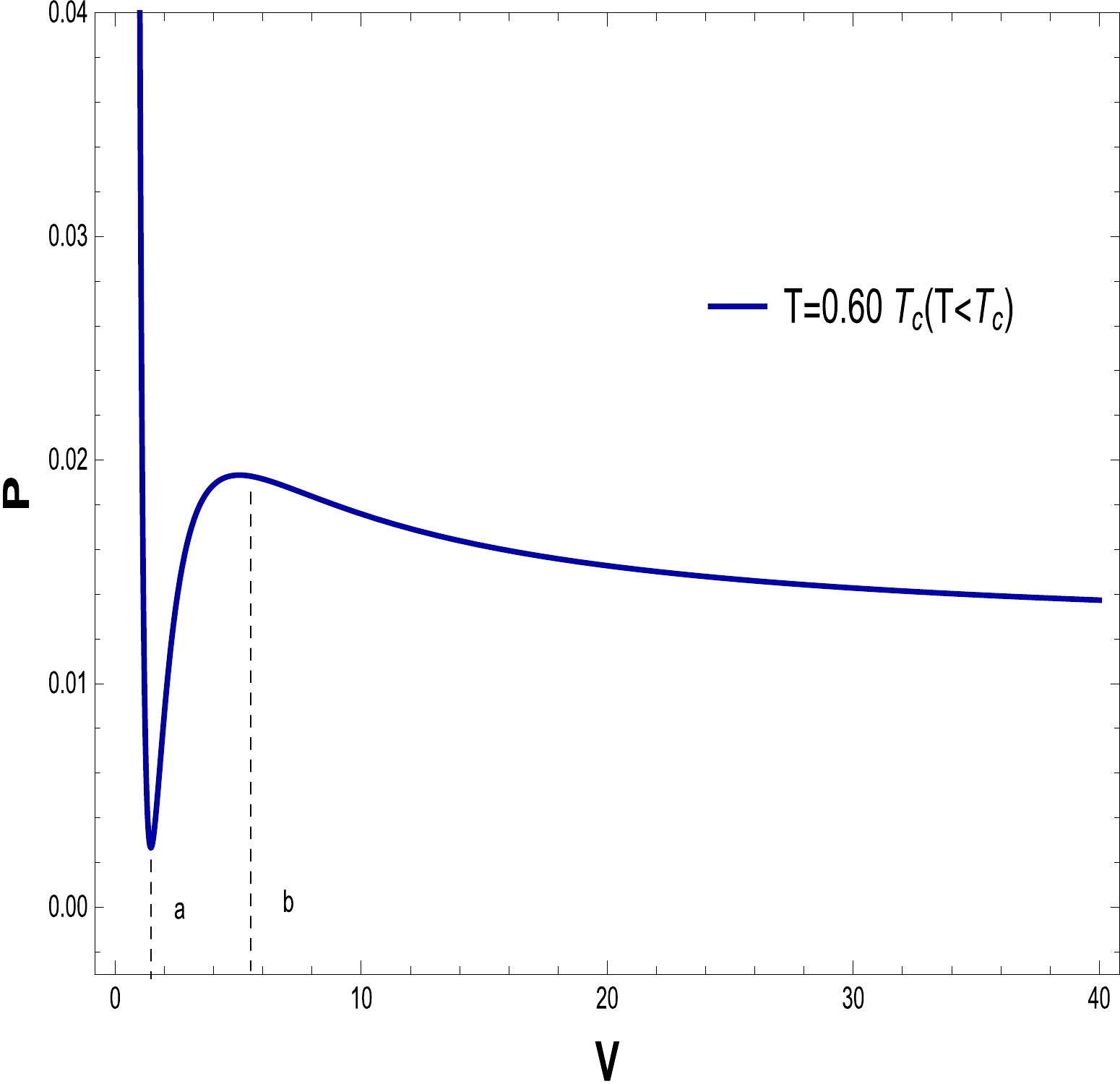
Figure 20. (color online) The graph of P as a function of V for
$ Q=1 $ ,$ \alpha=0.30 $ , and$ T=0.07704 $ .$ r_{c}=\frac{\sqrt{6} Q}{\sqrt{2 \alpha Q+1}}, $

(26) $ V_{c}=\frac{2 \left(\sqrt{6} Q\right)}{\sqrt{2 \alpha Q+1}}, $

(27) $ T_{c}= \frac{\frac{4 \sqrt{6} \alpha ^2 Q^2}{\sqrt{2 \alpha Q+1}}+\frac{4 \sqrt{6} \alpha Q}{\sqrt{2 \alpha Q+1}}+\frac{\sqrt{6}}{\sqrt{2 \alpha Q+1}}}{18 \pi Q}, $

(28) $ P_{c}=\frac{9 Q^3 \sqrt{2 \alpha Q+1}+9 \alpha Q r_+^4 \sqrt{2 \alpha Q+1}+2 \sqrt{6} r_+^3 (2 \alpha Q+1)^2-9 Q r_+^2 (2 \alpha Q+1)^{3/2}}{72 \pi Q r_+^4 \sqrt{2 \alpha Q+1}}. $ 
(29) Further, using Eqs. (27)–(29), we obtain
$V_{c}= 2.14834$ ,$ T_{c}= {0.4031}/{\pi } $ , and$ P_{c}= 0.034350. $ The next step is to investigate the critical exponents, which demonstrate the feature of phase transitions generally. In the vicinity of the critical point, there are four critical exponents that describe the specific heat, parameter order, isothermal compressibility, and critical isotherm, i.e., α, β, γ, and δ, which are frequently used to define the phase transition, e.g., the van der Waals phase transition. We define$ \tau= \frac{T}{T_{c}}-1 = t-1, $

where
$ t=\frac{T}{T_{c}}, $

(30) $ \omega = \frac{v-v_{c}}{v} = \frac{v}{v_{c}}-1 = \phi -1, $

(31) Here,
$ \phi = \frac{v}{v_{c}}. $

$ p = \frac{P}{P_{c}}, \,\,\,\,\,\,\,\Rightarrow P=pP_{c}. $

The critical exponents are identified as
$ t=1+ \tau \,\,\, \phi= 1+\omega. $ $ \begin{array}{*{20}{l}} p\approx 0.9514+ {\tau}-{\tau \omega}- {1.972\omega^{3}}+ O(\tau \omega^{2}, \omega^{4} ). \end{array} $

(32) The black hole sustains a step change from small to large, and the temperature, pressure, and thermodynamic volume remain constant. The equation of state Eq. (32) holds:
$ \begin{aligned}[b] p =& 0.9514+ {\tau}-{\tau \omega_{s}}- {1.972\omega_{s}^{3}}\\=& 0.9514+ {\tau}-{\tau \omega_{l}^{3}}- {1.972\omega_{l }^{3}}. \end{aligned} $

(33) The Maxwell's area law (
$\oint v {\rm d}p=0$ ) during phase transition holds:$ \begin{array}{*{20}{l}} \int_{\omega_{s}}^{\omega_{l}} \omega {\rm d}p= \int_{\omega_{s}}^{\omega_{l}}(\omega(p_{c}+5.916 \omega^{2}))\omega {\rm d}p, \end{array} $

(34) After a certain calculation, one can obtain
$ \begin{array}{*{20}{l}} \omega_{l}=-\omega_{s}, \end{array} $

(35) and we obtain
$ \omega_{l}=\sqrt{1.333 \tau}. $

$ 1. $ The specific heat at a constant value$ S = \pi r^{2} $ is governed by$ "\alpha_{1}" $ $ \begin{array}{*{20}{l}} C_{v}= T \frac{\partial S} {\partial T}|_{v} \varpropto |\tau|,^{-\alpha_{1}} \end{array} $

(36) $ \Rightarrow \frac{\partial S}{\partial T}=0. $

The entropy S is autonomously from T; thus, we obtain
$\alpha_{1} = 0.$ 2. Exponent β describes the order parameter
$ \eta = V_{s} - V_{l} $. $ \begin{array}{*{20}{l}} \eta = V^{s}- V_{l} \varpropto |\tau|^{\beta}, \end{array} $

(37) which simplifies to
$ \eta = V_{s} - V_{l} = V_{c}(1+\omega_{s})- V_{c}(1+\omega_{l}), $

$ \eta = |\tau|^{\frac{1}{2}}, $

and thus,
$ \Rightarrow \beta = \frac{1}{2}. $

(38) $ 3. $ The exponent γ determines the isothermal compressibility$ k\tau $ . From Eq. (32), we have$ k\tau = \frac{-1}{V} \frac{\partial V}{\partial P}|_{T} \varpropto |\tau|^{-\gamma}, $

(39) $ k\tau = \frac{-1}{V} \frac{\partial V}{\partial P}|_{T} \varpropto |\tau|^{-1},$

(40) and thus,
$ \begin{array}{*{20}{l}} \Rightarrow \gamma = 1. \end{array} $

(41) $ 4. $ As$ T=T_{c} $ , a critical isotherm is given by$ \begin{array}{*{20}{l}} |P-P_{c}|_{T_{c}} \varpropto |V-V_{c}|^{\delta}, \end{array} $

(42) $ \begin{array}{*{20}{l}} \alpha_{1} + \beta (\delta +1) = 2, \end{array} $

(43) which implies that
$ \delta = 3 $ . Hence, the critical elements connected to the exact BH with the NLED field include critical behavior, phase transition, and critical exponents, which is a universal pattern of phase transition. -
In this research, we explored the phase structure and critical behavior of a BH, as well as the extended thermodynamics for an AdS charged BH with NLED, by using the thermodynamic pressure as the cosmological constant. The mass M, charge Q, coupling constant α, and cosmological constant define the AdS charged BH.
We investigate the features of such NLED BHs in order to determine their stability and transition by computing the appropriate thermodynamical statistics.The horizon of the charged AdS BH solution is obtained by considering
$ N(r)=0 $ , which demonstrates that as the electric charge Q improves, the BH size shrinks with fixed values of α and l. When we study the Hawking temperature, we can see that as the electric charge decreases, the temperature increases to a maximum. In the absence of electric charge Q, it gives the Schwarzschild AdS BH temperature. Black hole entropy is calculated in accordance with the first law. The heat capacity with the cosmological constant, which reveals information about the stability plotted in Figs. 7 and 8 for different values of charge with fixed α and l values. The heat capacity for the specified charge values is perfectly discontinuous at the critical values, as can be seen. The heat capacity determines the stability of small radius BHs and shows the instability of large radius BHs. When a BH undergoes a phase change, its thermodynamic stability is described by the GFE. It is important to investigate the fundamental characteristics and behavior of the BH. With the negative values of pressure at$ p=-0.1,-0.3 $ , the GFE expresses the stability of the thermodynamical system and remains stable for large radius BHs. Pressure with positive values indicate an unstable system. In order to obtain information about critical aspects, we investigate the associated P-V depiction in Figs. 11 and 12. When$ T<T_{c} $ , one may have an unstable region, when the critical isotherm indicates a point of inflection. Finally, when$ T>T_{c} $ , the system behaves as an ideal gas. Critical exponents describe how physical variables behave when they are close to a continuous phase transition. The critical exponent values are found to increase with the charge and decrease with an increase in the coupling constant.
Extended phase space thermodynamics of black hole with non-linear electrodynamic field
- Received Date: 2022-12-07
- Available Online: 2023-06-15
Abstract: This paper deals with the thermodynamical properties of the black hole formulated in Einstein's theory of relativity associated with a nonlinear electromagnetic field. The transition of the black hole is analyzed using the mass, electric charge, coupling constant, and cosmological constant. We examine the thermodynamical aspects of exact black hole solutions to compute the black hole mass, temperature, entropy, Gibbs free energy, specific heat, and critical exponents in the phase space. Further, we study the stability of the black hole solution using the specific heat and Gibbs free energy. We examine the first and second phase changes and show a P-V criticality, which is similar to the van der Waals phase change. We also examine the equation of the state and the critical exponents.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: