-
Nuclear fission presents a unique example of non-equilibrium large-amplitude collective motion in a multi-dimensional space where all nucleons participate with complex correlation effects. Fission is considered one of the most complex processes in nuclear physics and offers a rich laboratory for a broad variety of scientific research on nuclear properties and general physics. Therefore, the study of fission is always at the frontier of nuclear physics.
Since its discovery, the evolution of a nucleus from a single ground-state shape into two separate fragments in nuclear fission has been described in terms of potential energy surfaces (PESs) that are functions of suitable shape coordinates [1–3]. Therefore, in all current approaches to fission that rely on the adiabatic approximation, the first step is to define the most relevant collective coordinates and compute the PESs. Two types of models, that is, the macroscopic-microscopic (MM) approach [4, 5] and energy density functional theory (DFT) [6], are widely used to calculate the PESs for nuclear fission.
The MM approach consists of viewing the nucleus as a finite chunk of nuclear matter, the energy of which is parameterized as a function of the charge, mass, and deformations of the nucleus. The total energy includes macro energy, shell correction energy, and pairing energy. The MM approach has a series of versions characterized by different parameterizations of the nuclear surface of the liquid drop and different phenomenological nuclear potentials, such as the five-dimensional finite-range liquid-drop model [7–9], macroscopic-microscopic Woods-Saxon model [10, 11], macroscopic-microscopic Lublin-Strasbourg drop (LSD) model in three-quadratic-surface parameterization [12, 13], LSD in Fourier shape parameterization [14], and two-center shell model [15]. Based on the obtained multi-dimensional PESs, various methods for dynamical evolution in the collective space have also been performed, generally reproducing experimental measurements [7, 16–22].
Self-consistent approaches based on the nuclear DFT have recently demonstrated that a microscopic description has the potential for both qualitative and quantitative descriptions of fission data [6, 23–27]. In the DFT framework, the wave functions along the fission path are generally determined by the minimization of the energy of the nucleus within a given set of constraints and assumed symmetries. Currently, large-scale calculations for fission up to scission are generally performed in two dimensions, for example, axially symmetric quadrupole and octupole deformations, and have been conducted based on the non-relativistic Gogny and Skyrme energy density functionals (EDFs) [28–39] and relativistic (covariant) EDFs [40–45]. For instance, Dubray
$ et\; al. $ [31] used the constrained Hartree-Fock-Bogoliubov method with the Gogny D1S functional to calculate the PESs of the fissioning nuclei$ ^{226} $ Th and$ ^{256,258,260} $ Fm as functions of quadrupole and octupole moments. Corresponding fragment properties at scission were derived yielding fragment deformations, deformation energies, energy partitioning, neutron multiplicities, total fragment kinetic energies, and so on. Schunck$ et\; al. $ [35] employed the Skyrme EDFs SkM$ ^* $ , UNEDF0, and UNEDF1 to calculate the PESs of$ ^{240} $ Pu in different two-dimensional (2D) spaces. In particular, the effects of the triaxial degree of freedom and nucleon number in the neck of the scission have been extensively studied. We also previously performed constrained relativistic mean-field calculations in the collective space of axially symmetric quadrupole and octupole deformations, based on the EDF PC-PK1, to determine the PES, scission line, and collective masses for the induced fission of$ ^{226} $ Th [40].The self-consistent approach guarantees that the shape for a given set of constraints is optimal, although nonconstrained degrees of freedom are not fixed. However, the results provided with this method are not always unique [46] because one can easily land in one of the local minima for a given set of constraints. As a consequence, discontinuities are often observed for PESs in restricted deformation space, especially for large elongated configurations. In fact, these discontinuities are entirely spurious because locally enlarging the collective space can easily restore the continuity of the full PES [46]. In addition, continuous PESs give additional flexibility to define the scission configurations and improve the predictive power of the theory. Recently, microscopic calculations of PESs in a fully three-dimensional (3D) collective space were performed for fission up to scission, such as for the PES of
$ ^{228} $ Th in axial quadrupole and octupole deformations as well as an isoscalar pairing degree of freedom [47], and the PESs of$ ^{252} $ Cf and$ ^{258} $ No in axial quadrupole, octupole, and hexadecapole moments [48].In this study, we take the compound nucleus
$ ^{236} $ U as an example to calculate the fully 3D PES in axial quadrupole and octupole deformations$ (\beta_2, \beta_3) $ as well as the nucleon number in the neck$ q_N $ based on covariant DFT (CDFT). It has been well demonstrated that the$ q_N $ degree of freedom provides a mechanism to pass continuously from a single whole nucleus to two distinct fragments [33, 34, 49]. Therefore, we mainly focus on the impact of the additional degree of freedom$ q_N $ on the fission modes and scission configurations. Section II briefly introduces the theoretical framework. The details of the calculation and the results for the PESs, scission configurations, and estimated total kinetic energies are described and discussed in Section III. Finally, Section IV contains a summary of the results and an outlook for future studies. -
The EDF in the point-coupling version of CDFT can be written as
$ \begin{aligned}[b] {{E}_{\rm CDF}}=&\int{{\rm d}}\mathbf{r}{{\varepsilon }_{\rm CDF}}(\mathbf{r}) \\ =&\sum\limits_{k}{\int{\rm d}}\mathbf{r}\upsilon _{k}^{2}{{{\bar{\psi }}}_{k}}(\mathbf{r})(-{\rm i}\mathbf{\gamma }\mathbf{\nabla} +m){{\psi }_{k}}(\mathbf{r}) \\ &+\int{{\rm d}\mathbf{r}\left( \frac{{{\alpha }_{S}}}{2}\rho _{S}^{2}+\frac{{{\beta }_{S}}}{3}{{\rho}_S^{3}}+\frac{{{\gamma }_{S}}}{4}\rho _{S}^{4}+\frac{{{\delta }_{S}}}{2}{{\rho }_{S}}\Delta {{\rho }_{S}} \right.} \\ &+\frac{{{\alpha }_{V}}}{2}{{j}_{\mu }}{{j}^{\mu }}+\frac{{{\gamma }_{V}}}{4}{{({{j}_{\mu }}{{j}^{\mu }})}^{2}}+\frac{\delta_V}{2}{{j}_{\mu }}\Delta {{j}^{\mu }}+\frac{{e}}{2}{{\rho }_{p}}{{A}^{0}} \\ &\left. +\frac{{{\alpha }_{TV}}}{2}j_{TV}^{\mu }\cdot {{(j_{TV})}_{\mu }}+\frac{{{\delta }_{TV}}}{2}j_{TV}^{\mu }\cdot \Delta (j_{TV})_{\mu } \right) \end{aligned}$

(1) with the local densities and currents
$\begin{aligned}[b] {{\rho }_{S}}(\mathbf{r})&=\sum\limits_{k}{v_{k}^{2}}{{\bar{\psi }}_{k}}(\mathbf{r}){{\psi }_{k}}(\mathbf{r})\\ {{j}^{\mu }}(\mathbf{r})&=\sum\limits_{k}{v_{k}^{2}}{{\bar{\psi }}_{k}}(\mathbf{r}){{\gamma }^{\mu }}{{\psi }_{k}}(\mathbf{r})\\ j_{TV}^{\mu }(\mathbf{r})&=\sum\limits_{k}{v_{k}^{2}}{{\bar{\psi }}_{k}}(\mathbf{r}){{\gamma }^{\mu }}\tau_3{{\psi }_{k}}(\mathbf{r}), \end{aligned} $

(2) where ψ is the Dirac spinor of the nucleon, and
$ \rho_p $ and$ A^0 $ are the proton density and Coulomb field, respectively. The coupling constants$ (\alpha, \beta, \gamma, \delta) $ are determined via PC-PK1 parameterization [50] in this study. The subscripts indicate the symmetry of the couplings, where S stands for scalar, V for vector, and T for isovector.From the variation in the EDF with respect to the densities and currents, we can then obtain the relativistic Kohn-Sham equation, which has the form of a single-particle Dirac equation,
$\begin{array}{*{20}{l}} \{-{\rm i}\mathbf{\alpha}\cdot\mathbf{\nabla} +V(\mathbf{r})+\beta [M+S(\mathbf{r})]\}\psi_k(\mathbf{r})=\varepsilon_k\psi_k(\mathbf{r}). \end{array}$

(3) The single-particle effective Hamiltonian contains local scalar
$ S(\mathbf{r}) $ and vector$ V(\mathbf{r}) $ potentials, which are functions of densities and currents,$ \begin{aligned}[b] S(\mathbf{r})=&\alpha_S \rho_S+\beta_S\rho_S^2+\gamma_S\rho_S^3+\delta_S\Delta\rho_S\\ V^\mu (\mathbf{r})=&\alpha_V j^\mu+\gamma_V(j_\nu j^\nu)j^\mu+\delta_V\Delta j^\mu+eA^\mu\frac{1-\tau_3}{2}\\ & +\tau_3(\alpha_{TV}j^\mu_{TV}+\delta_{TV}\Delta j_{TV}^\mu). \end{aligned}$

(4) Pairing correlations between nucleons are treated using the Bardeen-Cooper-Schrieffer (BCS) approach with a δ pairing force [51]. Owing to the broken translational symmetry, we must consider the center-of-mass (c.m.) correction energy for the motion of the c.m., and the phenomenological formula
$ E_{\rm c.m.}=-\dfrac{3}{4}\cdot 41A^{-1/3} $ is adopted. Finally, the total energy reads as$ \begin{array}{*{20}{l}} E_{\rm tot}=E_{\rm CDF}+E_{\rm pair}+E_{\rm c.m.}. \end{array} $

(5) To calculate the multi-dimensional PES in a large deformation space, we must solve the Dirac equation (Eq. (3)) with high precision and efficiency. One way to achieve this is by expanding the Dirac spinor in a two-center harmonic oscillator (TCHO) basis, which contains eigenfunctions in an axially symmetric TCHO potential,
$ \begin{array}{*{20}{l}} V\left(r_{\perp}, z\right)=\frac{1}{2} M \omega_{\perp}^{2} r_{\perp}^{2}+ \begin{cases}\dfrac{1}{2} M \omega_{1}^{2}\left(z+z_{1}\right)^{2}, & z<0 \\ \dfrac{1}{2} M \omega_{2}^{2}\left(z-z_{2}\right)^{2}, & z \geq 0\end{cases} \end{array}$

(6) in the cylindrical coordinate system. A TCHO can be regarded as two off-center harmonic oscillators connected at
$ z=0 $ , while$ z_1 (z_2) $ and$ \omega_1 (\omega_2) $ denote the distance from$ z=0 $ to the center of the left (right) harmonic oscillator and its frequency, respectively. In practice, we set$ z_1=z_2= 2.24\sqrt{4.32{{\beta }_{2}}-2.38}-3.21 $ fm and$ \omega_1 = \omega_2= 3.81 $ MeV/$ \hbar $ . Details can be found in Refs. [52, 53].The entire map of the energy surface in 3D collective space for fission is obtained by imposing constraints on the three collective coordinates: quadrupole deformation
$ \beta_2 $ , octupole deformation$ \beta_3 $ , and the number of nucleons in the neck$ q_N $ $ \begin{equation} \langle E_{\rm tot}\rangle+\sum\limits_{k=2,3}C_k(\langle\hat Q_k\rangle-q_k)^2+C_N(\langle\hat Q_N\rangle-q_N)^2, \end{equation} $

(7) where
$ \langle E_{\rm tot}\rangle $ is the total energy of CDFT,$ \hat Q_2 $ ,$ \hat Q_3 $ , and$ \hat Q_N $ denote the mass quadrupole and octupole operators, and the Gaussian neck operator, respectively, and$ q_k $ and$ q_N $ are the constraint values of these operators. The Gaussian neck operator is generally chosen as$\hat Q_N= \exp[-(z- z_N)^2/a^2_N]$ , where$ a_N $ = 1 fm, and$ z_N $ is the position of the neck determined by minimizing$ \langle\hat Q_N\rangle $ [33]. The left and right fragments are defined as parts of the whole nucleus with$ z\leq z_N $ and$ z\geq z_N $ , respectively.Once the constraint on
$ q_N $ is adopted, the variation in the configurations around the scission becomes smooth and continuous. Therefore, the Coulomb energy between the left and right fragments is calculated using$ \begin{equation} E_{\rm C} (\beta_2, \beta_3, q_N)={\rm e}^2\int {\rm d}\mathbf{r} {\rm d}\mathbf{r^\prime} \frac{\rho^L_p(\mathbf{r})\rho^R_p(\mathbf{r^\prime})}{|\mathbf{r}-\mathbf{r^\prime}|}, \end{equation} $

(8) where
$ \rho_p^L $ ($ \rho_p^R $ ) is the proton density of the left (right) fragment at the configuration$ (\beta_2, \beta_3, q_N) $ , which is also smooth around the scission and can be used to estimate the total kinetic energy (TKE). -
In this section, we present the results of an illustrative study on the 3D PES for the fission of the compound nucleus
$ ^{236} $ U. In the first step, a large-scale deformation-constrained CDFT calculation is performed to generate the 2D PES in the$ (\beta_2, \beta_3) $ plane. The range of collective variables is –1.02$ - $ 7.34 for$ \beta_{2} $ with a step$ \Delta \beta_{2} = 0.08 $ , and from 0.00$ - $ 3.76 for$ \beta_{3} $ with a step$ \Delta \beta_{3} $ = 0.08. Then, we extend the 2D PES to three dimensions via the constraint on$ q_N $ from a thick neck to one as thin as possible with a step$ \Delta q_N = 0.5 $ for the configurations with the neck in the 2D calculation. The EDF PC-PK1 [50] is used for the effective interaction in the particle-hole channel, and a δ-force pairing with strengths$ V_n = 344 $ MeV fm$ ^3 $ and$ V_p = 371 $ MeV fm$ ^3 $ determined by the empirical pairing gap parameters of$ ^{236} $ U, which are calculated using a five-point formula [54]. The self-consistent Dirac equation for single-particle wave functions is solved by expanding the nucleon spinors in an axially deformed TCHO basis in cylindrical coordinates with 20 major shells.Figure 1 shows the 2D PES calculated using constrained CDFT with the PC-PK1 functional. The equilibrium shape is located at
$ (\beta_{2}, \beta_{3})\sim (0.30, 0.00) $ . A double-humped fission barrier is predicted along the optimal fission path, and the calculated heights are 6.85 and 6.05 MeV for the inner and outer fission barriers, respectively. At$ \beta_2 > 2.0 $ , a symmetric valley with up to large elongation is found, and the symmetric and asymmetric fission valleys are separated by a ridge from$ (\beta_2, \beta_3) \approx (1.7, 0.0) $ to$ (3.5, 1.0) $ . In addition, we can see a fission valley from the equilibrium shape to large octupole deformation,$ (\beta_{2}, \beta_{3})\sim (1.8,~ 3.8)$ , passing through a saddle point at$(\beta_{2}, \beta_{3})\sim (1.3,~ 2.1)$ . This describes super-asymmetric fission strongly related to cluster radioactivity, and the saddle point reaches more than$ 30 $ MeV. Note that the overall topography of the 2D PES is similar to that calculated with the Skyrme SkM* functional [38].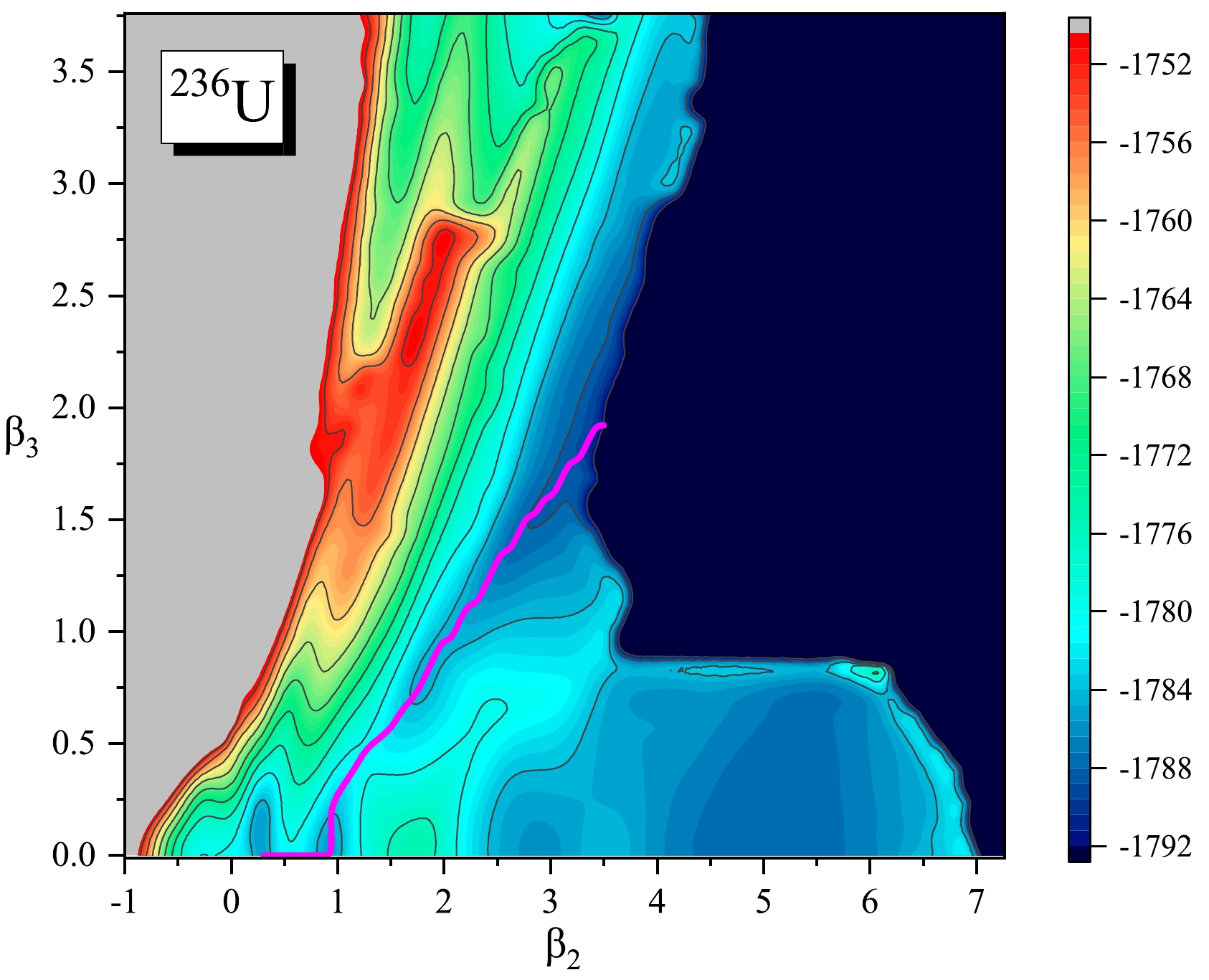
Figure 1. (color online) Potential energy surface of
$^{236}$ U in the$(\beta_{2}, \beta_{3})$ plane calculated using constrained CDFT with the PC-PK1 functional. The solid magenta line denotes the optimal fission path in the$(\beta_2, \beta_3)$ plane. The energy difference between neighboring contour lines is 4.0 MeV.Visualizing a 3D PES is a difficult task that can be facilitated if one of the variables is fixed and the PES for the remaining two variables is plotted as a contour plot. Such a procedure is followed, as shown in Fig. 2, for
$ ^{236} $ U, where sections of the PES for fixed values of$ \beta_3 $ are presented as maps in the$ (\beta_2, q_N) $ space. Here, we mainly focus on the region from saddle to scission. The solid magenta lines and star symbols denote the optimal fission paths and corresponding scission points in the$ (\beta_2, q_N) $ planes, respectively. Overall, the PES descends toward large elongation and a thin neck, as shown by the solid magenta lines. Remarkably, the PES broadens to form a wide "estuary" in the$ (\beta_2, q_N) $ subspace for$ q_N<6 $ ; the energy surface is shallow across a large range of quadrupole deformations. We check whether this wide "estuary" also exists in the$ (\beta_3, q_N) $ subspace for small$ q_N $ . This should manifest itself as a sizable broadening of the yields and total kinetic energies, which is presented in detail in Fig. 4.
Figure 2. (color online) Contour plots for the sections of the 3D PES of
$ ^{236} $ U. In each panel, the energy is shown as a function of$ \beta_2 $ and$ q_{N} $ when$ \beta_{3} $ is fixed at a certain value. The solid magenta lines and star symbols denote the optimal fission paths in the$ (\beta_2, q_N) $ planes and the corresponding scission points defined by$ q_N=2 $ , respectively. The energy difference between neighboring contour lines is 2.0 MeV.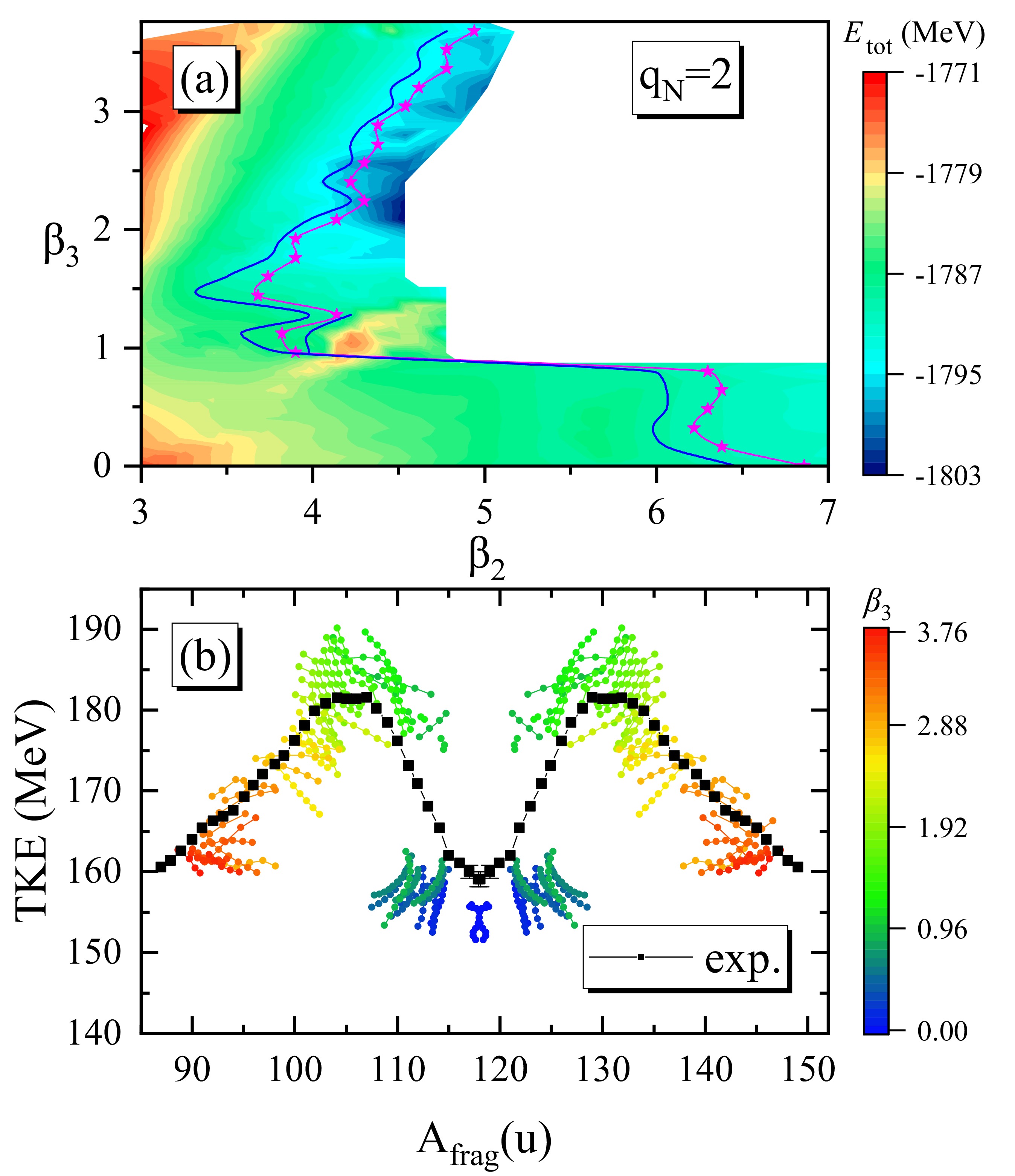
Figure 4. (color online) (a) Contour plot for the section of the 3D PES with fixed
$q_N=2$ . The solid magenta line denotes the optimal scission line, the star symbols on which correspond to the optimal scission points, as shown in Fig. 2. The solid blue lines denote configurations with energies equal to$E_\star+1$ MeV, where$E_\star$ is the total binding erergy of the star symbol. (b) Calculated Coulomb energies between two fragments using Eq. (8) to estimate the TKEs for configurations with energies lower than$E_\star+1$ MeV, denoted by the solid blue lines in panel (a). The dot colors indicate the variation in$\beta_3$ of the configurations, with blue to red corresponding to$\beta_3$ from$0.00$ to$3.76$ . The experimental TKE distribution for the thermal neutron induced fission of$^{235}$ U [56] is shown for comparison.Specifically, for
$ \beta_3\lesssim 0.80 $ , the 2D PESs in the$ (\beta_2, q_N) $ plane are all extended to large quadrupole deformations,$ \beta_2>6.0 $ , and the density distribution for one of the configurations is shown in Fig. 3(a). Evidently, both the fissioning nucleus and its pre-fragments are greatly elongated. As the asymmetric octupole deformation$ \beta_3 $ increases to 0.96, two fission valleys corresponding to the compact and elongated fission modes coexist and are separated by a shallow ridge. The optimal fission mode is the compact one, whose density distribution is also illustrated in Fig. 3(b). It is well known that the compact mode is driven by the double shell closure$ Z=50 $ and$ N=82 $ . The coexistence of these two fission valleys lasts until$ \beta_3=1.28 $ , which corresponds to the end of the ridge that separates the symmetric and asymmetric fission valleys in the 2D PES in Fig. 1. When$ \beta_3>1.44 $ , the pattern of the contour plots is similar, but only the optimal fission paths shift to larger$ \beta_2 $ . There are mainly two fission modes in this region, the compact one shown in Fig. 3(b) for$ \beta_3\lesssim 2.0 $ , and the one shown in Fig. 3(c) characterized by octupole-deformed pre-fragments [55] for the region with larger$ \beta_3 $ .
Figure 3. (color online) Density distributions of
$^{236}$ U for the configurations with$q_N=2$ and$(\beta_2, \beta_3) = (6.22, 0.80)$ (a), (3.90, 0.96) (b), and (3.90, 2.08) (c).To demonstrate the impact of the additional degree of freedom
$ q_N $ on the scissions and consequent fragment masses and TKEs, we present the contour plot for the section of the 3D PES with fixed$ q_N=2 $ and the calculated Coulomb energies between two fragments for the configurations around the optimal scission line in Fig. 4. In panel (a), we find that the energy surface is shallow around the optimal scission line (solid magenta line) for both the symmetric and asymmetric fission valleys. Within$ \pm 1 $ MeV, the quadrupole and octupole deformations can even extend to$ \sim 0.5 $ unit. This will certainly broaden the distributions of the yields and TKEs, which is quantitatively estimated in Fig. 4(b). We show the calculated Coulomb energies between two fragments using Eq. (8) to estimate the TKEs for configurations with energies lower than$ E_\star+1 $ MeV, considering the fluctuation of the collective current in the dynamical process [57]. For a certain fragment partitioning, the estimated TKE can fluctuate by approximately several to ten MeV or more at the mass of the heavy fragment$ A_{\rm H}\sim 132 $ . Moreover, for$122\lesssim A_{\rm H}\lesssim 128$ , note that lower-than 160 MeV and higher-than 178 MeV are simultaneously obtained owing to the coexistence of the elongated and compact fission modes in the region with$0.9\lesssim \beta_3\lesssim 1.3$ (c.f. Fig. 2). The measured TKE may be an average of those of different fission modes with corresponding probabilities. Finally, we would like to emphasize that, for asymmetric fission with$ A_{\rm H}>130 $ , the broadening of the energy surface around the scission can lead to a fluctuation of the fragment masses by several to approximately ten nucleons, which is consistent with the width of the asymmetric peak of the yield distribution in the actinides. -
In summary, we perform a fully 3D calculation to generate the PES for the fission of the compound nucleus
$ ^{236} $ U using constrained covariant DFT with constraints on the axial quadrupole and octupole deformations$ (\beta_2, \beta_3) $ as well as the nucleon number in the neck$ q_N $ . By considering the additional degree of freedom$ q_N $ , coexistence of the elongated and compact fission modes is predicted for$ 0.9\lesssim \beta_3 \lesssim 1.3 $ , and remarkably, the PES broadens to form a wide "estuary" in the$ (\beta_2, q_N) $ subspace for$ q_N<6 $ ; the energy surface is shallow across a large range of quadrupole deformations. This wide "estuary" also exists in the$ (\beta_3, q_N) $ subspace for small$ q_N $ . Therefore, the scission line in the$ (\beta_2, \beta_3) $ plane extends to a shallow band and hence leads to fluctuations of several to ten MeV in the estimated TKE and of several to approximately ten nucleons in the fragment masses. Certainly, this is a simple estimation of the fluctuation of the fission observables. More precise calculations should be performed by investigating the dynamical evolution of the collective wave packet on the 3D PES, for example, using the time-dependent generator coordinate method [58]. Such research is in progress.
Three-dimensional potential energy surface for fission of 236U within covariant density functional theory
- Received Date: 2023-02-06
- Available Online: 2023-06-15
Abstract: We calculate the three-dimensional potential energy surface (PES) for the fission of the compound nucleus





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: