-
Atomic nuclei are complicated many-body systems composed of protons and neutrons. With exact treatment of all correlations among valence nucleons, the spherical shell model (SM) is able to provide a good description of not only the low-lying states of spherical nuclei but also those of transitional and deformed nuclei (see, for example, Refs. [1–6]). In addition, it has been shown that collective motions also emerge in the description of the no-core shell model for light nuclei [7–9]. Yet, for most transitional and deformed nuclei in the medium-heavy and heavy regions, the full SM space is too large, which prohibits diagonalization.
Owing to the attractive and short-range characteristics of effective nucleon-nucleon interactions, the pairing correlation plays a crucial role in atomic nuclei and nuclear matter [10], and low-energy nucleon pairs are believed to be key building blocks for the low-lying states of nuclei [11]. Significant efforts have been devoted to various pair-truncation schemes, such as BCS theory [12–16] and the generalized seniority scheme [17, 18], where the spin-0 S-pair correlation is emphasized, and the interacting boson model (IBM) [19–23], where collective spin-0 S and spin-2 D pairs are represented by
$ sd $ bosons. The nucleon-pair approximation (NPA) [24, 25] is also a pair-truncation scheme. In the NPA, collective nucleon pairs with arbitrary spins can be adopted to build the configuration space and are treated exactly in the technique [26, 27]. When all possible pairs are considered, the NPA results are exactly equivalent to the SM results; when only a few selected pairs are considered, the SM space is efficiently truncated.The structures of collective pairs play a crucial role in the validity of pair truncations. In the NPA, pair structures are usually determined within the generalized seniority scheme, or in a scheme where the S-pair structure is defined based on a spherical BCS state and the D pair is taken to be the two-particle state corresponding to the quadrupole excitation out of the S pair [28, 29]. For spherical nuclei, that is, semi-magic nuclei and open-shell nuclei close to doubly-magic nuclei, it has been shown that using one set of collective pairs whose structures are defined within the generalized seniority scheme, the SM wave functions of different low-lying states can be represented by corresponding NPA wave functions [30, 31] and furthermore well approximated to be one-dimensional pair states [32–34].
For transitional and deformed nuclei, the quadrupole collectivity has (well) developed, and its interplay with the pairing correlation is key for a good description of the low-lying states of these nuclei. Recently, the three approaches outlined below were presented to optimize the structures of coupled collective pairs. Using these, improved descriptions of the low-lying states of transitional and deformed nuclei were achieved. First, collective pairs are defined based on a Hartree-Fock state [35, 36]; second, collective pairs are defined based on a condensate of uncoupled collective pairs [37, 38]; and third, pair structures are numerically optimized to give the energy minimum for the ground state in the NPA calculation [39].
Yet, one fundamental question remains unanswered, that is, whether the structures of relevant collective pairs are robust throughout low-lying yrast states. In this study, we investigate the robustness of pair structures along the yrast lines of deformed and transitional nuclei. For each yrast state, we consider optimized pair structures to be those providing the energy minimum for the state. To find the minimum, many full NPA calculations with varying pair structures are performed, and the numerical optimization procedure of the conjugate gradient method is implemented. This paper is organized as follows: In Sec. II, we give a brief introduction to our theoretical framework, including pair basis states and the SM Hamiltonian with an effective interaction. Sec. III presents and discusses our results. In Sec. IV, we summarize our study.
-
We start with the definition of a collective nucleon pair. The creation operator of a collective pair with spin r is defined by
$ \begin{aligned}[b] A^{(r) \dagger} \equiv A^{(r) \dagger}_{\mu} = \sum\limits_{j_1j_2} y(j_1j_2r) A^{(r) \dagger} (j_1j_2) \; , \end{aligned} $

$ \begin{aligned}[b]A^{(r) \dagger} (j_1j_2) \equiv A^{(r) \dagger}_{\mu} (j_1j_2) = \left( a^\dagger_{j_1} \times a^\dagger_{j_2} \right)^{(r)}_{\mu}\; , \end{aligned} $

(1) where
$ A^{(r) \dagger} (j_1j_2) $ is a non-collective pair, and$\left(a^\dagger_{j_1} \times a^\dagger_{j_2} \right)^{(r)}_{\mu}= \sum_{m_1 m_1} C^{r \mu}_{j_1 m_1 j_2 m_2}a^\dagger_{j_1m_1} a^\dagger_{j_2m_2}$ , with$ C^{r \mu}_{j_1 m_1 j_2 m_2} $ as the Clebsch-Gordan coefficient. Here, we denote the creation operator of a particle in the orbit associated with the quantum numbers$ (n,l,j,m) $ using$ a_{j m}^\dagger \equiv a_{n l j m}^\dagger $ . A collective pair creation operator$ A^{(r) \dagger} $ is given by the linear combination of all non-collective pairs with spin r.$ y(j_1j_2r) $ are the so-called structure coefficients, which define the structure of the collective pair.Pair basis states are constructed by coupling nucleon pairs successively. For a system with
$ 2N $ identical valence nucleons, the pair basis state is given by$ \begin{eqnarray} [ ( A^{(r_1) \dagger} \times A^{(r_2) \dagger} )^{(J_2)} \times \cdots \times A^{(r_N) \dagger} ]^{(J_N)}|0\rangle\; . \end{eqnarray} $

(2) -
The shell-model Hamiltonian with an effective interaction is given in a form with isospin symmetry,
$ \begin{aligned}[b] H =& \sum \limits_{j} \varepsilon_{j} N_{j} + \sum \limits_{j_1\leq j_2} \sum \limits_{j_3\leq j_4} \sum \limits_{J M} \sum \limits_{T M_T} \frac{V_{JT}(j_1 j_2 j_3 j_4)}{\sqrt{(1+\delta_{j_1 j_2})(1+\delta_{j_3 j_4})}} \\ & \times A^{(JT) \dagger}_{MM_T}(j_1 j_2) A^{(JT)}_{MM_T}(j_3 j_4)\; . \\ \end{aligned} $

(3) Here,
$ N_j=\sum_{m\tau} a^\dagger_{jm\frac{1}{2}\tau} a_{jm\frac{1}{2}\tau} $ , with τ as the isospin projection of the orbit. The pair creation operator with both good spin J and isospin T is given by$ \begin{aligned}[b] & A^{(JT) \dagger}_{MM_T}(j_1 j_2) = \sum \limits_{m_1 m_2} \sum \limits_{\tau_1 \tau_2} C_{j_1m_1j_2m_2}^{JM} C_{\frac{1}{2}\tau_1 \frac{1}{2}\tau_2}^{T M_T} a_{j_1m_1\frac{1}{2}\tau_1}^{\dagger} a_{j_2m_2\frac{1}{2}\tau_2}^{\dagger}\; . \end{aligned} $

$ \varepsilon_{j} $ are single-particle energies, and$ V_{JT}(j_1 j_2 j_3 j_4) $ are normalized two-body interaction matrix elements.In the NPA calculation, we decompose the above SM Hamiltonian into proton, neutron, and proton-neutron parts, that is,
$ \begin{aligned}[b]\\& H = \sum \limits_{\sigma=\pi,\nu} H_\sigma + H_{\pi\nu}\; , \\& H_\sigma = \sum \limits_j \varepsilon_j n_{j_\sigma} + \sum \limits_{j_{1\sigma}\leq j_{2\sigma}} \sum \limits_{j_{3\sigma}\leq j_{4\sigma}} \sum\limits_J \frac{V_{JT=1}(j_1 j_2 j_3 j_4)}{\sqrt{(1+\delta_{j_1j_2})(1+\delta_{j_3j_4})}} \hat{J} \left( A^{(J) \dagger} (j_{1\sigma} j_{2\sigma}) \times \tilde{A}^{(J)} (j_{3\sigma} j_{4\sigma}) \right)^{(0)}\; , \end{aligned} $ 
$ \begin{aligned}[b] & H_{\pi\nu} = -\sum \limits_{j_{1\pi} j_{2\nu} j_{3\pi} j_{4\nu}} \sum \limits_{J} V^{\pi\nu}_{J}(j_{1\pi} j_{2\nu} j_{3\pi} j_{4\nu}) \hat{J} \left( ( a^{\dagger}_{j_{1\pi}} \times a^{\dagger}_{j_{2\nu}} )^{(J)} \times ( \tilde{a}_{j_{3\pi}} \times \tilde{a}_{j_{4\nu}} )^{(J)} \right)^{(0)}\; , \\ & V^{\pi\nu}_{J}(j_{1\pi} j_{2\nu} j_{3\pi} j_{4\nu}) = \frac{1}{2} \left( V_{JT=1}(j_1 j_2 j_3 j_4)+V_{JT=0}(j_1 j_2 j_3 j_4) \right) \sqrt{(1+\delta_{j_1j_2})(1+\delta_{j_3j_4})}\; . \end{aligned} $

(4) Here,
$ n_{j} = \displaystyle\sum_{m} a_{j m}^{\dagger} a_{j m} $ ,$ \hat{J}=\sqrt{2J+1} $ , and for the time-reversed operator of single-particle (or pair) destruction, we use the convention$ \tilde{a}_{j m}=(-)^{j-m} a_{j,-m}\; $ . To calculate the matrix elements of$ H_{\pi\nu} $ in the NPA, we further express$ H_{\pi\nu} $ in terms of proton-neutron multipole-multipole interactions. Denoting$ j_{1\pi}\equiv j_\pi $ ,$ j_{2\nu}\equiv j_\nu $ ,$ j_{3\pi}\equiv j_\pi' $ , and$ j_{4\nu}\equiv j_\nu' $ , we have$ \begin{eqnarray} H_{\pi\nu}= \sum \limits_{j_\pi j_\pi'} \sum \limits_{j_\nu j_\nu'} \sum \limits_{k} \left( \sum \limits_{J} (-)^{J+j_\nu+j_\pi'} (2J+1) \left\{ \begin{array}{ccc} j_\pi & j_\nu & J \\ j_\nu' & j_\pi' & k \end{array} \right\} V^{\pi\nu}_{J}(j_\pi j_\nu j_\pi' j_\nu') \right) (-)^k \hat{k} \left( Q^{(k)} (j_\pi j_\pi') \times Q^{(k)} (j_\nu j_\nu') \right)^{(0)}\; . \end{eqnarray} $ 
(5) Here,
$ Q^{(k)} (j_\sigma j_\sigma')=(a^\dagger_{j_\sigma} \times \tilde{a}_{j'_\sigma})^{(k)} $ , and$ \{^{j_\pi \; \; j_\nu \; \; J} _{j_\nu' \; \; j_\pi' \; \; k}\} $ is the 6j-symbol. -
In this study, we investigate the robustness of pair structures for nuclear yrast states, that is, whether the structures of relevant collective pairs as building blocks of different yrast states are the same. We focus on deformed and transitional nuclei because the pattern for spherical nuclei can be inferred from previous studies [30–34]. We investigate the yrast states of three selected examples,
$ ^{28} $ Si,$ ^{50} $ Cr, and$ ^{132} $ Xe, using the NPA and (realistic) effective SM interactions.$ ^{28} $ Si,$ ^{50} $ Cr, and$ ^{132} $ Xe have experimental$ R_{4/2} $ values of 2.60, 2.40, and 2.16, respectively, and are thus expected to represent nuclei with different degrees of quadrupole collectivity. Meanwhile, the valence particles of these three nuclei reside in different major shells, that is, the$ 0d1s $ shell,$ 0f1p $ shell, and 50–82 shell consisting of$ 0g_{7/2}1d2s $ orbits and the$ 0h_{11/2} $ intruder orbit.For each nucleus, we perform two sets of NPA calculations, denoted as NPA-1 and NPA-2. Considering collective pairs with given spins and parities,
● in NPA-1, pair structures are optimized with regard to each yrast state and then adopted to build the NPA wavefunction of the corresponding yrast state;
● in NPA-2, pair structures are optimized with regard to the ground state and then adopted to build the NPA wavefunctions of all considered yrast states.
We compare the results of the NPA-1 and NPA-2 calculations, and calculate explicit overlaps between the two sets of NPA wavefunctions. In doing so, we study whether the optimized pair structures of each yrast state remain unchanged in comparison with those optimized with respect to the ground state. We also present available SM results for comparison.
We denote the state with respect to which pair structures are optimized, to be the reference state. The energy of the reference state (denoted as
$ E^{\rm ref.} $ ) can be regarded as a function of the structure coefficients of all adopted pairs,$ \begin{eqnarray} E^{\rm ref.}(y_1,y_2,...,y_n)\; , \end{eqnarray} $

(6) because the NPA wave function and corresponding energy for a state are obtained via diagonalization in the configuration space spanned by the nucleon-pair basis states in the form of Eq. (2). Here,
$ y_i $ denotes the ith pair-structure coefficient. We consider optimized pair-structure coefficients to be those providing the energy minimum for the reference state because the reference state is taken to be a yrast state in all cases in this study. Similar to the numerical procedure of Ref. [39], with which pair structures were optimized with respect to the ground state, in this study, to find the minimum$ E^{\rm ref.} $ for each reference state, many full NPA calculations with varying$ y_1,y_2,...,y_n $ are performed, and the numerical optimization process of the conjugate gradient method [40] is implemented. -
We start with
$ ^{28} $ Si and$ ^{50} $ Cr. For$ ^{28} $ Si, we use the USDB effective interaction of the$ 0d1s $ shell [41], and for$ ^{50} $ Cr, we use the KB3G effective interaction of the$ 0f1p $ shell [42]. For the two nuclei, we consider$ SDG $ pairs for both the proton and neutron parts in the NPA calculations, and the pair structures are determined as previously described.We first discuss the yrast states of
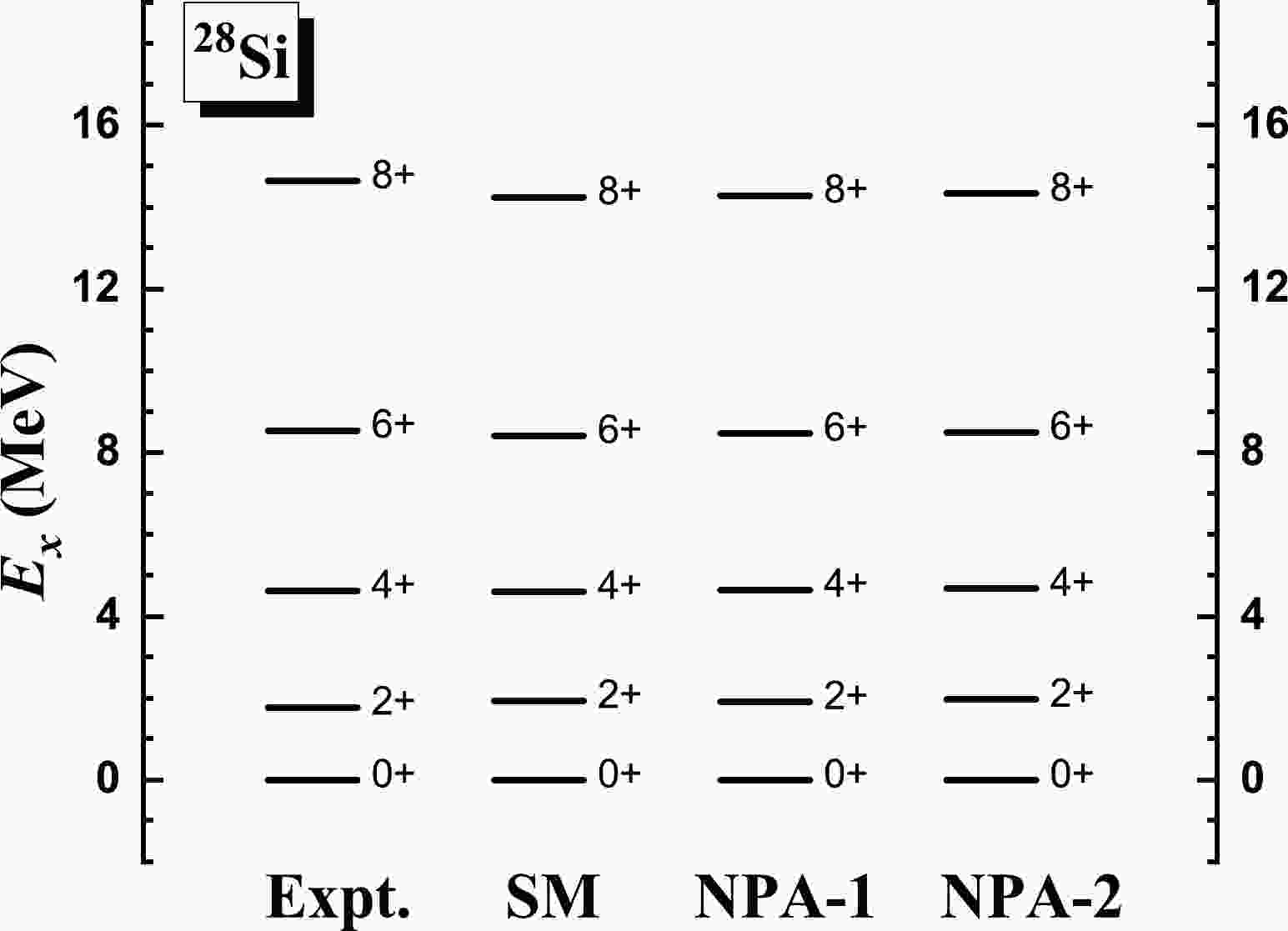
$ ^{28} $ Si, whose experimental$ R_{4/2} $ is 2.60. In Fig. 1, we present the calculated excitation energies of the yrast states of$ ^{28} $ Si given by the NPA-1 and NPA-2 calculations, in comparison with experimental data [43]. We also perform an SM calculation for$ ^{28} $ Si, in which all possible pairs are adopted to construct the full valence space. In Fig. 2, we present the theoretical and experimental results of the$ E2 $ transition energies. In Table 1, we present the quadrupole moments given by the three sets of calculations as well as available experimental data [43]. The effective charges are taken to be the standard values$ e_\pi=1.5e $ and$ e_\nu=0.5e $ . As shown in Figs. 1 and 2 and Table 1, the results given by the SM, NPA-1, and NPA-2 calculations are close to each other. Moreover, as shown in Figs. 1 and 2, the experimental excitation and transition energies are well reproduced by the three sets of calculations.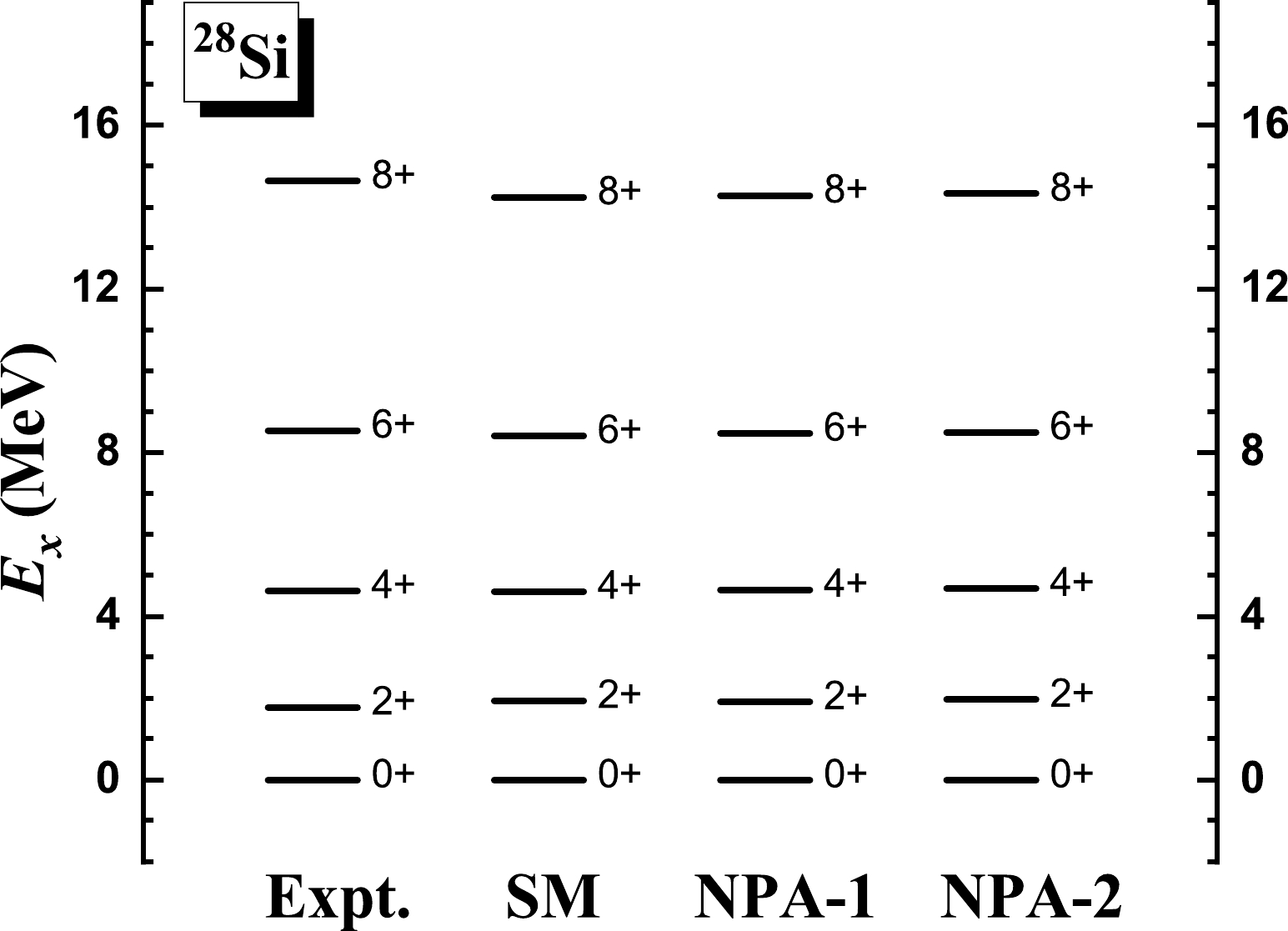
Figure 1. Excitation energies given by the NPA-1 and NPA-2 calculations, in comparison with experimental data [43] and the SM results, for the yrast states of
$ ^{28} $ Si. In NPA-1, the structures of the adopted$ SDG $ pairs are optimized with regard to each yrast state and then used to build the corresponding yrast state. In NPA-2, the pair structures are optimized with regard to the ground state and then adopted to build all the considered yrast states. In the SM calculation, all possible pairs are adopted to construct the full valence space. The USDB effective interaction [41] is used in the three sets of calculations.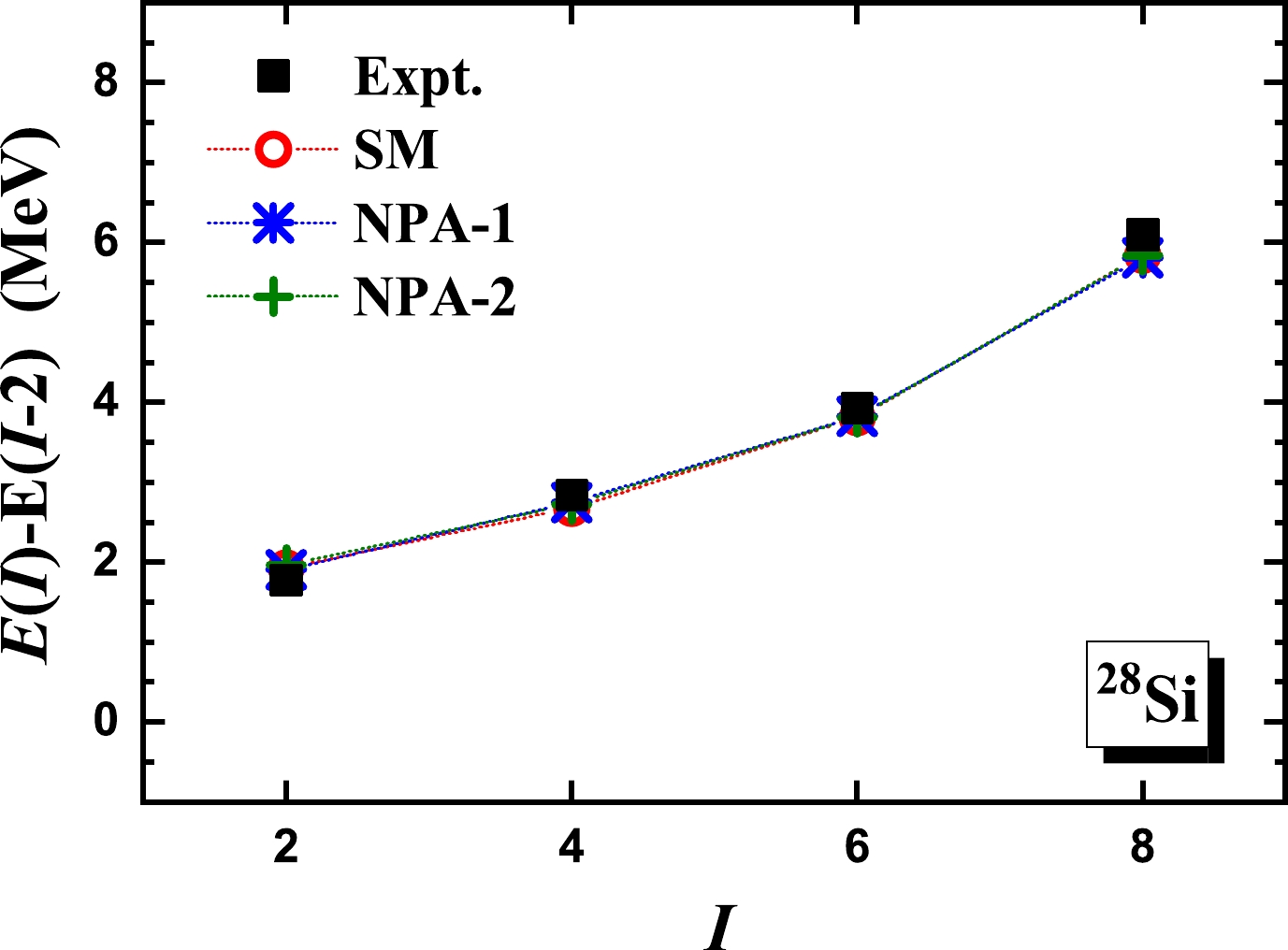
Figure 2. (color online)
$ E2 $ transition energy, denoted as$ E(I)-E(I-2) $ , versus the spin of the initial state I, given by the NPA-1 and NPA-2 calculations, in comparison with experimental data [43] and the SM results, for the yrast states of$ ^{28} $ Si.Expt. SM NPA-1 NPA-2 Q $Q^{\rm intr.}$ 

Q $Q^{\rm intr.}$ 

Q $Q^{\rm intr.}$ 

Q $Q^{\rm intr.}$ 

$2^+_1$ 

16(3) −56(11) 20.9 −73.2 21.3 −74.4 21.0 −73.6 $4^+_1$ 

$-$ 

$-$ 

25.6 −70.4 26.1 −71.9 25.7 −70.8 $6^+_1$ 

$-$ 

$-$ 

31.6 −78.9 31.8 −79.5 31.6 −79.0 $8^+_1$ 

$-$ 

$-$ 

29.1 -69.1 30.3 -72.0 29.5 -70.1 Table 1. Quadrupole moments Q and intrinsic quadrupole moments
$ Q^{\rm intr.} $ (both in units of efm$ ^2 $ ) given by the NPA-1 and NPA-2 calculations, as well as the SM results and available experimental data [43] for the yrast states of$ ^{28} $ Si. In the three sets of calculations, the effective charges are taken to be the standard values$ e_\pi=1.5e $ and$ e_\nu=0.5e $ . Based on the Q value, Eq. (8) is used inversely with$ K=0 $ to obtained the$ Q^{\rm intr.} $ value.Now, we discuss the yrast states of
$ ^{28} $ Si from the perspective of collective rotation. In the description of the rotation of an axially symmetric nucleus, energies of states within a$ K=0 $ band (with K denoting the angular-momentum projection of the intrinsic state along the intrinsic symmetry axis) follow the pattern below (see, for example, Ref. [44]).$ \begin{eqnarray} E(I) = E_0 + \frac{\hbar^2}{2\mathcal{J}} I(I+1)\; , \end{eqnarray} $

(7) where
$ \mathcal{J} $ denotes the moment of inertia with respect to the rotation axis, which is perpendicular to the intrinsic symmetry axis. Furthermore, the observed quadrupole moments Q for states within a rotational band are related to the quadrupole moment of the intrinsic state (denoted as$ Q^{\rm intr.} $ ) as below (see, for example, Ref. [44]).$ \begin{eqnarray} Q(I)=\frac{3K^2-I(I+1)}{(I+1)(2I+3)}Q^{\rm intr.}\; . \end{eqnarray} $

(8) As shown in Figs. 1 and 2, for the yrast states of
$ ^{28} $ Si, the level structure, as well as the approximate linear behavior of the$ E2 $ transition energy versus the spin of the initial state, is consistent with Eq. (7). In addition, based on the quadrupole moment Q, we calculate the intrinsic moment$ Q^{\rm intr.} $ using Eq. (8) inversely and with$ K=0 $ . The results are presented in Table 1, where the$ Q^{\rm intr.} $ values given by the Q values of the$ 2^+_1 $ ,$ 4^+_1 $ ,$ 6^+_1 $ , and$ 8^+_1 $ states are close to each other. This suggests that the considered yrast states of$ ^{28} $ Si manifest as members of a rotational band.In Fig. 3, we present the explicit overlaps between the SM and NPA-1 wavefunctions, the SM and NPA-2 wavefunctions, and the NPA-1 and NPA-2 wavefunctions for the yrast states of
$ ^{28} $ Si. As shown, these overlaps are all close to 1. The overlaps between the SM and NPA-1 wavefunctions suggest that for the considered yrast states of$ ^{28} $ Si, the SM wavefunctions are well represented by the wavefunctions of$ SDG $ -pair approximation with optimized pair structures. It is worth noting that for a system with six neutrons and six protons in the$ sd $ shell, the result of Elliot's$ S U $ (3) model [45, 46] suggests two degenerate ground bands, which are shown in Ref. [47] to be exactly reproduced by$ SD $ -pair approximation and$ SDG $ -pair approximation. Yet, for the realistic case, that is, for$ ^{28} $ Si, G pairs are essential in reproducing the ground band of the SM result according to our calculation. In other words, such a degeneracy in Elliot's model is broken. In Fig. 3, the overlaps between the NPA-1 and NPA-2 wavefunctions suggest that for a deformed nucleus, optimized pair structures remain the same in all the states within a rotational band.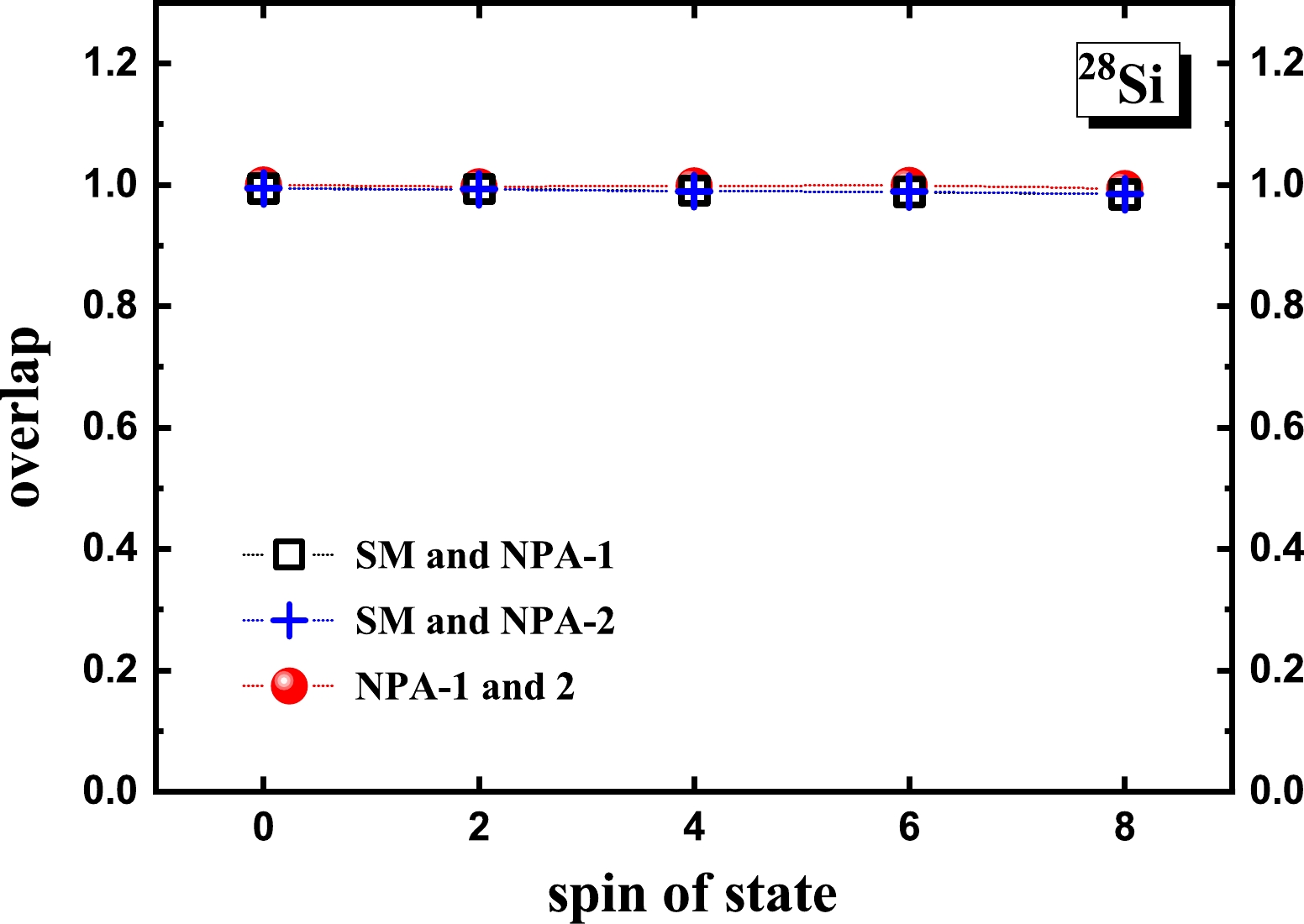
Figure 3. (color online) Overlaps between the SM and NPA-1 wavefunctions, the SM and NPA-2 wavefunctions, and the NPA-1 and NPA-2 wavefunctions, for the yrast states of
$ ^{28} $ Si.Next, we discuss the yrast states of
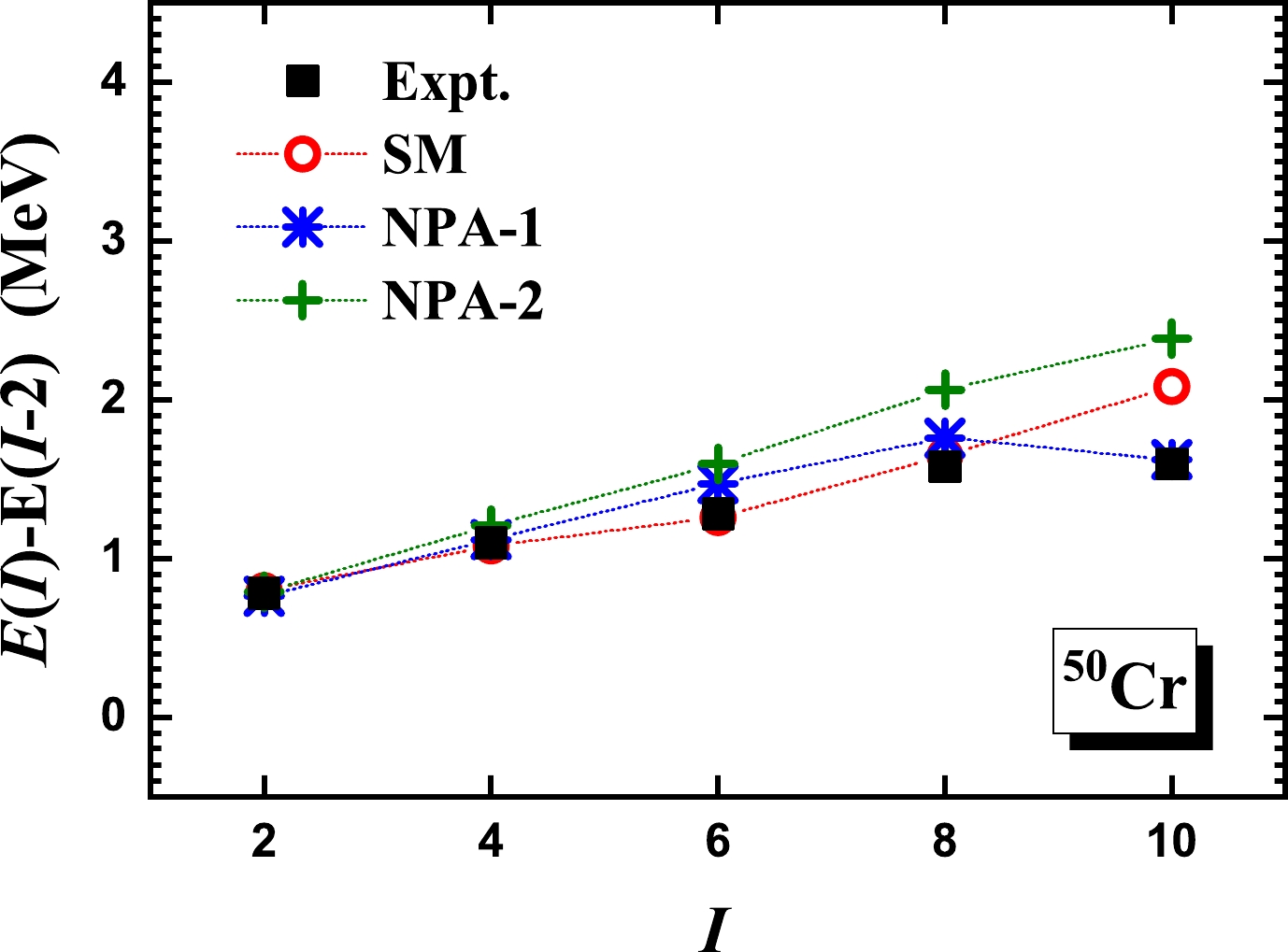
$ ^{50} $ Cr, whose experimental$ R_{4/2} $ is 2.40. In Figs. 4 and 5, we present the excitation and$ E2 $ transition energies given by NPA-1 and NPA-2, in comparison with experimental data [43] and the SM results of Ref. [36]. In Table 1, we present the quadrupole moments and corresponding intrinsic quadrupole moments given by the NPA-1 and NPA-2 calculations, as well as the SM results of Ref. [2] and available experimental data [43]. In the SM calculation of Ref. [36], the KB3G effective interaction was adopted, the same as in our NPA calculations. In the SM calculation of Ref. [2], the KB3 effective interaction [48] was adopted. The KB3 [48] and KB3G interactions [42] are two versions of the Kuo-Brown interaction [49] with small modifications. According to Ref. [42], the two interactions are approximately equivalent in describing the low-lying states of$ ^{50} $ Cr. For effective charges, the standard values, that is,$ e_\pi=1.5 e $ and$ e_\nu=0.5 e $ , are adopted in both our NPA calculations and the SM calculation of Ref. [2].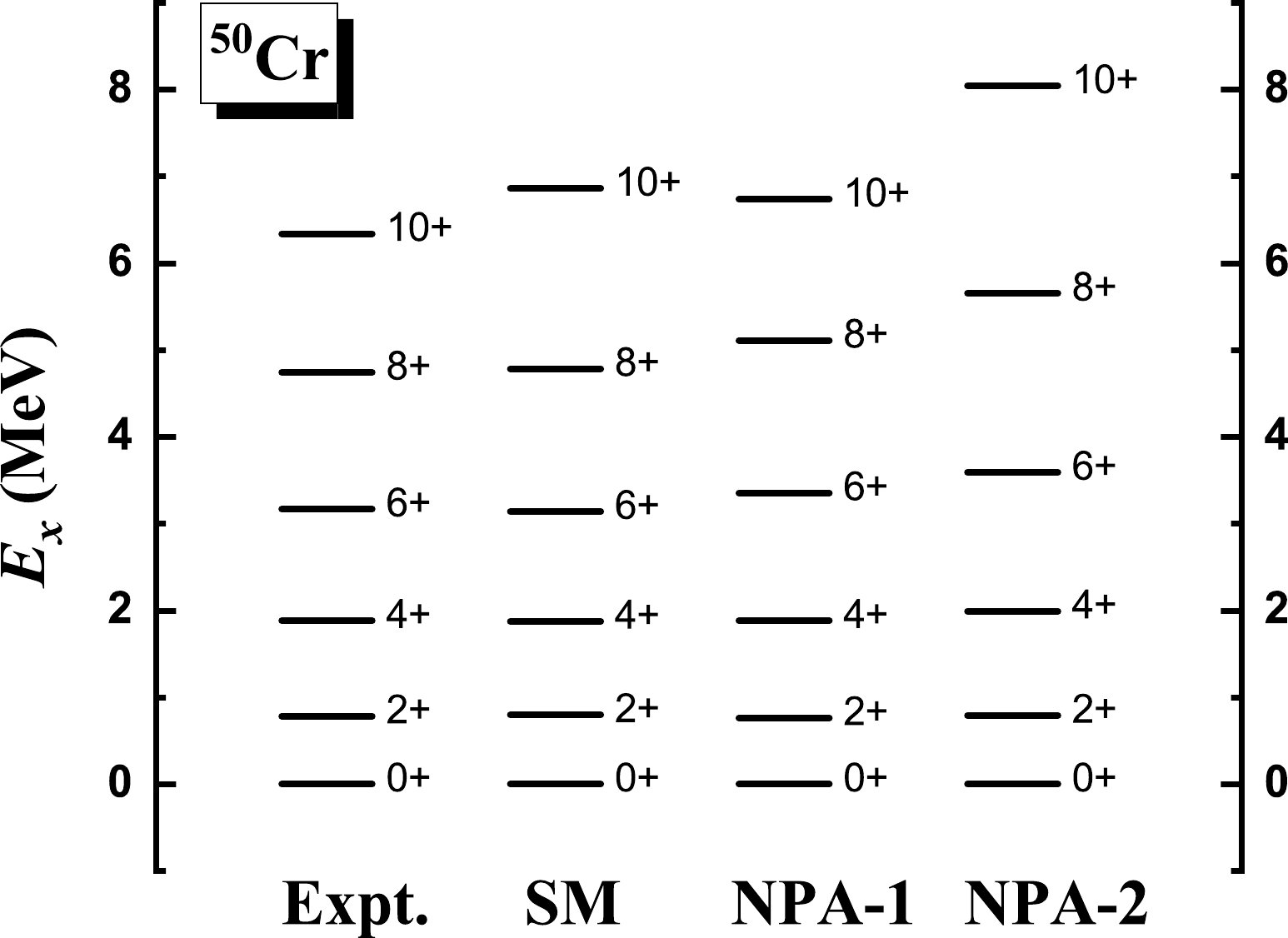
Figure 4. Excitation energies given by the NPA-1 and NPA-2 calculations, in comparison with experimental data [43] and the SM results [36], for the yrast states of
$ ^{50} $ Cr. The pair structures for$ ^{50} $ Cr in NPA-1 and NPA-2 are determined in the same ways as those for$ ^{28} $ Si. In both our NPA calculations and the SM calculation of Ref. [36], the KB3G effective interaction [42] is used.In Figs. 4 and 5, up to the
$ 8^+_1 $ state, the excitation and transition energies given by the three sets of calculations are close to each other, and the experimental data are well reproduced. In Table 2, the quadrupole moments given by NPA-1 are close to the SM results of Ref. [2], which indicates that the NPA-1 and SM wavefunctions should be close to each other.Expt. SM NPA-1 NPA-2 Q $Q^{\rm intr.}$ 

Q $Q^{\rm intr.}$ 

Q $Q^{\rm intr.}$ 

Q $Q^{\rm intr.}$ 

$2^+_1$ 

−36(7) 126(25) −26.8 93.8 −30.3 105.9 −30.0 104.9 $4^+_1$ 

$-$ 

$-$ 

−33.1 91.0 −38.0 104.5 −38.2 105.1 $6^+_1$ 

$-$ 

$-$ 

−17.7 44.3 −37.6 94.0 −40.4 101.0 $8^+_1$ 

$-$ 

$-$ 

−17.1 40.6 −26.8 63.6 −40.0 95.0 $10^+_1$ 

$-$ 

$-$ 

23.7 −54.5 20.7 −47.6 −38.1 87.7 Table 2. Quadrupole moments Q and intrinsic quadrupole moments
$ Q^{\rm intr.} $ (both in units of efm$ ^2 $ ) given by the NPA-1 and NPA-2 calculations, as well as the SM results [2] and available experimental data [43], for the yrast states of$ ^{50} $ Cr. In the SM calculation of Ref. [2], the KB3 effective interaction [48] was adopted, which is approximately equivalent to the KB3G interaction [42] in describing the low-lying states of$ ^{50} $ Cr according to Ref. [42]. The standard effective charges$ e_\pi=1.5 e $ and$ e_\nu=0.5 e $ are adopted in both our NPA calculations and the SM calculation of Ref. [2]. Based on the Q value, the$ Q^{\rm intr.} $ value is obtained in the same way as that for$ ^{28} $ Si.As shown in Table 2, for the SM results [2] and our NPA-1 results, the
$ Q^{\rm intr.} $ value changes significantly, that is, the sign changes, at the$ 10^+_1 $ state. This indicates backbending at the$ 10^+_1 $ state in the two sets of descriptions, which is also consistent with the HFB description given in Ref. [2]. In contrast, for the NPA-2 results, the$ Q^{\rm intr.} $ value remains almost the same for all the yrast states up to$ |10^+_1\rangle $ , which indicates no backbending in the description given by NPA-2. In Fig. 6, we present the overlaps between the NPA-1 and NPA-2 wavefunctions. The overlaps are close to 1 for the yrast states up to$ |8^+_1\rangle $ . In contrast, the overlap for the$ 10^+_1 $ state is small, that is,$ \sim $ 0.45. Theses indicate that optimized pair structures remain the same in the states within a rotational band, which is consistent with the case of$ ^{28} $ Si discussed previously, whereas optimized pair structures change substantially when backbending occurs, that is, when the structure of the intrinsic state changes.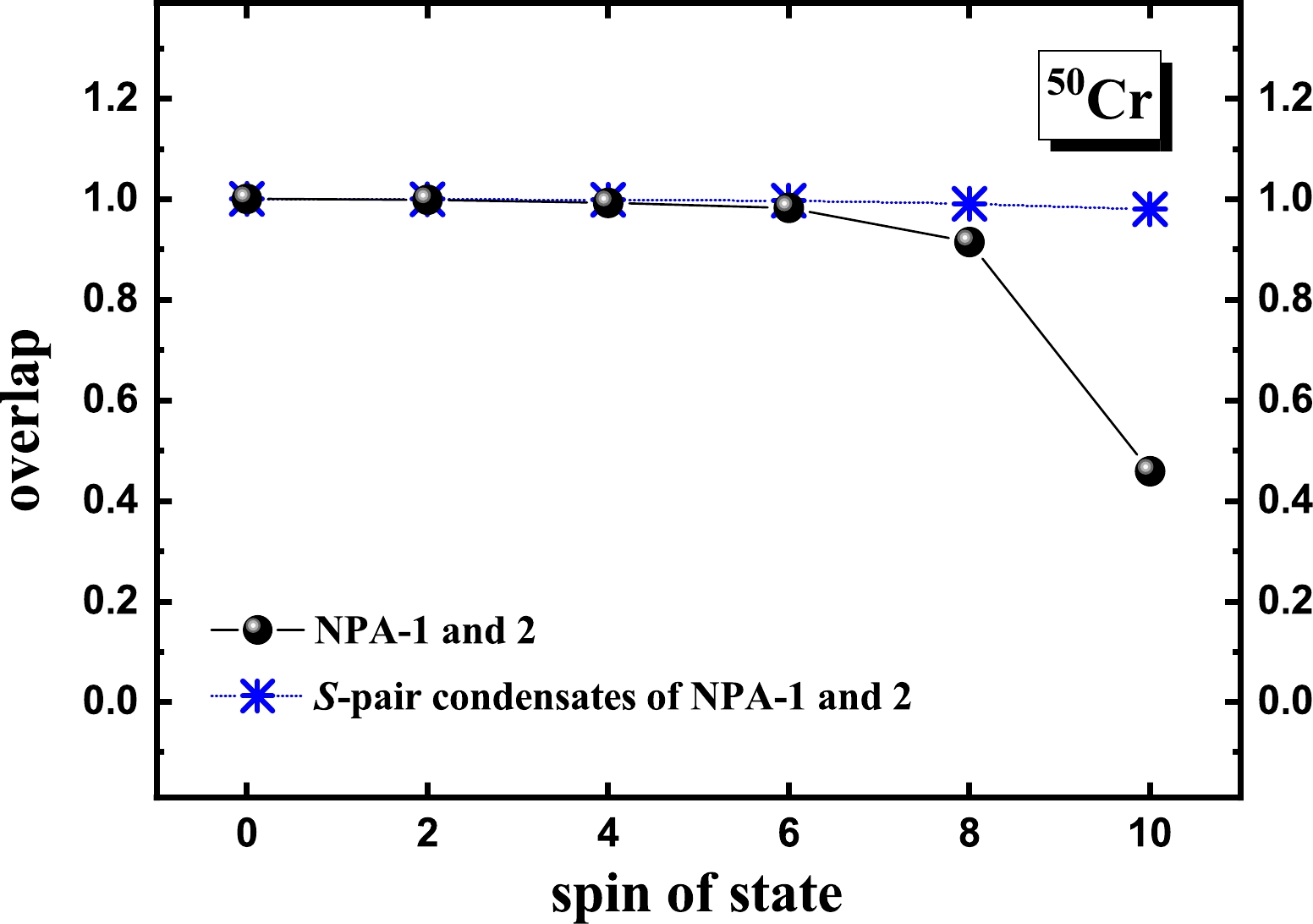
Figure 6. (color online) Overlap between the NPA-1 and NPA-2 wavefunctions for the yrast states of
$ ^{50} $ Cr, and the overlap between the S-pair condensate state constructed by the S pairs of NPA-1 and that constructed by the S pairs of NPA-2. For the latter, recall that in NPA-1, the structures of the$ SDG $ pairs are optimized to give the energy minimum for the reference state, and in NPA-2, the structures of the$ SDG $ pairs are optimized to give the energy minimum for the ground state. Here, the overlap between the two S-pair condensate states is presented versus the spin of the corresponding reference state in NPA-1.In Fig. 6, we also present the overlap between the S-pair condensate state constructed by the S pairs of NPA-1 and that constructed by the S pairs of NPA-2. Recall that in NPA-1, the structures of the
$ SDG $ pairs are optimized to give the energy minimum for the reference state and then used in building this reference state, whereas in NPA-2, the structures of the$ SDG $ pairs are optimized to give the energy minimum for the ground state and then used in building all the yrast states considered in this study. Here, the overlap between the two S-pair condensate states is presented versus the spin of the corresponding reference state in NPA-1. The results are all close to 1, suggesting that the structure of the S pair, which is the key to building the pairing correlation, remains the same along the entire yrast line. In other words, it is robust with regard to the change in the intrinsic state. -
Finally, we discuss the yrast states of
$ ^{132} $ Xe, whose experimental$ R_{4/2} $ value is 2.16. We present our NPA-1 and NPA-2 results in comparison with experimental data [5, 6, 43]. In the NPA calculations, the monopole-optimized effective interaction for the 50–82 major shell of Ref. [50], which is based on a G-matrix interaction [51] renormalized from the CD-Bonn potential [52], is adopted. For comparison, we also present the SM results of Refs. [5, 6], both of which adopted the$ jj55 $ interaction [53]. The$ jj55 $ interaction [53] is an effective interaction renormalized from the CD-Bonn potential [52] via the G-matrix and Q-box methods [51] successively, and with the Coulomb interaction additionally included.For the pair configuration space, we consider collective
$ SDG $ pairs for both the proton and neutron parts. Because non-collective pairs coupled by two$ h_{11/2} $ neutron holes, particularly those with high spins, are important in building the low-lying states of nuclei in the$ ^{132} $ Sn region with$ N<82 $ [33, 37, 54–58], we adopt additional non-collective pairs of two$ h_{11/2} $ neutron holes with spins of$ 6, 8, 10 $ , that is,$ (a^\dagger_{h_{11/2}}\times a^\dagger_{h_{11/2}})^{(J)} $ with$ J=6, 8, 10 $ . For brevity, such non-collective pairs are denoted as H pairs. Note that the pair structures of collective pairs are optimized as described previously with the presence of the non-collective pairs, that is, the optimized collective$ SDG $ pairs and non-collective H pairs together provide the energy minimum for the reference state (ground state) in the NPA-1 (NPA-2) calculation.In Figs. 7 and 8, for the yrast states of
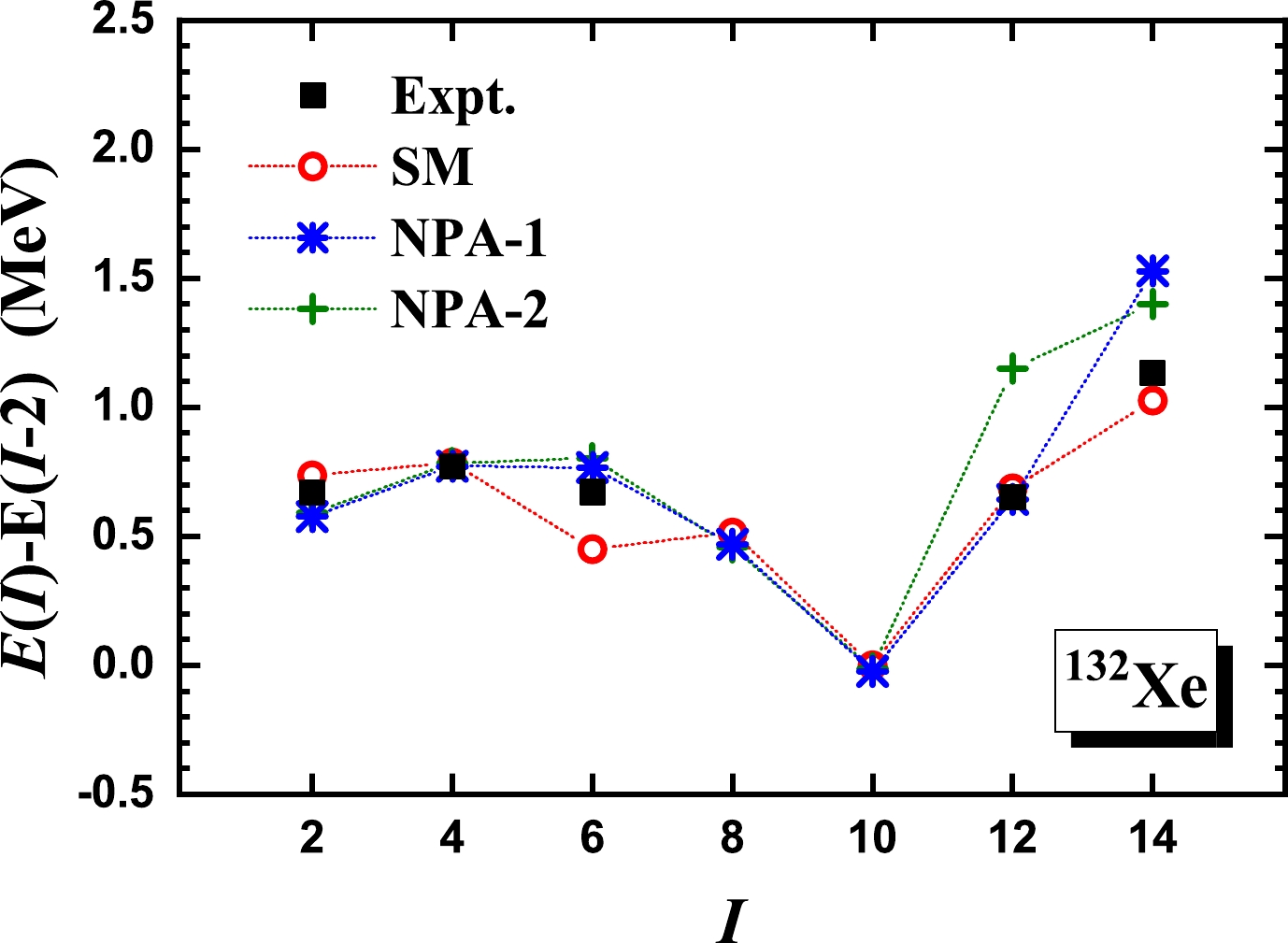
$ ^{132} $ Xe, we present the excitation and$ E2 $ transition energies given by NPA-1 and NPA-2, in comparison with experimental data [5, 43] and the SM results [5]. In Table 3, we present the$ B(E2) $ values and g factors for the yrast states given by NPA-1, in comparison with available experimental data [43] and the SM results [6]. The effective charges for$ B(E2) $ adopted in the NPA-1 calculation are$ e_{\pi}=1.5 e $ for valence protons and$ e_{\nu}=-0.68 e $ for neutron holes, and the orbital and spin g factors are taken to be$ g^l_{\pi}=1.13 \mu_N $ and$ g^s_{\pi}=5.586\times0.7 \mu_N $ for valence protons, and$ g^l_{\nu}=0 \mu_N $ and$ g^s_{\nu}=-3.826\times0.7 \mu_N $ for neutron holes. The effective charges and proton orbital g factor are optimized via fitting to available experimental data. As shown in Figs. 7 and 8, the experimental excitation energies and$ E2 $ transition energies are well reproduced by the NPA-1 calculation up to the$ 12^+_1 $ state. As shown in Table 3, the available experimental$ B(E2) $ values and g factors are reasonably well reproduced by our NPA-1 calculation and the SM calculation of Ref. [6].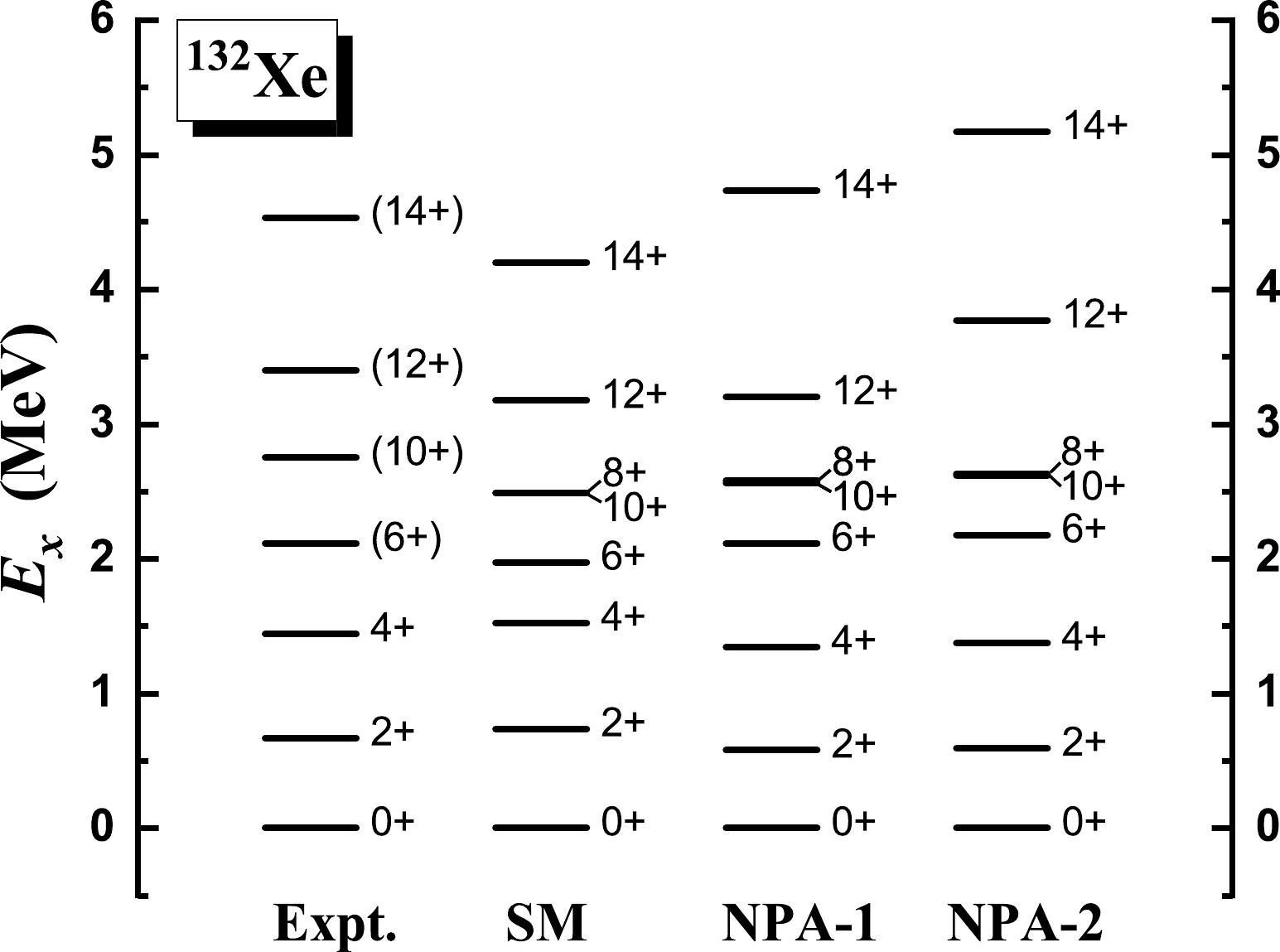
Figure 7. Excitation energies of the yrast states of
$ ^{132} $ Xe given by the NPA-1 and NPA-2 calculations, in comparison with experimental data [5, 43] and the SM results [5]. The collective$ SDG $ pairs and non-collective neutron-hole pairs,$(a^\dagger_{h_{11/2}}\times $ $ a^\dagger_{h_{11/2}})^{(J)}$ with$ J=6,8,10 $ , are adopted. For$ ^{132} $ Xe, with the presence of the non-collective pairs, the structures of the collective pairs in NPA-1 and NPA-2 are optimized in the same ways as those for$ ^{28} $ Si and$ ^{50} $ Cr. In our NPA calculations, the monopole-optimized realistic effective interaction of Ref. [50] is used. For the SM results taken from Ref. [5], the realistic effective interaction$ jj55 $ [53] is used.$B(E2)$ (W.u.)

Expt. SM NPA-1 $2^+_1\rightarrow0^+_1$ 

23.1(15) 24.4 18.5 $4^+_1\rightarrow2^+_1$ 

28.6(23) 35.1 31.7 g factor ( $\mu_N$ )

Expt. SM NPA-1 $2^+_1$ 

0.3255(120) 0.336 0.342 $4^+_1$ 

0.60(10) 0.407 0.328 $10^+_1$ 

(-)0.195(5) $-$ 

−0.213 Table 3.
$ B(E2) $ values (in units of W.u.) and g factors (in units of$ \mu_N $ ) for the yrast states of$ ^{132} $ Xe given by the NPA-1 calculation, in comparison with available experimental data [43] and the SM results [6]. The effective charges for$ B(E2) $ adopted in the NPA-1 calculation are$ e_{\pi}=1.5 e $ for valence protons and$ e_{\nu}=-0.68 e $ for neutron holes, and the orbital and spin g factors are taken to be$ g^l_{\pi}=1.13 \mu_N $ and$ g^s_{\pi}=5.586\times0.7 \mu_N $ for valence protons, and$ g^l_{\nu}=0 \mu_N $ and$ g^s_{\nu}=-3.826\times0.7 \mu_N $ for neutron holes. For the SM results taken from Ref. [6], neither the effective interaction nor the effective charges are the same as those adopted in this study.For transitional nuclei, one might expect a low-lying yrast state to be a mixture of spherical configurations and deformed ones. In Figs. 7 and 8, the results of NPA-1 indicate that the quadrupole collectivity develops in the
$ 2^+_1 $ ,$ 4^+_1 $ , and$ 6^+_1 $ states but deteriorates dramatically in the$ 8^+_1 $ and$ 10^+_1 $ states. After the$ 10^+_1 $ state, the quadrupole collectivity develops again in the$ 12^+_1 $ and$ 14^+_1 $ states. In other words, deformed configurations play an important role in the$ 2^+_1 $ ,$ 4^+_1 $ ,$ 6^+_1 $ ,$ 12^+_1 $ , and$ 14^+_1 $ states, whereas spherical configurations are dominant in the$ 8^+_1 $ and$ 10^+_1 $ states.In Fig. 9, we present the overlap between the NPA-1 and NPA-2 wavefunctions. The overlaps are all close to 1 up to the
$ 10^+_1 $ state, whereas for the$ 12^+_1 $ and$ 14^+_1 $ states, the overlaps decrease. Because pair structures are robust in different spherical states [30–34], we expect that the above decrease is due to the difference between the structures of pairs as building blocks of the important deformed configurations for the$ 12^+_1 $ and$ 14^+_1 $ states and those of pairs as building blocks of the important deformed configurations for the$ 2^+_1 $ ,$ 4^+_1 $ , and$ 6^+_1 $ states. In Fig. 9, we also present the overlap between the NPA-1 wavefunction and the wavefunction (denoted as NPA-1$ ' $ ) built solely by the$ SDG $ pairs of NPA-1, that is, without including the H pairs. These overlaps suggest that the non-collective H pairs are approximately irrelevant in the$ 2^+_1 $ ,$ 4^+_1 $ , and$ 6^+_1 $ states but are essential in the$ 12^+_1 $ and$ 14^+_1 $ states. This indicates that the important deformed configurations for the$ 12^+_1 $ and$ 14^+_1 $ states and those for the$ 2^+_1 $ ,$ 4^+_1 $ , and$ 6^+_1 $ states might correspond to two different intrinsic states. Then, we find that the results for the transitional$ ^{132} $ Xe nucleus is consistent with the previous conclusion drawn for the deformed$ ^{50} $ Cr nucleus, that is, the change in the optimized pair structures along the yrast line of a deformed nucleus arises from the change in the intrinsic state.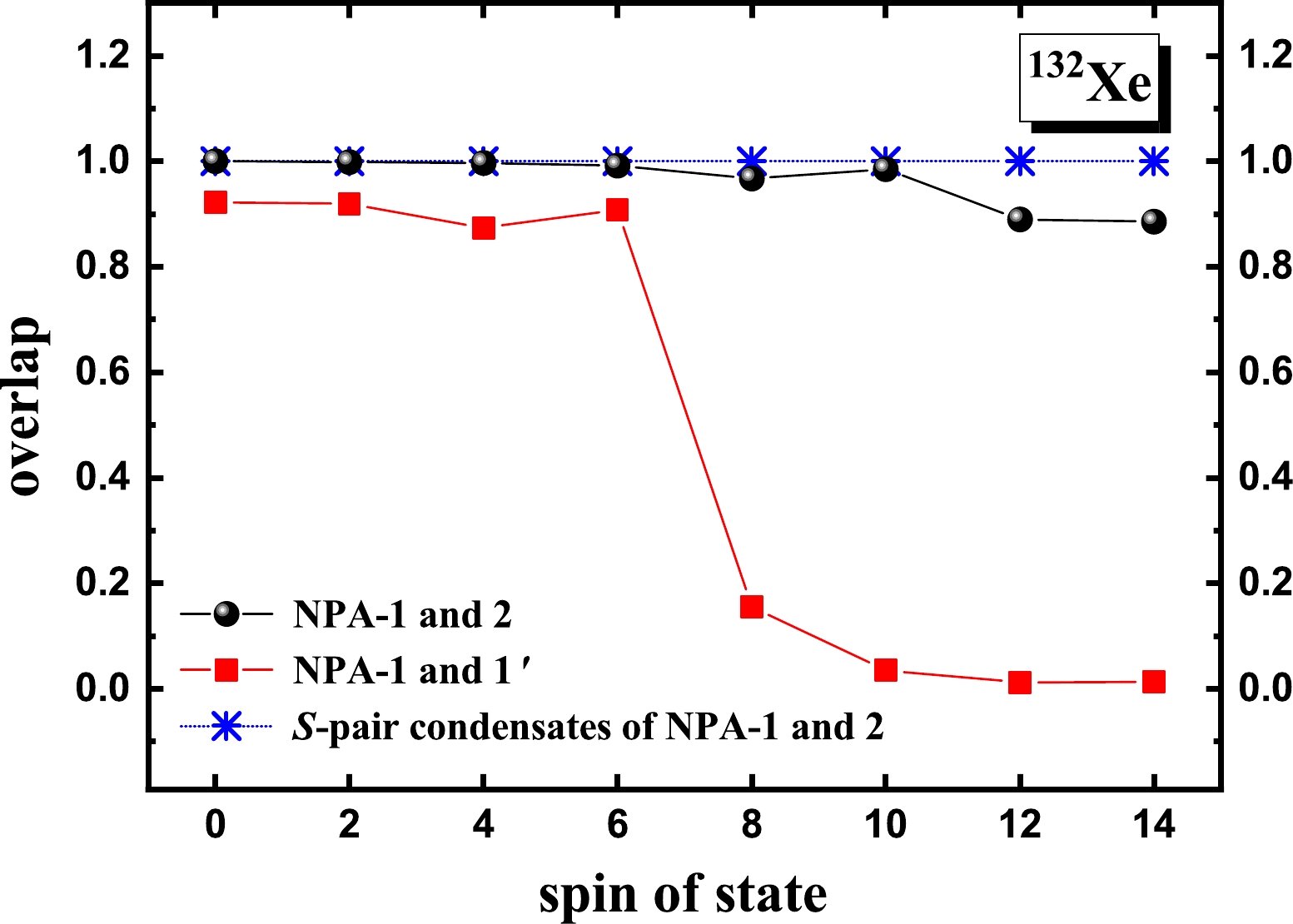
Figure 9. (color online) Overlap between the NPA-1 and NPA-2 wavefunctions, and the overlap between the NPA-1 and NPA-1
$ ' $ wavefunctions, for the yrast states of$ ^{132} $ Xe. In NPA-1$ ' $ , the pair configuration space is constructed solely by the$ SDG $ pairs of NPA-1, that is, without including non-collective H pairs. The overlap between the S-pair condensate state constructed by the S pairs of NPA-1 and that constructed by the S pairs of NPA-2 versus the spin of the corresponding reference state in NPA-1 is also presented.In Fig. 9, we also present the overlap between the S-pair condensate state constructed by the S pairs of NPA-1 and that constructed by the S pairs of NPA-2 versus the spin of the corresponding reference state in NPA-1. As shown in Fig. 6, regarding the deformed
$ ^{50} $ Cr nucleus, the S-pair structure is robust with respect to the change in the intrinsic state, whereas the structures of the$ DG $ pairs change significantly. Meanwhile, for a spherical nucleus, the structures of all relevant pairs are robust along the yrast line [30–34]. Then, one would expect that the S-pair structure remains the same along the entire yrast line of the transitional$ ^{132} $ Xe nucleus, which is indeed the case, as shown in Fig. 9. -
In this study, a fundamental problem in the validity of pair truncations is rigorously studied, to the best of our knowledge, for the first time, that is, whether the structures of relevant collective pairs are robust throughout low-lying yrast states. The yrast states of
$ ^{28} $ Si,$ ^{50} $ Cr, and$ ^{132} $ Xe, which have experimental$ R_{4/2} $ values of 2.60, 2.40, and 2.16, respectively, and are expected to represent nuclei with different degrees of the quadrupole collectivity, are studied using the NPA and (realistic) effective SM interactions. For each yrast state, we consider optimized pair structures to be those providing the energy minimum for this state. To find the energy minimum for a yrast state, many full NPA calculations with varying pair structures are performed, and the numerical optimization process of the conjugate gradient method is implemented.The results of
$ ^{28} $ Si suggest that optimized pair structures remain the same for all the states within a rotational band. The results of$ ^{50} $ Cr are consistent with those for$ ^{28} $ Si and further suggest that the structure of the S pair, which is essential in building the monopole pairing correlation, is also robust with respect to backbending, that is, to the change in the intrinsic state, whereas the structures of the non-$ S DG $ pairs, which are essential to building the quadrupole correlation, change significantly. In other words, one must take special care when backbending occurs. For the transitional$ ^{132} $ Xe nucleus, we consider its yrast states as mixtures of spherical and deformed configurations, and the pattern in regard to the robustness of pair structures along its yrast line is consistent with that for the deformed nuclei shown in this paper and that for spherical nuclei inferred from previous studies [30–34].
Robustness of pair structures for nuclear yrast states
- Received Date: 2023-01-16
- Available Online: 2023-06-15
Abstract: In this study, we investigate the robustness of pair structures for nuclear yrast states, that is, whether the structures of relevant collective pairs as building blocks of different yrast states are the same. We focus on deformed and transitional nuclei and study the yrast states of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: