Explaining the W boson mass anomaly and dark matter with a U(1) dark sector

The CDF collaboration recently reported a direct measurement of the W boson mass with increased precision [1],

which has a deviation from the standard model (SM) expectation presented in [2]

at a confidence level of $ 7\sigma $. This result soon attracted many discussions and explorations in particle physics [3–48]. However, the recent CDF result is in tension with previous W boson mass measurements from other experimental groups [49–52] and requires further verification with future LHC measurements. At present, details of the CDF measurements, such as calibrations and experimental uncertainties, as well as details of data analysis, such as the CDF selection rules and fitting assumptions, need to be better understood before any conclusive statement can be made on the new CDF result. Nevertheless, this intriguing result still points to new physics beyond the SM. In this paper, we discuss a possible explanation of the W boson mass anomaly and the nature of dark matter with an extra $ U(1) $ dark sector.

Dark sectors with new interactions and hypothetical particles are usually introduced to explain puzzles beyond the SM. Among them, $ U(1) $ dark sectors are the simplest and are well-motivated by grand unified theories and string theory [53–55]. The dark $ U(1) $ gauge field may mix with the $ U(1) $ hypercharge via gauge kinetic terms [56–58]. However, we find that for this case, such kinetic mixing can only generate at most a 10 MeV mass enhancement to the W boson according to various experimental constraints. While the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM can easily generate 77 MeV enhancement of the W boson mass, explaining the new CDF result. In addition, fermions only charged under the extra $ U(1) $ gauge group are natural dark matter candidates. The massive neutral vector bosons of the theory act as a vector portal between the dark sector and SM particles. The dark fermion can in principle annihilate through vector bosons exchange into SM fermion pairs and satisfy the current observed value of the dark matter relic density.

This paper is organized as follows. In Sec. II, we introduce the $ U(1)_x $ extension of the SM and explain the kinetic mixing between the $ U(1)_x $ dark sector and the SM. In Sec. III, we discuss the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM. In Sec. IV, we review the $S,~T,~U$ effective Lagrangian approach and calculate the effective shifts in the oblique parameters for the two $ U(1) $ extensions of the SM, which are essential in explaining W boson mass enhancement. Fitting various experimental constraints, we investigate how these two models explain W boson mass enhancement. We then focus on the fermionic $ U(1) $ dark matter candidate in the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM in Sec. V. We calculate the dark matter relic abundance and fit our benchmark points with direct and indirect detection bounds. Finally, we conclude our study in Sec. VI.

We first briefly discuss the dark $ U(1)_x $ extension of the SM. The mixing of the $ U(1) $ dark sector with the SM can be generated through either the gauge kinetic terms [56] or the mass terms [59–61]. In this section, we only discuss the kinetic mixing effect [56, 57]. The kinetic terms of the gauge fields are given by

where $W^a_{\mu \nu},~B_{\mu \nu},~C_{\mu \nu}$ are the $SU (2)_L,~U(1)_Y,~U(1)_x$ field strengths, and δ is the kinetic mixing parameter. Because we only consider the kinetic mixing effect in this section, we do not go into detail about the $ U(1)_x $ breaking mechanism. The $ U(1)_x $ gauge field $ C_\mu $ can obtain a mass $ M_1 $ from either the Higgs mechanism or Stueckelberg mechanism. In the gauge eigenbasis $V^{T}=(C,~B,~A^{3})$, the $ U(1)_x $ gauge boson C mixes with the SM gauge bosons via the following matrices:

A simultaneous diagonalization of both the kinetic mixing matrix $\mathcal{\boldsymbol K}$ and the mass-squared matrix ${\boldsymbol M}^{2}$ leads to the relation between the mass eigenbasis $E^{T}=(Z^{\prime},~A_{\gamma},~Z)$ and the original gauge eigenbasis as $ V=RE $, where R is the transformation matrix, given by

where $ c_{\delta}=1/\sqrt{1-\delta^{2}} $, $ s_{\delta}=\delta/\sqrt{1-\delta^{2}} $, $ s_W=\sin \theta_W $, $ c_W= \cos \theta_W $, and the mixing angle ψ is given by

where $ M_0 = \dfrac{v}{2} \sqrt{g_2^2 + g_Y^2} $ is the Z boson mass in the SM. In this paper, we focus on the $ Z^\prime $ mass region of the order of TeV and further define a parameter $ \epsilon^2 \equiv M_0^2/M_1^2 \ll 1 $. The above diagonalization leads to a massless photon and massive Z and $ Z^\prime $ gauge bosons with respective masses of

The $ U(1)_x $ dark sector in general includes dark fermions. The simplest case is to consider a Dirac fermion χ charged under $ U(1)_x $ but not under the SM gauge groups. The dark fermion part of the Lagrangian can be written as

where the dark fermion χ has mass $ m_\chi $ and carries the $ U(1)_x $ charge $ Q_\chi $.

The interactions of gauge bosons and fermions can be obtained using the transformation matrix R.

In the mass eigenbasis, Z and $ Z^\prime $ gauge bosons couple to dark fermions and all SM fermions, whereas the photon has exactly zero couplings with dark fermions. After the mixing, Z boson to SM fermion couplings are modified to be

where $Q^i,~ T_3^i$ are the electric charge and the third component of the weak isospin of the SM fermions, respectively. The Z boson also couples to dark sector fermions,

The couplings of the $ Z^\prime $ gauge boson to fermions are calculated as

The couplings of neutral gauge bosons $ Z,Z^\prime $ to SM fermions can be written in the standard form as

where

We notice that in the expression of $v_i,~a_i$ the change to the $ Z\bar f f $ coupling is proportional to $ \delta^2 \epsilon^2 \lesssim 10^{-6} $, which is a small modification.

We now discuss a general $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM, where the $ U(1) $ charge $ Q=\mathbf{A} Y+\mathbf{B} q $ is a linear combination of the hypercharge Y and any possible charge q, and $ \mathbf{A},\mathbf{B} $ are free parameters. For example, the combination $ \mathbf{A} Y+\mathbf{B}(B-L) $ is the most general anomaly-free combination with the inclusion of three generations of right-handed neutrinos. The choice of q can be family-dependent, for example, $ L_{\mu}-L_{\tau} $ [62], $ B_{1}+B_{2}-2B_{3} $ [63], and can also be any hidden quantum number with which SM fields are not charged. This $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ symmetry is broken by a complex scalar field ϕ at some scale higher than the electroweak scale. The complex scalar ϕ does not carry any SM gauge charges. The covariant derivatives acting on the SM Higgs doublet Φ and the complex scalar ϕ are written as

where $A_{\mu}^{a},~B_{\mu},~C_{\mu}$ are the $S U(2)_L,~U(1)_{Y},~U(1)_{\mathbf{A} Y+\mathbf{B} q}$ gauge fields, respectively. The vevs of the scalar fields are given by

The scalar fields $ \Phi,\phi $ can mix via the scalar potential of the following form:

and we assume the scalar mixing is small due to the choice of parameters.

We are interested in the case that the SM Higgs does not carry the q quantum number. In this case, the neutral gauge bosons are mixed through the mass matrix

where we define $ g_{\mathbf{A}}\equiv \mathbf{A} g_{Y} $. A diagonalization of the above mass matrix gives rise to a change in the gauge boson basis into the mass eigenbasis as

The angle ψ is given by

where $ M_{0}=\dfrac{v}{2}\sqrt{g_{2}^{2}+g_{Y}^{2}} $ is again the original Z boson mass in the SM. The modified Z and $ Z^\prime $ boson masses are respectively given by

For the case in which the dark fermion χ carries zero hypercharge, the interactions of the Z boson with fermions are calculated as

The $ Z^{\prime} $ interactions with fermions are given by

In Eqs. (28) and (29), the value of $ Y_i $ depends on the left- and right-handedness of the SM fermions.

Expressing the $ Z,Z^\prime $ interactions with the SM fermions in the standard form, we have

where

where $ Q^i, T_3^i $ are the electric charge and the third component of the weak isospin of the SM fermions, respectively, and $ q_i $ is the q quantum number carried by the SM fermions, and are set to zero in Sec. V, although in a more general setup, $ q_i $ could be nonzero.

Looking into Eqs. (31) and (32), we notice that the change to the original SM Z boson coupling is proportional to $ \sin \psi g_x \lesssim 10^{-4} $, which is a small modification. We also notice that although $ g_{\mathbf{A}}= \mathbf{A} g_Y $, where $ \mathbf{A}\sim \mathcal{O}(1) $, can have a similar size to $ g_Y $, it only appears at the mixing angle $ \psi \lesssim 10^{-3} $(cf. Eq. (25)), and thus, the value of $ g_{\mathbf{A}} $ does not impose an additional constraint on the model.

Here, we would like to emphasize that this is the key to resolving W boson mass enhancement using the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ model. On the one hand, W boson mass is enhanced through the mixing effect, which is sensitive to the $ g_{\mathbf{A}} $value (cf. Eqs. (41) and (45)). On the other hand, the modification to the couplings of the Z boson with SM fermions is proportional to $ \sin \psi g_x $, whereas the $ Z^\prime $ to SM fermion couplings depend mainly on $ g_x $. Thus, with suitable values of $ g_x $ and $ M_{Z^\prime} $, all the current experimental constraints can be satisfied.

The Peskin-Takeuchi oblique parameters $S,~ T, ~U$ are a set of three measurable quantities, which parameterize new physics contributions to electroweak radiative corrections [64, 65]. Under the $S,~ T,~ U$ effective Lagrangian formulation [66, 67], new physics contributions are recast into effective operators using the original SM gauge fields, giving rise to small shifts in the $S,~ T,~ U$ parameters. With the inclusion of an extra $ U(1) $ gauge boson mixing with the SM gauge bosons, the $S,~ T,~ U$ parameters can be expressed by the changes in the redefinition of the gauge fields as well as the mass shifts of the SM gauge bosons [66],

with $ \delta_A,\delta_Z,\delta_{AZ} $, and $ \tilde{\delta}_Z $ given by

where $A_{\rm SM},~Z_{\rm SM}$ are the original photon and Z gauge fields from the SM, whereas $A,~Z$ are the physical photon and Z boson in the final mass eigenbasis, respectively.

Under this formalism, values of all original SM parameters may alter with the presence of new physics. All physical fields in the final mass eigenbasis as well as all altered physical quantities, such as the electromagnetic fine-structure constant, take the observed experimental values [67]. The shifts in $S,~ T,~ U$ can generate an enhancement of the W boson mass [65, 67],

For the dark $ U(1)_x $ extension of the SM, as described in Sec. II, with some manipulation of Eqs. (5) and (7), we find to the lowest order,

leading to

where δ is the kinetic mixing parameter, and $ \epsilon = M_0 / M_{Z^\prime} $. For the case in which the heavy dark $ U(1)_x $ gauge field only mixes with the SM via gauge kinetic terms, we notice that both the $S,~T$ parameters have negative values, whereas a combination of the two generates an enhancement of the W boson mass. The U parameter is zero to this order and thus offers no contribution. The signs of $S,~T$ may change after considering the mass mixing effect [68].

For the general $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM, as described in Sec. III, with some manipulation of Eqs. (24) and (26), we find to the lowest order,

leading to

where $ g_{\mathbf{A}} = \mathbf{A} g_Y $, $ g_x $ is the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ gauge coupling, and $v,~u$ are the Higgs vev and extra scalar vev, respectively. For the case in which the heavy $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ gauge field mixes with the SM through the gauge boson mass-square matrix, T offers a positive and dominant contribution, whereas S takes a negative value, and a combination of the two generates an enhancement of the W boson mass. The U parameter is still zero and thus offers no contribution.

Under the $S,~ T,~ U$ effective Lagrangian formulation, all altered SM physical quantities take the observed experimental values, considering the new physics effects. Thus, for the models under consideration, the redefined Z boson has the mass [2]

We would like to emphasize that the Z boson mass measurement error bar does not correspond to the change in the original SM Z boson mass, shown in Eqs. (7) and (26). In both of the models under discussion, the measured Z boson mass from the experiment is identified as the modified Z boson after $ U(1) $ mixing in the final mass eigenbasis.

Current experiments set strong constraints on the mass and couplings of the extra $ U(1) $ gauge bosons. Constraints from $ e^+e^- $ colliders originate from the resonance production of $ e^+e^-\to \ell^+ \ell^- $ processes. At the LHC, the $ Z^\prime $ boson can be detected through Drell-Yan processes or by examining dijet resonances. A stringent bound was recently set on an extra large $ Z^\prime $ gauge boson by ATLAS [69]. Using ATLAS and CMS data, a model-independent study [70] was performed, and the upper limit on the couplings of $ Z^\prime $ to quarks was found, corresponding to a set of $ M_{Z^\prime} $ and $ \Gamma_{Z^\prime} $ values. The $ Z^\prime $ couplings to quarks from both our models (shown in Eqs. (17) and (18), and Eqs. (33) and (34)) are well below the limits presented in Ref. [70].

The limit of models with an extra $ U(1) $ with coupling $ g_{Z^\prime \bar{\ell} \ell} $ to SM leptons can be written as

which is a stringent constraint for $ U(1) $ dark sectors connecting with the SM through mixing effects. All benchmark points in the figures presented in this paper have taken into account the above constraints.

The combined results [71] from the Fermilab E989 [72] and Brookhaven E821 [73] experiments show a $ 4.2\sigma $ deviation from the SM prediction [74], which is

This combined result may suggest new physics contributions. The $ Z^\prime $ contribution to muon $ g-2 $ is given by

However, for a TeV scale $ Z^\prime $ gauge boson with a very weak coupling strength to muon pairs, this contribution is negligible.

We also investigate the implications of the two models discussed in the previous sections on the precisely determined observables in the electroweak sector. In particular, we find that the modified Z decay widths of both models are within the error bars of the current measurements. A detailed analysis is given in Appendix A.

For the dark $ U(1)_x $ extension of the SM with kinetic mixing, the $ \delta-M_{Z^\prime} $ plot is shown in Fig. 1. The blue region can explain the W boson mass enhancement considering the experimental error bar and theoretical uncertainties. The dark blue line corresponds to the central value of the W boson mass enhancement $ \Delta M_W\sim77 $ MeV. To achieve 77 MeV enhancement, $ M_{Z^\prime} $ can only stay in the region of several hundred GeV with a rather large $ \mathcal{O}(1) $ kinetic mixing. Such kinetic mixing will generate $ Z^\prime $ to SM fermion coupling strengths $ \sim \delta g_Y $(cf. Eq. (13)) for $ {Z^\prime \bar{f} f} $ couplings. Thus, the entire red region is ruled out by experimental constraints, as mentioned above. The reason is simple. For the dark $ U(1)_x $ extension of the SM, kinetic mixing generates both the W boson mass enhancement and $ Z-Z^\prime $ mixing. Achieving the desired value of the W boson mass enhancement requires $ \mathcal{O}(1) $ kinetic mixing, rendering a large $ Z-Z^\prime $ mixing. As a result, $ Z^\prime \bar{f}f $ couplings are comparable with $ Z\bar{f}f $ couplings, and thus such $ Z^\prime $ faces severe restrictions from experiments. With the current experimental bounds, the dark $ U(1)_x $ extension of the SM with only kinetic mixing can offer an enhancement of 10 MeV at most to the W boson mass, corresponding to the δ upper limit line shown in Fig. 1.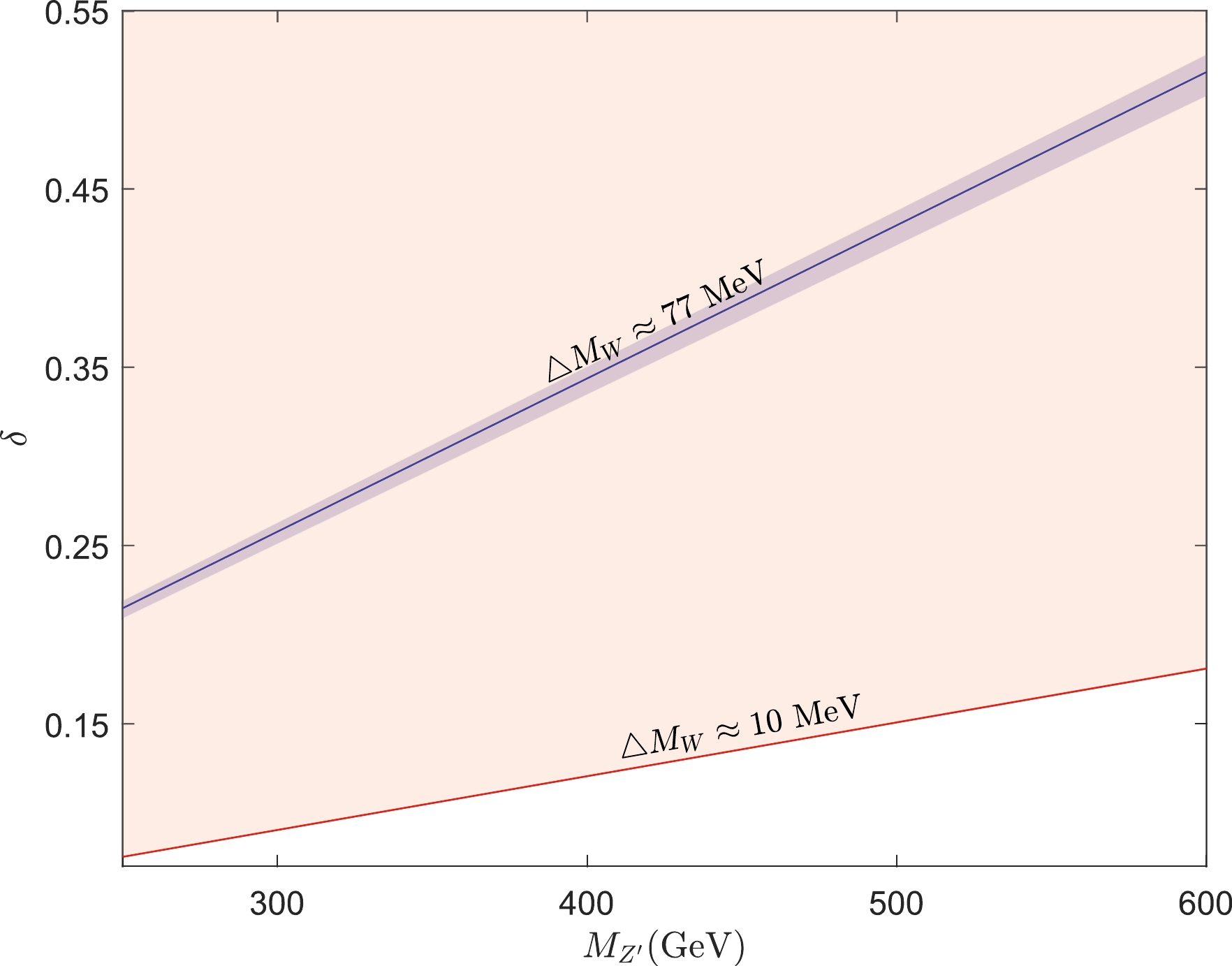

Figure 1.  (color online) W boson mass enhancement generated by the dark $ U(1)_x $ extension of the SM with the $ U(1)_x $ gauge field mixed with the SM through gauge kinetic terms. δ is the kinetic mixing parameter. The dark blue line corresponds to the central value of the W boson mass enhancement $ \Delta M_W\sim77 $ MeV, and the light blue region takes into account the experimental error bar and theoretical uncertainties. The region in red is ruled out by experimental constraints. The lower boundary of the red region shows the upper limit of δ, corresponding to 10 MeV enhancement of the W boson mass.

We now turn to the general $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM, the $ g_{\mathbf{A}} - M_{Z^\prime} $ plot is shown in Fig. 2. The blue region effectively explains the W boson mass enhancement considering the experimental error bar and theoretical uncertainties. The dark blue line corresponds to the central value of the W boson mass enhancement of 77 MeV. As already mentioned at the end of Sec. III, for this case, the mixing is generated via the $ \mathbf{A} Y $ part of the gauged $ U(1) $; thus, we have the freedom to tune the $ U(1) $ gauge coupling $ g_x $ as well as the $ Z^\prime $ mass. As a consequence, various experimental constraints are not difficult to satisfy for the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM. The entire blue region in Fig. 2 can pass all current experiential constraints with a suitable choice of $ g_x $ and $ Z^\prime $ mass, which is fairly easy to achieve.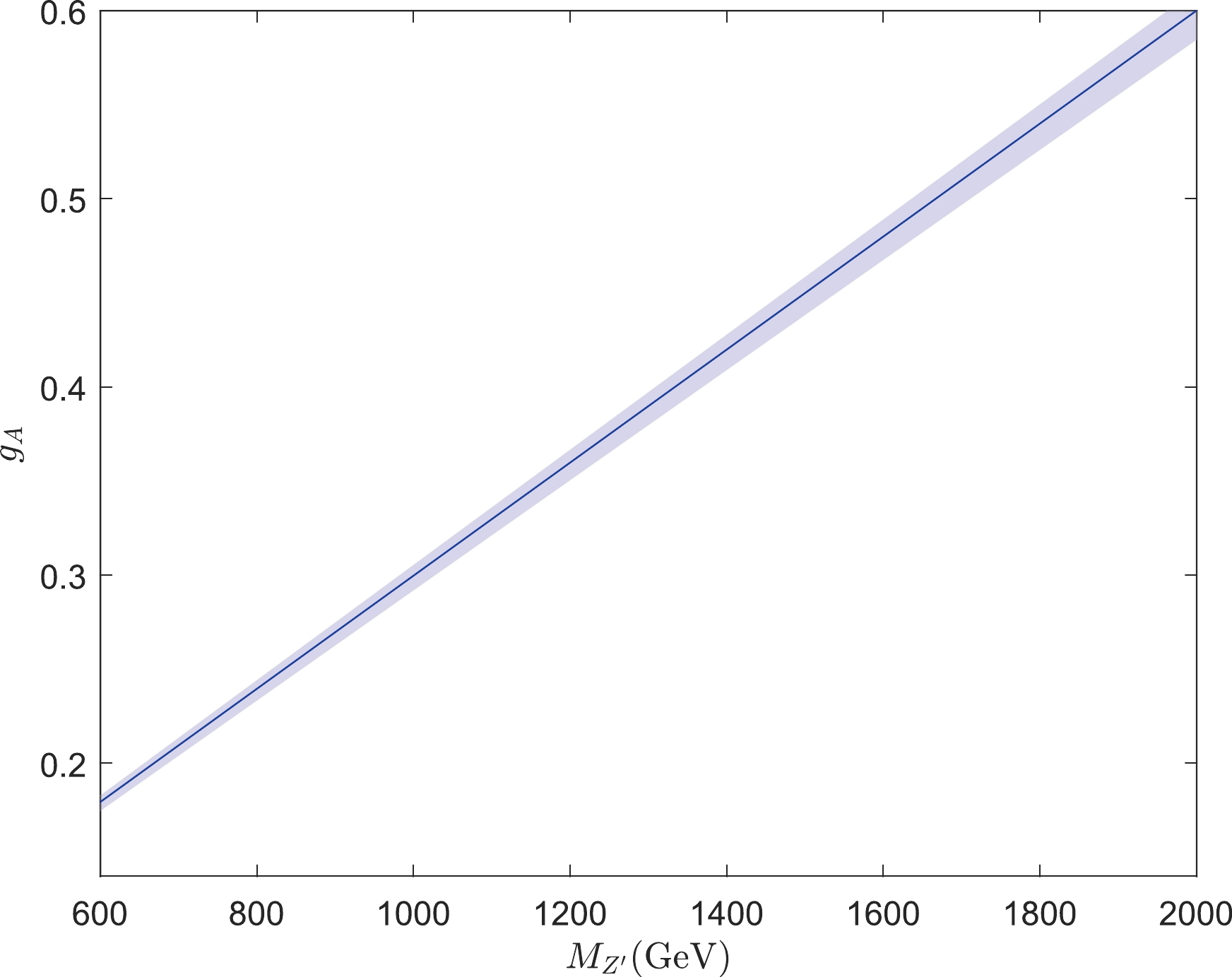

Figure 2.  (color online) W boson mass enhancement from the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM. The dark blue line corresponds to the central value of the W boson mass enhancement $ \Delta M_W\sim77 $ MeV, and the light blue region takes into account the experimental error bar and theoretical uncertainties. The entire blue region can satisfy all current experiential constraints with a suitable choice of $ g_x $ and $ M_{Z^\prime} $.

Despite the great success of the SM, the nature of dark matter remains a mystery in particle physics and cosmology. The $ U(1) $ dark sector includes dark fermions only charged under the extra $ U(1) $ gauge group, which are stable and thus natural dark matter candidates. We now investigate the dark fermion as a dark matter candidate in the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM. The dark fermion part of the Lagrangian is given by Eq. (9), and we consider that the dark fermion χ carries the $ U(1) $ charge $ Q_\chi = +1 $. Here, we assume dark fermions carry zero hypercharge, and thus they couple to the Z boson only through the mass mixing effect. We also assume that the SM fermions carry no q quantum number for simplicity, and thus, they couple to $ Z^\prime $ only through $ \mathbf{A} Y $ and mass mixing.

The mass mixing between $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ and the SM mediates interactions between dark fermions and SM particles, which can be an efficient mechanism to reduce the dark fermion primordial density and achieve the current observed value of the dark matter relic density via the freeze-out process. The dark fermion $\chi,~ \bar{\chi}$ can annihilate^① through the Z and $ Z^\prime $ poles to pairs of SM fermions $ f_i $, i.e.,

Using the vector and axial couplings in Eqs. (31)–(34), the cross-section of these processes are given by

where $ f_i $ are SM fermions with masses $ m_i $, $ N_c $ is the color factor, $ m_\chi $ is the dark matter mass, and the form factor is given by

The modified Z boson decay width is presented in Appendix A, whereas the $ Z^\prime $ decay width can be calculated as

where

With the processes in Eq. (51), dark fermions annihilate to SM fermion pairs and freeze out as the Universe cools down. The dark matter relic density can be computed as

where $ x_f $ is the dark matter mass over the freeze-out temperature, defined as, at $ x_f $, as $ Y - Y_{\rm EQ} \sim cY_{\rm EQ} $, and c is an $ \mathcal{O}(1) $ value. The thermal averaging cross-section is given by

For a heavy $ Z^\prime $ gauge boson with $ \mathcal{O}({\rm TeV}) $ mass, we consider that the dark fermions annihilate via a narrow Breit-Wigner $ Z^\prime $ resonance, which can generate a sufficiently large annihilation cross-section in accordance with the observed dark matter relic abundance, and thus the mass of dark matter is approximately half the $ Z^\prime $ mass.

The mass of the corresponding dark matter candidate is shown in Fig. 3, with two different values of dark sector gauge couplings $ g_x $. To accommodate the observed dark matter relic abundance using the Wigner enhancement effect, the mass of dark matter is approximately half the $ Z^\prime $ mass. As $ M_{Z^\prime} $ increases and $ g_x $ decreases, the mass of dark matter approaches closer to half the $ {Z^\prime} $ mass to achieve the observed dark matter relic density. The most stringent constraint on the model originates from dark matter direct detection experiments. We plot the spin-independent cross-section against dark matter mass in Fig. 4. For the model under discussion, data points above the black lines are excluded by current direct detection experiments [75–77]. For example, for the $ U(1) $ gauge coupling $ g_x=0.08 $, data points with dark matter masses less than $ \sim900 $ GeV are excluded by experiments. While data points with $ g_x=0.05 $ are still viable dark matter candidates and will be in reach of the next generation of dark matter direct detection experiments. Future improved experiments on the large mass region of dark matter with better sensitivities should be able to test this model.

Figure 3.  (color online) Dark matter mass versus the mass of$ Z^\prime $ with two different dark sector gauge couplings. The data points on the lines represent the observed values of dark matter relic density.

Figure 4.  (color online) Current constraints from dark matter direct detection experiments as well as benchmark points of dark matter from the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM. Data points above the black lines showing the bounds of direct detection experiments are excluded.

For stable dark matter, the indirect detection bound arises mostly from dark matter annihilation into SM particles. In Fig. 5, we plot the constraints from CMB (green) [78], AMS-02 (red) [79, 80], and Fermi (blue) [81] for various SM final states. We take the larger $ g_x=0.08 $ value used in dark matter analyses (Fig. 3 and Fig. 4), which gives a larger annihilation cross section. Other indirect detection bounds also include dark matter annihilation into the $\gamma\gamma,~gg,~hh$ final states, which are absent in our model.

Figure 5.  (color online) Current constraints from dark matter indirect detection experiments as well as benchmark points of dark matter from the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM with $ g_x = 0.08 $. All benchmark points are below the current constraints.

Recently, the CDF collaboration announced a more precise measurement of the W boson mass, with a central value significantly larger than the SM prediction of approximately 77 MeV with a $ 7\sigma $ deviation. This result is in favor of the presence of new physics beyond the SM. It is thus crucial to explore the phenomenological implications of the new CDF result on the W boson mass measurement. In this paper, we perform a comprehensive study of two extra $ U(1) $ extensions of the SM. One is the dark $ U(1)_x $ extension, and the other is the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension. The mixing effects between the extra $ U(1) $ dark sector and the SM are discussed in detail. For the scenario in which the dark $ U(1)_x $ has only kinetic mixing with the SM, the W boson mass can be enhanced by 10 MeV at most according to various experimental constraints. While we demonstrate that for the $ U(1)_{\mathbf{A} Y+\mathbf{B} q} $ extension of the SM, a consistent scenario in agreement with all existing experimental results can be achieved and explain the W boson mass enhancement $ \sim77 $ MeV as well as the nature of dark matter. Mixing mediates interactions between dark fermions and SM particles through the exchange of a Z boson as well as an $ \mathcal{O}({\rm TeV}) $ $ Z^\prime $ gauge boson. Dark fermions can annihilate through $ Z,Z^\prime $ poles and become a relic in the Universe; thus, they are natural dark matter candidates. We calculate the dark matter relic density and fit our model points with the direct and indirect dark matter detection experimental bounds. The viable benchmark points of the model offer dark matter candidates within the reach of future direct dark matter detection experiments.

We now investigate the implications of the analyses in the previous sections on the precisely determined observables in the electroweak sector. One need to make sure the modified Z boson, now carrying a tiny fraction of $ Z^\prime $, passes the electroweak precision test. The couplings of the Z boson to SM fermions are elevated from the tree level expressions

where $ \rho_i,\kappa_i $ are given in [61]. For the pure kinetic mixing ${\boldsymbol U}(1)$ model, the two parameters $ C_1,C_2 $ are

whereas for the $U(1)_{\mathbf{A} Y+\mathbf{B} q}$ model

The decay of the Z boson into lepton and anti-lepton as well as quark and anti-quark pairs (excluding the top) in the on-shell renormalization scheme is given by [61, 82]

where $ \mu_i=m_i/M_Z $, $ \Gamma_o=G_F M_Z^3 / 6 \sqrt{2} \pi $.

For the kinetic mixing $ U(1) $ model, we show that the modified Z boson decay width of two benchmark points are taken from the two edges of the red lower bound from Fig. 1, which can only enhance the W boson mass by approximately 10 MeV. We find

All other points from Fig. 1 also fall into the experimental error bars of the Z boson decay width measurement.

For the $ U(1)_{\mathbf{A} Y + \mathbf{B} q} $ model, we compute the Z decay width using the two different $ g_x $ values used in the discussion of dark matter in Sec. V. For each $ g_x $ value, we evaluate two edge points on the plot of Fig. 2, which can achieve a W boson mass enhancement of 77 MeV. For $ g_x=0.05 $,

and for $ g_x=0.08 $,

where $\Gamma_Z^{EX}\approx 2.4952~\text{GeV}\pm 0.0023~\text{GeV}$ [71]. Compared with the Z boson decay width, other precision electroweak data set weaker constraints on our models. A detail analysis was performed in, for example, [58, 61], showing that their model fits well to the experimental data, in which a significantly larger $ U(1) $ mixing was considered compared to those in the two models discussed in this paper. Thus, both of our models are safe confronting precision electroweak data.