-
The phase transition between quark-gluon plasma (QGP) and the hadron phase is one of the most interesting topics in relativistic heavy ion physics. As the QGP cannot be detected directly, the heavy quarkonium consisting of a heavy quark and a heavy antiquark has been proposed as a probe for the early stage of the hot medium in heavy-ion collisions [1–11]. The non-relativistic approximation is usually taken in studies of heavy quarkonium, due to its large mass [7, 12–15]. Such an approximation is usually reasonable at zero temperature when the mass or radius is calculated, because the typical energy scale of the potential is smaller than the masses of heavy quarks.
However, dissociation with a screened potential is different. The temperature as a new low energy scale comes in. The potential pulls the quarks together into a meson, and the temperature weakens the attraction. Around the maximum survival temperature, that is, the dissociation temperature
$ T_d $ , the balance between the attractive potential and the screening can be destroyed even by a relatively small contribution in the potential. Therefore, it is interesting to check how much a change in temperature can rebalance the relativistic correction. Determining the in-medium properties of quarkonium is crucial for extracting the heavy quark potential at finite temperatures and also the hot medium information with quarkonium probes. Some theoretical studies [16–18] on the relativistic effect have been conducted in open and hidden heavy flavors based on the two body Dirac equation (TBDE) [19–22].An analog to heavy quarkonia is the
$ B_c $ meson [23–27], since it is composed of two heavy quarks. It is a cleaner probe than heavy quarkonia, because (i) it is composed of heavy quarks with different flavors, so the number of possible processes is less than that for heavy quarkonia, and (ii)$ B_c $ is a pseudo-scalar meson, so the spin structure is simpler. It is therefore urgent to study the properties of the$ B_c $ meson at finite temperatures. In experiments, the nuclear modification factor of$ B_c $ mesons has been measured, and more helpful results can be expected in the future [28]. In this study, we employ the TBDE compared with the Schrödinger equation to study the relativistic correction on$ B_c $ dissociation temperature. -
The TBDE is a generalization of the free Dirac equation. It is both relativistic and Schrödinger-like, and it has been used to calculate the meson spectra in vacuum and at finite temperature. In general, it involves complicated coupled equations [16, 22]. For a (pseudo-)scalar meson, it decouples from the spin triplet components, and its equation can greatly be simplified. We rewrite its radial equation as
$ \begin{eqnarray} \left[-\frac{ \text{d}^2}{ \text{d} r^2}+\Phi_{SI}+\Phi_1\right]U(r)&=&b^2 U(r), \end{eqnarray} $

(1) with
$ \Phi_{SI}=2m_wS+2\varepsilon_w A+S^2-A^2, $

(2) $ \Phi_{1}=\frac{1}{R}\frac{ \text{d}^2}{ \text{d} r^2}R, $

(3) $ R=r\sqrt{\frac{(m_1 \varepsilon_2+m_2 \varepsilon_1)X}{ \varepsilon_1M_2+ \varepsilon_2M_1-A(M_1+M_2)}}, $

(4) $ M_i=\sqrt{m_i^2+Y/X},\quad i=1,2, $

(5) $ Y=2m_wS+S^2, $

(6) $ X=1-\frac{2A}{m_m}. $

(7) Here, r is the radius of the relative motion. The quantities denoted by capital letters are all r-dependent functions. This convention is also followed elsewhere in this paper except for conventional special functions, the temperature T, and r itself. The r-independent quantities are the constituent mass of each quark
$ \varepsilon_i $ , the reduced mass$ m_w $ , the energy$ \varepsilon_w $ of the imaginary particle for relative motion, and the eigenvalue-like term$ b^2 $ , which are defined as$ \varepsilon_i=\frac{m_m^2+2m_i^2-m_1^2-m_2^2}{2m_m},\quad i=1,2, $

(8) $ m_w=\frac{m_1m_2}{m_m}, $

(9) $ \varepsilon_w=\frac{m_m^2-m_1^2-m_2^2}{2m_m}, $

(10) $ b^2=\frac{m_m^4-2(m_1^2+m_2^2)m_m^2+(m_1^2-m_2^2)^2}{4m_m^2}. $

(11) The inputs of this equation are the charm quark mass
$ m_1 $ , the bottom quark mass$ m_2 $ , and the potential between them divided into a scalar part S and a vector part A, while the outputs are both the mass$ m_m $ of the$ B_c $ meson and its radial wave function$ U(r) $ ; therefore, the probability to find the quark pairs in a spherical shell$ r\sim r+ \text{d} r $ is proportional to$ |U^2(r)| \text{d} r $ . Note that$ m_m $ appears on both sides of the equation. Therefore, it is actually not a typical eigen equation.In the non-relativistic limit
$ A, S\ll m_1, m_2, m_w, m_m $ ①, one finds$ X\rightarrow 1 $ ,$ M_i\rightarrow m_i $ ,$ R\rightarrow r $ ,$ \Phi_1\rightarrow 0 $ ,$ \varepsilon_w\rightarrow m^S $ ,$ m_w\rightarrow m^S $ with the non-relativistic reduced mass$m^S= \dfrac{m_1m_2}{m_1+m_2}$ , the spin-independent term$ \Phi_{SI}\rightarrow 2m^SV^S $ with$ V^S=A+S $ being the non-relativistic potential, and$ b^2\rightarrow 2m^S \varepsilon $ , with$ \varepsilon=m_m-m_1-m_2 $ being the eigen energy in a Schrödinger equation. As expected, it reduces to a Schrödinger equation$ \begin{eqnarray} \left[-\frac{1}{2m^S}\frac{ \text{d}^2 }{ \text{d} r^2}+V^S \right]U(r)&=& \varepsilon U(r), \end{eqnarray} $

(12) or
$ \begin{eqnarray} \left[-\frac{1}{2m^S}\frac{ \text{d}^2 }{ \text{d} r^2}+\overline{V}^S\right]U(r)&=&-\Delta \varepsilon^S U(r), \end{eqnarray} $

(13) with the non-relativistic binding energy
$ \Delta \varepsilon^S= m_1+m_2+ v_{\infty}-m_m $ . Here, we introduce the shifted potential$ \overline{V}^S=V^S-v_{\infty} $ ,$ v_{\infty}=\lim\limits_{r\rightarrow +\infty}V^S $ , so that$ \overline{V}^S $ vanishes at$ r\rightarrow +\infty $ . Such a bar-symbol is also used for other potentials in the following.A widely used potential
$ V^S $ in vacuum is the Cornell potential, which contains a Coulomb-like potential$A=-\dfrac{\alpha}{r}$ , and a linear potential$ S=\sigma r $ . Charmonium and bottomonium spectra can be fitted with$ \alpha=\pi/12 $ and$ \sigma=0.2 $ GeV$ ^2 $ [12]. At finite temperature, we take the screened Cornell potential [12] as a function of the screening mass μ and radius r,$ V^S(r,\mu)=A(r,\mu)+S(r,\mu), $

(14) $ A(r,\mu)=-\alpha\mu\left(\frac{{\rm e}^{-\mu r}}{\mu r}+1\right), $

(15) $ S(r,\mu)=\frac{\sigma}{\mu\Gamma\left(\dfrac{3}{4}\right)}\left[ \frac{\Gamma\left(\dfrac{1}{4}\right)}{2^{\frac{3}{2}}}-\frac{(\mu r)^{\frac{1}{2}}}{2^{\frac{3}{4}}}K_{\frac{1}{4}}(\mu^2 r^2) \right]. $

(16) We attribute the screened Coulomb-like potential to A, and the screened confining potential to S, as it is at zero temperature [29]. This is our assumption in the main part of this paper, and we revisit it at the end. The only temperature dependent parameter is the screening mass μ, which we fit from the lattice result [30] as
$ \mu(\overline{T})/\sqrt{\sigma}= s\overline{T}+\sqrt{\frac{\pi}{2}}a\sigma_{t}\left[ \text{erf}\left(\frac{b}{\sqrt{2}\sigma_{t}}\right)- \text{erf}\left(\frac{b-\overline{T}}{\sqrt{2}\sigma_t}\right)\right],\\ $

(17) with
$ \overline{T}=T/T_c $ ,$\text{erf}(t)=\dfrac{2}{\sqrt{\pi}}\int_{0}^{t}{\rm e}^{-x^2} \text{d} x$ ,$ s=0.587 $ ,$ a=2.150 $ ,$ b=1.054 $ , and$ \sigma_t=0.07379 $ .The only free parameters left are quark masses
$ m_1 $ and$ m_2 $ . We fit masses of scalar heavy mesons composed of a charm quark and/or a bottom quark in experiments [31] to obtain$ m_1 $ and$ m_2 $ both in the TBDE and in the Schrödinger equation. The results are listed in Table 1. We denote the results or parameters for the Schrödinger equation with a superscript$ ^S $ and those for TBDE with a superscript$ ^D $ to distinguish them when necessary.$ m_1 $ 

$ m_2 $ 

$ m_{\eta_c} $ 

$ m_{\eta_b} $ 

$ m_{B_c} $ 

Schrödinger Eq. 1.19 4.59 2.991 9.415 6.256 TBDE 1.27 4.62 2.997 9.421 6.254 Experiments − − 2.984 9.399 6.274 Table 1. Mass parameters in the Schrödinger equation and those in TBDE. The masses are all in GeV. Experimental data are from the Particle Data Group [31].
-
At finite temperature, the binding energy
$ \Delta \varepsilon $ of$ B_c $ is defined as the energy difference between the lowest scattering state and the bound state$ \Delta \varepsilon^D = v_{\infty}+\sqrt{v^2_{\infty}+(m_1+m_2)^2}-m_m^D, $

(18) while in the non-relativistic limit, it becomes
$\Delta \varepsilon^S = v_{\infty}+m_1+m_2-m_m^S$ as mentioned above. The temperature dependence of the binding energy$ \Delta \varepsilon $ and that of the average radius$ \begin{eqnarray} \langle r \rangle&=& \frac{\int \text{d} r\ r |U(r)|^2}{\int \text{d} r |U(r)|^2}, \end{eqnarray} $

(19) and the r dependence of the wave functions U of
$ B_c $ are shown in Fig. 1, Fig. 2, and Fig. 3, respectively. It can be seen that, in both cases, the higher the temperature, the weaker the binding between the two heavy quarks, as expected. The dissociation temperature$ T_d $ , at which the binding energy reduces to zero, increases from$ 1.45T_c $ to$ 1.9T_c $ when the relativistic correction is considered.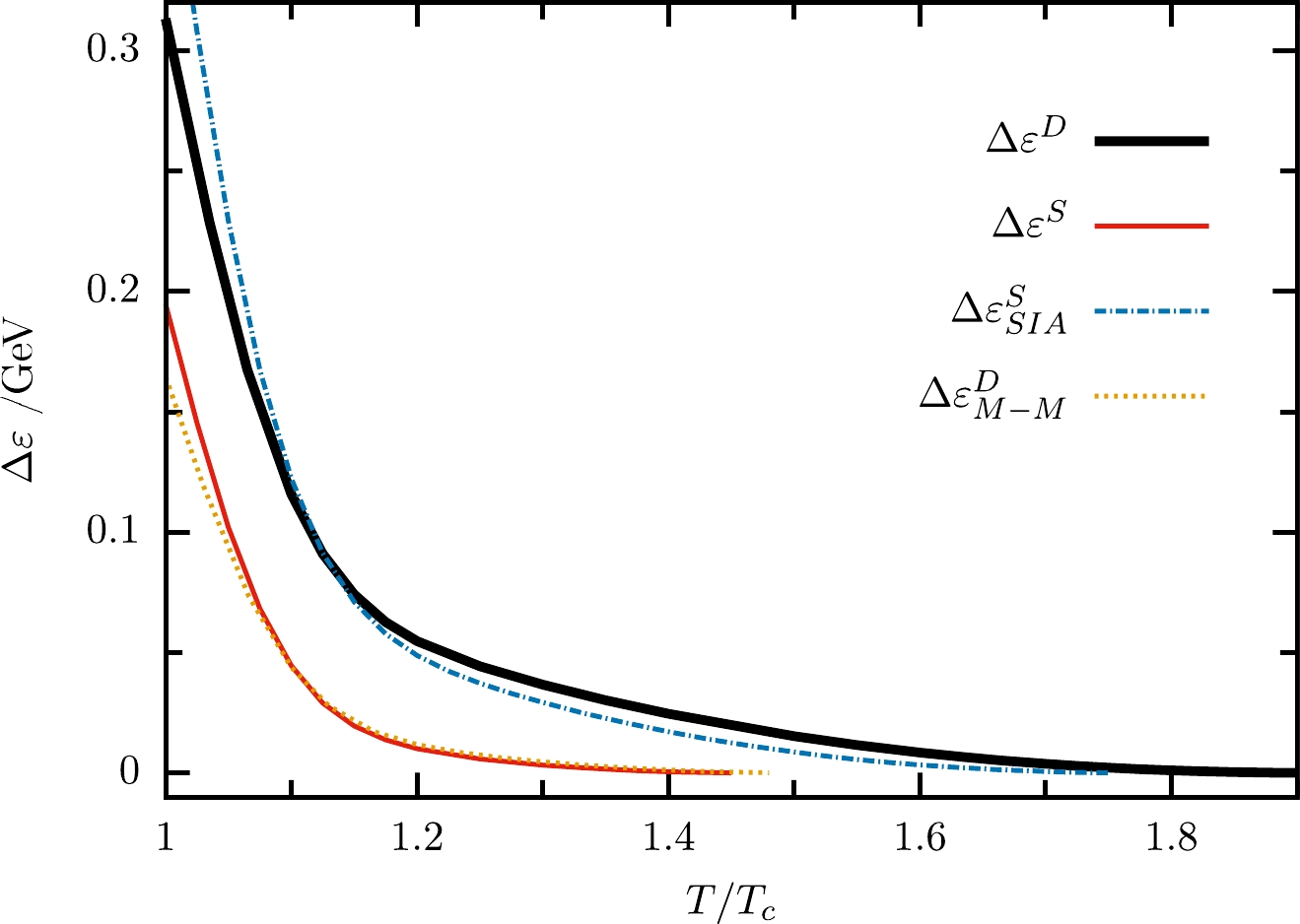
Figure 1. (color online) Binding energy
$ \Delta \varepsilon $ as a function of temperature T compared with the non-relativistic limit.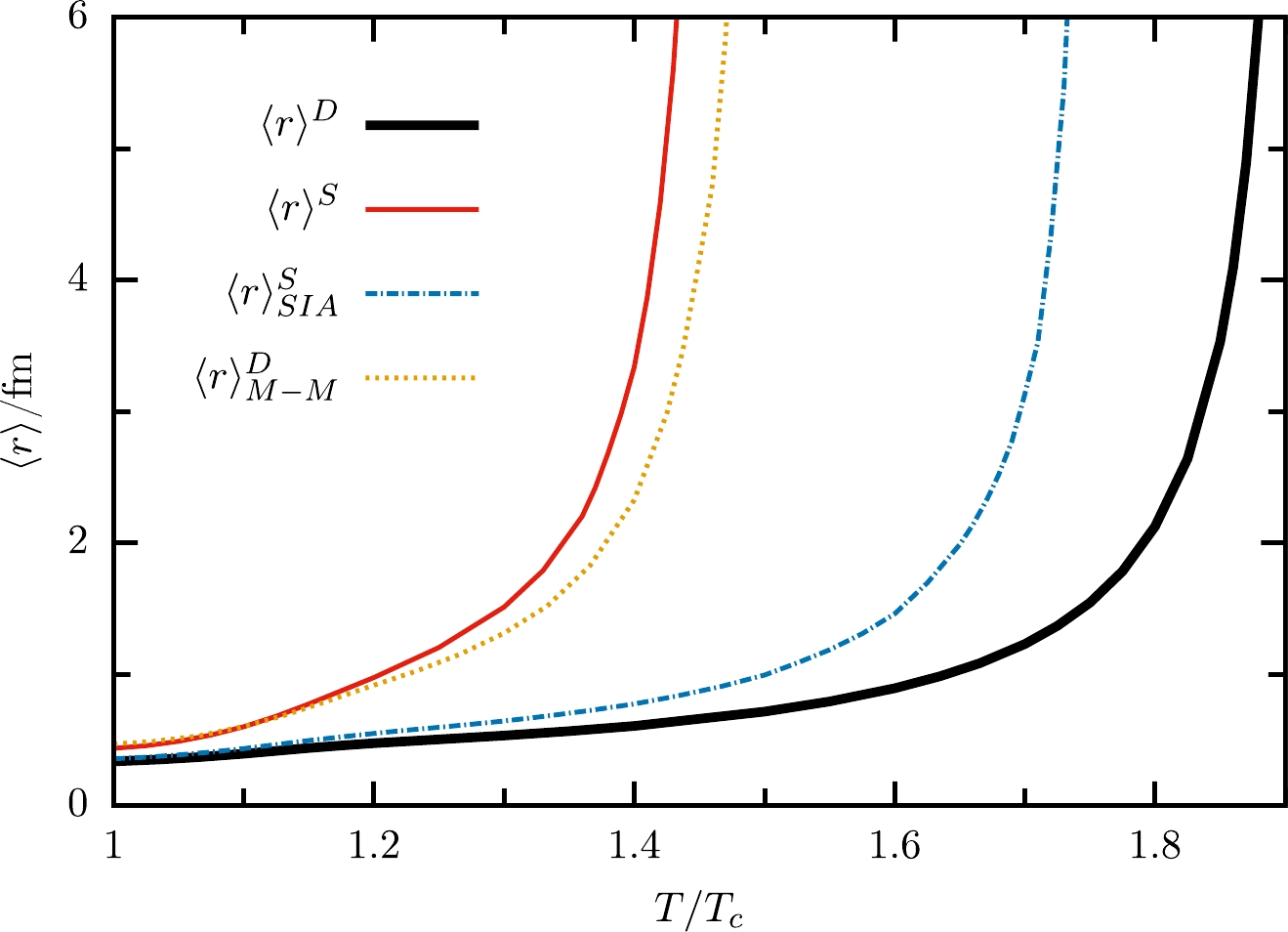
Figure 2. (color online) Average radius as a function of temperature T compared with the non-relativistic limit.

Figure 3. (color online) Wave functions at different temperatures
$ T=0 $ ,$ T=T_c $ , and$ T=1.4T_c $ .To understand the differences, we first check the dependence of parameters
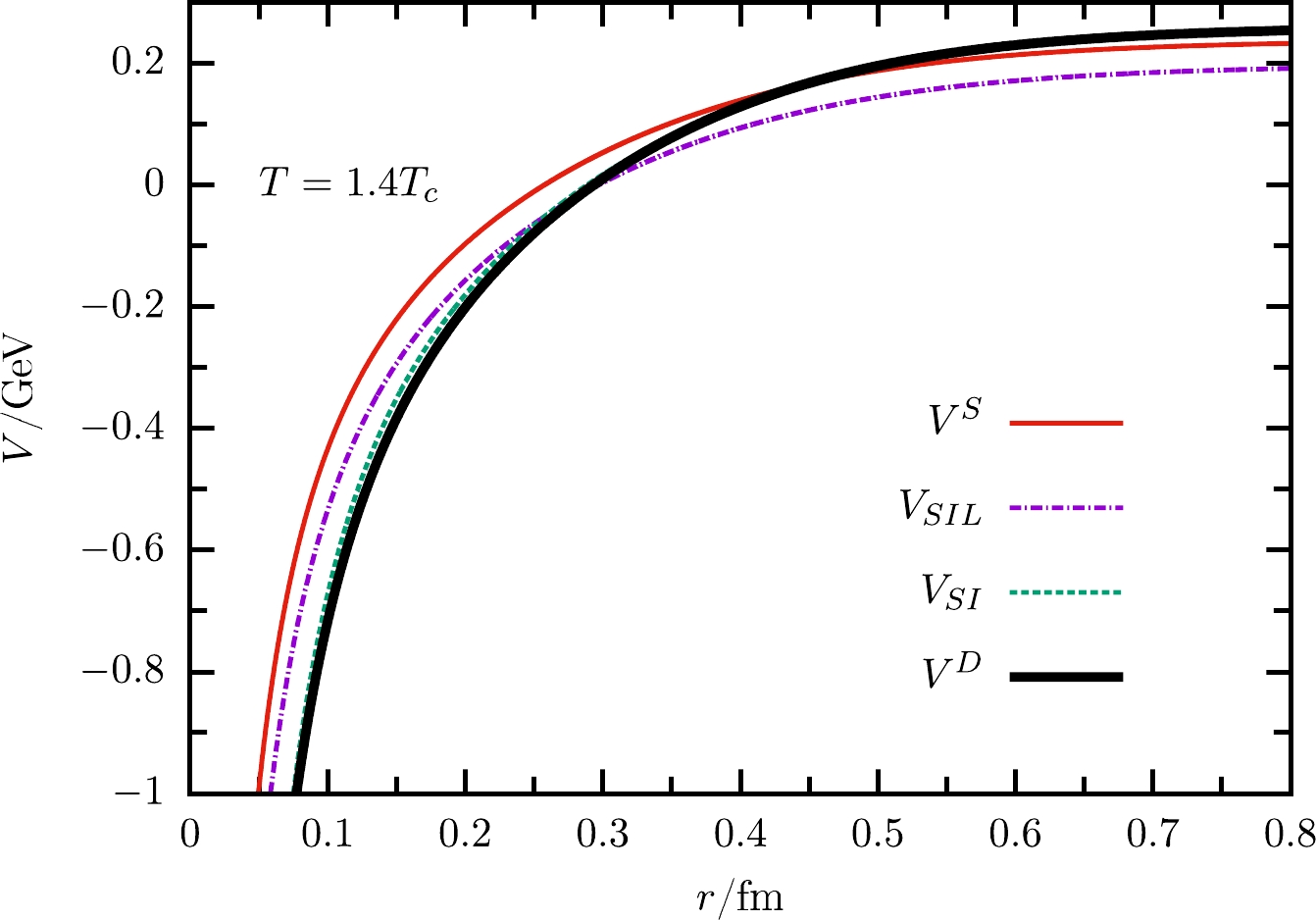
$ m_1 $ and$ m_2 $ . It is found that this factor is less important. For example, if the TBDE parameters$ m_1 $ and$ m_2 $ (see the middle row in Table 1) are used instead in the Schrödinger equation, the dissociation temperature$ T_d $ increases only by approximately$ 0.05T_c $ . This indicates that the differences in$ T_d $ are mainly due to the relativistic corrections in the equations, instead of the parameter difference in Table 1.Now we turn to the difference in equations. A direct comparison is to compare Φ②. However, a potential is more intuitive. Therefore, we consider potentials V with and without the relativistic corrections at different temperatures
$ T_c $ and$ 1.4T_c $ , with$ V^D\equiv \dfrac{1}{2m^S}\left( \Phi_{SI}+\Phi_1 \right) $ . It can be seen in Fig. 4 that, at$ r\rightarrow 0 $ , the temperature dependence of$ {V} $ is weak, because at a short distance it is dominated by the Coulomb term of the potential A, and the screening is weak. The effective potential$ V^D $ in TBDE is deeper than the potential$ V^S $ in the Schrödinger equation at a short range mainly because of the$ -A^2\approx-\alpha^2/r^2 $ term. At a large value of r, the difference between$ V^D $ and$ V^S $ is much smaller, which is reasonable, since a large radius corresponds to a low energy scale, and the relativistic effect is less important. The differences are from the constant term in the screening potentials. In short, the potential well becomes deeper at lower temperatures and/or in the relativistic case.
Figure 4. (color online) Potentials as functions of radius r at temperatures
$ T=T_c $ and$ T=1.4T_c $ .The potential term is dominated by
$ \Phi_{SI} $ , which means that the dissociation temperature of the$ B_c $ meson is not sensitive to the spin structure. Actually, up-to the next-to-leading order of the non-relativistic approximation, we have$ R= r\left(1+\frac{\sec^2\theta}{m_m}A-\frac{\sec^2\theta+\tan^2\theta}{m_m}S\right), $

(20) with
$ \sin\theta=(m_1-m_2)/m_m $ . The leading term of$ \Phi_1 $ is$ \begin{aligned}[b] \Phi_1 =& \frac{1}{m_mr}\left[\sec^2\theta (rA)''-(\sec^2\theta+\tan^2\theta) (rS)''\right] \sim \frac{\mu^2}{m_m}\overline{V}^S, \end{aligned} $

(21) which implies that
$ \Phi_1 $ is smaller than$ m_mV^S $ by a factor of approximately$ \dfrac{\mu^2}{m_m^2} $ and thus smaller than$\Phi_{SI}\approx 2m_wV^S$ by a factor of approximately$ \dfrac{\mu^2}{2m_1m_2} $ . At the temperature that the$ B_c $ meson dissociates, the screening mass is approximately$ 0.6 $ GeV, so$ \Phi_1 $ is only as small as a few percent of$ \Phi_{SI} $ and can thus be neglected, as shown in Fig. 5 with$ V_{SI}=\Phi_{SI}/(2m^S) $ and$ V^{D}=(\Phi_{SI}+\Phi_1)/(2m^S) $ . In this case, the TBDE can be deduced as a relativistic two body equation for spinless particles [22].The leading term in
$ \Phi_{SI} $ is$ \Phi_{SIL}=2m_wS+2 \varepsilon_wA $ , which differs from the non-relativistic potential in the mass terms. The masses at$ T=T_c $ and$ T=1.4T_c $ are listed in Table 2. It can be seen that the modification to the scalar part of the potential is relatively small (a few percent), while that to the vector part is relatively large ($ \varepsilon_w/m^S-1\approx 0.3 $ ). As a result, the modification due to the mass coefficient is roughly of the order of$15$ % (see the curve of$ {V}_{SIL}=\Phi_{SIL}/(2m^S) $ in Fig. 5).$ T/T_c $ 

$ m_m $ 

$ m^S $ 

$ m_w $ 

$ \varepsilon_w $ 

1.0 6.217 0.945 0.944 1.262 1.4 6.111 0.945 0.960 1.177 Table 2. Masses in
$ \Phi_{SIL} $ . The masses are all in GeV.Note that there is some ambiguity from the non-relativistic potential
$ V^S $ to the potential$ \Phi_{SI}+\Phi_1 $ in the TBDE, because it depends on how it is divided into the vector part A and the scalar part S, especially when the potential is given numerically as in the lattice QCD. We attempt to attribute both the$ v_{\infty} $ terms to the scalar potential, leaving$A=-\alpha {\rm e}^{-\mu r}/r$ . Then, the dissociation temperature shifts from$ 1.9T_c $ to$ 1.7T_c $ . Actually, we can rewrite$ \Phi_{SI} $ under the approximation$ m_w\approx m^{S} $ and$ \varepsilon_w\approx m^S $ as$\Phi_{SI}\approx \Phi_{SIA}= 2m^SV^{S}[1+(S-A)/(2m^S)]$ . Therefore, the larger the value of$ S-A $ , the deeper the well. In the trial scheme in this paragraph,$ S-A $ becomes smaller, and the binding is looser. The results from the Schrödinger equation with the above$ \Phi_{SIA} $ are shown by the blue dotted-dashed curves in Figs. 1 and 2. The results are closer to the TBDE results as expected. Another way one may be interested in approximating the interaction of quarks is to attribute the constant potential to quark masses [32, 33], i.e., using$m_b'= m_b+v_{\infty}/2$ and$ m_c'=m_c+v_{\infty}/2 $ to absorb the constant term$ v_{\infty} $ in the potentials. The results are shown by the yellow dotted curves in Figs. 1 and 2. In this case, the dissociation temperature is slightly higher than the Schrödinger results. -
In summary, the dissociation temperature of the
$ B_c $ meson in the QGP is calculated by the TBDE, and it is found to be higher than that calculated by the Schrödinger equation. The spin dependent part is negligible, and the increase is mainly due to the square terms$ S^2-A^2 $ in the spin independent part of the potential$ \Phi_{SI} $ . In the case in which S is finite and A approaches$ -\alpha/r $ around$ r=0 $ , the potential well becomes deeper at small r. The constant term in the potential, which is not important in the Schrödinger equation, is significant in the TBDE. -
Liu is grateful to Prof. Xingyu Guo for helpful discussions.
Relativistic correction to the dissociation temperature of Bc mesons in a hot medium
- Received Date: 2022-08-08
- Available Online: 2023-02-15
Abstract: By solving two body Dirac equations with potentials at finite temperature, we calculate the dissociation temperature





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: