-
The search for exotic hadrons, made of more than three quarks (antiquarks), is one of the most interesting subjects in hadron physics because they may contain more low-energy strong interaction information than ordinary hadrons. A large quantity of new hadrons have been observed by experiments since the Belle Collaboration’s discovery of the state
$ X(3872) $ in 2003 [1]. Some of these new observed hadron states cannot be explained as conventional mesons because they are charged states, such as$ Z_c^+ $ , and some others cannot be explained very well in the traditional$ qq\rm{-} $ meson or$ qqq\rm{-} $ baryon framework. Multiquark states have therefore attracted much attention theoretically.Recent experimental studies of heavy meson spectroscopy revealed several new states, such as
$ T_{cc} $ reported by the LHCb Collaboration [2, 3], and$ X_{cc\bar{s}\bar{s}} $ by the Belle Collaboration [4], which cannot be simply accommodated in the quark-antiquark ($ q\bar{q} $ ) picture [5]. These states may be good candidates of multiquark states. The simplest multiquark system is a tetraquark, made up of two quarks and two antiquarks. Heavy tetraquarks are of particular interest, because the presence of a heavy quark will increase the binding energy of the bound system. As a consequence, such tetraquarks will have masses below the thresholds and forbid the strong decays to mesons with open heavy flavor with the small decay width generated by the weak and electromagnetic decay. Therefore, it is important to investigate the possible stability of$ QQ\bar{q}\bar{q} $ tetraquarks because they are explicitly exotic states with the heavy flavor number equal to 2. Further, their observation will be a direct proof of the existence of multiquark states.Until now, many theoretical studies have been conducted about the double-heavy tetraquarks with various phenomenological methods, such as the constituent quark model, chiral perturbation theory, string model, lattice quantum chromodynamics (QCD), and QCD sum rule approach [6–36]. Most of them predicted that
$ cc\bar{u}\bar{d} $ ,$ bb\bar{u}\bar{d} $ with$ 0(1^+) $ and$ cc\bar{u}\bar{s} $ ,$ bb\bar{u}\bar{s} $ with$ \dfrac{1}{2}(1^+) $ have stable masses below the corresponding thresholds. However, none of them has so far been confirmed experimentally, except$ T_{cc} $ . Moreover, the states with masses above some two-hadron thresholds become resonances with often a large fall-apart decay width and can be experimentally observable in the future.Following our previous study about
$ T_{cc} $ and$ T_{bb} $ [37], the purpose of this work is to systematically study the tetraquarks with two heavy quarks$ QQ (Q=b,c) $ and two light/strange quarks$ us $ or$ ss $ with possible quantum numbers constrained by the Pauli principle and try to find stable bound states and resonance states in the strong interaction in the non-relativistic chiral quark model. According to previous results about$ T_{cc} $ , the different quark pictures can lead to diverse conclusions. For instance, the diquark-antidiquark structure leads to deeply bound states, whereas the meson-meson picture brings about a weakly bound state. When considering the coupling of the two pictures, we can obtain deeper bound states, but the weakly bound state disappears. We may look forward to more precise experimental data and determine if there exist states with much deeper binding energy.Moreover, along with the discoveries of new hadron states in experiments, we are blessed with new opportunities and faced with new challenges, such as the chiral quark model. In the quark model, the quark-quark interactions have a good achievement on hadron spectrum, where the unique color structure, color-singlet, is accepted. Nowadays, we usually generalize the quark-quark interactions used in color-singlet baryons and mesons to multiquark systems, such as those using Casimir scaling [38]. With the accumulation of experimental data, our understanding of the hadron-hadron interactions can be deepened and may shed light on the properties of the newly observed exotic states.
In our present work, different quark configurations such as the meson-meson picture, the diquark-antidiquark picture, and their couplings are also considered to show the stability of states. For
$ T_{cc} $ states, the$ S U(2) $ flavor symmetry is applied, and for the double-heavy tetraquarks with strangeness, the$ S U(2) $ flavor symmetry may be a good choice, but the Goldstone boson K meson exchanges will be inoperative. Thus, for the strange double-heavy tetraquarks, when introducing the Hamiltonian for the hadron states, the octet Goldstone boson exchanges$ V^{\pi, K, \eta} $ are considered. However, the$ S U(3) $ flavor symmetry breaking is also taken into account, with the different masses of the$u,~d$ and s quarks, and it gives rise to different masses of π and K. In the construction of the wavefunctions, we also take the mass differences into consideration.We find no bound stats for strange double-heavy tetraquarks when pure meson-meson or diquark-antidiquark pictures are considered, but we find a bound state for
$ cc\bar{u}\bar{s} $ and$ bb\bar{u}\bar{s} $ with isospin and spin-parity$ I(J^P)=\dfrac{1}{2}(1^+) $ only when considering the coupling of the meson-meson and diquark-antidiquark pictures having a binding energy of 7.0 and 104.4 MeV, respectively. Further, for$ bb\bar{u}\bar{s} $ with$ I(J^P)=\dfrac{1}{2}(1^+) $ , the K meson exchange is much larger than that of the$ cc\bar{u}\bar{s} $ system, and it plays a role in obtaining the deeper bound energy. Meanwhile, the possible resonance states are also searched with the real scaling method (RSM) [39] in the full channel-coupling calculations. With the help of the RSM, we obtain some observable resonances for double-heavy tetraquarks with strangeness.The article is organized as follows. In the next section we present the framework of the chiral quark model and the wave functions of the tetraquark states. In Sec. III, we present analyses of our results. We conclude with a summary and outlook in Sec. IV.
-
As we all know, QCD has three important properties, asymptotic freedom, color confinement, and approximate chiral symmetry and its spontaneous breaking. Until now, it is still difficult for us to obtain the hadron spectra analytically from the QCD Lagrangian. The QCD-inspired chiral quark model is widely regarded as an effective tool to obtain the hadron spectra and understand the hadron-hadron interactions. In the chiral quark model, the quark-quark interactions within the confinement scale (
$ \sim $ 1 fm) have undergone a wide check in the hadron spectra, where the unique color structure, color-singlet, is accepted. For the multiquark system with various color structures, the effects of these color structures are considered by the Casimir operator$ \boldsymbol{\lambda}_i^c\cdot \boldsymbol{\lambda}_j^c $ [38].In the chiral quark model, the Hamiltonian of the four-quark system is as follows:
$ \begin{aligned}[b] H = &\sum_{i=1}^4 m_i +\frac{{\boldsymbol p}^2_{12}}{2\mu_{12}}+\frac{{\boldsymbol p}^2_{34}}{2\mu_{34}} +\frac{{\boldsymbol p}^2_{r}}{2\mu_{r}} \quad \\ & + \sum_{i<j=1}^4 \left[ V_{ij}^{C}+V_{ij}^{G}+\sum_{\chi=\pi,K,\eta} V_{ij}^{\chi} +V_{ij}^{\sigma}\right], \end{aligned} $

(1) where
$ m_i $ is the constituent mass of ith quark (antiquark).$\dfrac{{\boldsymbol p}^2_{ij}}{2\mu_{ij}} (ij=12; 34)$ and$\dfrac{{\boldsymbol p}^2_{r}}{2\mu_{r}}$ represent the inner kinetic of two-cluster and the relative motion kinetic between two clusters, respectively, with$ {{\boldsymbol p}}_{12}=\frac{m_2{{\boldsymbol p}}_1-m_1{{\boldsymbol p}}_2}{m_1+m_2}, \tag{2a}$

$ {{\boldsymbol p}}_{34}=\frac{m_4{{\boldsymbol p}}_3-m_3{{\boldsymbol p}}_4}{m_3+m_4}, \tag{2b} $

$ {{\boldsymbol p}}_{r}= \frac{(m_3+m_4){{\boldsymbol p}}_{12}-(m_1+m_2){{\boldsymbol p}}_{34}}{m_1+m_2+m_3+m_4}, \tag{2c}$

$ \mu_{ij}=\frac{m_im_j}{m_i+m_j}, \tag{2d}$

$ \mu_{r}=\frac{(m_1+m_2)(m_3+m_4)}{m_1+m_2+m_3+m_4}. \tag{2e} $

The potential energy is constituted from pieces describing quark confinement "
$ V_{ij}^C $ ," one-gluon-exchange (OGE) "$ V_{ij}^G $ ," Goldstone boson exchange "$ V_{ij}^{\chi=\pi, K, \eta} $ ," and scalar σ meson exchange. Their central part form for the four-quark system is as follows [40]:$ V_{ij}^{C}= ( -a_c r_{ij}^2-\Delta ) \boldsymbol{\lambda}_i^c \cdot \boldsymbol{\lambda}_j^c , \tag{3a}$

$ \begin{aligned}[b] V_{ij}^{G}&= \frac{\alpha_s}{4} \boldsymbol{\lambda}_i^c \cdot \boldsymbol{\lambda}_{j}^c \left[\frac{1}{r_{ij}}-\frac{2\pi}{3m_im_j}\boldsymbol{\sigma}_i\cdot \boldsymbol{\sigma}_j \delta(\boldsymbol{r}_{ij})\right], \\ \delta{(\boldsymbol{r}_{ij})} & = \frac{{\rm e}^{-r_{ij}/r_0(\mu_{ij})}}{4\pi r_{ij}r_0^2(\mu_{ij})}, r_0(\mu_{ij}) =s_0/\mu_{ij}, \end{aligned}\tag{3b} $

$ V_{ij}^{\pi}= \frac{g_{ch}^2}{4\pi}\frac{m_{\pi}^2}{12m_im_j} \frac{\Lambda_{\pi}^2}{\Lambda_{\pi}^2-m_{\pi}^2}m_\pi v_{ij}^{\pi} \sum_{a=1}^3 \lambda_i^a \lambda_j^a, \tag{3c} $

$ V_{ij}^{K}= \frac{g_{ch}^2}{4\pi}\frac{m_{K}^2}{12m_im_j} \frac{\Lambda_K^2}{\Lambda_K^2-m_{K}^2}m_K v_{ij}^{K} \sum_{a=4}^7 \lambda_i^a \lambda_j^a, \tag{3d} $

$ \begin{aligned}[b] V_{ij}^{\eta} =& \frac{g_{ch}^2}{4\pi}\frac{m_{\eta}^2}{12m_im_j} \frac{\Lambda_{\eta}^2}{\Lambda_{\eta}^2-m_{\eta}^2}m_{\eta} v_{ij}^{\eta} \\& \times \left[\lambda_i^8 \lambda_j^8 \cos\theta_p - \lambda_i^0 \lambda_j^0 \sin \theta_p \right], \\ v_{ij}^{\chi} =& \left[ Y(m_\chi r_{ij})- \frac{\Lambda_{\chi}^3}{m_{\chi}^3}Y(\Lambda_{\chi} r_{ij}) \right] \boldsymbol{\sigma}_i \cdot\boldsymbol{\sigma}_j, \end{aligned}\tag{3e} $

$ \begin{aligned}[b] V_{ij}^{\sigma}&= -\frac{g_{ch}^2}{4\pi} \frac{\Lambda_{\sigma}^2}{\Lambda_{\sigma}^2-m_{\sigma}^2}m_\sigma \times \left[ Y(m_\sigma r_{ij})-\frac{\Lambda_{\sigma}}{m_\sigma}Y(\Lambda_{\sigma} r_{ij})\right] , \\ Y(x) &= e^{-x}/x. \end{aligned}\tag{3f} $

$ \boldsymbol{\sigma} $ denotes the$S U(2)$ Pauli matrices;$ \boldsymbol{\lambda} $ and$ \boldsymbol{\lambda}^c $ are the$ S U(3) $ flavor and color Gell-Mann matrices, respectively;$ g^2_{ch}/4\pi $ is the chiral coupling constant, determined from the π-nucleon coupling; and$ \alpha_s $ is an effective scale-dependent running coupling [40],$ \alpha_s(\mu_{ij})=\frac{\alpha_0}{\ln\left[(\mu_{ij}^2+\mu_0^2)/\Lambda_0^2\right]}. $

(4) $\Lambda_0,~\alpha_0,~\mu_0,~s_0$ are adjustable model parameters, and$ \theta_p $ is fixed by η and$ \eta^{'} $ mixing.It is important to note that the noncentral parts of the OGE, tensor and spin-orbit forces, between quarks are omitted in the present calculations because only
$ S\rm{-} $ wave tetraquarks are studied here, and the contributions of the noncentral part are small or approximatively zero. Second, for$QQ\bar{q}\bar{s}\; (Q=c, b; q=u, s)$ systems, the Goldstone bosons potential$ V^{\pi} $ and$ V^{\sigma} $ will be zero herein. Lastly, we present the model parameters [41] in Table 1. We note that, in reference [41], the confinement item takes the form$V^{C}_{ij}=\big[-a_c(1-{\rm e}^{-\mu_c r_{ij}}\big)+\Delta](\boldsymbol{\lambda}_i^c \cdot \boldsymbol{\lambda}_j^c)$ . In our present calculations, the usual quadratic confinement$ V^{C}_{ij}=( -a_c r_{ij}^2-\Delta ) \boldsymbol{\lambda}_i^c \cdot \boldsymbol{\lambda}_j^c $ is employed, and thus, some parameters such as quark mass,$ a_c $ , and Δ are different.Quark masses $ m_u=m_d $ 

313 /MeV $ m_s $ 

536 $ m_c $ 

1728 $ m_b $ 

5112 Goldstone bosons $ m_{\pi} $ 

0.70 (fm $ ^{-1} \sim 200\, $ MeV)

$ m_{\sigma} $ 

3.42 $ m_{\eta} $ 

2.77 $ m_{K} $ 

2.51 $ \Lambda_{\pi}=\Lambda_{\sigma} $ 

4.2 $ \Lambda_{\eta}=\Lambda_{K} $ 

5.2 $ g_{ch}^2/(4\pi) $ 

0.54 $ \theta_p(^\circ) $ 

−15 Confinement $ a_c $ /MeV· fm

$ ^{-2} $ 

101 Δ /MeV −78.3 OGE $ \alpha_0 $ 

3.67 $\Lambda_0/{\rm fm}^{-1}$ 

0.033 $ \mu_0 $ /MeV

36.98 $ s_0 $ /MeV

28.17 Table 1. Model parameters, determined by fitting the meson spectra.
In this work, using the model parameters, we calculated the ground-state masses of most mesons, especially the relevant mesons D,
$ D^* $ ,$ D_s $ ,$ D_s^* $ , B,$ B^* $ ,$ B_s $ , and$ B_s^* $ , which are listed in Table 2. From the table, we can find that the quark model achieves great success in describing the hadron spectra, especially for the ground-state heavy mesons.Meson $ I(J^P) $ 

Mass PDG [42] π $ 1(0^-) $ 

139.3 139.6 K $ \frac{1}{2}(0^-) $ 

493.9 493.7 ρ $ 1(1^-) $ 

772.0 770.0 $ K^* $ 

$ \frac{1}{2}(1^-) $ 

914.0 892.0 ω $0 (1^-)$ 

701.6 782.7 η $ 0(0^-) $ 

669.2 547.0 $ \phi(1020) $ 

$ 0(1^-) $ 

1016.5 1019.4 $ \eta_c(1s) $ 

$ 0(0^-) $ 

2986.3 2983.6 $ J/\Psi $ 

$ 0(1^-) $ 

3096.4 3096.9 $ D^0 $ 

$ \frac{1}{2}(0^-) $ 

1862.6 1864.8 $ D^{*0} $ 

$ \frac{1}{2}(1^-) $ 

1980.6 2007.0 $ D_s^+ $ 

$ 0(0^-) $ 

1950.2 1968.3 $ D_s^{*+} $ 

$ 0(1^-) $ 

2079.9 2112.2 $ B^- $ 

$ \frac{1}{2}(0^-) $ 

5280.8 5279.3 $ B^{*-} $ 

$ \frac{1}{2}(1^-) $ 

5319.6 5325.2 $ \bar{B_s}^0 $ 

$ 0(0^-) $ 

5367.7 5366.8 $ \bar{B_s^*}^0 $ 

$ 0(1^-) $ 

5410.2 5415.4 $ \eta_b(1s) $ 

$ 0(0^-) $ 

9334.7 9399.1 $ \Upsilon(1s) $ 

$ 0(1^-) $ 

9463.9 9460.3 Table 2. Ground-state masses of the mesons in the chiral quark model in comparison with the experimental data [42] (unit: MeV).
-
The properties of the double-heavy tetraquark states can be obtained with a complete wave function, which should be a direct product of the orbital, spin, color, and flavor wave functions that contribute to a given well defined quantum number
$ I(J^P) $ .For the orbital part, in our calculations, the orbital wave function is
$ \Psi_{L}^{M_{L}}=\left[[\Psi_{l_1}({\boldsymbol r})\Psi_{l_2}({\boldsymbol R})]_{l_{12}}\Psi_{L_r}(\boldsymbol{Z}) \right]_{L}^{M_{L}}, $

(5) where
$\boldsymbol{r}$ ,$\boldsymbol{R}$ , and$\boldsymbol{Z}$ are the relative spatial coordinates, and one of the definitions of the Jacobi coordinates can be written as follows:$ \begin{aligned}[b] {\boldsymbol{r}}&=r_1-r_2, \\ \boldsymbol{R}&=r_3-r_4, \\ \boldsymbol{Z}&=\frac{m_1{\bf r}_1+m_2{\bf r}_2}{m_1+m_2}-\frac{m_3{\bf r}_3+m_4{\bf r}_4}{m_3+m_4}, \\ \boldsymbol{R}_c&=\frac{m_1{\bf r}_1+m_2{\bf r}_2+m_3{\bf r}_3+m_4{\bf r}_4}{m_1+m_2+m_3+m_4}. \end{aligned} $

(6) $\boldsymbol{R}_c$ is the center-of-mass coordinate. In Eq. (5),$ l_1 $ ,$ l_2 $ is the inner angular momentum of the two sub-cluster;$ L_r $ is the relative angular momentum between two sub clusters. L is the total orbital angular momentum of the four-quark system, with$ L=l_1 \oplus l_2 \oplus L_r $ . In the present work, we just consider the low-lying$ S\rm{-} $ wave double heavy tetraquark states, and hence, it is natural to assume that all the orbital angular momenta are zeros. The parity of the double-heavy tetraquarks$ QQ\bar{q}\bar{s} $ can be expressed in terms of the relative orbital angular momenta, with$ P=(-1)^{l_1+l_2+L_r} =+1 $ . Therefore, to obtain reliable information of the four-quark system, a high precision numerical method, the Gaussian expansion method (GEM) [43], is applied in our work. In the GEM, any relative motion wave function can be expanded in a series of Gaussian basis functions,$ \Psi_{l}^{m}(\mathbf{x}) = \sum_{n=1}^{n_{\rm max}} c_{n}N_{nl}x^{l} {\rm e}^{-\nu_{n}x^2}Y_{lm}(\hat{\mathbf{x}}), $

(7) where
$ N_{nl} $ denotes normalization constants,$ N_{nl}=\left[\frac{2^{l+2}(2\nu_{n})^{l+\frac{3}{2}}}{\sqrt{\pi}(2l+1)} \right]^\frac{1}{2}. $

(8) $ c_n $ represents the variational parameters, which are determined dynamically. The Gaussian size parameters are chosen according to the following geometric progression:$ \nu_{n}=\frac{1}{r^2_n}, \quad r_n=r_1a^{n-1}, \quad a=\left(\frac{r_{n_{\rm max}}}{r_1}\right)^{\frac{1}{n_{\rm max}-1}}. $

(9) This procedure enables optimization of the expansion using just a small number of Gaussians. For example, to obtain the stable ground-state masses of mesons in Table 2, we take
$ \begin{equation} r_1=0.01\; {\rm fm}, \quad {r}_{{n}_{\rm max}}=2\; {\rm fm}, \quad {n}_{\rm{max}}=12. \end{equation} $

(10) For the spin part, we first write down the wave functions for the two-quark system,
$ \chi_{11}=\alpha\alpha, \tag{11a} $

$ \chi_{10}=\frac{1}{\sqrt{2}}(\alpha\beta+\beta\alpha), \tag{11b}$

$ \chi_{1-1}=\beta\beta, \tag{11c} $

$ \chi_{00}=\frac{1}{\sqrt{2}}(\alpha\beta-\beta\alpha). \tag{11d} $

If the spin of one cluster is coupled to
$ S_1 $ and that of another cluster to$ S_2 $ , the total spin wave function of the four-quark system can be obtained as$ S=S_1 \oplus S_2 $ ,$ \chi_{00=0\oplus0}^{\sigma1}=\chi_{00}\chi_{00}, \tag{12a} $

$ \chi_{00=1\oplus1}^{\sigma2}=\sqrt{\frac{1}{3}}(\chi_{11}\chi_{1-1}-\chi_{10}\chi_{10}+\chi_{1-1}\chi_{11}), \tag{12b} $

$ \chi_{11=0\oplus1}^{\sigma3}=\chi_{00}\chi_{11}, \tag{12c} $

$ \chi_{11=1\oplus0}^{\sigma4}=\chi_{11}\chi_{00},\tag{12d} $

$ \chi_{11=1\oplus1}^{\sigma5}=\frac{1}{\sqrt{2}}(\chi_{11}\chi_{10}-\chi_{10}\chi_{11}), \tag{12e} $

$ \chi_{22=1\oplus1}^{\sigma6}=\chi_{11}\chi_{11}. \tag{12f} $

The subscript of χ represents the
$ SM_S=S_1 \oplus S_2 $ , and$ M_S $ is the third projection of the total spin S.For the meson-meson picture, the indices of particles are "1234," and for the diquark-antidiquark picture, the indices are "1324." For the color part, in the meson-meson picture, the colorless wave functions can be obtained from
$ \big[[Q\bar{q}]_{1_c}[Q\bar{s}]_{1_c}\big]_1 $ or$ \big[[Q\bar{q}]_{8_c}[Q\bar{s}]_{8_c}\big]_1 $ . In the diquark-antidiquark picture, the color representation of the diquark maybe antisymmetrical$ [QQ]_{\bar{3}_c} $ or symmetrical$ [QQ]_{6_c} $ , and for the antidiquark, the color form is antisymmetrical$ [\bar{q}\bar{s}]_{3_c} $ or symmetrical$ [\bar{q}\bar{s}]_{\bar{6}_c} $ . There are two rules to couple the diquark and antidiquark into a colorless wave function: one is the good diquark with attractive interaction$ \big[[QQ]_{\bar{3}_c}[\bar{q}\bar{s}]_{3_c}\big]_1 $ , and another is the bad diquark with repulsive interaction$ \big[[QQ]_{6_c}[\bar{q}\bar{s}]_{\bar{6}_c}\big]_1 $ . Thus, we can easily write down the color wave functions in the meson-meson picture and the diquark-antidiquark picture, respectively.$ \chi^{c1}_{1 \otimes 1}=\frac{1}{3}(r\bar{r}+g\bar{g}+b\bar{b})_{12}(r\bar{r}+g\bar{g}+b\bar{b})_{34}, \tag{13a}$

$ \begin{aligned}[b] \chi^{c2}_{8 \otimes 8}=&\frac{\sqrt{2}}{12}(3r\bar{b}b\bar{r}+3r\bar{g}g\bar{r}+3g\bar{b}b\bar{g}+3b\bar{g}g\bar{b} +3g\bar{r}r\bar{g}\\ &+3b\bar{r}r\bar{b}+2r\bar{r}r\bar{r}+2g\bar{g}g\bar{g}+2b\bar{b}b\bar{b}-r\bar{r}g\bar{g} \\ &-g\bar{g}r\bar{r}-b\bar{b}g\bar{g} -b\bar{b}r\bar{r}-g\bar{g}b\bar{b}-r\bar{r}b\bar{b})_{1234}, \end{aligned}\tag{13b} $

$ \begin{aligned}[b] \chi^{c3}_{\bar{3} \otimes 3}=&\frac{\sqrt{3}}{6}(rg\bar{r}\bar{g}-rg\bar{g}\bar{r}+gr\bar{g}\bar{r}-gr\bar{r}\bar{g} +rb\bar{r}\bar{b}-rb\bar{b}\bar{r}\\&+br\bar{b}\bar{r}-br\bar{r}\bar{b} +gb\bar{g}\bar{b}-gb\bar{b}\bar{g}+bg\bar{b}\bar{g}-bg\bar{g}\bar{b})_{1324}, \end{aligned}\tag{13c} $

$ \begin{aligned}[b] \chi^{c4}_{6 \otimes \bar{6}}=&\frac{\sqrt{6}}{12}(2rr\bar{r}\bar{r}+2gg\bar{g}\bar{g}+2bb\bar{b}\bar{b}+rg\bar{r}\bar{g} \\ &+rg\bar{g}\bar{r}+gr\bar{g}\bar{r}+gr\bar{r}\bar{g}+rb\bar{r}\bar{b} \\ &+rb\bar{b}\bar{r}+br\bar{b}\bar{r}+br\bar{r}\bar{b}+gb\bar{g}\bar{b} \\ &+gb\bar{b}\bar{g}+bg\bar{b}\bar{g}+bg\bar{g}\bar{b})_{1324}. \end{aligned}\tag{13d} $

For the flavor wave functions of the
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ systems, the quarks, Q and s, have no contributions to the total isospin, which is only determined by the flavor of$ \bar{q} $ . There are six types of the flavor wave functions in the diquark-antidiquark picture,$ \chi^{d1}=(QQ\bar{s}\bar{s})_{1324},\tag{14a} $

$ \chi^{d2}=(QQ\bar{u}\bar{s})_{1324},\tag{14b} $

$ \chi^{d3}=(QQ\bar{s}\bar{u})_{1324}, \tag{14c} $

$ \chi^{d4}=(bc\bar{s}\bar{s})_{1324}, \tag{14d} $

$ \chi^{d5}=(bc\bar{u}\bar{s})_{1324}, \tag{14e} $

$ \chi^{d6}=(bc\bar{s}\bar{u})_{1324}. \tag{14f} $

For the meson-meson picture, the flavor wave functions can be expressed as
$ \chi^{t1}=(Q\bar{s}Q\bar{s})_{1234},\tag{15a} $

$ \chi^{t2}=(Q\bar{u}Q\bar{s})_{1234}, \tag{15b} $

$ \chi^{t3}=(Q\bar{s}Q\bar{u})_{1234},\tag{15c} $

$ \chi^{t4}=(b\bar{s}c\bar{s})_{1234},\tag{15d} $

$ \chi^{t5}=(b\bar{u}c\bar{s})_{1234},\tag{15e} $

$ \chi^{t6}=(b\bar{s}c\bar{u})_{1234}.\tag{15f} $

We note that the subscripts of the wave functions for color and flavor stand for the indices of particles. Taking all the degrees of freedom into account, we present the spin-flavor-color basis of the
$ S\rm{-} $ wave$ QQ\bar{q}\bar{s}\; (Q= c, b; q= u, s) $ systems constrained by the Pauli principle in Table 3. Finally, the complete wave function$ \Psi_{IJ}^{M_IM_J} $ is obtained by coupling the orbital and spin, flavor, and color wave functions. Actually, a real physical state should be the mixture of these basis with the same quantum numbers$ I(J^P) $ . Moreover, we can obtain the ground-state masses and the eigenvectors of the double-heavy strange tetraquarks by solving the Schrödinger equation with the Rayleigh-Ritz variational principle,$ QQ\bar{s}\bar{s} $ 

$ QQ\bar{u}\bar{s} $ 

$ bc\bar{s}\bar{s} $ 

$ bc\bar{u}\bar{s} $ 

$ 0(0^+) $ 

$ 0(1^+) $ 

$ 0(2^+) $ 

$ \frac{1}{2}(0^+) $ 

$ \frac{1}{2}(1^+) $ 

$ \frac{1}{2}(2^+) $ 

$ 0(0^+) $ 

$ 0(1^+) $ 

$ 0(2^+) $ 

$ \frac{1}{2}(0^+) $ 

$ \frac{1}{2}(1^+) $ 

$ \frac{1}{2}(2^+) $ 

$ (\sigma1,t1,c1) $ 

$ (\sigma3,t1,c1) $ 

$ (\sigma6,t1,c1) $ 

$ (\sigma1,t2,c1) $ 

$ (\sigma3,t2,c1) $ 

$ (\sigma6,t2,c1) $ 

$ (\sigma1,t3,c1) $ 

$ (\sigma3,t3,c1) $ 

$ (\sigma6,t3,c1) $ 

$ (\sigma1,t5,c1) $ 

$ (\sigma3,t5,c1) $ 

$ (\sigma6,t5,c1) $ 

$ (\sigma1,t1,c2) $ 

$ (\sigma3,t1,c2) $ 

$ (\sigma6,t1,c2) $ 

$ (\sigma1,t2,c2) $ 

$ (\sigma3,t2,c2) $ 

$ (\sigma6,t2,c2) $ 

$ (\sigma1,t3,c2) $ 

$ (\sigma3,t3,c2) $ 

$ (\sigma6,t3,c2) $ 

$ (\sigma1,t5,c2) $ 

$ (\sigma3,t5,c2) $ 

$ (\sigma6,t5,c2) $ 

$ (\sigma2,t1,c1) $ 

$ (\sigma4,t1,c1) $ 

$ (\sigma6,d1,c3) $ 

$ (\sigma2,t2,c1) $ 

$ (\sigma4,t2,c1) $ 

$ (\sigma6,t3,c1) $ 

$ (\sigma2,t3,c1) $ 

$ (\sigma4,t3,c1) $ 

$ (\sigma6,d3,c3) $ 

$ (\sigma2,t5,c1) $ 

$ (\sigma4,t5,c1) $ 

$ (\sigma6,t6,c1) $ 

$ (\sigma2,t1,c2) $ 

$ (\sigma4,t1,c2) $ 

$ (\sigma2,t2,c2) $ 

$ (\sigma4,t2,c2) $ 

$ (\sigma6,t3,c2) $ 

$ (\sigma2,t3,c2) $ 

$ (\sigma4,t3,c2) $ 

$ (\sigma2,t5,c2) $ 

$ (\sigma4,t5,c2) $ 

$ (\sigma6,t6,c2) $ 

$ (\sigma1,d1,c4) $ 

$ (\sigma5,d1,c3) $ 

$ (\sigma1,t3,c1) $ 

$ (\sigma5,t2,c1) $ 

$ (\sigma6,d2,c3) $ 

$ (\sigma1,d3,c4) $ 

$ (\sigma5,t3,c1) $ 

$ (\sigma1,t6,c1) $ 

$ (\sigma5,t5,c1) $ 

$ (\sigma6,d5,c3) $ 

$ (\sigma2,d1,c3) $ 

$ (\sigma1,t3,c2) $ 

$ (\sigma5,t2,c2) $ 

$ (\sigma6,d3,c3) $ 

$ (\sigma2,d3,c3) $ 

$ (\sigma5,t3,c2) $ 

$ (\sigma1,t6,c2) $ 

$ (\sigma5,t5,c2) $ 

$ (\sigma6,d5,c4) $ 

$ (\sigma2,t3,c1) $ 

$ (\sigma3,t3,c1) $ 

$ (\sigma3,d3,c3) $ 

$ (\sigma2,t6,c1) $ 

$ (\sigma3,t6,c1) $ 

$ (\sigma6,d6,c3) $ 

$ (\sigma2,t3,c2) $ 

$ (\sigma3,t3,c2) $ 

$ (\sigma4,d3,c4) $ 

$ (\sigma2,t6,c2) $ 

$ (\sigma3,t6,c2) $ 

$ (\sigma6,d6,c4) $ 

$ (\sigma1,d2,c4) $ 

$ (\sigma4,t3,c1) $ 

$ (\sigma5,d3,c3) $ 

$ (\sigma1,d5,c3) $ 

$ (\sigma4,t6,c1) $ 

$ (\sigma2,d2,c3) $ 

$ (\sigma4,t3,c2) $ 

$ (\sigma1,d5,c4) $ 

$ (\sigma4,t6,c2) $ 

$ (\sigma1,d3,c4) $ 

$ (\sigma5,t3,c1) $ 

$ (\sigma2,d5,c3) $ 

$ (\sigma5,t6,c1) $ 

$ (\sigma2,d3,c3) $ 

$ (\sigma5,t3,c2) $ 

$ (\sigma2,d5,c4) $ 

$ (\sigma5,t6,c2) $ 

$ (\sigma3,d2,c4) $ 

$ (\sigma1,d6,c3) $ 

$ (\sigma3,d5,c3) $ 

$ (\sigma4,d2,c3) $ 

$ (\sigma1,d6,c4) $ 

$ (\sigma3,d5,c4) $ 

$ (\sigma5,d2,c3) $ 

$ (\sigma2,d6,c3) $ 

$ (\sigma4,d5,c3) $ 

$ (\sigma3,d3,c4) $ 

$ (\sigma2,d6,c4) $ 

$ (\sigma4,d5,c4) $ 

$ (\sigma4,d3,c3) $ 

$ (\sigma5,d5,c3) $ 

$ (\sigma5,d3,c3) $ 

$ (\sigma5,d5,c4) $ 

$ (\sigma3,d6,c3) $ 

$ (\sigma3,d6,c4) $ 

$ (\sigma4,d6,c3) $ 

$ (\sigma4,d6,c4) $ 

$ (\sigma5,d6,c3) $ 

$ (\sigma5,d6,c4) $ 

Table 3. Spin-flavor-color basis of S-wave
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ systems constrained by the Pauli principle. For simplicity, in the table, we use the superscripts of χ to represent the wave functions, such as$ \chi_{00=0\oplus0}^{\sigma1}=\sigma1 $ ,$ \chi^{c1}_{1 \otimes 1} = c1 $ , and$ \chi^{d1}=d1 $ .$ H \, \Psi^{\,M_IM_J}_{IJ}=E^{IJ} \Psi^{\,M_IM_J}_{IJ}. $

(16) -
In the framework of the chiral quark model, we present a systematic calculation about the double-heavy tetraquarks with strange flavor
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ . The converged numerical ground-state masses are obtained by solving the four-body Schrödinger equation with the GEM. As we all know, a system always tends to take the position with the lowest energy. For a four-quark system, there is a stable configuration with two well separated mesons, which we call the threshold and plays an important role here. A tetraquark state should be stable against strong interaction if its energy lies below all possible two-meson thresholds, and the decay must be weak or electromagnetic interaction. If the state has the energy higher than the sum of the masses of two mesons, the tetraquark state can fall apart into two mesons via strong interaction. Resonance states may exist. In the following, we will present our numerical results of looking for possible bound states and resonance states for$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ . -
In this subsection, we try to find the promising stable bound states for
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ . The chiral quark model predictions on the lowest energies of the double-heavy strange tetraquark states with a set of given$ I(J^P) $ are presented in Table 4. In the table,$ E_{\rm{MM}} $ and$ E_{\rm{DA}} $ represent the ground-state mass only in the pure meson-meson (MM) and diquark-antidiquark (DA) pictures, respectively.$ E_{cc} $ is the ground-state energy considering the coupling of the MM and DA pictures. We express the theoretical lowest threshold of the double-heavy strange tetraquark as$ E_{\rm{Theo}} $ , with$ E_{\rm{Theo}}= $ Mass(meson1) + Mass(meson2). The relevant masses of mesons can be found in Table 2. The binding energy of the states can be therefore defined asFlavor $ I(J^P) $ 

$ E_{\rm{MM}} $ 

$ E_{\rm{DA}} $ 

$ E_{cc} $ 

$ E_{\rm{Theo}} $ 

$ E_{\rm{B}} $ 

$ cc\bar{s}\bar{s} $ 

$ 0(0^+) $ 

3906.5 4217.4 3906.5 3900.4( $ D_s^+D_s^+ $ )

6.1 $ 0(1^+) $ 

4033.8 4281.9 4033.8 4030.1( $ D_s^+D_s^{*+} $ )

3.7 $ 0(2^+) $ 

4161.2 4345.5 4161.0 4159.8( $ D_s^{*+}D_s^{*+} $ )

1.2 $ bb\bar{s}\bar{s} $ 

$ 0(0^+) $ 

10736.5 10891.0 10736.5 10735.4( $ \bar{B}_s^0\bar{B}_s^0 $ )

1.1 $ 0(1^+) $ 

10778.8 10916.4 10778.8 10777.9( $ \bar{B}_s^0\bar{B}_s^{*0} $ )

0.9 $ 0(2^+) $ 

10820.9 10943.9 10820.9 10820.4( $ \bar{B}_s^{*0}\bar{B}_s^{*0} $ )

0.5 $ cc\bar{u}\bar{s} $ 

$ \dfrac{1}{2}(0^+) $ 

3814.3 4193.5 3814.2 3812.8( $ D^0D_s^+ $ )

1.4 $ \dfrac{1}{2}(1^+) $ 

3933.0 4020.9 3923.8 3930.8( $ D^{*0}D_s^+ $ )

−7.0 $ \dfrac{1}{2}(2^+) $ 

4063.0 4289.1 4062.9 4060.5( $ D^{*0}D_s^{*+} $ )

2.4 $ bb\bar{u}\bar{s} $ 

$ \dfrac{1}{2}(0^+) $ 

10649.2 10834.9 10649.2 10648.5( $ B^-\bar{B}_s^0 $ )

0.7 $ \dfrac{1}{2}(1^+) $ 

10687.8 10615.9 10582.9 10687.3( $ B^{*-}\bar{B}_s^0 $ )

-104.4 $ \dfrac{1}{2}(2^+) $ 

10730.9 10877.5 10730.9 10729.8( $ B^{*-}\bar{B}_s^{*0} $ )

1.1 $ bc\bar{s}\bar{s} $ 

$ 0(0^+) $ 

7322.1 7650.7 7322.1 7317.9( $ \bar{B}_s^0D_s^+ $ )

4.2 $ 0(1^+) $ 

7364.3 7662.2 7364.3 7360.4( $ \bar{B}_s^{*0}D_s^+ $ )

3.9 $ 0(2^+) $ 

7491.1 7696.3 7491.1 7490.1( $ \bar{B}_s^{*0}D_s^{*+} $ )

1.0 $ bc\bar{u}\bar{s} $ 

$ \dfrac{1}{2}(0^+) $ 

7232.0 7317.8 7231.6 7230.3( $ \bar{B}_s^0D^0 $ )

1.3 $ \dfrac{1}{2}(1^+) $ 

7274.1 7334.2 7272.4 7269.8( $ B^{*-}D_s^{+} $ )

2.6 $ \dfrac{1}{2}(2^+) $ 

7392.2 7582.0 7392.1 7390.8( $ \bar{B}_s^{*0}D^{*0} $ )

1.3 Table 4. Ground-state mass of double-heavy strange tetraquarks
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ (unit: MeV).$ \begin{equation} E_{\rm{B}}=E_{cc}-E_{\rm{Theo}}. \end{equation} $

(17) In the table, we find that the energies are always lower in the MM picture than those in the DA picture except the
$ bb\bar{u}\bar{s} $ state with$ \dfrac{1}{2}(1^+) $ , and the coupling of the two pictures are small for the ground state for the double-heavy strange tetraquarks except the$ cc\bar{u}\bar{s} $ and$ bb\bar{u}\bar{s} $ states with$ \dfrac{1}{2}(1^+) $ . In our previous work about$ cc\bar{u}\bar{d} $ and$ bb\bar{u}\bar{d} $ tetraquarks, we also obtained the lower energies for the DA picture and the coupling of the two pictures cannot be neglected either [37]. In the last column in Table 4, we find two promising stable bound states. For the$ cc\bar{u}\bar{s} $ state with$\dfrac{1}{2}(1^+)$ , the chiral quark model indicates that the binding energy is approximately 7.0 MeV, which is well consistent with the lattice QCD result with 7.7 MeV binding energy [20]. For$ bb\bar{u}\bar{s} $ with$ \dfrac{1}{2}(1^+) $ , it has binding energy of 104.4 MeV. For the other double-heavy strange tetraquark states in Table 4, they all lie above the corresponding lowest thresholds within the chiral quark model.In Table 5, the contributions of each potential in the system Hamiltonian of the
$ cc\bar{u}\bar{s} $ and$ bb\bar{u}\bar{s} $ systems with$ I(J^P)=\dfrac{1}{2}(1^+) $ are given for comparison. From the table, we can easily find that, for the$ bb\bar{u}\bar{s} $ system, the K meson exchange is much larger than that for the$ cc\bar{u}\bar{s} $ system and plays a role in obtaining the deeper bound energy. Because of the larger mass of the b quark compared to that of the c quark, the relative kinetic energy will diminish. The repulsion of the system will decrease, and attraction will be predominant. The original stable state is broken, which leads to a smaller distance between quarks. For the K meson exchange, it will become larger with the decrease in quark distance.$ cc\bar{u}\bar{s} $ 

$ bb\bar{u}\bar{s} $ 

$ K_1 $ 

434.6 546.0 $ K_2 $ 

384.0 394.2 $ K_3 $ 

202.7 166.8 $ V^{\rm{C}} $ 

−457.5 −507.5 $ V^{\rm{Coul}} $ 

−648.8 −658.1 $ V^{\rm{CMI}} $ 

−204.3 −212.9 $ V^{\eta} $ 

−17.0 −40.5 $ V^{\pi} $ 

0.0 0.0 $ V^{\sigma} $ 

−24.9 −47.2 $ V^{K} $ 

−74.9 −178.1 E 3923.8 10582.9 $ \Delta E $ 

−7.0 −104.4 Table 5. Contributions of each potential in the system Hamiltonian of the
$ cc\bar{u}\bar{s} $ and$ bb\bar{u}\bar{s} $ systems with$ I(J^P)=\frac{1}{2}(1^+) $ , when considering the coupling of the meson-meson structure and diquark-antidiquark structure.$ K_1 $ ,$ K_2 $ , and$ K_3 $ represent the inner kinetic energy and relative kinetic energy between two clusters.$ \Delta E $ is the binding energy of the system (unit: MeV).In our previous work about
$ T_{cc} $ states with$ 0(1^+) $ , we obtained a deep bound state when all the structures, meson-meson and diquark-antidiquark, were considered. Further, the model can obtain a very shallow bound state, which is very consistent with the experimental data, if the structure is limited to the meson-meson one. Now, when we replace the d quark with the heavier s quark, we reach different conclusions. We cannot find the bound states in the pure meson-meson or diquark-antidiquark structures, but a shallow bound state with binding energy of −7.0 MeV is obtained in the calculations of structure coupling. It would perhaps helpful to trace the appearance of the deep bound state in nonstrange systems (or equivalently, the absence of the deep bound state in the strange system). Thus, to understand the difference in the binding energy of$ T_{cc} $ and$ cc\bar{u}\bar{s} $ , we give the contributions of each potential in the system Hamiltonian by considering the couplings of the meson-meson and diquark-antidiquark structures in Table 6. We can easily find that for$ T_{cc} $ , π meson exchange plays an important role in obtaining a bound state. In comparison, for the$ cc\bar{u}\bar{s} $ system, the kaon exchange is weaker than the pion exchange because of the s quark's larger mass.$ T_{cc} $ 

$ cc\bar{u}\bar{s} $ 

$ K_1 $ 

321.8 434.6 $ K_2 $ 

929.7 384.0 $ K_3 $ 

189.9 202.7 $ V^{\rm{C}} $ 

−432.8 −457.5 $ V^{\rm{Coul}} $ 

−645.8 −648.8 $ V^{\rm{CMI}} $ 

−346.4 −204.3 $ V^{\eta} $ 

75.4 −17.0 $ V^{\pi} $ 

−464.6 0.0 $ V^{\sigma} $ 

−48.8 −24.9 $ V^{K} $ 

0 −74.9 E 3660.7 3923.8 $ \Delta E $ 

−182.5 −7.0 Table 6. Contributions of each potential in the system Hamiltonian of
$ T_{cc} $ states with$ I(J^P)=0(1^+) $ and$ cc\bar{u}\bar{s} $ system with$ I(J^P)=\frac{1}{2}(1^+) $ , when considering the coupling of the meson-meson and diquark-antidiquark structures.$ \Delta E $ is the binding energy of the state (unit: MeV).In Table 7, we list the binding energies (
$ \Delta E $ ) of the diquark$ \bar{u}\bar{d} $ and$ \bar{u}\bar{s} $ , along with the contributions of each potential in the system Hamiltonian. The second and third columns indicate that$ \bar{u}\bar{d} $ is much easier to be the bound state than$ \bar{u}\bar{s} $ . If we take the mass of the s quark to be that of the d quark, we obtain the deeper bound energy due to the stronger kaon exchange in the fourth column. If we take the mass of K to be that of π, the kaon exchange does not seem to change significantly. By tuning$ m_s $ and$ m_K $ , we find that the main reason for the shallow bound state of the$ cc\bar{u}\bar{s} $ system is the heavier mass of the s quark.$ \bar{u}\bar{d} $ 

$ \bar{u}\bar{s} $ 

$ \begin{aligned}M_s=536,\\M_K=494 \end{aligned}$ 

$ \begin{aligned}M_s=313,\\M_K=494\end{aligned} $ 

$ \begin{aligned}M_s=536,\\M_K=139\end{aligned} $ 

$ K_2 $ 

970.4 686.9 1133.8 624.2 $ V^{\rm{C}} $ 

−85.8 −87.3 −103 −82.9 $ V^{\rm{Coul}} $ 

−208.9 −184.3 −224 −176.2 $ V^{\rm{CMI}} $ 

−330.4 −204.7 −393 −180.9 $ V^{\eta} $ 

80.4 −40.2 −93.9 −35.2 $ V^{\pi} $ 

−495.3 0 0 0 $ V^{\sigma} $ 

−51.1 −46.9 −54.4 −44.7 $ V^{K} $ 

0 −176.7 −411.8 −156.8 $ \Delta E $ 

−120.7 −53.2 −146.3 −52.5 Table 7. Mass of the diquark
$ \bar{u}\bar{d} $ and$ \bar{u}\bar{s} $ .$ \Delta E $ is the binding energy of the state (unit: MeV).Moreover, in Table 8, we present the binding energy of the state
$ bb\bar{u}\bar{s} $ with$ \dfrac{1}{2}(1^+) $ within various theoretical methods for comparison. In the table, most of the studies obtain the bound state for this state, but the binding energy is different from each other. In general, the value is approximately 10$ \sim $ 50 MeV in the quark model [8, 9, 13–15, 27, 30], 100 MeV in the lattice QCD calculations [10, 20, 21, 26], and 180$ \sim $ 500 MeV in the QCD sum rules [22, 28]. In references [31, 32], the authors obatined no bound states for$ bb\bar{u}\bar{s} $ with$ \dfrac{1}{2}(1^+) $ in the relativistic quark model. Our results for$ bb\bar{u}\bar{s} $ with$ \dfrac{1}{2}(1^+) $ state are also well consistent with the lattice QCD calculations [10, 20, 21, 26].Table 8. Stable tetraquark state
$ bb\bar{u}\bar{s} $ with quantum numbers$ I(J^P)=\frac{1}{2}(1^+) $ in various methods (unit: MeV). -
Next we try to find possible resonance states for double-heavy strange tetraquarks
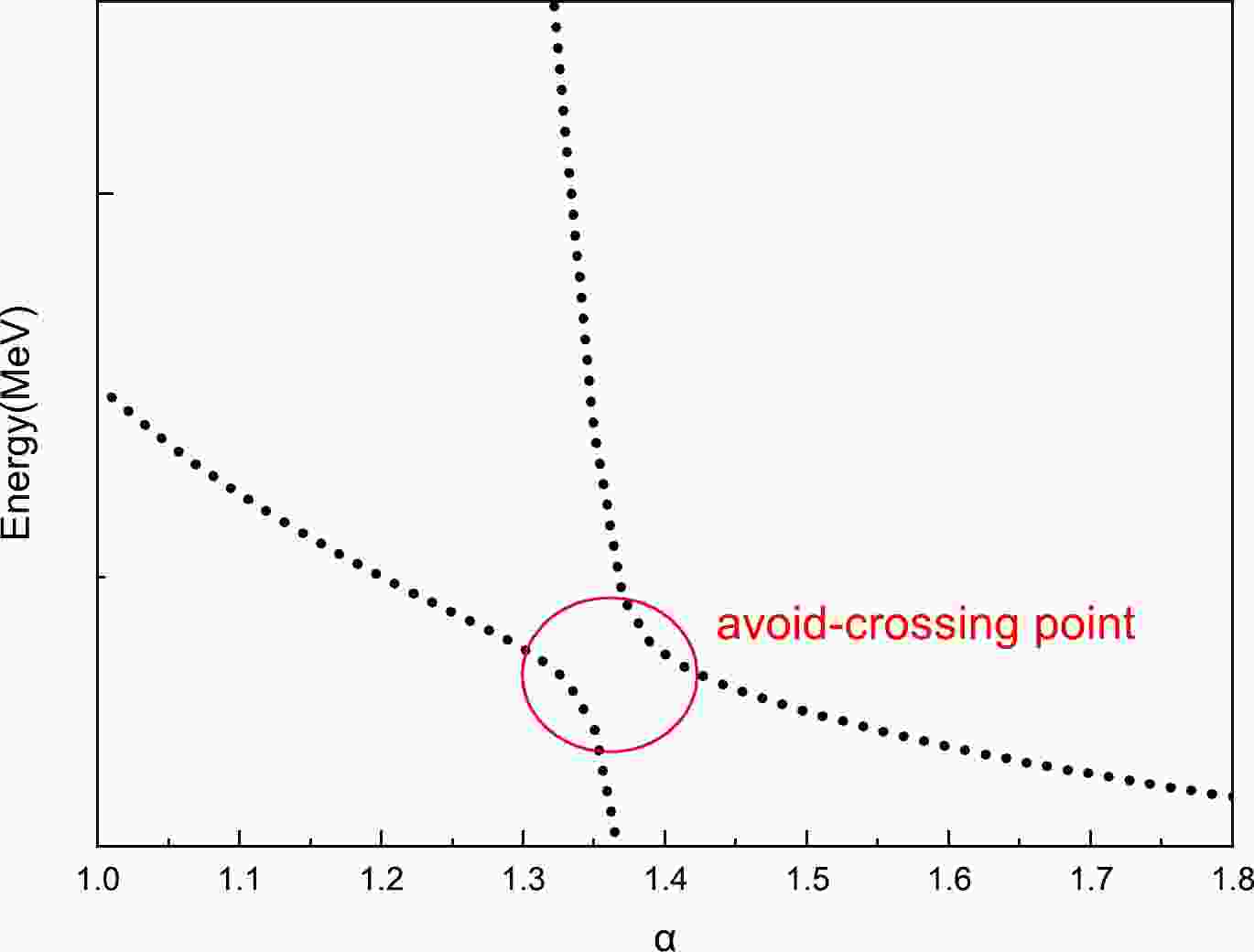
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ . Herein, the RSM [39] is applied to find the genuine resonances. In the RSM, the Gaussian range parameters$ r_n $ in Eq. (9), only for the meson-meson picture with the color singlet-singlet configuration, are scaled as$ r_n \rightarrow \alpha r_n $ . In our calculations, α takes values from 1.0 to 3.0. When α is varied, the distance of the two color-singlet mesons is scaled with α. The energy eigenvalues of the scattering states decrease as α increases. For the bound states, they are shown as straight lines, and resonance states appear as an avoid-crossing structure such as that in Fig. 1. Thus, the α dependence of energy eigenvalues can be used to distinguish resonance states from scattering states. The results are presented in Figs. 2 to 7.
Figure 2. (color online) Stabilization plots of the energies of
$ cc\bar{s}\bar{s} $ states with respect to the scaling factor α (unit: GeV).
Figure 7. (color online) Stabilization plots of the energies of
$ bc\bar{u}\bar{s} $ states with respect to the scaling factor α (unit: GeV).In Fig. 2, for the state
$ cc\bar{s}\bar{s} $ with$ 0(0^+) $ , the blue lines represent the theoretical thresholds$ D_s^+D_s^+ $ and$ D_s^{*+}D_s^{*+} $ . The red lines are the two possible resonance states with masses of 4176 and 4250 MeV. By analyzing the components of the resonance states, we found that, for the resonance with energy of 4176 MeV, the$ D_s^*D_s^* $ channel with the hidden color component takes up a larger proportion,$54$ %. For the resonance with energy of 4250 MeV, the$ D_sD_s $ channel with the hidden color component occupies a larger proportion,$ 44 $ %. We note that the wave function of resonance is not square-integrable and the proportions of different channels are defined in the sense of finite volume. The proportions of the resonances could be changed by varying the "finite volume." In our work, we normalize the scattering state in the finite space occupied by the bound state (in the calculation without open channels involved); then, the proportions of the various components in the resonances will not depend on the "finite volume" anymore. The details can be found in Ref. [44]. Besides, these proportions can reflect the strengths of the coupling between the resonances and the corresponding channels. For the$ 0(1^+) $ and$ 0(2^+) $ states, we find no resonance states. In Ref. [19], the authors also obtained a resonance state with an energy of 4256 MeV for$ 0(0^+) $ in the quark delocalization color screening model (QDCSM), which is well consistent with our results.In Fig. 3, for
$ bb\bar{s}\bar{s} $ states, we find one resonance for$ 0(0^+) $ ,$ 0(1^+) $ , and$ 0(2^+) $ with masses of 11343, 11354, and 11363 MeV, respectively. The resonance mechanism of these resonances also comes from the hidden color structure because the hidden color component occupies a large proportion.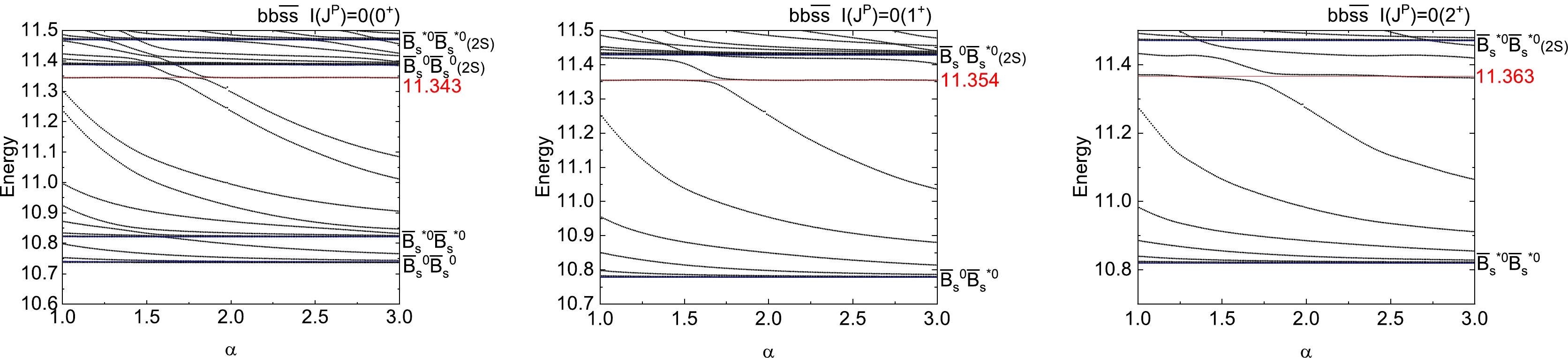
Figure 3. (color online) Stabilization plots of the energies of
$ bb\bar{s}\bar{s} $ states with respect to the scaling factor α (unit: GeV).In Fig. 4, there are more resonances for
$ bc\bar{s}\bar{s} $ . For example, we find one resonance with an energy of 7698 MeV for$ 0(0^+) $ coming from the hidden color channel resonance mechanism. For$ 0(1^+) $ , two possible resonances between 7.5 and 7.7 GeV are found. One with the energy of 7660 MeV comes from the diquark-antidiquark with$ 6\otimes\bar{6} $ color resonance mechanism, and the other with an energy of 7683 MeV comes from the$ B_s^*D_s $ hidden color channel resonance mechanism. For$ 0(2^+) $ , there are two resonances between 7.7 and 8.1 GeV, with energies of 7702 and 8089 MeV. They both come from the colorful channel resonance mechanism, with$ B_s^*D_s^* $ hidden color$ (71) $ % and diquark-antidiquark with$ 3\otimes\bar{3} $ $ (74) $ %, respectively.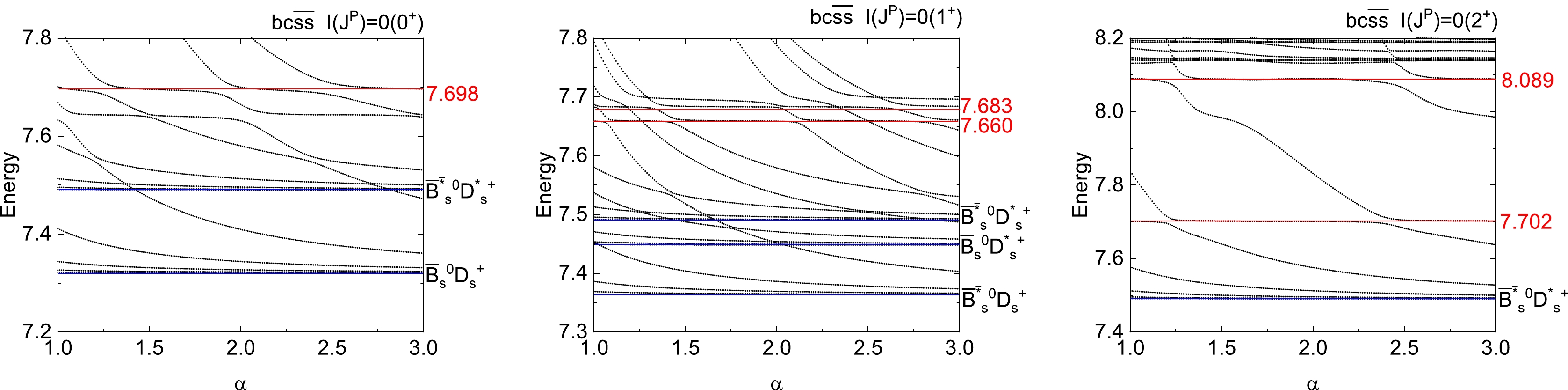
Figure 4. (color online) Stabilization plots of the energies of
$ bc\bar{s}\bar{s} $ states with respect to the scaling factor α (unit: GeV).For
$ cc\bar{u}\bar{s} $ , in Fig. 5, there is no resonance state for$ \dfrac{1}{2}(0^+) $ ,$ \dfrac{1}{2}(1^+) $ , and$ \dfrac{1}{2}(2^+) $ .
Figure 5. (color online) Stabilization plots of the energies of
$ cc\bar{u}\bar{s} $ states with respect to the scaling factor α (unit: GeV).For the
$ bb\bar{u}\bar{s} $ system in Fig. 6, we found no resonances for both$ \dfrac{1}{2}(0^+) $ and$ \dfrac{1}{2}(1^+) $ , but there is one resonance with an energy of 11307 MeV for$ \dfrac{1}{2}(2^+) $ . With a lower energy than that of the$ B^*B_s^*(2S) $ channel, this resonance state may come from the bound state of$ B^*B_s^*(2S) $ .
Figure 6. (color online) Stabilization plots of the energies of
$ bb\bar{u}\bar{s} $ states with respect to the scaling factor α (unit: GeV).In Fig. 7, for the
$ bc\bar{u}\bar{s} $ system, there are two resonance states for$ \dfrac{1}{2}(2^+) $ with energies of 7560 MeV and 7890 MeV. They also come from the color resonance mechanism because the hidden color channel and the diquark-antidiquark channels occupy a large component.Succinctly, we collect all the resonance states in Table 9.
Flavor $ I(J^P) $ 

Resonance states $ cc\bar{s}\bar{s} $ 

$ 0(0^+) $ 

4.176 4.250 $ 0(1^+) $ 

··· $ 0(2^+) $ 

··· $ bb\bar{s}\bar{s} $ 

$ 0(0^+) $ 

11.343 $ 0(1^+) $ 

11.354 $ 0(2^+) $ 

11.363 $ cc\bar{u}\bar{s} $ 

$ \dfrac{1}{2}(0^+) $ 

··· $ \dfrac{1}{2}(1^+) $ 

··· $ \dfrac{1}{2}(2^+) $ 

··· $ bb\bar{u}\bar{s} $ 

$ \dfrac{1}{2}(0^+) $ 

··· $ \dfrac{1}{2}(1^+) $ 

··· $ \dfrac{1}{2}(2^+) $ 

11.307 $ bc\bar{s}\bar{s} $ 

$ 0(0^+) $ 

7.698 $ 0(1^+) $ 

7.660 7.683 $ 0(2^+) $ 

7.702 8.089 $ bc\bar{u}\bar{s} $ 

$ \dfrac{1}{2}(0^+) $ 

··· $ \dfrac{1}{2}(1^+) $ 

··· $ \dfrac{1}{2}(2^+) $ 

7.56 7.89 Table 9. Possible resonance states of double-heavy strange tetraquarks
$ QQ\bar{q}\bar{s}\; (Q=c, b; q= u, s) $ (unit: GeV).Furthermore, the decay widths of the resonances can be approximately estimated from the two-state crossing formula presented in Ref. [39]:
$ \Gamma=4|V(\alpha)|\frac{\sqrt{|S_r||S_c|}}{|S_c-S_r|}, $

(18) where
$ V(\alpha) $ is the energy difference between the upper and lower branches at the avoid-crossing point with the same value α.$ S_r $ and$ S_c $ are the slopes of the two crossing levels, continuum and resonance, respectively. It should be noted that the decay width is the partial strong two-body decay width to$ S\rm{-} $ wave channels included in the calculation. For example, for$ cc\bar{s}\bar{s} $ with$ 0(0^+) $ , there are two resonance states with energies of 4176 and 4250 MeV, which have decay widths of 18 and 24 MeV, respectively. This decay values are just the partial widths to the$ D_s^+D_s^+ $ and$ D_s^{*+}D_s^{*+} $ channels. For the other resonance states in Figs. 3 to 7, we found that the slopes of the resonance states lines approximately equal zero; thus, the partial two-body strong decay width may be very small, and the decay width may come from the width of the excited mesons themselves. -
We systematically studied the double-heavy tetraquark states
$ QQ\bar{q}\bar{s} $ with all the possible quantum numbers constrained by the Pauli principle, where$ Q=c,b; q=u, s $ within the framework of the chiral quark model.To search for the possible stable states against strong interaction, the meson-meson picture, the diquark-antidiquark picture, and the coupling calculations are considered. The results predict that the
$ cc\bar{u}\bar{s} $ and$ bb\bar{u}\bar{s} $ tetraquarks with$ \dfrac{1}{2}(1^+) $ are bound states against strong interactions, with binding energies of 7.0 and 104.4 MeV, respectively, which may be explored in experiments in the near future. Meanwhile, some resonance states are also found with the RSM.Until now, none of the stable or resonant double heavy tetraquarks with strange flavor have been observed in experiments, and therefore, we need further investigation on their properties. The future experimental values will provide an opportunity to verify the availability of the different theoretical models.
Double-heavy tetraquarks with strangeness in the chiral quark model
- Received Date: 2022-06-22
- Available Online: 2023-02-15
Abstract: Recently, some progress has been made in the experiments on double-heavy tetraquarks, such as






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





























 DownLoad:
DownLoad: