-
The flagship of modern particle physics, the LHC, is expected to continue running for another 10 years or more. However, planning for next generation colliders has already begun.
It is widely believed that the next major collider project will be a high-energy, high-luminosity electron-positron collider. Currently, four advanced projects involving
$ e^+e^- $ colliders are under consideration: two linear colliders, the CLIC [1] and ILC [2], and two circular colliders, the CEPC [3] and FCC-ee [4].Scientific programs for future
$ e^+e^- $ colliders are well developed. The main goals are study of Higgs boson physics, high-precision measurements at the Z pole energy, study of top quark physics, and searches for new physics phenomena. In this study, we investigate the prospects of another branch of the experimental program: the physics of two photon collisions.The collisions of (quasi-)virtual photons are responsible for a significant fraction of the total event rate at electron-positron colliders. They are especially abundant at linear colliders owing to high acceleration gradients. Such events represent an unpleasant background for the studies of other physics processes. However, two-photon collisions themselves provide opportunities for interesting physics studies. In this paper, we analyze several topics that can be investigated using two-photon collisions at future
$ e^+e^- $ colliders.At linear colliders, the rate and energy spectrum of two-photon collisions depend on the particular configuration of beams. Therefore, our study is restricted to the case of circular colliders, where the differential gamma-gamma luminosity can be predicted from first principles.
Both the CEPC and FCC are expected to take large data sets at a center-of-mass energy of 240 GeV (a point close to the maximum yield of Higgs bosons). The expected integrated luminosity of the CEPC is 5.6 ab
$ ^{-1} $ . The FCC plans to collect at least 5 ab$ ^{-1} $ at 240 GeV, followed by 1.7 ab$ ^{-1} $ at the energies of top pair production (340–365 GeV). In this paper, we use the CEPC planned energy and luminosity as a benchmark scenario; however, our qualitative results are also applicable to the FCC, which has a similar expected performance. -
The era of two-photon physics began in the early 1970s when a relatively high cross section of the 4-th order QED process
$ e^+e^-\to e^+e^-e^+e^- $ was observed [5] at the Budker Institute of Nuclear Physics (Novosibirsk).It should be noted that the first theoretical predictions of pion photoproduction [6, 7] in
$ e^+e^- $ collision was made around 1960; however, the calculated cross-sections were deemed unmeasurably small, and no further elaboration was performed until the late 60s. At that time, a series of papers on the multiple final states of$ e^+e^- $ colliders was published. It was only after experimental observation in Novosibirsk that the most remarkable mechanism of cross-section enhancement due to the small virtuality of photons emitted by electrons was revealed [8].It is the small virtuality of intermediate photons that features the two main characteristics of two-photon processes: enhancement of the yield with increasing colliding beam energies and the possibility of studying a new type of process
$ \gamma\gamma\to X $ with two variable parameters - the virtualities of intermediate photons.The two-photon process can occur at electron-positron or electron-electron colliders:
$ e^\pm+e^-\to e^\pm+e^- +\gamma^*+\gamma^*\to e^\pm+e^- +X, $

where X represents an arbitrary final state. It is not possible for simply any final state to be produced in the two-photon process; because two photons have even C parity, only states with C = +1 are possible. As mentioned above, the two-photon cross-section slowly increases with energy and becomes greater than that of the annihilation channel at
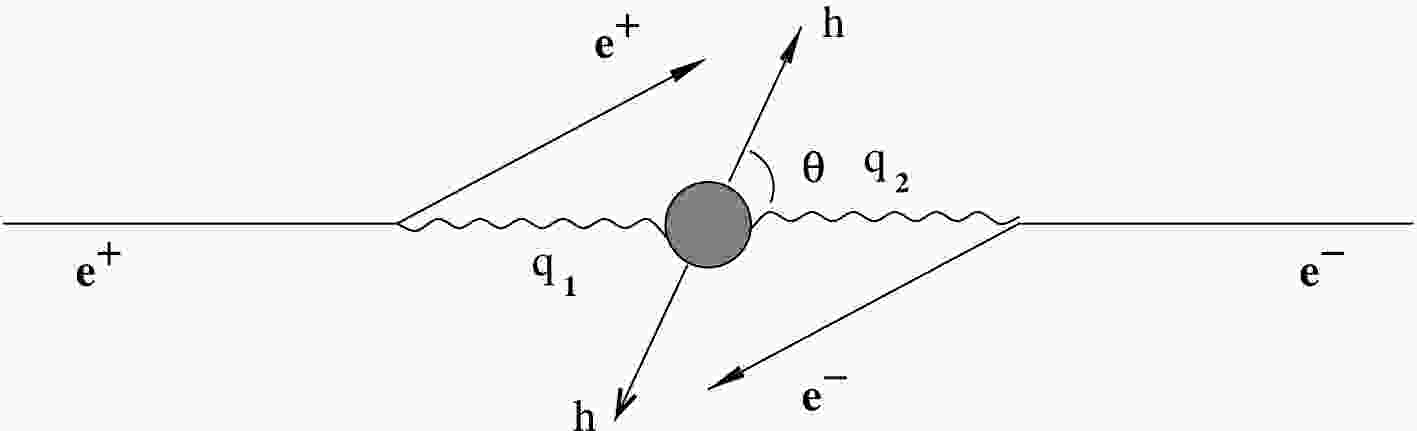
$ \sqrt{s}/2 \gtrsim 1 $ GeV.In a two-photon process, the initial particles (electrons and/or positrons) emit two photons with virtualities
$ q_1 $ and$ q_2 $ , and the latter merges in a final system of particles X with the invariant mass square$ W^2={(q_1+q_2)^2} $ (see Fig. 1).The cross-section of the two-photon scattering of electrons (positrons) can be calculated as a convolution of amplitudes describing the emission of virtual photons off the initial particle and
$ \gamma\gamma\to X $ transition. The former is calculated within QED, and the latter can be expanded in independent tensors, the choice of which is arbitrary up to the conservation of Lorenz, T-, and gauge invariances. For the sake of physical interpretation, it is encoded in five structure functions. Three of these can be expressed through the cross section$ \sigma_{a,b} $ for scalar ($ a,b=S $ ) and transverse ($ a,b=T $ ) photons. The other structure functions$ \tau_{TT} $ and$ \tau_{TS} $ correspond to transitions with spin-flip for each of the photons with total helicity conservation [9]:$ \begin{aligned}[b] \rm{d}\sigma=& \frac{\alpha^2}{16\pi^4q_1^2q_2^2}\sqrt{\frac{(q_1q_2)^2-q_1^2q_2^2}{(p_1p_2)^2-m_e^2m_e^2}} \biggl( 4\rho^{++}_1\rho^{++}_2\sigma_{TT} +2|\rho_1^{+-}\rho_2^{+-}|\tau_{TT}\cos(2\tilde{\phi}) \\& +2\rho^{++}_1\rho^{00}_2\sigma_{TS} +2\rho^{00}_1\rho^{++}_2\sigma_{ST} +\rho^{00}_1\rho^{00}_2\sigma_{SS} -8|\rho^{+0}_1\rho^{+0}_2|\tau_{TS}\cos(\tilde{\phi}) ) \frac{ \rm{d}^3 p_1' \rm{d}^3p_2'}{E_1 E_2}, \end{aligned} $ 
(1) where
$ \rho_{i}^{ab} $ are the density matrices of the virtual photon in the$ \gamma\gamma $ -helicity basis,$ p_i, (p_i') $ corresponds to the momentum and energy of the initial (scattered) leptons,$ E_i $ represents scattered lepton energies,$ \tilde{\phi} $ is the angle between the scattering planes of colliding particles at the c.m.s. of photons, and$ m_e $ is the mass of the initial lepton.The exact formula (1) provides an accurate estimation of the two-photon process at any kinematical region and may be used for quantitatively correct simulations [10, 11]. At the limit
$ q_i^2\to 0 $ , one can observe a logarithmic enhancement of the cross-section, with the natural kinematic "regularization" value at$ m_e^2 $ .The small
$ q^2_i $ domain gives the main contribution to the cross-section of the process under consideration. In this limit, the expression for (1) can be simplified under a procedure known as equivalent photon approximation (Weizacher-Williams' method).Keeping this approximation in mind and considering only leading terms, we can see that the cross-section of the two-photon process factorizes into two different parts: one is connected to the emission of two real photons by initial particles, and the other is final state production by the two photons [12]:
$ \begin{eqnarray} \frac{ \rm{d}\sigma^{(0)}}{ \rm{d} W^2 \rm{d}\Gamma}=2\biggl(\frac{\alpha}{\pi})^2 \frac{1}{W^2}\ln^2\frac{E}{m_e} f\left(\frac{W}{2E}\right)\frac{ \rm{d}\sigma_{\gamma\gamma\to X}(W^2)}{ \rm{d}\Gamma}, \end{eqnarray} $

(2) where E is the energy of the initial particles,
$ \begin{eqnarray} f(\gamma)=-(2+\gamma^2)^2\ln\gamma-(1-\gamma^2)(3+\gamma^2) \end{eqnarray} $

(3) is the factor describing the luminosity dependence over the invariant mass of the colliding photons, and Γ represents the phase volume of the final state X.
The cost of this simplicity is the underestimation of the cross-section in certain specific kinematics, the loss of information on the initial particle scattering angle, and missing the deep virtual scattering behaviour of the cross-section when one of the photons has a large invariant mass. Of course, events with a large virtuality of an intermediate photon are considerably more rare because there is no
$ q_i^2 $ pole enhancement.A small
$ q^2_i $ invariant mass of emitted photons indicates that the scattered leptons proceed undetected (so called no-tag events); however, owing to the large cross-section of the process, no-tag events can be selected even without full final state recovery [13] using the requirements of the small total transverse momentum of the produced system and the small value of its invariant mass ($ W\ll 2E $ ). Gamma-gamma collisions tend to occur at c.m.s. energies significantly lower than the nominal collider energy, as shown in Fig. 2 (left). Nevertheless, the amount of collisions at high energies is also significant and can be used to study different aspects of two-photon physics.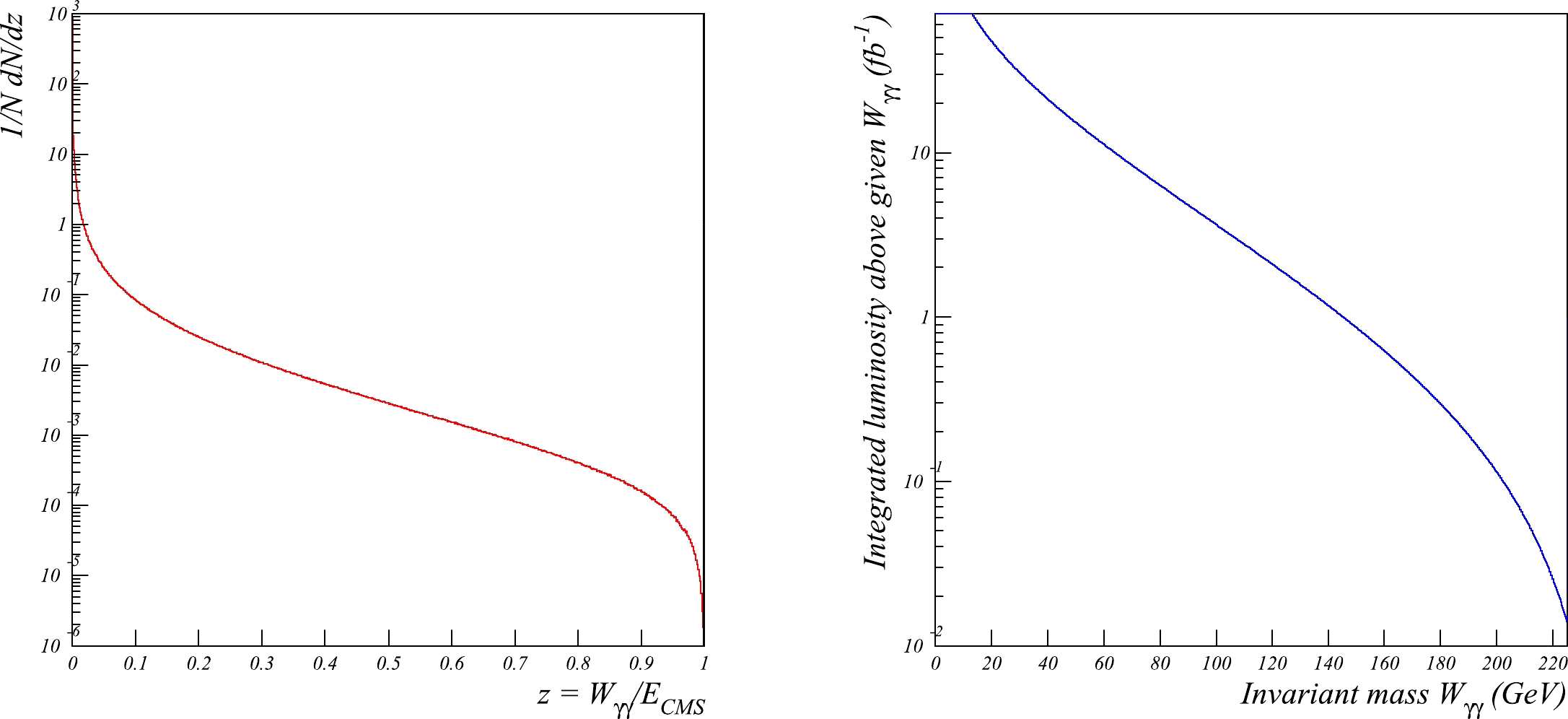
Figure 2. (color online) Left: Number of
$ \gamma\gamma $ collisions as a function of the$ \gamma\gamma $ invariant mass relative to the$ e^+e^- $ CMS energy. Right: Integrated luminosity of$ \gamma\gamma $ collisions above a certain collision energy, under the assumption of a 5.6 ab$ ^{-1} $ integrated luminosity of$ e^+e^- $ collisions.Practically, two photon events can be tagged via the detection of one or both scattered electrons (single tag or double tag mode). Tagging allows one to significantly suppress background at the cost of a steep reduction in available statistics. In this case, the requirement of lepton tagging at a given energy and angular range indicates non-vanishing virtualities of photon mass and allows the possibility of measuring the
$ q_i^2 $ dependence of the two-photon cross-section (1). In this paper, we assume that scattered particles can be tagged in the luminosity monitor. A typical CEPC and FCC-ee acceptance down to 30 mrad is assumed.Two-photon processes have always been of interest to physicists owing to the fascinating opportunity to study the conversion of pure light to matter. In this paper, we cover conservative and well-established topics in two-photon physics, namely, quarkonium spectroscopy, Higgs production, tau pair production, and photon hadronic structure. All suggested measurements are aimed at significantly improving the precision of existing experiments and are certainly achievable under the planned characteristics of future
$ e^+e^- $ colliders. The integrated luminosity of gamma-gamma collisions above the$ W^+W^- $ threshold (see Fig. 2, right) is slightly less than 1 fb$ ^{-1} $ , which is comparable to the total$ e^+e^- $ luminosity recorded by LEP2 experiments. -
A quarkonium is regarded as a simple hadronic system used to explore QCD aspects at low energy regimes through its spectroscopy [14].
Quarkonia, the bound states of a heavy quark c or b and the corresponding antiquark, can be most effectively studied at
$ e^+e^- $ colliders. Since the discovery of$ J/\psi $ in 1974, considerable information on bounded$ b\bar b $ and$ c \bar c $ states has been accumulated.A quarkonium can be described as a bound quark-antiquark state, with a Coulombic short-distance potential that has a logarithmic modification of the coupling strength and linear long-distance potential for a description of quark confinement [14, 15].
Although there are numerous different ways of quantitatively describing quarkonia, e.g., lattice QCD methods [16], NRQCD methods [17], the light front quark model [18], or the exotic like instanton liquid model [19], there are still many inconsistencies between the predicted and measured radial excitation mass spectra of quarkonium states.
Owing to the negative charge parity of photons, only neutral particles with an even charge conjugation
$ C=1 $ can be produced in two-photon collisions. There are many interesting areas of study involving light mesons composed of light$ u, d $ quarks, such as π, η,$ \eta' $ , and their excited states; however, we expect that CEPC experiments will be insensitive to hadronic systems with masses below 3 GeV owing to issues regarding detector resolution and the experimental environment. Therefore, the most straightforward studies can be performed with heavy c and b quarks, which lead us to charmonium and bottomonium spectroscopy.Charmonium states with an even charge conjugation
$ C=1 $ up to the$ \eta_c(2S) $ mass of 3637 GeV have been well studied, and their radiative decays to photons have been observed and measured.$ \chi_{c_ 1} $ production in two-photon collision was recently detected by the BELLE collaboration [20]. However, only the upper limit on the branching ratio is available to date (see Table 1). From the numerical estimation of event number (see Sect. III.B, double tag set-ups), we can conclude that it is possible to improve the accuracy of the$ \gamma\gamma $ branching ratio for the$ \chi_{c_ 1} $ and$ \eta_c(2S) $ charmonium states and measure, at least, the$ Q^2 $ dependence of resonance formation in a single-tag set-up, where we expect approximately$ 10^4 $ events for each charmonium state.Fraction $ \eta_c $ 

$ \chi_{c_ 0} $ 

$ \chi_{c_ 1} $ 

$ \chi_{c_ 2} $ 

$ \eta_c(2S) $ 

$ 10^{-4} $ 

$ 1.57\pm 0.12 $ 

$ 2.04\pm 0.09 $ 

$<6.3 \times 10^{-2} $ 

$ 2.85\pm0.1 $ 

$ 1.9\pm 1.3 $ 

Table 1. Charmonium low state radiative decay branching ratio.
The event yield estimation of charmonium production with masses larger than that of
$ \eta_c(2S) $ is more difficult. From one perspective,$ c\bar c $ spectroscopy in this region of mass states is interesting owing to a lack of knowledge on the internal structure and two photon branching ratio of resonances (see Table 2); hence, any measurement results or lower limit estimations of$ \gamma\gamma $ width are highly appreciated. Moreover, the measurement of the$ Q^2 $ dependence of resonance formation may provide a hard restriction over the quantum numbers and internal structure of the resonances under consideration.Name $ J^{PC} $ 

Width/MeV $ \Gamma_{\gamma\gamma} $ 

Nature $ \chi_{c0}(3860) $ 

$ 0^{++} $ 

$ 201\pm101 $ 

observed $ c\bar c $ +possible non-

$ q\bar q $ states

$ \chi_{c1}(3872) $ 

$ 1^{++} $ 

$ 1.19\pm0.21 $ 

observed candidate for an exotic structure X(3915) 0 or $ 2^{++} $ 

$ 20\pm 5 $ 

observed $ c\bar c $ +possible non-

$ q\bar q $ states

$ \chi_{c2}(3930) $ 

$ 2^{++} $ 

$ 24\pm6 $ 

observed $ c\bar c $ +possible non-

$ q\bar q $ states

X(3940) $ ?^{??} $ 

$ 37\pm17 $ 

− $ c\bar c $ +possible non-

$ q\bar q $ states

X(4050) $ ?^{?+} $ 

$ 82\pm28 $ 

− candidate for an exotic structure X(4100) $ ?^{??} $ 

$ 152\pm70 $ 

− candidate for an exotic structure $ \chi_c1 $ (4140)

$ 1^{++} $ 

$ 22\pm7 $ 

not observed candidate for an exotic structure X(4160) $ ?^{??} $ 

$ 139\pm60 $ 

− $ c\bar c $ +possible non-

$ q\bar q $ states

X(4250) $ ?^{?+} $ 

$ 177\pm70 $ 

− candidate for an exotic structure $ \chi_{c1} $ (4274)

$ 1^{++} $ 

$ 49\pm12 $ 

− candidate for an exotic structure X(4350) $ ?^{?+} $ 

$ 13\pm10 $ 

observed $ c\bar c $ +possible non-

$ q\bar q $ states

$ \chi_{c0} $ (4500)

$ 0^{++} $ 

$ 92\pm29 $ 

− candidate for an exotic structure $ \chi_{c0} $ (4700)

$ 0^{++} $ 

$ 120\pm50 $ 

− candidate for an exotic structure Table 2. Charmonium exotic states that could be observed in a
$ \gamma\gamma $ collision.Charmonium bound states with masses above the open charm threshold cannot be described only in the frames of the constituent quark model that describes the observed meson spectrum as
$ q\bar q $ bound states (see Table 2). To explain the unexpected quantum numbers, masses, branching ratios, and other properties of the heavy resonances that form the charmonium spectrum, various possibilities of new physics states are considered: meson states composed of bound gluons (glueballs), qq-pairs with an excited gluon (hybrids), multiquark color singlet states, such as qqqq (tetraquarks), molecular bound states of four-quark systems, and six-quark and "baryonium" bound states.The other side of the problem is that without knowledge of the internal structure, it is not possible to conduct a firm estimation of charmonium state production. Even a basic equivalent photon approximation with a narrow resonance approximation is not applicable owing to the unknown branching ratio of the two photons.
We suggest conducting a rough estimation of the production rate under the assumption that all charmonium states mostly consist of
$ c\bar c $ states. We know that the branching ratio of two photon quarkonium decay at the lowest order does not depend on the state mass and has a slight (up to several factors) dependence on its quantum numbers (see Ref. [21] and Table 1). Therefore, the two photon branching ratio could be estimated at the level of$ 10^{-4} $ . This estimation provides approximately$ 10^7-10^8 $ events in the no-tag mode (although we do not observe scattered leptons, it is possible to reduce background events by imposing a strict transverse-momentum balance along the beam axis for the final-state hadronic system [22]) and approximately$ 10^4 $ events in the single (minimal angle of detection at 6 degrees) and double tag (using a luminosity calorimeter) modes. All estimations are made with the accelerator parameters described in Sect. III.B. For estimations in the no-tag mode, events with scattered electrons are also accepted, with negligible contribution to the total event yield.As a result, we can conclude that if the recently discovered charmonium resonances (Table 2) are similar to the charm quark bound state, we can discover their quantum numbers and measure the two photon branching ratios.
For the bottomonium states, only the ground state
$ \eta_b(9399) $ decay to two photons has been observed, and other$ C=+1 $ state radiative decays have not been measured [23]; hence, any information about them, such as the upper limit on the two photon branching or decay event observation, are highly appreciated.In Sect. III.B, we estimate the low bottomonium states
$ 1S, 1P,2S $ . The event number of positive charge parity states with higher radial quantum numbers, namely,$ \chi_{b0}(2P) $ ,$ \chi_{b1}(2P) $ ,$ \chi_{b2}(2P) $ ,$ \chi_{b1}(3P) $ , and$ \chi_{b2}(3P) $ , are estimated as counterparts with radial quantum numbers equal to unity.With a number of bottomonium state events of approximately
$ 10^5 $ in the no-tag mode and$ 10^2 $ in the double-tag mode, we may conclude that an upper limit can at least be placed on the radiative decay branching of bottomonium states. -
We can theoretically estimate the full cross-section of two photon meson production with the help of the equivalent photon approximation formula (2), where the cross-section of mesons with spin J and mass M photoproduction can be estimated via
$ \sigma_{\rm mes}(W^2)=(2J+1)8\pi^2 \frac{\Gamma_{\gamma\gamma}}{M} \frac{1}{\pi}\frac{M\Gamma}{(M^2-W^2)^2+M^2\Gamma^2}, $

(4) where
$ \Gamma_{\gamma\gamma} $ and Γ are the two photon and total widths of meson decay, respectively. -
A simulation is performed using GALUGA [10, 11, 24], a two photon production generator, where the virtualities
$ Q^2 $ of photons are fully considered through five structure functions describing photon scattering with different polarizations. Such a consideration allows for a robust estimation of meson production at large photon virtualities (large electron or positron scattering angle). Resonance formation in two-photon scattering is calculated in the framework of the constituent-quark model [11].The expected event yields are presented at the total beam energy
$ \sqrt{s}=240 $ GeV and integrated luminosity$ 5 $ ab$ ^{-1} $ .Quarkonium production is estimated in three different modes: no tag, where no final scattered electron or positron is detected (there is no limitation on the polar angle of the scattered electron/position), single tag, where the electron or positron is detected, and double tag, in which both the electron and positron are detected. The minimal angles are taken to be equal to 6 or 10 degrees (various detector characteristics are considered), and a value of 1.9 degrees is used when the scattered electron or positron can be detected in the luminosity calorimeter.
From Tables 3 and 4, we can see that the number of registered mesons is drastically dependent on the minimal angle of scattered lepton detection. Using the luminosity calorimeter for scattered lepton detection (minimal detection angle of 1.9 degrees), we can enhance the statistics of registered mesons by two orders of magnitude. This emphasizes the significance of a low-angle calorimeter in two-photon physics.
Name No Tag S Tag 10 S Tag 6 D Tag 6 D Tag 6–1.9 D Tag 1.9–1.9 $ \eta_c $ 

$ 1.\times 10^9 $ 

$ 5 .3\times 10^5 $ 

$ 1 .7\times 10^5 $ 

$ 7 .6\times 10^2 $ 

$ 1 .2\times 10^4 $ 

$ 8 .6\times 10^4 $ 

$ \chi_{c_ 0} $ 

$ 2.\times 10^8 $ 

$ 6 .5\times 10^4 $ 

$ 2 .2\times 10^4 $ 

$ 6 .3\times 10^1 $ 

$ 9.\times 10^2 $ 

$ 8 .3\times 10^3 $ 

$ \chi_{c_ 1} $ 

$ 7.\times 10^6 $ 

$ 4 .4\times 10^4 $ 

$ 1 .1\times 10^4 $ 

$ 1 .7\times 10^2 $ 

$ 2 .4\times 10^3 $ 

$ 1 .7\times 10^4 $ 

$ \chi_{c_ 2} $ 

$ 9 .5\times 10^7 $ 

$ 3 .1\times 10^4 $ 

$ 9 .8\times 10^3 $ 

$ 5 .4\times 10^1 $ 

$ 7 .2\times 10^2 $ 

$ 6 .7\times 10^3 $ 

$ \eta_c(2S) $ 

$ 2 .4\times 10^8 $ 

$ 2 .1\times 10^5 $ 

$ 6 .4\times 10^4 $ 

$ 4 .1\times 10^2 $ 

$ 6.\times 10^3 $ 

$ 4 .1\times 10^4 $ 

Table 3. Estimation of event number for charmonium states. Singe tag, no tag, and double tag set-ups are considered. Cuts on the electron or positron scattering angle are 1.9, 6, and 10 degrees.
Name No Tag S Tag 10 S Tag 6 D Tag 6 D Tag 6–1.9 D Tag 1.9–1.9 $ \eta_b (9399) $ 

$ 1.3\times 10^6 $ 

$ 1.4\times 10^4 $ 

$ 3.9\times 10^3 $ 

$ 1.1\times 10^2 $ 

$ 1.\times 10^3 $ 

$ 3.6\times 10^3 $ 

$ \chi_{b_0}(1P) $ 

$ 9.6\times 10^4 $ 

$ 5.2\times 10^2 $ 

$ 1.4\times 10^2 $ 

$ 2.7 $ 

$ 3.\times 10^1 $ 

$ 1.5\times 10^2 $ 

$ \chi_{b_1}(1P) $ 

$ 3.9\times 10^3 $ 

$ 5.1\times 10^2 $ 

$ 1.3\times 10^2 $ 

$ 6.6 $ 

$ 5.3\times 10^1 $ 

$ 1.4\times 10^2 $ 

$ \chi_{b_2}(1P) $ 

$ 8.3\times 10^4 $ 

$ 4.9\times 10^2 $ 

$ 1.2\times 10^2 $ 

$ 3.4 $ 

$ 3.4\times 10^1 $ 

$ 1.6\times 10^2 $ 

$ \eta_b(9999) $ 

$ 4.6\times 10^5 $ 

$ 5.8\times 10^3 $ 

$ 1.6\times 10^3 $ 

$ 4.9\times 10^1 $ 

$ 4.4\times 10^2 $ 

$ 1.5\times 10^3 $ 

Table 4. Estimation of event number for bottomonium states. Singe tag, no tag, and double tag set-ups are considered. Cuts on the electron or positron scattering angle are 1.9, 6, and 10 degrees.
In the no-tag mode, where no leptons are registered at the final state, we expect a large number of events, that is,
$ 10^7-10^8 $ for quarkonium states and$ 10^5 $ for bottomonium states. However, the absence of kinematical constraints in the no-tag mode results in large background contamination. Several special techniques, such as strict transverse-momentum balance for the final state, can be applied to reduce background. The exact estimation of no-tag quarkonium sensitivities may only be produced using a detailed detector simulation.For quarkonium two-photon physics at the CEPC, we suggest using a conservative estimation, namely, the single-tag mode (one detected lepton helps to reconstruct final state kinematics and drastically reduces background events) and an efficiency of detection of approximately
$10$ %. It this case, we reconstruct approximately$ 10^2-10^4 $ events for each charmonium state. For bottomonium states, we can measure low-state$ \eta_b $ with approximately$ 4\times10^2 $ registered events and possibly observe several events or apply an upper bound for higher bottomonium states. -
The vertex
$ H\gamma\gamma $ is forbidden in the standard model (SM) at tree level. The decay process$ H \rightarrow \gamma\gamma $ as well as the production process$ \gamma\gamma \rightarrow H $ proceed mostly through the top-quark and W loops and are sensitive to contributions from new charged particles; hence, an observation of excess in the$ \gamma\gamma \rightarrow H $ process would indicate new physics phenomena, e.g., a contribution of the anomalous$ H\gamma\gamma $ vertex.At
$ e^+e^- $ colliders, the main background in the process$ \gamma\gamma \rightarrow H $ (referred to as the "signal" hereafter) is Higgs boson production via the fusion of virtual Z bosons ($ ZZ\rightarrow H $ ) and$ \gamma\gamma $ collisions with final states identical to those of Higgs decays but without formation of the intermediate Higgs boson. The background from$ \gamma\gamma $ collisions can be strongly suppressed by selecting "single-tag" events, where one of the beam particles is scattered at a significant angle and detected in the luminosity calorimeter. The signal reduction due to this selection is relatively small (by only a factor of 3 to 5) because Higgs boson production is characterized by a large$ q^2 $ transfer. In the following, we assume event selection with a beam particle scattered by at least 30 milliradians, which is well within the acceptance of the luminosity monitor [25]. The signal and main background sources are simulated using the PYTHIA generator [26]. No detailed detector simulation is performed; however, the main features of the proposed CEPC detector [25] are considered. -
Currently, Higgs photoproduction at future lepton colliders attracts a surprisingly low level of attention.
Nevertheless, there was a vigorous discussion in the frames of Higgs boson production in ultraperipheral collisions (UPC) at the LHC (proton and heavy ion collision cases were considered, see Silveira talk [27] and references therein), where estimations of Higgs photoproduction were made for different set-ups and energies.
Recently, a paper [28] devoted to the estimation of the photoproduction of Higgs bosons at the LHeC [29], a proposed electron-proton collider at the LHC, was published.
Moreover, there are numerous estimations and proposals for double Higgs photoproduction measurement at photon colliders, particularly owing to the possibility of probing trilinear Higgs interactions [30, 31].
-
For the estimation of the Higgs production rate due to the two-photon mechanism, we can utilize the equivalent photon approximation, elaborated in Refs. [6, 32] and [9],
$ \sigma_{ee\to eeH} \approx 2\left(\frac{\alpha}{\pi}\right)^2\left(\ln\frac{E}{m_e}\right)^2 \times \int_0^{4E^2} \frac{ \rm{d} W^2}{W^2}f \left(\frac{W}{2E}\right) \sigma_{\gamma\gamma\to H}(W), $

where
$ \sigma_{\gamma\gamma\to H}(W) $ represents the Higgs photoproduction cross-section estimation, and the function f is defined in Eq. (3). Here, we consider only leading logarithm approximation.The subprocess cross section for two photon Higgs production can be calculated via the narrow resonance estimation [33],
$ \begin{aligned}[b] \sigma_{\gamma\gamma\to H}(W)\approx & 8\pi^2 \frac{\Gamma_{\gamma\gamma}}{M_{\rm H}}\frac{1}{\pi}\frac{M_{\rm H}\Gamma}{(M_{\rm H}^2-W^2)^2+M_{\rm H}^2\Gamma^2} \\ \approx & 8\pi^2\frac{\Gamma_{\gamma\gamma}}{M_{\rm H}}\delta(W^2-M_{\rm H}^2),\end{aligned}$

where
$ \Gamma_{\gamma\gamma} $ and Γ are the two photon and total widths of Higgs decay, respectively, and$M_{\rm H}$ is the Higgs mass.Given the energy of the initial electron beam
$ E= 120 $ GeV and$ \Gamma_{\gamma\gamma}=2.27 \times10^{-3}\Gamma $ ,$ \Gamma\approx 4.2 $ MeV [23], we can roughly estimate Higgs two photon production at CEPC energies of the level of$ 0.25 $ fb.It is interesting that the Higgs production rates through the two photon mechanism at the CEPC and LHC are comparable. In the latter case, the estimation gives a cross section of approximately
$ 0.1 $ fb (see Refs. [34–36]). -
The energy dependencies of the signal
$ \gamma\gamma \rightarrow H $ and background$ ZZ\rightarrow H $ processes [26] are compared in Fig. 3. At high energy colliders, the$ ZZ\rightarrow H $ background rate is significantly higher than that of the signal. However, at$ e^+e^- $ CMS energies near 240 GeV, the background decreases abruptly and becomes comparable to the signal. The CEPC and FCC-ee colliders are therefore perfectly suited to study the$ \gamma\gamma \rightarrow H $ process.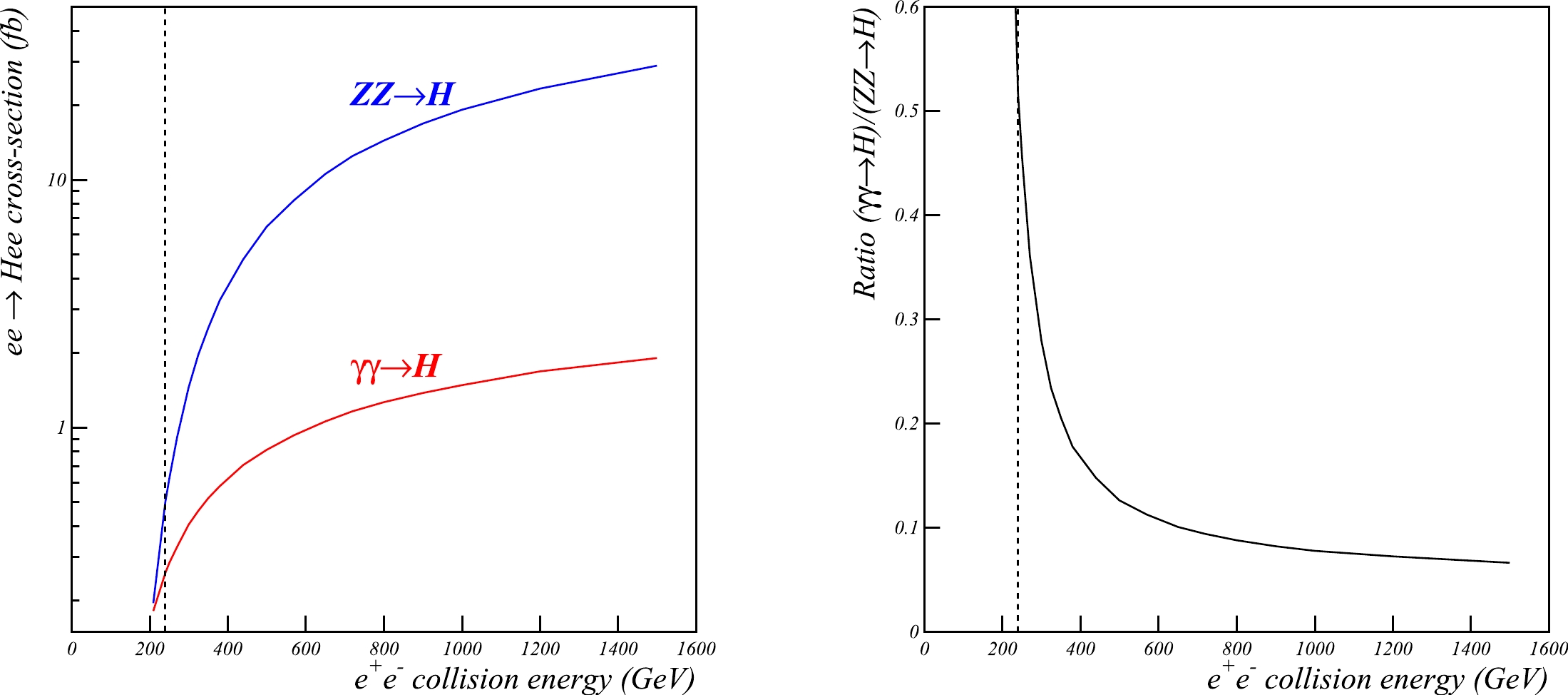
Figure 3. (color online) Left: Energy dependence of the
$e^+e^- \rightarrow He^+e^-$ cross-section for the signal$\gamma\gamma \rightarrow H$ and background$ZZ \rightarrow H$ contributions. Right: Energy dependence of the signal to background ratio. The vertical lines indicate a CMS energy of 240 GeV.At 240 GeV, the total signal cross-section is 0.26 fb [26], compared with 0.50 fb for the
$ ZZ \rightarrow H $ background. The background can be significantly reduced using the fact that the typical$ q^2 $ transfer in$ ZZ \rightarrow H $ events is significantly larger than that in the$ \gamma\gamma \rightarrow H $ process. The distribution of the scattering angle is presented in Fig. 4. Nearly all the background is removed by applying the requirement that the beam particles are scattered by less than 24$ ^\circ $ .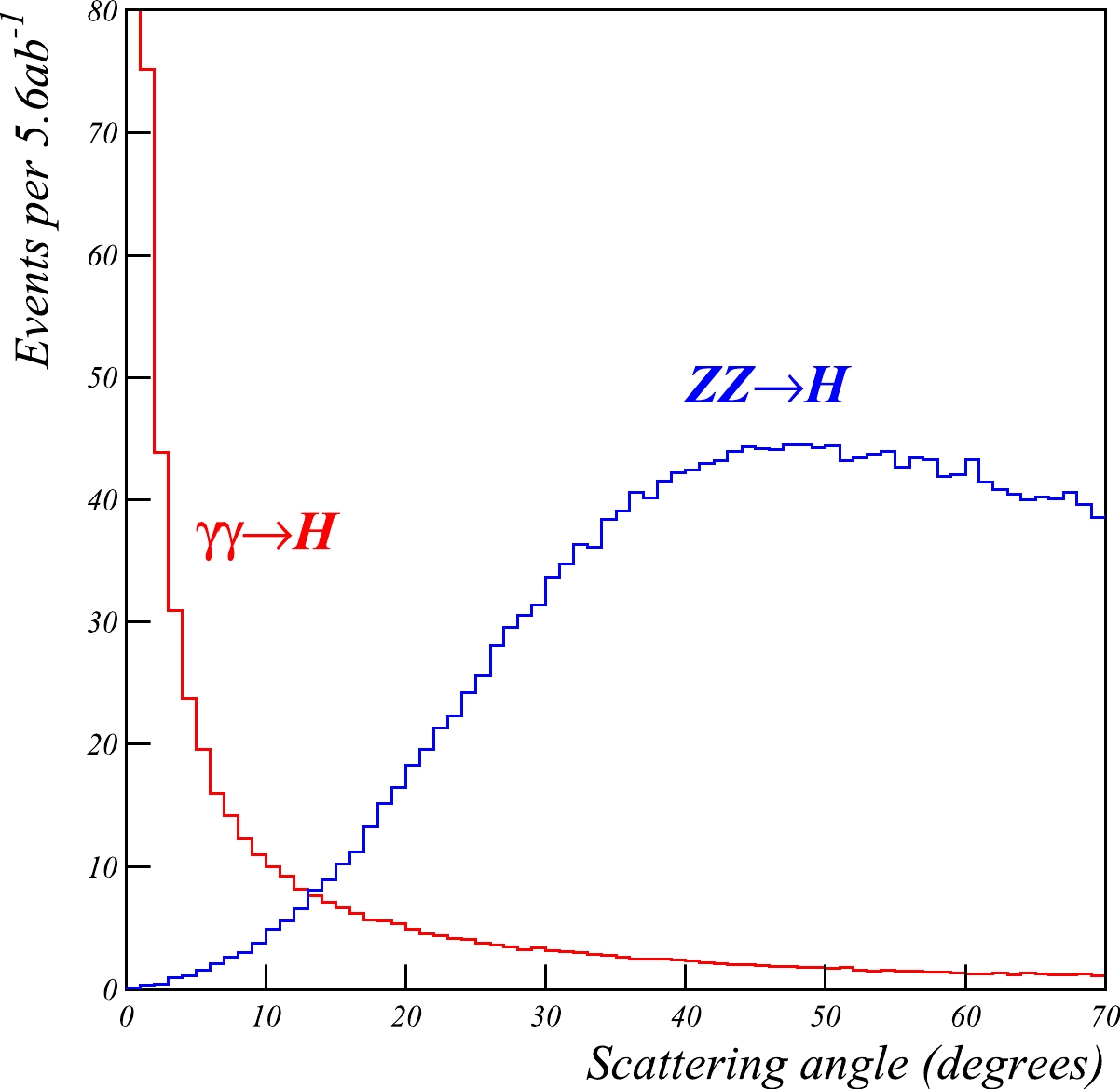
Figure 4. (color online) Distribution of the beam particle scattering angle for the
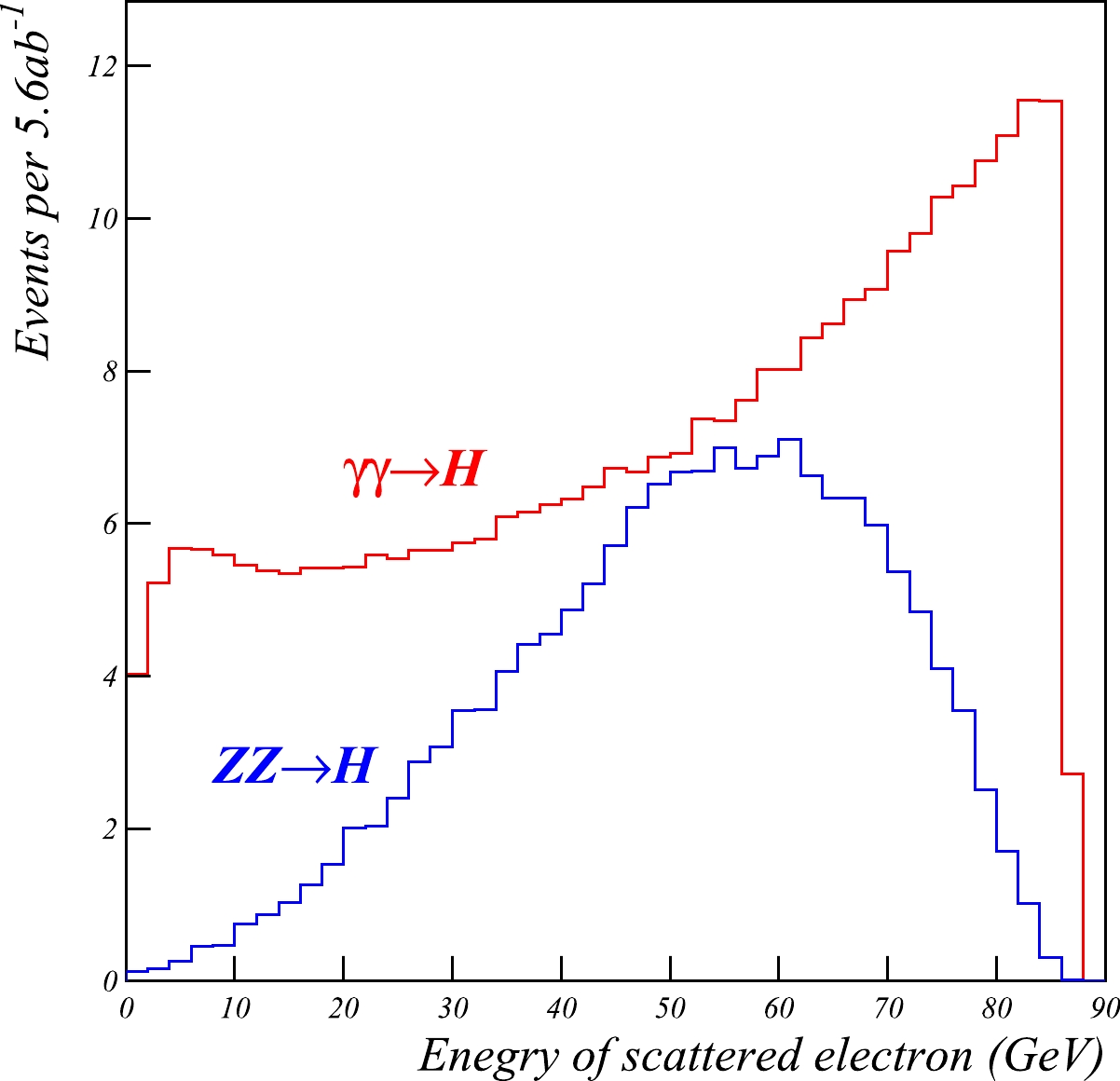
$\gamma\gamma \rightarrow H$ signal and$ZZ \rightarrow H$ background. The number of events is normalized to an integrated luminosity of 5.6 ab$^{-1}$ .Figure 5 shows the energy distribution of the scattered beam particles with a scattering angle between 30 mrad and 24
$ ^\circ $ . An additional energy cut,$ E > 15 $ GeV, is applied to the scattered particles to ensure reliable identification in the luminosity calorimeter. After the cuts on the angle and energy of the scattered particles, the cross-section is 0.049 fb for the signal and 0.027 fb for the$ ZZ \rightarrow H $ background. Assuming an integrated luminosity of 5.6 ab$ ^{-1} $ , this corresponds to 273 and 154 events, respectively. -
The Higgsstrahlung
$ e^+e^- \rightarrow ZH $ is the most abundant Higgs production process at the 240 GeV collision energy. The "single-tag" signal can be caused by an electron from Z-boson decay. The cross-section of$e^+e^- \rightarrow ZH \rightarrow eeH$ is 6.7 fb. The requirement that one of the electrons must be found in the "single-tag" region between 30 mrad and 24$ ^\circ $ reduces the effective cross-section to 1.4 fb. Further background reduction is achieved by the requirement that the second electron is not reconstructed in the tracker. Events with the second electron outside the tracking system (less than 10 degrees from the beam) correspond to 0.030 fb, which is similar to the background from ZZ fusion. This electron can be reconstructed in the luminosity calorimeter. Although the reconstruction efficiency is not perfect, the background can be reduced to a negligible level compared to that in ZZ fusion. Electrons outside the luminosity calorimeter (less that 30 mrad from the beam) correspond to 0.001 fb, which is also negligible.Another "standard" mechanism of Higgs boson production is the WW fusion
$ e^+e^- \rightarrow H\nu\nu $ . The "single-tag" signal can be produced by an ISR photon at an angular acceptance between 30 mrad and 10$ ^\circ $ (at larger angles, photons are distinguished from electrons by the tracking system). The total WW fusion cross-section is approximately 5 fb at 240 GeV. The presence of the "tag" photon reduces this to 0.032 fb, which is similar to the ZZ fusion background. Further background reduction is based on the large missing transverse momentum in$ H\nu\nu $ events. A loose cut,$P_T^{\rm miss} < 20$ GeV/c, rejects only 4% of the signal, while the WW fusion background is reduced to 0.008 fb, which is only a small fraction of the ZZ fusion background.W pair production is a potentially dangerous background owing to its high cross-section (approximately 15 pb at 240 GeV). The "single-tag" signal can be produced by electrons from leptonic W decays. However, this background is reduced by several large factors: the branching of
$ WW \rightarrow cse\nu $ decays (factor 14), the probability of simultaneous fake b-tagging of both c and s quarks (factor of at least 500), electron production outside the tracking system (factor 70), reconstruction of hadronic W decay with a Higgs boson mass (factor of at least 20), and the requirement of a low$P_T^{\rm miss}$ (factor of 7). Taken together, the above factors reduce$ e^+e^- \rightarrow W^+W^- $ to a negligible level. -
The most abundant (58%) Higgs decay channel is
$ H \rightarrow bb $ . In this channel, the most significant background is the non-resonant production of b quark pairs in$ \gamma\gamma $ collisions ($ \gamma\gamma \rightarrow bb $ ). In addition, there is a reducible background$ \gamma\gamma \rightarrow cc $ , where both jets from c quarks are tagged asb jets. The background from light quarks can be neglected because it is efficiently suppressed by b-tagging. With the "single-tag" selection described above, the
$ \gamma\gamma \rightarrow bb $ cross-section is 94 fb for the full range of bb invariant masses. This is reduced to 0.77 fb for$ M_{bb} > $ 100 GeV. According to the CEPC CDR [25], the invariant mass resolution in$ H \rightarrow bb $ decays is approximately 5 GeV. Within the$ \pm 1\sigma $ window around the Higgs mass ($ 120 < M_{bb} < 130 $ GeV), the$ \gamma\gamma \rightarrow bb $ background is 0.124 fb, which is more than five times higher than that of the signal (considering the branching fraction of$ H \rightarrow bb $ decay).The total cross-section of single-tag
$ \gamma\gamma \rightarrow cc $ production is 2086 fb. This is reduced to 13.6 fb for$ M_{cc} > $ 100 GeV and 1.8 fb for$ 120 < M_{cc} < 130 $ GeV. Although the cc background is almost two orders of magnitude higher than the signal, it can be efficiently reduced by b-tagging. According to the the CEPC CDR, the c jet rejection factor is 10 for the 80% b jet efficiency. Applying b-tagging to both jets, a 64% efficiency is obtained for signal tagging, and a reduction factor of 100 is obtained for the charm background, making the latter considerably smaller than the$ \gamma\gamma \rightarrow bb $ background.The non-resonant background can be additionally reduced using a cut on the direction of the produced b and c jets. Figure 6 shows the distribution of the quark polar angle. The background jets are concentrated near the beam axis. We apply a polar angle cut
$ \Theta > 20^\circ $ to both quarks. Within this acceptance, we assume (for the signal and background) a 75% efficiency to reconstruct both jets from b or c quarks.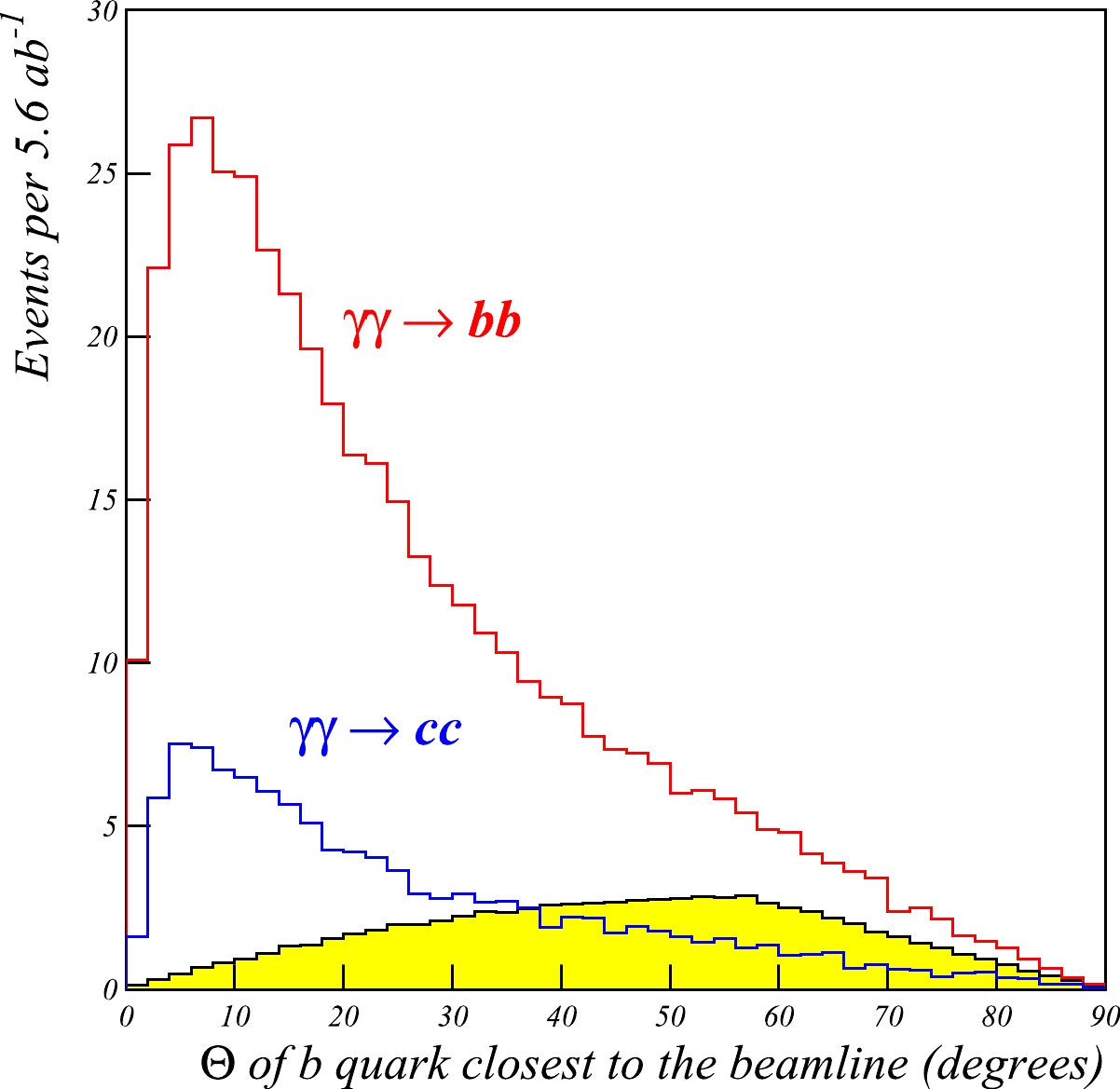
Figure 6. (color online) Distribution of the polar angle of the quark closest to the beam line. Shaded area is the
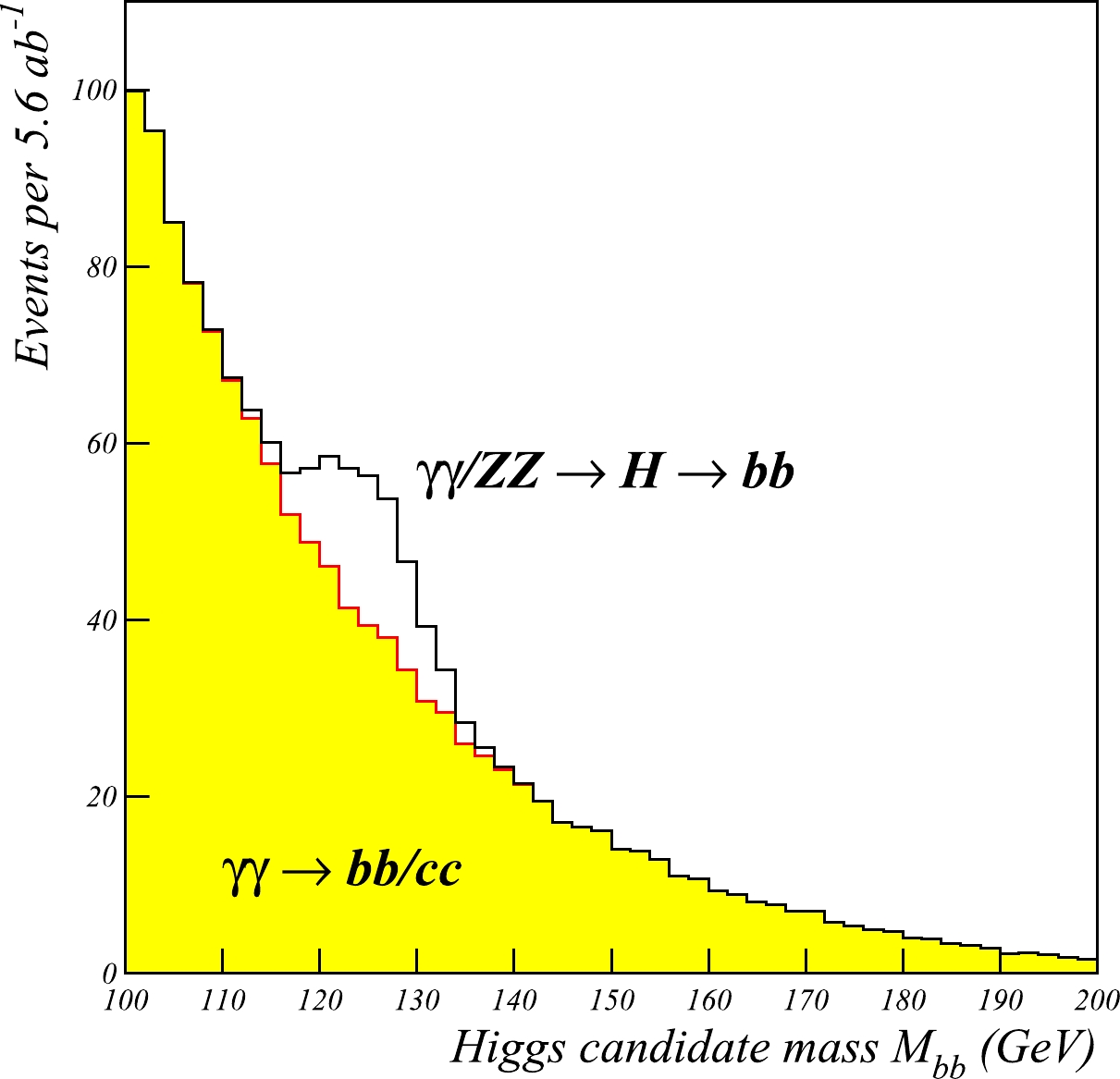
$\gamma\gamma \rightarrow H$ signal, and open histograms represent the non-resonant background. The events are shown within the invariant mass window$118 < M_{bb} < 132$ GeV.The
$ M_{bb} $ invariant mass distribution is presented in Fig. 7. The Higgs signal is smeared assuming a 5 GeV mass resolution. Within the 118–132 GeV window, the expected signal is 57 events, the peaking ZZ background is 33 events, and the non-peaking background is 278 events. A fit to the signal and background yields results at a signal significance of approximately$ 4.1\sigma $ for the$ H \rightarrow bb $ channel after the subtraction of the$ ZZ \rightarrow H $ background. The signal significance can be further improved by including other Higgs decay modes. We conclude that the$ \gamma\gamma \rightarrow H $ signal can be reliably observed with the planned CEPC luminosity. -
At present, the anomalous magnetic moments of electrons and muons are measured with enormous precision, that is, better than one per billion and one per million, respectively. These measurements provide an extremely important test of the SM. At the same time, the anomalous magnetic moment of the tau lepton,
$ a_\tau $ , is known with poor accuracy.The measurement of
$ a_\tau $ is interesting in two respects. First, the large$ a_\tau $ mass is sensitive to the contributions of new physics at higher scales. Second, many theoretical models predict that new physics effects manifest themselves only in the properties of third-generation fermions. Thus, the overwhelming success of the SM observed in the field of anomalous magnetic moments might simply be a consequence of performing high precision measurements with only first generation leptons.The most precise determination of
$ a_\tau $ (17 permille) was performed by the DELPHI experiment at LEP2. The total luminosity was approximately 0.5 fb$ ^{-1} $ , taken at c.m.s. energies between 182 and 208 GeV. The tau anomalous magnetic moment was extracted from the absolute cross-section of tau pair production in gamma-gamma collisions. The simplest final state was selected with one tau decaying into an electron and another into a muon. The precision of the DELPHI cross-section measurement was approximately 4%.At the CEPC, the integrated luminosity will be increased by four orders of magnitude with respect to LEP2. Thus, an improvement in
$ a_\tau $ precision by a large factor can be expected.At a collision energy of 240 GeV, the QED cross-section of the
$ e^+e^- \rightarrow e^+e^-\tau^+\tau^- $ process is 570 pb [37]. This corresponds to nearly 3 billion events with an integrated luminosity of 5 ab$ ^{-1} $ , or 165 millions events with the$ e-\mu $ final state.At LEP2, the selection efficiency of the
$ e-\mu $ final state was 15%–20%. In the CEPC environment, a tighter selection might be necessary to cope with the high background. We conservatively consider the following severe cuts: at least one of the two tracks must have the transverse momentum$ p_T > 5 $ GeV/c, whereas the other track must have$ p_T > 3 $ GeV/c. In addition, the directions of both tracks must be more than 20 degrees from the beam axis, and the total energy of the two particles must be less than 30 GeV to remove annihilation events.Figure 8 shows the distribution of the transverse momentum of the leading and subleading tracks in
$ \gamma\gamma \rightarrow \tau\tau \rightarrow e\mu $ events. Only a small fraction of the events satisfy the selection cuts. Figure 9 shows the distribution of the invariant mass of the electron and muon after applying the selection cuts.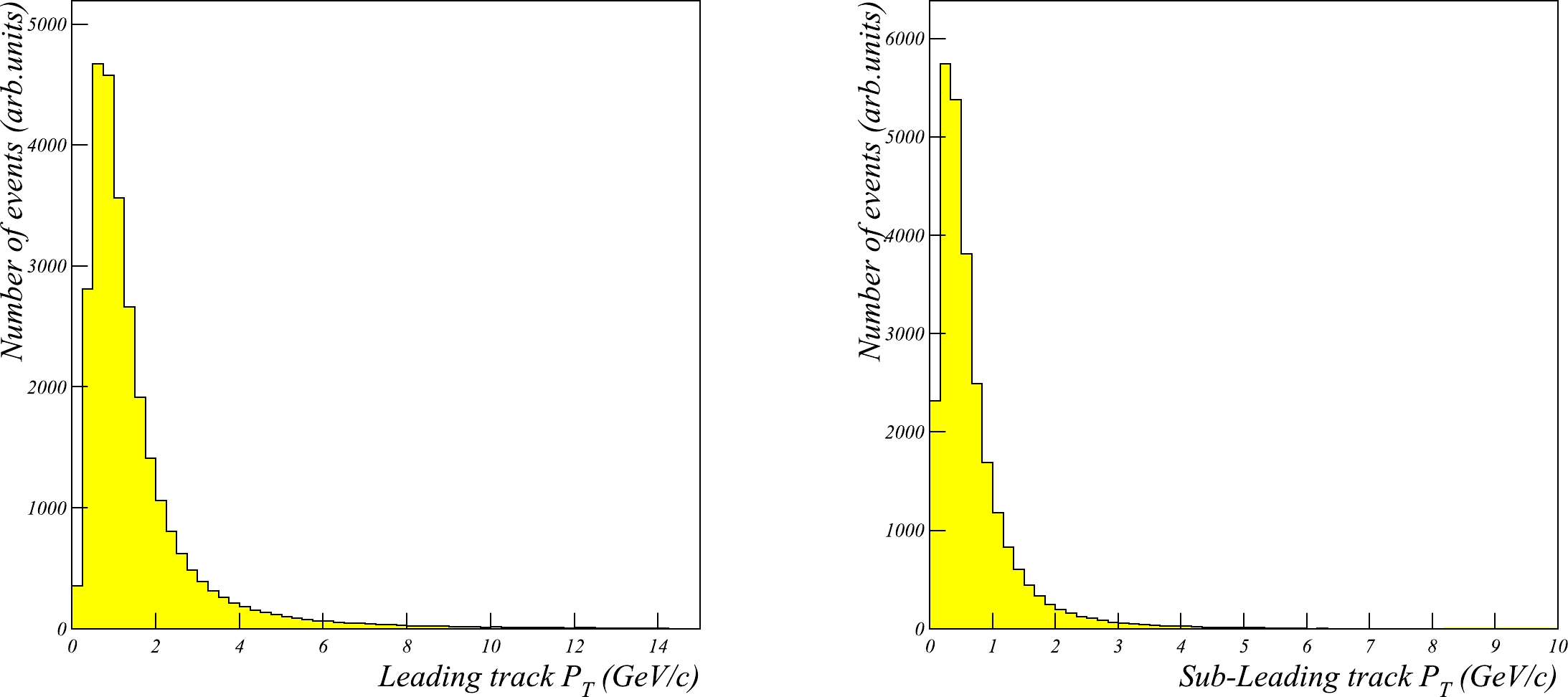
Figure 8. (color online) Distribution of the transverse momentum of the leading (left) and subleading (right) tracks in
$\gamma\gamma \rightarrow \tau\tau \rightarrow e\mu$ events.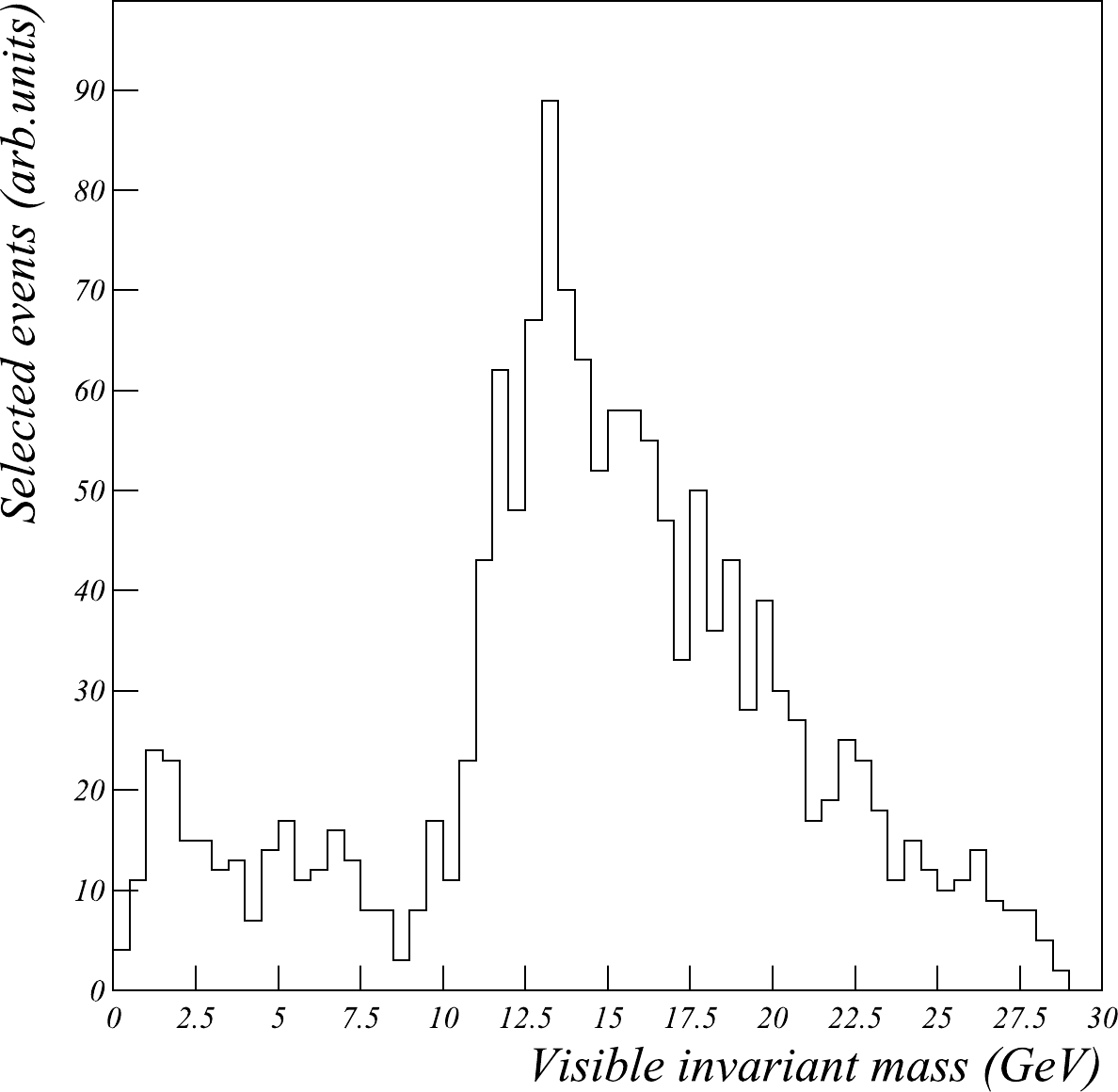
Figure 9. Distribution of the visible invariant masses of the selected
$\gamma\gamma \rightarrow \tau\tau \rightarrow e\mu$ events.The above selection has a generator-level efficiency of 0.42%, corresponding to the total statistics of approximately 700 thousands events. Thus, the statistical error is expected to be at the permille level, and the measurement is likely to be systematically limited.
Given the clean and simple final state, one can optimistically expect to maintain the total systematic error at the 0.5% level. This will include the absolute luminosity determination (0.1%), tracking and particle identification efficiency (0.15% per track for tracking and a similar number for the PID), trigger efficiency, and residual background.
With the above systematic error, the DELPHI precision can be improved by a factor of 8 for the cross-section measurement, and the sensitivity to the anomalous magnetic moment would be improved by a similar factor. Adding other final states (such as
$ e-\rho $ and$ \mu-\rho $ ) is not expected to significantly improve the total error because the measurement will be systematically dominated. However, these channels will have partially independent systematic uncertainties, providing important cross-checks and a certain reduction in the overall systematic errors. -
The measurement of the photon structure function (PSF) has a long history. Although the photon is considered a point-like particle, it can fluctuate to a quark pair or rho meson owing to quantum effects. These two processes are usually described as point-like and hadron contributions to the PSF, respectively. The latter has been estimated in the framework of the vector meson dominance model [32], whereas the former was calculated within the quark model in leading order QCD corrections [38] and later in a series of papers at NLO [39, 40] and NNLO accuracy [41].
The most recent measurement of the PSF was performed at the LEP approximately 20 years ago. Since then, publications have been scarce; the latest review on the state-of-the-art can be found in [42–44].
The photon hadronic structure can be tested via the measurement of inclusive hadron production in the gamma-gamma collisions
${e^+e^-} \rightarrow {e^+e^-} \gamma \gamma^* \rightarrow {e^+e^- +} { hadrons}$ . A high-virtuality photon,$ \gamma^* $ , is radiated off an electron, which scatters at a relatively large angle and can be detected in the experimental setup ("tagged electron"). The second electron is usually scattered at a small angle and thus remain undetected ("untagged electron"). The γ photon radiated by the untagged electron can be considered quasi-real.The overall reaction can be described as a deep inelastic scattering (DIS)
$ \rm{e}\gamma $ of the tagged electron on the real photon. In such scattering, the hadronic nature of the target photon is effectively revealed.A pioneering experiment on the PSF
$ F_2 $ measurement was conducted at DESY by the PLUTO collaboration in 1981 [45] within the range$ Q^2\in(1,15) $ GeV2 at an average beam energy of$ 15.5 $ GeV. Since then, many experiments have contributed to increasing the$ Q^2 $ range up to 780GeV2 at PLUTO [46, 47], ALEPH [48, 49] AMY [50, 51], DELPHI [52, 53], JADE [54], L3 [55, 56], OPAL [57], TASSO [58], TOPAZ [59], and TCP$ /2\gamma $ [60].The most recent experiments were performed at the LEP by the ALEPH, L3, and OPAL collaborations with similar characteristics: center of mass energy
$ \approx 200 $ GeV and integrated luminosity$ \approx $ 600 pb$ ^{-1} $ , while the minimum angle for detection in the luminosity calorimeter was$ 0.024 $ ,$ 0.03 $ , and$ 0.033 $ rad, respectively. Comparing this data with similar CEPC parameters, namely, a c.m.s. energy of 240 GeV, an integrated luminosity of 5 ab$ ^{-1} $ , and a minimal detection angle of approximately 1.9 degrees ($ 0.03 $ rad), one can naively estimate the number of events at the CEPC to be approximately$ 10^4 $ times larger than that at the LEP.The hadronic PSF
$ F^\gamma_2(x,Q^2) $ can be extracted from the differential cross-section${\rm d}\sigma/{\rm d}Q^2{\rm d}x{\rm d}y$ , where$ Q^2 $ is the virtuality of$ \gamma^* $ , and$ x,y $ are the Bjorken scaling variables.In the case of single-tagged events, when one of the photons is almost real (photon invariant mass
$ P\approx 0 $ ), the general process cross-section,$ e^+e^-\to e^+e^-\gamma\gamma\to e^+e^-X $ $ \frac{{\rm d}\sigma(ee\to ee X)}{{\rm d} x {\rm d} z {\rm d} Q^2 {\rm d} P^2}=f_{\gamma/e} \frac{{\rm d}\sigma(e\gamma\to e X)}{{\rm d} x {\rm d} Q^2}, $

(5) is factorized into an almost real photon luminosity function
$ f_{\gamma/e} $ $ f_{\gamma/e}=\frac{\alpha}{2\pi}\left(\frac{1+(1-z^2)}{z}\frac{1}{P^2}-\frac{2m_e^2z}{P^4}\right), \; \; \; z={E_\gamma}/{E_{\rm beam}} $

(6) and deep inelastic proton-electron scattering cross-section [32]
$ \frac{{\rm d}\sigma(e\gamma\to e X)}{{\rm d} x {\rm d} Q^2}= \frac{2\pi\alpha^2}{x Q^4}((1+(1-y)^2) F_2^\gamma-y^2F_L^\gamma). $

(7) Neglecting the virtuality of the quasi-real photon, one obtains
$Q^2 = 2E_{\rm beam}E_{\rm tag}(1 - {\rm cos}\theta_{\rm tag})$ ,$ x = Q^2/(Q^2+W^2) $ , and$y = 1 - (1 + {\rm cos}\theta_{\rm tag})E_{\rm tag}/(2E_{\rm beam})$ , where W is the$ \gamma \gamma^* $ invariant mass, which is experimentally measured as the mass of the hadronic system, and$\theta_{\rm tag}$ and$E_{\rm tag}$ are the scattering angle and energy of the tagged lepton, respectively.Usually, the experimentally accessible kinematic region corresponds to small values of y (
$ y^2\ll1 $ ); hence, the contribution of the term proportional to the longitudinal structure function$ F_L^\gamma $ is negligible, and one can determine PSF$ F_2^\gamma $ directly from the cross-section (7).Measurement of the energy
$E_{\rm tag}$ and polar angle$\theta_{\rm tag}$ of the scattered electron is straightforward. The most difficult part of the analysis is the reconstruction of the hadronic invariant mass W. In addition to the finite detector resolution and efficiency, W reconstruction is affected by the acceptance issue because the hadronic system is typically boosted along the beam axis and part of it remains undetected or poorly reconstructed. A sophisticated unfolding procedure is required to convert the measured visible invariant mass into the true value. An additional difficulty is regarding the background from overlapping interactions. This background has little impact on hard processes but must be carefully considered in studies on gamma-gamma collisions.The scattered electron can be reconstructed either in the luminosity monitor (probing the small
$ Q^2 $ values with high statistics) or the forward electromagnetic calorimeter. In the latter case, the domain of high$ Q^2 $ values can be accessed. The available range of high$ Q^2 $ is limited by low statistics owing to the steeply falling spectrum of scattering angles. Given the unprecedented luminosity, future$ e^+e^- $ colliders will be able to study the PSF in the high$ Q^2 $ domain, which has never been accessed by previous experiments.At LEP2, the explored range of
$ Q^2 $ was limited to approximately$ 10^3 $ GeV2, mainly due to the available statistics. At the CEPC, the collision energy will be comparable to LEP2. However, the large statistics expected at future colliders (an increase of several orders of magnitude) will allow the exploration of kinematical regions that were inaccessible in past experiments owing to limited statistics. Among them, the following can be mentioned:● Measurement of the PSF at high virtualities
$ Q^2 $ , corresponding to large electron scattering angles.● Double-tagged events, where both beam particles are detected. In this situation, the entire event is fully reconstructed, which will dramatically reduce the systematic uncertainty at the expense of low available statistics.
The case of deeply virtual target photons,
$Q^2\gg P^2\gg\Lambda_{\rm QCD}$ , is interesting because it is purely perturbative and allows one to compare experimental values with absolute QCD predictions. -
In this study, we investigate several interesting topics involving two-photon physics that could be considered at the CEPC and FCC-ee, two future electron-positron colliders. As a reference, we take the planned CEPC set-up with a c.m.s. energy
$ \sqrt{s}=240 $ GeV and an integrated luminosity of 5.6$\rm ab^{-1}$ and assume that a forward electromagnetic calorimeter will cover polar angles down to$ 1.9 $ degrees. Our qualitative results can be applied to the FCC-ee project, considering its similar expected performance.We consider a limited set of topics in two-photon physics, namely, quarkonium spectroscopy, Higgs and tau pair production, and the photon hadronic structure. Our estimations are based on a conservative approach, and the quantitative characteristics will undoubtedly be surpassed in real experiments. New physics problems such as the search for MSSM heavy Higgs, anomalous top quark interactions, and new physics states will be considered elsewhere.
In Sect. III, we consider quarkonium two-photon physics in three possible detection modes: no-tag, single-, and double tag. We find that the use of a low-angle calorimeter (1.9 degree minimal detection angle) may drastically improve the statistics of tagged events by two orders of magnitude. In the no-tag mode, we expect approximately
$ 10^7 $ –$ 10^8 $ quarkonium and$ 10^5 $ bottomonium events. Considering the efficiency of detection to be approximately$ 10\ $ % and using the single-tag mode for better reconstruction of the final state and background event reduction, we estimate approximately$ 10^2-10^4 $ registered events for charmonium states. For bottomonium, we can expect approximately$ 4\times10^2 $ low-state$ \eta_b $ and possibly observe several events or apply an upper bound for higher states.In Sect. IV, we find that the photoproduction of Higgs can be observed with a total cross-section of approximately
$ 0.25 $ fb and a collider luminosity of 5.6$\rm ab^{-1}$ . Possible background issues from non-resonant$ \gamma\gamma $ collisions and$ ZZ\to H $ are discussed, and it is shown that, by choosing appropriate selection cuts, a signal significance of more than$ 4\sigma $ may be achieved for the$ H\to bb $ channel.The tau pair production cross-section and anomalous magnetic moment measurement can be improved by up to a factor of 8 compared with the precision of the DELPHI experiment at the LEP (Sect. V).
The statistical error on the PSF measurement (Sect. VI) can be improved by approximately two orders of magnitude compared to the LEP experiments. Furthermore, we expect that, owing to the high luminosity of future colliders, it will be possible to perform PSF measurements at high virtualities
$ Q^2 $ .A more detailed analysis and thorough simulation of events, background, and systematic and statistical errors on physical quantities can be performed once the exact characteristics of the planned colliders and detectors are known.
-
The authors are grateful to prof. Li Haibo for fruitful discussions, which inspired this study.
Two-photon physics at future electron-positron colliders
- Received Date: 2022-02-05
- Available Online: 2023-01-15
Abstract: Two photon collisions offer a variety of physics phenomena that can be studied at future electron-positron colliders. Using the planned CEPC parameters as a benchmark, we consider several topics within two-photon collisions. With the full integrated luminosity, Higgs boson photoproduction can be reliably observed, and large statistics on various quarkonium states can be collected. The LEP results for the photon structure function and tau lepton anomalous magnetic moment can be improved by 1-2 orders of magnitude.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: