-
The hadron
$ X(3872) $ has attracted considerable attention since it was first observed by Belle in the exclusive decay$ B^{\pm}\to K^{\pm}\pi^+\pi^-J/\Psi $ [1]. Though$ X(3872) $ has been confirmed by many experimental collaborations, such as the CDF [2], D0 [3], Babar [4], and LHCb [5], with quantum numbers$ J^{PC}=1^{++} $ and isospin$ I=0 $ , there are still many uncertainties. Because the mass of$ X(3872) $ is close to the$ D^0\bar D^{*0} $ threshold, several authors interpret it as a loosely bound molecular state [6–10], in which the building blocks are hadrons [11]. Others regard$ X(3872) $ as a compact tetraquark state [12–15], in which the building blocks are quarks and anti-quarks. There are other explanations, such as$ c\bar c g $ hybrid meson [16, 17] and glueballs [18]. Though there are many different exotic hadron state interpretations of$ X(3872) $ , it has not been ruled out that the first radial excitation of the$ 1P $ charmonium state$ \chi_{c1}(1P) $ is the most natural assignment [19–21]. Note that$ X(3872) $ was renamed$ \chi_{c1}(3872) $ by the Particle Data Group (PDG) [22].Many studies on the production and decays of
$ X(3872) $ have been performed to investigate the inner structure of$ X(3872) $ [23–26]. In Ref. [26], the authors calculated$ \Gamma(X(3872)\to J/\psi \pi^+\pi^-) $ using QCD sum rules and concluded that X(3872) is approximately$97$ % a charmonium state with a small molecular component. Many B meson decays with$ X(3872) $ in the final states have been studied using different approaches [27–33]. In Ref. [28], the authors studied the$ B\to \chi_{c1}(1P,2P)K $ decays using the QCD factorization (QCDF) approach and argued that$ X(3872) $ has a dominant$ c\bar c $ component but mixes with the$ D^0\bar D^{*0}+D^{*0}\bar D^0 $ continuum component. The$ B_c\to X(3872)\pi(K) $ decays were studied both using the covariant light-front (CLF) approach [29] and generalized factorization (GF) approach [30], respectively. In the former,$ X(3872) $ was identified as a$ 1^{++} $ charmonium state, whereas a tetraquark state was assumed in the latter. One may expect different results for the same decays under the different structure hypotheses of$ X(3872) $ . The$ B\to X(3872)K $ decay has also received significant attention from many researchers. In Refs. [31, 32], the authors assumed$ X(3872) $ to be a loosely bound S-wave molecular state of$ D^0\bar D^{*0}(D^{*0}\bar D^0) $ and estimated the branching ratio of the$ B^+\to X(3872)K^+ $ decay to be$ (0.07\sim1)\times10^{-4} $ . Furthermore, they considered the branching ratio of the$ B^0\to X(3872)K^0 $ decay to be suppressed by more than one order of magnitude compared with that of the$ B^+\to X(3872)K^+ $ decay, which indicates that there is large isospin symmetry between the$ B^+\to X(3872)K^+ $ and$ B^0\to X(3872)K^0 $ decays. If this type of large isospin symmetry is observed in experiments, any charmonium interpretation of$ X(3872) $ will be disfavored. Two years later, the branching ratio of the$ B^+\to X(3872)K^+ $ decay was calculated using the perturbative QCD (PQCD) approach, assuming$ X(3872) $ as a regular$ c\bar c $ charmonium state, in Ref. [33]; a large value of$ {\rm Br}(B^+\to X(3872)K^+)= (7.88^{+4.87}_{-3.76})\times10^{-4} $ was obtained. Clearly, this result is significantly larger than the present experimental upper limits given by Belle [34] and BaBar [35] at the$ 90\ $ % C.L.,$ {\rm Br}(B^+\to X(3872)K^+)<2.6\times10^{-4} \;\;\;(\rm{Belle}) , $

(1) $ {\rm Br}(B^+\to X(3872)K^+)<3.2\times10^{-4} \;\;\;(\rm{BaBar}). $

(2) Here, we conduct a systematic study of the
$ B_{c,u,d}\to X(3872)P $ decays using the PQCD approach, where P represents a light pseudoscalar meson (K or π). The layout of this paper is as follows. We present the analytic calculations of the amplitudes of the$ B_{c,u,d}\to X(3872)P $ decays in Section II. The numerical results and discussions are given in Section III, where we compare our results with other theoretical predictions and experimental data. The conclusions are presented in Section IV. -
Because the PQCD approach based on
$ k_T $ factorization has been successfully applied to many two-body charmed B meson decays [36–39], we use this approach to investigate the$ B_{c,u,d}\to X(3872)P $ decays in this study. First, the effective Hamiltonian for the$ B^+_c\to X(3872)\pi^+ (K^+) $ decays can be written as [40]$ \begin{eqnarray} {H}_{\rm eff}=\frac{G_{\rm F}}{\sqrt2}V^*_{cb}V_{uq}\left[C_1(\mu)O_1(\mu)+C_2(\mu)O_2(\mu)\right]+ {\rm H.c.}, \end{eqnarray} $

(3) where the Fermi coupling constant
$G_{\rm F}\simeq1.166\times 10^{-5}$ GeV$ ^{-2} $ [22],$ V^*_{cb}V_{uq} $ is the product of the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements with$ q=d $ ($ q=s $ ) for$ B^+_c\to X(3872)\pi^+ $ ($ B^+_c\to X(3872)K^+ $ ) decay,$ C_{i}(\mu)(i=1,2) $ are the Wilson coefficients at the renormalization scale μ, and$ O_{i}(i=1,2) $ are the local four-quark operators,$ \begin{aligned}[b] O_1=&\bar d_{\alpha}\gamma_{\mu}(1-\gamma_5)u_{\beta}\otimes\bar c_{\beta}\gamma_{\mu}(1-\gamma_5)b_{\alpha},\\ O_2=&\bar d_{\alpha}\gamma_{\mu}(1-\gamma_5)u_{\alpha}\otimes\bar c_{\beta}\gamma_{\mu}(1-\gamma_5)b_{\beta},\; \end{aligned} $

(4) where α and β are the
$S U(3)$ color indices, and the summation convention over repeated indices is understood. Because the four quarks in the operators are different, there is no penguin contribution and thus no CP violation. Here, we analyze the$ B^+_c\to X(3872)\pi^+ $ decay as an example, and its Feynman diagrams are given in Fig. 1, where only the factorizable and non-factorizable emission diagrams need to be considered at the leading order①. The amplitude for the factorizable emission diagrams in Fig. 1(a) and Fig. 1(b) can be written as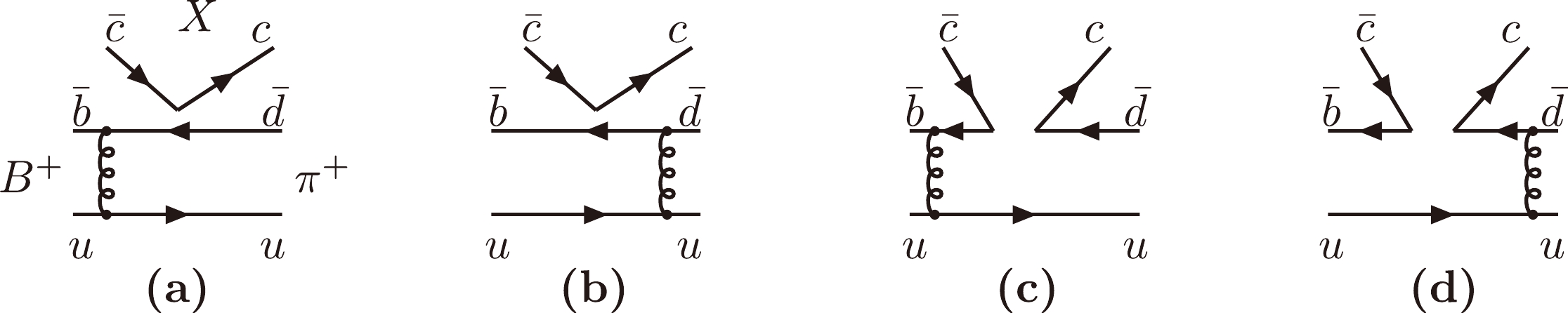
Figure 1. Feynman diagrams contributing to the
$ B^+_c\to X(3872)\pi^+ $ decay at the leading order.$ \begin{aligned}[b] F^{LL}_{B_c\to X}=&2\sqrt{\frac{2}{3}}\pi C_{\rm F} m^4_{B_c}f_{\pi}f_{B_c}\sqrt{1-r_X^2}\int_0^1 {\rm d} x_2 \int_0^\infty b_1 {\rm d} b_1 b_2 {\rm d} b_2 \exp\left(-\frac{\omega^2_{B_c}b^2_1}{2}\right)\\ & \left\{\left[ \Psi^L(x_2)(x_2-2r_b)+\Psi^t(x_2)(r_b-2x_2)\right]E_e(t_a)h(\alpha,\beta_a,b_1,b_2)S_t(x_2)\right.\\ &\left. -\Psi^L(x_2)(r_c+r_X^2(x_1-1))E_e(t_b)h(\alpha,\beta_b,b_2,b_1)S_t(x_1) \right\}, \end{aligned} $ 
(5) where the superscript
$ LL $ denotes the contribution from the$ (V-A)(V-A) $ operators, the color factor$ C_F=4/3, f_{\pi(B_c)} $ is the decay constant for the meson$ \pi(B_c) $ , the mass ratio$ r_{X(b,c)}=m_X(m_b,m_c)/m_{B_c} $ , the exponent$ \exp(-\omega^2_{B_c}b^2_1/2) $ originates from the$ B_c $ meson wave function, and$ \Psi^{L,t}(x_2) $ are the distribution amplitudes for$ X(3872) $ (given in Sec. III).The amplitude for the non-factorizable spectator diagrams in Fig. 1(c) and Fig. 1(d) is given as
$ \begin{aligned}[b]\\ M^{LL}_{B_c\to X}=&\frac{8}{3}\pi C_{\rm F} m^4_{B_c}f_{B_c}\sqrt{1-r_X^2} \int_0^1 {\rm d}x_2 \int_0^\infty b_1 {\rm d} b_1 b_3 {\rm d} b_3 \exp\left(-\frac{\omega^2_{B_c}b^2_1}{2}\right) \phi^A_\pi(x_3)\\ &\left\{[\Psi^L(x_2)(x_3-x_1)(1-r_X^2) +r_X\Psi^t(x_2)(1-x_1-x_2)]E_{cd}(t_c)h(\alpha,\beta_c,b_1,b_3) \right.\\ &\left. +[\Psi^L(x_2)(r_X^2(x_2-x_3)+2x_1+x_2+x_3-2)+r_X\Psi^t(x_2)(1-x_1-x_2)]\right. E_{cd}(t_d)h(\alpha,\beta_d,b_1,b_3)\Big\}. \end{aligned} $

(6) Note that the hard function h originates from the Fourier transform of the virtual quark and gluon propagators, which is defined as
$ h(\alpha,\beta,b_1,b_2)=h_1(\alpha,b_1)\times h_2(\beta,b_1,b_2), $

(7) $ \begin{eqnarray} h_1(\alpha,b_1)=\left\{\begin{matrix}K_0(\sqrt{\alpha}b_1), & \alpha > 0,\\ K_0({\rm i}\sqrt{-\alpha}b_1), & \alpha < 0, \\\end{matrix}\right. \end{eqnarray} $

(8) $ \begin{aligned}[b]& h_1(\beta,b_1,b_2)\\=&\left\{\begin{matrix}\theta(b_1-b_2) I_0(\sqrt{\beta}b_2) K_0(\sqrt{\beta}b_1)+(b_1\leftrightarrow b_2), & \beta > 0,\\ \theta(b_1-b_2) J_0(\sqrt{-\beta}b_2) K_0({\rm i}\sqrt{-\beta}b_1)+(b_1\leftrightarrow b_2), & \beta < 0, \\\end{matrix}\right. \end{aligned} $

(9) where
$ J_0 $ is the Bessel function, and$ K_0,I_0 $ are the modified Bessel functions with$K_0({\rm i}x)=\pi(-N_0(x)+{\rm i}J_0(x))/2.$ In Eqs. (5) and (6), α and$ \beta_{a,b,c,d} $ in the hard function h are the invariant masses of the internal quarks and gluons, respectively. The hard scales$ t_{a,b,c,d} $ are given as the maximum energy scale appearing in each Feynman diagram to remove the large logarithmic radiative corrections. Their expressions are listed in the appendix. The evolution factors$ E_e(t),E_{cd}(t) $ evolving the Sudakov exponent and jet function$ S_t(x) $ can be found in Refs. [38, 41]. For the reader's convenience, their explicit forms are also summarized in the appendix.Second, the effective Hamiltonian for the
$ B_{u,d}\to X(3872)\pi(K) $ decays is written as$ \begin{aligned}[b] {H}_{\rm eff}=&\frac{G_{\rm F}}{\sqrt2}\Bigg[V^*_{cb}V_{cq}(C_1(\mu)O^c_1(\mu)+C_2(\mu)O^c_2(\mu))\\&- V^{*}_{tb}V_{tq}\sum^{10}_{i=3}C_i(\mu)O_i(\mu)\Bigg], \end{aligned} $

(10) where
$ V^*_{c(t)b}V_{c(t)q} $ is the product of the CKM matrix elements,$ q=d $ or s. The local four-quark operators$ O_i(\mu) $ and corresponding QCD-corrected Wilson coefficients$ C_i(\mu) $ can be found in Ref. [40]. Here, we analyze$ B^+\to X(3872)\pi^+ $ as an example, and its Feynman diagrams are given in Fig. 2. The amplitudes for the factorizable and nonfactorizable emission diagrams from the$ (V-A)(V-A) $ operators are denoted as$ F^{LL}_{B\to \pi} $ and$ M^{LL}_{B\to\pi} $ , respectively. Their analytical expressions are given as$ \begin{aligned}[b] F^{LL}_{B\to \pi}=&\frac{8\pi C_{\rm F} m^4_Bf_{X}}{\sqrt{1-r^2_X}}\int_0^1 {\rm d} x_1 {\rm d} x_3 \int_0^\infty b_1 {\rm d} b_1 b_3 {\rm d} b_3\phi_B(x_1,b_1) \left\{\left[ \left(r^2_X-1)\phi^A_\pi(x_3)((r^2_X-1) x_3-1\right)\right.\right. \\ &\left.\left. +(r^2_X-1)\phi^P_\pi(x_3)r_\pi(2x_3-1)+\phi^T_\pi(x_3)r_\pi(2x_3(r_X^2-1)+1+r^2_X)\right] \right.\\ &\left.\times E_{e'}(t'_a)h(\alpha',\beta'_a,b_1,b_3)S_t(x_3) -2r_\pi(1-r_X^2)\phi^P_\pi(x_3)\right.\left. E_{e'}(t'_b)h(\alpha',\beta'_b,b_3,b_1)S_t(x_1) \right\}, \end{aligned} $ 
(11) $ \begin{aligned}[b] M^{LL}_{B\to\pi}=&\frac{32}{\sqrt6}\frac{1}{\sqrt{(1-r_X^2)}}\pi C_{\rm F} m^4_B \int_0^1 {\rm d} x_1 {\rm d} x_2 \int_0^\infty b_1 {\rm d} b_1 b_2 {\rm d} b_2\phi_B(x_1,b_1)\Big\{\Big[\Psi^L(x_2)(\phi^A_\pi(x_3)(r_X^2-1)\\ &+2\phi^T_\pi(x_3)r_\pi)(r_X^2(x_1+x_3-2x_2)+x_1-x_3) +4r_\pi r_Xr_c\phi^T_\pi(x_3)\Psi^t(x_2)\Big]\Big\}E_c(t'_c)h(\alpha',\beta'_c,b_1,b_2), \end{aligned} $

(12) where the evolution factors
$ E_{e'}(t),E_{c}(t) $ evolving the Sudakov exponent are given in the appendix. Besides the upper two$ (V-A)(V-A) $ type amplitudes, there are factorizable and nonfactorizable emission diagram contributions from the$ (V-A)(V+A) $ and$ (S-P)(S+P) $ operators, which are expressed as$ F^{LR}_{B\to\pi} $ and$ M^{SP}_{B\to\pi} $ , respectively.$ F^{LR}_{B\to\pi}=-F^{LL}_{B\to \pi}, $

(13) $ \begin{aligned}[b] M^{SP}_{B\to\pi}=&-\frac{32}{\sqrt6}\frac{1}{\sqrt{(1-r_X^2)}}\pi C_{\rm F} m^4_B \int_0^1 {\rm d} x_1 {\rm d} x_2 \int_0^\infty b_1 {\rm d} b_1 b_2 {\rm d} b_2\phi_B(x_1,b_1)\\ & \times \left\{\left[\Psi^L(x_2)(\phi^A_\pi(x_3)(r_X^2-1)+2\phi^T_\pi(x_3)r_\pi)(r_X^2(x_1+x_3-2x_2)+x_1-x_3) -4r_\pi r_Xr_c\phi^T_\pi(x_3)\Psi^t(x_2)\right]\right\}E_c(t'_c)h(\beta'_c,\alpha',b_2,b_1), \end{aligned} $ 
(14) where
$ \alpha',\beta'_{a,b,c} $ in the upper hard function and the hard scales$ t'_{a,b,c} $ are defined in the appendix.By combining the amplitudes from the different Feynman diagrams, the total decay amplitudes for the considered decays are given as
$ \begin{eqnarray} \mathcal{A}(B_c\to X(3872)P)=V^*_{cb}V_{uq}\left[a_1F^{LL}_{B_c\to X}+C_1M^{LL}_{B_c\to X}\right], \end{eqnarray} $

(15) $ \begin{aligned}[b] \mathcal{A}(B_{u,d}\to X(3872)P)=&V^*_{cb}V_{cq}\left[a_2F^{LL}_{B\to P}+C_2M^{LL}_{B\to P}\right]\\&-V^*_{tb}V_{tq}\left[(a_3+a_9-a_5-a_7)F^{LL}_{B\to P}\right.\\ &\left.+(C_4 + C_{10})M^{LL}_{B\to P} + (C_6 + C_8)M^{SP}_{B\to P}\right], \end{aligned} $

(16) where the combinations of the Wilson coefficients
$ a_1=C_1/3+C_2, a_2=C_1+C_2/3, a_i=C_i+C_{i+1}/3 $ with$ i= $ 3, 5, 7, and 9, and$ q=d $ ($ q=s $ ) corresponds to the decays induced by the$ b\to d $ ($ b\to s $ ) transition. -
We use the following input parameters for the numerical calculations [22, 29, 30]:
$\begin{aligned}[b]f_{B_c}= & 0.398^{+0.054}_{-0.055}~ {\rm GeV},~~ f_{B}=0.19~{\rm GeV},\\ f_{X}= & 0.234\pm0.052~{\rm GeV}, \end{aligned} $

(17) $ \begin{aligned}[b] M_{B_{c}}=& 6.275~{\rm GeV}, ~~M_B=5.279~{\rm GeV},\\ M_{X}= & 3.87169~{\rm GeV}, \end{aligned} $

(18) $ \begin{aligned}[b] \tau_{B_c}=&0.510\times 10^{-12} {\rm s},\quad \tau_B^\pm=1.638\times 10^{-12} {\rm s},\\\tau_{B^0}=&1.519\times 10^{-12} {\rm s}. \end{aligned} $

(19) For the CKM matrix elements, we adopt the Wolfenstein parameterization and the updated values
$ A=0.814 $ ,$ \lambda=0.22537,~ \bar\rho=0.117\pm0.021 $ , and$ \bar\eta=0.353\pm0.013 $ [22]. With the total amplitudes, the decay width can be expressed as$ \begin{eqnarray} \Gamma(B\to X(3872)P)=\frac{G^2_{\rm F}}{32\pi m_B}(1-r^2_{X})|\mathcal{A}(B\to X(3872)P)|^2. \end{eqnarray} $

(20) The wave functions of
$ B, \pi $ , and K have been well defined in many studies, whereas those of$ B_c $ and$ X(3872) $ still have many uncertainties. For the$ B_c $ meson, we use its wave function in the nonrelativistic limit [42],$ \begin{eqnarray} \Phi_{B_c}(x)=\frac{{\rm i}f_{B_c}}{4N_C}\left[( \not p _{B_{c}} +M_{B_{c}})\gamma_5\delta(x-r_c)\right] \exp\left(-\frac{b^2\omega^2_{B_c}}{2}\right), \end{eqnarray} $

(21) where b is the conjugate space coordinate of the parton transverse momentum
$ k_T $ , and the shape parameter$ \omega_{B_c}=0.6 $ GeV. The last exponent term reveals the$ k_T $ dependence.For the light cone distribution amplitude of
$ X(3872) $ , we adopt a similar formula to that of the$ \chi_{c1} $ meson [33, 43],$ \begin{aligned}[b]& \langle X(p,\epsilon_L)|\bar c_\alpha(z)c_{\beta}(0)|0\rangle\\=&\frac{1}{\sqrt{2N_c}}\int {\rm d} x {\rm e}^{{\rm i} x p\cdot z} \left\{m_X[\gamma_5 \not \epsilon _L]_{\beta\alpha}\phi^L_X(x)+[\gamma_5 \not \epsilon _L {\not p} ]_{\beta\alpha}\phi^t_X(x)\right\}, \end{aligned} $

(22) where
$ \epsilon_L $ is the longitudinal polarization vector, and$ m_X $ is the$ X(3872) $ mass. Here, only the longitudinal polarization contributes to the considered decays, and the asymptotic models of the twist-2 distribution amplitude$ \phi^{L}_X(x) $ and twist-3 distribution amplitude$ \phi^{t}_X(x) $ are given as$ \begin{aligned}[b] \phi^{L}_X(x)=&24.68\frac{f_X}{2\sqrt{2N_c}}x(1-x)\\&\times\left\{\frac{x(1-x)(1-2x)^2\left[1-4x(1-x)\right]}{[1-3.47x(1-x)]^3} \right\}^{0.7}, \end{aligned} $

(23) $ \begin{aligned}[b] \phi^{t}_X(x)=&13.53\frac{f_X}{2\sqrt{2N_c}}(1-2x)^2\\&\times\left\{\frac{x(1-x)(1-2x)^2\left[1-4x(1-x)\right]}{[1-3.47x(1-x)]^3} \right\}^{0.7}, \end{aligned} $

(24) where
$ f_X $ is the$ X(3872) $ decay constant.Using the input parameters and wave functions specified in this section, we present the branching ratios of the
$ B^+_c\to X(3872)\pi^{+}(K^+) $ decays as follows:$ {\rm Br}(B^+_c\to X(3872)\pi^+)=(2.7^{+1.4+0.9+0.7+0.2}_{-1.0-0.6-0.5-0.1})\times10^{-4}, $

(25) $ {\rm Br}(B^+_c\to X(3872)K^+)=(2.5^{+1.3+0.8+0.6+0.2}_{-1.0-0.6-0.4-0.1})\times10^{-5}, $

(26) where the first error arises from the
$ X(3872) $ decay constant,$ f_{X}=0.234\pm0.052 $ GeV, the second and third uncertainties are caused by the shape parameter$ \omega_{B_c}=0.6\pm0.1 $ GeV and decay constant$ f_{B_c}=0.398^{+0.054}_{-0.055} $ GeV, respectively, and the final error is from the variation in the hard scale from$ 0.8t $ to$ 1.2t $ , which characterizes the size of the next-to-leading-order QCD contributions. The branching ratios are sensitive to the decay constant$ f_{X} $ because the dominant contributions for these two channels are from the factorization emission amplitudes, which are proportional to$ f_{X} $ . The branching ratio of$ B^+_c\to X(3872)\pi^{+} $ is approximately one order of magnitude larger than that of$ B^-_c\to X(3872)K^{-} $ , which is mainly induced by the difference between the CKM elements$ V_{ud}=1-\lambda^2/2 $ and$ V_{us}=\lambda $ . From Table 1, it is shown that our predictions are consistent with the results given in the covariant light-front quark model within errors [29]; however, they are significantly larger than those calculated using the generalized factorization approach [30].Mode This study CLF [29] GF [30] $ B^+_{c}\to X(3872)\pi^{+}(\times10^{-4}) $ 

$ 2.7^{+1.4+0.9+0.7+0.2}_{-1.0-0.6-0.5-0.1} $ 

$ 1.7^{+0.7+0.1+0.4}_{-0.6-0.2-0.4} $ 

$ 0.60^{+0.22+0.14}_{-0.18-0.07} $ 

$ B^+_{c}\to X(3872)K^{+}(\times10^{-5}) $ 

$ 2.5^{+1.3+0.8+0.6+0.2}_{-1.0-0.6-0.4-0.1} $ 

$ 1.3^{+0.5+0.1+0.3}_{-0.5-0.2-0.3} $ 

$ 0.47^{+0.17+0.11}_{-0.14-0.05} $ 

Similarly, the branching ratios of the
$ B\to X(3872)P $ decays are calculated as follows:$ {\rm Br}(B^+\to X(3872)K^+)=(3.8^{+0.9+0.6+0.3}_{-0.8-0.5-0.2})\times10^{-4}, $

(27) $ {\rm Br}(B^0 \to X(3872)K^{0})=(3.5^{+0.7+0.5+0.3}_{-0.6-0.4-0.2})\times10^{-4}, $

(28) $ {\rm Br}(B^+\to X(3872)\pi^+)=(9.3^{+1.5+0.9+0.5}_{-1.3-0.8-0.4})\times10^{-6}, $

(29) $ {\rm Br}( B^0\to X(3872)\pi^{0})=(4.3^{+0.7+0.5+0.3}_{-0.6-0.4-0.3})\times10^{-6}, $

(30) where the first uncertainty arises from the shape parameter
$ \omega_{B}=0.4\pm0.04 $ GeV in the B meson wave function, the second error is from the decay constant$ f_{X}=0.234\pm0.052 $ GeV of$ X(3872) $ , and the third error arises from the choice of hard scales, which vary from$ 0.8t $ to$ 1.2t $ . From the results, we find that the branching ratios of the$ B^+\to X(3872)K^{+} $ and$ B^0 \to X(3872)K^{0} $ decays are similar because they differ only in the lifetimes between$ B^+ $ and$ B^0 $ in our formalism. Our prediction for the branching ratio of the$ B^+\to X(3872)K^{+} $ decay is less than the previous PQCD calculation result$ (7.88^{+4.87}_{-3.76})\times10^{-4} $ [33]. However, it is still slightly larger than the upper limits$ 2.6\times10^{-4} $ given by Belle [34] and$ 3.2\times10^{-4} $ given by BaBar [35]. If the present experimental upper limits are confident, a pure charmonium assignment for$ X(3872) $ may not be suitable under the PQCD approach. We expect that the branching ratios of the$ B^{0,+}\to X(3872)K^{0,+} $ decays can be precisely measured at the current LHCb and SuperKEKB experiments, which will help probe the inner structure of$ X(3872) $ .However, note that
$ X(3872) $ was renamed$ \chi_{c1}(3872) $ by the current PDG [22], which seems to assume it is a radial excited state of$ \chi_{c1}(1P) $ . As we know, the$ \chi_{c1}(1P) $ meson is another P-wave charmonium state with the same quantum numbers$ J^{(PC)}=1^{++} $ and a slightly lighter mass of$ 3.511 $ GeV. In this case, they should have similar properties in B meson decays. For example, the branching ratio of the$ B^{+}\to \chi_{c1}(1P) K^+ $ decay is measured as$(4.85\pm 0.33)\times 10^{-4}$ [22], which is consistent with the result predicted using the PQCD approach$ (4.4^{+1.9}_{-1.6})\times10^{-4} $ [43]. The corresponding decay$ B^{+}\to X(3872) K^+ $ should have a similar but slightly smaller branching ratio. Comparisons of the branching ratios of the$ B\to X(3872)\pi(K) $ and$ B\to \chi_{c1}(1P)\pi(K) $ decays can be found in Table 2, where the theoretical predictions for the branching ratios of the$ B\to \chi_{c1}(1P)\pi(K)) $ decays are taken from other PQCD calculations [43]. From Table 2, we know that calculations for the$ B\to X(3872)P $ decays using the PQCD approach are under control and credible. Therefore, we suggest that experimental researchers measure these decays at LHCb and Belle II to help discriminate the inner structure of$ X(3872) $ from different assumptions.Mode $ (\times10^{-4}) $ 

$ B^+\to X(3872)K^{+} $ 

$ B^+\to \chi_{c1}(1P)K^{+} $ 

$ B^0\to X(3872)K^{0} $ 

$ B^0\to \chi_{c1}(1P)K^{0} $ 

PQCD $ 3.8^{+0.9+0.6+0.3}_{-0.8-0.5-0.2} $ 

$ 4.4^{+1.9}_{-1.6} $ 

$ 3.5^{+0.7+0.5+0.3}_{-0.6-0.4-0.2} $ 

$ 4.1^{+1.8}_{-1.6} $ 

Exp. − $ 4.85\pm0.33 $ 

− $ 3.95\pm0.27 $ 

Mode ( $ \times10^{-5}) $ 

$ B^+\to X(3872)\pi^{+} $ 

$ B^+\to \chi_{c1}(1P)\pi^{+} $ 

$ B^0\to X(3872)\pi^{0} $ 

$ B^0\to \chi_{c1}(1P)\pi^{0} $ 

PQCD $ 0.93^{+0.15+0.09+0.05}_{-0.13-0.08-0.04} $ 

$ 1.7\pm0.6 $ 

$ 0.43^{+0.07+0.05+0.03}_{-0.06-0.04-0.03} $ 

$ 0.8\pm0.3 $ 

Exp. − $ 2.2\pm0.5 $ 

− $ 1.12\pm0.28 $ 

In Table 3, we compare our predictions with the results calculated using the generalized factorization approach [30]. It is interesting that the branching ratios of the
$ B\to X(3872)\pi(K) $ decays calculated with these two different approaches are consistent with each other within errors. We find that${\rm Br}(B^+\to X(3872)\pi^{+})\simeq 2 {\rm Br}(B^0\to X(3872)\pi^{0})$ , which is supported by the isospin symmetry.Mode This study GF [30] $ B^+\to X(3872)K^{+}(\times10^{-4}) $ 

$ 3.8^{+0.9+0.6+0.3}_{-0.8-0.5-0.2} $ 

$ 2.3^{+1.1}_{-0.9}\pm0.1 $ 

$ B^0\to X(3872)K^{0}(\times10^{-4}) $ 

$ 3.5^{+0.7+0.5+0.3}_{-0.6-0.4-0.2} $ 

$ 2.1^{+1.0}_{-0.8}\pm0.1 $ 

$ B^+\to X(3872)\pi^{+}(\times10^{-6}) $ 

$ 9.3^{+1.5+0.9+0.5}_{-1.3-0.8-0.4} $ 

$ 11.5^{+5.7}_{-4.5}\pm0.3 $ 

$ B^0\to X(3872)\pi^{0}(\times10^{-6}) $ 

$ 4.3^{+0.7+0.5+0.3}_{-0.6-0.4-0.3} $ 

$ 5.3^{+2.6}_{-2.1}\pm0.2 $ 

Table 3. Our predictions for the branching ratios of the
$ B\to X(3872)\pi(K) $ decays, along with the results from the generalized factorization (GF) approach [30].In the following we discuss the CP asymmetries in the
$ B\to X(3872)P $ decays. As we know, CP asymmetry arises from the interference between the tree and penguin amplitudes; however, there are no contributions from the penguin amplitudes for the$ B^+_c\to X(3872)\pi^+(K^+) $ decays. Therefore, the corresponding direct CP violation is zero. For the charged decays$B^+\to $ $ X(3872)\pi^{+}(K^+)$ , we only need to consider the direct CP violation$A^{\rm dir}_{CP}$ , which is defined as$ \begin{eqnarray} A^{\rm dir}_{CP}=\frac{|\mathcal{\bar A}|^2-|\mathcal{A}|^2}{|\mathcal{ \bar A}|^2+|\mathcal{A}|^2}, \end{eqnarray} $

(31) where
$ \mathcal{ \bar A} $ is the CP-conjugate amplitude of$ \mathcal{A} $ . For neutral B meson decays, there is another type of CP violation that must be considered, known as as time-dependent CP asymmetry, which is induced by interference between the direct decay and the decay via oscillation. Time-dependent CP violation can be defined as$ \begin{eqnarray} A(t)_{CP}=A_f\cos(\Delta mt)+S_f\sin(\Delta mt), \end{eqnarray} $

(32) where the subscript f represents a CP eigenstate,
$ \Delta m $ is the mass difference of the two neutral B meson mass eigenstates, and the direct CP asymmetry$ A_f $ and mixing-induced CP asymmetry$ S_f $ are expressed as$ \begin{eqnarray} A_f=\frac{|\lambda_f|^2-1}{|\lambda_f|^2+1}, \;\;S_f=\frac{2{\rm Im}(\lambda_f)}{|\lambda_f|^2+1}, \end{eqnarray} $

(33) with
$ \begin{eqnarray} \lambda_f=\eta_f {\rm e}^{-2{\rm i}\beta}\frac{\mathcal{\bar A}}{\mathcal{A}}, \end{eqnarray} $

(34) where
$ \eta_f $ is$ 1(-1) $ for a CP-even (CP-odd) final state f, and β is the CKM angle [22]. Because the charged decay channel and corresponding neutral mode are the same, except for the lifetime and isospin factor in the amplitudes, they have the same direct CP asymmetries. Therefore, we only need to consider the neutral decays, whose direct CP asymmetries are calculated as$ A_{X(3872)K^0}=(1.2^{+0.0+0.0+0.2}_{-0.0-0.0-0.3})\times10^{-3}, $

(35) $ A_{X(3872)\pi^0}=(2.7^{+0.1+0.0+0.4}_{-0.2-0.0-0.4})\times10^{-2}, $

(36) where the errors are induced by the same sources as those for the branching ratios; however, the direct CP violations are less sensitive to the nonperturbative parameters within their uncertainties, except for the hard scale t. Compared to the tree contributions, the penguin amplitudes are loop suppressed by one to two orders of magnitude. At the same time, the product of the CKM matrix elements associated with the tree amplitudes is approximately four times larger than that of penguin amplitudes. Hence, direct CP violations, which arise from interference between the tree and penguin contributions, are very small. Because the final state
$ X(3872)K^0 $ and its CP conjugate state are flavor-specific, we should use the CP-odd eigenstate$ X(3872)K^0_S $ to analyze the mixing-induced CP violations. The results for the mixing-induced CP violations are calculated as$ S_{X(3872)K^0_S}=(70.3^{+0.0+0.0+0.9}_{-0.0-0.0-1.2}){\text{%}}, $

(37) $ S_{X(3872)\pi}=(-60.8^{+0.0+0.0+1.5}_{-0.0-0.0-1.4}){\text{%}}, $

(38) where the errors are similar to those listed in the direct CP violations and are not sensitive to the nonperturbative parameters given in the wave functions. We find that
$ S_{X(3872)K^0_S} $ is highly consistent with the current world average value$ \sin2\beta=0.699\pm0.017 $ [44], which is obtained from$ B^0 $ decays to charmonium and$ K^0_S $ . Therefore, we can check the nature of$ X(3872) $ by extracting the CKM phase β from future experimental data on the$ B^0\to X(3872)K^0_S $ decay. Conversely, the mixing-induced CP asymmetry of the$ B^0\to X(3872)\pi^0 $ decay exhibits a significant deviation from the world average value of$ \sin2\beta $ because the imaginary parts of the total amplitudes for this channel and its CP-conjugate process exhibit a large difference. Our results can be tested in future experiments. -
In this study, we analyze the
$ B_{c,u,d}\to X(3872)\pi(K) $ decays using the PQCD approach by assuming$ X(3872) $ to be a$ 1^{++} $ charmonium state. Comparing our predictions for the branching ratios and CP asymmetries of the considered decays with other theoretical results and available experimental data, we find the following results:(1) The branching ratios of the
$ B^-_c\to X(3872)\pi^- $ and$ B^-_c\to X(3872) K^- $ decays can reach orders of$ 10^{-4} $ and$ 10^{-5} $ , respectively, which are consistent with the results obtained via the covariant light-front approach within errors but larger than those given by the generalized factorization approach. These results can be discriminated at the current LHCb and Belle II experiments.(2) Our predictions for the branching ratio of the
$ B\to X(3872) K $ and$ B\to X(3872)\pi $ decays are consistent with the results given by the generalized factorization approach. The branching ratio of the$ B\to X(3872) K) $ decay can reach the order of$ 10^{-4} $ , which is significantly larger than that of the$ B\to X(3872) \pi $ decay induced by the$ b\to d $ transition. On the experimental side, it is helpful to probe the inner structure of$ X(3872) $ by measuring the branching ratios and testing the$S U(3)$ and isospin symmetries of these considered decays.(3) The direct CP violations of the
$ B\to X(3872)\pi(K) $ decays are small (only$ 10^{-3}\sim 10^{-2} $ ). The mixing-induced CP violation of the$ B\to X(3872)K^0_S $ decay agrees with the current world average value$ \sin2\beta=(69.9\pm1.7)\ $ %. However, it is different for the value of$ S_{X(3872)\pi^0} $ because the imaginary parts of the total amplitudes of the$ B\to X(3872)\pi^0 $ decay and its CP-conjugate process exhibit a large difference. -
The invariant masses of virtual quarks and gluons are given as follows:
$ \begin{eqnarray} \alpha=(x_2+x_1-1)(r_X^2(1-x_2)-x_1)m^2_{B_c}, \end{eqnarray}\tag{A1} $

$ \begin{eqnarray} \beta_a=(r_b^2-x_2(1-r^2_X(1-x_2))m^2_{B_c}, \end{eqnarray}\tag{A2} $

$ \begin{eqnarray} \beta_b=(r_c^2-(1-x_1)(r^2_X-x_1))m^2_{B_c}, \end{eqnarray} \tag{A3}$

$ \begin{eqnarray} \beta_c=-(1-x_1-x_2)(r_X^2(1-x_2-x_3)+x_3-x_1)m^2_{B_c}, \end{eqnarray}\tag{A4} $

$ \begin{eqnarray} \beta_d&=&-(1-x_1-x_2)(r_X^2(x_3-x_2)+1-x_3-x_1)m^2_{B_c}, \end{eqnarray}\tag{A5} $

$ \begin{eqnarray} \alpha'=x_1x_3(1-r_X^2)m^2_{B}, \end{eqnarray} \tag{A6}$

$ \begin{eqnarray} \beta'_a=x_3(1-r_X^2)m^2_{B}, \end{eqnarray} \tag{A7}$

$ \begin{eqnarray} \beta'_b=x_1(1-r_X^2)m^2_{B}, \end{eqnarray} \tag{A8}$

$ \begin{eqnarray} \beta'_c=(r_c^2+(x_1-x_2)(x_3+r_X^2(x_2-x_3)))m^2_B. \end{eqnarray}\tag{A9}$

The hard scale t is chosen as the maximum of the virtuality of the internal momentum transition in each amplitude, including
$ 1/b_i(i=1,2,3) $ $ \begin{eqnarray} t_{a(b)}=\max(\sqrt{|\alpha|},\sqrt{|\beta_{a(b)}|},1/b_1,1/b_2), \end{eqnarray}\tag{A10} $

$ \begin{eqnarray} t_{c(d)}=\max(\sqrt{|\alpha|},\sqrt{|\beta_{c(d)}|},1/b_1,1/b_3), \end{eqnarray}\tag{A11} $

$ \begin{eqnarray} t^\prime_{a(b)}=\max(\sqrt{|\alpha'|},\sqrt{|\beta'_{a(b)}|},1/b_1,1/b_3), \end{eqnarray}\tag{A12} $

$ \begin{eqnarray} t'_c=\max(\sqrt{|\alpha'|},\sqrt{|\beta'_c|},1/b_1,1/b_2). \end{eqnarray}\tag{A13} $

The functions
$ E_{e(c,d)}(t) $ are defined by$ \begin{eqnarray} E_e(t)=\alpha_s(t)\exp[-S_{B}(t)-S_X(t)], \end{eqnarray}\tag{A14} $

$ \begin{eqnarray} E_{cd}=\alpha_s(t)\exp[-S_B(t)-S_X(t)-S_\pi(t)]|_{b_1=b_2}, \end{eqnarray} \tag{A15}$

$ \begin{eqnarray} E_{e'}(t)=\alpha_s(t)\exp[-S_{B}(t)-S_\pi(t)], \end{eqnarray} \tag{A16}$

$ \begin{eqnarray} E_c=\alpha_s(t)\exp[-S_B(t)-S_X(t)-S_\pi(t)]|_{b_1=b_3}, \end{eqnarray}\tag{A17} $

where the Sudakov factors can be written as
$ \begin{eqnarray} S_B(t)=s \left(x_1\frac{m_B}{\sqrt2},b_1\right)+2\int^t_{1/b_1}\frac{{\rm d}\bar\mu}{\bar\mu}\gamma_q(\alpha_s(\bar\mu)), \end{eqnarray} \tag{A18}$

$ \begin{aligned}[b] S_{X}(t)=s\left(x_2\frac{m_B}{\sqrt2},b_2\right)+s\left((1-x_2)\frac{m_B}{\sqrt2},b_2\right)\end{aligned} $

$ \begin{aligned}[b] \;\;\;\;\;\quad\quad +2\int^t_{1/b_2}\frac{{\rm d}\bar\mu}{\bar\mu}\gamma_q(\alpha_s(\bar\mu)), \end{aligned} \tag{A19}$

$ \begin{aligned}[b] S_{\pi}(t)=&s\left(x_3\frac{m_B}{\sqrt2},b_3\right)+s\left((1-x_3)\frac{m_B}{\sqrt2},b_3\right)\\&+2\int^t_{1/b_3}\frac{{\rm d}\bar\mu}{\bar\mu}\gamma_q(\alpha_s(\bar\mu)), \end{aligned}\tag{A20} $

where the quark anomalous dimension
$ \gamma_q=-\alpha_s/\pi $ , and the expression for$ s(Q,b) $ in the one-loop running coupling constant is used,$ \begin{aligned}[b] s(Q,b)=&\frac{A^{(1)}}{2\beta_1}\hat{q}\ln\left(\frac{\hat{q}}{\hat{b}}\right)-\frac{A^{(1)}}{2\beta_1}(\hat{q}-\hat{b}) +\frac{A^{(2)}}{4\beta^2_1}\left(\frac{\hat{q}}{\hat{b}}-1\right)\\ &-\left[\frac{A^{(2)}}{4\beta^2_1}-\frac{A^{(1)}}{4\beta_1}\ln\left(\frac{{\rm e}^{2\gamma_E-1}}{2}\right)\right] \ln\left(\frac{\hat{q}}{\hat{b}}\right), \end{aligned}\tag{A21} $

with the variables defined by
$ \hat{q}= \ln[Q/(\sqrt2\Lambda)], \; \hat{q}= \ln[1/(b\Lambda)] $ and the coefficients$ A^{(1,2)} $ and$ \beta_{1} $ expressed as$ \begin{eqnarray} \beta_1=\frac{33-2n_f}{12},\quad A^{(1)}=\frac{4}{3}, \end{eqnarray} \tag{A22}$

$ \begin{eqnarray} A^{(2)}=\frac{67}{9}-\frac{\pi^2}{3} -\frac{10}{27}n_f+\frac{8}{3}\beta_1\ln\left(\frac{1}{2}{\rm e}^{\gamma_{\rm E}}\right), \end{eqnarray}\tag{A23} $

$ n_f $ is the number of quark flavors, and$\gamma_{\rm E}$ is Euler's constant.As we know, the double logarithms
$\alpha_s\ln^2x$ produced by the radiative corrections are not small expansion parameters when the end point region is important. To improve the perturbative expansion, the threshold resummation of these logarithms to all orders is required, which leads to a quark jet function$ \begin{eqnarray} S_t(x)=\frac{2^{1+2c}\Gamma(3/2+c)}{\sqrt{\pi}\Gamma(1+c)}[x(1-x)]^c, \end{eqnarray} \tag{A24}$

with
$ c=0.3 $ . It is effective to smear the end point singularity with a momentum fraction$ x\to0 $ .
Insights into the nature of X(3872) through B meson decays
- Received Date: 2022-08-16
- Available Online: 2023-01-15
Abstract: We study the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






























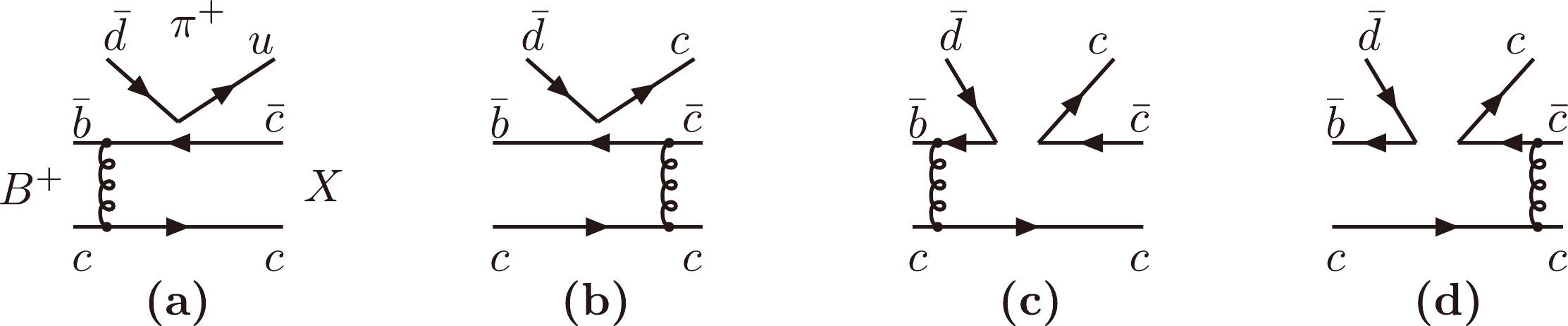



 DownLoad:
DownLoad: