Anisotropic stars in modified gravity: An extended gravitational decoupling approach

Modifications in the gravitational sector have been proposed from time to time because of the correction in the gravitation action. These corrections have become inevitable, when already existing gravitational theories are unable to address certain key issues of the present universe. Several corrections have recently been incorporated for cosmological applications [1, 2], string theory [3, 4], teleparallel gravity [5], unimodular gravity [6], $ f(R) $ gravity [7, 8], $ f(R,G) $ gravity [9, 10], $ f(Q,T) $ gravity [11], etc. Multiple cosmological observations have confirmed the late time cosmic acceleration phenomenon, which has altered our understanding of the universe. This recent development has generated novel concepts and ideas. The late time cosmic acceleration phenomenon is attributed to an exotic form of energy called dark energy, and general relativity (GR) has certain limitations in addressing this issue. There are various exotic matter fields that simulate negative pressure and positive energy density to explain this bizarre phenomenon; however, a proper geometrical modification without the addition of any exotic matter can possibly resolve this issue. Harko et al. [12] proposed the $ f(R,T) $ gravity by assuming a weak coupling between matter and geometry. The geometrical part of Einstein-Hilbert action has been modified by assuming the arbitrary function $ f(R,T) $, where R and T denote the Ricci scalar and the trace of the energy momentum tensor, respectively. The trace incorporated in this function may associate with the existence of exotic imperfect fluids. The functions are suggested in three forms: (i) $ f(R,T)=R+2f(T) $, (ii) $ f(R,T)=f_1(R)+f_2(T) $ , and (iii) $ f(R,T)=f_1(R)+f_2(R)f_3(T) $, where $ f_1(R) $, $ f_2(R) $, $ f(T) $, $ f_2(T) $ , and $ f_3(T) $ are arbitrary functions of their respective arguments. The first case can be reduced to GR under certain conditions, and this has been widely used to solve cosmological and astrophysical problems.

Recently, $ f(R,T) $ gravity theory has been of great interest and used widely in literature to address many issues related to astrophysics and cosmology. The issues of late time cosmic dynamics and the anisotropy behavior of the expansion have been partially addressed in $ f(R,T) $ gravity. Some of the key findings in $ f(R,T) $ gravity are given here. Alvarenga et al. [13] have studied the evolution of scalar cosmological perturbations, in metric formalism. Balakin and Bochkarev [14] have investigated the rip cosmology, whereas Noureen et al. [15] have shown the implications of shear-free condition on the instability range of an anisotropic fluid. Baffou et al. [16] have solved the cosmological evolution of the cosmological parameters numerically in $ f(R,T) $ gravity. Mishra et al. [17] have introduced the hybrid scale factor to study the dynamical behavior of the cosmological model of the universe and also introduced the squared trace model [18] in $ f(R,T) $ gravity. In order to address the singularity issue, bouncing cosmology has also been studied in $ f(R,T) $ gravity. Shabani and Ziaie [19] have introduced the effective fluid by defining the effective energy density and pressure to present the bouncing cosmological model. Tripathy et al. [20] have studied the bouncing cosmology in $ f(R,T) $ gravity and performed the stability analysis of the models under linear homogeneous perturbations to solve the bouncing. The $ f(R,T) $ gravity theory has also been significant in the study of wormhole solutions. Zubair et al. [21] have obtained the wormhole solutions in $ f(R,T) $ gravity and shown that the wormhole can be constructed without exotic matter in few regions of space-time. Elizalde and Khurshudyan [22] have obtained the wormhole solution and explored the observational possibilities for testing these models. Yousaf et al. [23] have investigated the irregularity factors of self-gravitating spherical star that evolves in the presence of an imperfect fluid. Das et al. [24] have studied the gravastar in $ f(R,T) $ gravity and obtained a set of singularity-free, and exact solution of the gravastar. Abbas et al. [25] have studied the charged perfect fluid spherically symmetric gravitational collapse and commented that the singularity is formed earlier than the apparent horizons.

In the context of GR, the charged compact objects have been investigated with the interpretation of anisotropic systems from Einstein-Maxwell field equations. The anisotropic factor has been mimicked from the electric field intensity, and the model with this assumption helps in obtaining the stability of static fluid in presence of charge. The solution of Einstein-Maxwell equations has been instrumental in describing the astrophysical compact objects [26–29]. However, since the last decade, researchers have given attention to construct charged compact star model in $ f(R,T) $ gravity to understand its behavior in the geometrically extended gravity. Moraes et al. [30] have studied the stellar equilibrium configurations of compact stars in $ f(R,T) $ gravity. Islam and Basu [31] have constructed model of a compact star in presence of magnetic fluid and suggested that these solutions will enable to describe the interior of compact objects. With the Krori-Barua solutions in an anisotropic distribution, Sharif and Waseem [32] have analyzed the effects of charge on the nature of relativistic compact star candidates. In the scope of this extended gravity, Yadav et al. [33] have proposed the existence of non-exotic compact star, that validates the energy conditions and stability of the model. Biswas et al. [34] have studied the anisotropic spherically symmetric strange star and have shown the validity of the conditions used in the model. Maurya et al. [35] have suggested an embedded approach to study the existence of compact structures that describes anisotropic matter distributions in the framework of matter geometry coupling. Also, Maurya and Tello-Ortiz [36] have extended the isotropic Durgapal-Fuloria model and investigated the high dense charged anisotropic compact structure in an isotropic background. Rahaman et al. [37] have predicted the exact redii of the values of the coupling parameter involved in $ f(R,T) $ gravity by considering the observed mass values of six compact stars. Rej et al. [38] have obtained singularity free model of charged anisotropic compact star in $ f(R,T) $ gravity.

The standard model is based on the homogeneity of space and large scale isotropy; however, a small scale of anisotropy can be expected in the universe [39–44]. The isotropy and homogeneity can be observed through the space-time under consideration. However, the space-time of compact objects leads to anisotropic features with the inhomogeneous matter distribution. Anisotropic pressure is the result of the difference between the radial and tangential component pressures. This anisotropy feature influences the physical properties, such as gravitational redshift, energy density, and total mass. There are numerous causes for anisotropy, including pion condensation [45], phase transitions [46], immense magnetic fields of neutron stars [47], and strong electric fields [48] (the refs. therein provide further explanation [49–51]). In addition to these, the form of gravitational tidal effects is believed to be a reason for anisotropy in the compact star, and this has been responsible for deformation [52–57].

A review of the relevant literature reveals that several modified/extended theories of gravity are now employed to investigate compact stellar models. Therefore, it is crucial to comprehend the inherent geometry of spacetime and the procedure for embedding a 4D space-time. In line with this, Karmarkar [58] has embedded 4-dimensional spacetime into 5-dimensional Euclidean space. This embedding simplifies the process of solving the Einstein field equations. From the historical background, according to Eddigton [59] the 4-dimensional surfaces in higher dimension will not change the metric at all. Further, different types of manifolds are linked by embedding 4-dimensional Einstein field equations into 5-dimensional flat spacetime [60, 61]. It is well known that the n dimensional manifold $ V_n $ can always be embedded in Pseudo-Euclidean space of $ m[= n(n+1)/2] $ dimensions, and the minimum extra dimensions $ (m-n)[= n(n-1)/2] $ of pseudo-Euclidean space needed for the embedding is called the embedding Class of $ V_n $. According to this definition, Schwarzschild’s interior and exterior solutions are of Class I and Class II, respectively; the class of general spherical and plane symmetric spacetimes are II and III, respectively; and the well known Kerr metric is of Class V [62–65].

It is notable that in general relativistic background, Maurya et al. [64] have obtained the exact generalized model for anisotropic compact stars of embedding Class I and tested the viability of the model by performing different physical tests, including energy conditions, stability analysis, and mass-radius relation. It should also be mentioned that Salako et al. [66] have studied the existence of strange starts in $ f({\cal{T}},T) $ gravity, where $ {\cal{T}} $ is the torsion tensor. Waheed et al. [67] used the Karmarkar condition [58] to find the physically acceptable solution for compact stars in $ f(R,T) $ gravity. In $ f(R,T) $ gravity, Ahmed and Abbas [68] have studied the gravitational collapse using the Karmarkar condition [58] to the spherically symmetric non-static radiating star.

Under the aforementioned discussion, we now explain our technique for efficiently solving the Einstein field equations in an anisotropic domain. The newly adopted method, known as the gravitational decoupling (GD) approach, allows one to decouple the Einstein equations [69–73] ^①. This gravitational decoupling approach is applied in a system using minimal geometric deformation (MGD) and its extension, called extended MGD or complete geometric deformation (CGD).

Before presenting a literature review for GD works, we would like to highlight the origin of the gravitational decoupling, which starts with a simple matter distribution $ {T}_{i j} $. Thereafter, it is extended to a more complex source (i) without violating the spherically symmetry condition and (ii) by adding a new source through a dimensionless coupling constant β as follows:

In a similar way, one can extend the new energy momentum tensor $ \tilde{T}^{(1)}_{ij} $ and repeat the similar procedure up to n times. The simple initial solution of $ f(R,T) $ field equation linked with the source $ T_{ij} $ can then be extended in a more generalized form associated with the source $ T_{ij}=\tilde{T}^{(n)}_{ij} $ , in a stepwise and systematic procedure. This is a new procedure to anisotropize the initial (or seed) solutions obtained from the perfect fluid, as well as anisotropic matter distributions. However, it is necessary to note here that each distinct component for the source $ {T}^{n}_{ij} $ is independently conserved. Moreover, the MGD technique can be employed in a reverse order to find solution for the self-gravitating compact objects.

Specifically, we have applied the CGD approach by defining the modified action for total energy momentum tensor for the anisotropic matter distribution which includes the extra source $ \theta_{\mu\nu} $. In this situation, the field equations for complete or original system will contain eight unknown functions for anisotropic fluid matter distribution. By taking this into account, we solve these field equations using gravitational decoupling via CGD approach by transforming the metric potentials $ \lambda(r) $ and $ y(r) $ as: $ \lambda \rightarrow - \ln[\xi+\beta\, h(r)] $ and $ y(r) = \eta+\beta\,g(r) $. In this way, we arrive at the two systems of equations corresponding to the source $ T_{ij} $ and $ \theta_{ij} $, respectively. The first system will be for pure $ f(R,T) $-gravity system, while the second system is for extra source $ \theta_{ij} $. After solving both systems individually, we combine the solutions together and obtain the complete solution of the original decoupled system.

The abovementioned techniques have been employed by many investigators to tackle the system efficiently [79–98]. Moreover, some recent works on gravitational decoupling using MGD and CGD have been explored by Zubair and collaborators in different context [99–105]. Here, the extended MGD or CGD is used to investigate the exact solution for compact stars in modified gravity theory without imposing a deformation function. The systematic approach of this technique is described in detail in the following sections.

The paper is organized as follows. In Sec. II, some preliminaries of the $ f(R,T) $ gravity for gravitational decoupling along with the Einstein's field equations and the Class I condition are discussed. In Sec. III, we adopt a systematic procedure to solve the field equations for decoupled systems. In Sec. IV, the matching conditions for the astrophysical system are elaborated. The physical analysis of the problem is described in Sec. V, and in Sec. VI, discussions and conclusions are presented.

The generalized integral action for $ f(R,T) $ formulation with an extra source is given by [74]

where $ {L}_{m} $ denotes the matter Lagrangian, β denotes a coupling constant, and $ {L}_{X} $ is the Lagrangian density of a new sector. Here, $ {L}_{X} $ is not required to be essentially defined by GR, however this can create the alterations in GR as argued in [74].

Let us now vary the action with respect to the metric tensor $ g^{\mu\nu} $ , which yields the field equations as follows

where $ f_{R}(R,T)=\partial f(R,T)/\partial R $ and $ f_{T}(R,T)=\partial f(R,T)/\partial T $.

Again, the energy-momentum tensor (EMT) $ T_{\mu\nu} $ , and extra source $ \theta_{\mu\nu} $, along with $ \Theta_{\mu\nu} $ can be provided as

where the conceptual meaning of this special tensor $ \Theta_{\mu\nu} $ will be physically meaningful later on.

Hence, the Einstein tensor $ G_{\mu\nu} $, after rearranging of Eq. (3), can be given as

The respective conservation equation now leads to

The energy-momentum tensor $ T_{\mu\nu} $ for the anisotropic matter distribution can be taken as

where $ {u^{\mu}} $ is the four velocity, satisfying $ u_{\mu}u^{\mu}=-1 $ and $ u_{\mu}\nabla^{\nu}u_{\mu}=0 $ , while ρ, $ p_r $ , and $ p_t $ are the matter density, radial pressure, and tangential pressure of the system, respectively.

Here, the matter Lagrangian considered as, $ {L}_m=-{\cal{P}} $, where $ {\cal{P}}=-\big({1}/{3}\big)\big(p_r+2\,p_t) $. It is important to note that the matter Lagrangian appears in the field Eq. (7), and the conservation Eq. (8) can be realized according to its choice (see Ref. [106] for detailed consultation). However, in the context of GR, this choice would not affect the observational outcomes. Therefore, when the matter field is described as a perfect fluid, it is important to choose a particular form of the matter Lagrangian. The choice we mention here is consistent since it provides a well-established Lagrangian density. Consequently, from Eq. (4), we can obtain

Now, using $ \delta\,g_{\mu \nu}/\delta\,g^{\gamma \epsilon}=-g_{\mu\sigma}g_{\nu \zeta}\delta^{\sigma \zeta}_{\gamma \epsilon} $, the above equation becomes

Plugging (11) in (6), we obtain

Again, employing (4) and $ {L}_m=-{\cal{P}} $, we finally get

Now, taking into account the work of Harko et al. [12], we consider the linear form of $ f(R,T) $ as

where χ is dimensionless, and known as the coupling constant. The linear form of $ f(R,T) $ is quite successful in the context of astrophysical and cosmological models. We have elaborated its successes in Section I. However, in the limit $ \chi\rightarrow 0 $, it reduces to the anisotropic fluid distribution in the context of GR [107].

By substituting the $ f(R,T) $ functional (14) in Eq. (7) we find

where we denote $ \hat{T}_{\mu\nu} $ as

with $ {T}_{\mu\nu} $ as given by Eq. (9).

Hence, from the conservation of (15) one obtains

At this stage we would like to mention the terms $ {\cal{P}} $ and T as

We consider the most general line element to describe a spherically symmetric and static spacetime, which is given by

where the metric potential y and λ are functions of the radial coordinate r only, i.e., $ y=y(r) $ and $ \lambda=\lambda(r) $.

Let us write the non-zero components of the field equations under the static spherically symmetric line element (18), which can be given as

In the preceding expression, a "prime" denotes differentiation with respect to the radial coordinate r. Moreover, $ \hat{T}^{0}_{\ 0} $ and $ \hat{T}^{1}_{\ 1} $ are expressed as

Now our aim is to solve the system of Eqs. (19)–(21) by using a complete geometric deformation approach, which we discuss in the next section.

A close observation on the field Eqs. (19)–(21) reveals that a closed exact solution is not a simple and trivial task. Therefore, we employ the CGD technique for solving these system of equations in a unique way. This CGD technique provides a systematic approach consisting of the following steps: first, split the decoupled system into two subsystems; then, solve these subsystems individually.

In this approach, we basically deform the gravitational potentials $ {\lambda(r)} $ and $ {y(r)} $ over a linear transformation given as

where $ h(r) $ and $ g(r) $ denote the decoupling functions corresponding to the radial and the temporal components of the line element (18), respectively. Here, we consider the deformation in conjunction with both the radial and the temporal components, i.e., $ f(r)\ne 0 $ and $ g(r) \ne 0 $ , so that it is known for the CGD. Also, it is always possible to separate the new piece $ \theta_{\mu\nu} $ from the seed matter sector for pure $ f(R,T) $ system.

Now, inserting Eqs. (25) and (26) into the system of Eqs. (19)–(21), we can have

where

where $ \Psi(r) $ is given by the Eq. (30).

Clearly, the limit $ \chi \rightarrow 0 $ and $ \beta \rightarrow 0 $ will provide the usual mass function expression for an anisotropic compact structure in the arena of GR. From Eq. (31), we have extra contributions due to the $ f(R,T) $ and CGD scenarios as $ m_{\rm frt}(r) $ and $ m_{\rm CGD}(r) $, respectively. At this point, it should be mentioned that the mixture $ f(R,T) $ + CGD goes beyond the pure GR scope and thereby helps to enhance the compactness, at least from the theoretical point of view.

One can note from the right hand side of Eqs. (27) – (29) that we have separated all the first terms from the new terms involved such as β and the decoupling functions, $ h(r) $ and $ g(r) $. Here, we apply the gravitational decoupling via CGD through the deformation of the original metric potentials $ {\rm e}^{y(r)} $ and $ {\rm e}^{\lambda(r)} $ , by adding to new functions $ h(r) $ and $ g(r) $. These decoupling functions are responsible for defining a new set of equations for extra source, $\theta_{\mu\nu}$. However, the symbols ξ and η will describe the solution for pure $ f(R,T) $-gravity.

Now, the separated field equations and their corresponding conservation law can be written as

By virtue of the above set of Eqs. (32) – (34), the following conservation equation $ \nabla^{\mu}\big( T_{\mu\nu}+\hat{T}_{\mu\nu}\big)=0 $, i.e., (17), under the condition $ \beta=0 $, provides

Eq. (33) can be termed as the modified Tolman-Oppenheimer-Volkoff (TOV) [108, 109] equation in the arena of $ f(R,T) $ gravity theory. It is noticeable that Eq. (35) converts into the hydrostatic equilibrium condition for standard GR for $ \chi=0 $. However, the corresponding solution can be given from the following static spacetime as

In this scenario, the gravitational mass for anisotropic matter distribution in $ f(R,T) $-gravity can be determined by

Here, $ m_0 $ is the mass function in pure $ f(R,T) $ scenario. Henceforth, we shall mention the system of Eqs. (32)–(34) as a "seed system" and the corresponding solution as a "seed solution." The spacetime (36) described by a seed solution will be known as a "seed spacetime."

Let us now look at the factor β, so that the field equations for $ \theta_{\mu\nu} $ becomes

with

Hence, in view of Eq. (17), we obtain $ \nabla^{\mu}\theta_{\mu\nu}=0 $ in the following conservation equation for system of Eqs. (38) – (40)

In addition to this, now we use the pressure anisotropy condition in Eqs. (28) and (29), i.e., $ G^1_1=G^2_2 $, which provides

where $ \hat{\Delta}={(8\pi+2\chi)}\,(p_t-p_r) $.

This demonstrates that condition (42) is the same as the anisotropic condition in GR. Since $ f(R,T) $ gravity is an extended form of GR for the linear choice of $ f(R,T) $, we can say that the solution of the field equations in $ f(R,T) $ theory can be obtained by the known solution of GR. The coupling parameter χ will only affect the matter variable. Using Eqs. (22) – (24), we can obtain ρ, $ p_r $, and $ p_t $ from Eqs. (32) – (33) with respect to the radial coordinate as

To find the contribution of $ f(R,T) $, it is required to separate ρ, $ p_r $ , and $ p_t $, because the term $ \hat{T} $contains ρ, $ p_r $, and $ p_t $in Eqs. (32)–(34), respectively. If we interpret the term $ \rho+\hat{T}^{0}_{\ 0} $ in Eq. (32) as the effective seed density (similarly $ p_r-\hat{T}^{1}_{1} $ in (33) and $ p_r-\hat{T}^{2}_{2} $ in 34 as the effective seed pressures), then the system of equations can be treated as the set of Einstein's field equations. The $ f(R,T) $ contribution is hidden within the redefined thermodynamic quantities, as mentioned in Eqs. (43)–(45). We would like to mention here that no substantial effect has been noticed in Eqs. (43)–(45) $ f(R,T) $ since θ-sector is separated by applying the CGD. Hence, in order to close the problem at least mathematically and to check the physical viability, we need to find a solution for the system $ \{\theta_{\mu\nu},h,g\} $.

Let us now define the following new physical parameters:

where the effective thermodynamic variables characterize the matter distribution of the model.

Here, we can observe the effects of CGD on the mass function $ m(r) $ from $ m_{\rm CGD}(r) $. Moreover, the effective anisotropy factor Δ can be given as

Here, we would like to highlight an important point that the CGD induced an extra contribution $ \Delta_{\rm CGD} $ in the seed anisotropy $ \Delta_{\rm FRT} $ which may enhance the anisotropy within the matter distribution. This contribution may also improve the equilibrium mechanism of the stellar system via the anisotropic force. Now our main objective is to solve both systems of equations separately to obtain the solution of the original system (19)–(21). The solution of the second system (38)–(40) is dependent on the solution of the first system (32)–(34). Therefore, we beign by solving the first system using the embedding Class I condition, which is discussed in the following section.

The metric (18), which refers to the 4-dimensional spherically symmetric spacetime, essentially describes a spacetime of Class II. We would like to mention here that embedding requires a 6-dimensional pseudo-Euclidean space. Regarding this, Gupta et al. [110] have provided the 6-dimensional Euclidean spacetime in the form

with the particular transformation as follows:

Then, Eq. (50) readily takes the form

After comparing from Eqs. (4) and (51), we have

and

Further, to be a Class I static and non-static spherically symmetric spacetime, it must satisfy the following Karmarkar condition [58]

subject to $ R_{2323}\neq 0 $ [111], where the quantities regarding the Riemann components for the metric (36) are given as

Notably, the abovementioned Karmarker condition was derived using a relation between Remannian components, and this condition provides a relation between metric potential of the spacetime that guarantees the 4-dimensional spherically symmetric spacetime can be embedded within the 5-dimensional flat or Euclidean spacetime. Moreover, when solving the field equation, additional conditions are required due to the number of unknowns involved in the system of equations. This Class I condition aids in the solution of the system of equations.

After inserting the Riemann components in condition (16), we obtain

with $ \xi \neq 1 $.

To be a Class I spacetime of the aforementioned differential Eq. (56), there is a requirement to maintain the spacetime (18). Therefore, after integrating (17), the gravitational potentials are related as follows

where A is the integration constants.

Hence, in connection to Eqs. (52) and (57), it can be ensured that the transformation involved in Eq. (50) provides 5-dimensional Euclidean spacetime in order to describe the embedding Class I spacetime under the condition $ \mathbb{Z}=0 $ and $ A={K^2}/{4} $.

In view of the condition (57), we consider the following Class I spacetime in $ f(R,T) $ gravity as,

where X and B are constants and $ Y=8\,A\,B^2 $ , while the seed metric potentials are: $ {\rm e}^{\eta(r)}=(X+Br^2)^2 $, and $\xi(r)= (1+Yr^2)^{-1}.$ A literature survey shows that the temporal and radial components of the chosen seed spacetime corresponds to the well-known Adler [112] and Finch-Skea [113], respectively. Furthermore, this seed Class I spacetime was previously discussed in $ f(R,T) $ gravity in the context of MGD approach [75]. Therefore, the hybridization which we are considering here is reasonable.

Then, the density and the pressures in $ f(R,T) $ scenario [using Eqs. (43) – (45)] characterizing this model can be given as

where we considered $ C=B/X $ for simplicity; $ \psi_1(r)= \chi (3 + 8 Yr^2 + 2 r^4 Y^2) $, $ \psi_2(r)=6 \pi (4 + 3 Yr^2 - r^4 Y^2) $, $ \psi_3(r)= [\chi\,Y r^2 + 3 \pi (1 + Yr^2)] $, and $ \psi_4(r)=(9 + 4Yr^2 +Y^2 r^4 ) $.

Now that we have already specified the ξ and η, we only need to determine the deformation functions $ h(r) $ and $ g(r) $ to close the θ-sector completely. Therefore, we apply two different approaches to find deformation functions $ h(r) $ and $ g(r) $ , as discussed below.

There are several ways for determining the radial deformation function, such as EOS or particular choice of expression. However, the mimic constraints to density approach has some physical significance. If we apply the mimic constraints to density approach, we can easily find the effective density as$ (1+\beta) $ times the seed density, and as a result, the mass function will also be$ (1+\beta) $ times the seed mass. It means that the total mass of the object is now controlled by the decoupling constant, which yields the extra packing of the mass.

Hence, in this case we shall consider the mimic constraints for the density

which leads to

where F is a constant of integration.

Now, using Eqs. (59) and (63), we find the deformation function $ h(r) $

where the coefficient used in $ h(r) $ can be provided as

In Eq. (63), we take the arbitrary constant $ F=0 $ to avoid the singularity at $ r=0 $. Moreover, in Eq. (64), we avoid the singularity in the expression of $ f(r) $ as follows: (i) expansion of $ \tan^{-1}(x) $, where $x=\sqrt{C}\,r\; \; {\rm or}\; \; \sqrt{Y}\,r$, up to the linear term by using the Taylor series around $ x = 0 $, and (ii) the integration constant involved in the solution has been taken to be zero.

For clarity purposes, we would like to note that mimic constraints only pertain to the matching of two particular functions [69]. As can be seen, we have two unknown deformation functions, $ h(r) $ and $ g(r) $, that are involved in θ-sector components (Eqs. (43) – (45)). Typically, authors solve the problem by assuming a particular form for one of the deformation functions. However, this is the first work in $ f(R,T) $-gravity where we did not consider any particular form of the deformation function. We have determined the exact expression for both the functions, $ h(r) $ and $ g(r) $, by solving the θ-system. From Eq. (43), only the first derivative of h is given and the deformation function g is not present in this equation. Then, it is easy to show that, using the mimicking of $ \rho(r)=\theta^0_0(r) $ , the effective density $ \rho^{\rm eff} $ will become $ (1+\beta) $ times the seed density ρ, i.e., $ \rho^{\rm eff}=(1+\beta)\rho $ , and the behavior of this effective density can be controlled by the decoupling parameter β. In addition, it is advantageous to control the mass of the object because the mass is directly related to the energy density.

The other deformation function $ g(r) $ will be obtained by taking a linear equation of state (EOS) between the θ-components. For this, let us now consider the following linear EOS

where α and γ are the constants.

The first order linear differential equation obtained provides the expression for $ g(r) $ as

where

Now, the θ components can be given as

The coefficient used in the expressions (67)–(69) have been mentioned in the appendix.

Then, the deformed spacetime can be given by

where $ h(r) $ and $ g(r) $ are given in Eqs. (64) and (66).

Thus, the effective quantities are given as

In the relativistic astrophysical system, the matching of the spacetime geometries leads to the system's physical viability so that any spherically symmetric stellar object serves as a strict limiting case. Accordingly, the stellar distribution at the surface of the star ($ r=R $) between the interior ($ r<R $) and exterior ($ r>R $) solutions should be smooth and continuous. The $ f(R,T) $ theory of gravity can describe a non-minimal coupling between the geometry and matter. The non-trivial coupling between the gravity and matter sectors can contribute to the matter content of the outer space time that surrounds the compact structure. Also, the junction conditions in $ f(R,T) $ gravity needs to be established. Therefore, the field equations of $ f(R,T) $ gravity (15) for the functional $ f(R,T)= R+2\chi T $ is required to be expressed in terms of the Ricci tensor and matter distribution. Moreover, to analyze the contribution of the extended gravity on the outer space time matter distribution, we shall ignore the $ \theta_{\mu\nu} $ term. Now, we can establish a relation between the trace and Ricci scalar from (15) as

Subsequently, we can obtain the field equations as

Now, to obtain insights into the matching condition, it is instructive to consider the contribution of $ T_{\mu\nu} $ and $ f(R,T) $ gravity sector within the compact object. For brevity, we consider $ T_{\mu\nu}=0 $, so that the trace, energy density and the pressures terms vanish. Here we consider the geometry of outer spacetime as the Schwarzschild exterior metric. This is possible because of the linear relation between the Ricci scalar and trace of the energy-momentum tensor (14). If the gravity-matter coupling were represented by the functional $ f(R,T) $, such that non-linear terms would exist between them, and as a result, obtaining R and T explicitly becomes difficult. However, the minimal coupling further allows the decoupling of $ \theta_{\mu\nu} $ and the seed source would violate this. Hence, the Schwarzschild metric as the exterior spacetime that surrounds the collapsed configuration is given by

In this context, the deformed solution can be given by the most general interior spacetime as

Now, at the boundary Σ, the matching of the geometries can be performed smoothly between the outer manifold $ {\rm d}s^2_+ $ (76) and the inner manifold $ {\rm d}s^2_- $ (77) , as per the junction conditions following the continuity equation. Thus, one may easily get the first and second fundamental forms across the surface Σ, where in the first fundamental form, the inner geometry can be described by the metric tensor $ g_{\mu\nu} $ induced by $ {\rm d}s^2_- $ and $ {\rm d}s^2_+ $ on the interface. This can be provided as

Explicitly, it reads

where

Furthermore, the second fundamental form is associated with the continuity of the extrinsic curvature $ K_{\mu\nu} $ through the $ {\cal{M}}^{-} $ and $ {\cal{M}}^{+} $ on Σ. Then, by matching of interior ($ {\cal{M}}^{-} $) and outer ($ {\cal{M}}^{+} $) , the manifold at the Σ gives

Now, in principle, the θ-sector might influence the outer spacetime and matter content. Because of this, the second fundamental form (82) can be expressed as follows:

where $ p_r(r_b)=p_r^{-}(r_b) $.

After substituting the value of $ (\theta^{1}_{\ 1})^{-}(r_b) $ from Eq. (39), the above expression reads

where $ y^{\prime}\equiv \partial_r\,y^{-} $.

In order to find out $ (\theta^1_1)^{+}(r_b) $ in (50), we employ Eqs. (39), (76) and (80), obtaining

where $ h^{\ast}(r_b) $ and $ g^{\ast}(r_b) $ denote the deformation functions for exterior solution under the extra source $ \theta_{\mu\nu} $, which can be given by following in the exterior metric as

If this the exterior solution (86) is given by the Schwarzschild solution (76), then we must substitute $ h^{\ast}(r_b)=0 $ and $ g^{\ast}(r_b)=0 $ in (86). Then, Eq. (85) yields the following

The above condition (87) can be also written as

The constants involves in the solutions will be determined by the necessary and sufficient conditions (79), (80) and (87). Therefore, by using the boundary conditions we have obtained the values of the constants

where $ M_0=m_0(r_b) $. Also, we avoid writing the expression for the constant B due to its long cumbersome form.

Note that the regular behavior of the solution depends on the deformed metric functions $ e^{\lambda} $ and $ e^{y} $ , which are $ e^{\lambda(0)}=1 $ and $ e^{y(0)}>0 $ , together with the monotonic increasing function of r to describe the realistic objects. In the present case we see that $ e^{\lambda(r)} $ and $ e^{y} $ are solely dependent on the parameters $ \xi,\; \eta,\; h,\; g $. Since ξ and η are metric functions corresponding to the seed space-time which are already well behaved, then only the testing of the physical validity of the deformation functions, $ h(r) $ and $ g(r) $ are required. At the center, $ r=0 $, $ f(r) $ and $ g(r) $ must be freed from singularity, and $ f(r) $ must vanish to preserve $ e^{\lambda(0)}=1 $.

In addition, the following conditions also must be satisfied:

Case I: For $ \beta>0 $

1. If $ h(r)\geq0 $, $ g(r)\geq0 $, and for all $ r\in[0,R] $, both are increasing, then the deformed metric function $ e^{\lambda(r)}>0 $, $ e^{y(r)}>0 $, mass function $ m(r)>0 $ are also increasing, when the growth of $ \xi(r) $ is faster than $ h(r) $.

2. If $ h(r)\leq0 $, $ g(r)\leq0 $, and for all $ r\in[0,R] $, both are decreasing, then the deformed metric function $ e^{\lambda(r)}>0 $, $ e^{y(r)}>0 $, mass function $ m(r)>0 $ are increasing, when the growth of $ \eta(r) $ is faster than $ g(r) $.

3. If $ h(r)\le 0 $and$ g(r)\ge0 $ for all $ r\in[0,R] $, then the deformed metric function $ e^{\lambda(r)}>0 $, $ e^{y(r)}>0 $, and mass function $ m(r)>0 $ and increasing automatically.

4. If $ h(r)\ge 0 $and $ g(r)\le0 $ for all $ r\in[0,R] $, then the growth of $ \xi(r) $ and $ \eta(r) $ must be respectively faster than $ h(r) $ and $ g(r) $, to maintain the deformed metric function $ e^{\lambda(r)}>0 $, $ e^{y(r)}>0 $, and the mass function $ m(r)> $ and its increasing behavior.

Case II: For $ \beta<0 $

1. For non-negative and increasing $ h(r) $ and $ g(r) $, $ \forall $ $ r\in[0,R] $, the deformed metric function $ e^{\lambda(r)} $, $ e^{y(r)} $ and the mass function $ m(r) $ will be positive and increasing, when the growth of $ \eta(r) $ is higher than $ g(r) $.

2. If $ h(r) $ and $ g(r) $ are non-positive and decreasing for all $ r\in[0,R] $, then growth of $ \xi(r) $ must be higher than $ h(r) $ in order to preserve the increasing and positive behavior of $ e^{\lambda(r)} $, $ e^{y(r)} $, and the mass function $ m(r) $.

3. If $ h(r)\le 0 $ and $ g(r)\ge0 $, $ \forall $$ r\in[0,R] $, then the deformed metric function $ e^{\lambda(r)} $, $ e^{y(r)} $, and the mass function $ m(r) $ will be positive and increasing, if the growths of $ \xi(r) $ and $ \eta(r) $ are higher than $ h(r) $ and $ g(r) $, respectively.

4. If $ h(r)\ge 0 $ and $ g(r)\le0 $, $ \forall $$ r\in[0,R] $, then it yields positive and increasing behavior of $ e^{\lambda(r)} $, $ e^{y(r)} $, and $ m(r) $, automatically.

The adiabatic index Γ is defined as the ratio of two specific heats [114] as follows:

This provides amethod for analyzing the density profile and the stiffness of EOS in a spherically symmetric system [115–120]. It is argued that Γ can play a key role in explaining the dynamical stability of a stellar system by applying an infinitesimal radial adiabatic perturbation [121–128]. It is important to note that $ \Gamma>{4}/{3} $ is prescribed for a stable Newtonian sphere, while $ \Gamma={4}/{3} $ gives rise to a neutral equilibrium [129]. In the scenario of relativistic fluid distribution, an additional term may create a correction in the previous bound, which can be expressed as [130, 131]

where $ \rho_{0} $, $ p_{r0} $, and $ p_{t0} $ are the initial density, radial pressure, and tangential pressure when the matter distribution is in static equilibrium, respectively. The first term in the bracket in the above inequality describes the relativistic corrections to the Newtonian perfect fluid, while the last term in the bracket is due to anisotropy.

However, for an anisotropic, stable and relativistic dynamical system, $ \Gamma>{4}/{3} $ [114, 131, 132], since positive anisotropy factor may slow down the growth of instability. The relativistic correction to the adiabatic index Γ could introduce some instabilities inside the star [133]. To solve this, Moustakidis [134] proposed a more strict condition on the adiabatic index Γ and achived a stable stellar structure. This condition leads to the existence of a critical value for the adiabatic index Γ, denoted by $ \Gamma_{\rm crit} $, which depends on the amplitude of the Lagrangian displacement from equilibrium and the compactness factor $ u=M/R $ (where M and R being the total mass and radius of the spherical system). Specifically, the critical relativistic adiabatic index under in $ f(R,T) $ theory can be given as

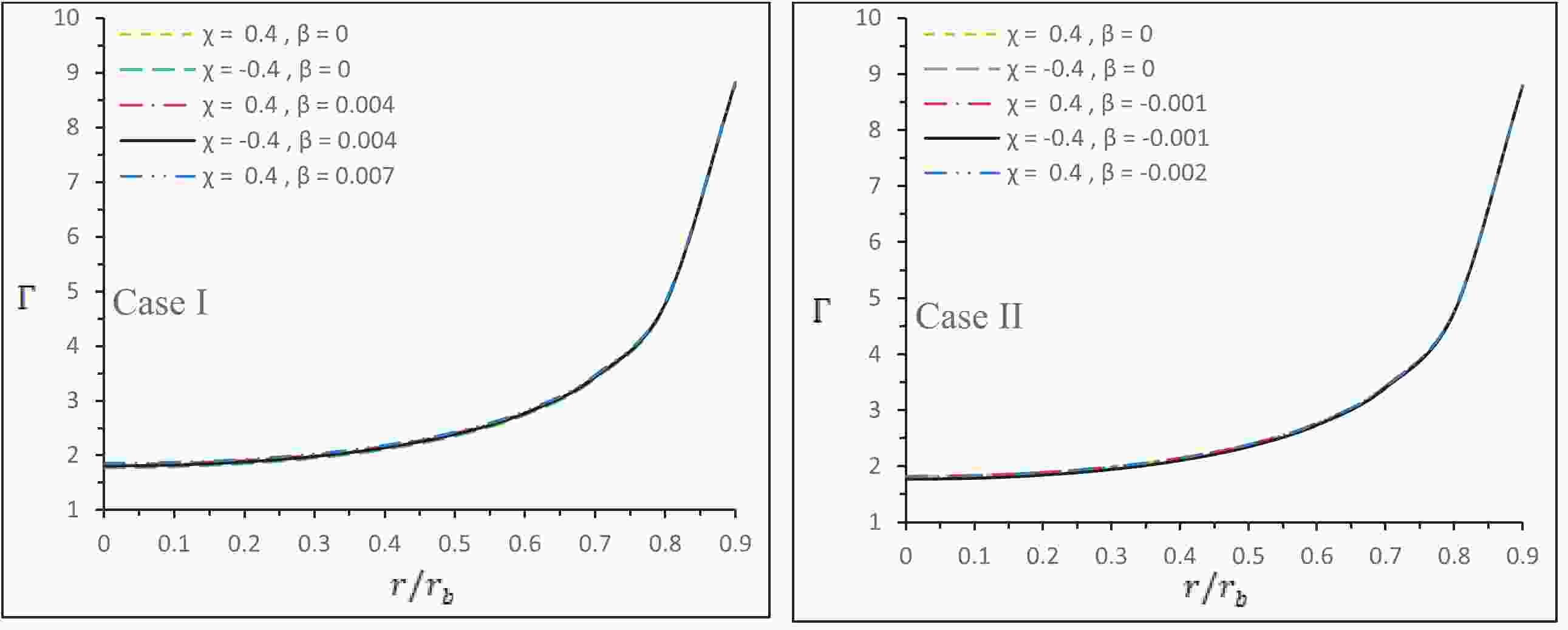
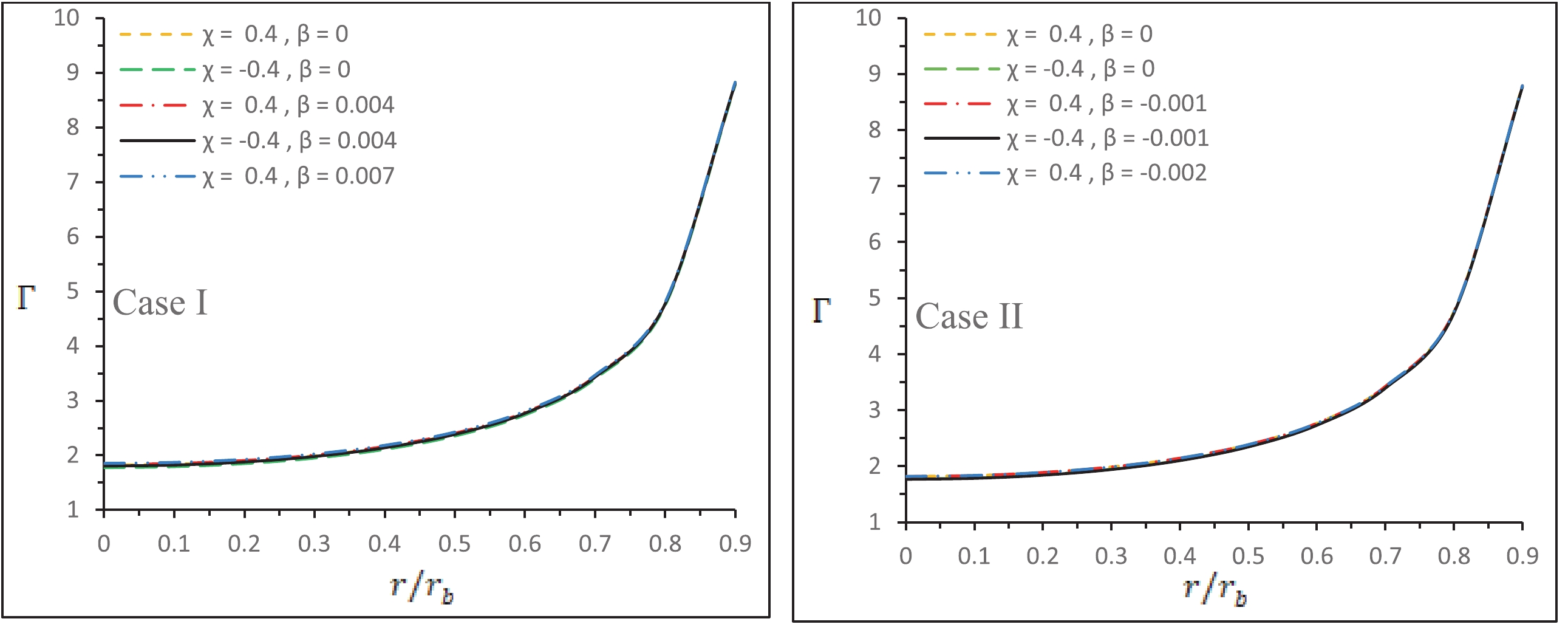
The variation of the adiabatic index (Γ) with respect to the radial coordinate $ r/r_b $ is shown in Fig. 1 , which is physically satisfactory.

Figure 1.  (color online) Variation in the adiabatic index (Γ) with respect to the radial coordinate $ r/r_b $.

In the present case, the obtained modified form of Tolman [108] and Oppenheimer-Volkoff (TOV) [108, 109] equations, which comply with the hydrostatic equilibrium of the stellar structure, can be written as

The aforementioned modified TOV equation can be expressed in terms of several force components, such as hydrostatic force $ F_{h}=- \Big[p^{\prime}_r-\beta\,\left(\theta^{1}_{\ 1}\right)^{\prime} \Big]$, gravitational gradient force $ F_g = -\bigg[\dfrac{\eta^{\prime}}{2}\,(\rho + p_r)+\dfrac{\beta\,g^\prime}{2}(p_r + \rho)+\beta\,\dfrac{y^{\prime}}{2}\left(\theta^{0}_{\ 0} - \theta^{1}_{\ 1}\right)\bigg] $, anisotropic force $F_a=\,\bigg[\,\dfrac{2}{r}\,(p_t-p_r)\,-\dfrac{2}{r}\,\left(\theta^{2}_{\ 2}-\,\theta^{1}_{\ 1}\right)\bigg]$, and coupling force due to $ f(R,T) $-gravity $ F_{\chi}=\;\,\dfrac{\chi\,(3\rho^{\prime}-p^{\prime}_r-2p^{\prime}_t)}{6\,(4\,\pi+\chi)} $ , such that $ F_h+F_g+F_a+F_\chi=0 $.

We have shown the features of all the forces for different parameter values in Fig. 2. From this figure, it can be observed that the fluid distribution possesses a stable equilibrium as the combined effect of all the forces involved in Eq. (94) related to the stellar configuration becomes zero.

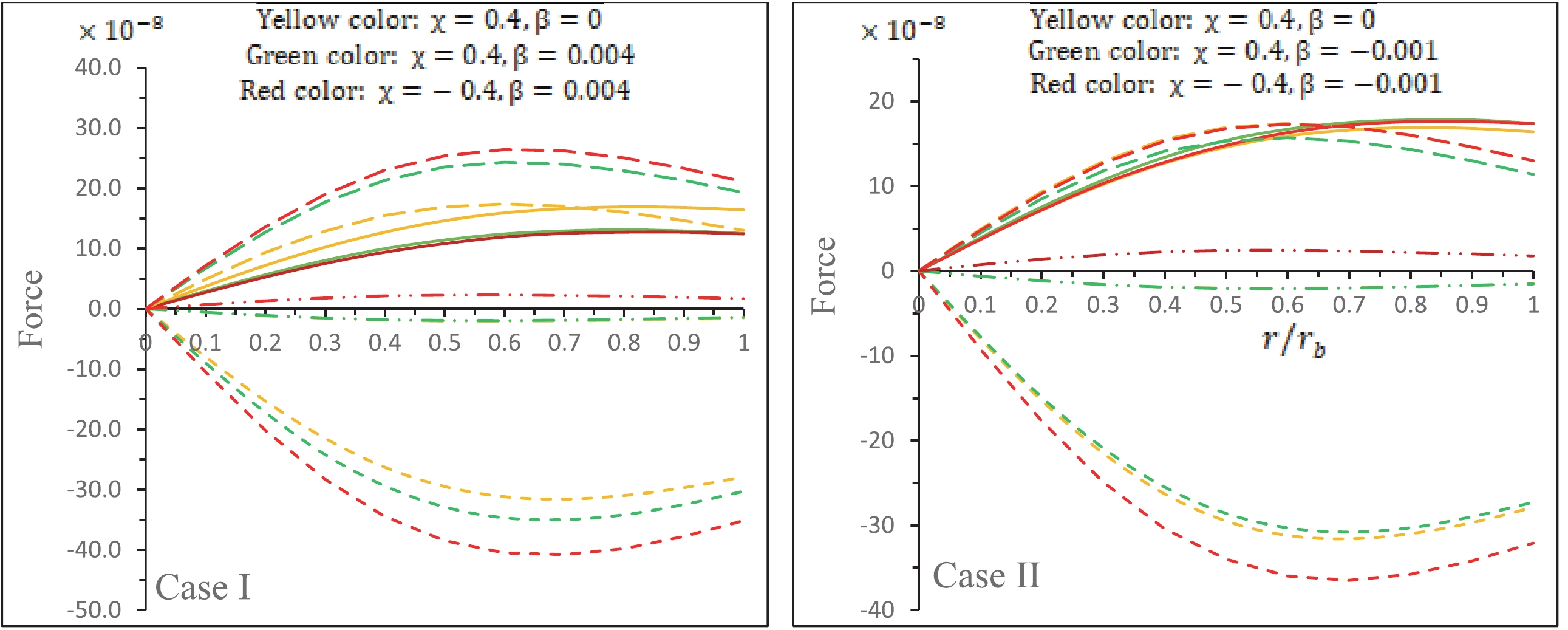
Figure 2.  (color online) Variation in different forces: $ F_g $is denoted by short dash curves, $ F_h $is denoted by long dashed curves, $ F_a $is denoted by solid curves, and $ F_\chi $is denoted by long dot dashed curves, with respect to the radial coordinate $ r/r_b $, for Case I (left panel) and Case II (right panel).

In the present investigation, we deal with the decoupling gravitational sources in $ f(R,T) $ gravity under anisotropic matter distribution. However, the energy-momentum tensor $ T_{\mu\nu} $ used here under the CGD, is not the usual one as in Eq. (9). Instead, for the present study, we consider the matter Lagrangian to be $ {L}_m=-{\cal{P}} $, where $ {\cal{P}}=-\dfrac{1}{3}\big(p_r+2\,p_t) $. The basis of this particular choice is not a general one, as the matter Lagrangian enters explicitly in the field Eq. (7), and different choices lead to different equations of motion. The adopted technique of the CGD for solving the system of equations seems a unique approach. This technique provides a systematic approach as follows: (1) split the decoupled system into two subsystems, and (2) solve these subsystems individually. A detailed discussion on this aspect has been provided in the preliminary Sec. V. Based on the aforementioned approach, we have, essentially, an extended case of all similar studies that were previously conducted. The results of the present study are generally interesting, distinctive, and satisfactory as far as physical viability is concerned.

Some salient features of the present investigation can be discussed as follows:

(i) We have shown the variation of the radial deformation function $ f(r) $ and temporal deformation function $ h(r) $ with respect to the radial coordinate $ r/r_b $ in Fig. 3. From this figure, for $ f(r) $ and $ h(r) $, we note that both are negative and decreasing functions$ \forall $$ r\in (r,R] $ , giving the scenario of point 2 in Case I.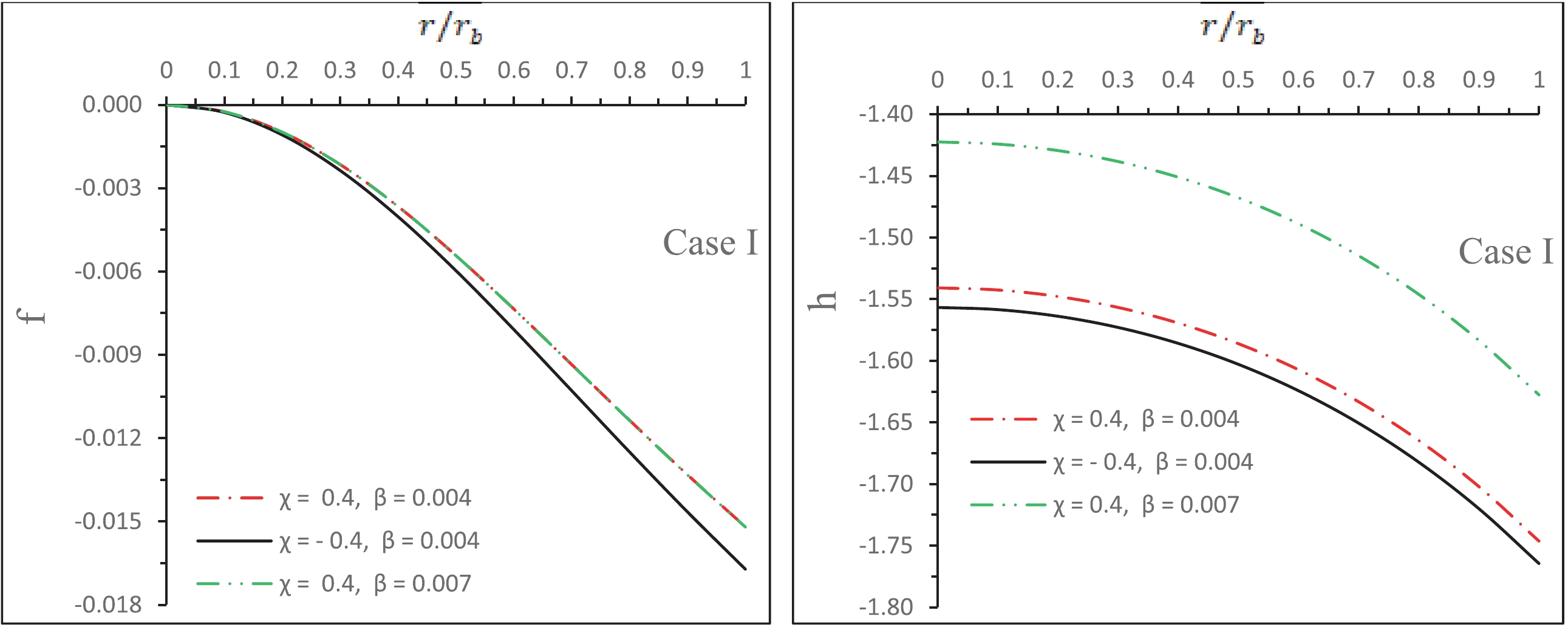

Figure 3.  (color online) Variation in the radial deformation function $ f(r) $ and temporal deformation function $ h(r) $ with respect to the radial coordinate $ r/r_b $. For plotting of this figure, we use the numerical values of the constants as $ \alpha=1.4 $, $ \gamma=-0.002 $, $ {M_0}/{R}=0.2 $, and $ Y=0.005 $. Henceforth, we shall use this same data set for plotting other figures.

(ii) In Fig. 4, the metric functions $ \lambda(r)=-\ln[\xi(r)+ \alpha\,f(r)] $ and $ \nu(r)=\eta(r)+\alpha\,h(r) $ are both increasing and positive throughout the star, which implies that the growth of $ \eta(r) $ is faster than the deformation function $ h(r) $.

Figure 4.  (color online) Variation in the metric functions $ e^{\lambda} $ and $ e^{\nu} $ with respect to the radial coordinate $ r/r_b $.

(iii) In Fig. 5, the left panel shows the effective radial pressure ($ p^{\rm{eff}}_r $) and the right panel shows the effective tangential pressure ($ p^{\rm{eff}}_t $) with respect to the radial coordinate $ r/r_b $. Since the constants χ and β influence the radial and tangential pressures, the following observations can be made from Fig. 5:

Figure 5.  (color online) The left panel shows the effective radial pressure ($ p^{\rm{eff}}_r $), and the right panel shows the effective tangential pressure ($ p^{\rm{eff}}_t $) with respect to the radial coordinate $ r/r_b $.

For fixing χ: when we increase β, both $ p^{\rm{eff}}_r $ and $ p^{\rm{eff}}_t $ increase at the core of compact object;

For fixing β: $ p^{\rm{eff}}_r $ and $ p^{\rm{eff}}_t $ show decreasing values at the core of the star when we move χ from a negative to positive value.

(iv) Variation of the effective energy density ($ \rho^{\rm{eff}} $) with respect to $ r/r_b $ is shown in Fig. 6. We set the same numerical values as used in Fig. 3. Since the effective energy density is $ \rho^{\rm{eff}}=(1+\beta)\,\rho $, therefore, the value of the effective energy density at the core and boundary of the stellar object will be decreasing for decreasing values of β. Evidently, values of the effective energy density of Case I are higher than those of Case II at each point of the stellar model.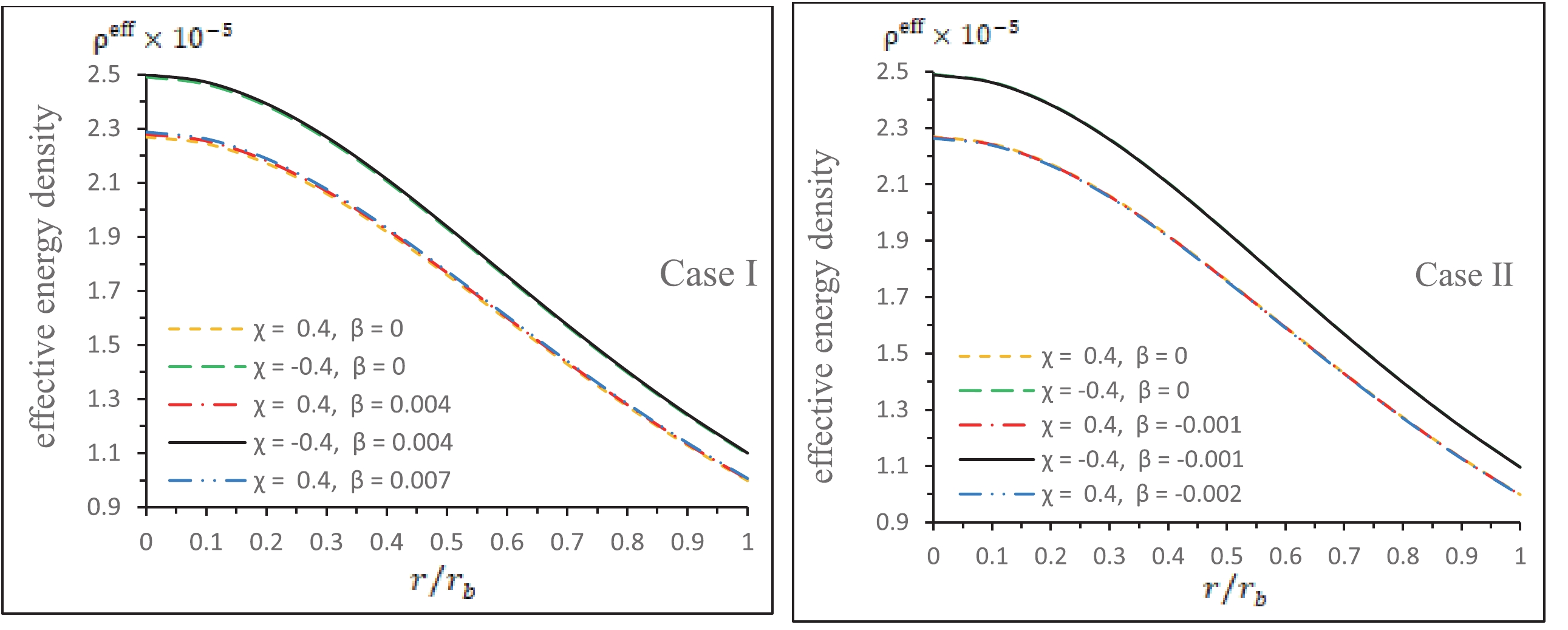

Figure 6.  (color online) The left panel shows the effective density $ \rho^{\text{eff}}_r $ for Case I, and the right panel shows the effective density $ \rho^{\text{eff}}_r $ for Case II with respect to the radial coordinate $ r/r_b $.

(v) The left panel of Fig. 7 shows the anisotropy for the CGD contribution ($\Delta_{\rm CGD}$) and the right panel shows the effective anisotropy ($ \Delta^{\rm{eff}} $) with respect to $ r/r_b $. We set the same numerical values as used in Fig. 3. One can observe from the Fig. 7that the anisotropic contribution $ \Delta_{\rm CGD} $ due to CGD shows negative and decreasing behavior within the stellar model, while the effective anisotropy is still increasing when $ \beta\ge0 $, which shows that the growth of seed anisotropy ($ \Delta_{\rm FRT} $) is faster than $ \Delta_{\rm CGD} $. Moreover, it should be noted that when β is positive, the effective anisotropic force $ F_a=\dfrac{2\,\Delta^{\rm{eff}}}{r} $ will produce less effect to balance the system to achieve the hydrostatic equilibrium near the surface.

Figure 7.  (color online) The left panel shows the anisotropy for the CGD contribution ($\Delta_{\rm CGD}$), and the right panel shows the effective anisotropy ($ \Delta^{\rm{eff}} $) with respect to $ r/r_b $.

(vi) Variation of the radial deformation function $ f(r) $ and the temporal deformation function $ h(r) $ with respect to the radial coordinate $ r/r_b $ are depicted in Fig. 8. For this figure, we use the numerical values of constants as $ \beta = 0.004 $, $ \alpha=1.4 $, $ \gamma=-0.002 $, ${M_0}/{R}=0.2 $, and $ Y= $ 0.005. In Case II, the deformation functions $ f(r) $ and $ h(r) $ are also negative and decreasing functions $ \forall $$ r\in (r,R] $, similar to those in Case I; see Fig. 8.

Figure 8.  (color online) Variation in the radial deformation function, $ f(r) $, and the temporal deformation function, $ h(r) $, with respect to the radial coordinate $ r/r_b $. For plotting this figure, we use the numerical values of the constants as $ \alpha=1.4 $, $ \gamma=-0.002 $, $ {M_0}/{R}=0.2 $, and $ Y=0.005 $. Henceforth, we shall use this same data set for plotting other figures.

(vii) Variation of the metric functions $ e^{\lambda} $ and $ e^{\nu} $ with respect to the radial coordinate $ r/r_b $ are featured in Fig. 9. For this figure, we use the same numerical values of constants as used in Fig. 3. It can be observed that the deformation functions $ f(r) $ and $ h(r) $ are negative and decreasing function throughout the stellar model, and both metric functions $ \lambda(r)=-\ln[\xi(r)+\alpha\,f(r)] $ and $ \nu(r)=\eta(r)+ \alpha\,h(r) $ are increasing as well as positive $ \forall $$ r\in[0,R] $. This clearly shows that the growth of $ \eta(r) $ is faster than the deformation function $ h(r) $ in Case II.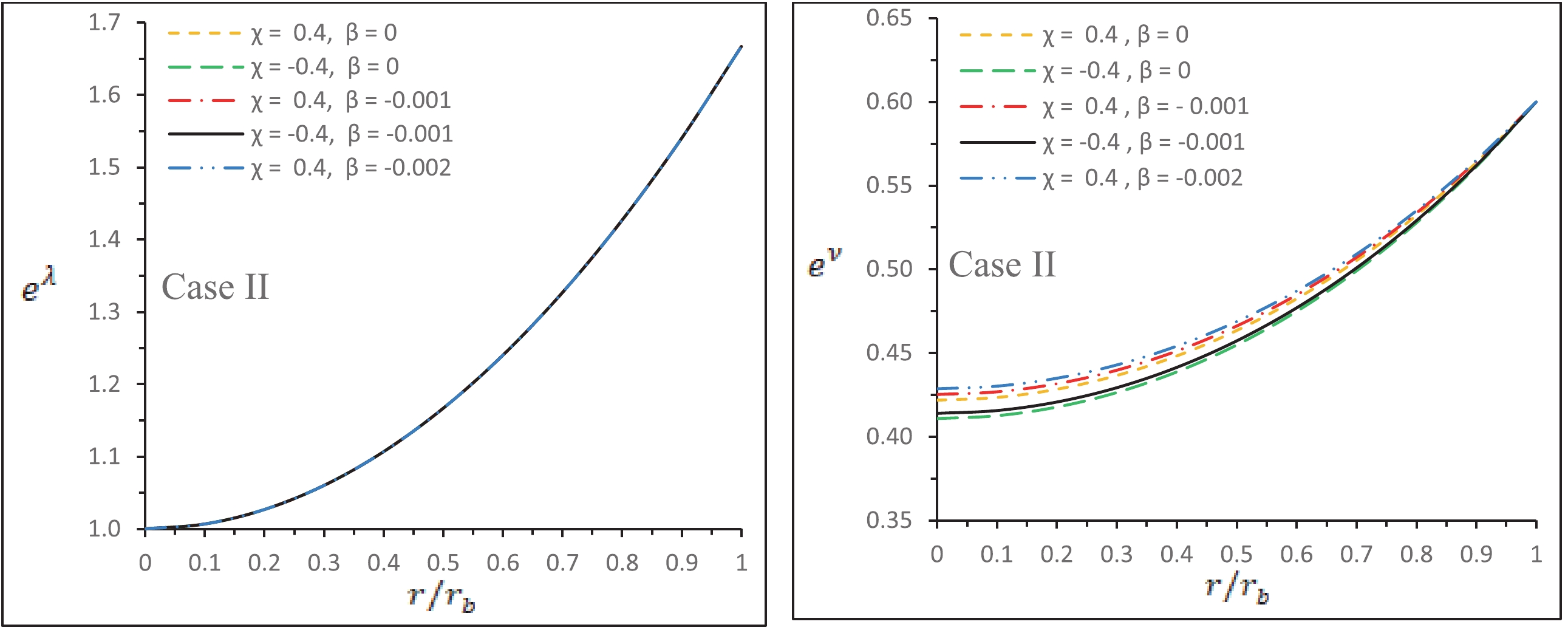

Figure 9.  (color online) Variation in the metric functions $ e^{\lambda} $ and $ e^{\nu} $ with respect to the radial coordinate $ r/r_b $.

(viii) In Fig. 10, the left panel shows the effective radial pressure ($ p^{\rm{eff}}_r $) and the right panel shows the effective tangential pressure ($ p^{\rm{eff}}_t $) with respect to the radial coordinate $ r/r_b $. We set the same numerical values as used in Fig. 3. Here, the constants χ and β also influence the radial and tangential pressures ($ p^{\rm{eff}}_r $ and $ p^{\rm{eff}}_t $), and we observe the following important points from Fig. 5: when we fix β and χ to move from positive to negative, the values of the pressures $ p^{\rm{eff}}_r $ and $ p^{\rm{eff}}_t $ at the core of stellar object increase, but when β is decreasing, $ p^{\rm{eff}}_r $ and $ p^{\rm{eff}}_t $ at the core also decrease while fixing χ. Further, if we compare Case I ($ \beta>0 $) and Case II ($ \beta<0 $), the pressure at the core in Case I is higher than that in Case II (see Tables 1 and 2 as well as Figs. 5 and 10).

χ and β	$\rho^{\rm{eff} }_0\times10^{13}({\rm gm/cm^3})$	$\rho^{\rm{eff} }_s\times10^{13} ({\rm gm/cm}^3)$	$p^{\rm{eff} }_0\times10^{33}({\rm dyne/cm^2})$
χ = 0.4, β = 0	3.06204	1.34680	1.84404
χ = −0.4, β = 0	3.36193	1.47900	2.02227
χ = 0.4, β = 0.004	3.07614	1.35285	2.39666
χ = −0.4, β = 0.004	3.37324	1.48417	2.60919
χ = 0.4, β = 0.007	3.08677	1.35739	2.83532

Table 1.  The numerical values of physical parameters effective central density ($ \rho^{\rm{eff}}_0 $), effective surface density ($ \rho^{\rm{eff}}_s $), and effective central pressure ($ p^{\rm{eff}}_0 $) for $ \beta = 0.004 $, $ \alpha=1.4 $, $ \gamma=-0.002 $, and $ Y=0.005 $.

χ and β	$\rho^{\rm{eff} }_0\times10^{13}({\rm gm/cm}^3)$	$\rho^{\rm{eff} }_s\times10^{13}( {\rm gm/cm}^3)$	$p^{\rm{eff} }_0\times10^{33}({\rm dyne/cm}^2)$
χ = 0.4, β = 0	3.06204	1.34680	1.84404
χ = −0.4, β = 0	3.36193	1.47900	2.02227
χ = 0.4, β = −0.001	3.05853	1.34528	1.71146
χ = −0.4, β = −0.001	3.35909	1.47771	1.88101
χ = 0.4, β = −0.002	3.05502	1.34377	1.58106

Table 2.  The numerical values of physical parameters ($ \rho^{\rm{eff}}_0 $), effective surface density ($ \rho^{\rm{eff}}_s $), and effective central pressure ($ p^{\rm{eff}}_0 $) for $ \beta = 0.004 $, $ \alpha=1.4 $, $ \gamma=-0.002 $, and $ Y=0.005 $.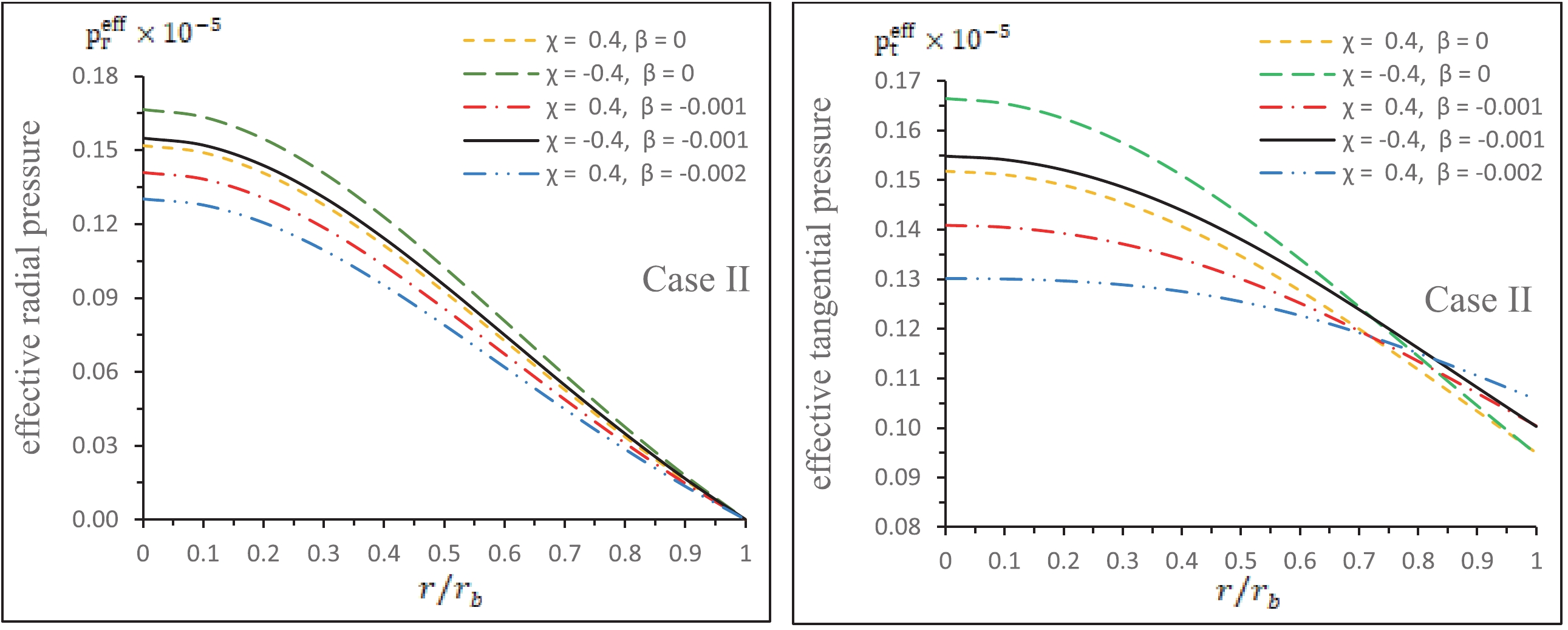

Figure 10.  (color online) The left panel shows the effective radial pressure ($ p^{\rm{eff}}_r $) and the right panel shows the effective tangential pressure ($ p^{\rm{eff}}_t $) with respect to the radial coordinate $ r/r_b $.

(ix) In Fig. 11, the left panel shows the anisotropy for the CGD contribution ($ \Delta_{\rm CGD} $) and the right panel shows the effective anisotropy ($ \Delta^{\rm{eff}} $) with respect to $ r/r_b $. We set the same numerical values as used in Fig. 8. Here, we find an interesting observation, i.e., when we look at the left panel of Fig. 11, the anisotropic contribution $ \Delta_{\rm CGD} $ is increasing throughout the compact star model, which shows that CGD approach can also introduce a stronger anisotropy within the object since the effective anisotropy $ \Delta^{\rm{eff}}=\Delta_{\rm FRT}+\Delta_{\rm CGD} $ will be higher than seed anisotropy $ \Delta_{\rm FRT} $. Due to this, the effective anisotropic force $ F_a={(2\,\Delta^{\rm{eff}})}/{2} $ will produce stronger effects to balance the system in order to achieve the hydrostatic equilibrium near the surface.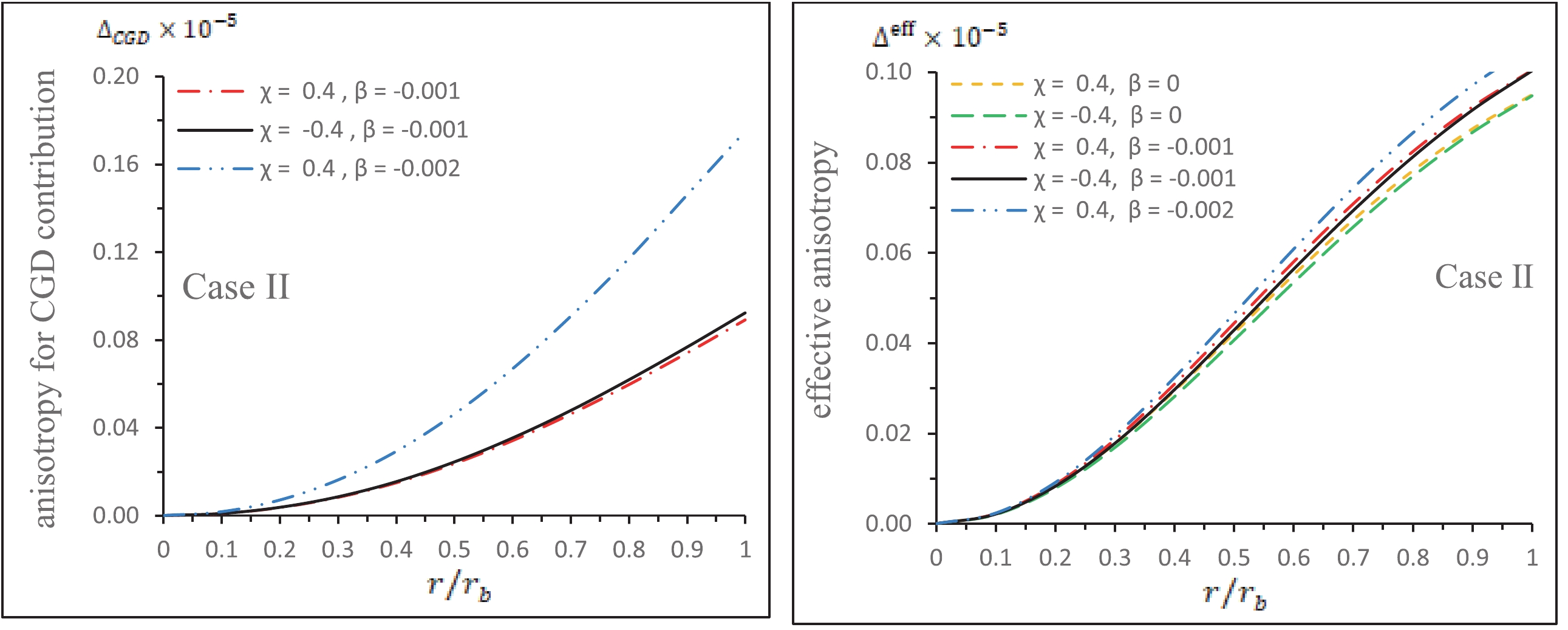

Figure 11.  (color online) The left panel shows the anisotropy for the CGD contribution ($\Delta_{\rm CGD}$) and the right panel shows the effective anisotropy ($ \Delta^{\rm{eff}} $) with respect to $ r/r_b $.

(x) Variations in the adiabatic index (Γ) with respect to the radial coordinate $ r/r_b $ are featured in Fig. 1. Here, we set the numerical values of constants as $ \beta = 0.004 $, $ \alpha=1.4 $, $ \gamma=-0.002 $, $ {M_0}/{R}=0.2 $, and $ Y=0.005 $. We have mentioned earlier that the anisotropy may improve the stability of the model. Here, we can note from Fig. 1 that the value of the adiabatic index Γ for both Cases I and II is higher in the presence of gravitational decoupling. On the other hand, we notice from Fig. 2 that the adiabatic index Γ is monotonically increasing towards the surface. Tables 3 and 4 show that the adiabatic index $ \Gamma_0 >\Gamma_{\rm crit} $ for both Cases I and II and hence is stable against the radial adiabatic infinitesimal perturbations. One can note that we have chosen very small values for the intensity parameter β, and hence, an obvious issue may be the following: what will be the scenario if one chooses $ \beta>0.1 $? If we take a higher value for the parameter β, say $ \beta>0.1 $, then the effective tangential pressure becomes negative, and consequently, we will obtain an increasing energy density. In a similar way, for the physical analysis, the mass-radius ratio has been fixed to 0.2 for the seed solution. However, in connection to the physical consistency for the other mass-radius ratios or against some other real star values, we have checked that the assigned mass-radius ratio is consistent with star LMC X-4 of radius 9.51 km.

β	$u={M}/{R}$	$ z_s $	$ \Gamma_0 $	$\Gamma_{\rm crit}$
β = 0	0.2	0.29113	1.81430	1.51434
β = 0.004	0.20009	0.29119	1.82829	1.51437
β = 0.007	0.20012	0.29124	1.84826	1.51439

Table 3.  The numerical values of physical parameters mass-radius ratio $ \big({M}/{R}\big) $, surface red-shift ($ z_s $), central adiabatic index ($ \Gamma_0 $), and $ \Gamma_{\rm crit} $ for different β with $ \alpha=1.4 $, $ \gamma=-0.002 $, $ Y=0.005 $, and $ \chi=0.4 $.

β	$u={M}/{R}$	$ z_s $	$ \Gamma_0 $	$\Gamma_{\rm crit}$
β = 0	0.2	0.29113	1.81430	1.51434
β = −0.001	0.200055	0.291112	1.81400	1.514335
β = −0.002	0.200047	0.291095	1.81547	1.514328

Table 4.  The numerical values of physical parameters mass-radius ratio $ \big({M}/{R}\big) $, surface red-shift ($ z_s $), central adiabatic index ($ \Gamma_0 $), and $ \Gamma_{\rm crit} $ for different β with $ \alpha=1.4 $, $ \gamma=-0.002 $, $ Y=0.005 $, and $ \chi=0.4 $.

(xi) As mentioned earlier, when the anisotropic contribution $ \Delta_{\rm CGD} $ due gravitational decoupling is negative and decreasing, then the anisotropic force will show less impact as compared to hydrostatic force for balancing the system of Case I, which can be seen from Fig. 2 (left panel), while in Case II, the anisotropic force is stronger than the hydrostatic force near the surface. Moreover, this force increases throughout the star, which implies that the anisotropic force in Case 2 will introduce a strong repulsive force to avoid the gravitational collapse.

As a final comment, we would like to add here that, although the present work is an extension of the work of Maurya et al. [75], the obtained results widely differ due to the particular CGD technique, as can be observed from all the case studies in connection to the above descriptions on Figs. 1–11. The literature survey reveals that this is the first study to solve field equations in $ f(R,T) $ gravity under the extended gravitational decoupling approach, where CGD is employed to successfully generate physically viable solutions for anisotropic systems.