-
While hyperons, i.e., baryons with a strangeness content, play an important role in compact star mergers and core-collapse events [1], there are limited experimental data on doubly strange hypernuclear systems, and the systems containing higher strangeness are almost unknown. Different phenomenological models have been developed for the nucleon-hyperon (NY) and hyperon-hyperon (YY) interactions. Nonetheless, recent developments in computational technologies and theoretical progress in Lattice QCD methods facilitated the derivation of
$ \Omega N $ ,$ \Omega \Omega $ ,$ \Lambda \Lambda $ , and$ N \Xi $ interactions [2–4], close to the physical pion masses$ m_{\pi} \simeq 146 $ MeV and Kaon masses$ m_k\simeq525 $ MeV, by the HAL QCD Collaboration [5, 6], where their physical values are$ m_{\pi} \simeq 135 $ MeV and$ m_k\simeq497 $ MeV. The$ N\Omega $ and di-$ \Omega $ interactions were suggested and predicted before the lattice QCD simulation in [7, 8].The potentials are obtained on a large space-time volume
$ L^{4}=(8.1\ {\rm{fm}})^{4} $ with a lattice spacing$ a=0.0846 $ fm. While there are sophisticated calculations to study$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ hypernucleus [9–18], in this work, we examine the HAL QCD$ \Lambda \Lambda $ interactions, which are the most consistent potential with the LHC ALICE data [19, 20], to study the ground state properties of the$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ hypernucleus. Similarly, we explore the$ \Omega \Omega \alpha $ system with lattice QCD-based interactions.The following motivated our exploration for possible implications of the attractive nature of the
$ \Omega N $ and$ \Omega \Omega $ interactions on few-body$ \Omega \Omega \alpha $ systems on the basis of first-principle lattice QCD-based interactions. In few-body systems the presence of additional nucleons may increase the binding, as demonstrated in many straightforward examples in nature. Although there are no dibaryon bound states with strangeness$ =-1 $ ($ \Lambda $ -nucleon system), hypertriton$ _{\Lambda}^{3} $ H, consisting of a neutron, a proton, and a$ \Lambda $ -particle, is bound with a separation energy of$ 0.41 \pm 0.12 $ MeV [21, 22]. In the case of strangeness$ =-2 $ , in systems containing$ \Xi $ -particles, an enhancement in the binding energy per baryon is observed by increasing the number of nucleons [23–25]. The Extended-Soft-Core (ESC08c) model of Nijmegen interaction [26] supports the bound states of$ \Xi N $ and$ \Xi N N \ (T=1/2, \ J^{\pi} = 3/2^+) $ with energies$ -1.56 $ and$ -17.2 $ MeV, respectively [23, 24, 27]. Recently Garcilazo et al. have implemented$ \Omega N $ and$ \Omega \Omega $ interactions derived by the HAL QCD Collaboration [2, 3, 28] to study three-body systems containing more strangeness number, i.e.,$ \Omega N N $ and$ \Omega \Omega N $ with strangeness$ = -3 $ and$ -6 $ [26]. As a result, they obtained$ \Omega d \ (0, \ 5/2^+) $ binding energy of about$ -20 $ MeV and two resonance states$ \Omega nn \ (1, \ 3/2^+) $ and$ \Omega \Omega N \ (1/2, \ 1/2^+) $ , with resonance energies of$ 1 $ and$ 4.6 $ MeV, correspondingly. Besides the$ \Omega $ -deuteron bound state, the$ \Omega \Omega \alpha $ bound state would be an interesting system to benchmark the$ \Omega \alpha $ and$ \Omega \Omega $ interactions in a three-body system.As the femtoscopic analysis of two-particle correlation functions in heavy-ion collisions provides information on hadron-hadron interactions at low energies [29, 30], investigating the
$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ system can also be interesting for this purpose. The correlation function in multistrange systems such as$ \Lambda \Lambda $ [31, 32] and$ p \Omega $ [20, 33, 34] have been measured recently in high-energy nuclear collisions. Furthermore, as a next step in femtoscopic analyses, the hadron-deuteron correlation functions would be promising. So far, experimental investigations of correlations for pd, dd and even for light nuclei have been already performed [35–37], whereas the$ K^{-}d $ case is currently in progress [38, 39], and$ \Lambda d $ correlation function is in the pipeline [40, 41]. A method to probe the momentum correlation functions of$ \Omega \Omega $ is proposed in Ref. [42]. Very recently, the production of$ \Omega NN $ and$ \Omega \Omega N $ in ultra-relativistic heavy-ion collisions using the Lattice QCD$ \Omega N $ ,$ \Omega \Omega $ potentials has been studied in Ref. [43]. Since the di-Omega appears with the binding energy approximately$ 1.6 $ MeV in$ ^1S_{0} $ channel [2], there is a possibility that our results could help the future study of$ \Omega \Omega -\alpha $ (like$ d-\alpha $ [44]) two-particle momentum correlation functions, and can be measured in high energy heavy-ion collisions. We explore this hypothetical system for the first time, and to the best of our knowledge, there is no other study performed on this system thus far.In the present work, we study the ground state properties of
$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ and$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ hypernuclei as a three-body$ (\alpha + Y + Y) $ bound state. For this, we solve two coupled Faddeev equations in configuration space with the hyperspherical harmonics expansion method to calculate the ground state binding energy and the geometrical structures of these hypernuclei. In our study, we use the HAL QCD$ \Lambda \Lambda $ and$ \Omega \Omega $ interactions, Isle-type Gaussian potential for$ \alpha \Lambda $ interactions and a Woods-Saxon type potential for$ \alpha \Omega $ interaction.In 2001, the KEK emulsion/scintillating-fiber hybrid experiment [45], known as the Nagara event, reported a uniquely identified double-
$ \Lambda $ hypernucleus$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ with binding energy of$ -7.25\pm0.19 $ MeV. The re-analysis of the Nagara event using the new$ \Xi $ mass of$ 1321.71 $ MeV [46], revised the binding energy to$ -6.91\pm0.16 $ MeV [47, 48], considerably shallower than the earlier measured value$ -10.9\pm0.8 $ MeV [49]. In the recent J-PARC E07 experiment emulsion analysis, several hypernuclear events have been observed. For example, the$ Be $ double$ \Lambda $ hypernucleus has been identified as an event called the “MINO event” [50], and a new$ \Xi $ -nuclear deeply bound state has been reported [51]. Furthermore, the high precision spectra for light to heavy multi-strange hypernuclei are planned to be measured in the future at JLab and with the new high-intensity high-resolution line at [51, 52].Hiyama et al. performed a three-body calculation for
$ \Lambda+\Lambda+{}_{ }^4{{\rm{He}}} $ , with the Gaussian expansion method, using properly tuned$ \Lambda \Lambda $ Nijmegen interactions to reproduce the Nagara event data [9, 10]. Nemura et al. studied$ \Lambda \Lambda $ hypernuclei with the stochastic variational method using effective phenomenological$ \Lambda N $ and$ \Lambda\Lambda $ potentials [11, 12]. Moreover, Filikhin et al. have studied$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ by solving the differential Faddeev equations (DFE) in configuration space using different models of Nijmegen$ YY $ interactions [13–16]. Recently, double-strangeness hypernuclei were studied in an effective field theory approach using the stochastic variational method at leading order [17] and with the Jacobi no-core shell model at the next-to-leading order [18]. The cluster structure of light hypernuclei [53, 54] has been studied with different methods, including the generator coordinate method [55], orthogonality condition model [56], Gaussian expansion method [57, 58], and Tohsaki-Horiuchi-Schuck-Röpke wave function approach [59].The Faddeev-Yakubovsky (FY) equations are extensively used to study the structure of three- and four-body bound states, with identical and non-identical particles, in different sectors of physics [60–65]. FY equations are solved with different techniques such as direct projection in momentum space [66], hyperspherical harmonics (HH) [67], adiabatic hyperspherical [68], and variational methods [69, 70]. The HH method has been implemented to study the complex structure of
$ {\rm{{^{6}}}He} $ and$ {\rm{{^{11}}}Li} $ halo nuclei in a three-body picture [67, 71]. In this work, we apply this method to study the ground state properties of double hyperon nuclei in a three-body picture as$ Y+Y+\alpha $ .In Sec. II, we briefly review the HH formalism for
$ Y+Y+\alpha $ three-body bound state. In Sec. III, we introduce$ YY $ and$ \alpha Y $ two-body potentials used to study the structure of double-hyperon nuclei. Our numerical results for the ground state binding energies and geometrical properties of$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ and$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ hypernuclei are presented and discussed in Sec. IV. A summary and outlook is provided in Sec. V. -
The total wave function
$ \Psi^{j \mu} $ of the three-body system$ (YY \alpha) $ for a given total angular momentum$ j $ by projection$ \mu $ , composed of two$ Y $ particles and one$ \alpha $ particle, is given as a sum of three Faddeev components$ \psi_i^{j \mu} $ $ \Psi^{j \mu}=\sum\limits_{i=1}^{3}\psi_{i}^{j \mu}\left({\boldsymbol{x}}_{i}, {\boldsymbol{y}}_{i}\right). $

(1) Each component
$ \psi_i^{j \mu} $ is expressed in terms of two Jacobi coordinates$ ({\boldsymbol{x}}_{i}, {\boldsymbol{y}}_{i}) $ and can be obtained from the solution of coupled Faddeev equations$ \begin{array}{l} \left(H_0 - E\right)\psi_{i}^{j \mu}+V_{jk}\left(\psi_{i}^{j \mu}+\psi_{j}^{j \mu}+\psi_{k}^{j \mu}\right)=0, \end{array} $

(2) where
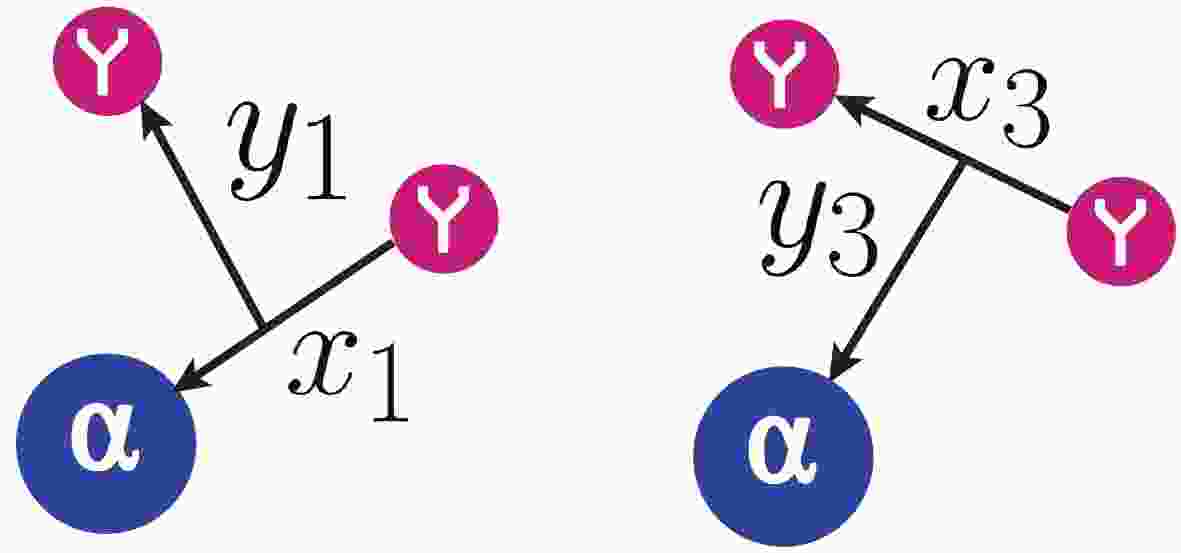
$ H_0 $ is the free Hamiltonian,$ E $ is 3B binding energy, and$ V_{jk} $ is the two body interaction (both the Coulomb and nuclear interactions) between the corresponding pair. The indexes$ i, j, k $ run through$ \left(1, 2, 3\right) $ in circular order. To solve the coupled Faddeev equations (2) in configuration space, one needs two different sets of Jacobi coordinates$( {\boldsymbol x}_1, {\boldsymbol y}_1)$ and$( {\boldsymbol x}_3, {\boldsymbol y}_3)$ , as shown in Fig. 1, defined by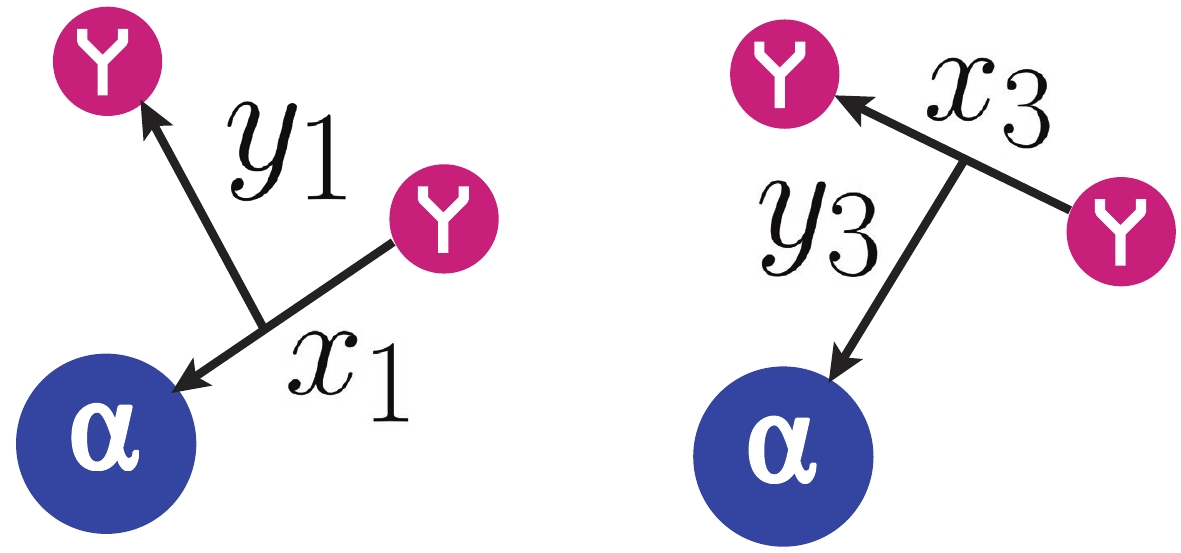
Figure 1. (color online) Two sets of Jacobi coordinates
$(Y\alpha, Y)$ and$(YY, \alpha)$ for a description of the$YY \alpha$ three-body system.$ \begin{aligned}[b] {\boldsymbol x}_i =& \sqrt{A_{jk}} \ {\boldsymbol r}_{jk} = \sqrt{A_{jk}} \ ( {\boldsymbol r}_j - {\boldsymbol r}_k) , \\ {\boldsymbol y}_i =& \sqrt{A_{(jk)i}} \ {\boldsymbol r}_{(jk)i} = \sqrt{A_{(jk)i}} \left( {\boldsymbol r}_i - \frac{A_j {\boldsymbol r}_j + A_k {\boldsymbol r}_k}{A_j+A_k} \right) , \end{aligned} $

(3) where
${\boldsymbol r}_i$ is the position vector of particle$ i $ ,${\boldsymbol r}_{jk}$ is the relative distance between the pair particles$ (jk) $ , and${\boldsymbol r}_{(jk)i}$ is the distance between the spectator particle$ i $ and the center of mass of pair$ (jk) $ . The reduced masses are$ A_{jk}=\dfrac{A_jA_k}{A_j+A_k} $ and$ A_{(jk)i}=\dfrac{(A_j+A_k)A_i}{A_i+A_j+A_k} $ , where$ A_i=\dfrac{m_i}{m} $ ,$ m=1 $ a.m.u., and$ m_i $ is the mass of particle$ i $ in a.m.u.The projection of coupled Faddeev equations onto the Jacobi coordinates
$( {\boldsymbol x}_i , {\boldsymbol y}_i )$ leads to two-dimensional partial differential equations that can be transformed into two sets of coupled one-dimensional equations using the hyperspherical coordinates$ ( \rho_i, \Omega_i ) $ . The hyperradius is defined by$ \rho_i^{2}=x_i^{2}+y_i^{2} $ ; the angular part$\Omega_i \equiv \{ \theta_i, \hat{ {\boldsymbol x}}_i, \hat{ {\boldsymbol y}}_i \}$ denotes a set of hyperspherical angles, with the hyperangle$ \theta_i=\arctan (x_i/y_i) $ and other angles associated with the unit vectors$\hat{ {\boldsymbol x}}_i$ and$\hat{ {\boldsymbol y}}_i$ . The projection of Faddeev components$ \psi_{Y} $ and$ \psi_{\alpha} $ , hereafter shown as$ \psi_{ Q} $ , for a given total angular momentum$ j $ and its projection$ \mu $ onto the spherical coordinates is given by [72, 73],$ \psi_{ Q}^{j \mu} (\rho_i, \Omega_i ) = \rho_i^{-5/2} \sum\limits_{\beta}\mathcal{R}_{\beta}^{j} (\rho_i )\mathcal{Y}_{\beta}^{j \mu} (\Omega_i), $

(4) $ \mathcal{Y}_{\beta}^{j\mu}\left(\Omega_{i}\right) $ is written in terms of hyperspherical harmonics$ \Upsilon_{Kl}^{l_{x_{i}}l_{y_{i}}}\left(\Omega_{i}\right) $ , which are eigenstates of the hypermomentum harmonics operator$ \hat{K} $ as$ \begin{array}{l} \mathcal{Y}_{\beta}^{j\mu}\left(\Omega\right)=\left\{ \left[\Upsilon_{Kl}^{l_{x}l_{y}}\left(\Omega\right)\otimes\phi_{S_{x}}\right]_{j_{ab}}\otimes\kappa_{I}\right\} _{j\mu}, \end{array} $

(5) $ \begin{array}{l} \Upsilon_{Klm_{l}}^{l_{x}l_{y}}\left(\Omega \right)=\varphi_{K}^{l_{x}l_{y}}\left(\theta \right)\left[Y_{l_{x}}\left(\hat{x}\right)\otimes Y_{l_{y}}\left(\hat{y}\right)\right]_{lm_{l}}, \end{array} $

(6) $ \begin{array}{l} \varphi_{K}^{l_{x}l_{y}}\left(\theta\right)=N_{K}^{l_{x}l_{y}}\left(\sin\theta\right)^{l_{x}}\left(\cos\theta\right)^{l_{y}}P_{n}^{l_{x}+1/2, l_{y}+1/2}\left(\cos2\theta\right), \end{array} $

(7) where
$ P_{n}^{a, b} $ is the Jacobi polynomial of order$ n=\left(K-l_{x}-l_{y}\right)/2 $ , and$ N_{K}^{l_{x}l_{y}} $ is a normalizing coefficient. The parameter$ \beta \equiv \{ K, l_{x}, l_{y}, l, S_{x}, j_{ab}\} $ represents a set of quantum numbers of a specific channel coupled to$ j $ .$ K $ is the hyperangular quantum number,$ l_{x} $ and$ l_{y} $ are the orbital angular momenta of the Jacobi coordinates$ x $ and$ y $ ,${\boldsymbol{l}}={\boldsymbol{l}}_{x}+{\boldsymbol{l}}_{y}$ is total orbital angular momentum,$ S_{x} $ is the total spin of the pair particles associated with the coordinate$ x $ , and${\boldsymbol{j}}_{ab}={\boldsymbol{l}}+{\boldsymbol{S}}_{x}$ .${\boldsymbol{I}}$ denotes the spin of the third particle, and the total angular momentum$ j $ is${\boldsymbol{j}}={\boldsymbol{j}}_{ab}+{\boldsymbol{I}}$ . In Eq. (5),$ \phi_{S_{x}} $ is the spin wave function of two-body subsystem, and$ \kappa_{I} $ is the spin function of the third particle. Applying this expansion in the Faddeev equations and performing the hyperangular integration, one obtains a set of coupled differential equations for the wave functions$ \mathcal{R}_{\beta}^{j}\left(\rho\right) $ of Eq. (4) as$ \begin{aligned}[b]& \left[-\frac{\hbar^{2}}{2m}\left(\frac{{\rm d}^{2}}{{\rm d}\rho^{2}}-\frac{\left(K+3/2\right)\left(K+5/2\right)}{\rho^{2}}\right)-E\right]\mathcal{R}_{\beta}^{j}\left(\rho\right) \\& +\mathop{\sum\limits_{\beta^{\prime}}}V_{\beta\beta^{\prime}}^{j\mu}\left(\rho\right)\mathcal{R}_{\beta^{\prime}}^{j}\left(\rho\right)=0, \end{aligned} $

(8) The coupling potentials are the hyperangular integrations of the two-body interaction
$ V_{\beta\beta^{\prime}}^{j\mu}\left(\rho_{i}\right)= \langle \mathcal{Y}_{\beta}^{j\mu}\left(\Omega_{i}\right) \left| {\hat{V}_{ij}} \right|\mathcal{Y}_{\beta^{\prime}}^{j\mu}\left(\Omega_{j}\right)\rangle $ , and$ \hat{V}_{ij} $ are the two-body potentials between particles$ i $ and$ j $ , which will be introduced in Section III.In order to solve these coupled equations, the hyperradial wave functions
$ \mathcal{R}_{\beta}^{j} (\rho) $ are expanded in a finite basis set of$i_{\max}$ hyperradial excitations as$ \mathcal{R}_{\beta}^{j} (\rho)=\sum\limits_{i=0}^{i_{\max}}C_{i\beta}^{j}R_{i\beta}(\rho), $

(9) where the coefficients
$ C_{i\beta}^{j} $ can be obtained by diagonalizing the three-body Hamiltonian for$i=0, ..., i_{\max}$ basis functions. The hyperradial functions$ R_{i\beta}(\rho) $ can be written in terms of Laguerre polynomials.By having the three-body wave function
$ \Psi^{j \mu} $ in the hyperspherical coordinates, one can study the geometrical structure of$ YY \alpha $ systems by calculating the matter radius$r_{\rm mat}=\sqrt{\langle r^{2}\rangle }$ and the correlation densities, giving the probability to have definite distances between the particles in the three-body system:$ P(r_{jk}, r_{(jk)i}) = \frac{r^2_{jk} r^2_{(jk)i}}{2j+1} \sum\limits_{\mu} \int {\rm d} \hat{x}_{i} {\rm d}\hat{y}_{i} \left| {\psi^{j \mu} (x_i, y_i)} \right|^2. $

(10) -
In this section, we present the two-body interactions, which we use in our calculations for the bound state of
$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ three-body systems. -
For
$ \Lambda \Lambda $ interaction, we use HAL QCD potentials in$ ^{1}S_{0} $ channel with isospin$ T=0 $ [4]$ \begin{aligned}[b] V_{\Lambda\Lambda}(r)=& \sum\limits_{i=1}^{2} \alpha_{i}\exp(-r^{2}/\beta_{i}^{2}) \\ &+ \lambda_{2} \left (1-\exp(-r^{2}/\rho_{2}^{2}) \right)^{2} \left( \frac{\exp(-m_{\pi}r)}{r} \right)^{2}. \end{aligned} $

(11) The effective
$ \Lambda \Lambda $ interaction is handled by the coupled-channel formalism [74] at three imaginary-time distances of$ t/a=11, 12, 13 $ , where the potential parameters are fitted to$ \chi^{2}/d.o.f = 1.30(40), \ 0.76(18) $ , and$ 0.74(30) $ , respectively. The$ t $ -dependence is insignificant within the statistical errors. The fitted potential parameters to Eq. (11) are given in Table 1, where the pion mass is$ m_{\pi}=146 $ MeV.$t/a$ 

$\alpha_{1} / {\rm{MeV} }$ 

$\beta_{1} / { {\rm{fm} } }$ 

$\alpha_{2} / {\rm{MeV} }$ 

$\beta_{2} / {\rm{fm} }$ 

$\lambda_{2} / {\rm{MeV \cdot fm} }^{2}$ 

$\rho_{2} / {\rm{fm} }$ 

11 1466.4 0.160 407.1 0.366 −170.3 0.918 12 1486.7 0.156 418.2 0.367 −160.0 0.929 13 1338.0 0.143 560.7 0.322 −176.2 1.033 Table 1. Fitted parameters of
$V_{\Lambda \Lambda}(r)$ potential, shown in Eq. (11), taken from Ref. [4]. The statistical errors in fitted parameters are not taken into account in our calculations.The low-energy data derived from this interaction indicate no bound or resonant di-hyperon around the
$ \Lambda\Lambda $ threshold in (2+1)-flavor QCD at nearly physical quark masses. These data predict a scattering length$ a_{0}^{\left(\Lambda\Lambda\right)}=-0.81\pm0.23_{-0.13}^{+0.00} $ fm and an effective range$ r_{ {\rm{eff}}}^{\left(\Lambda\Lambda\right)}=5.47\pm0.78_{-0.55}^{+0.09} $ fm. The central values and the statistical errors are extracted from phase shifts at$ t/a=12 $ , whereas the systematic errors are estimated from the central values at$ t/a=11 $ and$ 13 $ [4]. The systematic errors are estimated by the difference between the results obtained by the fit range, and the statistical errors are estimated by the jackknife sampling of the lattice QCD configurations. The source of systematic error is the contamination from inelastic states.For the
$ \Lambda \alpha $ interaction we use the Isle-type Gaussian potential [14]$ \begin{array}{l} V_{\Lambda\alpha}(r)=450.4 \exp(-(r/1.25)^{2})-404.9 \exp(-(r/1.41)^{2}). \end{array} $

(12) This potential reproduces the experimental data for the lifetime and binding energy of the
$ _{\Lambda}^{5}\rm He $ hypernucleus with$ \tau = 3.02_{-0.09}^{+0.10}\times10^{-10} $ s and$ E_{B} = -3.1 $ MeV [75]. -
The HAL QCD
$ \Omega \Omega $ potential in the$ ^{1}S_{0} $ channel is fitted to an analytical function as [2]$ V_{\Omega\Omega}(r)=\sum\limits_{j=1}^{3}c_j {\rm e}^{-(r/d_j)^{2}}, $

(13) where the potential parameters, without considering the statistical errors, are
$ (c_{1}, \ c_{2}, \ c_{3}) = (914, \ 305, \ -112) $ MeV and$ (d_{1}, \ d_{2}, \ d_{3}) = (0.143, \ 0.305, \ 0.949) $ fm. Using a single-folding potential method, an$ \Omega\alpha $ interaction has been recently extracted from a separable HAL QCD$ \Omega N $ potential. This potential supports an$ \Omega\alpha $ bound state with a binding energy of approximately$ -22 $ MeV and is parameterized in the form of the Woods-Saxon type potential [76]$ V_{\Omega\alpha}(r)=-61 \left (1+ \exp \left (\frac{r-1.7}{0.47} \right) \right) ^{-1}. $

(14) All two-body interactions for
$ YY $ ($ \Lambda\Lambda $ and$ \Omega\Omega $ ) and also$ Y\alpha $ ($ \Lambda\alpha $ and$ \Omega\alpha $ ) subsystems are shown in Fig. 2.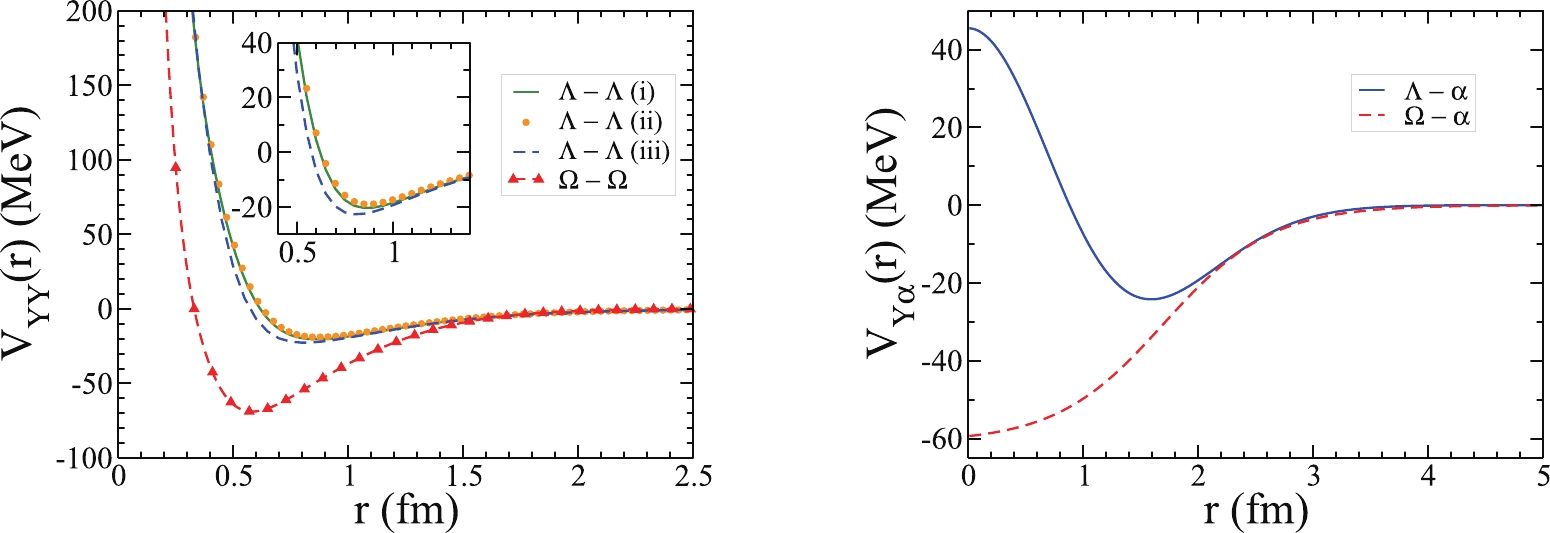
Figure 2. (color online) Left panel: YY potentials for three models of the HAL QCD
$\Lambda\Lambda$ potential of Eq. (11) with the parameters given in Table 1 at the imaginary-time distances$t/a=11, 12, 13$ (shown as model i, ii, iii) and the HAL QCD$\Omega\Omega$ potential of Eq. (13). Right panel:$Y\alpha$ potentials for the Isle-type$\Lambda\alpha$ potential given in Eq. (12) and the Woods-Saxon type$\Omega\alpha$ potential given in Eq. (14).In our calculations, we consider the Coulomb interaction in the
$ \Omega\Omega\alpha $ system using a hard-sphere model as [77]$ \begin{array}{ll} V_{\rm Coul}\left(r\right)=Z^{2}e^{2}\times\begin{cases} \dfrac{1}{r_{\rm Coul}}\left(\dfrac{3}{2}-\dfrac{r^{2}}{2r_{\rm Coul}^{2}}\right), & r\leq r_{\rm Coul}\\ \dfrac{1}{r}, & r > r_{\rm Coul} \end{cases} \end{array} $

(15) with a Coulomb radius
$r_{\rm Coul} = 1.47$ fm. -
To calculate the ground state binding energy and the geometrical properties of
$ \Lambda \Lambda \alpha $ and$ \Omega \Omega \alpha $ , we solve the coupled Faddeev equations (2) by implementing the FaCE computational toolkit [78] using the two-body interactions discussed in Sec. III. To discretize the continuous hyperradius coordinate$ \rho_i $ , we use the Gauss-Laguerre quadrature with 100 grid points, while the hyperangular integrations are performed using the Gauss-Jacobi quadrature with 60 grid points. The hyperradius cutoffs are selected high enough to achieve the cutoff-independent binding energies, converging with four significant figures. In our calculations, the masses of particles are$ m_{N} $ = 939 MeV,$ m_{\Lambda} $ = 1127.42 MeV,$ m_{\Omega}=1672.45 $ , and$ m_{\alpha} $ = 3727.38 MeV. Table 2 shows the convergence of the three-body ground state binding energy$ E_{3} $ and nuclear matter radius$r_{\rm mat}$ as a function of the maximum values of hyperangular quantum number$K_{\max}$ and hyperradial excitations$i_{\max}$ . The spin and isospin of$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ systems are equal to zero. The number of strange quark content for$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ is equal to 2 and 6, respectively. The Coulomb interaction of Eq. (15) is considered in$ \Omega\Omega\alpha $ systems leading to an increase of approximately$ 6 $ MeV in 3B binding energy.$\Lambda\Lambda\alpha$ 

$\Omega\Omega\alpha$ 

$i_{\max}$ 

$E_{3}$ /MeV

$r_{\rm mat}$ /fm

$E_{3}$ /MeV

$r_{\rm mat}$ /fm

5 −7.442 1.930 −67.19 1.327 10 −7.467 1.954 −67.21 1.326 15 −7.468 1.955 −67.21 1.326 20 −7.468 1.955 −67.21 1.326 25 −7.468 1.955 −67.21 1.326 $K_{\max}$ 

$E_{3}$ /MeV

$r_{\rm mat}$ /fm

$E_{3}$ /MeV

$r_{\rm mat}$ /fm

5 −6.897 1.953 −66.58 1.327 10 −7.321 1.948 −67.04 1.326 15 −7.404 1.951 −67.14 1.326 20 −7.446 1.953 −67.19 1.326 25 −7.456 1.954 −67.20 1.326 30 −7.463 1.955 −67.21 1.326 35 −7.465 1.955 −67.21 1.326 40 −7.466 1.955 −67.21 1.326 45 −7.467 1.955 −67.21 1.326 50 −7.467 1.955 −67.21 1.326 55 −7.467 1.955 −67.21 1.326 60 −7.468 1.955 −67.21 1.326 65 −7.468 1.955 −67.21 1.326 70 −7.468 1.955 −67.21 1.326 75 −7.468 1.955 −67.21 1.326 80 −7.468 1.955 −67.21 1.326 Table 2. Convergence of three-body ground state binding energy
$E_{3}$ and nuclear matter radius$r_{\rm mat}$ calculated for$\Lambda\Lambda\alpha$ and$\Omega\Omega\alpha$ systems as a function of maximum hyperradial excitations$i_{\max}$ (with$K_{\max}=80$ ) and hyperangular quantum number$K_{\max}$ (with$i_{\max}=25$ ).Since
$ \Omega \alpha $ interaction is completely attractive, faster convergence is reached in the calculation of ground state binding energy and nuclear matter radius of$ \Omega\Omega\alpha $ to$ -67.21 $ MeV and$ 1.326 $ fm. For the$ \Lambda\Lambda\alpha $ system, a convergence can be reached at larger values of$K_{\max}$ and$i_{\max}$ . For$ \Lambda\Lambda\alpha $ , the ground state binding energy and nuclear matter radius converge to$ -7.468 $ MeV and$ 1.955 $ fm. The listed results for$ \Lambda\Lambda\alpha $ are obtained for the$ \Lambda\Lambda $ interaction with imaginary-time distance$ t/a=12 $ , whereas for$ t/a=11 $ and$ t/a=13 $ , the calculated ground state binding energies are$ -7.605 $ MeV and$ -7.804 $ MeV, respectively.In Table 3, in addition to the converged 3B binding energies for
$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ systems, we list the binding energy of two-body$ YY $ and$ Y \alpha $ subsystems. Furthermore, the 3B binding energies in which the 2B interactions between identical hyperons are set to zero, i.e.,$ V_{YY}=0 $ , are listed. Our numerical results show that the relative percentage difference$ (B_3 (V_{YY}=0) - 2B_2(V_{Y\alpha}) ) / B_3 (V_{YY}= 0) \times 100 $ varies between$ 4 $ to 6%. As one can see in Table 3, the$ \Omega\Omega\alpha $ has a deeper bound state by having two bound subsystems. Our numerical analysis shows that the uncertainties in the HAL QCD$ \Omega\Omega $ ($ \Lambda \Lambda $ ) potential parameters impact the$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ ($ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ ) ground state binding energy for approximately$ 4 $ ($ 0.1 $ ) MeV and the$r_{\rm mat}$ for less than$ 0.01 $ ($ 0.007 $ ) fm. While the employed$ \Omega \alpha $ potential in our calculations is derived based on the dominant$ ^{5}S_{2} $ channel of$ N \Omega $ interactions [3, 79], the contribution of the$ ^{3}S_{1} $ channel can be reasonably ignored. Although the implemented two-body interactions in our calculations are restricted to only one angular momentum channel, we should point out that, to the best of our knowledge, no lattice two-body interactions developed to higher channels. This restriction in the interactions should explain the deep binding of the$ \Omega $ particles to the$ \alpha $ as possible contributions of repulsive channels, which are not taken into account, even though their contributions appear to be small [79].$YY \alpha$ System

$E_{2}\; (YY )$ 

$E_{2}\; (Y \alpha)$ 

$E_{3}$ 

$E_{3}$ (

$V_{YY }=0$ )

$\Lambda\Lambda\alpha \; (t/a=12)$ 

Not Bound $-3.146$ 

$-7.468$ 

$-6.463$ 

$\Omega\Omega\alpha$ 

$-1.408$ 

$-22.01$ 

$-67.21$ 

$-48.96$ 

Table 3. Three-body ground state binding energies
$E_{3}$ in MeV for$YY \alpha$ systems. The last column shows our results for 3B binding energies with zero interaction in$YY$ subsystems. Two-body binding energies$E_{2}$ for$YY $ and$Y \alpha$ subsystems are also shown in MeV.In Table 4, we compare our numerical results with other theoretical results such as those of the Gaussian expansion method (GEM), stochastic variational method (SVM), differential Faddeev equations (DFE), quark-cluster-model (QCM) by different
$ YY $ interaction models like the Nijmegen model D (ND), simulating Nijmegen hard-core model F$ (NF_{s}) $ , modified simulating Nijmegen hard-core model D$ (mND_{s}) $ , simulating Nijmegen hard-core model D$ (ND_{s}) $ , spin-flavor$ SU6 $ quark-model (fss2), Nijmegen soft-core model (NSC97e), G-matrix interaction based on the bare ND interaction (ND(G)), and Nijmegen extended soft-Core (ESC00) model as well as the experimental data (Exp).Ref. $YY$ Model

$E_{3}$ /MeV

present HAL QCD $(t/a=11)$ 

$-7.605$ 

present HAL QCD $(t/a=12)$ 

$-7.468$ 

present HAL QCD $(t/a=13)$ 

$-7.804$ 

[10] (GEM) ND $-7.25$ 

[12] (SVM) $NF_{s}$ 

$-7.52$ 

[12] (SVM) $mND_{s}$ 

$-7.53$ 

[12] (SVM) $ND_{s}$ 

$-7.93$ 

[80] (DFE) fss2 $-7.653$ 

[14] (DFE) NSC97e $-6.82$ 

[14] (DFE) ND $-9.10$ 

[14] (DFE) ND(G) $-10.1$ 

[14] (DFE) ESC00 $-10.7$ 

[81] (QCM) ND $-9.7 $ 

[81] (QCM) ND(G) $-9.4 $ 

[82] (GEM) ND $-9.34$ 

[83](G-matrix) ND(G) $-9.23$ 

[47, 48] (Exp.) – $-6.91 \pm 0.16$ 

[45] (Exp.) – $-7.25\pm0.19$ 

[49] (Exp.) – $-10.9\pm0.8$ 

Table 4. Comparison between our results for three-body ground state binding energy
$E_{3}$ of$\Lambda\Lambda\alpha$ system and other theoretical and experimental data.By having 3B wave functions of
$ YY \alpha $ systems in terms of the HH basis, we calculate the geometrical quantities, i.e., the r.m.s. distances between the particles and the r.m.s. matter radius, presented in Table 5. In our calculations, we consider the$ \alpha $ matter radius of$ 1.47 $ fm. For comparison, we also present the DFE results in Ref. [14]. Since the studied 3B systems consist of two identical hyperons and one alpha particle, interacting by scalar potentials, three particles form a ground state, where the most probable positions of the particles have the shape of an isosceles triangle. As shown in Table 5, our numerical results for the expectation values of the Jacobi coordinates in$ (YY, \alpha) $ and$ (Y\alpha, Y) $ configurations satisfy the following Pythagorean theorem with high accuracy$(YY \alpha)$ system

$\langle r_{YY} \rangle$ /fm

$\langle r_{Y \alpha} \rangle$ /fm

$\langle r_{(YY )\alpha} \rangle$ /fm

$ \left| {\Delta} \right| $ /fm

$^2$ 

$\langle \rho^{2}\rangle^{1/2}$ /fm

$r_{\rm mat}$ /fm

$\Lambda\Lambda\alpha\; (t/a=11)$ 

3.598 (3.36) 2.902 (2.70) 2.276 (2.11) 0.005 (0.015) 3.943 1.944 $\Lambda\Lambda\alpha\; (t/a=12)$ 

3.629 2.926 2.295 0.002 3.976 1.955 $\Lambda\Lambda\alpha\; (t/a=13)$ 

3.555 2.867 2.248 0.007 3.895 1.929 $\Omega\Omega\alpha$ 

1.521 1.293 1.047 0.003 2.037 1.326 Table 5. Expectation values of Jacobi coordinates in
$\Lambda\Lambda\alpha$ and$\Omega\Omega\alpha$ systems.$\langle r_{YY} \rangle$ is the separation between identical hyperons,$\langle r_{Y\alpha} \rangle$ is the separation between$Y\alpha$ pairs, and$\langle r_{(YY)\alpha} \rangle$ is the separation between the center of mass of$YY$ pair and the spectator$\alpha$ particle.$\langle \rho^{2}\rangle^{1/2}$ is the r.m.s. matter radius of the three-body system containing only point particles, and$r_{\rm mat}$ is the r.m.s. matter radius. The numbers in parentheses are from the DFE calculations using the Nijmegen model D (ND)$ YY $ interaction [14].$\Delta$ shows the accuracy of satisfaction of the Pythagorean theorem in Eq. (16).$ \Delta = \langle r_{(YY)\alpha} \rangle^2 + \frac{1}{4} \langle r_{YY} \rangle^2 - \langle r_{Y\alpha} \rangle^2 = 0. $

(16) In Table 6, we present the contribution of different channels, indicated by the quantum numbers
$ \{ K, l_{x_i}, l_{y_i}, l, S_{x_i}, j_{ab}\} $ , to the total norm of 3B ground state wave functions of$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ systems in both$ (Y\alpha-Y) $ and$ (YY-\alpha) $ Jacobi coordinates. As one can see, the main contributions in 3B wave functions come from the$ s $ -wave channels, whereas the higher partial wave channels substantially have an insignificant contribution.$K$ 

$l_{x_i}$ 

$l_{y_i}$ 

$l$ 

$S_{x_i}$ 

$j_{ab}$ 

$W$ 

$(\Lambda\alpha-\Lambda)$ Jacobi

0 0 0 0 0.0 0.0 0.980 2 0 0 0 0.0 0.0 0.004 4 2 2 0 0.0 0.0 0.012 $(\Lambda\Lambda-\alpha)$ Jacobi

0 0 0 0 0.5 0.5 0.980 2 1 1 0 0.5 0.5 0.004 4 1 1 0 0.5 0.5 0.001 4 0 0 0 0.5 0.5 0.010 $(\Omega\alpha-\Omega)$ Jacobi

0 0 0 0 0.0 0.0 0.993 2 0 0 0 0.0 0.0 0.005 $(\Omega\Omega-\alpha)$ Jacobi

0 0 0 0 1.5 1.5 0.993 2 1 1 0 1.5 1.5 0.005 Table 6. Contributions of different partial wave channels
$W$ to the total norm of 3B ground state wave functions of$\Lambda\Lambda\alpha$ and$\Omega\Omega\alpha$ systems. For each system, the upper panel shows the contributions in$(Y\alpha-Y)$ Jacobi coordinates, and the lower panel shows the contributions in$(YY-\alpha)$ Jacobi coordinates. Channels with a contribution greater than 0.001% are listed.In Fig. 3, we show the first three dominant hyperradial components
$ \rho^{5/2}R_{\beta}(\rho) $ for the ground state wave functions of$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ systems, obtained by$i_{\max} =25$ . As the binding energy of the 3B system increases from the left to right panel, the system becomes more compact in the configuration space. In Fig. 4, we illustrate the probability density of 3B ground states of$ \Lambda\Lambda\alpha $ and$ \Omega\Omega\alpha $ systems as a function of$ \langle r_{YY} \rangle $ , the distance between the two identical$ Y $ hyperons, and$ r_{(YY) \alpha} $ , the distance between the$ \alpha $ particle and the center of mass of two$ Y $ particles. As we can see for both systems, the distributions along the$ \langle r_{YY} \rangle $ direction are broader than those along the$ r_{(YY) \alpha} $ direction,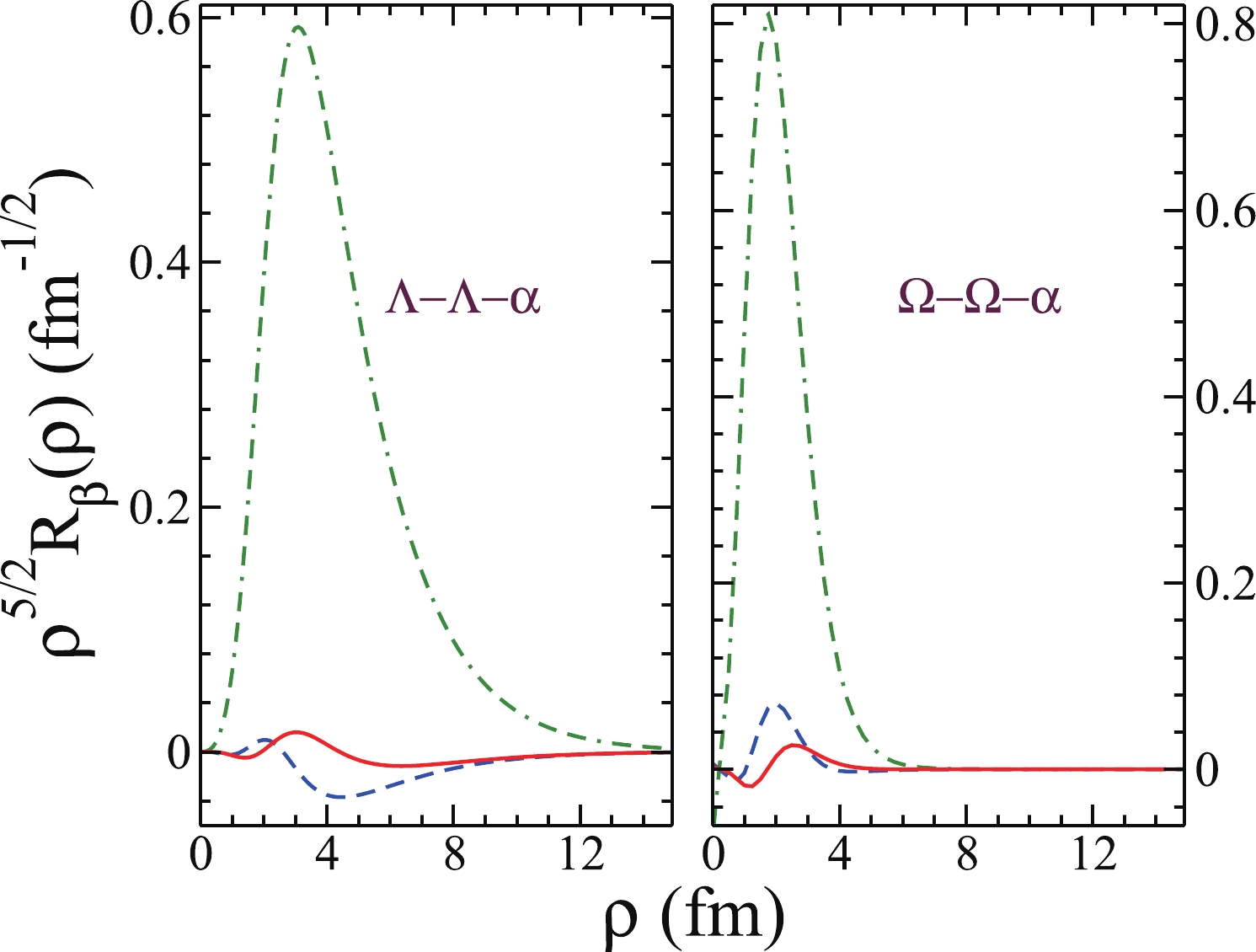
Figure 3. (color online) Hyperradial wave function
$\rho^{5/2}R_{\beta}(\rho)$ for the first three dominant channels,$\beta \equiv $ {0, 0, 0, 0, 0, 0} (green dash-dotted line),$\beta \equiv $ {2, 0, 0, 0, 0, 0} (blue dashed line), and$\beta \equiv$ {4, 0, 0, 0, 0, 0} (red solid line), of the ground state wave functions of$\Lambda\Lambda\alpha$ and$\Omega\Omega\alpha$ systems.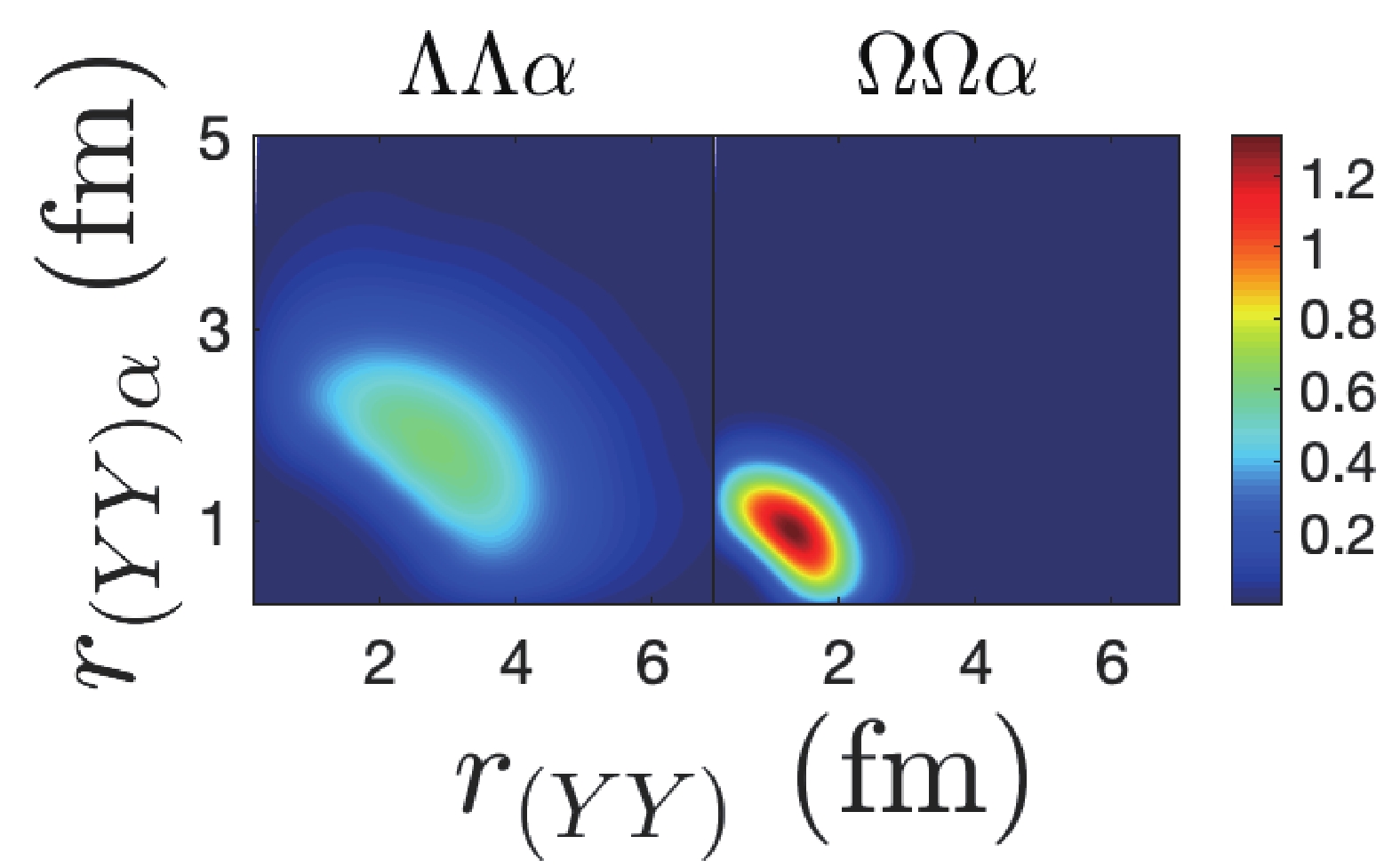
Figure 4. (color online) 3B ground state probability density of
$\Lambda\Lambda\alpha$ and$\Omega\Omega\alpha$ systems as a function of$\langle r_{YY} \rangle$ , the distance between$YY$ pair, and$r_{(YY) \alpha}$ , the distance between$\alpha$ particle and the center of mass of the$YY$ pair.confirming that the distance between identical
$ Y $ hyperons is greater than the distance between the spectator$ \alpha $ particle and the center of mass of the$ YY $ pair. -
In this study, we invetigated the ground-state properties of multi-strangeness hypernuclei
$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ and$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ in a hyperharmonic three-body model of$ (YY \alpha) $ . For this, we solved two coupled Faddeev equations in configuration space with the hyperspherical harmonics expansion method using the most modern two-body interactions, including the recent lattice QCD potentials, to calculate the ground state binding energies and geometrical properties. In our numerical analysis, we checked the convergence of 3B ground state binding energies and nuclear matter radii as a function of the maximum value of hyperradial excitations$i_{\max}$ and hyperangular quantum number$K_{\max}$ . Our numerical results show that the ground state binding energy of$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ using three models of$ \Lambda\Lambda $ lattice interactions changes in the domain of$ (-7.468 , \ -7.804) $ MeV, while$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ has a deep binding energy of$ -67.21 $ MeV. We should indicate that the implemented$ \Omega \alpha $ potential in our calculations is restricted to one angular momentum channel only, whereas the contribution of repulsive channels is not considered. Thus, this could explain the deep binding of the$ \Omega \alpha $ and consequently the$ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ system.We studied the geometrical properties of the aforementioned
$ ^6 $ He double hyperon by calculating the expectation values of the Jacobi coordinates and the r.m.s. matter radius and correlation density. Our numerical results confirm that the studied 3B systems, composed of two identical hyperons and one alpha particle, form isosceles triangles, where the most probable positions of the particles perfectly satisfy the Pythagorean theorem. Our numerical analysis on the structure of 3B ground state wave functions shows that the main contributions of over 99% are from the$ s $ -wave channels. Our numerical results for$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ are in agreement with the results of other theoretical studies.Considering the contributions of the coupled channels in
$ \Lambda \Lambda- \Xi N $ ($ \Omega N-\Lambda\Xi - \Sigma \Xi $ ) interactions is a complementary task to be implemented in the FaCE toolkit to include the coupled components in the wave function of$ {}_{\Lambda\Lambda }^{\;\;\;6}{{\rm{He}}} $ ($ {}_{\Omega\Omega }^{\;\;\;6}{{\rm{He}}} $ ). As shown in Refs. [81, 84], the contribution of the coupled channels leads to an increase of approximately$ 0.1 \sim 0.4 $ MeV in the$ \Lambda\Lambda\alpha $ binding energy, while using an effective single-channel interaction leads to a reduction of approximately$ 0.3 $ MeV [14]. This reduction is due to the tight$ \alpha $ cluster binding, which inhibits the effectiveness of the$ \Lambda \Lambda-\Xi N $ coupling. We assume that this should also be valid for the$ \Omega \Omega \alpha $ system. Moreover, while the contribution of transition potentials to the inelastic channels [85], i.e.,$ \Omega N-\Lambda\Xi - \Sigma \Xi $ , are expected to be small [79], they have not yet been derived from the lattice QCD calculations and can be considered in a future study when they are developed. -
F.E. thanks T. Hatsuda and J. Casal for helpful discussions and suggestions.
Three-body Faddeev calculations for ${{}_{\boldsymbol\Lambda \boldsymbol\Lambda }^{\;\;\;\;\bf 6}{\bf{He}}}$ and ${{}_{\boldsymbol\Omega \boldsymbol\Omega }^{\;\;\;\;\bf 6}{\bf{He}}} $ hypernuclei
- Received Date: 2022-04-07
- Available Online: 2022-10-15
Abstract: We study the ground-state properties of the







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF






























 DownLoad:
DownLoad: