-
The discovery of Ω baryon dates back to 1964; nevertheless, it continues to be the least observed in experiments worldwide.
$ \Omega^{-} $ holds a place in the decuplet family with isospin I = 0 and strangeness S = –3 with sss quarks. The search for missing resonances is the prime aim of hadron spectroscopy to understand the internal dynamics of the quarks inside the system ranging from light to heavy as well as exotic hadrons as depicted by few recent reviews [1, 2]. The motivation behind the current study is to exploit all resonance masses with possible spin-parity assignment. This is the extension of the previous study for non-strange [3, 4] and strange baryons with S = –1, –2 [5].Ω baryon purely belongs to the decuplet representation in a similar manner to Δ, whereas, in principle, Σ and Ξ can be realized as a mixture of octet and decuplet states. In terms of multi-strangeness, Ω baryon is similar to Ξ as both are not easily observed in experiments and no further information has been readily available since the publishing of bubble chamber data. In a recent study of strong decays in the constituent quark model with relativisitc corrections, it was highlighted that, unlike other light baryons, Ω with only strange quarks may be a tool to reach the valence quarks in the baryons when other kaon cloud effects are somehow excluded [6]. Pervin et al. [7] have vividly described that multi-strange baryons are produced only as a part of the final state with a very small production cross-section, which complicates the analysis for their study. Recent studies at Belle experiments have provided some results regarding Ω(2012) through
$ e^{+}e^{-} $ annihilations and into$ \Xi^{0}K^{-} $ as well as$ \Xi^{-}\bar K^{0} $ decay channels [8]. Earlier, BaBar collaboration attempted to study the spin of$ \Omega^{-} $ (1672) for$ J={3}/{2} $ through processes like$ \Omega_{c}^{0}\rightarrow \Omega^{-} K^{+} $ and$ \Xi_{c}^{0}\rightarrow \Omega^{-} \pi^{+} $ [9]. All these observations pose a challenge regarding the underlying mystery of multi strange baryons, especially for S=–3. The upcoming experimental facility at FAIR,$ \bar P $ ANDA-GSI is expected to perform a dedicated study of hyperons, especially at low energy regime [10]. Moreover, a part of BESIII experiment shall be including the strange quark systems [11] and J-PARC facility [12].The three star state Ω(2012) has been a puzzling one appearing in Table 1 as the second known state. The discovery of Ω(2012) by the Belle collaboration sparked a lot of theoretical work on the issue, with pictures inspired by quark models as well as molecular pictures based on the meson-baryon interaction. In various quark models, the masses of the first orbital excitations of states were deemed to Ω(2012). A recent study has proposed this state to be a molecular one. This state is slightly below Ξ(1530){
$ \bar K $ } threshold so that the binding mechanism could be a coupled channel dynamics [13]. Its characteristic signature could be a three body channel Ξ{$ \bar K $ }π. Some studies argue that the present information is not sufficient for considering it as a molecular state [15, 16], whereas others disapprove the proposed state [17]. Moreover, a study has been revisited to check the compatibility of molecular picture of 2012 within the coupled channel unitary approach [18]. Xiao et al. have studied the strong decays within chiral quark model to understand the structure of the Ω(2012) state [19]. There are several models to study the Ω baryon properties theoretically and phenomenologically such as quark pair-creation [20], QCD Sum rule [21], Glozman-Riska model [22], algebraic model by Bijker [23], and large-$ N_{c} $ analysis [24, 25]. Recently, A. Arifi et al. have investigated the decay properties of Ξ and Ω baryons including Roper-like resonances using relativistic corrections in the constituent quark model [6]. Our group has also attempted to explore light, strange baryon through Regge Phenomenology [26]. The Nambu-Jona-Lasinio (NJL) approach has been used for calculating the mixing of three and five components in low-lying Ω states with negative parity [27]. The partial wave analysis of light baryons is also a very important tool for the spectroscopy of narrow experimental states [28–31]. The details of these models through comparison are described in Section III.State $ J^{P} $ 

Status Ω(1672) ${3}/{2}^{+}$ 

**** Ω(2012) $?^{-} $ 

*** Ω(2250) *** Ω(2380) ** Ω(2470) ** Table 1. PDG Ω baryon [14].
In the present article, we study the resonance mass spectra of
$ \Omega^{-} $ baryon through a non-relativistic model. Section II describes the potential terms used to obtain the resonance mass with spin-dependent and correction parts. Section III sketches the results obtained through the model and summarizes the comparison with other models. Sections IV and V exploit the Regge trajectories and magnetic moment properties leading to the conclusion of the study. -
The present study is based on the hypercentral Constituent Quark Model (hCQM), i.e., a non-relativistic approach [32, 33]. The baryons are composed of three quarks confined within and interacting by a potential that is considered to be hypercentral. The hyperspherical coordinates are given by the angles
$ \Omega_{\rho} $ ,$ \Omega_{\lambda} $ along with hyperradius x and hyperangle ξ , which are written in terms of Jacobi coordinates as in Fig. 1 [34, 35],
Figure 1. (color online) Representation of the three-body system [36].
$ {\mathit{\boldsymbol{\rho}}} = \frac{1}{\sqrt{2}}({{\boldsymbol{ r}}_{1}} -{{\boldsymbol{ r}}_{2}}), \tag{1a} $

$ \begin{align} {\mathit{\boldsymbol{\lambda}}} = \frac{(m_{1}{{\boldsymbol{ r}}_{1}} + m_{2}{{\boldsymbol{ r}}_{2}} - (m_{1}+m_{2}){{\boldsymbol{ r}}_{3}})}{\sqrt{m_{1}^{2} + m_{2}^{2} + (m_{1}+m_{2})^{2}}}, \end{align} \tag{1b} $

where
$ r_{i} $ and$ m_{i} $ correspond to the internal distance between given two quarks and their masses, respectively.The hyperradius and hyperangle are defined as
$ \begin{equation} x = \sqrt{{\bf \rho^{2}} + {\bf \lambda^{2}}} , \quad \xi = {\rm arctan}\left(\frac{\rho}{\lambda}\right). \end{equation} $

(2) The hyperradius x is a one-dimensional coordinate, which encloses, simultaneously, the effects of the three-body interaction. The quarks are pictured as connected by gluonic strings where the potential increases linearly with the radius x. The reduced masses with Jacobi co-ordinates
$ \mathit{\boldsymbol{\rho}} $ and$ \mathit{\boldsymbol{\lambda}} $ are given by$ \begin{equation} m_{\rho}=\frac{2m_{1}m_{2}}{m_{1}+m_{2}}, \quad m_{\lambda}=\frac{2m_{3}(m_{1}^{2}+ m_{2}^{2}+m_{1}m_{2})}{(m_{1}+m_{2})(m_{1}+m_{2}+m_{3})}. \end{equation} $

(3) The kinetic energy operator in the center of mass frame is written as
$ \begin{equation} -\frac{\hbar^{2}}{2m}(\Delta_{\rho} + \Delta_{\lambda})= \frac{\hbar^{2}}{2m}\left(\frac{\partial^{2}}{\partial x^{2}} + \frac{5}{x}\frac{\partial}{\partial x} + \frac{L^{2}(\Omega)}{x^{2}}\right). \end{equation} $

(4) Here,
$ L^{2}(\Omega)= L^{2}(\Omega_{\rho}, \Omega_{\lambda}, \xi) $ is the quadratic Casimir operator for the six-dimensional rotational group whose eigenfucntions are hyperspherical harmonics satisfying$ \begin{equation} L^{2}(\Omega_{\rho}, \Omega_{\lambda}, \xi) Y_{[\gamma]l_{\rho}l_{\lambda}}(\Omega_{\rho}, \Omega_{\lambda}, \xi) = -\gamma(\gamma + 4 )Y_{[\gamma]l_{\rho}l_{\lambda}}(\Omega_{\rho}, \Omega_{\lambda}, \xi), \end{equation} $

(5) $ \gamma = 2n + l_{\rho} + l_{\lambda} $ is the grand angular quantum number. Thus, the hyper-radial part of the wave-function, as determined by hypercentral Schrodinger equation, is$ \begin{equation} \left[\frac{{\rm d}^{2}}{{\rm d}x^{2}} + \frac{5}{x}\frac{\rm d}{{\rm d}x} - \frac{\gamma(\gamma +4)}{x^{2}}\right]\psi(x) = -2m[E-V(x)]\psi(x). \end{equation} $

(6) Here
$ l(l+1) \rightarrow {15}/{4} + \gamma (\gamma + 4) $ . The hyperradial wave-function$ \psi(x) $ is completely symmetric for exchange of the quark coordinates using the orthogonal basis [37]. The expansion of the quark interaction term is written as$ \begin{equation} \sum_{i<j}V(r_{ij})= V (x) + ... \end{equation} $

(7) The potential with the first term gives the hypercentral approximation, which has three-body character as not a single pair of coordinates can be disentangled from the third one. The Hamiltonian of the system is written with a potential term solely dependent on the hyperradius x of the three body system.
$ \begin{equation} H = \frac{P^{2}}{2m} + V^{0}(x) + V_{SD}(x), \end{equation} $

(8) where
$ m=\dfrac{2m_{\rho}m_{\lambda}}{m_{\rho}+m_{\lambda}} $ is the reduced mass. The potential is solely hyperradius dependent. So, it consists of a Coulomb-like term and a linear term acting as confining part.$ \begin{equation} V^{0}(x) = -\frac{\tau}{x} + \alpha x. \end{equation} $

(9) Here,
$ \tau = ({2}/{3})\alpha_{s} $ with$ \alpha_{s} $ representing the running coupling constant.$ \alpha_{s}= {\frac{\alpha_{s}(\mu_{0})}{1+ {\left(\dfrac{33-2 n_{f}}{12\pi}\right)} \alpha_{s}(\mu_{0}) {\rm ln}{\left(\dfrac{m_{1}+m_{2}+m_{3}}{\mu_{0}}\right)}}}. $

(10) Here,
$ \alpha_{s} $ is 0.6 at$ \mu_{0}=1 \;{\rm GeV} $ and$ n_{f} $ is the number of active quark flavors whose value here is 3, whereas α is the string tension of the confinement part of the potential. Moreover, α is state dependent and is obtained by fixing the value using the experimental ground state mass of the baryon [38, 39]. The constituent quark mass is considered as$ m_{s} $ = 0.500 GeV. The model parameters used for the groundstate are as shown in Table 2.$ m_{s} $ /GeV

$ \alpha_{s} $ 

$ \alpha/{\rm GeV}^{2} $ 

0.500 0.5109 0.0129 Table 2. Ground state model parameters.
If considering the chiral quark model, the low-energy regime shall be well established as the spontaneously broken SU(3) chiral symmetry scale is different from that of the QCD confinement scale. For three body higher excited states, the relative position of positive and negative parity states can be fixed by the interplay of relativistic kinematics and pion exchange interaction, playing the role of one-gluon exchange potential. Thus, the higher terms in Goldstone exchange will allow us to incorporate the hyperfine, and spin-singlet and triplet splitting [40–42].
The
$ V_{SD}(x) $ is added for incorporating spin-dependent contributions through$ V_{SS}(x) $ ,$ V_{\gamma S}(x) $ and$ V_{T}(x) $ as spin-spin, spin-orbit, and tensor terms, respectively. These interactions arise due to$ {\nu^{2}}/{c^{2}} $ effects in non-relativistic expansion and by the standard Breit-Fermi expansion as described by Voloshin [43].$ \begin{aligned}[b] V_{SD}(x) =& V_{SS}(x)({\boldsymbol {S_{\rho}\cdot S_{\lambda}}}) + V_{\gamma S}(x)({\boldsymbol {\gamma \cdot S}}) \\& + V_{T} \left[S^{2}- \frac{3({\boldsymbol {S\cdot x}})({\boldsymbol {S\cdot x}})}{x^{2}}\right], \end{aligned} $

(11) $ \quad\quad \;\begin{equation} V_{SS}(x)=\frac{1}{3m_{\rho}m_{\lambda}}\nabla^{2}V_{V}, \end{equation} $

(12) $\quad\quad \; \begin{equation} V_{\gamma S}(x)=\frac{1}{2m_{\rho}m_{\lambda}x}\left(3\frac{{\rm d}V_{V}}{{\rm d}x}-\frac{{\rm d}V_{S}}{{\rm d}x}\right), \end{equation} $

(13) $ \quad\quad \;\begin{equation} V_{T}(x)=\frac{1}{6m_{\rho}m_{\lambda}}\left(3\frac{{\rm d}^{2}V_{V}}{{\rm d}x^{2}}-\frac{1}{x}\frac{{\rm d}V_{V}}{{\rm d}x}\right), \end{equation} $

(14) where
$ V_{V} = {\tau}/{x} $ and$ V_{S} = \alpha x $ are the vector and scalar part of the potential. However, instead of the spin-spin interaction presented by delta function, we have employed a smear function of the form, which is detailed in previous works [33, 44, 45]. Further,$ {{S\mathit{\boldsymbol{}}}= {S\mathit{\boldsymbol{}}}_{\rho} + {S\mathit{\boldsymbol{}}}_{\lambda}} $ , where$ {S\mathit{\boldsymbol{}}}_{\rho} $ and$ {S\mathit{\boldsymbol{}}}_{\lambda} $ are the spin vectors associated with the$ \boldsymbol \rho $ and$ \boldsymbol \lambda $ variables, respectively.$ \begin{equation} V_{SS}(x)=\frac{-A}{6m_{\rho}m_{\lambda}} \frac{{\rm e}^{{-x}/{x_{0}}}}{xx_{0}^{2}}. \end{equation} $

(15) Here,
$ x_{0} $ is the hyperfine parameter, with value$ x_{0}=1 $ and A is a state dependent parameter consisting of an arbitrary constant. The form of A is chosen as$ A=A_{0}/ \sqrt{n+l+\dfrac{1}{2}} $ , wherein the value of$ A_{0}=28 $ for determining the ground state value ($ 1S({3}/{2})^{+} $ 1672 MeV) as well as other radially excited states. Similarly, the other parameters are determined for obtaining the experimentally known ground state mass, i.e., 1672 MeV, in the case of Ω. In addition, masses with first order correction as$ \dfrac{1}{m}V^{1}(x) $ are taken into account through$ \begin{equation} V^{1}(x)= -C_{F}C_{A}\frac{\alpha_{s}^{2}}{4x^{2}}, \end{equation} $

(16) where
$ C_{F}=\dfrac{2}{3} $ and$ C_{A}=3 $ are Casimir elements of the fundamental and adjoint representation.Numerical solutions of Schrodinger equation has been obtained using Mathematica notebook [46].
-
In the present work, 1S–4S, 1P–4P, 1D–3D, and 1F–2F states have been obtained for
$ S={1}/{2} $ and$ S={3}/{2} $ spin configurations with all possible$ J^{P} $ values in Tables 3–6. Moreover,$ Mass_{\rm cal}1 $ and$ Mass_{\rm cal}2 $ correspond to the resonance masses without and with the first order correction term, respectively. Tables 7 and 8 show comparisons of the obtained results with various approaches for positive and negative parity states. The ground state Ω(1672) is nearly the same for many approaches with a variation of 20–30 MeV in few cases depending on the approach.State $ J^{P} $ 

$ Mass_{\rm cal} $ 1

$ Mass_{\rm cal} $ 2

1S $ {3}/{2}^{+} $ 

1672 1672 2S $ {3}/{2}^{+} $ 

2057 2068 3S $ {3}/{2}^{+} $ 

2429 2449 4S ${3}/{2}^{+} $ 

2852 2885 Table 3. Resonance masses of S-state 1S–4S without and with first order correction to the potential (in MeV).
State $J^{P}$ 

$Mass_{\rm cal}$ 1

$Mass_{\rm cal}$ 2

$1^{2}F_{5/2}$ 

${5}/{2}^{-}$ 

2585 2614 $1^{2}F_{7/2}$ 

${7}/{2}^{-}$ 

2552 2579 $1^{4}F_{3/2}$ 

${3}/{2}^{-}$ 

2622 2653 $1^{4}F_{5/2}$ 

${5}/{2}^{-}$ 

2595 2625 $1^{4}F_{7/2}$ 

${7}/{2}^{-}$ 

2562 2590 $1^{4}F_{9/2}$ 

${9}/{2}^{-}$ 

2521 2548 $2^{2}F_{5/2}$ 

${5}/{2}^{-}$ 

3027 3069 $2^{2}F_{7/2}$ 

${7}/{2}^{-}$ 

2986 3027 $2^{4}F_{3/2}$ 

${3}/{2}^{-}$ 

3072 3115 $2^{4}F_{5/2}$ 

${5}/{2}^{-}$ 

3039 3081 $2^{4}F_{7/2}$ 

${7}/{2}^{-}$ 

2998 3040 $2^{4}F_{9/2}$ 

${9}/{2}^{-}$ 

2949 2999 Table 6. Resonance masses of F-state 1F–2F without and with first order correction to the potential (in MeV).
$ J^{P} $ 

$ Mass_{\rm cal}1 $ 

$ Mass_{\rm cal}2 $ 

[47] [48] [49] [7] [50] [51] [52] [54] [55] $ {1}/{2}^{+} $ 

2291 2311 2301 2182 2232 2175 2140 2220 2190 2232 2350(63) 2699 2733 2202 2191 2255 2210 2256 2481(51) 3157 3201 $ {3}/{2}^{+} $ 

1672 1672 1678 1673 1672 1656 1694 1635 1675 1642(17) 2057 2068 2173 2078 2159 2170 2282 2165 2065 2177 2470(49) 2269 2288 2304 2208 2188 2182 2280 2215 2236 2276 2295 2332 2263 2245 2345 2265 2287 2429 2449 2671 2703 2681 2713 2852 2885 3122 3166 3134 3178 $ {5}/{2}^{+} $ 

2250 2267 2401 2224 2303 2178 2280 2225 2253 2257 2275 2260 2252 2210 2345 2265 2312 2646 2676 2656 2686 3092 3135 3102 3146 $ {7}/{2}^{+} $ 

2233 2249 2369 2205 2321 2183 2295 2210 2292 2623 2652 3065 3107 Table 7. Comparison of present masses with other approaches based on
$ J^{P} $ value with positive parity described in the increasing order for all possible spin-parity assignment (in MeV).$ J^{P} $ 

$ Mass_{\rm cal}1 $ 

$ Mass_{\rm cal}2 $ 

[47] [48] [49] [7] [50] [51] [52] [54] [55] $ {1}/{2}^{-} $ 

1987 1996 1941 2015 1957 1923 1837 1950 2020 1992 1944(56) 1983 2001 2463 2410 2456 2716(118) 2345 2363 2580 2490 2498 2352 2370 2550 2758 2788 2767 2797 3218 3264 3229 3276 $ {3}/{2}^{-} $ 

1978 1985 2038 2015 2012 1953 1978 2000 2020 1976 2049(32) 1983 1991 2537 2604 2440 2446 2755(67) 2332 2349 2636 2495 2507 2339 2356 2524 2622 2653 2564 2740 2770 2594 2749 2779 3072 3115 3196 3240 3207 3252 $ {5}/{2}^{-} $ 

1970 1997 2653 2490 2528 2321 2338 2534 2585 2614 2554 2595 2625 2617 2726 2755 3027 3069 3039 3081 3178 3221 $ {7}/{2}^{-} $ 

2562 2590 2599 2531 2998 3040 2577 $ {9}/{2}^{-} $ 

2521 2548 2649 2606 2949 2999 Table 8. Comparison of present masses with other approaches based on
$ J^{P} $ value with negative parity described in the increasing order for all possible spin-parity assignment (in MeV).State $J^{P}$ 

$Mass_{\rm cal}$ 1

$Mass_{\rm cal}$ 2

$1^{2}P_{1/2}$ 

${1}/{2}^{-}$ 

1987 1996 $1^{2}P_{3/2}$ 

${3}/{2}^{-}$ 

1978 1985 $1^{4}P_{1/2}$ 

${1}/{2}^{-}$ 

1992 2001 $1^{4}P_{3/2}$ 

${3}/{2}^{-}$ 

1983 1991 $1^{4}P_{5/2}$ 

${5}/{2}^{-}$ 

1970 1997 $2^{2}P_{1/2}$ 

${1}/{2}^{-}$ 

2345 2363 $2^{2}P_{3/2}$ 

${3}/{2}^{-}$ 

2332 2349 $2^{4}P_{1/2}$ 

${1}/{2}^{-}$ 

2352 2370 $2^{4}P_{3/2}$ 

${3}/{2}^{-}$ 

2339 2356 $2^{4}P_{5/2}$ 

${5}/{2}^{-}$ 

2321 2338 $3^{2}P_{1/2}$ 

${1}/{2}^{-}$ 

2758 2788 $3^{2}P_{3/2}$ 

${3}/{2}^{-}$ 

2740 2770 $3^{4}P_{1/2}$ 

${1}/{2}^{-}$ 

2767 2797 $3^{4}P_{3/2}$ 

${3}/{2}^{-}$ 

2749 2779 $3^{4}P_{5/2}$ 

${5}/{2}^{-}$ 

2726 2755 $4^{2}P_{1/2}$ 

${1}/{2}^{-}$ 

3218 3264 $4^{2}P_{3/2}$ 

${3}/{2}^{-}$ 

3196 3240 $4^{4}P_{1/2}$ 

${1}/{2}^{-}$ 

3229 3276 $4^{4}P_{3/2}$ 

${3}/{2}^{-}$ 

3207 3252 $4^{4}P_{5/2}$ 

${5}/{2}^{-}$ 

3178 3221 Table 4. Resonance masses of P-state 1P–4P without and with first order correction to the potential (in MeV).
State $J^{P}$ 

$Mass_{\rm cal}$ 1

$Mass_{\rm cal}$ 2

$1^{2}D_{3/2}$ 

${3}/{2}^{+}$ 

2269 2288 $1^{2}D_{5/2}$ 

${5}/{2}^{+}$ 

2250 2267 $1^{4}D_{1/2}$ 

${1}/{2}^{+}$ 

2291 2311 $1^{4}D_{3/2}$ 

${3}/{2}^{+}$ 

2276 2295 $1^{4}D_{5/2}$ 

${5}/{2}^{+}$ 

2257 2275 $1^{4}D_{7/2}$ 

${7}/{2}^{+}$ 

2233 2249 $2^{2}D_{3/2}$ 

${3}/{2}^{+}$ 

2671 2703 $2^{2}D_{5/2}$ 

${5}/{2}^{+}$ 

2646 2676 $2^{4}D_{1/2}$ 

${1}/{2}^{+}$ 

2699 2733 $2^{4}D_{3/2}$ 

${3}/{2}^{+}$ 

2681 2713 $2^{4}D_{5/2}$ 

${5}/{2}^{+}$ 

2656 2686 $2^{4}D_{7/2}$ 

${7}/{2}^{+}$ 

2623 2652 $3^{2}D_{3/2}$ 

${3}/{2}^{+}$ 

3122 3166 $3^{2}D_{5/2}$ 

${5}/{2}^{+}$ 

3092 3135 $3^{4}D_{1/2}$ 

${1}/{2}^{+}$ 

3157 3201 $3^{4}D_{3/2}$ 

${3}/{2}^{+}$ 

3134 3178 $3^{4}D_{5/2}$ 

${5}/{2}^{+}$ 

3103 3146 $3^{4}D_{7/2}$ 

${7}/{2}^{+}$ 

3065 3107 Table 5. Resonance masses of D-state 1D–3D without and with first order correction to the potential (in MeV).
Faustov et al. [47] have employed a relativistic quark model approach considering a quark-diquark system. The lower excited states are found to be in strong accordance, whereas for higher excitations, an exact comparison is not possible. In ref [48], the authors studied the spectrum through hyperfine interactions due to two-gluon exchange. For the available states, our current results are very close to those reported, within 50 MeV. Another non-relativistic constituent quark model approach has been utilized by [49]. Y. Oh [50] has investigated the Ω spectrum using Skyrme model. Refs [51] and [52] have exploited the quark model based on chromodynamics, with which some of the present states are also in accordance. E. Klempt [53] has reproduced the few known states through a new baryon mass formula. U. Löring et al. have studied the whole light spectrum within a relativistic covariant quark model based on Bethe-Salpeter equation [54]. The BGR collaboration [55] results are based on chirally improved (CI) quarks. For higher
$ J^{P} $ values, few approaches are available for comparison.One puzzling issue remains regarding the Ω(2012) state, i.e. our results vary by 30 MeV and do not exactly reproduce previous measurements. Moreover, this study is not able to precisely comment on the proposed molecular nature of this state. So, the future experimental results would serve as a key towards its understanding.
The results described in Tables 3–6 have been summarized in the increasing order for each
$ J^{P} $ value including positive parity in Table 7 and negative parity in Table 8. All the mentioned models appearing in the table for comparison are not sufficient to segregate each state based on the$ J^{P} $ value. The ground state Ω(1672) with$ J^{P}={3}/{2}^{+} $ is close to those in [47–49] and [52]. The first state with$ J^{P}={1}/{2}^{+} $ is nearly comparable to that in the relativistic approach by Faustov et al.The first excited states with
$ J^{P}={5}/{2}^{+} $ and$ J^{P}={7}/{2}^{+} $ are not very far from most of the comparison. As in the case on negative parity states$ J^{P}={3}/{2}^{-} $ , [48], [49], [51] and [52], the results are close to 2012 MeV, whereas the present study could not identify exactly the proposed Ω(2012) state. The state$ J^{P}={7}/{2}^{-} $ is very close to the results from [47] and [54].Here, we attempt to assign a tentative spin-parity to the three and two starred states. The Ω(2250) with an experimental mass at
$ 2252 \pm 9 $ is quite comparable to our 1D with$ J^{P}={5}/{2}^{+} $ . The fourth state Ω(2380) may possibly be a member of the 2P family with$ J^{P}={1}/{2}^{-} $ matching our value at 2370 MeV. The last state of Ω(2470) with a mass as$ 2474 \pm 12 $ might be assigned a 3S state with$ J^{P}={3}/{2}^{+} $ as the calculated state 2429 or 2449 MeV.The present model has attempted to distinguish all the possible spin-parity assignment of the excited states. However, due to limited data obtained by various compared models, exact state-wise comparison is not possible. Thus, this study is expected to provide a possible range of masses for upcoming experiments, which shall identify the existence of a particular state.
-
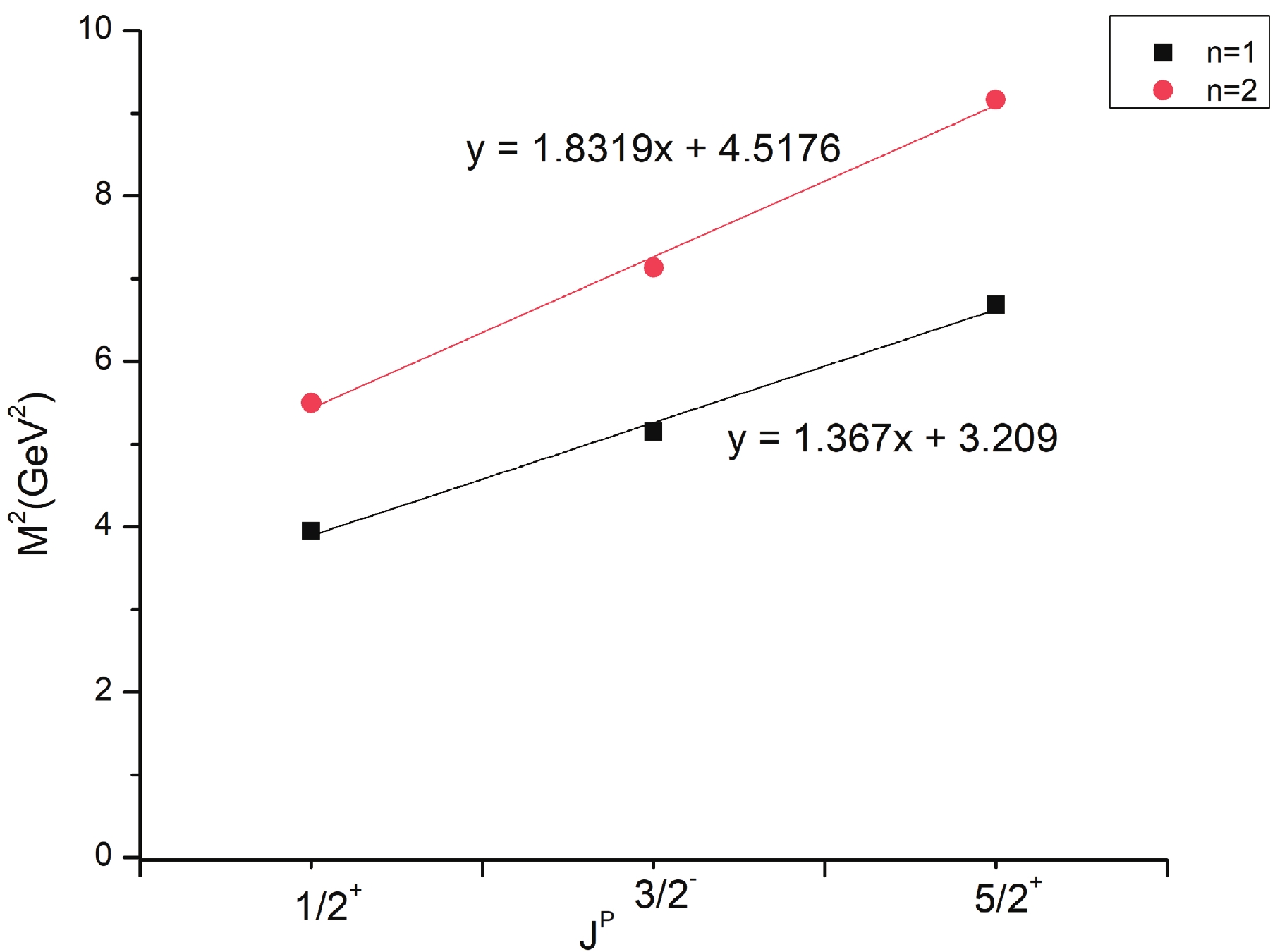
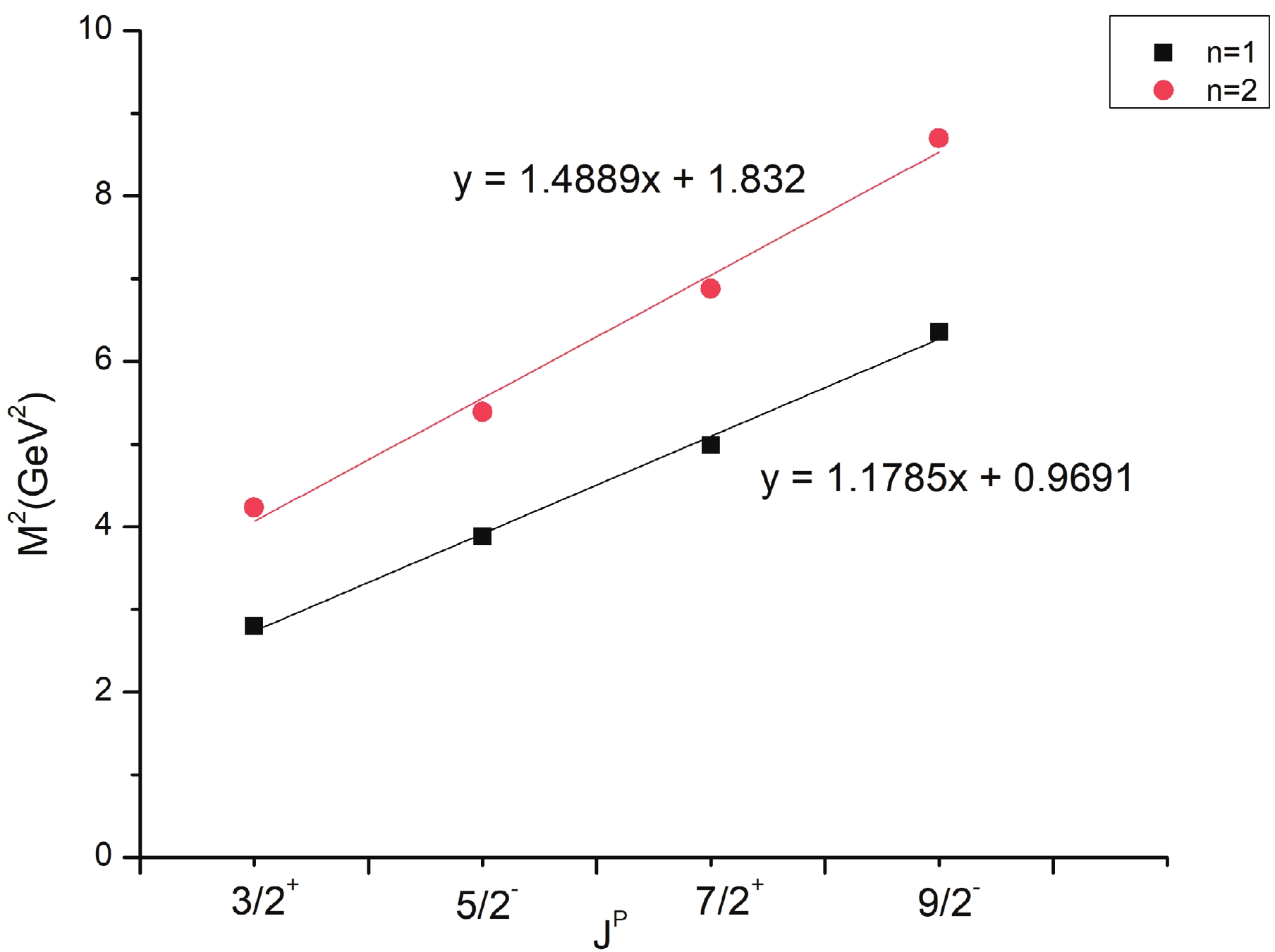
Regge trajectories have been of importance in spectroscopic studies. The total angular momentum J and principal quantum number n are plotted against the square of resonance mass
$ M^{2} $ to obtain the non-intersecting and linearly fitted lines. Figure 2 shows a linear behaviour with almost all the points following the trend for$ n-M^{2} $ . Figures 3 and 4 are plotted with few natural and unnatural parity states for available results. These plots point toward the fact that the spin-parity assignment of a given state in the present calculation could possibly be correct. The linear fitting parameters are mentioned in the respective plots.
Figure 2. (color online) Regge trajectory
$ n \rightarrow M^{2} $ for S, P, D and F state masses and linearly fitted.$ J = aM^{2} + a_{0},\tag{17a} $

$ n = b M^{2} + b_{0}. \tag{17b}$

Faustov et al. [47] have shown the total angular momentum J against the square of mass trajectories using the resonances obtained with the relativistic quark model. The slope and intercept values have been given as 0.712
$ \pm $ 0.002 and –0.504$ \pm $ 0.007, respectively. The similar plot with natural parity for present masses gives the value as 1.1785$ \pm $ 0.048 and 0.9691$ \pm $ 0.154 respectively. The values for slope and intercept with standard error for (n,$ M^{2} $ ) plot are listed in Table 9. However, due to the lack of more experimental data, we are unable to comment on the exact comparison of the values.Trajectory b $ b_{0} $ 

S 1.76838 ± 0.12837 0.84426 ± 0.35156 P 2.07004 ± 0.1839 1.52458 ± 0.50364 D 2.20397 ± 0.17905 2.67895 ± 0.3868 F 2.34116 4.01428 Table 9. Regge slopes and intercepts for (n,
$ M^{2} $ ). -
The electromagnetic properties of baryons are a challenging realm, especially for short-lived
$ J^{P}={3}/{2}^{+} $ decuplet baryons. Many theoretical approaches have attempted to investigate strange baryon magnetic moments. They served as an asset for the study of decay properties as well as intrinsic dynamics of quarks. The generalized form of magnetic moment is [45]$ \begin{equation} \mu_{B}= \sum\limits_{q} \langle \phi_{sf} \vert \mu_{qz}\vert \phi_{sf} \rangle, \end{equation} $

(18) where
$ \phi_{sf} $ is the spin-flavour wave function. The contribution from individual quark appears as$ \begin{equation} \mu_{qz}= \frac{e_{q}}{2m_{q}^{\rm eff}}\sigma_{qz}, \end{equation} $

(19) $ e_{q} $ being the quark charge,$ \sigma_{qz} $ being the spin orientation, and$ m_{q}^{\rm eff} $ being the effective mass, which may vary from the model based quark mass due to interactions. In case of Ω,$ \sigma_{qz}=s \uparrow s \uparrow s \uparrow $ , which leads to$ 3\mu_{s} $ . Table 10 summarizes the calculated magnetic moment alongwith other comparison results [56–62]. -
A hypercentral Constituent Quark Model with a linear confining term, spin-dependent terms, and a correction term has been helpful to obtain mass spectra for higher excited states up to nearly 3 GeV. Even though the scarcity of experimental data does not allow us to completely validate the findings, comparisons with theoretical models with varied assumptions are of keen interest. The low-lying states are in good accordance with some models but not exactly matching for higher
$ J^{P} $ values.It is noteworthy that the current findings could not comment on the debated state of Ω(2012) for molecular structure. However, the mass varies within 30 MeV with
$ J^{P}={3}/{2}^{-} $ , which may be identified as a negative parity state of 1P family. As the$ J^{P} $ value for any other state is not experimentally known, an exact comparison still depends on the availability of more findings in future. However, the probable spin-parity assignment according to the obtained value can be given. Thus, Ω(2250) could be the$ 1D_{{5}/{2}^{+}} $ state, Ω(2380) could be$ 2P_{{1}/{2}^{-}} $ , and Ω(2470) may be associated to 3S with$ {3}/{2}^{+} $ .The magnetic moment differs by 0.5
$ \mu_{n} $ from PDG and other results. The Regge trajectories show a linear nature, hinting that the spin-parity assignments may be correct. However, the validation of any of the results depends on the future experimental facilities to exclusively study the strange baryon properties, especially by$ \bar P $ ANDA at FAIR-GSI [10] and BESIII [11].
Spectroscopic study of strangeness = –3 Ω– baryon
- Received Date: 2022-04-21
- Available Online: 2022-10-15
Abstract:






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: