-
The absence of a rigorous formalism to predict elastic and diffractive processes, the so-called soft scattering states, makes soft interactions a significant challenge for quantum chromodynamics (QCD). As a complementary difficulty, the use of asymptotic theorems in high energy physics are also complicated as no indication exists when they must begin to be applied, i.e., where the asymptotia should begin. Furthermore, they also emerge in different contexts in the S-matrix, a pre-QCD formalism.
A few of the rigorous theorems are crucially important for high energy physics, particularly for the asymptotic energy domain. In this paper, we analyze two of the most outstanding among them, namely the Froissart–Martin bound and Pomeranchuk theorem, both concerning particle–particle and antiparticle–particle total cross sections (
$ \sigma_{\rm{tot}} $ ), which are forward quantities (zero transferred momentum).The Froissart–Martin bound [1–4], as well as its recent modification [5], is probably the most relevant asymptotic bound in forward high energy scattering as it imposes a form of physical limit on the increase in the total cross section as the collision energy increases. This theoretical result is the effect of the analyticity of elastic scattering amplitude and rigorous consequence of the most general properties of quantum field theory (QFT), namely, causality, unitarity, and the polynomial boundness [2, 3]. This asymptotic bound is pre-QCD and functions as a general parameterization for several models concerning the increase in
$ \sigma_{\rm{tot}} $ . In the QCD framework, no formal derivation of this bound exists from the first principles but from the functional integral approach [6]. However, the absence of a non-perturbative QCD corroboration does not contradict the robustness of such an inequality.Another interesting forward asymptotic result is given by the Pomeranchuk theorem [7], and it involves the difference between
$ \sigma_{\rm{tot}} $ for particle–particle and antiparticle–particle interactions. As is well known, this theorem is the consequence of the crossing property and an effect of the analyticity of the scattering amplitude. The Pomeranchuk theorem predicts that, for sufficiently high energies, the difference between these total cross sections should vanish. The general belief about this result imposes the necessity for a particle exchange as being responsible for the vanishing difference as the collision energy increases. This particle is called the leading Regge pole [8], or Pomeron for short, and it does not differentiate a particle from an antiparticle because it has the vacuum quantum numbers. The usual picture in which the Pomeron is considered a pair of gluons is attributed to Low and Nussinov [9, 10]. Despite the large amount of experimental data, no evidence exists for the Pomeron up to the present-day energies.In the phenomenological context, the above two theorems remain fundamental to imposing constraints on the increase in
$ \sigma_{\rm{tot}} $ as the collision energy increases. However, they are not isolated when we discuss forward quantities. The optical theorem is a remarkable result connecting the total cross section and imaginary part of the forward scattering amplitude [11]. Moreover, the derivative dispersion relations (DDR) can be used to connect the imaginary part of the forward scattering amplitude with the real part [12]. Thus, at least in the forward collision context, a entire scattering amplitude can be constructed based on a few theoretical results.Note that if we assume that the crossing property is valid despite its lack of theoretical and experimental evidence, we can obtain the forward scattering amplitude of particle–particle events from the forward scattering amplitude of antiparticle–particle scattering (and vice–versa).
In this paper, we use the crossing property, the DDR, and the optical theorem to obtain some theoretical results on the increase in
$ \sigma_{\rm{tot}} $ . In particular, based on these results, we present a simple fitting model for the proton–proton ($ pp $ ) and antiproton–proton ($ \bar{p}p $ ) total cross sections. Our results indicate that, asymptotically, a Pomeron intercept$ \alpha_{\mathbb{P}}=1 $ . Moreover, we estimate the energy range in which the asymptotic regime should begin.The remainder of this paper is organized as follows. In section II, some considerations on the total cross section are discussed. Section III provides a detailed description of experimental databases considered in the paper and corresponding procedures for approximation. Section IV presents the parameters obtained in the fitting procedure. Discussion and projections for some global scattering parameters are presented in Section V. Section VI provides conclusions and final remarks.
-
As is well known, the crossing property has never been proven (see, for instance, [13]), but generally, based on it, we can postulate that scattering amplitudes can be analytically continued between the different channels of the collision process. Subsequently, we assume that the scattering amplitude in terms of auxiliary even (+) and odd (–) amplitudes can be expressed as
$ 2f_\pm(s,t)=F_{pp}(s,t) \pm F_{\bar{p}p}(s,t), $

(1) where
$f_\pm(s,t)={\rm{Re}}f_\pm(s,t)+{\rm i}{\rm{Im}}f_\pm(s,t)$ are the crossing amplitudes, and$ F_{pp}(s,t) $ and$ F_{\bar{p}p}(s,t) $ are the complex-valued scattering amplitudes for$ pp $ and$ \bar{p}p $ processes; s is the square of the collision energy and$ -t $ is the square of transferred momentum, both in the center–of–mass system.Based on the above definition, the DDR up to the first-order approximation for the odd and even amplitudes (1) in the forward direction (
$ t=0 $ ) can be expressed as [12, 14]$ \frac{{\rm{Re}}f_+(s)}{s}=\frac{k}{s}+\Bigg[\frac{\pi}{2}\frac{\rm d}{{\rm d}\ln s}\Bigg]\frac{{\rm{Im}}f_+(s)}{s},\tag{2a} $

$ \frac{{\rm{Re}}f_-(s)}{s}=\Bigg[\frac{\pi}{2}\Bigg(1+\frac{{\rm d}}{{\rm d}\ln s}\Bigg)\Bigg]\frac{{\rm{Im}}f_-(s)}{s},\tag{2b} $

where
$ f_{\pm}(s,0) \equiv f_{\pm}(s) $ , and k is the subtraction constant. Without loss of generality, we adopt$ k=0 $ since the influence of such parameter is restricted to the low energy domain [8]. Notice the addition of high-order derivative terms in Equation (2) may make this representation more sensitive to describe high-energy experimental data. Considering the representation (1) and DDR (2), the following simple scheme summarizes the use of such odd and even amplitudes:$ {\rm{Im}}F_{xp}(s)\longrightarrow {\rm{Im}}f_{\pm}(s)\longrightarrow {\rm{Re}}f_{\pm}(s)\longrightarrow {\rm{Re}}F_{xp}(s), $

where
$ x=p, \bar{p} $ . This scheme reveals the importance of phenomenological information (the input) about the imaginary part of the forward scattering amplitude. Furthermore, through the optical theorem, the forward imaginary part can be used to define the behavior of the total cross section. As is well known, the optical theorem is in the core of high energy physics, and it was proved to be valid for all energies and scattering angles [11], being expressed as$ \sigma_{\rm{tot}}^{xp}(s)={\rm{Im}}F_{xp}(s) / s. $

(3) The optical theorem (3) and DDR (2), can be used to obtain the two following results concerning the behavior of
$ \sigma_{\rm{tot}} $ as s increases:$ \frac{{\rm d}\Delta_{\rm{tot}}(s)}{{\rm d}\ln s}= \frac{2}{s}\left\{\frac{1}{\pi}\bigl[{\rm{Re}}F_{\bar{p}p}(s)-{\rm{Re}}F_{pp}(s)\bigr]+{\rm{Im}}f_-(s)\right\}, \tag{4a}$

$ \frac{{\rm d}\Sigma_{\rm{tot}}(s)}{{\rm d}\ln s}=\frac{2}{\pi s}\bigl[{\rm{Re}}F_{\bar{p}p}(s)+{\rm{Re}}F_{pp}(s)\bigr], \tag{4b}$

where the difference and sum of the
$ pp $ and$ \bar{p}p $ total cross sections are expressed, respectively, as$ \Delta_{\rm{tot}}(s) \equiv \sigma_{\rm{tot}}^{\bar{p}p}(s) - \sigma_{\rm{tot}}^{pp}(s), \tag{5a}$

$ \Sigma_{\rm{tot}}(s) \equiv \sigma_{\rm{tot}}^{\bar{p}p}(s) + \sigma_{\rm{tot}}^{pp}(s). \tag{5b}$

One can note the relation (4a) implies the independence of
$\Delta_{\rm{tot}}(s)}$ and$\mathrm{Im}f_{-}(s)$ on each other for further calculations which in turn is based on the above definitions of the parameters$\Delta_{\rm{tot}}(s)}$ and$\Sigma_{\rm{tot}}(s)$ via only measuring quantities ($\sigma_{\rm{tot}}^{xp}$ ) without possible consequent transition to the imaginary parts of amplitudes.The experimentally measured
$ pp $ and$ \bar{p}p $ total cross sections can be expressed using the above results as follows:$ 2\sigma_{\rm{tot}}^{\bar{p}p}(s)=\Sigma_{\rm{tot}}(s) + \Delta_{\rm{tot}}(s), \tag{6a}$

$ 2\sigma_{\rm{tot}}^{pp}(s)=\Sigma_{\rm{tot}}(s) - \Delta_{\rm{tot}}(s). \tag{6b}$

Equations (4a) and (4b) can be analyzed by considering some expected particularities for
$ {\rm{Im}}F_{xp}(s) $ and$ {\rm{Re}}F_{xp}(s) $ . First, at very high energies, from the phenomenological perspective, we expect that$ {\rm{Re}}F_{xp}(s) \ll {\rm{Im}}F_{xp}(s), $

(7) which means an
$ almost $ complete absorptive scattering. However, the Froissart–Martin bound states that for$ pp $ and$ \bar{p}p $ forward collisions, the total cross section obeys the inequality$ \left.\sigma_{\rm{tot}}(s)\right|_{s \to \infty} \leq C\ln^2\varepsilon, $

(8) where C is a constant,
$ \varepsilon \equiv s/s_0 $ , and$ s_0 $ is a fixed scale that is generally unspecified. The scale can be selected to hadronic particles as the reasonable one$ s_0=1 $ GeV2 [15]. At this choice of$ s_{0} $ , the axiomatic quantum field theory (AQFT) resulted in$ C=\pi/m_{\pi}^2\approx 62.8 $ mb [3, 4], whereas the twice smaller value$ \pi/2m_{\pi}^2\approx 31.4 $ mb was recently derived [5] with$ m_{\pi} $ being the charged pion mass [16]. It is well known that bound (8) cannot be improved using only analyticity in the momentum transfer, unitarity, and boundedness by a polynomial in s, even if oscillations were permitted [17].The theoretical results (3) and (8) facilitate the construction of a wide scope to accommodate several functional forms of
$ {\rm{Re}}F_{xp}(s) $ , which satisfies the phenomenological condition (7). The simplest suggestion among them is to select a sufficiently small constant (which is always possible) to satisfy relation (7) at asymptotically high energies. Subsequently, from an energy$ \sqrt{s_a} $ , and considering the onset of the asymptotic region in the elastic scattering case, we can assume that (i)$ {\rm{Re}}F_{xp}(s)=0 $ , (ii)$ {\rm{Re}}F_{xp}(s)/s=c_x\neq 0 $ is a small real number depending on x, or (iii)$ {\rm{Re}}F_{xp}(s)/s=c\neq 0 $ , where c is a small real number.Considering the assumption (i) in (2b), we obtain a simple expression for the odd auxiliary function
$ {\rm{Im}}f_-(s) / s = a_{1}/\varepsilon, $

(9) where
$ a_1 $ is an integration constant. For simplicity, hereafter we adopt the lower limit of integration as$ s_0 $ . Using result (9) and assumption (i), from (4a) we obtain$ \Delta_{\rm{tot}}(s)= -2a_{1}/\varepsilon. $

(10) Notice that the sign of
$ a_1 $ determines which of either total cross section increases faster as s increases. For example, if$ a_1<0 $ , we obtain$ \sigma_{\rm{tot}}^{\bar{p}p}(s)\gtrsim\sigma_{\rm{tot}}^{pp}(s) $ for asymptotic energies.At the end of the 1950s, the general belief was that the total cross section decreases with increasing collision energy, as shown by experimental data. As is well known, this conviction was only modified with the Intersecting Storage Rings (ISR) measurement of the
$ pp $ total cross section conducted in 1973 showing the increase in$ \sigma_{\rm{tot}}^{pp}(s) $ with energy.Possibly, the first theoretical result using the asymptotic condition to obtain useful ground in high energy physics is the Pomeranchuk theorem [7]. The original version assumes that if the forward elastic scattering amplitude increases slower than s, then the difference between
$ \bar{p}p $ and$ pp $ total cross sections tends to zero as$ s\rightarrow \infty $ $ \Delta_{\rm{tot}}(s) \rightarrow 0, \; {\rm{if}}\; |F(s)|<s. $

(11) The Pomeranchuk proof uses dispersion relations and other additional intuitive assumptions, removed in other versions of the Pomeranchuk result, often expressed as [18–20]
$ R_{\rm{tot}}^{\bar{p}/p}(s) \equiv \sigma_{\rm{tot}}^{\bar{p}p}(s) / \sigma_{\rm{tot}}^{pp}(s) \rightarrow 1, \; {\rm{if}}\; s \rightarrow \infty, $

(12) which is not the same result expressed by (11).
Under the present assumption (i), when
$ s\rightarrow \infty $ result (10) vanishes asymptotically, corroborating the Pomeranchuk theorem. In contrast, if we use assumption (ii), it implies the following result:$ \bigl[{\rm{Re}}F_{\bar{p}p}(s)-{\rm{Re}}F_{pp}(s)\bigr] / s= c_{\bar{p}}-c_p. $

(13) In this case, from (2b), we obtain
$ {\rm{Im}}f_-(s) / s = (c_{\bar{p}}-c_p)/\pi+a_{2}/\varepsilon. $

(14) where
$ a_2\neq 0 $ is an integration constant. Using the above result, the difference between the total cross sections is expressed as$ \Delta_{\rm{tot}}(s)= \bigl[4(c_{\bar{p}}-c_p)/\pi \bigr]\ln \varepsilon - 2a_{2}/\varepsilon, $

(15) which does not corroborate the Pomeranchuk theorem unless
$ c_{\bar{p}}=c_p $ . The last assumption (iii) implies$ c_{\bar{p}}=c_p=c $ ; thus, in this case, the difference is null:$ {\rm{Re}}F_{\bar{p}p}(s)-{\rm{Re}}F_{pp}(s) = 0. $

(16) The above result implies an asymptotic behavior for the total cross section similar to (10). From this simple analysis, we can conclude that
$ {\rm{Re}}F_{xp}(s)=0 $ or$ {\rm{Re}}F_{xp}(s)/s=c $ at high energies since both results corroborate with the Pomeranchuk theorem.Equation (4b) can also provide physical information on the behavior of
$ \Sigma_{\rm{tot}}(s) $ . Considering assumption (i), from certain$ s_a $ values, we obtain$ \Sigma_{\rm{tot}}(s)= a_{0}, $

(17) where
$ a_{0} $ is a real constant. Not that this result does not violate any theorem in high energy physics, and it appears to indicate the existence of a taming mechanism (for example, the mini-jet [21]) to the increase in$ \sigma_{\rm{tot}}(s) $ as s increases.In contrast, for a non-null real part given by assumption (ii), we obtain
$ \Sigma_{\rm{tot}}(s)= \bigl[2(c_{\bar{p}}+c_p)/\pi \bigr]\ln \varepsilon, $

(18) which notably reveals that, in the asymptotic limit, the sum of the cross sections follows the logarithm of the collision energy, i.e., with a Pomeron intercept
$ \alpha_{\mathbb{P}}=1 $ . Considering assumption (iii), we can derive a similar result:$ \Sigma_{\rm{tot}}(s)= (4c/\pi)\ln \varepsilon. $

(19) We can observe that results (18) and (19) do not violate the Froissart–Martin theorem (8) even in its modified version [5].
For clarity, all the above results are summarized in Table 1. From this table, we observe that for (i), although
$ \Delta_{\rm{tot}}(s) $ obeys the Pomeranchuk theorem, the sum$ \Sigma_{\rm{tot}}(s) $ does not appear to correspond to the behavior exhibited by the experimental data, at least at present-day energies. However, for the results expressed by (ii), we observe that$ \Delta_{\rm{tot}}(s) $ does not obey the Pomeranchuk theorem, unless$ c_{\bar{p}}=c_p $ . The results given by (iii) appear to be reasonable in terms of the experimental data, representing a Pomeron intercept$ \alpha_{\mathbb{P}}=1 $ [8].Assumption $ {\rm{Re}}F_{xp}(s)/s $ 

$ {\rm{Im}}f_{-}(s)/s $ 

$ \Delta_{\rm{tot}}(s) $ 

$ \Sigma_{\rm{tot}}(s) $ 

(i) 0 $ a_1/\varepsilon $ 

$ -2a_1/\varepsilon $ 

$ a_{0} $ 

(ii) $ c_x $ 

$ (c_{\bar{p}}-c_p)/\pi+a_2/\varepsilon $ 

$ [4(c_{\bar{p}}-c_p)/\pi]\ln \varepsilon-2a_2/\varepsilon $ 

$ [2(c_{\bar{p}}+c_p)/\pi]\ln \varepsilon $ 

(iii) c $ a_1/\varepsilon $ 

$ -2a_1/\varepsilon $ 

$ (4c/\pi)\ln \varepsilon $ 

Table 1. Summary of the theoretical results obtained assuming the asymptotic condition
$ s\rightarrow \infty $ .Therefore, we may conclude that the
$ pp $ and$ \bar{p}p $ real parts of the forward elastic amplitude are null above a certian energy$ \sqrt{s_a} $ or that they are equal. Both conclusions preserve the Pomeranchuk theorem and Froissart–Martin bound. However, they result in different asymptotic behaviors for$ \Sigma_{\rm{tot}}(s) $ , which represents a puzzle that apparently cannot be solved at present-day energies. It is important to emphasize that considering the results shown in Table 1 and in (6), we can obtain analytic expressions for experimentally measured quantities$ \sigma_{\rm{tot}}^{\bar{p}p}(s) $ and$ \sigma_{\rm{tot}}^{pp}(s) $ at asymptotically high energies.Now, we can apply the above procedure to study the behavior of the ρ-parameter as the collision energy increases. This parameter is defined as
$ \rho^{xp}(s)={\rm{Re}}F_{xp}(s) /\, {\rm{Im}}F_{xp}(s), $

(20) which measures the increase in the absorptive part of the forward scattering amplitude (relative to the real part) as s increases.
If condition (i) is used, for certain
$ s_{a} $ values, the only possible result is$ \rho^{xp}(s_a < s)=0 $ , which does not contradict any theorem but has no predictive capability for non-asymptotic energies. In contrast, adopting, assumption (iii) for instance, we obtain$ \rho^{xp}(s)=c/\bigl[\pm a_1/\varepsilon+(2c/\pi)\ln \varepsilon \bigr], $

(21) where the sign
$ +/- $ is for$ pp/\bar{p}p $ , respectively. For a sufficient high energy, the term$ a_1/\varepsilon $ can be disregarded, resulting in the prediction that$ \rho^{pp}(s)=\rho^{\bar{p}p}(s) $ and the ρ-parameter approaches its asymptotic value ($ \rho_{a} $ )$ \left.\rho^{xp}(s)\right|_{s \to \infty} \to \rho^{xp}_{a}(s) \equiv (\pi /2)\ln^{-1} \varepsilon. $

(22) It is important to emphasize that (22) is independent of any external parameter, as the collision energy is the only variable of interest. It appears to be reasonable since we expect the same parameters that drive
$ {\rm{Im}}F_{xp}(s)/s $ should also control$ {\rm{Re}}F_{xp}(s)/s $ , at least for the high energy regime. Furthermore, the asymptotic result (22) agrees well with the "standard" picture of high energy elastic diffraction in which amplitude$ f_{-}(s) $ becomes negligible compared with the crossing-even amplitude$ f_{+}(s) $ as s increases. The property of analyticity implies$ \rho\propto \ln^{-1}\varepsilon $ [22].The results obtained for measured forward scattering parameters for
$ \bar{p}p $ and$ pp $ within assumptions under consideration are summarized in Table 2. It is interesting to note that if we assume$ \rho(s) $ as given by assumptions (i), (ii), or (iii), then the use of DDR tends to become similar to those obtained in [17]. In particular, assumptions (ii) and (iii) for$ \rho(s) $ result in$ \sigma_{\rm{tot}} $ as given by the Froissart–Martin bound, which means that it cannot be improved using the methods employed here.Assumption $ \sigma_{\rm{tot}}^{\bar{p}p}(s) $ 

$ \sigma_{\rm{tot}}^{pp}(s) $ 

$ \rho^{\bar{p}p}(s) $ 

$ \rho^{pp}(s) $ 

(i) $ a_{0}/2-a_{1}/\varepsilon $ 

$ a_{0}/2+a_{1}/\varepsilon $ 

0 0 (ii) $ \dfrac{3c_{\bar{p}}-c_{p}}{\pi}\ln \varepsilon-\dfrac{a_2}{\varepsilon} $ 

$ \dfrac{3c_{p}-c_{\bar{p}}}{\pi}\ln \varepsilon+\dfrac{a_2}{\varepsilon} $ 

$ \dfrac{c_{\bar{p}}}{[(3c_{\bar{p}}-c_p)/\pi]\ln \varepsilon-a_2/\varepsilon} $ 

$ \dfrac{c_{p}}{[(3c_{p}-c_{\bar{p}})/\pi]\ln \varepsilon+a_2/\varepsilon} $ 

(iii) $ \dfrac{2c}{\pi}\ln \varepsilon - \dfrac{a_1}{\varepsilon} $ 

$ \dfrac{2c}{\pi}\ln \varepsilon + \dfrac{a_1}{\varepsilon} $ 

$ \dfrac{c}{(2c/\pi)\ln \varepsilon - a_1/\varepsilon} $ 

$ \dfrac{c}{(2c/\pi)\ln \varepsilon + a_1/\varepsilon} $ 

Table 2. Summary of the results for measured forward parameters assuming the asymptotic condition
$ s\rightarrow \infty $ .In the framework of the present approach based on the crossing property, DDR (2), and optical theorem (3), both
$ pp $ and$ \bar{p}p $ elastic collisions are characterized by similar energy dependencies for the total cross section and ρ-parameter at asymptotically high energies, namely,$ \forall\,x=p, \bar{p}: \sigma_{\rm{tot}}^{xp}(s) \propto \ln \varepsilon $ ,$ \rho^{xp} \propto \ln^{-1}\varepsilon $ within more realistic assumptions (ii) and (iii), which are considered in the paragraph below.It seems the dependence
$ \sigma_{\rm{tot}}^{xp}(s) $ for$ x=p, \bar{p} $ from Table 2 in the collision energy domain under consideration appears to be functionally close to the increase in$ \sigma_{\rm{tot}}^{pp}(s) $ deduced within the Regge–Eikonal approach [23]. However, note that$ \forall\,x=p, \bar{p}: \sigma_{\rm{tot}}^{xp}(s) $ exhibits a weaker increase with s than that within the AQFT and semiclassical color glass condensate (CGC) approach, which implies that$ \sigma_{\rm{tot}}(s) $ is functionally close to the Froissart–Martin limit (8) in the region of at least$ {\cal{O}} $ (100 TeV) energies [24]. The asymptotic behavior$ \forall\,x=p, \bar{p}: \left.\rho^{xp}(s)\right|_{s \to \infty} \propto \ln^{-1}\varepsilon $ is qualitatively similar in functional sense to the corresponding AQFT$ \rho(s) $ dependencies for$ pp $ and$ \bar{p}p $ considering the values of fit parameters [25, 26]. -
The set of the global scattering parameters
${\cal{G}}_{1} \equiv \{{\cal{G}}_{1}^{i}\}_{i=1}^{4}= \{\sigma_{{{\rm{tot}}}}^{pp}, \sigma_{{{\rm{tot}}}}^{\bar{p}p},\rho^{pp},\rho^{\bar{p}p}\}$ contains only observables that are independent of each other as well as directly measured in experiments. In contrast, the set$ {\cal{G}}_{2} \equiv \{{\cal{G}}_{2}^{i}\}_{i=1}^{3}= \{\Delta_{{{\rm{tot}}}}, \Sigma_{{{\rm{tot}}}},R_{{{\rm{tot}}}}^{\bar{p}/p}\} $ is formed strictly by the parameters that depend on experimentally measurable quantities; moreover, terms of$ {\cal{G}}_{2} $ are independent of each other and the terms of$ {\cal{G}}_{1} $ . In this paper, the sets of scattering parameters and their combinations$ {\cal{G}}_{j} $ ,$ j=1,2 $ are studied. Additionally, the joined ensemble$ {\cal{G}}={\cal{G}}_{1} \bigcup\,{\cal{G}}_{2} $ is considered for completeness of information①.The experimental database for
$ {\cal{G}}_{1} $ containing the ensembles for$ \sigma_{{\rm{tot}}}^{xp} $ ,$ \rho^{\,xp} $ from [16] is denoted as DB20, whereas the database considering the above samples and results from STAR for$ \sigma_{{\rm{tot}}}^{pp} $ at$ \sqrt{s}=0.20 $ TeV [27] and from TOTEM for$ \rho^{pp} $ at$ \sqrt{s}=13 $ TeV [28] is denoted as DB20+. The last paper leads to some uncertainty, which results in two perspectives for database creation. Two values$ \left.\rho_{1}^{pp}\right|_{\sqrt{s}=13\,{\rm{TeV}}}=0.09 \pm 0.01 $ and$ \left.\rho_{2}^{pp}\right|_{\sqrt{s}=13\,{\rm{TeV}}}= 0.10 \pm 0.01 $ were obtained in [28] for one quantity and collision energy without any preference for one value of$ \rho^{pp} $ over the other. However, the one result should be included in the corresponding data sample because$ \rho^{pp} $ was measured under the same experimental conditions (detector, kinematic parameters, etc.). It should be stressed that such request is fully within the rules were applied for creation of experimental databases in various analyzes, for instance, for elastic slope [29] as well as in jet physics [30] and femtoscopy [31]. The weighted average [16] can be used as an estimation for$ \rho^{pp} $ at$ \sqrt{s}=13 $ TeV:$ \left.\langle \rho^{pp}\rangle\right|_{\sqrt{s}=13\,{\rm{TeV}}}=0.095 \pm 0.007 $ . Therefore, two versions of the DB20+ are considered here, namely, the database with one value$ \left.\langle \rho^{pp}\rangle\right|_{\sqrt{s}=13\,{\rm{TeV}}} $ is denoted as DB201+, whereas the database containing both results ($ \rho_{1}^{pp} $ ,$ \rho_{2}^{pp} $ ) at$ \sqrt{s}=13 $ TeV is denoted as DB202+. Table 3 summarizes the main features of the databases of experimental results used in this paper for the set of the scattering parameters$ {\cal{G}}_{1} $ .Database Parameter from the set $ {\cal{G}}_{1} $ 

$ \sigma_{{\rm{tot}}}^{pp} $ 

$ \sigma_{{\rm{tot}}}^{\bar{p}p} $ 

$ \rho^{pp} $ 

$ \rho^{\bar{p}p} $ 

DB20 [16] [16] [16] [16] DB201+ [16, 27] –//– [16] and $ \left.\langle \rho^{pp}\rangle\right|_{\sqrt{s}=13\,{\rm{TeV}}} $ 

–//– DB202+ –//– –//– [16, 28] –//– Table 3. Databases for the set of global scattering parameters
$ {\cal{G}}_{1} $ .Within the main objectives of this paper, the values for each term
$ \{{\cal{G}}_{2}^{i}\}_{i=1}^{3} $ are calculated using relations (5) and (12) and measured values of$ \sigma_{{\rm{tot}}}^{pp} $ and$ \sigma_{{\rm{tot}}}^{\bar{p}p} $ for completeness of analysis. In the following, these ensembles of calculated values are called data samples for$ {\cal{G}}_{2} $ similar to the set$ {\cal{G}}_{1} $ only in the sense that the value of each term$ \{{\cal{G}}_{2}^{i}\}_{i=1}^{3} $ at certain s values is only defined by experimental results for$ xp $ cross sections. The data sample for each term of$ {\cal{G}}_{2} $ is based on the corresponding subensembles for$ \sigma_{{\rm{tot}}}^{pp} $ and$ \sigma_{{\rm{tot}}}^{\bar{p}p} $ at identical or, at least, close energies. The energy values for the measured$ \sigma_{{\rm{tot}}}^{pp} $ and$ \sigma_{{\rm{tot}}}^{\bar{p}p} $ are considered close if$ P_{\Delta} \equiv |P_{1}-P_{2}| \leq 0.02 $ GeV or$ P_{1} $ and$ P_{2} $ coincide within errors, where$ P_{i} $ is the laboratory momentum for the term$ {\cal{G}}_{1}^{i} $ ,$ i=1, 2 $ . On can note that the first condition for the closeness of$ P_{1} $ and$ P_{2} $ was previously used in [32]. The relative fraction of the pairs ($ \sigma_{{\rm{tot}}}^{pp} $ ,$ \sigma_{{\rm{tot}}}^{\bar{p}p} $ ) with finite$ P_{\Delta} $ is 64.8% and almost all of such measurements are at$ \sqrt{s} < 3.63 $ GeV. In these cases the average momentum$ \langle P\rangle $ is assigned for the initial energy for corresponding estimation of the each term$ {\cal{G}}_{2}^{i} $ ,$ i=1-3 $ and$ \langle P\rangle $ is calculated as simple average$ \langle P\rangle = 0.5(P_{1}+P_{2}) $ with$ \Delta\langle P\rangle = 0.5|P_{1}-P_{2}| $ if$ \exists\, i: \Delta P_{i}=0 $ or$ \langle P\rangle $ and its uncertainty is estimated with the help of the weighted average technique [16] on the contrary case. As shown in Table 3, the subensembles for$ \sigma_{{\rm{tot}}}^{pp} $ and$ \sigma_{{\rm{tot}}}^{\bar{p}p} $ from [16] are only used to calculate each term of$ {\cal{G}}_{2} $ and, consequently, one database for$ {\cal{G}}_{2} $ corresponds to DB20 for$ {\cal{G}}_{1} $ . As expected from definitions (5) and (12), the energy range covered by experiments is identical for all terms of$ {\cal{G}}_{2} $ . A detailed analysis shows that this range is limited to$ \sqrt{s} < 0.5 $ TeV with a wide gap between the highest ISR energy$ \sqrt{s} \approx 0.06 $ TeV and the high energy boundary$ \sqrt{s}=(0.47 \pm 0.08) $ TeV for the energy domain under discussion.No prediction exists for the asymptotic energy
$ \sqrt{s_{a}} $ from the first principles of QCD (for instance), and the search for the onset of the asymptotic energy domain remains a non-trivial task. Thus, no consensus exists for the beginning of the so-called asymptotia. For example, the asymptotic regime may be defined by using the first change in the sign of the curvature parameter C in the impact parameter representation [33]. For the Chou–Yang model [34], for instance, the asymptotia begins at$ \sqrt{s_a}\approx 2 $ TeV, where C changes its sign. However, recent studies have shown model-dependent estimations for$ s_{a} $ , and these values lie in a very wide energy range. From the experimental perspective, the most optimistic estimation for$ \sqrt{s_{a}} $ appears to be$ {\cal{O}} $ (100 TeV) in order of magnitude, and it was qualitatively obtained from a study on the functional behavior of$ \sigma_{\rm{tot}}^{pp}(s) $ within the AQFT and CGC approach at ultra-high energies [24]. This result agrees with the conclusion from the Regge–Eikonal model for$ \sigma_{\rm{tot}}^{pp}(s) $ and forward slope for$ pp $ interaction [23].Detailed analyes of the ratio of the elastic–to–total cross sections for
$ pp $ and$ \bar{p}p $ collisions [32] as well as the approach of the partonic disks [35] permit only the indication$ \sqrt{s_{a}} \sim 5-10 $ PeV. Consideration of some other signatures of the "truly asymptotic regime" within the Regge–Eikonal model [23] results in a much more conservative estimation for$ s_{a} $ . In particular, the onset of the asymptotic regime can be expected in grand unified theory (GUT) energy domain in order of magnitude, i.e.$ \sqrt{s_{a}} \gtrsim 10^{12}-10^{13} $ GeV.Thus, there are only 1 – 2 measurements for
$ \sigma_{{\rm{tot}}}^{pp} $ in ultra-high energy cosmic rays even for lowest estimation for$ \sqrt{s_{a}} $ . Therefore, a phenomenological approximation will be a priori at collision energies smaller than the possible onset of the asymptotic region. Consequently, the request for the validity of the Pomeranchuk theorem appears to be redundant for the energy range under fit, and we can consider hypotheses (ii) and (iii) for the functional forms of the terms of$ {\cal{G}} $ within the fitting procedure. As previously investigated [25, 26], the parameterizations shown in Tables 1 and 2 for hypotheses (ii) and (iii) will be applied to approximate the energy dependence of different terms of$ {\cal{G}} $ only for$ s \geq s_{\min} $ , where$ s_{\min} $ is an empirical low boundary. During the analysis procedure, the$ s_{\min} $ value will be decreased as much as possible to describe the wider energy domain with a statistically reasonable fit quality. -
This section presents a detailed description of the results of simultaneous fits for the sets
$ {\cal{G}}_{i} $ ,$ i=1, 2 $ and the corresponding discussion. -
The energy dependence of the terms of
$ {\cal{G}}_{1} $ is approximated at$ \sqrt{s_{\min}}=0.03, 0.04, 0.05, 0.06, 0.1, 0.5, 1, 5 $ , and 10 TeV using the corresponding formulas in Table 2 within hypotheses (ii) and (iii). At the lowest$ s_{\min} $ considered here, the fit quality$ \chi^{2}/{\rm{n.d.f.}} \approx 26 $ with a rapid decrease in the growth of the low boundary of fitted range for hypotheses (ii) and (iii). For both hypotheses considered, the statistically reasonable fit qualities are only observed for$ \sqrt{s_{\min}} \geq 0.06 $ TeV. This approach facilitates a reasonable description of$ {\cal{G}}_{1} $ within narrower energy ranges than that of AQFT equations [25, 26] as$ s_{\min} $ shifts towards larger values. In general, this result is expected because the asymptotic behavior of the total cross sections and ρ–parameter is studied here for$ pp $ and$ \bar{p}p $ collisions. Thus, the discussion below is focused on the results for$ \sqrt{s_{\min}} \geq 0.06 $ TeV.As shown in Table 3, the databases considered here differ from each other very slightly; more precisely, the maximum difference between DB20 and DB202+ occurs on three points. Furthermore, all the experimental results that are added with respect to the DB20 agree well with the general trends in the energy dependence of the corresponding observable. Therefore, according to the hypothesis confirmed in [26], we can expect a negligible effect of the additional points on the values of fit parameters for various databases at fixed
$ s_{{\min}} $ values. A detailed analysis fully confirms the correctness of this suggestion for the results of simultaneous fits for$ {\cal{G}}_{1} $ with databases DB201+ and DB202+ differing from each other only on one point (Table 3). The values of all fit parameters agree within errors for DB201+ and DB202+ for each$ s_{{\min}} $ and hypotheses (ii) and (iii) considered here. Moreover, the identity is observed between the numerical values of the fit parameters and their uncertainties for DB201+ and the values of the corresponding quantities for DB202+ for the noticeable part of low boundaries$ s_{{\min}} $ , particularly within hypothesis (iii). The approximation quality$ \chi^{2}/{\rm{n.d.f.}} $ is very close for the simultaneous fits of DB201+ and DB202+ with a subtle improvement for the last case at any fixed$ s_{{\min}} $ . All these enable us to consider the fit results obtained for DB20 and DB201+ in the following.The numerical results of the simultaneous fits of
$ {\cal{G}}_{1} $ in various energy ranges are shown in Tables 4 for hypotheses (ii) and (iii). At a fixed$ s_{{\min}} $ , the first and second lines show results for DB20 and DB201+, respectively. Experimental data from DB201+ for the terms$ {\cal{G}}_{1}^{i} $ ,$ i=1-4 $ and fit curves are shown in Fig. 1 for$ \sqrt{s_{\min}}= $ 0.06 TeV (solid lines) and for$ \sqrt{s_{\min}}=1 $ TeV (dashed lines). The thick curves are obtained within hypothesis (ii), whereas the two remaining lines correspond to hypothesis (iii).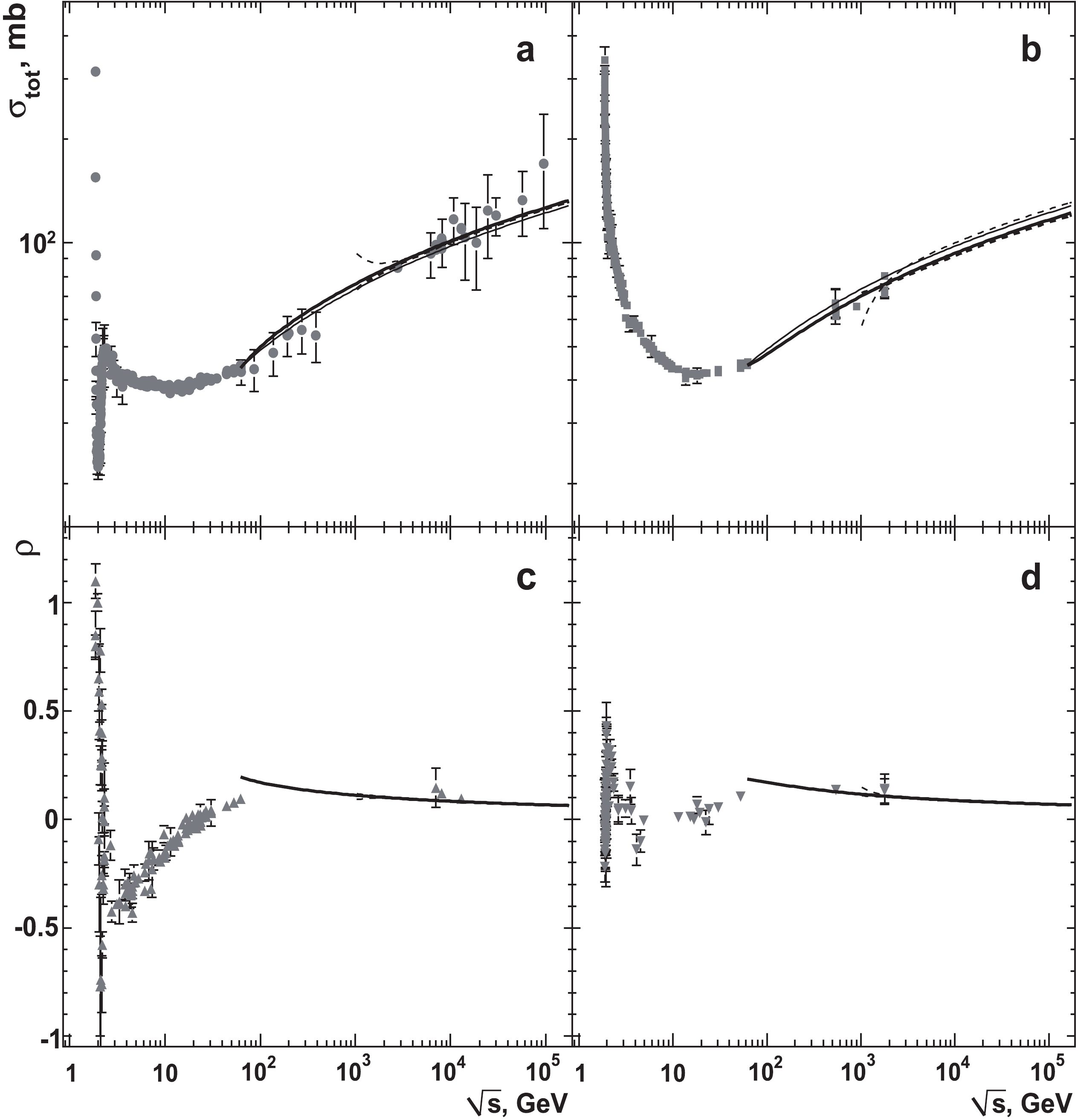
Figure 1. Energy dependence of the measurements for the terms of
$ {\cal{G}}_{1} $ and results of simultaneous fits of all these terms. Experimental results are from DB201+. The solid lines correspond to the fit at$ \sqrt{s_{\min}}=0.06 $ TeV, the dashed lines are at$ \sqrt{s_{\min}}=1 $ TeV. The thick lines show the fit curves for hypothesis (ii) and the other lines correspond to hypothesis (iii).$ \sqrt{s_{{\min}}} $ , TeV

hypothesis (ii) hypothesis (iii) $ c_{p} $ , mbarn

$ c_{\bar{p}} $ , mbarn

$ a_{2} $ , mbarn

$ \chi^{2}/{\rm{n.d.f.}} $ 

c, mbarn $ a_{1} $ , mbarn

$ \chi^{2}/{\rm{n.d.f.}} $ 

0.06 $ 8.484 \pm 0.029 $ 

$ 8.12 \pm 0.04 $ 

$ (-9.0 \pm 0.9) \times 10^{3} $ 

$ 97.7/45 $ 

$ 8.342 \pm 0.024 $ 

$ (-1.9 \pm 0.6) \times 10^{3} $ 

$ 170/46 $ 

$ 8.468 \pm 0.029 $ 

$ 8.12 \pm 0.04 $ 

$ (-8.5 \pm 0.9) \times 10^{3} $ 

$ 108/47 $ 

$ 8.339 \pm 0.024 $ 

$ (-1.8 \pm 0.6) \times 10^{3} $ 

$ 174/48 $ 

0.1 $ 8.35 \pm 0.04 $ 

$ 7.91 \pm 0.06 $ 

$ (-1.0 \pm 0.4) \times 10^{5} $ 

$ 39.6/34 $ 

$ 8.31 \pm 0.04 $ 

$ (2.8 \pm 1.5) \times 10^{5} $ 

$ 124/35 $ 

$ 8.35 \pm 0.04 $ 

$ 7.91 \pm 0.06 $ 

$ (-1.2 \pm 0.5) \times 10^{5} $ 

$ 43.7/36 $ 

$ 8.28 \pm 0.04 $ 

$ (2.2 \pm 0.9) \times 10^{4} $ 

$ 134/37 $ 

0.5 $ 8.38 \pm 0.05 $ 

$ 8.00 \pm 0.11 $ 

$ (3.1 \pm 1.4) \times 10^{5} $ 

$ 37.1/30 $ 

$ 8.48 \pm 0.05 $ 

$ (2.04 \pm 0.25) \times 10^{6} $ 

$ 62.3/31 $ 

$ 8.39 \pm 0.05 $ 

$ 8.01 \pm 0.11 $ 

$ (3.5 \pm 1.2) \times 10^{5} $ 

$ 41.0/31 $ 

$ 8.48 \pm 0.05 $ 

$ (2.0 \pm 0.4) \times 10^{6} $ 

$ 65.2/32 $ 

1 $ 8.28 \pm 0.17 $ 

$ 7.6 \pm 0.6 $ 

$ (-1.9 \pm 0.5) \times 10^{7} $ 

$ 33.0/23 $ 

$ 8.54 \pm 0.05 $ 

$ (1.8 \pm 0.4) \times 10^{7} $ 

$ 34.9/24 $ 

$ 8.4 \pm 0.3 $ 

$ 8.0 \pm 1.1 $ 

$ (-2.4 \pm 0.8) \times 10^{6} $ 

$ 37.3/24 $ 

$ 8.54 \pm 0.05 $ 

$ (1.9 \pm 0.4) \times 10^{7} $ 

$ 37.9/25 $ 

5 $ 9.3 \pm 0.4 $ 

$ 9.9 \pm 2.6 $ 

$ (-3.1 \pm 0.6) \times 10^{8} $ 

$ 20.3/17 $ 

$ 9.03 \pm 0.21 $ 

$ (-3.1 \pm 0.8) \times 10^{8} $ 

$ 20.5/18 $ 

$ 9.35 \pm 0.15 $ 

$ 10.0 \pm 1.9 $ 

$ (-3.1 \pm 0.6) \times 10^{8} $ 

$ 21.4/18 $ 

$ 9.06 \pm 0.22 $ 

$ (-3.3 \pm 0.9) \times 10^{8} $ 

$ 22.8/19 $ 

10 $ 9.4 \pm 1.7 $ 

$ 10.1 \pm 2.7 $ 

$ (6.5 \pm 0.5) \times 10^{7} $ 

$ 1.08/6 $ 

$ 9.1 \pm 1.0 $ 

$ (6.5 \pm 0.7) \times 10^{7} $ 

$ 1.08/7 $ 

$ 9.8 \pm 0.5 $ 

$ 10.0 \pm 2.6 $ 

$ (-1.3 \pm 0.9) \times 10^{9} $ 

$ 2.16/7 $ 

$ 9.9 \pm 0.6 $ 

$ (-1.7 \pm 0.8) \times 10^{9} $ 

$ 2.26/8 $ 

Table 4. Parameters for simultaneous fitting of
$ {\cal{G}}_{1}(s) $ within various hypotheses at different stages of DB: DB20 (first line) and DB201+ (second line).The use of the multi-TeV values of
$ \sqrt{s_{\min}} $ and the available experimental data within a certain database stipulates that the approximation procedure consequently transits from the simultaneous fit of the full set$ {\cal{G}}_{1} $ to the simultaneous fit of the$ pp $ observables$ \{\sigma_{{{\rm{tot}}}}^{pp},\rho^{pp}\} $ only at$ \sqrt{s_{\min}}=5 $ TeV and even to the individual fit of the$ \sigma_{{{\rm{tot}}}}^{pp} $ at the highest$ \sqrt{s_{\min}}=10 $ TeV for DB20. In the last case, hypothesis (ii) reduces to hypothesis (iii) because the available experimental data permit the fix only with the combination$ (3c_{p}-c_{\bar{p}}) $ . No fitting function for which there would be at least one experimental point at$ \sqrt{s} \geq 10 $ TeV, and this function would contain parameter$ c_{p} $ or$ c_{\bar{p}} $ in the separate term. Moreover, we expect the smooth joining for the energy-dependent$ \bar{p}p $ global observables,$ \sigma_{{\rm{tot}}}^{\bar{p}p}(s) $ and$ \rho^{\bar{p}p}(s) $ , in the experimentally measured range and in the domain$ \sqrt{s} \geq 5\,(10) $ TeV described by the curve calculated from the fit results at$ \sqrt{s_{\min}}=5\,(10) $ TeV. This expectation is established by the absence of the any signature for new physics beyond the Standard Model (SM) that could result in the sudden change in the energy dependence of any global scattering parameter in$ pp/\bar{p}p $ collisions.Only few points for
$ \rho^{xp}(s) $ exist in the TeV-energy domain; moreover, the experimental values$ \rho^{xp} \sim 10^{-2} $ at$ \sqrt{s} > 1 $ TeV; the consideration mentioned in Sec. II implies that the smooth behavior of the curves for$ \rho^{xp}(s) $ is dominated by the values of$ c_{x} $ / c parameters within hypotheses (ii) and (iii). Furthermore, changes in these curves are slow ($ \propto \ln^{-1}\varepsilon $ ) at sufficiently high s. All of these evidences result in the relatively robust behavior of the curve for$ \rho^{\bar{p}p}(s) $ at$ \sqrt{s_{\min}}=5 $ , 10 TeV and a reasonable agreement between experimental value of$ \left.\rho^{\bar{p}p}(s)\right|_{\sqrt{s} \approx 2\,\rm{TeV}} $ and analytic approximation in multi-TeV energy domain without any additional request for the smooth joining. A detailed analysis indicates an influence of the request of the smooth joining for$ \sigma_{{\rm{tot}}}^{\bar{p}p}(s) $ on the fit results within hypothesis (ii) for DB201+ at$ \sqrt{s_{\min}}=10 $ TeV. For this case, the numerical values of the fit parameters obtained considering the necessity of smooth joining for$ \sigma_{{\rm{tot}}}^{\bar{p}p}(s) $ are shown in Table 4, while the results without additional request are as follows:$ c_{p}= (10.5 \pm 0.8) $ mbarn,$ c_{\bar{p}}=(13.2 \pm 2.8) $ mbarn,$ a_{2}=(6.0 \pm 0.6) \times 10^{7} $ mbarn, and$ \chi^{2}/{\rm{n.d.f.}}= 1.08/7 $ .As observed, the request of the smooth joining for
$ \sigma_{{\rm{tot}}}^{\bar{p}p}(s) $ influences the value of parameter$ a_{2} $ and the fit quality. If one releases the need under consideration, then we provide the agreement between values of$ a_{2} $ for various databases within hypothesis (ii) at almost identical$ \chi^{2}/{\rm{n.d.f.}} $ Such an exception results in the expected discrepancy between values of$ a_{2} $ and$ \chi^{2}/{\rm{n.d.f.}} $ obtained using simultaneous fits within various hypotheses for database DB201+. Note that the change in the fit quality for the last two cases is noticeable but not at a first glance. It is important to emphasize that$ \chi^{2}/{\rm{n.d.f.}} $ remains statistically acceptable for simultaneous fit of DB201+ within hypothesis (ii) at the highest$ s_{\min} $ , independent of additional requests of the smooth joining for$ \sigma_{{\rm{tot}}}^{\bar{p}p}(s) $ .As observed in Table 4, hypothesis (ii) enables the simultaneous approximation of all terms of
$ {\cal{G}}_{1} $ with reasonable quality at$ \sqrt{s_{\min}} \geq 0.06 $ TeV and with statistically acceptable quality at$ \sqrt{s_{\min}} \geq 0.1 $ TeV for any databases considered. The relation$ c_{p} > c_{\bar{p}} $ is valid for the simultaneous fit versions within hypothesis (ii) up to$ \sqrt{s_{\min}}=0.5 $ TeV. In contrast, the values of$ c_{p} $ and$ c_{\bar{p}} $ coincide within errors for approximations at$ \sqrt{s_{\min}} \geq 1 $ TeV. These statements are valid for both databases DB20 and DB201+. It is important to note that for hypothesis (iii), in contrast to (ii), a reasonable value of$ \chi^{2}/{\rm{n.d.f.}} $ can be obtained only at$ \sqrt{s_{\min}} \geq 0.5 $ TeV and a statistically acceptable$ \chi^{2}/{\rm{n.d.f.}} $ only at$ \sqrt{s_{\min}} \geq 1 $ TeV. This characteristic is in full agreement with Table 4: as consequence of the considered relations between$ c_{p} $ and$ c_{\bar{p}} $ at various$ s_{\min} $ , we can expect that reducing the parameters$ c_{p} $ and$ c_{\bar{p}} $ to c would be possible to start, at least, at similar collision energies④. Thus, hypothesis (iii) reasonably describes the experimental data for$ {\cal{G}}_{1} $ at significantly higher s values than hypothesis (ii) owing to the "extremely" asymptotic nature of the corresponding relations in Table 2. Hypotheses (ii) and (iii) already qualitatively describe the energy-dependent behavior of$ \sigma_{{\rm{tot}}}^{xp} $ at$ \sqrt{s_{\min}}=0.06 $ TeV (Fig. 1a, b). However, they provide overestimates for$ \rho^{xp} $ at$ \sqrt{s} < 0.1 $ TeV (Fig. 1c, d), which enables the qualitative assumption that the discrepancy between experimental values of$ \rho^{xp} $ and smooth curves within hypotheses (ii) and (iii) at$ \sqrt{s} < 0.1 $ TeV is the main reason for the large values of$ \chi^{2}/{\rm{n.d.f.}} $ for simultaneous fits at small values of the low boundary of the fitted range considered here ($ \sqrt{s_{\min}}=0.03, 0.04 $ , and 0.05 TeV).A comparative analysis of the fit parameters obtained for databases DB20 and DB201+ and shown in Table 4 results in the following conclusions: (a) close values of
$ \chi^{2}/{\rm{n.d.f.}} $ are for both databases at any fixed$ s_{\min} $ ; (b) values of$ c_{p} $ and$ c_{\bar{p}} $ within hypothesis (ii) agree within errors for various databases at the corresponding$ s_{\min} $ value and values of c in for hypothesis (iii); (c) the last statement is also mostly valid for parameter$ a_{2} / a_{1} $ for hypothesis (ii)/(iii).In general, the versions (ii) and (iii) of the asymptotic model suggested within this paper describe the experimental data for the set
$ {\cal{G}}_{1} $ at higher energies than the AQFT [25, 26], particularly for hypothesis (iii). The comparison between the asymptotic model and AQFT is possible only at$ \sqrt{s_{\min}}=0.06 $ TeV, and the fit quality is noticeably worse in the first case than that for AQFT. Such a relationship between the phenomenological models is expected, since the approach considered here is a priori asymptotic, i.e., as reasonably expected, the model based on the suggestions for the asymptotic energy domain will describe the experimental data well at higher asymptotic energies.The ensemble of experimental results that includes only accelerator data is also considered for databases DB20, DB201+, and DB202+. These ensembles are denoted as DBac20, DBac201+, and DBac202+, respectively. The energy dependence of the terms of
$ {\cal{G}}_{1} $ is approximated at$ \sqrt{s_{\min}}= $ 0.03, 0.04, 0.05, 0.06, 0.1, 0.5, 1, 5 and 10 TeV by the corresponding formulas from Table 2 within hypotheses (ii) and (iii) for ensembles DBac20, DBac201+, and DBac202+ and for the full databases above. The statement made for DB20, DB201+ and DB202+ regarding the fit qualities is valid for this case. Therefore, the discussion below for samples DBac20, DBac201+ and DBac202+ focuses on the results for$ \sqrt{s_{\min}} \geq 0.06 $ TeV.The values of all fit parameters agree considerably well within the errors for DBac201+ and DBac202+ for each
$ s_{{\min}} $ and hypotheses (ii) and (iii) considered here. The approximation quality$ \chi^{2}/{\rm{n.d.f.}} $ is very close for the simultaneous fits of accelerator data ensembles DBac201+ and DBac202+ with subtle improvement for the last case at any fixed$ s_{{\min}} $ . These statements are valid with exception of the highest$ \sqrt{s_{\min}}=10 $ TeV, which is analyzed below in more detail. As well as for the full databases, all these enables us to consider the fit results for DBac20 and DBac201+.The numerical results of the simultaneous fits of
$ {\cal{G}}_{1} $ in various energy ranges are shown in Table 5 for hypotheses (ii) and (iii) considering the accelerator data only. At fixed$ s_{{\min}} $ , the first and second lines show results for DBac20 and DBac201+, respectively. Experimental data from DBac201+ for the terms$ {\cal{G}}_{1}^{i} $ ,$ i=1-4 $ along the with fit curves are shown in Fig. 2 for$ \sqrt{s_{\min}}=0.06 $ TeV (solid lines) and at$ \sqrt{s_{\min}}=1 $ TeV (dashed lines). The thick curves are obtained within hypothesis (ii) and the two other lines correspond to hypothesis (iii). The energy domain$ \sqrt{s} \geq 0.06 $ TeV is considered in Fig. 2 in contrast to Fig. 1 to show fit curves clearer for different$ s_{\min} $ values and hypotheses.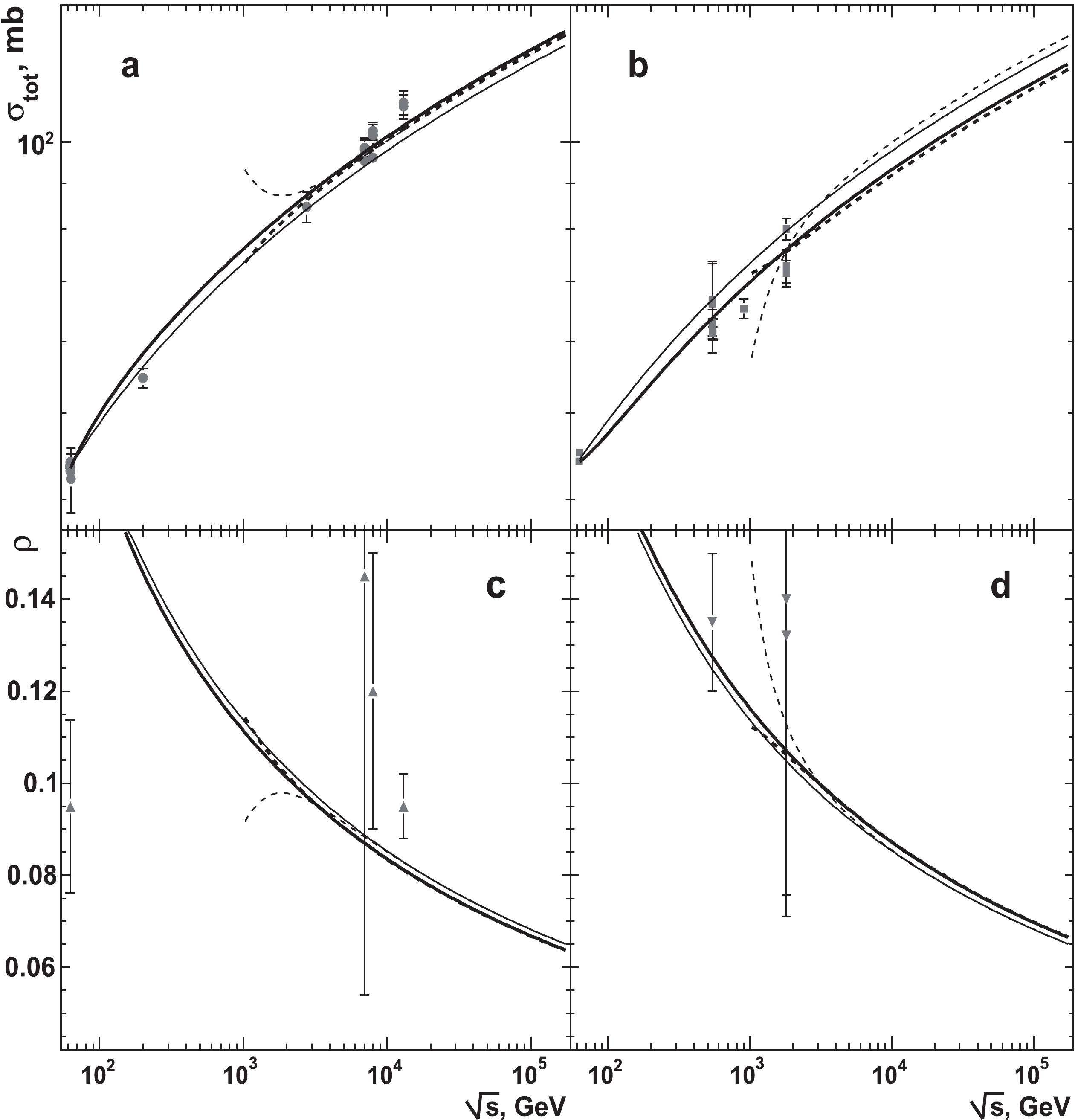
Figure 2. Comparison of the data from accelerator experiments for the terms of
$ {\cal{G}}_{1} $ and approximating curves from simultaneous fits of all these terms at$ \sqrt{s} \geq 0.06 $ TeV. The experimental results are from the subsample DBac201+. The notations for the curves and experimental data base are identical to that in Fig. 1.$ \sqrt{s_{{\min}}} $ ,TeV

hypothesis (ii) hypothesis (iii) $ c_{p} $ , mbarn

$ c_{\bar{p}} $ , mbarn

$ a_{2} $ , mbarn

$ \chi^{2}/{\rm{n.d.f.}} $ 

c, mbarn $ a_{1} $ , mbarn

$ \chi^{2}/{\rm{n.d.f.}} $ 

0.06 $ 8.49 \pm 0.03 $ 

$ 8.12 \pm 0.04 $ 

$ (-9.1 \pm 0.9) \times 10^{3} $ 

$ 92.1/31 $ 

$ 8.343 \pm 0.024 $ 

$ (-1.9 \pm 0.6) \times 10^{3} $ 

$ 165/32 $ 

$ 8.471 \pm 0.029 $ 

$ 8.12 \pm 0.04 $ 

$ (-8.6 \pm 0.9) \times 10^{3} $ 

$ 103/33 $ 

$ 8.339 \pm 0.024 $ 

$ (-1.8 \pm 0.6) \times 10^{3} $ 

$ 169/34 $ 

0.1 – – $ 8.35 \pm 0.04 $ 

$ 7.91 \pm 0.06 $ 

$ (-1.2 \pm 0.6) \times 10^{5} $ 

$ 40.2/23 $ 

$ 8.28 \pm 0.04 $ 

$ (4.4 \pm 0.8) \times 10^{4} $ 

$ 129/24 $ 

0.5 $ 8.38 \pm 0.05 $ 

$ 8.00 \pm 0.11 $ 

$ (3.1 \pm 1.4) \times 10^{5} $ 

$ 35.0/21 $ 

$ 8.48 \pm 0.05 $ 

$ (2.03 \pm 0.25) \times 10^{6} $ 

$ 59.9/22 $ 

$ 8.38 \pm 0.05 $ 

$ 8.01 \pm 0.11 $ 

$ (3.5 \pm 0.9) \times 10^{5} $ 

$ 39.0/22 $ 

$ 8.48 \pm 0.05 $ 

$ (2.03 \pm 0.25) \times 10^{6} $ 

$ 62.9/23 $ 

1 $ 8.29 \pm 0.16 $ 

$ 7.7 \pm 0.5 $ 

$ (-1.7 \pm 0.8) \times 10^{7} $ 

$ 31.0/14 $ 

$ 8.54 \pm 0.05 $ 

$ (1.9 \pm 0.4) \times 10^{7} $ 

$ 32.8/15 $ 

$ 8.39 \pm 0.05 $ 

$ 8.02 \pm 0.11 $ 

$ (-2.4 \pm 0.5) \times 10^{6} $ 

$ 35.3/15 $ 

$ 8.54 \pm 0.05 $ 

$ (1.9 \pm 0.4) \times 10^{7} $ 

$ 35.8/16 $ 

5 $ 9.34 \pm 0.16 $ 

$ 10.0 \pm 2.7 $ 

$ (-2.9 \pm 0.7) \times 10^{8} $ 

$ 19.0/8 $ 

$ 9.01 \pm 0.23 $ 

$ (-3.0 \pm 0.9) \times 10^{8} $ 

$ 19.2/9 $ 

$ 9.33 \pm 0.16 $ 

$ 10.0 \pm 1.9 $ 

$ (-2.9 \pm 0.8) \times 10^{8} $ 

$ 20.1/9 $ 

$ 9.04 \pm 0.23 $ 

$ (-3.2 \pm 0.7) \times 10^{8} $ 

$ 21.5/10 $ 

10 – – – $ 10.5 \pm 0.7 $ 

$ (-2.7 \pm 0.7) \times 10^{9} $ 

$ 0.05/1 $ 

Table 5. Parameters for simultaneous fitting of
$ {\cal{G}}_{1}(s) $ within teh two hypotheses at different stages of the accelerator subsample of DB: DBac20 (first line) and DBac201+ (second line).Numerical values for the fit parameters agree within errors for Tables 4 and 5 at a fixed
$ s_{\min} $ and hypothesis. Therefore, most of conclusions above for the full databases DB20, DB201+, and DB202+ are valid for the corresponding ensembles of the accelerator experimental results with the following features and interpretations. Agreements, within errors, are observed between the numerical values of the corresponded fit parameters for ensembles DBac20 and DBac201+ for a certain hypothesis and fixed$ s_{\min} $ . Furthermore, values are identical for free parameters at$ \sqrt{s_{\min}}=0.5 $ and 1 TeV within hypothesis (iii). Consequencetly, the fit curves for various hypotheses are close to each other at any fixed$ s_{\min} $ considered in Fig. 2 for each observable from the set$ {\cal{G}}_{1} $ .Table 5 shows a noticeable decrease in the relative uncertainties for c at
$ \sqrt{s_{\min}}=1 $ TeV, for$ c_{\bar{p}} $ at$ \sqrt{s_{\min}} \geq 1 $ TeV, for$ a_{2} $ at$ \sqrt{s_{\min}}=0.5 $ , and 1 TeV at the transition from the ensemble DBac20 to the ensemble DBac201+ for hypothesis (ii). The similar effect is absent for pairs of any other ensembles within a certain hypothesis. The datasets for approximation are identical for$ \sqrt{s_{\min}}=0.1 $ and 0.5 TeV for the sample DBac20; therefore, the fit results are only shown for the last case in Table 5. The fits are impossible at the highest$ \sqrt{s_{\min}}=10 $ TeV owing to lack of the required number of data points with the exception of the cases of DBac201+ for hypothesis (iii), shown in Table 5 and ensemble DBac202+ for both hypotheses under study. In the last case, the following results are obtained using the simultaneous fit at the highest$ \sqrt{s_{\min}}=10 $ TeV:$ c_{p}= (10.00 \pm 0.13) $ mbarn,$ c_{\bar{p}}=(10.0 \pm 1.7) $ mbarn,$ a_{2}=(-1.8 \pm 1.0) \times 10^{9} $ mbarn,$ \chi^{2}/{\rm{n.d.f.}}=0.88/1 $ for the hypothesis (ii), and$ c=(10.5 \pm 0.7) $ mbarn,$ a_{1}=(-2.7 \pm 0.7) \times 10^{9} $ mbarn,$ \chi^{2}/{\rm{n.d.f.}}=0.55/2 $ for hypothesis (iii).These data confirm all the above conclusions regarding the agreement between the fitting results for DBac201+ (Table 5) and DBac202+ for hypothesis (iii) and between the full databases DB201+ and DB202+ and the corresponding ensembles of accelerator experimental results for hypothesis (ii) at
$ \sqrt{s_{\min}}=10 $ TeV considering the closeness of the results of approximation established above for DB201+ and DB202+.Note that the fitting results are obtained with the request for the smooth joining of
$ \sigma_{{\rm{tot}}}^{\bar{p}p}(s) $ and$ \rho^{\bar{p}p}(s) $ in the experimentally measured range and in the domain$ \sqrt{s} \geq 5\,(10) $ TeV within hypothesis (ii) at$ \sqrt{s_{\min}}=5 $ TeV for the ensembles DBac20 and DBac201+ (Table 5) and at$ \sqrt{s_{\min}}=5 $ and 10 TeV for DBac202+. As shown in Tables 4 and 5, the exception of the cosmic ray (CR) measurements result in the deterioration in the quality of the approximation for the ensembles DBac20 and DBac201+ regarding the corresponding full databases⑤. Only statistically reasonable values of$ \chi^{2}/{\rm{n.d.f.}} $ are obtained for ensembles of accelerator results for any$ \sqrt{s_{\min}} \geq 0.06 $ TeV in contrast to the full databases. Consequently, hypotheses (ii) and (iii) facilitate the qualitative description of energy dependence of$ {\cal{G}}_{1} $ only. Figure 2 depicts the qualitative agreement of the curves from simultaneous fits of the terms of$ {\cal{G}}_{1} $ with data points at any considered$ s_{\min} $ . The main features of the behavior of these fit curves with respect to the experimental results are similar to those observed in Fig. 1 at corresponding$ s_{\min} $ values.In general, we can conclude that the exclusion of the CR data from the fitted samples results in to significant narrowing of the experimentally available energy domain owing to the decrease in the maximal energy boundary from
$ \sqrt{s}=95^{+5}_{-8} $ TeV [36] to$ \sqrt{s}=13 $ TeV at the LHC and the noticeable deterioration in the approximation quality in most cases. Therefore, the full databases from Table 3 and corresponding fitting results from Table 4 are considered below, unless otherwise stated.Note that the curves obtained within hypothesis (iii) at
$ \sqrt{s_{\min}}=1 $ TeV exhibit a peculiar behavior close to the lower boundary of the fitted range (Figs. 1 and 2). This behavior is dominated by the standard-fit procedure, namely, by the request to obtain a better fit quality and the absence of experimental points close to$ \sqrt{s_{\min}}=1 $ TeV. Therefore, this peculiar behavior is an artificial effect owing to the data analysis procedure. Furthermore, the fit at$ s \geq s_{\min} $ does not consider data points at lower s values; consequently, the behavior under consideration does not contradict any physical results and it has no physical meaning. Hypothesis (ii) is less sensitive to the absence/presence of the data points closer to$ \sqrt{s} \approx 1 $ TeV than hypothesis (iii). Accordingly, the curves obtained within hypothesis (ii) at$ \sqrt{s_{\min}}=1 $ TeV has a smooth behavior without any features at the low energy edge (thick dashed lines in Figs. 1 and 2) whereas the curves obtained using hypothesis (iii) at$ \sqrt{s_{\min}}=1 $ TeV exhibits a peculiar behavior at the low energy edge (thin dashed lines in Figs. 1 and 2) owing to the aforementioned reasons.In summary, for this subsection, simultaneous fit results obtained for the full databases DB20, DB201+, and DB202+ and for the corresponding ensembles of accelerator data DBac20, DBac201+, and DBac202+ generally demonstrate the robustness of the fit results for each hypothesis under consideration for fixed
$ s_{\min} $ , and on the value of the lower boundary of fitted range for$ \sqrt{s_{\min}} \geq 0.06 $ TeV within certain hypotheses (Tables 4 and 5). Consequently, the corresponding curves are closer to each other in Figs. 1 and 2. -
Figure 3 shows the energy dependence for
$ {\cal{G}}_{2} $ , namely$ \Delta_{{{\rm{tot}}}} $ (a),$ \Sigma_{{{\rm{tot}}}} $ (b), and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ (c), with the values of points multiplied by 0.1 in Fig. 3b for$ \Sigma_{{{\rm{tot}}}}(s) $ to use the one scale for the Y–axis for the terms$ {\cal{G}}_{2}^{1} $ and$ {\cal{G}}_{2}^{2} $ . The plots for the terms of$ {\cal{G}}_{2} $ indicate that values of any term$ {\cal{G}}_{2}^{i} $ ,$ i=1-3 $ decrease at$ \sqrt{s} \lesssim 10 $ GeV, particularly rapidly at$ \sqrt{s} < 3 $ GeV. For higher energies, the slowdown is observed in the decrease of$ \Delta_{{{\rm{tot}}}} $ (Fig. 3a) and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ (Fig. 3c), and is paticularly noticeable in the last case; a broad minimum occurs for$ \Sigma_{{{\rm{tot}}}} $ (Fig. 3b), followed by a moderate increase at$ \sqrt{s} \gtrsim 20 $ GeV.
Figure 3. Energy dependence of the measurements for the terms of
$ {\cal{G}}_{2} $ and results of simultaneous fits of all these terms. Points are calculated using the experimental results from DB20. The point values and fit curves are multiplied by 0.1 for$ \Sigma_{{{\rm{tot}}}} $ (b). The solid lines correspond to the fit at$ \sqrt{s_{\min}}=0.03 $ TeV, and the dashed lines are at$ \sqrt{s_{\min}}=0.06 $ TeV. The thick lines show the fit curves for hypothesis (ii) and two other lines correspond to hypothesis (iii).Note that the values of
$ \Delta_{{{\rm{tot}}}} $ and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ at the highest available energy are larger than the previous measurements, particularly in the first case. However, since this is the only point for each parameter$ \Delta_{{{\rm{tot}}}} $ and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ , this increase can be only considered as an indication of a possible transition to growth at$ \sqrt{s} > 62 $ GeV, i.e., at energies larger than the maximum energy of ISR, in the corresponding energy dependence. Except for three points with large errors$ \Delta_{{{\rm{tot}}}} \geq 1-2 $ mb;$ R_{{{\rm{tot}}}}^{\bar{p}/p} > 1 $ although it approaches the asymptotic value (12) from above with an accuracy level better than 2% at ISR energies. However, indications of the change in the behavior of$ \Delta_{{{\rm{tot}}}}(s) $ and$ R_{{{\rm{tot}}}}^{\bar{p}/p}(s) $ at higher energies, the absence of an exact reaching of the asymptotic levels and continuation of this trend at any higher energies, as well as other numerous studies, make it possible to exclude the reach of the asymptotic regime at ISR energies.The energy dependence of the terms of
$ {\cal{G}}_{2} $ is approximated at$ \sqrt{s_{\min}}= $ 3, 5, 10, 15, 20, 25, 30, 40, 50, 60, and 100 GeV using the corresponding formulas from Table 1 within hypotheses (ii) and (iii). It should be noted that the fitted samples and, as consequence, numerical values of the fit parameters are identical for the pairs (25, 30) GeV and (40, 50) GeV of the values of$ \sqrt{s_{\min}} $ . Through a detailed analysis, we observe that analytic formulas from Table 1 quite poorly decribe the energy dependence of the terms of$ {\cal{G}}_{2} $ at most of values of$ \sqrt{s_{\min}} $ for hypotheses (ii) amd (iii). The qualitative analysis indicates that large values of$ \chi^{2}/{\rm{n.d.f.}} $ are mostly dominated by the large discrepancy between fit curves and data points for$ \Sigma_{{{\rm{tot}}}}(s) $ . For both hypotheses, the value of$ \chi^{2}/{\rm{n.d.f.}} $ decreases rapidly at the growth of the low boundary of the fitted range, and the qualitative agreement is achieved for fitted curves and data points at$ \sqrt{s_{\min}} \geq 25 $ GeV. Reasonable fit qualities are only observed for$ \sqrt{s_{\min}} \geq 40 $ GeV. As well as for$ {\cal{G}}_{1} $ , such a relation between fits and data can be considered as expected because the formulas in Table 1 are asymptotic, particularly for hypothesis (iii). In contrast, experimental data for$ {\cal{G}}_{2} $ are only available for$ \sqrt{s} < 0.5 $ TeV. This energy range is significantly narrower even than that for$ {\cal{G}}_{1} $ , and such collision energies are far from any estimation for the onset of the asymptotic region. Thus, the discussion below is focused on the results for$ \sqrt{s_{\min}} \geq 0.03 $ TeV considering the identity of data samples for$ \sqrt{s_{\min}}=25 $ and 30 GeV noted above.Figure 3 shows the results of the simultaneous fits of corresponding data samples using (5) and (12) as solid (dashed) lines for
$ \sqrt{s_{\min}}=0.03 $ (0.06) TeV. The thick lines show the fit curves for hypothesis (ii) and the two other lines correspond to hypothesis (iii). The curves are also multiplied by 0.1 in Fig. 3b to correspond to the scaled data points for$ \Sigma_{{{\rm{tot}}}}(s) $ . The numerical values of fit parameters are shown in Table 6 for$ \sqrt{s_{\min}} \geq 0.03 $ TeV. For hypothesis (ii), the fit is impossible at the highest$ \sqrt{s_{\min}}=0.10 $ TeV considered in this section owing to the lack of the required number of data points.$ \sqrt{s_{{\min}}} $ ,TeV

hypothesis (ii) hypothesis (iii) $ c_{p} $ , mbarn

$ c_{\bar{p}} $ , mbarn

$ a_{2} $ , mbarn

$ \chi^{2}/{\rm{n.d.f.}} $ 

c, mbarn $ a_{1} $ , mbarn

$ \chi^{2}/{\rm{n.d.f.}} $ 

0.03 $ 8.72 \pm 0.03 $ 

$ 8.78 \pm 0.03 $ 

$ -900 \pm 200 $ 

$ 398/12 $ 

$ 8.750 \pm 0.024 $ 

$ (-1.27 \pm 0.12) \times 10^{3} $ 

$ 404/13 $ 

0.05 $ 8.49 \pm 0.06 $ 

$ 8.46 \pm 0.06 $ 

$ (-2.7 \pm 0.5) \times 10^{3} $ 

$ 31.3/9 $ 

$ 8.475 \pm 0.028 $ 

$ (-2.1 \pm 0.4) \times 10^{3} $ 

$ 31.4/10 $ 

0.06 $ 8.34 \pm 0.04 $ 

$ 8.44 \pm 0.04 $ 

$ -0.15 \pm 0.07 $ 

$ 7.64/6 $ 

$ 8.39 \pm 0.03 $ 

$ (-1.9 \pm 0.5) \times 10^{3} $ 

$ 8.17/7 $ 

0.10 – $ 7.7 \pm 0.7 $ 

$ (-4.5 \pm 0.6) \times 10^{4} $ 

$ 2.17/1 $ 

Table 6. Parameters for simultaneous fitting of
$ {\cal{G}}_{2}(s) $ within various hypotheses.As shown in Table 6, the values of
$ c_{p} $ and$ c_{\bar{p}} $ a agree with each other within a 1.25 standard deviation or better at$ \sqrt{s_{\min}} \geq 0.03 $ TeV, i.e., for the fits described data points, at least, qualitatively. The values of$ c_{p} $ and$ c_{\bar{p}} $ decrease continuously with the increase in$ \sqrt{s_{\min}} $ , except for$ c_{\bar{p}} $ at the highest available$ \sqrt{s_{\min}}=0.06 $ TeV, which coincides with the value of the parameter at$ \sqrt{s_{\min}}=0.05 $ TeV. A similar scenario is observed in Table 6 for parameter c under hypothesis (iii).It is not possible to identify any trend in the behavior of
$ a_{1} $ depending on$ s_{\min} $ because of the small number of obtained values of the free parameter for hypothesis (ii). For the other hypothesis studied here,$ a_{1} $ is almost constant within uncertainties except for the value at the highest available$ \sqrt{s_{\min}}=0.10 $ TeV. A detailed analysis shows that the fit results are not sufficiently stable at the highest available$ s_{\min} $ for both hypotheses. The corresponding approximated curves for$ \Delta_{{{\rm{tot}}}}(s) $ and$ R_{{{\rm{tot}}}}^{\bar{p}/p}(s) $ can exhibit very sharp behavior with clear contradictions to both the data points and the general trends in the energy dependence of$ \Delta_{{{\rm{tot}}}} $ and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ . This scenario is similar to that observed for the set$ {\cal{G}}_{1} $ and is discussed in Subsec. IV.A. Therefore, by analogy with the study of$ {\cal{G}}_{1} $ , Table 6 shows the values of fitted parameters obtained accounting for the additional request of smooth behavior of curves and their qualitative agreement with nearest data points at smaller collision energies for$ \sqrt{s_{\min}}=0.06 $ / 0.10 TeV for hypotheses (ii) and (iii).Figure 3a shows that the curve for
$ \Delta_{{{\rm{tot}}}} $ obtained from the simultaneous fit at$ \sqrt{s_{\min}}=0.03 $ TeV within hypothesis (ii) corresponds at qualitative level to the main features of the energy dependence of data points, namely, the decrease in$ \Delta_{{{\rm{tot}}}}(s) $ at$ \sqrt{s} \lesssim 60 $ GeV and the possible increase of this parameter at higher collision energies, despite the large$ \chi^{2}/{\rm{n.d.f.}} $ In contrast, the formulas in Table 1 for$ \Delta_{{{\rm{tot}}}}(s) $ and$ \Sigma_{{{\rm{tot}}}}(s) $ within hypothesis (iii) indicate only a smooth decrease ($ \propto \varepsilon^{-1} $ ) or increase ($ \propto \ln \varepsilon $ ), respectively, without any dependence on the fitted energy range and, as consequence, it is difficult to describe the change in behavior of the s–dependence of terms of the set$ {\cal{G}}_{2} $ within hypothesis (iii) as observed most clearly in Fig. 3a for$ \Delta_{{{\rm{tot}}}}(s) $ . The fitted curves for$ \Sigma_{{{\rm{tot}}}} $ (Fig. 3b) and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ (Fig. 3c) are (very) close to each other at$ \sqrt{s_{\min}}=0.03 $ and 0.06 TeV within a particular hypothesis and for various hypotheses at fixed$ s_{\min} $ .In summary, the detailed analysis of the energy dependence of terms of set
$ {\cal{G}}_{2} $ excludes the possibility of an asymptotic regime at ISR energies, which agrees with numerous studies. The analytic functions deduced within hypotheses (ii) and (iii) for the energy dependence of terms$ \{{\cal{G}}_{2}^{i}\}_{i=1}^{3} $ describe the experimental data at a qualitative level for$ \sqrt{s_{\min}} \geq 40 $ GeV only. The curves for$ \Delta_{{{\rm{tot}}}}(s) $ obtained with the aid of the simultaneous fits for$ {\cal{G}}_{2} $ are sensitive to both hypotheses and the value of$ s_{\min} $ (Fig. 3a). In contrast, simultaneous fit results result in the curves for$ \Sigma_{{{\rm{tot}}}} $ (Fig. 3b) and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ (Fig. 3c), which are almost independent on the hypothesis type for a fixed$ s_{\min} $ and the value of$ s_{\min} $ for certain hypotheses. -
The simultaneous fit of the terms of
$ {\cal{G}} $ is not possible because, as emphasized in Sec. III, the databases for the terms of$ {\cal{G}}_{2} $ are calculated from the experimental values of some parameters of$ {\cal{G}}_{1} $ , namely, the measurements of$ \sigma_{\rm{tot}}^{xp} $ ,$ x=p, \bar{p} $ . One can note this situation principally differs from the situation for databases for$ \sigma_{\rm{tot}} $ , elastic ($ \sigma_{\rm el} $ ) and inelastic ($ \sigma_{\rm{inel}} $ ) cross sections which are related by the optical theorem. There are number of experiments measured$ \sigma_{\rm{inel}} $ directly, for instance, [37]. Therefore the databases for the set$ \{\sigma_{\rm{tot}}, \sigma_{\rm el}, \sigma_{\rm{inel}}} $ } can be considered as, at least, particularly independent. In contrast, all terms of the joined ensemble$ {\cal{G}} $ are defined by one set of the free parameters within hypothesis (ii) or (iii) suggested within this paper. Therefore, the energy dependence for the terms of one set from$ {\cal{G}}_{1} $ and$ {\cal{G}}_{2} $ can be calculated using the values of free parameters obtained from the simultaneous fit of the terms of the another set called the "adjoint set," i.e., the curves for smooth energy dependence of the terms of$ {\cal{G}}_{1} $ at fixed$ s_{\min} $ can be calculated with the free parameter values obtained for$ {\cal{G}}_{2} $ using the simultaneous fit at the same$ s_{\min} $ , and vice versa.Figure 4 shows the energy dependence for the terms of
$ {\cal{G}} $ derived within hypothesis (ii) at$ \sqrt{s_{{\min}}}=0.06 $ TeV. Database DB201+ is used for the terms of$ {\cal{G}}_{1} $ . The thick curves are from the simultaneous fits for the terms of$ {\cal{G}}_{i} $ ,$ i=1 $ , 2, whereas the thin lines correspond to the results of the calculations for some terms from$ {\cal{G}}_{i} $ ,$ i=1 $ , 2 using the values of free parameters obtained for the adjoined set$ {\cal{G}}_{j} $ ,$ j \ne i $ using the simultaneous fit, and is shown in Tables 4 and 6 for$ \sqrt{s_{{\min}}}=0.06 $ TeV. The lines corresponding to the fit results and calculations are close to each other for$ {\cal{G}}_{1} $ (Figs. 4a – d), but the results are different for most terms of$ {\cal{G}}_{2} $ . A dramatic discrepancy is obtained between the fitted and calculated curves for$ \Delta_{{{\rm{tot}}}}(s) $ in Fig. 4e, whereas the parameter$ \Sigma_{{{\rm{tot}}}} $ is not sensitive to the technique of the creation of smooth curve (Fig. 4f); two curves exhibit a similar behavior in the functional sense at$ \sqrt{s} \geq 0.2 $ TeV, but a quantitative difference is observed between them for$ R_{{{\rm{tot}}}}^{\bar{p}/p}(s) $ in Fig. 4g.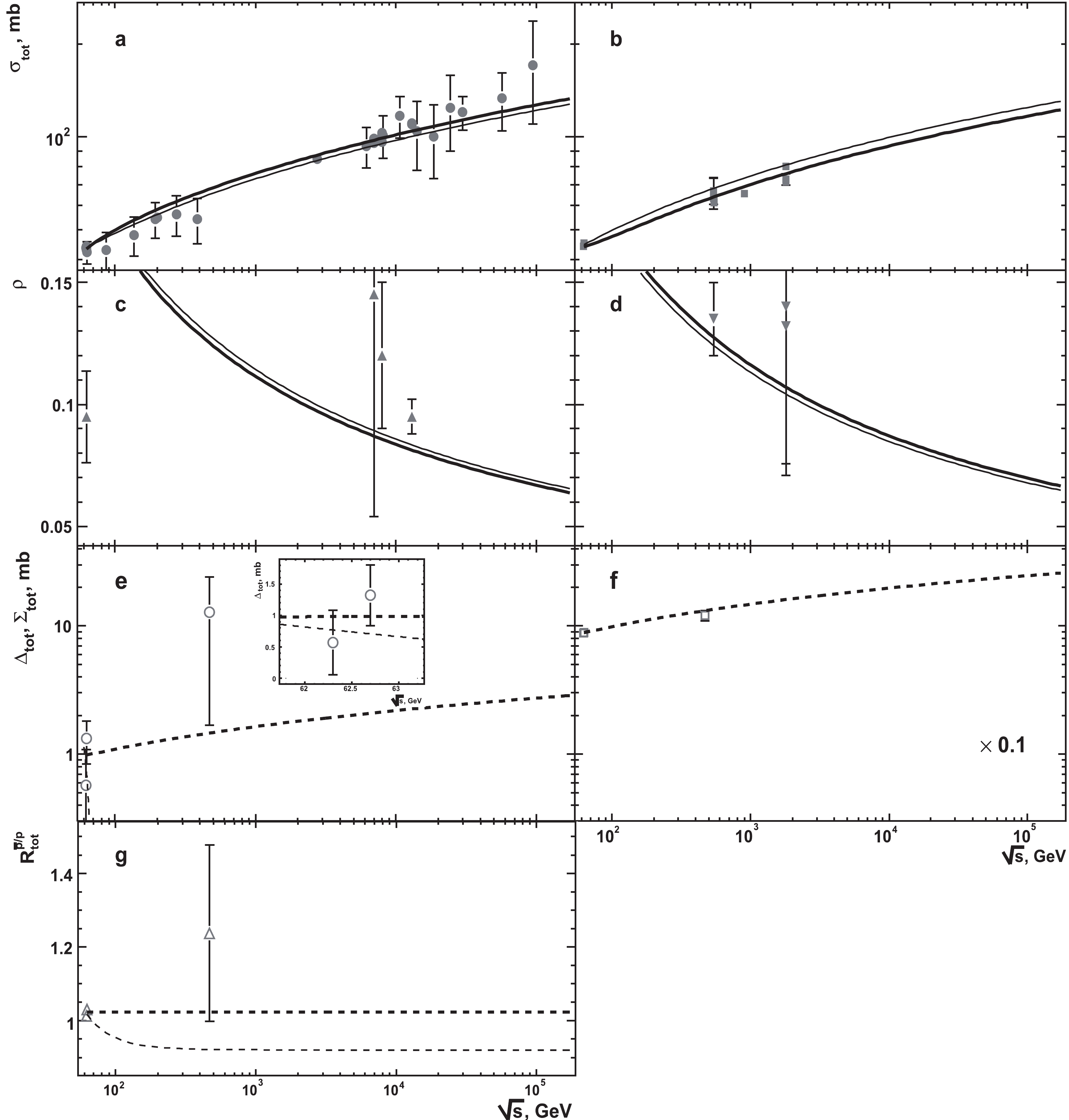
Figure 4. Energy dependence for the terms of the joined set
$ {\cal{G}} $ and curves obtained using the results shown in Table 4 for database DB201+ and in Table 6 within hypothesis (ii). The experimental results and curves are shown at$ \sqrt{s} \geq 0.06 $ TeV. The inner panel for$ \Delta_{{{\rm{tot}}}} $ (e) shows the narrow energy range close to$ \sqrt{s}=62.5 $ GeV. The point values and curves are multiplied by 0.1 for$ \Sigma_{{{\rm{tot}}}} $ (f). The solid lines correspond to the curves for the terms of$ {\cal{G}}_{1} $ , and the dashed lines are for$ {\cal{G}}_{2} $ . The thick curves are from the simultaneous fit results of the corresponding$ {\cal{G}}_{i} $ ,$ i=1 $ , 2; the thin lines are calculated using the values of free parameters obtained from the simultaneous fit of the terms of the adjoint set, i.e., the curves for the terms of$ {\cal{G}}_{1} $ are calculated with the free parameter values obtained for$ {\cal{G}}_{2} $ using the simultaneous fit at$ \sqrt{s_{\min}}=0.06 $ TeV and vice versa.These features for the terms of
$ {\cal{G}}_{2} $ are driven by the unstable behavior of the fit results for$ {\cal{G}}_{2} $ at$ \sqrt{s_{{\min}}}=0.06 $ TeV within hypothesis (ii) as well as the special request added for the simultaneous fit for$ {\cal{G}}_{2} $ described in Subsec. IV.B. This suggestion is confirmed in Fig. 5, which shows the energy dependence for the terms of$ {\cal{G}} $ derived within hypothesis (iii) at$ \sqrt{s_{{\min}}}=0.06 $ TeV. In this case, the fit results for$ {\cal{G}}_{2} $ are stable and additional requests are not used for the fit procedure. Figure 5 shows the full identity of the fitted and calculated curves for each term of the joined ensemble$ {\cal{G}} $ owing to the agreement of the values of free parameters within errors in Table 4 and 6 for hypothesis (iii) at$ \sqrt{s_{{\min}}}=0.06 $ TeV.
Figure 5. Energy dependence for the terms of the joined set
$ {\cal{G}} $ and curves obtained using the results shown in Table 4 for database DB201+ and in Table 6 within hypothesis (iii). The experimental results and curves are shown at$ \sqrt{s} \geq 0.06 $ TeV. The inner panel for$ \Delta_{{{\rm{tot}}}} $ (e) shows the narrow energy range close to the$ \sqrt{s}=62.5 $ GeV. The point values and curves are multiplied by 0.1 for$ \Sigma_{{{\rm{tot}}}} $ (f). The solid lines correspond to the curves for the terms of$ {\cal{G}}_{1} $ , and dashed lines are for$ {\cal{G}}_{2} $ . The thick curves are from the simultaneous fit results of the corresponding$ {\cal{G}}_{i} $ ,$ i=1 $ , 2; the thin lines are calculated using the values of free parameters obtained from the simultaneous fit of the terms of the adjoint set, i.e., the curves for the terms of$ {\cal{G}}_{1} $ are calculated with the free parameter values obtained for$ {\cal{G}}_{2} $ using the simultaneous fit at$ \sqrt{s_{\min}}=0.06 $ TeV and vice versa.It should be noted from Figs. 4 and 5 that, in general, we can obtain the smooth energy dependence for the terms of
$ {\cal{G}}_{1} $ in the multi-TeV range using the fit results for$ {\cal{G}}_{2} $ at significantly smaller collision energies. Moreover, the calculated curves for$ {\cal{G}}_{1} $ agree reasonably with both the experimental points and corresponding fitted curves. Thus, the trends in the s–dependence of the terms of$ {\cal{G}}_{2} $ observed at$ \sqrt{s} \lesssim 0.5 $ TeV and driven by the behavior of the$ \sigma_{\rm{tot}}^{xp}(s) $ ,$ x=p, \bar{p} $ enable us to obtain the correct energy dependence for the terms of$ {\cal{G}}_{1} $ in a much wider energy domain up to the highest s available in experiments.Summarizing this subsection, the energy dependence for each term of the joined set
$ {\cal{G}} $ can be calculated using the free parameter values obtained for any separate set$ {\cal{G}}_{i} $ ,$ i=1 $ , 2 using the simultaneous fit within the validity of the additional request of stability for the results of that simultaneous fit for$ {\cal{G}}_{i} $ ,$ i=1 $ , 2. -
First, the results shown in Table 4 facilitate the qualitative estimation of the onset of the asymptotic energy domain
$ s_{a} $ . As discussed in the text,$ c_{p} $ and$ c_{\bar{p}} $ agree with c within errors as well as$ a_{2} $ with$ a_{1} $ for simultaneous fits within hypotheses (ii) and (iii) at$ \sqrt{s_{\min}} \geq 5 $ TeV. Thus, the fitting results can be considered as evidence for possible transition from hypothesis (ii) to (iii) at$ \sqrt{s}\gtrsim 5 $ TeV. Thus, this transition imposes a small energy-dependence on the parameters involved in the fitting procedures, which are not considered here.Furthermore, the term
$ \propto \varepsilon^{-1} $ should be negligibly small in the parameterization of$ \sigma_{{\rm{tot}}}^{xp}(s) $ ,$ x=p, \bar{p} $ (Table 2) to obtain the validation of the Pomeranchuk theorem in both the classical (11) and generalized formulation (12).Considering the condition
$ a/\varepsilon \lesssim \delta $ for the energy range$ s \geq s_{a} $ as, at least, one of the possible signatures of the onset of the asymptotic energy region, we can assume that the model under consideration enables us to estimate$ s_{a} $ in order of magnitude. Here,$ a \equiv |a_{1}|= |a_{2}| $ within uncertainties for certain databases, DB20 or DB201+, at fixed values of$ \sqrt{s_{\min}} \geq 5 $ TeV and$ \delta \ll 1 $ mbarn is the empirical boundary. Considering the range$ a \sim (6.5 \times 10^{7} - 1.7 \times 10^{9}) $ mbarn, which represents a variation in two orders in magnitude, and the choice$ \delta=0.1 $ mbarn, a small contribution resulting from the non-logarithmic term, we can estimate$ \sqrt{s_{a}} \sim 25.5 - 130 $ TeV. The lower value of the range of$ \sqrt{s_{a}} $ is close to the nominal energy of the high–energy LHC (HE–LHC) mode [38], whereas the upper one agrees reasonably well with the estimation deduced within the approaches mentioned in Sec. II and III [23, 24]. Hopefully, this upper value can be achieved within the newest option of the Future Circular Collider (FCC) project [39] with a proton beam energy of 75 TeV.The above estimates for
$ \sqrt{s_{a}} $ are rather crude, considering the wide range of the absolute values of$ a_{1,2} $ obtained using simultaneous fits in the multi-TeV region$ \sqrt{s_{\min}} \geq 5 $ TeV (Table 4). Moreover, as stressed earlier, only experimental data for$ pp $ are approximated at$ \sqrt{s_{\min}} \geq 5 $ TeV. All these enable only a preliminary statements at a qualitative level to be made regarding of the onset of the asymptotic energy domain.The analytic functions deduced within various hypotheses (Tables 1, 2) and numerical fit results (Tables 4, 6) enable the phenomenological projections for the terms of the wide set
$ {\cal{G}} $ of global scattering parameters and their derivative quantities, in particular for energies$ {\cal{O}} $ (100 TeV) and higher. The main features for such predictions are described in detail in [26, 32]. Simultaneous fit results obtained for database DB201+ (Table 4) enable predictions of the joined set$ {\cal{G}} $ since DB201+ is one of the most complete databases considered here; however, this database satisfies the general requirements used in the formation of databases. To obtain estimates at (ultra–)high energies, it may be reasonable to use the fitted results for$ s_{{\min}} \geq 1 $ TeV2. Therefore, predictions for the joined set$ {\cal{G}} $ are calculated and analyzed below for$ \sqrt{s_{{\min}}}=1 $ , 5, and 10 TeV. Calculations are performed for both collisions considered in the paper ($ pp, \bar{p}p $ ) at$ \sqrt{s} \geq 14 $ TeV.Within hypothesis (ii), the values of both
$ \sigma_{\rm{tot}}^{xp} $ and$ \rho^{xp} $ do not depend on the type of collision for a given$ s_{{\min}} $ , nor$ s_{{\min}} $ indicated above for a fixed type of interaction within errors. The$ \rho^{xp} $ reaches the asymptotic level (22) within uncertainty at the smallest$ \sqrt{s} = 14 $ TeV under consideration at any$ s_{{\min}} $ . Relative uncertainties for the estimations of$ \sigma_{\rm{tot}}^{xp} $ ($ \delta_{\sigma}^{xp} $ ) are almost constant for all$ s_{{\min}} $ values, except for the highest$ \sqrt{s_{{\min}}}=10 $ TeV, for which, after a certain decrease (increase), a fairly rapid transition to a constant level is observed at$ \sqrt{s} \approx 25 $ (50) TeV for$ pp $ ($ \bar{p}p $ ) collisions. The accuracy of estimates for$ pp $ is noticeably better than that for$ \bar{p}p $ , deteriorating for both collision types with an increase in$ s_{{\min}} $ , particularly for the transition from lower values of$ s_{{\min}} $ to the highest$ \sqrt{s_{{\min}}}=10 $ TeV under consideration. For$ pp $ ($ \bar{p}p $ ), the values of$ \delta_{\sigma}^{xp} $ are at the level of 0.09 (0.22) at$ \sqrt{s_{{\min}}}=1 $ TeV, slightly increasing to 0.11 (0.27) at$ \sqrt{s_{{\min}}}=5 $ TeV. The decrease in$ \delta_{\sigma}^{pp} $ is observed from 0.17 to 0.15 at$ \sqrt{s} \gtrsim 25 $ TeV, whereas a smooth increase in$ \delta_{\sigma}^{\bar{p}p} $ occurs from 0.36 to a constant level of 0.38 at$ \sqrt{s} \gtrsim 50 $ TeV at$ \sqrt{s_{{\min}}}=10 $ TeV. For$ \rho^{xp} $ , in general, a similar scenario is observed for$ \delta^{xp}_{\rho} $ in the functional sense as well as for$ \delta^{xp}_{\sigma} $ : for$ pp $ , the$ \delta^{pp}_{\rho} $ quantity is approximately constant for all$ s_{{\min}} $ except for$ \sqrt{s_{{\min}}}=10 $ TeV, for which the approach to the constant level is observed at$ \sqrt{s} \gtrsim 25 $ TeV after a certain decrease in$ \delta^{pp}_{\rho}(s) $ ; for$ \bar{p}p $ ,$ \delta^{\bar{p}p}_{\rho}(s) $ agrees with the constant reasonably well at the lowest value$ \sqrt{s_{{\min}}}=1 $ TeV under discussion, and relative uncertainty$ \delta^{\bar{p}p}_{\rho} $ exhibits an increase for other$ s_{{\min}} $ , which is particularly noticeable at highest$ \sqrt{s_{{\min}}}=10 $ TeV reaching a constant level at$ \sqrt{s} \gtrsim 50 $ TeV. The relative uncertainties in projections of the ρ-parameter are smaller than those for the total cross section for any of the collision types considered here at any fixed$ s_{{\min}} $ . For$ pp $ , the$ \delta^{pp}_{\rho}(s) $ quantity agrees well with a constant 0.068 for$ \sqrt{s} \geq 14 $ TeV at$ \sqrt{s_{{\min}}}=1 $ TeV, whereas a decrease is observed for higher$ s_{{\min}} $ , particularly for the highest$ \sqrt{s_{{\min}}}=10 $ TeV. The$ \delta^{pp}_{\rho}(s) $ decreases with the increase in s from 0.106 (0.151) at$ \sqrt{s}=14 $ TeV to the constant level of 0.105 (0.133) at$ \sqrt{s} \geq 20 $ (200) TeV for$ \sqrt{s_{{\min}}}=5 $ (10) TeV.$ \delta^{\bar{p}p}_{\rho}(s) $ is approximately equal to the constant level$ 0.078 $ for$ \sqrt{s} \geq 14 $ TeV at$ \sqrt{s_{{\min}}}=1 $ TeV and$ \delta^{\bar{p}p}_{\rho} $ increases from 0.082 (0.112) to a constant of 0.085 (0.127) at$ \sqrt{s} \gtrsim 30 $ (150) TeV for$ \sqrt{s_{{\min}}}=5 $ (10) TeV. Thus, for the ρ-parameter, the inverse energy dependence of the relative uncertainty is observed compared with that of the$ \sigma_{\rm{tot}}^{xp} $ at$ \sqrt{s_{{\min}}} > 1 $ TeV.Estimates for each term of the set
$ {\cal{G}}_{1} $ , calculated within hypothesis (iii), are characterized by significantly better accuracy than those for hypothesis (ii) for each$ s_{{\min}} $ used for the derivation of numerical estimates.Within hypothesis (iii), the values of
$ \sigma_{\rm{tot}}^{xp} $ do not depend on the type of collision within the errors for a given$ s_{{\min}} $ as well as for hypothesis (ii). However, in contrast to hypothesis (ii), an increase in the estimations of$ \sigma_{\rm{tot}}^{xp} $ at fixed s is observed with an increase in$ s_{{\min}} $ , particularly in the transition from$ \sqrt{s_{{\min}}} = 1 $ TeV to the highest$ \sqrt{s_{{\min}}} = 10 $ TeV under consideration. The ratios of the estimates obtained for a fixed type of collision at a given s and different$ s_{{\min}} $ –$ R^{\,xp}_{\sigma, 2/1} \equiv {\left.\sigma_{\rm{tot}}^{xp}(s)\right|_{s_{{\min,2}}}}\big/ {\left.\sigma_{\rm{tot}}^{xp}(s)\right|_{s_{{\min,1}}}} $ – reach constant levels with an increase in s, and this generally occurs at different s values dependent on both the$ s_{{\min}} $ and the collision type. The numerical values of these constant levels are$ \forall\,x=p, \bar{p}: R^{\,xp}_{\sigma, 2/1}=1.06 \pm 0.03 $ ,$ 1.16 \pm 0.07 $ , and$ 1.09 \pm 0.07 $ at$ \sqrt{s} \gtrsim 60 $ , 50, and 40 (60, 70, and 140) TeV in$ pp $ ($ \bar{p}p $ ) interactions for the pairs of lower boundary values for fitted ranges$ (\sqrt{s_{{\min,1}}}, \sqrt{s_{{\min,2}}}\,)=(1,\; 5) $ , (1, 10) and (5, 10) in TeV, respectively. Thus the values of these constants with uncertainties do not depend either on the type of collision or the choice of the specific pair$ (s_{{\min,1}},s_{{\min,2}}) $ . The quantity$ \delta_{\sigma}^{xp} $ agrees reasonably well with a constant at$ \sqrt{s} \geq 14 $ TeV and does not depend on the type of interaction for all$ s_{{\min}} $ values, except for$ \sqrt{s_{{\min}}} = 10 $ TeV, for which the onset of constant behavior is observed at$ \sqrt{s} \approx 100 $ TeV after a decrease from 0.075 (0.065), at the smallest$ \sqrt{s}=14 $ TeV under consideration for$ pp $ ($ \bar{p}p $ ) collisions. The constant values of$ \delta_{\sigma}^{xp} $ are approximately 0.006, 0.024, and 0.061 at$ \sqrt{s_{{\min}}} = 1 $ , 5, and 10 TeV, respectively. The quantity$ \delta^{xp}_{\rho} $ does not depend on the type of interaction and, owing to the reasons indicated in Sec. II, it becomes small, namely,$ < 10^{-4} $ at$ \sqrt{s} \gtrsim 30 $ , 125, and 350 TeV for$ \sqrt{s_{{\min}}} = 1 $ , 5, and 10 TeV, respectively. Furthermore, the$ \delta^{xp}_{\rho} $ rapidly decreases with increasing s. Therefore, within the framework of hypothesis (iii), the$ \delta^{xp}_{\rho} $ can be considered equal to zero at$ \sqrt{s} \gtrsim 30 $ , 125, and 350 TeV for$ \sqrt{s_{{\min}}} = 1 $ , 5, and 10 TeV, respectively. Accounting for the aforementioned specific scenario with the uncertainties for estimates of the$ \rho^{xp} $ -parameter, only the median values of these estimates are discussed in this paragraph. The median values of the ρ-parameter are almost independent of the type of collision and coincide with the asymptotic level (22) with an accuracy of$ 10^{-3} $ at the smallest considered$ \sqrt{s}=14 $ TeV for$ \sqrt{s_{{\min}}} = 1 $ TeV. This type of interaction has no dependence on the ρ-parameter, and the median values of$ \rho^{xp} $ coincide with$ \rho^{xp}_{a} $ (22) with an accuracy of$ 10^{-3} $ at$ \sqrt{s} \gtrsim 50 $ (100) TeV in the case of$ \sqrt{s_{{\min}}} = 5 $ (10) TeV. The scenario for the ratio of estimates of ρ obtained for a fixed type of interaction at a given s and different$ s_{{\min}} $ –$ R^{\,xp}_{\rho, 2/1} \equiv {\left.\rho^{xp}(s)\right|_{s_{{\min,2}}}} \big/ {\left.\rho^{xp}(s)\right|_{s_{{\min,1}}}} $ – is generally similar to that observed for$ \sigma_{\rm{tot}}^{xp} $ . However, unlike on total cross sections,$ \forall\,x=p, \bar{p}: R^{\,xp}_{\rho, 2/1} $ agree with unity with high accuracy better than$ 7 \times 10^{-4} $ at$ \sqrt{s} \geq 100 $ TeV for any pair$ (s_{{\min,1}},s_{{\min,2}}) $ considered here.The detailed analysis above for the predictions for the terms of the set
$ {\cal{G}}_{1} $ unambiguously indicates that the terms$ \Delta_{{{\rm{tot}}}} $ and$ R_{{{\rm{tot}}}}^{\bar{p}/p} $ of the set$ {\cal{G}}_{2} $ coincide with their asymptotic values (11) and (12) within the uncertainties at$ \sqrt{s} \geq 14 $ TeV for both hypotheses (ii) and (iii) at any$ s_{{\min}} \geq 1 $ TeV2. The smooth increase is observed for$ \sigma_{\rm{tot}}^{xp} $ with the increase in s for any$ s_{{\min}} $ . Therefore, we can conclude that the realization of the scenario according to the Pomeranchuk theorem (12) appears to be more preferable at asymptotic energies than the scenario with the formulation (11) for any hypotheses discussed in this paper.Furthermore, the aforementioned study of energy behavior of projections for the terms of the joined ensemble
$ {\cal{G}} $ shows that, in general, physical quantities and their uncertainties reach corresponding asymptotic or constant levels at energies$ {\cal{O}} $ (100 TeV). This can be considered as indirect evidence in favor of the range for$ \sqrt{s_{a}} $ , derived using the condition for$ a/\varepsilon $ .Some numerical values for the estimates of global scattering parameters are shown in Table 7 for
$ pp $ collisions in the energy range from the nominal$ \sqrt{s} $ of the LHC up to the high boundary of the PeV domain$ \sqrt{s}=10 $ PeV based on the detailed analysis above and the reasons discussed in other papers [26, 32]. The fitted results for DB201+ at$ \sqrt{s_{{\min}}}=5 $ TeV are used to calculate the estimates of terms of the set$ {\cal{G}}_{1} $ . The choice of the value$ \sqrt{s_{{\min}}}=5 $ TeV for Table 7 is based on the detailed analysis in subsec. IV.A and in this section. In particular, the simultaneous fit for$ {\cal{G}}_{1} $ at this$ s_{{\min}} $ is characterized first by a sufficient number of experimental points in fitted sample and statistically acceptable$ \chi^{2}/{\rm{n.d.f.}} $ in difference with smaller$ s_{{\min}} $ . Second, it is characterized by the higher robustness of fit results in comparison with the$ \sqrt{s_{{\min}}}=10 $ TeV. As shown in Table 7, the predictions for$ \sigma_{{{\rm{tot}}}}^{pp} $ and$ \rho^{pp} $ coincide within the uncertainties for various hypotheses under consideration. A direct comparison is impossible for the results in Table 7 and the projections within the AQFT [26] because of noticeably different$ s_{{\min}} $ values used for simultaneous fits and, consequently, for the estimates of$ \sigma_{{{\rm{tot}}}}^{pp} $ and$ \rho^{pp} $ . Nevertheless, accounting for this characteristic, we can observe the following: the estimates obtained within this paper are characterized with significantly better precision than those within the AQFT [26], particulary for the ρ-parameter; the estimates mostly agree within uncertainties for two approaches for any global scattering parameters under discussion, except for$ \sigma_{{{\rm{tot}}}}^{pp} $ at ultra–high energies$ \sqrt{s} \geq 5 $ PeV. In general, this discrepancy can be expected because the present approach provides$ \sigma_{{{\rm{tot}}}}^{pp} \propto \ln\varepsilon $ at$ s \to \infty $ , i.e., the slowest increase in the total cross section at (ultra–)high energies, and this functional form for$ \sigma_{{{\rm{tot}}}}^{pp} $ should result in the continuously increasing difference with the results of AQFT with the increase in s.Parameter $ \sqrt{s} $ , TeV

(HL–)LHC, HE–LHC, LHC-ultimate SPPC, FCC-hh, VLHC-I, II 14 27 42 40 70.6 100 125 150 175 $ \sigma_{{{\rm{tot}}}}^{pp} $ , mbarn

$ 108 \pm 12 $ 

$ 117 \pm 13 $ 

$ 122 \pm 13 $ 

$ 122 \pm 13 $ 

$ 128 \pm 14 $ 

$ 132 \pm 14 $ 

$ 135 \pm 14 $ 

$ 137 \pm 15 $ 

$ 139 \pm 15 $ 

$ 108.5 \pm 2.7 $ 

$ 117.3 \pm 2.8 $ 

$ 122.7 \pm 2.9 $ 

$ 122.1 \pm 2.9 $ 

$ 129 \pm 3 $ 

$ 133 \pm 3 $ 

$ 135 \pm 3 $ 

$ 138 \pm 3 $ 

$ 139 \pm 3 $ 

$ \rho^{pp} \times 10^{3} $ 

$ 87 \pm 9 $ 

$ 80 \pm 8 $ 

$ 77 \pm 8 $ 

$ 77 \pm 8 $ 

$ 73 \pm 8 $ 

$ 71 \pm 7 $ 

$ 69 \pm 7 $ 

$ 68 \pm 7 $ 

$ 67 \pm 7 $ 

$ 83.6 \pm 0.4 $ 

$ 77.3 \pm 0.1 $ 

$ 73.89 \pm 0.03 $ 

$ 74.24 \pm 0.04 $ 

$ 70.38 \pm 0.01 $ 

$ 68.24 \pm 0.01 $ 

$ 66.93 $ 

$ 65.91 $ 

$ 65.06 $ 

VLHC-II ultra-high energy cosmic rays higher energies 200 110 170 250 500 750 $ 10^{3} $ 

$ 5 \times 10^{3} $ 

$ 10^{4} $ 

$ \sigma_{{{\rm{tot}}}}^{pp} $ , mbarn

$ 140 \pm 15 $ 

$ 133 \pm 14 $ 

$ 138 \pm 15 $ 

$ 143 \pm 15 $ 

$ 151 \pm 16 $ 

$ 155 \pm 17 $ 

$ 159 \pm 17 $ 

$ 172 \pm 19 $ 

$ 185 \pm 20 $ 

$ 141 \pm 3 $ 

$ 134 \pm 3 $ 

$ 139 \pm 3 $ 

$ 143 \pm 3 $ 

$ 151 \pm 4 $ 

$ 156 \pm 4 $ 

$ 159 \pm 4 $ 

$ 178 \pm 4 $ 

$ 186 \pm 4 $ 

$ \rho^{pp} \times 10^{3} $ 

$ 67 \pm 7 $ 

$ 70 \pm 7 $ 

$ 68 \pm 7 $ 

$ 66 \pm 7 $ 

$ 62 \pm 7 $ 

$ 60 \pm 6 $ 

$ 59 \pm 6 $ 

$ 53 \pm 6 $ 

$ 51 \pm 5 $ 

$ 64.35 $ 

$ 67.67 $ 

$ 65.22 $ 

$ 63.19 $ 

$ 59.85 $ 

$ 58.06 $ 

$ 56.85 $ 

$ 50.92 $ 

$ 48.73 $ 

Table 7. Predictions for
$ pp $ based on the simultaneous fit of$ {\cal{G}}_{1} $ for DB201+ at$ \sqrt{s_{{\min}}}=5 $ TeV; the first and second lines in the cell are for hypotheses (ii) and (iii), respectively. -
The asymptotic behavior of the wide set
$ {\cal{G}} $ of scattering parameters is studied with the aid of the crossing property, the DDR, and the optical theorem in$ pp $ , and$ \bar{p}p $ collisions. Note that we obtained an intercept$ \alpha_{\mathbb{P}}=1 $ , typical of a soft Pomeron (low momentum transfer). This is a consequence of the use of the first-order approximation for the DDR. In contrast, the introduction of higher derivative orders to describe the dispersion relation may introduce subleading contributions at high energies, which can result in a Pomeron intercept different from 1. The simplest functional form for the real part of the forward scattering amplitude is used for the asymptotic energy domain to deduce the analytic expressions for$ \sigma_{\rm{tot}}^{xp} $ and$ \rho^{xp} $ ,$ x=p, \bar{p} $ as well as for some combinations of total cross sections, which are important for verification of the Pomeranchuk theorem. Within that form, for$ {\rm{Re}}F_{xp} $ , two hypotheses – (ii) and (iii) – are maintained with non-zero constants for$ {\rm{Re}}F_{xp} $ at asymptotic energies.Three consequent stages are considered for the most current database for global scattering parameters in elastic
$ pp $ and$ \bar{p}p $ scattering, namely, the latest PDG sample (DB20) and all available experimental results (DB201+, DB202+). The analytic parameterizations deduced considering both hypotheses provide a quantitative description of the energy dependence of measured global scattering parameters – set$ {\cal{G}}_{1} $ – with mostly robust values of fit parameters for any DBs. The fit qualities are reasonable for the energy range$ \sqrt{s} \geq 0.06 $ TeV, and the quantity is statistically acceptable at the low boundary for the fit domain$ \sqrt{s_{{\min}}} \geq 0.1 $ TeV for hypothesis (ii). The corresponding ranges are significantly shifted to the higher energies and they are$ \sqrt{s} \geq 0.5 $ TeV and$ \sqrt{s} \geq 1 $ TeV for statistically reasonable and acceptable quantities, respectively, for hypothesis (iii) owing to its "extremely" asymptotic nature. A detailed analysis of accelerator data only shows that hypotheses (ii) and (iii) enable the qualitative description for these data up to$ \sqrt{s_{{\min}}}=5 $ TeV. The experimental database created for some interrelations between$ \sigma_{{{\rm{tot}}}}^{\bar{p}p} $ and$ \sigma_{{{\rm{tot}}}}^{pp} $ – set$ {\cal{G}}_{2} $ – covers the energy domain$ \sqrt{s} < 0.5 $ TeV only, and most of the points are at$ \sqrt{s} \lesssim 0.06 $ TeV. The analytic expressions deduced for terms of the set$ {\cal{G}}_{2} $ within hypotheses (ii) and (iii) only provide a qualitative description of the energy dependence of these terms at$ \sqrt{s_{{\min}}} \geq 0.04 $ TeV. In general, such a relation between simultaneous fits and data is expected since the formulas for the terms of the set$ {\cal{G}}_{2} $ , as well as for the set$ {\cal{G}}_{1} $ , are asymptotic for both hypotheses under study. Nevertheless, the consideration of the joined ensemble$ {\cal{G}} $ indicates that, in general, we can obtain the smooth energy dependence for the terms of$ {\cal{G}}_{1} $ in the multi-TeV range using the fit results for$ {\cal{G}}_{2} $ at significantly smaller collision energies, and the calculated curves for$ {\cal{G}}_{1} $ reasonably agree with both the experimental data and the corresponding fitted curvesA study of empirical conditions for the functional forms of the analytic expressions for measured global scattering parameters enables the following crude estimation of collision energy for the onset of the asymptotic region
$ \sqrt{s_{a}} \sim 25.5 - 130 $ TeV.Based on the simultaneous fit results, the estimations are calculated for the total cross section and ρ-parameter, considering the elastic
$ pp $ scattering at different s values, up to an energy frontier of$ \sqrt{s}=10 $ PeV. These estimations with uncertainties are robust for various$ \sqrt{s_{{\min}}} \geq 1 $ TeV and types of collisions. The numerical values of the estimations for$ \sigma_{{{\rm{tot}}}}^{pp} $ and$ \rho^{pp} $ obtained using the simultaneous fit of$ {\cal{G}}_{1} $ for DB201+ at$ \sqrt{s_{{\min}}}=5 $ TeV agree for hypotheses (ii) and (iii) within the errors. The estimations for$ \sigma_{{{\rm{tot}}}}^{pp} $ can be considered conservative owing to the functional form of this quantity at (ultra–)high energies, which results in a slow increase in$ \sigma_{{{\rm{tot}}}}^{pp} $ as s increases. A detailed analysis of the predictions for terms of the joined ensemble$ {\cal{G}} $ unambiguously indicates that the realization of the scenario with the generalized formulation of the Pomeranchuk theorem may be more suitable at asymptotic energies than the scenario with the original formulation of this theorem for any hypotheses discussed in the paper. The aforementioned study shows that, in general, physical quantities and their uncertainties reach corresponding asymptotic or constant levels at energies$ {\cal{O}} $ (100 TeV). As commented earlier, it can be considered an indirect indication to support the range for$ \sqrt{s_{a}} $ obtained by considering the empirical conditions described in this work.As a final comment, at very high energies, possible non-linearities on the elastic forward quantities may be considered by using higher-order derivative terms in the dispersion relations. This procedure may result in corrections on the results presented here. This question is presently under study and will be published in a future paper.
-
S.D.C. thanks to UFSCar for the financial support. The work of V.A.O. was supported partly by NRNU MEPhI Program "Priority 2030".
Optical theorem, crossing property, and derivative dispersion relations: implications on the asymptotic behavior of ${\boldsymbol{\sigma_{\bf tot}(s)}}$ and ${\boldsymbol{\rho(s)}}$
- Received Date: 2022-02-25
- Available Online: 2022-08-15
Abstract: In this paper, we present some results on the behavior of the total cross section and ρ-parameter at asymptotic energies in proton–proton (








 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: