-
Neutrinos are among the most fascinating and enigmatic particles in nature. They are also the second most abundant particles after photons in the visible universe. Unlike photons, the interactions of neutrinos are extremely weak. Neutrinos are the lightest of all known particles; they also do not interact with normal matter. When they are produced in stellar interiors, they can easily absorb energy that would otherwise take much longer to be transported to the surface by radiation or convection. The resulting energy sink in the center of the star can dictate the star's rate of nuclear burning, structure and evolution, and ultimately how its life ends. Any process that produces neutrinos in stellar interiors acts as a sink of stellar energy, as the mean free path of neutrinos is much longer than the scale of the stellar radius. Neutrinos are very important in high energy physics, astrophysics, and cosmology [1–4]. Gamov and Pontecorvo were the first to indicate the important role played by neutrinos in the evolution of stars. Therefore, the neutrino emissions process may affect the properties of matter at high temperatures and also affect stellar evolution. The properties of neutrinos have been increasingly researched over the last sixty years. The possible electromagnetic properties of massive neutrinos include a charged radius, an anapole moment, a dipole magnetic, and an electric moment [5–12]. Research on neutrino mass, whether they are Dirac or Majorana particles, oscillations, and form factors and especially on the magnetic moment is of great significance for the choice of the theory of elementary particles and for clarifying phenomena such a supernova dynamics, stellar evaluation, and the production of sun neutrinos. The energy loss due to neutrino pair production is huge, and it is an important process in a wide range of astrophysical problems, such as in the red giant stages of stellar evolution, neutron stars, supernova collapse, and for the cooling of white dwarfs [13–17]. While the three thermal neutrino processes, namely plasmon decay (
$ \gamma_{\rm plasmon} \rightarrow \nu_e + \overline{\nu}_e $ ), photo neutrino production ($ e^-+\gamma \rightarrow e^- + \nu_e + \overline{\nu}_e $ ), and pair annihilation ($ e^- + e^+ \rightarrow \nu_e + \overline{\nu}_e $ ) are dominant, the bremstrahlung ($ e^- + Z \rightarrow e^- + Z + \nu_e + \overline{\nu}_e $ ) and recombination processes ($ e^-_{\rm continuum} \rightarrow e^-_{\rm bound} + \nu_e + \overline{\nu}_e $ ) play a smaller role in astrophysics and cosmology. The energy loss rates of these processes have already been calculated at various temperature values and matter densities in different models [18–29].The most general expression for the effective vertex of the interaction
$ \nu\overline{\nu} \gamma $ is given by [5, 29–31]$\begin{aligned}[b] \Gamma_\mu =& e \gamma_\mu F_1(q^2) + ({\rm i}e/2m_\nu) \sigma_{\mu \lambda} q^\lambda F_2(q^2) \\&+ (e/2m_\nu) \sigma_{\mu \lambda} q^\lambda \gamma_5 F_3(q^2) \\&+ e\left(\gamma_\mu - \frac{{ {\not {q}}}q_\mu}{q^2}\right) \gamma_5 q^2 F_4(q^2) \end{aligned} $

(1) for the diagonal cases, where
$ q^\lambda $ is the photon momentum and$ F_{1,2,3,4}(q^2) $ are the electromagnetic form factors of the neutrino. Note that in the derivations of the decomposition in Eq. (1), the demands based on the Lorentz invariance and the electromagnetic gauge invariance are taken into account. The charge radius, magnetic moment, electric dipole moment, and anapole moment are defined as [8]$\begin{aligned}[b]& <r^2> = 6 \frac{{\rm d} F_1(q^2) }{{\rm d}q^2}\Bigg|_{q^2=0}, \quad {m_e \over m_\nu}F_2(q^2=0)=\mu_\nu, \\& {e \over 2m_\nu}F_3(q^2=0)=d_\nu, \quad F_4(q^2=0)=a. \end{aligned}$

(2) A Dirac neutrino has a charge, a magnetic moment, an electric dipole moment (which is absent in the CP invariant theory), and an anapole moment. However, a Majorana neutrino has only a diagonal anapole moment, as its antiparticle is equal to itself (imposing the restriction of the C-, -P, -T-properties). In addition, Majorana neutrinos can have as many transition moments as Dirac neutrinos.
There have been studies on the energy loss in the annihilation processes in the frame of SM and the extension of SM [11, 12, 25, 26]. In Sec. II of this study, we calculate the cross sections and energy loss rate of a pair annihilation process in the extended SM, which includes the neutrino electromagnetic form factor (especially the charge radius and anapole moment) effects on the neutrino cross section and takes into account the
$ \gamma \nu \overline{\nu} $ vertex for the Dirac neutrinos [7–10, 29, 30]. To the best of our knowledge this has not been previously studied. In Sec. III, we present and discuss the numerical results. -
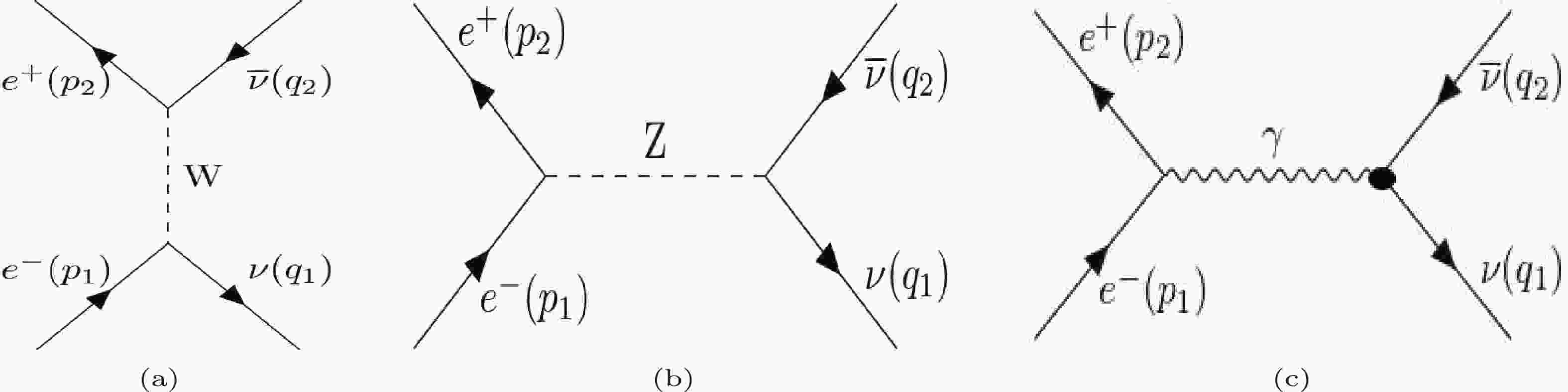
The lowest order diagrams for the process
$ e^-(p_1) + e^+(p_2) \rightarrow \nu_e(q_1) + \overline{\nu}_e(q_2) $ are given in Fig. 1. The matrix element of the process due to SM (Figs. 1 (a), (b)) in the low energy limit are given by making a Fierz transformation, as follows: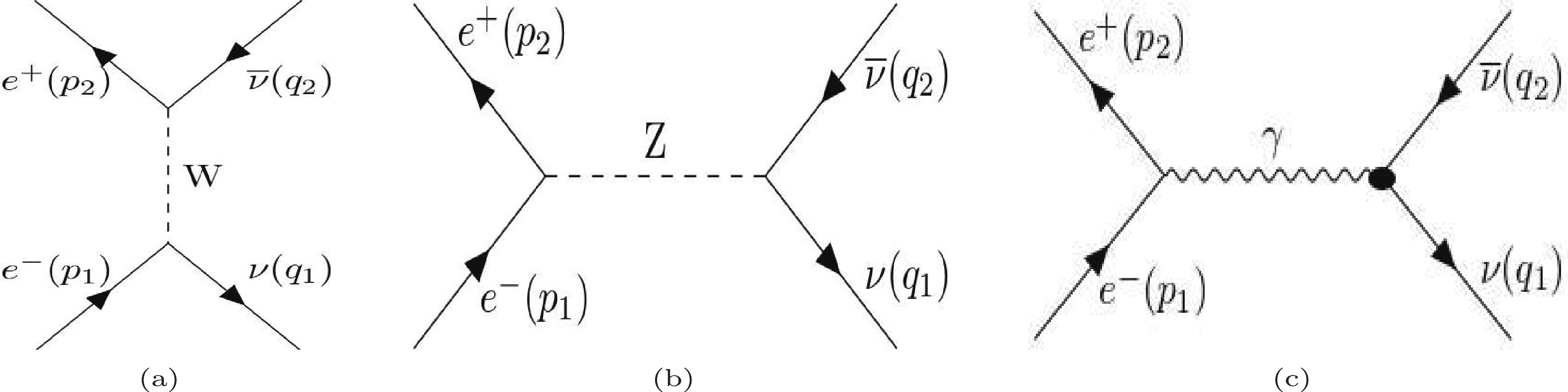
Figure 1. The lowest order Feynman diagrams for the process
$ e^{+}+e^{-}\rightarrow \nu_e +\overline{\nu}_e $ . The symbols in the parantheses are the momenta of the particles. The black disc in (c) represents the interaction arising from the effective neutrino interaction beyond the SM.$ \mathcal{M}^{(\rm SM)} = {{\rm i} G_{\rm F} \over \sqrt{2}} \overline{ {u}} (q_1) \gamma_\beta (1-\gamma_5) {v}(q_2) \overline{ {v}}(p_2) \gamma^\beta (C_V-C_A \gamma_5) {u}(p_1), $

(3) where
$ C_V={1 /2} +2 \sin^2 \theta_W $ and$ C_A={1/ 2} $ for$ \nu_e $ , and$ C_V=-{1 /2} +2 \sin^2 \theta_W $ and$ C_A=-{1/ 2} $ for$ \nu_\mu $ and$ \nu_\tau $ because electron neutrinos interact with both W and Z bosons, but muon and tau neutrinos interact only with Z bosons (see the case in Fig. 1(b)).The matrix element due to electromagnetic interactions ( Fig. 1(c)) is given by [32]
$ \mathcal{M}^{(\gamma)}= \mathcal{M}^{(Q)} + \mathcal{M}^{(\mu)}, $

(4) with
$ \mathcal{M}^{(Q)} = {4\pi\alpha \over q^2} \overline{ {u}}(q_1) (\gamma^\beta - {q^\beta { {\not{q}}} \over q^2}) \left[ {q^2 \over 6} <r_\nu^2> \right] {v}(q_2) \overline{ {v}}(p_2) \gamma^\lambda {u}(p_1), $

$ \mathcal{M}^{(\mu)} = -{\rm i} {2\pi\alpha \over q^2} \overline{ {u}}(q_1) \sigma^{\beta \lambda} q_\lambda \left[ \mu \right] {v}(q_2) \overline{ {v}}(p_2) \gamma^\lambda {u}(p_1), $

where
$ \alpha=e^2/4\pi $ ,$ <r_\nu>=<r^2>+6 \gamma_5 a $ , and$ \mu=\mu_\nu+{\rm i} \gamma_5 d_\nu $ . The effect of$ \gamma_5 $ is simply a multiplication of the abovementioned formulas for the ultra-relativistic neutrino by a factor of$ -1 $ .The total matrix element of the process is as follows:
$ \mathcal{M}_t = \mathcal{M}^{(\rm SM)}+ \mathcal{M}^{(Q)} + \mathcal{M}^{(\mu)} . $

(5) There is no interference between the helicity-conserving (
$ \mathcal{M}^{(\rm SM)} $ and$ \mathcal{M}^{(Q)} $ ) and helicity-flipping ($ \mathcal{M}^{(\mu)} $ ) amplitudes. Combining the helicity-conserving amplitudes and using$ q_\mu J^\mu(q)=0 $ , we find$ \begin{aligned}[b] \mathcal{M}^{(\rm SM)} + \mathcal{M}^{(Q)} =& {{\rm i} G_{\rm F} \over \sqrt{2}} \overline{ {u}} (q_1) \gamma_\beta (1-\gamma_5) {v}(q_2) \overline{ {v}}(p_2)\\&\times \gamma^\beta (C'_V-C_A \gamma_5) {u}(p_1), \end{aligned} $

(6) where
$ C'_V=C_V + ({\sqrt{2} \pi \alpha /3 G_{\rm F}}) <r_\nu^2> $ .When evaluating the cross section, we even considered the neutrino mass; however, we ignored it in the calculations due to its negligible contribution. Then, we obtained the following absolute total matrix element squared
$ \begin{aligned}[b] | \mathcal{M}_t|^2 = & | \mathcal{M}^{(\rm SM)} + \mathcal{M}^{(Q)}|^2 + | \mathcal{M}^{(\mu)}|^2 \\ = & G_{\rm F}^2 \left\{ {\alpha \over G_{\rm F}^2} (\mu_\nu^2 + d_\nu^2) {(q_1 \cdot q_2)(q_2 \cdot p_1) \over (p_1+p_2)^2} \right. \\ & + (C'_V + C_A)^2 (p_1 \cdot q_1)(p_2 \cdot q_2)\\ & + (C'_V - C_A)^2 (p_2 \cdot q_1)(p_1 \cdot q_2) \\ & + m_e^2 ({C'_V}^2 - {C_A}^2)(q_1 \cdot q_2) \left. \right\}. \end{aligned} $

(7) Squaring
$ \mathcal{M}_t $ , summing and averaging over the spins, and integrating over the final momenta by using Lenard's formula$ \int {{\rm d}^3 q_1 \over 2 w_1} {{\rm d}^3 q_2 \over 2 w_2} \delta^4 (q-q_1-q_2) q_1^\mu q_2^\nu = {1 \over 24} \pi (2q^\mu q^\nu + g^{\mu \nu} q^2), $

(8) we have
$ \begin{aligned}[b] \sigma v = & {1 \over (2 \pi)^2}{1 \over 4 E_1 E_2} \int {{\rm d}^3 q_1 \over 2 w_1} {{\rm d}^3 q_2 \over 2 w_2} \delta^4 (p_1+p_2-q_1-q_2) \sum_s | \mathcal{M}_t|^2 \\ = & {G_{\rm F}^2 \over 48 \pi E_1 E_2} \Bigg\{ 8 {\alpha \pi\over G_{\rm F}^2}(\mu_\nu^2 + d_\nu^2)(2m_e^2+p_1 \cdot p_2) \\&+ ({C'_V}^2+{C_A}^2)\left[2(p_1 \cdot p_2)^2 + 3m_e^2(p_1 \cdot p_2)+m_e^4\right] \ \\ & + 12 ({C'_V}^2 -{C_A}^2) \left[ m_e^2 (p_1 \cdot p_2) + m_e^4 \right] \Bigg\}, \end{aligned} $

(9) where
$ E_1 $ and$ E_2 $ are the energies of the electron and positron, and$ \overrightarrow{v} $ is the electron-positron relative velocity.The rate of the energy loss per cubic centimeter per second
$ \mathcal{Q} $ arising from the pair process depends not only on the cross-section (σ) but also on the available densities of electrons and positrons. It is given by$ \begin{aligned}[b] \mathcal{Q} =& {4 \over (2\pi)^6} \int {{\rm d}^3 p_1 \over {\rm{exp}}[(E_1-\mu_e)/k_{\rm B} T]+1} \\&\times{{\rm d}^3 p_2 \over {\rm{exp}}[(E_2+\mu_ e)/k_{\rm B} T]+1} (E_1 + E_2) v \sigma ,\end{aligned} $

(10) where σ is the process cross-section and
$ \dfrac{1} {{ \rm{exp}}[(E_{1,2} \mp \mu_e)/k_{\rm B} T]+1} $

is the Fermi-Dirac distribution function for electrons/positrons,
$ \mu_e $ is the electron chemical potential, T is the stellar temperature and$ k_{\rm B} $ is the Boltzmann constant. We will assume that the star consists of a completely ionized gas in thermal equilibrium at a temperature T with a density ρ.Now, according to [17], if we define
$ \lambda=({k_{\rm B} T})/{ m_e} $ and$ \nu={\mu_e}/({ k_{\rm B} T}) $ where$ m_e $ is the electron mass, then we will get the function$ G_n^\pm(\lambda,\nu) = \lambda^{3+2n} \int_{\lambda^{-1}}^ \infty {\rm d}x {x^{2n+1}(x^2-\lambda^{-2}) \over {\rm{exp}}(x\pm\nu)+1 } . $

(11) The energy loss rate for all values of λ and ν in Eq. (10) can be written in terms of the integrals given in Eq. (11) as
$ \begin{aligned}[b] \mathcal{Q} = & {G_{\rm F}^2 m_e^9 \over 18 \pi^5} \Bigg\{ {12 \pi \alpha \over G_{\rm F}^2 m_e^2} (\mu_\nu^2+ d_\nu^2) \Big[2 (G_0^+G_{-1/2}^- + G_0^-G_{-1/2}^+) + G_0^-G_{1/2}^+ \\ & + G_0^+G_{1/2}^- \Big] + 2 ({C'_V}^2 + {C_A}^2) \Big[5 (G_0^+G_{-1/2}^- + G_0^-G_{-1/2}^+) \\ & + 7 (G_0^-G_{1/2}^+ + G_0^+G_{1/2}^-) - (G_1^-G_{-1/2}^+ + G_1^+G_{-1/2}^-) \\ &+ 8 (G_1^-G_{1/2}^+ + G_1^+G_{1/2}^-) \Big] + 36 ({C'_V}^2 - {C_A}^2) \\&\times\Big[ G_0^+G_{-1/2}^- + G_0^-G_{-1/2}^+ + G_0^-G_{1/2}^+ + G_0^+G_{1/2}^- \Big] \Bigg\} . \\[-15pt] \end{aligned} $

(12) Unfortunately, these integrals cannot be calculated analytically for any values of λ and ν. We evaluated them for special ranges of the temperatures and densities. In order to compare the results with previously obtained ones in the SM for electron-positron pair annihilation, we evaluated
$ \mathcal{Q} $ in various regions of λ and ν, and also calculated the ratio$\dfrac {\delta \mathcal{Q} }{ \mathcal{Q}^{\rm SM}} = \dfrac{ \mathcal{Q} - \mathcal{Q}^{\rm SM} }{ \mathcal{Q}^{\rm SM}} $ .In region I (
$\rho \le 10^5 \;{\rm gr/cm^3}, \;3 \times 10^8 \le T \le 3 \times 10^9\; {\rm K}$ );$ \lambda \ll 1,\; \nu \ll 1/\lambda $ (nonrelativistic and nondegenerate case)$ \mathcal{Q}_1 = {G_{\rm F}^2 \over \pi^4} m_e^6 T^3 {\rm e}^{-2m_e/T} \left[ { \alpha \pi \over G_{\rm F}^2 m_e^2} (\mu_\nu^2 + d_\nu^2) + {C'}_V^2 \right], $

(13) and in region II (
$ 10^4 \; \le \rho \le 10^6 \;{\rm gr/cm^3},\; T \le 3 \times 10^8 \;{\rm K} $ );$ \lambda \ll 1, \;1/\lambda < \nu < 2/\lambda $ (nonrelativistic and mildly degenerate case)$ \begin{aligned}[b] \mathcal{Q}_{\rm II} =& {\sqrt{2\pi}G_{\rm F}^2 \over \pi^3} m_e^6 \left( {\rho \over \mu_e} N_A \right) \left( {T \over m_e} \right)^{3/2} \\&\times {\rm e}^{-(m_e+\mu_e)/T} \left[ { \alpha \pi \over G_{\rm F}^2 m_e^2} (\mu_\nu^2 + d_\nu^2) + {C'}_V^2 \right], \end{aligned} $

(14) then, we get
$ {\delta \mathcal{Q}_{\rm I} \over \mathcal{Q}^{\rm SM}_{\rm I}} = {\delta \mathcal{Q}_{\rm II} \over \mathcal{Q}^{\rm SM}_{\rm II}} = { \left[C_V + \dfrac {\sqrt{2}\pi \alpha}{ 3 G_{\rm F}} < r_\nu^2> \right]^2 + \dfrac { \pi \alpha }{ G_{\rm F}^2 m_e^2} (\mu_\nu^2 + d_\nu^2 ) \over C_V^2 } -1 . $

Similarly, in region III (
$ 10^7 \;{\rm gr/cm^3} \le \rho, \; 6 \times 10^7 \, {\rm K} < T $ );$ \lambda \ll 1, \;1 \ll \lambda \nu $ (relativistic and nondegenerate case),$ \mathcal{Q}_{\rm III} = {\sqrt{2\pi}G_{\rm F}^2 \over 20 \pi^3} m_e^4 \mu_e^2 \left( {\rho \over \mu_e} N_A \right) \left( {T \over m_e} \right)^{3/2} {\rm e}^{-(m_e+\mu_e)/T} \left[ {C'}_V^2 + C_A^2\right], $

(15) in region IV (
$ 10^7 \;{\rm gr/cm^3} \le \rho $ );$ 1 \ll \lambda,\; \nu \ll 1 $ (relativistic and nondegenerate case)$ \mathcal{Q}_{\rm IV} = {7 \zeta(5) G_{\rm F}^2 \over 12 \pi} (T)^9 \left[ {C'}_V^2 + C_A^2\right], $

(16) and in region V (
$ 10^8 \;{\rm gr/cm^3} \le \rho $ ,$10^{10} \; {\rm K} \le T$ (at the lowest),$ 10^{10}\;{\rm gr/cm^3} \le \rho $ ,$ 10^{10} \le T \le 10^{11} \; {\rm K} $ (at the extendable));$ 1 \ll \lambda, \;1 \ll \nu $ (relativistic and degenerate case)$ \mathcal{Q}_V = {2G_{\rm F}^2 \over 5 \pi^3} (T)^4 \mu_e^2 \left( {\rho \over \mu_e} N_A \right) {\rm e}^{-\mu_e/T} \left[ {C'}_V^2 + C_A^2\right], $

(17) and again one can get
$ {\delta \mathcal{Q}_{\rm III} \over \mathcal{Q}^{\rm SM}_{\rm III}} = {\delta \mathcal{Q}_{\rm IV} \over \mathcal{Q}^{\rm SM}_{\rm IV}} = {\delta \mathcal{Q}_{\rm V} \over \mathcal{Q}^{\rm SM}_{\rm V}} = { \left[C_V + \dfrac{\sqrt{2}\pi \alpha }{ 3 G_{\rm F}} < r_\nu^2> \right]^2 + C_A ^2 \over C_V^2 + C_A^2 } -1 . $

Notice that the typical approximation for these regions (
$ {\rm III-V} $ ) only considers the terms for the dominant powers, so there is no dependence on the$ \mu_\nu $ and$ d_\nu $ of the neutrino. -
As the magnetic moment contribution has been already studied by many researchers ([25, 26] and references therein), for the purpose of originality, we will try to obtain the effects of the form factors numerically from the proposed analytical expressions, especially the effect of the charge radius (or anapole moment) of the Dirac neutrino on the energy loss rates through the physical process of pair-annihilation
$ e^+ + e^- \rightarrow \nu_e + \overline{\nu}_e $ .As is known, this process is one of the main mechanisms of neutrino pair production relevant for neutrino luminosity. We obtained the approximated formula for energy loss (Q) and the correction contribution in comparison with those of the SM. We investigated both the degenerate and non-degenerate Fermi gas for the case
$ d_\nu=0 $ using the values of the parameters given in [25, 26, 33–37].The dependence of
$ Q_{\rm I} $ as a function of temperature (T) is visualized in Fig. 2. It is seen that as the temperature increases, the stellar energy loss rate also increases.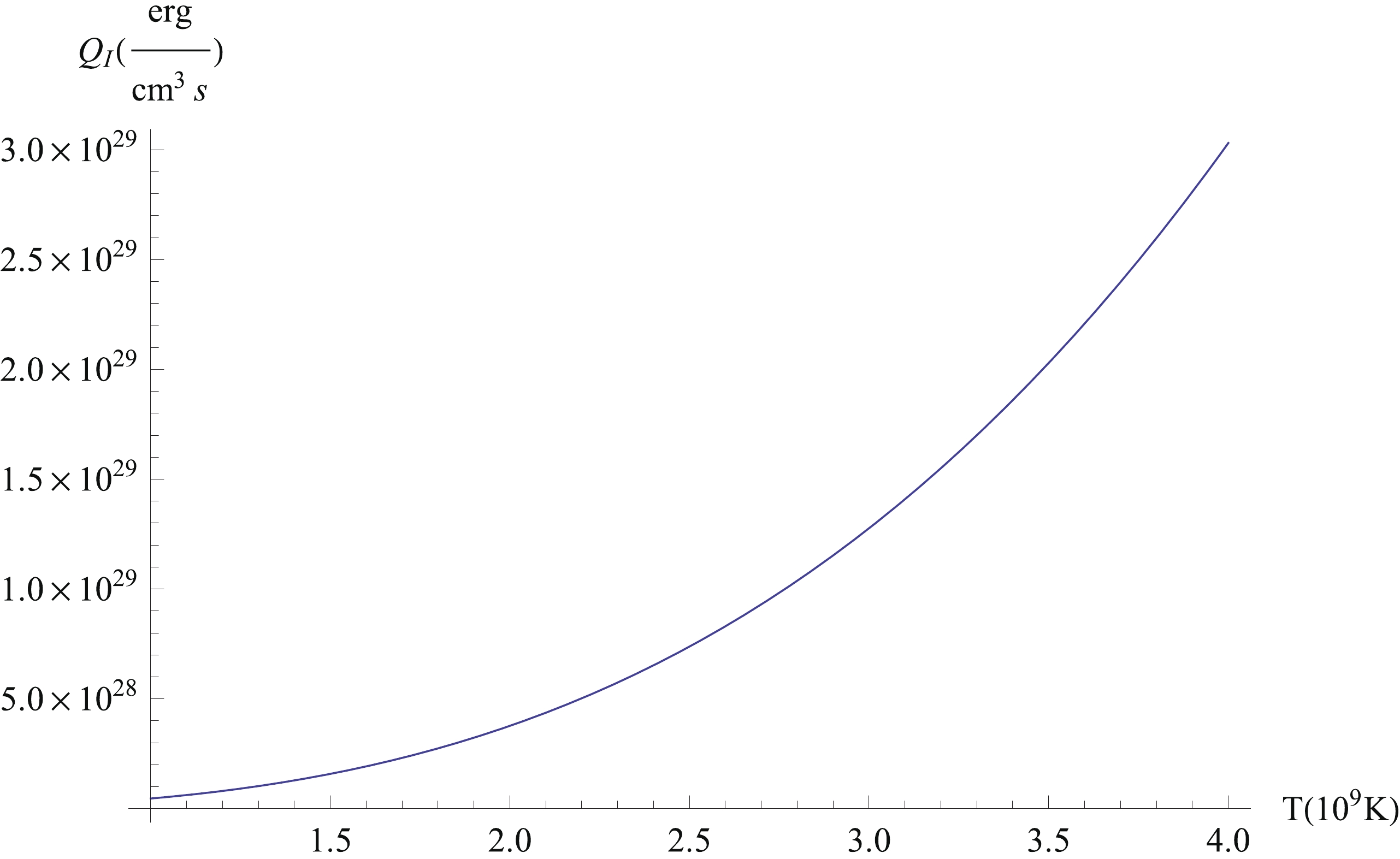
Figure 2. (color online) Energy loss rate (
$ Q_{\rm I} $ ) as a function of temperature (T) for the case$ \mu_\nu=1.58 \times 10^{-12} \mu_B $ and$< r_\nu^2 > =1.5 \times 10^{-32} {\rm cm^2}.$ In Fig. 3 the dependence of
$ Q_{\rm II} $ on the pair of parameters of the charge radius with the degeneration parameter ν (Fig. 3(a) in this case, the magnetic moment is taken as zero) and the magnetic moment with the degeneration parameter ν (Fig. 3(b) in this case, the charge radius is taken as zero) are displayed. As can be seen, Q decreases with an increase in ν as ν is inversely proportional to the temperature T. In addition, the effect of the charge radius on the energy loss compared with the magnetic moment can be observed more clearly.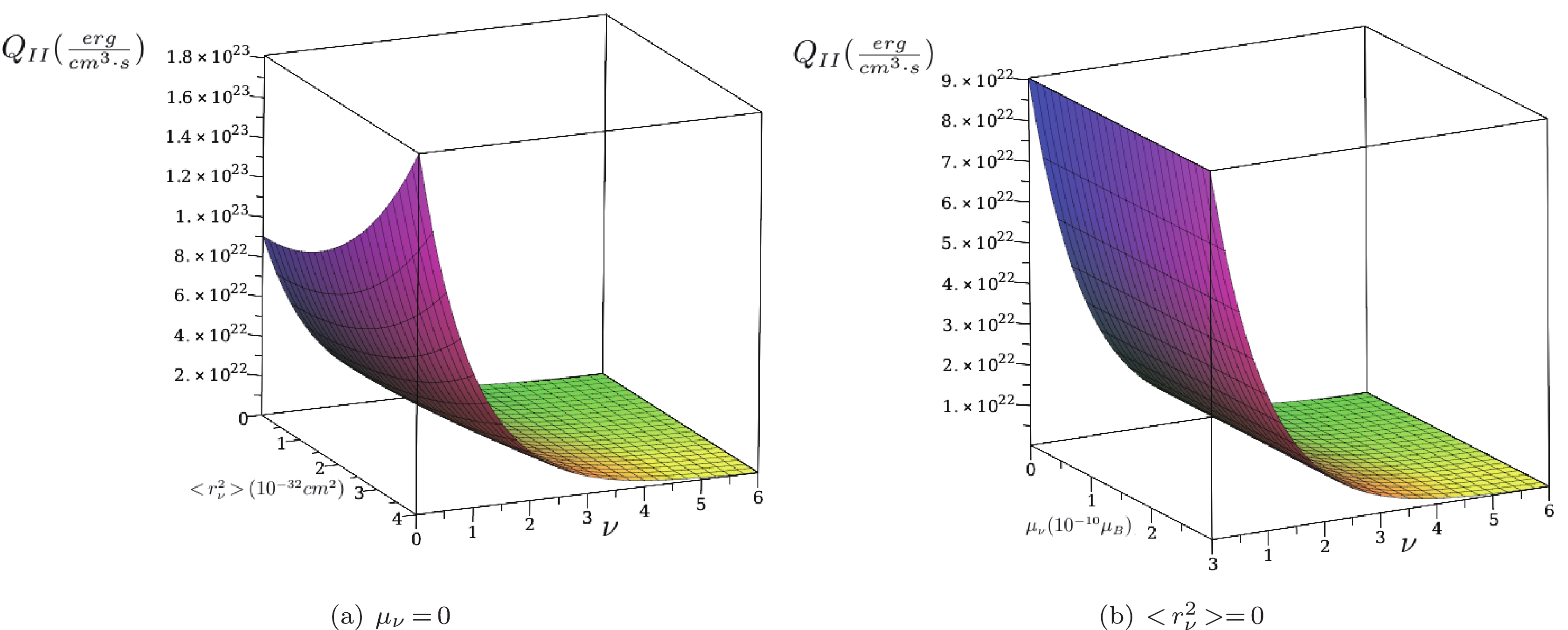
Figure 3. (color online) The energy loss rate (
$ Q_{\rm II} $ ) as a function of$ \nu={\mu_e /(k_{\rm B} T)} $ and the charge radius ($ <r_\nu^2> $ ), and ν and the magnetic moment ($ \mu_\nu $ ) for the case$\rho= 1.1 \times 10^6\;{\rm gr/cm^3}.$ We have compared the effect of the change on the order of the magnetic moment from
$ 10^{-12} $ to$ 10^{-10} \mu_B $ on$ Q_{\rm II} $ in Fig. 4. It can be seen that as the magnetic moment becomes larger, even the order of the energy loss rate stays almost at the same level. Again, the effect of the magnetic moment is more pronounced for the large value case (Fig. 4(b)) and is dominant in the contribution obtained for the standard model. In the case of the magnetic moment of the electron neutrino, the best bound is derived from the globular cluster red giant energy loss$ \mu_{\mu_e} < 3 \times 10^{-12} \mu_B $ [25, 34, 38]. If one takes a magnetic moment on the order of$ 10^{-14} \mu_B $ [39], the effect of the considered formulation in the numerical calculation will not be observed effectively. The contribution of the charge radius still exists in the calculations.
Figure 4. (color online) The energy loss rate (
$ Q_{\rm II} $ ) as a function of the magnetic moment ($ \mu_\nu $ ) and charge radius ($ <r_\nu^2> $ ) for the case$ T=3 \times 10^8\;{\rm K} $ and$ \rho= 1.1 \times 10^6 \;{\rm gr/cm^3}. $ Finally, in Fig. 5 we display the behavior of
$ {\delta \mathcal{Q} / \mathcal{Q}^{\rm SM}} $ with respect to the charge radius for the cases$ \rm III, \;IV $ , and V. It has already been stated that the ratio depends only on the charge radius due to the negligible effect of the dipole moment ($ \mu_\nu $ ).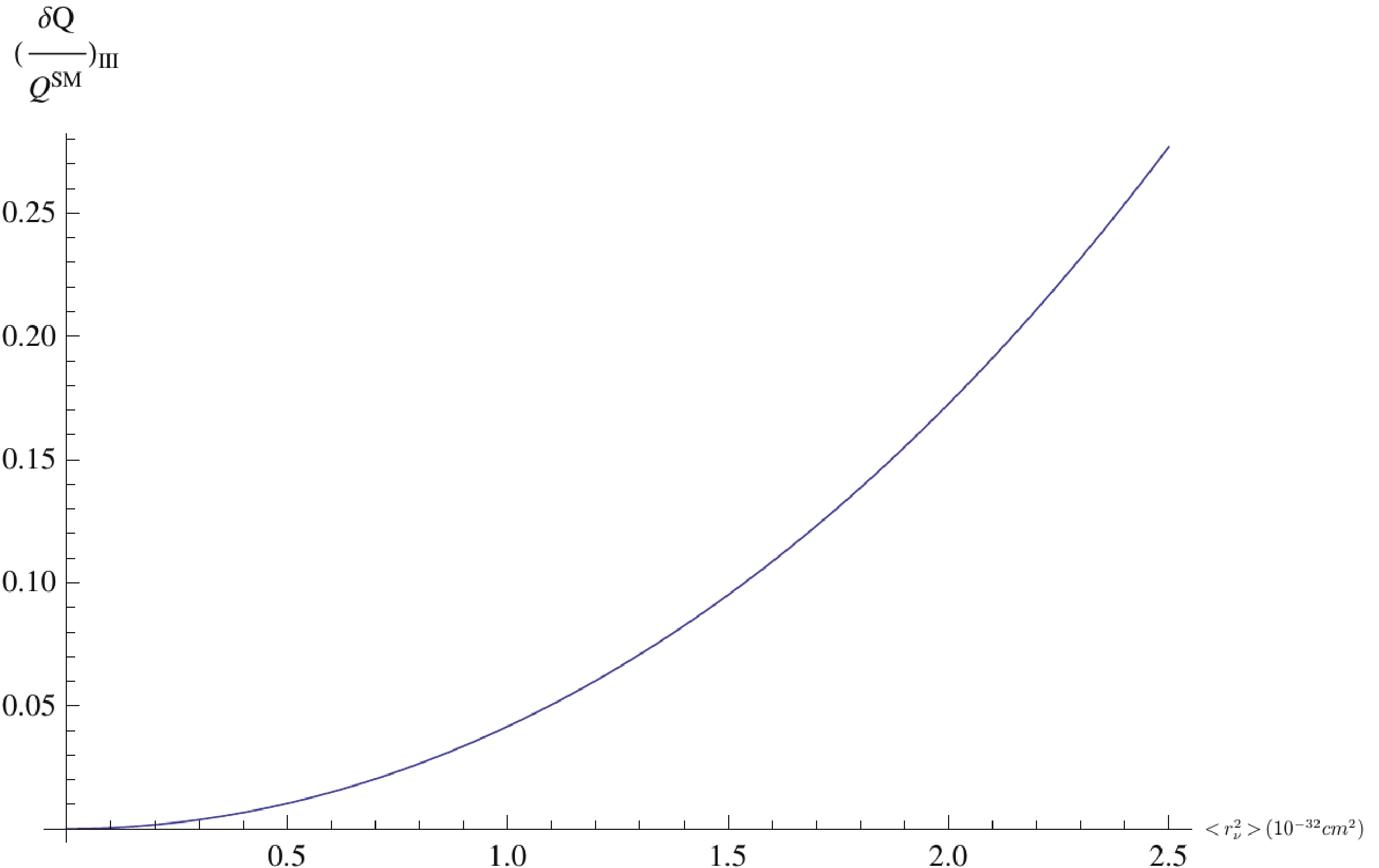
Figure 5. (color online) The ratio
$({\delta \mathcal{Q} / \mathcal{Q}^{\rm SM}})_{\rm III} = ({( \mathcal{Q} - \mathcal{Q}^{\rm SM})/ \mathcal{Q}^{\rm SM}})_{\rm III}$ as a function of the charge radius ($ <r_\nu^2>$ ).To conclude, in this study, we have calculated the charge radius and magnetic moment effects numerically for the electron neutrino. If τ neutrinos are considered, when their magnetic moments are
$ 10^6 $ times greater then of the electron neutrino, the effect of the indicated term becomes dominant, and the contribution of the magnetic moment becomes greater than the contribution of the charge radius for this situation. As an extension of this study, similar calculations can be done for plasmon decay and photo neutrino production. -
The author would like to express special thanks to Prof. Konstantin A. Kouzakov and Prof. A. Gutierrez-Rodriguez for their comments and useful discussions.
Role of neutrino form factors in the energy loss rates of the pair annihilation process
- Received Date: 2022-02-12
- Available Online: 2022-07-15
Abstract: The stellar energy loss rates due to the production of neutrino pairs






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: