-
Experimental measurements for the weak decays of charm and bottom mesons have inspired several theoretical studies exploring their dynamics [1–8]. The phenomenological analyses of the two-body hadronic decays of heavy flavor mesons have indicated the presence of significant nonfactorizable contributions. In the naïve factorization scheme, two QCD related coefficients, a1 and a2, are treated as parameters to be fixed from the experimental data while ignoring the nonfactorizable contribution to decay amplitudes [9–11]. Initially, data on the branching fractions of
$ D \to \bar K\pi $ decays seemed to require$ {a_1} \approx {c_1} = 1.26,\quad {a_2} \approx {c_2} = - 0.51, $ leading to destructive interference between color-favored (CF) and color-suppressed (CS) processes for$ {D^ + } \to {\bar K^0}{\pi ^ + }, $ thereby implying the$ {N_c} \to \infty $ limit [12, 13]. This limit, which was thought to be justified with the hope that the nonfactorizable part relative to the factorizable amplitude is of the order of$ 1/{N_c}, $ was expected to perform even better for B- meson decays, where the final state particles carry larger momenta than those of charm meson decays.However, the measurement of
$ \bar B \to D\pi $ meson decays did not later favor this result empirically because these decays require$ {a_1} \approx 1.03, $ and$ {a_2} \approx 0.23, $ i.e., a positive value of$ {a_2} $ , in sharp contrast to the expectations based on the large$ {N_c} $ limit. Thus, B- meson decays, revealing constructive interference between the CF and CS diagrams for$ {B^ - } \to {\pi ^ - }{D^0}, $ seem to favor$ {N_c} = 3 $ (real value). Even in the D-meson sector, the choice of the universal parameters$ {a_1} $ and$ {a_2} $ proved to be problematic when more accurate measurements were obtained for other decay modes of D-mesons, even after including final state interaction (FSI) effects [14, 15]. Consequently, charm meson decays have been thoroughly reinvestigated to explicitly study the nonfactorization contributions. Using the isospin analysis for the$ D \to \bar K\pi /\bar K\rho /{\bar K^*}\pi $ decay modes [16–19], these contributions are expressed in terms of two reduced matrix elements$ A_{1/2}^{nf},\;A_{3/2}^{nf}, $ and systematics were recognized. It was observed that in all these decays, the nonfactorizable isospin reduced amplitude$ A_{1/2}^{nf} $ not only has the same sign but also bears the same ratio (-1.12) as the$ A_{3/2}^{nf} $ reduced amplitude, within the experimental errors. It is worth noting that these systematics were also found to be consistent with those of the p-wave meson emitting decays of charm mesons,$D \to \bar K{a_1}/\pi {\bar K_1}/ \pi {\bar K_{ -1} }/ \pi {\bar K_0}/\bar K{a_2}$ [18].Extensive work has also been conducted to study nonfactorization contributions in charmed hadronic B-decays over the past two decades. Nonfactorizable terms may appear for several reasons, such as FSI rescattering effects and soft-gluon exchange around a basic weak vertex. The rescattering effects on the outgoing mesons have been studied in detail for bottom meson decays [20, 21]. Moreover, flavor SU(3) symmetry and the factorization assisted topological (FAT) approach have been employed for the study of such nonfactorizable contributions because they have the advantage of absorbing various types of contributions lump-sum in terms of a few parameters, which are to be fixed empirically [22, 23].
Inspired by these efforts, we investigate nonfactorizable contributions to the weak hadronic decays of bottom mesons, including the strong interaction phases possibly through FSI. It is well known that the strong phases of the decay amplitude in B-decays are significant, and many recent analyses of
$ \bar B \to \pi D/\rho D/\pi {D^*} $ decays have shown large strong phases. Because non-pertubative nonfactorizable contributions cannot be calculated from first principles, we employ isospin symmetry, which is reliable for hadronic interactions to gain insight into these contributions. We perform isospin analysis to study$ \bar B \to \pi D/\rho D/\pi {D^*} $ decay modes. Our aim is to investigate if such systematics, which were observed in charm meson decays, is valid for these decay modes, because their decay products also involve two different isospin states$ I = 1/2 $ and$ 3/2. $ We introduce strong phases, which affect the interference between the isospin-1/2 and isospin-3/2 amplitudes. Using the experimental measurements for their branching fractions, we first obtain three free parameters the two isospin amplitudes$ {A_{1/2}},\;{A_{3/2}} $ , and their relative strong phase. By determining the factorizable decay amplitudes for$ {N_c} = 3, $ we estimate the nonfactorizable isospin reduced amplitudes corresponding to these isospin states. We finally observe that the ratio of the nonfactorizable reduced amplitude in these isospin channels also follows a universal value for both decay modes$ \bar B \to \pi D/\bar B \to \rho D $ and$ \bar B \to \pi {D^*}. $ -
The effective weak Hamiltonian for CKM enhanced B-meson decays is given by
$ {H_w} = \frac{G_{\rm F}}{{\sqrt 2 }}{V_{cb}}V_{ud}^ * \left[ {{c_1}\left( {\overline d u} \right)\left( {\overline c b} \right) + {c_2}\left( {\overline c u} \right)\left( {\overline d b} \right)} \right], $

(1) where
${\bar q_1}{q_2} = {\bar q_1}{\gamma _\mu }\left( {1 - {\gamma _5}} \right){q_2}$ denotes the color singlet V−A Dirac current, and the QCD coefficients [23, 24] on the bottom mass scale are$ {c_1} = 1.132,\quad \quad {c_2} = - 0.287. $

(2) Because the current operators in the weak Hamiltonian are expressed in terms of fundamental quark fields, it is appropriate to have the Hamiltonian in a form such that one of these currents carries the same quantum numbers as one of the mesons emitted in the final state of bottom meson decays. Consequently, the hadronic matrix elements of an operator O receives contributions from the operator itself and the Fierz transformation of O, which generates the factorizable and nonfactorizable parts through the Fierz identity,
$\begin{aligned}[b](\bar du)(\bar cb) =& \frac{1}{{{N_c}}} (\bar cu)(\bar db) \\&+ \frac{1}{2}\left( {\overline c {\lambda ^a}\,u} \right)\left( {\overline d {\kern 1pt} {\lambda ^a}b} \right), \end{aligned}$

(3) where
${\bar q_1}{\lambda ^a}\,{q_2} \equiv \,{\bar q_1}{\kern 1pt} {\gamma _\mu }\,\left( {1 - {\gamma _5}\,} \right){\lambda ^a}{q_2}$ represents the color octet current. Performing a similar treatment on the other operator$(\overline c u)(\overline d b)$ , the weak Hamiltonian becomes$ H_w^{\rm CF} = \frac{G_{\rm F}}{{\sqrt 2 }}{V_{cb}}V_{ud}^ * \left[ {{a_1}{{\left( {\overline d u} \right)}_H}{{\left( {\overline c b} \right)}_H} + {c_2}H_w^8} \right], $

(4) $ H_w^{\rm CS} = \frac{G_{\rm F}}{{\sqrt 2 }}{V_{cb}}V_{ud}^ * \left[ {{a_2}{{\left( {\overline c u} \right)}_H}{{\left( {\overline d b} \right)}_H} + {c_1}\tilde H_w^8} \right], $

(5) $ {a_{1,2}} = {c_{1,2}} + \frac{{{c_{2,1}}}}{{{N_c}}}, $

(6) $\begin{aligned}[b]& H_w^8 = \frac{1}{2}\sum\limits_{a = 1}^8 {\left( {\overline c {\lambda ^a}\,u} \right)\left( {\overline d {\kern 1pt} {\lambda ^a}b} \right)} ,\\& \tilde H_w^8 = \frac{1}{2}\sum\limits_{a = 1}^8 {\left( {\overline d {\kern 1pt} {\lambda ^a}u} \right)\left( {\overline c {\lambda ^a}\,b} \right)} , \end{aligned}$

(7) which describe the color-favored (CF) and color-suppressed (CS) processes, respectively. Here, the index H in (4) and (5) indicates the change from the quark current to hadron field operator [4]. The matrix elements of the first terms in (4) and (5) lead to the factorizable contributions [4], and the second terms, involving the color octet currents, generate nonfactorized contributions.
-
The branching fraction for B-meson decay into two pseudoscalar mesons is related to its decay amplitude as follows:
$\begin{aligned}[b] B\left( {\bar B \to {P_1}{P_2}} \right) =& {\tau _B}{\left| {\frac{G_{\rm F}}{{\sqrt 2 }}{V_{cb}}V_{ud}^ * } \right|^2}\frac{p}{{8\pi m_B^2}}\\&\times{\left| {A\left( {\bar B \to {P_1}{P_2}} \right)} \right|^2} , \end{aligned}$

(8) where
$ {\tau _B} $ denotes the lifetime of B-mesons taken from [1],$\begin{aligned}[b] {\tau _{{{\bar B}^0}}} = (1.519 \pm 0.004) \times {10^{ - 12}}\;{\rm s}, \\ {\tau _{{B^ - }}} = (1.638 \pm 0.004) \times {10^{ - 12}}\;{\rm s}, \end{aligned}$

$ {V_{ud}}{V_{cb}}$ is the product of the Cabibbo–Kobayashi–Maskawa (CKM) matrix elements [1],$ {V_{ud}} = 0.975,{\kern 1pt} \;\;\;\;\;\;{V_{cb}} = 0.041 , $

and p is the magnitude of the three-momentum of the final state particles in the rest frame of the parent B- meson,
$\begin{aligned}[b] p =& \left| {{p_1}} \right| = \left| {{p_2}} \right| = \frac{1}{{2{m_B}}}\left[ \left\{ {m_B^2 - {{\left( {{m_1} + {m_2}} \right)}^2}} \right\}\right.\\&\times\left.\left\{ {m_B^2 - {{\left( {{m_1} - {m_2}} \right)}^2}} \right\} \right]^{1/2}. \end{aligned}$

(9) In heavy flavor meson decays, it has been observed that long distance strong FSI rescattering [20–21] of out-going mesons significantly affects their branching fractions. In general, such FSI phenomena can affect a decay amplitude in two ways: The decay amplitude may itself be modulated or it may acquire a phase. It has been shown by Kamal [25] that, in the weak scattering limit, the elastic FSI effect is mainly used to obtain a phase factor, i.e.,
$ {A^{\rm FSI}} = A\;{{\rm e}^{{\rm i}\delta }}. $

(10) Consequently, mixing of final states with the same quantum numbers can take place. Initially, it was expected that bottom meson decays may not be affected by FSI because the produced particles may not have sufficient time to interact, and there are no meson resonances near the B- meson mass corresponding to the quantum numbers of the final state. However, experimental data do not fulfill this naïve expectation [26].
To demonstrate this, we employ the isospin framework, in which
$ \bar B \to \pi D $ decay amplitudes are represented in terms of isospin reduced amplitudes, including the strong interaction phases$ \delta _{1/2}^{\pi D},\,\;\delta _{3/2}^{\pi D} $ in the Isospin -1/2 and 3/2 final states, respectively, as$ \begin{aligned}[b] A({{\bar B}^0} \to {\pi ^ - }{D^ + }) =& \frac{1}{{\sqrt 3 }}\left[ {A_{3/2}^{\pi D}{{\rm e}^{{\rm i}\delta _{3/2}^{\pi D}}} + \sqrt 2 A_{1/2}^{\pi D}{{\rm e}^{{\rm i}\delta _{1/2}^{\pi D}}}} \right], \\ A({{\bar B}^0} \to {\pi ^0}{D^0}) =& \frac{1}{{\sqrt 3 }}\left[ {\sqrt 2 A_{3/2}^{\pi D}{{\rm e}^{{\rm i}\delta _{3/2}^{\pi D}}} - A_{1/2}^{\pi D}{{\rm e}^{{\rm i}\delta _{1/2}^{\pi D}}}} \right], \\ A({B^ - } \to {\pi ^ - }{D^0}) =& \sqrt 3 A_{3/2}^{\pi D}{{\rm e}^{{\rm i}\delta _{3/2}^{\pi D}}}. \end{aligned} $

(11) These lead to the following relations:
$ \begin{aligned}[b] A_{1/2}^{\pi D} =& \left[{ \left| A({{\bar B}^0} \to {\pi ^ - }{D^ + }) \right|}^2 + \left| {A({{\bar B}^0} \to {\pi ^0}{D^0})} \right|^2\right. \\&\left. - \frac{1}{3}\left| {A({B^ - } \to {\pi ^ - }{D^0})} \right|^2 \right]^{1/2}, \\ A_{3/2}^{\pi D} = &\sqrt {\frac{1}{3}} \left| {A({B^ - } \to {\pi ^ - }{D^0})} \right|, \end{aligned} $

(12) and the relative phase difference,
$ \delta _{}^{\pi D} = \delta _{1/2}^{\pi D} - \delta _{3/2}^{\pi D}, $ is given by$\begin{aligned}[b]\\[-5pt] {Cos} \delta _{}^{\pi D} = \frac{{(3{{\left| {A({{\bar B}^0} \to {\pi ^ - }{D^ + })} \right|}^2} - 6{{\left| {A({{\bar B}^0} \to {\pi ^0}{D^0})} \right|}^2} + {{\left| {A({B^ - } \to {\pi ^ - }{D^0})} \right|}^2})}}{{6\sqrt 2 \left| {A_{1/2}^{\pi D}} \right|\left| {A_{3/2}^{\pi D}} \right|}}.\\ \end{aligned}$ 
(13) Thus,
$ A_{1/2}^{\pi D} $ and$ A_{3/2}^{\pi D} $ can be treated as real quantities in the following analysis:Using the experimental values [1]
$ B\left( {{{\bar B}^0} \to {\pi ^ - }{D^ + }} \right) = \left( {2.52 \pm 0.13} \right) \times {10^{ - 3}}, $

$ B\left( {{{\bar B}^0} \to {\pi ^0}{D^0}} \right) = \left( {2.63 \pm 0.14} \right) \times {10^{ - 4}}, $

$ B\left( {{B^ - } \to {\pi ^ - }{D^0}} \right) = \left( {4.68 \pm 0.13} \right) \times {10^{ - 3}}, $

we obtain
$\begin{aligned}[b] A_{1/2}^{\pi D}{\,^{\exp }} = &\pm \left( {1.273 \pm 0.065} \right){\;\rm Ge{V^3}},\\A{_{3/2}^{\pi D\,}\,^{\exp }} =& \pm \left( {1.323 \pm 0.018} \right){\;\rm Ge{V^3}}, \end{aligned}$

(14) and the phase difference
$ {\delta ^{\pi D}} = \left( {28 \pm 7} \right){^\circ } , $

(15) which agrees with the final state rescattering analysis [22]. Although this phase difference is relatively smaller than that of the
$ D \to \bar K\pi $ mode$ {\delta ^{}} = \left( {86 \pm 7} \right){^\circ } , $ it certainly indicates the presence of non-vanishing strong phases in the B- meson sector.We express the decay amplitude as a sum of the factorizable and nonfactorizable parts,
$ A(\bar B \to \pi D) = {A^f}(\bar B \to \pi D) + {A^{n{\kern 1pt} f}}(\bar B \to \pi D), $

(16) arising from the respective terms of the weak Hamiltonian given in (4) and (5).
Using the factorization scheme, the spectator-quark parts of the decay amplitudes arising from W- emission① diagrams are derived for the following classes of
$ \bar B \to \pi D $ decays:(a) Class I: Color favored (CF)
$ {A^f}({\bar B^0} \to {\pi ^ - }{D^ + }) = {a_1}{f_\pi }\left( {m_B^2 - m_D^2} \right){\kern 1pt} F_0^{\bar BD}\left( {m_\pi ^2\,} \right), $

(17) (b) Class II: Color Suppressed (CS)
$ {A^f}({\bar B^0} \to {\pi ^0}{D^0}) = - \frac{1}{{\sqrt 2 }}{a_2}{f_D}\left( {m_B^2 - m_\pi ^2} \right){\kern 1pt} F_0^{\bar B\pi }\left( {m_D^2\,} \right), $

(18) (c) Class III : Interference of CF and CS
$\begin{aligned}[b] {A^f}({B^ - } \to {\pi ^ - }{D^0}) =& {a_1}{f_\pi }\left( {m_B^2 - m_D^2} \right){\kern 1pt} F_0^{\bar BD}\left( {m_\pi ^2\,} \right) \\&+ {a_2}{f_D}\left( {m_B^2 - m_\pi ^2} \right){\kern 1pt} F_0^{\bar B\pi }\left( {m_D^2\,} \right)\,. \end{aligned}$

(19) We calculate the values of the factorization contributions for
$ {N_c} = 3 $ (real value) using numerical inputs for decay constants taken as$\begin{aligned}[b] {f_D} =& \left( {0.207 \pm 0.009} \right){\;\rm GeV},\\{f_\pi } =& \left( {0.131 \pm 0.002} \right)\;{\rm GeV}, \end{aligned}$

(20) from the leptonic decays of D and π mesons, respectively [27].
Assuming nearest pole dominance, momentum dependence of the form-factors, appearing in the decay amplitudes given in (17–19), is taken as
$ {F_0}\left( {{q^2}} \right) = \frac{{{F_0}\left( 0 \right)}}{{{{\left( {1 - {\raise0.7ex\hbox{${{q^2}}$} \mathord{\left/ {\vphantom {{{q^2}} {m_s^2}}}\right.} \lower0.7ex\hbox{${m_s^2}$}}} \right)}^n}}}, $

(21) where the pole masses are given by the scalar meson carrying the quantum number of the corresponding weak current, which are ms = 5.78 GeV and ms = 6.80 GeV, and n = 1 for the monopole formula. The form-factors
$ F _0^{}\left( {0\,} \right) $ at q2 =0 are taken from [28], as given below.$ \begin{aligned}[b] {\kern 1pt} F_0^{\bar B\pi }\left( {0\,} \right) =& \left( {0.27 \pm 0.05} \right), \\ F_0^{\bar BD}\left( {0\,} \right) =& \left( {0.66 \pm 0.03} \right). \end{aligned} $

(22) We finally obtain
$ \begin{aligned}[b] {A^f}({{\bar B}^0} \to {\pi ^ - }{D^ + }) = 2.180 \pm \;0.099\;{{\rm{GeV}}^3}, \hfill \\ {A^f}({{\bar B}^0} \to {\pi ^0}{D^0}) = - 0.111 \pm \;0.021\; {{\rm{GeV}}^3}, \hfill \\ {A^f}({B^ - } \to {\pi ^ - }{D^0}) = 2.339 \pm \;0.103 \;{{\rm{GeV}}^3}. \hfill \\ \end{aligned} $

(23) Exploiting the following isospin relations:
$ \begin{gathered} A_{1/2}^f(\bar B \to \pi D) = \frac{1}{{\sqrt 3 }}\left\{ {\sqrt 2 {A^f}({{\bar B}^0} \to {\pi ^ - }{D^ + }) - {A^f}({{\bar B}^0} \to {\pi ^0}{D^0})} \right\}, \hfill \\ A_{3/2}^f(\bar B \to \pi D) = \frac{1}{{\sqrt 3 }}\left\{ {{A^f}({{\bar B}^0} \to {\pi ^ - }{D^ + }) + \sqrt 2 {A^f}({{\bar B}^0} \to {\pi ^0}{D^0})} \right\}, \hfill \\ \end{gathered} $

(24) we obtain
$\begin{aligned}[b] A_{1/2}^f =& \left( {1.845 \pm 0.082} \right){\kern 1pt} {\kern 1pt} {{\rm{GeV}}^3},\\ A_{3/2}^f =& \left( {1.168 \pm 0.060} \right){\kern 1pt} {\rm{GeV}}{^3}. \end{aligned}$

(25) Using isospin C. G. coefficients with the convention used in [17, 18], the nonfactorizable part of the decay amplitudes can be expressed in terms of the scattering amplitudes for the spurion +
$ \bar B \to \pi D $ process.$ \begin{aligned}[b] &{A^{n{\kern 1pt} f}}({{\bar B}^0} \to {\pi ^ - }{D^ + }) = \frac{1}{3}{c_2}\left( {\left\langle {\pi D\left\| {\left. {H_w^8} \right\|} \right.} \right.{{\left. {\bar B} \right\rangle }_{3/2}} + 2\left\langle {\pi D\left\| {\left. {H_w^8} \right\|} \right.} \right.{{\left. {\bar B} \right\rangle }_{1/2}}} \right), \\ &{A^{n{\kern 1pt} f}}({{\bar B}^0} \to {\pi ^0}{D^0}) = \frac{{\sqrt 2 }}{3}{c_1}\left( {\left\langle {\pi D\left\| {\left. {\tilde H_w^8} \right\|} \right.} \right.{{\left. {\bar B} \right\rangle }_{3/2}} - \left\langle {\pi D\left\| {\left. {\tilde H_w^8} \right\|} \right.} \right.{{\left. {\bar B} \right\rangle }_{1/2}}} \right), \\ & {A^{nf}}({B^ - } \to {\pi ^ - }{D^0}) = {c_2}\left\langle {\pi D\left\| {\left. {H_w^8} \right\|} \right.} \right.{\left. {\bar B} \right\rangle _{3/2}} + {c_1}\left\langle {\pi D\left\| {\left. {\tilde H_w^8} \right\|} \right.} \right.{\left. {\bar B} \right\rangle _{3/2}}. \end{aligned} $

(26) At present, there is no available technique to exactly calculate these quantities from the theory of strong interactions. Therefore, by subtracting the factorizable part (25) from the experimental decay amplitude (14), we determine the nonfactorizable isospin reduced amplitudes,
$\begin{aligned}[b] A_{1/2}^{nf} =& - \left( {0.572 \pm 0.105} \right)\;{\rm Ge{V^3}},\\ A_{3/2}^{nf} =& - \left( {2.491 \pm 0.062} \right)\;{\rm Ge{V^3}},\end{aligned} $

(27) by choosing positive and negative values for
$ A_{1/2}^{nf} $ and$ A_{3/2}^{nf} $ , respectively. Their ratio is$ \alpha = {{A_{1/2}^{nf}}}/{{A_{3/2}^{nf}}} = 0.229 \pm 0.042. $

(28) There are several calculations for form factors, obtained from different approaches in literature, which are given in Table 1.
Table 1. Form-factor of
$ \bar B \to D $ and$ \bar B \to \pi $ transitions at maximum recoil (q2 =0).To observe the effect of form-factor variation on our analysis, we give the ratio
$ \alpha $ in Table 2 for the maximum and minimum values of the form-factors, which are consistent with (28) within errors.$ F_0^{\bar BD}\left( {0\,} \right) $ 

0.69 0.69 0.63 0.63 $ F_0^{\bar B\pi }\left( {0\,} \right) $ 

0.32 0.22 0.32 0.22 $ \alpha $ 

0.262 0.249 0.207 0.195 Table 2. Ratio
$ \alpha = {{A_{1/2}^{nf}}}/{{A_{3/2}^{nf}}} $ for maximum and minimum values of form-factors.We also plot the dependence of
$ \alpha $ on form-factors$ F_0^{\bar BD}(0) $ and$ F_0^{\bar B\pi }(0) $ in Fig. 1, which shows that$ \alpha $ is not quite sensitive to them. -
Using the branching fraction,
$ B\left( {\bar B \to PV} \right) = {\tau _B}{\left| {\frac{G_{\rm F}}{{\sqrt 2 }}{V_{cb}}V_{ud}^ * } \right|^2}\frac{{{p^3}}}{{8\pi m_V^2}}{\left| {A\left( {\bar B \to PV} \right)} \right|^2}. $

(29) Because the isospin structure of
$ \bar B \to \rho D $ decays is exactly the same as that of$ \bar B \to \pi D $ decays,$ \begin{aligned}[b] &A({{\bar B}^0} \to {\rho ^ - }{D^ + }) = \frac{1}{{\sqrt 3 }}\left[ {A_{3/2}^{\rho D}{{\rm e}^{{\rm i}\delta _{3/2}^{\rho D}}} + \sqrt 2 A_{1/2}^{\rho D}{{\rm e}^{{\rm i}\delta _{1/2}^{\rho D}}}} \right], \hfill \\ & A({{\bar B}^0} \to {\rho ^0}{D^0}) = \frac{1}{{\sqrt 3 }}\left[ {\sqrt 2 A_{3/2}^{\rho D}{{\rm e}^{{\rm i}\delta _{3/2}^{\rho D}}} - A_{1/2}^{\rho D}{{\rm e}^{{\rm i}\delta _{1/2}^{\rho D}}}} \right], \hfill \\ & A({B^ - } \to {\rho ^ - }{D^0}) = \sqrt 3 A_{3/2}^{\rho D}{{\rm e}^{{\rm i}\delta _{1/2}^{\rho D}}}. \hfill \\ \end{aligned} $

(30) We repeat the same procedure as before. Using the experimental branching fractions
$ \begin{gathered} B\left( {{{\bar B}^0} \to {\rho ^ - }{D^ + }} \right) = \left( {7.6 \pm 1.2} \right) \times {10^{ - 3}}, \hfill \\ B\left( {{{\bar B}^0} \to {\rho ^0}{D^0}} \right) = \left( {3.21 \pm 0.21} \right) \times {10^{ - 4}}, \hfill \\ B\left( {{B^ - } \to {\rho ^ - }{D^0}} \right) = \left( {1.34 \pm 0.18} \right) \times {10^{ - 2}}, \hfill \\ \end{gathered} $

we obtain the total isospin reduced amplitudes
$ \begin{aligned}[b]&A{_{1/2}^{\rho D}\,^{\exp }} = \pm \left( {0.143 \pm 0.025} \right)\;{\rm Ge{V^2}},\\&A{_{3/2}^{\rho D}\,^{\exp }} = \pm \left( {0.149 \pm 0.010} \right)\;\rm Ge{V^2},\end{aligned} $

(31) and the phase difference
$ {\delta ^{\rho {\kern 1pt} {\kern 1pt} D}} \equiv \delta _{1/2}^{\rho D} - \delta _{3/2}^{\rho D} = {\left( {8\;_{ - 8}^{ + 30}} \right)^ \circ }. $

(32) The factorizable decay amplitudes of the spectator-quark diagrams can be expressed as
$ \begin{gathered} {A^f}({{\bar B}^0} \to {\rho ^ - }{D^ + }) = 2{a_1}{m_\rho }{f_\rho }F_1^{\bar BD}\left( {m_\rho ^2} \right), \hfill \\ {A^f}({{\bar B}^0} \to {\rho ^0}{D^0}) = - \sqrt 2 {a_2}{f_D}{m_\rho }A_0^{\bar B\rho }\left( {m_D^2} \right), \hfill \\ {A^f}({B^ - } \to {\rho ^ - }{D^0}) = {a_1}2{m_\rho }{f_\rho }F_1^{\bar BD}\left( {m_\rho ^2} \right) + {a_2}{f_D}2{m_\rho }A_0^{\bar B\rho }\left( {m_D^2} \right). \hfill \\ \end{gathered} $

(33) It has been noted in the BSW II model [3] that consistency with heavy quark symmetry requires certain form- factors, such as
$ {F_1}(0) $ and$ {A_0}(0), $ to have dipole q2 dependence (n=2) in$\begin{aligned}[b] {F_1}\left( {{q^2}} \right) = \frac{{{F_1}\left( 0 \right)}}{{{{\left( {1 - {\raise0.7ex\hbox{${{q^2}}$} \mathord{\left/ {\vphantom {{{q^2}} {m_V^2}}}\right.} \lower0.7ex\hbox{${m_V^2}$}}} \right)}^n}}},\;\;\; {A_0}\left( {{q^2}} \right) = \frac{{{A_0}\left( 0 \right)}}{{{{\left( {1 - {\raise0.7ex\hbox{${{q^2}}$} \mathord{\left/ {\vphantom {{{q^2}} {m_P^2}}}\right.} \lower0.7ex\hbox{${m_P^2}$}}} \right)}^n}}}, \end{aligned}$

(34) where the vector V(1–) meson and pseudoscalar P(0–) meson pole masses are 6.34 and 5.27 GeV, respectively.
Decay constant values are taken from [27] as
$\begin{aligned}[b]& {f_D} = \left( {0.207 \pm 0.009} \right)\;{\rm GeV},\\&{f_\rho } = \left( {0.215 \pm 0.005} \right)\;{\rm GeV}, \end{aligned}$

(35) and form-factors for
$ \bar B \to V $ transitions are chosen from [33],$ {\kern 1pt} A_0^{\bar B\rho }\left( {0\,} \right) = 0.356 \pm 0.042, $

(36) where the
$ F_0^{\bar BD}\left( {0\,} \right) $ value is taken from Eq. (22).$ {\kern 1pt} F_1^{\bar BD}\left( {0\,} \right) = F_0^{\bar BD}\left( {0\,} \right) = 0.66 \pm 0.03. $

(37) Thus, we calculate the factorizable contributions to the decay amplitudes,
$ \begin{aligned}[b] & {A^f}({{\bar B}^0} \to {\rho ^ - }{D^ + }) = \left( {0.235 \pm 0.011} \right)\;{\rm Ge{V^2}}, \hfill \\ & {A^f}({{\bar B}^0} \to {\rho ^0}{D^0}) = - \left( {0.010 \pm 0.001} \right)\;{\rm Ge{V^2}}, \hfill \\ & {A^f}({B^ - } \to {\rho ^ - }{D^0}) = \left( {0.248 \pm 0.011} \right)\;{\rm Ge{V^2}}, \hfill \\ \end{aligned} $

(38) thereby the isospin reduced amplitudes of the factorized amplitudes are calculated as
$\begin{aligned}[b]& A_{1/2}^f = \left( {0.197 \pm 0.009} \right) \;{\rm Ge{V^2}},\\& A_{3/2}^f = \left( {0.127 \pm 0.006} \right) \;{\rm Ge{V^2}}. \end{aligned}$

(39) Following the procedure discussed for
$ \bar B \to \pi D $ , we determine the nonfactorizable reduced isospin amplitudes$\begin{aligned}& A_{1/2}^{nf} = - \left( {0.054 \pm 0.026} \right){\kern 1pt} {\kern 1pt} \;{\rm Ge{V^2}},\\& A_{3/2}^{nf} = - \left( {0.277 \pm 0.012} \right){\kern 1pt} \;{\rm Ge{V^2}}, \end{aligned}$

(40) which bear the following ratio:
$ \alpha = \frac{{A_{1/2}^{nf}}}{{A_{3/2}^{nf}}} = 0.200 \pm 0.096. $

(41) There are also existing calculations for
$ A_0^{\bar B\rho }\left( {0\,} \right) $ , which are given in Table 3. To show the effect of form-factors on our analysis, we obtain the ratio$ \alpha = {{A_{1/2}^{nf}}}/{{A_{3/2}^{nf}}} $ for the maximum and minimum value of the form factors given in Table 4, which are consistent with (41) within errors. This is also shown in Fig. 2.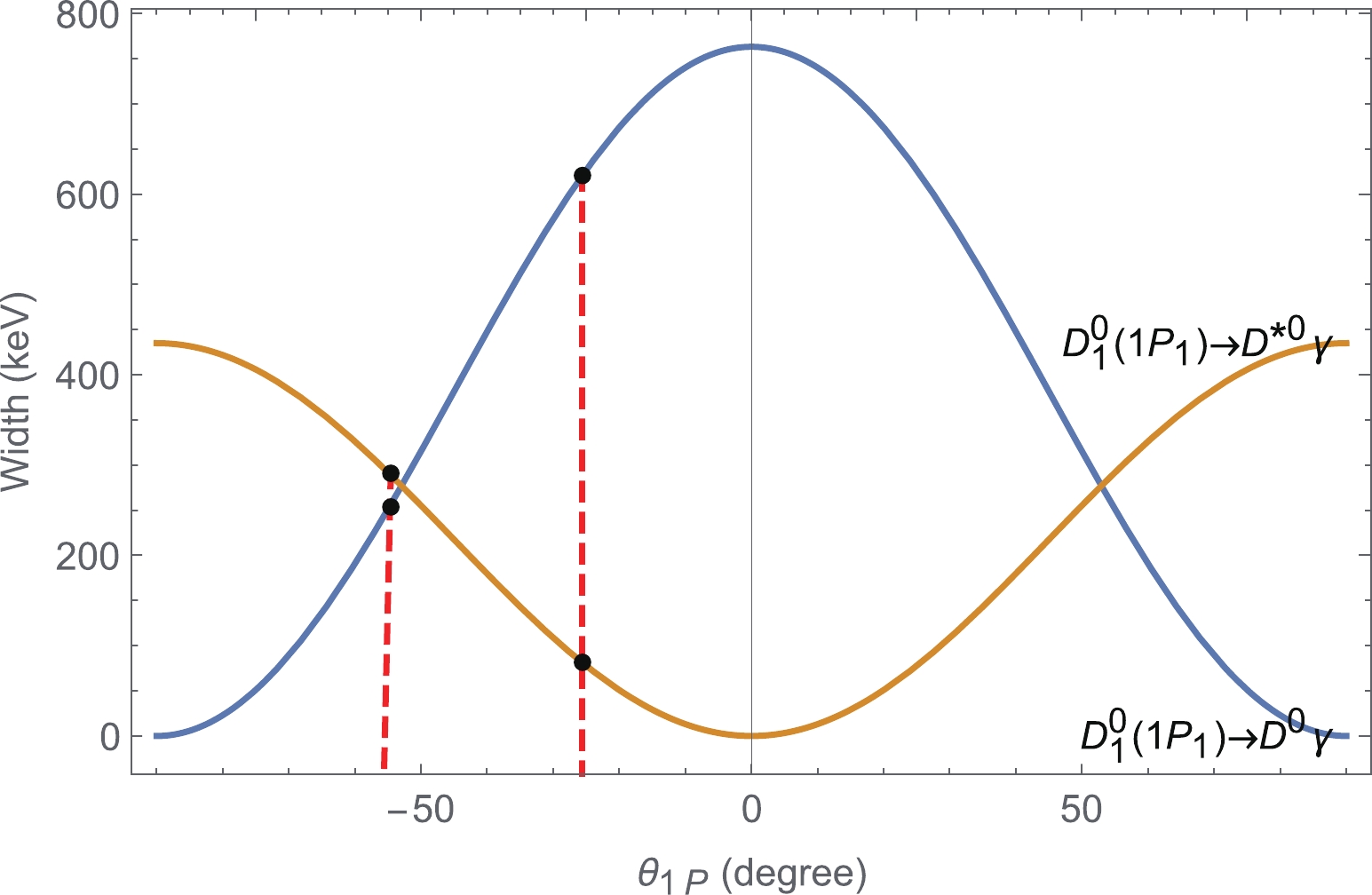
Figure 2. (color online) Variation in
$ \alpha $ with form factors$ F_0^{\bar BD}(0) $ and$ F_0^{\bar B\rho }(0) $ .Table 3. Form-factor of
$ \bar B \to \rho $ transitions at maximum recoil (q2 =0).$ F_0^{\bar BD}\left( {0\,} \right) $ 

0.69 0.69 0.63 0.63 $ A_0^{\bar B\rho }\left( {0\,} \right) $ 

0.40 0.31 0.40 0.31 $ \alpha $ 

0.226 0.219 0.171 0.158 Table 4. Ratio
$ \alpha = {{A_{1/2}^{nf}}}/{{A_{3/2}^{nf}}} $ for maximum and minimum values of form-factors. -
Including the strong phases between the isospin I=1/2 and 3/2 states, the decay amplitudes are given by
$ \begin{aligned}[b] &A({{\bar B}^0} \to {\pi ^ - }{D^*}^ + ) = \frac{1}{{\sqrt 3 }}\left[ {A_{3/2}^{\pi {D^*}}{{\rm e}^{{\rm i}\delta _{3/2}^{\pi {D^*}}}} + \sqrt 2 A_{1/2}^{\pi {D^*}}{{\rm e}^{{\rm i}\delta _{1/2}^{\pi {D^*}}}}} \right], \hfill \\ &A({{\bar B}^0} \to {\pi ^0}{D^*}^0) = \frac{1}{{\sqrt 3 }}\left[ {\sqrt 2 A_{3/2}^{\pi {D^*}}{{\rm e}^{{\rm i}\delta _{3/2}^{\pi {D^*}}}} - A_{1/2}^{\pi {D^*}}{{\rm e}^{{\rm i}\delta _{1/2}^{\pi {D^*}}}}} \right], \hfill \\ &A({B^ - } \to {\pi ^ - }{D^*}^0) = \sqrt 3 A_{3/2}^{\pi {D^*}}{{\rm e}^{{\rm i}\delta _{3/2}^{\pi {D^*}}}}. \hfill \\ \end{aligned} $

(42) Using the experimental values of branching fractions [1],
$ \begin{aligned}[b] & B\left( {{{\bar B}^0} \to {\pi ^ - }{D^{* + }}} \right) = \left( {2.74 \pm 0.13} \right) \times {10^{ - 3}}, \hfill \\ & B\left( {{{\bar B}^0} \to {\pi ^0}{D^{*0}}} \right) = \left( {2.20 \pm 0.60} \right) \times {10^{ - 4}}, \hfill \\ & B\left( {{B^ - } \to {\pi ^ - }{D^{*0}}} \right) = \left( {4.90 \pm 0.17} \right) \times {10^{ - 3}}, \hfill \\ \end{aligned} $

we calculate the total isospin reduced amplitudes
$\begin{aligned}[b]& A{_{1/2}^{\pi {D^*}}\,^{\exp }} = \pm \left( {0.226 \pm 0.042} \right)\;{\rm Ge{V^2}},\\&A{_{3/2}^{\pi {D^*}}\,^{\exp }} = \pm \left( {0.231 \pm 0.040} \right)\;{\rm Ge{V^2}},\end{aligned} $

(43) and the phase difference
$ {\delta ^{\,\pi {D^*}}} = {\left( {24 \pm 24} \right)^ \circ }. $

(44) Therefore, the
$ \bar B \to PV $ decays also indicate the presence of strong FSI phases, as also observed in [17, 18].The factorizable amplitudes for this mode are
$ \begin{aligned}[b] {A^f}({{\bar B}^0} \to {\pi ^ - }{D^{ * + }}) =& 2{a_1}{m_{{D^ * }}}{f_\pi }A_0^{\bar B{D^ * }}\left( {m_\pi ^2} \right), \hfill \\ {A^f}({{\bar B}^0} \to {\pi ^0}{D^{ * 0}}) =& - \sqrt 2 {a_2}{f_{{D^ * }}}{m_{{D^ * }}}F_1^{\bar B\pi }\left( {m_{{D^ * }}^2} \right), \hfill \\ {A^f}({B^ - } \to {\pi ^ - }{D^{ * 0}}) =& {a_1}2{m_{{D^ * }}}{f_\pi }A_0^{\bar B{D^ * }}\left( {m_\pi ^2} \right) \\&+ {a_2}{f_{{D^ * }}}2{m_{{D^ * }}}F_1^{\bar B\pi }\left( {m_{{D^ * }}^2} \right). \hfill \\ \end{aligned} $

(45) Using the decay constant values [27]
$\begin{aligned}[b]& {f_{{D^*}}} = \left( {0.245 \pm 0.034} \right)\;{\rm GeV},\\& {f_\pi } = \left( {0.131 \pm 0.002} \right)\;{\rm GeV}, \end{aligned}$

(46) and the form-factor
$ A_0^{\bar B{D^*}}\left( {0\,} \right) = \left( {0.68 \pm 0.04} \right), $

(47) taken from [27], with pole masses
$ V({1^ - }) = 5.32 $ GeV and$ P({0^ - }) = 6.28 $ GeV for$ {q^2} $ -dependence (34),$ F_1^{\bar B\pi }\left( {0\,} \right) = F_0^{\bar B\pi }\left( {0\,} \right) = (0.27 \pm 0.05), $

we calculate the factorized amplitudes as
$ \begin{aligned}[b] & {A^f}({{\bar B}^0} \to {\pi ^ - }{D^{ * + }}) = \left( {0.371 \pm 0.022} \right)\;{\rm Ge{V^2}}, \hfill \\ & {A^f}({{\bar B}^0} \to {\pi ^0}{D^{ * 0}}) = - \left( {0.023 \pm 0.004} \right)\;{\rm Ge{V^2}}, \hfill \\ & {A^f}({B^ - } \to {\pi ^ - }{D^{ * 0}}) = \left( {0.403 \pm 0.023} \right)\;{\rm Ge{V^2}}, \hfill \\ \end{aligned} $

(48) which in turn yield the isospin reduced amplitudes
$\begin{aligned}[b]& A_{1/2}^f = \left( {0.317 \pm 0.018} \right){\kern 1pt} \;{\rm Ge{V^2}},\\& A_{3/2}^f = \left( {0.196 \pm 0.013} \right){\kern 1pt} \;{\rm Ge{V^2}}. \end{aligned}$

(49) Subtracting the factorizable parts from the total experimental amplitudes, we calculate
$\begin{aligned}[b] &A_{1/2}^{nf} = - \left( {0.090 \pm 0.046} \right){\kern 1pt} \;{\rm Ge{V^2}},\\& A_{3/2}^{nf} = - \left( {0.426 \pm 0.042} \right){\kern 1pt} \;{\rm Ge{V^2}}, \end{aligned}$

(50) with the following ratio:
$ \alpha = \frac{{A_{1/2}^{nf}}}{{A_{3/2}^{nf}}} = 0.211 \pm 0.109. $

(51) In literature, we find different values of the
$ A_0^{\bar B{D^ * }}\left( {0\,} \right) $ form-factor, as shown in Table 5. We calculate the ratio$ \alpha $ for the maximum and minimum values of the form-factors, as shown in Table 6, and plot the variation in$ \alpha $ in Fig. 3. Although$ \alpha $ remains insensitive to the$ F_0^{\bar B\pi }(0) $ form-factor, it increases slowly for large values of$ A_0^{\bar B{D^*}}(0) $ . However, considering the near equality of the ratio$ \alpha $ for$ \bar B \to \pi D/\rho D/\pi {D^*}, $ we expect a higher value of$ A_0^{\bar B{D^*}}(0) $ is less likely.
Figure 3. (color online) Variation in
$ \alpha $ with form factors$ A_0^{\bar B{D^*}}(0) $ and$ F_0^{\bar B\pi }(0) $ Table 5. Form-factor of the
$ \bar B \to {D^*} $ transitions at maximum recoil (q2 =0).$ A_0^{\bar B{D^*}}\left( {0\,} \right) $ 

0.72 0.72 0.64 0.64 $ F_0^{\bar B\pi }\left( {0\,} \right) $ 

0.32 0.22 0.32 0.22 $ \alpha $ 

0.264 0.245 0.192 0.173 Table 6. Ratio
$\alpha = {{A_{1/2}^{nf}}}/{{A_{3/2}^{nf}}}$ for maximum and minimum values of form-factors. -
The purpose of performing an isospin analysis on the
$ \bar B \to \pi D $ and$ \bar B \to \rho D/\pi {D^*} $ decays is to search for systematics, which have previously been identified in the charm sector [17, 18]. By choosing a positive sign for$ A_{1/2}^{\exp } $ and a negative sign for$ A_{3/2}^{\exp } $ in each case, we obtain the same value of the ratio of the corresponding nonfactorizable reduced matrix elements$ A_{1/2}^{nf} $ and$ A_{3/2}^{nf} $ , i.e.,$ \begin{gathered} \frac{{A_{1/2}^{nf}(\bar B \to \pi D)}}{{A_{3/2}^{nf}(\bar B \to \pi D)}} = \frac{{A_{1/2}^{nf}(\bar B \to \rho D)}}{{A_{3/2}^{nf}(\bar B \to \rho D)}}\, = \frac{{A_{1/2}^{nf}(\bar B \to \pi {D^*})}}{{A_{3/2}^{nf}(\bar B \to \pi {D^*})}}\quad , \hfill \\ 0.229 \pm 0.042\;\;\;\;\;\;\;0.200 \pm 0.096\;\;\;\quad \;0.211 \pm 0.109 \\[-10pt] \end{gathered} $

(52) and note that
$ A_{1/2}^{nf} $ has a negative sign for the cases$ A_{1/2}^{nf}(\bar B \to \pi D) = - \left( {0.572 \pm 0.105} \right)\;{\rm Ge{V^3}}, $

(53) $ A_{1/2}^{nf}(\bar B \to \rho D) = - \left( {0.054 \pm 0.026} \right)\;{\rm Ge{V^2}}, $

(54) $ A_{1/2}^{nf}(\bar B \to \pi {D^ * }) = - \left( {0.090 \pm 0.046} \right)\;{\rm Ge{V^2}}. $

(55) We can generically predict the sum of the branching fractions of the
$ {\bar B^0} - $ meson decays in the respective modes considered here as$ \begin{aligned}[b]&{B_{ - \, + }} + {B_{0\,0}}\\=& \frac{{{\tau _{{{\bar B}^0}}}}}{{3{\tau _{{B^ - }}}}}{B_{0 - }}\left[ {1 + {{\left\{ {\alpha + \frac{{\left( {\sqrt 2 - \alpha } \right)A_{ - + }^f - \left( {1 + \sqrt 2 \alpha } \right)A_{00}^f}}{{{A_{0 - }}}}} \right\}}^2}} \right], \end{aligned}$

(56) where
$ \alpha $ has been defined previously (27), and the experimental decay amplitude of the$ {B^ - } $ decays is$ {A_{0 - }} = \sqrt {\frac{{{B_{0 - }}}}{{{\tau _{{B^ - }}} \times \left( {\rm kinematic\;factor} \right)}}} \;, $

where the subscripts -+, 00, and 0- denote the charge states of the non-charm and charm mesons emitted in each case. Taking the average value of α = 0.22, we predict
$ \begin{aligned}[b] B\left( {{{\bar B}^0} \to {\pi ^ - }{D^ + }} \right) + B\left( {{{\bar B}^0} \to {\pi ^0}{D^0}} \right) =& (0.28 \pm 0.02){\text{%}}\quad {\rm Theo}, \\ = &(0.28 \pm 0.01){\text{%}}\quad {\rm Expt}; \end{aligned} $

(57) $ \begin{aligned}[b] B\left( {{{\bar B}^0} \to {\rho ^ - }{D^ + }} \right) + B\left( {{{\bar B}^0} \to {\rho ^0}{D^0}} \right) =& (0.76 \pm 0.13){\text{%}}\quad {\rm Theo}, \\ =& (0.79 \pm 0.12){\text{%}}\quad {\rm Expt}; \end{aligned} $

(58) $ \begin{aligned}[b] B\left( {{{\bar B}^0} \to {\pi ^ - }{D^{* + }}} \right) + B\left( {{{\bar B}^0} \to {\pi ^0}{D^{*0}}} \right) =& (0.29 \pm 0.04){\text{%}}\quad {\rm Theo}, \\ =& (0.30 \pm 0.01){\text{%}}\quad {\rm Expt}; \\ \end{aligned} $

(59) which are in good agreement with the experiment. To show that this agreement is not coincidental and to study the sensitivity of the sum of the
$ {\bar B^0} $ branching fractions with the ratio α, we plot$\sum {B\left( {{{\bar B}^0} \to\rm decays} \right)}$ against α by treating it as a free parameter for all three cases, which are shown in Figs. 4, 5, and 6. Clearly, the experiment data indicate α = 0.22 consistently. The broken curves represent the errors due to the decay constant, form factors, and branching fractions. The horizontal lines correspond to the experimental value of the sum, and its errors are indicated by broken lines.
Figure 4. (color online) Variation in the sum of
$ B\left( {{{\bar B}^0} \to {\pi ^ - }{D^ + }} \right) $ and$ B\left( {{{\bar B}^0} \to {\pi ^0}{D^0}} \right) $ with the ratio$ \alpha = {{A_{1/2}^{nf}} \mathord{\left/ {\vphantom {{A_{1/2}^{nf}} {A_{3/2}^{nf}}}} \right. } {A_{3/2}^{nf}}}. $ 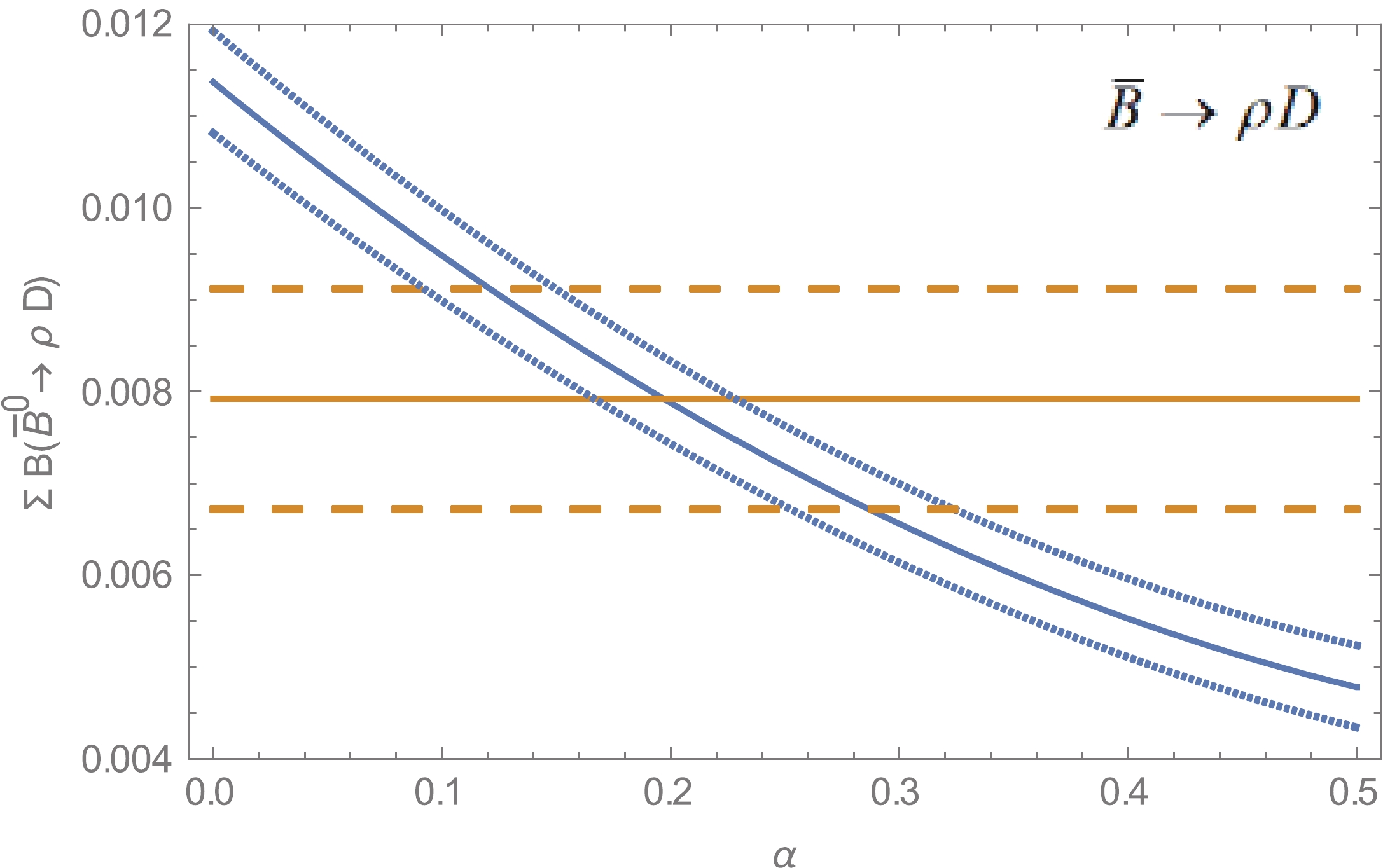
Figure 5. (color online) Variation in the sum of
$ B\left( {{{\bar B}^0} \to {\rho ^ - }{D^ + }} \right) $ and$ B\left( {{{\bar B}^0} \to {\rho ^0}{D^0}} \right) $ with the ratio$ \alpha = {{A_{1/2}^{nf}} \mathord{\left/ {\vphantom {{A_{1/2}^{nf}} {A_{3/2}^{nf}}}} \right. } {A_{3/2}^{nf}}}. $ 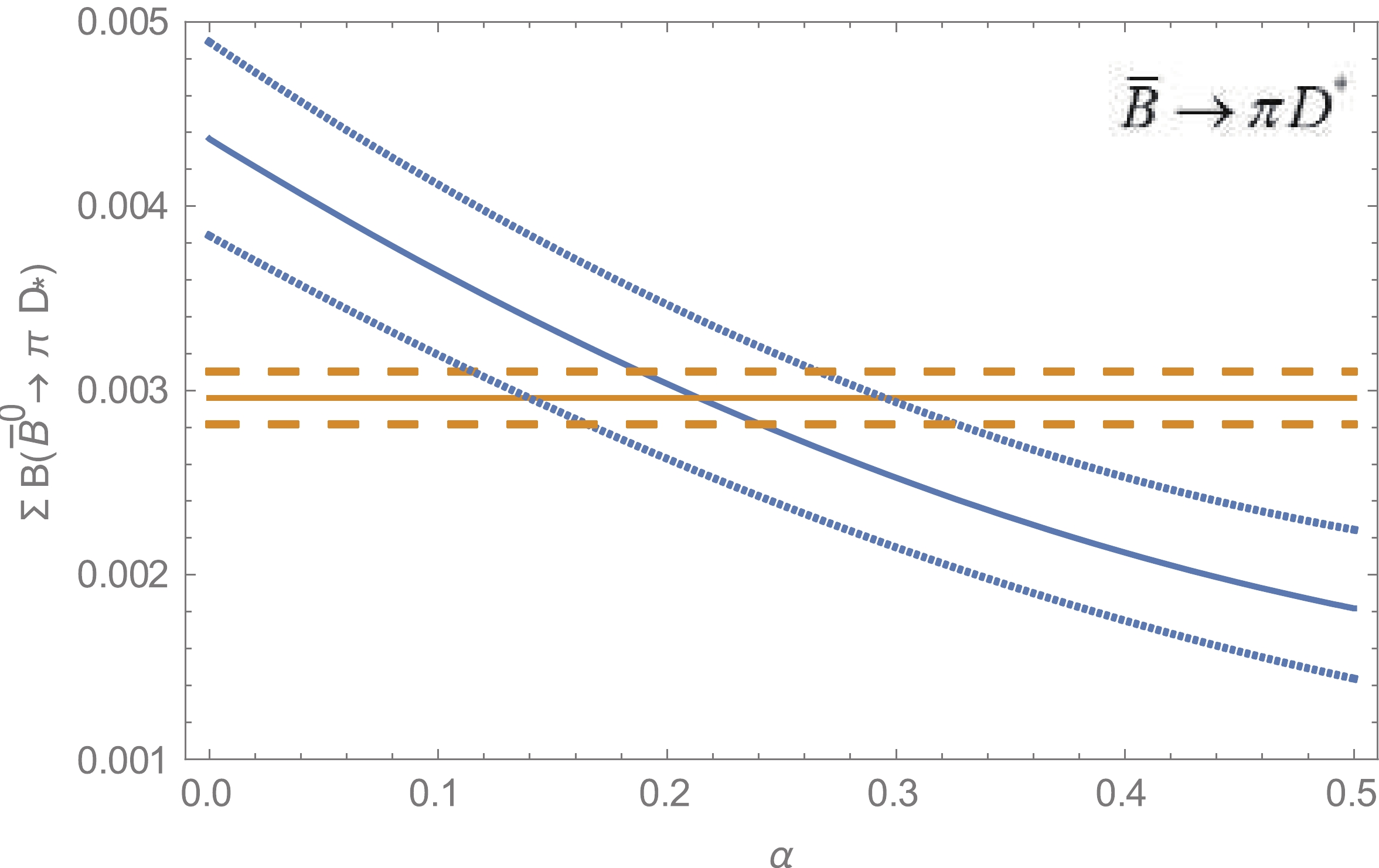
Figure 6. (color online) Variation in the sum of
$ B\left( {{{\bar B}^0} \to {\pi ^ - }{D^{* + }}} \right) $ and$ B\left( {{{\bar B}^0} \to {\pi ^0}{D^{*{\kern 1pt} 0}}} \right) $ with the ratio$ \alpha = {{A_{1/2}^{nf}} \mathord{\left/ {\vphantom {{A_{1/2}^{nf}} {A_{3/2}^{nf}}}} \right. } {A_{3/2}^{nf}}}. $ We wish to remark that similar observations have also been made in the FAT approach [23] analysis used for B- meson decays, which separates the factorizable and nonfactorizable contributions in each topological quark level diagram. The most important result in this approach is that the non-perturbative parameters
$ {\chi ^{C,{\kern 1pt} E}} $ and$ {\varphi ^{C,{\kern 1pt} E}} $ , representing the nonfactorizable contributions, are found to be universal for all the$ \bar B \to \pi D/\rho D/\pi {D^*} $ decay modes, which is consistent with the systematics recognized in our analysis. -
We perform an analysis of CKM-favored two-body hadronic decays,
$ \bar B \to \pi D/\rho D/\pi {D^*} $ , which involve two isospin states in the decay products, by including nonfactorizable contributions arising from the part of the weak Hamiltonian involving colored currents. Because non-perturbated nonfactorizable contributions are difficult to calculate, from the theory of strong interactions, we employ the isospin formalism and find that in all the decay modes, the nonfactorizable isospin reduced amplitude$ A_{1/2}^{nf} $ consistently bears the same ratio, 0.22, as$ A_{3/2}^{nf} $ , within the experimental errors, and maintains the same sign. It is important to note that similar universality in nonfactorizable contributions has also been observed [23] in a recent analysis of B- decays using the FAT approach.Because similar systematics observed for charm mesons decaying into s-wave mesons [16] have been found to be consistent with those of their p-wave meson emitting decays [18], we further expect that this universality of nonfactorizable terms in
$ \bar B \to \pi D/\rho D/\pi {D^*} $ may also hold true for the p-wave meson emitting decays of bottom mesons and can be used to make predictions of the branching fractions, for which experimental measurements are not yet available.The present experimental data for
$ B $ -decays clearly indicate the presence of FSI strong phase differences, and our values agree with other analyses performed for these decays [20, 21]. We also wish to mention that we are aware of a study by Sharma and Katoch [38], who assumed that the ratio of the non-factorizable amplitudes was equal to -0.828 in the absence of experimental data at that time and predicted the sum of the branching fractions of$ {\bar B^0} $ -decays, which was not in agreement with the latest experimental measurements. Moreover, their approach was different from ours because they did not consider the final state interaction effects.
Searching systematics for nonfactorizable contributions to $ {{\boldsymbol B^ - }} $ and $ {\bar {\boldsymbol B}^{\bf 0}}$ hadronic decays
- Received Date: 2021-11-23
- Available Online: 2022-07-15
Abstract: The two-body weak decays








 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
































 DownLoad:
DownLoad: