-
The hyperfine transition of the cosmic hydrogen atom, which is known as the 21 cm signal, provides a powerful probe to the physics in the early universe; for reviews, see Refs. [1-3]. Recently, the Experiment to Detect the Global Epoch of Reionization Signature (EDGES) has reported a new measurement on the sky-averaged radio spectrum centered at
$ \nu = 78 $ MHz, which corresponds to the 21 cm absorption signal of the primordial hydrogen gas at redshift$ z\simeq 17 $ [4]. The differential brightness temperature$ T_{21} $ measured by the EDGES experiment at redshift$ z\simeq17 $ is [4]$ T_{21} = -500^{+200}_{-500}\; {\rm mK}, $

(1) which is about a factor of two larger than the value expected in the standard cosmology [4, 5]. This hints that either the cosmic microwave background (CMB) could be hotter than expected [6-9], or the hydrogen gas could be colder than expected [10-27].
If the EDGES measurement is interpreted as caused by a colder gas, the question is how to cool the hydrogen gas? One simple solution is that, if there exist some sort of particle interactions between dark matter (DM) and hydrogen atom, the primordial hydrogen gas can be cooled by DM, which is colder than gas.① However, there exist very strong constraints from the CMB measurements, as well as from other early universe measurements on DM interactions with standard model particles. Millicharged DM is one of the leading DM candidates to explain the EDGES anomaly, because its interaction with baryons is proportional to
$ v^{-4} $ , where$ v $ is the relative velocity, thus leading to a much smaller interaction cross section in the early universe than that needed at$ z\simeq 17 $ for the EDGES interpretation so that the early universe constraints can be significantly alleviated. Millicharged DM has been extensively investigated for the interpretation of the EDGES anomaly [10-15, 19-22]. The parameter space of the millicharged DM is constrained by various experiments, including accelerator experiments [28], the CMB anisotropy [19, 20, 29-31], the SN1987A [32], and the Big Bang Nucleosynthesis (BBN) [12, 33, 34]; the allowed parameter space is that the millicharged DM mass is$ 0.1 $ MeV$ \lesssim m_\chi \lesssim 10 $ MeV, the millicharge is$ 10^{-6} \lesssim $ $ Q/e \lesssim 10^{-4} $ , and the mass fraction of the millicharged DM is$ 0.0115\% \lesssim f \lesssim 0.4$ %. However, as pointed out by Ref. [21], such a parameter space is ruled out by the$ N_{\rm eff} $ limit with the Planck 2018 data if the relic abundance of the millicharged DM is set by thermal freeze-out. Recently, Ref. [22] proposed a new millicharged DM model in which the sub-component millicharged DM has a sizable interaction cross section with the other DM components so that the millicharged DM can be cooled by the other DM components; this reopens the parameter space that was previously excluded by various experimental constraints.In this paper, we propose a new DM model that consists of two DM components: the lighter DM component is the millicharged DM, and the heavier DM component is unstable, which decays into the lighter DM component. In our model, the millicharged DM is primarily produced after the recombination, so that the stringent constraints from CMB can be alleviated. We show that such a model can explain the 21 cm anomaly observed by EDGES and satisfy various experimental constraints. The rest of the paper is organized as follows. We present our model in Sec. II. We compute the number density of the two DM components as a function of redshift in Sec. III. The temperature change due to the heavier DM decays is derived in Sec. IV. We provide the time evolution equations for four different physics quantities in Sec. V. The results of our numerical analysis are given in Sec. VI. We summarize our findings in Sec. VII.
-
We extend the standard model (SM) by introducing a hidden sector that consists of three
$ U(1) $ gauge bosons,$ X^i_\mu $ ($ i = 1, 2, 3 $ ), and one Dirac fermion$ \chi $ that is charged under both$ X^2_\mu $ and$ X^3_\mu $ gauge bosons. We use the Stueckelberg mechanism [35-40] to provide mass to the three$ U(1) $ gauge bosons; the new Lagrangian is given by$ \begin{aligned}[b] \Delta {\cal L} = &- \sum_{i = 1,2,3} {1\over 4} X_{i \mu \nu} X_{i}^{\mu \nu} + \bar \chi ({\rm i}\gamma^\mu \partial_\mu - m_\chi) \chi \\& + g^\chi_2 X_{2}^{\mu} \bar \chi \gamma^\mu \chi + g^\chi_3 X_{3}^{\mu} \bar \chi \gamma^\mu \chi \\ &- {1 \over 2} ( \partial_\mu \sigma_1 + m_{1}^{\prime} X_{1}^{\mu})^2 - {1 \over 2} ( \partial_\mu \sigma_2 + m_{1} X_{1}^{\mu} + m_{2} X_{2}^{\mu} )^2 \\& - {1 \over 2} ( \partial_\mu \sigma_3 + m_{3} X_{3}^{\mu} + m_{4} B^{\mu} )^2, \end{aligned} $

(2) where
$ \sigma_1 $ ,$ \sigma_2 $ , and$ \sigma_3 $ are the axion fields in the Stueckelberg mechanism,$ B_\mu $ is the SM hypercharge boson,$ m_\chi $ is the dark fermion mass,$ g^\chi_2 $ and$ g^\chi_3 $ are the gauge couplings, and$ m_1^{\prime} $ ,$ m_1 $ ,$ m_2 $ ,$ m_3 $ , and$ m_4 $ are the Stueckelberg mass terms. The Stueckelberg mechanism can be commonly seen in extra dimension models, strings, and D branes [41]. The Stueckelberg mechanism can also be viewed as a particular limit of the abelian Higgs mechanism, in which the Higgs mass goes to infinity and the Higgs vacuum expectation value is kept to be fixed [42]. However, unlike in the Higgs mechanism, mass is generated below the spontaneous symmetry breaking temperature in the early universe, in the Stueckelberg mechanism the vector boson can retain a mass to an arbitrary high temperature [43].After the spontaneous symmetry breaking in the SM, the mass matrix
$ M^2 $ of the neutral gauge bosons in the basis$ (X_1,X_2, X_3, B, A^3) $ , where$ A^3 $ is the third component of the$ SU(2)_{\rm L} $ gauge bosons in the SM, is given by$ \left\{ \begin{array}{*{20}{c}} m_1^{\prime 2} + m_1^2 & m_1 m_2 & 0 & 0 &0 \\ m_1 m_2 & m_2^2 & 0 & 0 &0 \\ 0 & 0 & m_3^2 & m_3 m_4 & 0 \\ 0 & 0 & m_3 m_4 & m_4^2 + {g_{\rm Y}^2 v^2/4} & - {g_{\rm Y} g_2 v^2/4} \\ 0 & 0 & 0 & - {g_{\rm Y} g_2 v^2/4} & {g_2^2 v^2/4} \end{array}\right\}, $

(3) where
$ v $ is the vacuum expectation value of the SM Higgs, and$ g_2 $ and$ g_{\rm Y} $ are the$ SU(2)_{\rm L} $ and$ U(1)_{\rm Y} $ gauge couplings in the SM respectively. The mass matrix has a vanishing determinant such that there exists a massless mode to be identified as the SM photon. Because the mass matrix is block-diagonal, one can diagonalize the first two gauge bosons and the last three gauge bosons separately.The mass matrix of the first two gauge bosons (the upper-left two by two block matrix in Eq. (3)) can be diagonalized via a rotation matrix
$ {\cal R} $ which is parameterized by a single angle$ \theta $ $ {\cal R} = \begin{pmatrix} \cos\theta & {-\sin\theta} \cr {\sin\theta} & \cos\theta \end{pmatrix}. $

(4) The mass eigenstates,
$ Z_1 $ and$ Z_2 $ , are related to the gauge states via$ Z_i = {\cal R}_{ji} X_{j} $ . The rotation matrix$ {\cal R} $ leads to an interaction between$ \chi $ and$ Z_1 $ such that$ {\cal L}_{\rm int} = $ $ \sin\theta g^\chi_2 Z_{1}^{\mu} \bar \chi \gamma^\mu \chi \equiv v_{Z_1}^\chi Z_{1}^{\mu} \bar \chi \gamma^\mu \chi $ . We are interested in the parameter space where$ \theta \ll 1 $ so that$ Z_1 \sim X_1 $ and$ Z_2 \sim X_2 $ . In our analysis, we take$ m_1^\prime \sim 2 m_\chi $ ,$ m_2 < m_\chi $ , and$ m_1 \ll m_2 $ so that the two mass eigenstates have masses$ m_{Z_1} \simeq m_1^\prime $ and$ m_{Z_2} \simeq m_2 $ , and the mixing angle$ \theta $ is given by$ \theta \simeq $ $ m_1 m_2 /(m_1^{\prime 2}-m_2^2) $ .The mass matrix of the last three gauge bosons (the bottom-right three by three block matrix in Eq. (3)) can be diagonalized by an orthogonal matrix
$ {\cal O} $ such that$ E_i = {\cal O}_{ji} G_{j} $ , where$ G_j = (X_3, B, A^3) $ are the gauge states, and$ E_i = (Z', Z, \gamma) $ are the mass eigenstates. Here,$ \gamma $ is the photon,$ Z $ is the neutral gauge boson in the weak interaction, and$ Z' $ is the new massive vector boson. Thus, we have$ {\cal O}^T M_{3\times 3}^2 {\cal O} = {\rm diag} (m^2_{Z'}, m^2_{Z}, 0) $ , where$ M_{3\times 3}^2 $ is the bottom-right three by three block matrix in Eq. (3). Such a matrix diagonalization also leads to interactions between matter fields (both hidden sector fermion$ \chi $ and SM fermions$ f $ ) and the three mass eigenstates ($ \gamma $ ,$ Z $ , and$ Z' $ ). The interaction Lagrangian can be parameterized as follows$ \bar f \gamma_\mu (v^f_i - \gamma_5 a^f_i) f E^\mu_i + v^\chi_i \bar \chi \gamma_\mu \chi E^\mu_i, $

(5) where the vector and axial-vector couplings are given by
$ v^f_i = (g_2 {\cal O}_{3i} - g_Y {\cal O}_{2i})T^{3 }_f/2 + g_Y{\cal O}_{2i}Q_f , $

(6) $ a^f_i = (g_2 {\cal O}_{3i} - g_Y{\cal O}_{2i})T^{3 }_f/2, $

(7) $ v^\chi_i = g_{\chi} {\cal O}_{1i}. $

(8) Here,
$ Q_f $ is the electric charge of the SM fermion, and$ T_f^3 $ is the quantum number of the left-hand chiral component under SU(2)$ _{\rm L} $ .Thus, the hidden sector fermion
$ \chi $ has a vector current interaction with the SM photon,$ v_3^\chi A_\mu \bar \chi \gamma^\mu \chi \equiv \epsilon e A_\mu \bar \chi \gamma^\mu \chi, $

(9) where we have defined an electric charge
$ \epsilon $ for the$ \chi $ particle. In our analysis, we adopt the following model parameters:$ m_3 = 100 $ TeV, and$ m_4/m_3 \ll 1 $ . In this case, the electric charge$ \epsilon $ is given by$ \epsilon \simeq - (m_4/m_3) \cos\theta_W (g_3^\chi /e) $ , where$ \theta_W $ is the weak rotation angle in the SM. Since$ m_4/m_3 \ll 1 $ in our analysis, we have$ \epsilon \ll 1 $ , which is often referred to as millicharge.$ \chi $ is then the millicharged particle. -
There are two DM particles in the hidden sector, the
$ Z_1 $ boson and the hidden Dirac fermion$ \chi $ . In the very early universe,$ Z_1 $ is the dominant DM component, which is assumed to be nonthermally produced. The$ Z_1 $ DM component is long-lived and decays into$ \bar \chi \chi $ . The decay width of the$ Z_1 $ boson is given by$ \begin{aligned}[b] \Gamma (Z_1\rightarrow \bar\chi\chi) = & \frac{m_{Z_1}}{12\pi} \sqrt{1-4\frac{m_\chi^2}{m_{Z_1}^2}} \left( 1+2\frac{m_\chi^2}{m_{Z_1}^2} \right) (v_{Z_1}^\chi)^2 \\ \simeq& {\sqrt{m_{Z_1} \, \Delta m } \over 4 \sqrt{2} \pi} \left( {g^\chi_2 \theta} \right)^2, \end{aligned} $

(10) where
$ v_{Z_1}^\chi = g^\chi_2 \sin \theta \simeq g^\chi_2 \theta $ ,$ \Delta m \equiv m_{Z_1} - 2 m_\chi $ , and we have assumed$ \Delta m \ll m_{Z_1} $ . In our analysis, we have$ \theta \ll 1 $ and$ \Delta m \ll m_{Z_1} $ so that$ Z_1 $ is long-lived with a lifetime$ {\tau (Z_1) \simeq \sqrt{ {\rm MeV} \over m_{Z_1}} \sqrt{ {\rm meV} \over \Delta m} \left( { 2.3 \times 10^{-16} \over g^\chi_2 \theta } \right)^2 \, \tau_{17}, } $

(11) where
$ \tau_{17} \sim 7 \times 10^{15} $ second is the time between the early universe and$ z = 17 $ .The value of
$ \Delta m $ cannot be very large, otherwise the DM$ \chi $ will be significantly heated by the decay process$ Z_1 \to \bar \chi \chi $ so that$ \chi $ is unable to cool the baryons. The velocity of the$ \chi $ particle is$ v_\chi \simeq \sqrt{\Delta m/m_\chi} $ in the rest frame of$ Z_1 $ , under the assumption of$ \Delta m \ll m_\chi $ . For the case where$ m_\chi \sim 100 $ MeV and$ \Delta m \sim {\cal O} $ (meV), we have$v_\chi \sim 3.2 \times $ $ 10^{-6}$ . Thus, in our analysis, we assume a sufficiently small mass difference,$ \Delta m \sim {\cal O} $ (meV), such that the$ Z_1 $ decay does not heat the$ \chi $ DM significantly.The
$ \chi $ DM component is mainly produced via the decay process$ Z_1 \to \bar \chi \chi $ in the universe. We assume that the initial number density of$ \chi $ is negligible. The relic density of$ \chi $ can also be produced via thermal freeze-out. There are two processes that contribute to the$ \chi $ DM annihilation cross section:$ \bar \chi \chi \to \gamma \to \bar f f $ and$ \bar \chi \chi \to Z_2 Z_2 $ . In our analysis,$ \sigma(\bar \chi \chi \to Z_2 Z_2) \gg \sigma(\bar \chi \chi \to \bar f f) $ . The$ \bar \chi \chi $ annihilation cross section into on-shell$ Z_2 $ bosons is given by [44]$ \langle \sigma v \rangle (\bar \chi \chi \to Z_2 Z_2) \simeq { (g_2^\chi)^4 \over 16 \pi m_\chi^2} {(1-r^2)^{3/2} \over (1-r^2/2)^{2}}, $

(12) where
$ r = m_{Z_2}/m_\chi $ . For the case where$ g_2^\chi = 1 $ ,$ r = 1/2 $ , and$ m_\chi = 5 $ MeV, one has$ \langle \sigma v \rangle (\bar \chi \chi \to Z_2 Z_2) \simeq 0.3 $ barn, leading to a mass fraction as$ f_\chi \sim 10^{-11} $ . Thus, the contribution to the relic density of$ \chi $ from thermal freeze-out is negligible, and the constraints imposed on thermal freeze-out millicharged DM (e.g. Ref. [21]) are not directly applicable to our model.The total number of
$ Z_1 $ particles in a comoving volume at time$ t $ is given by$ N_{Z_1}(t) = N_{Z_1} (0) {\rm e}^{ - t / \tau } , $

(13) where
$ \tau $ is the lifetime of the$ Z_1 $ particle,$ N_{Z_1} (0) $ is the total number of$ Z_1 $ particles at time$ t = 0 $ , and we have assumed that$ Z_1 $ is non-relativistic. In our analysis, we set$ t = 0 $ at redshift$ z_0 = 10^6 $ ; the abundance of$ Z_1 $ at$ z_0 = 10^6 $ is given by$ \rho_{Z_1}(z_0) \simeq \rho_{\rm DM, 0}(1+z_0)^3 $ , where$ \rho_{\rm DM, 0} $ is the current DM density. The number of$ \chi $ particles at time$ t $ in a comoving volume is$ N_\chi (t) = 2N_{Z_1}(0) - 2N_{Z_1}(t). $ Thus, the number density of$ \chi $ is related to the number density of$ Z_1 $ via$ n_\chi = 2( {\rm e}^{t/\tau}-1) n_{Z_1} . $

(14) where
$ n_{Z_1}\ (n_\chi) $ is the number density of the$ {Z_1}\ (\chi) $ particle. In our analysis$ m_{Z_1} \simeq 2 m_\chi $ , so the mass fraction of the millicharged DM$ \chi $ at redshift$ z $ in the total DM is given by$ f_\chi (z) \simeq (1-{\rm e}^{-t(z)/\tau}), $

(15) where
$ t(z) $ is the time between early universe (which we take to be$ z_0 = 10^6 $ ) and redshift$ z $ ②. Fig. 1 shows the mass fraction of$ \chi $ as a function of the redshift$ z $ for different lifetimes$ \tau $ . CMB observations provide strong constraints on millicharged DM; only 0.4% DM can be millicharged, unless the millicharge is negligible [19, 20, 31]. This leads to a lower bound on the$ \tau $ , which is$ \sim 3.6 \times 10^{15} $ s.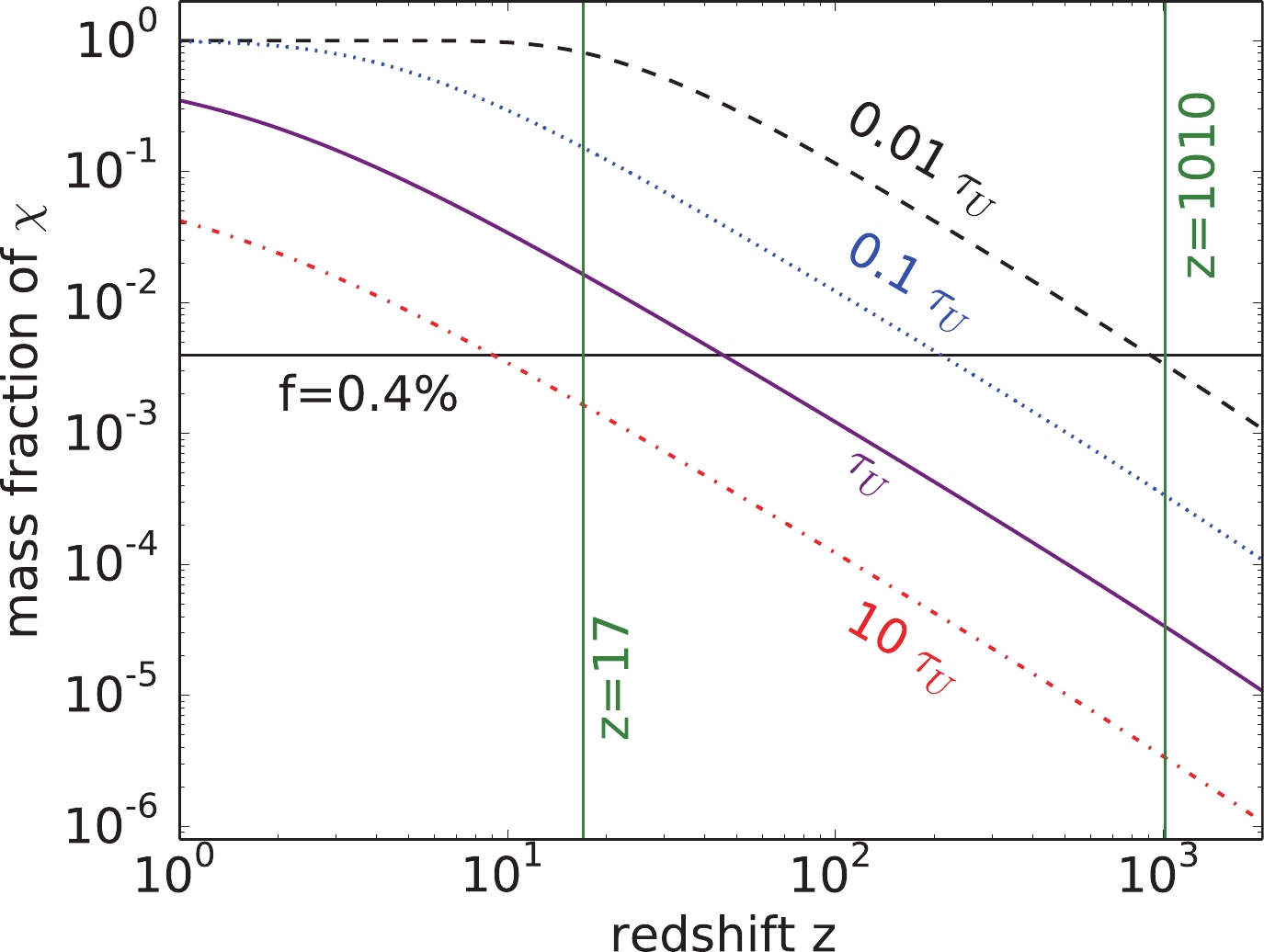
Figure 1. (color online) Mass fraction of
$ \chi $ in the total DM as a function of the redshift.$ \tau_U \simeq 4.3 \times 10^{17} $ s is the age of the universe.Because
$ \Delta m \ll m_\chi $ , the total DM density$ \rho_{Z_1} + \rho_\chi $ at redshift$ z $ is given by$ \rho_{Z_1} + \rho_\chi = \rho_{\rm DM, 0} \, (1+z)^3. $ Thus, the number density of$ \chi $ particles at redshift$ z $ is given by$ n_\chi (z) = {\rho_{\rm DM,0} \over m_\chi} \, (1+z)^3 \, f_\chi(z) \simeq {\rho_{\rm DM,0} \over m_\chi} \, (1+z)^3 \, (1-{\rm e}^{-t(z)/\tau}), $

(16) where
$ \rho_{\rm DM, 0} = \Omega_{\rm DM} \, \rho_{\rm cr,0} $ and$ \rho_{\rm cr,0} = 1.054 h^2\times 10^4 $ eV cm$ ^{-3} $ is the critical density [45]. In our analysis, we use$ \Omega_{\rm DM} h^2 = 0.1186 $ [46]. -
The DM
$ \chi $ is heated by the$ Z_1 \to \chi \bar \chi $ decay process because of the difference between the$ Z_1 $ mass and twice of the$ \chi $ mass. To compute this effect, consider the kinetic energy$ \Delta q $ that goes into the$ \chi \bar \chi $ final state for the decay process$ Z_1 \to \chi\chi $ $ \Delta{q} = \Delta{m}+\frac{3}{2}k_{\rm B}T_{Z_1}, $

(17) where
$ 3k_{\rm B}T_{Z_1}/2 $ is the averaged kinetic energy of$ Z_1 $ with$ T_{Z_1} $ being the temperature of the$ Z_1 $ particle and$ k_{\rm B} $ being the Boltzmann constant③. Here, we have assumed that$ Z_1 $ is non-relativistic and$ \Delta m $ is sufficiently small, such that$ \chi $ is also non-relativistic. The change in the particle numbers in the comoving volume per unit time due to decay is given by$ \dot N_{Z_1} = - \Gamma_{Z_1} N_{Z_1} $ and$ \dot N_\chi = -2 \dot N_{Z_1}, $ where the dot denotes the derivative with respect to time,$ N_\chi $ ($ N_{Z_1} $ ) is the particle number of$ \chi $ ($ Z_1 $ ), and$ \Gamma_{Z_1} $ is the decay width for the process$ Z_1\rightarrow \chi\chi $ . The total kinetic energy transfer to the$ \chi $ particles per unit time from$ Z_1 $ decays is given by$ \Delta q |\dot N_{Z_1}|, $ which is equal to the change of the kinetic energy of the$ \chi $ particles per unit time$ \Delta q |\dot N_{Z_1}| = \frac{\rm d}{{\rm d}t} \left( \frac{3}{2} k_{\rm B} T_\chi N_\chi \right) = \frac{3}{2} k_{\rm B} (T_\chi \dot N_\chi +N_\chi \dot T_\chi). $

(18) Thus, the
$ \chi $ temperature change per unit time due to$ Z_1 $ decays is given by$ \dot T_\chi^{d} = \frac{n_{Z_1}}{n_\chi} \left[ \frac{2}{3k_{\rm B}} \Delta m +T_{Z_1} -2T_\chi \right] \Gamma_{Z_1}. $

(19) -
To compute the baryon temperature at redshift
$ z = 17 $ , we numerically solve the temperature evolutions for various quantities.The time evolution equation of the baryon temperature
$ T_b $ is given by (see e.g. [10, 47])$ \frac{{\rm d}T_b}{{\rm d}t} = -2HT_b+\frac{2}{3}\frac{{\rm d}Q_b}{{\rm d}t} +\Gamma_C(T_\gamma-T_b), $

(20) where
$ H $ is the Hubble parameter④,$ T_\gamma $ is the CMB temperature,$ Q_b $ is the energy transfer term due to DM-baryon scatterings, and$ \Gamma_{\rm C} $ is the Compton scattering rate which describes the effects due to CMB-baryon interactions. The Compton scattering rate is given by [10]$ \Gamma_{\rm C} = \frac{8\sigma_{\rm T} x_e} {3(1+f_{\rm He})m_e} U $

(21) where
$ \sigma_{\rm T} $ is the Thomson cross section,$ f_{\rm He} $ is the Helium fraction, and$ U $ is the energy density. In our analysis, we use$\sigma_{\rm T} = 6.65 \times 10^{-25}$ cm$ ^2 $ [45],$ f_{\rm He} = 0.08 $ [10], and$ U = (\pi^2/15) \, T_\gamma^4 = 0.26(1+z)^4\ \rm{eV/cm^3} $ [48, 49].The time evolution equation of the temperature
$ T_\chi $ of the lighter DM component$ \chi $ is given by$ \frac{{\rm d}T_\chi}{{\rm d}t} = -2HT_\chi +\frac{2}{3}\frac{{\rm d}Q_\chi}{{\rm d}t} + \dot T_\chi^{d}, $

(22) where
$ Q_\chi $ is the energy transfer term due the interaction between DM$ \chi $ and baryons, and$ \dot T_\chi^{d} $ is given in Eq. (19). The first two terms on the right-hand side of Eq. (22) represent the effects due to universe expansion and the DM-baryon scattering respectively, which are similar to the first two terms in Eq. (20). The third term on the right-hand side of Eq. (22) is new and is due to the decay of the$ Z_1 $ particle in our model, as discussed in Sec. IV.In addition, we also solve the time evolution equation of the relative bulk velocity between baryon and DM,
$ V_{\chi b} = | \vec V_{\chi b} | $ where$ \vec V_{\chi b} \equiv \vec V_{\chi} - \vec V_{b} $ [47],$ \frac{{\rm d}V_{\chi b}}{{\rm d}t} = -HV_{\chi b}-D(V_{\chi b}), $

(23) and the time evolution equation of the ionization fraction
$ x_e \equiv n_e/n_H $ [50]$ \frac{{\rm d}x_e}{{\rm d}t} = -C \left[ n_H\alpha_B {x_e}^2 -4(1-x_e)\beta_B \exp\left( {3E_0 \over 4T_\gamma} \right) \right]. $

(24) We follow Ref. [50] to obtain the various coefficients in Eq. (24). The formulas of
$ Q_b $ ,$ Q_\chi $ , and$ D(V_{\chi b}) $ for millicharged DM used in our analysis are given in Appendix B. -
We simultaneously solve the four time evolution equations for
$ T_b $ ,$ T_\chi $ ,$ V_{\chi b} $ , and$ x_e $ from redshift$ z = 1010 $ to$ z = 10 $ . The baryon temperature$ T_b $ at$ z = 1010 $ is assumed to be equal to the CMB temperature$ T_\gamma = T_0 \, (1+z) $ ,where$ T_0 = 2.7 $ K, since these two components are tightly coupled in the early universe. The temperatures for both DM components are assumed to be negligible in the early universe, so we set$ T_{Z_1} = 0 $ and$ T_\chi = 0 $ at$ z = 1010 $ . This is due to the fact that in our model,$ Z_1 $ does not interact with the SM particles and$ \Delta m \ll m_\chi $ . We also set$ x_e = 0.05 $ [51] and$ V_{\chi b} = 29 $ km/s [10] at redshift$ z = 1010 $ .We scan the parameter space spanned by
$ {\epsilon} $ and$ m_\chi $ for three different decay lifetimes of$ Z_1 $ :$ \tau = 2 \times 10^{16} $ ,$ 3 \times 10^{17} $ , and$ 8 \times 10^{17} $ s. In our analysis, we fix$ \Delta m = 1 $ meV. In order to explain the EDGES data, the baryon temperature$ T_b $ has to be at least$ 5.1 $ K at$ z = 17 $ within the 99% CL [22]. Fig. 2 shows the parameter space where the baryon temperature can be cooled to$ T_b = 5.1 $ K at$ z = 17 $ for three different lifetimes of$ Z_1 $ :$ 2 \times 10^{16} $ (blue dot-dashed),$ 3 \times 10^{17} $ (purple dashed), and$ 8 \times 10^{17} $ s (red solid)⑤. Millicharged DM is mainly constrained by CMB around$ z \simeq 10^3 $ [61]. The mass fractions of$ \chi $ at$ z = 1100 $ are about$ 0.06$ %,$ 0.004$ %, and$ 0.001$ % for the lifetimes$ \tau = 2\times 10^{16} $ ,$ 3 \times 10^{17} $ , and$ 8\times 10^{17} $ s, respectively, which satisfy the CMB bound$ f_\chi <0.4$ % [20]. However, in our model, the mass fraction of the millicharged DM increases with redshift. Energy injections after the recombination can further influence the CMB power spectrum and thus, are constrained by the CMB data (see Refs. [62-66]). Thus, we compute the mass fractions of$ \chi $ at$ z = 600 $ , which are about$ 0.15$ %,$ 0.01$ %, and$ 0.004$ % for the lifetimes$ \tau = 2 \times 10^{16} $ ,$ 3 \times 10^{17} $ , and$ 8 \times 10^{17} $ s, respectively. Because the mass fractions for all the models considered in this analysis are smaller than$ 0.4$ % for redshift$ z>600 $ , the CMB constraints are satisfied [20]⑥. We find that the viable parameter in our model is much larger than the minimal millicharged DM model⑦, which is indicated by the black dotted line for 0.4% millicharged DM [22]. Various experimental constraints are considered in Fig. 2. These include, the underground dark matter direct detection (DMDD) experiments [22, 58], the XQC experiment [58, 59], SN1987A [60], and the accelerator experiments: SLAC electron beam dump [28], CMS [52], MiniBooNE [53], LSND [53], ArgoNeuT [54], and milliQan demonstrator [55]. Two benchmark model points that can explain the 21 cm anomaly while satisfying various constraints are presented in Table 1. The mass fractions of the$ \chi $ DM at today are 100%, 77%, and 42% for the lifetimes$ \tau = 2\times 10^{16} $ ,$ 3 \times 10^{17} $ , and$ 8\times 10^{17} $ s, respectively. We find that the$ Z_1 $ lifetime$ 2 \times 10^{16} $ is nearly excluded by both the underground DMDD and the XQC constraints. In order to evade the XQC constraints, the$ Z_1 $ lifetime has to be$ \geqslant 2 \times 10^{16} $ s.
Figure 2. (color online) Parameter space spanned by the millicharge
$ \epsilon $ and the DM mass$ m_\chi $ . Model points in which$ T_b = 5 $ K at$ z = 17 $ correspond to three different lifetimes:$ \tau = 2\times 10^{16} $ s (blue dot-dashed),$ \tau = 3 \times 10^{17} $ s (purple dashed), and$ \tau = 8\times 10^{17} $ s (red solid), with the mass fraction of the millicharged DM component being$ 0.06$ %,$ 0.004$ %, and$ 0.001$ % at$ z = 1100 $ , and 100%, 77%, and 42% today, respectively. The green shaded region is excluded by various accelerator experiments, including SLAC electron beam dump [28], CMS [52], MiniBooNE and LSND [53], ArgoNeuT [54], milliQan demonstrator [55], and others [56, 57]. The gray shaded region indicates the parameter region excluded by the dark matter direct detection (DMDD) experiments; above the DMDD region, millicharged DM is absorbed by the rocks on top of underground labs [22, 58]. The magenta region is ruled out by the rocket experiment XQC for mass fractions:$ f = 100$ % (solid) [59],$ f = 1$ % (solid) [59], and$ f = 0.4$ % (solid) [58]. The brown shaded region is excluded by the SN1987A data [60]. The black dashed vertical line indicates the upper bound on DM mass due to$ \Delta N_{\rm eff} $ from CMB [12, 33]. The black dotted line indicates the parameter space of the minimal millicharged DM model with a mass fraction of 0.4% to explain EDGES data [22].Model $m'_1$ 

$m_1$ 

$m_2$ 

$m_3$ 

$m_4$ 

$m_\chi$ 

$\Delta m$ 

$\theta$ 

$\epsilon$ 

$\tau_{Z_1}/{\rm s}$ 

A 160 $10^{-13}$ 

1.55 $10^8$ 

$2.76 \times 10^3$ 

$\sim$ 80

$10^{-9}$ 

$6.1 \times 10^{-18}$ 

$8\times 10^{-5}$ 

$8 \times 10^{17}$ 

$B$ 

400 $10^{-8}$ 

$1.25 \times 10^{-4}$ 

$10^8$ 

$3.45 \times 10^3$ 

$\sim$ 200

$10^{-9}$ 

$7.8 \times 10^{-18}$ 

$1 \times 10^{-4}$ 

$3 \times 10^{17}$ 

Table 1. Benchmark model points. All the masses are in unit of MeV. We take
$ g_2^\chi = g_3^\chi = 1 $ in our analysis. -
We construct a new millicharged DM model to explain the recent 21 cm anomaly. In our model, the millicharged DM
$ \chi $ is a subcomponent in the early universe and is mainly produced via decays of the other DM component$ Z_1 $ . The DM annihilation cross section$ \bar \chi \chi \to Z_2 Z_2 $ is so strong that the relic abundance of$ \chi $ due to thermal freeze-out is negligible. We compute the heating term due to the decay process$ Z_1 \to \bar \chi \chi $ and include it in our numerical calculations of the time evolution equation of the DM temperature. We find that the model can explain the EDGES 21 cm anomaly while satisfying various experimental constraints, including those from accelerators, XQC, underground DMDD, and CMB. -
We thank Ran Ding and Mingxuan Du for helpful discussions.
-
The time
$ t(z) $ at redshift$ z $ is given by$ t(z) = \int_z^{z_0} {{\rm d}z' \over H(z')(1+z')}, \tag{A1} $

where
$ H $ is the Hubble parameter. Here, we use$ {z_0} = 10^6 $ . We compute the Hubble parameter at redshift$ z $ via$ H(z) = H_0 \sqrt{\Omega_R(1+z)^4+\Omega_m(1+z)^3+\Omega_\Lambda}, \tag{A2} $

where
$ H_0 \equiv 100h\ {\rm km\ s^{-1} \ Mpc^{-1}} $ is the present Hubble parameter,$ \Omega_R $ ,$ \Omega_m $ , and$ \Omega_\Lambda $ are the density of radiation, matter, and dark energy, respectively. In our analysis, we adopt the following values:$ \Omega_R = 2.47\times10^{-5}/h^2 $ [67],$ \Omega_m = 0.308 $ ,$ \Omega_\Lambda = 0.692 $ , and$ h = 0.678 $ [46]. -
We provide the formulas of
$ \sigma_{0,t} $ ,$ Q_b $ ,$ Q_\chi $ , and$ D(V_{\chi b}) $ for millicharged DM used in our analysis.The scattering cross section between millicharged DM and baryons can be parameterized as
$ \sigma_t = \sigma_{0,t}v^{-4} $ where$ v $ is the relative velocity between DM and baryons, and$ \sigma_{0,t} = 2 \pi \alpha^2 \epsilon^2 \xi / \mu_{\chi t}^2 $ where$ \alpha $ is the fine structure constant,$ \epsilon $ is the millicharge,$ \mu_{\chi t} $ is the reduced mass of DM$ \chi $ and the target particle$ t $ , and$ \xi $ is the Debye logarithm [10, 68]$ \xi = \ln \left[ { 9 T_b^3 / (4 \pi \epsilon^2 \alpha^3 x_e n_H)} \right]. $ The baryon heating term due to interactions with millicharged DM is given by [10, 47]
$ \begin{aligned}[b] \frac{{\rm d}Q_b}{{\rm d}t} =& n_\chi {x_e} \sum_{t = e,p} \frac{m_t m_\chi }{(m_\chi+m_t)^2} \frac{\sigma_{0,t}}{u_{{\rm th},t}} \\&\times\left[\sqrt{\frac{2}{\pi}}\frac{{\rm e}^{-r_t^2/2}}{u_{{\rm th},t}^2}(T_\chi-T_b) +m_\chi\frac{F(r_t)}{r_t}\right], \end{aligned}\tag{B1} $

where
$ u_{\rm th}^2 \equiv T_b/m_b+T_\chi/m_\chi $ ,$ r \equiv V_{\chi b}/u_{\rm th} $ , and$ F(r) = $ $ {\rm erf}\left({r/\sqrt{2}} \right)-\sqrt{{2}{\pi}} r {\rm e}^{-r^2/2}. $ Here, we assume that electron and proton share a common temperature$ T_b $ with the hydrogen atom. The DM heating term due to interactions with baryons is given by$ \begin{aligned}[b] \frac{{\rm d}Q_\chi}{{\rm d}t} = n_H x_e\sum_{t = e,p} \frac{m_\chi m_t}{(m_\chi+m_t)^2} \frac{\sigma_{0,t}}{u_{{\rm th,}t}} \end{aligned} $

$\tag{B2} \begin{aligned}[b] \times \left[\sqrt{\frac{2}{\pi}}\frac{{\rm e}^{-r_t^2/2}}{u_{{\rm th,}t}^2}(T_b-T_\chi) +m_t\frac{F(r_t)}{r_t}\right], \end{aligned} $

where
$ n_e = n_p = n_H x_e $ is assumed.The
$ D $ term in Eq. (23) is given by [47]$ D(V_{\chi b}) = { \rho_m \sigma_0 \over m_\chi + m_b } { F(r) \over V_{\chi b}^2 }, \tag{B3}$

where we consider both electron and proton as the target baryons.
Two-component millicharged dark matter and the EDGES 21 cm signal
- Received Date: 2021-11-01
- Available Online: 2022-04-15
Abstract: We propose a two-component dark matter explanation to the EDGES 21 cm anomalous signal. The heavier dark matter component is long-lived, and its decay is primarily responsible for the relic abundance of the lighter dark matter, which is millicharged. To evade the constraints from CMB, underground dark matter direct detection, and XQC experiments, the lifetime of the heavier dark matter has to be larger than






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: