-
In a nuclear collision, the interaction between two nuclei may lead to the formation of a compound nucleus (CN) along with other competing mechanisms. However, the fusion threshold barrier opposes the amalgamation of two positively charged nuclei owing to a mutual repulsive Coulomb potential. If a projectile nucleus has sufficient kinetic energy, it may overcome/penetrate the barrier posed by the mutual interaction of colliding partners and a new nuclear entity may be synthesized.
The fusion barrier characteristics are sensitive to mass/charge number, deformation, orientation, excitation energy, and angular momentum. The present study is constrained to analyze the impact of nuclear deformations (up to
$ \beta_3 $ ) and the related orientation degree of freedom in terms of barrier characteristics and the consequent effect on the fusion probability by selecting various spherical-plus-deformed nuclei. For the synthesis of heavy and superheavy elements, either of the two nuclear mechanisms, namely hot and cold fusion processes, are used [1-5]. These fusion phenomena have been described successfully when either one or both of the colliding nuclear partners are deformed [6-9]. For these types of target-projectile combinations, the fusion barrier extracted from the total interaction potential depends on the deformation and orientation of the deformed nucleus relative to the direction of approach of the colliding partner (spherical or deformed). To illustrate, the lowest barrier height and largest interaction distance between the colliding nuclei exhibit the polar orientation (θ = 0° or 180°) of a prolate ($ \beta_2^+ $ or$ \beta_2>0 $ ) nucleus and leads to the formation of a cold fusion configuration. On the other hand, the highest barrier height and smallest interaction distance related to the equatorial orientation (θ = 90° ) of $ \beta_2^+ $ leads to a hot fusion process. The theories used to illustrate the concept of hot and cold fusion processes are developed based on the uniquely fixed or optimum orientation of quadrupole deformed nuclei [10-12]. These optimum orientations depend on the +/- signs of quadrupole deformation. As a consequence, an enhancement is observed in the fusion probability of heavy/superheavy nuclear systems, with the inclusion of$ \beta_2 $ -deformed nuclei as the target, projectile, or both the colliding partners [13-21]. In addition, the relevance of higher-order deformations (with axial- and reflection-symmetries) is also analyzed in reference to the fusion barrier characteristics [22-26]. The impact of the reflection symmetry-breaking pear shapes of octupole deformed nuclei requires further exploration to better understand the fusion process. Unlike quadrupole deformed nuclei, there are very few experimentally observed octupole ($ \beta_3 $ ) deformed nuclei [27-34]. However, the exploration of octupole deformed nuclei is important for extracting the appropriate nuclear structure because significant enhancements can be found in electric dipole moments (EDMs) [27]. Also, in the nuclear fusion process, it has been observed that [35] the nonzero EDMs in one of the fusion partners (16O+144Ba and 224Ra) may have a significant impact on the fusion barrier and corresponding cross-sections.In a recent study [36], we worked on the optimum orientations (
$\theta_{\rm opt.}$ ) after the inclusion of deformations up to$ \beta_3 $ for the ‘cold or noncompact’ and ‘hot or compact’ fusion configurations. The octupole deformation ($ \beta_3 $ ), which distorts the spherically symmetric or quadrupole deformed ($ \beta_2 $ ) nuclei into pear shapes, significantly modifies$\theta_{\rm opt.}$ , in reference to those obtained for$ \beta_2 $ -deformed nuclei. The selection of$\theta_{\rm opt}.$ for$ \beta_3 $ -deformed nuclei is sensitive to the magnitude as well as the sign of$ \beta_3 $ -deformation; hence, the considered octupole nucleus options belonging to different mass-regions of the Periodic Table are categorized as (i) the nuclei with weak or little octupole deformation compared to quadrupole deformation and (ii) the nuclei with strong octupole deformation. The first type of configuration is called the soft-pear shape ($ |\beta_2|>|\beta_3| $ ) and the second is called the rigid-pear shape ($ |\beta_2|\leqslant |\beta_3| $ ). The main objective of the present study is to investigate in detail the influence of cold and hot optimum oriented octupole deformed nuclei on the fusion barrier characteristics (barrier height$ V_B $ and barrier position$ R_B $ ) and hence on the fusion cross-sections for energies across the Coulomb barrier. To study the ‘cold’ and ‘hot’ optimum cases of octupole deformed nuclei in nuclear fusion reactions, the static deformations are considered. The dynamical effect of quadrupole, octupole, or higher-order deformations will be explored for the fusion-fission mechanisms in future research.The deformation and orientation degrees of freedom are introduced in the interaction potential to obtain the related barrier characteristics through the spherical harmonic function of nuclear radii terms (see [37, 38] and Eq. (6) of the manuscript). The radius of a nucleus is estimated from the center to the surface region. Unlike spherical-symmetric quadrupole (
$ \beta_2 $ ) deformed nuclei, the center point of the symmetry-breaking pear shape is not situated exactly at the center. One can visualize (in the graphical representation of Fig. 1) the change in the interaction distance between the centers of the spherical-octupole pairs of colliding nuclei and that of spherical-quadrupole combination for the cold/noncompact and hot/compact fusion configurations. This point motivates us to observe the corresponding effects on the fusion barrier ($ V_B $ and$ R_B $ ) as well as the fusion cross-sections ($\sigma_{\rm fus}$ ). To extract the exclusive role of deformations up to octupole, the$ \beta_3 $ results are compared with the corresponding$ \beta_2 $ -case. For heavy-ion induced reactions, the total interaction potential constitutes the repulsive and attractive potential terms; these contributing potentials, that is, the long-range repulsive Coulomb and centrifugal potentials, are well known [39]. However, the short range attractive nuclear potential can be obtained using microscopic as well as phenomenological approaches. It is relevant to mention that the optimum orientations obtained for deformations up to$ \beta_3 $ in Ref. [36] are independent of the choice in nuclear potential and the nuclear radius term. Therefore, in this study, we obtained the nuclear potential from the ‘pocket formula’ by Blocki et al. [40].
Figure 1. (color online) The graphical representation of the ‘cold or elongated’ and ‘hot or compact’ fusion configurations of the 16O+280Ra (
$ \beta_{22} = 0.069 $ ,$ \beta_{32} = -0.163 $ ) reaction. The upper panel represents the spherical-plus-quadrupole deformed combination, and lower panel presents spherical-plus-octupole deformed colliding partners.This study explores the effect of octupole deformation and the related optimum orientations on approximately 200 spherical-octupole pairs of colliding nuclei. For this combination, the doubly magic nuclei 16O and 48Ca are used as projectiles to strike an octupole deformed target. The considered options for the soft- and rigid-pear shapes of octupoles belong to different mass-regions of the Periodic Table. For the previously mentioned reactions, Section II describes the formalism used to determine the fusion barrier and cross-sections. In Section III, we discuss the calculation and results; it is observed that the cold configuration criteria of
$ \beta_3 $ could reproduce the experimental data of the 16O+150Sm ($ \beta_{22} = 0.205, $ $ \beta_{32} = -0.055 $ ) reaction [1] across the Coulomb barrier energies. Finally, in Section IV, a brief summary is given. -
The total interaction potential
$ V_T(R,\theta_2) $ for spherical-deformed pairs is defined as a function of the separation distance R between the centers of colliding nuclei. To find the fusion barrier, the$ V_T(R,\theta_2) $ is calculated at a distance (barrier position$ R_B $ ) where a repulsive Coulomb ($ V_C $ ) and an attractive nuclear potential ($ V_N $ ) are balanced. Note that the barrier curvature ($ \hbar\omega_B $ ) at$ R_B $ is evaluated by taking the second derivative of$ V_T(R,\theta_2) $ , that is,$\hbar\omega_B = \hbar[|{\rm d}^2V_T(R,\theta_2)/{\rm d} R^2|_{R = R_B}/\mu]^{1/2}$ .For the spherical-deformed case, the repulsive Coulomb potential for co-planar nuclei is given as [39]
$ \begin{aligned}[b] V_C =& \frac{Z_1Z_2e^2}{R}+Z_1Z_2e^2\sum\limits_{\lambda = 2,3}\left(\frac{R_2^{\lambda}(\alpha_2)}{R^{\lambda+1}}\right)\beta_{\lambda}Y_{\lambda}^{(0)}\\&\times \left[\frac{3}{2\lambda+1}+\left(\frac{12}{7(2\lambda+1)}\right)\beta_{\lambda}Y_{\lambda}^{(0)}\right], \end{aligned} $

(1) where
$ \beta_{\lambda} $ ,$ Y_{\lambda}^{(0)} $ , and$ R_2(\alpha_2) $ represent the deformation parameter, spherical harmonic function, and nuclear radius terms for a target nucleus.$ \lambda = 2,3 $ represent the quadrupole and octupole deformations, respectively, which are taken from the Nuclear Data Table of ground-state deformations [41].The nuclear proximity potential (
$ V_N $ ) is obtained from Blocki et al. [40]. Here, a collective formulation for the deformed and coplanar oriented nuclei is considered [14, 26, 42-45], and$ V_N $ reads as$ V_N = 4\pi\bar{R}\gamma b\Phi(s_0), $

(2) where
$ V_N $ is a product of two terms; one [$ 4\pi\bar{R}\gamma b $ ] depends on the shape and geometry (relative orientation) of the colliding nuclei and the other [$ \Phi(s_0) $ ] is a function of a single parameter, that is, the minimum separation distance ($ s_0 $ ) between two colliding surfaces. In the first term, the mean curvature$ \bar{R} $ is expressed in terms of the radii of curvature$ R_{i1} $ and$ R_{i2} $ , as given below for coplanar nuclei ($ \phi = 0 $ ).$ \frac{1}{\bar{R}^2} = \frac{1}{R_{11}R_{12}}+\frac{1}{R_{21}R_{22}}+\frac{1}{R_{11}R_{22}}+\frac{1}{R_{21}R_{12}}, $

(3) where the principal radii of curvature (
$ R_{11} $ and$ R_{12} $ ) for a spherical projectile (i = 1) are given as$ \begin{aligned}[b] R_{11}(\alpha_1) =& \frac{\left[R_1^2(\alpha_1)+R_1^{'2}(\alpha_1)\right]^{3/2}}{R_1^2(\alpha_1)+2R_1^{'2}(\alpha_1)-R_1(\alpha_1)R_1^{''}(\alpha_1)} = R_1(\alpha_1) \\& \because R_1(\alpha_1) = R_{01} \Rightarrow R_1^{'}(\alpha_1) = R_1^{''}(\alpha_1) = 0,\\ R_{12}(\alpha_1) =& \frac{R_1(\alpha_1)\sin\alpha_1}{\cos(\pi/2-\alpha_1-\delta_1)} = \frac{R_1(\alpha_1)\sin\alpha_1}{\cos(\pi/2-\alpha_1-\theta_1+\alpha_1)}\\ =& R_1(\alpha_1). \end{aligned} $

(4) Here,
$ \delta_1 = \theta_1-\alpha_1 $ ,$\theta_1 = 0^\circ$ , and$\alpha_1 = 180^\circ$ .For the deformed target (
$ i = 2 $ ), the principal radii of curvature ($ R_{21} $ and$ R_{22} $ ) are given as$ \begin{aligned}[b] R_{21}(\alpha_2) =& \frac{\left[R_2^2(\alpha_2)+R_2^{'2}(\alpha_2)\right]^{3/2}}{R_2^2(\alpha_2)+2R_2^{'2}(\alpha_2)-R_2(\alpha_2)R_2^{''}(\alpha_2)}, \\ \\ R_{22}(\alpha_2) =& \frac{R_2(\alpha_2)\sin\alpha_2}{\cos(\pi/2-\alpha_2-\delta_2)}. \end{aligned} $

(5) The angles (
$ \alpha_i $ and$ \delta_i $ ) for the deformed target (i = 2) are depicted in Fig. 2, and further details may be seen in references [36, 44]. In Eqs. (4) and (5),$ R^{'}_i(\alpha_i) $ and$ R^{''}_i(\alpha_i) $ represent the first and second order derivatives, respectively, of radius vector$ R_i(\alpha_i) $ with respect to the angle$ \alpha_i $ .
Figure 2. Schematic configuration of spherical-plus-octupole axially symmetric deformed and oriented nuclei lying in the same plane.
The nuclear radius parameter for the spherical projectile in Eq. (4) is
$ R_1(\alpha_1) = R_{01} $ , and that of the deformed nuclei$ R_2 $ ($ \alpha_2 $ ) in Eq. (5) is described in terms of the spherical harmonic function [37, 38], as given follows:$ R_2(\alpha_2) = R_{02}\left[1+\sum\limits_{\lambda = 2,3}\beta_{\lambda}Y_{\lambda}^{(0)}(\alpha_2)\right]. $

(6) Here,
$ R_{0i} $ ($ = 1.28A^{1/3}_i-0.76+0.8A^{-1/3}_i $ ) in fm, from Ref. [40], represents the radius of the equivalent spherical nucleus.In Eq. (2), the value of the surface thickness b = 0.99 fm and the surface energy constant term ‘γ’ is expressed as follows for the axially symmetric nuclear shapes:
$ \gamma = 0.9517\left[1-1.7826\left(\frac{N-Z}{A}\right)^2\right] {\rm{MeV\,fm^{-2}}}. $

Further, the second term of Eq. (2) is the Universal function, given as
$ \Phi ({s_0}) = \left\{ \begin{array}{l} - \dfrac{1}{2}{({s_0} - 2.54)^2} - 0.0852{({s_0} - 2.54)^3}\\ - 3.437\exp \left( { - \dfrac{{{s_0}}}{{0.75}}} \right) \end{array} \right., $

(7) respectively, for
$ s_0\leqslant 1.2511 $ and$ s_0>1.2511 $ . Here,$ s_0 $ is defined in units of the surface diffuseness factor b. It is to be noted that the optimum orientations obtained in Ref. [36] for both the hot and cold fusion configurations of octupole deformed nuclei are independent of the choice in nuclear potentials and the radius term ‘$ R_{0i} $ ’.Different iterative methods to fix ‘
$ s_0 $ ’ are available [42, 46]. In the proximity potential, the shortest distance$ s_0 $ is taken parallel to the separation distance R along the collision axis. The minimized separation distance$ s_0 $ in terms of nuclear radii is defined for the co-planar case as follows:$ \begin{aligned}[b] s_0 = &R-X_1-X_2 = R-R_1(\alpha_1)\cos(\theta_1-\alpha_1)\\ & -R_2(\alpha_2)\cos(180+\theta_2-\alpha_2), \end{aligned} $

(8) with the minimization conditions
$ \begin{aligned}[b] \tan(\theta_1-\alpha_1) =& \tan(\delta_1) = -\frac{R_1^{'}(\alpha_1)}{R_1(\alpha_1)},\\ \tan(180+\theta_2-\alpha_2) = &\tan(\delta_2) = -\frac{R_2^{'}(\alpha_2)}{R_2(\alpha_2)}. \end{aligned} $

(9) The fusion barrier characteristics (
$ V_B $ ,$ R_B $ and$ \hbar\omega_B $ ), as a function of deformation and orientation degrees of freedom, derived with the help of Eqs. (1) to (9) are used in the calculation of fusion cross-sections, as discussed below. -
To determine the fusion cross-sections for the spherical-deformed projectile-target combinations, we used the well known Wong approach [39]. The effect of deformation and orientation is introduced via barrier characteristics (barrier height
$ V_B $ , barrier position$ R_B $ and barrier curvature$ \hbar\omega_B $ ), which are the input terms of the Wong formula, as given below.$ \sigma_{\rm fus}(E_{\rm c.m.},\theta_2) = \frac{R_B^2\hbar\omega_B}{2E_{\rm c.m.}}\ln\left[1+\exp\left(\frac{2\pi}{\hbar\omega_B}(E_{\rm c.m.}-V_B)\right)\right]. $

(10) For the above formula, Wong conducted ℓ-summation under several approximations: (i)
$ \hbar\omega_B^{\ell}\approx\hbar\omega_B^0 $ ,$ R_B^{\ell}\approx R_B^0 $ and (ii)$ V_B^{\ell}\approx V_B^0+\dfrac{\hbar^2\ell(\ell+1)}{2\mu {R_B^0} ^2} $ . Using these approximations, the Wong formula (Eq. (10)) was expressed for$ \ell = 0 $ case. Further, the formula was modified by Gupta and collaborators via explicit ℓ-summation [47]. In other words, the fusion cross-sections calculated using the extended ℓ-summed Wong model is expressed as a function of ℓ-dependent barrier characteristics ($ V_B^{\ell} $ ,$ R_B^{\ell} $ and$ \hbar\omega_B^{\ell} $ ) and is given as$ \sigma_{\rm fus}(E_{\rm c.m.},\theta_2) = \frac{\pi}{k^2}\sum\limits_{\ell = 0}^{\ell_{\max}}(2\ell+1)T(E_{\rm c.m.}), $

(11) where
$k = \sqrt{\dfrac{2\mu E_{\rm c.m.}}{\hbar^2}}$ and μ is the reduced mass. The value of$\ell_{\max}$ is obtained using the sharp cut-off model [48] for the above barrier energies and extrapolated for the below barrier energies.$T(E_{\rm c.m.})$ is the quantum-mechanical transmission probability for the$ \ell^{th} $ -partial wave. The formulation of transmission/penetration probability$T(E_{\rm c.m.})$ is expressed as$ T(E_{\rm c.m.}) = \left[1+\exp\left(\frac{2\pi}{\hbar\omega_B^{\ell}}(V_B^{\ell}-E_{\rm c.m.})\right)\right]^{-1}. $

(12) Furthermore, to observe the effect of octupole deformed nuclei over all orientations, the fusion cross-sections are integrated over
$ \theta_2 $ , as follows:$ \sigma_{\rm int}(E_{\rm c.m.}) = \int_{\theta_2}\sigma(E_{\rm c.m.},\theta_2)\sin{\theta_2}{\rm d}\theta_2. $

(13) The above equation is for coplanar nuclei of reactions that involve spherical projectiles and deformed targets.
-
The octupole deformation (
$ \beta_3 $ ) that distorts the quadrupole ($ \beta_2 $ ) deformed nuclei into a (reflection symmetry-breaking) pear shape significantly modifies the uniquely fixed or optimized orientations ($\theta_{\rm opt}$ ) for the hot and cold fusion configurations [36]. Based on this observation, this study explores the impact of deformations up to$ \beta_3 $ and the related$\theta_{\rm opt}$ on the fusion barrier (barrier height$ V_B $ and barrier position$ R_B $ ) and fusion cross-sections ($\sigma_{\rm fus}$ ), in reference to the results obtained for$ \beta_2 $ -deformation. The above analysis is applied to spherical+deformed pairs of colliding nuclei in which 16O and 48Ca are used as projectiles and the octupole deformed nucleus is used as the target.There are approximately 700 deformed nuclei that have both the quadrupole
$ \beta_2 $ and octupole$ \beta_3 $ deformations [41]. The magnitude of the$ \beta_2 $ and$ \beta_3 $ deformations shown in Fig. 3 is represented by the open triangle and solid circle symbols, respectively. From this figure, one can identify the nuclei that have a larger$ \beta_2 $ magnitude than$ \beta_3 $ magnitude (also called soft-pear shapes of the octupole). On the other hand, nuclei with larger or equal$ \beta_3 $ magnitudes than$ \beta_2 $ are called rigid-pear shapes of the octupole. Most of the soft-pear shapes exist in the regions Z = 53-60 and 76-88 with a mass range of A = 103-115, 140-150, 188-195, and 210-230. Its rigid counterparts are found in abundance in the regions Z = 37-40, 59-68, and >80 with the masses A = 124-131, 189-196, 215-224, and 272-291. We have considered these pear shapes from their respective regions① in further calculations.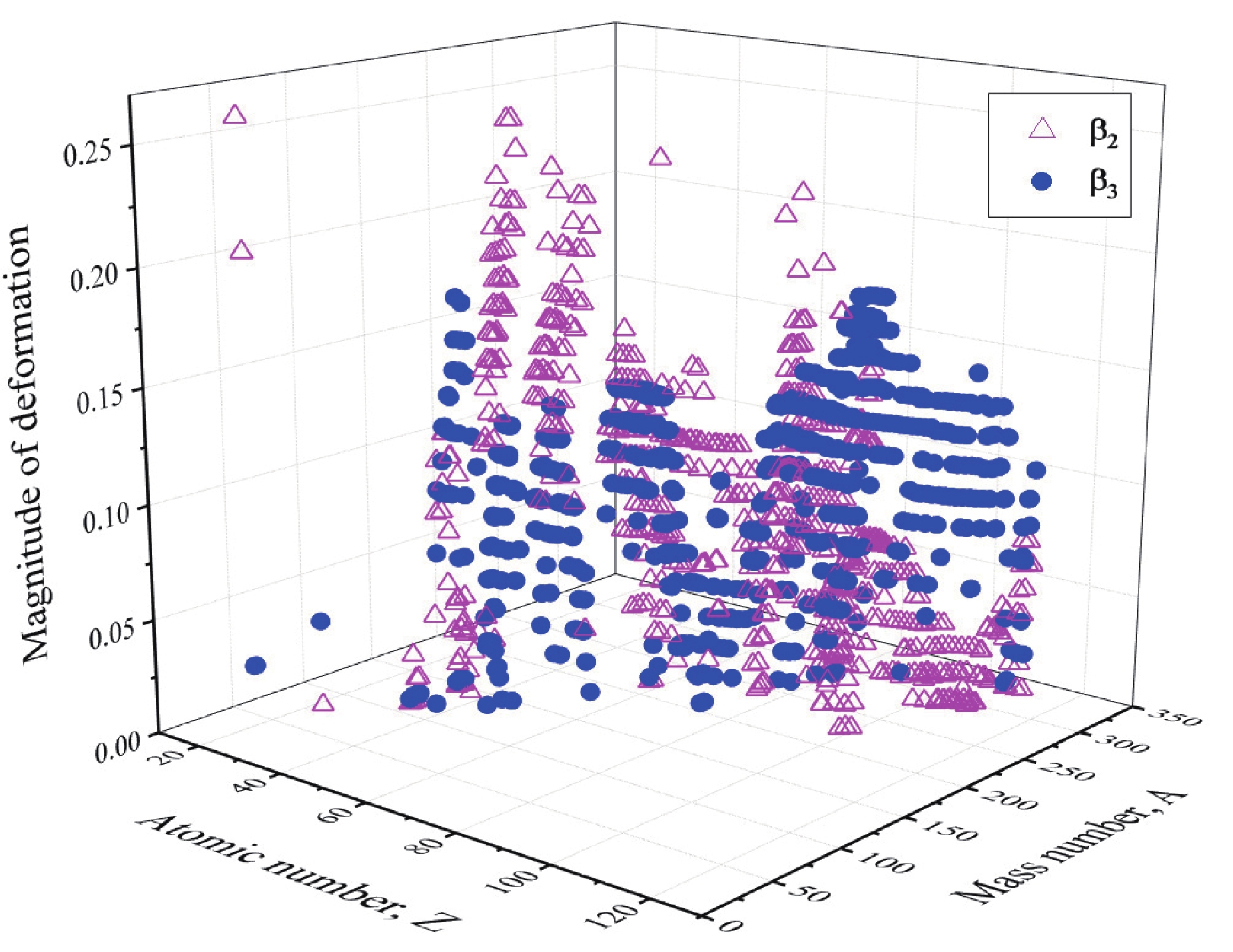
Figure 3. (color online) The magnitude of deformations provided in the Nuclear Data Table of [41] for nuclei belonging to different mass-regions of the Periodic Table.
Initially, to illustrate, we plotted the total interaction potential
$ V_T $ (MeV) as a function of separation distance R (fm) in Fig. 4 for the 16O+144Ba (soft-pear shape;$ |\beta_2|>|\beta_3| $ ) and 280Ra (rigid-pear shape;$ |\beta_2|\leq|\beta_3| $ ) reactions. For the synthesis of a compound nucleus via cold or hot fusion process, the orientation of a deformed nucleus is fixed or optimized in two ways: (i) the noncompact (or elongated) configuration, which occurs owing to the lowest barrier and largest interaction distance between the centers of two nuclei and (ii) the most-compact configuration occurs at the highest barrier and shortest interaction distance. The steps (i) and (ii) correspond to the ‘optimum cold’ and ‘optimum hot’ fusion configurations, respectively. By considering$ \beta_2 $ in the targets of the above reactions, the cold optimum orientation occurs at either$\theta_{\rm opt}^{\beta_2} =$ 0° or 180 ° . However, by including deformation up to $ \beta_3 $ , the noncompact or cold fusion configuration does not occur at$\theta_{\rm opt}^{\beta_2} =$ 180° but at $\theta_{\rm opt}^{\beta_3} =$ 0° because the pear-shape or octupole deformed nucleus does not have the same configuration at angles 0 ° and 180 ° (see Fig. 1). For the hot optimum case, the corresponding $\theta_{\rm opt}$ for$ \beta_2 $ occurs at 90°; however, this situation is justified at angles $\theta_{\rm opt}^{\beta_3} =$ 75$ \pm $ 2° and 180° due to a small $ \beta_3 $ in soft-pear shapes and the strong contribution of$ \beta_3 $ in rigid-pear shapes, respectively (see Ref. [36]). The above analysis shown in panels (a)-(d) of Fig. 4 illustrates that the change in$\theta_{\rm opt}^{\beta_2}$ owing to inclusion of$ \beta_3 $ also has a significant influence on fusion barrier characteristics. For the soft-pear shapes, these remarkable effects can be seen on$ V_B $ and$ R_B $ , mainly for the noncompact fusion configuration, as shown in Fig. 4(a) and (b). However, by considering the rigid-pear shape, a significant impact is observed on the fusion barrier of both the compact and noncompact fusion configurations (see panels (c) and (d) of Fig. 4). For further calculations, this analysis is applied to approximately 200 pear shapes of octupole deformed nuclei that belong to different mass-regions of the Periodic Table.
Figure 4. (color online) The total interaction potential
$ V_T $ (MeV) as a function of separation distance R (fm) is shown for the cold and hot fusion configurations in panels (a) and (b), respectively, for the 16O+144Ba ($ \beta_{22} = 0.163 $ ,$ \beta_{32} = -0.124 $ ) reaction, and in (c) and (d) for the 16O+280Ra ($ \beta_{22} = 0.069 $ ,$ \beta_{32} = -0.163 $ ) reaction.$\theta_{\rm opt}^{\beta_2}$ and$\theta_{\rm opt}^{\beta_3}$ represent the optimum angles for deformations$ \beta_2 $ and up to$ \beta_3 $ . -
The soft-pear shapes belonging to regions Z = 53-60 and 76-88 have different values of
$ \beta_2 $ and$ \beta_3 $ and are considered targets in 16O-induced reactions. Furthermore, to observe the impact of this shape on the fusion barrier at both the hot and cold optimum orientations, we observed the change in the barrier height$ V_B $ and barrier position$ R_B $ owing to the inclusion of deformations up to$ \beta_3 $ from that of$ \beta_2 $ . Figure 5 shows the variation of$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ and$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ for the cold optimum case in panels (a) and (b), respectively, with respect to the difference in the magnitude of the$ \beta_2 $ and$ \beta_3 $ deformations. The soft-pear shapes have a larger$ \beta_2 $ magnitude than$ \beta_3 $ magnitude; therefore, the difference$ |\beta_2|-|\beta_3| $ is greater than zero. In Fig. 5(a), the positive values obtained from$ V_B(\beta_2) $ -$ V_B(\beta_2,\beta_3) $ illustrate the extent with which$ V_B(\beta_2,\beta_3) $ decreases from$ V_B(\beta_2) $ . For the soft-pear shapes of mass-regions A = 103-115 (open square) and 140-150 (open circle) belonging to Z = 53-60, the difference increases to 3.5 MeV as the magnitude of$ \beta_3 $ becomes comparable to$ \beta_2 $ (that is,$ |\beta_2|-|\beta_3|\rightarrow0 $ ). On the other hand, for the heavy-mass regions A = 188-195 (solid circle) and 210-230 (stars) of Z = 76-88, the difference$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ reaches 5.5 MeV for$ |\beta_2|-|\beta_3|\rightarrow 0 $ . In the lower panel of Fig. 5, the difference between$ R_B(\beta_2) $ and$ R_B(\beta_2,\beta_3) $ is depicted for the above fusion configuration and mass-regions. The negative value obtained from$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ indicates that the inclusion of$ \beta_3 $ enlarges the interaction distance between the centers of two colliding nuclei, in reference to that of$ \beta_2 $ . A large negative value of up to 0.8 fm is obtained for$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ as one goes from lighter to the heavier mass systems. It is clear to see from this discussion that, for the cold optimum orientation of heavy-mass soft-pear shapes, there is a significant impact on the fusion barrier height$ V_B $ and barrier position$ R_B $ , particularly when$ \beta_3 $ approaches the$ \beta_2 $ -value.
Figure 5. (color online) The difference in barrier height
$ V_B $ and barrier position$ R_B $ obtained owing to deformations up to$ \beta_2 $ and$ \beta_3 $ , that is, (a)$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ and (b)$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ , shown with respect to the difference in the magnitude of$ \beta_2 $ and$ \beta_3 $ . Note that the above analysis is performed for the ‘cold or noncompact’ fusion configuration of 16O+soft-pear shape combinations.Further, in Fig. 6, the negative and positive values obtained for
$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ and$R_B(\beta_2)- $ $ R_B(\beta_2,\beta_3)$ , respectively, represent the case of the hot optimum orientation of soft-pear shapes belonging to the previously mentioned mass-regions. In Fig. 6(a), for mass-regions A = 103-115 and 140-150 belonging to Z = 53-60, the change in$ V_B(\beta_2,\beta_3) $ from$ V_B(\beta_2) $ increases to 0.75 MeV as$ |\beta_2|-|\beta_3| $ approaches zero. On the other hand, for A = 188-195 and 210-230,$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ gives a value of approximately 1.5 MeV. In the case of barrier position, the positive value of$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ increases up to 0.2 fm for heavy mass systems, which is relatively higher than that of lighter-mass soft-pear nuclei, as shown in Fig. 6(b). In the other words, for the hot or compact configuration, the interaction distance becomes shorter with the inclusion of deformations up to$ \beta_3 $ than that of$ \beta_2 $ , which in turn increases$ V_B(\beta_2,\beta_3) $ from$ V_B(\beta_2) $ . The results obtained for both the cold and hot fusion configurations of the 16O+soft-pear shape combinations in Fig. 5 and Fig. 6 indicate that the octupole deformation of soft-pear shapes has a significant impact on$ V_B $ and$ R_B $ mainly for the cold fusion configuration.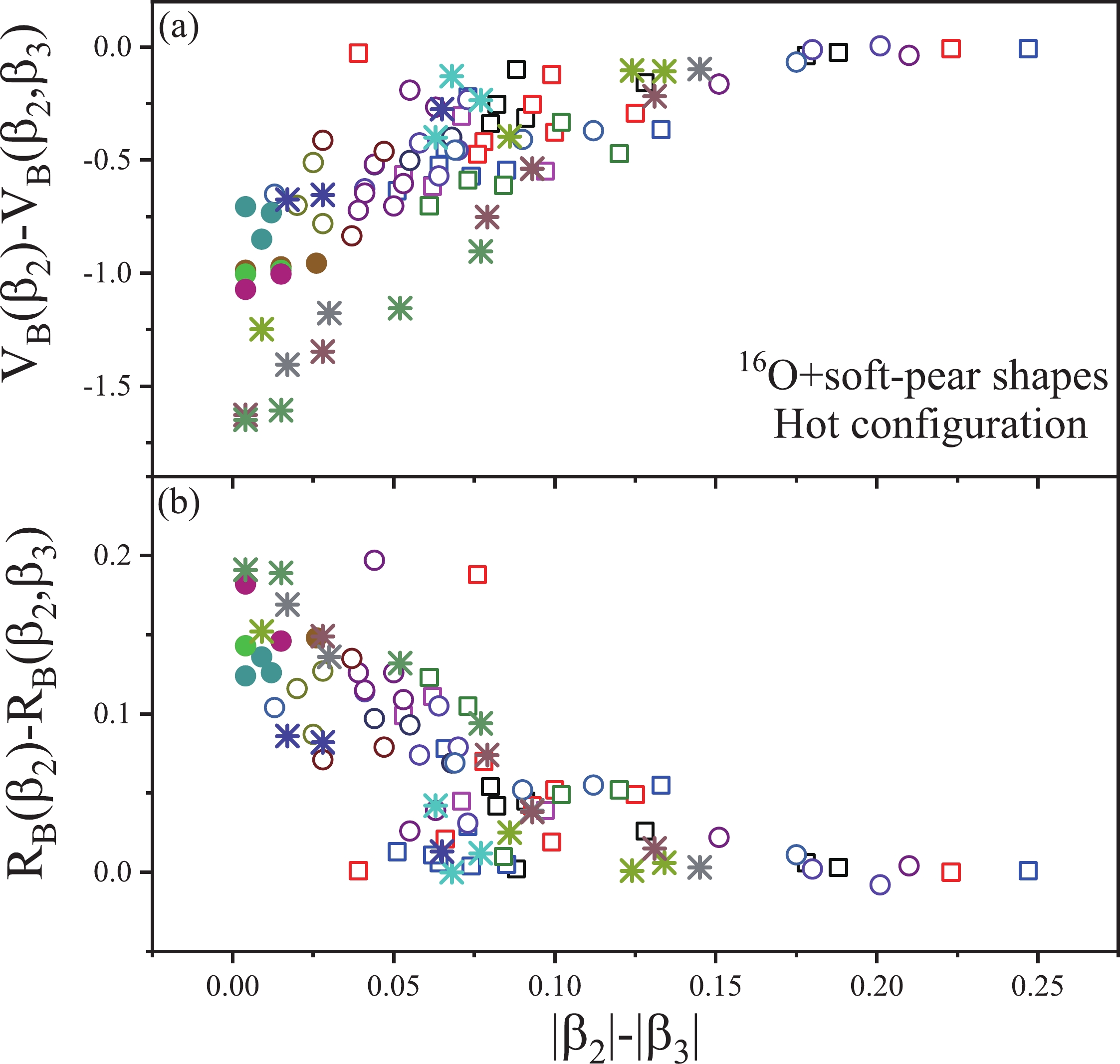
Figure 6. (color online) Same as Fig. 5, but for ‘hot or compact’ fusion configuration.
Moreover, we considered the rigid-pear shapes of the octupole (with stronger values of
$ \beta_3 $ than$ \beta_2 $ ) as the target in 16O-induced reactions to observe their corresponding effects on the fusion barrier, in reference to the results obtained for$ \beta_2 $ deformation. The considered options for rigid-pear shapes belong to mass-regions A = 124-131, 189-196, 215-225, and 272-291 of Z = 37-40, 59-68, and >80 (see Fig. 3). Furthermore, the variation of the differences$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ and$R_B(\beta_2)- $ $ R_B(\beta_2,\beta_3)$ is shown with respect to$ |\beta_2|-|\beta_3| $ for the cold fusion configuration of 16O+rigid-pear shape combinations in panels (a) and (b) of Fig. 7, respectively. In rigid-pear shapes, the magnitude of$ \beta_3 $ is greater or equal to that of$ \beta_2 $ ; therefore, the difference$ |\beta_2|-|\beta_3| $ is less than zero. For mass-regions A = 124-131 (open square) and 189-196 (open circle) of Z = 37-40 and 59-68, respectively, the positive value of$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ increases to 4 MeV, irrespective of the choice of$ |\beta_2|-|\beta_3| $ . On the other hand, for heavy-mass regions A = 215-224 (solid circle) and 272-291 (stars) of Z = 80-88 and 85-102, respectively,$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ increases up to 7 MeV (see Fig. 7(a)). In the case of barrier position, the negative value of the difference$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ for the cold optimum case reaches nearly 1.5 fm as one goes from lighter to heavy-mass regions, as shown in Fig. 7(b).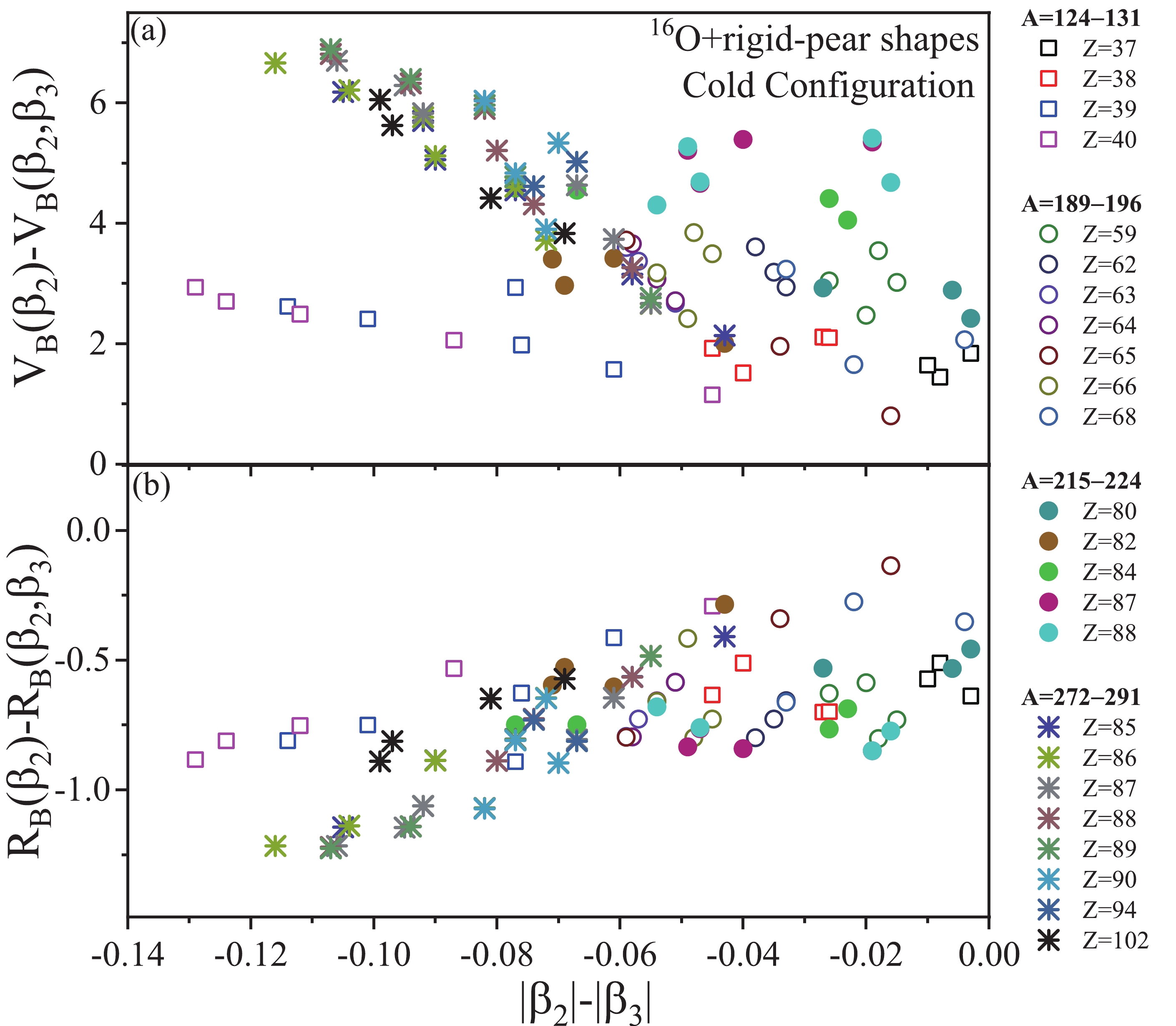
Figure 7. (color online) Same as Fig. 5, but for 16O+rigid-pear shape combinations.
In the case of hot or compact fusion configuration, the rigid-pear shapes show a change in
$ V_B(\beta_2,\beta_3) $ of approximately 2 MeV from$ V_B(\beta_2) $ for the lighter mass-region. For heavy-mass regions, the difference$ V_B(\beta_2)-V_B(\beta_2,\beta_3) $ increases to 6.5 MeV, as shown in Fig. 8(a). In the case of barrier position, the negative value of the difference$ R_B(\beta_2)-R_B(\beta_2,\beta_3) $ reaches nearly 0.8 fm with an increase in the mass of the rigid-pear shape. The results obtained from Figs. 5-8 for the 16O+deformed reactions signify that, irrespective of the choice of$ |\beta_2|-|\beta_3| $ , the rigid-pear shapes with$ |\beta_3|\geqslant |\beta_2| $ have a relatively stronger influence on the fusion barrier for hot and cold optimum cases than that of soft-pear shapes. The above analysis has also been repeated for 48Ca+deformed pairs of colliding nuclei, which involve the octupoles of soft- and rigid-pear shapes as targets. As a consequence, we have observed similar results as that of 16O-induced reactions for both the compact and noncompact fusion configurations.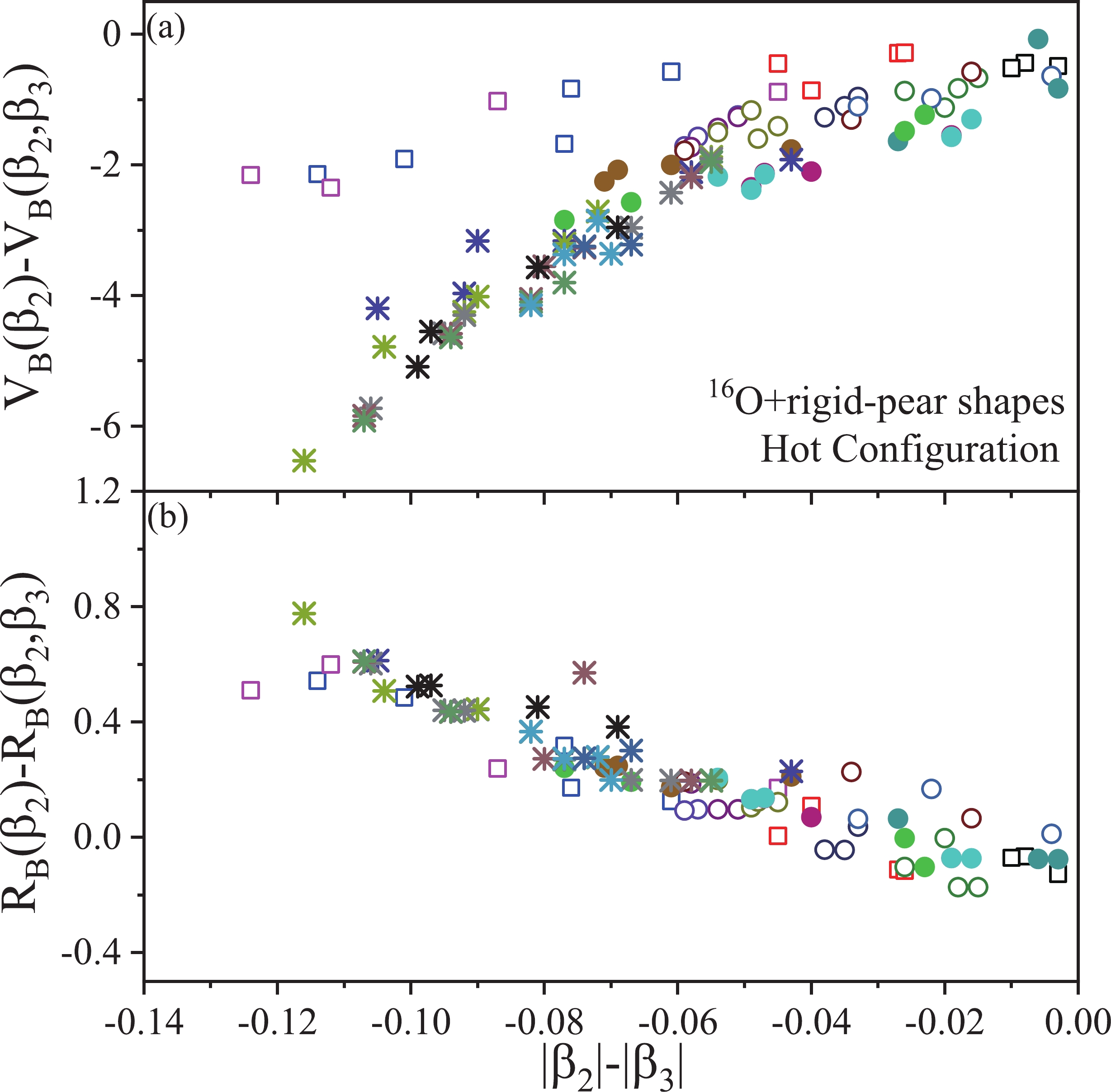
Figure 8. (color online) Same as Fig. 5, but for the hot fusion configuration of 16O+rigid-pear shape combinations.
-
So far, the role of octupole deformation (
$ \beta_3 $ ) has been analyzed for fusion barrier characteristics by employing the cold and hot optimum orientations. This analysis tested for 16O, 48Ca+soft- and rigid-pear shape reactions is compared with the results obtained for quadrupole ($ \beta_2 $ ) deformations. In addition, we calculated the fusion cross-sections to address the exclusive role of$ \beta_3 $ -deformations. For the calculation of fusion cross-section, which is a function of the center of mass energy$E_{\rm c.m.}$ and barrier characteristics (barrier height$ V_B $ , barrier position$ R_B $ , and barrier curvature$ \hbar\omega_B $ ), we used the Wong formula [39]. As we know, the fusion barrier parameters are sensitive to the deformation and orientation degrees of freedom; therefore, the fusion cross-sections ($\sigma_{\rm fus}$ ) are illustrated as a collective effect of the barrier characteristics of the spherical-plus-octupole deformed pairs of colliding nuclei. In view of this, we plotted$\sigma_{\rm fus}$ (mb) at$E_{\rm c.m.} = V_B$ for the above fusion configurations of the 16O, 48Ca+octupole deformed nucleus reactions.From Fig. 5, by considering soft-pear shapes as the target in 16O- and 48Ca-induced reactions, we discover a relatively higher impact on the fusion barrier as the magnitude of
$ \beta_3 $ becomes comparable to$ \beta_2 $ or$ |\beta_2|-|\beta_3|\rightarrow 0 $ . Thus, in the calculation of$\sigma_{\rm fus}$ , we considered the octupole deformed nuclei$ ^{145,146,148} {\rm{Nd}}$ and$ ^{149,150} {\rm{Sm}}$ , which are stable in nature [49] and can also be used for future fusion experiments. For the cold or noncompact fusion configuration, shown in panels (a) and (c) of Fig. 9, there is an enhancement in$\sigma_{\rm fus}$ owing to$ \beta_3 $ from that of$ \beta_2 $ . The change in$\sigma_{\rm fus}(\beta_2,\beta_3)$ from$\sigma_{\rm fus}(\beta_2)$ is relatively higher for the octupole deformed targets ($ ^{145,146,148} {\rm{Nd}}$ ), which have small differences in magnitude of the$ \beta_2 $ and$ \beta_3 $ -deformations, that is,$ |\beta_{22}|-|\beta_{32}|\leq0.112 $ . This analysis holds true for both the 16O- and 48Ca-induced reactions, as shown in panels (a) and (c) of Fig. 9. On the other hand, in the case of the compact or hot fusion configuration of soft-pear shapes, the change observed in the fusion barrier is relatively less. As a consequence, the fusion cross-sections obtained owing to the weak$ \beta_3 $ of soft-pear shapes differ by a smaller amount when compared with the$ \beta_2 $ -case, as shown in panels (b) and (d) of Fig. 9. Furthermore, the nuclei 147Eu and 223Ra of the rigid-pear shapes with sufficient half-lives [49] are considered targets of 16O, 48Ca-induced reactions and are studied for their corresponding effects on fusion cross-sections. As observed in section III.A, the rigid-pear shapes have a relatively higher impact on the fusion barrier of both the cold and hot fusion configurations than the soft-pear shapes. Consequently, there is a corresponding impact on the fusion cross-sections. The maximum change observed in$\sigma_{\rm fus}(\beta_2,\beta_3)$ from$\sigma_{\rm fus}(\beta_2)$ for the cold and hot fusion configurations is approximately 400mb and 15mb, respectively, which is larger than that of soft-pear shapes. In future experiments, it would be interesting to use octupole deformed nuclei (soft- and rigid-pear shapes) in nuclear fusion reactions to form new nuclei or isotopes.
Figure 9. (color online) The fusion cross-sections calculated using the Wong formula [39] for the (a), (c) cold and (b), (d) hot fusion configurations of the 16O, 48Ca+soft-pear shape (
$ ^{145,146,148} {\rm{Nd}}$ and$ ^{149,150} {\rm{Sm}}$ ) reactions, at$E_{\rm c.m.} = V_B$ .In [1], the experimentally determined fusion cross-sections are given across the Coulomb barrier energy for the 16O+150Sm (
$ \beta_{22} = 0.205 $ ,$ \beta_{32} = -0.055 $ ) reaction, which has an octupole deformed target of the soft-pear shape. In view of this, we calculated the fusion cross-sections with the inclusion of higher-order deformation (up to$ \beta_3 $ ) and compared the results with the experimental values. In this discussion, the Wong formula is used for the calculation of fusion cross-sections at$E_{\rm c.m.} = V_B$ because Wong conducted ℓ-summation under several approximations and produced the formula for the$ \ell = 0 $ case. Further, the ℓ-summation is performed explicitly in [47], which is called the extended ℓ-summed Wong model. The fusion cross-section determined using this extended version of the Wong formula is expressed in terms of quantum-mechanical transmission probability$T(E_{\rm c.m.})$ (see Eq. (11)). First, we analyzed the variation in$T(E_{\rm c.m.})$ with respect to$ E_{c.m.} $ for the above reaction. In Fig. 10(a), one can see the behavior of$T(E_{\rm c.m.})$ across the Coulomb barrier energies for the hot and cold fusion configurations of the above reaction. Across the Coulomb barrier energies, there is a relatively larger possibility of penetration due to the inclusion of deformations up to$ \beta_3 $ . On the other hand, for the hot or compact fusion configuration of the spherical-deformed combination, there is a highly nominal value observed for$T(E_{\rm c.m.})$ , especially below and near the barrier energies. The above observation is further analyzed in terms of fusion cross-sections ($\sigma_{\rm fus}$ ) using the extended ℓ-summed Wong model. The calculation of$\sigma_{\rm fus}$ , performed with the inclusion of$ \beta_2 $ and up to$ \beta_3 $ -defomrations for both the hot and cold configurations, are compared with the available data, as shown in Fig. 10(b). In Fig. 10, the target 150Sm is a soft-pear shape of the octupole nucleus; hence, the results obtained for the hot fusion configuration either with the involvement of$ \beta_2 $ or up to$ \beta_3 $ are similar and show hindrance from the data. On the other hand, the$\sigma_{\rm fus}$ obtained at the cold optimum orientation of$ \beta_3 $ provides better results than that of quadrupole deformation. In other words, the fusion cross-sections calculated for the cold or noncompact fusion configuration of the octupole deformed target (150Sm) effectively reproduce the experimental data across the Coulomb barrier energies.
Figure 10. (color online) (a) The transmission probability
$T(E_{\rm c.m.})$ calculated as a function of the center of mass energy$E_{\rm c.m.}$ (MeV), and (b) fusion cross-sections obtained using the extended ℓ-summed Wong model [47] for the 16O+150Sm ($ \beta_{22} = 0.205,\beta_{32} = -0.055 $ ) reaction [1] at both the hot and cold optimum orientations [36] related to quadrupole and octupole deformations across the Coulomb barrier energies.Also, we explored the average effect of
$ \beta_3 $ deformation in terms of$\sigma_{\rm fus}$ for the 16O+150Sm reaction by integrating$\sigma_{\rm fus}$ over the orientation$ \theta_2 $ , as shown in Fig. 11. This shows a relatively better comparison with the data than that of the$ \beta_2 $ -case (see Fig. 11(a)). However, we notice fusion hindrance even after the inclusion of$ \beta_3 $ -deformation. In this case, extra energy is required to fuse such systems, called extra-push energy. In view of this, many authors have implemented this idea and analyzed the influence of different factors (such as channel-coupling effects, dynamical deformations, and phenomenological model), which in turn provides extra-push energy below the barrier region to address fusion hindrance [50-55]. In our study, the main aim is to find the exclusive role of the optimum orientations ($\theta_{\rm opt}$ ) related to the static deformations of octupole ($ \beta_3 $ ) deformed nuclei on the barrier characteristics and subsequently on the fusion cross-sections; this is in reference to the results obtained with the inclusion of static quadrupole ($ \beta_2 $ ) deformations and the related$\theta_{\rm opt}$ . In this context, the fusion hindrance is addressed by employing a modified version of Prox77, that is, Prox88 [56]. Due to different values of the coefficient$ \gamma_0 $ ,$ k_s $ = 1.2496 MeV fm-2, and 2.3 used in Prox88, the barrier height$ V_B $ decreases and the barrier position$ R_B $ increases from that in Prox77. Consequently, the integrated fusion cross-sections obtained owing to the inclusion of deformations up to$ \beta_3 $ within the Prox88 potential produce a better fit to the experimental data of the 16O+150Sm reaction (see in Fig. 11(b)) than the$ \beta_2 $ -case. The fusion cross-sections shown in Figs. 10 and 11 represent the case for soft-pear targets of the 16O-induced reaction because its experimental data is available. The exclusive role of octupole deformation on the rigid-pear shape will be more prominent in reference to the$ \beta_2 $ -case. However, we have not shown this type of comparison for rigid-pear nuclei owing to unavailability of experimental data.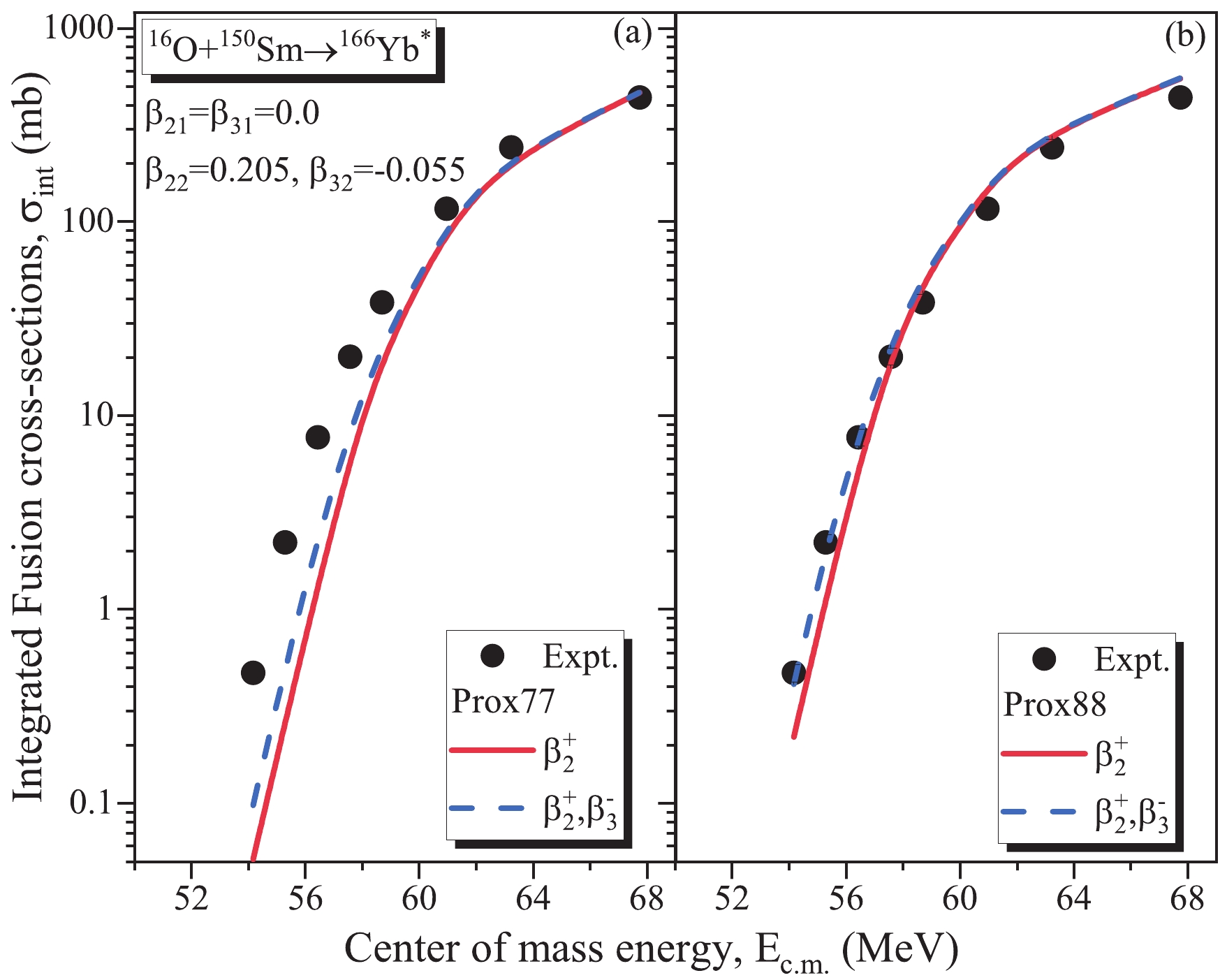
Figure 11. (color online) The fusion cross-sections integrated (
$\sigma_{\rm int}$ ) over orientations$ \theta_2 $ , calculated using (a) Prox77 and (b) Prox88, for the 16O+150Sm ($ \beta_{22} = 0.205,\beta_{32} = -0.055 $ ) reaction is varied as a function of the center of mass energy$E_{\rm c.m.}$ (MeV). -
For the synthesis of a compound nucleus via either cold or hot fusion processes, information on the fusion barrier characteristics (barrier height
$ V_B $ and barrier position$ R_B $ ) is extracted from the total interaction potential, which depends on the deformation and orientation degrees of freedom. The octupole deformation, which distorts the spherical-symmetric quadrupole deformed nucleus into a symmetry-breaking pear shape, produces different values of optimum orientations ($\theta_{\rm opt}$ ) for the ‘compact or hot’ and ‘elongated or cold’ fusion configurations, in reference to$\theta_{\rm opt}$ obtained for$ \beta_2 $ . In view of this, this study shows the influence of higher order deformations up to$ \beta_3 $ and the related$\theta_{\rm opt}$ on fusion barrier parameters. The elongated configuration of an octupole deformed nucleus has a significant impact on the fusion barrier compared to the most compact case. Similar results have been observed in the estimation of fusion cross-sections ($\sigma_{\rm fus}$ ) for 16O, 48Ca+octupole deformed nuclei (soft-pear shapes$ \rightarrow^{145,146,148} {\rm{Nd}}$ ,$ ^{149,150} {\rm{Sm}}$ , and rigid-pear shapes$ \rightarrow^{147} {\rm{Eu}}$ , 223Ra). The calculation of$\sigma_{\rm fus}$ with the inclusion of deformations up to$ \beta_3 $ at a cold optimum orientation reproduces the experimental data across the Coulomb barrier for the 16O+150Sm ($ \beta_{22} = 0.205 $ ,$ \beta_{32} = -0.055 $ ) reaction using the extended ℓ-summed Wong model. Also, we integrated the fusion cross-sections ($\sigma_{\rm int}$ ) over all orientations, by including$ \beta_2 $ and then$ \beta_3 $ -deformation of the deformed target in the above reaction. Even though the inclusion of deformations up to$ \beta_3 $ enhances$\sigma_{\rm int}$ from that of$ \beta_2 $ , we noticed fusion hindrance at the below-barrier region, where extra-push energy is required to fuse such systems. In view of this, a modified version of Prox77, that is, Prox88 is employed, which has a relatively lower barrier height and larger barrier position. As a consequence, the involvement of$ \beta_3 $ -deformation within the Prox88 potential gives better agreement with the experimental data for the 16O+150Sm reaction. Thus, nuclear potentials such as Prox88, which give a lower barrier height, provide extra-push below the Coulomb barrier energies to account for fusion hindrance.We conclude that octupole deformed nuclei in fusion reactions can be used for the synthesis of new isotopes of heavy and super-heavy nuclei. The
$ \beta_3 $ -induced optimum orientations play an important role in addressing the behavior of barrier characteristics and the associated fusion cross-sections. The orientation criteria for the fusion of quadrupole-plus-octupole and octupole-plus-octupole pairs of colliding nuclei will be investigated in the near future. Additionally, it would be of interest to investigate the impact of the choice in different nuclear potentials and hexadecapole deformations ($ \beta_{4} $ ) in view of the hot and cold optimum orientations of fusion processes.
Fusion of spherical-octupole pairs of colliding nuclei for compact and elongated configurations
- Received Date: 2021-04-23
- Available Online: 2022-01-15
Abstract: The deformation and associated optimum/uniquely fixed orientations play an important role in the synthesis of compound nuclei via cold and hot fusion reactions, respectively, at the lowest and highest barrier energies. The choice of optimum orientation (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: