-
Particle collision near a black hole background has long history. The possibility of having an infinite center-of-mass energy collision near a black hole was first pointed out by Piran, Shaham, and Katz in 1975 [1]. In 2009, Bañados, Silk, and West [2], rediscovered this mechanism, known as the BSW process and pointed out that because of the infinite center-of-mass energy caused by this collision, the rotating black holes can act as particle accelerators [2, 3]. Along this line, many aspects of the BSW mechanism with various black hole backgrounds have been investigated. Examples are the Kerr naked singularity [4], charged spinning black hole [5], Kerr-(anti)de-Sitter black hole spacetime [6], and the universal property of rotating black holes was given in Ref. [7]. Other research related to a higher or lower dimensional spacetime background [8–10] is also interesting, such that a five-dimensional Kerr black hole can be found in Ref. [8] and a three-dimensional rotating charged hairy black hole has been studied in Ref. [10]. Furthermore, the BSW mechanism can help us optimize the collisional penrose process, which extracts energy from a black hole through particle collision [11–19].
In three-dimensional spacetime, there is a typical stationary black hole solution with a negative cosmological constant that was first discovered by Bañados-Teitelboim-Zanelli (BTZ) [20]. This black hole solution, because of its similarity and simplicity compared with the (3+1)-dimensional Kerr black hole, has recently received increasing attention. For example, the spinless particles collision around the BTZ black hole has been the subject of study in Ref. [21]. Researchers are interested in the (2+1)-dimensional BTZ black hole, as it can be a good toy model, which helps gain a deeper understanding of the same problem in Kerr spacetime. This is becausethe analytical expression is usually possible in the BTZ background [22–24], while in the Kerr spacetime the same analytical treatment for the same problem is generally very difficult. For example, the collision of fast rotating dust thin shells in the (2+1)-dimension is significantly more simple compared with the (3+1)-dimensional Kerr spacetime [22–25].
In contrast, numerous authors focus on the point particle, whose trajectory is a geodesic. However, a real particle should be an extended body with inclusion of self-interaction. Compared with the spinless particle, the orbit of a spinning test particle is no longer a geodesic, and it has been shown [26–32] that the equations of motion of spinning particles around a given spacetime background are discribed by the Mathisson-Papapetrou-Dixon (MPD) equations [33–35]. By collecting these results, the authors in Ref. [30] show that the collision center-of-mass energy could be divergent for the extremal Kerr black hole. With these motivations, our research in this study is devoted to investigate the collision of spinning particles around the BTZ black hole.
The paper is organized as follows: In Sec. 2, we introduce Mathission-Papapetrou-Dixon (MPD) equations, which describe the spinning particles' motion in curved spacetime, and apply it to the Bañados-Teitelboim-Zanelli (BTZ) black hole. In Sec. 3, we obtain the collision center-of-mass energy of spinning particles and find the condition for the divergence of center-of-mass energy with either of the particle possessing critical total angular momentum. Subsequently, in Sec. 4, the motion of spinning particles with critical and subcritical angular momentum near the event horizon is analyzed in detail, and it is shown that a spinning particle with subcritical total angular momentum is allowed to exist on or outside the horizon. In Sec. 5, the collision of two spinning particles with subcritical total angular momenta near the horizon are calculated, and the diverging center-of-mass energy in the critical limit is obtained. Conclusions are provided in Sec. 6. Throughout the paper, we adopt the convention that the speed of light
$ c = 1 $ . -
The metric of the BTZ black hole in the Boyer-Lindquist coordinates reads [20]
$ {\rm{d}}s^2 = -g(r){\rm{d}}t^2+{{\rm{d}}r^2\over g(r)}+r^2\left({\rm{d}}\phi-{r_{+}r_{-}\over lr^2}{\rm{d}}t\right)^2, $

(1) where
$ g(r) ={(r^2-r_{+}^2)(r^2-r_{-}^2)\over l^2r^2}, $

(2) and
$ M = {r_{+}^2+r_{-}^2\over 8Gl^2}, $

(3) $ J = {r_{+}r_{-}\over 4Gl}, $

(4) and
$ r = r_{+} $ is the outer horizon,$ r = r_{-} $ is the inner horizon, M is the ADM mass, J is the angular momentum and l is a parameter determined by the negative cosmological constant$ \Lambda $ ($ l^2 = -\Lambda/3 $ ). Note that for the angular momentum J,$ {|J| }\leq M l $ must be satisfied. When the black hole is extremal ($ r_{+} = r_{-} $ ), we have$ |J| = M l $ .Under the given BTZ spacetime, the spinning particle's motion can be described by MPD equations [28, 30]
$ \frac{D}{D\tau }P^{a} = -\frac{1}{2}R_{bcd}^{a} v ^{b}S^{cd}, $

(5) $\frac{D}{D\tau }S^{ab} = P^{a} v^{b}-P^{b} v^{a}. $

(6) Along the center-of-mass world line
$ z(\tau) $ ,$ \upsilon ^{a} = (\frac{\partial }{\partial \tau })^{a} $ is the tangent vector,$ \frac{D}{D\tau } $ is the covariant derivative,$ P^{a} $ is the momentum of the spinning particles, and$ S^{ab} $ is the spinning angular momentum tensor.To obtain the detailed relation between
$ P^a $ and$ v^a $ , supplementary conditions need to be imposed: [30, 31]$ S^{ab}P_{b} = 0, $

(7) $ P^a v_a = -m , $

(8) where
$ \tau $ is not necessarily the proper time of the spinning particle. Combining Eqs. (5), (7), and (8), the difference between$ v^{a} $ and$ u^{a} $ reads [30, 34]$ mv^{a}-P^{a} = \frac{S^{ab}R_{bcde}P^{c}S^{de}}{2\left(m^{2}+\dfrac{1}{4}R_{bcde}S^{bc}S^{de}\right)}. $

(9) With direct calculation, we find that
$ v^a = u^a $ in BTZ spacetime, where$ u^a\equiv {P^a / m} $ . Notably, the velocity$ v^a $ is parallel to the momentum$ u^a $ in the specific property in (2+1)-dimensions, and in general not valid in four-dimensional spacetime.There are two Killing vector fields
$ \xi ^a = \left(\partial/\partial t\right)^a $ and$ \phi^a = \left(\partial/\partial \phi\right)^a $ in BTZ spacetime, and because BTZ spacetime is axi-symmetric and stationary, they can be expanded in the orthonormal triad basis$ {e_{a}^{(\nu)}} $ as$ \begin{align} \xi_a& = -\sqrt{g(r)}e_{a}^{(0)}-{r_{+}r_{-}\over lr}e_{a}^{(2)},\\ \phi_a& = r e_{a}^{(2)} , \end{align} $

(10) where
$ \begin{align} e_{a}^{(0)}& = \sqrt{g(r)}({\rm{d}}t)_a, \\ e_{a}^{(1)}& ={1\over \sqrt{g(r)}}({\rm{d}}r)_a, \\ e_{a}^{(2)}& =r\left(({\rm{d}}\phi)_a-{r_{+}r_{-}\over lr^2}({\rm{d}}t)_a\right). \end{align} $

(11) Then, a corresponding conserved quantity can be defined by the Killing vector field
$ \xi^{a} $ as follows:$ Q_{\xi } = P^{a}\xi _{a}-\frac{1}{2}S^{ab}\triangledown_{b}\xi_{a}. $

(12) From the equation above, two conserved quantities can be obtained, namely the energy of per unit mass of the particle
$ E_m $ and the angular momentum per unit mass of the particle$ J_m $ :$ \begin{align} E_m& =-u^a\xi _a+\frac{1}{2m}S^{ab}\nabla _b\xi _a,\\ J_m& =u^a\phi _a-\frac{1}{2m}S^{ab}\nabla _b\phi _a. \end{align} $

(13) Combining these with Eqs. (6) and (7), we can introduce the spin s of the particle as
$ s^2: = \frac{1}{2m^2}S^{ab}S_{ab}, $

(14) where s is the spin of unit mass. Moreover, combining with Eqs. (5), (6), and (7), the spin tensor can be written reversely as
$ S^{(a)(b)} = -m\varepsilon ^{(a)(b)}_{\; \; \; \; \; \; (c)}u^{(c)}s, $

(15) where
$ \varepsilon _{(a)(b)(c)} $ is the completely anti-symmetric tensor with the component$ \varepsilon _{(0)(1)(2)} = 1 $ .From Eq. (15), the non-zero components of the spin tensor can be expressed in terms of
$ u^{(a)} $ as$ \begin{align} S^{(0)(1)}& =-msu^{(2)},\\ S^{(0)(2)}& =msu^{(1)},\\ S^{(1)(2)}& =-msu^{(0)}. \end{align} $

(16) The explicit expressions of the energy and the angular momentum per unit mass
$ E_{{m}} $ and$ J_{{m}} $ in terms of$ u^{(a)} $ can be obtained using Eq. (16) and Eq. (13) as:$ E_m = \sqrt{g(r)}u^{(0)}+\left({r_{+}r_{-}\over lr}+{rs\over l^2}\right)u^{(2)}, $

(17) $ J_m = s\sqrt{g(r)}u^{(0)}+\left({r_{+}r_{-}s\over lr}+r\right)u^{(2)}. $

(18) Solving Eq. (17) and Eq. (18) gives
$ u^{(0)} = \frac{l \left(l E_m \left(l r^2+r_- r_+ s\right)-J_m \left(l r_- r_++r^2 s\right)\right)}{r \sqrt{\left(r^2-r_-^2\right) \left(r^2-r_+^2\right)} (l^2-s^2)}, $

(19) $ u^{(2)} = \frac{J_m-E_m s}{r-\dfrac{r s^2}{l^2}}. $

(20) By considering the normalization condition of momentum
$ u^{(a)}u_{(a)} = -m^2 $ , we obtain the$ u^{(1)} $ as follows:$ (u^{(1)})^2 = (u^{(0)})^{2}-(u^{(2)})^2-m^2. $

(21) For direct comparison to the spinless case in [21], now express the momentum in the coordinate basis:
$ p^t(r) ={{\rm{d}}t\over{\rm{d}}\tau} = {W(r)\over g(r)}, $

(22) $ p^r(r) = {{\rm{d}}r\over{\rm{d}}\tau} = \rho\sqrt{Y(r)}, $

(23) $ p^\phi(r) ={{\rm{d}}\phi\over{\rm{d}}\tau} = {r_{+}r_{-}W(r)\over lg(r)r^2}+{l^2(J_m-E_ms)\over r^2(l^2-s^2)}, $

(24) where
$ W(r) = \frac{E_{{m}} l \left(l r^2+r_{-} r_{+} s\right)-J_{{m}} \left(l r_{-} r_{+}+r^2 s\right)}{r^2 \left(l^2-s^2\right)}, $

(25) $ Y(r) = W^2(r)-\left(m^2+\left({J_{{m}}-E_{{m}}s\over r(1-{s^2\over l^2})}\right)^2\right)g(r), $

(26) $\rho = +1$ for the outward direction, –1 for the inward direction.We define the critical angular momentum as
$ J_c\equiv{E_ml(lr_{+}+r_{-}s)\over lr_{-}+r_{+}s}, $

(27) and a particle with critical angular momentum
$ J_c $ corresponds to:$ W_i(r_{+}) = 0, $

(28) where
$ i = 1,2 $ refers to particle 1 or particle 2 in the collision process. When the particle's spin$ s = 0 $ , the critical angular momentum introduced here will be reduced to the spinless case, which has already been investigated in Ref. [21].The timelike constraint of Eq. (22) indicates
$ p^t(r)>0 $ outside the horizon for massive particles, which in turn implies$ W_i(r)>0 $ . Therefore, for particles with the angular momentum$ J_m\leqslant J_c $ , the positivity of$ W_i(r) $ gives rise to a constraint on the particle's spin, as$ l^2-s^2>0 $ . Therefore, in the following sections, we restrict ourselves to the case$ -l<s<l $ . -
In this section, we intend to find the condition required for infinite center-of-mass energy collision of two spinning massive particles near the BTZ horizon. These are particles
$ i = 1,2 $ that start at infinity with masses$ m_i $ , energy per unit mass$ E_{mi} $ , total angular momenta per unit mass$ J_{mi} $ , and spins$ s_i $ , falling to the black hole and colliding near the event horizon. Then, the collision center-of-mass energy$ E_{\rm cm} $ is given by [21, 30]:$ \begin{split} E^2_{\rm cm}\equiv &-(p^\mu_1(r)+p^\mu_2(r))(p_{1\mu}(r)+p_{2\mu}(r)) \\ =& \;m_1^2+m_2^2 +{W_1(r)W_2(r)-\sqrt{Y_1(r)Y_2(r)}\over g(r)}\\ &-2{l^4(J_{m1}-E_{m1}s_1)(J_{m2}-E_{m1}s_2)\over r^2(l^2-s_1^2)(l^2-s_2^2)}, \end{split} $

(29) where
$ Y_i(r) $ and$ W_i(r) $ are defined by Eqs. (25) and (26) with$ i = 1,2 $ again labeling particle 1 or particle 2.We find that the third term of Eq. (29) is a
$ {0\over 0} $ type when r approaches the event horizon$ r_{+} $ , hence we first need to regularize this term as$ \mathop {\lim }\limits_{r \to {r_ + }} 2\frac{{{W_1}(r){W_2}(r) - \sqrt {{Y_1}(r){Y_2}(r)} }}{{g(r)}} = \frac{{{W_2}({r_ + })}}{{{W_1}({r_ + })}}{Z_1} + \frac{{{W_1}({r_ + })}}{{{W_2}({r_ + })}}{Z_2},$

(30) in which
$ Z_i = \left(m_i^2+\left({J_{mi}-E_{mi}s_i\over r\left(1-\dfrac{s_i^2} {l^2}\right)}\right)^2\right)>0. $

(31) It is easy to see that
$ E^2_{\rm cm} $ blows up with$ r\rightarrow r_{+} $ if one of the particles has the critical angular momentum$ J_c $ (which means$ W_i(r_{+}) = 0 $ ). If both particles possess$ J_c $ , then we have,$ {W_2(r_{+})\over W_1(r_{+})} = {W'_2(r_{+})\over W'_1(r_{+})} = \frac{E_{m1}(l r_-+ r_+ s_2)}{E_{m2} (l r_-+ r_+ s_1)}, $

(32) in which
$ ' $ denotes the derivative with respect to r. For an equal spin collision ($ s_1 = s_2 $ ), the ratio$ {W_2(r_{+})\over W_1(r_{+})} = {E_{m1}\over E_{m2}} $ becomes a finite value, which is similar to the spinless case [21]. Therefore, the only possibility for the center-of-mass energy to approach infinity is one of the spin, for example,$ s_1 $ , satisfies$ s_1 = s_c = -{lr_{-}\over r_{+}}. $

(33) However, this is equivalent to require
$ J_{m1} = J_{c1} $ to be infinity according to Eq. (27) and thus impossible to achieve in practice. -
In the previous section, we showed that if one of the collision particle possesses critical angular momentum, the center-of-mass energy
$ E_{\rm cm} $ will blow up. However, to solidify this conclusion, we still need to verify whether the particle with critical angular momentum$ J_c $ can satisfy other constraints, such as the timelike constraint in subsection IVA and radial equation of motion, which guarantees that the particles can reach the horizon. Therefore, the aim of this section is to discuss these constraints carefully.First, we note that for the spinless case [21], a particle with critical total angular momentum
$ J_m = J_c $ is not allowed to exist outside the event horizon, while one with subcritical angular momentum can be allowed. Later, we shall investigate the same issue by taking account of the spin effect in subsections IVB to IVC. -
The first subsection is devoted to the timelike constraint of
$ p^t(r) $ . To avoid superluminality,$ p^t(r) $ should be non-negative. From Eq. (22) we have$ p^t(r) = {W(r)\over g(r)}\geqslant 0, $

(34) since
$ f(r)>0 $ , the above equation is equivalent to$ W(r) = \frac{l \left(l E_m \left(l r^2+r_- r_+ s\right)-J_m \left(l r_- r_++r^2 s\right)\right)}{r (l^2-s^2)}\geqslant 0. $

(35) Eq. (35) states a restriction of
$ J_m $ to ensure$ p^t(r)\geqslant 0 $ near the event horizon, where the infinite center-of-mass energy collision takes place. Considering an extremal black hole and the case$ -l<s<l $ , this leads to$ J_m\leqslant E_m l = J_c, $

(36) which means that for
$ J_m<J_c $ , the timelike condition is satisfied. However, for a massive particle, when the total angular momentum assumes the critical value$ J_m = J_c $ , the timelike condition is violated. Therefore, in the following sections, we consider the subcritical total angular momentum$ J_m<J_c $ . -
Now we come to the radial motion of the particle, starting with the expression of
$ p^r(r) $ Eq. (23), and obtain the radial equation of motion of the spinning particle:$ {1\over 2}{p^r(r)}^2+V(r) = 0, $

(37) where
$ V(r) $ is the radial effective potential defined by$ V(r)\equiv -Y(r)/2 $ , and$ \tau $ is the geodesic parameter. Particles are only allowed to exist in regions where$ V(r)\leqslant 0 $ or$ Y(r)\geqslant 0 $ from Eq. (37).For a massive particle with
$ m\ne 0 $ , we consider that the tendency of$ Y(r) $ at infinity is$ \mathop {\lim }\limits_{r \to \infty } Y(r) = - {m^2} \times \infty < 0, $

(38) which implies that a massive particle cannot escape to infinity. As the expression of
$ Y(r) $ for massive particle is complicated, we investigate it with subcritical total angular momentum in IVC, especially for an extremal black hole. -
In the last subsection, we already know that particles with critical total angular momentum cannot exist outside the event horizon. Thus, we consider a particle with subcritical total angular momentum
$ J_m $ ($ J_m\leqslant J_c $ for the case$ -l<s<l $ according to Eq. (36)):$ J_m\equiv J_c-{\tilde{\delta}} = {E_ml(lr_{+}+r_{-}s)\over lr_{-}+r_{+}s}-{\tilde{\delta}}, $

(39) and attempt to find the range of
$ {\tilde{\delta}} $ that enables the particle to exist outside the black hole (i.e.$ Y(r)\geq 0 $ ). With this well-defined subcritical total angular momentum, we obtain the corresponding function$ Y(r) $ as follows:$ \begin{split} Y(r) =Y_c(r)+\frac{{\tilde{\delta}}(-2E_ml(r^2-r_{+}^2)(l^2-s^2)(lr_{+}+r_{-}s)-(lr_{-}+r_{+}s)(l^2(-r^2+r_{-}^2+r_{+}^2)+2lr_{-}r_{+}s+r^2s^2){\tilde{\delta}})} {r^2(l^2-s^2)^2(lr_{-}+r_{+}s)}, \end{split} $

(40) where
$ Y_c(r) = -{(r^2-r_{+}^2)\over r^2}\left({E_m^2l^2(r_{+}^2-r_{-}^2)\over (lr_{-}+r_{+}s)^2}+{m^2(r^2-r_{-})^2\over l^2}\right). $

(41) When the spin s is taken as zero, our result will reduce to the spinless case by identifying
$ {\tilde{\delta}} = \frac{r_+l}{r_-}\delta $ with$ \delta $ introduced in Ref. [21]. From Eq. (40), a particle with subcritical total angular momentum can exist on the event horizon or nearby outside of the black hole, since$ Y(r_{+}) = \left({(lr_{-}+r_{+}s){\tilde{\delta}}\over r_{+}(l^2-s^2)}\right)^2>0. $

(42) We proceed to discuss
$ Y'(r) $ , which is the derivative of$ Y(r) $ with respect to r, determining how far the collision point departs from the event horizon$ r_+ $ [21]. First,$ Y'(r) $ with critical total angular momentum (i.e.$ {\tilde{\delta}} = 0 $ ) is$ Y_c'(r_+) = \frac{2 \left(r_-^2-r_+^2\right) \left(l^4 E_m^2+m^2 \left(l r_-+r_+ s\right){}^2\right)}{l^2 r_+ \left(l r_-+r_+ s\right){}^2} $

(43) on the event horizon. For the extremal case with critical total angular momentum, since we have
$ r_+ = r_- $ , using Eqs. (41) and (43), we obtain$ Y(r_+) = Y'(r_+) = 0 $ on the event horizon.Then, with subcritical total angular momentum,
$ Y'(r) $ is relevant to$ {\tilde{\delta}} $ $ Y'(r) = Y'_c(r)-{2l{\tilde{\delta}}(-2E_mr_{+}^2(l^2-s^2)(lr_{+}+r_{-}s)+(lr_{-}+r_{+}s)(l(r_{-}^2+r_{+}^2)+2r_{-}r_{+}s){\tilde{\delta}})\over r^3(lr_{-}+r_{+}s)(l^2-s^2)^2}.\\ $

(44) On the event horizon, the above equation becomes
$ Y'(r_{+}) = D_2{\tilde{\delta}}^2+D_1{\tilde{\delta}}+D_0, $

(45) where the coefficients read
$ D_2 = -\frac{2 l \left(l \left(r_-^2+r_+^2\right)+2 r_- r_+ s\right)}{r_+^3 \left(l^2-s^2\right)^2}, $

(46) $ D_1 = \frac{4 l E_m \left(l r_++r_- s\right)}{r_+ \left(l^2-s^2\right) \left(l r_-+r_+ s\right)}, $

(47) $ D_0 =\frac{2 \left(r_-^2-r_+^2\right) \left(l^4 E_m^2+m^2 \left(l r_-+r_+ s\right){}^2\right)}{l^2 r_+ \left(l r_-+r_+ s\right){}^2}. $

(48) The coefficient
$ D_2<0 $ by considering$ s^2< l^2 $ , the sign of$ D_2 $ is the same as in the spinless case [21]. Along the same line as in Ref. [21], by solving Eq. (45), we found that there exists a$ E_{\max} $ $ E_{\max} = \frac{m \sqrt{r_+^2-r_-^2} \sqrt{l r_-^2+l r_+^2+2 r_+ r_- s}}{l^{3/2} r_-}, $

(49) if the unit mass energy
$ E_m<E_{\max} $ . The corresponding$ Y'(r_{+}) $ is always negative; on the contrary if$ E_m\geq E_{\max} $ , which is more interesting, the corresponding$ Y'(r_{+}) $ can be non-negative in the range of$ {\tilde{\delta}}_{\rm L}\leqslant{\tilde{\delta}}\leqslant{\tilde{\delta}}_{\rm R} $ , and it is negative elsewhere with the boundaries defined as$ \begin{split} {\tilde{\delta}}_{\rm L}& =\frac{l^3 E_m r_+^2 (l^2-s^2) \left(l r_++r_- s\right)-\sqrt{\Delta}}{l^3 \left(l r_-+r_+ s\right) \left(l \left(r_-^2+r_+^2\right)+2 r_- r_+ s\right)},\\ {\tilde{\delta}}_{\rm R}& =\frac{l^3 E_m r_+^2 (l^2-s^2) \left(l r_++r_- s\right)+\sqrt{\Delta}}{l^3 \left(l r_-+r_+ s\right) \left(l \left(r_-^2+r_+^2\right)+2 r_- r_+ s\right)}, \\ \Delta =& l^3 r_+^2 (l^2-s^2)^2 \left(l r_-+r_+ s\right){}^2 \\ &\times\left(l^3 E_m^2 r_-^2+m^2 \left(r_-^2-r_+^2\right) \left(l \left(r_-^2+r_+^2\right)+2 r_- r_+ s\right)\right). \end{split} $

(50) For the extremal black hole,
$ E_{\max} = 0 $ . It is worth noting that particles with subcritical total angular momenta$ J_c-{\tilde{\delta}} $ satisfying$ {\tilde{\delta}}_{\rm L}\leqslant{\tilde{\delta}}\leqslant{\tilde{\delta}}_{\rm R} $ have$ Y(r_+)>0 $ with$ Y'(r_+)>0 $ . Furtunately, they can exist outside the event horizon, which is in contrast to the non-existence of particles with critical total angular momentum in subsection 4.1.For the spinless particle, the infinite center-of-mass energy collision occurs at the extreme point of
$ Y(r) $ , which usually serves as return point of the particle. This is because in BTZ spacetime, except in the point where the particle starts to fall,$ Y(r) $ has no other zero point, which is usually taken as the collision point [21]. To find this turning point of radial motion, we solve the equation$ Y'(r) = 0 $ with the positive root$ r_m $ :$ r_m = r_{+}\left(1+{Y'(r_{+})l^2\over 2r_{+}m^2}\right)^{1\over 4}. $

(51) Consequently, whether
$ r_m $ is greater than event horizon$ r_+ $ relies directly on the sign of$ Y'(r_+) $ that has been analyzed above. When$ E_m\geqslant E_{\max} $ and$ {\tilde{\delta}}_{\rm L}\leqslant{\tilde{\delta}}\leqslant{\tilde{\delta}}_{\rm R} $ are satisfied, we have$ Y'(r_{+})\geqslant 0 $ , which in turn implies$ r_m\geqslant r_{+}, $

(52) Eq. (52) indicates that the turning point of radial motion is on or outside the event horizon.
After applying the extremal condition
$ r_{-} = r_{+} $ ,$ E_{\max} = 0 $ , the boundaries of Eq. (50) become:$ \begin{split} {\tilde{\delta}}_{\rm L}& =\frac{1}{2} E_m \left(l-s-\sqrt{(l-s)^2}\right),\\ {\tilde{\delta}}_{\rm R}& =\frac{1}{2} E_m \left(l-s+\sqrt{(l-s)^2}\right). \end{split}$

(53) Thus, the relation between
$ r_m $ and$ r_{+} $ can be summarized as follows:Since
$ -l<s<l $ , we have$ {\tilde{\delta}}_{\rm L} = 0\leqslant{\tilde{\delta}}\leqslant E_m(l-s) = {\tilde{\delta}}_{\rm R} $ or equivalently$ E_ms\leqslant J_m\leqslant E_m l $ ,$ r_m\geqslant r_{+} $ ; for other values of$ {\tilde{\delta}} $ ,$ r_m<r_{+} $ , which is disfavored by the current discussion.In Fig. 1,
$ {\tilde{\delta}} $ is assumed to be 0.01, and we compare the effective potentials of radial motion$ V(r) = -Y(r)/2 $ of a particle with different spins s and a subcritical total angular momentum$ J_m = E_ml-{\tilde{\delta}} $ in an extremal BTZ spacetime, in which the minimum points mark$ r_m $ , where the particle is about to return, and it is shown that$ r_m $ with spins satisfying$ -l<s<l $ are greater than$ r_{+} $ .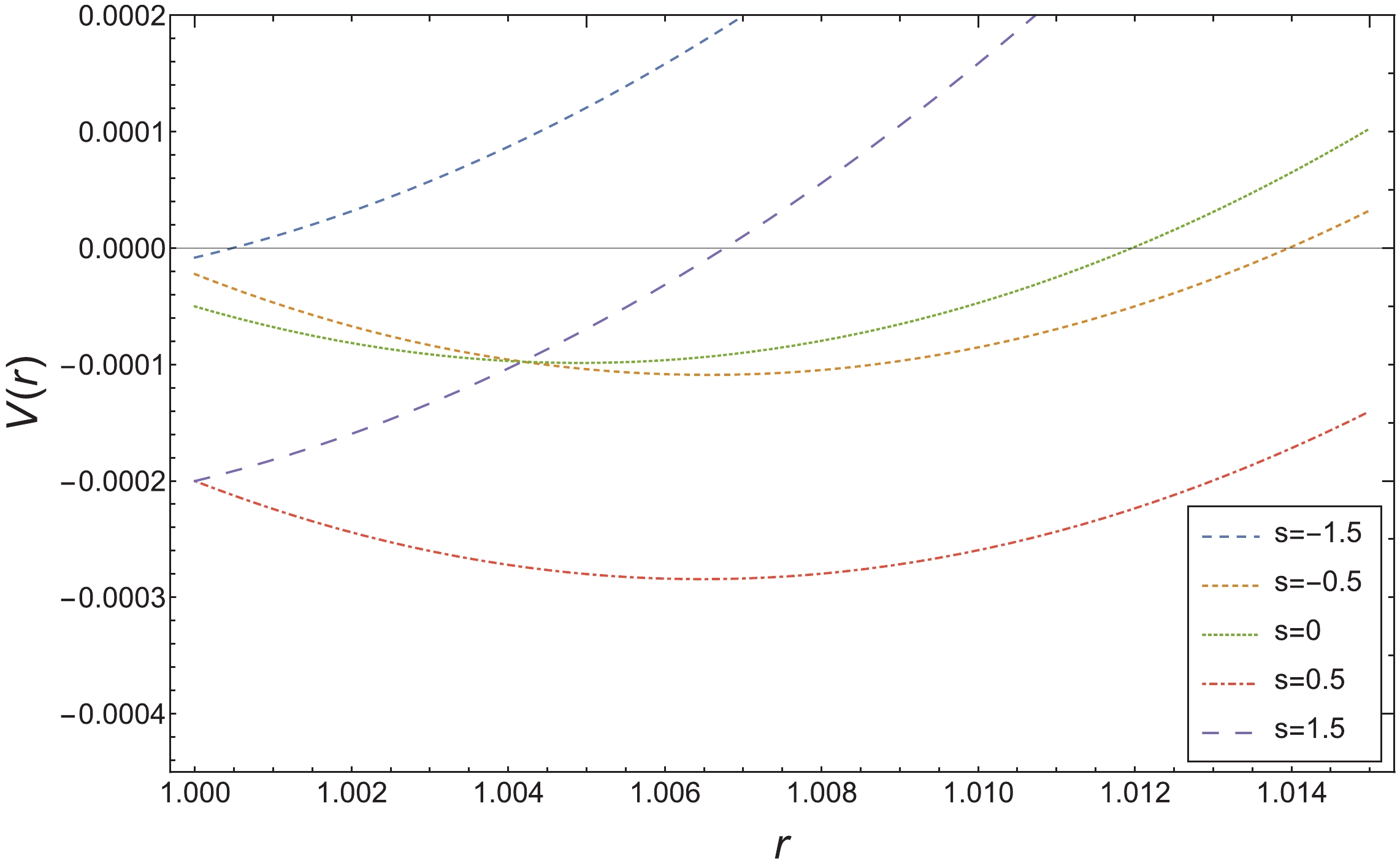
Figure 1. (color online) Effective potential of radial motion
$ V(r) = -{1\over 2}Y(r) $ of a particle with different spins s and a subcritical total angular momentum$ J_m = E_ml-{\tilde{\delta}}<J_c $ in an extremal BTZ spacetime. The minimum point of$ V(r) $ :$ r_m $ with spin$ s = -0.5,\;0,\;0.5 $ is greater than$ r_{+} $ . Here,$ r_{-} = r_{+} = E_m = l = m = 1,{\tilde{\delta}} = 0.01 $ , and the longitudinal axis marks the event horizon$ r_{+} $ . -
The divergence condition for center-of-mass energy with critical total angular momentum
$ J_c $ in Sec. 3 was found to be unavailable in subsection IVA. Because of the timelike constraint, both spinning particles are required to possess subcritical values of total angular momentum$ J_{m1} = E_{m1}l-{\tilde{\delta}}_1,\;J_{m2}\leqslant E_{m2}l $ , with$ {\tilde{\delta}}_{\rm L1}\leqslant{\tilde{\delta}}_1\leqslant{\tilde{\delta}}_{\rm R1} $ because we pick$ r_{m1} $ as the collision point. Then, we consider the collision center-of-mass energy$ E^2_{\rm cm} $ by taking the limit$ {\tilde{\delta}}_1\rightarrow 0 $ .$ \lim_{{\tilde{\delta}}_1\rightarrow 0}E_{\rm cm}^2(r_{m}) = m_1^2+m_2^2+Q-{2l^4(E_{m1}(l-s_1))J_{m2}\over r_+^2(l^2-s_1^2)(l^2-s_2^2)}, $

(54) in which
$ Q \equiv \mathop {\lim }\limits_{r \to {r_m}} 2\frac{{{W_1}({r_m}){W_2}({r_m}) - \sqrt {{Y_1}({r_m}){Y_2}({r_m})} }}{{g({r_m})}}.$

(55) Both numerator and denominator of Q tend to zero in the limit of
$ {\tilde{\delta}}_1\rightarrow 0 $ . For this reason, we express Q using L'Hopital's rule with respect to$ {\tilde{\delta}}_1 $ as$ \begin{split} Q& = \lim_{{\tilde{\delta}}_1\rightarrow 0}{W_2(r_m)\over \dot{g}(r_m)}\left(2\dot{W}_1(r_m)-{\dot{Y}_1(r_m)\over \sqrt{Y_1(r_m)}}\right)\\ & = \lim_{{\tilde{\delta}}_1\rightarrow 0}{W_2(r_m)\over \dot{g}(r_m)}\left(2\dot{W}_1(r_m)-2\sqrt{\dot{W}_1(r_m)\over(l-s_1)}\right), \end{split}$

(56) with · indicating derivative with respect to
$ {\tilde{\delta}}_1 $ , in which$ \lim_{{\tilde{\delta}}_1\rightarrow 0}\dot{W}_1(r_m) = \frac{E_{m1}^2 l^4+m_1^2 r_{+}^2 (l+s_1)^2}{m_1^2 r_{+}^2 (l-s_1) (l+s_1)^2}, $

(57) and after a series expansion,
$ \dot{g}(r_m) $ becomes:$ \lim_{{\tilde{\delta}}_1\rightarrow 0}\dot{g}(r_m) = \frac{2 {\tilde{\delta}}_1 E_{m1}^2 l^4}{m_1^4 r_{+}^2 \left(l^2-s_1^2\right)^2}. $

(58) Eventually, collecting all the above ingredients, Q can be expressed as
$ \begin{split} Q& = \lim_{{\tilde{\delta}}_1\rightarrow 0}{W_2(r_m)\over \dot{g}(r_m)}\left(2\dot{W}_1(r_m)-2\sqrt{\dot{W}_1(r_m)\over(l-s_1)}\right) \\&= 2k\lim_{{\tilde{\delta}}_1\rightarrow 0}{W_2(r_m)\over \dot{g}(r_m)}\dot{W}_1(r_m)\\ & = k\lim_{{\tilde{\delta}}_1\rightarrow 0}W_2(r_m)\frac{m_1^2 (l-s_1) \left(E_{m1}^2 l^4+m_1^2 r_{+}^2 (l+s_1)^2\right)}{ {\tilde{\delta}}_1 E_{m1}^2 l^4}. \end{split} $

(59) where k is
$\begin{split} k = 1-\sqrt{\dot{W}_1(r_m)\over(l-s_1)}/\dot{W}_1(r_m) = 1-\sqrt{\frac{m_1^2 r_{+}^2 (l+s_1)^2}{E_{m1}^2 l^4+m_1^2 r_{+}^2 (l+s_1)^2}}>0. \end{split}$

(60) Therefore, the collision center-of-mass energy
$ E^2_{\rm cm} $ of the two spinning particles is easily observed to diverge, as Q diverges at the point$ r = r_m $ in the limit$ {\tilde{\delta}}_1\rightarrow 0 $ . -
We analyzed the collision center-of-mass energy of two spinning particles near the BTZ black hole. Our result shows that the center-of-mass energy of two ingoing spinning particles in the near horizon limit can be arbitrarily large if one of the particles possesses a critical angular momentum, and the other has a noncritical angular momentum. However, a particle with critical angular momentum cannot exist outside of the horizon due to the violation of the timelike constraint. Moreover, we proved that the particle with a subcritical angular momentum is allowed to exist in the neighbourhood of an extremal BTZ black hole and the corresponding collision center-of-mass energy of two spinning particles taking place at the point near an extremal BTZ black hole can be arbitrarily large in the
$ {\tilde{\delta}}_1\rightarrow 0 $ limit.Notably, there are still many important issues that need to be investigated in the future. For example, inspired by the BSW mechanism, people found that the efficiency of extracting energy from a rotating black hole, which is usually called the Penrose process, can be significantly improved, especially for spinning particles [12, 13, 19, 36]. Therefore, with the BSW mechanism for spinning particles, studying the corresponding Penrose process becomes possible. We hope to address this issue in the near future.
Collision of spinning particles near BTZ black holes
- Received Date: 2019-12-31
- Available Online: 2020-06-01
Abstract: We study the collision property of spinning particles near a Bañados-Teitelboim-Zanelli (BTZ) black hole. Our results show that although the center-of-mass energy of two ingoing particles diverges if one of the particles possesses a critical angular momentum, the particle with critical angular momentum cannot exist outside of the horizon due to violation of the timelike constraint. Further detailed investigation indicates that only a particle with a subcritical angular momentum is allowed to exist near an extremal rotating BTZ black hole, and the corresponding collision center-of-mass energy can be arbitrarily large in a critical angular momentum limit.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: