Key factor for determining relation between radius and tidal deformability of neutron stars: Slope of symmetry energy

The equation of state (EOS) of dense neutron-rich matter plays a dominant role in determining the properties of neutron stars. In turn, observations of neutron stars can place strict constraints on the EOS. Currently, the most widely used observation to constrain the EOSs is the maximum observed mass of pulsars J1614-2230 with mass $M = 1.908\pm0.016$ $M_\odot$ [1, 2] and J0348+0432 with $M = 2.01\pm0.04$ $M_\odot$ [3]. Many soft EOSs, which cannot support such high mass have been excluded. Recently, the newly reported pulsar J0740+6620 with $M = 2.14^{+0.10}_{-0.09}$ $M_\odot$ [4] introduced a new theoretical challenge in satisfying the constrained pressure band for several typical microscopic nuclear EOSs with maximum mass $M_{\rm max}>2.14$ $M_\odot$ [5].

Except for the mass, the radius of neutron stars is another observable that constrains the EOSs. To extract the radii, special attention is given to the quiescent low-mass X-ray binaries [6, 7] or the isolated cooling neutron stars [8], and various analyses have been performed [9–18]. However, due to the significant difficulties in e.g., determining the precise distance of the source and compositions of atmosphere, large uncertainties still exist, and additional information is required to estimate the correct radii (see, e.g., Refs. [12, 19–22] for recent reviews).

The first joint gravitational and electromagnetic observation of GW170817 initiated the era of multimessenger astronomy [23, 24] and further motivated an abundance of studies on the EOS in both astrophysics and nuclear physics communities (see, e.g., Refs. [25-28] for recent reviews). In a coalescing binary neutron star system, one neutron star suffers tidal deformation induced by the strong tidal field of its companion. The corresponding tidal deformability can be extracted by different methods. The dimensionless tidal deformability of the canonical neutron stars was first extracted [23] and then refined as $\Lambda_{1.4} = 190^{+390}_{-120}$ at 90% confidence level by assuming that both neutron stars are described by the same EOS and spin at low-spin prior [29]. Considering the maximum observed mass of PSR J0348+0432, Ref. [30] improved the lower limit of $\Lambda_{1.4}>120$ based on a generic family of neutron-star-matter EOSs that interpolate between theoretical results at low and high baryon density. Similarly, Ref. [31] modified the lower limits as $\Lambda_{1.4}>290$ $(35.5)$ at 3$\sigma$ for neutron stars without (with) phase transition. Thereafter, various constraints have been placed on the properties of nuclei and neutron stars, such as the neutron-skin thickness of ²⁰⁸Pb [32-34], radius R [29–33, 35–43], and maximum mass $M_{\rm max}$ [44-51] of neutron stars.

As the dimensionless tidal deformability $\Lambda$ is related to radius R by $\Lambda = 2k_2/3(c^2R/GM)^5$ [52, 53] where $k_2$ is the second Love number, an underlying relation may exist between $\Lambda$ and $R$ when the mass is fixed. If the relation is explicit, one quantity can be extracted when the other is measured/determined. However, as the $k_2$ is solved by a complicated differential equation coupled to TOV equations [54, 55], the exact relation between the radius and tidal deformability of canonical neutron stars ($R_{1.4}\sim\Lambda_{1.4}$ relation) is still not well determined. The $R_{1.4}\sim\Lambda_{1.4}$ relation has been fitted in Refs. [30, 32, 33, 35, 37–39, 56–58] based on the EOSs calculated from relativistic mean field (RMF) theory, Skyrme Hartree-Fock (SHF) theory, microscopic theories, or parameterized EOSs, which are summarized in Fig. 1. We observe that, though all fitted equations are found within a narrow band in the $R_{1.4}\sim\Lambda_{1.4}$ plane, the uncertainty remains.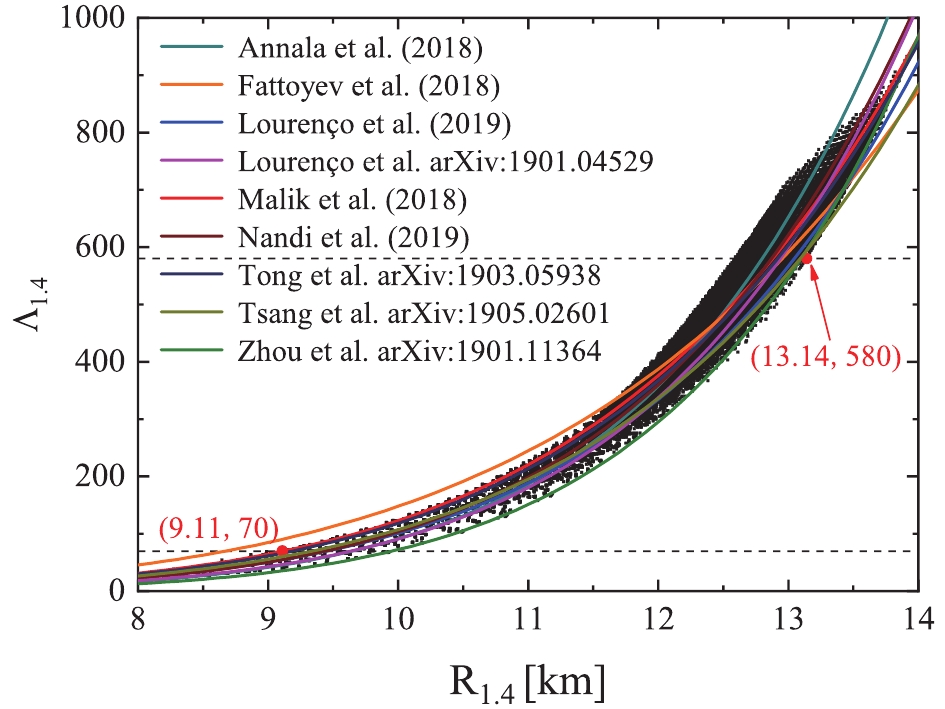

Figure 1.  (color online) Tidal deformability $\Lambda_{1.4}$ as a function of radius $R_{1.4}$ of canonical neutron stars based on isospin-dependent parameterized EOS. Parameters L, $K_{\rm sym}$, $J_{\rm sym}$, and $J_0$ are valued in steps of 5, 50, 100, and 50 MeV within their uncertainties, respectively. The horizontal dashed lines represent the refined constraints of $70<\Lambda_{1.4}<580$ (90% confidence level) extracted by LIGO and Virgo Collaborations [29]. Red dots labeled by the coordinates represent the constrained upper and lower limits on $R_{1.4}$. Solid lines correspond to the fitted equations suggested by different studies.

In the present study, we focus on two approaches regarding the relation between radius and tidal deformability: (1) Delineating the dependence of the $R_{1.4}\sim\Lambda_{1.4}$ relation on the parameters of nuclear matter based on an isospin-dependent parameterized EOS; (2) Revealing the mass dependence of $R\sim\Lambda$ relation. The theoretical framework is summarized in Section 2. The discussion on the $R_{1.4}\sim\Lambda_{1.4}$ relation and its dependence on EOS parameters and mass is presented in Section 3, and the conclusions are provided in Section 4.

Recently, the study in Ref. [59] constructed an isospin-dependent parameterized EOS describing the neutron stars with a core consisting of a neutron, proton, electron, and muon at $\beta$-equilibrium (charge neutral $npe\mu$ matter) and developed a numerical technique of inverting the TOV equations to constrain the EOS and symmetry energy based on the observations of radius, tidal deformability, and maximum mass, or physical requirement, such as the causality condition (speed of sound is lower than speed of light) [5, 51, 60]. The construction and demonstration are presented in detail in Ref. [59]. For completeness and ease of discussion, we first summarize the key aspects of the model. An EOS is mainly determined by the EOS of asymmetric nucleonic matter $E_b(\rho,\delta)$ with isospin asymmetry $\delta = (\rho_{\rm{n}}-\rho_{\rm{p}})/\rho$ at density $\rho$ through $\epsilon(\rho, \delta) = \rho [E_b(\rho,\delta)+M_N]+\epsilon_l(\rho, \delta)$, and $E_b(\rho,\delta)$ is thus approximated as [61]

where $E_0(\rho)$ is the EOS of symmetric nuclear matter (SNM), and $E_{\rm sym}$ is the symmetry energy. We parameterize $E_0(\rho)$ and $E_{\rm sym}(\rho)$ as

using the saturation density of SNM $\rho_0$, the incompressibility $K_0$ and skewness $J_0$ of SNM, as well as the slope $L$, curvature $K_{\rm sym}$, and skewness $J_{\rm sym}$ of the symmetry energy.

The above equations have the same form as the widely used Taylor expansions around $\rho_0$. With increasing density, the convergence problem appears for Taylor expansions. However, as demonstrated in great detail in Ref. [59], the above equations can still be used to simulate nuclear matter at high density if we see the coefficients as free parameters that should be determined by the observations. The parameterizations (2) and (3) naturally become Taylor expansions when $\rho\rightarrow \rho_0$. As free parameters, in principle, they can be varied. In this case, it is infeasible to perform a study with seven free parameters. To reduce the freedom of parameters, we first fixed the well constrained parameters as their currently known most probable values around $\rho_0$ extracted from terrestrial nuclear laboratory experiments, namely, $E_0(\rho_0) = -15.9$ MeV [62], $E_{\rm{sym}}(\rho_0) = 31.7$ MeV [63-65], and $K_0 = 230$ MeV [66, 67]. As the uncertainty of $L$ is constrained as $\approx 58.7\pm 28.1$ MeV [63–65] but $J_0$, $K_{\rm sym}$, and $J_{\rm sym}$ are less constrained ($-800\leq J_0 \leqslant 400$ MeV, $-400\leqslant K_{\rm sym}\leqslant100$ MeV, and $-200\leqslant J_{\rm sym}\leqslant 800$ MeV) [68, 69], we fixed $L = 58.7$ MeV and studied how the observations of maximum observed mass $M_{\rm max}$, radius $R_{1.4}$, and tidal deformability $\Lambda_{1.4}$ of canonical neutron stars, as well as the causality condition can constrain the EOS and symmetry energy in the three-dimensional $K_{\rm sym}-J_{\rm sym}-J_0$ parameter space [51]. We found that $J_0$, and thereby $E_0$, have slight effects on the radius and tidal deformability of canonical neutron stars. Then, the effects of the symmetry energy on the properties of neutron stars were delineated in the three-dimensional $L-K_{\rm sym}-J_{\rm sym}$ parameter space [60]. In the present study, the overall effects of $L-K_{\rm sym}-$$J_{\rm sym}-J_0$ parameters on $R_{1.4}$, $\Lambda_{1.4}$, and the $R_{1.4}\sim\Lambda_{1.4}$ relation are discussed. To enlarge the samples of EOSs, the parameter combinations are adopted within the whole parameter space constrained by experiments and theories mentioned above, and thus the causality condition is not considered in the present study.

Using the parameterized EOS to describe the core of neutron stars, the outer and inner crusts are replaced by BPS [70] and NV EOSs [71], where the transition density is self-consistently calculated by investigating the incompressibility [72-75]:

Once the $K_\mu$ becomes negative, the thermodynamical instability grows by forming clusters, indicating a transition from the uniform core to the clustered crust. Notably, the crust EOSs have little effect on the maximum mass and tidal deformability [76, 77]. However, the crust EOSs have an apparent effect on the radius, e.g., in Ref. [76, 78]. The main purpose of the present study is to investigate the dependence of the $R\sim\Lambda$ relation on the core EOSs; hence, the effects of crust EOSs are not discussed.

For a given EOS, the mass and radius can be calculated by solving the TOV equations [54, 55]:

and the tidal deformability can be obtained by solving a complicated differential equation coupled to TOV equations [52, 53].

The radius of neutron stars is sensitive to the symmetry energy at around two times the saturation density [79, 80]. The dependence of $\Lambda_{1.4}$ on symmetry energy was first discussed in Refs. [81, 82], where the authors concluded that the tidal deformability of low mass neutron stars is only sensitive to the slope $L$ of the symmetry energy, while the tidal deformability of massive neutron stars is sensitive to the high density behavior of symmetry energy. Recently, Ref. [57] studied the relation between $\Lambda_{1.4}$ and the parameters of symmetry energy $E_{\rm sym}$ and EOS of SNM $E_0$ based on more than 200 Skyrme EOSs and found a strong relationship between $\Lambda_{1.4}$ and the curvature $K_{\rm sym}$ of symmetry energy. Ref. [83] found that $R_{1.4}$ is almost independent of $L$ with respect to the constraints from the chiral effective field theory.

In several previous studies, we showed the individual results of $R_{1.4}$ and $\Lambda_{1.4}$ in the three-dimensional parameter space of $K_{\rm sym}-J_{\rm sym}-J_0$ by fixing $L = 58.7$ MeV [51, 59] and $L-K_{\rm sym}-J_{\rm sym}$ by fixing $J_0 = -180$ MeV [60]. We found that the slope $L$ and curvature $K_{\rm sym}$ of the symmetry energy play almost equally important roles in determining the individual values of $R_{1.4}$ and $\Lambda_{1.4}$. To further clarify the $R_{1.4}\sim\Lambda_{1.4}$ relation and its dependence on the symmetry energy and EOS of SNM, the tidal deformability $\Lambda_{1.4}$ as a function of radius $R_{1.4}$ of canonical neutron stars based on the isospin-dependent parameterized EOS is depicted by black dots in Fig. 1. The parameters $L$, $K_{\rm sym}$, $J_{\rm sym}$, and $J_0$ are valued in steps of 5, 50, 100, and 50 MeV within their uncertainties, respectively. The horizontal dashed lines depict the refined constraints of $70<\Lambda_{1.4}<580$ (90% confidence level) extracted by LIGO and Virgo Collaborations [29]. The red dots labeled by the coordinates represent the constrained upper and lower limits of $R_{1.4}$. The solid lines correspond to the equations fitted by other studies mentioned in the introduction. We see that almost all fitted equations are represented by present calculations, except the one from Ref. [32], where only EOSs with $R_{1.4}>12.5$ km are adopted to fit the equation and the $R_{1.4}\sim\Lambda_{1.4}$ relation is extrapolated with larger errors for smaller radii. Thus, the parameterized EOSs are sufficient to study the $R_{1.4}\sim\Lambda_{1.4}$ relation. Considering the constraint of tidal deformability, as labeled by red dots, the radius can be constrained as $9.11<R_{1.4}<13.14$ km. This upper limit is largely consistent with Ref. [30] using EOSs interpolation between the chiral effective theory at low density and perturbative quantum chromo dynamics at high baryon density, and Ref. [84] using available terrestrial laboratory data on the isospin diffusion in heavy-ion reactions at intermediate energies. Considering the constraint of $2.01$ $M_\odot$ from Ref. [3] or the newly reported $2.14$ $M_\odot$ from Ref. [4], more parameter sets with small radii can be excluded and thus raise the lower limit of $R_{1.4}$ significantly, as discussed in Ref. [30].

As the $E_0(\rho)$ and $E_{\rm sym}(\rho)$ have been parameterized in our calculations, apart from showing the overall $R_{1.4}\sim\Lambda_{1.4}$ relation, the individual effects of each parameter of $E_0(\rho)$ and $E_{\rm sym}(\rho)$ on the $R_{1.4}\sim\Lambda_{1.4}$ relation can likewise be studied. To study the effects of $K_{\rm sym}$ and $J_{\rm sym}$, the tidal deformability $\Lambda_{1.4}$ as a function of radius $R_{1.4}$ of canonical neutron stars when $L$ ($J_0$) is fixed as 30, 60, and 90 MeV (0 and 400 MeV), as shown in Fig. 2. $J_{\rm sym}$ increases from –200 to 800 MeV when $K_{\rm sym}$ is fixed at –400, –300, –200, –100, 0, and 100 MeV for each panel. Solid lines correspond to the fitted curves in the form of $\Lambda_{1.4} = aR_{1.4}^b$. The corresponding coefficients ($a$, $b$) of the fitted equation are given in Table 1. We observe that the increase of $K_{\rm sym}$, $J_{\rm sym}$, or $J_0$ can shift the data to larger $\Lambda_{1.4}$ and $R_{1.4}$ along the fitted curves for fixed $L$. Using the fitted curve of $L = 30$ MeV and $J_0 = 0$ MeV as a reference, the deviation between the data and fitted curve by varying $K_{\rm sym}$ and $J_{\rm sym}$ (top left panel) is less than 5%, except several points with small radii. If considering the effects of L, i.e., varying L from 30 MeV to 90 MeV (bottom left panel), the deviation increases to about 20%. Further, an additional 2% deviation is added when changing $J_0$ from 0 to 400 MeV (bottom right panel).

		L/MeV
		30	60	90
$J_0$/MeV	0	(10.25, 7.040)	(4.943, 7.277)	(4.353, 7.283)
	400	(13.38, 6.937)	(5.110, 7.268)	(5.892, 7.173)

Table 1.  Coefficients ($a\times10^6$, b) of fitted equation $\Lambda_{1.4} = aR_{1.4}^b$ for different L and $J_0$ parameter sets given in Fig. 2, respectively.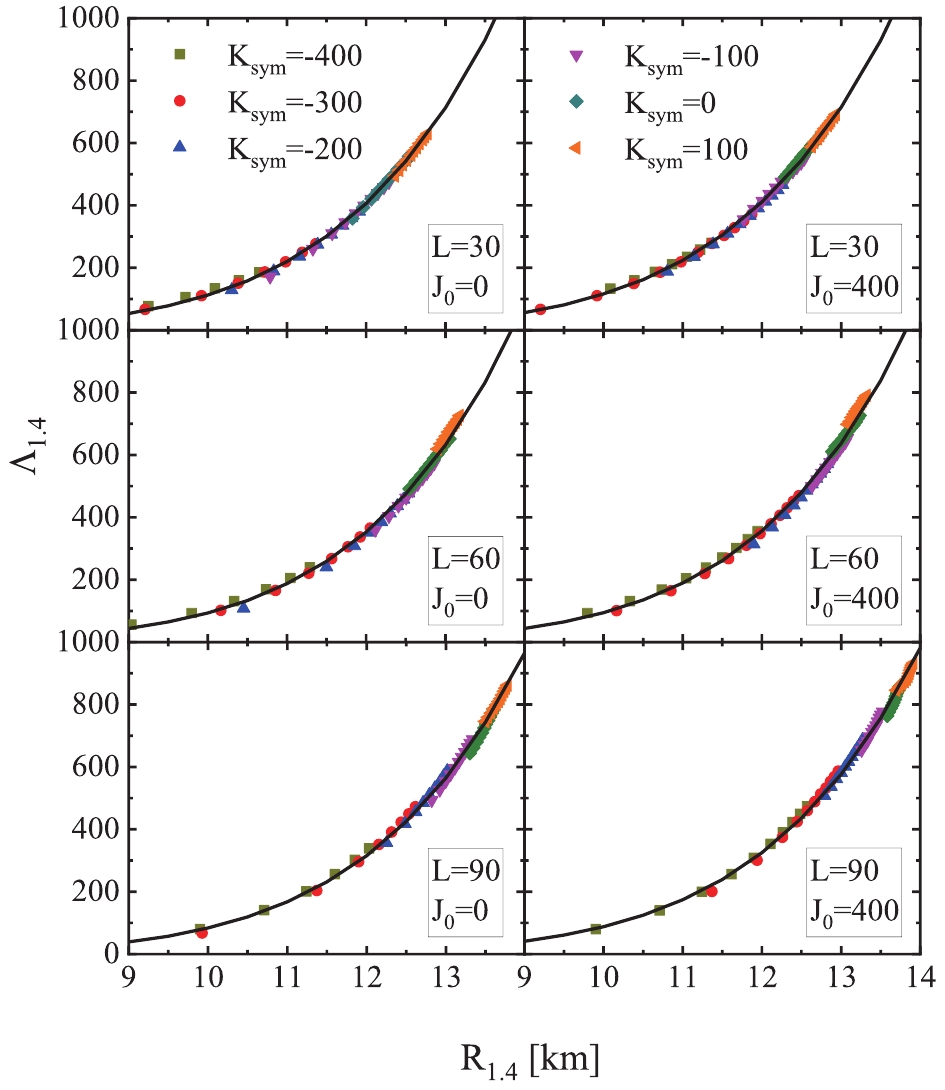

Figure 2.  (color online) Tidal deformability $\Lambda_{1.4}$ as a function of radius $R_{1.4}$ of canonical neutron stars when L ($J_0$) is fixed as 30, 60, and 90 MeV (0 and 400 MeV), respectively. The $J_{\rm sym}$ is varied from –200 to 800 MeV when $K_{\rm sym}$ is fixed as –400, –300, –200, –100, 0, and 100 MeV for each plot. Solid lines correspond to the fitted curves.

To present the above discussion more clearly, we summarize the six fitted curves in Fig. 3. The black, blue, and red lines correspond to the results of $L = 30$, $60$, and $90$ MeV. The solid and dashed lines correspond to the results of $J_0 = 400$ MeV and $0$ MeV. We observe that although $J_0$ changes from 400 MeV to 0 MeV, the $R_{1.4}\sim\Lambda_{1.4}$ relation is almost unchanged. However, when $L$ changes from 30 to 90 MeV, the $R_{1.4}\sim\Lambda_{1.4}$ relation changes significantly. We conclude that the slope $L$ of the symmetry energy plays the dominant role in determining the $R_{1.4}\sim\Lambda_{1.4}$ relation, although $L$ and $K_{\rm sym}$ play almost equally important roles in determining the individual values of $R_{1.4}$ and $\Lambda_{1.4}$ [60]. Thus, the precise measurement of $L$ is crucial to determine the exact relation between $R_{1.4}$ and $\Lambda_{1.4}$, which are expected to be measured by the LIGO and Virgo Collaborations and Neutron star Interior Composition ExploreR (NICER), respectively. Notably, the exact dependence of fitted coefficients (a, b) on $L$ is not found in the present study.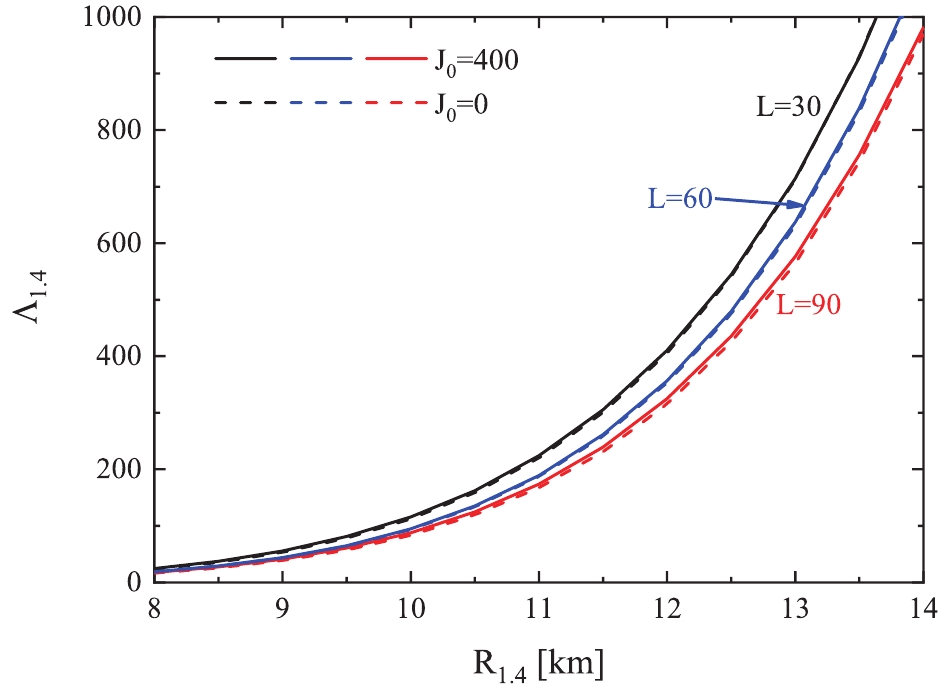

Figure 3.  (color online) Fitted curves for different L and $J_0$ parameter sets given in Fig. 2 with $K_{\rm sym}$ and $J_{\rm sym}$ varying within their uncertainties. Black, blue, and red lines correspond to results of L = 30, 60, and 90 MeV. The solid and dashed lines correspond to results of $J_0 = 400$ and 0 MeV.

In fact, the effects of $J_0$ have been shown in Refs. [51, 59]. The constant surfaces of $R_{1.4}$ and $\Lambda_{1.4}$ are almost parallel to the $J_0$ axis in the $K_{\rm sym}-J_{\rm sym}-J_0$ parameter space for $L = 58.7$ MeV, which shows the weak dependence on $J_0$ for $R_{1.4}$ and $\Lambda_{1.4}$, thereby the $R_{1.4}\sim\Lambda_{1.4}$ relation.

Besides, the $R\sim\Lambda$ relation is normally studied for neutron stars with $M = 1.4$ $M_\odot$. To determine whether the $R\sim\Lambda$ relation still holds for low mass or massive neutron stars (e.g., $R_{1.0}\sim\Lambda_{1.0}$ relation or $R_{1.8}\sim\Lambda_{1.8}$ relation) requires further studies. To verify the mass dependence of the above discussions, we calculate the tidal deformability as a function of radius for neutron stars with $1.0$ $M_\odot$ (black dots), $1.4$ $M_\odot$ (red dots), and $1.8$ $M_\odot$ (blue dots) and show the results in Fig. 4. Compared to the results of neutron stars with $1.4$ $M_\odot$, we observe that wider ranges can be covered for neutron stars with $1.0$ $M_\odot$. This is evident, as the $\Lambda$ decreases with increasing M for a given EOS (see, e.g., Ref. [60]). Moreover, as the central density of neutron stars with $1.8$ $M_\odot$ is significantly larger than that of the stars with $1.4$ $M_\odot$, the high order parameters in Eqs. (2) and (3) start to play more important roles in determining the properties of neutron stars and thus break the well-fitted $R\sim\Lambda$ relation for canonical neutron stars.

Figure 4.  (color online) Tidal deformability as a function of radius for neutron stars with 1.0 $M_\odot$ (black dots), 1.4 $M_\odot$ (red dots), and 1.8 $M_\odot$ (blue dots) based on isospin-dependent parameterized EOS.

Employing an isospin-dependent parameterized EOS, we study the relation between $R$ and $\Lambda$ of neutron stars and its dependence on the symmetry energy $E_{\rm sym}$ and EOS of SNM $E_0$ when the mass is fixed at $1.4$ $M_\odot$, $1.0$ $M_\odot$, and $1.8$ $M_\odot$. We find that, although the changes of high order parameters of $E_{\rm sym}$ and $E_0$ are capable of shifting the individual values of $R_{1.4}$ and $\Lambda_{1.4}$ to different values, the $R_{1.4}\sim\Lambda_{1.4}$ relation remains approximately at the same fitted curve. The slope L of the symmetry energy plays the dominant role in determining the $R_{1.4}\sim\Lambda_{1.4}$ relation, and the precise measurement of L is crucial to determine the exact relation between $R_{1.4}$ and $\Lambda_{1.4}$. Compared to the results of neutron stars with $1.4$ $M_\odot$, wider ranges in the $R\sim\Lambda$ plane can be covered for neutron stars with $1.0$ $M_\odot$ and $1.8$ $M_\odot$. Hence, the well-fitted $R\sim\Lambda$ relation for 1.4 $M_\odot$ is broken for massive neutron stars.

A possible relation among $L-R_{1.4}-\Lambda_{1.4}$ is found in the present study. All three relations remain inconclusive to date. Any progress on heavy-ion reactions, measurement of radius (such as, NICER), or gravitational wave events (such as, LIGO and Virgo Collaborations) may help to break the degeneracy and constrain the other two quantities. Fortunately, Refs. [85, 86] recently reported the estimation of the radius and mass of PSR J0030+0451 based on the pulse-profile modeling of NICER data. The determination of the influence of newly reported constraints of mass and radius on the properties of neutron stars based on the parameterized EOS is in progress.

We would like to thank Prof. Bao-An Li for constructive suggestions and comments.