-
In 1974, Stephen Hawking proved that the black hole emitts quantum radiation with a temperature
$ T = \frac{\kappa }{2\pi } $ [1]. This discovery promoted investigations of the thermodynamics of black holes, and since then it is believed that a black hole could be viewed as a thermodynamic system [2,3]. There have been many works on the thermodynamics of black holes, such as on the four laws of thermodynamics [4,5], quantum effects [1,6,7], phase transitions [8,9] etc.. In these studies, the AdS space-time has been frequently used, in which the cosmological constant can be considered as a thermodynamic variable [10]. The thermodynamic phase space is thus extended, and new thermodynamic phenomena emerge. There have been many works on the extended phase space of black holes. In particular, if the cosmological constant and its conjugate quantity are viewed as the pressure and volume of a black hole, it is possible to construct the extended first law of thermodynamics [11]. In addition, the$ P-V $ critical behavior can be studied [11-13]. In this framework, some interesting phenomena, such as the Van der Waals phase transition [14-16], the engine cycle [17-19], can be investigated.Until recently, attention has been mainly focused on the first law of thermodynamics and phase transitions of black holes in the extended phase space. The second law of thermodynamics and the weak cosmic censorship conjecture (WCCC) have been rarely reported. The premise that the first law of thermodynamics is valid does not mean that the second law of thermodynamics and WCCC hold. Therefore, it is extremely important and necessary to check the validity of the second law of thermodynamics and WCCC in the extended phase space.
The thermodynamics and WCCC in the extended phase space were recently investigated in Ref. [20]. This work is based on the Gedanken experiment proposed in Ref. [21]. After a test particle is absorbed by a black hole, the change of the location of the event horizon was studied. It was found that the first law of thermodynamics and WCCC are always valid for the charged Reissner-Nordström AdS black hole, while the second law of thermodynamics is not valid for the extremal and near-extremal black holes. As there is no general method to prove WCCC in a gravity system, different space-times need to be checked one by one. Based on the idea of Ref. [20], the thermodynamics and WCCC in the extended phase space of a series of black holes have been investigated [22-34].
In this paper, we study the thermodynamics and WCCC of an AdS black hole with a global monopole. On the one hand, we discuss the influence of the global monopole on the thermodynamics and WCCC of the black hole, and on the other, we explore whether higher order corrections of the mass of the absorbed particle affect WCCC. In Ref. [20], it was found that WCCC is valid in the extended phase space for the extremal and near-extremal Reissner Nordström-AdS black holes. However, only the first order correction of the mass was considered. Higher order corrections are important for investigating WCCC. Recently, WCCC was studied in Refs. [35-38] taking into account the second order correction of the mass of the black holes. It was found that WCCC is valid for the non-extremal black holes, a result which is different from the previous study where higher order corrections were neglected. In this study, we find that the global monopole does not have an effect on the thermodynamic laws. As in [20], the first law is valid, while the second law may be violated. Since we consider the second order correction of the mass of the absorbed particle, we find that WCCC can be violated, which is different from the result in [20].
The remainder of the paper is as follows. In Sec. 2, we briefly review the motion of a charged particle in an AdS black hole with a global monopole. In Sec. 3, we investigate the first and second laws of thermodynamics in the extended phase space. In Sec. 4, we investigate WCCC in the extended phase space, considering in particular the second order correction of the mass of the absorbed particle. Our conclusions are presented in Sec. 5. We use throughout the system
$ G = c = \hbar = 1 $ . -
The spherically symmetric AdS black hole solution with a global monopole can be expressed as [39]
$ {{\rm d}s}^2 = -F\left(\tilde{r}\right){\rm d}\tilde{t}^2+\frac{1}{F\left(\tilde{r}\right)}{\rm d}\tilde{r}^2+\tilde{r}^2\left({\rm{d}}\theta ^2+\sin ^2\theta {\rm{d}}\phi^2\right), $

(1) where
$ F\left(\tilde{r}\right) = 1-8\pi \eta _0^2-\frac{2\tilde{m}}{\tilde{r}}+\frac{\tilde{q}^2}{\tilde{r}^2}+\frac{\tilde{r}^2}{l^2}, $

(2) in which,
$ \eta _0 $ is a parameter related to symmetry breaking,$ \tilde{m} $ and$ \tilde{q} $ correspond to the mass and charge,$ l $ is the radius of the AdS space, which is related to the cosmological parameter as$ \Lambda = -\frac{3}{l^2} $ . In this gravitational system, the non-zero electromagnetic four-vector component is$ \tilde{A}_{\tilde{t}} = -\frac{\tilde{q}}{\tilde{r}}. $

(3) In order to study various properties of black holes more easily, we introduce the coordinate transformation
$ \tilde{t} = \left(1-8\pi \eta _0^2\right){}^{-1/2}t, \tilde{r} = \left(1-8\pi \eta _0^2\right){}^{1/2}r, $

(4) and redefine the following physical quantities
$ m = \left(1-8\pi \eta _0^2\right){}^{-3/2}\tilde{m},~ q = \left(1-8\pi \eta _0^2\right){}^{-1}\tilde{q},~ \eta ^2 = 8\pi \eta _0^2. $

(5) The metric in Eq. (1) can then be written as
$ {{\rm d}s}^2 = -f(r){{\rm d}t}^2+\frac{1}{f(r)}{{\rm d}r}^2+\left(1-\eta ^2\right)r^2\left({\rm{d}}\theta^2+\sin ^2\theta {\rm{d}}\phi ^2\right), $

(6) with
$ f(r) = 1-\frac{2m}{r}+\frac{q^2}{r^2}+\frac{r^2}{l^2}. $

(7) The potential of the black hole is then
$ A_t = -\frac{q}{r}. $

(8) In this case and for
$ \eta = 0 $ , the black hole is a four-dimensional Reissner-Nordström AdS black hole. The existence of the global monopole also affects the mass and the charge of the black hole, which are$ M = \left(1-\eta ^2\right)m,\quad Q = \left(1-\eta ^2\right)q. $

(9) We consider now the energy-momentum relation of the charged particle when it is absorbed by the black hole. In the potential field
$ A_\mu $ , the Hamilton-Jacobi equation can be expressed as$ g^{\mu \nu }\left(p_{\mu }-{eA}_{\mu }\right)\left(p_{\nu }-{eA}_{\nu }\right)+u^2 = 0, $

(10) where
$ u $ is the mass,$ e $ is the charge, and$ p_{\mu } $ is the momentum of the particle, which can be expressed as$ p_{\mu } = \partial _{\mu }{\cal{I}}, $

(11) where
$ {\cal{I}} $ is the Hamiltonian action of the particle. Considering the symmetry of the gravitational system, this action can be separated into$ {\cal{I}} = -E t+{\cal{I}}_r(r)+{\cal{I}}_{\theta }(\theta )+L \phi, $

(12) where
$ E $ and$ L $ are the energy and angular momentum of the particle. From Eq. (6), we can get the inverse metric of the black hole$\begin{split} g^{\mu \nu }\partial _{\mu }\partial _{\nu } =& -f(r)^{-1}\left(\partial _t\right)^2+f(r)\left(\partial _r\right)^2\\ &+\left[\left(1-\eta ^2\right)r^2\right]^{-1}\left(\partial _{\theta }^2+\sin ^{-2}\theta \partial _{\phi }^2\right). \end{split} $

(13) In this case, the Hamilton-Jacobi equation can be rewritten as
$ \begin{split}u^2 &-\frac{\left(E+{eA}_t\right)^2}{f(r)} +f(r)\left(\partial _r{\cal{I}}_r(r)\right)^2 \\&+\frac{\left(\left(\partial _{\theta }{\cal{I}}_{\theta }\right)^2+\sin ^{-2}\theta L^2\right)}{\left(1-\eta ^2\right)r^2} = 0. \end{split} $

(14) After separation of variables, Eq. (14) can be written as the angular and radial equations
$ K = \left(\partial _{\theta }{\cal{I}}_{\theta }\right)^2+\frac{1}{\sin ^2\theta }L^2, $

(15) and
$ \begin{split} K =& -\left(1-\eta ^2\right)u^2r^2+\frac{\left(1-\eta ^2\right)r^2}{f(r)}\left(-E-{eA}_t\right)^2 \\ &-\left(1-\eta ^2\right)r^2f(r)\left(\partial _r{\cal{I}}_r(r)\right)^2. \end{split} $

(16) We can then rewrite Eq. (12) as
$ {\cal{I}} = \frac{1}{2}m^2\lambda -{Et}+\int {{\rm d}r}\sqrt{R}+\int {{\rm d}\theta }\sqrt{\Theta }+{L\phi }, $

(17) where
$ \begin{split}{\cal{I}}_r =& \int {{\rm d}r}\sqrt{R}, \quad {\cal{I}}_{\theta } = \int {{\rm d}\theta }\sqrt{\Theta }, \quad \Theta = K-\frac{1}{\sin ^2\theta }L^2, \quad \\ R =& -\frac{K+\left(1-\eta ^2\right)u^2r^2}{\left(1-\eta ^2\right)r^2f(r)} \\ & +\frac{1}{\left(1-\eta ^2\right)r^2f(r)}\left(\frac{\left(1-\eta ^2\right)r^2}{f(r)}\left(-E-{eA}_t\right)^2\right). \end{split} $

(18) Using Eq. (17), the radial and angular momenta can be expressed as
$ p^r = f(r)\sqrt{\frac{1}{f^2(r)}\left(E+{eA}_t\right)^2-\frac{K+\left(1-\eta ^2\right)u^2r^2}{\left(1-\eta ^2\right)r^2f(r)}}, $

(19) $ p^{\theta } = \frac{1}{\left(1-\eta ^2\right)r^2}\sqrt{K-\frac{1}{\sin ^2\theta }L^2}. $

(20) We are mainly interested in the radial momentum of the particle. At the event horizon, we can write
$ E = \frac{q}{r_h}e+\left|p^r_h\right|. $

(21) We take a positive sign in front of
$ \left|p^r_h\right| $ since we want to ensure that the particle drops in the positive direction of time. In this case, the energy$ E $ and momentum$ p^r_h $ of the particle are positive. -
In order to study the thermodynamics of black holes, we need to express the physical quantities at the event horizon of the black hole. The event horizon of the black hole is defined at
$ r = r_h $ and its form can be obtained from$ f(r_h) = 0 $ . At the event horizon, the potential energy of the black hole is$ \Phi = \frac{q}{r_h}. $

(22) Using the definition of the surface gravity, the temperature of the black hole can be expressed as
$ T = \frac{\kappa }{2\pi } = \frac{1}{4\pi r_h}\left[1+\frac{3r_h^2}{l^2}-\frac{Q^2}{\left(1-\eta ^2\right)^2r_h^2}\right]. $

(23) The entropy of the black hole is then
$ S = \frac{A_{bh}}{4} = \pi \left(1-\eta ^2\right)r_h^2. $

(24) It has been show recently that the cosmological parameter could be regarded as the pressure of the thermodynamic system formed by the black hole, and the corresponded conjugate quantity as the volume of the system. In this case, the first law of thermodynamics holds [13], that is,
$ {{\rm d}M} = T {{\rm d}S}+\Phi {{\rm d}Q}+V {{\rm d}P}, $

(25) where
$ P = -\frac{\Lambda }{8\pi } = \frac{3}{8\pi l^2}, $

(26) $ \quad V = \frac{4}{3}\pi \left(1-\eta ^2\right)r_h^3. $

(27) Accordingly, the Smarr relation in the extended phase space can be obtained as
$ M = 2(T S-V P)+\Phi Q. $

(28) In the above equation,
$ M $ is not the internal energy, but the enthalpy. The relation between the enthalpy and the internal energy is$ M = U+P V. $

(29) When the black hole absorbs a charged particle, it is assumed that the energy and charge are conserved. According to the first law of thermodynamics, the energy and charge of the black hole increase, which implies
$ E = {\rm d} U = {\rm d}(M-P V), \quad e = {\rm d}Q. $

(30) Combining Eq. (30) and Eq. (21), we get
$ {{\rm d}U} = \frac{q}{r_h}{{\rm d}Q}+\left|p^r_h\right|. $

(31) After the charged particle is absorbed by the black hole, the enthalpy, charge, pressure and volume of the black hole change. The changes are labelled as
$ ({\rm d}M, {\rm d}Q, {\rm d}l) $ . The other quantities can be obtained in terms of these variables. Our goal is to obtain the first law of thermodynamics based on Eq. (31). Therefore, we discuss the change of entropy of the black hole after the absorption of a charged particle. From Eq. (24), we have$ {{\rm d}S} = 2\pi \left(1-\eta ^2\right)r_h{{\rm d}r}_h. $

(32) The change of the event horizon is determined by the parameters of the absorbed particle
$ (e, p_h^r) $ . Due to the change of the horizon, the function$ f(r) $ determining the location of the horizon also changes, namely$ {{\rm d}f}_h = \frac{\partial f_h}{\partial M}{{\rm d}M}+\frac{\partial f_h}{\partial Q}{{\rm d}Q}+\frac{\partial f_h}{\partial l}{{\rm d}l}+\frac{\partial f_h}{\partial r_h}{{\rm d}r}_h = 0, $

(33) where we have used the relation
$ f(r_h) = f(r_h+{\rm d}r_h) = 0 $ , and$ \begin{split} \frac{\partial f_h}{\partial M} =& \frac{2}{r_h \left(\eta ^2-1\right)}, \quad \frac{\partial f_h}{\partial Q} = \frac{2Q}{\left(\eta ^2-1\right)^2r_h^2}, \quad \frac{\partial f_h}{\partial l} = -\frac{2r_h^2 }{l^3}, \\ \frac{\partial f_h}{\partial r_h} =& \frac{2r_h}{l^2}-\frac{2\left(\left(\eta ^2-1\right){Mr}_h+Q^2\right)}{\left(\eta ^2-1\right)^2r_h^3}. \end{split} $

(34) In addition, as
$ M $ is the enthalpy, Eq. (31) can be rewritten as$ {{\rm d}M}-{\rm d}(P V) = \frac{q}{r_h} {{\rm d}Q}+p^r_h. $

(35) Combining Eq. (33) and Eq. (35), we can remove the
$ {\rm d}l $ term. Interestingly, we find that$ {\rm d}Q $ and$ {\rm d}M $ are also eliminated. Therefore, we finally get$ {{\rm d}r}_h = \frac{2l^2p^r_hr_h}{2l^2\left(\left(1-\eta ^2\right)r_h-M\right)+\left(1-\eta ^2\right)r_h^3} . $

(36) From Eqs. (24), (27) and (36), the variations of entropy and volume of the black hole can be written as functions of particle momentum, and are
$ {{\rm d}S} = \frac{4\left(1-\eta ^2\right)\pi l^2p^r_hr_h^2}{2l^2\left(\left(1-\eta ^2\right)r_h-M\right)+\left(1-\eta ^2\right)r_h^3}, $

(37) $ {{\rm d}V} = \frac{8\left(1-\eta ^2\right)\pi l^2p^r_hr_h^3}{2l^2\left(\left(1-\eta ^2\right)r_h-M\right)+\left(1-\eta ^2\right)r_h^3}. $

(38) Combining Eqs. (38), (37), (23) and (24), we find
$ T {{\rm d}S}-P {{\rm d}V} = p^r_h. $

(39) In this case, the energy-momentum relation Eq. (31) becomes
$ {\rm d} U = \Phi {\rm d}Q+T {\rm d}S-P{\rm d}V. $

(40) In the extended phase space, the mass of the black hole was already defined as the enthalpy. We can express the internal energy in the above equation as the enthalpy using Eq. (29), namely
$ {\rm d}M = {\rm d}U+P{\rm d}V+V{\rm d}P. $

(41) Substituting Eq. (41) into Eq. (40), we obtain
$ {\rm d}M = T{\rm d}S+\Phi {\rm d}Q+V{\rm d}P, $

(42) which is the same as Eq. (25). Obviously, the first law of thermodynamics holds after the charged particle is absorbed by the AdS black hole with a global monopole.
We now turn to the second law of thermodynamics of the black hole. It is well known that the black hole entropy does not decrease in the clockwise direction. In other words, in the process of absorbing a charged particle, the black hole entropy increases. We would like to check whether this is true in the extended phase space using Eq. (37).
We first discuss the case of the extremal black hole. A typical feature of the extremal black hole is that its temperature vanishes. Based on this fact and Eq. (23), we can get the mass of the extremal black hole. Substituting the mass into Eq. (37), we obtain
$ {{\rm d}S}_{\rm{extreme}} = -\frac{4\pi l^2p^r_h}{3 r_h}<0. $

(43) Obviously, the change of entropy of the black hole is negative, implying that the second law of thermodynamics is not valid in this case.
We next discuss the near-extremal black hole. For a given mass
$ M $ and monopole parameter$ \eta $ , we find the charge$ Q_e $ that satisfies the extremal conditions using numerical approximation. The condition that the black hole can be formed is$ Q\leqslant Q_e $ . For a given mass and charge, we can find the event horizon$ r_h $ of the black hole from the equation$ f(r_h) = 0 $ . Using Eq. (37), we can get the variation of entropy$ {\rm d}S $ . As an example, we take the parameters$ M = 0.5 $ ,$ l = 1 $ . For$ \eta = 0.1 $ , we find that the extremal charge is$ Q_e = 0.462988 $ . For black holes with different charges, the location of the event horizon and the variation of entropy are listed in Table 1.$Q$ 

$r_h$ 

${\rm d}S$ 

0.462988 0.389008 -10.9783 0.46 0.425981 -28.2074 0.455 0.449251 -121.19 0.44 0.489249 35.1871 0.42 0.522924 19.2248 0.4 0.547731 15.0991 0.3 0.62191 10.2483 0.2 0.660347 9.15501 0.1 0.680281 8.74138 Table 1. Relation between
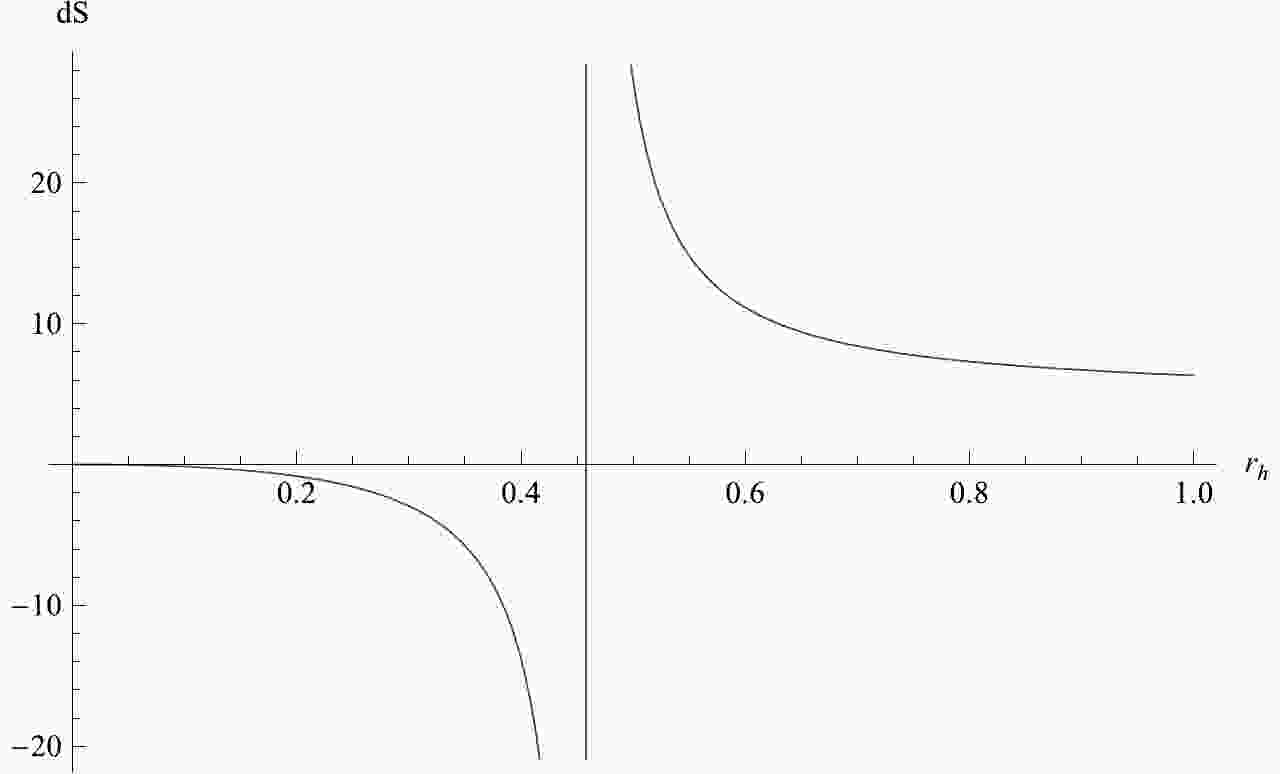
${\rm d}S$ ,$Q$ and$r_h$ for$\eta = 0.1$ .It is obvious that as the black hole charge decreases, the horizon radius gradually increases. The changes of entropy and charge are not related by a simple monotonic relation. When the charge approaches the extremal charge, the change of entropy is negative, while for a charge that is far from the extremal charge, the change of entropy is positive. In the positive and negative regions, the entropy decreases as the charge decreases. The near-extremal black hole violates the second law of thermodynamics, while the far-extremal black hole follows the second law of thermodynamics. In Fig. 1, we show the relation between the change of entropy and the event horizon.

Figure 1. Relation between
$ {\rm d}S $ and$ r_h $ for$ M = 0.5, l = p^r_h = 1 $ and$ \eta = 0.1 .$ Obviously, there is a phase transition at
$ r_h = $ 0.4566, which is larger than for the extremal black hole. When the event horizon radius is smaller than this value, the change of entropy is negative. Conversely, when the horizon radius is greater than this value, the change of entropy is positive. This conclusion is consistent with Table 1.In addition, we find that for different values of
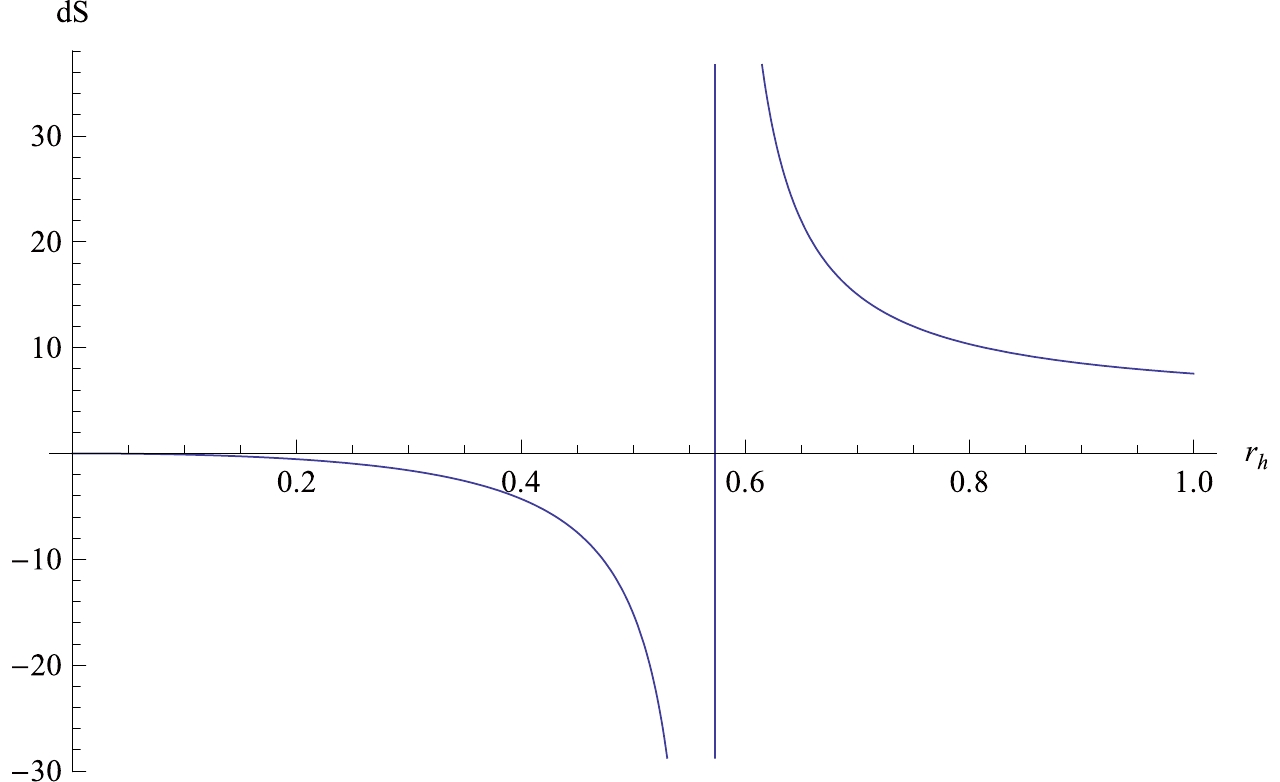
$ \eta $ the above conclusion does not change. For$ \eta = 0.5 $ , the extremal charge is$ Q_e = 0.448134 $ . The relation between the change of entropy, charge and horizon radius is given in Table 2.$Q$ 

$r_h$ 

${\rm d}S$ 

0.448134 0.466004 -9.09252 0.44 0.537818 -35.5889 0.43 0.571502 -1118.76 0.42 0.595534 64.6394 0.41 0.61485 36.8817 0.4 0.631209 27.7267 0.3 0.72788 13.1042 0.2 0.775407 11.0511 0.1 0.799693 10.3366 Table 2. Relation between
${\rm d}S$ ,$Q$ and$r_h$ for$\eta = 0.1$ .From Table 2, we also find that the change of entropy is negative in the case of a near-extremal black hole, and the second law of thermodynamics is violated. For the far-extremal black hole, the change of entropy is positive, and the second law of thermodynamics holds. The relation between the change of entropy and the event horizon is shown in Fig. 2. We find that the phase transition is at
$ r_h = 0.5727 $ , and the result shown in Fig. 2 is consistent with Table 2. -
In the extended phase space, we found that the second law of thermodynamics is not valid for the extremal black hole and the near-extremal black hole. Hence, we would like to check whether WCCC is valid in the extended phase space.
After a particle is absorbed by the black hole, the changes in the black hole are reflected in
$ M, Q, l $ . However, these physical quantities are ultimately related to the metric function$ f(M, Q, l, r) $ . Therefore, we discuss the changes in$ f(M, Q, l, r) $ . The function$ f(M, Q, l, r) $ has a minimum at$ r_{\min} $ which satisfies$ f(M,Q,l,r)\big|_{r = r_{\min}}\equiv f_{\min} = \delta\leqslant 0, $

(44) $ \partial_{r} f(M,Q,l,r)\big|_{r = r_{\min}}\equiv f'_{\min} = 0, $

(45) $ (\partial_{r})^2 f(M,Q,l,r)\big|_{r = r_{\min}}>0. $

(46) In the case of the extremal black hole,
$ \delta = 0 $ , and for the near-extremal black hole,$ \delta $ has a small negative value. The inner and outer horizons of the black hole are distributed on both sides of$ r_{\min} $ . After the absorption of a particle,$ (M, Q, l) $ change into$ (M + {\rm d}M, Q + {\rm d}Q, l + {\rm d}l) $ . Due to these changes, the position of the minimum of the function$ f(M, Q, l, r) $ and the position of the event horizon move to$ r_{{\min} }\rightarrow r_{{\min} }+{{\rm d}r}_{{\min} } $ ,$ r_h\rightarrow r_h+{{\rm d}r}_h $ . The metric function$ f(M, Q, l, r) $ also changes by$ {{\rm d}f}_{\min} $ . At$ r_{{\min} }+{{\rm d}r}_{{\min} } $ ,$ \partial_{r} f\big|_{r = r_{\min}+{\rm d}r_{\min}} = f'_{\min}+{\rm d}f'_{\min} = 0. $

(47) That is
$ \begin{split}{\rm d}f'_{\min} = \frac{\partial f'_{\min}}{\partial M}{\rm d}M+\frac{\partial f'_{\min}}{\partial Q}{\rm d}Q+\frac{\partial f'_{\min}}{\partial l}{\rm d}l+\frac{\partial f'_{\min}}{\partial r_{\min}}{\rm d}r_{\min} = 0, \end{split}$

(48) where
$ \begin{split}\frac{\partial f'_{{\min} }}{\partial M} =& \frac{2}{r_{{\min} }^2\left(1-\eta ^2\right)}, \frac{\partial f'_{{\min} }}{\partial Q} = -\frac{4Q}{\left(\eta ^2-1\right)^2r_{{\min} }^3}, \\ \frac{\partial f'_{{\min} }}{\partial l} =& -\frac{4r_{{\min} }}{l^3}, \\ \frac{\partial f'_{{\min} }}{\partial r_{{\min} }} =& \frac{2}{l^2}-\frac{4 M}{\left(1-\eta ^2\right)r_{{\min} }^3}+\frac{6Q^2}{\left(\eta ^2-1\right)^2r_{{\min} }^4}. \end{split}$

(49) At
$ r_{\min} + {{\rm d}r}_{\min} $ , the function$ f(M, Q, l,r) $ becomes$ \begin{split} &f(M+dM,Q+{\rm d}Q,l+{\rm d}l,r)\big|_{r = r_{\min}+{\rm d}r_{\min}} =f_{\min}+{\rm d}f_{\min}\\ &\quad = \delta+\left(\frac{\partial f_{\min}}{\partial M}{\rm d}M+\frac{\partial f_{\min}}{\partial Q}{\rm d}Q+\frac{\partial f_{\min}}{\partial l}{\rm d}l\right). \end{split} $

(50) In the above equation, we used the condition
$ f'_{\min} = 0 $ . The most important step is to get a specific form of Eq. (50). For the extremal black hole, we have$ r_h = r_{\min} $ , which means that Eq. (35) can be used. Using the condition$ f'_{\min} = 0 $ , we can get an equation for$ M $ , which we obtain as$ \begin{split} {{\rm d}M} =& \frac{l^2Q^2+3\left(\eta ^2-1\right)^2r_{{\min} }^4}{\left(\eta ^2-1\right)l^2r_{{\min} }^2}{{\rm d}r}_{{\min} } \\ &-\frac{2\left({{\rm d}l}\left(\eta ^2-1\right)^2r_{{\min} }^5+l^3Q r_{{\min} }{{\rm d}Q}\right)}{\left(\eta ^2-1\right)l^3r_{{\min} }^2}. \end{split} $

(51) From Eqs. (35) and (51), we find
$ {\rm d}f_{{\min} } = 0. $

(52) Therefore, we finally get
$ f(M+{\rm d}M,Q+{\rm d}Q,l+{\rm d}l,r)\big|_{r = r_{\min}+{\rm d}r_{\min}} = 0. $

(53) This result shows that the minimum of the function
$ f(r) $ does not change in the extended phase space. That is, as a charged particle is absorbed by the extremal black hole, the configuration of the black hole does not change, and the extremal black hole remains extremal.In the case of the near-extremal black hole, Eq. (35) can not be used since it is valid only at the horizon. However, we can expand it at
$ r_{\min} $ using the relation$ r_h = r_{\min}+\epsilon $ , which gives$ \begin{split} {{\rm d}M} =& \frac{\left( r_{{\min} }^5 \left(\eta ^2-1\right)^2 {{\rm d}l}-l^3 Q r_{{\min} } {{\rm d}Q} \right)}{ l^3 r_{{\min} }^2 \left(\eta ^2-1\right)} \quad \\ &+\frac{l^2 \left(Q^2-r_{{\min} }^2 \left(\eta ^2-1\right)^2\right)-3 r_{{\min} }^4 \left(\eta ^2-1\right)^2}{ l^2r_{{\min} }^2 \left(\eta ^2-1\right)} \\& +\frac{ l^3 Q r_{{\min} } {{\rm d}Q}+3 r_{{\min} }^5{{\rm d}l}+6 l r_{{\min} }^4 \eta ^2{{\rm d}r}_{{\min} }+3{ }r_{{\min} }^5 \eta ^4{{\rm d}l} }{l^3 r_{{\min} }^3 \left(\eta ^2-1\right)\epsilon^{-1}} \\ &-\frac{ l^3 Q^2{{\rm d}r}_{{\min} }+3{ }l r_{{\min} }^4{{\rm d}r}_{{\min} }+6{ }r_{{\min} }^5 \eta ^2{{\rm d}l}+3{ }l r_{{\min} }^4 \eta ^4{{\rm d}r}_{{\min} } }{l^3 r_{{\min} }^3 \left(\eta ^2-1\right) \epsilon^{-1}}\\& +{\cal {O}}(\epsilon )^2. \\[-12pt]\end{split} $

(54) Substituting Eq. (54) into Eq. (50), we have
$ \begin{split} {{\rm d}f}_{{\min} } =& \frac{ \left(l^2 \left(Q^2-r_{{\min} }^2 \left(\eta ^2-1\right)^2\right)-3 r_{{\min} }^4 \left(\eta ^2-1\right)^2\right){{\rm d}r}_{{\min} }}{l^2 r_{{\min} }^3 \left(\eta ^2-1\right)^2}\quad \\ & +\frac{2 \left({{\rm d}Q} l^3 Q r_{{\min} }+3{{\rm d}l} r_{{\min} }^5 \left(\eta ^2-1\right)^2\right) \epsilon }{l^3 r_{{\min} }^4 \left(\eta ^2-1\right)^2} \\ & -\frac{2 {{\rm d}r}_{{\min} } l \left(l^2 Q^2+3 r_{{\min} }^4 \left(\eta ^2-1\right)^2\right)\epsilon }{l^3 r_{{\min} }^4 \left(\eta ^2-1\right)^2} \\&+{\cal{O}}(\epsilon )^2. \end{split} $

(55) At
$ r_h = r_{\min}+\epsilon $ , we also get$ Q = \frac{r_{{\min} } \sqrt{l^2+3 r_{{\min} }^2} \left(\eta ^2-1\right)}{l}, $

(56) and
$ {{\rm d}Q} = \frac{\left(\left(l^3+6 l r_{{\min} }^2\right){{\rm d}r}_{{\min} }-3 r_{{\min} }^3{{\rm d}l}\right) \left(\eta ^2-1\right)}{l^2 \sqrt{l^2+3 r_{{\min} }^2}}. $

(57) Substituting Eqs. (56) and (57) into Eq. (55), we find
$ {\rm d}f_{{\min} } = {\cal{O}}(\epsilon^2 ), $

(58) so that
$ f_{\min}+{\rm d}f_{\min} = \delta+{\cal{O}}(\epsilon^2 ). $

(59) In Ref. [20], it was claimed that
$ {\rm d}f_{{\min} } $ can be neglected since$ {\cal{O}}(\epsilon^2 ) $ is a small quantity. However,$ \delta $ is also a small negative quantity, and we cannot directly determine which one is smaller. Therefore, for the near-extremal black hole in the extended phase space, we need to find the relation between$ \delta $ and$ {\cal{O}}(\epsilon^2 ) $ . Expanding$ f(r_h) $ to the second order, we have$ f\left(r_{{\min} }+\epsilon \right) = \delta +\frac{\left(l^2 Q^2+3 r_{{\min} }^4 \left(\eta ^2-1\right)^2\right)\epsilon ^2}{l^2 r_{{\min} }^4 \left(\eta ^2-1\right)^2}+{\cal{O}}(\epsilon^3 ) = 0, $

(60) where we used the relation
$ r_h = r_{\min}+\epsilon $ , and we obtain$ \delta = -\frac{\left(l^2 Q^2+3 r_{{\min} }^4 \left(\eta ^2-1\right)^2\right)\epsilon ^2}{l^2 r_{{\min} }^4 \left(\eta ^2-1\right)^2}-{\cal{O}}(\epsilon^3 ). $

(61) Similarly, expanding Eq. (35) to the second order and inserting the result into Eq. (50), we obtain
$ {{\rm d}f}_{{\min} } = \left(\frac{6 (1+{{\rm d}l})}{l^3}+\frac{2 {\rm d} r_{{\min} }}{ r_{{\min} }^3}\right) \epsilon ^2+{\cal{O}}(\epsilon^3 ). $

(62) For simplicity, we define.
$ \Delta _E = \frac{\delta +{{\rm d}f}_{{\min} }}{\epsilon ^2}. $

(63) Combining Eqs. (61), (62) and (63), we get
$ \Delta _E = \frac{6 (1+{{\rm d}l})}{l^3}-\frac{3}{l^2}+\frac{2r_{{\min} } {\rm d} r_{{\min} }-Q^2\left(\eta ^2-1\right)^{-2}}{ r_{{\min} }^4}. $

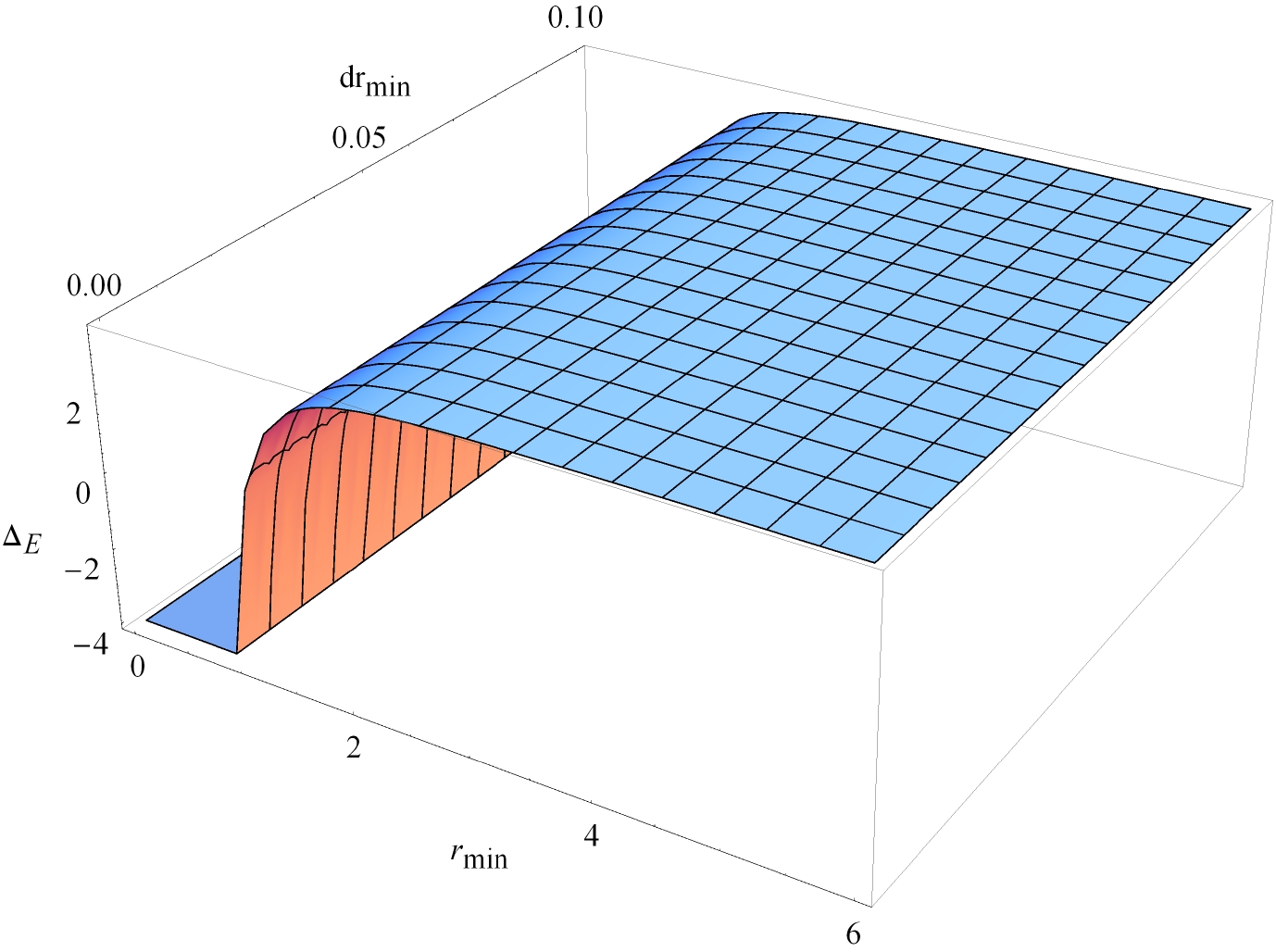
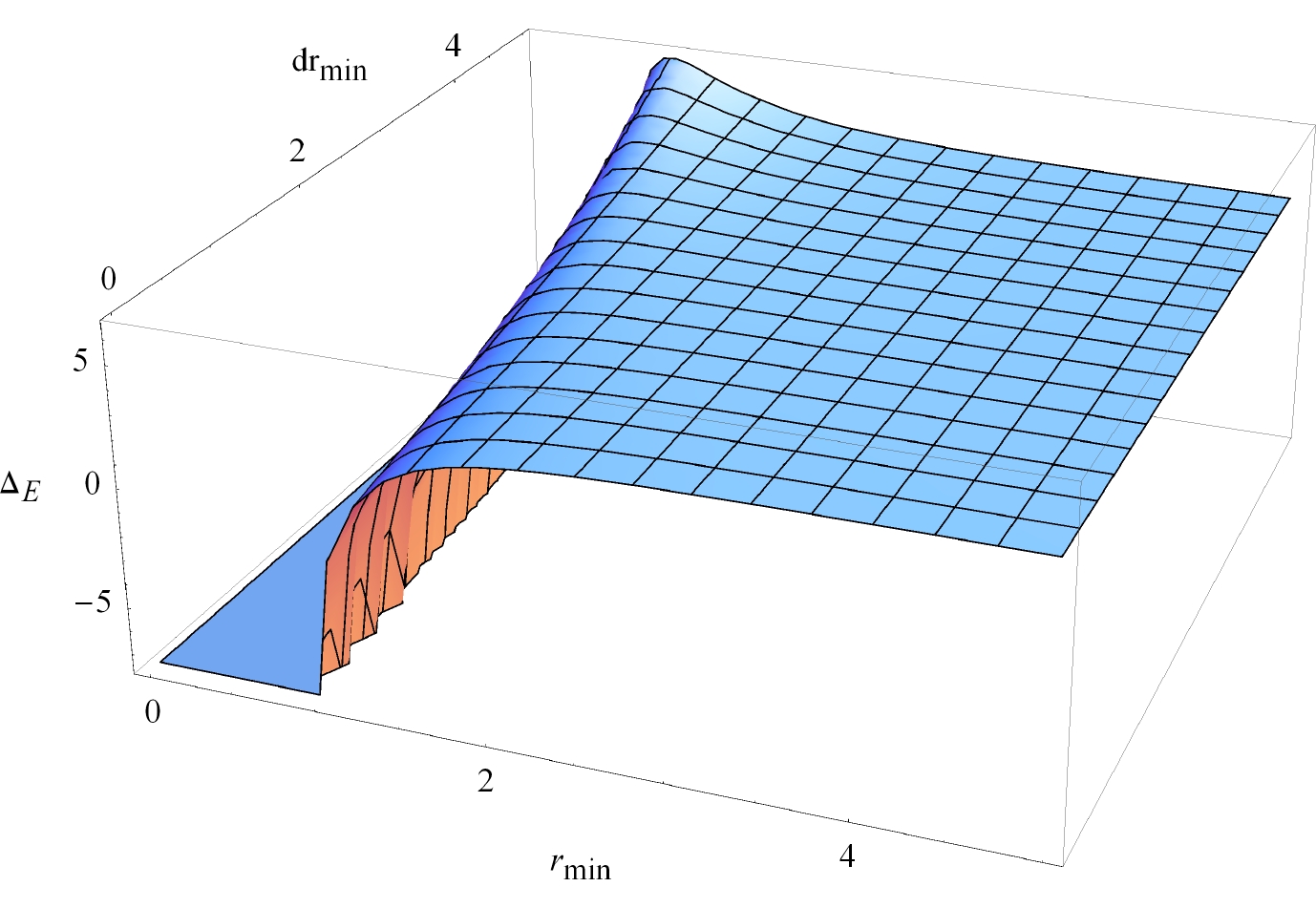
(64) Obviously, the value of
$ \Delta _E $ is directly related to$ (Q, \eta, r_{\min}, l, {\rm d}l) $ . In order to determine whether$ \Delta _E $ is positive or negative, we plot it in Fig. 3 and Fig. 4 for different values of$ (Q, \eta, r_{\min}, l, {\rm d}l) $ . For$ \Delta _E $ positive, the horizon does not exist since the equation$ f(r) = 0 $ does not have a solution. For$ \Delta _E $ negative, the horizon always exists. Therefore, WCCC is violated for$ \Delta _E>0 $ .From Fig. 3 and Fig. 4, we see that depending on the values of
$ (Q, \eta, r_{\min}, l, {\rm d}l) $ ,$ \Delta _E $ may be positive or negative. That is, in the extended phase space, WCCC can be violated for the near-extremal black hole. This result is different from Ref. [20], where WCCC was found to be always valid. Our result is more precise and comprehensive since we consider higher order corrections to the mass of the absorbed particle. -
The thermodynamics of black holes provides an effective means for studying the relation between gravity, thermodynamics and quantum theory. An in-depth study of the thermodynamics of black holes is helpful for further understanding of the nature of gravity. We studied the laws of thermodynamics and WCCC in the extended phase space in the case of charged particle absorption. Based on the Hamilton-Jacobi equation, we first obtained the relation between the particle momentum and energy. From this relation, we obtained the first law of thermodynamics in the extended phase space, which was found to be valid. Using the methods of numerical analysis, we obtained the variation of entropy for the extremal black hole, near-extremal black holes, and far-extremal black holes. It was shown that for the extremal black hole and the near-extremal black holes, the change of the black hole entropy is negative, while for the far-extremal black hole, it is positive. Therefore, the second law of thermodynamics of the black hole is only valid for the far-extremal black hole.
We also checked WCCC in the extended phase space. We studied the change of the minimum of the function
$ f(r ) $ which determines the location of the event horizon. In the case of the extremal black hole, we showed that$ f(r_{\min}) $ does not change when a charged particle is absorbed, that is the extremal black hole remains extremal. Hence, WCCC is still valid for the extremal black hole. However, we found that$ f(r_{\min}+{\rm d}r_{\min}) > 0 $ could occur in the case of the near-extremal black hole. Thus, WCCC is not valid for the near-extremal black hole. This result is different from Ref. [20] because we did not neglect the contributions of$ \delta $ and$ {\cal{O}}(\epsilon^2 ) $ as we considered the second order correction of the mass of the particle. Hence, our conclusion is more precise and comprehensive.
Thermodynamics and weak cosmic censorship conjecture of an AdS black hole with a monopole in the extended phase space
- Received Date: 2019-11-18
- Available Online: 2020-05-01
Abstract: The first law of black hole thermodynamics has been shown to be valid in the extended phase space. However, the second law and the weak cosmic censorship conjecture have not been investigated extensively. We investigate the laws of thermodynamics and the weak cosmic censorship conjecture of an AdS black hole with a global monopole in the extended phase space in the case of charged particle absorption. It is shown that the first law of thermodynamics is valid, while the second law is violated for the extremal and near-extremal black holes. Moreover, we find that the weak cosmic censorship conjecture is valid only for the extremal black hole, and that it can be violated for the near-extremal black holes, which is different from the previous results.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: