-
With increasing temperature or baryon chemical potential, it is generally assumed that strong interaction matter undergoes a phase transition from the hadronic matter to quark-gluon plasma (QGP), which is expected to appear in ultrarelativistic heavy ion collisions. The basic theory describing these strong interactions is quantum chromodynamics (QCD). Drawing a phase diagram of strong interaction matter at finite temperature and finite density is an important goal of current high nuclear physics studies. Although Lattice Monte Carlo simulations have made significant progress in the studies of finite temperature and low chemical potential, they encounter the so-called sign problem when dealing with large chemical potentials. Therefore, calculations of large chemical potentials based on effective theories of QCD are irreplaceable at present.
Currently, people usually describe the phase transition of strong interaction matter under the condition of large chemical potential from two different physical pictures. One is based on the quark-gluon degree of freedom, while the other is from the hadron degree of freedom. First, we look at the phase transition of strong interaction matter in the case of large chemical potentials derived from quark-gluon degree of freedom. In Ref. [1], based on a universal argument, when the chemical potential μ is smaller than a critical value
$ \mu_0 $ , the quark-number density vanishes identically. Namely,$ \mu_0 $ is a singularity that separates two the regions with different quark-number densities. The numerical value of the critical chemical potential$ \mu_0 $ in pure QCD (i.e., with electromagnetic interactions being switched off) is estimated to be$ \mu_0 = ({M}_N -16 ~\mbox{MeV})/{N}_c = 307 $ MeV (where$ {M}_N $ is the nucleon mass and$ {N}_c = 3 $ is the number of colors). This means that at temperature$ T = 0 $ , and when μ is greater than$ \mu_0 $ , the baryons will be excited from the QCD vacuum, which is a robust and model-independent prediction [1]. Along with the continuous increase in the quark chemical potential, it is believed that when the chemical potential is as large as a critical value$ \mu_c $ , the strong interaction matter will undergo the so-called chiral restoration and deconfinement phase transition [2,3]. Naturally, since the Lattice QCD cannot be employed to deal with the large chemical potential problem, the value of$ \mu_c $ depends on the phenomenological QCD model that is chosen. For example, the$ \mu_c $ predicted by NJL model, which is commonly used, has a value of ~330–380 MeV [4-6]. This means that the chemical potential required to excite a baryon from the QCD vacuum to a phase transition of strong interaction matter does not exceed dozens of MeV, which is unlikely. However, from the picture of hadron degrees of freedom, it is generally believed that strong interaction phase transitions are only possible when the density of nuclear matter is at least greater than four times the saturation density of the nuclear matter. Hence, the quark chemical potential corresponding to four times the saturation density of nuclear matter remains to be found. To address this, we use the relativistic mean field (RMF) method [7] to estimate the quark chemical potential corresponding to one to five times the saturation density of the nuclear matter, as shown in Table 1.Nuclear density ρ0 2ρ0 3ρ0 4ρ0 5ρ0 Quark chemical potential/MeV 323 371 469 580 692 Table 1 shows that the quark chemical potential corresponding to four times saturation density of the nuclear matter is about 580 MeV. Hence, from the picture of hadron degrees of freedom, in the case of zero temperature and finite chemical potential, the phase transition of strong interaction matter is likely to occur only when the quark chemical potential is at least greater than 580 MeV. The position of the phase change of the strong interaction matter obtained from the perspective of the picture of the hadron degree of freedom is significantly different from that derived from the quark-gluon degree of freedom. Therefore, there are huge contradictions between the results drawn from the quark-gluon degrees of freedom and the expected results derived from the hadron degrees of freedom. The main motivation of this study is to propose a new self-consistent mean field approximation to solve the above contradictions.
-
Before proposing a new approach for a self-consistent mean field approximation, we first review the mean field approximation usually adopted in the past. A mean field approximation replaces all interactions to any one body with an average or effective interaction, which reduces any many body problem into an effective one-body problem. Taking the Nambu–Jona–Lasinio (NJL) model [11,12] as an example, the Lagrangian is given by
$ {\cal{L}} = \bar\psi (i\not\!\!\partial-m)\psi+G[ (\bar\psi\psi)^2+(\bar\psi i\gamma^5 \tau \psi)^2], $

(1) where
$ m $ denotes current quark mass and$ G $ denotes the coupling constant. Performing Fierz transformation on the interaction part of the Lagrangian (1) in flavor, Dirac spinor, and color spaces, one obtains$\begin{split}{\cal{F}}[(\bar\psi\psi)^2+(\bar\psi i\gamma^5 \tau \psi)^2] =& \frac{1}{8N_c}[2(\bar\psi\psi)^2+2(\bar\psi i \gamma^5\tau\psi)^2-2(\psi\tau\psi)^2\\&-2(\bar\psi i \gamma^5\psi)^2\!\!-\! 4(\bar\psi\gamma^{\mu}\psi)^2\!\!-\!4(\bar\psi i\gamma^{\mu}\gamma^{5}\psi)^2\\&+(\bar\psi\sigma^{\mu\nu}\psi)^2-(\bar\psi\sigma^{\mu\nu}\tau\psi)^2], \end{split} $

(2) and the Lagrangian becomes
$ \begin{array}{l} {\cal{L}}_{F} = \bar\psi (i\not\!\!\partial-m)\psi+G{\cal{F}}[(\bar\psi\psi)^2+(\bar\psi i\gamma^5 \tau \psi)^2]. \end{array} $

(3) Because the Fierz transformation is a mathematically equivalent transformation, the original Lagrangian
$ {\cal{L}} $ and the Fierz-transformed Lagrangian$ {\cal{L}}_{F} $ are equivalent. However, when the mean field approximation is applied, especially in the case of an external field,$ \langle{\cal{L}}\rangle_{m} $ is no longer equal to$ \langle {\cal L}_{F}\rangle_{m} $ (the notation$ \langle \cdots \rangle_{m} $ denotes mean field approximation). For example, when we study the strong interaction phase transition at finite chemical potential, which can be regarded as the vector background field, the position of the phase transition calculated by$ \langle{\cal{L}}\rangle_{m} $ and$ \langle{\cal{L}}_{F}\rangle_{m} $ is very different [13]. Thus, a suitable Lagrangian in the mean field approximation remains to be found. Ref. [13] suggests the form$ 1/2(\langle{\cal{L}}\rangle_{m} +\langle{\cal{L}}_{F}\rangle_{m}) $ , as this form is Fierz invariant. Formally,$ \langle{\cal{L}}\rangle_{m} $ and$ \langle {\cal{L}}_{F}\rangle_{m} $ contributions are equal, and as there is no physical requirements for this, the two term contributions are identical.Considering that the original Lagrangian and Fierz-transformed Lagrangian are identical, the most general effective Lagrangian can be redefined as
${\cal{L}}_{R} = (1-\alpha){\cal{L}}+ $ $ \alpha{\cal{L}}_{F} $ , where α is an arbitrary c number. As$ {\cal{L}}_{R} = {\cal{L}} $ , redefining the effective Lagrangian of the system does not change the original Lagrangian of the system. However, in the presence of chemical potential, once the mean field approximation is made, the situation changes greatly (see below). In the standard NJL model (1), the interaction term in the scalar and pseudoscalar-isovector channels is used. As shown in the Walecka model [7,14], the vector-isoscalar channel is very important at non-zero densities. To reflect this fact, in some model studies, the vector-isoscalar term is added to the standard NJL model manually [13]. However, the current model is different from the standard NJL model. In fact, all the possible interaction channels are included in the standard NJL model, which can be reflected by Fierz transformation. In particular, there has been a great arbitrariness in the past when the self-consistent mean field approximation was applied in a standard NJL model. For example, when discussing the finite chemical potential, the vector-isoscalar channel is artificially added to the standard NJL model Lagrangian. Similarly, if the axial chemical potential is discussed (in this case, the isovector-isoscalar channel is very important), the isovector-isoscalar channel is also artificially added to the standard NJL model, which makes the standard NJL model lack predictive power. In contrast, our self-consistent mean field approximation avoids this arbitrariness and can be handled in a self-consistent manner for any background field (for example, in the case of a strong magnetic field).Applying the mean field approximation on the redefined Lagrangian, one has
$ \begin{split} \langle {\cal{L}}_{R}\rangle_m =& (1-\alpha)\langle{\cal{L}}\rangle_m+\alpha\langle{\cal{L}}_{F}\rangle_m.\\ =& \bar\psi (i\not\!\!\partial-m)\psi+(1-\alpha)G[ (\bar\psi\psi)^2+(\bar\psi i\gamma^5\cdot\tau \psi)^2]\\ &+\alpha\frac{G}{8N_c}[2(\bar\psi\psi)^2+2(\bar\psi i \gamma^5\tau\psi)^2-2(\psi\tau\psi)^2\\&- 2(\bar\psi i \gamma^5\psi)^2-4(\bar\psi\gamma^{\mu}\psi)^2-4(\bar\psi i\gamma^{\mu}\gamma^{5}\psi)^2\\&+(\bar\psi\sigma^{\mu\nu}\psi)^2 -(\bar\psi\sigma^{\mu\nu}\tau\psi)^2] . \end{split} $

(4) The gap equation is then given by
$ \begin{split} M=& m+ \left( 12- 11 \alpha \right) G\frac { M } { \pi ^ { 2 } } \int^{\Lambda} \frac { p ^ { 2 } } { E _ { p } }\\&\times [ 1 - n _ { p } \left( T , \mu _ { r } \right) - \overline { n } _ { p } \left( T , \mu _ { r } \right)]\mbox{d} p, \\ \end{split} $

(5) where
$ \begin{aligned} \mu_{r} = \mu- \frac { \alpha G } { N _ { c } }\frac { 6 } { \pi ^ { 2 } } \int^{\Lambda} p ^ { 2 } [ n _ { p } \left( T , \mu _ { r } \right) - \overline { n } _ { p } \left( T , \mu _ { r } \right)] \mbox{d} p. \end{aligned} $

(6) Here,
$ E_{p} = \sqrt{p^2+M^2} $ and$ \begin{split} n _ { p } ( T , \mu_{r} )=& \frac { 1 } { 1 + \exp \left( \displaystyle\frac { E _ { p } - \mu _ { r } } { T } \right) }, \\ \overline { n } _ { p } ( T , \mu_{r} )=& \frac { 1 } { 1 + \exp \left( \displaystyle\frac { E _ { p } + \mu _ { r } } { T } \right) },\end{split} $

(7) where the parameter α can not be determined in advance by theory, but only by fitting of the experimental results.
As mentioned above, in the case of a finite chemical potential, the new self-consistent mean field approximation is quite different from the previously applied mean field approximation. When the chemical potential approaches zero, the gap equation obtained from the self-consistent mean field approximation is reduced to the gap equation obtained from the conventional mean field approximation. Therefore, with the exception of the free parameter α (which must be fitted by finite density experimental data), other model parameters, such as cutoff Λ and current quark mass m, are identical to the conventional NJL model parameters. The details are provided for clarity as follows: the quantum number of QCD vacuum is
$ 0^{++} $ . In the presence of an external field, the vacuum responds by forming a vacuum condensate to ensure that the ground state of the composite system remains in the$ 0^{++} $ quantum state. Hence, when an external field is present, the contribution of the external field must be taken into account. In the case of vanishing chemical potential, at finite temperature or zero temperature, no vector condensate exists. Therefore, the gap equation of the effective Lagrangian at zero chemical potential has the same form, except for the coupling constant. From Eq. (5), the parameter α can be absorbed into the value of the coupling constant G at vanishing chemical potential, which reduces to the G in the original NJL model. In this case, there is no new model parameter introduced into the NJL model at finite temperature/or zero temperature.At the same time, since the NJL model parameters are obtained by fitting the pion mass, decay constant, and chiral condensation at zero temperature and zero chemical potential, the model parameters of this study are the same as in the previous NJL model. In addition, we also stress that the form
$ 1/2(\langle{\cal{L}}\rangle_{m} +\langle{\cal{L}}_{F}\rangle_{m}) $ proposed by Ref. [13] is only a special case with$ \alpha = 1/2 $ . Here, the effective Lagrangian defined by Eq. (4) is universal and can be applied to any strongly interacting system. For example, an important challenge of modern condensed matter physics is to develop a self-consistent method to determine the leading and sub-leading phase transition instabilities caused by various kinds of interaction. Recently, this issue has been widely studied in iron-based superconductors [15] and Dirac semimetal materials [16-18], however many problems were not satisfactorily resolved. In these strongly correlated systems, the fermionic excitations are subjected to several sorts of interactions, which lead to a number of competing long-range orders. The approach developed in this letter can be applied to study the phase-transition instabilities and ordering competition in condensed matter physics. The effective Lagrangian of strong correlated systems is naturally different from the NJL mode, and the corresponding parameter α can only be determined by experimental results in condensed physics. Indeed, different models should have different parameters α.Due to the lack of experimental data at large chemical potentials, the parameter α can not be determined by experiment and can be regarded as a free parameter. In this study, we first explore the dependence of the chiral phase transition on the parameter α at finite chemical potential and zero temperature, and investigate the effects of α on the chiral phase transition. To determine the order of the phase transition its location, the chiral susceptibility [19]
$ \begin{aligned} \chi_{m} = -\frac{\partial\langle\bar\psi\psi\rangle}{\partial m}, \end{aligned} $

(8) with different α is adopted.
Based on the numerical iterative algorithm, the quark gap equation is numerically solved at finite chemical potential and the corresponding quark number density and chiral susceptibility are obtained. The results are as follows: first, the critical value
$ \mu_{0} $ does not depend on the parameter α, that is, no matter how large α is, the value of$ \mu_0 $ is always the same. Based on the model parameters adopted in this letter, for example,$ \mu_{0} $ is always equal to 311$ \mbox{MeV} $ , which is quantitatively consistent with the prediction of Ref. [1]. Second, the chiral susceptibility exhibits different behaviors with different α. If α is less than the critical value$ \alpha_c = 0.71 $ , the chiral susceptibility is discontinuous at the critical chemical potential, therefore, the phase transition is a first order phase transition, see Fig. 1. In the previous mean field approximation, α is often assumed as 0.5, which is less than$ \alpha_c = 0.71 $ , therefore the strong interaction phase transition at low temperature and large chemical potential predicted by NJL model [13] represents the first order phase transition. Third, with the increase of α, the chiral susceptibility shows a smooth peak at the pseudo-critical chemical potential, and the phase transition is a crossover, see Fig. 2. Moreover, the pseudo-critical chemical potential increases with the parameter α at zero temperature. Therefore, the parameter α not only affects the value of the (pseudo) critical chemical potential, but also the order of the phase transition.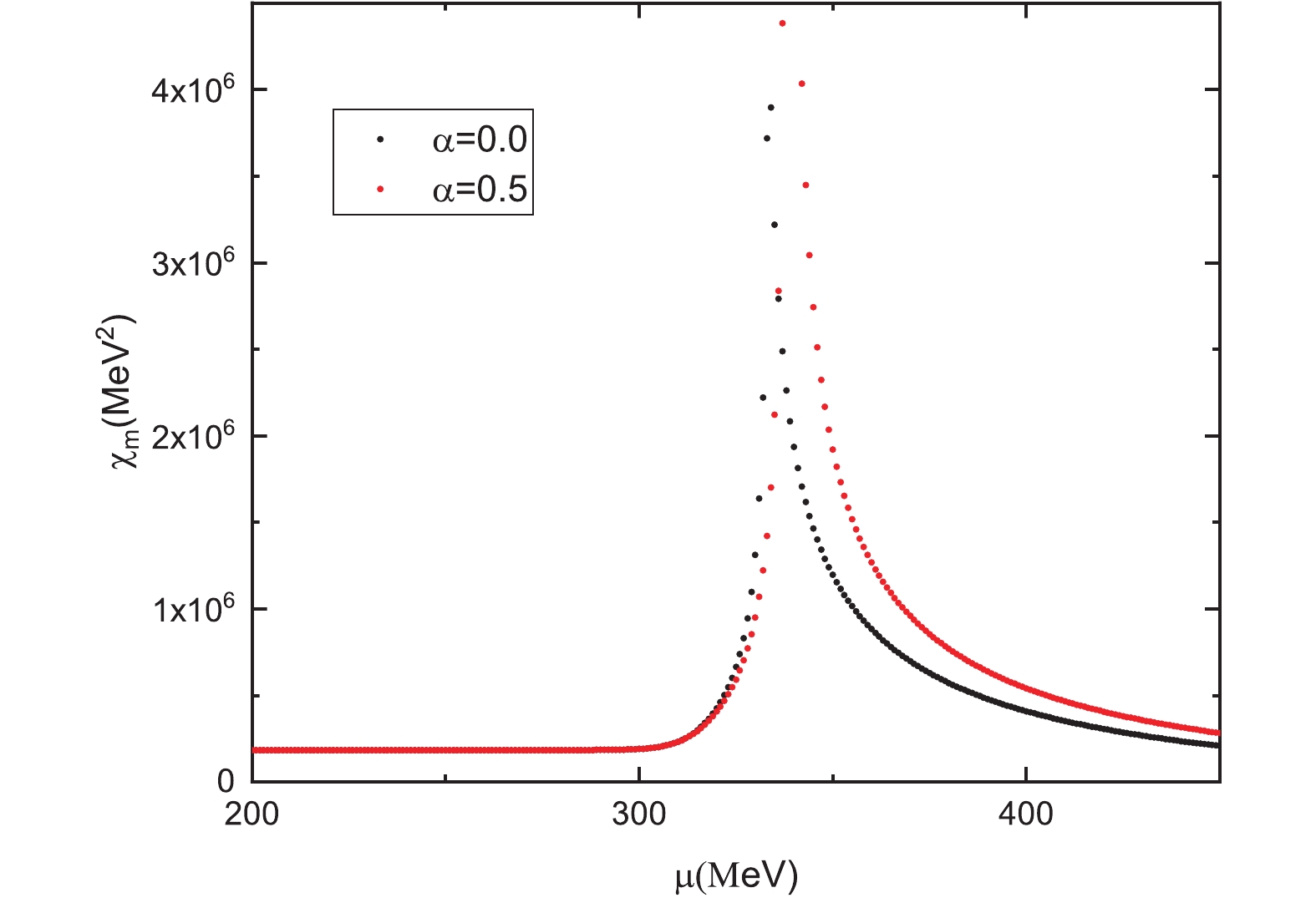
Figure 1. (color online) Chiral susceptibility as a function of chemical potential at zero temperature (α is less than
$ \alpha_c = 0.71 $ ). Parameters of the NJL model are given by$ G = 4.93\times 10^{-6} \mbox{MeV}^{-2} $ ,$ \Lambda = 653 \mbox{MeV} $ and$ m = 5.0 \mbox{MeV} $ [20].
Figure 2. (color online) Chiral susceptibility as a function of chemical potential at zero temperature (α is larger than
$ \alpha_c = 0.71 $ ). Parameters of the NJL model are the same as in Fig. 1.Indeed, the parameter α reflects the competition between different interaction channels and characterizes their relative weights, which is shown clearly in Eq. (4). All current–current interaction channels are taken into consideration using Fierz transformation.
$ \alpha = 0 $ and$ \alpha = 1/2 $ are usually adopted to perform calculations [13]. For the case of$ \alpha = 0 $ , the contributions of interaction channels in the second square bracket on the right hand side of Eq. (4) are discarded, which means that the vector interaction channel is ignored at finite chemical potential. This will obviously lead to an inconsistency in the mean field approximation. For the case of$ \alpha = 1/2 $ , the contributions of interaction channels in the first and second square bracket are equal, and there is no physical requirement for this choice. Phase transition occurs as a result of competition between different interaction channels. Thus, adjusting the parameter α can lead to different weights of different interaction channels, which can change the critical chemical potential of the chiral phase transition and its order.As mentioned above, the parameter α can not be currently determined by experiment. However, it is generally believed that the phase transition of strong interaction matter is at least four times the saturation density of nuclear matter. If this is considered as a physical requirement to constrain α, we find that when
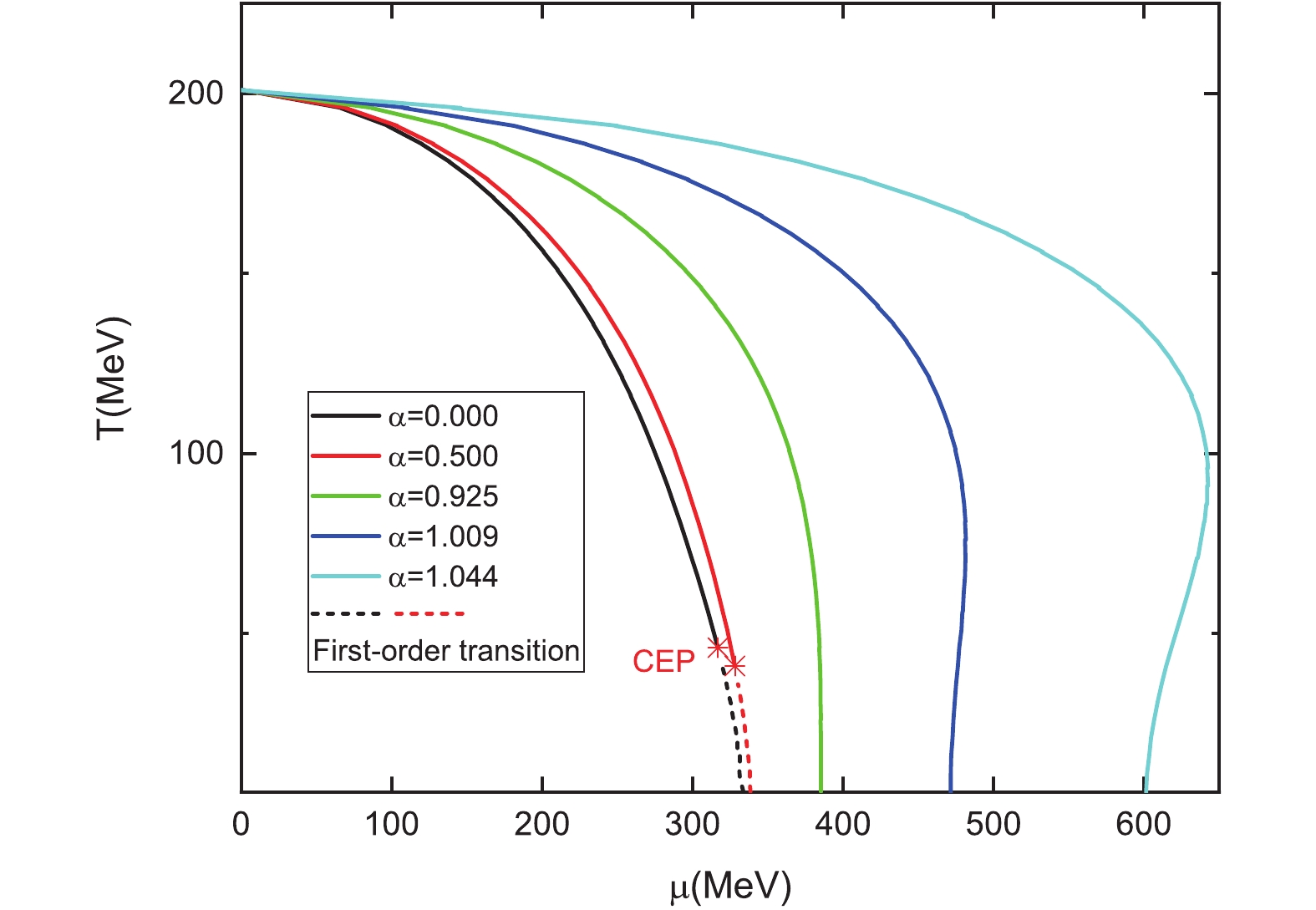
$ \alpha = 1.044 $ , that is, the corresponding pseudo-critical chemical potential$ \mu = 600 $ MeV, a strong interaction matter phase transition will occur. The self-consistent mean field method described above can be easily extended from two flavors to$ 2+1 $ flavor strong interaction matter, and thus the equation of state at zero temperature and finite chemical potential is obtained. This provides a good basis to study the neutron star mass radius relationship [9,10].Subsequently, the above approach is extended from zero temperature to finite temperature. At finite temperature with vanishing chemical potential, the chiral phase transition is a crossover, which is confirmed by lattice simulations [21]. Because of the fermion sign problem, lattice simulations can not perform calculations at large chemical potential. Many models show that the chiral phase transition at finite chemical potential is a first order phase transition [2,19]. Thus, the first order phase transition must be terminated at the critical temperature and chemical potential, which is the critical end point (CEP). Locating the possible CEP is an important target in the second phase energy scanning plan of the relativistic heavy ion collider (RHIC) [22–27]. However, in the new consistent mean field approach, the existence of CEP depends on the parameter α, as shown in Fig. 3. With the increase of α, the CEP ceases to exist, i.e., if α is larger than the critical value
$ \alpha_c = 0.71 $ , the chiral phase transition is a crossover at finite temperature and chemical potential, with no CEP. As a phase transition results from the competition between different interaction channels, at different temperatures, the competitive relationships between these channels are different, indicating that the pseudo critical chemical potential with$ \alpha > 1 $ is smaller at very small temperatures (Fig. 3). When α is larger than 1, the attractive interaction may become repulsive interaction, which likewise induces a change in the competitive relationships. The above results are evidently model dependent, and valid only if the mean field approximation can capture the nature of the strong interaction matter phase transition. -
We propose a new approach involving a universal self-consistent mean field approximation. We apply it in the study of a two flavor strong interaction matter phase transition. A free parameter α is introduced in the approach, which needs to be determined experimentally. We study the effects of α on the chiral phase transition and find that the parameter not only affects the value of the (pseudo)critical chemical potential, but also the order of the phase transition. The (pseudo) critical chemical potential increases with the parameter α. When
$ \alpha = 1.044 $ , the pseudo-critical chemical potential achieves values as high as ~600 MeV, which is in agreement with the expected results from the picture of hadron degrees of freedom. Moreover, with increasing α, the chiral phase transition becomes a crossover and therefore there is no CEP in QCD phase diagram at finite temperature and finite chemical potential. Finally, the determination of α is a highly intriguing task. α may be determined by observation of the binary neutron star merger, such as GW170817 [28], and the mass constraint of PSR J$ 0348+0432 $ [29], which we aim to investigate in a future study.The authors thank Professor Liu Guozhu and Luo Xiaofeng for their helpful discussions.
Novel self-consistent mean field approximation and its application in strong interaction phase transitions
- Received Date: 2019-03-26
- Available Online: 2019-08-01
Abstract: We propose a novel self-consistent mean field approximation method by means of a Fierz transformation, taking the Nambu-Jona-Lasinio model as an example. This new self-consistent mean field approximation introduces a new free parameter α to be determined experimentally. When α assumes the value of 0.5, the approximation reduces to the mean field calculation commonly used in the past. Subsequently, we study the influence of the undetermined parameter α on the phase diagram of the two-flavor strong interaction matter. The value of α plays a crucial role in the strong interaction phase diagram, as it not only changes the position of the phase transition point of strong interaction matter, but also affects the order of the phase transition. For example, when α is greater than the critical value





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: