-
One of the challenges in modern nuclear physics is exploring the mass and charge limits of atomic nuclei [1-8]. The prediction of the existence of an “island of stability” of superheavy nuclei (SHN) was made in the 1960s [9-14]. Currently, only the elements with
$ Z \leqslant 118 $ have been synthesized [15-17]. Various predictions of the center of the “island of stability” have been made [9-14, 18-20], but the position of this island is not well established. In contrast to the “island of stability,” the existence of a “shallow” of SHN has been well established theoretically and experimentally. This “shallow” connects the continent of stable nuclei to the “island of stability.” The center of this shallow is predicted to be around$ Z = 108 $ and$ N = 162 $ and consists of deformed SHN [21-24].$ ^{270}_{108} {\rm{Hs}} _{162} $ is a doubly magic deformed nucleus [25, 26] and offers a prototype for exploring the structure of SHN.There are currently two kinds of theoretical approaches for studying the structures and properties of SHN, the macroscopic-microscopic method (MMM) and the microscopic method. Generally, the surface of a nucleus is parameterized as [27]
$ R(\theta, \varphi) = R_{0}\left[ 1+\beta_{00}+ \sum\limits_{\lambda = 1}^{\infty} \sum\limits_{\mu = -\lambda}^{\lambda} \beta_{\lambda \mu}^{*} Y_{\lambda \mu}(\theta, \varphi)\right], $

(1) where
$ \beta_{\lambda\mu} $ is the deformation parameter and$ R_0 $ is the radius of a sphere with the same volume. However, there is an interesting consideration: how large should the dimension of the deformation space be when studying deformed SHN? In 1991, Patyk and Sobiczewski investigated the ground state properties of the heaviest even-even nuclei with proton numbers$ Z = 90 $ –114 and neutron numbers$ N = 136 $ –168 using the MMM and found that the$ \beta_6 $ degree of freedom is important for binding energies and the formation of deformed shells [23, 28]. Additionally,$ \beta_6 $ has a considerable influence on the moments of inertia [29, 30] and high-K isomers [31, 32]. The microscopic description of the structure of SHN can be achieved using density functional theories, with few studies investigating the influence of$ \beta_6 $ on the binding energy and shell structure of SHN to date.Covariant density functional theory (CDFT) is one of the most successful self-consistent approaches and has been used to describe ground and excited states of nuclei throughout the nuclear chart [33-41]. To investigate the ground state properties, potential energy surfaces (PESs), and fission barriers of heavy nuclei and SHN, multidimensionally-constrained (MDC) CDFTs have been developed [41-44]. MDC-CDFTs have been applied to investigate hypernuclei [45-48], the fission barriers and the PESs of actinide nuclei [42, 43, 49], the ground state properties and PESs of
$ ^{270} {\rm{Hs}}$ [50], the nonaxial octupole$ Y_{32} $ correlations in$ N = 150 $ isotones [51] and Zr isotopes [52], octupole correlations in MχD of$ ^{78} {\rm{Br}}$ [53] and Ba isotopes [54], etc. In MDC-CDFTs, reflection and axial symmetry are both broken, and the shape degrees of freedom$ \beta_{\lambda\mu} $ , where µ is an even number, are self-consistently included, such as$ \beta_{20},\;\beta_{22},\; $ $ \beta_{30},\;\beta_{32},\;\beta_{40},\;\beta_{42} $ , and$ \beta_{44} $ . Either the Bardeen-Cooper-Schrieffer (BCS) approach or the Bogoliubov transformation have been implemented to consider the pairing effects. With two different approaches to treat pairing correlations, there are two types of MDC-CDFTs: when using the BCS approach, the MDC relativistic mean-field (RMF) model is used, and for the Bogoliubov transformation, the MDC relativistic Hartree-Bogoliubov (RHB) theory is employed.In this study, we use the MDC-RMF model to investigate the ground state properties of SHN around the doubly magic deformed nucleus
$ ^{270} {\rm{Hs}}$ and focus on the influence of the higher-order deformations. This paper is organized as follows. The MDC-CDFTs is introduced in Sec. II. In Sec. III, the results and discussions are presented. Finally, we summarize the study in Sec. IV. -
In the CDFT, nucleons interact with each other through the exchange of mesons and photons or point-coupling interactions. To obtain accurate saturation properties of nuclear matter, the non-linear coupling terms or the density dependence of the coupling constants are introduced. Subsequently, there are four kinds of covariant density functionals: either meson exchange (ME) or point-coupling (PC) combined with the non-linear (NL) or density dependent (DD) couplings. In this study, both the ME and PC density functionals are used. The main formulae of the MDC-CDFTs can be found in Refs. [41, 43, 50, 52]. For convenience, we only introduce the MDC-RMF with the NL-PC effective interactions briefly.
The NL-PC Lagrangian is
$ {\cal{L}} = \bar{\psi}\left(\mathrm{i} \gamma_{\mu} \partial^{\mu} - M\right) \psi - {\cal{L}}_{\mathrm{lin}} - {\cal{L}}_{\mathrm{nl}} - {\cal{L}}_{\mathrm{der}} - {\cal{L}}_{\mathrm{Cou}}, $

(2) where the linear, nonlinear, derivative couplings, and the Coulomb terms respectively are
$ \begin{aligned}[b] {\cal{L}}_{{\rm{lin}}} =& \frac{1}{2} \alpha_{S} \rho_{S}^{2} +\frac{1}{2} \alpha_{V} \rho_{V}^{2} +\frac{1}{2} \alpha_{TS} {\boldsymbol{\rho}}_{TS}^{2} +\frac{1}{2} \alpha_{TV} {{\boldsymbol{\rho}}_{TV}}^{2} , \end{aligned} $

(3) $ {\cal{L}}_{\rm{nl}} = \frac{1}{3} \beta_{S} \rho_{S}^{3} +\frac{1}{4} \gamma_{S}\rho_{S}^{4} +\frac{1}{4} \gamma_{V}[\rho_{V}^{2}]^{2} , $

(4) $ \begin{aligned}[b] {\cal{L}}_{\rm{der}} =& \frac{1}{2} \delta_{S}[\partial_{\nu}\rho_{S}]^{2} +\frac{1}{2} \delta_{V}[\partial_{\nu}\rho_{V}]^{2} \\&+\frac{1}{2} \delta_{TS}[\partial_{\nu}{\boldsymbol{\rho}}_{TS}]^{2} +\frac{1}{2} \delta_{TV}[\partial_{\nu}{\boldsymbol{\rho}}_{TV}]^{2} , \end{aligned} $

(5) $ {\cal{L}}_{\rm{Cou}} = \frac{1}{4} F^{\mu\nu} F_{\mu\nu} +e\frac{1-\tau_{3}}{2} A_{0} \rho_{V} , $

(6) where M represents the nucleon mass, e is the unit charge, and
$ \alpha_{S} $ ,$ \alpha_{V} $ ,$ \alpha_{TS} $ ,$ \alpha_{TV} $ ,$ \beta_{S} $ ,$ \gamma_{S} $ ,$ \gamma_{V} $ ,$ \delta_{S} $ ,$ \delta_{V} $ ,$ \delta_{TS} $ , and$ \delta_{TV} $ are coupling constants. The isoscalar density$ \rho_{S} $ , isovector density$ {\boldsymbol{\rho}}_{TS} $ , the time-like components of isoscalar current$ \rho_{V} $ , and the time-like components of isovector currents$ {\boldsymbol{\rho}}_{TV} $ are defined as$ \rho_{S} = \bar{\psi} \psi,\; {\boldsymbol{\rho}}_{T S} = \bar{\psi} {\boldsymbol{\tau}} \psi,\; \rho_{V} = \bar{\psi} \gamma^{0} \psi,\; {\boldsymbol{\rho}}_{TV} = \bar{\psi} {\boldsymbol{\tau}} \gamma^{0} \psi. $

(7) The single particle wave function
$ \psi_{k}({{\boldsymbol{r}}}) $ with energy$ \epsilon_k $ of a nucleon is obtained by solving the Dirac equation$ \hat{h}\psi_{k}({\boldsymbol{r}}) = \epsilon_{k} \psi_{k}({\boldsymbol{r}}) , $

(8) with the Dirac Hamiltonian
$ \hat{h} = {\boldsymbol{\alpha}} \cdot {\boldsymbol{p}} + \beta \left[ M+S({\boldsymbol{r}}) \right] + V({\boldsymbol{r}}), $

(9) where the scalar potential
$ S({\boldsymbol{r}}) $ and vector potential$ V({\boldsymbol{r}}) $ are$ \begin{aligned}[b] S =& \; \alpha_{S} \rho_{S} + \alpha_{T S} {\boldsymbol{\rho}}_{T S} \cdot {\boldsymbol{\tau}} + \beta_{S} \rho_{S}^{2} + \gamma_{S} \rho_{S}^{3} \\ &+ \delta_{S} \Delta \rho_{S} + \delta_{T S} \Delta {\boldsymbol{\rho}}_{T S} \cdot {\boldsymbol{\tau}}, \\ V = &\alpha_{V} \rho_{V} + \alpha_{T V} {\boldsymbol{\rho}}_{T V} \cdot {\boldsymbol{\tau}} + \gamma_{V} \rho_{V}^{2} \rho_{V} \\ & + \delta_{V} \Delta \rho_{V} + \delta_{T V} \Delta {\boldsymbol{\rho}}_{T V} \cdot {\boldsymbol{\tau}} + e\frac{1-\tau_{3}}{2}A_0. \end{aligned} $

(10) In the MDC-CDFTs, the wave functions are expanded using the axially deformed harmonic oscillator (ADHO) basis [55, 56], which is obtained by solving the Schrödinger equation
$ \left[-\frac{\hbar^{2}}{2M}\nabla^{2}+V_{B}(z,\rho)\right]\Phi_{\alpha}({\boldsymbol{r}}\sigma) = E_{\alpha}\Phi_{\alpha}({\boldsymbol{r}}\sigma), $

(11) where
$ {\boldsymbol{r}} = (z,\rho) $ , where$ \rho = \sqrt{x^2+y^2} $ , and$ V_{B}(z,\rho) = \frac{1}{2} M ( \omega_{\rho}^{2} \rho^{2} + \omega_{z}^{2} z^{2}), $

(12) is the ADHO potential with the oscillator frequency, represented by
$ \omega_{\rho} $ ($ \omega_{z} $ ), perpendicular to (along) the z axis. More detailed formulae on the applications of ADHO in MDC-RMF can be found in Refs. [41, 43, 50, 52].After obtaining the ADHO basis, the single-particle wave functions can be expanded using the basis
$ \psi_{i}({\boldsymbol{r}}\sigma) = \left( \begin{array}{c} \sum\nolimits_{\alpha}f_{i}^{\alpha} \Phi_{\alpha}({\boldsymbol{r}}\sigma) \\ \sum\nolimits_{\alpha}g_{i}^{\alpha} \Phi_{\alpha}({\boldsymbol{r}}\sigma) \end{array} \right), $

(13) where α denotes a set of quantum numbers of the ADHO basis function,
$ \alpha\equiv\{n_{z},n_{\rho},m_{l},m_{s}\} $ , and$ f_{i}^{\alpha} $ and$ g_{i}^{\alpha} $ are the expansion coefficients. For the truncation of the ADHO basis, we follow Refs. [55, 57]. Finally, the wave functions are obtained by self-consistent iterations.$ ^{270} {\rm{Hs}}$ is an axially deformed nucleus in the ground state [50, 58, 59]. Reflection-asymmetric deformations normally occur only for ultra-neutron-rich nuclei with$ N \geqslant 182 $ in the SHN region [59]. Thus, we only consider the axially symmetric deformations$ \beta_\lambda $ , where λ is an even number, in this study. To investigate the influence of each shape degree of freedom on the bulk properties of SHN, constraint calculations on mass multipole moments are performed [27]. In MDC-CDFTs, a modified linear-constraint method is implemented [42, 43] and the Routhian reads$ E^{\prime} = E_{{\rm{RMF}}} + \sum\limits_{\lambda} \frac{1}{2} C_{\lambda}Q_{\lambda} . $

(14) After the nth iteration, the variable
$ C_{\lambda}^{(n+1)} $ is determined by$ C_{\lambda}^{(n+1)} = C_{\lambda}^{(n)} + k_{\lambda} \left( \beta_{\lambda}^{(n)} - \beta_{\lambda} \right), $

(15) where
$ C_{\lambda}^{(n)} $ is the value of the nth iteration,$ k_{\lambda} $ is a constant, and$ \beta_{\lambda} $ is the desired value of the deformation parameter.The intrinsic multipole moments are calculated as
$ Q_{\lambda,\tau} = \int {\rm d}^{3}{\boldsymbol{r}} \rho_{\tau}({\boldsymbol{r}}) r^{\lambda} Y_{\lambda 0}(\Omega), $

(16) where τ represents the nucleon (the neutron or the proton), and
$ \rho_{\tau} $ is the corresponding vector density. The deformation parameter$ \beta_{\lambda,\tau} $ is given by$ \beta_{\lambda,\tau} = \frac{4\pi} {3N_{\tau}R^{\lambda}} Q_{\lambda,\tau}, $

(17) where
$ R = r_0 A^{{1}/{3}} $ , with$ r_0 = 1.2 $ fm, and$ N_\tau $ represents the corresponding particle's number, A, N, or Z. -
To investigate the influence of higher-order deformations on the ground state properties of SHN, the doubly magic deformed nucleus
$ ^{270} {\rm{Hs}}$ , even-even Hs isotopes from$ ^{264} {\rm{Hs}}$ to$ ^{276} {\rm{Hs}}$ , and$ N = 162 $ isotones from$ ^{266} {\rm{Rf}}$ to$ ^{272} {\rm{Ds}}$ are analyzed. When investigating the ground state properties and the influence of higher-order deformations, the ADHO basis with$ N_f = 20 $ shells is adopted, leading to an accuracy of 0.1 MeV in total energy of$ ^{270} {\rm{Hs}}$ [50] in the MDC-RMF caclulations. In the particle-particle channel, a separable pairing force is adopted. Here, the strength and effective range of this force are taken to be the same as those in Ref. [50]:$ G = 1.1 G_0 $ , where$ G_0 = 728 $ MeV fm3, and$ a = 0.644 $ fm. The effective interactions PC-PK1 [60], PK1 [61], PKDD [61], DD-ME2 [62], and NL3* [63] are employed in the particle-hole channel.The ground state properties, including deformation parameters
$ \beta_\lambda $ ($ \lambda = 2, 4, 6, 8 $ , and$ 10 $ ), radii, and binding energies of even-even Hs isotopes with the above-mentioned five effective interactions are given in Table 1, and even-even isotones with$ N = 162 $ are listed in Table 2. The binding energies of one nucleus with five effective interactions differ from each other, e.g., the largest binding energy of$ ^{270} {\rm{Hs}}$ is 1973.77 MeV with PK1 and the smallest is 1967.41 MeV with PC-PK1. Such results are relatively close to the empirical values in AME2020,$ E_{\mathrm{B}} = 1969.65 $ MeV [64-66], and are also comparable to the predictions of other models, such as MMM, with$ E_{\mathrm{B}} = 1969.20 $ MeV [23], the Skyrme Hartree-Fock Bogoliubov mass model (HFB-24), with$ E_{\mathrm{B}} = 1968.45 $ MeV [67], the Weizsäcker-Skyrme (WS) mass formula WS4, with$ E_{\mathrm{B}} = 1970.27 $ MeV [68], the finite range droplet model (FRDM(2012)), with$ E_{\mathrm{B}} = 1971.48 $ MeV [58], and several RMF calculations [69-73]. For other nuclei, similar conclusions can also be drawn. From these two tables, it is clear that all considered nuclei are deformed in the MDC-RMF calculations with five effective interactions. This is consistent with the results obtained from MMM calculations [23, 58, 59] and other global studies [74, 75]. Additionally, it has been shown that the inclusion of the rotational energy correction (REC) can improve the description of binding energies with PC-PK1 [60]. In this study, after considering RECs in PC-PK1 calculations, the binding energy of$ ^{270} {\rm{Hs}}$ changes from 1967.45 to 1969.76 MeV, which is closer to the value provided in AME2020.$ \beta_{2,n} $ 

$ \beta_{2,p} $ 

$ \beta_{2} $ 

$ \beta_{4} $ 

$ \beta_{6} $ 

$ \beta_{8} $ 

$ \beta_{10} $ 

$ R_{n} $ /fm

$ R_{p} $ /fm

$ R_{\mathrm{t}} $ /fm

$ R_{\mathrm{c}} $ /fm

$ E_{\mathrm{B}} $ /MeV

PC-PK1 $ ^{264} {\rm{Hs}}$ 

0.270 0.280 0.274 −0.002 −0.060 −0.013 0.011 6.245 6.090 6.182 6.138 1924.415 $ ^{266} {\rm{Hs}}$ 

0.266 0.276 0.271 −0.021 −0.063 −0.004 0.014 6.267 6.101 6.200 6.148 1939.205 $ ^{268} {\rm{Hs}}$ 

0.262 0.273 0.266 −0.040 −0.063 0.004 0.015 6.288 6.111 6.217 6.158 1953.554 $ ^{270} {\rm{Hs}}$ 

0.257 0.269 0.261 −0.057 −0.061 0.012 0.015 6.306 6.120 6.232 6.167 1967.408 $ ^{272} {\rm{Hs}}$ 

0.245 0.258 0.250 −0.060 −0.049 0.013 0.010 6.330 6.131 6.252 6.178 1979.303 $ ^{274} {\rm{Hs}}$ 

0.216 0.228 0.221 −0.053 −0.038 0.009 0.006 6.344 6.135 6.263 6.182 1990.951 $ ^{276} {\rm{Hs}}$ 

0.188 0.198 0.192 −0.049 −0.027 0.007 0.003 6.357 6.139 6.273 6.185 2002.778 PK1 $ ^{264} {\rm{Hs}}$ 

0.253 0.258 0.255 0.006 −0.058 −0.016 0.011 6.228 6.058 6.159 6.105 1934.074 $ ^{266} {\rm{Hs}}$ 

0.253 0.258 0.255 −0.014 −0.065 −0.006 0.016 6.253 6.070 6.179 6.118 1947.952 $ ^{268} {\rm{Hs}}$ 

0.256 0.261 0.258 −0.034 −0.070 0.005 0.019 6.278 6.084 6.201 6.131 1961.285 $ ^{270} {\rm{Hs}}$ 

0245 0.251 0.248 −0.044 −0.062 0.010 0.016 6.297 6.091 6.216 6.138 1973.766 $ ^{272} {\rm{Hs}}$ 

0.211 0.216 0.213 −0.029 −0.053 0.005 0.010 6.305 6.090 6.221 6.137 1985.924 $ ^{274} {\rm{Hs}}$ 

0.194 0.198 0.195 −0.038 −0.040 0.006 0.010 6.322 6.097 6.234 6.144 1997.412 $ ^{276} {\rm{Hs}}$ 

0.178 0.182 0.180 −0.047 −0.028 0.007 0.007 6.342 6.105 6.250 6.151 2008.356 PKDD $ ^{264} {\rm{Hs}}$ 

0.250 0.255 0.252 0.001 −0.060 −0.015 0.011 6.207 6.053 6.145 6.101 1932.544 $ ^{266} {\rm{Hs}}$ 

0.253 0.258 0.255 −0.020 −0.066 −0.004 0.016 6.233 6.067 6.166 6.115 1946.294 $ ^{268} {\rm{Hs}}$ 

0.258 0.264 0.260 −0.041 −0.072 0.009 0.021 6.259 6.082 6.188 6.129 1959.686 $ ^{270} {\rm{Hs}}$ 

0.252 0.261 0.256 −0.059 −0.062 0.017 0.017 6.278 6.091 6.204 6.138 1972.399 $ ^{272} {\rm{Hs}}$ 

0.211 0.217 0.213 −0.030 −0.056 0.006 0.019 6.282 6.087 6.205 6.134 1983.376 $ ^{274} {\rm{Hs}}$ 

0.190 0.194 0.191 −0.039 −0.041 0.006 0.010 6.296 6.093 6.216 6.139 1994.504 $ ^{276} {\rm{Hs}}$ 

0.174 0.179 0.176 −0.048 −0.028 0.007 0.007 6.316 6.100 6.233 6.147 2004.934 DD-ME2 $ ^{264} {\rm{Hs}}$ 

0.260 0.267 0.263 −0.001 −0.061 −0.012 0.014 6.178 6.073 6.136 6.121 1928.426 $ ^{266} {\rm{Hs}}$ 

0.261 0.269 0.264 −0.023 −0.066 −0.001 0.019 6.200 6.086 6.154 6.133 1942.991 $ ^{268} {\rm{Hs}}$ 

0.259 0.269 0.263 −0.042 −0.068 0.011 0.021 6.220 6.097 6.171 6.144 1957.270 $ ^{270} {\rm{Hs}}$ 

0.252 0.264 0.257 −0.058 −0.060 0.017 0.017 6.236 6.105 6.184 6.152 1971.027 $ ^{272} {\rm{Hs}}$ 

0.213 0.222 0.216 −0.032 −0.054 0.007 0.012 6.240 6.101 6.185 6.148 1981.994 $ ^{274} {\rm{Hs}}$ 

0.196 0.204 0.199 −0.039 −0.041 0.007 0.010 6.256 6.107 6.198 6.154 1993.391 $ ^{276} {\rm{Hs}}$ 

0.178 0.186 0.181 −0.048 −0.027 0.008 0.007 6.271 6.113 6.210 6.160 2004.657 NL3* $ ^{264} {\rm{Hs}}$ 

0.265 0.271 0.267 0.004 −0.060 −0.014 0.013 6.260 6.079 6.186 6.126 1931.827 $ ^{266} {\rm{Hs}}$ 

0.263 0.270 0.266 −0.017 −0.065 −0.004 0.017 6.284 6.090 6.206 6.137 1945.933 $ ^{268} {\rm{Hs}}$ 

0.262 0.269 0.265 −0.036 −0.067 0.007 0.018 6.307 6.101 6.225 6.148 1959.582 $ ^{270} {\rm{Hs}}$ 

0.256 0.265 0.260 −0.054 −0.061 0.015 0.017 6.326 6.109 6.240 6.156 1972.574 $ ^{272} {\rm{Hs}}$ 

0.233 0.241 0.236 −0.045 −0.051 0.010 0.012 6.344 6.115 6.254 6.162 1984.027 $ ^{274} {\rm{Hs}}$ 

0.204 0.211 0.207 −0.039 −0.040 0.007 0.009 6.357 6.118 6.264 6.164 1995.465 $ ^{276} {\rm{Hs}}$ 

0.185 0.193 0.188 −0.047 −0.028 0.008 0.006 6.376 6.125 6.279 6.171 2006.648 Table 1. Ground state properties, including quadrupole deformation parameters, of neutrons and protons (
$ \beta_{2,n} $ and$ \beta_{2,p} $ ), deformation parameters$ \beta_2 $ ,$ \beta_4 $ ,$ \beta_6 $ ,$ \beta_8 $ , and$ \beta_{10} $ , mass radius$ R_{\rm t} $ , radii of protons and neutrons ($ R_p $ and$ R_n $ ), charge radius$ R_{\rm c} $ , and binding energy$ E_\mathrm{B} $ of Hs isotopes using MDC-RMF with five effective interactions: PC-PK1, PK1, PKDD, DD-ME2, and NL3*.$ \beta_{2,n} $ 

$ \beta_{2,p} $ 

$ \beta_{2} $ 

$ \beta_{4} $ 

$ \beta_{6} $ 

$ \beta_{8} $ 

$ \beta_{10} $ 

$ R_{n} $ /fm

$ R_{p} $ /fm

$ R_{\mathrm{t}} $ /fm

$ R_{\mathrm{c}} $ /fm

$ E_{\mathrm{B}} $ /MeV

PC-PK1 $ ^{266} {\rm{Rf}}$ 

0.261 0.274 0.266 −0.039 −0.060 0.005 0.013 6.303 6.083 6.218 6.129 1953.531 $ ^{268} {\rm{Sg}}$ 

0.260 0.274 0.266 −0.048 −0.063 0.009 0.015 6.304 6.102 6.225 6.149 1961.448 $ ^{270} {\rm{Hs}}$ 

0.257 0.269 0.261 −0.057 −0.061 0.012 0.015 6.306 6.120 6.232 6.167 1967.408 $ ^{272} {\rm{Ds}}$ 

0.249 0.258 0.253 −0.061 −0.055 0.015 0.012 6.308 6.139 6.240 6.186 1971.338 PK1 $ ^{266} {\rm{Rf}}$ 

0.256 0.265 0.260 −0.038 −0.062 0.007 0.017 6.296 6.053 6.202 6.100 1957.699 $ ^{268} {\rm{Sg}}$ 

0.257 0.268 0.261 −0.046 −0.067 0.010 0.018 6.299 6.075 6.211 6.122 1966.814 $ ^{270} {\rm{Hs}}$ 

0.245 0.251 0.248 −0.044 −0.062 0.010 0.016 6.297 6.091 6.216 6.138 1973.766 $ ^{272} {\rm{Ds}}$ 

0.225 0.228 0.226 −0.037 −0.054 0.007 0.012 6.292 6.104 6.217 6.151 1979.041 PKDD $ ^{266} {\rm{Rf}}$ 

0.256 0.266 0.260 −0.043 −0.063 0.009 0.018 6.272 6.050 6.186 6.097 1955.230 $ ^{268} {\rm{Sg}}$ 

0.259 0.272 0.264 −0.051 −0.070 0.013 0.020 6.277 6.073 6.197 6.120 1965.167 $ ^{270} {\rm{Hs}}$ 

0.252 0.261 0.256 −0.059 −0.062 0.017 0.017 6.278 6.091 6.204 6.138 1972.399 $ ^{272} {\rm{Ds}}$ 

0.241 0.245 0.242 −0.060 −0.056 0.017 0.015 6.278 6.107 6.210 6.154 1977.775 DD-ME2 $ ^{266} {\rm{Rf}}$ 

0.255 0.268 0.260 −0.040 −0.061 0.008 0.017 6.224 6.062 6.161 6.109 1955.711 $ ^{268} {\rm{Sg}}$ 

0.257 0.271 0.262 −0.048 −0.065 0.012 0.019 6.231 6.086 6.174 6.132 1964.571 $ ^{270} {\rm{Hs}}$ 

0.252 0.264 0.257 −0.058 −0.060 0.017 0.017 6.236 6.105 6.184 6.152 1971.027 $ ^{272} {\rm{Ds}}$ 

0.242 0.249 0.245 −0.060 −0.054 0.017 0.015 6.241 6.123 6.193 6.170 1975.320 NL3* $ ^{266} {\rm{Rf}}$ 

0.261 0.272 0.266 −0.038 −0.062 0.007 0.017 6.325 6.070 6.226 6.116 1956.503 $ ^{268} {\rm{Sg}}$ 

0.261 0.273 0.266 −0.047 −0.066 0.011 0.018 6.325 6.091 6.233 6.137 1965.582 $ ^{270} {\rm{Hs}}$ 

0.256 0.265 0.260 −0.054 −0.061 0.015 0.017 6.326 6.109 6.240 6.156 1972.574 $ ^{272} {\rm{Ds}}$ 

0.248 0.253 0.250 −0.058 −0.055 0.016 0.014 6.326 6.127 6.247 6.174 1977.689 Table 2. Ground state properties, including quadrupole deformation parameters, of neutrons and protons (
$ \beta_{2,n} $ and$ \beta_{2,p} $ ), deformation parameters$ \beta_2,\beta_4,\beta_6,\beta_8 $ and$ \beta_{10} $ , mass radius$ R_\mathrm{t} $ , radii of protons and neutrons ($ R_p $ and$ R_n $ ), charge radius$ R_c $ , and binding energies$ E_{\mathrm{B}} $ of$ N=162 $ isotones using MDC-RMF with five effective interactions: PC-PK1, PK1, PKDD, DD-ME2, and NL3*.To determine the dimension of the deformation space when investigating the ground states of SHN using MDC-CDFTs, we calculate the binding energies of Hs isotopes and isotones with
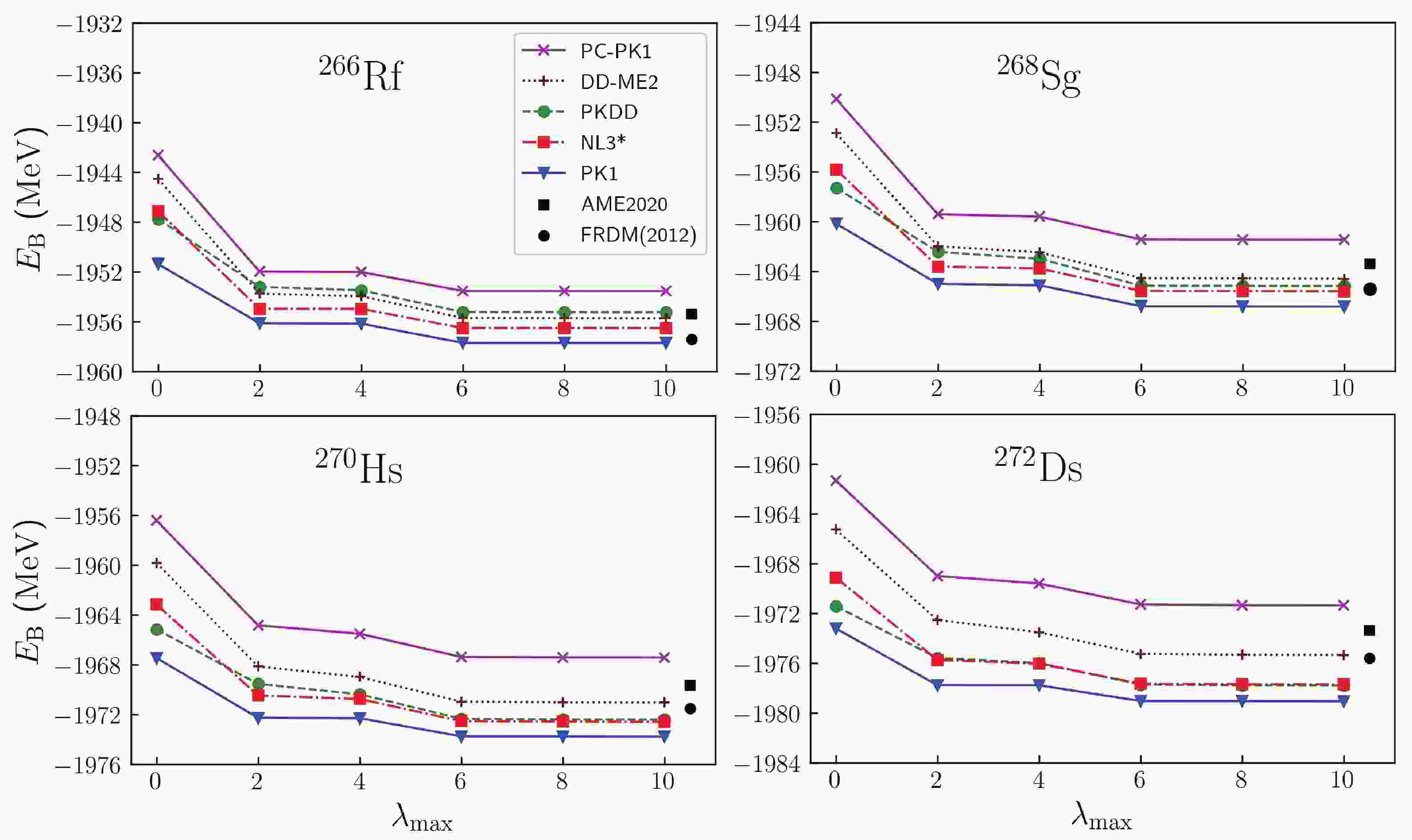
$ N = 162 $ in a different deformation space$ \{\beta_\lambda;\lambda = 0,2,\cdots, \lambda_\mathrm{max}\} $ with$ \lambda_\mathrm{max} $ being the maximum order of deformation parameters, meaning all deformation parameters$ \beta_{\lambda} \leqslant \beta_{\lambda_\mathrm{max}} $ are considered self-consistently, while other deformation parameters are constrained to zero. In Fig. 1, the binding energies of$ N = 162 $ isotones with five different effective interactions are plotted as a function of$ \lambda_{\mathrm{max}} $ . For convenience, we take$ ^{270} {\rm{Hs}}$ with the effective interaction PC-PK1 as an example to discuss the influence of each order of deformation on the binding energy in detail. When constraining$ ^{270} {\rm{Hs}}$ to be spherical, i.e., in the deformation space$ \left\{\beta_\lambda; \lambda = 0\right\} $ , the resulting binding energy is 1956.39 MeV, which is close to the prediction from the relativistic continuum Hartree-Bogoliubov theory, which is 1952.65 MeV [76], but not close to the value given in AME2020 (marked by a black square in Fig. 1). After considering the quadrupole deformation$ \beta_2 $ , the binding energy of$ ^{270} {\rm{Hs}}$ changes considerably (by approximately 8.43 MeV) and approaches that from AME2020. This result indicates the importance of the quadrupole deformation. The influence of the hexadecapole deformation$ \beta_4 $ on the binding energy is smaller, with a change of only 0.68 MeV. Considering$ \beta_6 $ , the energy change is approximately 1.87 MeV, which is larger than that of$ \beta_4 $ , and$ E_\mathrm{B} $ approaches the value provided in AME2020. Including$ \beta_8 $ and$ \beta_{10} $ does not affect the binding energy, which converges well at$ \{\beta_\lambda;\lambda = 0,2,\cdots,10\} $ . From these results, we can conclude that to obtain a proper description of$ ^{270} {\rm{Hs}}$ , one should consider the$ \beta_6 $ deformation at least with respect to the binding energy. Calculated binding energy versus$ \lambda_{\mathrm{max}} $ with other density functionals are also displayed in Fig. 1, and although the binding energies with five effective interactions differ from each other, the overall trend of$ E_\mathrm{B} $ changing with$ \lambda_{\mathrm{max}} $ are similar. The binding energy of$ ^{270} {\rm{Hs}}$ is predominantly changed by$ \beta_2 $ , then$ \beta_6 $ and$ \beta_4 $ . The influence of$ \beta_8 $ and$ \beta_{10} $ can be ignored. The RECs for$ ^{270} {\rm{Hs}}$ with PC-PK1 are 2.27, 2.03, 2.29, 2.31, and 2.31 MeV in deformation spaces$ \{\beta_\lambda;\lambda = 0,\cdots, \lambda_\mathrm{max}\} $ , with$ \lambda_{\mathrm{max}} = 2,4,6,8 $ , and$ 10 $ , respectively. The values of RECs change slightly in different deformation spaces and only minimally influence the trends of binding energies with respect to$ \lambda_\mathrm{max} $ .
Figure 1. (color online) Binding energies of
$ N = 162 $ isotones for PC-PK1, DD-ME2, PKDD, NL3*, and PK1 as a function of$ \lambda_\mathrm{max} $ . The black square and black circle represent the values from AME2020 and FRMD(2012), respectively.To check whether the above conclusion is valid for other SHN, we perform similar calculations for even-even isotones with
$ N = 162 $ and Hs isotopes, with the results also presented in Figs. 1 and 2. From these figures, we find that the binding energies of these nuclei are significantly changed by$ \beta_2 $ . The influence of$ \beta_4 $ and$ \beta_6 $ should also be considered, and the contribution to the total energy from$ \beta_6 $ is larger than that from$ \beta_4 $ . For Hs isotopes, with decreasing neutron number, the value of$ \beta_2 $ increases substantially and the differences of the total energies between the spherical case and in the ground states increase, which can be observed in Fig. 2. For isotones with$ N = 162 $ , the value of$ \beta_2 $ only minimally changes with proton number. For these nuclei, the relationship between binding energies and$ \beta_{\lambda_\mathrm{max}} $ are the same as for$ ^{270} {\rm{Hs}}$ .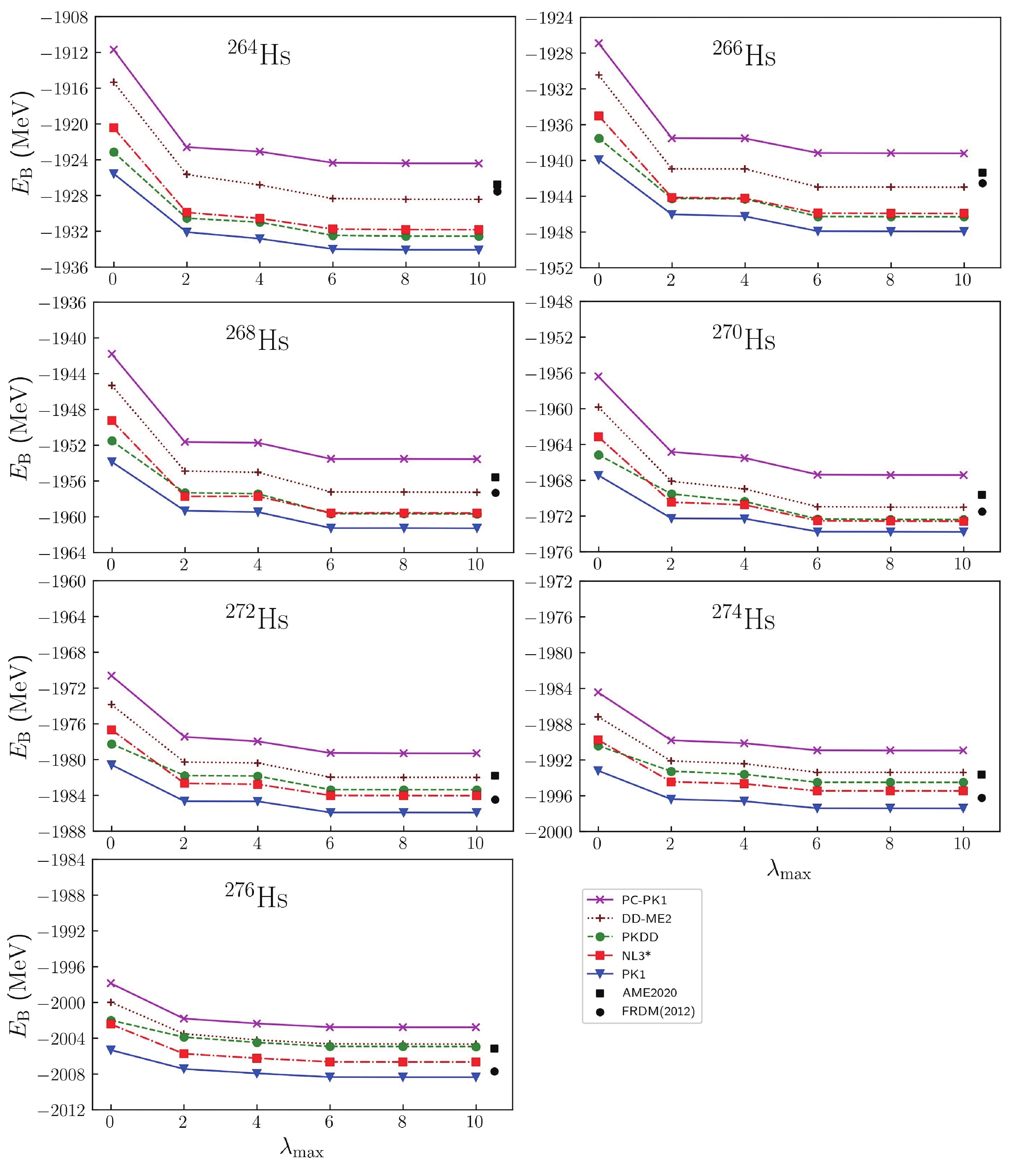
Figure 2. (color online) Binding energies of Hs isotopes for PC-PK1, DD-ME2, PKDD, NL3*, and PK1 as a function of
$ \lambda_\mathrm{max} $ . The black square and black circle represent the values from AME2020 and FRMD(2012), respectively.It is well known that shell structure is particularly important for SHN and very sensitive to the deformation of the nucleus [28]. Using
$ ^{270} {\rm{Hs}}$ as an example, we explore how the deformations influence the shell gaps at$ Z = 108 $ and$ N = 162 $ by investigating the structure of single-particle levels (SPLs) in different deformation spaces. In Fig. 3, we illustrate the SPLs for protons and neutrons of$ ^{270} {\rm{Hs}}$ versus$ \lambda_\mathrm{max} $ , calculated with PC-PK1. When$ \lambda_{\mathrm{max}} = 10 $ , i.e., for the ground state, the energy gaps at$ Z = 108 $ and$ N = 162 $ are approximately 1.34 MeV and 1.85 MeV, which are considerably large for such a heavy nucleus [77] and result in deformed shells.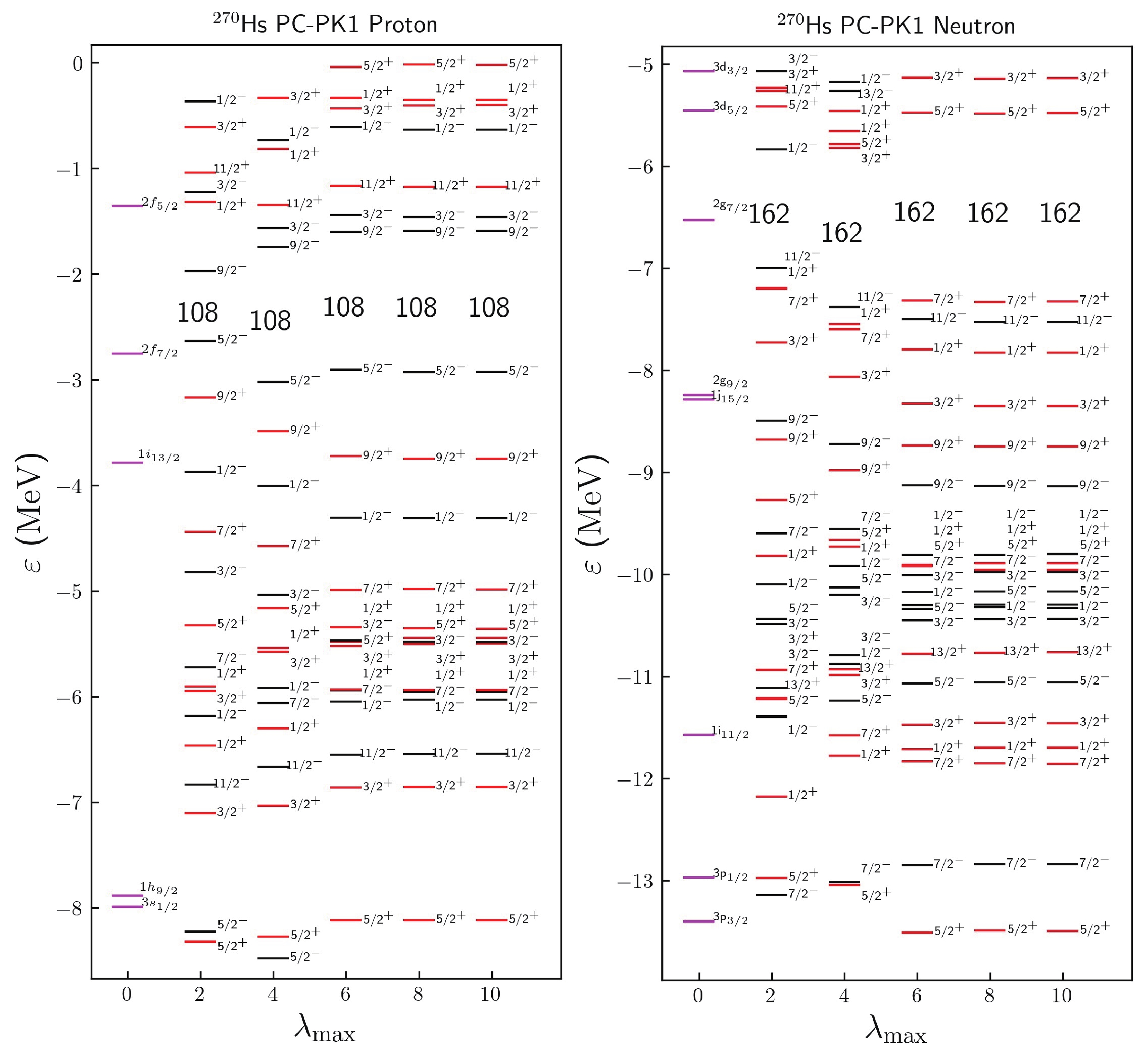
Figure 3. (color online) Single proton and neutron levels of
$ ^{270} {\rm{Hs}}$ from PC-PK1 calculations with different$ \lambda_\mathrm{max} $ . In the spherical case ($ \lambda_\mathrm{max} = 0 $ ), each level is labelled by$ |nlj\rangle $ . When$ \lambda_\mathrm{max}\neq0 $ , each level is labelled by the projection Ω of total angular momentum on the symmetry axis and the parity π. Single-particle levels with positive and negative parities are presented by red and black lines, respectively.In the spherical limit,
$ \lambda_{\mathrm{max}} = 0 $ , each single particle state is labelled by$ |nlj\rangle $ , where n, l, and j denote the radial quantum number, orbital angular momentum, and total angular momentum, respectively. It is obvious that there are no shell gaps at$ Z = 108 $ and$ N = 162 $ . After including$ \beta_2 $ , a spherical orbital$ |nlj\rangle $ with a degeneracy of$ 2j+1 $ splits into$ (2j+1)/2 $ levels, with each one represented by$ \Omega^\pi $ with the projection Ω of total angular momentum on the symmetry axis and the parity π. It is found that due to quadrupole correlations, the shell gaps at$ Z = 108 $ and$ N = 162 $ appear, with values of 0.66 MeV and 1.17 MeV, respectively. When including$ \beta_4 $ into the deformation space, the order of SPLs around the two gaps changes and the shell gaps at$ Z = 108 $ (up to approximately 1.28 MeV) and$ N = 162 $ (up to approximately 1.56 MeV) increase considerably. The impact of$ \beta_6 $ on the shell gap at$ Z = 108 $ is smaller, only 0.02 MeV. Although for neutrons, the shell gap at$ N = 162 $ increases by approximately 0.26 MeV. The inclusion of$ \beta_8 $ and$ \beta_{10} $ produces only extremely minimal changes in the shell gaps and the order of SPLs. From this, one can conclude that$ \beta_2 $ plays a vital role in the formation of the shell closures$ Z = 108 $ and$ N = 162 $ , which are further enhanced by$ \beta_4 $ . The influence of$ \beta_6 $ is relatively small and the effects of$ \beta_8 $ and$ \beta_{10} $ can be considered negligible. However, there remains a question: where do the$ Y_{60} $ correlations come from? By checking the SPLs, we find that two proton levels$ 1/2^+ $ originating from the spherical orbitals$ 3s_{1/2} $ and$ 1i_{13/2} $ are very close to each other and the mixing of these two spherical orbitals in the deformed SPLs results in$ Y_{60} $ correlations. For neutrons, these correlations originate from the mixing of the spherical orbitals 3$ p_{3/2} $ and 1$ j_{15/2} $ in the levels$ 3/2^- $ , close to the neutron Fermi energy. -
In this study, we investigate the ground state properties of SHN around
$ ^{270} {\rm{Hs}}$ in multidimensional deformation spaces using the MDC-RMF model with five density functionals. The influence of higher-order deformation parameters on the ground state of nuclei near$ ^{270} {\rm{Hs}}$ are investigated, including the binding energies and SPLs. We show that the binding energies of deformed SHN around$ ^{270} {\rm{Hs}}$ are significantly affected by higher-order deformations. In particular, the influence of$ \beta_6 $ on binding energy is larger than that of$ \beta_4 $ . For the doubly magic nucleus$ ^{270} {\rm{Hs}}$ , the deformed shell gaps at$ Z = 108 $ and$ N = 162 $ are mainly determined by quarupole correlations and are enhanced by the inclusion of$ \beta_4 $ . In conclusion, at least the$ \beta_6 $ degree of freedom should be considered in the investigation of SHN using CDFTs. It is also very interesting to investigate how the higher-order deformations influence other properties of SHN, such as the moment of inertia and energy spectra, by using density functional theories. Additionally, we would like to mention that the calculations performed in this study can also be performed using the deformation relativistic Hartree-Bogoliubov (DRHBc) theory [78-84], in which the scalar potential and densities are expanded in terms of the Legendre polynomials, though the DRHBc theory is much more time consuming than the MDC-RMF model. Very recently, the influence of higher-order deformations on possible bound nuclei beyond the drip line has also been investigated in the transfermium region from No ($ Z = 102 $ ) to Ds ($ Z = 110 $ ) using the DRHBc theory [85], and the development of a nuclear mass table using the DRHBc theory is in progress [86-89]. -
We thank Bing-Nan Lu, Yu-Ting Rong, and Kun Wang for helpful discussions. The results described in this paper were obtained on the High-performance Computing Cluster of ITP-CAS and the ScGrid of the Supercomputing Center, Computer Network Information Center of the Chinese Academy of Sciences.
Microscopic study of higher-order deformation effects on the ground states of superheavy nuclei around 270Hs
- Received Date: 2021-09-17
- Available Online: 2022-02-15
Abstract: We investigate the effects of higher-order deformations





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: