Dark matter subhalo evaporation by Coulomb-like interaction with galactic gas

A large number of cosmological and astrophysical observations indicate the existence of dark matter (DM), which makes up approximately 85% of the matter in our Universe. In the standard $ \rm \Lambda $CDM cosmology, DM is a cold, collisionless (CDM) particle, which fits well with our current observational constraints [1, 2]. However, there is still some potential evidence that the CDM model could be incomplete [3−17]. Although all the evidence we have for DM is derived from its gravitational interactions with ordinary matter, there is also the possibility that DM can have other, non-gravitational interactions with Standard Model (SM) particles and cause some observable effects throughout the Universe.

For the scattering between DM and SM particles, the relevant physical process can be described by the momentum transfer cross section, which characterizes the efficiency of momentum transfer and is largely captured as a power law function of the relative particle velocity v [18−29]. In recent years, DM with Coulomb-like interactions has been the subject of keen interest due to the anomalous observation by the Experiment to Detect the Global EoR Signature (EDGES) [30−32]. In such a scenario, the transfer cross section between DM and charged particles is proportional to $ v^{-4} $, which can cause an effective energy exchange between DM and baryons at later times and cool down baryons to explain the anomalous 21 cm absorption reported by the EDGES collaboration. A subclass of these models includes millicharged DM, which can couple to the SM photon and only scatter with charged particles. Effective coupling can be naturally produced in models with a hyper-charge portal via kinetic mixing [33, 34].

Elastic scattering between DM and charged particles can produce an observable effect throughout the Universe. These interactions can affect the cosmic microwave background (CMB) anisotropies and suppress the matter power spectrum on small scales [35−37]. Previous studies have constrained the momentum-transfer cross section between DM and protons by using measurements of CMB anisotropies from the Planck satellite [38−42]. Other observational probes of structure, including the measurements of Lyman-α forest power spectrum and abundance of Milky-Way satellite galaxies, have also been used to constrain DM-proton scattering [43−48].

Unlike previous studies, we start from a novel perspective and focus on the evaporation effects of subhalos due to the scattering between DM particles and ionized galactic gas. This process can be seen as ram-pressure evaporation, where the collision between low-velocity DM particles in the subhalo and particles in the host halo can cause the bound DM particles within the subhalo to escape. Considering that the transfer cross section of Coulomb-like scattering is proportional to $ v^{-4} $, it can produce prominent evaporation effects on DM subhalos at low velocity.

In the late Universe, ionized hotspots re-emerge in inner galactic regions. Our Milky Way is one such massive galaxy where the diffuse gas is predominantly ionized. When subhalos travel through such ionized regions, DM particles become gradually heated via soft scattering with ionized gas, to a point that they may escape the subhalo's gravitational binding. Thus, the survival of subhalos requires stringent limits on the strength of Coulomb-like scattering. One typical scenario to realize such interaction is the kinetically mixed $ U(1)' $ model, where the DM particles can develop a tiny electric charge and scatter with charged SM particles. In the following sections, we calculate the collision heating rate and place an upper limit on the DM’s transfer cross section by assuming the survival of subhalos in the ionized galactic region.

To implement Coulomb-like interactions, we consider a low energy phenomenological model [49, 50], in which the DM particle χ is a Dirac fermion, and it can interact with the charged particles, such as galactic protons. The effective interaction term between the DM particle χ and SM photon $ A_\mu $ is

where $ \epsilon $ is the kinetic mixing parameter, and $ g_\chi $ represents the gauge coupling under the dark $ U(1)' $. When setting $ g_\chi=e $, we can recover the scenario of millicharge DM.

The scattering process between DM and charged particles gives rise to a momentum transfer cross section that characterizes the efficiency of momentum transfer:

where θ is the scattering angle. For Coulomb-like interactions, the integration over Eq. (2) leads to a logarithmic divergence. To regulate the forward scattering singularity of the momentum-transfer integral, we use the Debye screening length as the maximal impact parameter [51]:

where $ n_p $, $ T_p $, and $ x_e $ denote the proton number density, proton temperature, and ionization fraction, respectively. For Coulomb-like interactions, the maximal impact parameter is equivalent to a minimal scattering angle

where we use $ \epsilon\ll1 $ and $ \mu_{\chi p} v^2/2\approx 3T_p/2 $. v represents the relative velocity between the DM and proton, and $ \mu_{\chi p}=\dfrac{m_\chi m_p}{ m_\chi+m_p} $ is their reduced mass. In terms of the cutoff scattering angle, the momentum-transfer cross section is given by

where $ \alpha_\chi\equiv g_\chi^2/4\pi $. As the relative velocity only appears as $ v^{-4} $ in the pre-factor, we can parameterize the transfer cross-section of the collision between DM and a proton as $ \sigma_T=\sigma_0 v^{-4} $, where $ \sigma_0 $ represents the velocity-stripped momentum transfer cross section.

When DM collides with ionized gas, the important physical quantity is energy transfer rate, which needs to be averaged over the velocity distributions of DM and hot gas. For gases primarily made of ionized hydrogen, the thermally averaged energy transfer rate of per unit time is given by Refs. [19, 52]:

where $ \rho_p $ is gas density, and $ \sigma_T $ is the transfer cross section. $ \vec{v}_{p} $ and $ \vec{v}_{\chi} $ denote the velocities of the proton and DM in the galactic frame, respectively, and $ \vec{v}_{\rm cm} $ is the DM-proton center-of-mass velocity. We can assume that DM velocity inside a subhalo follows a Maxwellian distribution,

where $ \vec{v}_0 $ represents the subhalo's collective velocity that circulates around the center of galaxy. For protons in hot gas, their velocity follows a Boltzmann distribution that may also have a collective motion velocity $ \vec{v}_{p0} $,

Substituting the transfer cross-section $ \sigma_T=\sigma_0 v^{n} $ into Eq. (6) and integrating out the velocity distributions, we obtain

with $ a=m_\chi/(m_\chi+m_p) $ and $ b=(T_\chi-T_p)/u_{\rm th}^2(m_\chi+m_p) $. The integrals $ I_{1}(n) $ and $ I_{2}(n) $ take the form

where $ u_{\rm th} $ and r are defined as $ u_{\rm th}^2= \dfrac{k_B T_p}{m_p}+\dfrac{k_B T_\chi}{m_\chi} $ and $ r=\dfrac{v}{u_{\rm th}} $, respectively, and v represents the relative velocity between the subhalo and galactic gas. For our case, taking $ n=-4 $ and the corresponding heating rate due to protons in gas, we obtain

where the function $ F(r) $ is

The additional heating by colliding with electrons in gas can be obtained by replacing $ m_p\rightarrow m_e $ and $ \rho_p\rightarrow \rho_e= \rho_p\cdot m_e/m_p $.

DM subhalos at a few kpc from the galactic center typically have $ v_0\sim 10^{-4} $ to $ 10^{-3} $. Thus, the relative velocity $ |\vec{v}_{\chi}-\vec{v}_{p}| $ between DM and a proton is much larger than the velocity dispersion inside the subhalo and gas. For DM-proton collision, we can take the limit where relative velocity v is dominated by $ |\vec{v}_0-\vec{v}_{p0}| $, and the energy transfer rate becomes insensitive to their temperature. In this case, the heating rate takes a much simpler expression:

where $ \rho_p $ is the proton's mass density. For DM-electron collision, this approximation may not hold. In dense ionized gas, thermal equilibrium between electrons and protons can occur rapidly; hence, they have the same temperature [53]. However, the thermal velocity of electrons in gas is much larger than that of protons; therefore, we need to use the full expression in Eq. (11) to calculate the energy transfer rate due to collision with electrons.

In previous studies, the cosmological constraints on the momentum transfer cross sections of DM–proton [38−40] and DM–electron [54−56] collisions are often investigated separately. In this study, we consider their combined contribution to DM subhalo evaporation by summing up the contributions from both protons and electrons in ionized gases. We first derive the constraint on $ \epsilon^2 \alpha_{\chi} $ for different DM masses and then we use Eq. (5) to obtain the constraints of DM–proton momentum transfer cross section, which is more convenient to compare with existing limits. Also note that, in Eq. (13), when $ m_\chi $ is much higher than the proton mass, and momentum transfer efficiency drops significantly; thus, we only focus on the DM mass range below the GeV scale, where the evaporation effects are prominent.

Given previous calculations, the time scale for an average DM particle to be heated to its host subhalo's escape velocity can be estimated as

where $ v_{\rm rms} $ is the root-mean-square velocity of DM inside the subhalo. Long-time stability of subhalos would require $ \tau_{\rm esc.} $ to be comparable to or longer than the age of a galaxy. Our Milky Way's age is approximately $ 10^{10} $ yr, so we use $ \tau_{\rm esc.}=10^{10} $ yr to calculate the evaporation limits of subhalos by collision with hot gas. A DM particle's root-mean-square velocity $ v_{\rm rms} $ and escape velocity $ v_{\rm esc} $ would depend on the subhalo size. For our galaxy, we use an empirical scaling relation for a particle's velocity dispersion $ \delta_v $ from the population of sizable subhalos that contain visible stars [57],

The scaling relation of velocity dispersion with the $ 1/3 $ power-law of halo mass is based on the predictions of the virial theorem. Evrard et al. [58] also verified this relation with high resolution N-body simulations. The root-mean-square velocity $ v_{\rm rms} $ and escape velocity $ v_{\rm esc} $ are related to the velocity dispersion $ \delta_v $ by an $ {\cal O}(1) $ factor, for a Maxwellian distribution as expressed in Eq. (7), with $ v_{\rm rms} = 1.73 \delta_v $ and $ v_{\rm esc}=2.44 \delta_v $.

Ionized galactic gases are distributed within a few kpc from the Milky Way's disk, where the average particle number density is 0.05 cm$ ^{-3} $, and the temperature is approximately 8000 K [53]. When subhalos travel through ionized gas near the galactic disk, collisions heat up DM subhalos toward their binding energy. For convenience of illustration, we choose two orbit radii at 1 and 10 kpc, and the respective circulating velocities are $ 10^{-4} $ and $ 10^{-3} $ around the center of the galaxy. We use the two benchmark velocities to estimate the evaporation limits. If a subhalo's orbit is not completely submerged in the gaseous region, a fraction of time ε would apply, and the corresponding evaporation time should scale as $ \tau_{\rm esc.}\rightarrow \varepsilon^{-1}\tau_{\rm esc.} $, where $ \sigma_0 $ limits scale as $ \varepsilon^{-1} $.

There are two common density distribution models for galactic hot gas. One is the disk-like model [59], which is used to describe the gas distribution near the disk, and another is the spherical distribution model [60], which can describe the gas distribution at a distance away from the galactic center. For the disk-like model, the gas density distribution can be parameterized as $ n= n_0 {\rm e}^{-R/R_0} {\rm e}^{-Z/Z_0} $, where R is the distance from the galactic center axis in cylindrical coordinates, and Z is the vertical height from the galactic disk. The typical parameter choices are $ R_0\sim $ 7 kpc and $ Z_0\sim $ 2 kpc. According to the disk-like model, we can estimate the magnitude of efficiency factor ε. For a 10 kpc circular orbit, the corresponding ε is between 0.15 and 1. $ \varepsilon=1 $ corresponds to an orbit on the disk, and $ \varepsilon=0.15 $ represents an orbit on a plane perpendicular to the disk.

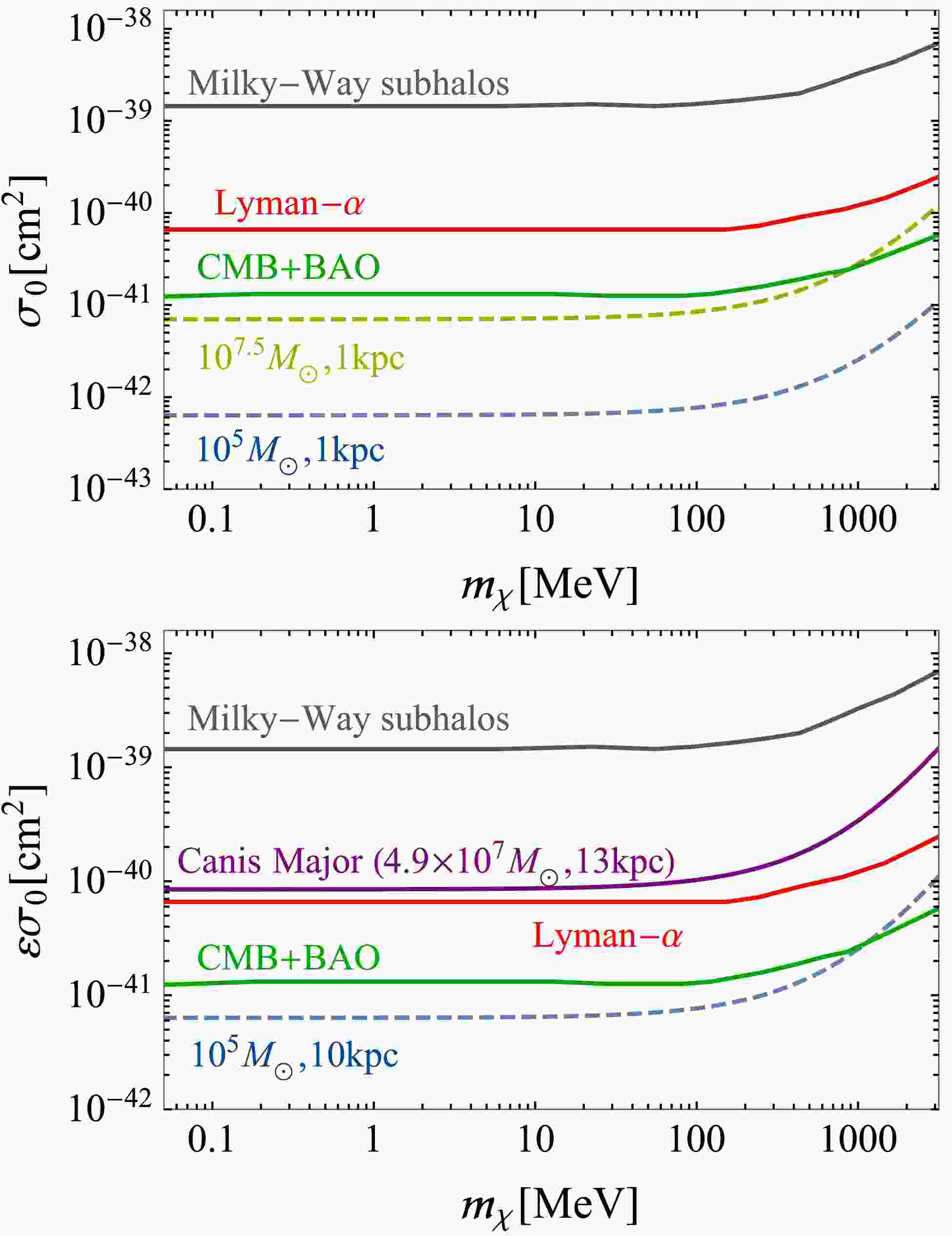
The Milky Way's observable subhalos typically have $ M \gtrsim 10^5 \;M_\odot $, and the current smallest known sample has a mass of approximately $ 10^5 \;M_\odot $, e.g., Segue1 [61] and Segue2 [62]. Therefore, for the first case, we use the subhalo mass $ 10^5 \;M_\odot $ to calculate the evaporation limits, although in principle, a lower-mass subhalo may also form [63, 64]. The evaporation limits for $ 10^5 \;M_\odot $ subhalos with $ \tau_{\rm esc.}= 10^{10} $ yr are shown by the blue dashed line in Fig. 1. The upper panel represents the evaporation limits in the case of subhalos with velocity $ v=10^{-4} $ and an orbit radius of 1 kpc, and the lower one represents those for subhalos at 10 kpc with velocity $ v=10^{-3} $. In the lower figure, ε is used at the $ \sigma_0 $ limit, which represents the time fraction of the subhalo's orbit in the gas-distributed region, where $ \varepsilon=1 $ corresponds to orbits entirely submerged in gaseous regions. It should be noted that, although these known $ 10^5 \;M_\odot $ subhalos are not very close to the galactic center, it is still reasonable to consider such subhalos as building blocks of our galactic halo given that the structure is developed from the bottom up. Therefore, we use $ 10^5 \;M_\odot $ as one benchmark, and the above limits are expected limits that apply to future observations.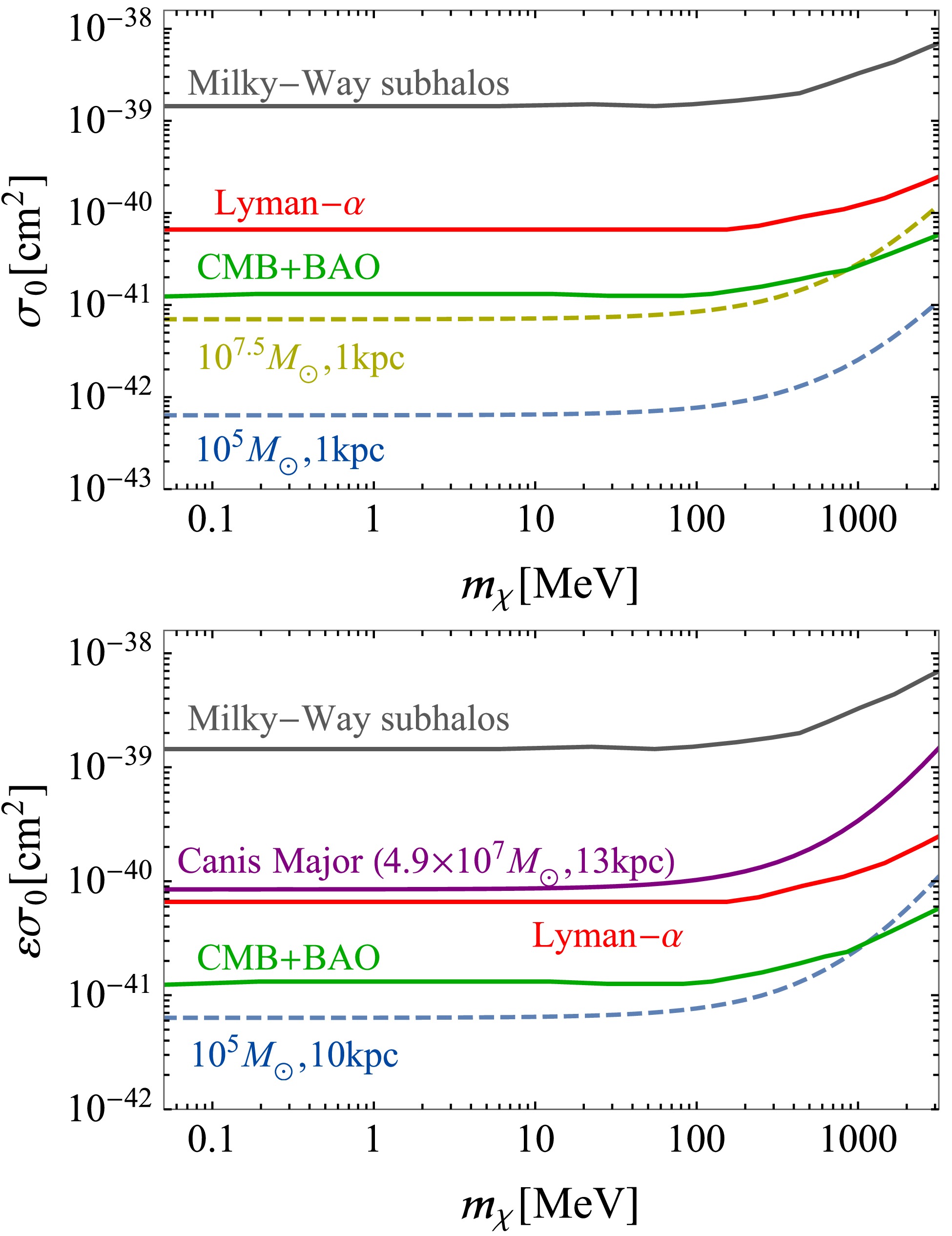

Figure 1.  (color online) Velocity-stripped momentum transfer cross-section $\sigma_0$ limits for $10^5 \;M_\odot$ (dashed blue) and $10^{7.5} \;M_\odot$ subhalos (dashed yellow) that survive a $10^{10}$ yr evaporation time. The evaporation limit of the Canis Major substructure is shown by the solid purple line. ε is the time fraction of the subhalo's orbit in the gas-distributed region, and $\varepsilon=1$ represents orbits entirely submerged in gaseous regions. The bounds from datasets of CMB+BAO (solid green), Lyman-α forest (solid red), and Milky-Way subhalos (solid gray) are also shown.

Another benchmark case we choose is $ 10^{7.5} \;M_\odot $ subhalos, and the expected evaporation limit is shown by the yellow dashed line. This line aims to illustrate the maximal soft scattering evaporation ability. For a DM mass below 1 GeV, with existing CMB+BAO limits, soft collisions alone can evaporate away $ 10^{7.5} \;M_\odot $ subhalos at 1 kpc distance from the galactic center. In the lower figure, we show a real example, the Canis Major substructure, which is located at a distance of approximately 13 kpc from the Milky Way's center and has a mass of approximately $ 4.9\times10^{7} \;M_\odot $ [65]. The center of the Canis Major Dwarf Galaxy lies around $ (1, b) \sim\left(240^{\circ}, -8^{\circ}\right) $ (l and b are the Galactic longitude and latitude, respectively), and its orbit is almost coplanar with the galactic disk. Current observations and N-body simulations indicate that it is being disturbed by the Milky Way's gravity, but its core still remains relatively stable [66]. The corresponding evaporation limit is shown by the purple solid line. The constraints from the datasets of CMB+BAO (solid green), Lyman-α forest (solid red) and Milky-Way subhalos (solid gray), which are from a recent study, are also shown for comparison [56].

Previous cosmological constraints on DM-baryon interactions can be briefly summarized as follows: the exchange of heat between DM and baryons would cool the baryons and lead to recombination occurring earlier, which can directly impact the CMB [41, 42]. Meanwhile, in the presence of DM-baryon interactions, baryon photon coupling can convey pressure to the DM, which damps the clustering of DM against structure formation and leads to a suppression on the matter power spectrum [35−37].

In this study, we investigate the evaporation of subhalos via Coulomb-like scattering between DM and ionized galactic gas. The subhalo evaporation limits are dependent on the gaseous environment of the inner galaxy and the location of subhalos. In case of $ 10^{5} \;M_\odot $ subhalos, which would survive at a 1 kpc orbit radius from the center of the Milky Way, the corresponding evaporation limit on $ \sigma_0 $ is one order of magnitude stronger than the current CMB+BAO constraint for a DM mass range below the GeV scale. For a larger 10 kpc orbit radius, the corresponding evaporation limit becomes comparable to the constraint from CMB+BAO.

In Fig. 1, it is not surprising that our evaporation limits for near-disk subhalo-gas scattering appear stronger than those from the average subhalo formation in the Milky-Way (gray solid) [56], which derives from the small-scale properties of the matter power spectrum for the extended galactic region and uses the Universe's average baryon number density for energy transfer calculation. As the ionized gas is more concentrated in the inner galactic region, the baryon number density in this region is much larger than the average baryon density of the Universe, which makes collision with ionized gas much more frequent and the evaporation limit more prominent for subhalos in this region. It is clear from Fig. 1 that, within the current CMB+BAO limits, fully ionized galactic gas can evaporate subhalos with masses below $ 10^{7.5} \;M_\odot $ at a 1 kpc orbit radius, and at a larger 10 kpc orbit, the affected subhalo mass drops to $ 10^{5} \;M_\odot $.

Direct-detection experiments can also constrain the same t-channel scattering process, which reflects the complementarity of cosmological probes. Next, we compare our limits to those from direct-detection experiments. For the electronic recoil direct detection experiments, the corresponding cross section is given by [67, 68]

where $ \overline{|\mathcal{M}|^2}|_{q=q_{\mathrm{ref}}} $ is the spin averaged amplitude-square at a reference transfer-momentum $ q=q_{\mathrm{ref}} $, and $ \mu_{\chi e} $ is the DM–electron reduced mass. A common choice for the reference transfer momentum for DM–electron scattering is $ q_{\mathrm{ref}}=\alpha m_e $ [69]. The t-channel spin averaged $ |{\cal M}|^2 $ for DM-electron scattering is

where t is the Mandelstam variable. The cross section is

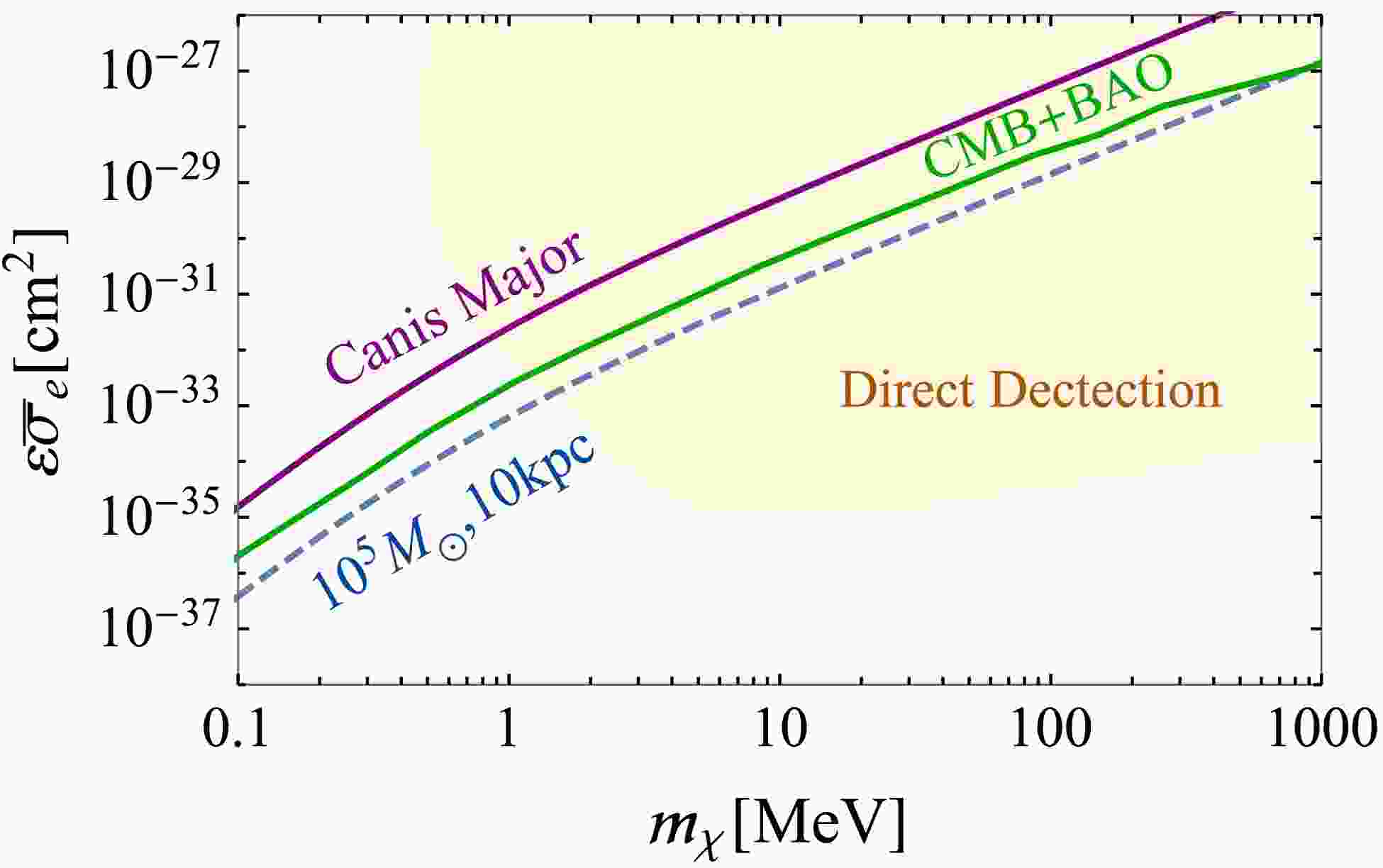
Similar to the constraints of velocity stripped DM-proton cross section $ \sigma_0 $, we substitute the constraint of $ \epsilon^2 \alpha_\chi $ for different DM masses into Eq. (18). The corresponding evaporation limits in terms of direct detection cross section $ \bar{\sigma}_e $ are shown in Fig. 2. The dashed blue line in this figure corresponds to the evaporation limit of $ 10^{5} \;M_\odot $ subhalos at a 10 kpc distance from galactic center, and the solid purple line indicates the evaporation limit of the Canis Major dwarf galaxy. The combined direct detection exclusion bounds [70−73] are shown as the orange shaded region (right-top) in the ($ m_\chi $, $ \bar{\sigma}_e $) plane. We also plot the CMB+BAO (solid green) constraints from Ref. [56] for comparison. The bounds from the Lyman-α forest and Milky-Way's average subhalos are not shown because they are weaker than those from CMB+BAO. It is clear from Fig. 2 that, for surviving subhalos located near the galactic center, their evaporation limits can readily extend to the sub-MeV DM mass range, where the direct detection experiments lose sensitivity.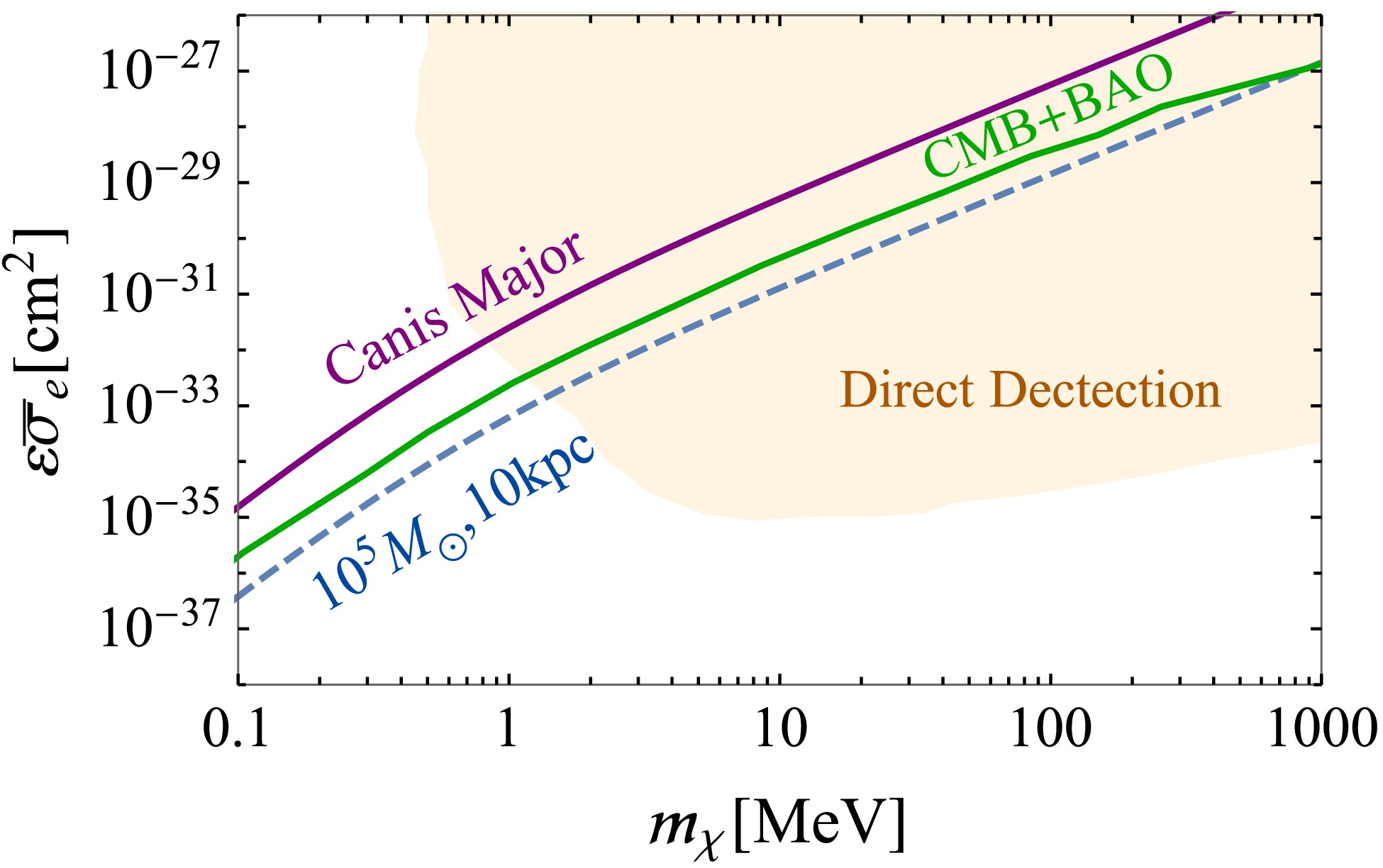

Figure 2.  (color online) Evaporation limit in terms of the electron-scattering direct-detection cross-section $\bar{\sigma}_e$ (dashed blue), which corresponds to subhalos with a $10^{5} \;M_\odot$ mass and a 10 kpc orbital distance to the galactic center. The solid purple line represents the evaporation limits of the Canis Major substructure. The combined direct-detection exclusion bounds obtained via DM-electron scattering experiments are shown by the orange shaped region. The bounds from datasets of CMB+BAO (solid green) are also shown for comparison.

In this study, we investigated the evaporation of subhalos by Coulomb-like interaction between DM and ionized gas in the inner galactic region. The typical feature of Coulomb-like scattering is that the momentum transfer cross section scales with relative particle velocity as $ v^{-4} $, which makes the collisional evaporation on DM subhalos very efficient at low velocity. Because the diffuse gas in our galaxy is mostly ionized and is concentrated near the galactic disk, subhalos in such a region may experience frequent soft collisions by Coulomb-like interaction, and their survival can be significantly affected by the evaporation effect.

Previous studies on the DM-baryon Coulomb-like interaction have mostly focused on the effects on CMB and structure formation. Soft collision with the fully ionized galactic gases can realize prominent evaporation effects on subhalos. In this study, we investigated the evaporation of subhalos in such a scenario for the first time. We calculated the evaporation rate of subhalos in the inner galaxy, and our results indicate that, when satisfying the existing CMB+BAO constraints for DM masses below the GeV scale, galactic ionized particles are capable of evaporating subhalos with masses below $ 10^{7.5} \;M_\odot $ over a $ 10^{10} $ year time span at a 1 kpc distance from the center of the Milky Way. At a larger 10 kpc orbit, such an effect can evaporate subhalos with masses below $ 10^5 \;M_\odot $, which is near the end of the galaxy’s visible DM structure profile. Evaporation by DM-gas collision is a non-negligible factor for the evolution of DM subhalos, which can potentially affect subhalo distribution around the galactic center. In comparison with the electronic-recoil direct detection constraints, the evaporation effects can readily extend to the sub-MeV range, which is unconstrained in direct detection experiments.

Low mass subhalos are also subject to tidal disruptions. However, the cuspy central regions of subhalos can still remain relatively intact [74, 75]. Recently, Bosch et al. [76, 77] used high resolution N-body simulations to conclude that the complete physical disruption of subhalos is rare, and tidal heating is not effective in the central regions of subhalos. In our study, the subhalo evaporation via Coulomb-like scattering can be an additional contribution for the disruption of subhalos. Considering that our Milky Way is far from being an active galaxy, the evaporation effects would be further enhanced in galaxies that are more active and have a higher amount of fully ionized gas than our Milky Way. Detecting these low mass subhalos may be a challenge due to the extremely low luminosity. In the future, programs like the Legacy Survey of Space and Time (LSST) conducted at the Vera C. Rubin Observatory [78] may uncover these extreme galaxies, which would support the evaporation scenario.