Towards a detection of reactor ${\overline {\boldsymbol v}_{\boldsymbol e} \bf\to \overline {\boldsymbol v}_{\boldsymbol\mu} }$ and ${\overline {\boldsymbol v}_{\boldsymbol e} \bf\to \overline {\boldsymbol v}_{\boldsymbol\tau} }$ oscillations with possible CP violation

The reactor-based neutrino experiments have played a crucial role in the developments of nuclear and particle physics [1, 2], such as the discovery of the electron antineutrino $ \overline{\nu}^{}_e $ [3], the discoveries of long- and short-baseline $ \overline{\nu}^{}_e \to \overline{\nu}^{}_e $ oscillations [4, 5], and the first measurement of the smallest lepton flavor mixing angles $ \theta^{}_{13} $ [5, 6]. The new flagship reactor neutrino oscillation experiment JUNO [7, 8], a medium-baseline facility which has just started data taking, aims to resolve another fundamental issue in particle physics and cosmology — the mass ordering of three active neutrinos.

It is well known that the flavor oscillations of reactor antineutrinos belong to the disappearance category, in the sense that the $ \overline{\nu}^{}_e $ events observed at the far detector are somewhat fewer than those recorded at the near detector. Although $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\tau $ oscillations do take place in a reactor experiment, they cannot be directly detected via the corresponding weak charged-current interactions associated with $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ [9]. The reason is simply that the reactor antineutrino beam energy is too low to produce the $ \mu^+ $ or $ \tau^+ $ events via the $ \overline{\nu}^{}_\mu + p \to \mu^+ + n $ or $ \overline{\nu}^{}_\tau + p \to \tau^+ + n $ processes in the detector. A burning question is therefore whether there exists a way out of this impasse in the coming precision measurement era.

The answer to this important question will be affirmative, if a dedicated measurement of the appearance of $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events can be done by means of their weak neutral-current interactions with the target material. In this note we are going to propose a novel method to detect the reactor $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\tau $ oscillations with the help of elastic antineutrino-electron scattering processes $ \overline{\nu}^{}_\alpha + e^- \to \overline{\nu}^{}_\alpha + e^- $ (for $ \alpha = e, \mu, \tau $), among which the $ \overline{\nu}^{}_e $ events can be singled out by detecting the $ \overline{\nu}^{}_e $ flux via the inverse beta decay $ \overline{\nu}^{}_e + p \to e^+ + n $ to a sufficiently high degree of accuracy. We find that such precision measurements will help open a new window for experimental neutrino physics at least in the following three aspects:

1. to directly confirm the appearance of $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events originating from the initial $ \overline{\nu}^{}_e $ events of a nuclear reactor via flavor oscillations, and thus to test the conservation of probability for reactor antineutrino oscillations by combining it with the $ \overline{\nu}^{}_e \to \overline{\nu}^{}_e $ disappearance.

2. to probe a fine difference between $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\tau $ oscillations, which is sensitive to both the μ-τ interchange symmetry and the leptonic CP violation, by precisely measuring the cross sections of elastic $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering reactions at the one-loop level.

3. to search for possible new physics either beyond the standard weak interactions or beyond the standard three-flavor oscillation scheme, or both of them.

We expect that the experimental and theoretical studies of this kind will find more applications at the low-energy luminosity or intensity frontiers of particle physics.

The present work is intended to provide a proof-of-concept investigation of points 1 and 2 listed above, with a very preliminary numerical illustration by taking the JUNO experiment for example. In particular, we highlight the novel possibility of probing or constraining the leptonic CP-violating phase from a precision measurement of the reactor $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\tau $ oscillations.

Let us focus on the standard three-flavor oscillation scheme, in which the $ 3\times 3 $ unitary Pontecorvo-Maki-Nakagawa-Sakata (PMNS) neutrino mixing matrix U [10, 11] can be parameterized as ¹

where $ c^{}_{ij} \equiv \cos \theta^{}_{ij} $, $ s^{}_{ij} \equiv \sin \theta^{}_{ij} $ and $ \hat{s}^{}_{13} \equiv s^{}_{13} e^{{\rm i}\delta} $ with $ \theta^{}_{ij} $ (for $ ij = 12, 13, 23 $) being the flavor mixing angles and δ being the nontrivial phase responsible for leptonic CP violation in neutrino oscillations. The probabilities of reactor $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\alpha $ oscillations in vacuum are given by

where $ F^{}_{ji} \equiv \left(m^2_j - m^2_i\right) L/(4E) $ with $ m^{}_{i,j} $ being the neutrino masses are defined (for $ i, j = 1, 2, 3 $), E represents the average antineutrino beam energy, L denotes the baseline length, $ \epsilon^{}_{e \alpha\beta} $ stands for the three-dimensional Levi-Civita symbol (for $ \alpha, \beta = e, \mu, \tau $), and

is the unqiue Jarlskog invariant of CP violation for the PMNS lepton flavor mixing matrix [13, 14].

It is obvious that the disappearance oscillation channel $ \overline{\nu}^{}_e \to \overline{\nu}^{}_e $ is CP-conserving, while the appearance oscillation channels $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\tau $ contain the CP-violating terms of the same magnitude but the opposite signs. That is why we find it useful to redefine

where $ D^{}_{ij} \equiv 4 {\rm Re}\left[ U^{}_{ei} U^*_{ej} \left( U^*_{\tau i} U^{}_{\tau j} - U^*_{\mu i} U^{}_{\mu j} \right) \right] $ characterize the effects of μ-τ interchange symmetry breaking for the PMNS matrix U. To be explicit, we obtain

which will vanish in the limit of the μ-τ permutation symmetry (i.e., $ \theta^{}_{23} = \pi/4 $ and $ \theta^{}_{13} = 0 $) or the μ-τ reflection symmetry (i.e., $ \theta^{}_{23} = \pi/4 $ and $ \delta = \pm \pi/2 $) [15]. Given the facts that the best-fit value of $ \theta^{}_{23} $ is really not far away from $ \pi/4 $ and the maximum value of $ |{\cal J}| $ is about 3% in a global analysis of current neutrino oscillation data [16, 17], we conclude that the magnitudes of $ D^{}_{ij} $ and $ {\cal J} $ are both suppressed, leading to an unfortunate suppression of $ P^{}_- $ as compared with $ P^{}_+ $.

Note that the reactor $ \overline{\nu}^{}_e \to \overline{\nu}^{}_e $ oscillations have been firmly established by measuring the survival $ \overline{\nu}^{}_e $ events at the far detector with the help of the weak charged-current $ \overline{\nu}^{}_e + p \to e^+ + n $ reactions. The first purpose of this work is to propose a careful precision measurement of $ P^{}_+ $ by use of elastic $ \overline{\nu}^{}_\alpha + e^- \to \overline{\nu}^{}_\alpha + e^- $ scattering (for $ \alpha = \mu, \tau $) via the weak neutral-current interactions in a reactor-based experiment like the JUNO, such that one may effectively test the consistency of the standard three-flavor neutrino oscillation framework by examining the conservation of probability associated with these pure quantum processes [i.e., $ P^{}_+ + P(\overline{\nu}^{}_e \to \overline{\nu}^{}_e) = 1 $ should hold].

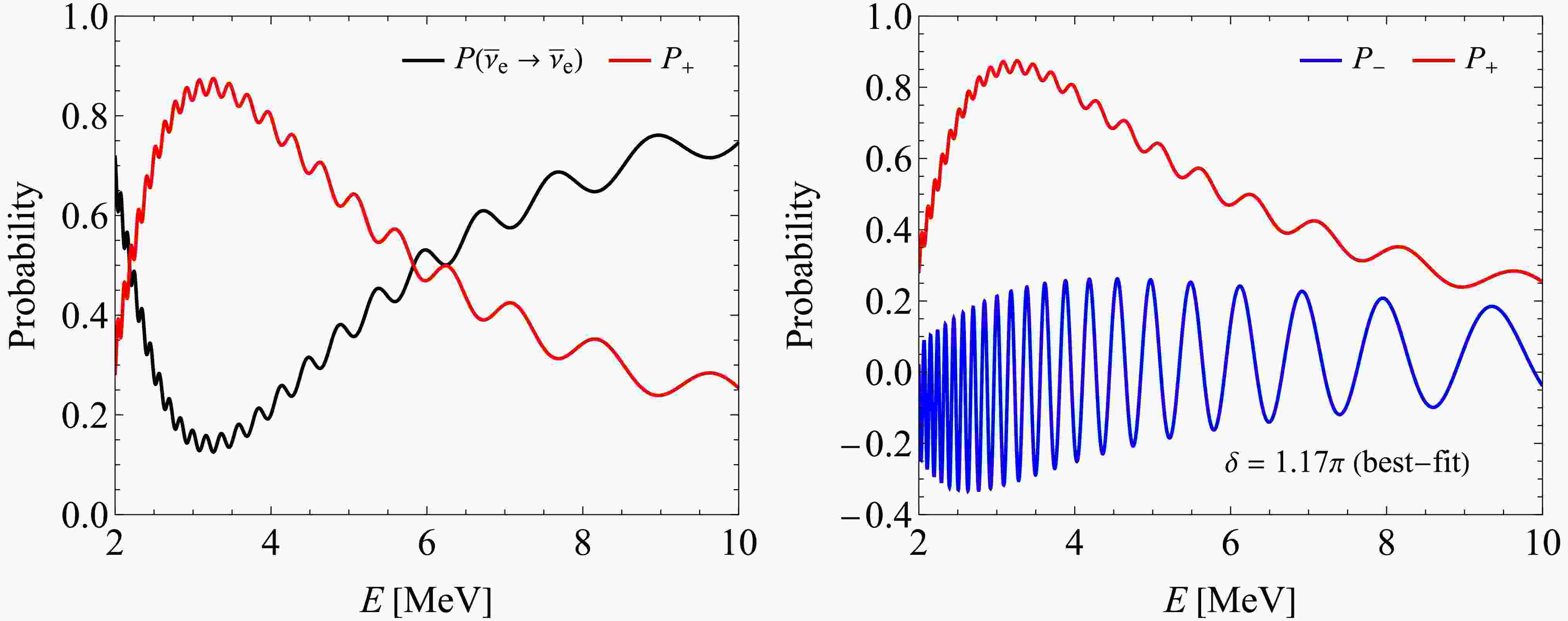
For the sake of illustration, we show the probabilities $ P^{}_+ $ and $ P(\overline{\nu}^{}_e \to \overline{\nu}^{}_e) $ changing with the reactor antineutrino beam energy E in the left panel of Fig. 1, where $ L = 53\; {\rm km} $ has been taken as a typical baseline length. In addition, the best-fit values of the oscillation parameters $ \sin^2 \theta^{}_{12} = 0.308 $, $ \sin^2 \theta^{}_{13} = 0.02215 $, $ \sin^2\theta^{}_{23} = 0.470 $ and $ \delta = 1.17\pi $, together with $ m^2_2 - m^2_1 = 7.49\times 10^{-5}\; {\rm eV}^2 $ and $ m^2_3 - m^2_1 = 2.513\times 10^{-3}\; {\rm eV}^2 $ (normal mass ordering) are taken from Ref. [16], where a perfect agreement with the results from an independent global-fit analysis of neutrino oscillation data in Ref. [17] can be found. From Fig. 1, it is clear that a significant fraction of the $ \overline{\nu}^{}_e $ events oscillate into the $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events, especially in the energy range $ E \in [2, 6]\; {\rm MeV} $. One may therefore expect that the antineutrinos of all three flavors are detectable in a liquid-scintillator detector.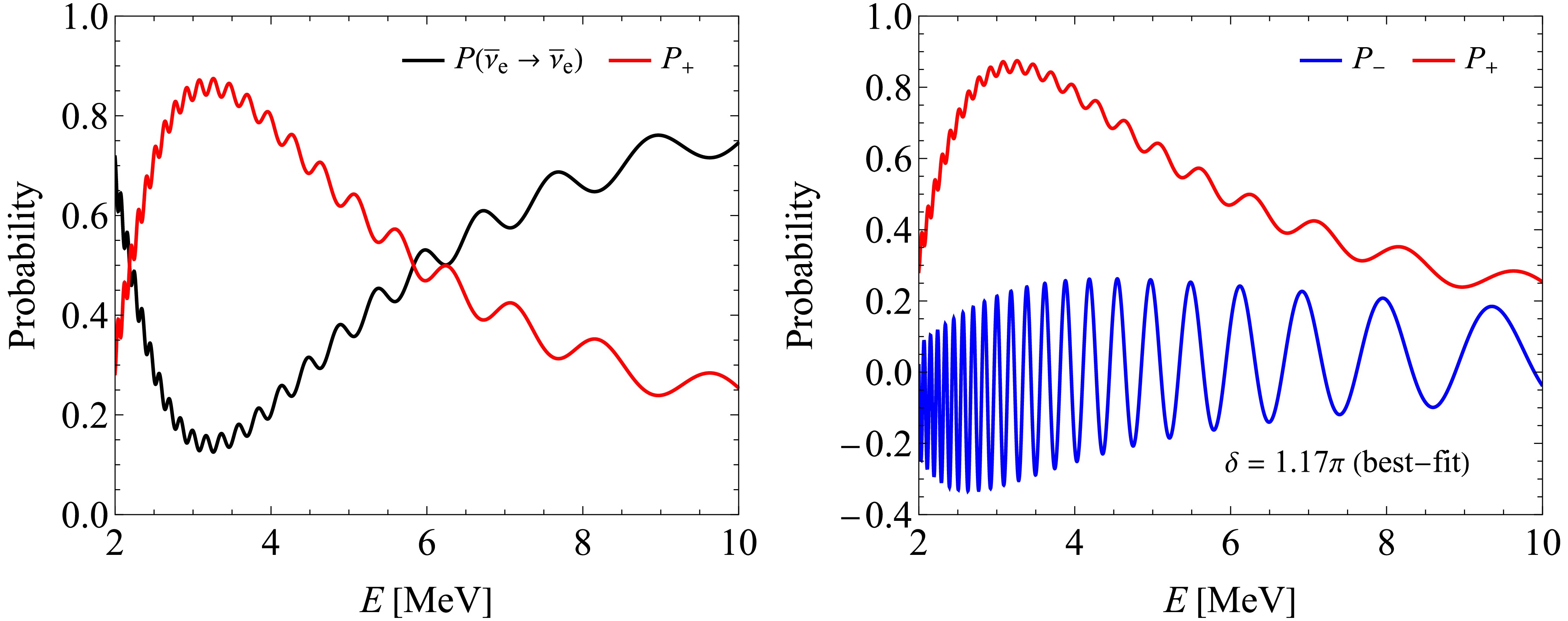

Figure 1.  (color online) The sum of the appearance oscillation probabilities $ P^{}_+ \equiv P(\overline{\nu}^{}_e \to \overline{\nu}^{}_\mu) + P(\overline{\nu}^{}_e \to \overline{\nu}^{}_\tau) $ versus the survival probability $ P(\overline{\nu}^{}_e \to \overline{\nu}^{}_e) $ changing with the beam energy E is shown in the left panel, while $ P^{}_+ $ and $ P^{}_- \equiv P(\overline{\nu}^{}_e \to \overline{\nu}^{}_\mu) - P(\overline{\nu}^{}_e \to \overline{\nu}^{}_\tau) $ in the right panel. The best-fit values of the relevant oscillation parameters $ \sin^2 \theta^{}_{12} = 0.308 $, $ \sin^2 \theta^{}_{13} = 0.02215 $, $ \sin^2\theta^{}_{23} = 0.470 $ and $ \delta = 1.17\pi $, together with $ m^2_2 - m^2_1 = 7.49\times 10^{-5}\; {\rm eV}^2 $ and $ m^2_3 - m^2_1 = 2.513\times 10^{-3}\; {\rm eV}^2 $ (normal mass ordering) have been input [16, 17], and the baseline length is set to $ L = 53\; {\rm km} $.

In comparison, it is certainly more ambitious and thus more challenging to detect $ P^{}_- $ by means of the same techniques, so as to probe or constrain the highly nontrivial effects of leptonic CP violation and μ-τ interchange symmetry breaking. The right panel of Fig. 1 illustrates how small $ P^{}_- $ is expected to be with respect to $ P^{}_+ $. A delicate measurement of the cross sections of elastic $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering at the one-loop level of accuracy is mandatory, in order to distinguish between the $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events that originate from the reactor $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\tau $ oscillations.

In view of the fact that the behaviors of reactor antineutrino oscillations in a medium-baseline experiment are essentially insensitive to terrestrial matter effects ², we shall not take into account such insignificant corrections in the following proof-of-concept analysis.

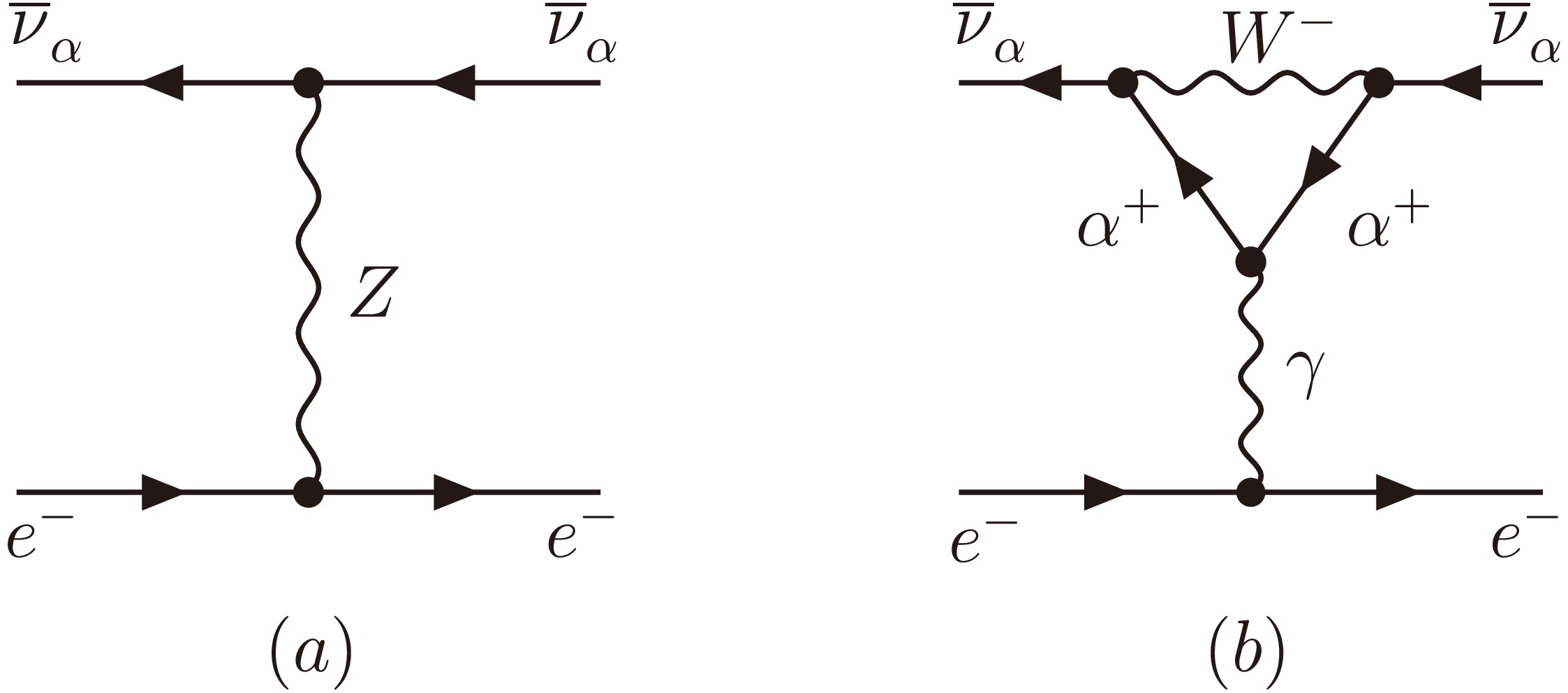
The elastic scattering of $ \overline{\nu}^{}_\mu $ or $ \overline{\nu}^{}_\tau $ with an electron takes place via the standard weak neutral-current interactions as typically illustrated in Fig. 2, whereas that of $ \overline{\nu}^{}_e $ with an electron occurs through both neutral- and charged-current interactions. After all the one-loop radiative corrections have been taken into account [22−25], the differential cross sections of elastic $ \overline{\nu}^{}_e $-$ e^- $, $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering reactions are found to be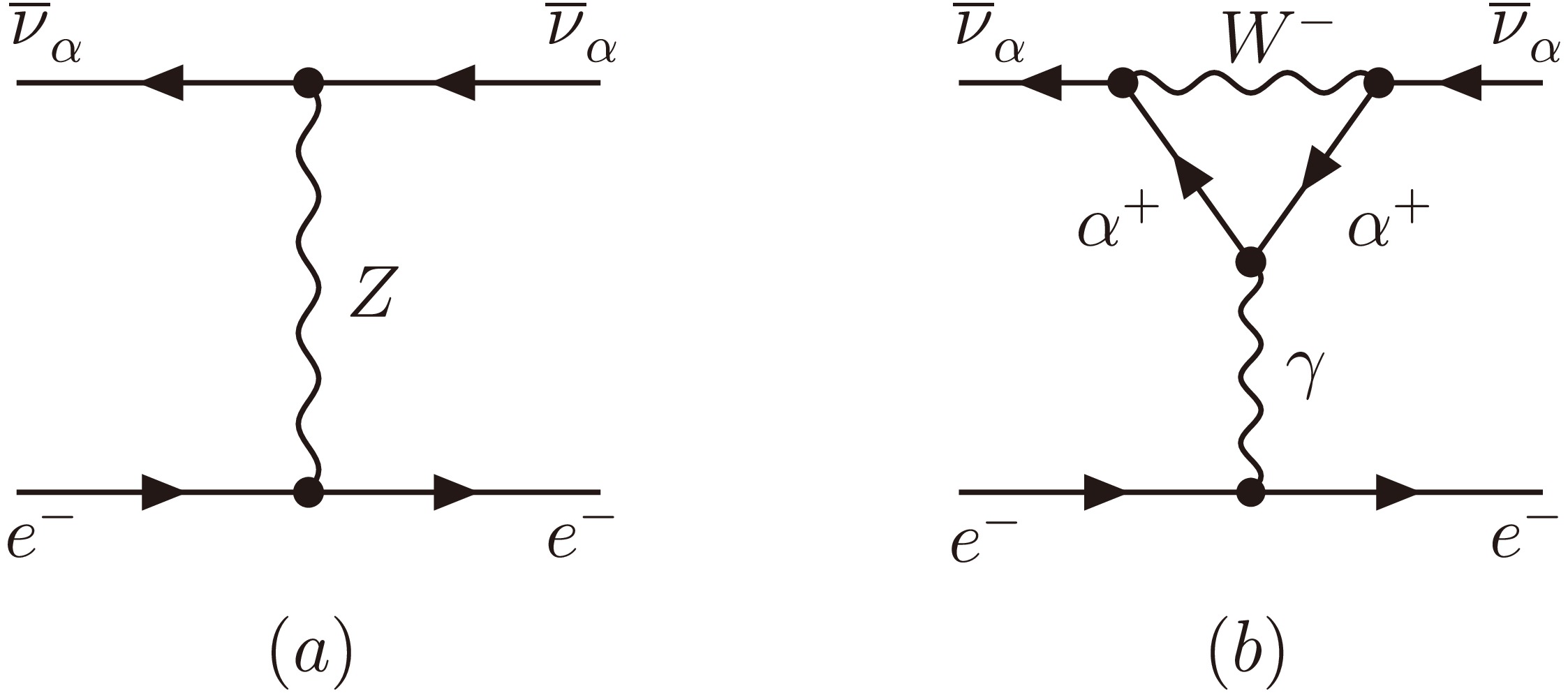

Figure 2.  The Feynman diagrams of elastic $ \overline{\nu}^{}_\alpha $-$ e^- $ scattering (for $ \alpha = \mu, \tau $) via weak neutral-current interactions: (a) the tree-level contribution; (b) the dominant one-loop contribution, where only one typical diagram is shown for illustration. It is the difference between the charged-lepton masses $ m^{}_\mu $ and $ m^{}_\tau $ that makes the $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering cross sections distinguishable. Note that a full set of the one-loop Feynman diagrams will be taken into account in our analytical and numerical calculations of the $ \overline{\nu}^{}_\alpha $-$ e^- $ scattering processes.

where $ T^{}_e \equiv E^{}_e - m^{}_e $ stands for the recoil energy of the final-state electron, $ G^{}_\mu $ is the Fermi coupling constant determined from a precision measurement of the muon lifetime, $ m^{}_e $ denotes the electron mass, E represents the initial neutrino energy, and $ s^{}_{\rm W} \equiv \sin\theta^{}_{\rm W} $ with $ \theta^{}_{\rm W} $ being the Weinberg angle. Moreover, the overall factor ρ in Eq. (6) is given by

where $ \alpha^{}_{\rm em} $ denotes the electromagnetic fine-structure constant, $ m^{}_h $, $ m^{}_W $ and $ m^{}_Z $ stand respectively for the Higgs-, W- and Z-boson masses, $ m^{}_f $ represents the charged-fermion mass, $ m^{}_\alpha $ refers to the charged-lepton mass, $ m^{}_q $ and $ m^{}_{q^\prime} $ are the respective up- and down-type quark masses, $ c^{}_{\rm W} \equiv \cos\theta^{}_{\rm W} $, $ V^{}_{q q^\prime} $ denote the elements of the Cabibbo-Kobayashi-Maskawa (CKM) quark flavor mixing matrix (for $ q = u, c, t $ and $ q^\prime = d, s, b $), the coefficient $ c^{}_Z $ and the function $ G(c^2_{\rm W} , x) $ are defined as

and the summation over q and $ q^\prime $ quarks in Eq. (7) should include their color factor "3". On the other hand, the flavor-dependent functions $ \kappa^{}_\alpha $ (for $ \alpha = e, \mu, \tau $) are expressed as

where $ q^2 = -2m^{}_e T^{}_e $ is the square of momentum transfer, and

In Eq. (9) the ultra-violet divergence term and the μ-dependence term stemming from dimensional regularization (with μ being the 't Hooft mass scale, $ d \equiv 4 - 2\epsilon $ being the spacetime dimension and $ \gamma^{}_{\rm E} \simeq 0.577 $ being the Euler-Mascheroni constant) will cancel the divergence terms associated with the one-loop self-energy functions of the gauge bosons $ \Sigma_{AZ}^{} (q^2) $, $ \Sigma_{W}^{} (m_W^2) $ and $ \Sigma_{Z}^{} (m_Z^2) $ [22].

It is obvious that switching off the one-loop radiative corrections is equivalent to taking $ \rho = 1 $ and $ \kappa^{}_e = \kappa^{}_\mu = \kappa^{}_\tau = 1 $, from which the tree-level equality $ \sigma^{}_\mu = \sigma^{}_\tau $ is simply obtained. Note that $ R^{}_\mu(q^2) $ and $ R^{}_\tau(q^2) $ arise respectively from the one-loop $ \overline{\nu}^{}_\mu $-$ \overline{\nu}^{}_\mu $-γ and $ \overline{\nu}^{}_\tau $-$ \overline{\nu}^{}_\tau $-γ vertices as typically illustrated by Fig. 2 (b), and their discrepancy is attributed to the difference between $ m^2_\mu $ and $ m^2_\tau $ as can be easily seen from Eq. (10). If the resulting discrepancy between elastic $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering cross sections is observed from a reactor antineutrino oscillation experiment, it will allows us to probe or constrain the fine effects of leptonic CP violation and μ-τ interchange symmetry breaking as described by $ P^{}_- $ in Eq. (4).

Let us proceed to calculate the rates of $ \overline{\nu}^{}_e $, $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events at the far detector. The initial reactor electron antineutrinos are produced from the nuclear beta decays, and the fluxes of $ \overline{\nu}^{}_\alpha $ events originating from $ \overline{\nu}^{}_e \to \overline{\nu}^{}_\alpha $ oscillations (for $ \alpha = e, \mu, \tau $) with a baseline length L are given as

where $ {\rm d}N^\prime_e/{\rm d}E $ is the rate for the initial $ \overline{\nu}^{}_e $ events. In the far detector, the event rates of elastic $ \overline{\nu}^{}_\alpha + e^- \to \overline{\nu}^{}_\alpha + e^- $ scattering turn out to be

where $ N^{}_{\rm T} $ is the total number of the target electrons in the far detector, T denotes the operation duration, $ T^\prime_e $ represents the observed energy in the detector corresponding to the electron recoil energy $ T^{}_e $ and the energy resolution $ \delta T^{}_e $ with a Gaussian distribution, the differential cross sections $ {\rm d}\sigma^{}_\alpha/{\rm d}T^{}_e $ and the fluxes $ \phi^{}_\alpha $ have been given in Eqs. (6) and (11) respectively.

To see the flavor effects in a clear way, we rewrite the integrand of the second integral in Eq. (12) and sum over the flavor index α. Then we are left with

where the expressions of $ P^{}_\pm $ have been given in Eq. (4). Since the $ \overline{\nu}^{}_e $ contribution can be subtracted from the total elastic scattering events by accurately measuring the $ \overline{\nu}^{}_e $ flux via the inverse beta decay $ \overline{\nu}^{}_e + p \to e^+ + n $, we are therefore able to observe the appearance of $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events as a whole. In other words, it is relatively easy to extract $ P^{}_+ $ from such a precision measurement, and extracting the information on $ P^{}_- $ will be very challenging. But the latter is highly nontrivial and deserves to be carefully studied, simply because it may open a new window to probe or constrain leptonic CP violation in the reactor-based experiments.

To illustrate, let us specify the nominal setup for a reactor antineutrino experiment by taking the JUNO detector for example, and calculate the elastic $ \overline{\nu}^{}_\alpha $-$ e^- $ scattering event rates (for $ \alpha = e, \mu, \tau $). Given the total thermal power $ P^{}_{\rm th} $ of the chosen nuclear reactors, the production rate of the reactor electron antineutrinos can be calculated by use of

where the subscript "i" refers to the radioactive isotopes $ {^{235}{\rm U}} $, $ {^{238}{\rm U}} $, $ {^{239}{\rm Pu}} $ and $ {^{241}{\rm Pu}} $, $ f^{}_i $ stands for the average fraction of each isotope, and $ \epsilon^{}_i $ denotes the thermal energy released per fission. The energy spectrum $ S^{}_i(E) $ of $ \overline{\nu}^{}_e $ from the beta decays of fission products is obtained with the help of a fifth-power fitting formula [26]. We assume $ P^{}_{\rm th} = 26.6\; {\rm GW} $, $ f^{}_i = \{0.561, 0.076, 0.307, 0.056\} $ and $ \epsilon^{}_i = \{202.36,205.99,211.12,214.26\}\; {\rm MeV} $ as the typical inputs in our numerical calculation ³, and use the values of $ \alpha^{}_{ij} $ from Ref. [26]. Then the elastic scattering event rates at the far detector can be calculated by convolving the antineutrino fluxes and the differential cross sections, given the total number of target electrons $ N^{}_{\rm T} \simeq 6.72\times 10^{33} $ corresponding to the 12% mass fraction of hydrogen and 88% of carbon in the 20 kiloton liquid scintillator. We show the final numerical results in Fig. 3. Some comments are in order.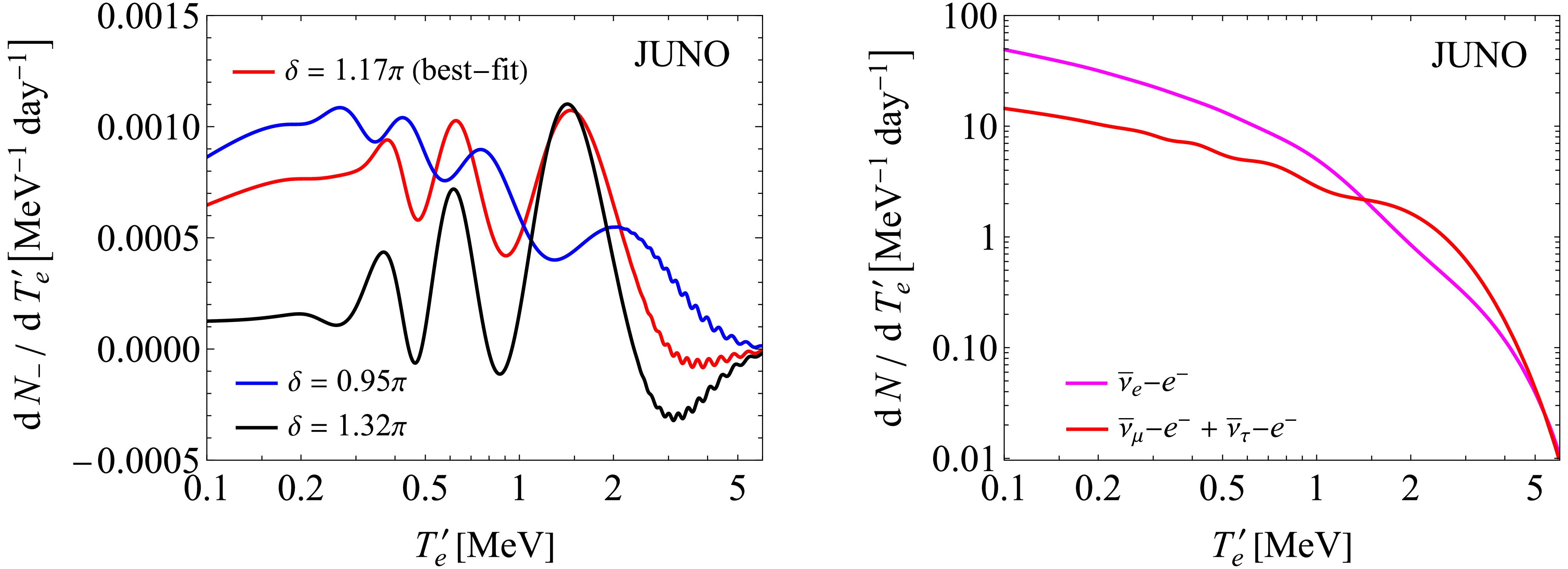

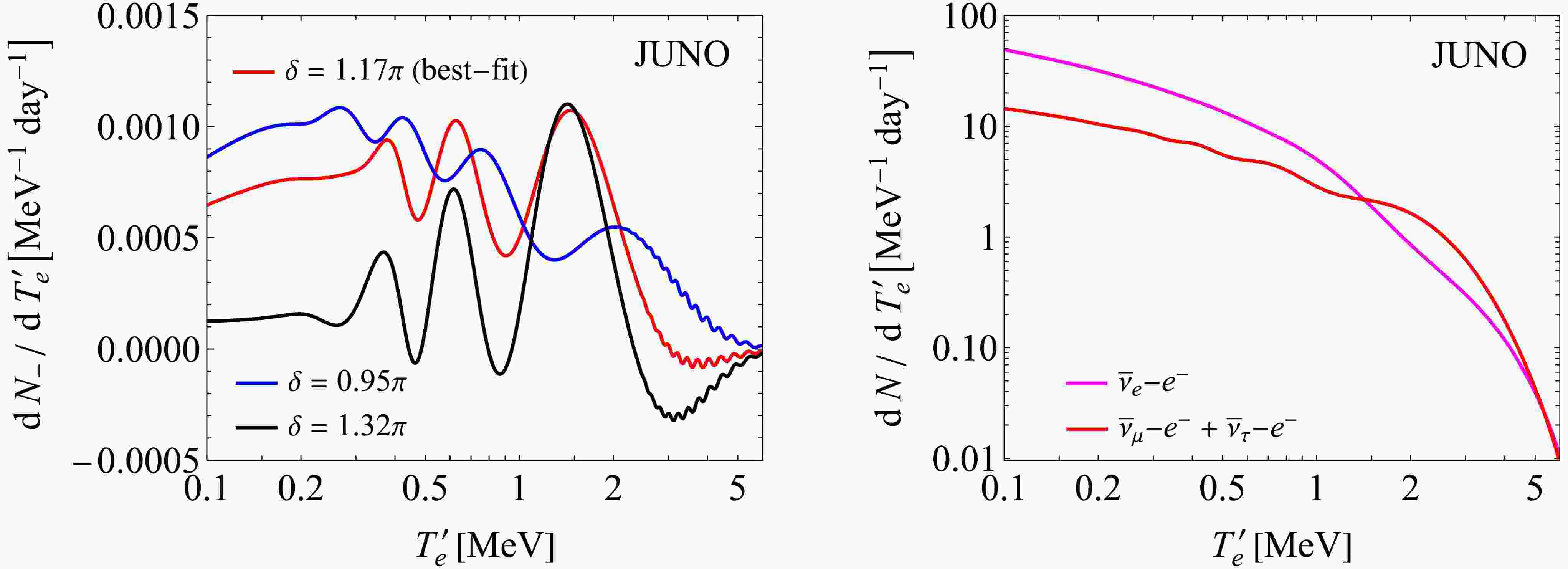
Figure 3.  (color online) In the left panel, the δ-dependent contribution $ P^{}_- \left( {\rm d}\sigma^{}_\mu/{\rm d}T^{}_e - {\rm d}\sigma^{}_\tau/{\rm d}T^{}_e\right)/2 $ to the event rate is denoted as $ {\rm d}N^{}_-/{\rm d}T^\prime_e $, and its numerical result is illustrated by inputting the best-fit value $ \delta = 1.17\pi $ and its $ 1\sigma $ lower (upper) bound $ \delta = 0.95\pi $ ($ 1.32\pi $). In the right panel, the event rate $ {\rm d}N^{}_e/{\rm d}T^\prime_e $ for $ \overline{\nu}^{}_e $-$ e^- $ scattering and the sum $ {\rm d}N^{}_\mu/{\rm d}T^\prime_e + {\rm d}N^{}_\tau/{\rm d}T^\prime_e $ of the event rates for $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering are presented. Here the JUNO detector with 20 kiloton liquid scintillator and an effective energy resolution $ \delta T^{}_e/T^{}_e = 3\%/\sqrt{T^{}_e/{\rm MeV}} $ have been taken into consideration.

• In the left panel, the contribution to the event rate in Eq. (12) from the last term on the right-hand side of Eq. (13) has been illustrated, where the dependence on the CP-violating phase δ is evident. For simplicity, we take the best-fit value $ \delta = 1.17\pi $ and its $ 1\sigma $ lower (upper) bound $ \delta = 0.95\pi $ ($ 1.32\pi $) from Ref. [16]. Note that this best-fit result agrees perfectly with $ \delta = 1.20\pi $ obtained from Ref. [17] in the case of normal neutrino mass ordering. Although $ {\rm d}N^{}_-/{\rm d}T^\prime_e $ is very sensitive to the values of δ, the variation of the event rates at the JUNO turns out to be $ 0.001\; {\rm MeV}^{-1} {\rm day}^{-1} $ at most. As indicated in Eq. (13), the suppression arises mainly from the difference between the one-loop cross sections for $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering. The ratio of such a difference to the tree-level cross section is about 1%, while the oscillation probability difference $ P^{}_- $ contributes some extra suppression. An experimental determination of the event rate at the level of $ 0.001\; {\rm MeV}^{-1} {\rm day}^{-1} $ is no doubt a big challenge.

• In the right panel, the sum $ {\rm d}N^{}_\mu/{\rm d}T^\prime_e + {\rm d}N^{}_\tau/{\rm d}T^\prime_e $ over the event rates for $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering is presented together with $ {\rm d}N^{}_e/{\rm d}T^\prime_e $ for $ \overline{\nu}^{}_e $-$ e^- $ scattering. Below $ T^\prime_e \approx 1.5\; {\rm MeV} $, the $ \overline{\nu}^{}_e $ event rate is always dominant. However, for $ T^\prime_e > 1.5\; {\rm MeV} $, we have more $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events. This observation can be easily understood as follows. The oscillation probability $ P^{}_+ $ is larger than $ P(\overline{\nu}^{}_e \to \overline{\nu}^{}_e) $ for the antineutrino beam energy $ E \in [2, 6]\; {\rm MeV} $, indicating that more $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events than $ \overline{\nu}^{}_e $ arrive in the far detector. As mentioned before, the $ \overline{\nu}^{}_e $ flux will be precisely measured through the inverse beta decay such that its contribution to the elastic scattering events can be reliably subtracted. For the visible energy $ T^\prime_e \in [0.1, 4]\; {\rm MeV} $, the appearance of $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ at the JUNO could be optimistically demonstrated by observing the elastic scattering events at the rate of $ (1\cdots 10)\; {\rm MeV}^{-1}\; {\rm day}^{-1} $.

Within the energy region $ T^\prime_e \in [0.1, 4]\; {\rm MeV} $, a number of backgrounds for observing the recoiled electrons should be taken into account, including the internal background due to the radioactivity of contaminants in the scintillator, the external backgrounds from the γ radioactivity of surrounding materials and beta decays of cosmogenic isotopes from the spallation of cosmic muons. According to the background analysis for the detection of solar neutrinos at the JUNO [27], in an ideal radiopurity scenario, the largest internal background comes from the $ ^{210}{\rm Pb} $ chain and the $ ^{238}{\rm U} $ chain with a total rate about $ 419 $ counts per kiloton per day in the range $ T^\prime_e \in [0.45, 1.6]\; {\rm MeV} $. The external γ background can be eliminated by only retaining the events within the spherical fiducial volume of a radius about $ 15 $ meters. The cosmogenic background is dominated by the beta decays of $ ^{11}{\rm C} $ at a rate of about $ 1761 $ counts per kiloton per day. In addition, the solar neutrinos themselves serve as an irreducible background, where the dominant contribution of $ 500 $ counts per kiloton per day is made by $ ^{7}{\rm Be} $ neutrinos. Obviously, the background rate is much larger than the signal rate associated with the flavor oscillations of reactor antineutrinos. One possible way out is to implement the directional information on the recoiled electrons such that the antineutrinos coming from the direction opposite to the nuclear reactors can be distinguished from the others.

Furthermore, the dependence on the leptonic CP-violating phase δ at the per-mille level will be relevant if the statistical uncertainty in the total number of $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering events reaches the same level, i.e., with $ 10^6 $ events. This can be realized by increasing the thermal power of reactors, optimizing the baseline in order to enhance the CP-violating effect and the antineutrino fluxes, and even constructing a much larger far detector.

We have carried out a proof-of-concept study of the possibility to observe the appearance of $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events in the far detector of a reactor antineutrino oscillation experiment. Taking the JUNO experiment for example, we have calculated the differential event rate for $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering and find that the total rate is about $ 9 $ counts per day for a 20 kiloton liquid-scintillator detector, while that for $ \overline{\nu}^{}_e $-$ e^- $ scattering is about $ 17 $ counts per day. However, the $ \overline{\nu}^{}_e $ events can be eliminated by precisely measuring the $ \overline{\nu}^{}_e $ flux through the inverse beta decay $ \overline{\nu}^{}_e + p \to e^+ + n $. We stress that it is important to experimentally verify the appearance of $ \overline{\nu}^{}_\mu $ and $ \overline{\nu}^{}_\tau $ events, so as to test the conservation of probability for reactor antineutrino oscillations.

When the one-loop correction to the cross sections for antineutrino-electron scattering is taken into account, the event rate becomes dependent on the leptonic CP-violating phase δ through the oscillation probability difference $ P^{}_- \equiv P(\overline{\nu}^{}_e \to \overline{\nu}^{}_\mu) - P(\overline{\nu}^{}_e \to \overline{\nu}^{}_\tau) $. Such dependence relies on both a nonzero $ P^{}_- $ and the difference in the cross sections of elastic $ \overline{\nu}^{}_\mu $-$ e^- $ and $ \overline{\nu}^{}_\tau $-$ e^- $ scattering, and hence it is highly suppressed. That is why we expect that an unprecedented precision measurement of elastic antineutrino-electron scattering events at the per-mille level is required to probe or constrain leptonic CP violation in the foreseeable future.

The authors are indebted to Jihong Huang for his kind technical helps and valuable discussions.