Lifetime measurement of high spin states in non-yrast bands in ¹⁷⁷Re

The neutron-deficient odd-Z nuclei with mass A ~ 175 provide an excellent opportunity to study the deformation-driving effects of various single-particle orbitals. In odd proton nucleus such as $ _{75}Re $, the proton Fermi level lie close to the low K, high-j $ \pi h_{9/2} $ (K = 1/2) and $ \pi i_{13/2} $ (K = 1/2) orbitals intruding from above the Z = 82 shell closure. The intruding orbitals are highly down-slopping as a function of deformation in the Nilsson diagram [1], so have a tendency to drive the nucleus to larger deformations for equilibrium shapes. In addition to these low-K, intruding orbitals, the high-K orbitals like $ h_{11/2} $ (K = 9/2) and $ d_{5/2} $ (K = 5/2) orbitals, also close to the Fermi surface. The high-K orbitals are upsloping as a function of deformation in the Nilsson diagram (i.e. have a positive slope), so have a tendency to drive the nucleus to smaller deformations. The deformation driving nature of this low-K, high-j $ \pi h_{9/2} $ intruder orbital was established in the lifetime measurement studies of $ ^{171,173}Ta $ and $ ^{177,179}Re $ nuclei, where indeed the deformation of the $ \pi h_{9/2}[541]1/2^- $ band was found to be ~ 20 % higher than the $ \pi d_{5/2}[402]5/2^+ $ orbital [2−5]. While a lot more has been investigated and said about the deformation driving capability of $ \pi h_{9/2} $ orbital, the studies about the deformation driving nature of low-K, high-j $ \pi i_{13/2} $ (K = 1/2) orbital is very rare in this mass region. It is primarily due to the fact that, though both the $ \pi h_{9/2} $ (K = 1/2) and the $ \pi i_{13/2} $ (K = 1/2) orbitals intrude from above the Z = 82 shell closure, the $ \pi i_{13/2} $ orbital lies at somewhat higher excitation from the Fermi level than the $ \pi h_{9/2} $ orbital, and therefore it is difficult to get populated in the nuclei of this mass region. The available data suggests that on the lower- Z side, $ ^{163}Lu $ is the lightest nucleus in which $ \pi i_{13/2} $ (K = 1/2) band has been identified. The results of the lifetime measurements done by Schmitz et al., [6] reveal that the deformation for this band is twice as large as that of normal deformed yrast band. On the higher Z- side, the $ ^{177}Re $ is the lightest nucleus where the $ \pi i_{13/2} $ (K = 1/2) band has been identified at high excitations in the experimental studies. In Rhenium isotopes (Z = 75), the $ \pi i_{13/2} $ (K = 1/2) orbital lies much closer to the Fermi surface than in case of Lutetium isotopes (Z = 71), but it is still expected to behave as a pure particle state and show its deformation driving capabilities. In $ ^{177}Re $ nucleus both $ \pi h_{9/2} $ (K = 1/2) and $ \pi i_{13/2} $ (K = 1/2) orbitals are present. However, looking at the experimental level scheme in Fig. 1 [7], it is clear that the $ \pi h_{9/2} $ (K = 1/2) band forms the yrast structure while the $ \pi i_{13/2} $ (K = 1/2) band is available at high excitations. So it is obvious that the $ \pi i_{13/2} $ state is farther than the $ \pi h_{9/2} $ orbital from the Fermi surface and therefore is expected to show more deformation driving tendency compared to $ \pi h_{9/2} $ orbital. In order to verify this, the measurement of quadrupole momemt is necessary in all the excited bands populated in $ ^{177} {\rm{Re}}$ nucleus with enough intensities. As the lifetime of excited nuclear states give direct information about the quadrupole deformation parameter in the given nucleus so the lifetime measurements have been done. Since in this mass region, the low spin excited states in populated bands have lifetime in the range of picosecond, so to measure such small lifetimes the recoil distance Doppler shift method (RDM) [8] has been considered for lifetime measurements. The RDM technique is based on Doppler's effect of light and is sensitive to measure the level lifetime of excited nuclear states having lifetimes in the range of picosecond to nanosecond.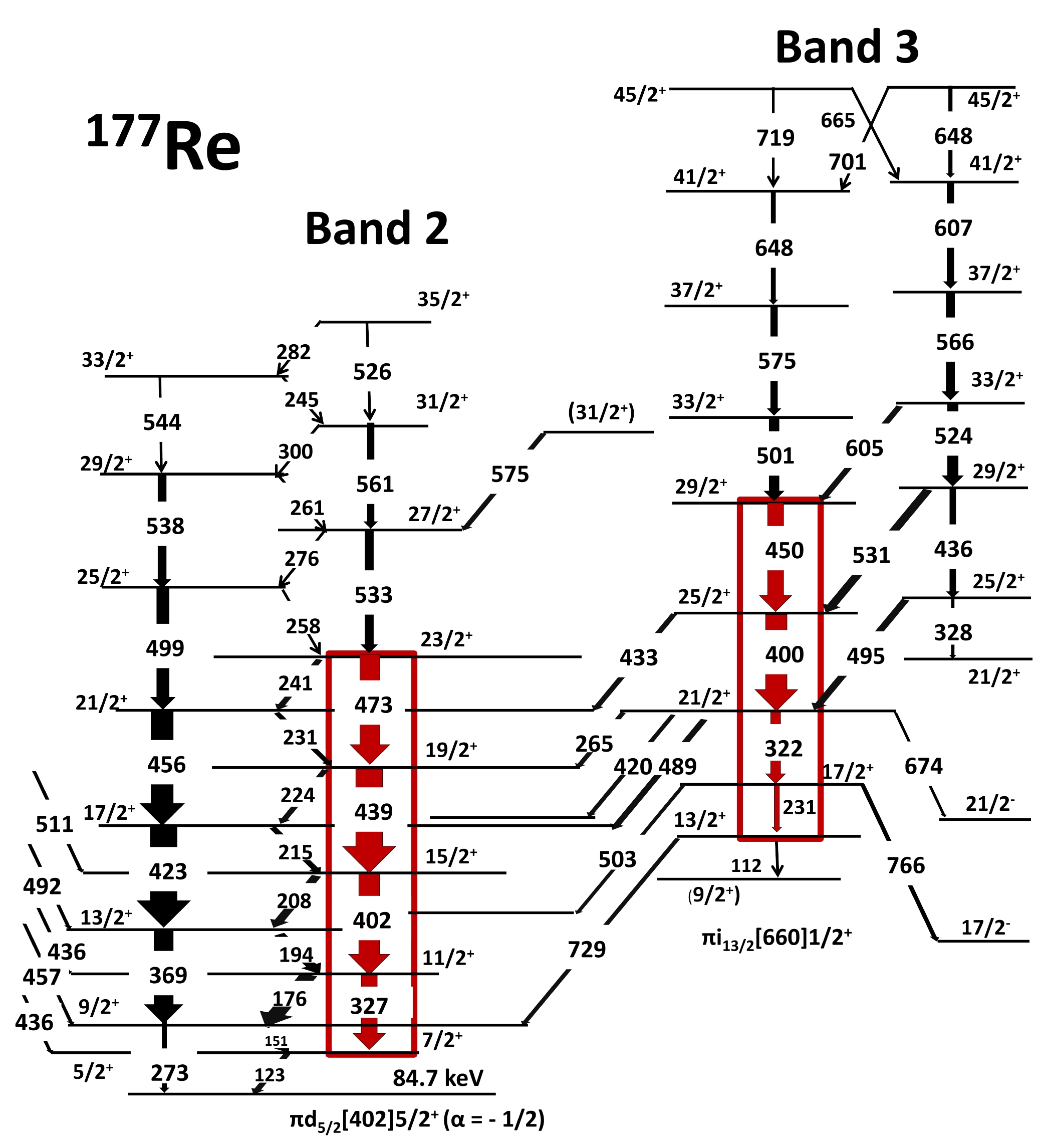

Figure 1.  (color online) Partial level scheme of ¹⁷⁷Re, relevant to this work showing the all eight γ-ray transitions of interest (marked with red color) in Band 2 ($ \pi d_{5/2}$, α = -1/2) and Band 3 ($ \pi i_{13/2}$) for which the lifetime measurement has been done in the present work. The complete level scheme appears in Ref [7].

The experiment was performed at the Inter-University Accelerator Centre (IUAC), New Delhi. For this purpose, the $ ^{177}Re $ nucleus was populated with $ ^{165} {\rm{Ho}}$ ($ ^{16} {\rm{O}}$, 4n)$ ^{177}Re $ reaction at 84 MeV of beam energy. In the experiment, a self-supporting foil of $ ^{165} {\rm{Ho}}$ (enrichment level 99.9%) of thickness ~ 780 μg/cm² was used as a target, and the stopper was made of highly pure natural Gold foil of thickness ~ 8 $ mg/cm^2 $. For the detection of gamma rays, the Gamma detector Array (GDA) setup [9, 10], consisting of 12 HPGe detectors and 14 elements BGO multiplicity filter was used. The HPGe detectors in the array were arranged in three different rings (4 detectors in each ring) at an angle of $ 50^{ \circ } $, $ 99^{ \circ } $, and $ 144^{ \circ } $ with respect to the beam direction. The 14 elements of BGO multiplicity filter were arranged in the array with 7 crystals up and 7 crystals down just above and below the target. The data was collected in the singles mode in coincidence with the BGO multiplicity condition M $ \geq 2 $ at 22 target-stopper distances (${\rm{D}} _{T-S} $), ranging from 10 – 10000 μm. The ‘singles mode’ means the event recorded in a single Ge detector of the GDA array under the condition that at least two gamma rays have been detected in the 14-element BGO crystals multiplicity array simultaneously. The BGO multiplicity gating helps to reduce the background contribution coming from the Coulomb excitation (low activity events), the radioactivity, and so on.The capacitance method [11] was used to measure small distances (less than ~ 50 $ \mu m $)) between the target and the stopper foils. The Capacitance method is useful at small distances when the target and the stopper foils in the RDM plunger set up behave like two plates of a parallel plate capacitor, so that the Capacitance between the target and the stopper foil assembly is inversely proportional to the distance between them. The minimum distance between the target and the stopper foils was obtained by the interpolation of fitting of the curve plotted between the inverse of capacitance (assuming the small gap between the target and stopper foil assembly as two plates of a parallel plate capacitor) as a function of increasing target stopper distance. The target-stopper distance was measured to the precession better than 1 $ \mu m $. This small variation in the measured distance was noticed due to the target heating of the beam. More details about the experimental setup, data acquisition, and method of data analysis can be found in [4].

In the experiment, the lowest gamma-ray transitions belonging to all populated bands like $ \pi h_{9/2} $[541]$ 1/2^- $ ($ \alpha= +1/2 $), $ \pi d_{5/2} $[402]$ 5/2^+ $ ($ \alpha= \pm 1/2 $), $ \pi h_{11/2} $[514]$ 9/2^- $ ($ \alpha= \pm 1/2 $), and $ \pi i_{13/2} $[660]$ 1/2^+ $ ($ \alpha= +1/2 $) have been detected. The results of lifetime analysis for $ \pi h_{9/2} $[541]$ 1/2^- $ ($ \alpha= +1/2 $), $ \pi d_{5/2} $[402]$ 5/2^+ $ ($ \alpha= + 1/2 $), and $ \pi h_{11/2} $[514]$ 9/2^- $ ($ \alpha= \pm 1/2 $) have already been reported previously (Ref.[4]). In the present manuscript we report the lifetimes results obtained for the four lowest gamma-ray transitions of $ \pi i_{13/2} $[660]$ 1/2^+ $ band, the 231 keV ($ 17/2^+ \rightarrow 13/2^+ $), the 322 keV ($ 21/2^+ \rightarrow 17/2^+ $), the 400 keV ($ 25/2^+ \rightarrow 21/2^+ $), and the 450 keV ($ 29/2^+ \rightarrow 25/2^+ $) and the four gamma-ray transitions in the $ \alpha = -1/2 $ signature partner of $ \pi d_{5/2} $[402]$ 5/2^+ $ band, the 327 keV ($ 11/2^+ \rightarrow 7/2^+ $), the 402 keV ($ 15/2^+ \rightarrow 11/2^+ $), the 439 keV ($ 19/2^+ \rightarrow 15/2^+ $), and 473 keV ($ 23/2^+ \rightarrow 19/2^+ $). For the sake of clarity the complete energy spectrum obtained with detectors at $ 144^{ \circ } $ (backward angle) for first target-stopper distance (${\rm{D}} _{T-S} $ = 8 μm) has been shown in in Fig. 2.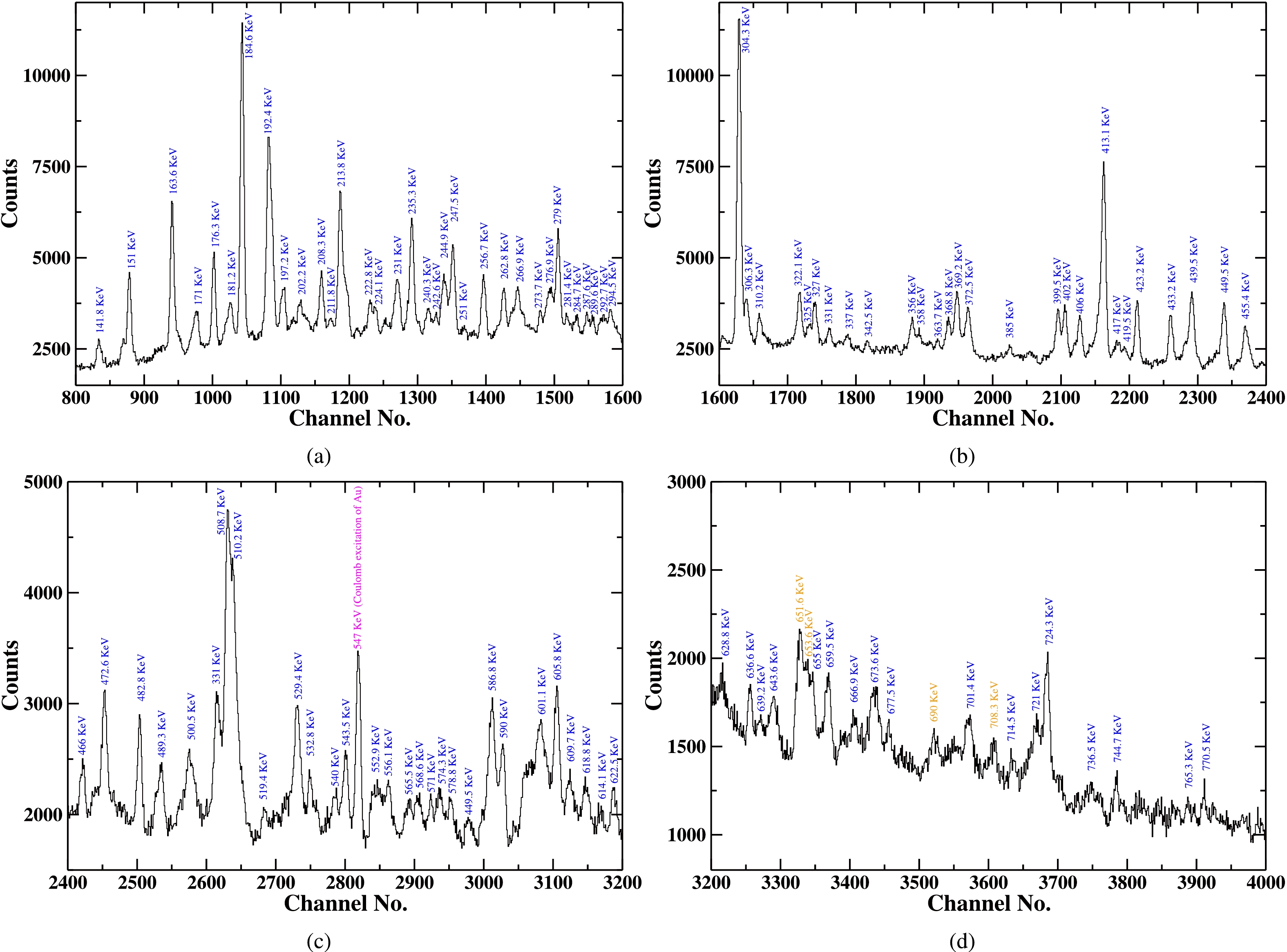

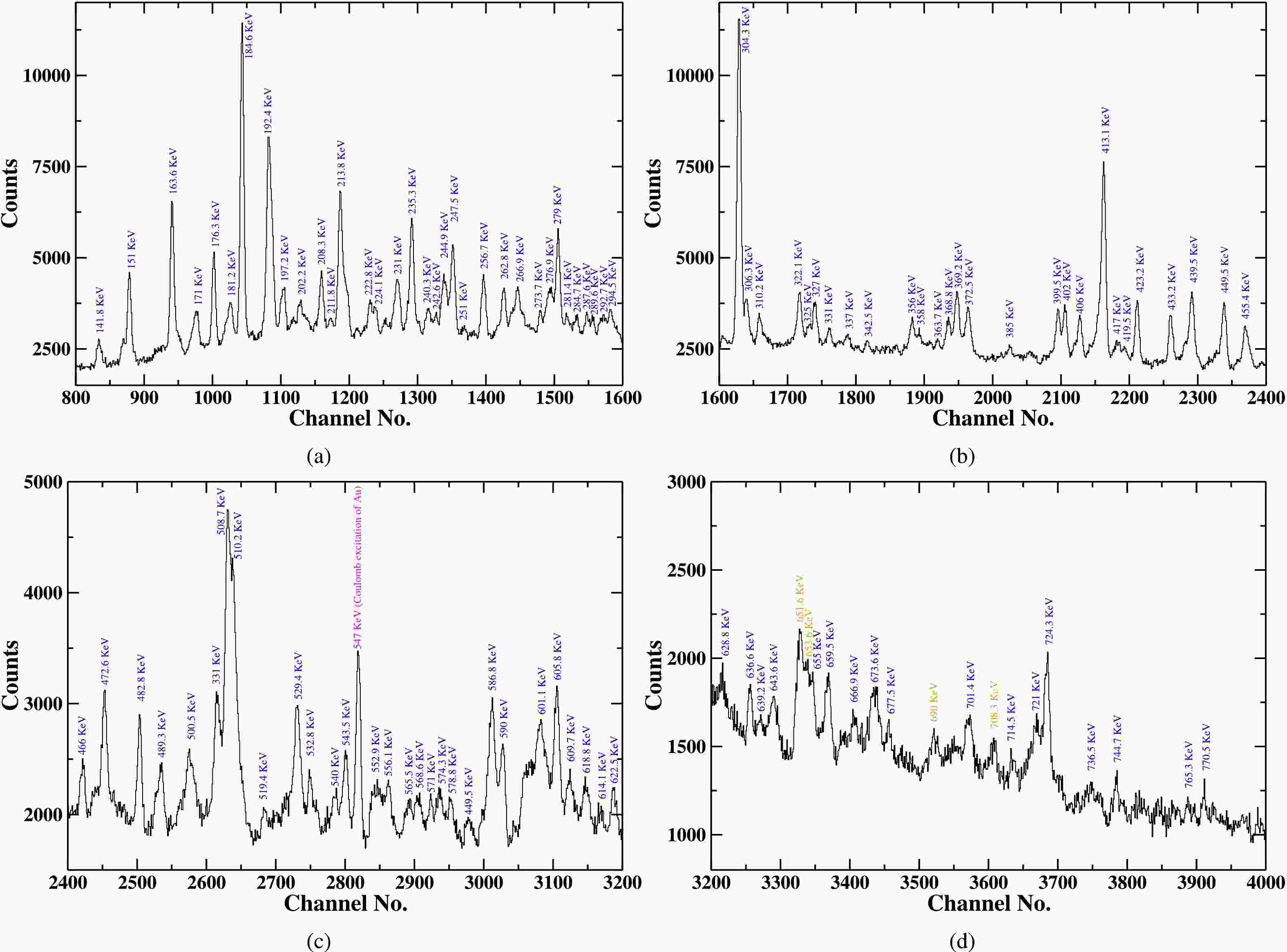
Figure 2.  (color online) The complete energy spectra obtained with detectors at $ 144^{ \circ } $ (backward angle) at first target-stopper distance (${\rm{D}} _{T-S} $ = 8 μm), showing gamma-ray transtions belonging to all bands populated in $ ^{177}Re $ nucleus in the present experiment and the γ-ray transitions (marked with orange colour) are the peaks of contamination.

For the observed gamma-ray transitions of interest, the data obtained with four HPGe detectors at one particular angle were first gain-matched and then added together to produce a total spectrum at that angle. In this way, three resultant spectra corresponding to detectors at $ 50^{ \circ } $ (forward angle), $ 99^{ \circ } $, and $ 144^{ \circ } $ (backward angle) were produced. As an extensive level scheme of $ ^{177}Re $ nucleus already exists [7], it was easy to identify the gamma-ray transitions of interest.

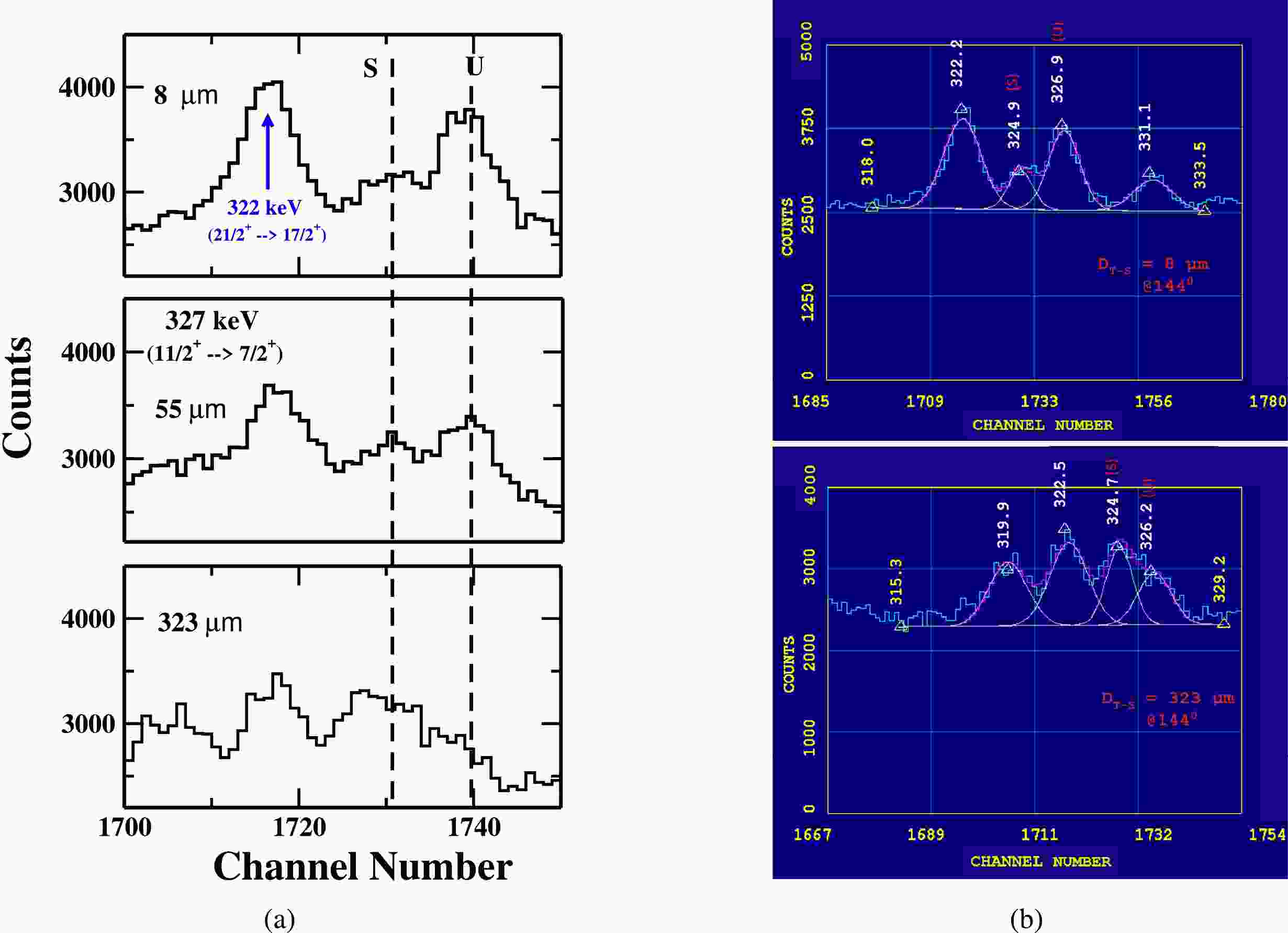
The gamma energy peak of 327 keV ($ 11/2^+ \rightarrow 7/2^+ $) is shown in Fig. 3. Having a finer look of the level scheme [7], it is observed that few close-by γ-ray energy transitions in the decay scheme could possibly contaminate our 327 keV γ-ray transition of interest. In this respect, the 328.35 keV ($ 25/2^+ \rightarrow 21/2^+ $) γ-ray transition in Band 4, the 325.01 keV ($ 13/2^+ \rightarrow 9/2^+ $) γ-ray transition in Band 1, and the the 327.97 keV ($ 23/2^+ \rightarrow 21/2^+ $) inter-connecting gamma transition between Band 1 and Band 2 could be the potential candidates for contamination. However, on careful examination of the entire γ-ray energy spectrum, it is noticed that the transitions belonging to Band 1 and Band 4 were not populated with enough intensity in the present measurement. From the spectrum Fig. 2.(b) it is clear that the intensity of first four lowest gamma-ray transitions of Band 1 i.e. 281 keV ($ 9/2^+ \rightarrow 7/2^+ $), 325 keV ($ 13/2^+ \rightarrow 9/2^+ $), 367 keV ($ 15/2^+ \rightarrow 11/2^+ $), and 405 keV ($ 17/2^+ \rightarrow 13/2^+ $) is less than 10% of the intensity of first three lowest energy gamma-ray transitions i.e. 327 keV ($ 11/2^+ \rightarrow 7/2^+ $), 369 keV ($ 13/2^+ \rightarrow 9/2^+ $), and 402 keV ($ 15/2^+ \rightarrow 11/2^+ $) of the πd-_5/2. On the other hand, the lowest gamma-ray transitions of Band 4, i.e. 328 keV ($ 25/2^+ \rightarrow 21/2^+ $), 436 keV ($ 29/2^+ \rightarrow 25/2^+ $), and 524 keV ($ 33/2^+ \rightarrow 29/2^+ $) are not visible in the spectrum Fig. 2 (b) and (c). So, there is no issue of any contamination of our γ-ray energy peak by those transitions. Hence the obtained intensity of 327 keV normalized to the intensity of 547 keV Coulomb excited γ-ray energy peak of Au observed in the spectrum is then used for the lifetime analysis. The intensity variation of the shifted (S) and unshifted (U) energy components of 327 keV γ-ray at three target-stopper distances is shown in Fig. 3 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 323 μm (distance of minimum intensity) is shown in Fig. 3 (b).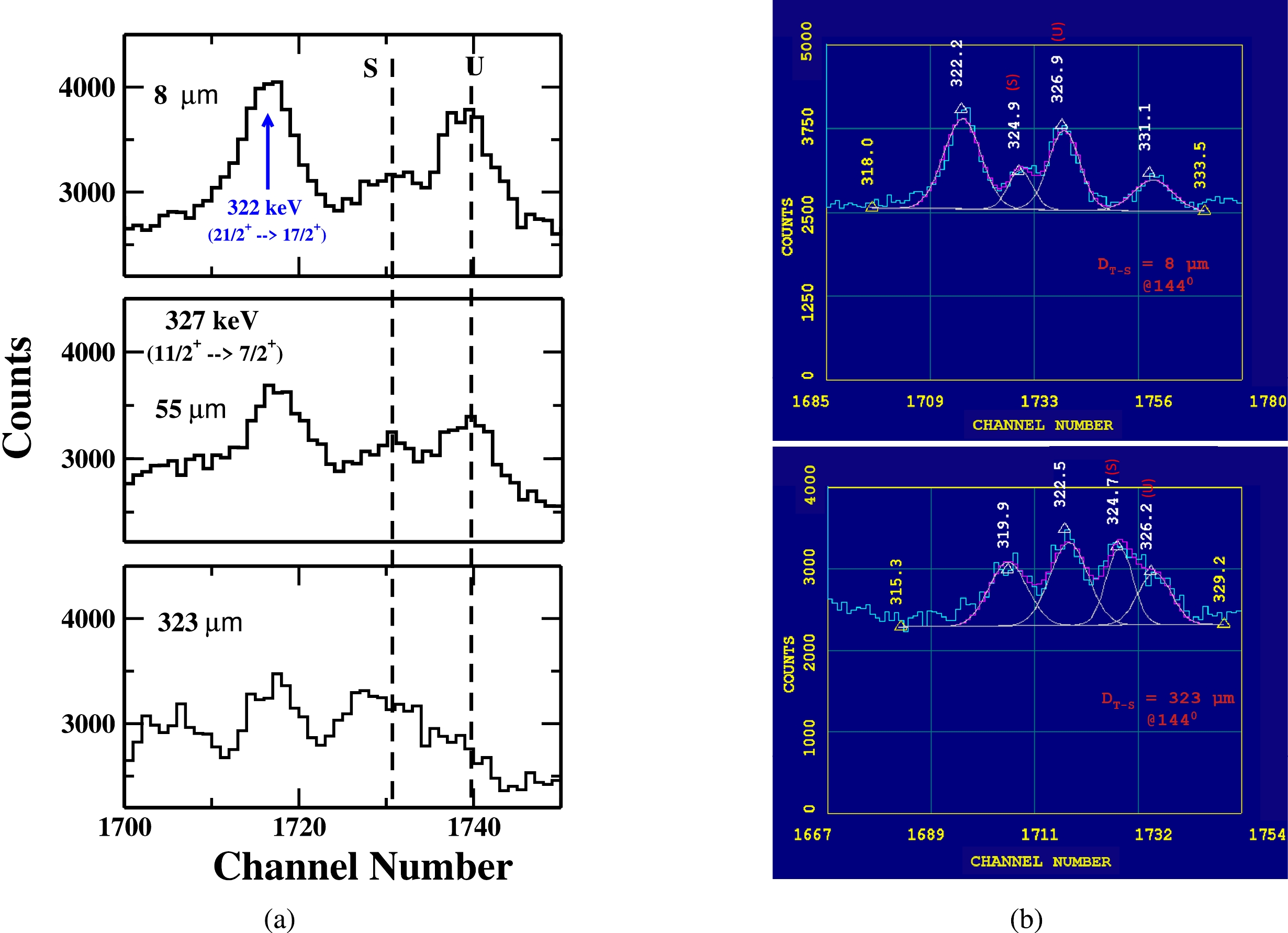

Figure 3.  (color online) (a) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 327 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 327 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 323 μm (distance of minimum intensity). Data is taken with detectors at $ 144^{ \circ } $ with respect to the beam direction.

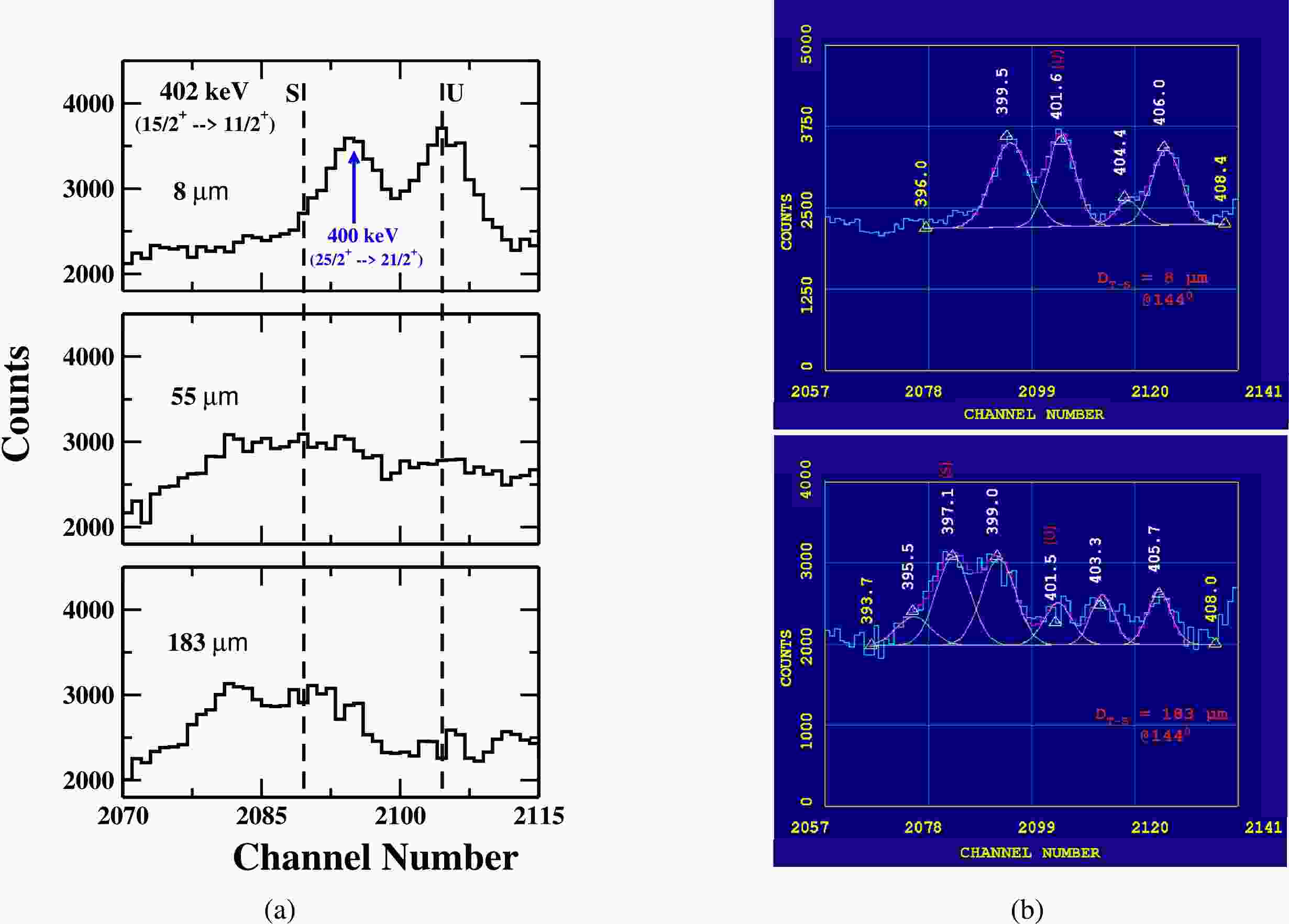
The gamma-ray energy peak of 402 keV ($ 15/2^+ \rightarrow 11/2^+ $) shown in Fig. 4, is clearly seen without any significant contamination from other decay transitions. So, to obtain the actual normalized intensity of 402 keV, the fitted intensity of only the unshifted component normalized to the intensity of 547 keV gamma-ray peak from the Coulomb excitation of gold. The intensity variation of the shifted (S) and unshifted (U) energy components of 402 keV γ-ray at three target-stopper distances is shown in Fig. 4 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 183 μm (distance of minimum intensity) is shown in Fig. 4 (b).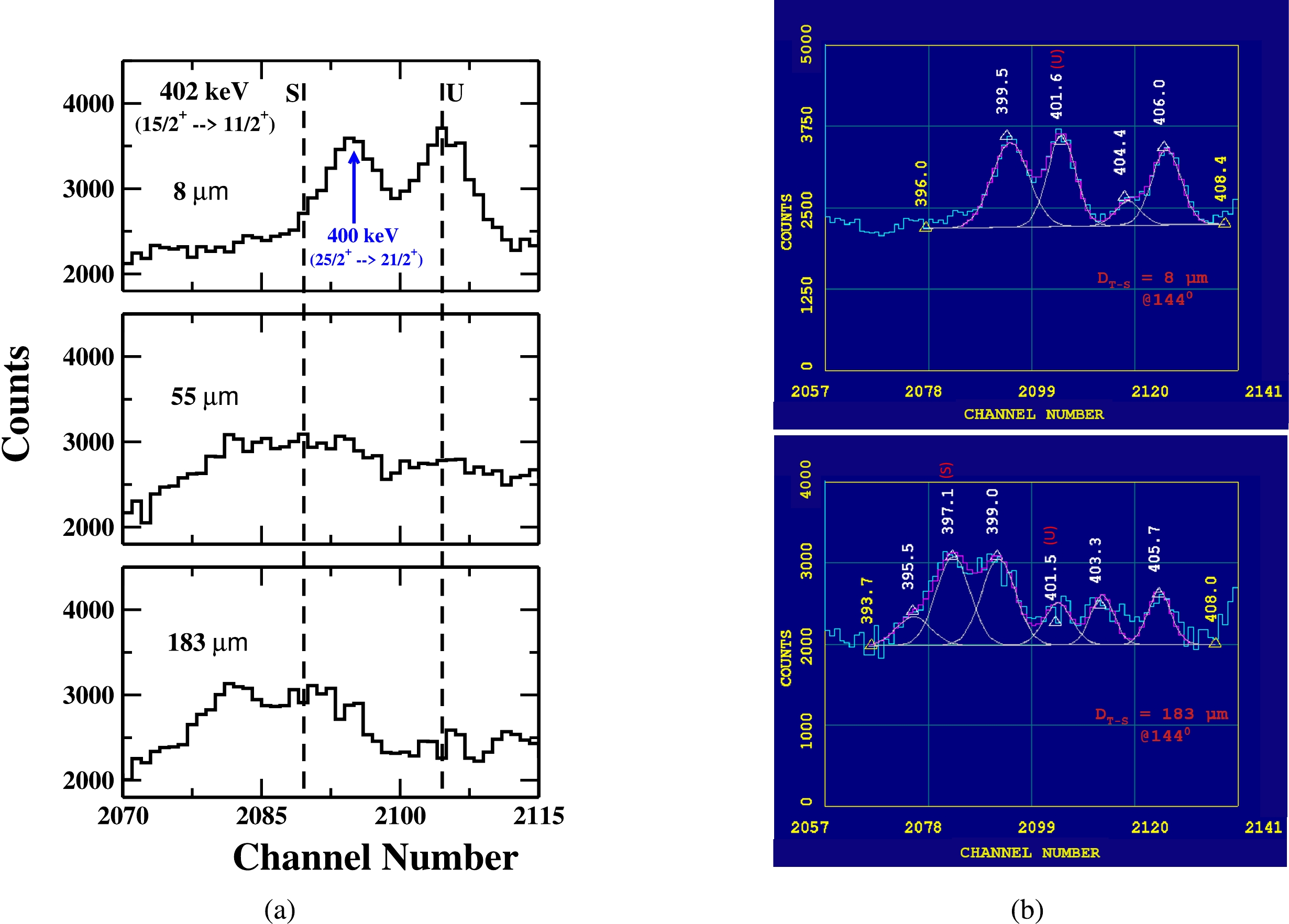

Figure 4.  (color online) (a) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 402 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 402 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 183 μm (distance of minimum intensity). Data is taken with detectors at $ 144^{ \circ } $ with respect to the beam direction.

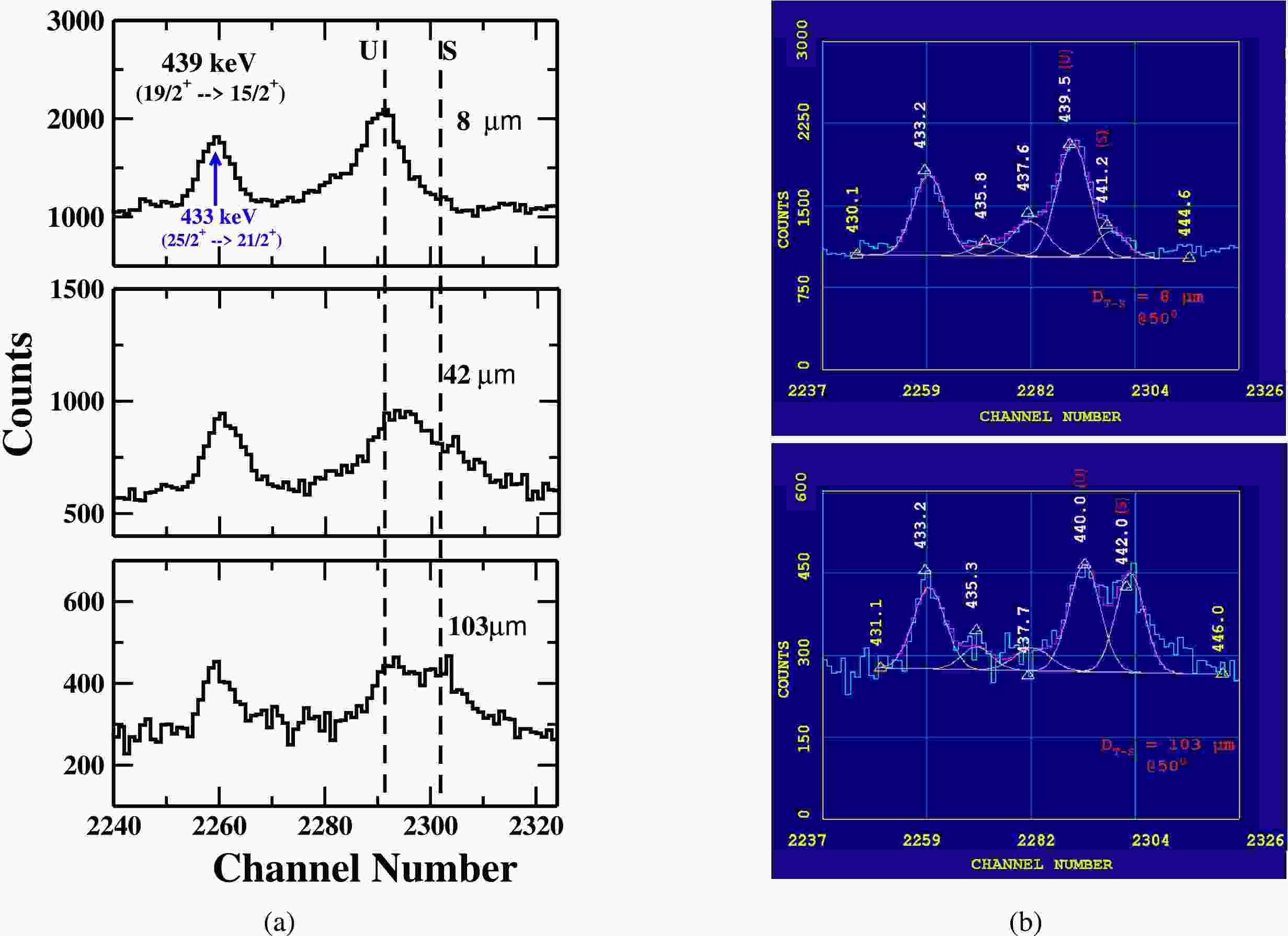
The gamma energy peak of 439 keV ($ 19/2^+ \rightarrow 15/2^+ $) as shown in Fig. 5 possibly has contributions in the intensity from two gamma-transitions of energy 437.48 keV ($ 19/2^+ \rightarrow 15/2^+ $) in Band 1 and energy 439 keV ($ 19/2^+ \rightarrow 15/2^+ $) in Band 2 (our gamma-ray transition of interest). However, on a careful look of the entire γ-ray energy spectrum, it is noticed that γ-ray energy transitions of Band 1 are not populated with enough intensity in the present measurement. So the possibility of contamination by the intensity of 437.48 keV ($ 19/2^+ \rightarrow 15/2^+ $) in Band 1 can be excluded. The intensity variation of the shifted (S) and unshifted (U) energy components of 439 keV γ-ray at three target-stopper distances is shown in Fig. 5 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 103 μm (distance of minimum intensity) is shown in Fig. 5 (b).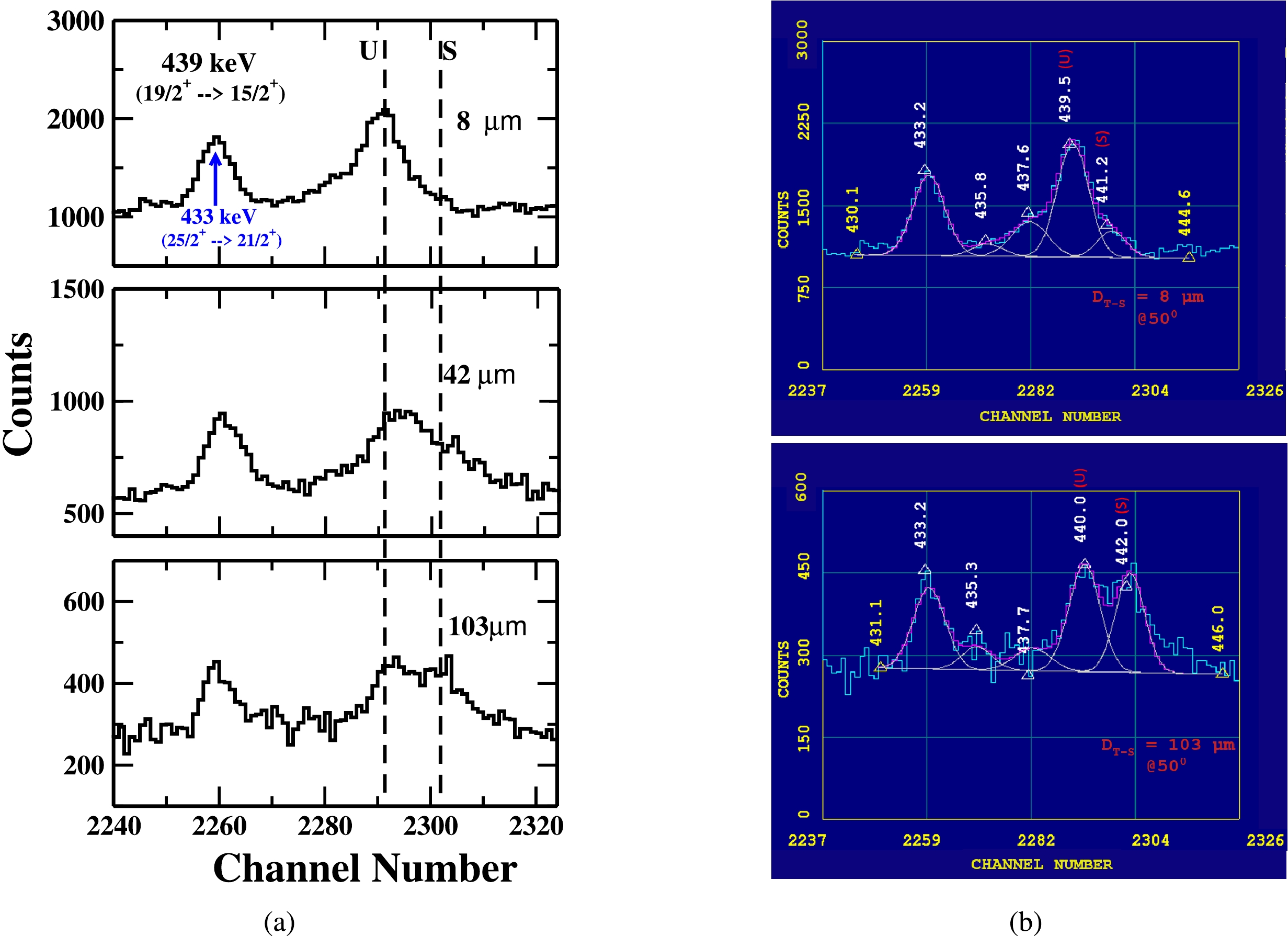

Figure 5.  (color online) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 439 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 439 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 103 μm (distance of minimum intensity). Data is taken with detectors at $ 50^{ \circ } $ with respect to the beam direction.

The gamma energy peak of 473 keV ($ 23/2^+ \rightarrow 19/2^+ $) as shown in Fig. 6 has the possibility of contamination from the two γ-ray transitions; the 472.14 keV ($ 31/2^+ \rightarrow 27/2^+ $) γ-ray transition in Band 6 and the 470.49 keV γ-ray transition in Band 10. On carefully looking at the level scheme and the entire γ-energy spectrum of $ ^{177}Re $ nucleus, it is observed that Band 10 is not populated in present measurements, as none of the lowest energy gamma-ray transitions are visible in the total energy spectrum. However, looking at the intensity of lowest gamma-ray transitions of 285 keV ($ 23/2^+ \rightarrow 19/2^+ $) in the total energy spectrum Fig. 2, it appears that the Band 6 is populated with intensity of less than 10 % compare to intensity of Band 2, so the possible contamination of 472.14 keV gamma-ray transition of Band 6 in our gamma-ray transition of interest of 473 KeV is less than 10 %. So, the γ-transitions of the energies 472.14 keV ($ 31/2^+ \rightarrow 27/2^+ $) in Band 6 and 470.49 keV in Band 10 can be easily excluded. Therefore, the net intensity of the gamma transition of 473 keV is then normalized to the intensity of 547 keV gamma ray peak from the Coulomb excitation of gold and used for the present lifetime analysis. The intensity variation of the shifted (S) and unshifted (U) energy components of 473 keV γ-ray at three target-stopper distances is shown in Fig. 6 (a), while the fit of the unshifted gamma-ray energy peak at two target-stopper distances; at 8 μm (first distance) and at 70 μm (distance of minimum intensity) is shown in Fig. 6 (b).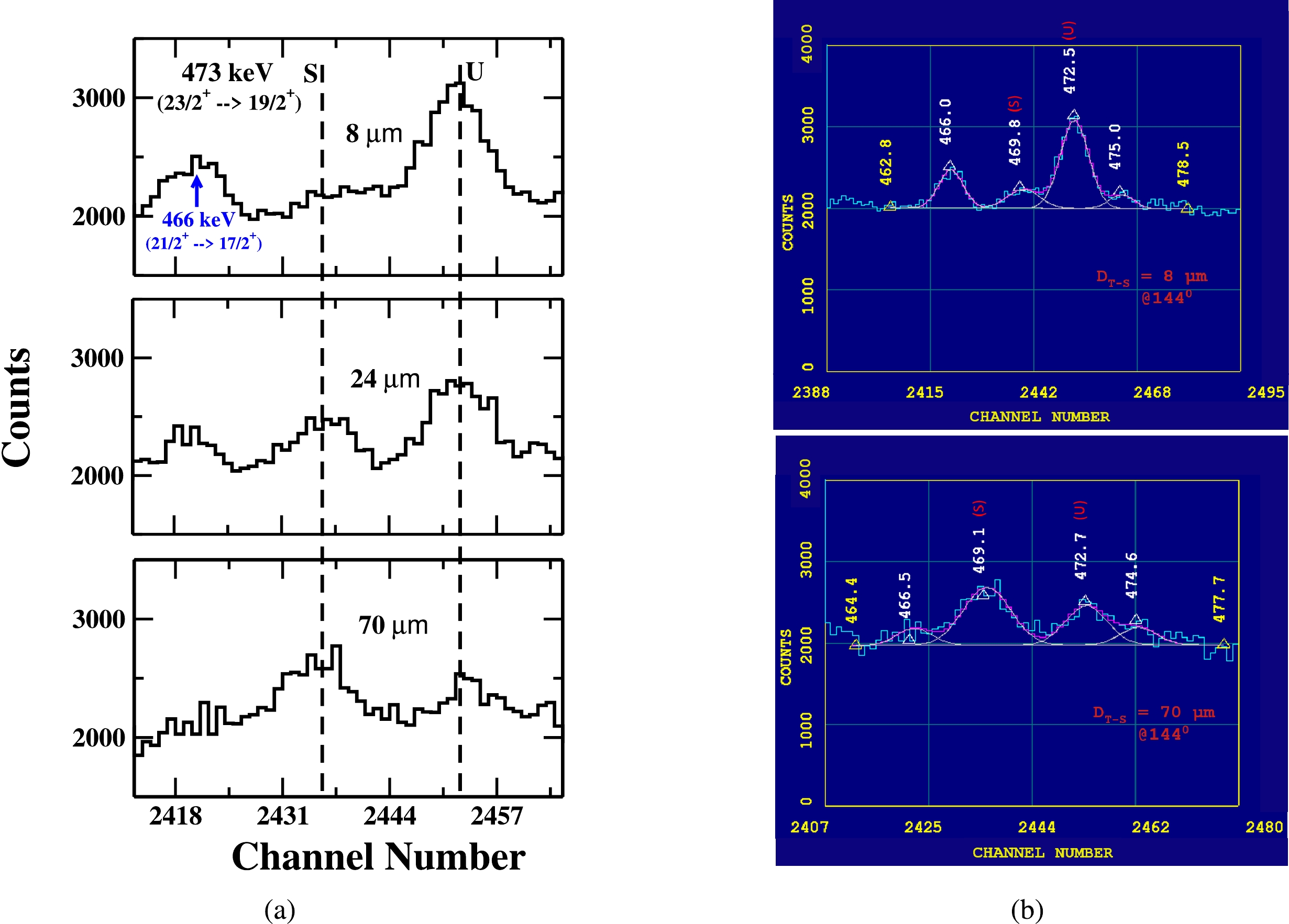

Figure 6.  (color online) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 473 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 473 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 70 μm (distance of minimum intensity). Data is taken with detectors at $ 144^{ \circ } $ with respect to the beam direction.

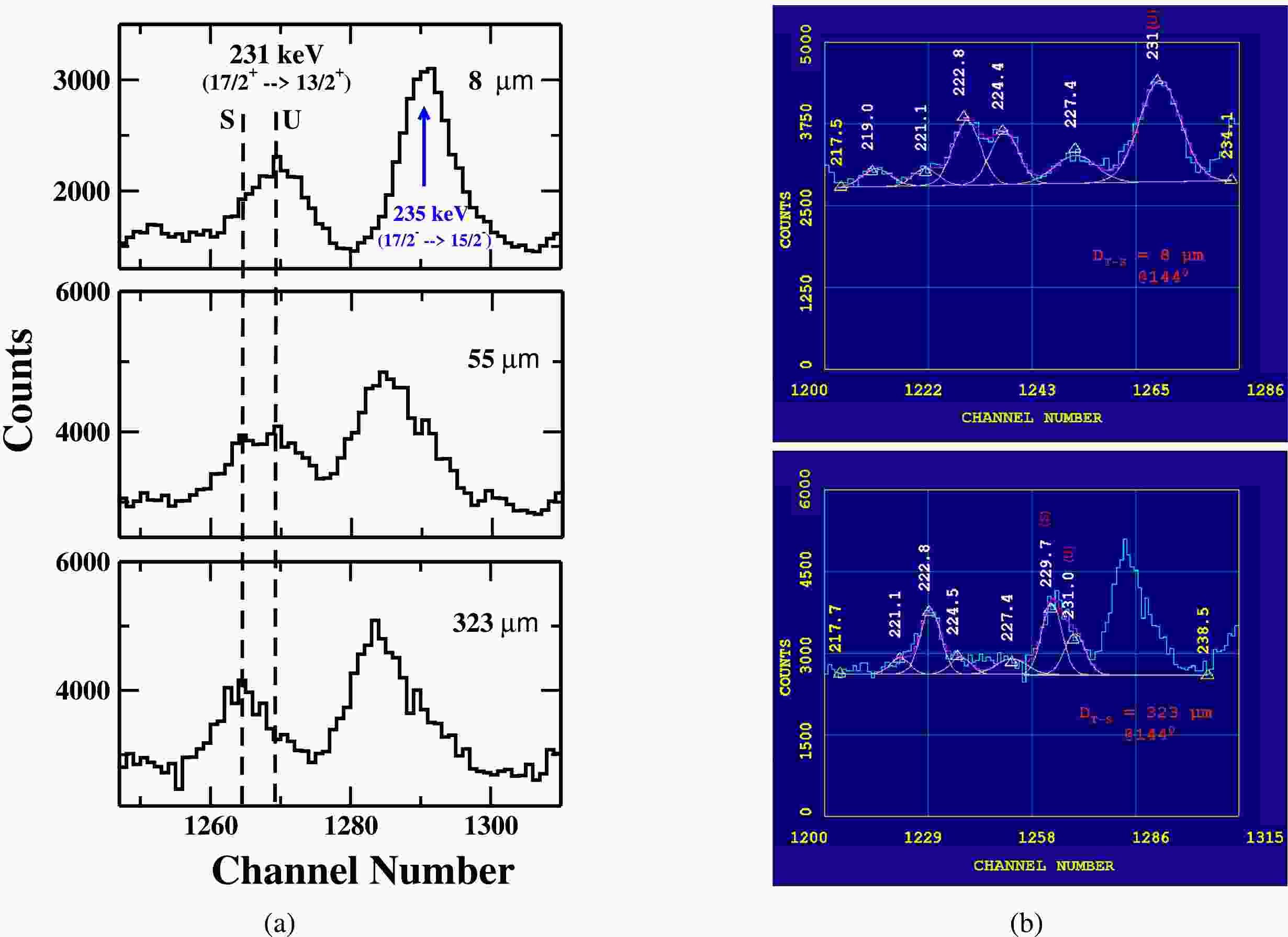
The gamma energy peak of 231 keV ($ 17/2^+ \rightarrow 13/2^+ $) belonging to Band 3 is shown in Fig. 7. On the careful look of the decay scheme of $ ^{177}Re $ nucleus point toward the possible contamination of this γ-ray transition by a few close by γ-ray transitions of energy, the 230.44 keV ($ 33/2^+ \rightarrow 31/2^+ $) γ-ray transition in Band 19 and, 231.26 keV ($ 21/2^+ \rightarrow 19/2^+ $) inter-connecting γ-ray transition in Band 2 are the possible candidates for the contamination. Since on close inspection of the entire energy spectrum, it is found that there is no gamma-ray energy peak at 230.44 keV which implies that Band 19 was not populated in the present measurement, so transition 230.44 keV ($ 33/2^+ \rightarrow 31/2^+ $) can be excluded as contaminant. So the 231 keV γ-energy transition shown in Fig. 7 can have contribution from only two close by energies, 231.26 keV ($ 21/2^+ \rightarrow 19/2^+ $) (inter-connecting γ-ray transition in Band 2) and 231 keV gamma-ray energy of our interest.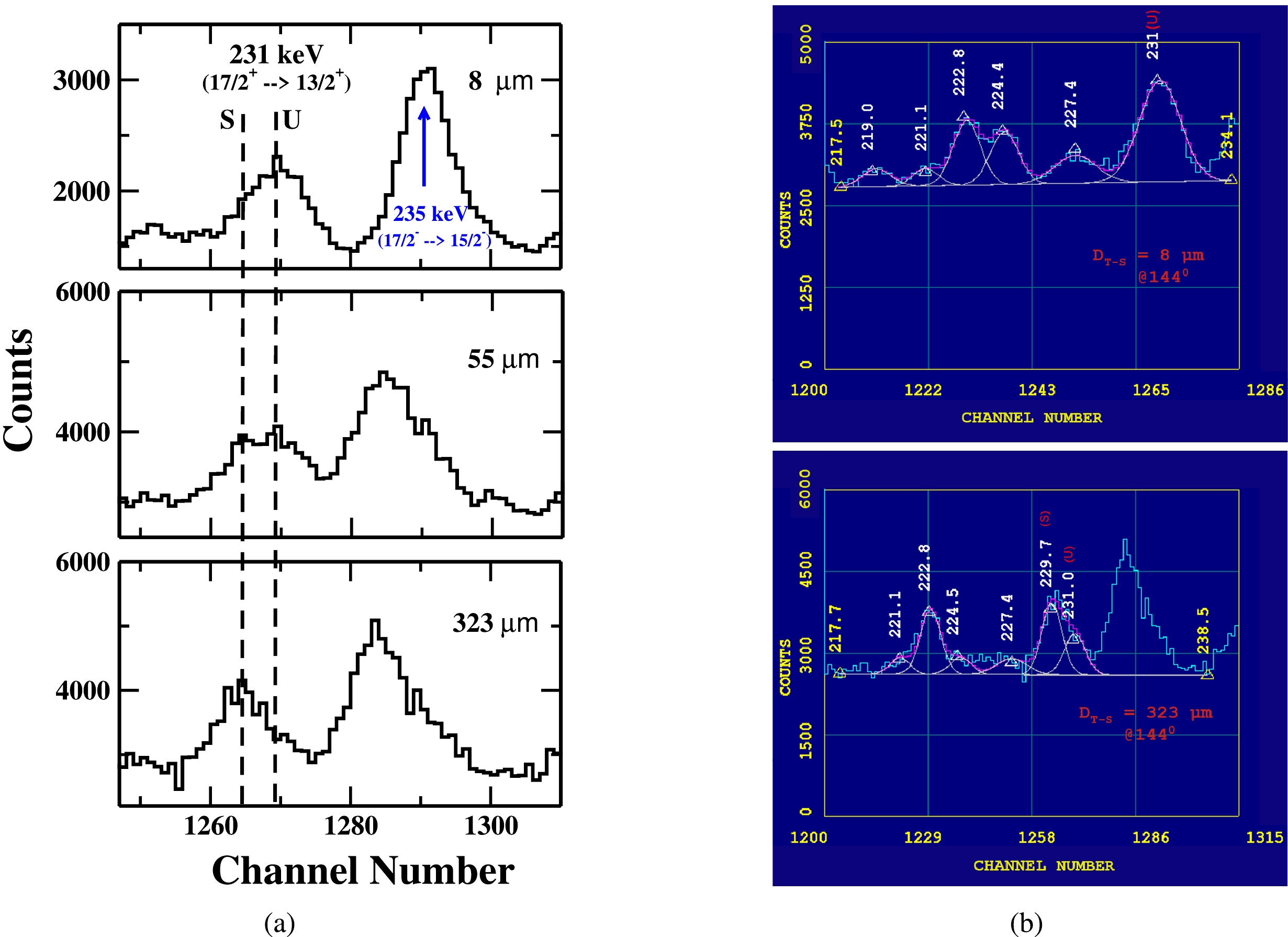

Figure 7.  (color online) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 231 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 231 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 323 μm (distance of minimum intensity). Data is taken with detectors at $ 144^{ \circ } $ with respect to the beam direction.

In order to show the relative population of Band 2 and Band 3 in our measurement compare to the relative population of the two bands in Ref. [7], we compared the intensities of 400 keV of Band 3 and 402 keV of Band 2 as observed in our measurements and the ones given in Ref. [7]. In our measurements, the ratio of intensity of 402 keV (Band 3) to the 400 keV (Band 2) is found to be 1.05 (3%) while the ratio of the intensities of the two transitions given in Ref. [7] is found to be 1.07 (2%). The same ratio (within experimental error) of population of two bands in our measurements and the one reported in Ref. [7] shows that the relative population of various bands in our measurements and one given in Ref. [7] appears to be same, despite using different reactions to populate bands. Therefore the data given in Ref. [7] for intensity of various gamma-ray transitions can be used in present analysis too. As per the intensity table [7], the intensity of 231 keV ($ 17/2^+ \rightarrow 13/2^+ $) is 54.1 and the intensity of other γ-transition 231.26 keV ($ 21/2^+ \rightarrow 19/2^+ $) in Band 2 is 117.5, respectively. So in the first step (step 1), the total intensity of 231 keV peak obtained in the experiment is divided in the ratio of 31.5 % and 68.5 % at each target-stopper distance. Also as for the interlinking γ-transition 231.26 keV ($ 21/2^+ \rightarrow 19/2^+ $) in Band 2 from the state (21/2⁺), the mean lifetime (τ = 4.4 ps, the upper limit of the lifetime) has been measured and already reported [4]. So in the second step (step 2) making use of the target-stopper distances covered and recoil velocity of nuclei obtained in this experiment, the intensity of 231.26 keV γ-transition at each target-stopper distance is found using the following expression:

Where d is the target-stopper distance, τ is the mean lifetime of state (21/2⁺) and v is the recoil velocity. In the present experiment, looking at the location of shifted (${\rm{E}} _s $) and unshifted (${\rm{E}} _u $) gamma-ray energy peaks for various gamma transitions of interest, and taking into account the angle of the detectors with respect to direction of beam, the recoil velocity of excited $ ^{177}Re $ nuclei is found to be 2.7 μm/ps using following well known formula [8]:

This recoil velocity has been obtained under the assumption that (i) Both target and stopper foils are thin enough to account for the loss of energy of the recoil nuclei when they pass through them (ii) all Re nuclei are getting produced in the excited state due to the reaction of the incoming beam particles with the target foil and no reaction is happening in the middle or anywhere else in the target (iii) there is complete vacuum between the target and stopper foils in the plunger setup so that no energy loss takes place for the recoil $ ^{177}Re $ nuclei (iv) the recoiling $ ^{177}Re $ nuclei after reaching at the stopper foil stopped immediately on its surface (v) both the target and stopper are of uniform thickness (vi) the detector opening angle is small so that there is no spread in the angle subtended by detector at the target foil. Now taking the difference of the two intensities (intensity in step 1 - intensity in step 2) at each target-stopper distance and adding that difference to the intensity obtained in step 1, the actual intensity of 231 keV (17/2$ ^+ \rightarrow $ 13/2⁺) γ-transition of Band 3 at each target-stopper (${\rm{D}} _{T-S} $) distance is obtained. The resulting intensity of 231 keV ($ 17/2^+ \rightarrow $ 13/2⁺) γ-transition obtained by using the limiting value (maximum possible) of lifetime value 21/2⁺ state in Band 2 was then normalized to the intensity of 547 keV gamma energy peak from the Coulomb excitation of gold to yield the normalized intensity and is used in the present lifetime analysis. The intensity variation of the shifted (S) and unshifted (U) energy components of 231 keV γ-ray at three target-stopper distances is shown in Fig. 7 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 323 μm (distance of minimum intensity) is shown in Fig. 7 (b).

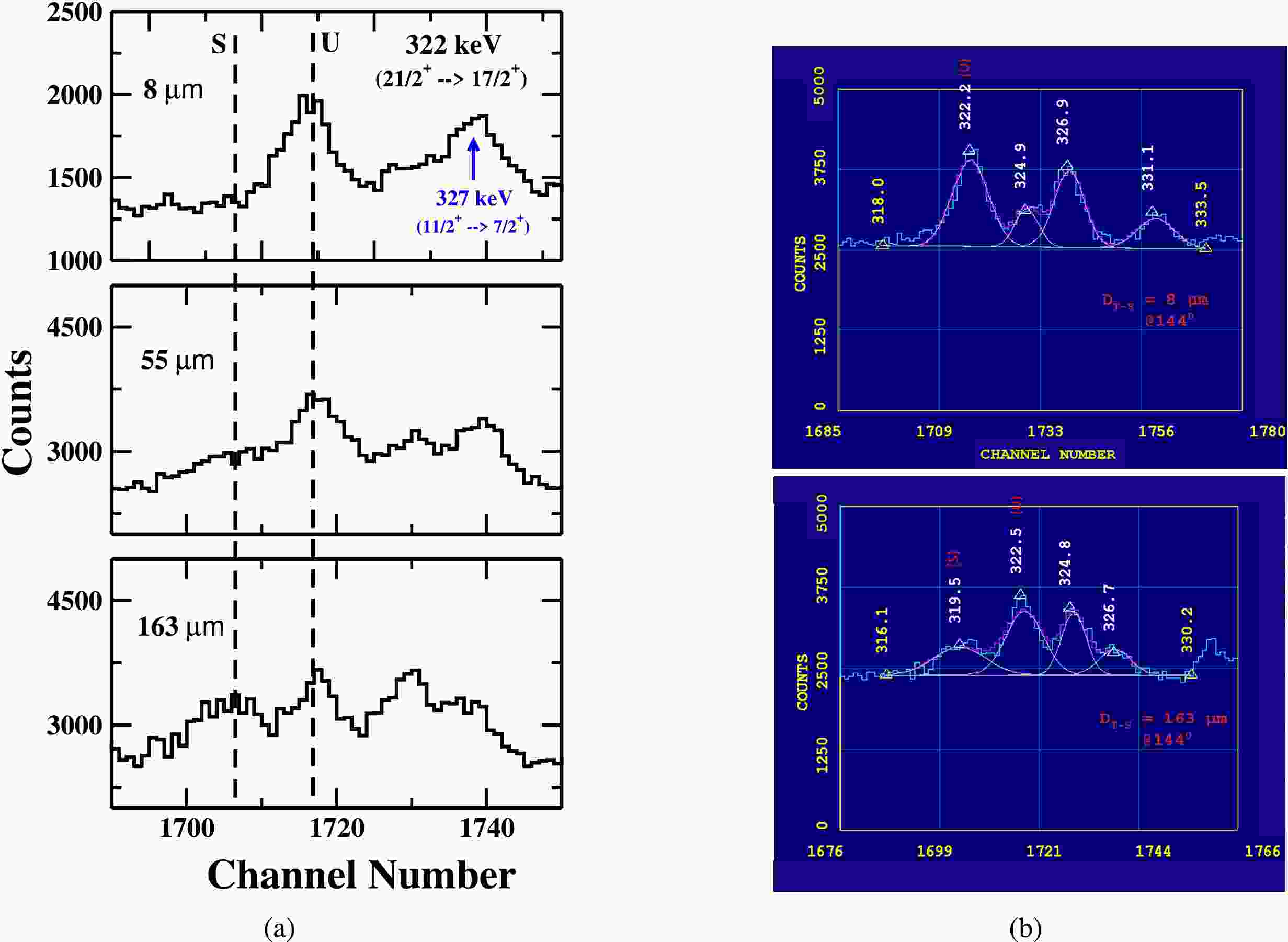
The gamma-ray energy peak 322 keV ($ 21/2^+ \rightarrow 17/2^+ $) is shown in Fig. 8. A careful look of the level scheme of $ ^{177}Re $ point towards the possible contamination of this γ-ray energy by the following γ-ray transitions: 322 keV ($ 43/2^+ \rightarrow 41/2^+ $) γ-ray transition in Band 19, the 323.19 keV ($ 39/2^+ \rightarrow 37/2^+ $) γ-ray transition in Band 18, the 323.97 keV ($ 43/2^+ \rightarrow 41/2^+ $) γ-ray transition in Band 20, the 319.32 keV ($ 15/2^- \rightarrow 11/2^- $) γ-ray transition in Band 7, and the 320.01 keV ($ 31/2^+ \rightarrow 29/2^+ $) inter-connecting γ-ray transition between Band 5 and Band 6. Looking at the full energy spectrum obtained in the present measurement and shown in Fig. 2, it looks that none of γ-ray energy transitions in Band 5, 6, 7, 18, 19, and 20 have been obtained with enough intensity. So the possibility of contamination of our γ-ray energy peak of interest by above mentioned five close by γ-transitions can be excluded. Therefore, net intensity of 322 keV as shown in Fig. 8 is the entire intensity of our gamma transition of interest. The intensity variation of the shifted (S) and unshifted (U) energy components of 322 keV γ-ray at three target-stopper distances is shown in Fig. 8 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 163 μm (distance of minimum intensity) is shown in Fig. 8 (b).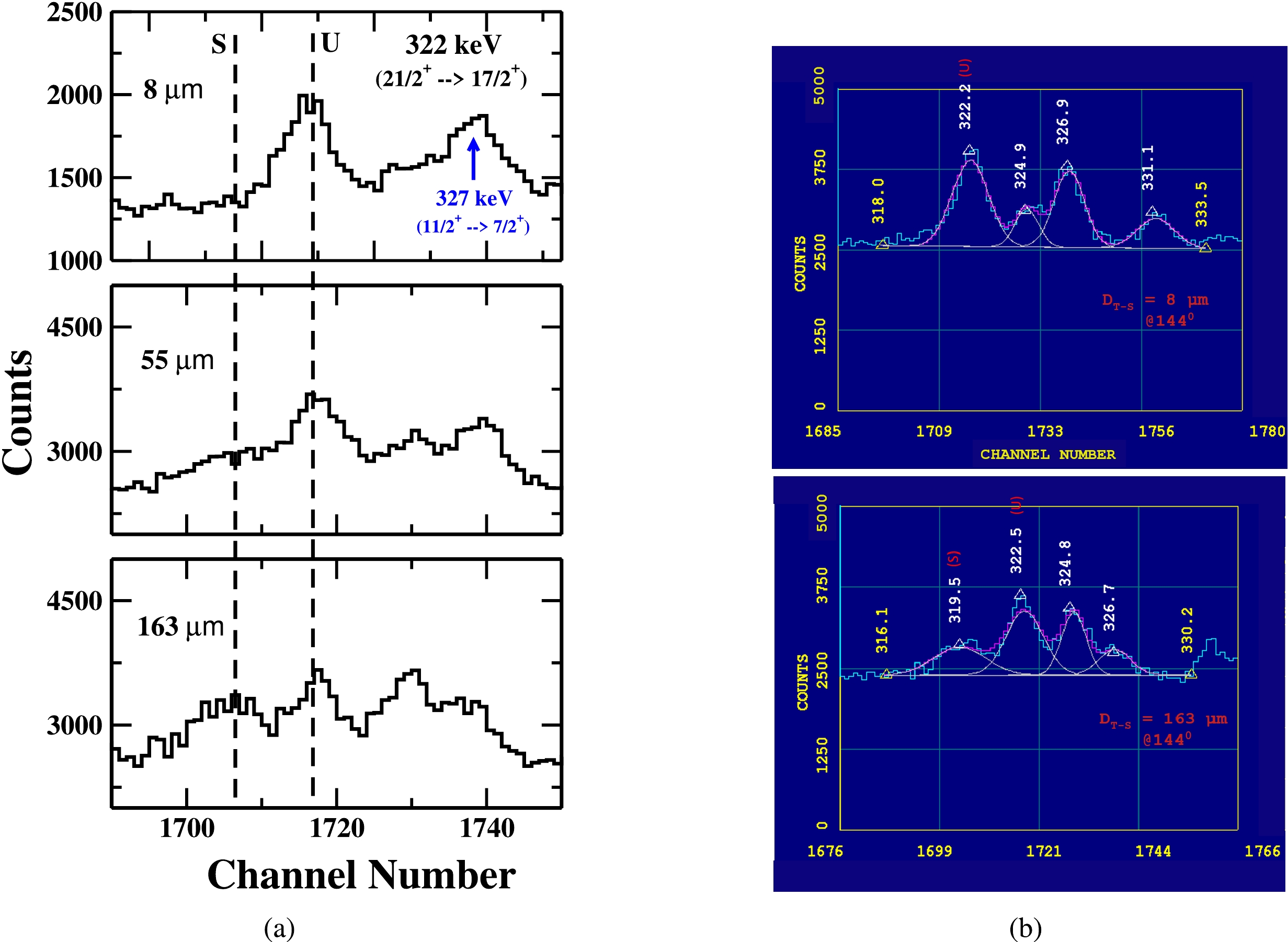

Figure 8.  (color online) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 322 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 322 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 163 μm (distance of minimum intensity). Data is taken with detectors at $ 144^{ \circ } $ with respect to the beam direction.

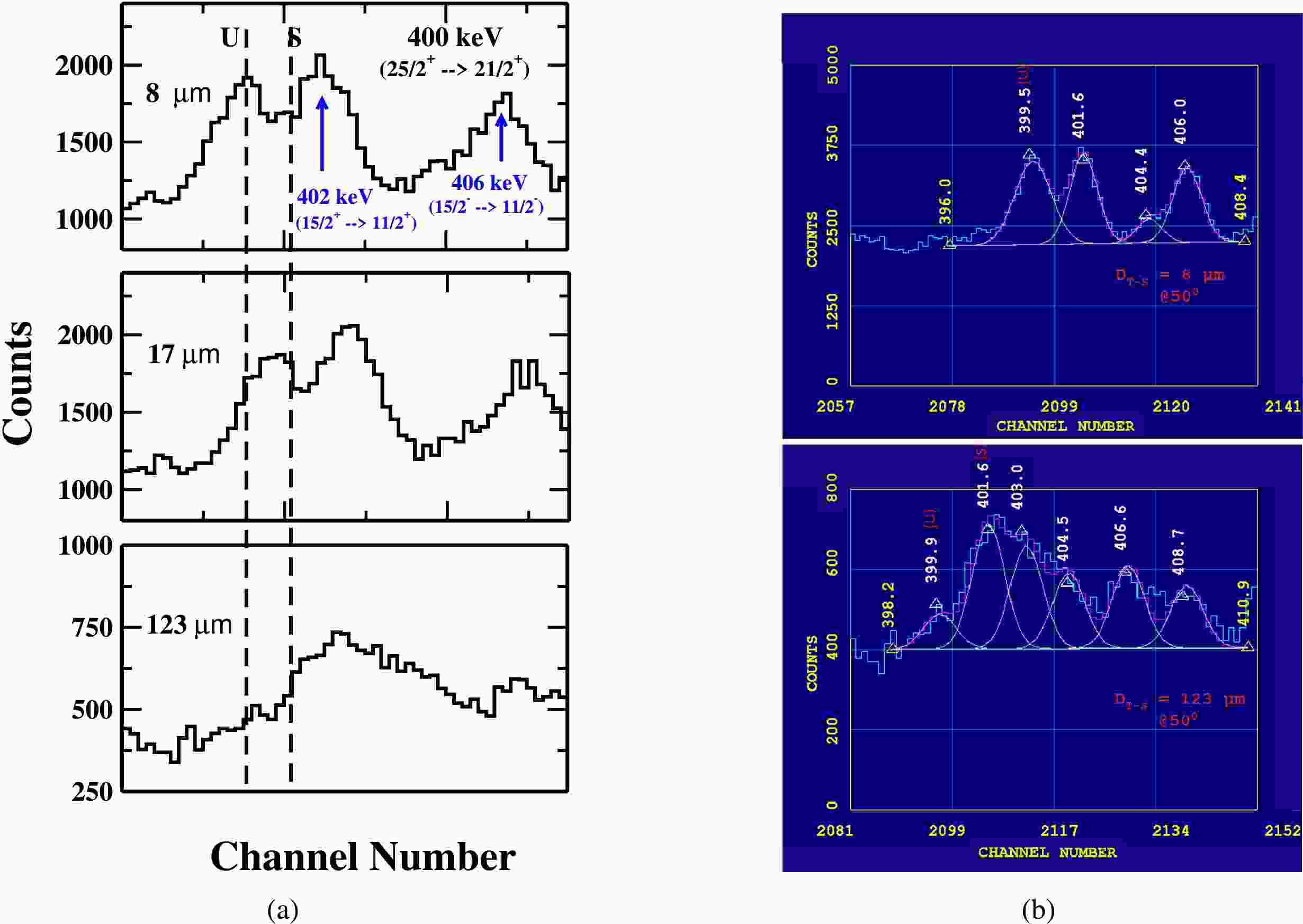
The gamma-ray energy peak of 400 keV ($ 25/2^+ \rightarrow 21/2^+ $) in Band 3 is shown in Fig. 9. This γ-ray peak is clearly seen without any significant contamination from other decay transitions. So the actual intensity of 400 keV γ-ray energy peak is used in the present lifetime analysis. The intensity variation of the shifted (S) and unshifted (U) energy components of 400 keV γ-ray at three target-stopper distances is shown in Fig. 9 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 123 μm (distance of minimum intensity) is shown in Fig. 9 (b).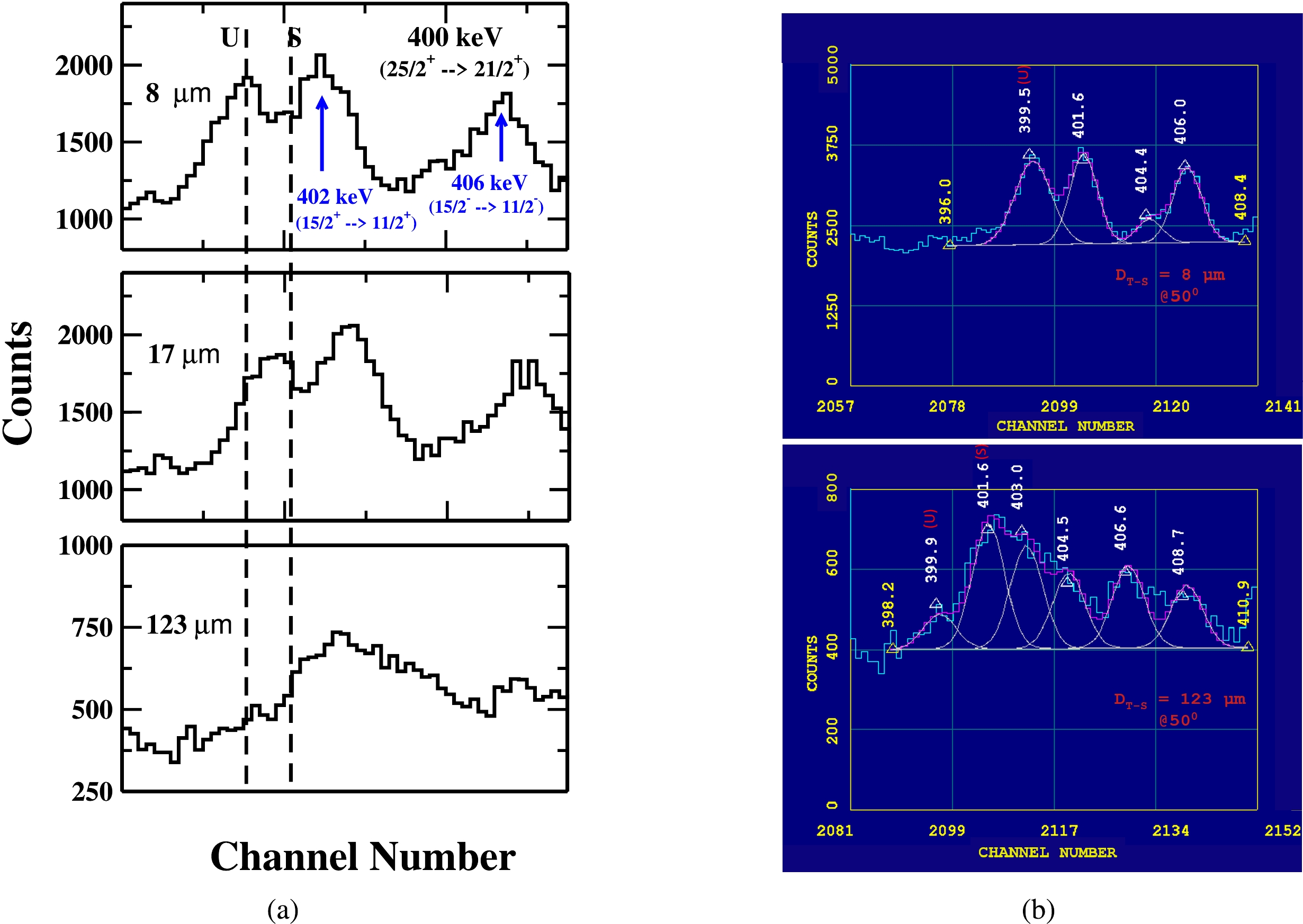

Figure 9.  (color online) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 400 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 400 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 123 μm (distance of minimum intensity). Data is taken with detectors at $ 50^{ \circ } $ with respect to the beam direction.

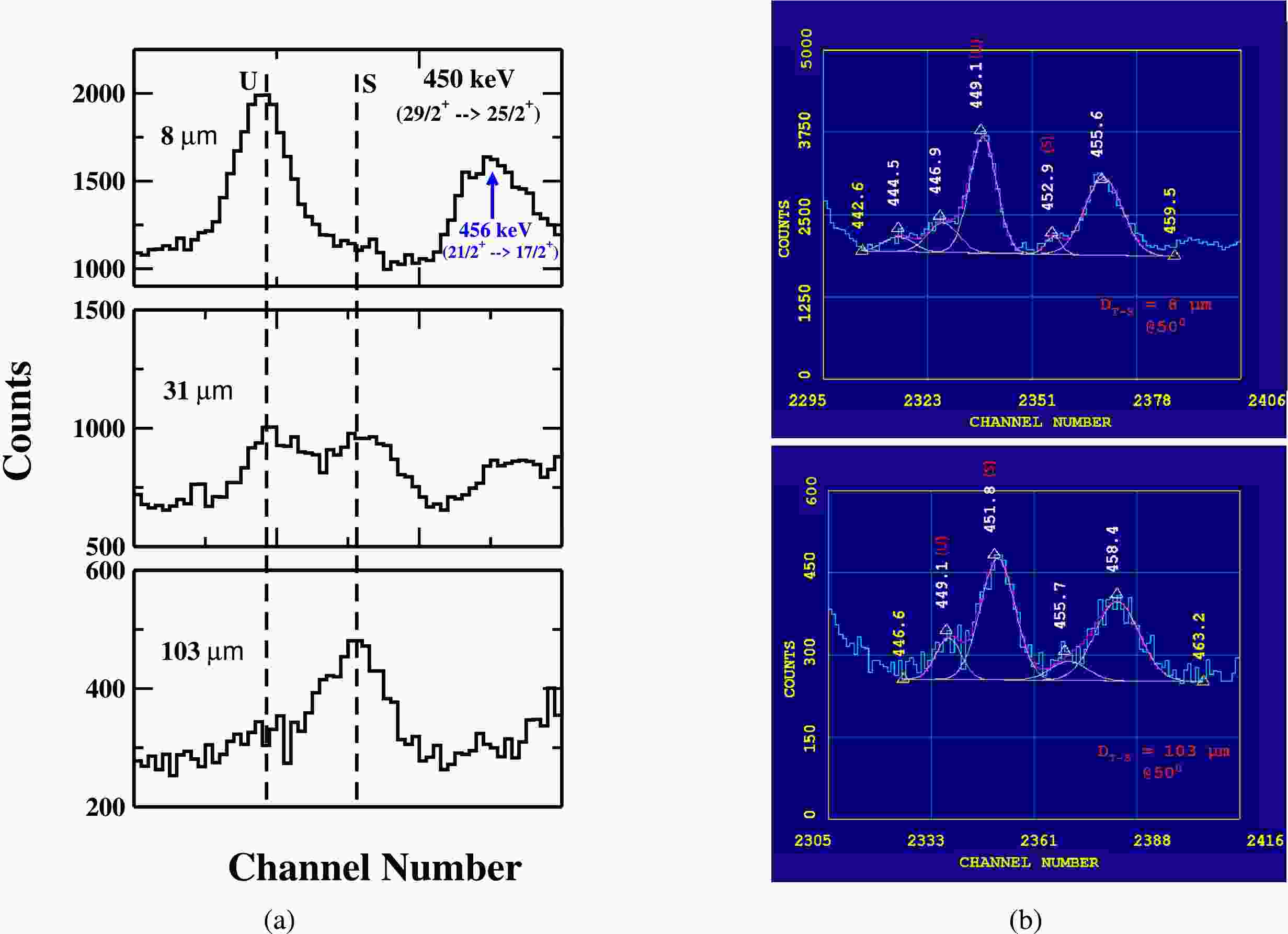
The gamma-ray energy peak of 450 keV ($ 29/2^+ \rightarrow 25/2^+ $) in Band 3 is shown in Fig. 10. Looking at the level scheme $ ^{177}Re $ nucleus carefully, it is noticed that this gamma-energy peak may be contaminated by other two γ-decay transitions, the 448.41 keV ($ 29/2^+ \rightarrow 25/2^+ $) in Band 17 and 449.08 keV ($ 17/2^- \rightarrow 13/2^- $) in Band 15. However, on scanning the complete energy spectrum it is clear that the transitions of Band 17 are not being populated in the present measurement. This has been concluded on the basis of the population of lowest four gamma-ray transitions of Band 17, i.e. 151 keV, 180 keV, 211 keV, and 391 keV in the complete energy spectrum shown in Fig. 2. Though, a large gamma-ray peak appear at 151 keV in complete energy spectrum, Fig. 2 (a), but it is 151.4 keV ($ 9/2^+ \rightarrow 7/2^+ $) transition from Band 2 and not from Band 17. Similarly, the peak at 181.2 keV in the spectrum (Fig. 2 (a)) is from Band 18 (transition from $ 27/2^+ \rightarrow 25/2^+ $) and there is no peak at 180 keV (Band 17) in complete energy spectrum. Again, a small peak seen at 211.2 keV in the complete energy spectrum, Fig. 2 (a) is the 211.10 keV ($ 17/2^+ \rightarrow 15/2^+ $) gamma-ray transition from Band 1 and not from Band 17. Corresponding to 391 keV gamma-ray transition from Band 17, there is no gamma-ray energy peak in the complete energy spectrum, Fig. 2 (b). So the contamination of intensity by the transition 448.41 keV ($ 29/2^+ \rightarrow 25/2^+ $) in Band 17 can be excluded from the intensity calculations. Now to separate the intensity of contaminant γ-transition 449.08 keV ($ 17/2^- \rightarrow 13/2^- $) of Band 15 from our peak of interest, the following procedure was adopted.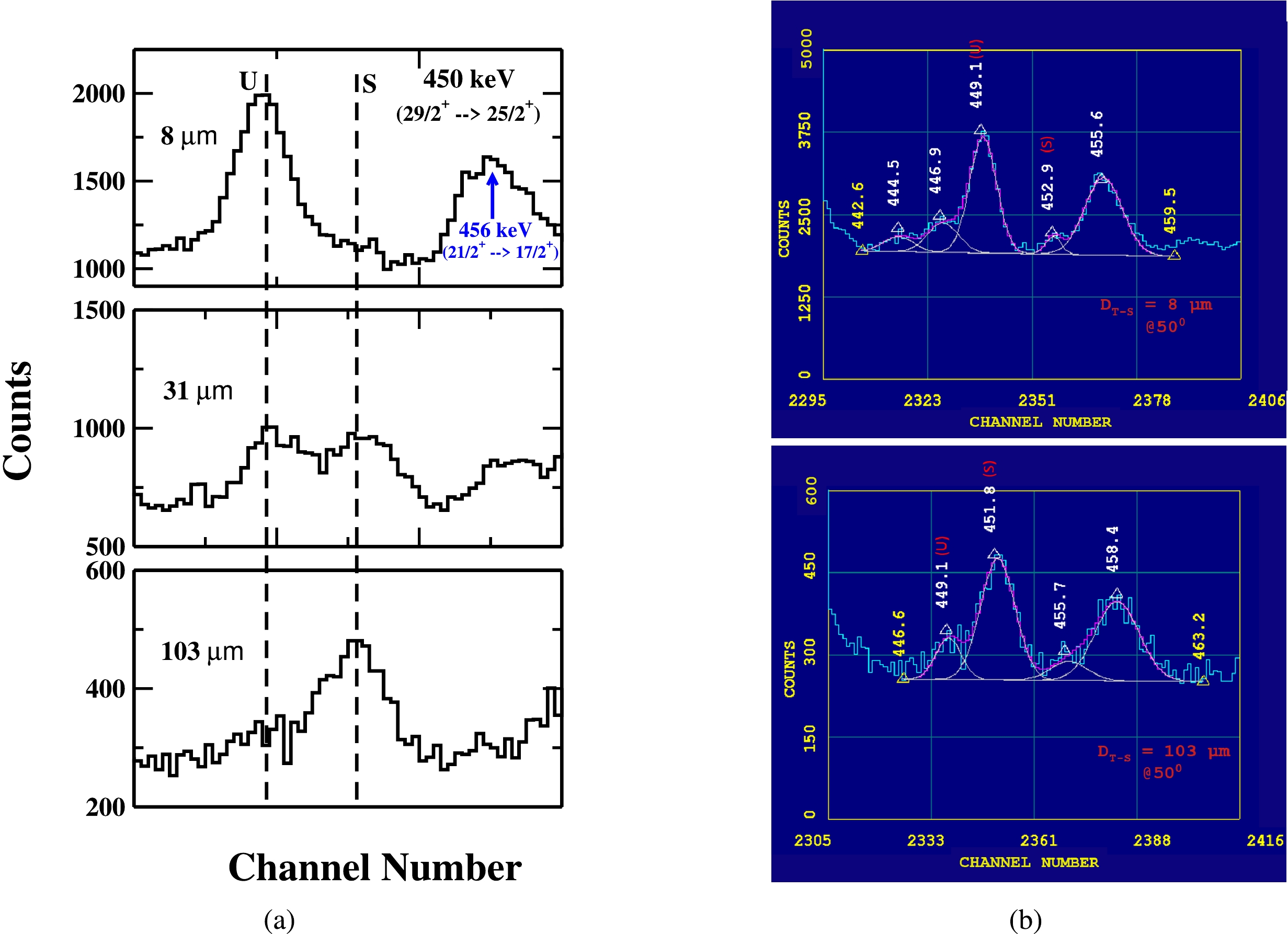

Figure 10.  (color online) A portion of energy spectrum showing the shifted (S) and unshifted (U) peaks of 450 keV γ-ray transition of yrast band in $ ^{177}Re $ at three different target-stopper distances (${\rm{D}} _{T-S} $) and (b) A potion of energy spectrum showing the fitting of unshifted energy (U) of 450 keV (our peaks of interest) at ${\rm{D}} _{T-S} $ = 8 μm (first distance) and ${\rm{D}} _{T-S} $ = 103 μm (distance of minimum intensity). Data is taken with detectors at $ 50^{ \circ } $ with respect to the beam direction.

As per the intensity table [7], the relative intensity of two gamma-transitions of energy 449.08 keV ($ 17/2^- \rightarrow 13/2^- $) and 450 keV ($ 29/2^+ \rightarrow 25/2^+ $) are 324 and 270 respectively. So, in the first step, the total intensity of 450 keV peak obtained in the experiment is divided in the ratio of 54.5 % and 45.5 % at each target-stopper distance. Also, the γ-ray transition of energy 449.08 keV, coming from the decay of state ($ 17/2^- $) of Band 15, which lie between the two decay states $ 19/2^- $ and $ 15/2^- $. As the lifetimes of both the states, $ 19/2^- $ and $ 15/2^- $ have already been measured and reported in previous studies [4]. So, to get the transition probability (i.e. B(E2) value) for the ($ 17/2^- \rightarrow 15/2^- $) transition, the average of the reported B(E2) values for ($ 19/2^- \rightarrow 15/2^- $) and ($ 15/2^- \rightarrow 11/2 $) gamma-ray transitions has been considered. With that B(E2) value so obtained for the ($ 17/2^- \rightarrow 15/2^- $) transition, the mean lifetime (τ = 2.4 ps) of the state ($ 17/2^- $) is obtained using the following relation:

Where, τ is the level lifetime (in ps), $ E_\gamma $, the γ-ray energy of transition (in MeV), $ B_\gamma $, the branching ratio and $ \alpha_t $, the total internal conversion coefficient.

Now using this lifetime of τ = 2.4 ps of $ 17/2^- $ state, the actual intensity of 450 keV ($ 29/2^+ \rightarrow 25/2^+ $) gamma-transition has been obtained using the same procedure as adopted to get the actual intensity of 231 keV γ-transition of Band 3 described above. In this way the actual intensity of our γ-transition 450 keV ($ 29/2^+ \rightarrow 25/2^+ $) in Band 3 has been obtained for various target-stopper distances and used for the lifetime analysis. The intensity variation of the shifted (S) and unshifted (U) energy components of 450 keV γ-ray at three target-stopper distances is shown in Fig. 10 (a), while the representative fit of the unshifted gamma-ray energy peak at two target-stopper distances; 8 μm (first distance) and 103 μm (distance of minimum intensity) is shown in Fig. 10 (b).

The basic strategy of the PSM approach is similar to the spherical shell model with the only difference that deformed basis are employed for diagonalizing the shell model Hamiltonian rather than the spherical one. The deformed basis are constructed by solving the triaxial Nilsson potential with optimum quadrupole deformation parameters of $ \epsilon$ and $ \epsilon' $. In principle, the deformed basis can be constructed with arbitrary deformation parameters, However, the basis is constructed with expected or known deformation parameters (so-called optimum) for a given system under consideration. These deformation values lead to an accurate Fermi surface, and it is possible to choose a minimal subset of the basis states around the Fermi surface for a realistic description of a given system. The Nilsson basis states are then transformed to the quasiparticle space using the simple Bardeen-Cooper-Schriefer (BCS) ansatz for treating the pairing interaction.

The inclusion of multi-quasiparticle basis space in PSM approach has made it feasible to study not only the ground-state properties but also the high-spin band structures in deformed and transitional nuclei [12]. Using the PSM approach, odd-proton systems have been studied earlier with the model space of one-proton and one-proton coupled to two-neutron quasiparticle states. However, to investigate the high-spin spectroscopy of these systems, the basis space needs to be extended by including proton aligning configurations, in addition to the neutron states. In the present work, the extended basis space has been implemented and the complete basis space in the generalized approach is given by $ : $

where $ |\Phi\rangle; $ is the triaxially-deformed quasiparticle vacuum state. $ P^I_{MK} $ is the three-dimensional angular-momentum-projection operator given by [13] $ : $

with the rotation operator

Here, $ ''\Omega'' $ represents the set of Euler angles ($ \alpha, \gamma = [0,2\pi],\, \beta= [0, \pi] $) and $ \hat{J}^{,}s $ are the angular-momentum operators. The angular-momentum projection operator in Eq. (5) not only projects out the good angular-momentum but also states having good K-values by specifying a value for K in the rotational matrix, $ "D" $ in Eq. (5). The constructed projected basis of Eq. (4) is then used to diagonalize the shell model Hamiltonian, consisting of the harmonic oscillator single-particle Hamiltonian and a residual two-body interaction comprising of quadrupole-quadrupole, monopole pairing, and quadrupole pairing terms. These terms represent specific correlations that are considered to be essential to describe the low-energy nuclear phenomena. The Hamiltonian has the following form:

In the above equation, $ \hat H_0 $ is the spherical single-particle part of the Nilsson potential [14]. The QQ-force strength, χ, in Eq. (7) is related to the quadrupole deformation $ \epsilon$ as a result of the self-consistent HFB condition, and the relation is given by [15]:

where $ \omega_\tau = \omega_0 a_\tau $, with $ \hslash\omega_0=41.4678 A^{-{1\over 3}} $ MeV, and the isospin-dependence factor $ a_\tau $ is defined as

with $ + (-) $ for $ \tau = $ neutron (proton). The harmonic oscillation parameter is given by $ b^2_\tau=b^2_0/a_\tau $ with $ b^2_0=\hbar/{(m\omega_0)}=A^{1\over 3} $ fm². The monopole pairing strength $ G_M $ (in MeV) is of the standard form

where the minus (plus) sign applies to neutrons (protons). In the present calculation, we choose $ G_1 $ and $ G_2 $ such that the calculated gap parameters reproduce the experimental mass differences. This choice of $ G_M $ is appropriate for the single-particle space employed in the present calculation, where three major oscillator shells are used for each type of nucleons (N$ =3,4,5 $ major shells for both neutrons and protons). The quadrupole pairing strength $ G_Q $ is assumed to be proportional to $ G_M $, the proportionality constant being fixed as usual to be 0.1. These interaction strengths, although not exactly the same, are consistent with those used earlier in the PSM calculations [16, 17]. Using the angular-momentum projected states as the basis, the spherical shell model Hamiltonian of Eq. (7) is diagonalized following the Hill-Wheeler approach. The generalized eigenvalue equation is given by

where the Hamiltonian and norm kernels are given by

The Hill-Wheeler wavefunction is given by

where $ f_{\kappa K}^{I} $ are the variational coefficients, and the index “κ“ designates the basis states of Eq. (4). The Hamiltonian in Eq. (7) is diagonalized using the projected basis. The obtained wavefunction can be written as

Here, the index “σ“ labels the states with same angular momentum and “κ“ the basis states. In Eq. (13), $ a^{\sigma}_{\kappa} $ are the amplitudes of the basis states κ. These wavefunctions are used to calculate the electromagnetic transition probabilities. The reduced electric quadrupole transition probability $ B(E2) $ from an initial state $ ( \sigma_i , I_i) $ to a final state $ (\sigma_f, I_f) $ is given by [18],

and transitional Quadruple moment can be obtained from B(E2) values using following relation:

As in our earlier publications [16, 17, 19−21], we have used the effective charges of 1.6 e (for protons) and 0.6 e (for neutrons). The effective charges are employed instead of the bare charges as core is used in the PSM approach and valance particles occupy only three major oscillator shells. In Ab-initio approaches with no core, only bare charges need to be used. PSM calculations proceed in several stages. In the first stage, the deformed basis space is constructed by solving the triaxially-deformed Nilsson potential. 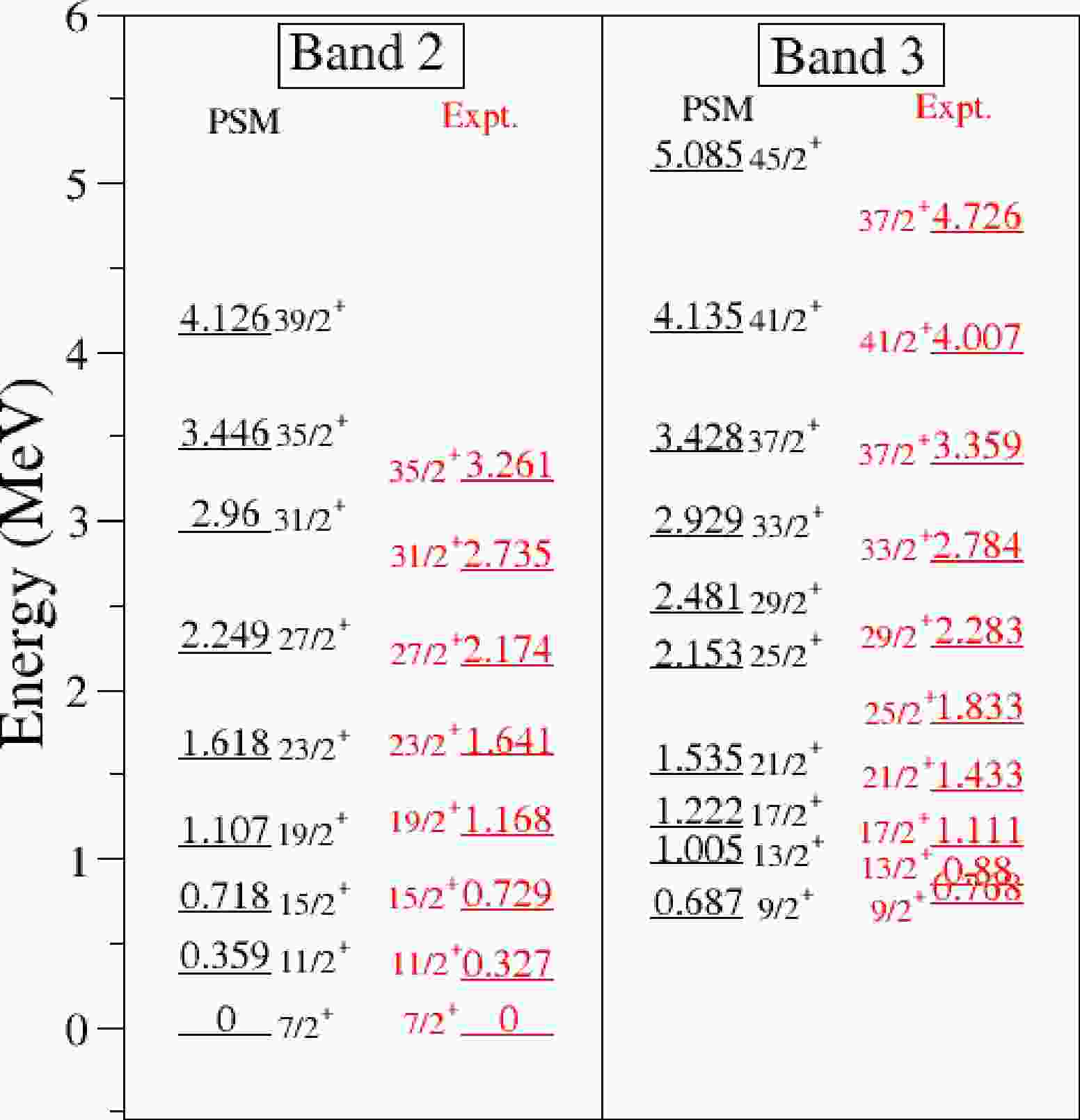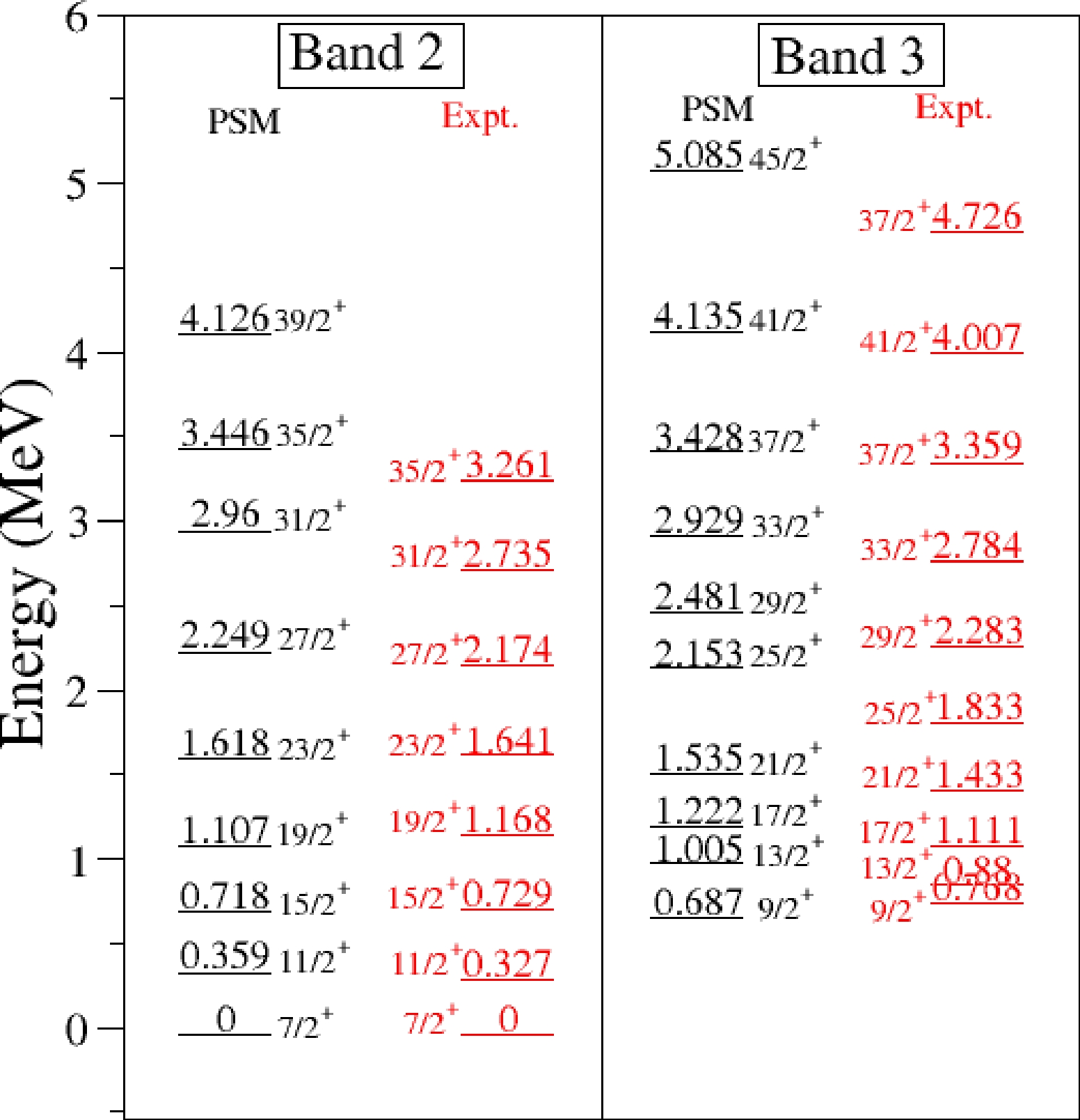In the present work, we have done PSM calculations with two deformation values, one with the deformation value of $ \epsilon=0.21 $ and the other with the larger value of $ \epsilon=0.28 $ [22]. In Tables 1 and 2, we present the B(E2) transition probabilities and $ Q_t $, and it is evident from the Tables that the measured values are reproduced with the larger value of $ \epsilon=0.28 $. In ref. [22], the deformation value has been calculated using Woods-Saxon potential and this value may not be the optimum one in the TPSM study. The non-axial deformation parameter $ \epsilon' = 0.100 $ has been chosen so that the behavior of the γ band is properly described. The configuration space employed corresponds to three principal oscillator shells $ \nu[4,5,6] $ and $ \pi[3,4,5] $. The pairing strengths have been parameterized in terms of two constants $ G_1 $ and $ G_2 $. In this work, we choose $ G_1 $ = 21.14 MeV and $ G_2 $ = 13.86 MeV; with these pairing strengths, we approximately reproduce the experimental odd-even mass differences in this region. The quadrupole pairing strength $ G_Q $ is assumed to be proportional to $ G_M $, and the proportionality constant was set to 0.18. In the second step, the good angular-momentum states are obtained from the deformed basis by employing the three-dimensional angular-momentum projection technique. The projected bands obtained from one and 3-quasiparticle states close to the Fermi surface, which is referred to as band diagram, are the diagonal matrix elements before band mixing. The projection from the 1-quasiparticle configuration gives rise to band structures with $ K=1/2,5/2,9/2,13/2 $, and 3-qp bands with $ K=3/2,7/2,11/2,15/2 $, corresponding to the K value of different rotational bands. In PSM calculation on $ ^{177} {\rm{Re}}$ nucleus, the band energies, obtained after diagonalization, are shown in Fig. 11 with the available experimental data. It is evident from the figure that PSM results are in excellent agreement with the known experimental energies.

Energy (${\rm{E}} _\gamma $) (keV)	Spin ($ \hslash $) $ (I^{\pi}_{i} \rightarrow I^{\pi}_{f}) $	lifetime ($ \tau $) (ps)	Conv. Coeff. ($ \alpha_t $)	B(E2) ($ e^2b^2 $)	${\rm{Q}} _t $ (eb)	B(E2) ($ e^2b^2 $) (PSM) $ \varepsilon = 0.28 $($ 0.21 $)	${\rm{Q}} _t $ (eb) (PSM) $ \varepsilon = 0.28 $($ 0.21 $)
327	11/2$ ^{+}\rightarrow $ 7/2$ ^{+} $	$ 17.0_{-1.2}^{+1.9} $	0.047 (7)	$ 0.36_{-0.09}^{+0.14} $	$ 4.6_{-0.6}^{+0.9} $	0.40 (0.52)	4.8 (6.0)
402	15/2$ ^{+}\rightarrow $ 11/2$ ^{+} $	$ 4.2_{-0.4}^{+0.2} $	0.028 (4)	$ 0.93_{-0.17}^{+0.08} $	$ 6.2_{-0.6}^{+0.3} $	0.94 (0.75)	5.9 (3.0)
439	19/2$ ^{+}\rightarrow $ 15/2$ ^{+} $	$ 2.8_{-0.5}^{+0.5} $	0.022 (4)	$ 1.29_{-0.29}^{+0.29} $	$ 6.7_{-0.7}^{+0.7} $	1.17 (0.94)	6.5 (7.0)
473	23/2$ ^{+}\rightarrow $ 19/2$ ^{+} $	< 1.7	0.019	> 1.70	> 7.4	1.01 (1.17)	7.1 (7.2)

Table 1.  The experimental and calculated B(E2)(PSM) results in the present experiment for different γ-ray transitions of interest of the $ \pi d_{5/2} $ (Band 2) $ ^{177}Re $ nucleus.

Energy (${\rm{E}} _\gamma $) (keV)	Spin ($ \hslash $) $ (I^{\pi}_{i} \rightarrow I^{\pi}_{f}) $	lifetime ($ \tau $) (ps)	Conv. Coeff. ($ \alpha_t $)	B(E2) ($ e^2b^2 $)	${\rm{Q}} _t $ (eb)	B(E2) ($ e^2b^2 $) (PSM) $ \varepsilon = 0.28 $($ 0.21 $)	${\rm{Q}} _t $ (eb) (PSM) $ \varepsilon = 0.28 $($ 0.21 $)	$ \tau_{SF} $ (ps) Side feeding
231	17/2$ ^{+}\rightarrow $ 13/2$ ^{+} $	$ 24.7_{-1.2}^{+1.4} $	0.116 (17)	$ 1.60_{-0.22}^{+0.25} $	$ 7.0_{-0.5}^{+0.6} $	1.70 (1.72)	7.1 (4.0)	1.5
322	21/2$ ^{+}\rightarrow $ 17/2$ ^{+} $	$ 3.8_{-0.2}^{+0.2} $	0.048 (7)	$ 1.95_{-0.29}^{+0.36} $	$ 7.6_{-0.6}^{+0.7} $	1.79 (1.62)	7.3 (3.0)	0.9
400	25/2$ ^{+}\rightarrow $ 21/2$ ^{+} $	$ 2.4_{-0.6}^{+0.7} $	0.028 (4)	$ 2.47_{-0.88}^{+0.80} $	$ 8.5_{-1.4}^{+0.5} $	2.24 (1.94)	7.9 (9.0)	1.1
450	29/2$ ^{+}\rightarrow $ 25/2$ ^{+} $	< 1.1	0.021	> 3.93	> 10.6	2.87 (1.64)	8.5 (3.0)	−

Table 2.  The experimental and calculated B(E2)(PSM) results in the present experiment for different γ-ray transitions of interest of the $ \pi i_{13/2} $ (Band 3) of $ ^{177}Re $ nucleus.

Figure 11.  (Color online) Comparison between the experimental and PSM results for the band structures of $ ^{177} {\rm{Re}}$.

For extracting the level lifetime information, the normalized intensity decay curves of unshifted γ-ray transitions of all eight gamma energies of interest have been analyzed with the computer program LIFETIME [23] (the details of LIFETIME program have been provided in Ref.[8]). The comprehensive details of lifetime analysis, including the extraction of B(E2) values and $ Q_t $ values through LIFETIME program described in [8]. The lifetime program uses sets of coupled differential equations called Batemanʼs equations [24] to determine the level population and the intensities of the shifted and the unshifted γ-ray energy for each transition of interest. At each level of the modelled band, the lifetime program considers two types of feeding, namely the cascade feeding from above and the side feeding. However, for the highest level, only the feeding from the top is considered through an unknown rotational band. The quadrupole moment for this feeding band was varied to have the best fit to the observed highest level. More details about the lifetime analysis through the LIFETIME program and the steps involved in it are given in [8]. For each γ-ray transition of interest, to find the error in the intensity a sum of the fitting error and the statistical error only is considered. The errors in the lifetimes have been calculated through the least-square minimization package, MINUIT [25] included in the LIFETIME program. This routine calculates true parameter errors by executing the behavior of the $ \chi^2 $ function over the unit interval on both side of the minimum $ \chi^2 $.

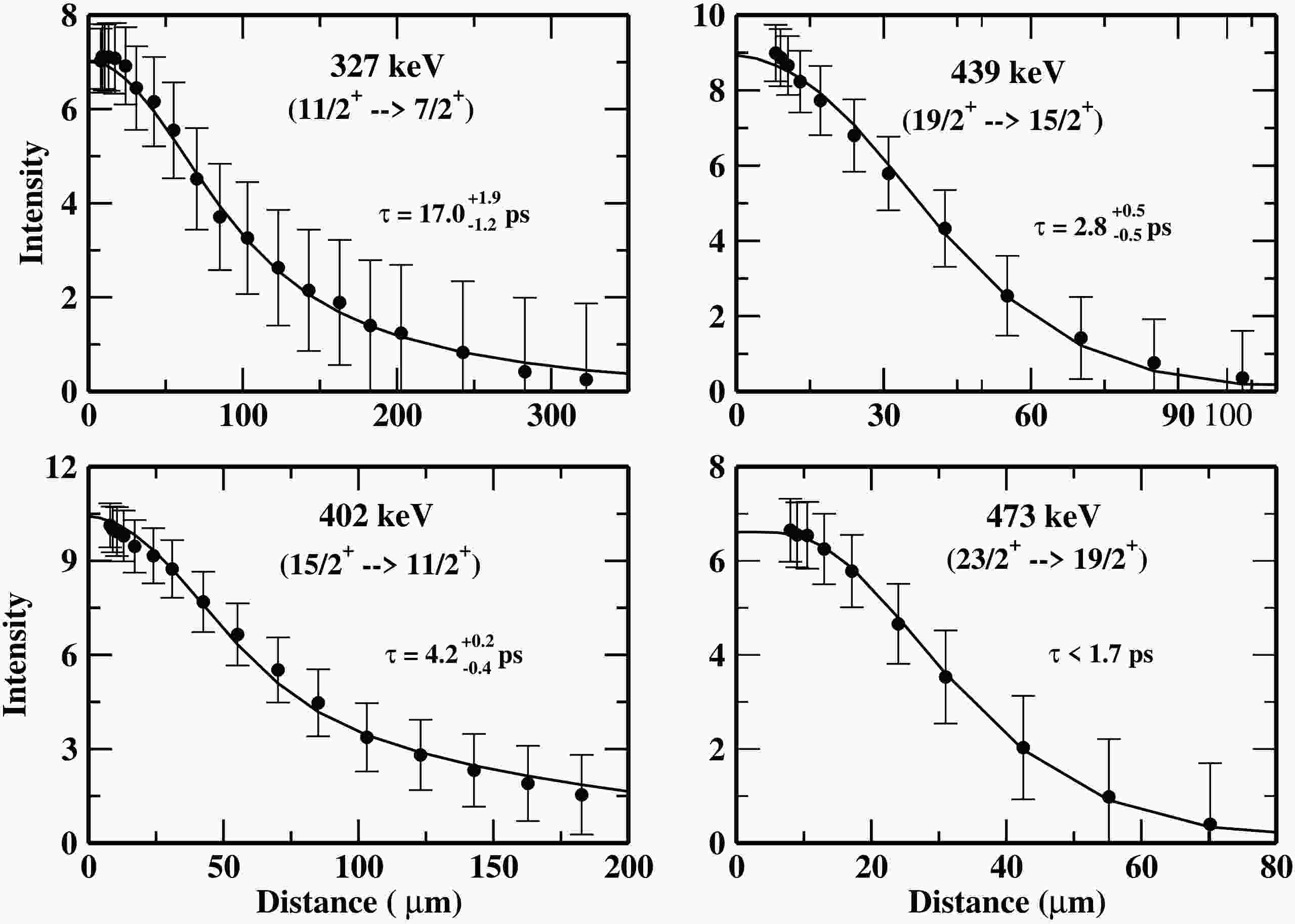
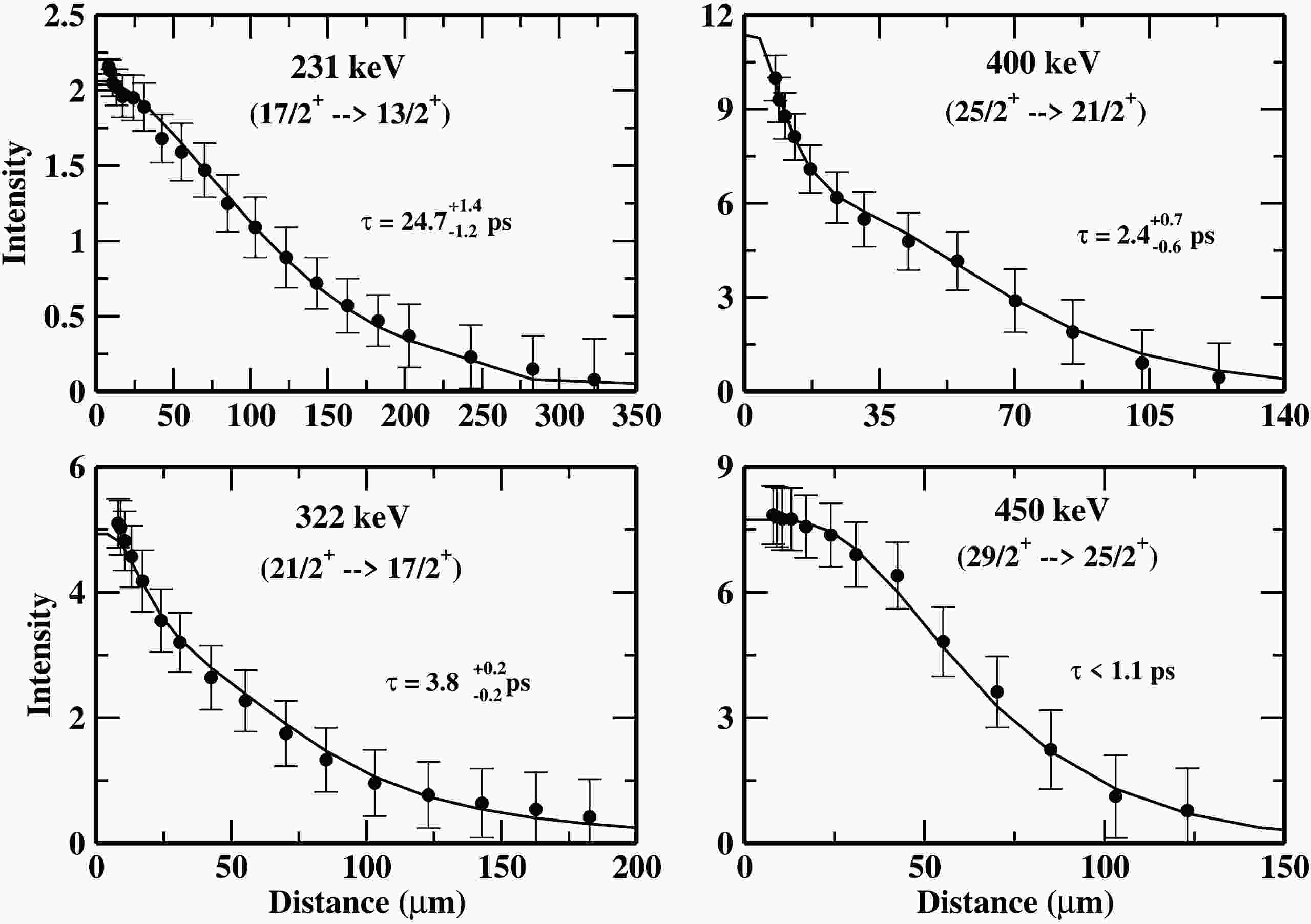
The intensity decay curves as a function of distance for various γ-ray energies of interest of $ \pi d_{5/2} $ (α = -1/2) (Band 2) and $ \pi i_{13/2} $ (α = +1/2)(Band 3) are analyzed through the LIFETIME code [23] and mean lifetime values for various excited states have been obtained. The resulting intensity decay curves of unshifted energies for the γ-transitions of interest in Band 2 and Band 3 are shown in Fig. 12 and Fig. 13 respectively. From the extracted mean lifetimes, the reduced electric quadrupole transition probability B(E2) values have been found using Eq. 2. From the B(E2) values the transitional quadrupole moment $ Q_t $ have been deduced using the following relation: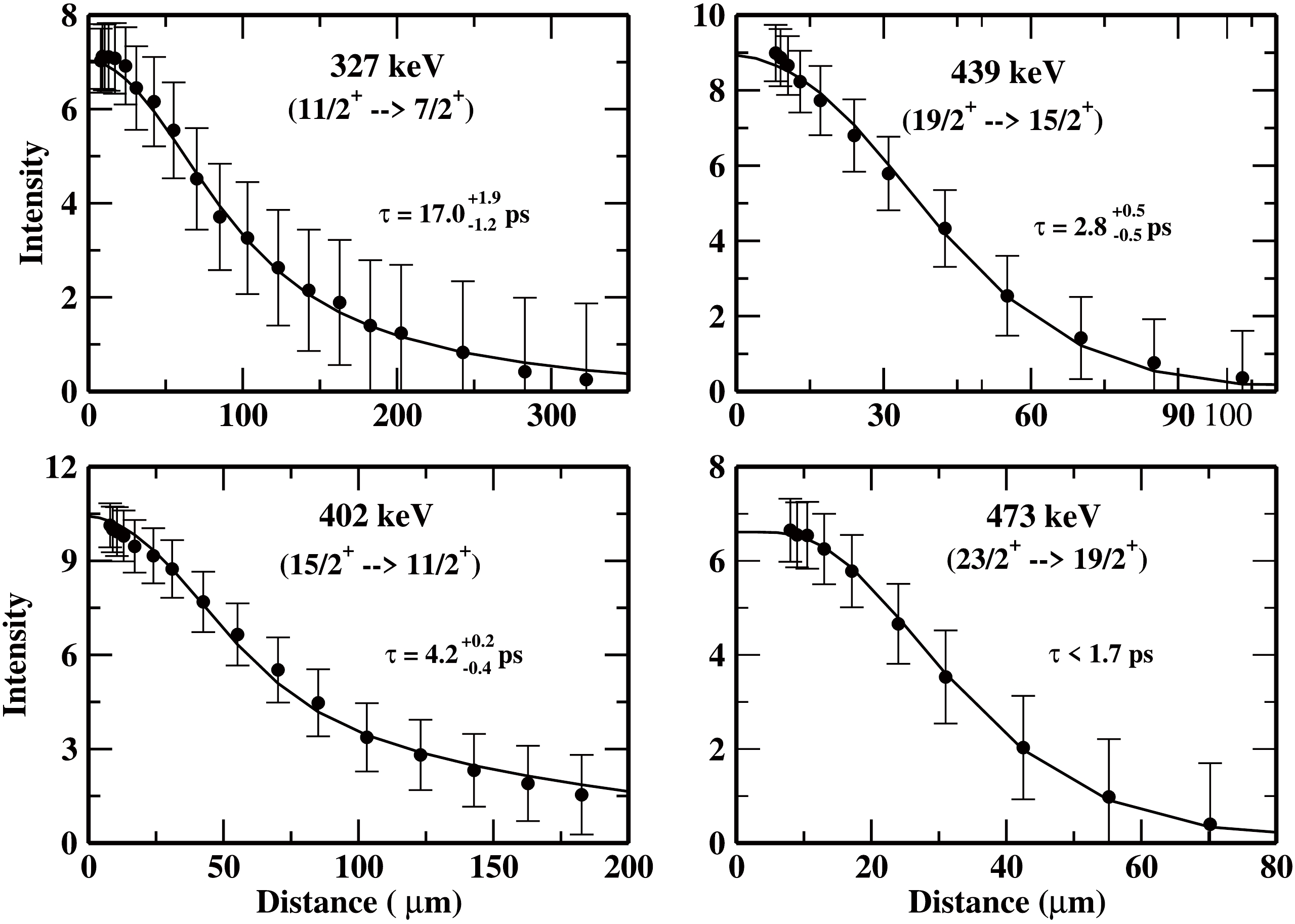

Figure 12.  Unshifted intensity decay curve for the γ-ray transitions of the Band 2 ($ \pi d_{5/2} $, α = -1/2) in $ ^{177} {\rm{Re}}$ nucleus obtained by fitting through the LIFETIME code.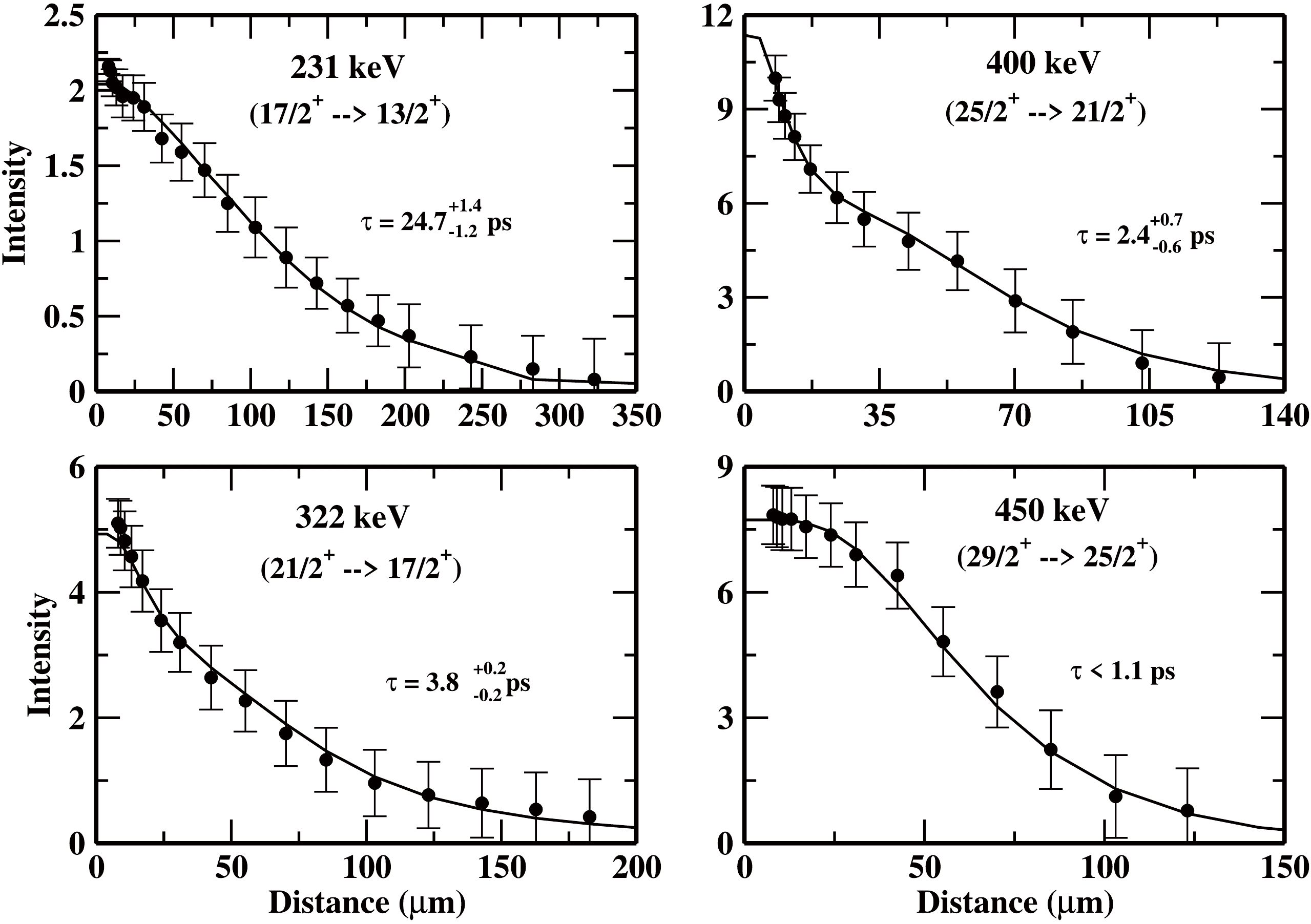

Figure 13.  Unshifted intensity decay curve for the γ-ray transitions of the Band 3 ($ \pi i_{13/2} $) in $ ^{177} {\rm{Re}}$ nucleus obtained by fitting through the LIFETIME code.

Where, $ \langle I2K0|I-2 K\rangle $ are the Clebsch-Gordon (C.G) coefficient, given by:

In the present work, K = 5/2 and 1/2 are used for Band 2 and Band 3 respectively. The results obtained are summarised in Table 1 for the $ \pi d_{5/2} $ (Band 2) and Table 2 for the $ \pi i_{13/2} $ (Band 3). The experimental results are also being compared to the results obtained with PSM model calculations in Table 1 & 2. Looking at the results for $ \pi d_{5/2} $ (Band 2) in Table 1, it is clear that the experimental B(E2) values are increasing smoothly between $ \frac{11}{2}^+ \hslash $ to $ \frac{15}{2}^+ \hslash $ state which suggest change in the structure of $ ^{177} {\rm{Re}}$ nucleus in this high -K configuration. Beyond $ \frac{15}{2}^+ \hslash $ state the BE(2) values look to be more or less same (within experimental error) which indicate the stability of the structure in this yrast configuration in $ ^{177} {\rm{Re}}$ nucleus. The results of the PSM calculations support the changing structure of the nucleus in this configuration as the calculated B(E2) values are also found to be increasing with spin, with an overall agreement with the experimental B(E2) values within the error bars. For the $ \pi i_{13/2} $ (α = +1/2) band, however, the behavior of B(E2) values with spin is found different from that of $ \pi d_{5/2} $ band. For this low-K high-j band as the results in Table 2 show, the experimental B(E2) values are constant (within error bars) up to $ \frac{21}{2}^+ \hslash $ spin and increase sharply increase thereafter at high spins. The increase in B(E2) value between $ \frac{21}{2}^+ \hslash $ to $ \frac{25}{2}^+ \hslash $ is found to be ~ 27 % and between $ \frac{25}{2}^+ \hslash $ to $ \frac{29}{2}^+ \hslash $ to ~ 59 %. The big increase in B(E2) values tend to suggest a major shape stretching happening in this intruder configuration at high spins. However, the results of the PSM calculations do not support this idea of observed shape stretching at high spins. As clear from Table 2, the PSM calculated B(E2) values are at significant difference from the experimental B(E2) values and tend to suggest an almost stable structure of $ ^{177} {\rm{Re}}$ nucleus in this low-K configuration. In Fig. 14, the variation of observed transitional quadrupole moment (${\rm{Q}} _t $) as a function of rotational frequency for various observed bands in $ ^{177} {\rm{Re}}$ is shown. From the figure, the following conclusion can be drawn:

Figure 14.  (Color online) The comparison of $ Q_t $ values for various observed quasi-proton bands in $ ^{177}Re $ nucleus, with the data for the $ d_{5/2} (\alpha = +1/2) $ band, and the data for the $ h_{11/2} $, band and the $ h_{9/2} $ band have been taken from reference [4].

● The average ${\rm{Q}} _t $ value for $ \pi i_{13/2} $ band is the highest (${\rm{Q}} _t $) among all the other observed bands, which clearly shows the strong deformation driving capability of this low-K intruder configuration.

● The higher average ${\rm{Q}} _t $ (~ 8.7 (6)) value for low-K $ \pi i_{13/2} $ intruder band compared to ${\rm{Q}} _t $ (~ 6.5 (4)) value for low-K $ \pi h_{9/2} $ intruder band, the average ${\rm{Q}} _t $ values for other high-K bands in $ ^{177} {\rm{Re}}$ nucleus, ${\rm{d}} _{5/2} $(α = +1/2, K= 5/2, ${\rm{Q}} _t $ ~ 5.3 (4)), ${\rm{d}} _{5/2} $(α = -1/2, K= 5/2, ${\rm{Q}} _t $ ~ 6.3 (5)) and ${\rm{h}} _{11/2} $(α = +1/2, K= 9/2, ${\rm{Q}} _t $ ~ 5.7 (5)) is indicative of the deformation driving character of this orbital.

● The almost constant nature of ${\rm{Q}} _t $ values as a function of rotational frequency for $ \pi h_{9/2} $, $ \pi d_{5/2} $ and $ \pi h_{11/2} $ bands within the error bars indicate the stable structure of the $ ^{177} {\rm{Re}}$ nucleus in these configurations. However, the sharply increasing trend of ${\rm{Q}} _t $ values at high spins in $ \pi i_{13/2} $ indicates the shape stretching of the nucleus in this intruder configuration.

● On comparing the nature of ${\rm{Q}} _t $ values for the two intruder configurations $ \pi h_{9/2} $[541]$ \frac{1}{2}^- $ and $ \pi i_{13/2} $[660]$ \frac{1}{2}^+ $ in the given figure, it is clear that though both are deformation driving the deformationdriving capability of $ \pi i_{13/2} $ orbital is more than the deformation driving capability of $ \pi h_{9/2} $ orbital. As both of these orbitals are well above the Fermi surface ($ \pi i_{13/2} $ orbital above the $ \pi h_{9/2} $ orbital), the higher average ${\rm{Q}} _t $ value for the $ \pi i_{13/2} $ band compared to the $ \pi h_{9/2} $ band is indicative of more particle nature of the $ \pi i_{13/2} $ band than the $ \pi h_{9/2} $ band in this nucleus.

To see the effect of proton and neutron Fermi surfaces on the deformation driving capabilities of the two intruder high-j orbitals ($ \pi i_{13/2} $ orbital and $ \pi h_{9/2} $ orbital), the average ${\rm{Q}} _t $ values for the $ \pi h_{9/2} $ and $ \pi i_{13/2} $ bands in $ ^{177}Re $ (present case), $ ^{179} {\rm{Ir}}$ [26] and $ ^{181} {\rm{Ir}}$ [27] have been tabulated in Table 3.

Nuceli	(Z, N)	$ Q_{avg} $ (eb) $ \pi h_{9/2} $	$ Q_{avg} $ (eb) $ \pi i_{13/2} $	% Change
$ ^{177}Re $	75,102	6.5 (4)	8.7 (6)	~ 33
$ ^{179}Ir $ [26]	77,102	< 6.0	$ \approx $ 7.8	~ 30
$ ^{181}Ir $ [27]	77,104	6.04 (33)	8.99 (37)	~ 50

Table 3.  The comparison of transitional quadrupole moment (${\rm{Q}} _t $) observed for $ \pi h_{9/2} $[541]$ \frac{1}{2}^- $ band and $ \pi i_{13/2} $[660]$ \frac{1}{2}^+ $ band in $ ^{177} {\rm{Re}}$, $ ^{179} {\rm{Ir}}$ and $ ^{181} {\rm{Ir}}$ nuclei.

Looking at the values in Table 3, it can inferred that the increase of proton Fermi surface from Re (Z = 75) to Ir (Z = 77) has almost no effect on the relative deformation driving capabilities of the two orbitals. However, on comparing the average ${\rm{Q}} _t $ values for the two orbitals in $ ^{179} {\rm{Ir}}$ and $ ^{181} {\rm{Ir}}$ (Z = 77) in the table, it can be concluded that an increase in neutron Fermi surface from N = 102 to 104 has almost no effect on the deformation driving capability of $ \pi h_{9/2} $ orbital, but has big influence on the deformation driving capability of the $ \pi i_{13/2} $ orbital. This is expected as in the case of Ir; the $ \pi h_{9/2} $ orbital is near to the Fermi surface and therefore acts more like a quasi-particle orbital whereas the $ \pi i_{13/2} $ orbital is still well above the Fermi surface ${\rm{E}} _{exc} $ ~ 1 MeV and so it still keeps its deformation driving capability.

The result for the lifetime measurements in $ ^{177}Re $ indicates that the gradual increment of B(E2) values for high-K $ \pi d_{5/2} $ ($ \alpha = -1/2) $ (Band 2) are gradually increasing with increase in spin at low spin values. This indicates a changing structure or a possible shape stretching (β-stretching) of the nucleus in this high -K configuration. For the $ \pi i_{13/2} $ (K =1/2) band, on the other hand, the B(E2) values are significantly higher than those of the B(E2) values of $ \pi d_{5/2} $ band, but show constant nature with increase in spin values. This indicates the larger collectivity and stable nuclear shape for $ ^{177}Re $ nucleus in this low -K configuration. Although the results of B(E2) values calculated using PSM model calculations do not match with the experimental values for both the bands but their behavior as a function of spin do support the different deformed structures of $ ^{177}Re $ nucleus in the two configurations. Also, when a comparison of $ Q_t $ values is done for the $ \pi h_{9/2} $ (K = 1/2) [4] and the $ Q_t $ values obtained for the $ \pi i_{13/2} $ band in the present measurement, the $ \pi i_{13/2} $ band is found to be more collective and hence has more deformation driving tendency compared to the $ \pi h_{9/2} $ band.

The authors would like to thank the support provided by the pelletron and support staff of the IUAC, New Delhi.