-
Stellar burning depends on the star's initial mass and can proceed through either the
$ p-p $ chain or the Carbon-Nitrogen-Oxygen (CNO) cycle, fusing hydrogen to helium through chain fusion processes - sequence of thermonuclear reactions that provides most of the energy radiated by the hot stars [1–3]. Unlike the$ p-p $ chain, the CNO cycle is a catalytic one that converts four protons into one helium nucleus but does so via reactions on the pre-existent seed isotopes of carbon, nitrogen, and oxygen nuclei. The carbon, nitrogen, and oxygen isotopes act just as catalysts in the CNO cycle. The CNO bi-cycle involves the following chains of nuclear reactions:$ ^{12}{\rm{C}}(p, \gamma )^{13}{\rm{N}}(\beta ^+\nu )^{13}{\rm{C}}(p, \gamma )^{14}{\rm{N}}(p, \gamma )^{15}{\rm{O}}(\beta ^+\nu )^{15}{\rm{N}} \begin{array}{l} \longrightarrow \;\; {}^{15}{\rm{N}}(p, \alpha )^{ {\rm{12}}}{\rm{C}} \\ \longrightarrow \;\;{}^{15}{\rm{N}}(p, \gamma )^{16} {\rm{O}}(p, \gamma )^{17}{\rm{F}}(\beta ^+\nu )^{17}{\rm{O}}(p, \alpha ){}^{14}{\rm{N}} . \end{array} $ 
(1) Therefore, the CNO bi-cycle produces three electron neutrinos from the
$ \beta ^{+} $ decay of 13N, 15O, and 17F and is also referred to as the "cold" CNO cycle [4]. The CN cycle contains no stable 13N and 15O isotopes that decay to the stable isotopes 13C and 15N, respectively. The catalytic nuclei are lost from the process via the leak reaction 15N($ p, \gamma $ )16O, and the subsequent reactions in (1) restore the catalytic material, generating 16O and heavier isotopes, leading to the accumulation of the 4He and 14N nuclei. This second branch produces 17F, which undergoes$ \beta ^{+} $ decay with the emission of the 1.74 MeV electron neutrinos. Thus, the 15N($ p, \gamma $ )16O process represents a branching reaction linking the alternative NO channel of the CNO cycle that produces the stable oxygen isotopes [5]. Therefore, in the CNO cycle, the proton capture reaction on 15N allows two possible channels: the branch of the cycle 15N($ p, ^{4} {\rm{He}}$ )12C and the branch of the cycle 15N($ p, \gamma $ )16 O reactions intersecting at the 15N nucleus.The rate of the CN with respect to the NO cycle depends on the branching ratio of the 15N(
$ p, \gamma $ )16O and 15N($ p, \alpha $ )12C reaction cross sections. The probability for the 15N($ p, \gamma $ )16O process to occur is about one for every thousand of the second [6]. Thus, the contribution to the overall nuclear energy production is negligible, while the consequences on the nucleosynthesis are critical [7]. Therefore, in the case of an active NO cycle, the correct evaluation of the 15N($ p, \gamma $ )16O reaction is crucial to properly predict the abundances of all the stable 16O, 17O, and 18O isotopes and their relative ratios [8–10]. The reaction rates ratio depends on how much nucleosynthesis of 16O, 17O, and 18O takes place during CNO burning [8].Since the first experimental study of the 15N(
$ p, \gamma $ )16O reaction in 1952 [11], experimental data [6, 12–17] for the total cross sections of the radiative$ p^{15} {\rm{N}}$ capture in the energy region from 80 keV to 2.5 MeV were collected [18, 19]. The analysis of existing experimental measurements of the low-energy 15N($ p, \gamma $ )16O reaction shows that the cross section data differ substantially at lower energies.In the past, multiple theoretical approaches from potential cluster models to multilevel
$R$ -matrix formalisms [5, 16, 20–23] were used to describe the 15N($ p, \gamma $ )16O reaction cross section at stellar energies and astrophysical S-factor, which is the main characteristic of this process at low energies. In the framework of the selective resonant tunneling model [24], the 15N($ p, \gamma $ )16O cross section and S-factor have been studied [25]. Most recently, the astrophysical$S$ -factor for the radiative proton capture process on the 15N nucleus at stellar energies are studied within the framework of the cluster effective field theory [26, 27]. The authors performed the single channel calculations considering only the contribution of the first resonance into a cross section [26] and then reported the results by including two low-energy resonances [27].This study continues the investigation on the reactions for the radiative capture of protons on light atomic nuclei [28, 29] and considers the radiative proton capture on 15N at astrophysical energies in the framework of a modified potential cluster model (MPCM). Within the MPCM, over thirty reactions of radiative capture of protons, neutrons, and other charged particles on light atomic nuclei were considered, and results are summarized in [30, 31]. References [28, 29] provide the basic theoretical framework of the MPCM approach for describing the charged-particle-induced radiative capture reactions. Calculation methods based on the MPCM of light nuclei with forbidden states (FS) are used [32]. The presence of allowed states (AS) and FS are determined based on the classification of the orbital states of clusters according to Young diagrams [33]. Our analysis is data driven: the potentials of intercluster interactions for scattering processes are constructed based on reproduction of elastic scattering phase shifts, considering their resonance behavior or the spectra of the levels of final nucleus. For bound state (BS) or ground state (GS) of nuclei in cluster channels, intercluster potentials are built based on a description of binding energy, asymptotic normalization coefficient (ANC), and mean square radius [28, 29, 31].
The modified model includes a classification of orbital states according to Young's diagrams. This classification leads to the concept of “forbidden states” in interaction potentials. In particular, for the GS of the
$ p^{15} {\rm{N}}$ system, the potential has a deeply bound state, which is the FS, and the second BS is the GS of the 16O nucleus in this channel. The concept of forbidden states makes it possible to effectively consider the Pauli principle for multinucleon systems when solving problems in cluster models for a single-channel approximation. The current study is based on the detailed classification of orbital states in the$ p \ + ^{15} {\rm{N}}$ channel using Young's diagrams, as described previously in Ref. [22].In this study, we investigate a radiative
$ p^{15} {\rm{N}}$ capture on the GS of 16O within the framework of the MPCM. For the first time, the contribution of the 3P1 scattering wave in the p + 15N channel due to$ {}^{3}P_{1}\longrightarrow {}^{3}P_{0} $ $ M1 $ transition is considered. Our approach allows us to analyze the explicit contribution of each transition into the S-factor and show the origin of the interference for$ E1 $ transitions.The rest of this paper is organized as follows. Section II presents a structure of resonance states and construction of interaction potentials based on the scattering phase shifts, mean square radius, asymptotic constant, and BS or GS of the 16O nucleus. The results of calculations of the astrophysical S-factor and reaction rate for the proton radiative capture on 15N are presented in Secs. III and IV, respectively. In the same sections we discuss a comparison of our calculation for the
$S$ -factor and reaction rate with existing experimental and theoretical data. Conclusions are presented in Sec. V. -
The
$ E1 $ transitions from resonant$ {}^{3}S_{1}- $ scattering states are the main contributions to the total cross section of the radiative proton capture on 15N to the GS of 16O [5]. There are two$ {}^{3}S_{1} $ resonances in the channel of p + 15N in continuum, given as follows:1. The first resonance appears at an energy of 335(4) keV with a width of 110(4) keV in the laboratory frame and has a quantum numbers
$ J^{\pi } $ ,$ T=1^{-} $ ,$ 0 $ (see Table 16.22 in [34]). This resonance is due to the triplet$ {}^{3}S_{1} $ scattering state and leads to$ E1 $ transition to the GS. In the center-of-mass (c.m.) frame, this resonance is at an energy of 312(2) keV with a width of 91(6) keV and corresponds to the resonant state of the 16O at an excitation energy of$ E_{{\rm{x}}}=12.440(2) $ MeV (see Table 16.13 in [34]). However, in the new database [35], an excitation energy of$ E_{ {\rm{x}}}=12.445(2) $ MeV and a width of$ \Gamma =101(10) $ keV in the c.m. are reported for this resonance.2. The second resonance is at an energy of 1028(10) keV with a width of 140(10) keV in the laboratory frame and has quantum numbers
$ J^{\pi }=1^{-} $ and$ T=1 $ [34]. This resonance is also due to the triplet$ {}^{3}S_{1} $ scattering, which results in$ E1 $ transition to the GS of 16O. In the c.m., the resonance emerges at an energy of 962(2) keV with a width of$ \Gamma =139(2) $ keV, corresponding to an excitation energy of$ E_{{\rm{x}} }=13.090(2) $ MeV of 16O in a new database [35]. In the database [34] for this resonance, an excitation energy of$ E_{{\rm{x}}}=13.090(8) $ MeV and a width of$ \Gamma = $ 130(5) keV in the c.m. are reported.The compilation of experimental data on the
$ {}^{3}S_{1} $ resonances is presented in Table 1.$ {}^{2S+1}L_{J} $ 

$E_{x}$ /MeV

$ E_{\rm{res}} $ /keV

$ \Gamma _{ \rm{res}} $ /keV

$ E_{\rm{theory}} $ /keV

$ \Gamma _{\rm{theory}} $ /keV

$ {}^{3}S_{1} $ (312)

12.440(2) [34] 312(2) [34] 91(6) [34] 312 $ 125-141 $ 

12.445(2)[35] 317(2) [35] 101.5(10) [35] $ {}^{3}S_{1} $ (962)

13.090(8) [34] 962(8) [34] 130(5) [34] 962 $ 131 $ 

13.090(2) [35] 962(2) [35] 139(2) [35] Table 1. Data on the
$ {}^{3}S_{1} $ resonance states in the p + 15N channel.$ E_{\rm{x}} $ is the excitation energy,$ E_{\rm{res}} $ and$ \Gamma _{\rm{res}} $ are the experimental resonance energy and width, respectively.$ E_{\rm{theory}} $ and$ \Gamma _{\rm{theory}} $ are the resonance energy and the width, respectively, obtained from the present calculationsThe other resonances are reported in databases [34, 35]. The third resonance has an energy of 1640(3) keV with a width of 68(3) keV in the laboratory frame and quantum numbers
$ J^{\pi } $ ,$ T=1^{+}, ~0 $ . This resonance can be due to the triplet$ {}^{3}P_{1} $ scattering, which results in the$ M1 $ transition to the GS. The resonance is at an energy of 1536(3) keV with a width of 64(3) keV in the c.m. that corresponds to an excitation energy of 13.664(3) MeV of 16O [34], and in Ref. [35], an excitation energy of 13.665(3) MeV and a width of 72(6) keV in the c.m. are reported. However, this resonance was observed only in measurements [13], and in the later measurements [16, 17], the resonance is absent. Therefore, we will not consider it in our calculations. The next resonance is excited at an energy of 16.20(90) MeV ($ J^{\pi } $ ,$ T=1^{-}, 0 $ ); it has a larger width of 580(60) keV in the c.m., and its contribution to the reaction rate will be small. In addition, in the spectra of 16O [34], another resonance is observed at an excitation energy of 16.209(2) MeV ($ J^{\pi } $ ,$ T=1^{+}, 1 $ ) with a width of 19(3) keV in the c.m. However, the resonance energy is too large and its width too small to make a noticeable contribution to the reaction rates.The cascade transitions via two very narrow 2– resonances, and the 0– and 3– resonances in the
$0.40 \lesssim E_{R}\lesssim $ 1.14 MeV range [17, 36, 37] are considered for the reaction rate calculations. These cascading transitions are included in the NACRE II [19] reaction rate calculations and appear at high$ T_{9} $ . There are two 2– resonances [17] at excitation energies of 12.53 MeV and 12.9686 MeV and widths of 97(10) eV and 1.34(4) keV [35]. When one considers transitions to the GS with 0+, only$ M2 $ transitions, which have a very small cross section, are possible here, and we do not consider them. In addition, due to such small widths, their contribution to the reaction rate will be very small. The measurement of the excitation functions of the three dominant cascade transitions allows one to estimate the contributions from these transitions. In Ref. [5], capture processes to the GS and three excited states$ E_{{\rm{x }}} $ $ =6.049 $ MeV, 6.130 MeV, and 7.117 MeV are considered, which gives$ S(0)= 41(3)\; {\rm{keV\cdot b}}$ in total and 40(3) keV·b for the GS. It is shown that the 1– and two 2+ resonances do not affect the value of the S-factor. Two 3– resonances at$E_{x}= 13.142$ MeV and 13.265 MeV decay into the GS due to the$ E3 $ transition, and their contribution is negligible [5].On the background of strong
$ E1 $ transitions, the next one in the long-wave expansion of the electromagnetic Hamiltonian is the magnetic dipole$ M1 $ transition [38]. In the case of 15N($ p, \gamma _{0} $ )16O,$ M1 $ transition is allowed by selection rules. It occurs as a direct capture from the non-resonance scattering wave$ {}^{3}P_{1} $ to the 16O$ {}^{3}P_{0} $ state. The intensity of the$ M1 $ partial transition depends on the distorted$ {}^{3}P_{1} $ wave only and is related to the corresponding interaction potential. Our$ M1 $ partial cross section estimations in plane-wave approximation show near order of magnitude suppression. The inclusion of the$ p $ -wave interaction in$ p+^{15} {\rm{N}}$ channel enhances the$ M1 $ transition. The interaction potential could be constructed based on an elastic 15N($ p, p $ )15N scattering to describe the$ {}^{3}P_{1} $ phase shift. The phase shifts should satisfy the following conditions: i) at$ E=0 $ ,$ \delta _{^{3}P_{1}}=180^{0} $ , according to the generalized Levinson theorem [32]; ii) fit the exsisting$ p $ -wave 15N($ p, p $ )15N scattereng data; iii) have a non-resonace behavior. Below, we find potential parameters that provide reasonable phase shifts. Therefore, in the calculations, we consider only the above two$ {}^{3}S_{1} $ resonance transitions and non-resonance$ {}^{3}P_{1} $ scattering for the$ M1 $ transition to the 16O GS.We should distinguish
$ M1 $ capture from the non-resonance$ {}^{3}P_{1} $ scattering wave to the 16O$ {}^{3}P_{0} $ state and$ M1 $ de-excitation of 1+ level at 13.665 MeV to the GS. As pointed by deBoer et al. [5], "The 1+ level at$ E_{x} $ = 13.66 MeV could decay by$ M1 $ de-excitation to the ground state but no evidence for this is observed (contrary to Ref. [13])." As mentioned above, we do not consider the contribution of$ M1 $ de-excitation (1+ level at 13.665 MeV) to$ S(E) $ .For total radiative capture cross section calculations, the nuclear part of the
$ p^{15} {\rm{N}}$ interaction potential is contracted using the Gaussian form [28, 29, 31]:$ V(r, JLS, \{f\})=-V_{0}(JLS, \{f\}){\rm exp}\left( -\alpha (JLS, \{f\})r^{2}\right) . $

(2) The parameters α and
$ V_{0} $ in Eq. (2) are the interaction range and strength of the potential, respectively.The strength and the interaction range of the potential (2) depend on the total and angular momenta, the spin,
$ JLS $ , and Young diagrams$ \{f\} $ [30, 31]. For a description of the$ {}^{3}S_{1} $ scattering states, we use the corresponding experimental energies and widths from Table 1. Coulomb potential is chosen as the point-like interaction potential.Construction of the potentials that give the energies and widths of
$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances reported in literature is challenging. One has to find the optimal parameters of the potentials for the description of$ E1 $ transitions that lead to the fitting of the experimental resonance energies and the widths of both interfering resonances. For the$ {}^{3}S_{1} $ (962) resonance, the obtained optimal parameters of the interaction potential for reproducing the resonance energy$ E_{{\rm{res}}}=962(1) $ keV and width$ \Gamma _{{\rm{res}}}=131 $ keV are reported in Table 2. The situation is more complicated with the$ {}^{3}S_{1} $ (312) resonance. While it is possible to reproduce the position and width of the$ {}^{3}S_{1} $ (312) resonance rather accurately, considering the interference of$ {}^{3}S_{1} $ resonances gives different sets of optimal parameters for the potential. We found three sets I – III of optimal values for$ V_{0} $ and α parameters reproducing exactly the energy of the first resonance$ E_{{\rm{theory}}}=312(1) $ keV. However, the width$ \Gamma _{{\rm{theory}}} $ varies in the$ 125-141 $ keV range.Set $ {}^{3}P_{0} $ , GS

$ {}^{3}S_{1} $ (312),

$ E1 $ 

$ {}^{3}S_{1} $ (962),

$ E1 $ 

$ {}^{3}P_{1} $ ,

$ M1 $ 

$ V_{0} $ 

α ANC $ C_{W} $ 

$ V_{0} $ 

α $ \Gamma _{ {\rm{theory}}} $ 

$ V_{0} $ 

α $ \Gamma _{{\rm{theory}}} $ 

$ V_{0} $ 

α I 976.85193 1.1 14.49 2.05 1.0193 0.0028 141 II 1057.9947 1.2 13.71 1.94 1.0552 0.0029 131 105.0675 1.0 131 14.4 0.025 III 1179.3299 1.35 12.85 1.8 1.0902 0.003 125 Table 2. Parameters of interaction potentials
$ V_{0} $ and α for the GS and continuum states. The$ C_{W} $ is a dimensionless constant that corresponds to the range of the experimental ANC of$ 12.88 - 14.76 $ fm−1/2 [21, 23]. The theoretical widths,$ \Gamma _{{\rm{theory}}} $ , for the resonances$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) are calculated using the corresponding parameters of the potentials.$ V_{0} $ and$ \Gamma _{{\rm{theory}}} $ are given in MeV and keV, respectively, α in fm-2, and ANC in fm-1/2.The dependence of the elastic
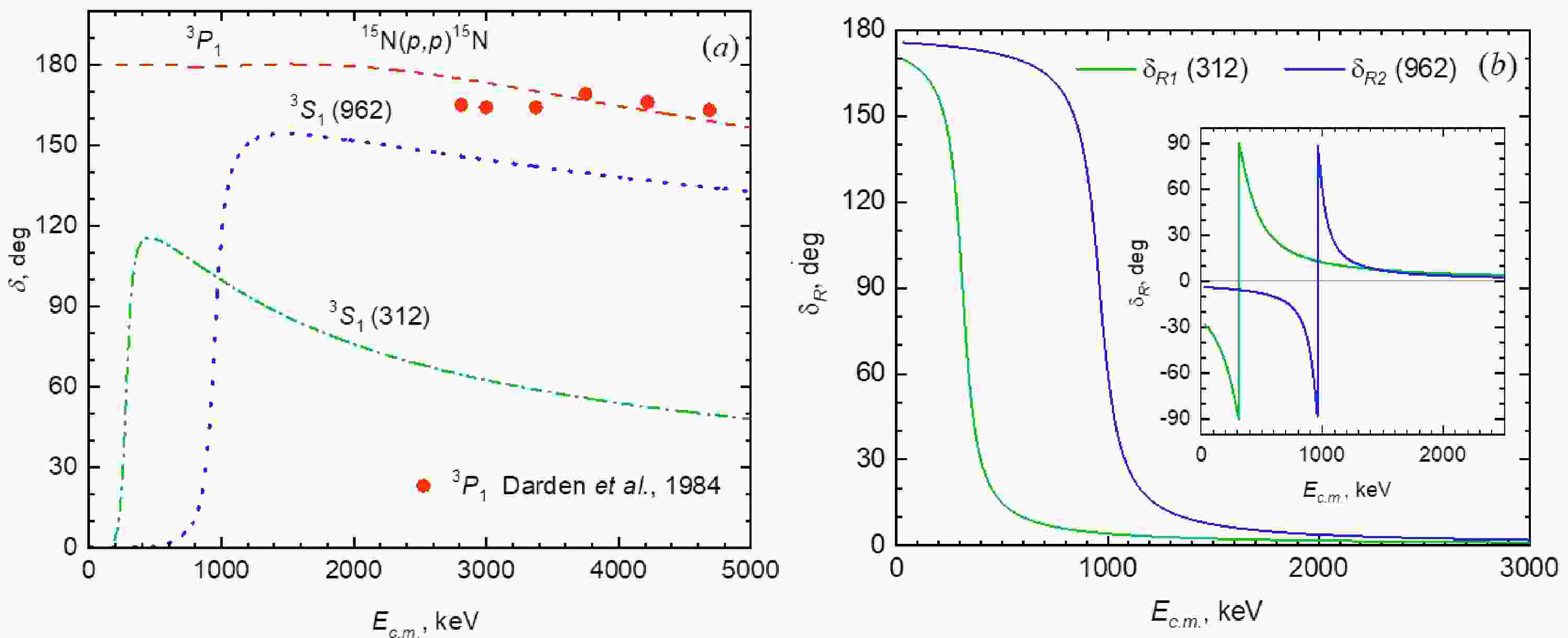
$ p^{15} {\rm{N}}$ scattering phase shifts for the$ E1 $ transitions on the energy is shown in Fig. 1(a). The calculation of the$ {}^{3}S_{1} $ phase shifts with the parameters for the S scattering potential without FS from Table 2 leads to a value of 90°(1) at energies 312(1) and 962(1) keV. Our calculations of the phase shifts for the$ {}^{3}S_{1} $ (312) resonance with the parameter sets I- III show very close energy dependence in the entire energy range up to 5 MeV at a fixed resonance position.
Figure 1. (color online) Dependence of the elastic
$ p^{15} {\rm{N}}$ scattering phase shifts on the energy. (a) Calculations are performed by using the potentials with parameters from Table 2. The phase shifts for the$ {}^{3}S_{1} $ (312) resonance is calculated using set I and is shown by the dash-dotted curve. The dotted and dashed curves represent the phase shifts for the$ {}^{3}S_{1} $ (962) resonance and$ {}^{3}P_{1} $ , respectively. The experimental data are from Ref. [39]. (b) Energy dependence of the resonant phase shifts$ \delta _{R1} $ and$ \delta _{R2} $ calculated using the experimental resonance widths of 91 keV and 130 keV, respectively. Reconstructed scattering resonant phase shifts$ \delta _{R1} $ and$ \delta _{R2} $ are calculated using Eq. (3) and considering the tangent function periodicity. The inset shows the result of the calculation using Eq. (3).In elastic
$ p^{15} {\rm{N}}$ scattering spectra at energies up to 5 MeV, there are no resonance levels with$ J^{\pi }=0^{+}, 1^{+}, 2 $ except for those the mentioned above and widths greater than 10 keV [34]. Therefore, for potentials of non-resonance$ {}^{3}P- $ waves with one bound FS, parameters can be determined based on the assumption that, in the energy region under consideration, their phase shifts are practically zero or have a gradually declining character [29]. For such potential, the optimal parameters are$ V_{p}=14.4 $ MeV and$ \alpha _{p}=0.025 $ fm-2. The result of calculating the$P$ -phase shifts with such potential at an energy of up to 5 MeV is shown in Fig. 1(a). To determine the values of phase shifts at zero energy, we use the generalized Levinson theorem [32]. Therefore, the phase shifts of the potential with one bound FS should begin from 180°. In the energy region$ E_{{\rm{ c.m.}}}<5 $ MeV, the$ {}^{3}P_{1} $ phase shift has gradual energy dependence and is almost constant up to$ E_{{\rm{c.m.}}}\lesssim 2.2 $ MeV.It is interesting to compare experimentally determined phase shifts with our calculations. Although in Ref. [40], the elastic scattering of protons from 15N was studied and authors measured the excitation functions of 15N(
$ p, p $ )15N over the proton energy range from 0.6 to 1.8 MeV at some laboratory angles, no phase shifts were reported. No systematic experimentally determined phase shifts have been reported at energies of astrophysical interest. Absolute differential cross sections were measured for the reactions 15N($ p, p $ )15N [41], and spins and parities are discussed, with resonances suggesting the existence of excited states in 16O. In Ref. [42], the authors carried out a phase-shift analysis of the cross section for the energy interval of 8$ - $ 15 MeV. Angular distributions of the cross section and analyzing power for the elastic scattering of protons from 15N were measured for the energy interval of 2.7$ - $ 7 MeV [39], and a phase-shift analysis of the data was performed. The results of our calculations for the$ {}^{3}P_{1} $ phase shift along with the experimental data [39] are presented in Fig. 1(a).The main assumption in all previous studies of the 15N(
$ p, \gamma $ )16O reaction was that direct and resonant radiative capture cross sections and their interferences contribute to the total cross section. The direct radiative capture process is considered, assuming a potential peripheral radiative capture for a hard sphere scattering [13, 43–46]. However, phase shifts are generally extracted from the experimental data analysis without separating the potential and resonant terms [47, 48]. We follow this ansatz. Consequently, the$ E1 $ transition amplitudes are constructed based on a single radial scattering wave function resembling a continuous and smooth resonance energy dependence. Both$ {}^{3}S_{1} $ phase shifts obtained with these scattering wave functions depend on the energy, as shown in Fig. 1(a). Therefore, we have only the interference between two partial$ E1 $ matrix elements, in contrast to all previous considerations.The resonant phase shift is given by the usual expression [13, 48]
$ \delta _{R}=\tan ^{-1}\frac{\Gamma }{2(E-E_{\rm res})}, $

(3) where Γ is the width of a resonance. In Fig. 1(b), the energy dependence of the resonant
$ \delta _{R1} $ and$ \delta _{R2} $ phase shifts for the resonance widths of 312 keV and 962 keV is presented, respectively. The comparison of the phase shifts for the$ E1 $ transitions via the$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances with the resonant phase shifts$ \delta _{R1} $ and$ \delta _{R2} $ shows their different energy dependence.We construct the potential for 16O in GS with Jπ, T = 0+, 0 in
$ p^{15} {\rm{N}}$ -channel based on the following characteristics: the binding energy of 12.1276 MeV, the experimental values of 2.710(15) fm and 2.612(9) fm [34] for the root mean square radii of 16O and 15N of [49], respectively, and a charge and matter proton radius of 0.8414 fm [50]. The potential should also reproduce the AC. The corresponding potential includes the FS and refers to the$ {}^{3}P_{0} $ state.Usually, for a proton radiative capture reaction of astrophysical interest, one assumes that it is peripheral, occurring at the surface of the nucleus. If the nuclear process is purely peripheral, then the final bound-state wave function can be replaced by its asymptotic form, so the capture occurs through the tail of the nuclear overlap function in the corresponding two-body channel. The Coulomb interaction determines the shape of this tail and is proportional to the asymptotic normalization coefficient. The role of the ANC in nuclear astrophysics was first discussed by Mukhamedzhanov and Timofeyuk [51] and in Ref. [52]. These works paved the way for using the ANC approach as an indirect technique in nuclear astrophysics; see Refs. [45, 53–60], the citations therein, and the most recent review [46].
We construct a potential with the FS
$ {}^{3}P_{0} $ state using the experimental ANC given in Ref. [21] that relates to the asymptotics of the radial wave function as$ \chi _{L}(R)= CW_{-\eta L+1/2}(2k_{0}R) $ . The dimensional constant C is linked with the ANC via the spectroscopic factor$ S_{F} $ . In our calculations, we exploited the dimensionless constant [61]$ C_{W} $ , which is defined in [29] as$ C_{W}=C/\sqrt{2k_{0}} $ , where$ k_{0} $ is wave number related to the binding energy. In Ref. [21], the values$ 192(26) $ fm-1 and 2.1 were reported for the ANC and spectroscopic factor, respectively. In Ref. [23], the dimensional ANC includes the antisymmetrization factor N in the radial overlap function, as clarified by the authors in [59]. The factor N is defined as$N = \left( \begin{matrix} A \\ x \end{matrix} \right) ^{1/2}=\sqrt{\dfrac{A!}{(A-x)!x!}},$ where$ {x} $ and$ {A} $ are the atomic mass numbers of the constituent nucleus from the$ {x} $ and$ {A-x} $ nucleons, respectively [62]. If$ x=1 $ , then$ N=\sqrt{A} $ and, for the reaction 15N($ p, \gamma _{0} $ )16O,$ N=4 $ . Thus, using the experimental square of the ANC of$ 192\pm 26 $ fm−1 [21, 23], we obtained the interval for the dimensionless AC used in our calculations:$ C_{W}=1.82-2.09 $ , which corresponds to the ANC of$ 12.88-14.76 $ fm-1/2. In our calculations, for the proton mass, we use$m_{p} = $ 1.00727646677 amu [50], 15N mass = 15.000108 amu [63], and the constant$ \hbar ^{2}/m_{0}=41.4686 $ MeV·fm2, where$ m_{0}=931.494 $ MeV is the atomic mass unit (amu).The 15N(
$ p, \gamma $ )16O is the astrophysical radiative capture process, in which the role of the ANC is elucidated [46]. In Table 2, three sets of parameters for the$ {}^{3}P_{0} $ GS potential and AC$ C_{W} $ are listed. The asymptotic constant$ C_{W} $ is calculated over averaging at the interval of$ 5-10 $ fm. Each set results in a binding energy of 12.12760 MeV, root mean square charge radius of 2.54 fm, and matter radius of 2.58 fm. However, the sets of$ C_{W} $ result in different widths of the$ {}^{3}S_{1} $ (312) resonance.Notably, there is one important benchmark for the choice of optimal sets for the interaction potential parameters for the first
$ E1 $ (312) resonance. The experimental values of the total cross section$ \sigma _{{\rm{exp}}}(312)=6.0\pm 0.6 $ μb [6] and$ 6.5\pm 0.6 $ μb [16] are in excellent agreement with the existing data, i.e,$ 6.3 $ μb [14] and$ 6.5\pm 0.7 $ μb [12]. Simultaneous variation of$ C_{W} $ for the GS and parameters$ V_{0} $ and α for the$ {}^{3}S_{1} $ (312) was implemented to ensure the value of the cross section$ \sigma _{{\rm{theory}}}(312)=5.8-5.9 $ μb matches the experimental data. The result of this optimization is presented in Table 2 as sets I - III.Table 2 summarizes the potential parameters used in the case where the MPCM works reasonably well for a radiative proton capture in the 15N(
$ p, \gamma _{0} $ )16O reaction.We sum up the procedure and choice of potential parameters as follows:
1. We construct the nucleon-nuclei potentials that produce the channel binding energy with the requested accuracy 10−5 MeV. There are a few such potentials;
2. The experimental ANC is used as a criterion for choosing the potential that provides the required asymptotic behavior of the radial wave function at the fixed binding energy. Thus, the variety of wave functions is constrained within the upper and lower limits for the ANC:
$ 12.88-14.76 $ fm−1/2 for 15N($ p, \gamma $ )16O;3. An additional test of the wave functions reproduces the matter and charge radii with a precision of ~ 5% and the
$ \sigma _{ {\rm{exp}}}(312) $ cross section within experimental uncertainties;4. For the continuous spectrum, the parameters of the potential are fixed using the resonance energy and width above threshold. An additional source of the S-factor uncertainty relates to uncertainties of the resonance energy and width;
5. This procedure gives the model's uncertainty bands for the S-factor.
-
The astrophysical S-factor is the main characteristic of any thermonuclear reaction at low energies. The present analysis focuses primarily on extrapolating the low-energy S-factor of the reaction 15N(
$ p, \gamma $ )16O into the stellar energy range. Since the first experimental study of the 15N($ p, \gamma _{0} $ )16O reaction in 1960 [12], experimental data [6, 13, 16, 17, 19] for total cross sections of the radiative$ p^{15} {\rm{N}}$ capture in the energy region from 80 keV to 2.5 MeV have been collected. These experimental studies verified and confirmed that the radiative$ p^{15} {\rm{N}}$ capture is dominated by the first two interfering resonances at 312 keV and 962 keV with the quantum numbers$ J^{\pi } $ ,$ T=1^{-} $ ,$ 0 $ and$ J^{\pi } $ ,$ T=1^{-} $ ,$ 1 $ , respectively. -
The
$ E1 $ transitions are the main input parts of the radiative capture amplitude for the 15N($ p, \gamma _{0} $ )16O reaction. Therefore, accurate determination of the resonance capture cross sections for these transitions is required to avoid one of the main sources of uncertainty. The radiative resonance capture to the BSs is reviewed in Ref. [46]. Following Ref. [29], after algebraic calculations using quantum numbers related to the 15N($ p, \gamma $ )16O reaction, one can write the cross section for the radiative capture$ p^{15} {\rm{N}}$ to the GS of 16O as$ \sigma _{E1}(E_{{\rm{c.m.}}})=\frac{4\pi {\rm e}^{2}}{9\hbar ^{2}}\left( \frac{K}{k }\right) ^{3}\left( \frac{1}{m_{p}}-\frac{7}{m_{^{15}{\rm{N}}}}\right) ^{2}\left\vert I(k;E1)\right\vert ^{2}. $

(4) In Eq. (4), μ is the reduced mass of the proton and 15N nucleus,
$ K=E_{\gamma }/\hbar c $ is the wave number of the emitted photon with energy$ E_{\gamma } $ , k is relative motion wave number, and$ \begin{aligned}[b] \left\vert I(k;E1)\right\vert ^{2}=&\left\vert {\rm e}^{-{\rm i}\delta _{^{3}S_{1}(312)}}I_{1}+{\rm e}^{-{\rm i}\delta _{^{3}S_{1}(962)}}I_{2}\right\vert ^{2}\\=&\left\vert I_{1}\right\vert ^{2}+\left\vert I_{2}\right\vert ^{2}+2\cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) I_{1}I_{2}. \end{aligned}$

(5) While constructing the radial matrix element in Eq. (4),squared by the modulus, we explicitly point out in Eq. (5) the importance of scattering
$S$ -matrix for analyzing the interference effects (see, for example, Ref. [43]).Note that, for non-interfering amplitudes, the phase-shift factor$ \exp(-\delta_{LJ}) $ converts to the unit in the final general expression for the total cross sections [29–31]. Below, we demonstrate that$ 2\cos\left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) I_{1}I_{2} $ of the interference term plays an important role in the whole treated energy region, especially for the reaction rate at low temperatures (see insert in Fig. 4).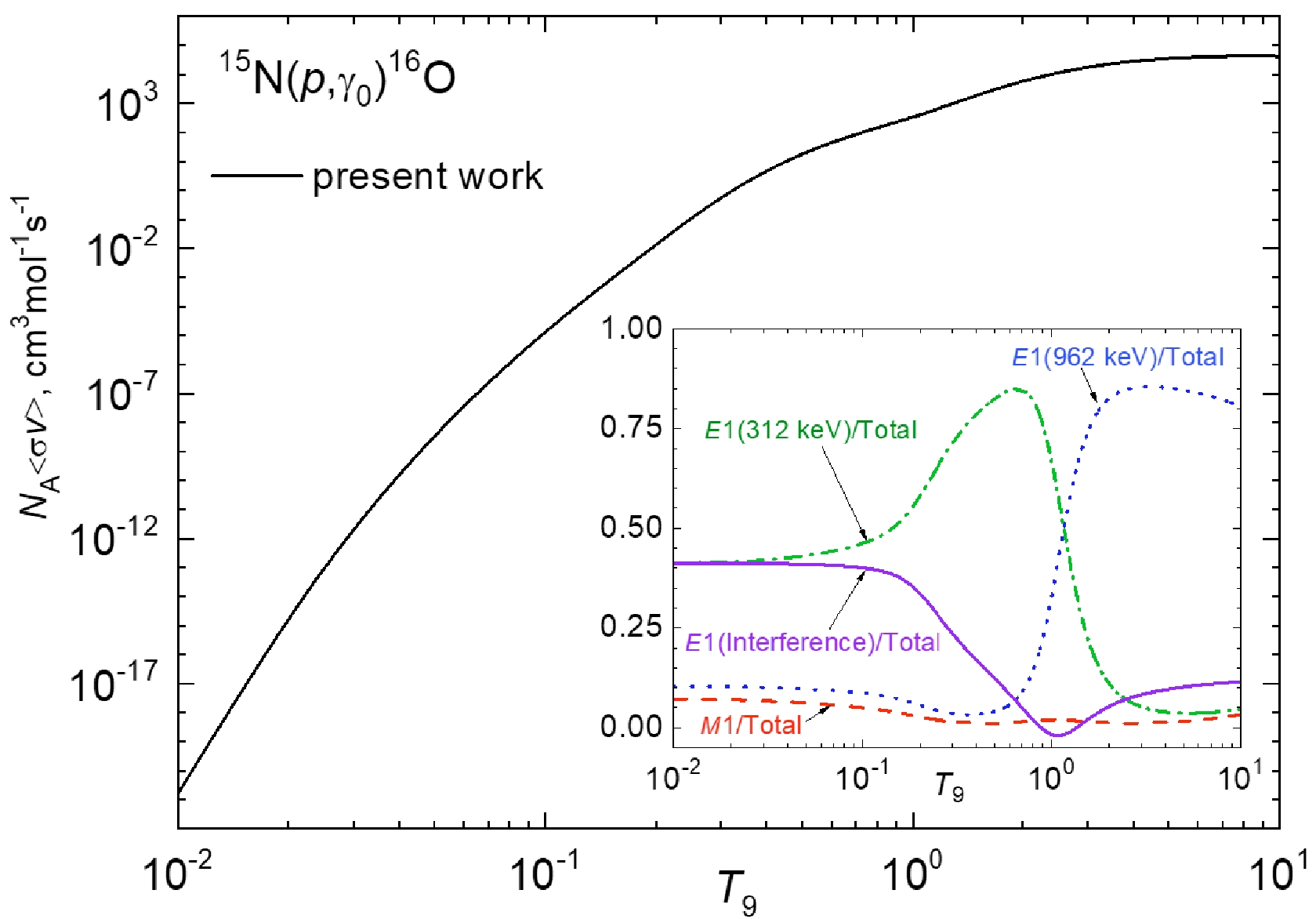
Figure 4. (color online) (a) Dependence of the reaction rate of the 15N(
$ p, \gamma _{0} $ )16O radiative capture on the astrophysical temperature. The solid curve presents our calculations for the sum of$ E1 $ and$ M1 $ transitions performed for potentials with the sets of parameters from Table 2. The inset shows the fractional contributions of the reaction rates from the$ {}^{3}S_{1} $ resonances at 312 keV and 962 keV and the non-resonance transition$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ , with respect to the reaction rate of 15N($ p, \gamma _{0} $ )16O, as functions of astrophysical temperature.In Eq. (5), the overlapping integral between the initial
$ \chi _{i} $ and final$ \chi _{f} $ state radial functions$I(k) = \int_{0}^{\infty} \chi^*_ir\chi_f {\rm d}r$ includes the interior and asymptotic regions via the continuous functions. The specific behavior of the proton relative motion in the field of the 15N nucleus is considered via the nuclear interaction potential$ V(r) $ . That is, according to the declared above ansatz. Note that in the cluster model's single-channel approach, the actual asymptotic behavior of radial WF is necessary for their proper normalizing [43].From Eq. (5), in the
$ E1 $ resonance$ \rightarrow $ GS transitions, the interference of$ {}^{3}S_{1}(312) $ and$ {}^{3}S_{1}(962) $ resonances contributes to the cross section. The interference is determined as the difference between the$ \delta _{^{3}S_{1}(312)} $ and$ \delta _{^{3}S_{1}(962)} $ phase shifts via the factor$ \cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) $ . We depict the behavior of this factor as a function of energy in Fig. 2(a) using the phase shifts shown in Fig. 1. One can conclude that the contribution of the interfering term into the$ E1 $ transition cross section is very significant at energies of up to 2.5 MeV.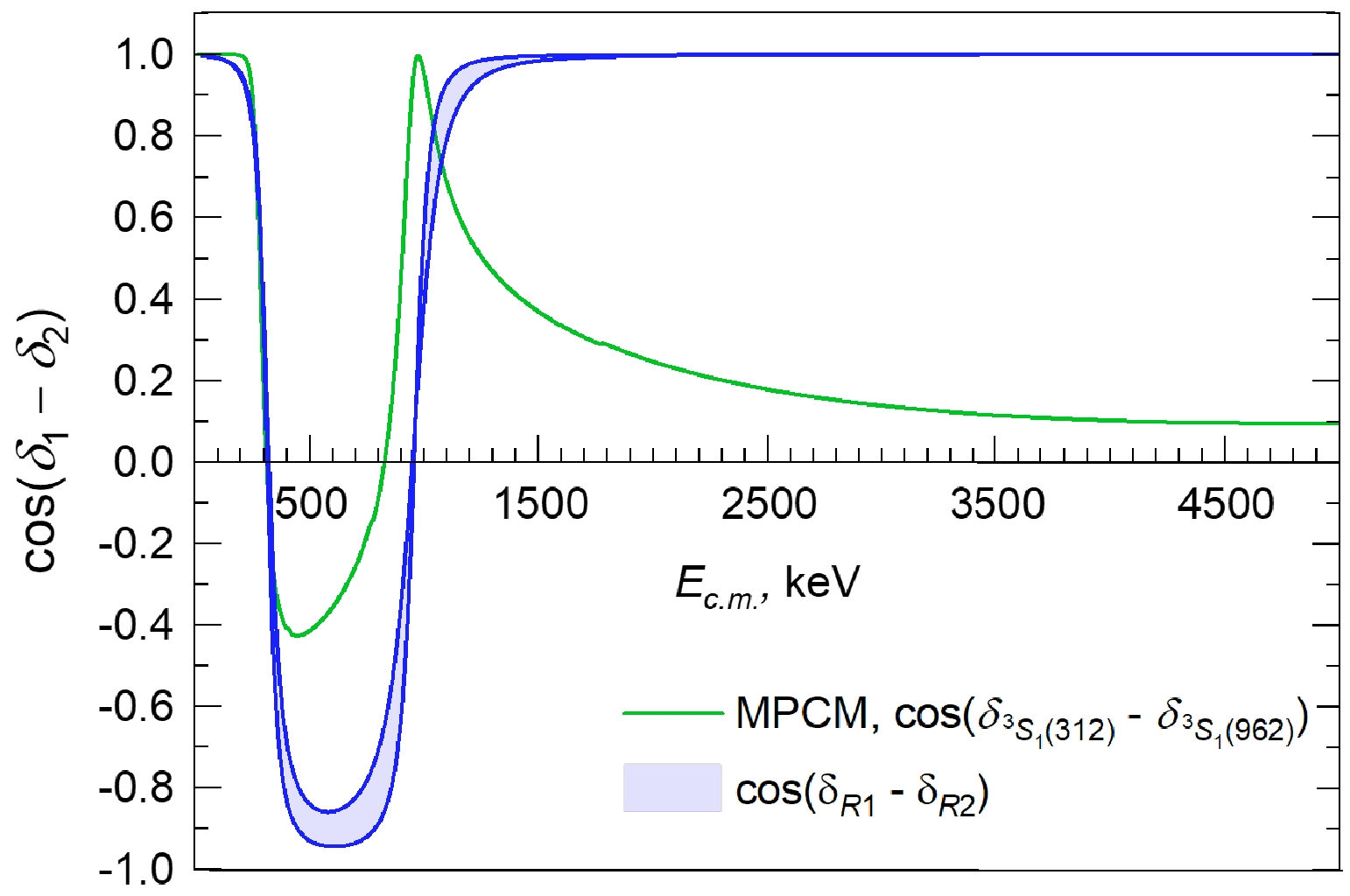
Figure 2. (color online) Energy dependence of the factors
$ \cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) $ (green curve) and$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ (shaded area). The upper and lower curves of the shaded area are obtained with the$ \delta _{R1} $ and$ \delta _{R2} $ resonant phase shifts calculated for the experimental$ \Gamma _{R1}=91 $ keV,$ \Gamma _{R2}=130 $ keV and arbitrary$ \Gamma _{R1}=120 $ keV,$ \Gamma _{R2}=250 $ keV widths, respectively.To illustrate the role of the factor
$ \cos \left( \delta _{^{3}S_{1}(312)}- \delta _{^{3}S_{1}(962)}\right) $ , we replace the$ \delta _{^{3}S_{1}(312)} $ and$ \delta _{^{3}S_{1}(962)} $ phase shifts by the resonant$ \delta _{R1} $ and$ \delta _{R2} $ (3). In this case, the factor$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ depends on the widths of the resonances. We calculate the energy dependence of the$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ by varying the width of the resonances from experimental values$ \Gamma _{R1}=91 $ keV and$ \Gamma _{R2}=130 $ keV [34] up to arbitrary values$ \Gamma _{R1}=120 $ keV and$ \Gamma _{R2}=250 $ keV (the upper and lower curves in Fig. 2, respectively). The results of the calculations are shown in Fig. 2 as a shaded area. We can conclude that the factor$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ is sensitive to the width of the resonances at the energy interval of about$ 400-800 $ keV and significantly increases the destructive interference term. -
The results of calculations for the astrophysical S-factor based on the potential parameters given in Table 2 and the compilation of experimental data [6, 13, 16, 17, 19] are presented in Fig. 3(a). Notice that the contribution of the 2+ level at the excitation energy of 12.97 MeV was considered in Ref. [5] using the
$R$ -matrix approach. The contribution of this transition to the GS is much smaller than the non-resonance$ M1 $ $ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ transition. The contribution of the interference of the$ {}^{3}S_{1}(312) $ and$ {}^{3}S_{1}(962) $ resonances results in a significant increase in the S-factor at energies of up to 300 keV. One can see the discrepancies between the experimental data and theoretical calculation at energies where the minimum of the S-factor is observed. This is related to the destructive interference of the$ {}^{3}S_{1}(312) $ and$ {}^{3}S_{1}(962) $ resonances at this energy due to the factor$ \cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) $ . This factor has its minimum at about 500 keV, as depicted in Fig. 2. The minimum of the S-factor is reproduced precisely within the$R$ -matrix approach [5] when the authors are considering the different reaction components' contributions in the fitting of the 15N($ p, \gamma $ )16O reaction data (see Fig. 49, [5]). Only by using the set of fitting parameters can it be described in the region of 0.5 MeV between the resonances for the S-factor [5].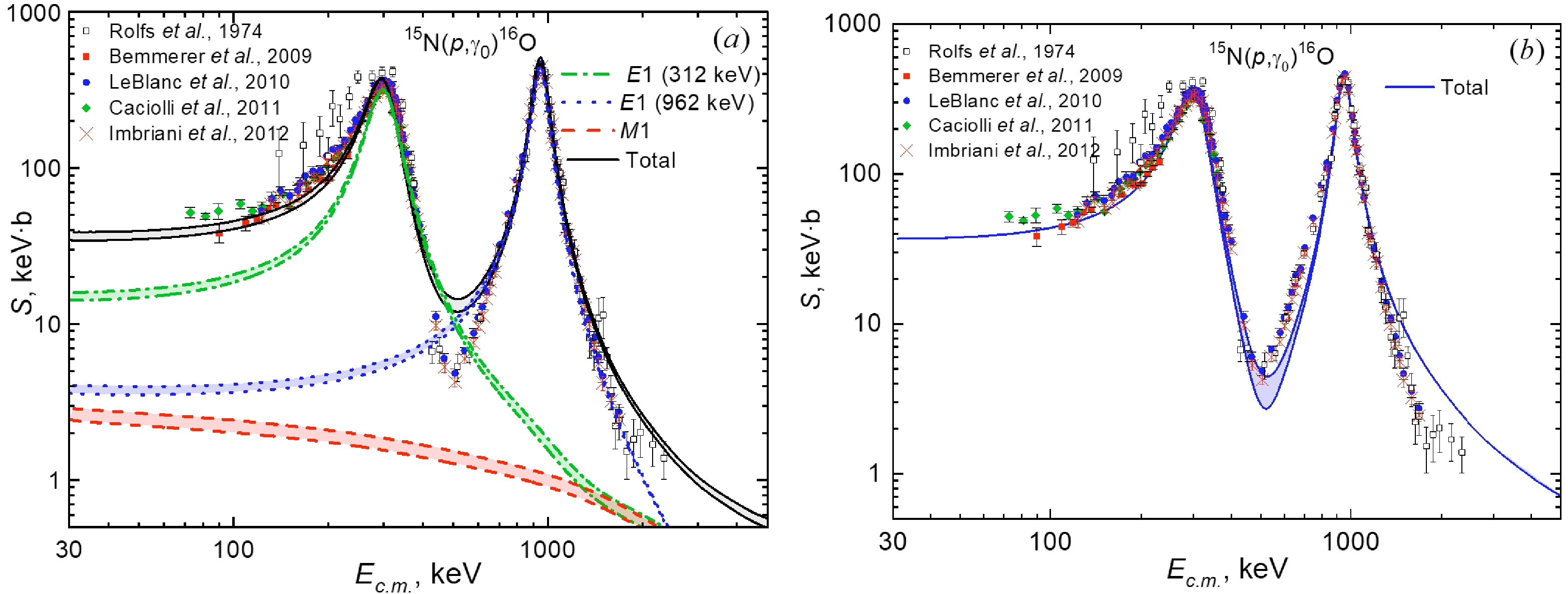
Figure 3. (color online) Astrophysical
$S$ -factor of radiative$ p^{15} {\rm{N}}$ capture on the GS of 16O. The shaded areas for the partial$ E1 $ and$ M1 $ and total S-factors correspond to the calculations with parameter sets I (upper curves) and III (lower curves), fromTable 2. (b) Astrophysical S-factor obtained with parameter set II, from Table 2. The shaded area refers to the variation of the cos($ \delta _{R1}- $ $ \delta _{R2} $ ) factor for the interference term and corresponds to the shaded area in Fig. 2.The shaded areas in Fig. 3(a) show the range of
$ S(E) $ changes for different AC values. Thus, the values of transition amplitudes are governed by the AC. At an energy of 30–60 keV, the S-factor is practically constant, and the corresponding value can be considered as the S-factor at zero energy. Thus, the theoretical calculation predicts the very smooth behavior of$ S(E) $ at very low energies that converge to$ S(0)=35.2(5) $ keV·b for$ C_{W}=1.8 $ (ANC of$ 12.85 $ fm-1/2). The increase in the AC leads to an increase in$ S(0) $ . The variation of the AC within the experimental uncertainties leads to the increase of the$S$ -factor up to$ S(0)=39.6(8) $ keV·b for$ C_{W}=2.05 $ (ANC of$ 14.49 $ fm−1/2). Therefore, depending on the value of the AC,$ S(0) $ varies in the range of$ 34.7-40.4 $ keV·b. Our predictions overlap with the$ S(0) $ factor reported in Ref. [21]. Note that in Ref. [27], the value of 29.8(1.1) keV·b was obtained in the effective field theory framework. However, [27] describes the experimental S-factor with resonances energies$ \approx $ 360–370 keV and widths$ \approx $ 250– 350 keV for the first resonance and resonances energies$ \approx $ 960–970 keV and widths$ \approx $ 155–160 keV for the second resonance, which are very far off from the experimental data.Let us consider, as an example, a different calculation scenario for the S-factor to understand the discrepancies between the experimental data and theoretical calculation at energies where the S-factor has the minimum. The value and position of the minimum are determined by the destructive interference of
$ {}^{3}S_{1}(312) $ and$ {}^{3}S_{1}(962) $ resonances. We calculate the S-factor using Eq. (5) and the parameter set II from Table 2. However, we replace the factor$ \cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) $ with$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ . The factor$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ is considered using the same parameters for the widths, as shown in Fig. 2. The result of the contributions of all transitions to the$ S(E) $ is shown by the shaded area in Fig. 3(b). Thus, we demonstrate that, by varying the factor$ -1<\cos \left( \delta _{R1}-\delta _{R2}\right) <1 $ and considering the widths of resonances as parameters, the MPCM can reproduce the position and value of the$ S(E) $ minimum. Notably, at very low energies, both factors$ \cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) $ and$ \cos \left( \delta _{R1}-\delta _{R2}\right) $ coincide:$ \cos \left( \delta _{^{3}S_{1}(312)}-\delta _{^{3}S_{1}(962)}\right) \simeq \cos \left( \delta _{R1}-\delta _{R2}\right) \approx 1 $ , as shown in Fig. 2. Thus,$ S(0) $ is not sensitive to this factor. However, the variation of this factor is important for describing the value and position of the$ S(E) $ minimum.The contribution of the
$ M1 $ non-resonant transition to the GS S-factor comes out of the MPCM through the$ {}^{3}P_{1} $ scattering state and has significance at energies$ E_{{\rm{c.m.}}}<500 $ keV. This contribution increases as the energy decreases. Considering the$ M1 $ transition requires experimental$ (p, p) $ phase shifts. The elastic 15N($ p, p $ )15N cross sections are measured only at energies higher than 2.7 MeV [42]. The low energy elastic scattering experimental data are desirable to evaluate the intensity of the$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ $ M1 $ transition.What is the contribution of each transition to the
$ S(0) $ ?$ E1 $ (312 keV) provides 15.5 keV·b (41%),$ E1 $ (962 keV) gives 3.9 keV·b (10%),$ M1 $ gives 2.6 keV·b (7%), and the interference term gives 15.7 keV·b (42%).$R$ -matrix calculations reproduce the interference minimum. Our consideration of the destructive interference of$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances did not reproduce the minimum of the S-factor precisely. Considering another state is thus justified if it has the same quantum numbers$ J^{\pi }=1^{-} $ as the resonances already considered. Such a state will interfere with the first two$ 1^{-} $ resonances. As mentioned in Sec. II, a resonance exists in the 16O spectrum at a very high excitation energy$ E_{{\rm{x}} }= $ 16.20(90) MeV. This is higher than the$ {}^{3}S_{1} $ (312) resonance by 3.76 MeV and 3.11 MeV higher than the$ {}^{3}S_{1} $ (962). Our numerical calculations revealed that the effect of this third state in the spectrum of$ 1^{-} $ resonances is negligible, and its interference does not influence the value or position of the S-factor minimum.In Table 3, the experimental data for the GS astrophysical S-factor in the measured energy ranges are given. The experimental range of energy is dramatically different, resulting in different values of
$ S(E_{\min }). $ In Ref. [13], the cross section is measured for the highest energy. The cross section for the lowest energy$ E_{{\rm{c.m.}}}=70 $ keV, which is near the Gamow range, is reported in Ref. [6]. It is obvious that the extrapolation of$ S(E) $ to the$ S(0) $ using each listed experimental energy range will yield different values of the$ S(0) $ , which may sometimes be dramatically different.Reference $E_{\text{c.m.}}$ /keV Experimental range

$E_{\min }$ /keV

$S(E_{\min })$ /keV·b

1 Hebbard et al., 1960 [12] $206-656$ 

230 $138.6\pm 15.2$ 

2 Brochard et al., 1973 [14] $234-1219$ 

256 $215.1\pm 27.3$ 

3 Rolfs & Rodney, 1974 [13] $139-2344$ 

139 $124.2\pm 52.6 $ 

4 Bemmerer et al., 2009 [15] $90-230$ 

90 $38.4\pm 5.4$ 

5 LeBlanc et al., 2010 [16] $123-1687$ 

123 $53\pm 7.1$ 

6 Caciolli et al., 2011 [6] $70-370$ 

70 $52\pm 4$ 

7 Imbriani et al., 2012 [17] $131-1687$ 

131 $48.4\pm 4.8$ 

Table 3. Experimental data on the astrophysical S-factor of the 15N(
$p, \gamma $ )16O reaction. The values of$S(E_{\min })$ listed in rows 1 and 2 are taken from Fig. 8 in Ref. [16].The determination of
$ S(0) $ relies on the dual approach of experimental measurement of the cross section complemented by theoretical interpretation and extrapolation from the experimental range of energy to zero energy. In Table 4, the estimates of the astrophysical S-factor at zero energy$ S(0) $ obtained using the$R$ -matrix fits of different sets of experimental data, different model calculations, and extrapolation of the experimental data are listed. By varying the fitting method, the authors obtained different values of$ S(0) $ (see, for example, Ref. [23]). The theoretical evaluation of astrophysical$ S(E) $ and its extrapolation to$ S(0) $ are also model dependent. Consequently, the uncertainties in the computed S-factor can be significant [64]. The extrapolation is of insufficient accuracy because of the difficulties in fully accounting for the complexities of the reaction mechanisms [65].Reference $S(0)$ / keV·b

Rolfs & Rodney, 1974 [13] 32 ([12]) $64\pm 6$ ([13])

Barker, 2008 [20] ≈ 50 – 55 ([13]) ≈ 35 ([12]) Mukhamedzhanov et al., 2008 [21] 36.0 ± 6 LeBlanc et al., 2010 [16] $39.6\pm 2.6$ 

Huang et al., 2010 [66] 21.1 Mukhamedzhanov et al., 2011 [23] $33.1-40.1$ 

Xu et al., 2013 [19] $45_{-7}^{+9}$ 

deBoer et al., 2013 [5] 40 ± 3 Dubovichenko et al., 2014 [22] $39.5-43.35$ 

Son et al., 2022 [26] 30.4 ([6]) Son et al., 2022 [27] $75.3\pm 12.1$ ([13])

$34.1\pm 0.9$ ([16])

$29.8\pm 1.1$ ([17])

Present work $34.7-40.4$ 

The results for $S(0)$ 35.2 ± 0.5a and 39.6 ± 0.8b are obtained for AC:

$C_{W}$ = 1.8a (ANC of 12.85 fm1/2) and

$C_{W}$ = 2.05b (ANC of 14.49 fm1/2).

Table 4. Values of the astrophysical
$S(0)$ factor of the 15N($p, \gamma $ )16O reaction. Estimations for the values of the$S(0)$ are obtained based on experimental data from the references listed in the parentheses.At ultra-low energies, the energy dependence of the S-factor can be modified using "a screening effect." The Coulomb screening effects in the laboratory plasma and astrophysical environment are discussed in detail in Refs. [67–70]. Despite various theoretical studies conducted over the past two decades, a theory has not yet been found to explain the cause of the exceedingly high values of the screening potential needed to explain the data [71].
Our expectation is that the screening considerations will increase
$ S(0) $ . The lack of parameters for the screening potential in the$ p^{15} {\rm{N}}$ medium does not allow us to estimate the role of the screening effect in the 15 N($ p, \gamma $ )16O reaction. However, if one considers the estimation in [72], the enhancement of the S-factor at energies of$ \sim $ 70 keV corresponding to the LUNA lower data is approximately 11%. -
The reaction rates for nuclear fusion are the critical components for stellar-burning processes and the study of stellar evolution [4]. In stellar interiors, where the interacting particles follow a Maxwell-Boltzmann distribution, the reaction rate describes the probability of nuclear interaction between two particles with an energy-dependent reaction cross section
$ \sigma (E) $ . The reaction rate of proton capture processes can be written as [48, 73]$\begin{aligned}[b] N_{A}\langle \sigma \nu \rangle =&N_{A}\left( \frac{8}{\pi \mu } \right) ^{1/2}\left( k_{B}T\right) ^{-3/2}\int \sigma (E)E\exp \left( -\frac{ E}{k_{B}T}\right) {\rm d}E\\=&N_{A}\left( \frac{8}{\pi \mu }\right) ^{1/2}\left( k_{B}T\right) ^{-3/2}\int S(E){\rm e}^{-2\pi \eta }\exp \left( -\frac{E}{k_{B}T} \right) {\rm d}E. \end{aligned} $

(6) In Eq. (6),
$ N_{A} $ is the Avogadro number, μ is the reduced mass of two interacting particles,$ k_{B} $ is the Boltzmann constant, T is the temperature of the stellar environment, and the factor${\rm e}^{-2\pi \eta }$ approximates the permeability of the Coulomb barrier between two point-like charged particles. -
The reaction rate can be numerically obtained in the framework of the standard formalism outline in Ref. [18] based on the S-factor, which includes the contributions of all transitions shown in Fig. 3 and the fractional contributions of
$ E1 $ transitions and the$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ $ M1 $ transition to the 15N($ p, \gamma _{0} $ )16O reaction rate. In Fig. 4, the reaction rate and fractional contributions of each transition to the reaction rate are presented. The inset in Fig. 4 shows the contribution of each resonance and$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ transition with respect to the total reaction rate as a function of the astrophysical temperature. Such a representation is useful to understand the relevance of each transition at a given temperature. At$ T_{9}=0.01 $ , the fractional contribution from the 312 keV resonance is 71%, while the fractional contributions of the 962 keV resonance and non-resonance transition$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ are 16% and 13%, respectively. In contrast, at temperature$ T_{9}=10 $ , the fractional contribution from the 962 keV resonance is 89%, and the contributions of the 312 keV resonance and$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ transition are commensurate: 6% and 5%, respectively. The$ E1 $ transitions from the 312 keV and 962 keV resonances have maximal fractional contributions of 95% and 93% at$ T_{9}=0.4 $ and$ T_{9}=4.1 $ , respectively. The fractional contribution from the non-resonance$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ transition increases as the energy decreases.The interference of the
$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances requires special consideration. The solid line in the inset in Fig. 4 shows the fractional contribution of the interference term between the$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances to the total reaction rate. In the Gamow CNO window$ T_{9}=0.01-0.03 $ , the contribution of the interference term to the total reaction rate is 41%, up to$ T_{9}=0.1 $ . In the temperature interval$ T_{9}=0.01-0.1 $ , the contribution of the interference term to the total reaction rate is$ \sim\, $ 40%, while at$ T_{9}=3-10 $ , the contribution of this term does not exceed$ \sim $ 11%. For the stellar CNO temperature range$ T_{9}=0.1-0.5 $ , the contribution of the interference term drops from$ \sim 40 $ % to$ \sim 12.5 $ %. The destructive interference is observed in the range from$ T_{9}=0.89 $ to$ T_{9}=1.36 $ but at a level of$ \sim $ 2%. From the end of this interval up to$ T_{9}=10 $ , a moderate constructive interference increase is observed from zero up to 11%.The dependence of the reaction rate of the 15N(
$ p, \gamma _{0} $ )16O radiative capture as a function of temperature for the astrophysical temperature between$ T_{9}=0.01 $ and$ T_{9}=10 $ is shown in Fig. 4. The results of the reaction rates for sets I$ - $ III are shown via a single solid curve in Fig. 4. The reaction rates for 15N($ p, \gamma $ )16O were reported earlier in Refs. [16, 18, 19]. We normalized the reaction rate obtained with the$R$ -matrix approach [16], NACRE [18], and NACRE II [19] reaction rates by dividing the corresponding data on the reaction rate obtained in the present calculation. The dependence of these ratios as a function of the astrophysical temperature is shown in Fig. 5. One can see the agreement between the reaction rate [16] obtained for the GS transition and our calculation. Notably, the agreement is also observed for the astrophysical factor; the range of our results for$ S(0) $ $ 34.7\leq S(0)\leq 40.4 $ keV·b and the range of$ 37\leq S(0)\leq $ 42.2 keV·b from [16] overlap. In the$ S(0) $ calculations in [16], the ANC of$ 23\pm 3 $ fm-1/2 used is approximately 3 times larger than the experimental value [21]. Therefore, one can conclude that the reaction rate is weakly responsive to the value of$ S(0) $ .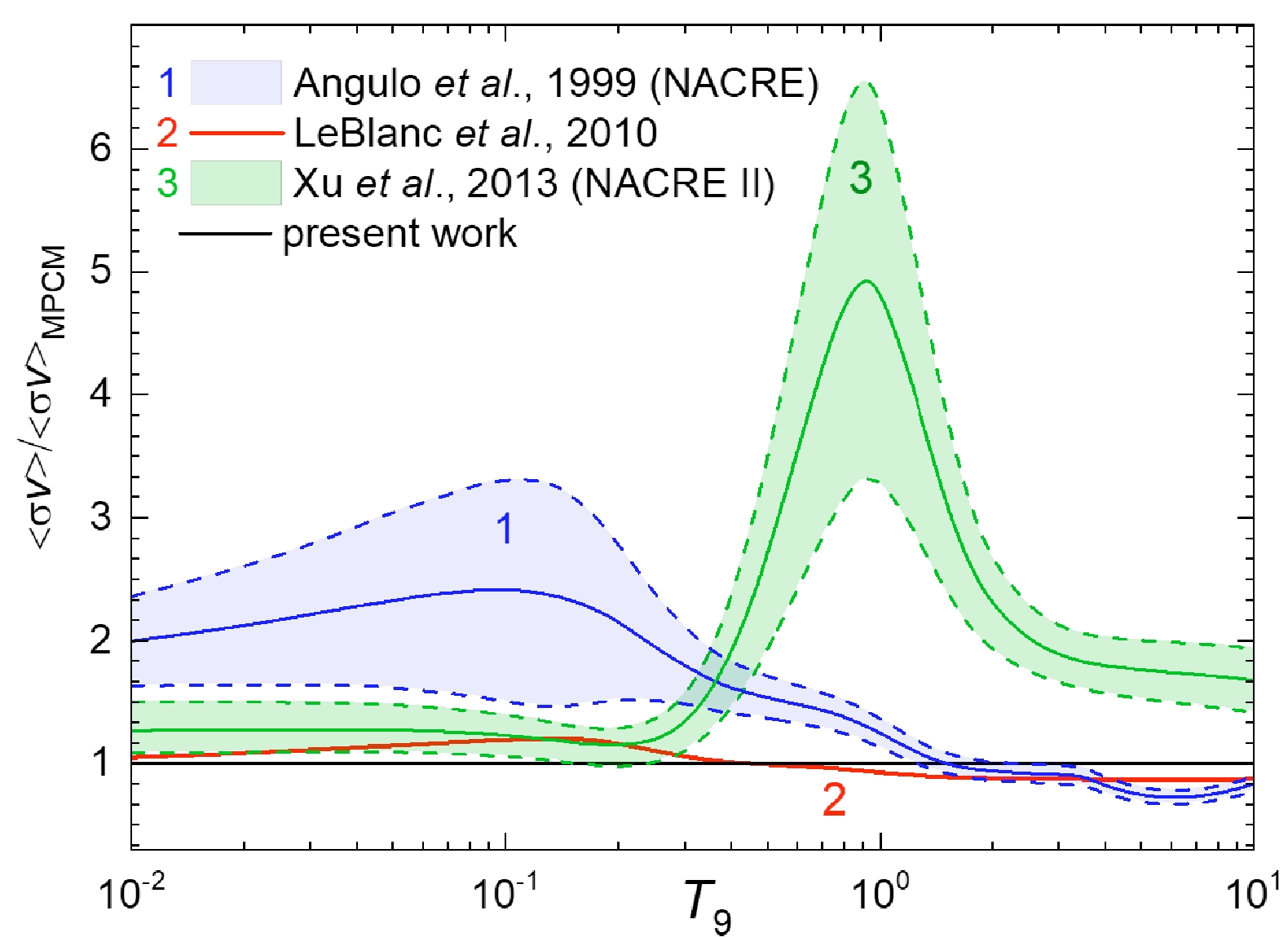
Figure 5. (color online) Dependence of the ratio of the proton radiative capture on the 15N reaction rate from NACRE [18] (curve 1), [16] (curve 2), NACRE II [19] (curve 3), and the present calculation on the astrophysical temperature in the range of
$ T_{9}=0.01-10 $ . The shaded areas within the dashed curves represent the uncertainties from NACRE and NACRE II. The calculations from NACRE [18], LeBlanc et al. [16], and the present study are given for the GS transition; the NACRE II parametrization includes the GS transition and transitions via two 2- resonances and 0 - and 3- resonances [19].One can see the significant discrepancies in the reaction rates, particularly, for NACRE [18] and NACRE II (includes the GS and two 2
$ {}^{-}, $ 0–, and 3– resonances) [19] data at temperatures$ T_{9}=0.1 $ and$ T_{9}=1 $ , respectively, where the ratios reach the maximum. While the difference between [16] and our 15N($ p, \gamma _{0} $ )16O and NACRE II at$ T_{9}>0.3 $ is understandable, the significant disagreement in the reaction rates between [16] and that obtained in the present study for the GS transition compared to NACRE [18], which is also parametrized for the GS transition, is puzzling. Perhaps, this disagreement is related to the experimental data [12, 13] used for the parametrization of the reaction rate reported in NACRE [18], which were excluded in NACRE II [19], in favor of the post-NACRE data.The reaction rates reported in [19] include cascade transitions via two 2– resonances and 0– and 3– resonances of 16O in the
$ 0.40\lesssim E_{R}\lesssim 1.14 $ MeV range [17, 34, 36, 64]. It is stated in Ref. [19] that the enhancement of the ratio around$ T_{9}={1} $ seen in Fig. 5 is owing to the contribution of the cascade transitions, which are not included in NACRE [18]. In Refs. [17, 37], partial cross sections of the radiative proton capture to the GS, 1${}^{\rm st}(0^{+})$ , 2${}^{\rm nd}(3^{-}),$ and 4${}^{\rm th}(1^{-})$ excited states are measured and converted to the astrophysical S-factors of the 15N($ p, \gamma _{0} $ )16O, 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O reactions. The experimental data on ($ p, \gamma _{1} $ ), ($ p, \gamma _{2} $ ), ($ p, \gamma _{4} $ ) were reported by Imbriani et al. [37] as cascade transitions. We estimate the contribution of these transitions in the framework of the MPCM based on the experimental data presented by Imbriani et al. [37] because the exact calculations of the cascade transitions are out of the scope of this study.The experimental data [17, 37] for the S-factors listed in the EXFOR database [74] (Hokkaido University Nuclear Reaction Data Centre) were used and interpolated with the Origin Pro 2018 software [75]. The interpolation enables the construction of the energy-dependent factor
$f(E)=\dfrac{{\rm{Total }}\;S-{\rm{factor}}}{{\rm{GS }}\; S-{\rm{factor}}}$ , where the "Total S-factor" corresponds to the sum of the 15N($ p, \gamma _{0} $ )16O and cascade transitions 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O, and "GS S-factor" refers to 15N($ p, \gamma _{0} $ )16O. Introducing this factor into Eq. (6),$ \begin{aligned}[b] \left[ N_{A}\langle \sigma \nu \rangle \right] _{{\rm{m}} }=&N_{A}\left( \frac{8}{\pi \mu }\right) ^{1/2}\left( k_{B}T\right) ^{-3/2}\int S(E)\\&\times f(E){\rm e}^{-2\pi \eta }\exp \left( -\frac{E}{k_{B}T} \right) {\rm d}E,\end{aligned} $

(7) one can estimate the contribution of the cascade transitions. Thus,
$ \left[ N_{A}\langle \sigma \nu \rangle \right] _{{\rm{m}}} $ is a modified GS reaction rate, which effectively includes the cascade transitions to the excited states of 16O: 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O.The dependence of factor
$ f(E) $ and the ratio of the total experimental S-factor, i.e., the sum of the contributions from the GS and cascade transitions and the reaction rate for the GS transition on the proton energy in the c.m. and astrophysical temperature, respectively, is shown in Fig. 6. The factor$ f(E) $ increases 14 times at$ E_{{\rm{c.m.}}}=600 $ keV. At temperatures above$ T_{9}=0.3 $ , the cascade gamma-ray transitions to the excited BSs contribute to the total reaction rate. Therefore, the enhancement of the ratio$ \left[ N_{A}\langle \sigma \nu \rangle \right] _{{\rm{m}}}/N_{A}\langle \sigma \nu \rangle _{{\rm{GS}}} $ at$ T_{9}>0.3 $ is due to the contribution of the cascade transitions: 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O. In the temperature range of about$ T_{9}=1-1.3 $ , we have a maximum of$ \sim $ 30% deviation of the total rate from the 15N($ p, \gamma _{0} $ )16O GS transition rate and a deviation of$ \sim $ 15% at$ T_{9}=10 $ . Thus, our estimations based on the experimental partial S-factors contradict the peculiar enhancement behaviour of the ratio reported in NACRE II at$ 0.4< $ $ T_{9}<10 $ . The latter calls for a careful theoretical investigation of the contributions of the two interfering 2– resonances at 12.530 MeV and 12.9686 MeV and the two interfering 3- resonances at 13.142 MeV and 13.265 MeV.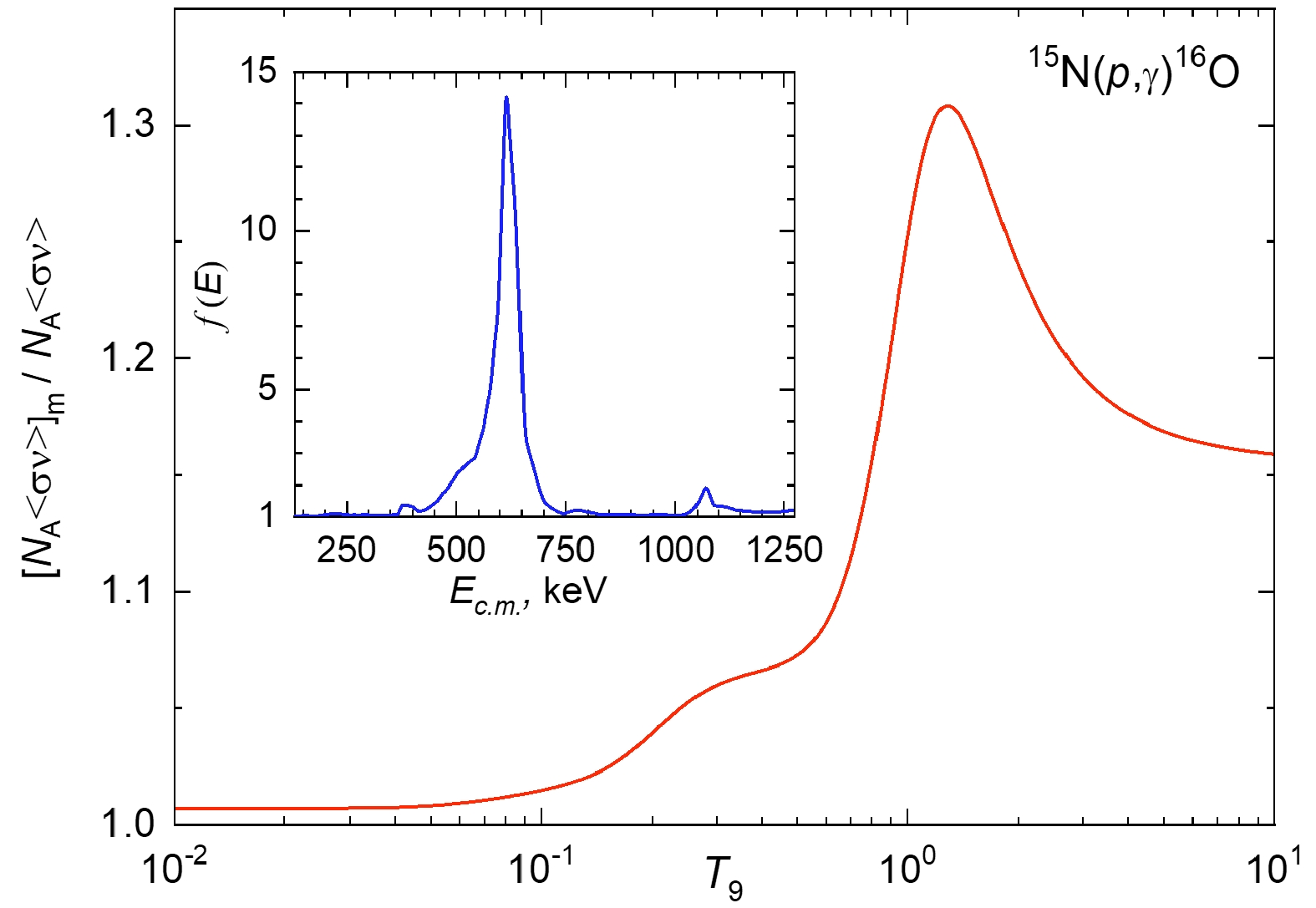
Figure 6. (color online) Dependence of the ratio of the total reaction rate, which is the sum of contributions from the 15N(
$ p, \gamma _{0} $ )16O and cascade transitions 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O and the reaction rate for the GS transition on temperature. The experimental data reported in Ref. [17] are used in calculations. The inset shows the dependence of the factor$ f(E) $ on the proton energy in the c.m.The results of the
$R$ -matrix calculations of the reaction rate [16] are parametrized in the form$\begin{aligned}[b] N_{A}\langle \sigma \nu \rangle =&\frac{a_{1}10^{9}}{T_{9}^{2/3}} \exp \left[ a_{2}/T_{9}^{1/3}-\left( T_{9}/a_{3}\right) ^{2}\right] \left[ 1.0+a_{4}T_{9}+a_{5}T_{9}^{2}\right] \\&+\frac{a_{6}10^{3}}{T_{9}^{3/2}}\exp \left( a_{7}/T_{9}\right) +\frac{a_{8}10^{6}}{T_{9}^{3/2}}\exp \left[ a_{9}/T_{9}\right]\end{aligned} $

(8) and calculations with the parameters from [16] yielded
$ \chi ^{2}=20.8 $ . However, by varying the parameters, we get a much smaller value of$ \chi ^{2}=0.4 $ . The corresponding parameters are given in the first column in Table A1 in the Appendix. The parametrization coefficients of the reaction rate obtained in the framework of MPCM for the analytical expression (8) with the parameters from Table 2 are presented in the Appendix and result in values of$ \chi ^{2}=0.084 $ ,$ \chi ^{2}=0.086 $ , and$ \chi ^{2}=0.09 $ for sets I, II, and III, respectively. We also present the parametrization coefficients for$ \left[ N_{A}\langle \sigma \nu \rangle \right] _{{\rm{m}}} $ for set II.Parameters for [16] Parameters for MPCM Parameters for MPCM Parameters for MPCM $ \chi ^{2}=0.4 $ 

Set I, $ \chi ^{2}=0.084 $ 

Set II, $ \chi ^{2}=0.086 $ 

Set II $ _{{\rm{m}}} $ ,

$ \chi ^{2}=0.093 $ 

Set III, $ \chi ^{2}=0.09 $ 

i $ a_{i} $ 

$ a_{i} $ 

$ a_{i} $ 

$ a_{i} $ 

$ a_{i} $ 

1 $ 0.4874952 $ 

$ 1.0375 $ 

$ 1.00436 $ 

$ 0.90521 $ 

$ 0.92832 $ 

2 $ -15.22289 $ 

$ -15.41934 $ 

$ -15.4231 $ 

$ -15.39278 $ 

$ -15.42226 $ 

3 $ 0.8597972 $ 

$ 2.19708 $ 

$ 2.17155 $ 

$ 2.09762 $ 

$ 2.16317 $ 

4 $ 6.734083 $ 

$ 0.10981 $ 

$ 0.10166 $ 

$ 0.47779 $ 

$ 0.11569 $ 

5 $ -2.462556 $ 

$ -0.01995 $ 

$ -0.01655 $ 

$ -0.04484 $ 

$ -0.01654 $ 

6 $ 0.7971639 $ 

$ 1.67272 $ 

$ 1.72304 $ 

$ 1.55827 $ 

$ 1.68868 $ 

7 $ -2.930568 $ 

$ -3.0594 $ 

$ -3.06727 $ 

$ -3.03021 $ 

$ -3.07264 $ 

8 $ 3.224569 $ 

$ 4.38681 $ 

$ 4.20809 $ 

$ 4.93559 $ 

$ 3.97887 $ 

9 $ -11.00680 $ 

$ -12.10183 $ 

$ -12.09517 $ 

$ -12.52017 $ 

$ -12.10662 $ 

Table A1. Parameters of analytical parametrization of the reaction rate of
$ p^{15} {\rm{N}}$ capture. The parameters for the reaction rate presented in Ref. [16] with$ \chi ^{2}=0.4 $ and results obtained in the present MPCM calculation. -
Two stable nitrogen isotopes, 14N and 15N, exist, and all other radioisotopes are short-lived. Among the short-lived isotopes, the longest-lived are 12N and 13N, with half-lives of about 11 ms and 9.965 min, respectively, and they are of nuclear astrophysics interest. A radiative proton capture on nitrogen isotopes in the reactions 12N(
$ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O produces the short-lived 13O, 14O, and 15O isotopes with half-lives of$ \sim $ 6 ms,$ \sim $ 71 s, and$ \sim $ 122 s, respectively, and a stable 16O nucleus. These radiative capture reactions caused by the electromagnetic interaction are significantly slower than reactions induced by strong interactions. Therefore, these slow reactions control the rate and time of cycles of oxygen isotope nucleosynthesis at particular astrophysical temperatures.The authors of Ref. [76] suggested and discussed three alternative paths for rapid processes of the CNO cycle leading to the formation of 14O through the breakout reactions 9C(
$ \alpha , p $ )12N and 11C($ p, \gamma $ )12N. These three branches of reaction sequences involve 12N($ p, \gamma $ )13O and 13N($ p, \gamma $ )14 O processes. Thus, these processes are of particular interest for nuclear astrophysics. In the MPCM framework, the radiative proton capture on nitrogen isotopes 12N, 13N, and 14N were investigated [28, 77, 78]. Because the reactions 12N($ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, and 14N($ p, \gamma $ )15O and the present study of 15N($ p, \gamma $ )16O are considered on the same footing within the MPCM, comparing the reaction rates helps in understanding the relevance of each process at a given astrophysical temperature. Thus, we compare the reaction rates for the 12N($ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O reactions involved in the different chains of the CNO cycles as follows:$\begin{aligned} & { }^{12} {\rm{~N}}(p, \gamma){ }^{13} {\rm{O}} {\rm{ - source\; of\; CNO\; seeds }}\;\left\{\begin{array}{l}\ldots{ }^{11} {\rm{C}}(p, \gamma)\fbox{${ }^{12} {\rm{~N}}(p, \gamma){ }^{13} {\rm{O}}$}\left(\beta^+ v\right)^{13} {\rm{~N}} \ldots[89 \%] \;{\rm { or }}\; \\ \ldots{ }^{11} {\rm{C}}(p, \gamma)\fbox{${ }^{12} {\rm{~N}}(p, \gamma){ }^{13} {\rm{O}}$}\left(\beta^+ p\right)^{12} {\rm{C}} \ldots[11 \%]\end{array}\right. \\ & { }^{13} {\rm{~N}}(p, \gamma){ }^{14} {\rm{O}} {\rm { - hot\; CNO\; only }}\; \qquad\qquad{ }^{12} {\rm{C}}(p, \gamma)\fbox{${ }^{13} {\rm{~N}}(p, \gamma){ }^{14} {\rm{O}}$}\left(\beta^+ v\right)\fbox{${ }^{14} {\rm{~N}}(p, \gamma){ }^{15} {\rm{O}}$}\left(\beta^+ v\right){ }^{15} {\rm{~N}}(p, \alpha){ }^{12} {\rm{C}} \\ & { }^{14} {\rm{~N}}(p, \gamma){ }^{15} {\rm{O}} {\rm { - cold\; and\; hot\; CNO }}\;\quad\left\{\begin{array}{l}{ }^{12} {\rm{C}}(p, \gamma){ }^{13} {\rm{~N}}\left(\beta^+ v\right){ }^{13} {\rm{C}}(p, \gamma)\fbox{${ }^{14} {\rm{~N}}(p, \gamma){ }^{15} {\rm{O}}$}\left(\beta^+ v\right){ }^{15} {\rm{~N}}(p, \alpha){ }^{12} {\rm{C}} \\ { }^{16} {\rm{O}}(p, \gamma){ }^{17} {\rm{~F}}\left(\beta^+ v\right){ }^{17} {\rm{O}}(p, \alpha)\fbox{${ }^{14} {\rm{~N}}(p, \gamma){ }^{15} {\rm{O}}$}\left(\beta^+ v\right)\fbox{${ }^{15} {\rm{~N}}(p, \gamma){ }^{16} {\rm{O}}$}\end{array}\right. \\ & { }^{15} {\rm{~N}}(p, \gamma){ }^{16} {\rm{O}} \;{\rm { - hot }}\; {\rm{CNO}} \qquad\qquad\qquad{ }^{17} {\rm{O}}(p, \gamma){ }^{18} {\rm{~F}}\left(\beta^+ v\right){ }^{18} {\rm{O}}(p, \gamma)\fbox{${ }^{15} {\rm{~N}}(p, \gamma){ }^{16} {\rm{O}}$}\left(\beta^+ v\right){ }^{17} {\rm{~F}}\left(\beta^+ v\right){ }^{17} {\rm{O}} & \end{aligned}$ 
(9) The reaction rates of the framed processes are calculated within the framework of the same model, MPCM. The temperature window, prevalence, and significance of each process are considered. The radiative proton 12N(
$ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O processes have the same Coulomb barrier, and, according to Eq. (6), the reaction rates will differ only due to the different values of$ S(E) $ and reduced mass μ of interacting particles in the entrance channel. The reduced masses of the pairs$ p^{12} {\rm{N}}$ ,$ p^{13} {\rm{N}}$ ,$ p^{14} {\rm{N}}$ , and$ p^{15} {\rm{N}}$ are always less than the proton mass and are within the range$ 0.9294 $ amu$ \leq \mu \leq 0.9439 $ amu. Therefore, the influence of the reduced mass on the reaction rates of proton capture on nitrogen isotopes is negligible and can be omitted. Therefore, the rates of these processes completely depend on the S-factor of the reaction. Figure 7 gives an overview of the reaction rates for typical CNO temperatures and explosive hydrogen burning scenarios. The 15N($ p, \gamma $ )16O reaction is the fastest one with the biggest rate up to$ T_{9}\sim 0.175 $ ;$ p^{14} {\rm{N}}$ is the slowest process up to$ T_{9}\sim 0.1 $ , and it controls the rate and time of nucleosynthesis cycles. Notably, the 15N($ p, \gamma $ )16O reaction rate becomes the dominant one at the temperature and explosive hydrogen burning scenarios in stars. The analysis of the result presented in the inset in Fig. 7 indicates that only in the temperature windows of$ 0.18\lesssim T_{9}\lesssim 1.14 $ and$0.66\lesssim T_{9}\lesssim 3$ is the reaction 15N($ p, \gamma $ )16O slower than the 13N($ p, \gamma $ )14O and 14N($ p, \gamma $ )15O reactions, respectively. Hence, this slow reaction controls the rate and time of nucleosynthesis cycles.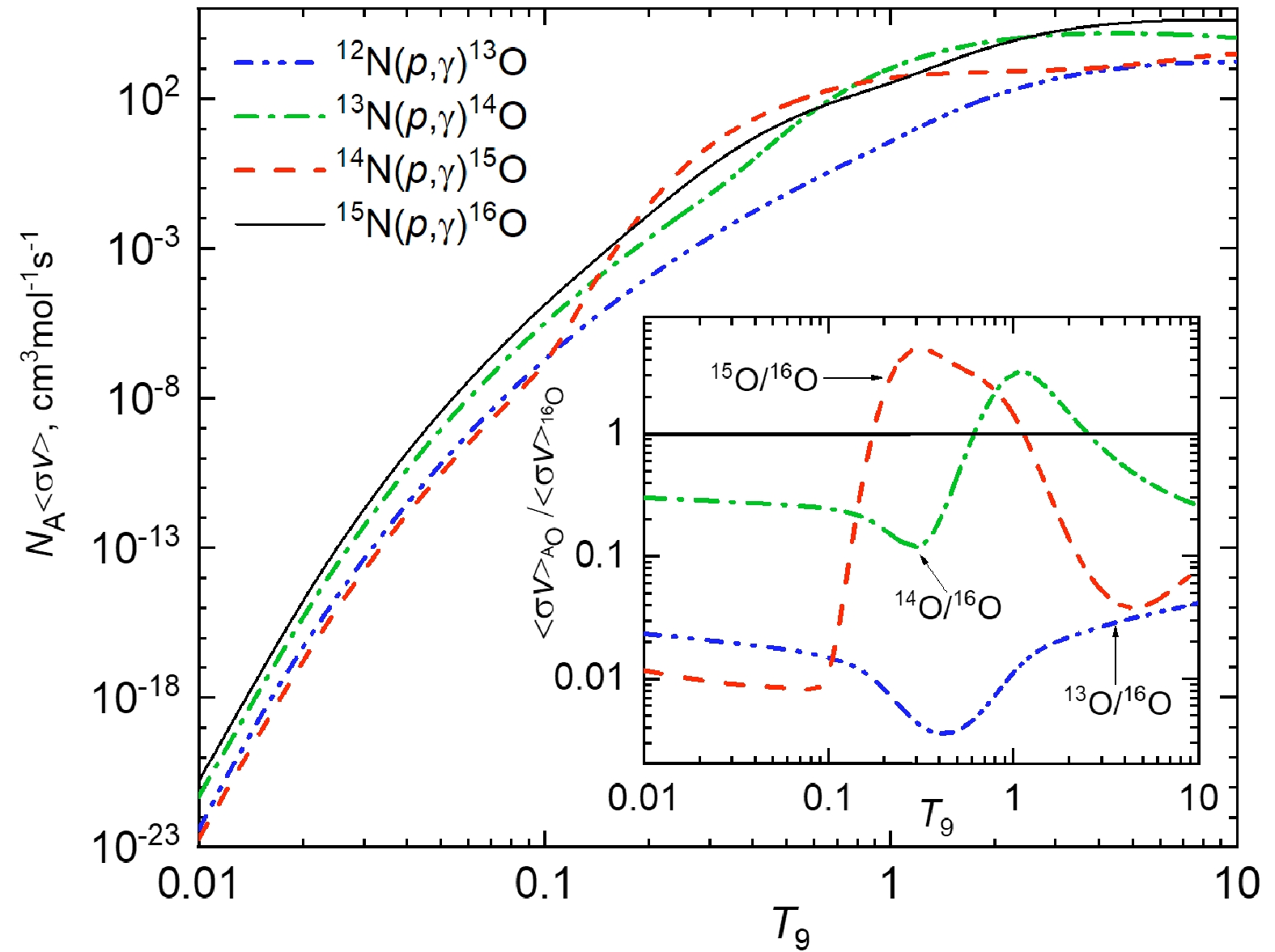
Figure 7. (color online) Reaction rates of the radiative proton capture on nitrogen isotopes leading to the production of oxygen isotopes as a function of astrophysical temperature. The inset shows the fractional contributions from 12N(
$ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, and 14N($ p, \gamma $ )15O with respect to the 15N($ p, \gamma $ )16O reaction rate as a function of astrophysical temperature.Presenting the reaction rates of proton radiative capture is important. The radiative hydrogen burning induced nucleosynthesis at specific temperatures has the Gamow peak energy [48, 79]
$ E_{0}=\left[ \frac{\pi ^{2}}{\hbar ^{2}}\left( Z_{1}Z_{2}{\rm e}^{2}\right) ^{2} \frac{\mu }{2}\left( k_{B}T\right) ^{2}\right] ^{\frac{1}{3}} $

(10) which is defined by the condition
$\dfrac{\rm d}{{\rm d}E}f_{G}(E, T)=0$ , where$f_{G}(E, T)={\rm e}^{-2\pi \eta }\exp \left( -\dfrac{E}{k_{B}T}\right)$ is a Gamow function. For the proton and nitrogen isotopes in the entrance channel$ Z_{1}=1 $ and$ Z_{2}=7 $ for (10) in keV for temperature$ T_{9} $ , one obtains$ E_{0}=466.4353\left[ \mu T_{9}^{2}\right] ^{\frac{1}{3}}, $

(11) and the effective energy range determined by the Gamow range
$ \Delta E_{G} $ (in keV) around the Gamow energy$ E_{0} $ is$ \Delta E_{G}=452.9821\left[ \mu T_{9}^{5}\right] ^{\frac{1}{6}}. $

(12) Thermonuclear reactions mainly occur over the Gamow energy window from
$ E_{0}-\Delta E_{G}/2 $ to$ E_{0}+\Delta E_{G}/2 $ except in the case of narrow resonances [48]. From Eqs. (11) and (12), clearly, the Gamow peak energies and ranges for the 12N($ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O reactions are completely determined by the astrophysical temperature. The variation of the reduced mass within$ 0.9294 $ amu$ \leq \mu \leq 0.9439 $ amu changes the Gamow peak energy and the energy range only within 0.5% and 0.3%, respectively.It is useful to present the reaction rate for a particular temperature range along with the Gamow window of CNO reactions for the radiative proton capture on nitrogen isotopes. The corresponding results of the calculations are shown in Figs. 8 and 9. Notably, the main difficulty in determining reliable reaction rates of the 12N(
$ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O reactions for the CNO cycles is the uncertainty in the very low cross sections at the Gamow range. Developments within the low-energy underground accelerator facility, LUNA, in the Gran Sasso laboratory [80] and recent improvements in the detection setup [81] make taking direct measurements of nuclear reactions near the Gamow range feasible. This advantage has been demonstrated in the 14N($ p, \gamma $ )15O reaction, which was successfully measured down to energies of 70 keV at LUNA [82].
Figure 8. (color online) (a) Dependence of the reaction rates of the radiative proton capture on nitrogen isotopes on the astrophysical temperature in the range of
$ T_{9}=0.01-0.03. $ (b) Stellar temperatures as a function of the Gamow energy for the CNO cycle of the 12N($ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O reactions.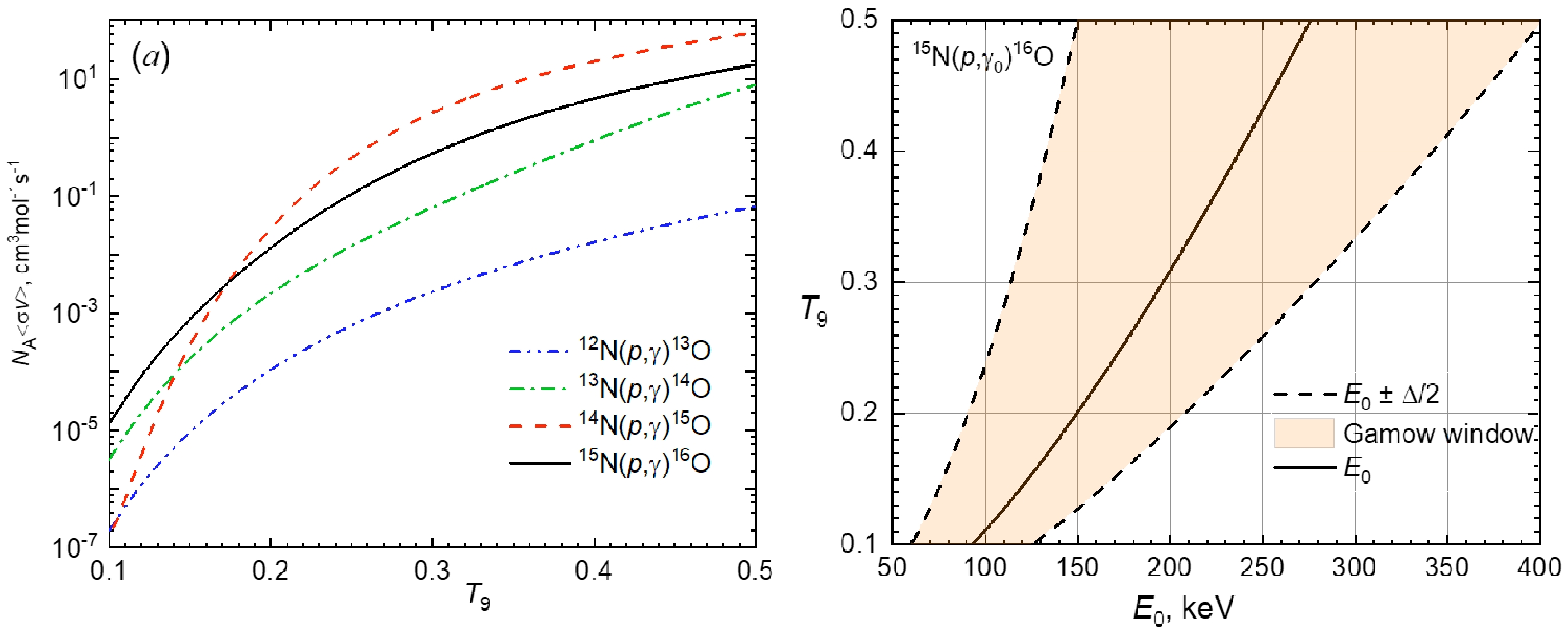
Figure 9. (color online) (a) Dependence of the reaction rates of the radiative proton capture on nitrogen isotopes on the astrophysical temperature in the range of 0.1
$T_{9}-0.5T_{9}.$ (b) Stellar temperatures as a function of the Gamow energy for the CNO cycle of the 12N($ p, \gamma $ )13O, 13N($ p, \gamma $ )14O, 14N($ p, \gamma $ )15O, and 15N($ p, \gamma $ )16O reactions. -
We present the results of the calculations and analysis of the astrophysical S-factor and reaction rate for the 15N(
$ p, \gamma $ )16O reaction in the MPCM framework with forbidden states, including low-lying$ {}^{3}S_{1} $ resonances and$ {}^{3}P_{1}\longrightarrow ^{3}P_{0} $ $ M1 $ transition. The intercluster potentials of the BS, constructed based on the obvious requirements for describing the binding energy and AC in the$ p^{15} {\rm{N}}$ channel of the GS, and the scattering potentials describing the resonances make it possible to reproduce the behavior of available experimental data for the total cross section of radiative proton capture on the 15N nucleus at astrophysical energies. However, it is not as precise as the$R$ -matrix fitting [5].The interference of the
$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances significantly increases the$ S- $ factor at energies of up to 300 keV. The consideration of the interfering$ {}^{3}S_{1} $ resonances and the contribution of the$ {}^{3}P_{1} $ scattering wave in the p + 15N channel due to the$ {}^{3}P_{1}\longrightarrow $ $ {}^{3}P_{0} $ $ M1 $ transition increases the$ S- $ factor at low energies. Our result for the$ M1 $ transition is related to the corresponding phase shifts. Within our model, we demonstrated that the contribution of the$ M1 $ transition from the non-resonance$ {}^{3}P_{1} $ scattering wave to the 15N($ p, \gamma _{0} $ )16O cross section really exists and contributes$ \sim $ 7% to the$ S(0) $ . Thus, systematic and precise low-energy elastic proton scattering data on 15N are needed to determine phase shifts at energies$ E_{c.m.}\lesssim 2 $ MeV. The extrapolation of the$ S- $ factor at a low energy yields 35.2$ \pm $ 0.5 keV·b and 39.6$ \pm $ 0.8 keV·b, depending on the value of the asymptotic constant, which turned out to be within$ 34.7-40.4 $ keV·b. This clarifies the important role of the asymptotic constant for the 15N($ p, \gamma _{0} $ )16O process, where the interfering$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances contribute the most to the cross section. Comparing our calculation for$ S(0) $ with existing experimental and theoretical data showed reasonable agreement with experimental measurements. Interestingly, the values of$ S(0) $ were consistent with each other, regardless of various$R$ -matrix method approaches [5, 16, 19–21, 23] and the present MPCM calculations. The deviations of$ S(0) $ in different approaches were within the accuracy of the main sources of uncertainties.The reaction rate was calculated and parametrized using the analytical expression at temperatures ranging from
$ T_{9}=0.01 $ to$ T_{9}=10 $ and compared with the existing rates. The reaction rate had negligible dependence on the variation of AC. However, it showed a strong impact on the interference of the$ {}^{3}S_{1} $ (312) and$ {}^{3}S_{1} $ (962) resonances, especially at$ T_{9} $ , in reference to the CNO Gamow windows. We estimated the contribution of the cascade transitions to the reaction rate. The enhancement of the ratio of the sum of the GS and cascade transitions and the GS transition at$ T_{9}>0.3 $ is due to the contribution of the 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O processes. -
The authors would like to thank A. M. Mukhamedzhanov for useful discussions.
-
Parametrization coefficients for the analytical expression (8) of the 15N(
$ p, \gamma $ )16O reaction rate data in Ref. [16] and those obtained within the framework of MPCM are presented in Table A1. The sets of parameters I, II, and III from Table 2 lead to the three sets of parametrization coefficients for Eq. (8). Set II$ _{{\rm{m}}} $ with$ \chi ^{2}=0.093 $ presents the parametrization coefficients for Eq. (8) when data [37] for the transitions 15N($ p, \gamma _{(6.050)} $ )16O, 15N($ p, \gamma _{(6.130)} $ )16O, and 15N($ p, \gamma _{(7.117)} $ )16O are considered based on Eq. (7).
Astrophysical S-factor and reaction rate for 15N(p,γ)16O within the modified potential cluster model
- Received Date: 2023-11-02
- Available Online: 2024-04-15
Abstract: We study radiative





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























 DownLoad:
DownLoad: