-
Magnetars are neutron stars with extremely strong magnetic fields exceeding
$ \sim 10^{13} $ G [1−3]. They have long rotational periods, typically lasting several seconds, and gradually spin down due to electromagnetic radiation. Magnetars are observationally recognized as soft gamma repeaters (SGRs), which persistently emit hard X-rays and soft gamma-rays [4−6]. Magnetar bursts usually have durations of$ \sim 0.1-1 \; \rm{s} $ and peak luminosities in the range of$ \sim 10^{39}-10^{41} \; \rm{erg s}^{-1} $ . Although it is widely accepted that the bursts are powered by strong magnetic fields, the triggering mechanism remains unclear. Many theoretical models have been proposed to explain the triggering mechanism of SGRs, such as crustquakes in neutron stars [7] and magnetic reconnection [8].There are already several studies on the statistical properties of SGRs, particularly focusing on the distributions of energy and waiting time [9−15]. The cumulative energy distribution of 111 bursts from SGR 1806−20 was found to be well described by a power-law function with an index
$ \gamma = 1.66 $ , which is very close to the index$ \gamma \approx 1.6 $ of the earthquake Gutenberg–Richter power law [9]. Chang et al. [12] investigated the cumulative distributions of SGR J1550−5418 and found that the distributions of fluence, peak flux, and duration were well fitted by a bent power law, while the distribution of waiting time followed a simple power law. In addition to the power-law distribution of magnetars bursts, the fluctuations of bursts exhibit scale-invariant properties [12, 14−16]. The probability density functions of fluctuations are well described by the Tsallis q-Gaussian function for fluence, peak flux, and duration of 384 bursts from SGR J1550−5418, with q values consistent across different scale intervals, indicating that the Tsallis q-Gaussian distribution of fluctuations is scale-invariant [12].The statistical similarity between SGRs and fast radio bursts (FRBs) has also been discussed [14, 15], motivated by the observed association between the Galactic FRB 200428 [17, 18] and the hard X-ray burst from SGR 1935+2154 [19−23]. Repeating FRBs exhibit properties similar to those of SGRs, including a power-law distribution for both energy and waiting time [24−29], as well as a scale-invariant Tsallis q-Gaussian distribution of fluctuations [14, 27, 28, 30, 31]. The power-law distribution of energy and the scale-invariant fluctuations are predicted by self-organized criticality (SOC) systems [32, 33], providing a potential explanation for the burst properties observed in both SGRs and repeating FRBs.
Recent studies have also explored the statistical properties of the time series of repeating FRBs and SGRs [30, 34, 35]. Zhang et al. [34] used the Pincus index and Lyapunov exponent to quantify the randomness and chaos of repeating FRBs 20121102A and 20190520B, comparing them to other natural phenomena such as pulsars, earthquakes, solar flares, and Brownian motion. Repeating FRBs were found to exhibit high randomness and low chaos, mimicking the behavior of Brownian motion in the randomness-chaos phase space. Similar dynamical stability analyses were applied to magnetar bursts from SGR J1550-5418 and SGR J1935+2154. It was found that these magnetar bursts are distinct from FRBs in the time domain but have no significant difference in the energy domain [35]. Another interesting phenomenon identified through the analysis of time series is the long-term memory, which has been observed in repeating FRBs [30, 36, 37] but not yet been studied in magnetar bursts.
In this study, we investigate the statistical properties of magnetar bursts using data from four active SGRs, comprising approximately 2000 bursts in total. We particularly focus on the long-term memory and dynamical stability of SGRs. The structure of this paper is as follows. Section II presents the dataset used in the study. Section III examines long-term memory. Section IV analyzes randomness and chaos. Finally, Section V provides a discussion and conclusions.
-
For this analysis, we use burst data from four SGR sources: SGR 1806−20, SGR 1900+14, SGR J1935+2154, and SGR J1550−5418. The first sample consists of 924 bursts from SGR 1806−20 detected by the Rossi X-ray Timing Explorer (RXTE) between 1996 and 2011. The second sample includes 432 bursts from SGR 1900+14, detected by RXTE between 1998 and 2006. Both samples are available in an online database
1 constructed by the high-energy astrophysics group at Sabancı University. The burst time and total count of each bursts can be found in the database. The third sample comprises 217 bursts from SGR J1935+2154, observed by the NICER telescope during the 1120s burst storm period on April 28, 2020 [38]. The database includes the burst start time, duration, and flux; the fluence can be calculated as the product of duration and time-averaged flux. The fourth sample consists of 384 bursts from SGR J1550-5418, observed during three active episodes in 2008-2009 by the Gamma-ray Burst Monitor onboard the Fermi Gamma-ray Space Telescope (Fermi/GBM) [39]. The$ T_{\rm 90} $ start time and fluence are given in the database. All four samples are summarized in Table 1, and the photon counts or fluence as a function of arrival time are depicted in Fig. 1.Table 1. SGR samples used in our analysis.
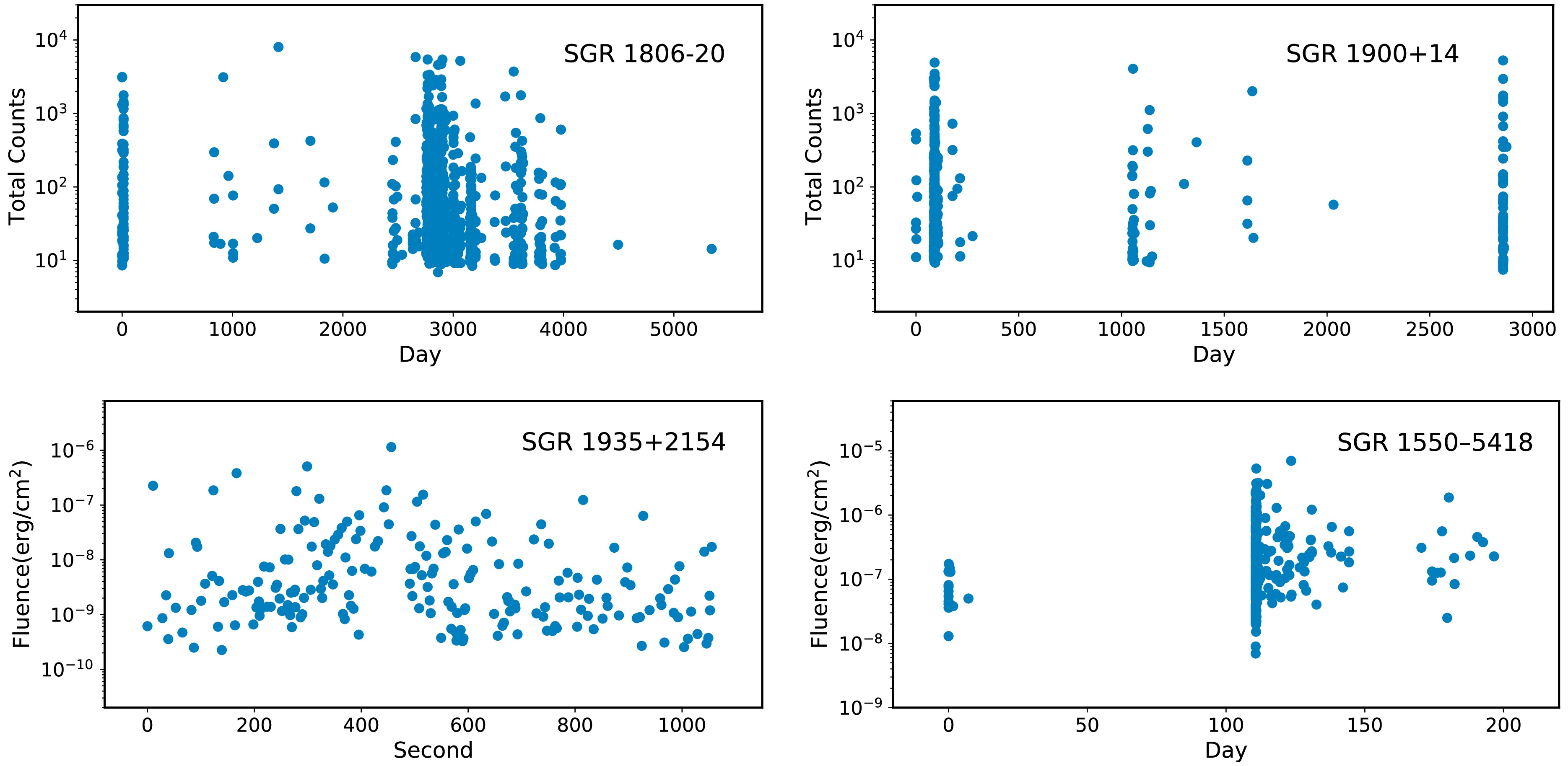
Figure 1. (color online) Photon counts or fluence vs. arrival time for all four SGR samples. The arrival time of the first burst is set to zero.
In this study, we investigate the long-term memory and dynamical stability of magnetar bursts by analyzing the time sequences of waiting time and energy. The waiting time is defined as the time difference between two successive bursts,
$ \Delta T = T_{i+1} - T_i $ . We use the burst time of SGR 1806−20 and SGR 1900+14, the burst start time of SGR J1935+2154, and the$ T_{\rm 90} $ start time of SGR J1550−5418 as the arrival time of the i-th burst$ T_i $ . Note that each sample consists of different observing sessions. The duration of an observing session is expected to be no more than a half of the orbital periods of satellites. The orbital periods of satellites around the Earth are 93, 93 and 95 minutes for the RXTE, NICER and Fermi satellites, respectively. Therefore, we use a uniform criterion to discard the waiting times longer than 1 hour to avoid long observing gaps. The burst energy is not a directly observable quantity. For a specific SGR source, the burst energy is proportional to the fluence or the photon counts. Rescaling the burst energy by a universal constant does not affect the results discussed below. Hence, we directly use the fluence or photon counts as representations of burst energy. Specifically, we use the time sequence of total counts for the SGR 1806−20 and SGR 1900+14 samples and the time sequence of fluence (flux multiplied by duration) for the SGR J1935+2154 and SGR J1550−5418 samples as the energy sequence in the subsequent analysis. -
Long-term memory observed in time series data is a fascinating phenomenon that has been identified in several natural events, such as earthquakes [40], solar flares [41] and repeating FRBs [30, 36, 37]. In this section, we present the measurement of long-term memory in magnetar bursts for the first time. We employ the rescaled range analysis (R/S analysis) to calculate the Hurst exponent H [42, 43], which quantifies long-term memory in time series data. If the R/S analysis yields
$ H > 0.5 $ , it indicates the presence of positive long-range correlations in the time series data. Conversely,$ H < 0.5 $ suggests negative long-range correlations. If$ H = 0.5 $ , it implies an absence of long-range correlations within the data.Here, we provide a concise introduction to the rescaled range analysis method [44−46]. A time series of length N is divided into l non-overlapping subseries, each of length n. For each subseries
$ X_m $ , where$m=1,2,\cdots,l$ , the R/S analysis proceeds as follows: (a) calculate the mean value$ E_m $ and standard deviation$ S_m $ for each subseries$ X_{m} $ ; (b) normalize the data in the subseries$ X_{m} $ by subtracting the mean value to obtain a mean-adjusted time series,$ Y_{i,m}=X_{i,m}-E_m $ for$i=1,2,\cdots,n$ ; (c) construct a cumulative deviation time series$ Z_{i,m}=\sum_{j=1}^i Y_{j,m} $ for$i=1,2,\cdots,n$ ; (d) determine the series range$R_m = \max \{Z_{1,m}, \cdots,Z_{n,m}\} - \min \{Z_{1,m},\cdots,Z_{n,m}\}$ ; and (e) rescale the range using the standard deviation,$ R_m/S_m $ . Finally, we calculate the mean value of the rescaled range across all subseries of length n,$ (R/S)_n = \frac{1}{l}\sum\limits_{m=1}^l R_m/S_m. $

(1) By varying the length n of the subseries, we construct a series of rescaled ranges, which asymptotically follow the relation:
$ (R/S)_n = Cn^H, $

(2) where H, the Hurst exponent, can be derived through linear regression on a logarithmic scale,
$ \ln (R/S)_n = \ln C + H \ln n. $

(3) In this study, we employ the R/S analysis on the time series of waiting time and energy of magnetar bursts. The public package
$\textsf{NOLDS}$ [47] is used for the analysis. Figure 2 illustrates the rescaled range series as a function of n for the four SGR samples, with the waiting time represented by green dots and energy by magenta squares. The points correspond to the rescaled range series derived from the sample data, and the straight lines represent the results of linear regression. As expected, the rescaled range series follows a simple power-law function of n. The data points fit well with a straight line in the log-log plot, where the slope of the line gives the Hurst exponent H. The best-fitting lines, obtained using the usual least-$ \chi^2 $ method, are shown in Fig. 2, with shaded regions representing the$ 1\sigma $ uncertainty. The Hurst exponents H for the waiting time and energy of the four SGR samples are summarized in Table 2. We also calculate the intrinsic scatter$ \sigma_\mathrm{int} $ , defined as the square root of the reduced chi-square. For the SGR 1806−20, SGR 1900+14, SGR J1935+2154, and SGR J1550−5418 samples, the Hurst exponents for waiting time are$ H=0.73 \pm 0.02 $ ,$ 0.64 \pm 0.03 $ ,$ 0.67 \pm 0.03 $ , and$ 0.73 \pm 0.03 $ , respectively. Similarly, the Hurst exponents for energy are$ H=0.56 \pm 0.01 $ ,$ 0.58 \pm 0.02 $ ,$ 0.64 \pm 0.02 $ , and$ 0.57 \pm 0.02 $ , respectively. The Hurst exponents are larger than$ 0.5 $ at$ \gtrsim 3\sigma $ confidence level for all the samples. Therefore, we conclude that long-term memory exists in the time series of both waiting time and energy for the magnetar bursts.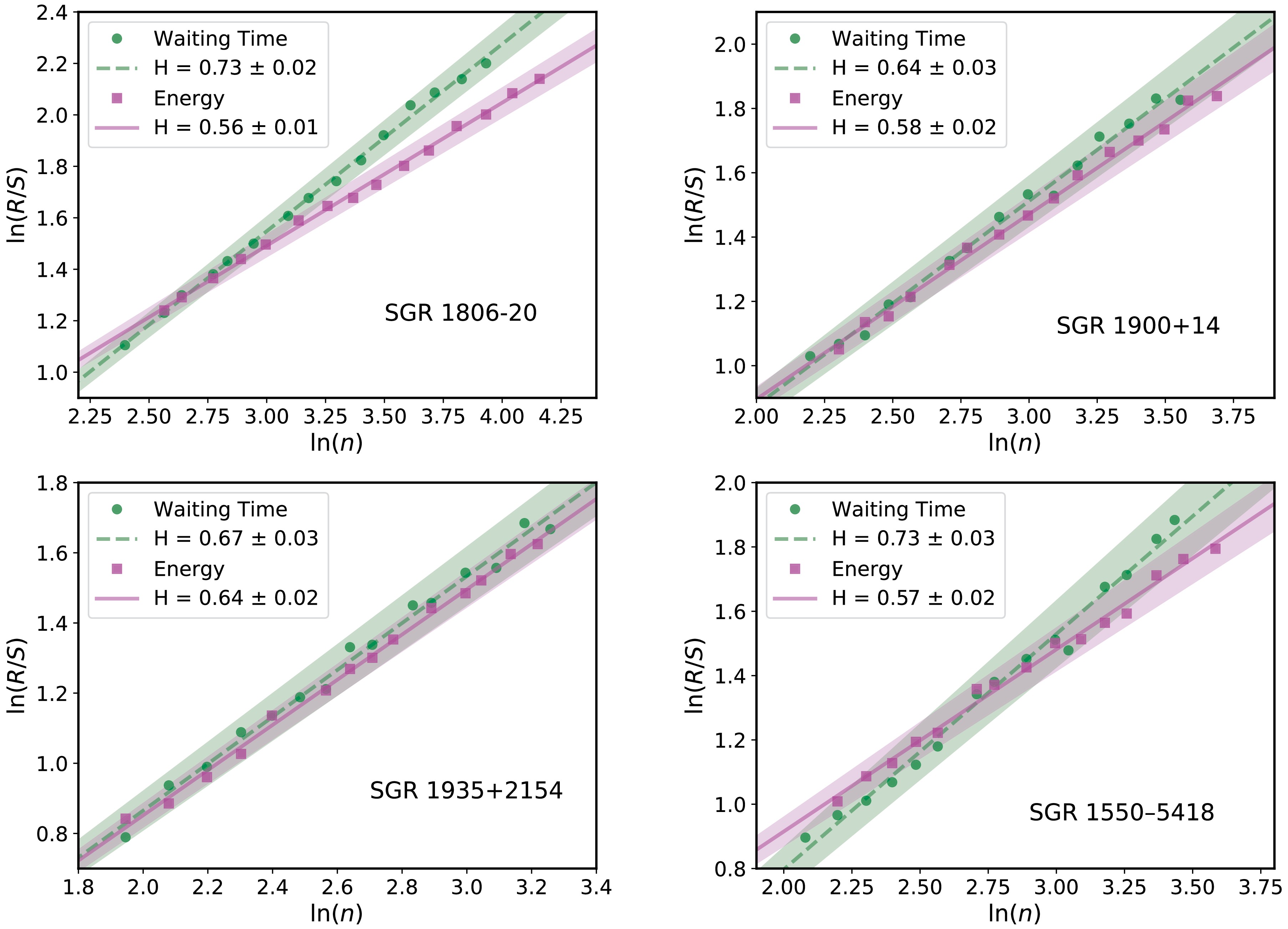
Figure 2. (color online) Rescaled range series of waiting time and energy for SGRs. The dashed lines and solid lines are the linear regression curves of waiting time and energy, respectively. The shaded regions represent the
$ 1\sigma $ uncertainty of linear regression.Waiting time Energy SGR 1806−20 0.73 $ \pm $ 0.02

0.56 $ \pm $ 0.01

SGR 1900+14 0.64 $ \pm $ 0.03

0.58 $ \pm $ 0.02

SGR J1935+2154 0.67 $ \pm $ 0.03

0.64 $ \pm $ 0.02

SGR J1550−5418 0.73 $ \pm $ 0.03

0.57 $ \pm $ 0.02

Table 2. Hurst exponent H of waiting time and energy for SGRs. The uncertainty is the intrinsic scatter of linear regression.
-
In this section, we explore the dynamical stability of magnetar bursts in terms of randomness and chaos. The randomness and chaos of a time series are quantified using the Pincus index (PI) [48] and the largest Lyapunov exponent (LLE) [49], respectively. We compute the PI and LLE values for the waiting time and energy in the four SGRs samples and illustrate the results in randomness-chaos phase space.
The PI value quantifies randomness in a dynamical system, and its calculation is based on the concept of approximate entropy. The approximate entropy of a time series
$ {u(i)} $ of length N is defined as [48, 50]$ \begin{aligned}[b] {\rm ApEn}(m,r,N) & \simeq -\frac{1}{N-m} \\ & \times \sum\limits_{i=1}^{N-m}\log \frac{\displaystyle\sum_{j=1}^{N-m}\theta({\rm dist}[x_{m+1}(j), x_{m+1}(i)]-r)}{\displaystyle\sum_{j=1}^{N-m} \theta({\rm dist}[x_{m}(j), x_{m}(i)]-r)}. \end{aligned} $

(4) Here,
$x_{m}(i)=[u(i),\cdots, u(i + m-1)]$ and$x_{m}(j)=[u(j),\cdots, u(j+m-1)]$ are the subseries of$ {u(i)} $ , and the embedding dimension m is the length of the subseries.$ {\rm dist}[x,y] $ is the Chebyshev distance between x and y.$ \theta(x) $ is the step function, i.e.$ \theta=1 $ for$ x\geq 0 $ , and$ \theta=0 $ for$ x<0 $ . We use the public code$\textsf{EntropyHub}$ [51] to compute ApEn in this paper. Following standard conventions, we set the embedding dimension$ m=2 $ and vary the distance threshold r in the range of [0.01,0.09] multiplied by the standard deviation of the data series. The maximum approximate entropy (MAE) [50, 52] is defined as the maximum value of ApEn across various values of r,$ {\rm MAE} = \max\limits_r [{\rm ApEn}(m,r,N) ]. $

(5) Using bootstrap sampling, we calculate the PI for a series, defined as the ratio of MAE of the original series to that of a randomly shuffled series,
$ {\rm PI} = \frac{{\rm MAE}_ {\rm{original}}}{{\rm MAE}_ {\rm{shuffled}}}. $

(6) The PI quantifies the randomness of a time series, with a value of zero indicating a completely ordered system and a value of unity representing complete randomness. In this study, we perform random shuffling on the original series 1000 times to obtain 1000 values of
$ {\rm MAE_{shuffled}} $ . The bootstrap sampling method also provides the uncertainty of the PI, propagated from the uncertainty of$ {\rm MAE_{shuffled}} $ ,$ \frac{\sigma_{\rm PI}}{\rm PI} = \frac{\sigma_{{\rm MAE}_ {\rm{shuffled}}}}{{\rm MAE}_ {\rm{shuffled}}}, $

(7) where
$ \sigma_{{\rm MAE}_ {\rm{shuffled}}} $ is defined as the standard deviation of the$ {\rm MAE} $ values of the randomly shuffled series.We calculate the MAE and PI values for the time series of waiting time and energy for the four SGR samples. Fig. 3 shows the MAE value for the original series using a magenta solid line and the distribution of MAE values for the 1000 shuffled series using a green histogram. The 16th, 50th, and 84th percentiles of the shuffled series distribution are plotted in blue, red, and black dashed lines, respectively. Table 3 lists the PI values and their uncertainties. We quantify the randomness of the samples through the distance between
$ {\rm MAE}_{ \rm{original}} $ and$ {\rm MAE}_{\rm{shuffled} }$ or directly through the PI values. As shown, the waiting time series of SGR 1900+14 and SGR J1550−5418 significantly deviate from a random organization, with PI values of$ 0.84 \pm 0.02 $ and$ 0.76 \pm 0.03 $ , respectively. For SGR 1806−20 and J1935+2154, the waiting time series also slightly differ from a completely random organization. Therefore, we conclude that the waiting time series are not completely random for all four SGRs samples. Regarding the energy series, the PI value of a completely random organization ($ {\rm PI}=1 $ ) lies within the$ 1 \sigma $ confidence interval of the PI values for SGR 1806−20 and SGR 1900+14. In contrast, the PI values for SGR J1935+2154 and SGR J1550−5418 deviate from complete randomness ($ {\rm PI}=1 $ ) at more than$ 2 \sigma $ confidence level. Hence, the energy series is completely random for SGR 1806−20 and SGR 1900+14 samples but less random for SGR J1935+2154 and SGR J1550−5418 samples.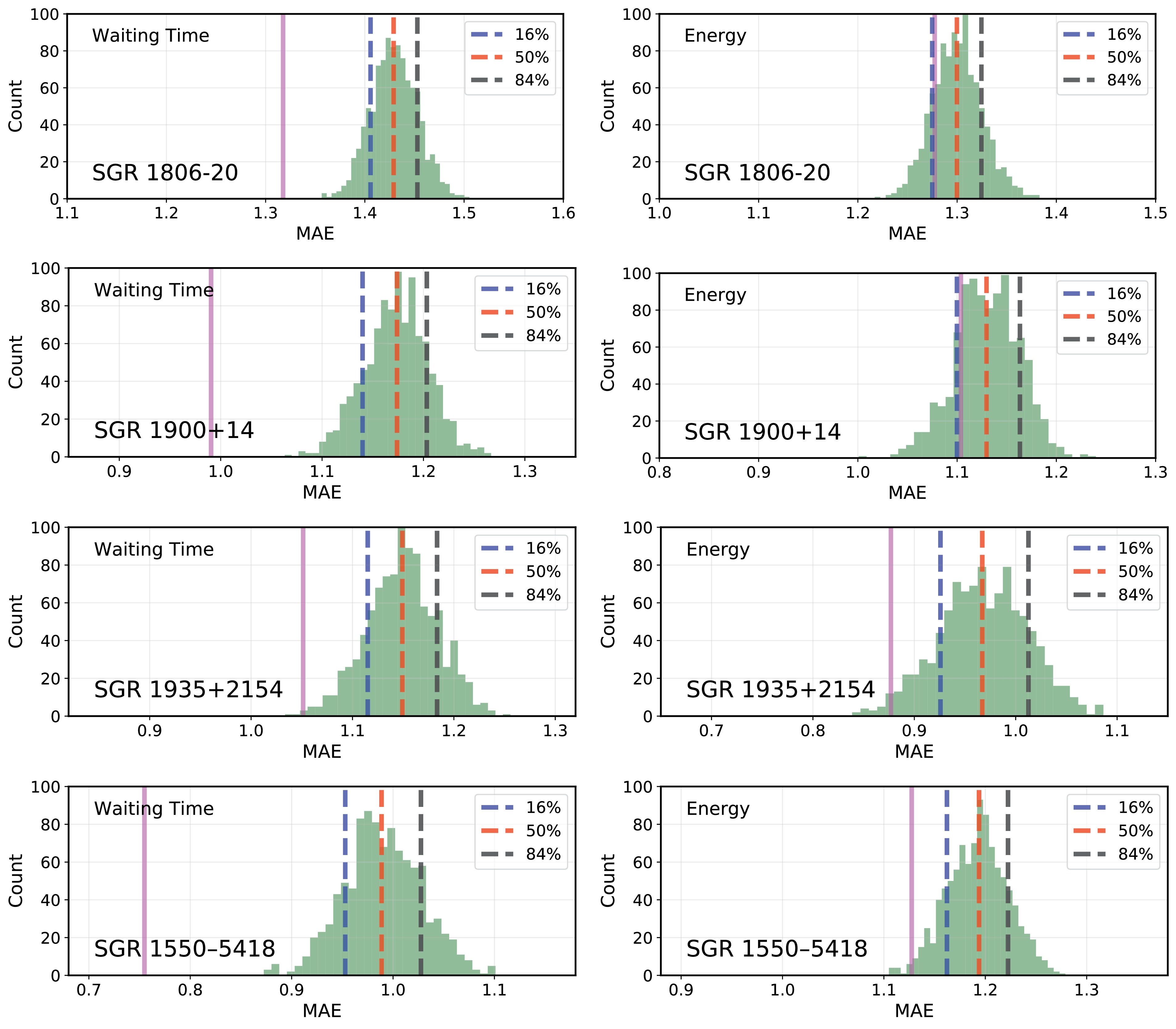
Figure 3. (color online) MAE distribution for SGRs. The magenta solid line represents the MAE of the original series. The green histogram represents the distribution of the MAE of the 1000 shuffled series. The blue, red, and black dashed lines represent the 16th, 50th, and 84th percentiles of the 1000 simulations, respectively.
Waiting time Energy SGR 1806−20 0.92 $ \pm $ 0.02

0.98 $ \pm $ 0.02

SGR 1900+14 0.84 $ \pm $ 0.02

0.98 $ \pm $ 0.03

SGR J1935+2154 0.92 $ \pm $ 0.03

0.91 $ \pm $ 0.04

SGR J1550−5418 0.76 $ \pm $ 0.03

0.95 $ \pm $ 0.02

Table 3. PI values of waiting time and energy for SGRs. The uncertainty is the standard deviation of the randomly shuffled series.
The LLE quantifies chaos in a non-linear dynamical system, along with quantifying the local stability features of attractors and other invariant sets in phase space. In an
$ m- $ dimensional phase space, an initially infinitesimal m-sphere of radius$ r_0 $ deforms into an m-ellipsoid due to the locally deforming nature of the phase flow. The length of the i-th ellipsoidal principal axis evolves exponentially with time$ r_i=r_0\exp(\lambda_it) $ . The Lyapunov exponents are defined as [49]$ \lambda_i=\lim\limits_{t\rightarrow \infty}\frac{1}{t}\ln\frac{r_i}{r_0},\; \; \; \; i=1,2,\cdots,m. $

(8) The LLE is the maximum value among the Lyapunov exponents
$ \lambda_i $ and quantifies the rate of separation of two adjacent trajectories in phase space. A positive LLE value indicates that two infinitely close trajectories in phase space diverge exponentially over time, implying the presence of chaos. Conversely, a negative LLE value suggests a stable system. We use the algorithm proposed by Rosenstein et al. [53] implemented in the public package$\textsf{NOLDS}$ [47] to calculate the LLE. The embedding dimension is set to the default value$ m=10 $ . Since the LLE represents the maximum value in the entire spectrum of Lyapunov exponents, defining its uncertainty is challenging. A possible method involves calculating the LLE values for varying embedding dimension m and using their standard deviation to estimate the uncertainty. However, we find that the LLE is nearly independent of the embedding dimension (as shown below), and therefore, we ignore the uncertainty of LLE in this analysis.Table 4 summarizes the LLE values of the waiting time and energy series for the four SGRs. Although all the LLE values are positive, they are very close to zero. Hence, we conclude that there is no strong evidence for the existence of chaos in any of the four SGR samples.Waiting time Energy SGR 1806−20 0.051 0.074 SGR 1900+14 0.056 0.079 SGR J1935+2154 0.034 0.061 SGR J1550−5418 0.137 0.046 Table 4. LLE values of waiting time and energy for SGRs.
In Fig. 4, we plot the LLE and PI values for each SGR in the randomness-chaos phase plane. For comparison, we also illustrate the LLE and PI values of four samples from three highly active repeating FRBs observed by the FAST telescope, i.e., FRB 20121102A, FRB 20201124A, and FRB 20220912A. The bursts from FRB 20201124A are divided into two samples, observed during two separate periods with an observational gap of approximately three months. The PI values of the four FRB samples were calculated in our previous study [31]. The LLE values were calculated by reanalyzing the same data samples using the method applied in this study. In the time domain (left panel of Fig. 4), the SGR samples except for SGR J1550−5418 and all four FRB samples concentrate in a small region, with average values of
$ {\rm PI}\sim 0.9 $ and$ {\rm LLE}\sim 0.05 $ . However, SGR J1550−5418 seems to be an outlier in the randomness-chaos phase plane, exhibiting a smaller PI ($ \sim 0.76 $ ) and a larger LLE ($ \sim 0.14 $ ) than the other SGRs and FRBs. This indicates that the waiting time of SGR J1550−5418 is less random but more chaotic than those of the other samples. In the energy domain (the right panel of Fig. 4), all the data samples concentrate in a small region of the randomness-chaos phase plane, with average values of$ {\rm PI}\sim 0.9 $ and$ {\rm LLE}\sim 0.06 $ . Notably, the two samples from FRB 20201124A do not significantly diverge in this plane, implying that there is no strong temporal variability in the burst activity. This finding aligns with our previous conclusion [31]. In summary, we conclude that there is no significant difference between SGRs and FRBs in the randomness-chaos phase plane for both waiting time and energy.
Figure 4. (color online) The randomness-chaos plane of waiting time (left-panel) and energy (right panel) for SGRs and FRBs. The dots and squares represent for SGRs and FRBs, respectively.
Both the PI and LLE values depend on the embedding dimension m. To assess the robustness of our results, we use different embedding dimensions m in the calculations of PI and LLE. The PI and LLE values as a function of m are depicted in Fig. 5 for the waiting time and energy of the four SGR samples. As shown, both PI and LLE values are not significantly affected by the choice of embedding dimension, confirming the robustness of our results.
-
In this study, we investigated the statistical properties of the waiting time and energy of magnetar bursts using four samples. Through rescaled range analysis, we calculated the Hurst exponent to measure long-term memory in magnetar bursts for the first time. Our findings indicate that long-term memory exists in the time series of both waiting time and energy for magnetar bursts. We also explored the dynamical stability of magnetar bursts by measuring randomness and chaos, quantified using the Pincus index and the largest Lyapunov exponent, respectively. In the time domain, all four SGR samples exhibited evidence of deviation from random organization. In the energy domain, the results were somewhat subtle: SGR 1806−20 and SGR 1900+14 were consistent with random organization, while SGR J1935+2154 and SGR J1550−5418 appeared less random. Furthermore, our analysis revealed that both waiting time and energy exhibit weak chaos across all four SGR samples. Finally, we compared the SGRs with repeating FRBs and found no significant difference between these two astronomical phenomena in the randomness-chaos phase space for both waiting time and energy.
Previous discussions on the statistical similarities between SGRs and repeating FRBs have primarily focused on the power-law distribution of observed quantities such as energy, waiting time, and burst duration, as well as the scale-invariant Tsallis q-Gaussian distribution of their fluctuations. In this study, we extend the scope of the investigation to include long-term memory and randomness-chaos characteristics. Our findings indicate that SGRs share similar properties with repeating FRBs. The Hurst exponent H for repeating FRBs are found to be around 0.6 [30], consistent with the H values for SGRs obtained in this study. This suggests that the long-range correlations in SGRs and FRBs are positive but not strong. Similarly, the PI values for FRBs and SGRs are also very similar, with a range of
$ {\rm PI}\sim 0.8-1.0 $ . These statistical similarities, along with the observation of the FRB-associated magnetar SGR 1935+2154 [17, 18], imply the possibility of a common emission mechanism between SGRs and FRBs.Repeating FRBs have also been compared with other physical phenomena in the randomness-chaos phase space. For instance, Zhang et al. [34] found that FRBs deviate significantly from pulsars, earthquakes, and solar flares. We found that, for both waiting time and energy, SGRs do not deviate significantly from FRBs within the randomness-chaos phase space. The randomness and chaos have also been investigated for two SGRs by Yamasaki et al. [35]. In their work, the authors compared SGRs and FRBs in the randomness-chaos plane and found that SGRs exhibit significantly lower randomness and a slightly higher degree of chaos compared to FRBs in the time domain, while exhibiting broad consistency in the energy domain. However, our results show that SGRs and FRBs are consistent with each other in both the time and energy domains, which contradicts the findings of Yamasaki et al. [35]. This discrepancy may be due to differences in the data samples used. Additionally, Yamasaki et al. [35] used the energy fluctuation in the analysis, while we used the energy itself. This issue needs to be further investigated with a larger data sample in the future.
Quantifying the memory and dynamical stability of magnetar bursts
- Received Date: 2024-10-14
- Available Online: 2025-03-15
Abstract: The time series of energy and waiting time in magnetar bursts carry important information about the source activity. In this study, we investigate the memory and dynamical stability of magnetar bursts from four soft gamma repeater (SGR) sources: SGR 1806−20, SGR 1900+14, SGR J1935+2154, and SGR J1550−5418. Based on the rescaled range analysis, we quantify the memory in magnetar bursts for the first time and find that there exists long-term memory in the time series of both waiting time and energy. We investigate the dynamical stability in the context of randomness and chaos. For all four SGR samples, we find that the waiting time is not completely random; however, the energy of two SGRs is consistent with a total random organization. Furthermore, both waiting time and energy exhibit weak chaos. We also find no significant difference between SGRs and repeating fast radio bursts (FRBs) in the randomness-chaos phase space. The statistical similarity between SGRs and repeating FRBs hints that there may be potential physical connection between these two phenomena.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: