-
Ultraperipheral collisions (UPCs) are important tools for investigating photoproduction at high energies [1-3]. UPCs can probe
$ \gamma $ -$ \gamma $ and$ \gamma $ -h interactions via vector meson production and dijet production [4]. UPCs have been studied at the Large Hadron Collider (LHC) and Relative Heavy Ion Collider (RHIC) for the photoproduction of several vector mesons, such as$ \rho $ ,$ \omega $ ,$ \phi $ , and$ J/\psi $ . The photoproduction of exotic particles by UPCs has also been investigated [5, 6].In UPCs, the impact parameter of two hadrons is larger than the sum radius of two hadrons. The direct strong interaction between two hadrons is thereby suppressed due to the large distance. However, the accelerated hadrons are surrounded by a cloud of photons with virtuality
$ Q^2<(\hbar c/R_A)^2 $ . If$ A>16 $ and$ Q^2 $ is less than$ ( $ 60$ \mathrm{MeV})^2 $ , a photon is almost a real photon in UPCs [3]. Therefore, electromagnetic interaction is important in UPCs since it is a long range interaction. The photon-hadron interaction can also be investigated in UPCs. Since the direct strong reaction between hadrons is suppressed in UPCs, the background of UPCs is cleaner than that of non-UPCs in hadron-hadron collisions.Recently, several narrow pentaquark states named
$ P_{c}(4312),\; P_{c}(4440), \; P_{c}(4457) $ have been observed in$ \Lambda _{b}\rightarrow $ $ J/\psi pK $ by the LHCb Collaboration [7, 8], which is an important progress in the search for exotic hadrons. Many theoretical models have been proposed to study the internal nature and production of pentaquark states$ P_c $ since their discovery [9-22].Since the intermediate particles in the above reaction process satisfy the on-shell condition, the contribution of triangular singularities in the
$ \Lambda _{b}\rightarrow J/\psi pK $ reaction cannot be ignored [23]. This means that it is currently difficult to determine whether these$ P_{c} $ states are genuine states. However, one can observe and study the$ P_{c} $ state via other scattering processes, such as photoproduction processes, thereby effectively avoiding the influence of triangular singularities in order to determine whether the$ P_{c} $ state is a genuine state. In Refs. [21, 22], combined with the latest experimental results, an in-depth study of$ P_{c} $ state production via$ \gamma p $ or$ \pi ^{-}p $ was carried out. Subsequently, the GlueX Collaboration reported their first measurement of the$ \gamma p\rightarrow J/\psi p $ process [24]. Although the GlueX group did not find the photoproduction of pentaquark states with the present precision [24], their data suggested a meaningful upper limit of production cross sections and hence a model dependent upper limit of the branching ratio$ \mathcal{B}(P_{c}\rightarrow J/\psi p) $ of a small percentage at most. The size of the branching ratio of$ P_{c}\rightarrow J/\psi p $ suggested by the experiment is largely consistent with the results in [22]. In Ref. [25], based on the previous predictions of the mass and width of the hidden bottom pentaquark$ P_{b} $ , a systematic study of the photoproduction of the$ P_{b} $ state was conducted. These photoproduction results of$ P_{c} $ and$ P_{b} $ are important foundations for studying the production of pentaquark states via UPCs.STARlight is a Monte-Carlo package for vector meson production simulation in UPCs [26]. It is widely used in
$ AA $ and$ pA $ UPCs at the LHC and RHIC. The cross section calculation of photon-proton to vector mesons is needed in the STARlight package, and the total cross section of vector mesons in UPCs can be obtained by multiplying the photon flux. We use the photon-induced cross section of the pentaquark states of$ P_c $ and$ P_b $ and implement the cross sections in STARlight. In this way, we can obtain the total cross sections of the vector mesons in UPCs and simulate the distributions. The output of STARlight is the four momentum of the final states. Using the four momentum of the final states, one can obtain the rapidity and pseudo-rapidity distributions of the vector mesons. We apply the STARlight package to simulate vector mesons in the pentaquark resonance s-channel and pomeron exchange t-channel. The pseudo-rapidity and rapidity distributions are presented in this paper.The aim of this paper is to study the production of hidden charm/bottom pentaquark states in UPCs. The relevant results can provide an important theoretical basis for finding
$ P_{c} $ and$ P_{b} $ states via future UPC experiments. This paper is organized as follows. The theoretical framework is presented in Section II. The numerical results are given in Section III, and a summary concludes the paper in Section IV. -
In UPCs, a real photon emitted from one nucleus can interact with a nucleus from the other direction. Because the photon number is proportional to the charge number of the hadrons, the photon flux emitted from a proton can be neglected when compared to the photon flux emitted from the nucleus in p-
$ A $ UPCs, for example, those of gold and lead. Thus, in p-$ A $ UPCs, we can neglect photons emitted from the proton, and we only consider the photons from the nucleus. Diagrams of the p-$ A $ processes in the s-channel and t-channel schemes are shown in Fig. 1. In the s-channel, the vector mesons are produced via pentaquark state resonance. In the t-channel, the photon interacts with a proton via pomeron exchange and produces vector mesons. As the cross section of the t-channel is dominant in photon-proton interactions, the cross section of the t-channel can be viewed as a background of the pentaquark resonance for the discovery of pentaquark states processes. Usually, for an electromagnetic scattering process, the scattering amplitude should meet the requirements of gauge invariance. In the process shown in Fig. 1, the s-channel amplitude$ {\cal M} $ satisfies the relation$ k\cdot {\cal M} = 0 $ , where k is the photon momentum. Moreover, the cross section of the t-channel can be calculated by a parameterized pomeron model rather than by constructing the amplitude. Therefore, for the current scattering process, we posit that the scattering amplitude roughly satisfies gauge invariance.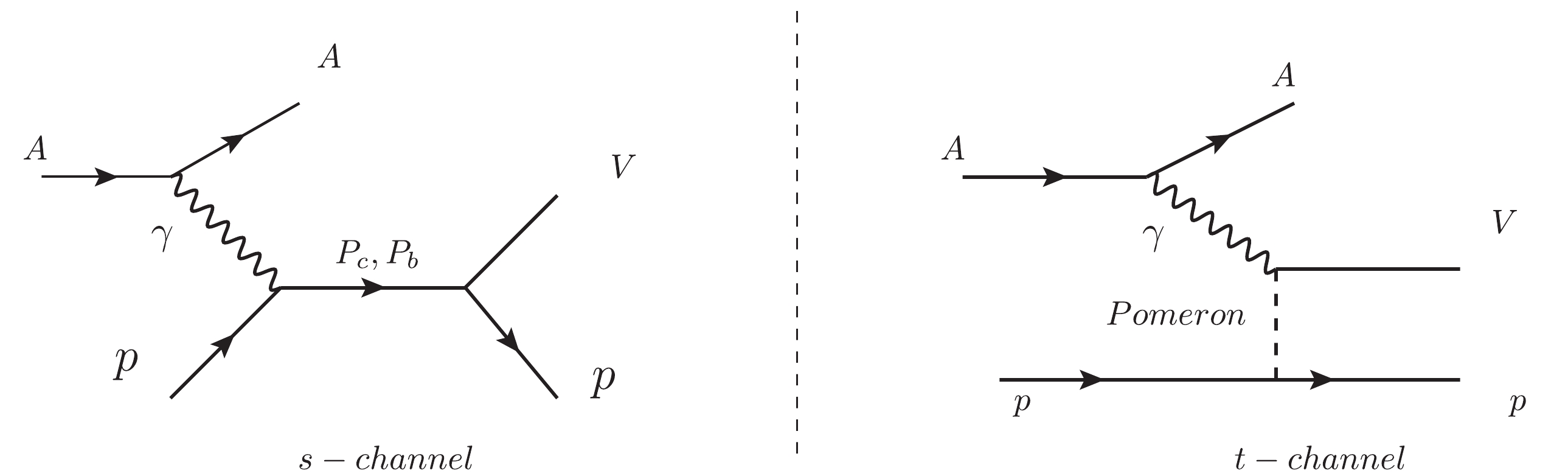
Figure 1. Processes of vector meson production in p-
$A $ UPCs via the s-channel (left) and t-channel (right).Because the impact parameter of two hadrons is large in UPCs, the production of pentaquark states via
$ \pi $ meson exchanging contributions in hadrons can be neglected since the$ \pi $ meson exchanging interaction is a short range interaction. We thus only consider the photon-induced pentaquark state production in UPCs, as depicted in Fig. 1.The cross section of the vector mesons in UPCs is computed by integrating the photon flux and photon-proton cross section. The photon flux can be obtained in QED calculations. The photon-proton cross section for vector mesons can be calculated by several models. In p-
$ A $ UPCs, the cross section of$ pA\rightarrow pAV $ is given as follows [26]$ \sigma (pA\rightarrow pAV) = \int {\rm d}k\frac{{\rm d}N_{\gamma }(k)}{{\rm d}k}\sigma _{\gamma p\rightarrow pV}(W), $

(1) where k is the momentum of the photon emitted from the nucleus, and W is the center of mass (c.m.) energy of the photon and proton system. The relationships of the rapidity of vector mesons y and k with W are
$ k = M_V/2{\rm exp}(y) $ and$ W = (2k\sqrt{s})^{1/2} $ . Using these equations, we obtain the rapidity distributions of the vector meson in UPCs [27]:$ \frac{{\rm d}\sigma}{{\rm d}{\mathrm{y}}} = k\frac{{\rm d}N_{\gamma }(k)}{{\rm d}k}\sigma _{\gamma p\rightarrow pV}(W). $

(2) The photon emitted from the nucleus is presented as [28]:
$ \frac{{\rm d}N_{\gamma }(k)}{{\rm d}k} = \frac{2Z^{2}\alpha }{\pi k}\big(XK_{0}(X)K_{1}(X)-\frac{X^{2}}{2}[K_{1}^{2}(X)-K_{0}^{2}(X)]\big),$

(3) where
$ X = b_{\rm min}k/\gamma_{\rm L} $ , and$ b_{\rm min} = R_{A}+R_{p} $ is the sum of the radii of the proton and nucleus.$ \gamma_L $ is the Lorentz boost factorm, and it is obtained by$ \gamma_{\rm L} = \sqrt{s}/2m_p $ .$ K_{0}(x) $ and$ K_{1}(x) $ are Bessel functions. By employing the cross section of the vector mesons in p-$ A $ UPCs, we obtain the total cross section in p-$ {\rm Au} $ UPCs in the RHIC experiments. From Eq. (3), it can be seen that the photon flux is proportional to the charge number of the hadrons. For example, the photon flux of gold is$ Z^2 \approx 6200 $ , which is larger than the photon flux of the proton,$ Z^2 = 1 $ . We can therefore neglect the contributions of the photons from the proton in p-A UPCs.In Refs. [22, 25], the cross sections of
$ \gamma p\rightarrow P_{c}\rightarrow J/\psi p $ and$ \gamma p\rightarrow P_{b}\rightarrow \Upsilon (1S) p $ via the s-channel were calculated based on the effective Lagrangian method and the vector-meson-dominance (VMD) model. In the photoproduction calculation, the branching ratio of$ P_{c}(4312)\rightarrow J/\psi p $ was taken as 3%, and the decay width of$ P_{b}(11080)\rightarrow \Upsilon (1S) p $ was taken as 0.38 MeV, as predicted in Ref. [29]. The numerical results show that the average value of the cross section from the$ P_{c}(4312) $ or$ P_{b}(11080) $ produced in photon-proton scattering reaches at least 0.1 nb with a bin of 0.1 GeV. In this work, we employ the results for$ P_{c}/P_{b} $ photoproduction from Refs. [22, 25] to calculate the production of$ P_{c}/P_{b} $ via UPCs.For the contribution of t-channel Pomeron exchange, the cross section of
$ \gamma p\to V p $ is given as [26]$ \sigma^t_{\gamma p\to V p}(W) = \sigma_p\cdot\Bigg(1-\frac{(m_p+m_{V})^2}{W^2} \Bigg)\cdot W^\epsilon, $

(4) with
$ \sigma_p $ = 4.06 nb and$ \epsilon = 0.65 $ for$ J/\psi $ and$ \sigma_p $ = 6.4 pb and$ \epsilon = 0.74 $ for$ \Upsilon (1S) $ ; these values are determined using experimental data for the$ \gamma p\to V p $ process.By employing the cross sections in the s-channel and t-channel, we can obtain the vector meson cross sections in p-
$ A $ UPCs. With the Monte-Carlo package STARlight, we can simulate the vector meson production processes and obtain the four momentum of the final states. We then obtain the spectrum of the vector mesons in the two channels. -
In this study, the cross sections of the vector mesons
$ J/\psi $ and$ \Upsilon (1S) $ in the t-channel can be calculated using Eqs. (1)-(4). We use the same calculation progress of vector mesons in the s-channel as in Refs. [22, 25]. The STARlight package is employed to simulate the vector mesons through the t-channel and s-channel in p-$ {\rm Au} $ UPCs at the RHIC and in p-$ {\rm Pb} $ UPCs at the LHC. Vector meson distributions are presented for the RHIC and LHC.First, we calculate the
$ J/\psi $ and$ \Upsilon (1S) $ cross sections in the$ s $ -channel and t-channel in p-$ {\rm Au} $ and p-$ {\rm Pb} $ UPCs. The cross sections are listed in Table 1 and Table 2, where the masses and decay widths are also listed. The event numbers are also included; they can be applied to estimate the event number for one-year running of the RHIC and LHC.resonance properties [8, 29] s-channel t-channel $ P_c(4312) $ 

mass $ 4311.9\pm 0.7_{-0.6}^{+6.8} $ MeV

$ J/\psi $ cross section

1.8 nb 2.2 μb decay width $ 9.8\pm 2.7_{-4.5}^{+3.7} $ MeV

event number 8.1 K 9.9 M $ P_b(11080) $ 

mass 11080 MeV $ \Upsilon (1S) $ cross section

0.10 nb 1.2 nb decay width 1.58 MeV event number 0.45 K 5.4 K Table 1. Cross sections of
$ J/\psi $ and$ \Upsilon (1S) $ in$ p{\rm Au}\rightarrow pV{\rm Au} $ in the s-channel and t-channel. The collision energy is$ \sqrt{s} $ = 200 GeV, and the luminosity of the$ p-{\rm Au} $ is 4.5$ \mathrm{pb}^{-1} $ [30].resonance properties [8, 29] s-channel t-channel $ P_c(4312) $ 

mass $ 4311.9\pm 0.7_{-0.6}^{+6.8} $ MeV

$ J/\psi $ cross section

7.4 nb 0.10 mb decay width $ 9.8\pm 2.7_{-4.5}^{+3.7} $ MeV

event number 7.4 K 0.10 G $ P_b(11080) $ 

mass 11080 MeV $ \Upsilon (1S) $ cross section

0.78 nb 0.22 μb decay width 1.58 MeV event number 0.78 K 0.22 M Table 2. Cross sections of
$ J/\psi $ and$ \Upsilon (1S) $ in$ p{\rm Pb}\rightarrow pV{\rm Pb} $ in the s-channel and t-channel. The collision energy is$ \sqrt{s} $ = 8.8 TeV, and the luminosity of the p-${\rm Pb} $ is 1$ \mathrm{pb}^{-1} $ [31].From Tables 1 and 2, it can be seen that the cross sections of the LHC are much larger than those of the RHIC in the t-channel, and in the s-channel, the cross sections of the LHC are several times larger than those of the RHIC. The reason is that the cross section of the t-channel is dependent on the W region. The W region at the LHC is broarder than that at the RHIC. However, in the s-channel, the W regions are of the same size at the RHIC and LHC.
Second, the pseudo-rapidity distributions corresponding to the angular distributions of two vector mesons of p-
$ {\rm Au} $ UPCs at the RHIC are illustrated in Fig. 2. It can be seen that$ J/\psi $ and$ \Upsilon (1S) $ in the s-channel are totally covered by the t-channel distributions. This is because the cross section of the t-channel is much larger than the$ J/\psi $ cross section through the pentaquark exchange s-channel. The sum of the s-channel and t-channel is the same as the t-channel. As a result, it is difficult to identify the pentaquark signal through the$ J/\psi+p $ invariant mass spectrum in pseudo-rapidity distributions. In contrast, in$ \Upsilon (1S) $ production, the s-channel signal is significant for identifying the pentaquark state$ P_b(11080) $ through the$ \Upsilon (1S)+p $ invariant mass spectrum in pseudo-rapidity distributions.
Figure 2. (color online) Pseudo-rapidity distributions of
$ J/\psi $ and$ \Upsilon (1S) $ produced from the pomeron exchange t-channel (black solid curve) and pentaquark resonance s-channel (red dashed curve) for p-$ {\rm Au} $ UPCs at$ \sqrt{s} = 200 $ GeV at the RHIC. The direction of the gold beam is the positive pseudo-rapidity direction.We also provide the rapidity distributions of two vector mesons in p-
$ {\rm Au} $ UPCs in Fig. 3. We can see that in the rapidity space, the vector mesons in the s-channel are not totally covered by the vector meson distributions in the t-channel. These results differ from the rapidity distributions in Ref. [6]. The rapidity distributions of$ J/\psi $ in the s-channel are totally covered by the t-channel$ J/\psi $ rapidity distributions in Ref. [6]. Moreover, it can be seen that the rapidity distributions differ from the pseudo-rapidity distributions because the energies in the same pseudo-rapidity region are different in Fig. 2 and Fig. 3.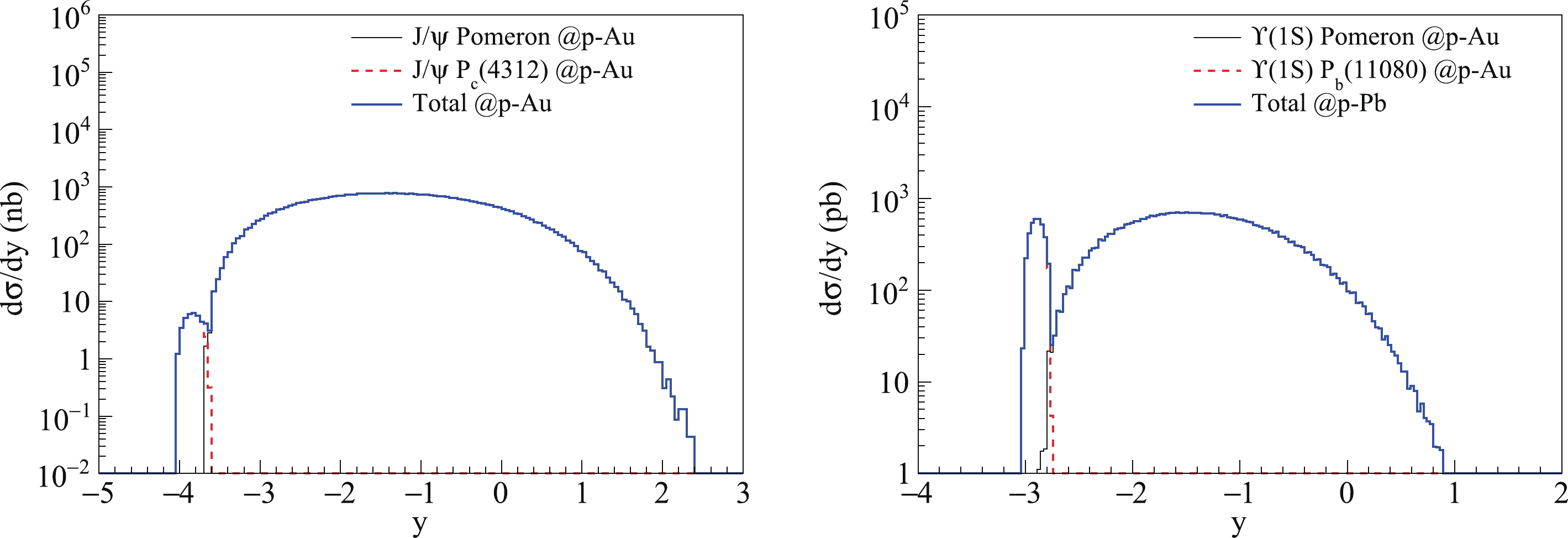
Figure 3. (color online) Rapidity distributions of
$ J/\psi $ and$ \Upsilon (1S) $ produced from the pomeron exchange t-channel (black solid curve) and pentaquark resonance s-channel (red dashed curve) for p-$ Au $ UPCs at$ \sqrt{s} = 200 $ GeV at the RHIC. The direction of the gold beam is the positive rapidity direction.Furthermore, we present the production of
$ J/\psi $ and$ \Upsilon(1S) $ via the s-channel and t-channel for p-$ {\rm Pb} $ UPCs at the LHC. The predictions are shown in Fig. 4 and Fig. 5. It is evident that the distributions of the t-channel at the LHC are larger than those at the RHIC. The background at the LHC is thus stronger than the background at the RHIC, making it more difficult to identify the pentaquark states at the LHC than at the RHIC.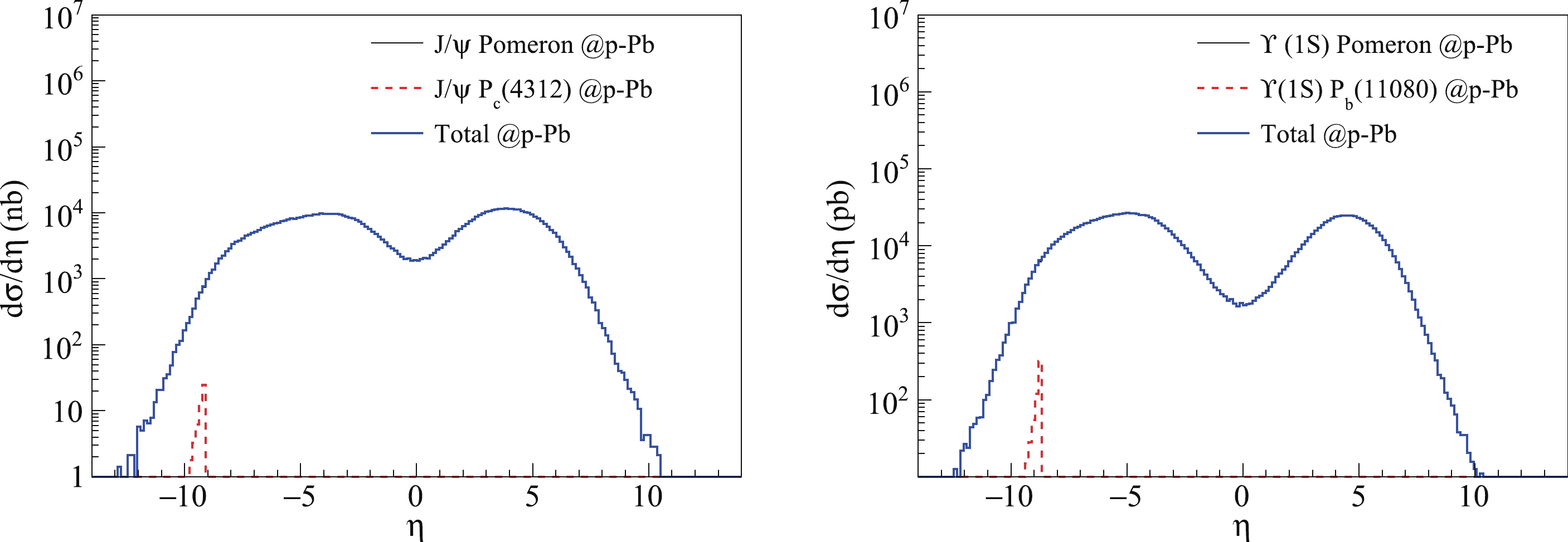
Figure 4. (color online) Pseudo-rapidity distributions of
$ J/\psi $ and$ \Upsilon (1S) $ produced from the pomeron exchange t-channel (black solid curve) and pentaquark resonance s-channel (red dashed curve) for p-$ {\rm Pb} $ UPCs at$ \sqrt{s} = 8.8 $ TeV at the LHC. The direction of the lead beam is the positive pseudo-rapidity direction.
Figure 5. (color online) Rapidity distributions of
$ J/\psi $ and$ \Upsilon (1S) $ produced from the pomeron exchange t-channel (black solid curve) and pentaquark resonance s-channel (red dashed curve) for p-$ {\rm Pb} $ UPCs at$ \sqrt{s} = 8.8 $ TeV at the LHC. The direction of the lead beam is the positive rapidity direction.Finally, the production of
$ J/\psi $ and$ \Upsilon (1S) $ is presented for p-$ {\rm Au} $ UPCs at the RHIC and p-$ {\rm Pb} $ at the LHC. The cross sections in the s-channel and t-channel, which can be used to predict the total detected event numbers at the RHIC and LHC, are listed in Tables 1 and 2. The pseudo-rapidity and rapidity distributions of$ J/\psi $ and$ \Upsilon (1S) $ in the two channels are illustrated for p-${\rm Au} $ at the RHIC and p-$ {\rm Pb} $ at the LHC. We can see that the pseudo-rapidity distributions and rapidity distributions are different. It is concluded that the RHIC is a better platform for the discovery of the pentaquark state than the LHC, and that$ P_{b}(11080) $ is a better candidate than$ P_c(4312) $ at RHIC because the background of$ \Upsilon (1S) $ is weaker than that of$ J/\psi $ at the RHIC. -
In this paper, we study the production of the vector mesons
$ J/\psi $ and$ \Upsilon (1S) $ in the pentaquark resonance channel in p-${\rm Au} $ UPCs at the RHIC and p-$ {\rm Pb} $ UPCs at the LHC. The cross sections of$ \gamma p\to Vp $ are computed via the two channels. The vector meson and proton production in the s-channel can be used to reconstruct pentaquark states. The vector meson and proton production in the t-channel can be viewed as background of the s-channel production. The cross sections of$ \gamma p\to J/\psi p $ and$ \gamma p\to \Upsilon (1S) p $ in the s-channel are calculated via the effective Lagrangian method. We apply the STARlight package to simulate vector meson production in p-$ {\rm Au} $ UPCs at the RHIC and p-$ {\rm Pb} $ UPCs at the LHC. We obtain several distributions for$ J/\psi $ and$ \Upsilon (1S) $ . The pseudo-rapidity and rapidity distributions of$ J/\psi $ and$ \Upsilon (1S) $ are illustrated in this work. From these distributions, we find that the background of the LHC is stronger than that of the RHIC due to the high collision energy. The RHIC is thus a better platform for identifying pentaquark states. Moreover, it can be concluded that the$ P_{c}(4312) $ state is difficult to identify through the$ J/\psi+p $ invariant mass spectrum in p-$ {\rm Au} $ UPCs at$ \sqrt{s} = 200 $ GeV at the RHIC. However,$ P_{b}(11080) $ may be discovered in the$ \Upsilon (1S)+p $ invariant mass spectrum in p-$ {\rm Au} $ UPCs at$ \sqrt{s} = 200 $ GeV at the RHIC, although a small energy bin width is necessary. Consequently, it is important to detect$ \Upsilon (1S) $ production in p-$ {\rm Au} $ UPCs at the RHIC to aid in the discovery of the pentaquark$ P_{b}(11080) $ .
Production of vector mesons in pentaquark state resonance channel in p-A ultraperipheral collisions
- Received Date: 2020-08-04
- Available Online: 2021-01-15
Abstract: Ultraperipheral collisions (UPCs) of protons and nuclei are important for the study of the photoproduction of vector mesons and exotic states. The photoproduction of vector mesons in the pentaquark resonance channel in p-






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

























 DownLoad:
DownLoad: