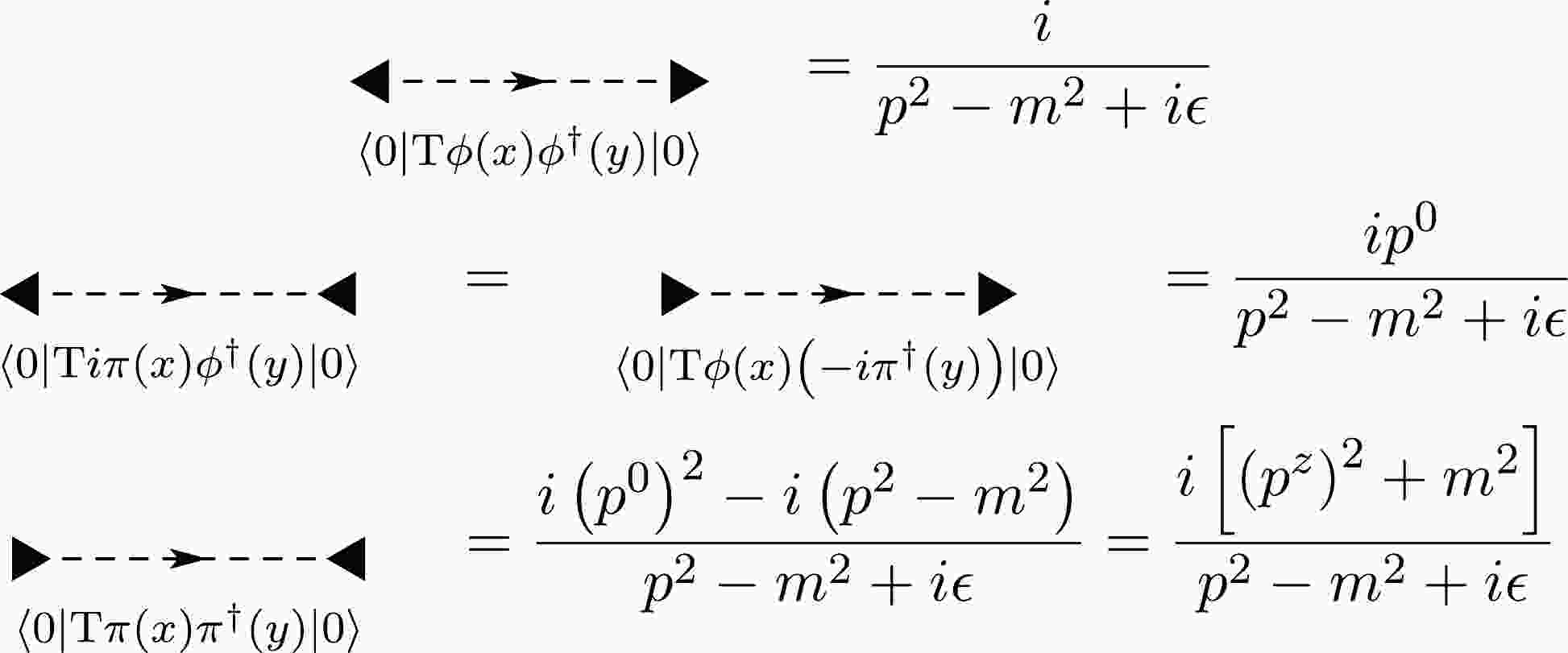-
Understanding the mass origin and the structure of baryons in the real world is a challenging problem. There is a conjecture dating back to the early days of the quark model that a baryon consists of a diquark (
$ qq $ pair) and another quark [1, 2]. The assumption of diquark reduces the number of levels in the baryon spectrum, which get closer to the experiment data than the three-body quark model. In this model, in order that the lowest-lying octet and decuplet baryons form a fully symmetric$ \mathbf{56} $ representation of the spin-flavor$ SU(6) $ , the diquark in lowest-lying baryons must be in a$ {}^3S_1 $ state, which corresponds to a spin-$ 1 $ boson. Later, some more realistic approaches derived from QCD also adopt the diquark picture [3−5], e.g., a Faddeev-type formulation which preserves the Lorentz and chiral symmetries. It is based on the observation that the gluon exchange between two quarks in the$ \bar{\mathbf{3}} $ representation of color$ SU(3) $ is known to be attractive, leading to a bound state. In this model the scalar diquarks play a significant role in the first baryon multiplet. Some recent progress can be found in, e.g., [6−9].In this work we consider the dynamics of quarks and diquarks in a two-dimensional toy model of QCD (
$ {\rm{QCD}}_2 $ ) with large-$ N_\mathrm{c} $ limit. For mesons consist of spinor quarks, this kind of model was first solved by 't Hooft [10], and was exhaustively studied in the subsequent works [11, 12, 14, 16–18, 46, 51]. For hadrons containing scalar quark and spinor antiquark. The two-dimensional scalar QCD (s$ {\rm{QCD}}_2 $ ) in the large-$ N_c $ limit has also been studied in the Feynman diagram approach [19], and in the Hamiltonian approach [20], both in the light-front quantization formalism. The interpretation of sQCD2 as a theory of diquark was also proposed in [21], where the mesonic bound states are thought as tetraquarks formed by a diquark-antidiquark pair. Recently, the equal-time quantization of sQCD2 in the Hamiltonian approach has been investigated in [22]. Following the same pattern, a baryon consists of a scalar quark and a spinor antiquark in two dimensions should be represented by the bound states of the spinor-scalar hybrid$ {\rm{QCD}}_2 $ . This kind of system was also studied in [23, 37] in the Feynman diagram approach and the light-front formalism.Our work focuses on the Hamiltonian approach and gives a thorough derivation of the light-front and equal-time quantization of both scalar and hybrid
$ {\rm{QCD}}_2 $ . We find that in s$ {\rm{QCD}}_2 $ , depending on the renormalizaion schemes of the mass, the renormalized mass in light-front may not coincide with that in equal-time. We derive the relation between these two renormalized masses. The novelty of our work is that the Hamiltonian approach is applied to the hybrid system. And we also carry out an exhaustive numerical analysis of the light-front and equal-time wave functions for scalar and hybrid bound state systems.The paper is organized as follows: In Sec. II, we review the derivation of the wave equation of the bound states in s
$ {\rm{QCD}}_2 $ , with an emphasis on the relation between the light-front and equal-time renormalizaion masses. In Sec. IIIA, we move on to the hybrid QCD2 and derive the wave equation for the scalar quark and spinor antiquark bound states. We exhibit the numerical results of the wave functions in Sec IV. We conclude in Sec. V. -
In this section we only focus on the bosonic quark. For simplicity, we consider only one single flavor of quark. The corresponding scalar
$ {\rm QCD}_2 $ lagrangian is entirely dictated by the$ SU(N_c) $ gauge invariance:$ \mathcal{L}_{\mathrm{sQCD}_2}= -\frac{1}{4}\left(F_{\mu\nu}^a\right)^2 + \left(D^{\mu}\phi\right)^{\dagger}D_{\mu}\phi - m^2\phi^{\dagger}\phi, $

(1) where ϕ denotes the complex scalar field, m represents the current quark mass, and
$ A_{\mu}^a $ represents the gluon field with color index$ a=1,2,\cdots, N_c^2-1 $ .$ F_{\mu\nu}^{a}\equiv\partial_{\mu}A_{\nu}^{a}- \partial_{\nu}A_{\mu}^{a}+g_{s}f^{abc}A_{\mu}^{b}A_{\nu}^{c} $ is the gluonic field strength tensor, and$ D_{\mu} = \partial_{\mu} - i g_{s} A_{\mu}^{a}T^a $ signifies the color covariant derivative. The generators of$ S U\left(N_c\right) $ group in the fundamental representation obey the following relation:$ \mathrm{tr}(T^{a}T^{b}) = \frac{\delta^{ab}}{2}, \tag{2a}$

$ \sum\limits_{a}T_{ij}^{a}T_{kl}^{a} = \frac{1}{2}\left(\delta_{il}\delta_{jk}-\frac{1}{N_c}\delta_{ij}\delta_{kl}\right). \tag{2b} $

The Lorentz two-vector is defined as
$ x^{\mu}=\left(x^{0},x^{z}\right) $ , with the superscript$ 0 $ and z representing the time and spatial indices. The Dirac γ-matrices in two space-time dimensions are represented by$ \gamma^{0}=\sigma_{1},\qquad \gamma^{z}=-i\sigma_{2},\qquad \gamma^{5}\equiv\gamma^{0}\gamma^{z}=\sigma_{3}, $

(3) where
$ \sigma^i $ ($ i=1,2,3 $ ) signifies the Pauli matrices.Throughout this work, we are interested in the so-called large-
$ N_\mathrm{c} $ limit:$ N_\mathrm{c} \rightarrow \infty,\qquad\qquad \lambda \equiv \frac{ g_\mathrm{s}^2 N_\mathrm{c}}{4\pi}\text{ fixed}, $

(4) with λ referring to the 't Hooft coupling constant.
-
The bound-state equation in the spinor QCD
$ _{2} $ was originally derived by 't Hooft in 1974, with the aid of diagrammatic Dyson-Schwinger/Bethe-Salpeter approach in the context of light-front quantization. Shortly after, the light-front bound-state equation in scalar QCD$ _{2} $ was also derived by Shei et al. in 1977 [19]. An equivalent approach to derive the bound-state equation is the Hamiltonian operator method, which has been widely applied in the context of the spinor QCD$ _{2} $ [25−31]. In 1978 Tomaras rederived the light-front bound-state equation in scalar QCD$ _{2} $ , verifying Shei et al.'s equations and elaborate on some subtlety about the quark mass renormalization [20] Loosely speaking, since a scalar bosonic quark may mimick a diquark to some extent, Grinstein et al. [21] in 2008 investigated the mesonic mass spectra in scalar QCD$ _{2} $ , which may shed some light on the tetraquark spectrum in the realistic QCD$ _4 $ .In this subsection, we revisit the operator approach derivation of the bound-state equations in scalar QCD
$ _{2} $ within the light-front quantization framework, paying special attention to the mass renormalization issue. -
Similar to spinor QCD
$ _{2} $ , the scalar QCD$ _{2} $ becomes significantly simplified once imposing the light-cone gauge$ A^{+a}=0 $ :$ \mathcal{L}_{\mathrm{sQCD}_2} = \frac{1}{2}\left(\partial_-A^{-a}\right)^2 + \left(\partial_-\phi^\dagger\right) D_+\phi + \left(D_+\phi\right)^\dagger \partial_-\phi - m^2\phi^\dagger\phi. $

(5) It is convenient to adopt the light-cone coordinates, which are defined through
$ x^\pm = x_\mp = \left(x^0 \pm x^z\right)/\sqrt{2} $ , with light-front time denoted by$ x^+ $ . The canonic conjugate momenta are given by$ \pi \equiv \dfrac{\partial\mathcal{L}}{\partial\left(\partial_+\phi^\dagger\right)} = \partial_-\phi,\:\pi^\dagger = \partial_-\phi^\dagger $ . One immediately arrives at the corresponding light-front Hamiltonian:$ \begin{aligned}[b] H_ \text{LF} =&\int dx^-\Bigg(-\frac{1}{2}\left(\partial_-A^{-a}\right)^{2}+ig_{s}A^{-a}\\&\times\left(\pi^{\dagger}T^{a}\phi-\phi^{\dagger}T^{a}\pi\right)+m^{2}\phi^{\dagger}\phi\Bigg). \end{aligned} $

(6) Since the light-front time derivative of the gluon field is absent in the lagrangian (5), the gluonic field
$ A^{-a} $ is no longer a dynamical variable. In fact, it is subject to a the following constraint:$ \begin{array}{*{20}{l}} \partial_-^2A^{-a} = g_\mathrm{s} J^a, \end{array} $

(7) where
$ J^{a}\equiv i\left(\phi^{\dagger}T^{a}\pi-\pi^{\dagger}T^{a}\phi\right) $ .Solving
$ A^{-a} $ in term of$ J^a $ in (7), and substituting back into (6), the light-front Hamiltonian then reduces to$ H_ \text{LF} =\int dx^-\left(m^{2}\phi^{\dagger}\phi-\frac{g_{s}^{2}}{2}J^{a}\frac{1}{\partial_-^{2}}J^{a}\right). $

(8) The light-front Hamiltonian actually becomes nonlocal. To see this, note that the rigorous meaning of
$ 1/\partial_-^2 J^a $ in (8) is$ \frac{1}{\partial_-^2} J^a\left(x^-\right) = \int dy^- G^{(2)}_\rho\left(x^–y^-\right) J^a\left(y^-\right), $

(9) where
$ G^{(2)} $ represents the Green function$ \partial_-^{2}G^{\left(2\right)}\left(x^-\right)=\delta\left(x^-\right). $

(10) The actual solution of the Green function turns out to be
$ G_\rho^{(2)}\left(x^–y^-\right) = -\int_{-\infty}^{+\infty} \frac{dk^+}{2\pi}\Theta\left(\left|k^+\right|-\rho\right) \frac{e^{ik^+\left(x^–y^-\right)}}{\left(k^+\right)^2}. $

(11) To make the Green function mathematically well-defined, we introduce an infrared cutoff ρ to regularize the severe IR divergence. This parameter may also be viewed as an artificial gauge parameter. Needless to say, this fictitious parameter must disappear in the final expressions for any physical quantities.
-
The task is to quantize the Hamiltonian (8) in equal light-front time. We Fourier-expand the ϕ and π fields in terms of the quark/antiquark's annihilation and creation operators:
$ \begin{aligned}[b] \phi^i\left(x^-\right) =& \int_0^\infty\frac{dk^+}{2\pi}\frac{1}{\sqrt{2k^+}} \Bigg[a^{i}\left(k^+\right)e^{-ik^+x^-}\\&+c^{i\dagger}\left(k^+\right)e^{ik^+x^-}\Bigg], \end{aligned} \tag{12a}$

$ \begin{aligned}[b] \pi^{j\dagger}\left(x^-\right) =& i\int_0^\infty\frac{dk^+}{2\pi} \sqrt{\frac{k^+}{2}}\Bigg[a^{j\dagger}\left(k^+\right)e^{ik^+x^-}\\&-c^{j}\left(k^+\right)e^{-ik^+x^-}\Bigg]. \end{aligned}\tag{12b} $

where
$ i,j=1,\cdots,N_c $ are color indices. The annihilation and creation operators are assumed to obey the standard commutation relations:$ \begin{array}{*{20}{l}} \left[a^i\left(k^+\right), a^{j\dagger}\left(p^+\right)\right] = \left[c^i\left(k^+\right), c^{j\dagger}\left(p^+\right)\right] = \left(2\pi\right)\delta\left(k^+-p^+\right)\delta^{ij}. \end{array} $

(13) A useful trick to diagonalize the Hamiltonian is the bosonization technique [25−31]. One first introduces the following four compound color-singlet operators:
$ \begin{aligned}[b] W\left(k^+,p^+\right) &\equiv\frac{1}{\sqrt{ N_\mathrm{c}}}\sum\limits_{i}c^{i}\left(k^+\right)a^{i}\left(p^+\right), \\ W^{\dagger}\left(k^+,p^+\right) &\equiv\frac{1}{\sqrt{ N_\mathrm{c}}}\sum\limits_{i}a^{i\dagger}\left(p^+\right)c^{i\dagger}\left(k^+\right) , \end{aligned} \tag{14a}$

$ \begin{aligned}[b] A\left(k^+,p^+\right) & \equiv\sum\limits_{i}a^{i\dagger}\left(k^+\right)a^{i}\left(p^+\right), \\ C\left(k^+,p^+\right)& \equiv\sum\limits_{i}c^{i\dagger}\left(k^+\right)c^{i}\left(p^+\right). \end{aligned}\tag{14b} $

It is straightforward to find the commutation relations among these four compound operators:
$ \begin{aligned}[b] &\left[W\left(k_{1}^+,P_{1}^+\right),W^{\dagger}\left(k_{2}^+,P_{2}^+\right)\right] \\=& \left(2\pi\right)^{2}\delta\left(k_{1}^+-k_{2}^+\right)\delta\left(P_{1}^+-P_{2}^+\right)+\mathcal{O}\left(\frac{1}{ N_\mathrm{c}}\right), \end{aligned} \tag{15a}$

$ \left[W\left(k_{1}^+,P_{1}^+\right),A\left(k_{2}^+,P_{2}^+\right)\right] = 2\pi\delta\left(P_{1}^+-k_2^+\right) W\left(k_1^+,P_{2}^+\right), \tag{15b} $

$ \left[W\left(k_{1}^+,P_{1}^+\right),C\left(k_{2}^+,P_{2}^+\right)\right] = 2\pi\delta\left(k_1^+-k_2^+\right) W\left(P_{2}^+,P_{1}^+\right), \tag{15c} $

$ \begin{aligned}[b] \left[A\left(k_{1}^+,P_{1}^+\right),A\left(k_{2}^+,P_{2}^+\right)\right] =& 2\pi\delta\left(P_{1}^+-k_2^+\right)A\left(k_1^+,P_{2}^+\right) \\& - 2\pi\delta\left(P_{2}^+-k_1^+\right) A\left(k_2^+,P_{1}^+\right), \end{aligned}\tag{15d} $

$ \begin{aligned}[b] \left[C\left(k_{1}^+,P_{1}^+\right),C\left(k_{2}^+,P_{2}^+\right)\right] =& 2\pi\delta\left(P_{1}^+-k_2^+\right)C\left(k_1^+,P_{2}^+\right) \\& - 2\pi\delta\left(P_{2}^+-k_1^+\right) C\left(k_2^+,P_{1}^+\right), \end{aligned}\tag{15e} $

$ \left[A\left(k_{1}^+,P_{1}^+\right),C\left(k_{2}^+,P_{2}^+\right)\right] = 0. \tag{15f}$

Substituting (12) into the Hamiltonian (8), and express everything in terms of the compound operator basis as given in (14), we can decompose the light-front Hamiltonian into three pieces:
$ H_{\rm LF} =H_{\rm LF;0}+\colon H_{\rm LF;2}\colon+\colon H_{\rm LF;4}\colon+\mathcal{O}\left(\frac{1}{\sqrt{N_{c}}}\right), $

(16) whose explicit expressions are
$ H_{\rm LF;0} = N_c \int \frac{dx^-}{2\pi}\Bigg(\int_0^\infty\frac{{m^{2}}{dk^+}}{2k^+}-{\pi\lambda}\int_0^\infty\frac{dk_{3}^+}{2\pi}\int_0^\infty \frac{dk_{4}^+}{2\pi}\frac{\left(k_{3}^+-k_{4}^+\right)^2}{\left(k_{3}^++k_{4}^+\right)^{2}{k_3^+k_4^+}} \Theta\left(|k_{3}^++k_{4}^+|-\rho\right)\Bigg), \tag{17a} $ 
$ \begin{aligned}[b] :H_{\rm LF;2}: =& {m^{2}}\int_0^\infty\frac{dk^+}{2\pi{2k^+}} \left[A\left(k^+,k^+\right)+C\left(k^+,k^+\right)\right] +\int_0^\infty\frac{dk_{1}^+}{2\pi}\int_{-\infty}^\infty\frac{dk_{2}^+}{2\pi}\frac{2\pi\lambda}{k_{1}^+ |k_{2}^+|}\left(\frac{k_{1}^++k_{2}^+}{k_{2}^+-k_{1}^+}\right)^{2} \\ &\times \Theta(|k_{2}^+-k_{1}^+|-\rho)[ A\left(k_{1}^+,k_{1}^+\right)+ C\left(k_{1}^+,k_{1}^+\right)] ,\end{aligned}\tag{17b} $

$ \begin{aligned}[b] :H_{\rm LF;4}: =& -{\pi^{3}\lambda} \int_0^\infty\frac{dk_{1}^+}{2\pi\sqrt{k_{1}^+}}\int_0^\infty\frac{dk_{2}^+}{2\pi\sqrt{k_{2}^+}} \int_0^\infty\frac{dk_{3}^+}{2\pi\sqrt{k_{3}^+}}\int_0^\infty\frac{dk_{4}^+}{2\pi\sqrt{k_{4}^+}} \frac{1}{\left(k_{3}^+-k_{4}^+\right)^{2}} \\ &\times\Theta\left(|k_{3}^+-k_{4}^+|-\rho\right) \left(k_{1}^++k_{2}^+\right)\left(k_{4}^++k_{3}^+\right) \big[W^{\dagger}\left(k_{4}^+,k_{1}^+\right) W\left(k_{3}^+,k_{2}^+\right) \delta\left(k_{1}^+-k_{2}^++k_{4}^+-k_{3}^+\right) \\ & + W^{\dagger}\left(k_{2}^+,k_{3}^+\right)W\left(k_{1}^+,k_{4}^+\right) \delta\left(k_{2}^+-k_{1}^++k_{3}^+-k_{4}^+\right)\big], \end{aligned}\tag{17c}$

with
$ :\;\:: $ denoting the normal ordering.$ H_{\rm LF;0} $ denotes the light-cone energy of the vacuum, which is severely IR divergent.Due to the confinement characteristics of QCD, the physical excitation must be the color singlets. The color-singlet compound operators A and C are not independent operators, which, at lowest order in
$ 1/N_c $ , actually can be expressed as the convolution between the color-singlet quark-antiquark pair creation/annihilation operators W and$ W^{\dagger} $ in (14a);$ A(k^+,p^+) \rightarrow \int_0^\infty\frac{dq^+}{2\pi} W^\dagger(q^+,k^+)W(q^+,p^+), \tag{18a} $

$ C(k^+,p^+) \rightarrow \int_0^\infty\frac{dq^+}{2\pi} W^\dagger(k^+,q^+)W(p^+,q^+). \tag{18b}$

Plugging (18) and into (17c) and (17f), and relabelling the momenta in
$ W^{(\dagger)}\left(k^+,p^+\right) $ by$ p^+=xP^+ $ ,$ k^+=(1-x)P^+ $ , at the lowest order in$ 1/N_{c} $ , we can rewrite the :$ H_{\rm LF;2}: $ and :$ H_{\rm LF;4} $ : pieces as$ \begin{aligned}[b] :H_{\rm LF;2}: =& \int_{0}^{\infty} \frac{dP^+(P^+)}{(2\pi)^2}\int_0^1 dx W^{\dagger}\left(\left(1-x\right)P^+,xP^+\right)W\left(\left(1-x\right)P^+,xP^+\right) \\ &\bigg[\frac{m^{2}}{2xP^+}+\frac{m^{2}}{2(1-x)P^+} +\frac{\lambda}{8xP^+}\int_{-\infty}^\infty\frac{dy}{|y|} \frac{\left(x+y\right)^2}{\left(y-x\right)^2}\Theta\left(|(y-x)P^+|-\rho\right) \\ &+\frac{\lambda}{8(1-x)P^+}\int_{-\infty}^\infty\frac{dy}{|1-y|} \frac{\left(2-x-y\right)^2}{\left(y-x\right)^2}\Theta\left(|(y-x)P^+|-\rho\right)\bigg], \end{aligned}\tag{19a} $ 
$ \begin{aligned}[b] :H_{\rm LF;4}: =& -\frac{\lambda}{2\left(2\pi\right)^{2}} \int_0^1 dx\int_0^1 dy\int_{0}^{\infty} \frac{dP^+\left(P^+\right)^{2}}{2\pi} W^{\dagger}\left(\left(1-x\right)P^+,xP^+\right)W\left(\left(1-y\right)P^+,yP^+\right)\\ &\frac{1}{\sqrt{xP^+}}\frac{1}{\sqrt{yP^+}}\frac{1}{\sqrt{(1-y)P^+}}\frac{1}{\sqrt{(1-x)P^+}}\frac{1}{[(x-y)P^+]^{2}} \\ & \Theta\left(|(x-y)P^+|-\rho\right)\left[\left(1-x\right)P^++\left(1-y\right)P^+\right]\left(yP^++xP^+\right). \end{aligned}\tag{19b} $

-
Our strategy of deriving the bound-state equation is via diagonalizing the light-front Hamiltonian (19). To this purpose, we introduce an infinite number of meson annihilation/creation operators:
$ w_{n}(P^{+}) $ /$ w_{n}^{\dagger}(P^{+}) $ , with n and$ P^{+} $ indicating the principal quantum number and the light-cone momentum of the "meson" in the physical spectrum. We assume that the$ w_{n}(P^{+}) $ /$ w_{n}^{\dagger}(P^{+}) $ operator basis is linked with the color-singlet quark-antquark pair creating/annihilation basis in the following specific fashion:$ W\left(\left(1-x\right)P^+,xP^+\right) =\sqrt{\frac{2\pi}{P^+}}\sum\limits_{n=0}^{\infty}\chi_{n}\left(x\right)w_{n}\left(P^+\right), \tag{20a} $

$ w_{n}\left(P^+\right) =\sqrt{\frac{P^+}{2\pi}}\int_{0}^{1}dx\chi_{n}\left(x\right)W\left(\left(1-x\right)P^+,xP^+\right). \tag{20b} $

with the coefficient function
$ \chi_n(x) $ interpreted as the light-cone wave function of the n-th meson.If one requests the mesonic annihilation and creation operators to obey the standard commutation relations,
$ \left[w_{n}\left(P_1^+\right),w_{m}^{\dagger}\left(P_2^+\right)\right] =2\pi\delta\left(P_1^+-P_2^+\right)\delta_{nm}, \tag{21}$

the light-cone wave function
$ \chi_{n}(x) $ must satisfy the following orthogonality and completeness conditions:$ \int_{0}^{1}dx\chi_{n}\left(x\right)\chi_{m}\left(x\right) =\delta_{nm},\tag{22a}$

$ \sum\limits_{n}\chi_{n}\left(x\right)\chi_{n}\left(y\right) =\delta\left(x-y\right). \tag{22b} $

The n-th mesonic state can be directly constructed via
$ |P_n^-,P^+\rangle =\sqrt{2P^+}w_{n}^{\dagger}(P^+)|0\rangle, $

(23) where
$ P_n^{-}=M_{n}^{2}/(2P^{+}) $ denotes the light-cone energy of the n-th excited mesonic state.In the
$ N_c\to \infty $ limit, the scalar$ {\rm QCD}_2 $ is composed of an infinite number of non-interacting mesons. To account for this, we anticipate that the light-front hamiltonian can be cast into a simple diagonal form in the mesonic annihilation/creation operators:$ H_{\rm LF} = H_{\rm LF;0} + \int\frac{dP^+}{2\pi}P_n^- w_{n}^{\dagger}\left(P^+\right)w_{n}\left(P^+\right). $

(24) In order to arrive at the desired form (24), all the non-diagonal terms in (19) after transformed in the
$ w_{n}/w_{n}^{\dagger} $ basis, such as$ w_n^\dagger w_m $ ($ m\neq n $ ),$ w^\dagger w^\dagger $ ,$ w w $ ,$ \cdots $ , must vanish. This condition imposes some nontrivial constraints on the light-cone wave function$ \chi_n(x) $ . After some manipulation, such constraint can be cast into an integral equation for$ \chi_n\left(x\right) $ :$ \begin{aligned}[b] &\Bigg(\frac{m^{2}}{x}+\frac{m^{2}}{1-x}+\frac{\lambda}{4x} {\rlap{—} \int }_{-\infty}^\infty\frac{dy}{|y|}\frac{\left(y+x\right)^{2}}{\left(y-x\right)^{2}} \\&+\frac{\lambda}{4(1-x)} {\rlap{—} \int }_{-\infty}^\infty\frac{dy}{|1-y|}\frac{\left(2-x-y\right)^{2}}{\left(y-x\right)^{2}}\Bigg)\chi_{n}\left(x\right) \\ &-\frac{\lambda}{2} {\rlap{—} \int }_0^1\frac{dy}{\left(x-y\right)^{2}}\frac{\left(2-x-y\right)\left(x+y\right)}{\sqrt{x\left(1-x\right)y\left(1-y\right)}} \chi_{n}\left(y\right)=M_{n}^{2}\chi_{n}\left(x\right). \end{aligned} $

(25) The potential IR divergence as
$ y\rightarrow {x} $ is overcome by the principal value (PV) prescription, denoted by the symbol$ {\rlap{—} \int } $ . Note the occurrence of the PV arises from taking the vanishing limit of the artificial IR regulator ρ first introduced in (11). Here we show two PV prescriptions defined in term of the regulator ρ [34, 35, 45]:$ \begin{aligned}[b] {\rlap{—} \int } dy\frac{f\left(y\right)}{\left(x-y\right)^2} & \equiv \lim\limits_{\rho\to 0^+} \int dy\frac{f\left(y\right)}{2}\left[\frac{1}{\left(x-y+i\rho\right)^2} +\frac{1}{\left(x-y-i\rho\right)^2}\right] \\ & = \lim\limits_{\rho\rightarrow0^+}\int dy\Theta\left(|x-y|-\rho\right)\frac{f\left(y\right)}{\left(x-y\right)^{2}}-\frac{2f\left(x\right)}{\rho}. \end{aligned} $

(26) -
Though the IR divergence is tamed by the principal value prescription, the bound-state equation in scalar
$ {\rm QCD}_2 $ , (25), is still plagued with logarithmic ultraviolet divergences. The logarithmic UV divergences arise as$ y\rightarrow {0} $ or$ y\to \pm \infty $ in the first integral in (25), also arise as$ y\rightarrow {1} $ or$ y\to \pm \infty $ in the second integral.As first pointed out by Shei and Tshao [20], it is essential to renormalize the quark mass m in order to eliminate the UV divergence. Concretely speaking, one introduce the renormalized
$ m_r $ according to$ m_{r}^{2} =m^{2}+\frac{\lambda}{2}\int_\delta^\Lambda\frac{dy}{y}, $

(27) where the mass counterterm logarithmically depends on the UV cutoffs
$ \Lambda\gg \sqrt{\lambda} $ and$ \delta\to 0^+ $ .The two integrals in the left side of (19) can be regularized and analytically worked out, which depend on
$ \ln\frac{\Lambda}{\delta} $ . In accordance with (27), these UV divergences can be absorbed into the bare quark mass, so that only the renormalized quark mass enters the bound-state equation [20]:$ \begin{aligned}[b]& \left(\frac{m_{r}^{2}-2\lambda}{x}+\frac{m_{r}^{2}-2\lambda}{1-x}\right)\chi_{n}\left(x\right) \\&-\frac{\lambda}{2} {\rlap{—} \int }_0^1\frac{dy}{\left(x-y\right)^{2}} \frac{\left(2-x-y\right)\left(x+y\right)}{\sqrt{x\left(1-x\right)y\left(1-y\right)}} \chi_{n}\left(y\right)\\ =& M_{n}^{2}\chi_{n}\left(x\right). \end{aligned} $

(28) This equation was first obtained by Shei and Tsao using diagrammatical approach [19]. Note that this bound-state equation is very similar to, albeit slightly more complicated than the 't Hooft's equation in spinor
$ {\rm QCD}_2 $ [10]. -
The
$ {\rm QCD}_2 $ in large$ N_c $ limit can also be solved in familiar equal-time quantization, whose formalism is considerably more complicated than the light-front quantization. The corresponding bound-state equation in spinor$ {\rm QCD}_2 $ was originally derived by Bars and Green in 1978 [12]. A comprehensive numerical studies of the Bars-Green equations have been conducted recently [17]. As for the scalar$ {\rm QCD}_2 $ , the bound-state equation was recently derived by Ji, Liu and Zahed in equal-time quantization, with the aid of the operator approach [22]. In this subsection, we the revisit bound-state equation for the scalar QCD$ _2 $ in equal-time quantization employing the operator approach. We add some new elements relative to [22]. For example, we elaborate some subtlety related to the mass renormalization scheme. We also present a new way of derivation of the mass-gap equation from the variational perspective. Moreover, for the first time, we also employ the diagrammatic technique to derive the bound-state equation in equal-time quantization. We devote Appendix A to a detailed explanation of the diagrammatic derivation. -
Like spinor
$ {\rm QCD}_2 $ , it is most convenient to choose the axial gauge$ A^{a\,z}=0 $ to quantize the scalar$ {\rm QCD}_2 $ in equal time, with the lagrangian reducing to$ \mathcal{L}_{\text{sQCD}_2}= \frac{1}{2}(\partial_{z}A_0^a)^2 + (D_0\phi)^{\dagger}D_0\phi - (\partial_z\phi^\dagger)\partial_z\phi - m^2\phi^{\dagger}\phi . $

(29) The canonical momenta are
$ \pi=D_{0}\phi $ ,$ \pi^{\dagger}=(D_{0}\phi)^{\dagger} $ . The Hamiltonian can be obtained through the Legendre transformation:$ H = \int dz\left(|\partial_z\phi|^2 + m^2|\phi|^2 + \pi^\dagger\pi\right) + \frac{ g_\mathrm{s}^2}{2}\int dz\left(J^{a}\frac{-1}{\partial_{z}^{2}}J^{a}\right), $

(30) where
$ J^{a}=i\left(\phi^{\dagger}T^{a}\pi-\pi^{\dagger}T^{a}\phi\right) $ .Similar to (9), one can express
$ {1\over \partial_z^2} J^a $ as the convolution between$ J^a $ and the Green function$ \widetilde{G}^{\left(2\right)} $ , which is defined through$ \tilde{G}_{\rho}^{\left(2\right)}(z) =-\int_{-\infty}^{+\infty}\frac{dk}{2\pi}\Theta\left(|k|-\rho\right)\frac{e^{ik z}}{k^2 }. $

(31) Analogous to (11), we again introduce an IR regulator ρ to make the Green function well-defined.
-
We plan to conduct the equal-time quantization for the Hamiltonian specified in (30). It is convenient to Fourier-expand the ϕ and
$ \pi^\dagger $ fields in the basis of the quark/antiquark's annihilation and creation operators:$ \phi^i\left(z\right) =\int\frac{dk}{2\pi\sqrt{2E_{k}}}e^{ikz}\left[a^{i}\left(k\right)+c^{i\dagger}\left(-k\right)\right], \tag{32a} $

$ \pi^{j\dagger}\left(z\right) =i\int\frac{dk}{2\pi}\sqrt{\frac{E_{k}}{2}}e^{-ikz}\left[a^{j\dagger}\left(k\right)-c^{j}\left(-k\right)\right], \tag{32b} $

where
$ E_k $ denotes the energy of a dressed quark. The concrete dispersion relation will be determined by the mass-gap equation in the following. The commutation relations between the quark annihilation and creation operators are the same as (13), except all the$ + $ -components are replaced with the z-components inside the δ functions.Analogous to the bosonizaion procedure used in the light-front case in Sec. IIB2, we introduce the following four color-singlet compound operators:
$ \begin{aligned}[b]& W\left(p,q\right) \equiv\frac{1}{\sqrt{N_{c}}}\sum\limits_{i}c^{i}\left(-p\right)a^{i}\left(q\right), \\& W^{\dagger}\left(p,q\right) \equiv\frac{1}{\sqrt{N_{c}}}\sum\limits_{i}a^{i\dagger}\left(q\right)c^{i\dagger}\left(-p\right), \end{aligned}\tag{33a} $

$ \begin{aligned}[b]& A\left(p,q\right) \equiv\sum\limits_{i}a^{i\dagger}\left(p\right)a^{i}\left(q\right), \\& C\left(p,q\right) \equiv\sum\limits_{i}c^{i\dagger}\left(-p\right)c^{i}\left(-q\right). \end{aligned}\tag{33b} $

The commutation relations among these compound operators are identical to (15) except replacing all the
$ + $ component with the z-components.Analogous to (16), we decompose the Hamiltonian (30) into three pieces:
$ H =H_{0}+\colon H_{2}\colon+\colon H_{4}\colon+\mathcal{O}\left(\frac{1}{\sqrt{N_{c}}}\right), \tag{34} $

whose explicit expressions read
$ \begin{aligned}[b] H_{0}= & N_c\int{dz}\Bigg(\int\frac{dk{(k^2+m^2)}}{2\pi\left(2E_k\right)}+\int\frac{dk{E_k}}{4\pi} \\&+\frac{\pi\lambda}{2}\int\frac{dk_1}{2\pi}\int\frac{dk_2}{2\pi}\frac{\left(E_{k2}-E_{k1}\right)^{2}}{\left(k_{1}-k_{2}\right)^{2}}\frac{1}{E_{k1}E_{k2}}\Bigg), \end{aligned}\tag{35a} $

$ \begin{aligned}[b] :H_{2}: =&\int\frac{dk}{2\pi}\Pi^+\left(k\right)\left(A\left(k,k\right)+C\left(k,k\right)\right) \\&+\sqrt{N_{c}}\int\frac{dk}{2\pi}\Pi^-\left(k\right)\left(W\left(k,k\right)+W^{\dagger}\left(k,k\right)\right), \end{aligned}\tag{35b} $

$ \begin{aligned}[b] :H_{4}: =&\frac{\lambda}{32\pi^{2}}\iiiint dk_{1}dk_{2}dk_{3}dk_{4}\\&\times\frac{\delta\left(k_{2}-k_{1}+k_{4}-k_{3}\right)}{\left(k_{4}-k_{3}\right)^{2}}\Theta\left(|k_4-k_3|-\rho\right) \\& \times \Big[-2f_+\left(k_{1},k_{2}\right)f_+\left(k_{3},k_{4}\right)W^{\dagger}\left(k_{1},k_{4}\right)\\&\times W\left(-k_{2},-k_{3}\right) +f_-\left(k_{1},k_{2}\right)f_-\left(k_{3},k_{4}\right)\\&\times W^{\dagger}\left(k_{1},k_{4}\right)W^{\dagger}\left(k_{3},k_{2}\right) \\ &+ f_-\left(k_{1},k_{2}\right)f_-\left(k_{3},k_{4}\right)W\left(k_{1},k_{4}\right)W\left(k_{3},k_{2}\right)\Big], \end{aligned} \tag{35c}$

with
$ \Pi^{\pm}(k) $ and$ f_{\pm} $ defined by$ \begin{aligned}[b] \Pi^{\pm}\left(k\right) =&\frac{1}{2}\left(\frac{k^{2}+m^{2}}{E_{k}}\pm E_{k}\right)\\&+\frac{\lambda}{4}\int dk_{1}\frac{\frac{E_{k_{1}}}{E_{k}}\pm\frac{E_{k}}{E_{k_1}}}{\left(k+k_{1}\right)^{2}}\Theta\left(|k+k_1|-\rho\right), \end{aligned}\tag{36a} $

$ f_{\pm}(k_{1},k_{2}) =\sqrt{\frac{E_{k_2}}{E_{k_1}}}\pm\sqrt{\frac{E_{k_1}}{E_{k_2}}}. \tag{36b}$

It is desirable to put the
$ :H_{2}: $ into a diagonalized form at the dressed quark level. To this purpose, the coefficient of the off-diagonal$ W+W^{\dagger} $ term in$ :H_{2}: $ should vanish. Requiring$ \Pi^{-}=0 $ then leads to a constraint for$ E_k $ [22]:$ \frac{k^{2}+m^{2}}{E_{k}}-E_{k}+\frac{\lambda}{2} {\rlap{—} \int } dk_{1}\left(\frac{E_{k_{1}}}{E_{k}}-\frac{E_{k}}{E_{k_{1}}}\right)\frac{1}{\left(k+k_{1}\right)^{2}} =0. $

(37) This integral equation can be solved numerically to determine the dispersion relation. Following the spinor
$ {\rm QCD}_2 $ case [12], we also call this equation as mass-gap equation.Here we provide an alternative perspective to derive the mass-gap equation (37). The physical requirement is that the vacuum energy
$ H_0 $ in (35a), albeit badly divergent, should be minimized with respect to all possible functional forms of$ E_k $ . This leads to a functional variational equation:$ \frac{\delta H_{0}[E_k]}{\delta E_{p}} =0. $

(38) After some straightforward algebra, we arrive at
$ \begin{aligned}[b] & \int\frac{dk_1}{2\pi}\frac{k^2+m^2}{-2E_{k1}}\delta(k_1-p)+\frac{1}{2}\int\frac{dk_1}{2\pi}E_{k1}\delta(k_1-p) \\ & +\frac{\pi\lambda}{2}\int\frac{dk_1}{2\pi}\int\frac{dk_2}{2\pi}\frac{1}{(k_1-k_2)^2} \left(\frac{E_{k1}}{E_{k2}}-\frac{E_{k2}}{E_{k1}}\right)\delta(k_1-p) = 0. \end{aligned} $

(39) Conducting the integration, we then reproduce the mass-gap equation (37).
The mass-gap equation (37) suffers from both IR and UV divergences. The IR divergence at
$ k_{1}\rightarrow -k $ can be tamed by the principal value prescription (26). Nevertheless, as$ |k_{1}|\rightarrow \infty $ , one can ascertain that$ E_{k1}\rightarrow |k_1| $ , and the integral in (37) exhibits a logarithmic UV divergence. Fortunately, the UV divergence can be absorbed in the quark mass through the renormalization procedure. One may follow [22] to introduce the following mass counterterm:$ m_{\tilde{r}}^{2} =m^2+\frac{\lambda}{2} {\rlap{—} \int } dk_1\frac{E_{k_1}}{k_1^2}. $

(40) Slightly differing from [22], we impose the principal value prescription to avoid the IR divergence arising from the
$ k_1\to 0 $ region. The renormalized mass-gap equation now becomes$ \frac{k^{2}+m_{\tilde{r}}^{2}}{E_{k}}-E_{k} + \frac{\lambda}{2} {\rlap{—} \int } dk_1 \left[ \left(\frac{E_{k_{1}}}{E_{k}}-\frac{E_{k}}{E_{k_{1}}}\right) \frac{1}{\left(k+k_{1}\right)^{2}} -\frac{E_{k_1}}{E_{k}}\frac{1}{k_{1}^2} \right] = 0. $

(41) Since the prescribed renormalization scheme in equal-time differs from that in the light-front quantization, the renormalized mass
$ m_{\tilde{r}}^{2} $ is generally different from$ m_{r} $ introduced in (27). We devote Appendix B to a detailed discussion the connection between these two renormalized quark masses. -
Following the same line of reasoning that leads to (18), the confinement feature of QCD implies that, at the lowest order in
$ 1/N_c $ , the compound operators A and C defined in (33) can be expressed as$ A\left(k_{1},k_{2}\right) \rightarrow \intop\frac{dp}{2\pi}W^{\dagger}\left(p,k_{1}\right)W\left(p,k_{2}\right), \tag{42a}$

$ C\left(k_{1},k_{2}\right) \rightarrow \intop\frac{dp}{2\pi}W^{\dagger}\left(k_{1},p\right)W\left(k_{2},p\right). \tag{42b}$

With this replacement, the Hamiltonian (34) can be built solely out of the W and
$ W^\dagger $ operators:$ \begin{aligned}[b] H =&\int\frac{dpdq}{4\pi^{2}}\left(\Pi^+\left(p\right)+\Pi^+\left(q\right)\right)W^{\dagger}\left(p,q\right)W\left(p,q\right) \\ & -\frac{\lambda}{32\pi^{2}}\int dP\iint dkdp\frac{O+Q}{(p-k)^{2}}\Theta\left(|p-k|-\rho\right), \end{aligned}\tag{43} $

where
$ O=2S_+\left(p,k,P\right)W^{\dagger}(P-p,p)W(P-k,k), \tag{44a} $

$ \begin{aligned}[b] Q=&S_-\left(p,k,P\right)\Big(W^{\dagger}\left(p,P-p\right)W^{\dagger}\left(P-k,k\right)\\&+W\left(p,P-p\right)W\left(P-k,k\right)\Big), \end{aligned}\tag{44b} $

with
$ S_{\pm}\left(p,k,P\right)=f_{\pm}\left(P-p,P-k\right)f_{\pm}\left(p,k\right). $

(45) To cast the Hamiltonian (43) in a diagonal form, it is most efficient to employ the Bogoliubov transformation [16]. The essence is to introduce a new set of color-singlet operators represented by w and
$ w^\dagger $ :$\begin{aligned}[b]& w=\mu W+ \nu W^{\dagger}, \\& w^{\dagger}=\mu W^{\dagger} + \nu W, \\& \mu^2 -\nu^2 =1. \end{aligned} $

(46) The coefficient μ and ν can be determined such that the Hamiltonian gets diagonalized in the new operator basis.
To our purpose, we introduce two infinite towers of color-singlet operators
$ w_{n} $ and$ w_{n}^{\dagger} $ , which are linear combinations of the W and$ W^{\dagger} $ operators. Inversely, we can express the W operators in terms of infinite sum of$ w_{n} $ and$ w_n^\dagger $ operators:$ \begin{aligned}[b] W\left(q-P,q\right) =&\sqrt{\frac{2\pi}{|P|}}\sum\limits_{n=0}^{\infty}\Big[w_{n}\left(P\right)\chi_{n}^+\left(q,P\right)\\&-w_{n}^{\dagger} \left(-P\right)\chi_{n}^-\left(q-P,-P\right)\Big],\end{aligned} $

$ \begin{aligned}[b] W^{\dagger}\left(q-P,q\right) =&\sqrt{\frac{2\pi}{|P|}}\sum\limits_{n=0}^{\infty}\Big[w_{n}^{\dagger}\left(P\right)\chi_{n}^+\left(q,P\right)\\&-w_{n}\left(-P\right)\chi_{n}^-\left(q-P,-P\right)\Big]. \end{aligned} $

(47) The operators
$ w_{n}(P) $ and$ w_{n}^{\dagger}(P) $ bear clear physical meaning, which represent the annihilation and creation operators for the nth mesonic state carrying momentum P. The coefficient functions$ \chi_{n}^{\pm} $ can be interpreted as the forward/backward-moving mesonic wave functions, playing the role of the Bogoliubov coefficients μ and ν in (46). The mesonic operators$ w_{n} $ and$ w_{n}^{\dagger} $ are anticipated to obey the standard commutation relations:$ \left[w_{n}\left(P\right),w_{m}^{\dagger}(P^{'})\right] =2\pi\delta_{nm}\delta\left(P-P^{'}\right), \tag{48a} $

$ \left[w_{n}\left(P\right),w_{m}\left(P^{'}\right)\right] =\left[w_{n}^{\dagger}\left(P\right),w_{m}^{\dagger}\left(P^{'}\right)\right]=0. \tag{48b}$

To fulfill these commutation relations, the mesonic wave functions
$ \chi_n^{\pm} $ must satisfy the following orthogonality and completeness conditions$ \int_{-\infty}^{+\infty}dp\left[\chi_+^{n}\left(p,P\right)\chi_+^{m}\left(p,P\right)-\chi_-^{n}\left(p,P\right)\chi_-^{m}\left(p,P\right)\right] =|P|\delta^{nm}, \tag{49a}$

$ \int_{-\infty}^{+\infty}dp\left[\chi_+^{n}\left(p,P\right)\chi_-^{m}\left(p-P,-P\right)-\chi_-^{n}\left(p,P\right)\chi_+^{m}\left(p,P\right)\right] =0, \tag{49b}$

$ \begin{aligned}[b]&\sum\limits_{n=0}^{\infty}\left[\chi_+^{n}(p,P)\chi_+^{n}\left(q,P\right)-\chi_-^{n}\left(p-P,-P\right)\chi_-^{n}\left(q-P,-P\right)\right] \\=&|P|\delta\left(p-q\right), \end{aligned} \tag{49c}$

$ \sum\limits_{n=0}^{\infty}\left[\chi_+^{n}\left(p,P\right)\chi_-^{n}\left(q,P\right)-\chi_-^{n}\left(p-P,-P\right)\chi_+^{n}\left(q-P,-P\right)\right] =0. \tag{49d}$

The true vacuum is defined by
$ w_n(P)|\Omega\rangle=0 $ , where$ \vert \Omega\rangle $ represents the physical vacuum, which may differ from the quark vacuum$ \vert 0\rangle $ at subleading order in$ 1/N_c $ . The n-th mesonic state can be constructed by$ |P_n^{0},P\rangle =\sqrt{2P_n^{0}}w_{n}^{\dagger}\left(P\right)|\Omega\rangle, $

(50) where
$ P_n^{0} $ denote the energy of the n-th mesonic state.Plugging (43) into (43), we desire to obtain the diagonalized Hamiltonian as follows
$ H=H_0^{'}+\int\frac{dP}{2\pi}\sum\limits_n P_n^{0}w_n^{\dagger}(P)w_n(P)+ \mathcal{O}\left(\frac{1}{\sqrt{N_c}}\right), $

(51) where
$ H_0^{\prime} $ is the shifted vacuum energy.Similar to the recipe of leading to (24) in the light-front case, we enforce that all the non-diagonal operators (43) in the new
$ w_{n}/w_{n}^{\dagger} $ basis, such as$ w_n^\dagger w_m $ ($ m\neq n $ ),$ w^\dagger w^\dagger $ ,$ w w $ ,$ \cdots $ , ought to vanish. This criterion imposes quite nontrivial constraints on the mesonic wave function$ \chi^\pm_n(x) $ . As a matter of fact, such constraint can be cast into two coupled integral equations for$ \chi_n^\pm $ :$ \begin{aligned}[b] & \left(\Pi^+\left(p\right)+\Pi^+\left(P-p\right)\mp P_n^{0}\right)\chi_{n}^{\pm}\left(p,P\right) \\ =&\frac{\lambda}{4} {\rlap{—} \int }\frac{dk}{\left(p-k\right)^{2}}\times\left(S_+\left(p,k,P\right)\chi_{n}^{\pm}\left(k,P\right)-S_-\left(p,k,P\right)\chi_{n}^{\mp}\left(k,P\right)\right), \end{aligned} $

(52) which agrees with the bound state equations first derived by Ji, Liu and Zahed for scalar
$ {\rm QCD}_2 $ in equal-time quantization [22].An important element of physics is that, when boosted to infinite-momentum frame (IMF), i.e., taking
$ P\to \infty $ limit, the backward-moving mesonic wave function$ \chi_{n}^{-} $ dies away, and the forward-moving mesonic wave function$ \chi_{n}^{+} $ approaches the light-cone wave function$ \chi_{n}(x) $ with$ x=p/P $ [22]. As a consequence, in the IMF the equal-time bound-state equations (52) descend to the light-cone bound-state equation (28). This pattern is identical to what was found in the spinor$ {\rm QCD}_2 $ case [12]. -
In this section, we aim to derive the bound-state equations for a new kind of hadron, a hybrid hadron or an exotic "baryon" composed of a bosonic quark and a fermionic anti-quark, in both light-front and equal-time quantization. If the bosonic quark can be interpreted as diquark, such hybrid hadron may in some sense resemble the ordinary baryon in the real world.
-
The bound-state equation for such a hybrid hadron in
$ {\rm QCD}_2 $ was first derived using diagrammatic approach in light-front quantization by Aoki in 1993 [23]. Shortly after the mass spectra of the hybrid hadrons were also studied by Aoki and Ichihara [37]. In this subsection, we use the Hamiltonian operator method to rederive the bound-state equation in hybrid QCD$ _2 $ in light-front quantization. -
We start from the hybrid
$ {\rm QCD}_2 $ lagrangian which contains both scalar and spinor quarks. Imposing the light-cone gauge$ A^{+a}=0 $ and utilizing the light-front coordinantes, the lagrangian can be expressed as$ \begin{aligned}[b] \mathcal{L}_{\text{hQCD}_2} =& \frac{1}{2}\left(\partial_-A^{-a}\right)^{2} + i\left(\psi_{R}^{\dagger}D_+\psi_{R}+\psi_{L}^{\dagger}\partial_-\psi_{L}\right) \\& - \frac{m_2}{\sqrt{2}}\left(\psi_{L}^{\dagger}\psi_{R}+\psi_{R}^{\dagger}\psi_{L}\right) \\ &+ \left(\partial_-\phi^\dagger\right) D_+\phi + \left(D_+\phi\right)^\dagger \partial_-\phi - m_1^{2}\phi^{\dagger}\phi. \end{aligned} $

(53) with
$ m_1 $ and$ m_2 $ represent the masses of the bosonic and fermionic quarks, respectively. Two sets of canonical momenta are$ \pi_\phi=\partial_-\phi, \pi_\psi=\psi_R $ . Note$ \psi_L $ is a constrained rather than canonical variable. After Legendre transformation, we obtain the following light-front Hamiltonian:$ H_\text{LF} = \int dx^- \Big[ \frac{m_2}{\sqrt{2}}\psi_{R}^{\dagger}\psi_{L}+ m_1^{2}\phi^{\dagger}\phi - \frac{ g_\mathrm{s}^2}{2}J^a\frac{1}{\partial_-^{2}}J^a\Big], $

(54) where
$ J^a \equiv i\left(\phi^{\dagger}T^{a}\pi-\pi^{\dagger}T^{a}\phi\right) + \psi_{R}^{\dagger}T^{a}\psi_{R}. $

(55) -
The scalar quark field has been Fourier-expanded in the annihilation/creation operator basis in (12). Analogously, the spinor quark field can be Fourier-expanded accordingly [18]:
$ \psi_{R}^{i}(x^-) =\int\frac{dk^+}{2\pi}[b^{i}\left(k^+\right)e^{-ik^+x^-}+d^{i^{\dagger}}\left(k^+\right)e^{ik^+x^-}]. $

(56) Following the bosonization technique in the preceding sections, here we introduce a set of compound color-singlet operators composed of the scalar/spinor quark annihilation and creation operators. Since we are studying the bound system composed of a fermion and a boson, we call this procedure as "Fermionization".
Besides the compound operators already introduced in (14), here we enumerate the new color-singlet compound operators:
$ B\left(k^+,p^+\right) \equiv\sum\limits_{i}b^{i\dagger}\left(k^+\right)b^{i}\left(p^+\right), \tag{57a} $

$ D\left(k^+,p^+\right) \equiv\sum\limits_{i}d^{i\dagger}\left(k^+\right)d^{i}\left(p^+\right). \tag{57b} $

$ K\left(k^+,p^+\right) \equiv\frac{1}{\sqrt{ N_\mathrm{c}}}\sum\limits_{i}d^{i}\left(k^+\right)a^{i}\left(p^+\right), \tag{57c} $

$ K^{\dagger}\left(k^+,p^+\right) \equiv\frac{1}{\sqrt{ N_\mathrm{c}}}\sum\limits_{i}a^{i\dagger}\left(p^+\right)d^{i\dagger}\left(k^+\right), \tag{57d} $

$ L\left(k^+,p^+\right) \equiv\frac{1}{\sqrt{ N_\mathrm{c}}}\sum\limits_{i}c^{i}\left(k^+\right)b^{i}\left(p^+\right), \tag{57e} $

$ L^{\dagger}\left(k^+,p^+\right) \equiv\frac{1}{\sqrt{ N_\mathrm{c}}}\sum\limits_{i}b^{i\dagger}\left(p^+\right)c^{i\dagger}\left(k^+\right). \tag{57f} $

The anticommutation relations among the fermionic compound operators K,
$ K^{\dagger} $ , L and$ L^{\dagger} $ turn out to be$ \begin{aligned}[b]& \left\{K\left(k_{1}^+,P_{1}^+\right), K^{\dagger}\left(k_{2}^+,P_{2}^+\right)\right\} \\=& \left(2\pi\right)^{2}\delta\left(k_{1}^+-k_{2}^+\right) \delta\left(P_{1}^+-P_{2}^+\right) + \mathcal{O}\left(\frac{1}{ N_\mathrm{c}}\right), \end{aligned}\tag{58a} $

$ \begin{aligned}[b]& \left\{L\left(k_{1}^+,P_{1}^+\right), L^{\dagger}\left(k_{2}^+,P_{2}^+\right)\right\} \\ =& \left(2\pi\right)^{2}\delta\left(k_{1}^+-k_{2}^+\right) \delta\left(P_{1}^+-P_{2}^+\right) + \mathcal{O}\left(\frac{1}{ N_\mathrm{c}}\right), \end{aligned}\tag{58b} $

$ \begin{aligned}[b]& \left\{K\left(k_{1}^+,P_{1}^+\right), L\left(k_{2}^+,P_{2}^+\right)\right\} \\=& \left\{K^{\dagger}\left(k_{1}^+,P_{1}^+\right), L\left(k_{2}^+,P_{2}^+\right)\right\} = 0, \end{aligned}\tag{58c} $

$ \begin{aligned}[b] &\left\{K\left(k_{1}^+,P_{1}^+\right),L^{\dagger} \left(k_{2}^+,P_{2}^+\right)\right\} \\=& \left\{K^{\dagger}\left(k_{1}^+,P_{1}^+\right), L^{\dagger}\left(k_{2}^+,P_{2}^+\right)\right\} = 0. \end{aligned}\tag{58d} $

The interaction term between the bosonic and spinor quark sector in (54) can be expressed in terms of the compound operators:
$ \begin{aligned}[b] & -\frac{1}{2}\left(ig_{s}\left(\phi^{\dagger}T^{a}\pi -\pi^{\dagger}T^{a}\phi\right)\right)\frac{1}{\partial_-^{2}} \left(g_{s}\psi_{R}^{\dagger}T^{a}\psi_{R}\right) =-4\pi\lambda\int_{0}^{\infty}\frac{dk_{1}^+}{2\pi\sqrt{2k_{1}^+}} \int_{0}^{\infty}\frac{dk_{2}^+}{2\pi\sqrt{2k_{2}^+}}\int_{0}^{\infty}\frac{dk_{3}^+}{2\pi} \int_{0}^{\infty}\frac{dk_{4}^+}{2\pi}\frac{(k_{1}^++k_{2}^+)}{\left(k_{3}-k_{4}\right)^{2}}\Theta\left(|k_3-k_4|-\rho\right) \\ &\left(K^{\dagger}\left(k_{4}^+,k_{1}^+\right)K\left(k_{3}^+,k_{2}^+\right)+L^{\dagger}\left(k_{2}^+,k_{3}^+\right)L\left(k_{1}^+,k_{4}^+\right)\right) \end{aligned}\tag{59}$ 
Again we can break the full light-front Hamiltonian into three pieces:
$ H_{\rm LF} =H_{\rm LF;0}+\colon H_{\rm LF;2}\colon+\colon H_{\rm LF;4}\colon+ \mathcal{O}(1/N_c) $ , with$ \begin{aligned}[b] :H_{\text{LF};2}: =& m^{2}\int_{-\infty}^{\infty}\frac{dx^-}{2\pi}\int_{0}^{\infty}\frac{dk^+}{2k^+}\left[ A\left(k^+,k^+\right)+C\left(k^+,k^+\right) +B\left(k^+,k^+\right)+D\left(k^+,k^+\right) \right]\\&+ \lambda\int_{0}^{\infty}\frac{dk^+}{2\pi}\left(\frac{1}{\rho}-\frac{1}{k^+}\right)\left[B\left(k^+,k^+\right)+D\left(k^+,k^+\right)\right]\\ &+ \frac{\lambda}{4}\int_{-\infty}^{\infty} dx^-\iint\frac{dk_{1}^+\cdot dk_{2}^+} {\left(2\pi\right) k_{1}^+k_{2}^+} \left(\frac{k_{1}^++k_{2}^+}{k_{2}^+-k_{1}^+}\right)^{2}\Theta\left(|k_2-k_1|-\rho\right)\left[A\left(k_{1}^+,k_{1}^+\right)+C\left(k_{2}^+,k_{2}^+\right)\right], \end{aligned}\tag{60a} $

$ \begin{aligned}[b] :H_{\text{LF};4}: =& - g_\mathrm{s}^2 N_\mathrm{c}\int_{0}^{\infty}\frac{dk_{1}^+}{2\pi\sqrt{2k_{1}^+}} \int_{0}^{\infty}\frac{dk_{2}^+}{2\pi\sqrt{2k_{2}^+}} \int_{0}^{\infty}\frac{dk_{3}^+}{2\pi}\int_{0}^{\infty}\frac{dk_{4}^+}{2\pi} \frac{\left(k_{1}^++k_{2}^+\right)}{\left(k_{3}-k_{4}\right)^{2}}\Theta\left(|k_3-k_4|-\rho\right) \\ &\left[K^{\dagger}\left(k_{4}^+,k_{1}^+\right)K\left(k_{3}^+,k_{2}^+\right) +L^{\dagger}\left(k_{2}^+,k_{3}^+\right)L\left(k_{1}^+,k_{4}^+\right)\right]. \end{aligned}\tag{60b} $

For simplicity, we have suppressed the explicit expression of the vacuum energy
$ H_{\rm LF;0} $ .As dictated by the confinement property of QCD, the color-singlet bosonic operators A, D, B and C are no longer independent, rather can be replaced by the convolution of the following fermionic compound operators:
$ A\left(p^+,q^+\right) \rightarrow \int_{0}^{\infty}\frac{dr^+}{2\pi} K^+\left(r^+,p^+\right)K\left(r^+,q^+\right), \tag{61a} $

$ D\left(p^+,q^+\right) \rightarrow \int_{0}^{\infty}\frac{dr^+}{2\pi} K^+\left(p^+,r^+\right)K\left(q^+,r^+\right), \tag{61b} $

$ C\left(p^+,q^+\right) \rightarrow \int_{0}^{\infty}\frac{dr^+}{2\pi} L^+\left(p^+,r^+\right)L\left(q^+,r^+\right), \tag{61c} $

$ B\left(p^+,q^+\right) \rightarrow \int_{0}^{\infty}\frac{dr^+}{2\pi} L^+\left(r^+,p^+\right)L\left(r^+,q^+\right). \tag{61d} $

Substituting these relations to (60a) and (60b), relabelling the light-cone momenta by
$ p^{+}=xP^{+} $ and$ k^{+}=(1-x)P^{+} $ , and only retaining the leading-order terms in 1/$ N_\mathrm{c} $ , the light-front Hamiltonian can be solely built out of the fermionic operators K and$ K^\dagger $ :$ \begin{aligned}[b] :H_{\rm LF;2}: = &\int_{0}^{\infty} \frac{dP^+\left(P^+\right)}{(2\pi)^{2}}\int_{0}^{1} dx K^{\dagger}((1-x)P^+,xP^+)K((1-x)P^+,xP^+) \\&\left\{ \frac{m^{2}}{2xP^+}+\frac{m^{2}}{2(1-x)P^+}+\frac{\lambda}{\rho}-\frac{\lambda}{(1-x)P^+}+\frac{1}{8xP^+}\int_{-\infty}^\infty\frac{dy}{ |y|}\frac{(x+y)^2}{(y-x)^2}\Theta\left(|y-x|-\frac{\rho}{P^+}\right)\right\}, \end{aligned}\tag{62a} $

$ \begin{aligned}[b] :H_{\rm LF;4}: =&-\frac{g_{s}^{2}}{2\left(2\pi\right)^{3}}\int_{0}^{\infty} dP^+\iint_{0}^{1} dxdyK^{\dagger}\left(\left(1-x\right)P^+,xP^+\right)K\left(\left(1-y\right)P^+,yP^+\right) \\&\frac{\left(P^+\right)^{2}}{\sqrt{2xP^+}\sqrt{2yP^+}}\frac{xP^++yP^+}{[\left(1-y\right)P^+-(1-x)P^+]^{2}}\Theta\left(|y-x|-\frac{\rho}{P^+}\right). \end{aligned}\tag{62b} $

-
Our goal is to diagonalize the light-front Hamiltonian (62). To this purpose, we introduce a new basis composed of the hybrid hadron annihilation/ creation operators:
$ k_{n}(P^{+}) $ /$ k_{n}^{\dagger}(P^{+}) $ , where n represents the principal quantum number, and$ P^{+} $ denotes the light-front momentum of the corresponding meson. We hypothesize that the K basis and the$ k_{n} $ basis are related by$ K\left(\left(1-x\right)P^+,xP^+\right) =\sqrt{\frac{2\pi}{P^+}}\sum\limits_{n=0}^{\infty}\varPhi_{n}\left(x\right)k_{n}\left(P^+\right),\tag{63} $

where
$ \varPhi_{n}(x) $ stands for the light-cone wave function of the n-th excited state in the hybrid hadron family.If we assume that the mesonic annihilation/creation operators
$ k_{n} $ obey the standard anticommutation relation:$ \left\{k_{n}\left(P_{1}^+\right),k_{m}^{\dagger}\left(P_{2}^{\text+}\right)\right\} =2\pi\delta\left(P_1^+-P_2^+\right)\delta_{nm}, \tag{64} $

the light-cone wave functions
$ \varPhi_{n}(x) $ must satisfy the following orthogonality and completeness relations:$ \int_{0}^{1}dx\varPhi_{n}\left(x\right)\varPhi_{m}\left(x\right) =\delta_{nm}, \tag{65a} $

$ \sum\limits_{n}\varPhi_{n}\left(x\right)\varPhi_{n}\left(y\right) =\delta\left(x-y\right). \tag{65b} $

The n-th hybrid state can be directly constructed as
$ |P_n^-,P^+\rangle =\sqrt{2P^+}k_{n}^{\dagger}(P^+)|0\rangle, $

(66) with the light-cone energy
$ P^{-}_n=M_{n}^{2}/(2P^{+}) $ , and$ M_{n}^{2} $ is the mass square of the n-th hybrid hadron.We wish the light-front Hamiltonian utimately bear the following diagonal form:
$ H_{\rm LF} =H_{\rm LF;0}+\int\frac{dP^+}{2\pi}P_n^-k_{n}^{\dagger}\left(P^+\right)k_{n}\left(P^+\right). $

(67) In order to arrive at this desired form, all the non-diagonal terms in (62) after converted in the
$ k_{n}/k_{n}^{\dagger} $ basis, such as$ k_n^\dagger k_m $ ($ m\neq n $ ),$ k^\dagger k^\dagger $ ,$ k k $ ,$ \cdots $ , have to vanish. This criterion imposes some nontrivial constraints on the light-cone wave function$ \varPhi_n(x) $ . After some manipulation, we end up the following light-front bound-state equation for the hybrid hadron:$ \begin{aligned}[b]& \left(\frac{m_{1r}^{2}-2\lambda}{x}+\frac{m_{2}^{2}-2\lambda}{\left(1-x\right)}\right)\varPhi_{n}\left(x\right)\\&-\lambda {\rlap{—} \int }_0^{1}\frac{dy}{\sqrt{xy}}\frac{\left(x+y\right)}{\left(x-y\right)^{2}}\varPhi_{n}\left(y\right)=M_{n}^{2}\varPhi_{n}\left(x\right). \end{aligned} $

(68) where the renormalized bosonic quark mass
$ m_{1r} $ is defined in (27).Equation (68) is in exact agreement with the light-front bound-state equation originally derived via diagrammatic method [37].
-
In this subsection, we attempt to derive the bound-state equation for the hybrid QCD
$ _2 $ from the perspective of equal-time quantization. To the best of our knowledge, the equal-time bound-state equation for hybrid hadron is derived for the first time. -
Imposing the axial gauge
$ A^{a\,z}=0 $ , the hybrid$ {\rm QCD}_2 $ lagrangian can be expressed as$ \begin{aligned}[b] \mathcal{L}_{\text{hQCD}_2} =& \frac{1}{2}\left(\partial_{z}A_{0}^{a}\right)^{2} + (D_0\phi)^{\dagger}D_0\phi - (\partial_z\phi^\dagger)\partial_z\phi \\& - m_1^{2}\phi^{\dagger}\phi + i\psi^{\dagger}\left(D_{0}+\gamma^{5}\partial_{z}\right)\psi-m_2\bar{\psi}\psi. \end{aligned} $

(69) Straightforward manipulation leads to
$ \begin{aligned}[b] H =&\int dz\Big[ \pi^{\dagger}\pi+|\partial_z\phi|^{2}+m_1^{2}|\phi|^{2}\\&+\psi^{\dagger}(-i\gamma^{5}\partial_{z}+m_2\gamma^{0})\psi -\frac{ g_\mathrm{s}^2}{2} J^a\frac{1}{\partial_{z}^{2}}J^a \Big], \end{aligned} $

(70) with
$ \begin{array}{*{20}{l}} J^a = \psi^{\dagger}T^{a}\psi - i\left(\pi^{\dagger}T^{a}\phi-\phi^{\dagger}T^{a}\pi\right). \end{array} $

(71) -
The bosonic quark field is Fourier-expanded in terms of the quark annihilation and creation operators in accordance with (32). The spinor quark field is Fourier-expanded as [18]
$ \psi^{i}\left(z\right) =\int\frac{dp}{2\pi}\frac{1}{\sqrt{2\widetilde{E}\left(p\right)}} \left[b^{i}\left(p\right)u\left(p\right)+d^{i\dagger}\left(-p\right)v\left(-p\right)\right]e^{ipz}, $

(72) with the energy of the dressed spinor quark
$ {\widetilde{E}(p)} $ is given by [12]$ \begin{aligned}[b] \widetilde{E}\left(p\right) =& m_2\cos\theta\left(p\right)+p\sin\theta\left(p\right)\\&+\frac{\lambda}{2}\int\frac{dk} {\left(p-k\right)^{2}}\Theta\left(|k-p|-\rho\right)\cos[\theta\left(p\right)-\theta\left(k\right)], \\ \end{aligned} $

(73) with
$ \theta(p) $ representing the so-called chiral-Bogoliubov angle, which can be determined by the mass-gap equation [12]. Note this dispersion relation depends on an artificial IR regulator. This can also be viewed as gauge artifact, since the energy of an colored object in QCD cannot be a physical quantity.Following the fermionization procedure introduced in Sec. 3.1.2, we introduce the following color-singlet compound operators:
$ B\left(p,q\right) \equiv\sum\limits_{i}b^{i\dagger}\left(p\right)b^{i}\left(q\right), \tag{74a} $

$ D\left(p,q\right) \equiv\sum\limits_{i}d^{i\dagger}\left(-p\right)d^{i}\left(-q\right), \tag{74b} $

$ M\left(p,q\right) \equiv\sum\limits_{i}d_i (-p) b_i (q), \tag{74c} $

$ M^{\dagger}\left(p,q\right) \equiv \sum\limits_{i}b_i^{\dagger} (q) d_i^\dagger(-p), \tag{74d} $

$ K\left(p,q\right) \equiv\frac{1}{\sqrt{N_{c}}}\sum\limits_{i}d^{i}\left(-p\right)a^{i}\left(q\right), \tag{74e} $

$ K^{\dagger}\left(p,q\right) \equiv\frac{1}{\sqrt{N_{c}}}\sum\limits_{i}a^{i\dagger}\left(q\right)d^{i\dagger}\left(-p\right), \tag{74f} $

$ L\left(p,q\right) \equiv\frac{1}{\sqrt{N_{c}}}\sum\limits_{i}c^{i}\left(-p\right)b^{i}\left(q\right), \tag{74g} $

$ L^{\dagger}\left(p,q\right) \equiv\frac{1}{\sqrt{N_{c}}}\sum\limits_{i}b^{i\dagger}\left(q\right)c^{i\dagger}\left(-p\right). \tag{74h} $

The anticommutation relations among the fermionic compound operators K,
$ K^{\dagger} $ , L and$ L^{\dagger} $ are$ \begin{aligned}[b]& \left\{ K\left(k_{1},P_1\right),K^{\dagger}\left(k_{2},P_2\right)\right\} \\ =&\left(2\pi\right)^{2}\delta\left(k_{1}-k_{2}\right)\delta\left(P_1-P_2\right)+\mathcal{O}\left(\frac{1}{ N_\mathrm{c}}\right), \end{aligned}\tag{75a} $

$ \begin{aligned}[b] &\left\{ L\left(k_{1}^+,P_1^+\right),L^{\dagger}\left(k_{2}^+,P_2^+\right)\right\} \\ =&\left(2\pi\right)^{2}\delta\left(k_{1}-k_{2}\right)\delta\left(P_1-P_2\right)+\mathcal{O}\left(\frac{1}{ N_\mathrm{c}}\right), \end{aligned}\tag{75b} $

$ \begin{array}{*{20}{l}} \left\{ K\left(k_{1},P_1\right),L\left(k_{2},P_2\right)\right\} =\left\{ K^{\dagger}\left(k_{1},P_1\right),L\left(k_{2},P_2\right)\right\} =0, \end{array}\tag{75c} $

$ \begin{array}{*{20}{l}} \left\{ K\left(k_{1},P_1\right),L^{\dagger}\left(k_{2},P_2\right)\right\} =\left\{ K^{\dagger}\left(k_{1},P_1\right),L^{\dagger}\left(k_{2},P_2\right)\right\} =0 \end{array}\tag{75d} $

The interaction term between the bosonic and fermionic sectors in (70) can be expressed as:
$ \begin{aligned}[b] & \frac{1}{2}g_{s}\psi^{\dagger}T^{a}\psi\frac{1}{\partial_{z}^{2}}\left(g_{s}i\left(\pi^{\dagger}T^{a}\phi-\phi^{\dagger}T^{a}\pi\right)\right) \\ =& \pi\lambda\int\frac{dP_1}{2\pi}\frac{1}{\sqrt{2\tilde{E}\left(P_1\right)}}\int\frac{dP_2}{2\pi}\frac{1}{\sqrt{2\tilde{E}\left(P_2\right)}}\\&\times\int\frac{dk_{1}}{2\pi}\int\frac{dk_{2}}{2\pi} \frac{1}{\left(k_{2}-k_{1}\right)^{2}} \\ &\Theta\left(|k_2-k_1|-\rho\right)2\pi\delta\left(P_2-P_1+k_2-k_1\right) \\ &\big\{-f_+\left(k_{1},k_{2}\right)\cos\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}L^{\dagger}\left(k_{2},P_1\right)L\left(k_{1},P_2\right) \\ &+f_-\left(k_{1},k_{2}\right)\sin\frac{\theta\left(k-P\right)-\theta\left(P-q\right)}{2}L^{\dagger}\left(k_{2},P_1\right)K^{\dagger}\left(P_2,k_{1}\right) \\ & -f_+\left(k_{1},k_{2}\right)\cos\frac{\theta\left(P-k\right)-\theta\left(P-q\right)}{2}K^{\dagger}\left(P_2,k_{1}\right)K\left(P_1,k_{2}\right) \\ & +f_-\left(k_{2},k_{1}\right)\sin\frac{\theta\left(P-k\right)-\theta\left(P-q\right)}{2}K\left(P_1,k_{2}\right)L\left(k_{1},P_2\right)\big\}. \end{aligned}\tag{76} $

In terms of the color-singlet compound operators, we can break the Hamiltonian (70) into three pieces:
$ H =H_{0}+\colon H_{2}\colon+\colon H_{4}\colon+\mathcal{O}(1/N_c) $ , with$ \begin{aligned}[b] :H_{2}: =& \int\frac{dk}{2\pi}\Pi^+\left(k\right)\left(A\left(k\right)+C\left(k\right)\right)+\sqrt{N_{c}}\int\frac{dk}{2\pi}\Pi^-(k)\left(N\left(k\right)+N^{\dagger}\left(k\right)\right) \\ &\int dpE(p)\left[B\left(p,p\right)+D\left(p,p\right)+M^{\dagger}\left(p,p\right)+M\left(p,p\right)\right], \end{aligned}\tag{77a} $

$ \begin{aligned}[b]:H_{ 4}:= & \pi\lambda\int\frac{dP_{1}}{2\pi}\frac{1}{\sqrt{2\widetilde{E}\left(P_1\right)}}\int\frac{dP_2}{2\pi}\frac{1}{\sqrt{2\tilde{E}\left(P_2\right)}}\int\frac{dk_{1}}{2\pi}\int\frac{dk_{2}}{2\pi}\frac{1}{\left(k_{2}-k_{1}\right)^{2}} \Theta\left(|k_2-k_1|-\rho\right)2\pi\delta\left(P_2-P_1+k_2-k_1\right) \\&\big\{-f_+\left(k_{1},k_{2}\right)\cos\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}L^{\dagger}\left(k_{2},P_1\right)L\left(k_{1},P_2\right) +f_-\left(k_{1},k_{2}\right)\sin\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}L^{\dagger}\left(k_{2},P_1\right)K^{\dagger}\left(P_2,k_{1}\right) \\ &-f_+\left(k_{1},k_{2}\right)\cos\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}K^{\dagger}\left(P_2,k_{1}\right)K\left(P_1,k_{2}\right)-f_-\left(k_{1},k_{2}\right)\sin\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}K\left(P_1,k_{2}\right)L\left(k_{1},P_2\right)\big\}. \end{aligned}\tag{77b} $

For simplicity, we have suppressed the explicit expressions of the vacuum energy
$ H_0 $ .Demanding that
$ :H_{\text{2}}: $ to bear the diagonal form separately for the dressed bosonic and fermionic quarks, we can obtain the mass-gap equations for both types of quarks. The mass-gap equation for bosonic quark is already given in (37). The mass-gap equation for spinor quark is well-known [12]:$ p \cos\theta(p)-m_2 \sin\theta(p) =\frac{\lambda}{2} {\rlap{—} \int }_{-\infty}^{+\infty}\frac{dk}{\left(p-k\right)^{2}} \sin\left[\theta\left(p\right)-\theta\left(k\right)\right]. \tag{78} $

As mentioned before, these two mass gap equations can also be deduced via variational approach, by requiring the minimized vacuum energy.
-
Like in the preceding subsection, the confinement property of QCD indicates that the color-singlet bosonic operators A, D, B and C are not independent, yet can be replaced by the convolution of the following fermionic compound operators at lowest order in
$ 1/N_c $ :$ A\left(k_{1},k_{2}\right) \rightarrow \intop\frac{dp}{2\pi}K^{\dagger}\left(p,k_{1}\right)K\left(p,k_{2}\right), \tag{79a} $

$ D\left(k_{1},k_{2}\right) \rightarrow \intop\frac{dp}{2\pi}K^{\dagger}\left(k_{1},p\right)K\left(k_{2},p\right), \tag{79b}$

$ C\left(k_{1},k_{2}\right) \rightarrow \intop\frac{dp}{2\pi}L^{\dagger}\left(k_{1},p\right)L\left(k_{2},p\right), \tag{79c}$

$ B\left(k_{1},k_{2}\right) \rightarrow \intop\frac{dp}{2\pi}L^{\dagger}\left(p,k_{1}\right)L\left(p,k_{2}\right). \tag{79d} $

Making these replacements in the Hamiltonian (77), and only retaining the leading-order terms in
$ 1/N_c $ , the Hamiltonian now only depend on the fermionic compound operators K, L and their Hermitian conjugates:$ \begin{aligned}[b] :H_{2}: & =\iint\frac{dPdq}{\left(2\pi\right)^{2}}\left(\Pi^+\left(q\right)+E\left(P-q\right)\right)K^{\dagger}\left(q-P,q\right)K\left(q-P,q\right)\\&-\left(\Pi^+\left(q\right)+E\left(P-q\right)\right)L^{\dagger}\left(q,q-P\right)L\left(q,q-P\right), \end{aligned}\tag{80a} $ 
$ \begin{aligned}[b] :H_{4}: =&-\frac{\lambda}{8\pi^{2}}\int dP\iint\frac{dqdk}{\left(k-q\right)^{2}}\Theta\left(|k-q|-\rho\right)\frac{1}{\sqrt{2E\left(k-P\right)}} \frac{1}{\sqrt{2E\left(k\right)}}\\ & \big\{f_+\left(k_{1},k_{2}\right)\cos\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}K^{\dagger}\left(q-P,q\right)K\left(k-P,k\right)\\ &-f_+\left(k_{1},k_{2}\right)\cos\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}L^{\dagger}\left(k,k-P\right)L\left(q,q-P\right)\\ & -f_-\left(k_{1},k_{2}\right)\sin\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2} N_{c}K\left(k-P,k\right)L\left(q,q-P\right) \\ &+f_-\left(k_{1},k_{2}\right)\sin\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}N_{c}L^{\dagger}\left(k,k-P\right)K^{\dagger}\left(q-P,q\right)\big\}, \end{aligned} \tag{80b}$

where the regularized dressed quark energy
$ E(p) $ is defined by [12]:$ \begin{aligned}[b] E\left(p\right) =& \tilde{E}\left(p\right)-\frac{\lambda}{\rho} = m\cos\theta\left(p\right)+p\sin\theta\left(p\right)\\&+\frac{\lambda}{2} {\rlap{—} \int }\frac{dk}{\left(p-k\right)^{2}} \cos[\theta\left(p\right)-\theta\left(k\right)]. \end{aligned}\tag{81} $

To diagonalize the Hamiltonian, we invoke the Bogoliubov transformation, expressing the compound quark operators K, L in terms of the annihilation/creation operators of the (anti)-hybrid hadrons:
$ \begin{aligned}[b] K\left(q-P,q\right) =&\sqrt{\frac{2\pi}{|P|}}\sum\limits_{n=0}^{\infty}\Big[m_{n}(P)\varPhi_{n}^+\left(q,P\right)\\&+\bar{m}_{n}^{\dagger}\left(-P\right) \varPhi_{n}^-\left(q-P,-P\right)\Big], \end{aligned}\tag{82a} $

$ \begin{aligned}[b] L\left(q-P,q\right) =&\sqrt{\frac{2\pi}{|P|}}\sum\limits_{n=0}^{\infty}\Big[\bar{m}_{n}\left(P\right)\varPhi_{n}^+\left(q,P\right)\\&+m_{n}^{\dagger}\left(-P\right)\varPhi_{n}^-\left(q-P,-P\right)\Big]. \end{aligned}\tag{82b} $

where
$ m_{n} $ and$ \bar{m}_{n}^{\dagger} $ represents the operator annihilating the n-th hybrid state composed of a bosonic quark and spinor anti-quark, while$ \bar{m}_{n}^{\dagger} $ represents the operator creating the n-th anti-hybrid state composed of a spinor quark and a bosonic anti-quark. The Bogoliubov coefficient functions$ \varPhi_{\pm}^{n} $ can be interpreted as the forward-moving/backward-moving wave functions of the n-th hybrid state. It is natural to anticipate that these hybrid annihilation and creation operators obey the following anticommutation relations:$ \{m_{n}\left(P\right),m_{m}^{\dagger}\left(P'\right)\} =2\pi\delta_{nm}\delta\left(P-P'\right), \tag{83a} $

$ \{\bar{m}_{n}\left(P\right),\bar{m}_{m}^{\dagger}\left(P'\right)\} =2\pi\delta_{nm}\delta\left(P-P'\right), \tag{83b} $

$ \{m_{n}\left(P\right),\bar{m}_{m}\left(P'\right)\} =\{m_{n}^{\dagger}\left(P\right),\bar{m}_{m}^{\dagger}\left(P'\right)\}=0. \tag{83c} $

The hadronic vacuum
$ \vert \Omega\rangle $ can be defined as$ m_{n}(P)|\Omega\rangle =0 $ for any P and n. One then construct the single hybrid hadron state as$ |P_n^{0},P\rangle =\sqrt{2P_n^{0}}m_{n}^{\dagger}\left(P\right)|\Omega\rangle, \tag{84}$

with
$ P_n^{0}=\sqrt{M_n^{2}+P^{2}} $ , and$ M_n $ denoting the mass of the n-th hybrid state.To be compatible with (83), the hybrid wave functions
$ \varPhi_{\pm}^{n} $ must obey the following orthogonality and completeness conditions:$\begin{aligned}[b]\\[-8pt] \int_{-\infty}^{+\infty}dp\left[\varPhi_+^{n}\left(p,P\right)\varPhi_+^{m}\left(p,P\right)+\varPhi_-^{n}\left(p,P\right)\varPhi_-^{m}\left(p,P\right)\right] =|P|\delta^{nm}, \end{aligned}\tag{85a}$ 
$ \int_{-\infty}^{+\infty}dp\left[\varPhi_+^{n}\left(p,P\right)\varPhi_-^{m}\left(p-P,-P\right)+\varPhi_-^{n}\left(p,P\right)\varPhi_+^{m}\left(p,P\right)\right] =0, \tag{85b} $

$ \sum\limits_{n=0}^{\infty}\left[\varPhi_+^{n}(p,P)\varPhi_+^{n}\left(q,P\right)+\varPhi_-^{n}\left(p-P,-P\right)\varPhi_-^{n}\left(q-P,-P\right)\right] =|P|\delta\left(p-q\right), \tag{85c} $

$ \sum\limits_{n=0}^{\infty}\left[\varPhi_+^{n}\left(p,P\right)\varPhi_-^{n}\left(q,P\right)+\varPhi_-^{n}\left(p-P,-P\right)\varPhi_+^{n}\left(q-P,-P\right)\right] =0. \tag{85d} $

Changing to the basis of
$ m_{n} $ and$ m_{n}^{\dagger} $ , we wish that all the non-diagonal terms in the Hamiltonian such as$ m_n^\dagger m_l $ ($ n\neq l $ ),$ m^\dagger m^\dagger $ ,$ m m $ all vanish, and end with the desired diagonal form:$ H =H_{0}^{'}+\int\frac{dP}{2\pi}\sum\limits_{n}P_n^{0}m_{n}^{\dagger}\left(P\right)m_{n}\left(P\right)+\mathcal{O}\left({\frac{1}{\sqrt{ N_\mathrm{c}}}}\right). \tag{86} $

In order to achieve this diagonal Hamiltonian, we find that the hadronic wave functions
$ \varPhi_{\pm}^{n} $ must satisfy the following coupled integral equations:$ \begin{aligned}[b] &\left(\Pi^+\left(p\right)+E\left(p-P\right)-P^{0}\right)\varPhi^+\left(p,P\right) \\ =&\frac{\lambda}{2} {\rlap{—} \int }\frac{dk}{\left(k-p\right)^{2}} \Big[f_+\left(k,p\right)\cos\frac{\theta\left(k-p\right)-\theta\left(q-p\right)}{2}\varPhi^+\left(k,P\right) \\ &+f_-\left(k,p\right)\sin\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}\varPhi^-\left(k,P\right)\Big],\\[-6pt] \end{aligned}\tag{87a} $

$ \begin{aligned}[b] &\left(\Pi^+\left(p\right)+E\left(p-P\right)+P^{0}\right)\varPhi^-\left(p,P\right)\\ =&\frac{\lambda}{2} {\rlap{—} \int }\frac{dk}{\left(k-p\right)^{2}} \Big[f_+\left(k,p\right)\cos\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}\varPhi^-\left(k,P\right) \\ &-f_-\left(k,p\right)\sin\frac{\theta\left(k-P\right)-\theta\left(q-P\right)}{2}\varPhi^+\left(k,P\right)\Big]. \end{aligned}\tag{87b} $

This is one of the main results of this paper.
When boosted to the IMF, one can show that these bound-state equations reduce to the bound-state equation derived in the light-front, (68). In the other word, as the hybrid hadron momentum is increasing, the backward-moving wave function
$ \varPhi_{-}^{n} $ quickly dies out, while the forward-moving wave function$ \varPhi_{+}^{n} $ approaches the light-front wave function$ \varPhi^{n}(x) $ . -
The numerical solution of bound-state wave functions have been widely discussed [42–49]. We follow the approach similar to [46] for the evaluation of light-cone wave functions and the Hermite function approach [51] for the equal-time wave functions. In order to simulate the physical mesons, we set the 't Hooft coupling to be
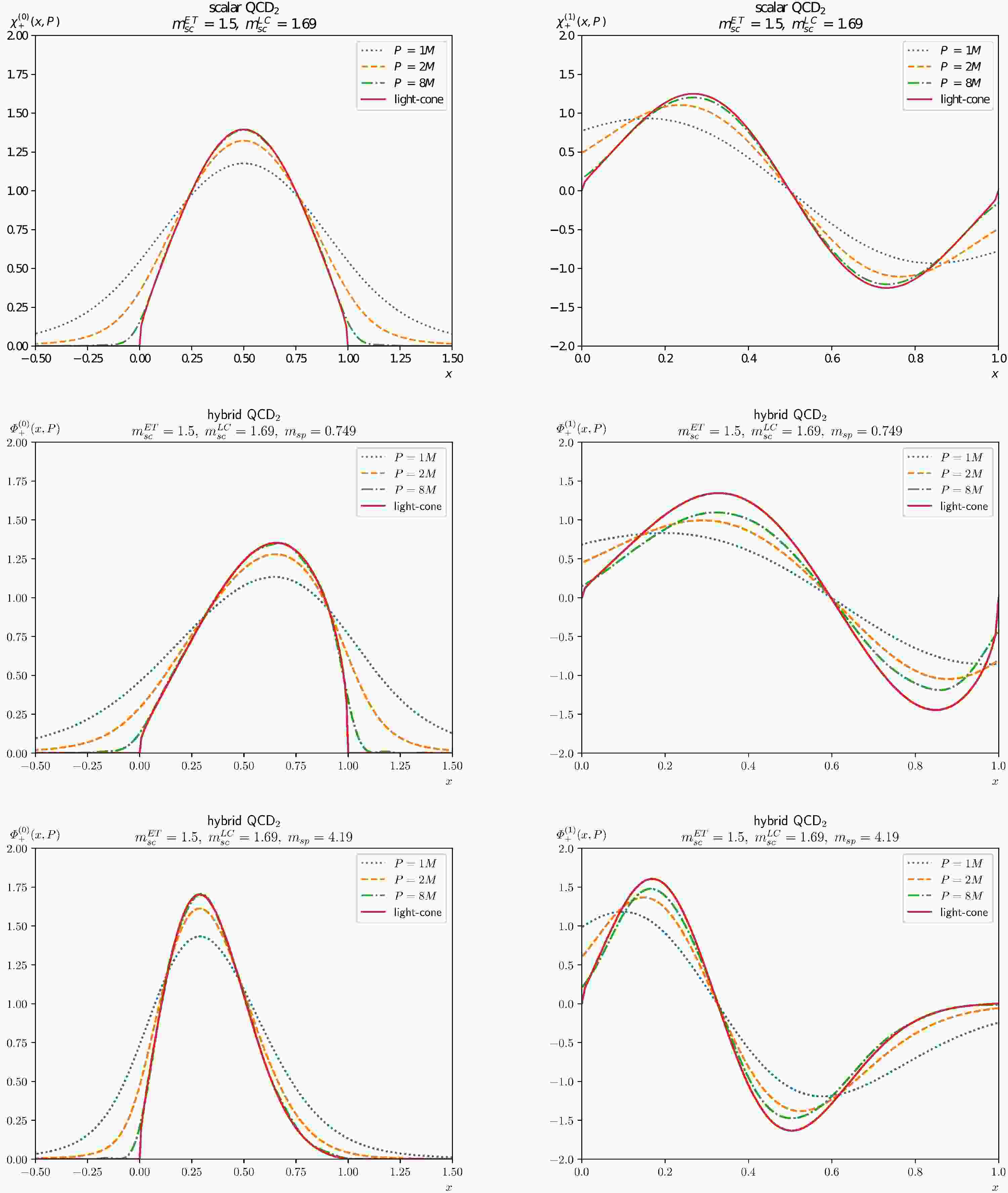
$ \sqrt{2\lambda}=340\text{ MeV} $ , which agrees with the value of string tension in$ {\rm{QCD}}_4 $ . For notational brevity, we use$ \sqrt{2\lambda} $ as the unit of mass in the rest of this section. The mass of scalar quark is assumed to be$ m_{sc}^\text{ET}\equiv m_{\tilde{r}}=1.5 $ ($ m_{sc}^\text{LC}\equiv m_{r} $ ). As for spinor quarks, we choose the mass of strange quark as$ m_{sp}=0.749 $ and charm quark as$ m_{sp}=4.19 $ .In Fig. 1, the meson mass spectra of different quark species are illustrated as functions of the principal quantum number n. It's exhibited that the square of the meson mass is linearly related to n. This phenomenon is analogous to the Regge trajectories in the 4 dimensional QCD where n is replaced by the spin J.
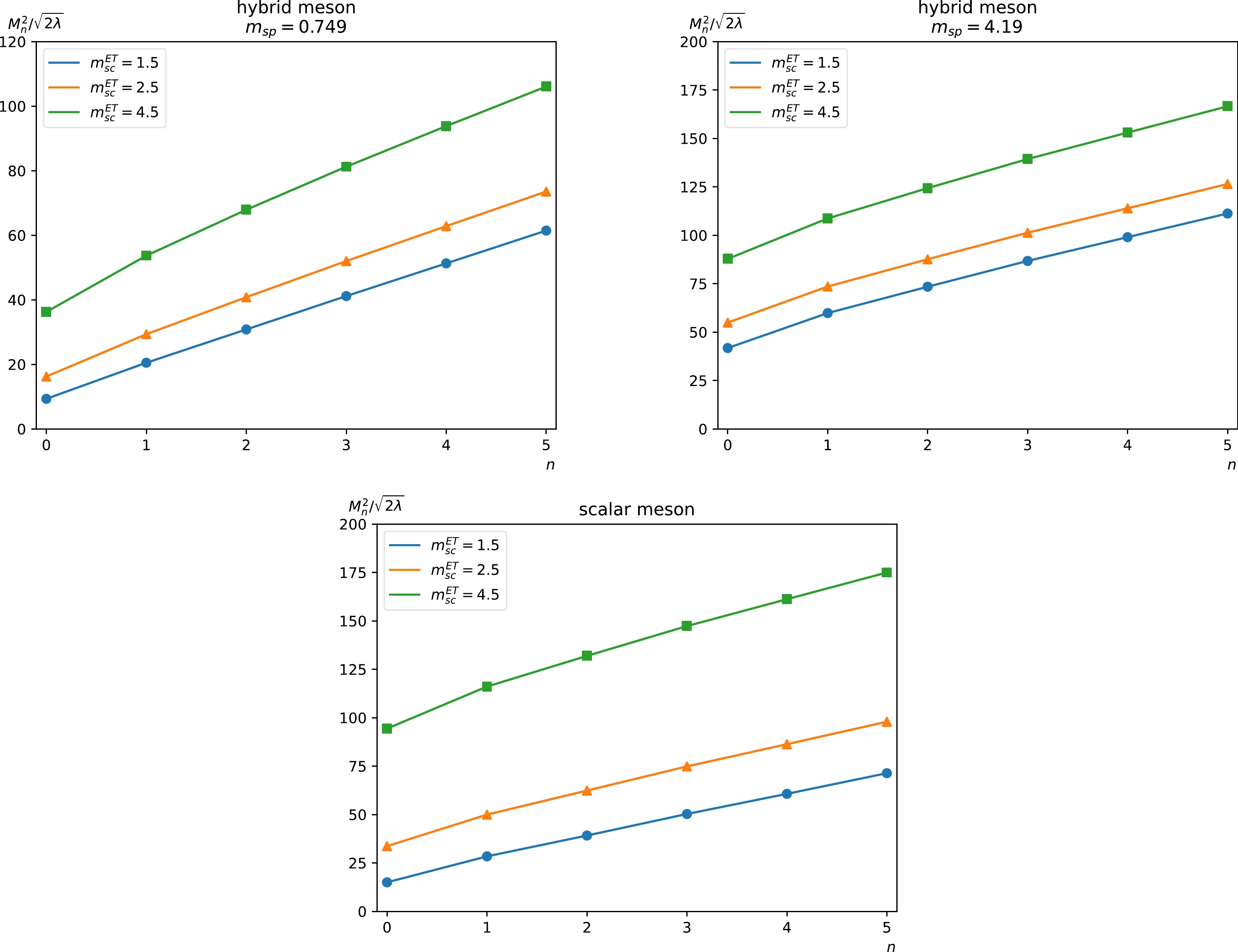
Figure 1. (color online) Mass spectra of a few low-lying mesonic levels with different quark mass. To facilitate the distinction between scalar quark and spinor quark,
$ m_{\tilde{r}}=m_{sc}^\text{ET} $ .We have numerically solved the bound state wave functions for scalar QCD
$ _2 $ and hybrid QCD$ _2 $ in the axial and light-cone gauges. In the process of calculation, we found that the renormalized scalar quark mass$ m_{sc}^\text{LC} $ in the light-front cannot be less than one, which corresponds to a strongly coupled region, where the asymptotic behavior of the wave function at the boundary is not a pure real number [50].In Fig. 2, we plot the equal-time and light-front (LF) meson wave functions in scalar and hybrid QCD
$ _2 $ , considering both the ground states and the first excited states. For single-flavor mesons consist of scalar quarks, the wave functions with even/odd n are symmetric/antisymmetric under the exchange$ x \leftrightarrow (1-x) $ due to the charge conjugation symmetry. The LF wave functions always vanish in both end points$ x = 0,1 $ . For heavy quark, the LF wave function possesses a much milder rising/falling shape near the end points and is mainly distributed at moderate values of x. When the mesons momentum goes to the infinity, the equal-time wave functions$ \chi_{+} $ and$ \varPhi_{+} $ will boost to the light-front bound state equation, while the$ \chi_{-} $ and and$ \varPhi_{-} $ components rapidly dies off. This phenomenon validates the large momentum effective theory (LaMET) and reflects the normative invariance of the theory. -
In this work, we have made a comprehensive study on the two-dimensional QCD, focusing on the bound-state equations for mesons composed of a scalar quark and scalar antiquark, as well as exotoic baryons composed of a fermionic quark and bosonic antiquark. These equations are obtained from both light-front quantization and equal-time quantization. Our major theoretical tool is the Hamiltonian operator approach. However, for the first time we also present a diagrammatical derivation of the mesonic bound-state equation in the equal-time quantization for scalar
$ {\rm QCD}_2 $ . We confirm the known equations for mesonic case and for the hybrid baryon in the light-front quantization, paying particular attention to the mass renormalization issue. We find that, in scalar$ {\rm{QCD}}_2 $ , the renormalized quark mass in light-front may not coincide with that in equal-time, depending on the chosen renormalization schemes. We establish the relationship between these two renormalized masses. For the first time, we also derive the bound-state equation for the exotic baryons in the equal-time quantization.We also conduct a comprehensive numerical study on the hadron spectroscopy and solving the bound-state wave functions of the ground and first-excited states. We utilize the concept of generalized functions to solve the mass-gap equation. We also explicitly verify the trend that as the hadron is boosted to infinite-momentum frame, the forward-moving bound-state wave function approach the light-front wave function.
-
In this Appendix, we utilize the Feynman diagrammatical method to redefine the bound-state equations for scalar
$ {\rm QCD}_2 $ in equal-time quantization. -
The s
$ {\rm QCD}_2 $ lagrangian is expanded as$ \begin{aligned}[b] \mathcal{L}_{\text{sQCD}_2} =& \mathrm{tr}\left(\partial_z A^0\right)^2 + \left(\partial^\mu\phi^\dagger\right)\partial_\mu\phi - m^2\phi^{\dagger}\phi \\ & -i g_\mathrm{s}\left(\partial_0\phi^\dagger\right) A^0\phi + i g_\mathrm{s}\phi^\dagger A^0\partial_0\phi + g_\mathrm{s}^2\phi^\dagger A^0A^0\phi. \end{aligned}\tag{A1} $

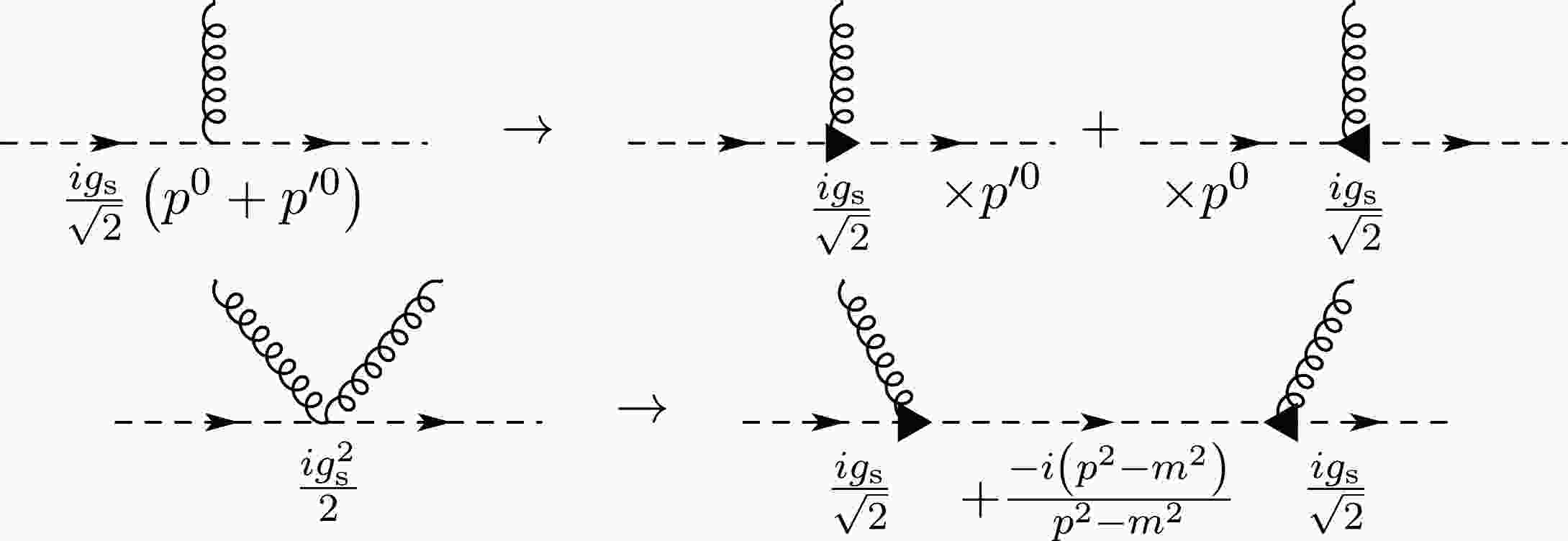
The Feynman rules can be derived directly from (88) and are shown in Table A1. The main obstacle of this approach in scalar
$ {\rm{QCD}}_2 $ compared with the case of spinor$ {\rm{QCD}}_2 $ is that the appearance of seagull vertices may mess up the rainbow-ladder topology at the leading order of$ 1/ N_\mathrm{c} $ .Building blocks Double lines Feynman rules 

$ {\dfrac{i}{\left(k^z\right)^2}} $ 



$ {\dfrac{i}{p^2 - m^2 + i\epsilon}} $ 



$ {\dfrac{i g_\mathrm{s}}{\sqrt{2}}\left(p^0 + p^{\prime0}\right)} $ 



$\dfrac{i g_{\mathrm{s}}^2}{2} $ 

Table A1. Original Feynman rules for sQCD2 in the axial gauge
The solution is straightforward. We break up each seagull vertex into two
$ q\bar{q}g $ vertices and reorganize its contribution into a new term of the quark propagator in between. However, this can not be done naively, since the Feynman rule of the$ q\bar{q}g $ vertex depends on the momenta of the two attached quark lines while a term in the quark propagator only knows about the momentum that flows through it. So we also need to break the$ q\bar{q}g $ vertex and move the momenta into the two attached quark propagators separately. This procedure is illustrated in Fig. A1. Note that in order to absorb the seagull vertex, we have to introduce four kinds of quark propagators, which are depicted in Fig. 2. With hindsight, these propagators are quite natural, and to some extent we can identify them with the propagators from$ \phi^\dagger\left(y\right), -i\pi^\dagger\left(y\right) $ to$ \phi\left(x\right), i\pi\left(x\right) $ in the Hamiltonian approach. The situation here is a bit similar (though not the same) to the relation between the canonical quantization and the path integral quantization of the massive vector field. The contact term from the seagull vertex cancels the$ \left(p^0\right)^2 $ numerator in the quark propagator to give the correct$ p^0 $ residue. For convenience we define$ \omega_p^2 \equiv \left(p^z\right)^2 + m^2 -i \epsilon $ .To simplify the calculation, we write the four quark propagators as a
$ 2\times2 $ matrix.$ D^{(0)}\left(p\right) = \frac{i\left(p^{0}\sigma_1 + \mathcal{P}_+ + \omega_p^2 \mathcal{P}_-\right)}{p^2-m^2+i\epsilon}, \tag{A2} $

where the projectors
$ \mathcal{P}_\pm \equiv \left(1\pm\sigma_3\right)/2 $ satisfy the orthogonality and completeness relations$ \mathcal{P}_\pm^2 = \mathcal{P}_\pm,\quad \mathcal{P}_\pm\mathcal{P}\mp = 0,\quad \mathcal{P}_+ + \mathcal{P}_- = 1, \tag{A3} $

and the following algebra
$ \sigma_1\mathcal{P}_\pm = \mathcal{P}_\mp \sigma_1,\quad \frac{\left(X\sigma_1 + Y\mathcal{P}_+ + Z \mathcal{P}_-\right)\left(X\sigma_1 - Z\mathcal{P}_+ - Y\mathcal{P}_-\right)} {X^2-YZ} = 1, \tag{A4} $

for scalars
$ X,Y,Z $ . It should be emphasized that the introduction of the Pauli σ matrices has nothing to do with spinors. In fact, the mass dimensions in (A2) don't even match. However, this particularly chosen matrix multiplication guarantees that only uniform-dimension terms in the matrix elements will be added together. The modified Feynman rules are summarized in Table A2.Building blocks Feynman rules 
$ {\dfrac{i}{\left(k^z\right)^2}} $ 


$ {\dfrac{i}{p^0\sigma_1 - \omega_p^2\mathcal{P}_{+} -\mathcal{P}_{-}}} $ 


$ {\dfrac{i g_\mathrm{s}}{\sqrt{2}}\sigma_1} $ 

Table A2. Modified Feynman rules for sQCD2 in the axial gauge.
-
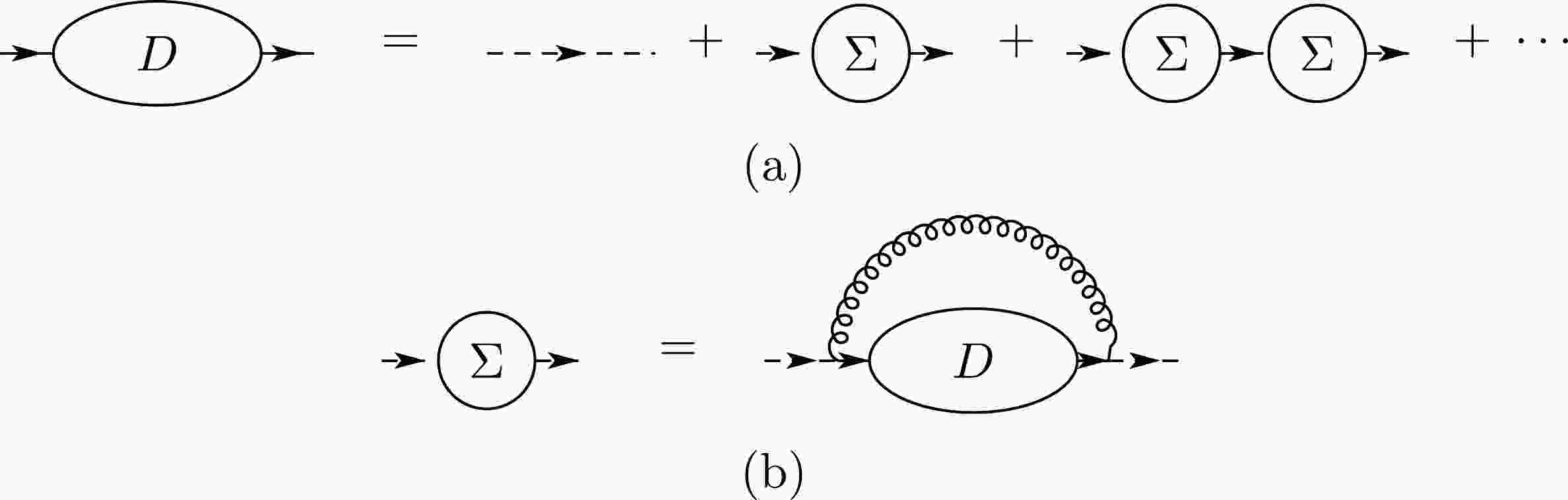
Let the contribution of one-particle irreducible (1PI) diagrams in the self-energy correction of quark propagator be given by
$ -i\Sigma\left(p\right) $ . The dressed quark propagator$ D\left(p\right) $ in the large-$ N_\mathrm{c} $ limit is governed by the rainbow diagrams (Fig. A3). It satisfies the recursive equations:$ D\left(p\right) = \frac{i}{p^0\sigma_1 - \omega_p^2 \mathcal{P}_+ - \mathcal{P}_- -\Sigma\left(p\right)}, \tag{A5a}$

$ -i\Sigma\left(p\right) = \frac{-i g_\mathrm{s}^2 N_\mathrm{c}}{2} {\rlap{—} \int }\frac{d^2 k}{\left(2\pi\right)^2} \frac{\sigma_1D\left(k\right)\sigma_1}{\left(p^z-k^z\right)^2}, \tag{A5b} $

where we have used
$ \frac{1}{X - Y} = X^{-1} + X^{-1}YX^{-1} + X^{-1}YX^{-1}YX^{-1} + \cdots. \tag{A6} $

Apparently
$ \Sigma\left(p\right) $ is independent of$ p^0 $ . The most general form is$ \Sigma\left(p\right) = A\left(p^z\right) \mathcal{P}_+ + B\left(p^z\right) \mathcal{P}_-. \tag{A7} $

The
$ \sigma_1 $ term does not appear in (A7) because we take the principal value of the$ k^0 $ integral in (A5b) at$ k^0=\infty $ , i.e., we take the average of the contour closed at the upper half-plane and the contour closed at the lower half-plane. The dressed quark propagator now becomes$ D\left(p\right) = i\frac{p^0\sigma_1 + \left(1+B\right)\mathcal{P}_+ +\left(\omega_p^2+A\right)\mathcal{P}_-} {\left(p^0\right)^2 - \left(1+B\right)\left(\omega_p^2+A\right)}. \tag{A8} $

Introducing the following magic variables,
$ E_p^2 \equiv \frac{\omega_p^2+A}{1+B},\quad F_p^2 \equiv \left(1+B\right)\left(\omega_p^2+A\right), \tag{A9} $

their advantage shows up immediately:
$ \begin{aligned}[b] D\left(p\right) =& i\frac{p^0\sigma_1 + \dfrac{F_p}{E_p}\mathcal{P}_+ + E_p F_p \mathcal{P}_-} {\left(p^0-F_p\right)\left(p^0+F_p\right)} \\ =& \frac{i}{2}\left( \frac{\sigma_1 + \dfrac{1}{E_p}\mathcal{P}_+ + E_p\mathcal{P}_-} {p^0 - F_p + i\epsilon} + \frac{\sigma_1 - \dfrac{1}{E_p}\mathcal{P}_+ - E_p\mathcal{P}_-} {p^0 + F_p - i\epsilon} \right), \end{aligned}\tag{A10} $

where we have made assumptions that
$ \omega_p^2+A>0 $ ,$ 1+B>0 $ . Substituting (A10) into (A5b), we find$ A\left(p^z\right) \mathcal{P}_+ + B\left(p^z\right) \mathcal{P}_- = \frac{\lambda}{2} {\rlap{—} \int } dk^z \frac{E_k\mathcal{P}_+ + \dfrac{1}{E_k}\mathcal{P}_-}{\left(p^z-k^z\right)^2}. \tag{A11} $

Matching the coefficients of
$ \mathcal{P} $ and utilizing (96), we find the equations for$ E_p $ and$ F_p $ :$ \begin{aligned}[b] F_p &= \frac{1}{E_p} \left( \omega_p^2 + \frac{\lambda}{2} {\rlap{—} \int } dk^z \frac{E_k}{\left(p^z-k^z\right)^2} \right) \\& = E_p \left( 1 + \frac{\lambda}{2} {\rlap{—} \int } dk^z \frac{1}{\left(p^z-k^z\right)^2}\frac{1}{E_k} \right). \end{aligned}\tag{A12} $

(From (A12) one can identify
$ E_p $ with$ E_p $ in the Hamiltonian approach and$ F_p $ with$ \Pi^+\left(p\right) $ .)Explicit calculation shows that the numerators of (A10) can be decomposed into outer products of two vectors:
$ \frac{\sigma_1 + \dfrac{1}{E_p}\mathcal{P}_+ + E_p\mathcal{P}_-}{2} = \xi\left(p\right) \tilde{\xi}\left(p\right)\sigma_1, \tag{A13a} $

$ \frac{\sigma_1 - \dfrac{1}{E_p}\mathcal{P}_+ - E_p\mathcal{P}_-}{2} = \eta\left(p\right) \tilde{\eta}\left(p\right)\sigma_1, \tag{A13b} $

where
$ \xi\left(p\right) = \frac{1}{\sqrt{2}}\left(1, E_p\right)^ \mathrm{T},\quad \tilde{\xi}\left(p\right) = \frac{1}{\sqrt{2}}\left(1, 1/E_p\right), \tag{A14a} $

$ \eta\left(p\right) = \frac{1}{\sqrt{2}}\left(1, -E_p\right)^ \mathrm{T},\quad \tilde{\eta}\left(p\right) = \frac{1}{\sqrt{2}}\left(1, -1/E_p\right). \tag{A14b} $

The dressed quark propagator can then be written as
$ D\left(p\right) = \frac{i\xi\left(p\right)\tilde{\xi}\left(p\right)\sigma_1} {p^0 - F_p + i\epsilon} + \frac{i\eta\left(p\right)\tilde{\eta}\left(p\right)\sigma_1} {p^0 + F_p - i\epsilon}. \tag{A15} $

-
In the large-
$ N_\mathrm{c} $ limit, The meson-$ q\bar{q} $ vertex$ \Gamma\left(p;q\right) $ satisfies the following Bethe-Salpeter equation (Fig. A4):$ \Gamma\left(p; q\right) = \frac{-i g_\mathrm{s}^2 N_\mathrm{c}}{2} {\rlap{—} \int }\frac{d^2 k}{\left(2\pi\right)^2} \frac{1}{\left(p^z - k^z\right)^2} \sigma_1D\left(k\right)\Gamma\left(k; q\right)D\left(k-q\right)\sigma_1. \tag{A16} $

$ \Gamma\left(p;q\right) $ is independent of$ p^0 $ , so we can perform the$ k^0 $ integration:$ \mathcal{I}\left(k; q\right) \equiv \int\frac{dk^0}{2\pi} D\left(k\right)\Gamma\left(k; q\right) D\left(k-q\right). \tag{A17} $

The interpretation of
$ \mathcal{I}\left(k; q\right) $ at the matrix-element level is$ \mathcal{I}\left(k; q\right) = \int dz\;e^{-ik^z z} \langle{\Omega}\vert \Phi\left(0, z\right) \Phi^\dagger\left(0, 0\right)\vert{M_n\left(q\right)}\rangle, \tag{A18} $

where
$ \Phi\left(x\right) = \left(\phi\left(x\right), i\pi\left(x\right)\right)^ \mathrm{T} $ and$ M_n $ is the n-th excitation of the bound states. Among the four projections of$ D\left(k\right) $ and$ D\left(k-q\right) $ , only two of them give nonzero residues. We arrive at$ \begin{aligned}[b] \mathcal{I}\left(k;q\right) =& \frac{ \xi\left(k\right)\left[ -i \tilde{\xi}\left(k\right)\sigma_1\Gamma\left(k;q\right)\eta\left(k-q\right) \right]\tilde{\eta}\left(k-q\right)\sigma_1 }{q^0_n - F\left(k-q\right)-F\left(k\right) + i\epsilon} \\ & + \frac{ \eta\left(k\right)\left[ -i \tilde{\eta}\left(k\right)\sigma_1\Gamma\left(k;q\right)\xi\left(k-q\right) \right]\tilde{\xi}\left(k-q\right)\sigma_1 }{- q^0_n - F\left(k-q\right)-F\left(k\right) + i\epsilon} \\ \equiv& -\chi^+_n\left(k^z;q^z\right) \sqrt{\frac{E_{k-q}}{E_k}} \xi\left(k\right)\tilde{\eta}\left(k-q\right)\sigma_1 \\ & - \chi^-_n\left(k^z;q^z\right) \sqrt{\frac{E_{k-q}}{E_k}} \eta\left(k\right)\tilde{\xi}\left(k-q\right)\sigma_1. \end{aligned}\tag{A19} $

From now on we drop the superscript z in spacial momenta for simplicity. Substituting (103) into (106), we get
$ \begin{aligned}[b] &\left[q^0_n - F\left(p-q\right)-F\left(p\right)\right]\chi^+_n\left(p;q\right) \\ =& -\lambda {\rlap{—} \int } \frac{d k}{\left(p-k\right)^2} \sqrt{\frac{E_pE_{k-q}}{E_kE_{p-q}}} \\& \times\Big[ \tilde{\xi}\left(p\right)\xi\left(k\right)\tilde{\eta}\left(k-q\right)\eta\left(p-q\right) \chi^+_n\left(k;q\right) \\ & + \tilde{\xi}\left(p\right)\eta\left(k\right)\tilde{\xi}\left(k-q\right)\eta\left(p-q\right) \chi^-_n\left(k;q\right) \Big], \end{aligned}\tag{A20a} $

$ \begin{aligned}[b] &\left[-q^0_n - F\left(p-q\right)-F\left(p\right)\right]\chi^-_n\left(p;q\right) \\ =& -\lambda {\rlap{—} \int } \frac{d k}{\left(p-k\right)^2} \sqrt{\frac{E_pE_{k-q}}{E_kE_{p-q}}} \\ & \times\Big[ \tilde{\eta}\left(p\right)\eta\left(k\right)\tilde{\xi}\left(k-q\right)\xi\left(p-q\right) \chi^-_n\left(k;q\right) \\ & + \tilde{\eta}\left(p\right)\xi\left(k\right)\tilde{\eta}\left(k-q\right)\xi\left(p-q\right) \chi^+_n\left(k;q\right) \Big]. \end{aligned}\tag{A20b} $

Using the fact that
$ \tilde{\xi}\left(p\right)\xi\left(k\right) = \tilde{\eta}\left(p\right)\eta\left(k\right)= \frac{E_p + E_k}{2E_p},\tag{A21a}$

$ \tilde{\xi}\left(p\right)\eta\left(k\right) = \tilde{\eta}\left(p\right)\xi\left(k\right) = \frac{E_p - E_k}{2E_p}, \tag{A21b}$

and defining
$ f_\pm\left(p, k\right) \equiv \frac{E_k \pm E_p}{\sqrt{E_pE_k}}, \tag{A22a} $

$ S_\pm\left(p, k; q\right) \equiv f_\pm\left(p,k\right)f_\pm\left(p-q,k-q\right), \tag{A22b} $

the bound state equations can be written as
$ \begin{aligned}[b] &\left[q^0_n - F\left(p-q\right)-F\left(p\right)\right]\chi^+_n\left(p;q\right) = -\frac{\lambda}{4} {\rlap{—} \int } \frac{d k}{\left(p-k\right)^2} \\&\quad \times\left[ S_+\left(p, k; q\right) \chi^+_n\left(k;q\right) - S_-\left(p, k; q\right) \chi^-_n\left(k;q\right) \right], \end{aligned}\tag{A23a} $

$ \begin{aligned}[b] &\left[-q^0_n - F\left(p-q\right)-F\left(p\right)\right]\chi^-_n\left(p;q\right) = -\frac{\lambda}{4} {\rlap{—} \int } \frac{d k}{\left(p-k\right)^2} \\ &\quad \times\left[ S_+\left(p, k; q\right) \chi^-_n\left(k;q\right) - S_-\left(p, k; q\right) \chi^+_n\left(k;q\right) \right]. \end{aligned}\tag{A23b} $

This equation is equivalent to (52).
-
In this appendix, we discuss some subtle issue about the mass renormalization in the scalar
$ {\rm QCD}_2 $ , in both equal-time and light-front quantization. We start from the equal-time quantization, and examine the asymptotic behavior of$ E_k $ and$ \Pi^+ $ in the large meson momentum limit.The integrals appear in
$ \Pi^\pm $ defined in (36) as$ k\to\infty $ can be calculated with the method of regions [36]. There are two regions of the integration variable$ k_1 $ : 1)$ m_{\tilde{r}} \sim \left|k_1\right| \ll k $ ; 2)$ m_{\tilde{r}} \ll \left|k_1\right| \sim k $ . We divide the integration regions, expand the integrand according to the different scaling of each region:$ \begin{aligned}[b]& {\rlap{—} \int } dk_{1}\left( \frac{\dfrac{E_{k_1}}{E_k}\pm\dfrac{E_k}{E_{k_1}}}{(k+k_1)^{2}} -\frac{E_{k_1}}{E_k}\frac{1}{k_1^2} \right) \\\approx &\frac{1}{k} {\rlap{—} \int }_{\left|k_1\right|<\Lambda} dk_{1} \left(\pm\frac{1}{E_{k_1}}-\frac{E_{k_1}}{k_1^2}\right) \\ &+ {\rlap{—} \int }_{\left|k_1\right|>\Lambda} dk_1\left( \frac{\dfrac{\left|k_1\right|}{k}\pm\dfrac{k}{\left|k_1\right|}}{\left(k+k_1\right)^2} -\frac{1}{k\left|k_1\right|} \right), \end{aligned}\tag{B1} $

where
$ m_{\tilde{r}}\ll\Lambda\ll k $ . For$ \Pi^+ $ , the bounds of each region can be extended to the whole momentum space since the asymptotic Λ dependence of each region cancels each other:$ {\rlap{—} \int } dk_{1} \left( \frac{\dfrac{E_{k_1}}{E_k}+\dfrac{E_k}{E_{k_1}}}{(k+k_1)^{2}} -\frac{E_{k_1}}{E_k}\frac{1}{k_1^2} \right) \approx \frac{1}{k}\left[ {\rlap{—} \int } dk_{1} \left(\frac{1}{E_{k_1}}-\frac{E_{k_1}}{k_1^2}\right) - 4 \right]. \tag{B2} $

For
$ \Pi^- $ , the integral is divergent for each region:$ \begin{aligned}[b]& {\rlap{—} \int } dk_{1}\left( \frac{\dfrac{E_{k_1}}{E_k}-\dfrac{E_k}{E_{k_1}}}{(k+k_1)^{2}} -\frac{E_{k_1}}{E_k}\frac{1}{k_1^2} \right) \\ \approx& \lim\limits_{\Lambda/k_1\to\infty} \frac{1}{k} \left[ {\rlap{—} \int }_{-\Lambda}^{\Lambda} dk_1 \left(-\frac{1}{E_{k_1}}-\frac{E_{k_1}}{k_1^2}\right) - 4 \ln\frac{k}{\Lambda} \right]. \end{aligned}\tag{B3} $

Define
$ k_0 $ as$ 4\ln k_{0} \equiv \lim\limits_{\Lambda/k_1\to\infty} {\rlap{—} \int }_{-\Lambda}^{\Lambda} dk_1 \left(-\frac{1}{E_{k_1}}-\frac{E_{k_1}}{k_1^2}\right) + 4\ln\Lambda. \tag{B4} $

the asymptotic behavior of
$ E_{k} $ can be derived from (41) as$ E_k approx k+\frac{1}{k}\left(\frac{m_{\tilde{r}}^{2}}{2} -\lambda\ln\frac{k}{k_0}\right). \tag{B5} $

The value of
$ E_k $ still can not be read directly from (125) since$ k_0 $ depends recursively on the functional form of$ E_{k_1} $ . Fortunately, however, when substituting (125) into$ \Pi^+ $ , the$ k_0 $ dependence cancels and we arrive at$ \Pi^+\left(k\right) \approx k+\frac{m_{\tilde{r}}^{2}}{2k} +\frac{\lambda}{4k}\left[ {\rlap{—} \int } dk_1 \left(\frac{1}{E_{k_1}}-\frac{E_{k_1}}{k_1^2}\right)-4\right], \tag{B6} $

Relabelling the momenta
$ k=xP $ in (52), and taking the large P limit, one finds that (52) approaches (28). The relation between the renormalization masses$ m_r $ and$ m_{\tilde{r}} $ can be found by matching two equations:$ m_{\tilde{r}}^2 + \frac{\lambda}{2} {\rlap{—} \int } dk_1 \left(\frac{1}{E_{k_1}}-\frac{E_{k_1}}{k_1^2}\right) = m_r^2. \tag{B7} $

Note that this relation is scheme dependent. Had we chosen the equal-time renormalized mass
$ m_{\hat{r}}^{2} = m^2+\frac{\lambda}{2}\int dk_1\frac{1}{E_{k_1}}, \tag{B8}$

we would get
$ m_{\hat{r}} = m_r $ .
Solving bound-state equations for scalar and hybrid QCD in two-dimensional spacetime
- Received Date: 2023-04-28
- Available Online: 2024-02-01
Abstract: We investigate the bound-state equations in two-dimensional QCD in the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

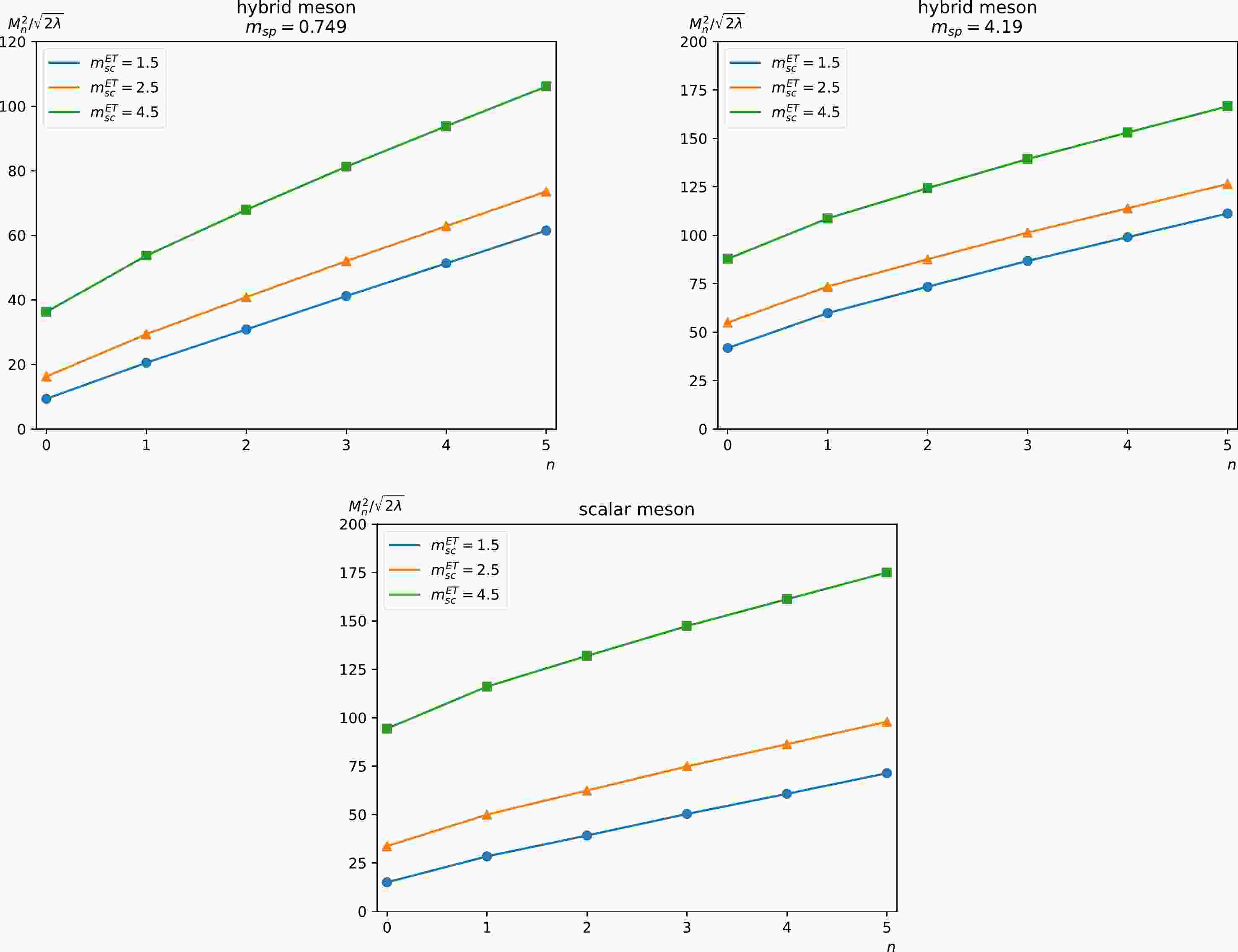










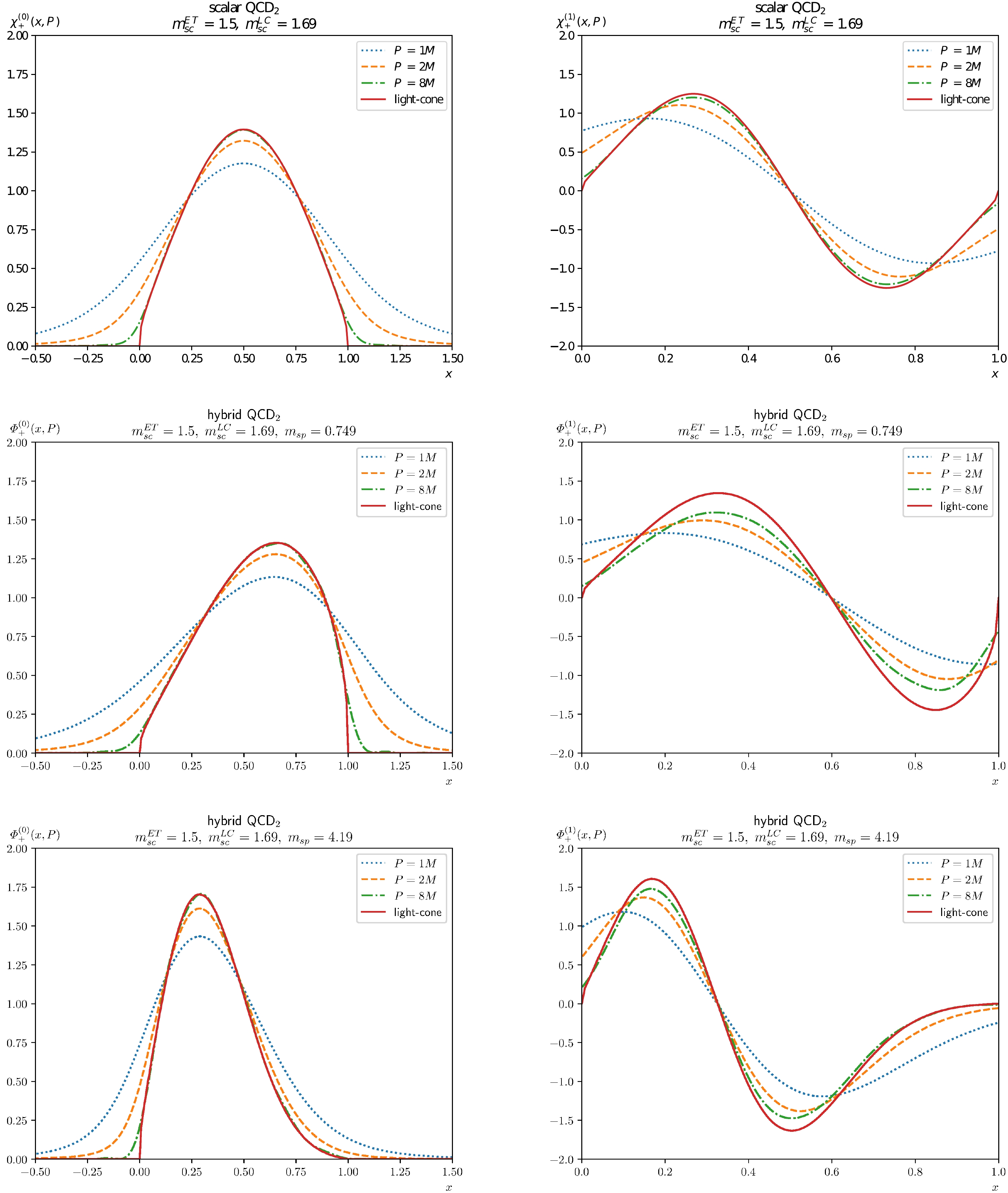
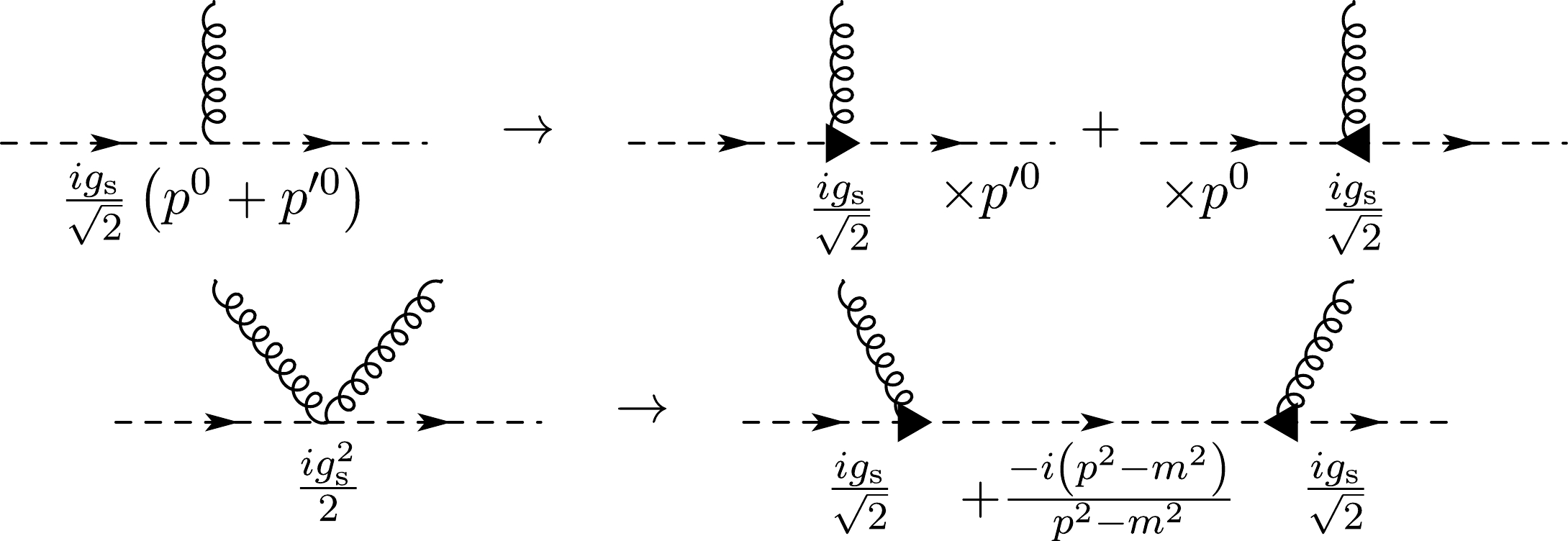
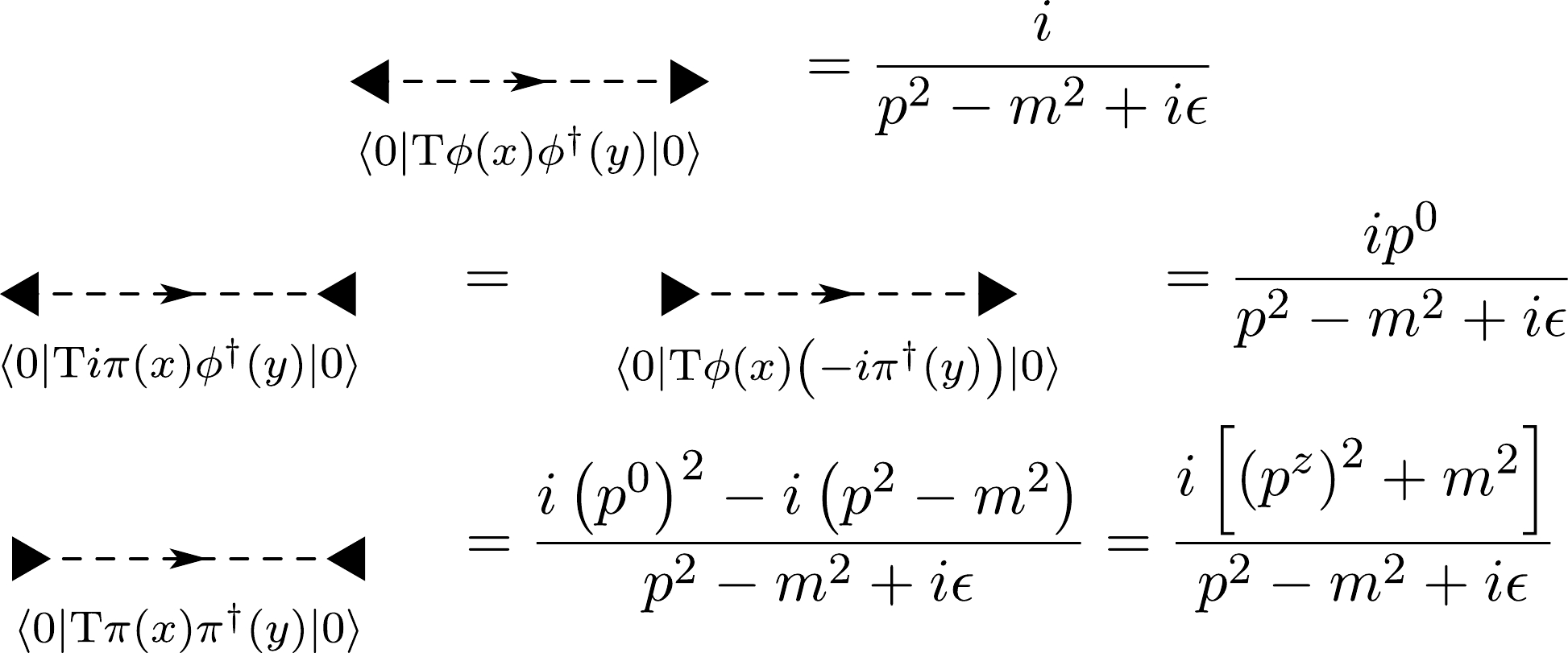
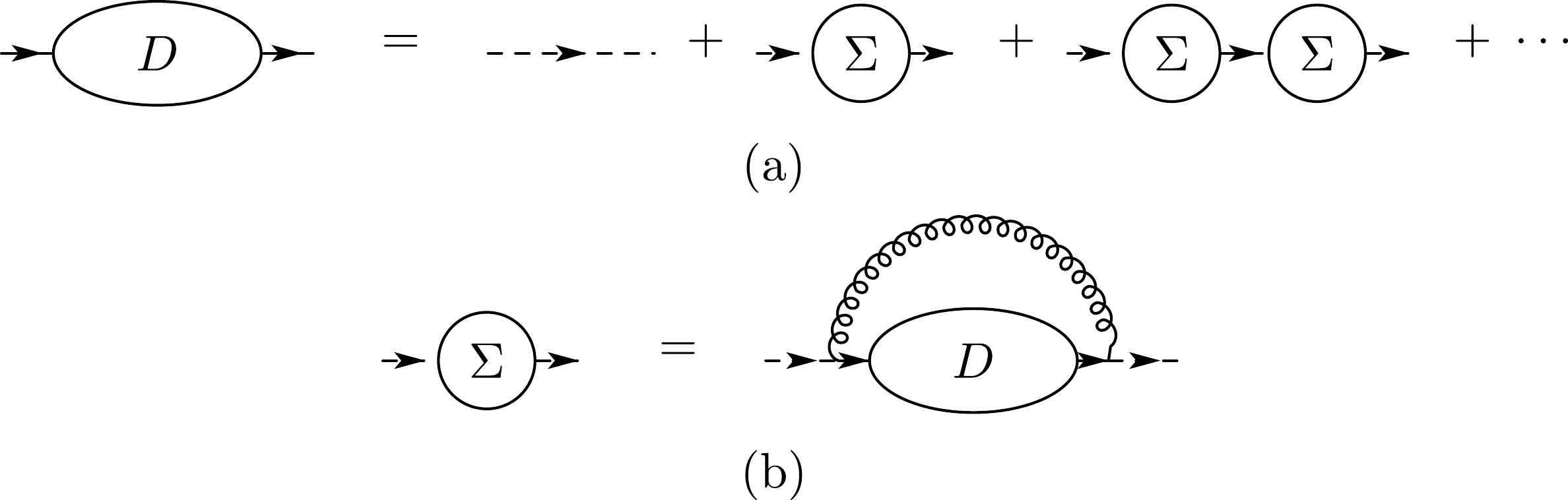




 DownLoad:
DownLoad: